A Review on Parametric Dynamic Models of Magnetorheological Dampers and Their Characterization Methods
Abstract
1. Introduction
2. MR Fluid Characteristics
3. Parametric Dynamic Models of MR Dampers
3.1. Bingham Dynamic Model
3.2. Gamota and Filisko Model
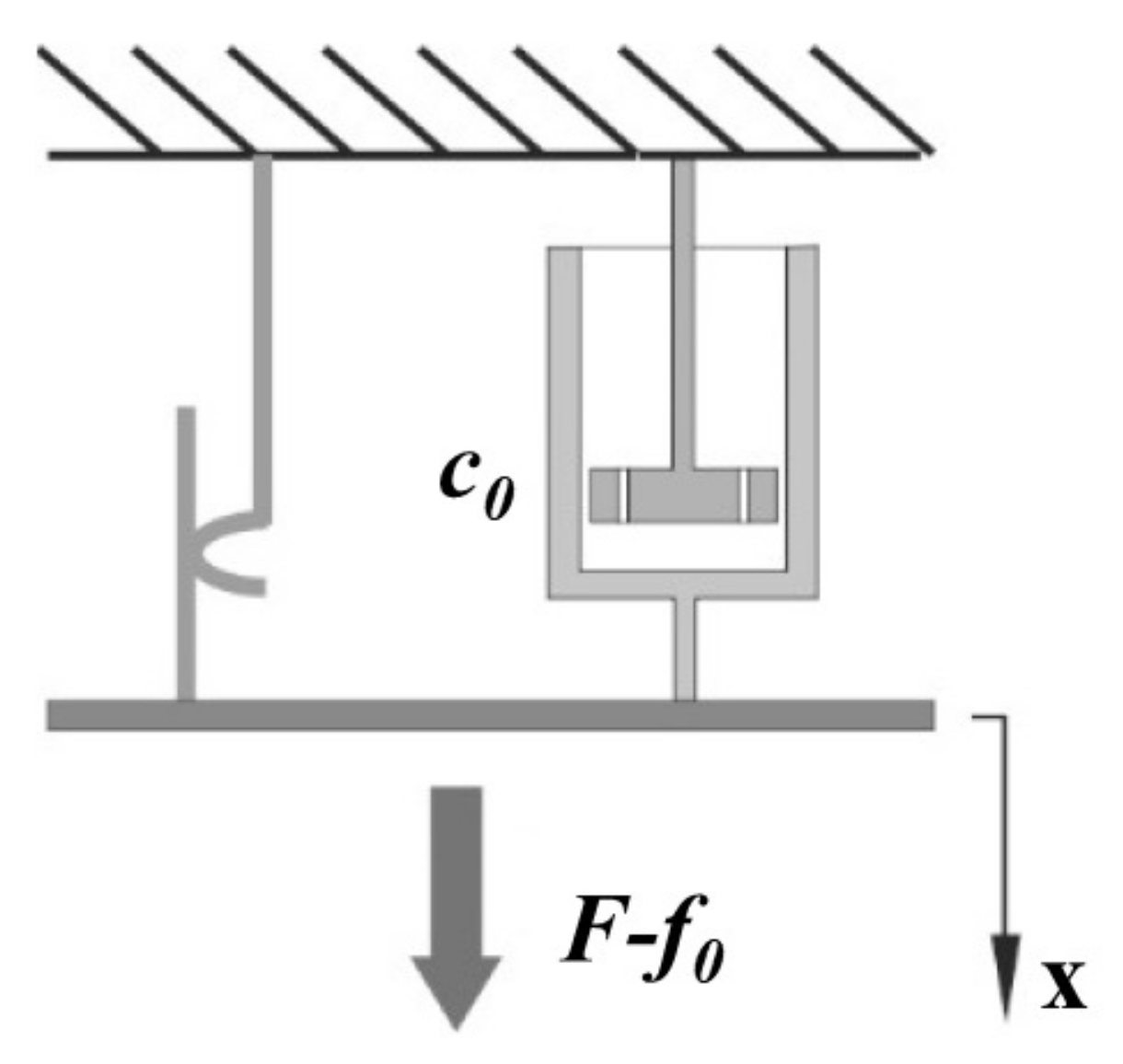
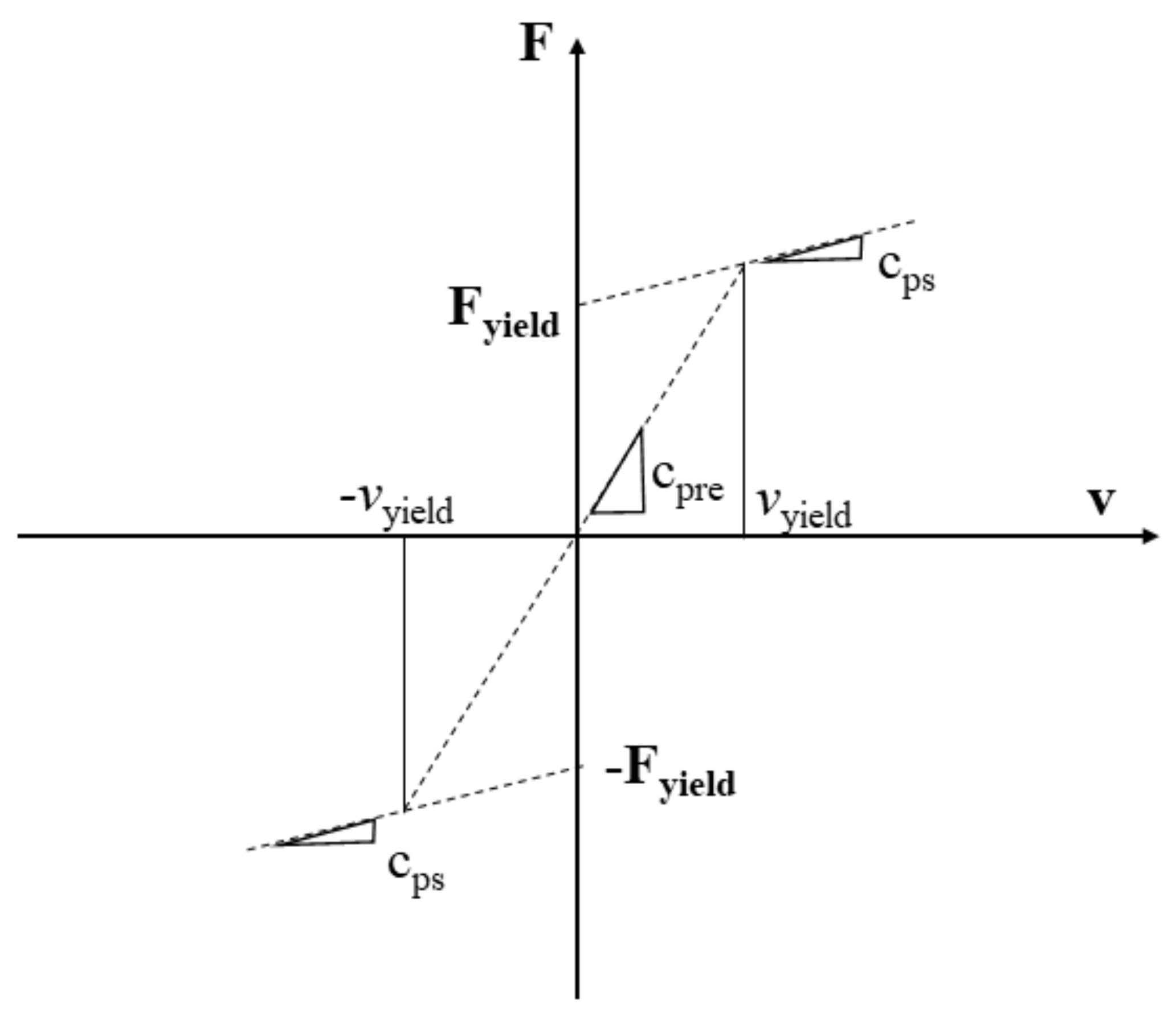
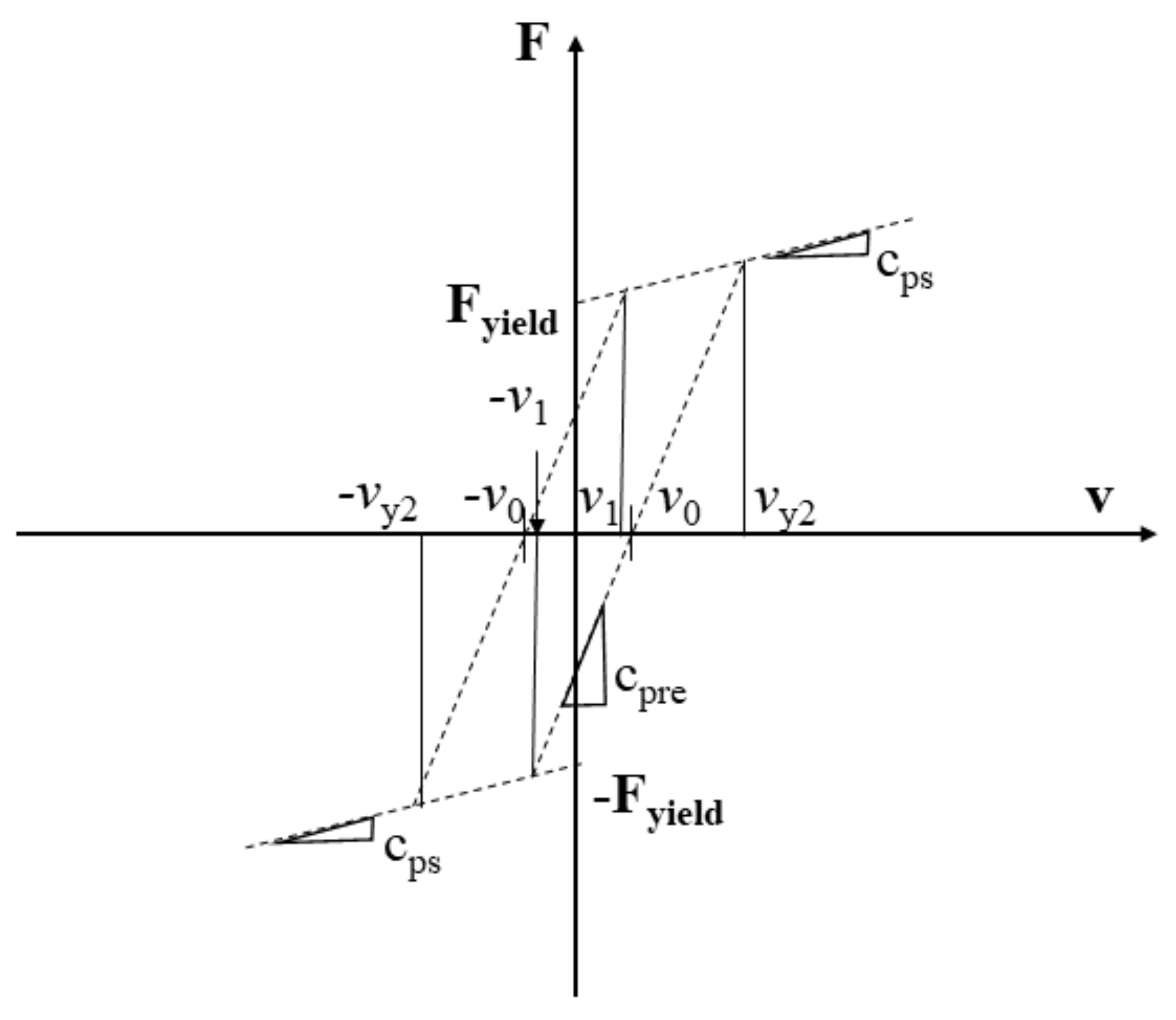
3.3. Bi-Viscous Models for MR Dampers
- an additional non linear function (quasi-steady velocity)
- the control signal of the damper
- the fluid compressibility and inertia
- the piston’s mass.
3.4. Bouc-Wen Model
3.5. Modified Bouc-Wen Model for Large-Scale MR Dampers
3.6. Spencer Dyke Model
3.7. Dominguez Model
3.8. Ali and Ramaswamy Model
3.9. Non-Symmetrical Bouc—Wen Model
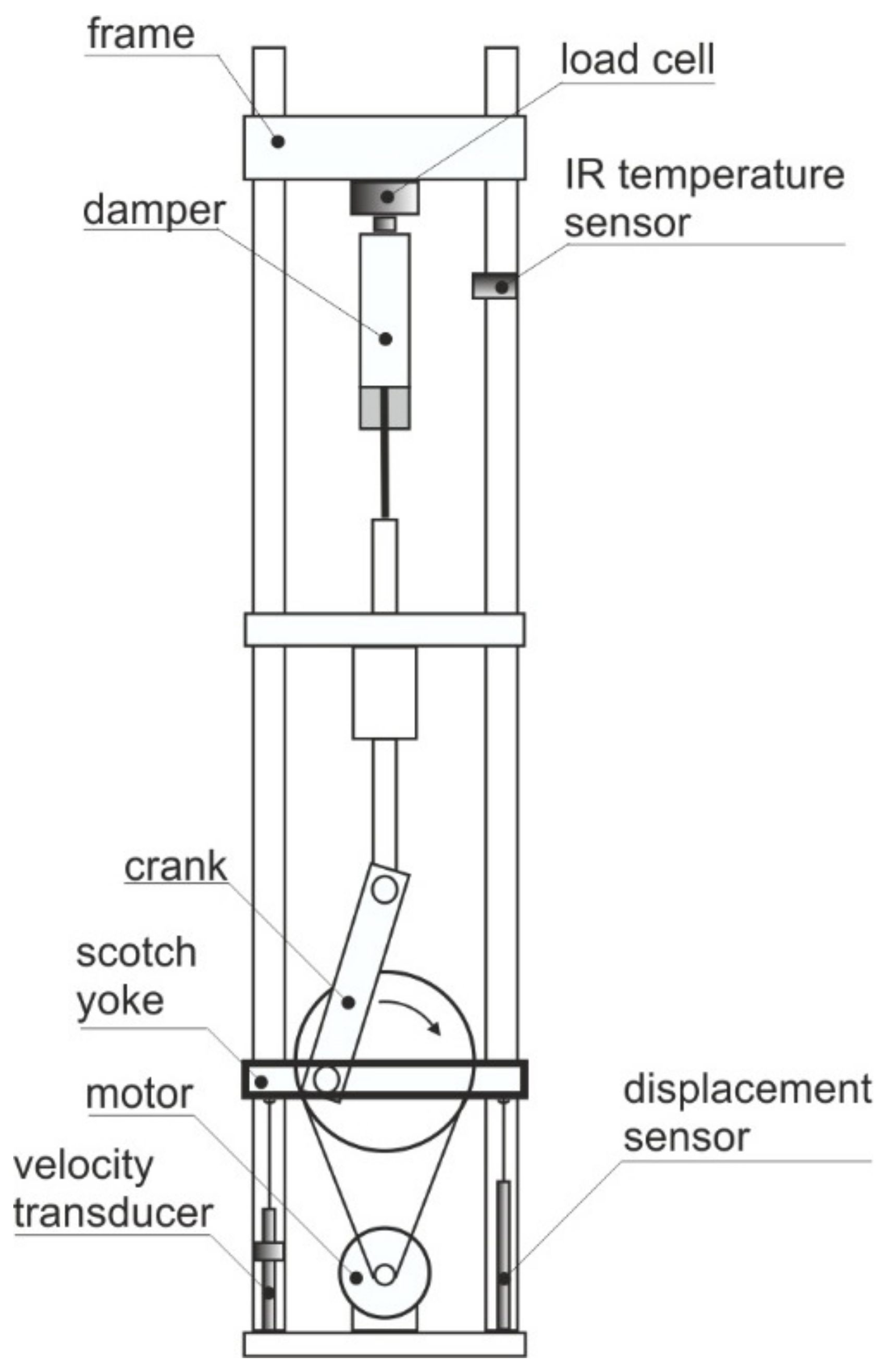
4. Characterization Methods for MR Dampers
5. Conclusions
Conflicts of Interest
References
- Herold, S.; Mayer, D. Adaptive Piezoelectric Absorber for Active Vibration Control. Actuators 2016, 5, 7. [Google Scholar] [CrossRef]
- Gao, J.; Xue, D.; Liu, W.; Zhou, C.; Ren, X. Recent Progress on BaTiO3-Based Piezoelectric Ceramics for Actuator Applications. Actuators 2017, 6, 24. [Google Scholar] [CrossRef]
- Botta, F.; Dini, D.; Schwingshackl, C.W.; di Mare, L.; Cerri, G. Optimal placement of piezoelectric plates to control multimode vibrations of a beam. Adv. Acoust. Vib. 2013, 2013, 905160. [Google Scholar] [CrossRef]
- Botta, F.; Marx, N.; Schwingshackl, C.W.; Cerri, G.; Dini, D. A wireless vibration control technique for gas turbine blades using piezoelectric plates and contactless energy transfer. In Proceedings of the ASME Turbo Expo, San Antonio, TX, USA, 3–7 June 2013; Volume 7A. [Google Scholar]
- Botta, F.; Dini, D.; de Lieto Vollaro, R. A new function for the optimal placement of piezoelectric plates to control multimode vibrations of a rotating beam. Int. J. Eng. Technol. 2013, 5, 4472–4488. [Google Scholar]
- Botta, F.; Marx, N.; Gentili, S.; Schwingshackl, C.W.; di Mare, L.; Cerri, G.; Dini, D. Optimal placement of piezoelectric plates for active vibration control of gas turbine blades: experimental results. In Proceedings of the SPIE—The International Society for Optical Engineering, San Diego, CA, USA, 12–16 August 2012; p. 8345. [Google Scholar]
- Sinn, T.; Barrett, R. Design, Manufacturing and Test of a High Lift Secondary Flight Control Surface with Shape Memory Alloy Post-Buckled Precompressed Actuators. Actuators 2015, 4, 156–171. [Google Scholar] [CrossRef]
- Tu, F.; Hu, S.; Zhuang, Y.; Lv, J.; Wang, Y.; Sun, Z. Hysteresis Curve Fitting Optimization of Magnetic Controlled Shape Memory Alloy Actuator. Actuators 2016, 5, 25. [Google Scholar] [CrossRef]
- Cianchetti, M.; Licofonte, A.; Follador, M.; Rogai, F.; Laschi, C. Bioinspired Soft Actuation System Using Shape Memory Alloys. Actuators 2014, 3, 226–244. [Google Scholar] [CrossRef]
- Nguyen, Q.-A.; Jorgensen, S.J.; Ho, J.; Sentis, L. Characterization and Testing of an Electrorheological Fluid Valve for Control of ERF Actuators. Actuators 2015, 4, 135–155. [Google Scholar] [CrossRef]
- Yang, G.; Spencer, B.; Jung, H.H.; Carlson, J.D. Dynamic Modeling of Large-Scale Magnetorheological Damper Systems for Civil Engineering Applications. J. Eng. Mech. 2004, 130, 1107–1114. [Google Scholar] [CrossRef]
- Wereley, N.; Pang, L. Nondimensional Analysis of Semi-Active Electrorheological and Magnetorheological Dampers Using Approximate Parallel Plate Models. Smart Mater. Struct. 1998, 7, 732–743. [Google Scholar] [CrossRef]
- Xiaocong, Z.; Xingjian, J.; Li, C. Magnetorheological fluid dampers: A review on structure design and analysis. J. Intell. Mater. Syst. Struct. 2012, 23, 839–873. [Google Scholar]
- Carlson, J.D. Magnetorheological Fluids, in Smart Materials; Taylor Francis Group; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Grunwald, A.; Olabi, A.G. Design of magnetorheological (MR) valve. Sens. Actuators A Phys. 2008, 148, 211–223. [Google Scholar] [CrossRef]
- Kciuk, M.; Turczyn, R. Properties and application of magnetorheological fluids. J. Achiev. Mater. Manuf. Eng. 2006, 18, 127–130. [Google Scholar]
- Alexandridis, A.A. The MagneRide System. In Proceedings of the US Vehicle Dynamics Expo, Novi, MI, USA, 8–10 May 2007. [Google Scholar]
- Yang, S.-Y.; Han, C.; Shin, S.-U.; Choi, S.-B. Design and Evaluation of a Semi-Active Magneto-rheological Mount for a Wheel Loader Cabin. Actuators 2017, 6, 16. [Google Scholar] [CrossRef]
- Wu, J.; Jiang, X.; Li, Q.; Yao, J.; Li, H.; Li, Z. Design and modelling of a novel multilayered cylindrical magnetorheological brake. Int. J. Appl. Electromagn. Mech. 2016, 53, 1–22. [Google Scholar] [CrossRef]
- Shiao, Y.; Quang-Anh, N.; Zhengyang, Z. Design and experiment of a new magnetorheological brake. Int. J. Appl. Electromagn. Mech. 2015, 48, 309–326. [Google Scholar] [CrossRef]
- Kwok, N.M.; Ha, Q.P.; Nguyen, T.H.; Li, J.; Samali, B. A novel hysteretic model for magnetorheological fluid dampers and parameter identification using particle swarm optimization. Sens. Actuators A 2006, 132, 441–451. [Google Scholar] [CrossRef]
- Dyke, S.J.; Spencer, B.F., Jr.; Sain, M.K.; Carlson, J.D. Modeling and Control of Magnetorheological Dampers for Seismic Response Reduction. Smart Mater. Struct. 1996, 5, 565–575. [Google Scholar] [CrossRef]
- Weber, F.; Distl, H.; Fischer, S.; Braun, C. MR Damper Controlled Vibration Absorber for Enhanced Mitigation of Harmonic Vibrations. Actuators 2016, 5, 27. [Google Scholar] [CrossRef]
- Sun, Q.; Wu, X.; Xue, X.; Zhang, L.; Zhang, L. Mechanics performance test of MR damper and its application in structural seismic response control. Int. J. Appl. Electromagn. Mech. 2010, 33, 1493–1501. [Google Scholar]
- Spelta, C.; Previdi, F.; Savaresi, S.M.; Fraternale, G.; Gaudiano, N. Control of magnetorheological dampers for vibration reduction in a washing machine. Mechatronics 2009, 19, 410–421. [Google Scholar] [CrossRef]
- Shin, Y.J.; You, W.-H.; Hur, H.-M.; Park, J.-H. Semi-active control to reduce carbody vibration of railway vehicle by using scaled roller rig. J. Mech. Sci. Technol. 2012, 26, 3423–3431. [Google Scholar] [CrossRef]
- Shin, Y.-J.; You, W.-H.; Hur, H.-M.; Park, J.-H.; Lee, G.-S. Improvement of Ride Quality of Railway Vehicle by Semiactive Secondary Suspension System on Roller Rig Using Magnetorheological Damper. Adv. Mech. Eng. 2014, 6, 1–10. [Google Scholar] [CrossRef]
- Ahmadian, M.; Poynor, J.C. An evaluation of magneto rheological dampers for controlling gun recoil dynamics. Shock Vib. 2001, 8, 147–155. [Google Scholar] [CrossRef]
- Powell, L.A.; Choi, Y.T.; Hu, W.; Wereley, N.M.; Birchette, T.S.; Bolukbasi, A.O. Adaptive Magnetorheological Landing Gear Dampers Employing Passive Valves to Maximize Applicable Sink Rate Range. In Proceedings of the American Helicopter Society 69th Annual Forum Technology Display, Phoenix, AZ, USA, 21–23 May 2013. [Google Scholar]
- Zhu, X.; Lai, C. Design and performance analysis of a magnetorheological fluid damper for drillstring. Int. J. Appl. Electromagn. Mech. 2012, 40, 67–83. [Google Scholar]
- Nakano, H.; Nakano, M. Active loading machine using MR fluid clutch for leg rehabilitation system. Int. J. Appl. Electromagn. Mech. 2012, 39, 463–469. [Google Scholar]
- Sk, F.; Ali, A. Ramaswami, Testing and Modeling of MR Damper and Its Application to SDOF Systems Using Integral Backstepping Technique. J. Dyn. Syst. Meas. Control 2009, 131, 11. [Google Scholar]
- Verotti, M.; Dochshanov, A.; Belfiore, N.P. Compliance Synthesis of CSFH MEMS-Based Microgrippers. J. Mech. Des. Trans. ASME 2017, 139, 022301. [Google Scholar] [CrossRef]
- Verotti, M.; Belfiore, N.P. Isotropic compliance in E(3): Feasibility and workspace mapping. J. Mech. Robot. 2016, 8, 061005. [Google Scholar] [CrossRef]
- Verotti, M.; Masarati, P.; Morandini, M.; Belfiore, N.P. Isotropic compliance in the Special Euclidean Group SE(3). Mech. Mach. Theory 2016, 98, 263–281. [Google Scholar] [CrossRef]
- Burson, K. Lord MR damping solutions for automotive applications. In Proceedings of the Vehicle Dynamics Expo, Novi, MI, USA, 2006. [Google Scholar]
- Yoo, J.-H.; Wereley, N. Design of a high-efficiency magnetorheological valve. J. Intell. Mater. Syst. Struct. 2002, 13, 679–685. [Google Scholar] [CrossRef]
- Bombard, A.J.F.; Antunes, L.S.; Gouvea, D. Redispersibility in magnetorheological fluids: Surface interactions between iron powder and wetting additives. J. Phys. Conf. Ser. 2009, 149, 12–38. [Google Scholar] [CrossRef]
- Bossis, G.; Lacisb, S.; Meuniera, A. Volkova, Magnetorheological fluids. J. Magn. Magn. Mater. 2008, 222, 2395–2407. [Google Scholar]
- Gołdasz, J.; Sapinski, B. Insight into Magnetorheological Shock Absorbers; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
- Strecker, Z.; Roupec, J.; Mazůrek, I.; Klapka, M. Limiting factors of the response time of the magnetorheological damper. Int. J. Appl. Electromagn. Mech. 2015, 47, 541–550. [Google Scholar]
- Lei, L.; Dong, L.; Yan, G. Magneto-rheological damper control system design. Int. J. Appl. Electromagn. Mech. 2010, 33, 1459–1467. [Google Scholar]
- Gamota, D.R.; Filisko, F.E. Dynamic Mechanical Studies of Electrorheological Materials: Moderate Frequencies. J. Rheol. 1991, 35, 399–425. [Google Scholar] [CrossRef]
- Ali, S.F.; Ramaswamy, A. Hybrid structural control using magnetorheological dampers for base isolated structures. Smart Mater. Struct. 2009, 18, 055011. [Google Scholar] [CrossRef]
- Kwok, N.M.; Ha, Q.P.; Nguyen, M.T.; Li, J.; Samali, B. Bouc-Wen model parameter identification for a MR fluid damper using computationally efficient GA. ISA Trans. 2007, 46, 167–179. [Google Scholar] [CrossRef] [PubMed]
- AAVV. Damper Testing Equipment 2VS/3VS/5VS/10VS/20VS/30VS; Roehrig Engineering Inc.: High Point, NC, USA, 2011; Volume 60. [Google Scholar]
- De Vicente, J.; Klingenberg, D.J. Hidalgo-Alvarez, Magnetorheological fluids: A review. Soft Matter 2011, 7, 3701–3710. [Google Scholar] [CrossRef]
- Jolly, M.R.; Bender, J.; Carlson, D.J. Properties and applications of commercial magnetorheological fluids. J. Intell. Mater. Syst. Struct. 1999, 1, 5–13. [Google Scholar] [CrossRef]
- Carlson, D.J.; Weiss, K.D. Magnetorheological Materials Based on Alloy Particles. U.S. Patent 5,382,373, 17 January 1995. [Google Scholar]
- Foister, R.T. Microspheres Dispersed in Liquid, Increase in Flow Resistance. U.S. Patent 5,667,715, 16 September 1997. [Google Scholar]
- Iyengar, V.R.; Foister, R.T. Durable Magnetorheological Fluid Compositions. U.S. Patent 6,599,439 B2, 29 July 2003. [Google Scholar]
- Iyengar, V.R.; Foister, R.T.; Johnson, J.C. MR Fluids Containing Magnetic Stainless Steel. U.S. Patent 6,679,999 B2, 20 January 2004. [Google Scholar]
- Lopez-Lopez, M.T.; Kuzhir, P.; Lacis, S.; Bossis, G.; Gonzalez-Caballero, F.; Duran, J.D.G. Magnetorheology for suspensions of solid particles dispersed in ferrofluids. J. Phys. Condens. Matter 2006, 18, 2803–2813. [Google Scholar] [CrossRef]
- Weiss, K.D.; Carlson, D.J.; Duclos, T.G.; Abbey, K.J. Temperature Independent Magnetorheological Materials. U.S. Patent No. 5599474, 4 February 1997. [Google Scholar]
- Weiss, K.D.; Carlson, D.J.; Nixon, D.A. Method and Magnetorheological Fluid Formulations for Increasing the Output of a Magnetorheological Fluid. U.S. Patent No. 6027664, 22 February 2000. [Google Scholar]
- Weiss, K.D.; Nixon, D.A.; Carlson, D.J.; Margida, A.J. Thixotropic Magnetorheological Materials. U.S. Patent No. 5645752, 8 July 1997. [Google Scholar]
- Kanno, H.; Shimada, K.; Ogawa, J.; Inoue, N. MR fluid damper composed of different size of particles. Int. J. Appl. Electromagn. Mech. 2007, 25, 109–112. [Google Scholar]
- Carlson, D.J.; Chrzan, M.J. Magnetorheological Fluid Dampers. U.S. Patent No. 5,277,281, 11 January 1994. [Google Scholar]
- Agraval, A.; Kaikarni, P.; Vieira, S.I.; Naganathan, N.G. An overview of magnetorheological and electrorheological fluids and their applications in fluid power systems. Int. J. Fluid Power 2001, 2, 5–36. [Google Scholar] [CrossRef]
- Jolly, M.R.; Nakano, M. Properties and applications of commercial controllable fluids. In Proceedings of the 6th International Conference on New Actuators, Bremen, Germany, 8 June 1998; pp. 411–416. [Google Scholar]
- Ginder, J.M.; Davis, L.C. Shear stresses in magnetorheological fluids: Role of magnetic saturation. Appl. Phys. Lett. 1994, 65, 3410–3412. [Google Scholar] [CrossRef]
- Phule, P.P.; Ginder, J.M. Synthesis and properties of novel magnetorheological fluids having improved stability and redispersibility. Int. J. Mod. Phys. B 1999, 13, 2019–2027. [Google Scholar] [CrossRef]
- Wang, D.H.; Liao, W.H. Magnetorheological fluid dampers: A review of parametric modelling. Smart Mater. Struct. 2011, 20, 34. [Google Scholar] [CrossRef]
- Gavin, H.P.; Hanson, R.D.; Filisko, F.E. Electrorheological dampers, part 1: Analysis and design. Trans. ASME J. Appl. Mech. 1996, 63, 669–675. [Google Scholar] [CrossRef]
- Gavin, H.P.; Hanson, R.D.; Filisko, F.E. Electrorheological dampers, part 2: Testing and modeling. Trans. ASME, J. Appl. Mech. 1996, 63, 676–682. [Google Scholar] [CrossRef]
- Wereley, N.M.; Pang, L. Nondimensional analysis of semi-active electrorheological and magnetorheological dampers using approximate parallel plate models. Smart Mater. Struct. 1998, 7, 732–743. [Google Scholar] [CrossRef]
- Chooi, W.W.; Oyadiji, S.O. Design, modelling and testing of magnetorheological (MR) dampers using analytical flow solutions. Comput. Struct. 2008, 86, 473–482. [Google Scholar] [CrossRef]
- Chooi, W.W.; Oyadiji, S.O. Mathematical modeling, analysis, and design of magnetorheological (MR) dampers. Trans. ASME J. Vib. Acoust. 2009, 131, 061002. [Google Scholar] [CrossRef]
- Chooi, W.W.; Oyadiji, S.O. Experimental testing and validation of a magnetorheological (MR) damper model. Trans. ASME J. Vib. Acoust. 2009, 131, 061003. [Google Scholar] [CrossRef]
- Hong, S.R.; John, S.; Wereley, N.M.; Choi, Y.T.; Choi, S.B. A unifying perspective on the quasi-steady analysis of magnetorheological dampers. J. Intell. Mater. Syst. Struct. 2008, 19, 959–976. [Google Scholar] [CrossRef]
- Yang, G.; Spencer, B.F., Jr.; Carlson, J.D.; Sain, M.K. Large-scale MR fluid dampers: Modeling and dynamic performance considerations. Eng. Struct. 2002, 24, 309–323. [Google Scholar] [CrossRef]
- Bouc, R. Mathematical model for hysteresis. Acustica 1971, 24, 16–25. [Google Scholar]
- Carlson, J.D.; Spencer, B.F., Jr. Magneto-Rheological Fluid Dampers for Semi-Active Seismic Control. In Proceedings of the 3rd International Conference on Motion and Vibration Control, Chiba, Japan, 1–6 September 1996. [Google Scholar]
- Spencer, B.F., Jr.; Dyke, S.J.; Sain, M.K.; Carlson, J.D. Phenomenological model for magnetorheological damper. J. Eng. Mech. 1997, 123, 230–238. [Google Scholar] [CrossRef]
- Dyke, S.J., Jr.; Spencer, B.F.; Sain, M.K.; Carlson, J.D. Experimental verification of semi-active structural control strategies using acceleration feedback. In Proceedings of the 3rd International Conference on Motion and Vibration Control, Chiba, Japan, 1–6 September 1996; Volume III, pp. 291–296. [Google Scholar]
- Wereley, N.M.; Pang, L.; Kamath, G.M. Idealized hysteresis modeling of electrorheological and magnetorheological dampers. J. Intell. Mater. Syst. Struct. 1998, 9, 642–649. [Google Scholar] [CrossRef]
- Pang, L.; Kamath, G.M.; Wereley, N.M. Analysis and testing of a linear stroke magnetorheological damper. In Proceedings of the AIAA/ASME/AHS Adaptive Structures Forum, Long Beach, CA, USA, 20–23 April 1998; Volume CP9803, pp. 2841–2856. [Google Scholar]
- Kamath, G.M.; Wereley, N.M.; Jolly, M.R. Characterization of magnetorheological helicopter lag dampers. J. Am. Helicopter Soc. 1999, 44, 234–248. [Google Scholar] [CrossRef]
- Snyder, R.A.; Kamath, G.M.; Wereley, N.M. Characterization and analysis of magnetorheological damper behavior under sinusoidal loading. AIAA J. 2001, 39, 1240–1253. [Google Scholar] [CrossRef]
- Stanway, R.; Sproston, J.L.; El-Wahed, A.K. Applications of electro-rheological fluids in vibration control: A survey. Smart Mater. Struct. 1996, 5, 464–482. [Google Scholar] [CrossRef]
- Sims, N.D.; Holmes, N.J.; Stanway, R. A unified modelling and model updating procedure for electrorheological and magnetorheological dampers. Smart Mater. Struct. 2004, 13, 100–121. [Google Scholar] [CrossRef]
- Sims, N.D.; Peel, D.J.; Stanway, R.; Johnson, A.R.; Bullough, W.A. The electrorheological long-stroke damper: A new modelling technique with experimental validation. J. Sound Vib. 2000, 229, 207–227. [Google Scholar] [CrossRef]
- Dominguez, A.; Sedaghati, R.; Tiharu, I.S. A new dynamic hysteresis model for magnetorheological dampers. Smart Mater. Struct. 2006, 15, 1179. [Google Scholar] [CrossRef]
- Paciello, V.; Pietrosanto, A. Magnetorheological Dampers: A New Approach of Characterization. IEEE Trans. Instrum. Meas. 2011, 60, 1718–1723. [Google Scholar] [CrossRef]
- Liao, W.H.; Lai, C.Y. Harmonic analysis of a magnetorheological damper for vibration control. Smart Mater. Struct. 2002, 11, 288–296. [Google Scholar] [CrossRef]
- Dyke, S.J.; Spencer, B.F., Jr.; Sain, M.K.; Carlson, J.D. An Experimental Study of MR Dampers for Seismic Protection. Smart Mater. Struct. 1997, 7, 693. [Google Scholar] [CrossRef]
- Facey, W.B.; Rosenfeld, N.C.; Choi, Y.-T.; Wereley, N.M. Design and testing of a compact magnetorheological damper for high impulsive loads. Int. J. Mod. Phys. B 2005, 19, 1549–1555. [Google Scholar] [CrossRef]
- Yao, G.Z.; Yap, F.F.; Chen, G.; Li, W.H.; Yeo, S.H. MR damper and its application for semi-active control of vehicle suspension system. Mechatronics 2002, 12, 963–973. [Google Scholar] [CrossRef]
- Ni, Y.Q.; Chen, Z.H. A Magnetorheological Damper with Embedded Piezoelectric Force Sensor: Experiment and Modeling. In Vibration Control; Mickaël Lallart: Rijeka, Croatia, 2010; ISBN 978-953-307-117-6. [Google Scholar]
- Metered, H.; Bonello, P.; Oyadiji, S.O. The experimental identification of magnetorheological dampers and evaluation of their controllers. Mech. Syst. Signal Process. 2010, 24, 976–994. [Google Scholar] [CrossRef]
- Batterbee, D.; Sims, N.D. Temperature Sensitive Controller Performance of MR Dampers. J. Intell. Mater. Syst. Struct. 2009, 20, 297–309. [Google Scholar] [CrossRef]
- ISO376:2011. Metallic Material—Calibration of Force-Proving Instruments Used for the Verification of Uniaxial Testing Machines; ISO: Geneva, Switzerland, 2011. [Google Scholar]
- JCGM 100:2008. Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement; BIPM Joint Committee for Guides in Metrology: Paris, France, 2008. [Google Scholar]
- Dahlberg, G. Materials Testing Machines Investigation of error sources and determination of measurement uncertainty. In Proceedings of the EUROLAB International Workshop organized by EMPA Academy Dubendorf, Dubendorf, Switzerland, 17–18 May 2001; pp. 57–68. [Google Scholar]
- Braz-César, M.T.; Barros, R.C. Experimental Behaviour and Numerical Analysis of MR dampers. In Proceedings of the 15th World Conference on Earthquake Engineering (WCEEE 2012), Lisbon, Portugal, 24–28 September 2012. [Google Scholar]
- De-Jesus Lozoya-Santos, J.; Morales-Menendez, R.; Ramirez-Mendoza, R.; Tudon-Martinez, J.; Sename, O.; Dugard, L. Magneto-Rheological Damper—An Experimental Study. J. Intell. Mater. Syst. Struct. 2012, 23, 1213–1232. [Google Scholar] [CrossRef]
- Chang, C.C.; Roschke, P. Neural network modeling of a magnetorheological damper. J. Intell. Mater. Syst. Struct. 1998, 9, 755–764. [Google Scholar] [CrossRef]
- Ehrgott, R.C.; Masri, S.F. Modeling the oscillatory dynamic behaviour of electrorheological materials in shear. Smart Mater. Struct. 1992, 1, 275–284. [Google Scholar] [CrossRef]
- Choi, S.B.; Lee, S.K.; Park, Y.P. A hysteresis model for the field-dependent damping force of a magnetorheological damper. J. Sound Vib. 2001, 245, 375–383. [Google Scholar] [CrossRef]
- Kim, K.J.; Lee, C.W.; Koo, J.H. Design and modeling of semi-active squeeze film dampers using magneto-rheological fluids. Smart Mater. Struct. 2008, 17, 035006. [Google Scholar] [CrossRef]
- Song, X.; Ahmadian, M.; Southward, S.; Miller, L. Modeling MR-dampers: A nonlinear blackbox approach. Commun. Nonlinear Sci. Numer. Simul. 2007, 12, 584–607. [Google Scholar] [CrossRef]
- Jin, G.; Sain, M.K.; Pham, K.D.; Billie, F.S., Jr.; Ramallo, J.C. Parametric study of nonlinear adaptive control algorithm with magneto-rheological suspension systems. Am. Control Conf. 2001, 1, 429–434. [Google Scholar]
- Jin, G.; Sain, M.K.; Spencer, B.F., Jr. Modeling MR-dampers: The ridgenet estimation approach. Proc. Am. Control Conf. 2002, 3, 2457–2462. [Google Scholar]
- Leva, A.; Piroddi, L. NARX-based technique for the modelling of magneto-rheological damping devices. Smart Mater. Struct. 2002, 11, 79–88. [Google Scholar] [CrossRef]
- Mori, M.; Sano, A. Local modeling approach to vibration control by MR damper. Proc. SICE Annu. Conf. 2004, 3, 2572–2577. [Google Scholar]
- Koga, K.; Sano, A. Query-based approach to prediction of MR damper force with application to vibration control. Proc. Am. Control Conf. 2006, 3259–3265. [Google Scholar]
- Chang, C.C.; Zhou, L. Neural network emulation of inverse dynamics for a magnetorheological damper. J. Struct. Eng. 2006, 128, 231–239. [Google Scholar] [CrossRef]
- Wang, X.; Chang, C.C.; Du, F. Achieving a more robust neural network model for control of a MR damper by signal sensitivity analysis. Neural Comput. Appl. 2002, 10, 330–338. [Google Scholar] [CrossRef]
- Xia, P.Q. An inverse model of MR damper using optimal neural network and system identification. J. Sound Vib. 2003, 266, 1009–1023. [Google Scholar] [CrossRef]
- Du, H.; Lam, J.; Zhang, N. Modelling of a magneto-rheological damper by evolving radial basis function networks. Eng. Appl. Artif. Intell. 2006, 19, 869–881. [Google Scholar] [CrossRef]
- Cao, M.; Wang, K.W.; Lee, K.Y. Scalable and invertible PMNN model for magneto-rheological fluid dampers. J. Vib. Control 2008, 14, 731–751. [Google Scholar] [CrossRef]
- Atray, V.S.; Roschke, P.N. Design, fabrication, testing and fuzzy modeling of a large magnetorheological damper for vibration control in a railcar. In Proceedings of the 2003 IEEE/ASME Joint Rail Conference, Chicago, IL, USA, 22–24 April 2003; pp. 223–229. [Google Scholar]
- Atray, V.S.; Roschke, P.N. Neuro-fuzzy control of railcar vibrations using semiactive dampers. Comput. Aided Civ. Infrastruct. Eng. 2004, 19, 81–92. [Google Scholar] [CrossRef]
- Kim, H.S.; Roschke, P.N.; Lin, P.Y.; Loh, C.H. Neuro-fuzzy model of hybrid semi-active base isolation system with FPS bearings and an MR damper. Eng. Struct. 2006, 28, 947–958. [Google Scholar] [CrossRef]
- Kim, H.S. Roschke, P.N. Fuzzy control of base-isolation system using multi-objective genetic algorithm. Comput. Aided Civ. Infrastruct. Eng. 2006, 21, 436–449. [Google Scholar] [CrossRef]
- Wang, D.H.; Liao, W.H. Modeling and control of magnetorheological fluid dampers using neural networks. Smart Mater. Struct. 2005, 14, 111–126. [Google Scholar] [CrossRef]
- Tsang, H.H.; Su, R.K.; Chandler, A.M. Simplified inverse dynamics models for MR fluid dampers. Eng. Struct. 2006, 28, 327–341. [Google Scholar] [CrossRef]
- Li, Z.-X.; Asce, M.; Xu, L.-H. Performance Tests and Hysteresis Model of MRF-04K Damper. J. Struct. Eng. 2005, 131, 1303–1306. [Google Scholar] [CrossRef]
- Bell, R.C.; Karli, J.O.; Vavreck, A.N.; Zimmerman, D.T.; Ngatu, G.T.; Wereley, N.M. Magnetorheology of submicron diameter iron microwires dispersed in silicone oil. Smart Mater. Struct. 2008, 17, 15–28. [Google Scholar] [CrossRef]
- Phulé, P.P.; Mihalcin, M.P.; Genc, S. The role of the dispersed-phase remnant magnetization on the redispersibility of magnetorheological fluids. J. Mater. Res. 1999, 14, 3037–3041. [Google Scholar] [CrossRef]
- Choi, J.S.; Park, B.J.; Cho, M.S.; Choi, H.J. Preparation and magnetorheological characteristics of polymer coated carbonyl iron suspensions. J. Magn. Mater. 2006, 304, 374–376. [Google Scholar] [CrossRef]
- Wu, W.P.; Zhao, B.Y.; Wu, Q.; Chen, L.S.; Hu, K.A. Reduced aggregation and sedimentation of zero-valent iron nanoparticles in the presence of guar gum. Smart Mater. Struct. 2006, 15, 94–98. [Google Scholar] [CrossRef]
- Phule, P.P. Magnetorheological Fluid. U.S. Patent 5985168, 16 November 1999. [Google Scholar]
- Chin, B.D.; Park, J.H.; Kwon, M.H.; Park, O.O. Rheological Properties and Dispersion Stability of Magnetorheological (MR) Suspensions. Rheol. Acta 2001, 40, 211–219. [Google Scholar] [CrossRef]
- De Vicente, J.; López-López, M.T.; González-Caballero, F.; Durán, J.D.G. A Rheological Study of the Stabilization of Magnetizable Colloidal Suspensions by Addition of Silica Nanoparticles. J. Rheol. 2003, 47, 1093–1109. [Google Scholar] [CrossRef]
- Rankin, P.J.; Horvath, A.T.; Klingenberg, D.J. Magnetorheology in viscoplastic media. Rheol. Acta 1999, 38, 471–477. [Google Scholar] [CrossRef]
- Guerrero-Sanchez, C.; Lara-Ceniceros, T.; Jimenez-Regalado, E.; Raşa, M.; Schubert, U.S. Magnetorheological Fluids Based on Ionic Liquids. Adv. Mater. 2007, 19, 1740–1747. [Google Scholar] [CrossRef]
- Kor, Y.K.; See, H.; Rasa, M.; Schubert, U.S. The electrorheological response of elongated particles. Rheol. Acta 2010, 49, 741–756. [Google Scholar] [CrossRef]
- Kanu, R.C.; Shaw, M.T. Enhanced electrorheological fluids using anisotropic particles. J. Rheol. 1998, 42, 657–670. [Google Scholar] [CrossRef]
- Otsubo, Y. Electrorheology of whisker suspensions. Colloids Surf. A Physicochem. Eng. Asp. 1999, 153, 459–466. [Google Scholar] [CrossRef]
- Felt, D.; Hagenbuchle, M.; Liu, J.; Richard, J. Rheology of a magnetorheological fluid. J. Intell. Mater. Syst. Struct. 1996, 7, 589–593. [Google Scholar] [CrossRef]
- Phillips, R.W. Engineering Applications of Fluids With a Variable Yield Stress. Ph.D. Thesis, University of California, Berkeley, CA, USA, 1969. [Google Scholar]
- Weiss, K.D.; Carlson, J.D.; Nixon, D.A. Viscoelastic properties of magneto- and electro-rheological fluids. J. Intell. Mater. Syst. Struct. 1994, 5, 772–775. [Google Scholar] [CrossRef]
- Ginder, J.M. Behavior of magnetorheological fluids. MRS Bull. 1998, 23, 26–28. [Google Scholar] [CrossRef]
- Jolly, M.; Carlson, J.D.; Munoz, B.C. A model of the behaviour of magnetorheological materials. Smart Mater. Struct. 1996, 5, 607–614. [Google Scholar] [CrossRef]
- Carlson, J.D. What makes a good MR fluid. J. Intell. Mater. Syst. Struct. 2002, 13, 413–435. [Google Scholar] [CrossRef]
- Carlson, J.D. Critical factors for MR fluids in vehicle systems. J. Veh. Des. 2003, 33, 207–217. [Google Scholar] [CrossRef]
- Rossi, A.; Orsini, F.; Scorza, A.; Botta, F.; Sciuto, S.A.; Di Giminiani, R. A preliminary characterization of a whole body vibration platform prototype for medical and rehabilitation application. In Proceedings of the 2016 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Benevento, Italy, 11–12 May 2016. [Google Scholar]
- Orsini, F.; Scorza, A.; Rossi, A.; Botta, F.; Sciuto, S.A.; Di Giminiani, R. A preliminary uncertainty analysis of acceleration and displacement measurements on a novel WBV platform for biologic response studies. In Proceedings of the 2016 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Benevento, Italy, 11–12 May 2016. [Google Scholar]
- Orsini, F.; Rossi, A.; Scorza, A.; Andrea Sciuto, S. Development and preliminary characterization of a novel system for the force platforms dynamic calibration. In Proceedings of the I2MTC 2017 IEEE International Instrumentation and Measurement Technology Conference, Torino, Italy, May 22–25 May 2017. [Google Scholar]
- Scorza, A.; Orsini, F.; Andrea Sciuto, S. Use of phantoms and test objects for local dynamic range evaluation in medical ultrasounds: A preliminary study. In Proceedings of the I2MTC 2017 IEEE International Instrumentation and Measurement Technology Conference, Torino, Italy, May 22–25 May 2017. [Google Scholar]
- Cesmeci, S.; Engin, T. Modeling and testing of a field-controllable magnetorheological fluid damper. J. Mech. Sci. 2010, 52, 1036–1046. [Google Scholar] [CrossRef]
- Suciua, B.; Koyanagib, K.; Sonodaa, K. Evaluation of the Dissipative and Thermal Characteristics of a Magneto-Rheological (MR) Damper for Automotive Suspension. In Proceedings of the 2nd International Conference on Intelligent Systems and Image Processing, Matsue, Japan, 26–29 September 2014. [Google Scholar]
- Raju, M.; Seetharamaiah, N.; Prasad, A.M.K.; Rahman, M.A. Experimental Analysis of Magneto-Rheological Fluid (MRF) Dampers under Triangular Excitation. Int. J. Mech. Eng. Technol. 2016, 7, 284–295. [Google Scholar]




| FIELD | RANGE | REF. |
|---|---|---|
| Automotive | ≤700 N, 1÷10 Hz, ±0.06 m s, ±8 mm | [18,19,20,21] |
| Civil Engineering | ≤1500 N, ±0.1 m s, 2.5 Hz | [22,23,24] |
| Washing Machine | 10 ÷ 90 N, 3 ÷ 24 Hz | [25] |
| Railway Vehicle | ≤15 kN, 3 ÷ 10 Hz, ±0.03 m s | [26,27] |
| Weapons | ≤1550 N, ≤2 m s | [28] |
| Aeronautical Industry | 18,000 N, 2 ÷ 8 m s | [29] |
| ISSUE | DESCRIPTION | REF. |
|---|---|---|
| Settling (iron particles) | Increase of response time | [36] |
| Saturation | Slow response | [37] |
| Abrasiveness of MR fluid | Premature wear (special additives are needed) | [38,39] |
| PHYSICAL PROPERTIES | DESCRIPTION | REF. |
|---|---|---|
| Static Yield stress τ0 | ≫ 20 kPa at 0.6 ÷ 1 T | [40,58] |
| Operative Temperature range | −40 up to 120 ◦C continuos exposure or up to 150 ◦C intermittent exposure | [17,40] |
| Shear rate | >105 s−1 at 1 m s−1 piston velocity (automotive applications) or up to 104 s−1 for rotary MR dampers | [40] |
| Liquid phase viscosity | 0.001 to 0.1 Pas at ambient temperature | [40] |
| Solid phase attributes | Density 2300–4120 kg/m3, Saturation magnetization 1.6–2.1 TParticle diameter 1 to 100 µm (typical), prefereably 1 to 10 µm Solid phase content by volume 20–22% to 40–48% | [40,47] |
| MODEL | DESCRIPTION | EXAMPLES | REF. |
|---|---|---|---|
| Quasi static | Based on the Bingham plastic model | Asymmetric models Parallel plate models | [63,64,65,66,67,68,69,70] |
| Dynamic parametric | The model requires the determination of a set of parameters by minimizing the error between the experimental results and the model outcomes | Bingham Biviscous Viscoelastic-plastic Stiffness-viscosity-elasto-slide Hysteresis Operator-based dynamic models: Bouc-Wen, Dahl, LuGre Function-based models: hyperbolic tangent, sigmoid. Equivalent models Phase transition | [43,44,45,46,63,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96] |
| Dynamic non parametric | Based on analytical expressions derived from experimental data and MR damper physics analysis. | Polynomial Multifunction Black-box Query Neural network Fuzzy Wavelets Ridgenet | [63,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115] |
| Dynamic models and inverse dynamic models | The relationship between the MR damper displacement and voltage/current supply should be known in order to be related to the damper forces. | Simplified inverse dynamics (SID) Feedforward neural network (FNN) Recurrent neural network (RNN) | [63,116,117] |
| Model | Advantages and/or Drawbacks | Ref. |
|---|---|---|
| Bingham models | ||
| Simple Bingham | Easy to implement and rapid computation time, the hysteresis behaviour not considered | [21,22,23,25,26,27,28,29,43,44,45,46,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141] |
| Gamota and Filisko | The viscoelastic behaviour is considered, but longer simulation time are needed | [43] |
| Bouc-Wen models | ||
| Simple Bouc-Wen | The hysteresis behaviour of MR fluids is implemented. A lot of parameters must be considered | [72] |
| Modified Bouc-Wen model (Yang and Spencer) | Other parameters are introduced to better describe the hysteresis behaviour of MR damper in civil engineering applications | [63,71,74] |
| Spencer and Dyke | It accurately predicts the response of the MR damper over a large range of operating conditions, as step excitation, random displacement at constant or random voltage | [11,21,73,74,75,83,87] |
| Dominguez | It models the hysteresis behaviour of a MR damper under any working conditions and the parameters have to be assessed only once | [44] |
| Ali and Ramaswamy | Applicable where the excitation is known a priori | [32] |
| Non-symmetrical Bouc Wen | Applicable when the MR behaviour is not symmetrical but a Genetic Algorythm approach is needed for the parameters evaluation | [45] |
| Model | Automotive | Civil Engineering | Microvibration | Behaviour Prediction | Real-Time Control |
|---|---|---|---|---|---|
| Bingham Models | |||||
| Simple Bingham | R | M | M | U | M |
| Gamota-Filisko | P | M | M | R | M |
| Bi-Viscous | |||||
| Hysteretic Bi-Viscous | P | M | M | R | P |
| Bouc-Wen models | |||||
| Simple Bouc-Wen | R | R | P | R | R |
| Yang and Spencer | P | R | P | R | P |
| Spencer and Dyke | R | R | P | R | R |
| Dominguez | R | R | P | M | M |
| Ali and Ramaswamy | P | R | P | R | R |
| Non symmetrical Bouc-Wen | P | R | M | M | P |
| Sensor Type | Range | Uncertainty | Ref. | |
|---|---|---|---|---|
| Force | S load cell | ±5.394 kN | ±0.03% FS | [85] |
| Multi-purpose ICP force sensor | 2.224 kN | ≤1% FS | [86] | |
| Load cell | 0.4 ÷ 500 kN | [88,89,90] | ||
| Acceleration | Accelerometer | 1.12 ÷ 15.00 m/s2 | [87] | |
| Velocity | Laser vibrometer | 20 ÷ 20,000 mm/s, ≤50 kHz | ±1.0% of rms at 25 ◦C | [86] |
| Computed fromdisplacement signal (e.g., LVDT) | −0.3 ÷ 0.3 m/s | [96,142] | ||
| Displacement | PCR-A-1 type | 150 mm | ±0.02% FS | [85] |
| Laser vibrometer | 81,920 µm | ±1.0% of rms reading | [86] | |
| LVDT | 0.07 ÷ 4.00 mm | [87,89,142] | ||
| Temperature | Thermocouple | 0 ÷ 75 ◦C | [90,91,92,143] | |
| IR temperature sensor | 20 ÷ 45 ◦C | ≤±10% of reading | [142,143,144] | |
| Frequency | Encoder, displacement sensors | 0.5 ÷ 12.0 Hz | [88,89,90] |
| Source | Example of Uncertainty (%) | Distribution |
|---|---|---|
| Drift | 0.04 | Rectangular |
| Mechanical and Electrical Noise | 0.1 | Rectangular |
| Resolution | 0.5 | Rectangular |
| Stability | Case dependent | |
| Backlash | 0.1 | Rectangular |
| Temperature compensation | 0.01 | Rectangular |
| Power Fluctuations | Case dependent | |
| Specimen alignment and preparation | Case dependent | |
| System zeroing | 0.1 | Rectangular |
| Display (readings error) | 0.5 | Normal |
| Test speed | 0.2 ÷ 10 | Rectangular |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rossi, A.; Orsini, F.; Scorza, A.; Botta, F.; Belfiore, N.P.; Sciuto, S.A. A Review on Parametric Dynamic Models of Magnetorheological Dampers and Their Characterization Methods. Actuators 2018, 7, 16. https://doi.org/10.3390/act7020016
Rossi A, Orsini F, Scorza A, Botta F, Belfiore NP, Sciuto SA. A Review on Parametric Dynamic Models of Magnetorheological Dampers and Their Characterization Methods. Actuators. 2018; 7(2):16. https://doi.org/10.3390/act7020016
Chicago/Turabian StyleRossi, Andrea, Francesco Orsini, Andrea Scorza, Fabio Botta, Nicola Pio Belfiore, and Salvatore Andrea Sciuto. 2018. "A Review on Parametric Dynamic Models of Magnetorheological Dampers and Their Characterization Methods" Actuators 7, no. 2: 16. https://doi.org/10.3390/act7020016
APA StyleRossi, A., Orsini, F., Scorza, A., Botta, F., Belfiore, N. P., & Sciuto, S. A. (2018). A Review on Parametric Dynamic Models of Magnetorheological Dampers and Their Characterization Methods. Actuators, 7(2), 16. https://doi.org/10.3390/act7020016







