Separation of Microparticles from Suspension Utilizing Ultrasonic Standing Waves in a Piezoelectric Cylinder Actuator
Abstract
:1. Introduction
2. Materials and Methods
2.1. Simulation Procedure
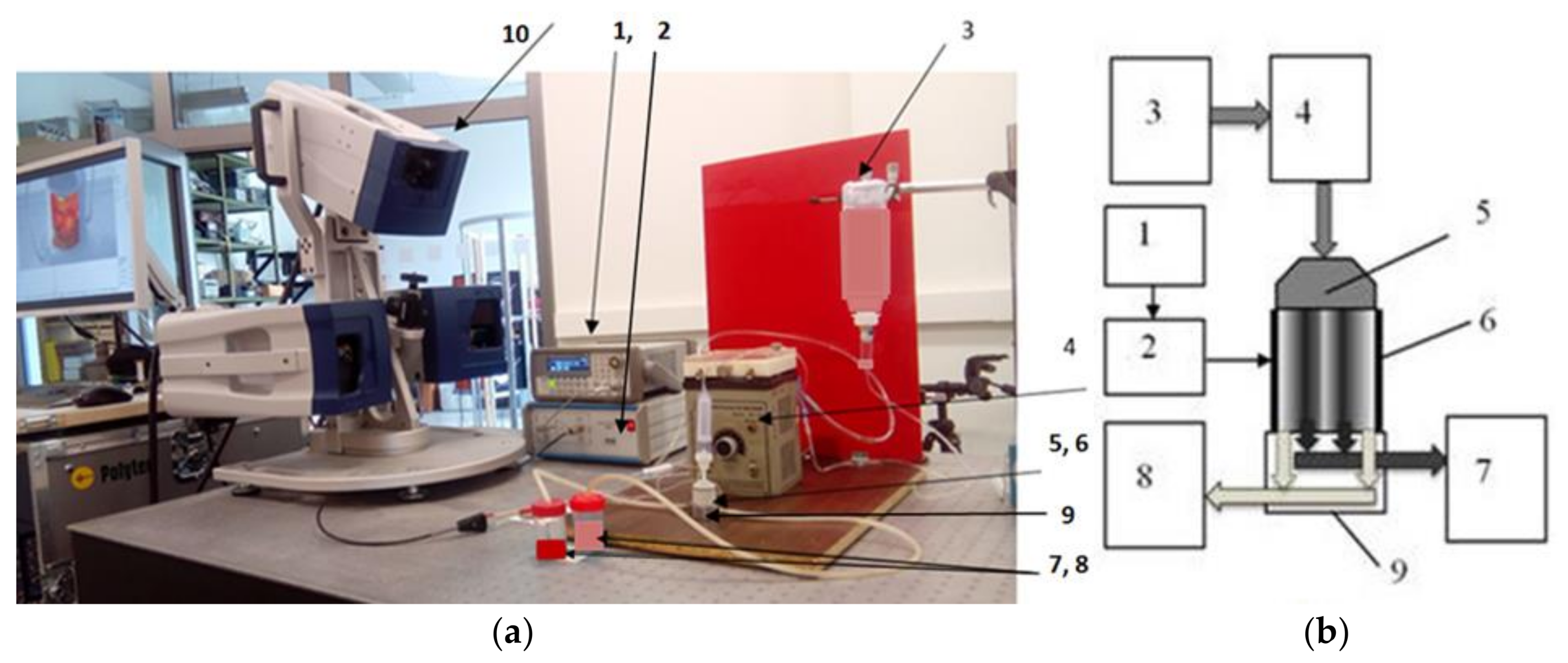
2.2. Experimental Validation Procedure
3. Results
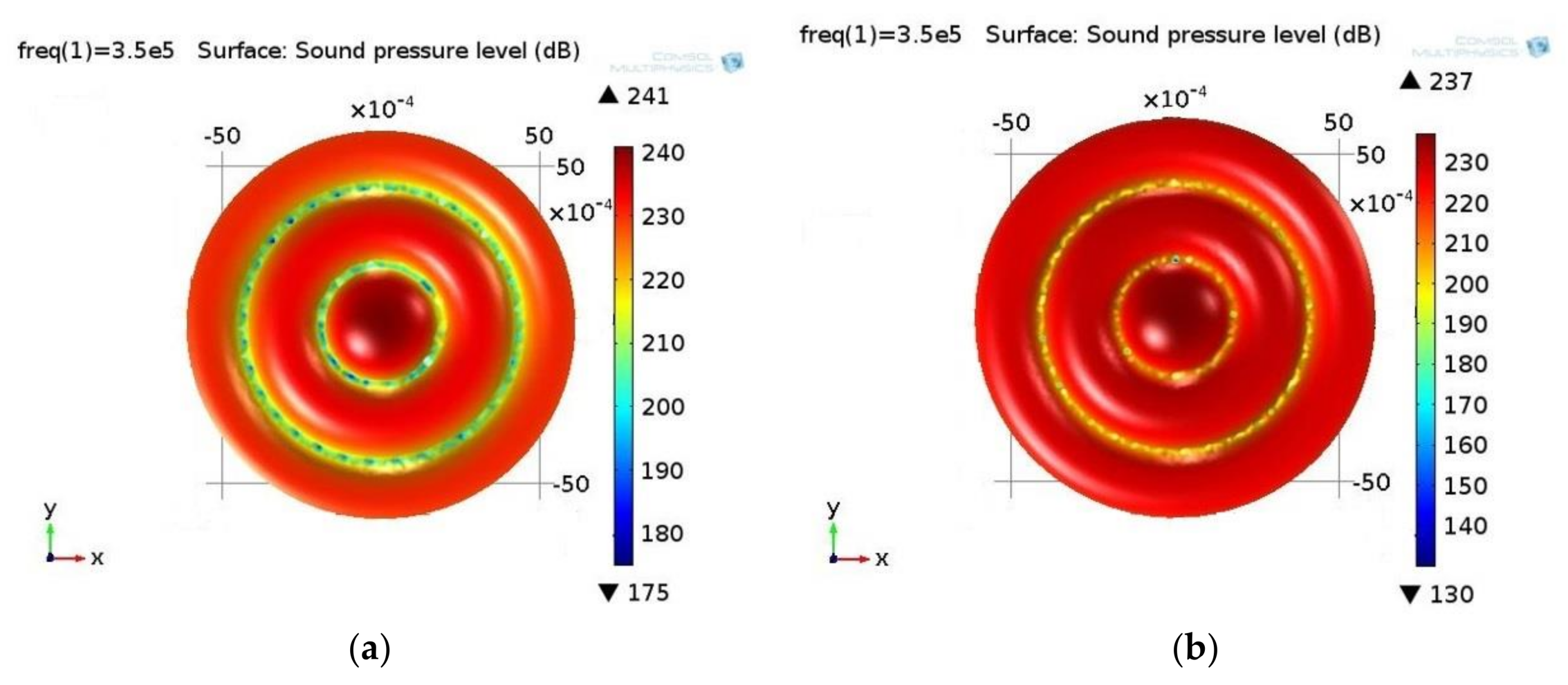
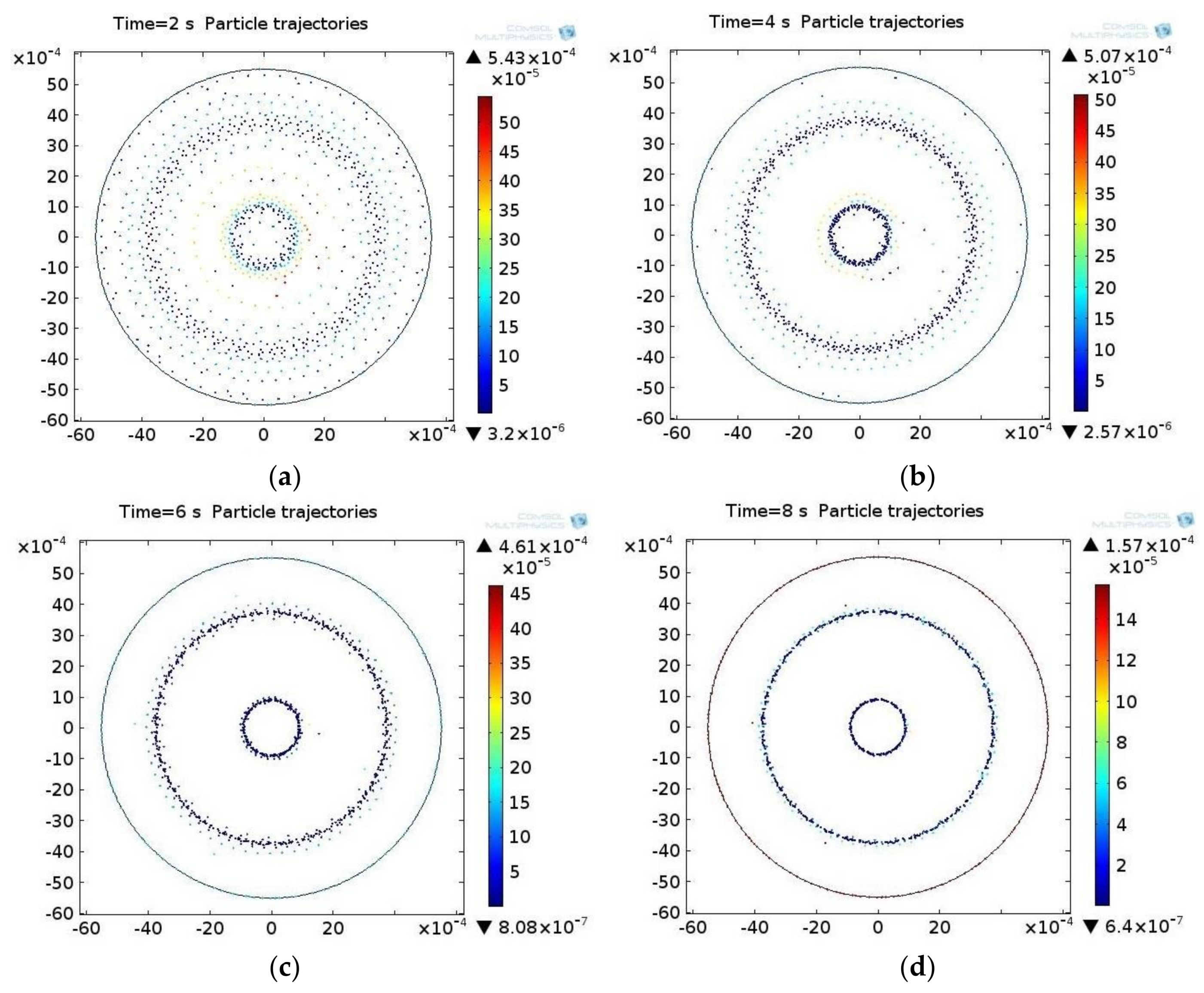
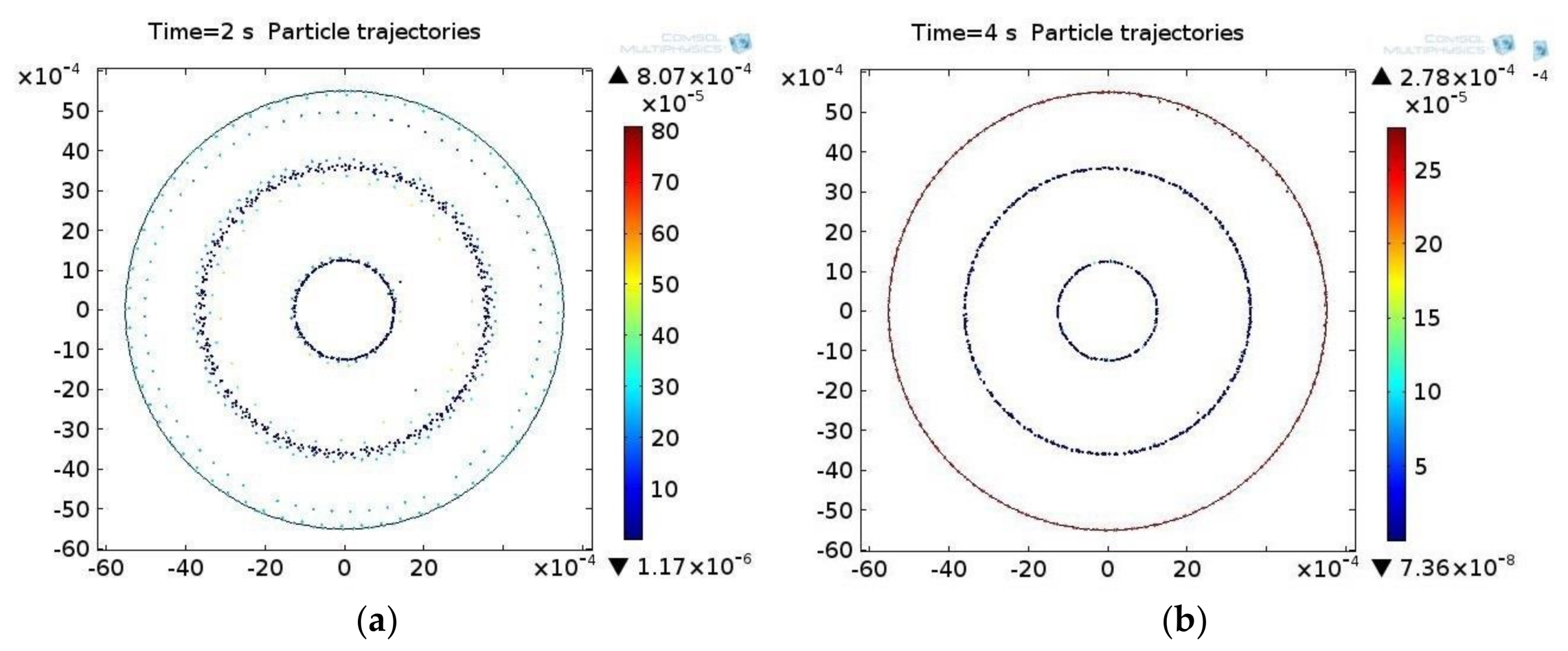
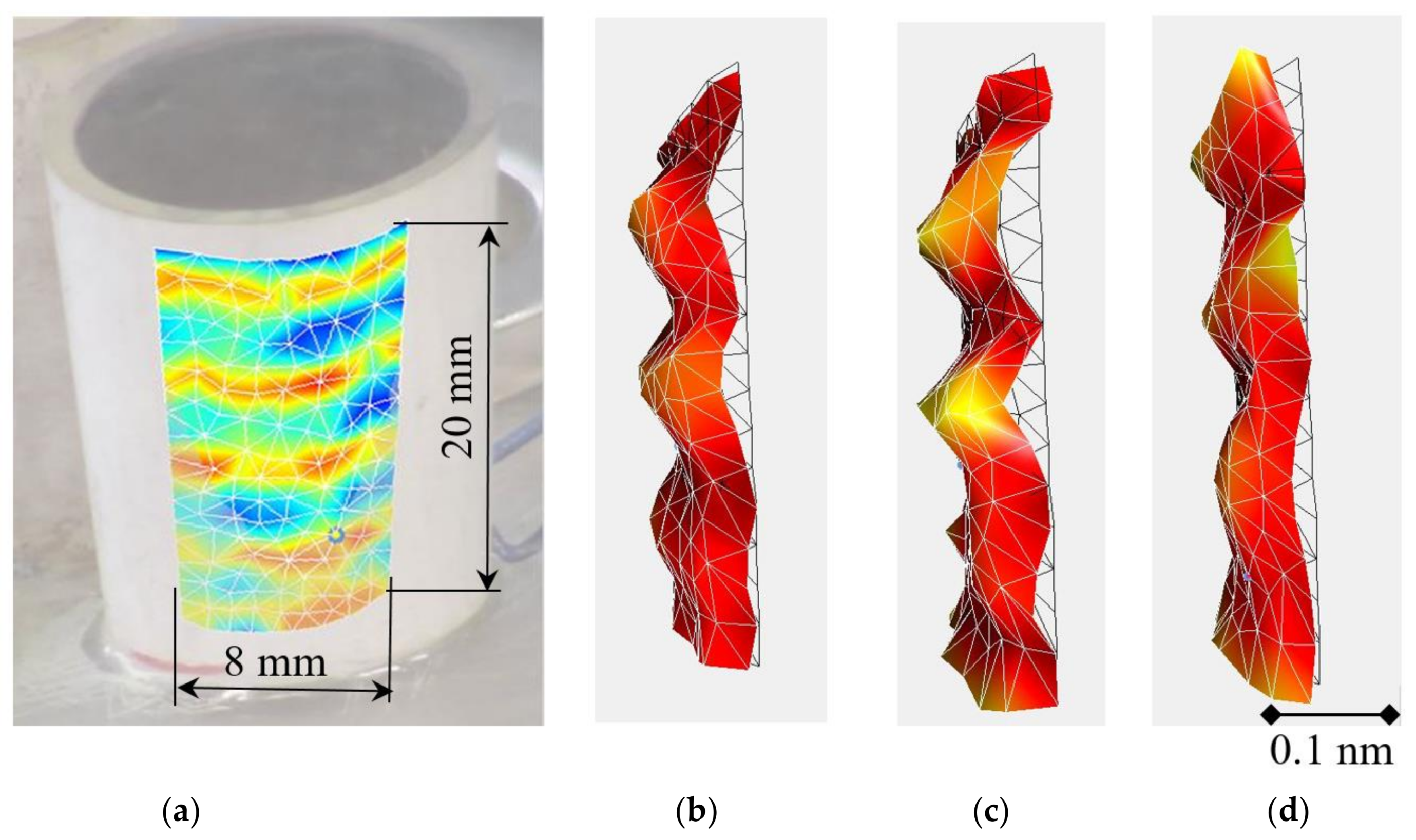
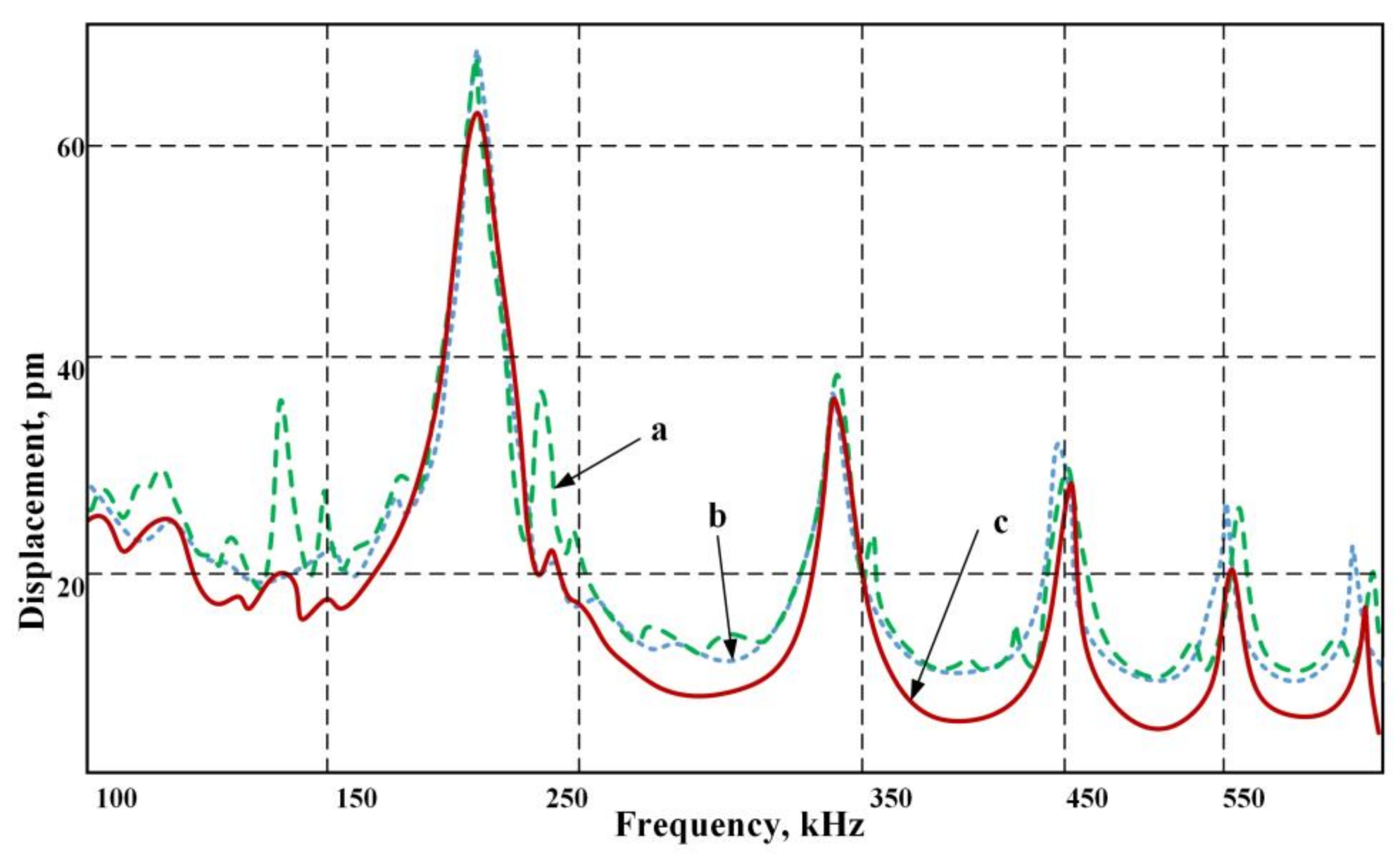
3.1. Simulation Results
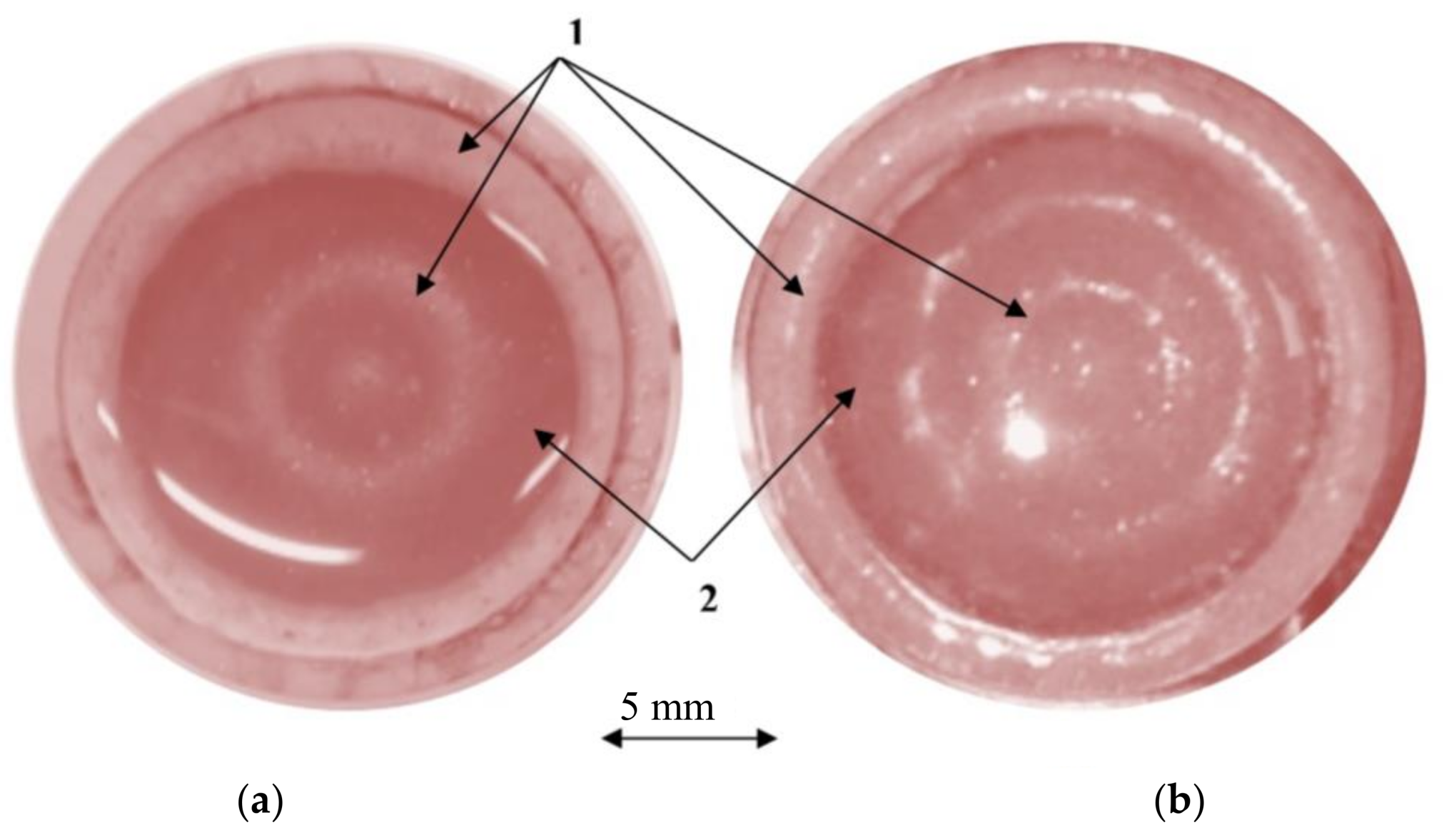
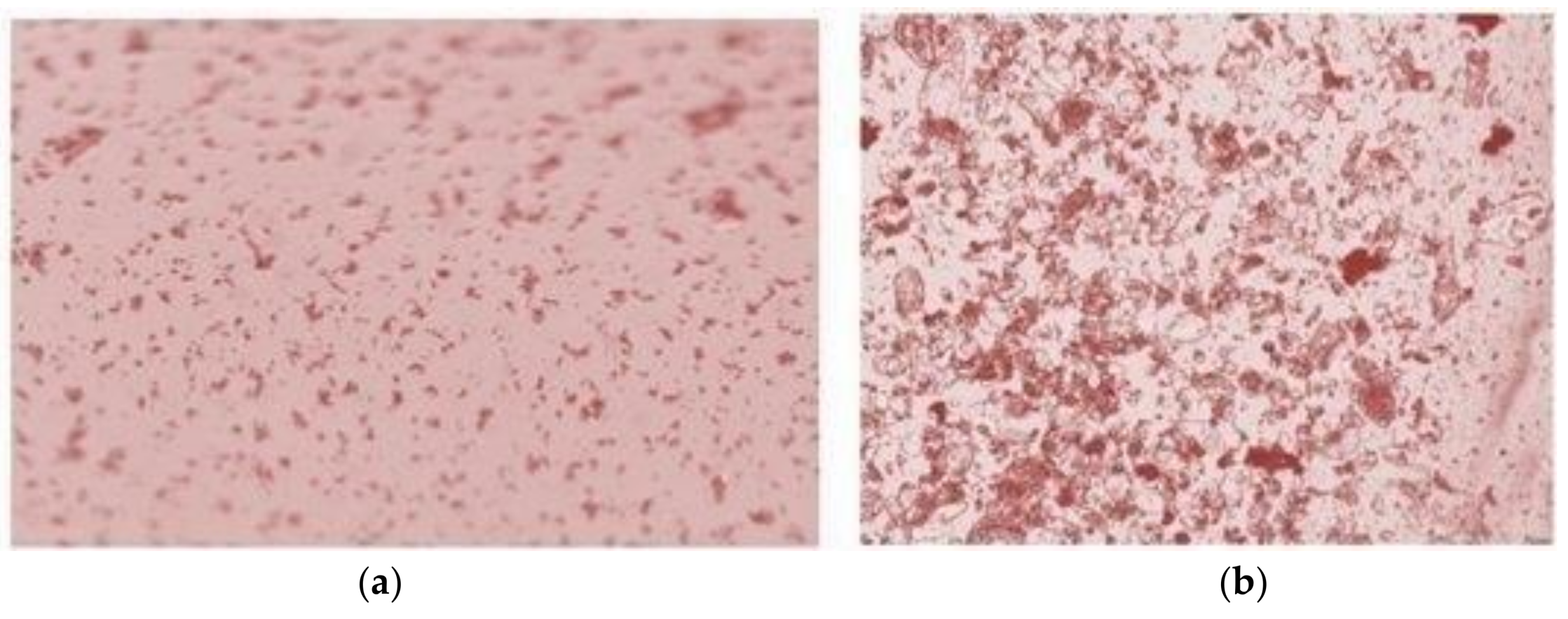
3.2. Experimental Results
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wloch, A.; Czyz, H.; Jasinski, T. Ultrasonic methods of the cells separation in human blood. Acta Phys. Pol. A 2015, 128, 234–236. [Google Scholar] [CrossRef]
- Lei, J.; Glynne-Jones, P.; Hill, M. Acoustic streaming in the transducer plane in ultrasonic particle manipulation devices. Lab Chip 2013, 13, 2133–2143. [Google Scholar] [CrossRef] [PubMed]
- Mohamed, M.A.; Fikry, N.M.; Mohamed, M.M. Experimental investigation of ultrasonic trapping of bioparticles using parallel plane cavity. Int. J. Biomed. Eng. Sci. 2014, 1, 21–34. [Google Scholar]
- Setayeshgar, A.; Lipsett, M.G.; Koch, C.R.; Nobes, D.S. Measurement of particle dynamics in a coherent acoustic field. In Proceedings of the 10th International Symposium on Particle Image Velocimetry, Delft, The Netherlands, 1–3 July 2013; p. 6. [Google Scholar]
- Westerweel, J. Fundamentals of digital particle image velocimetry. Meas. Sci. Technol. 1997, 8, 1379–1392. [Google Scholar] [CrossRef]
- Devendran, C.; Gralinski, I.; Neild, A. Separation of particles using acoustic streaming and radiation forces in an open microfluidic channel. Microfluid. Nanofluid. 2014, 17, 879–890. [Google Scholar] [CrossRef]
- Haddadi, B.; Fathipour, M. Numerical analysis of 3D model of the SSAW separator system. Int. J. Comput. Appl. 2016, 141, 7–12. [Google Scholar] [CrossRef]
- Kapishnikov, S.; Kantsler, V.; Steinberg, V. Continuous particle size separation and size sorting using ultrasound in a microchannel. J. Stat. Mech. Theory Exp. 2006, P01012. [Google Scholar] [CrossRef]
- Laurell, T.; Petersson, F.; Nilsson, A. Chip integrated strategies for acoustic separation and manipulation of cells and particles. Chem. Soc. Rev. 2007, 36, 492–506. [Google Scholar] [CrossRef] [PubMed]
- Oberti, S.; Möller, D.; Neild, A.; Duala, J.; Beyelerb, F.; Nelson, B.J.; Gutmann, S. Strategies for single particle manipulation using acoustic and flow fields. Ultrasonics 2010, 50, 247–257. [Google Scholar] [CrossRef] [PubMed]
- Petersson, F.; Nilsson, A.; Holm, C.; Jonsson, H.; Laurell, T. Separation of lipids from blood utilizing ultrasonic standing waves in microfluidic channels. R. Soc. Chem. J. Anal. 2004, 129, 938–943. [Google Scholar] [CrossRef] [PubMed]
- Böhm, H.; Briarty, L.G.; Lowe, K.C.; Power, J.B.; Benes, E.; Davey, M.R. Application of a novel h-shaped ultrasonic particle separator under microgravity conditions. In Proceedings of the Forum Acusticum 2002, Special Session PHA-01: Acoustics of Dispersed Particulate Matter, Sevilla, Spain, 16–20 September 2002. [Google Scholar]
- Sadikova, D.G.; Pashovkin, T.N. Cell concentration and separation in the field of a standing ultrasonic wave for medicine and biotechnology. Open J. Biophys. 2013, 3, 70–75. [Google Scholar] [CrossRef]
- Grösch, M.; Burger, W.; Handl, B.; Doblhoff-Dier, O.; Gaida, T.; Schmatz, C. Ultrasonic separation of suspended particles—Part III. Acta Acust. United Acust. 1998, 84, 815–822. [Google Scholar]
- Riera-Franco de Sarabia, E.; Gallego-Juárez, J.A.; Rodríguez-Corral, G.; Elvira-Segura, L.; González-Gómez, I. Application of high-power ultrasound to enhance fluid/solid particle separation processes. Ultrasonics 2000, 38, 642–646. [Google Scholar] [CrossRef]
- Andrade, M.A.B.; Buiochi, F.; Adamowski, J.C. Particle manipulation by ultrasonic progressive waves. Phys. Proc. 2010, 3, 283–288. [Google Scholar] [CrossRef]
- Rahman, S.; Haque, A. Mathematical modeling of blood flow. In Proceedings of the 2012 International Conference on Informatics, Electronics & Vision (ICIEV), Dhaka, Bangladesh, 18–19 May 2012; pp. 672–676. [Google Scholar]
- Fontaine, I.; Savery, D.; Cloutier, G. Simulation of ultrasound backscattering by red cell aggregates: Effect of shear rate and anisotropy. Biophys. J. 2002, 82, 1696–1710. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, W.K. Rheology of red blood cell aggregation by computer simulation. J. Comput. Phys. 2006, 220, 139–154. [Google Scholar] [CrossRef]
- Mason, T.J.; Joyce, E.; Phull, S.S.; Lorimer, J.P. Potential uses of ultrasound in the biological decontamination of water. Ultrason. Sonochem. 2003, 10, 319–323. [Google Scholar] [CrossRef]
- Yin, X.; Han, P.; Lu, X.; Wang, Y. A review on the dewaterability of bio-sludge and ultrasound pretreatment. Ultrason. Sonochem. 2004, 11, 337–348. [Google Scholar] [CrossRef] [PubMed]
- Saxena, A.; Tripathi, B.P.; Kumar, M.; Shahi, V.K. Membrane-based techniques for the separation and purification of proteins: An overview. Adv. Colloid Interface Sci. 2009, 145, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Yasuda, K.; Sakamoto, T. Cell separation device using ultrasound and electrophoresis. U.S. Patent 6245207 B112, 18 May 1999. [Google Scholar]
- Settnes, M.; Bruus, H. Forces acting on a small particle in an acoustical field in a viscous fluid. Phys. Rev. 2012, E85, 1–12. [Google Scholar] [CrossRef]
- Gor’kov, L.P. On the forces acting on a small particle in an acoustical field in an ideal fluid. Sov. Phys. Dokl. 1962, 6, 773. [Google Scholar]
- Stegmayr, B.G. A survey of blood purification techniques. Transf. Apher. Sci. 2005, 32, 209–220. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Nyborg, W.L. Ultrasound, cavitation bubbles and their interaction with cells. Adv. Drug Deliv. Rev. 2008, 60, 1103–1116. [Google Scholar] [CrossRef] [PubMed]
- Lewis, R.W.C.; Bowen, C.R.; Dent, A.C.E.; Jonas, K. Finite element and experimental analysis of the vibration response of radially poled piezoceramic cylinders. Ferroelectrics 2010, 389, 95–106. [Google Scholar] [CrossRef]
- Adams, J.D.; Ebbesen, C.L.; Brankob, R.; Yang, A.H.J.; Soh, H.T.; Bruus, H. High-throughput, temperature-controlled microchannel acoustophoresis device made with rapid prototyping. J. Micromech. Microeng. 2012, 22, 1–4. [Google Scholar] [CrossRef]


| Density (103 kg/m3) | 7.7 |
| Young’s modulus (1010 N/m) | 7.3 |
| Curie point (°C) | 350 |
| Mechanical Q | 1000 |
| Relative dielectric constant | 1725 |
| Dielectric loss (1 kHz) | 0.4 |
| k31 | 0.32 |
| kp | 0.54 |
| d31 (10−12 m/V) | −130 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ostasevicius, V.; Jurenas, V.; Golinka, I.; Gaidys, R.; Aleksa, A. Separation of Microparticles from Suspension Utilizing Ultrasonic Standing Waves in a Piezoelectric Cylinder Actuator. Actuators 2018, 7, 14. https://doi.org/10.3390/act7020014
Ostasevicius V, Jurenas V, Golinka I, Gaidys R, Aleksa A. Separation of Microparticles from Suspension Utilizing Ultrasonic Standing Waves in a Piezoelectric Cylinder Actuator. Actuators. 2018; 7(2):14. https://doi.org/10.3390/act7020014
Chicago/Turabian StyleOstasevicius, Vytautas, Vytautas Jurenas, Ievgeniia Golinka, Rimvydas Gaidys, and Algiment Aleksa. 2018. "Separation of Microparticles from Suspension Utilizing Ultrasonic Standing Waves in a Piezoelectric Cylinder Actuator" Actuators 7, no. 2: 14. https://doi.org/10.3390/act7020014
APA StyleOstasevicius, V., Jurenas, V., Golinka, I., Gaidys, R., & Aleksa, A. (2018). Separation of Microparticles from Suspension Utilizing Ultrasonic Standing Waves in a Piezoelectric Cylinder Actuator. Actuators, 7(2), 14. https://doi.org/10.3390/act7020014





