Role of α and β Transmembrane Domains in Integrin Clustering
Abstract
:1. Introduction
2. Material and Method
2.1. Method
2.2. Models and Simulation Details
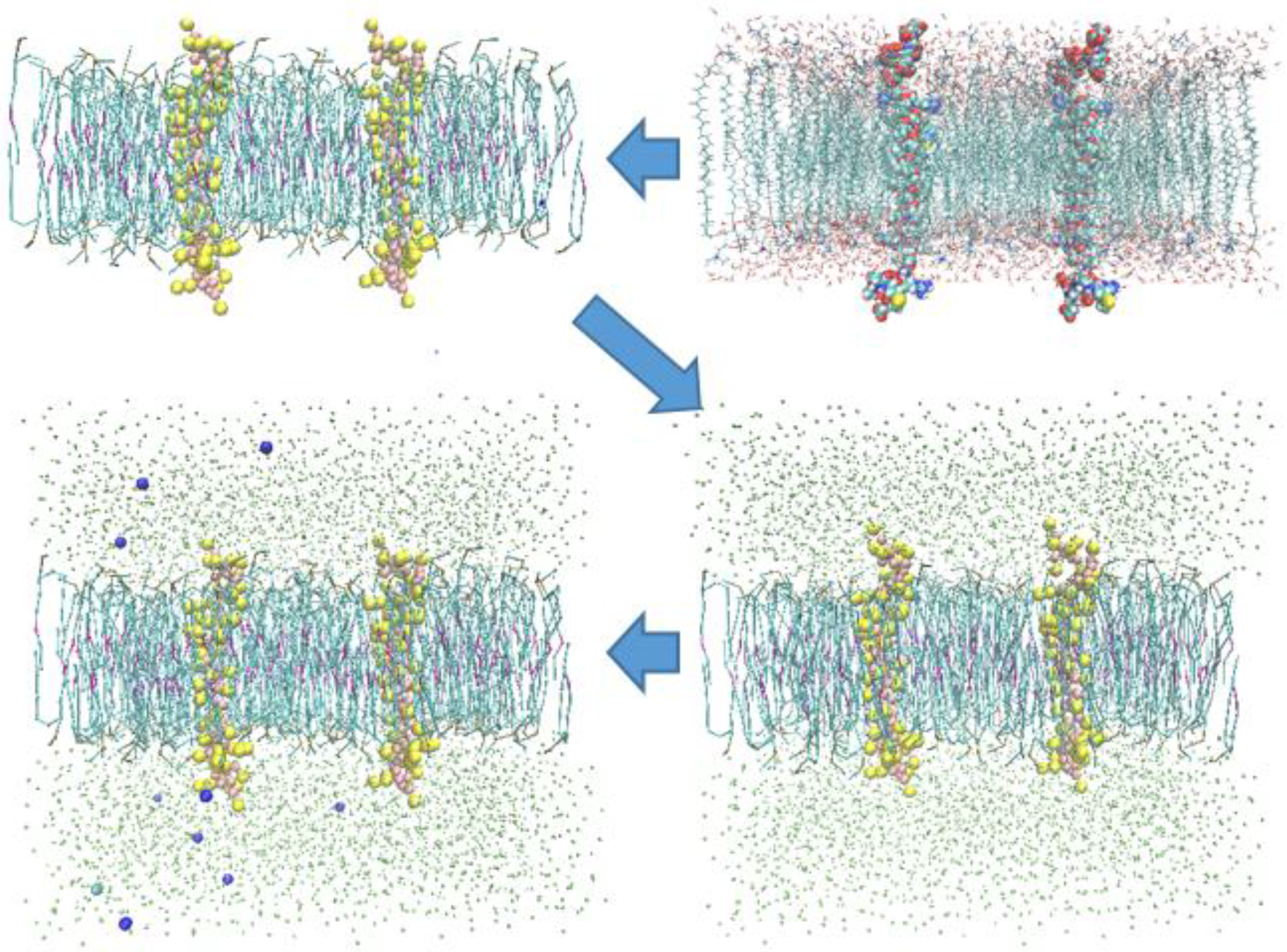
3. Results and Discussion
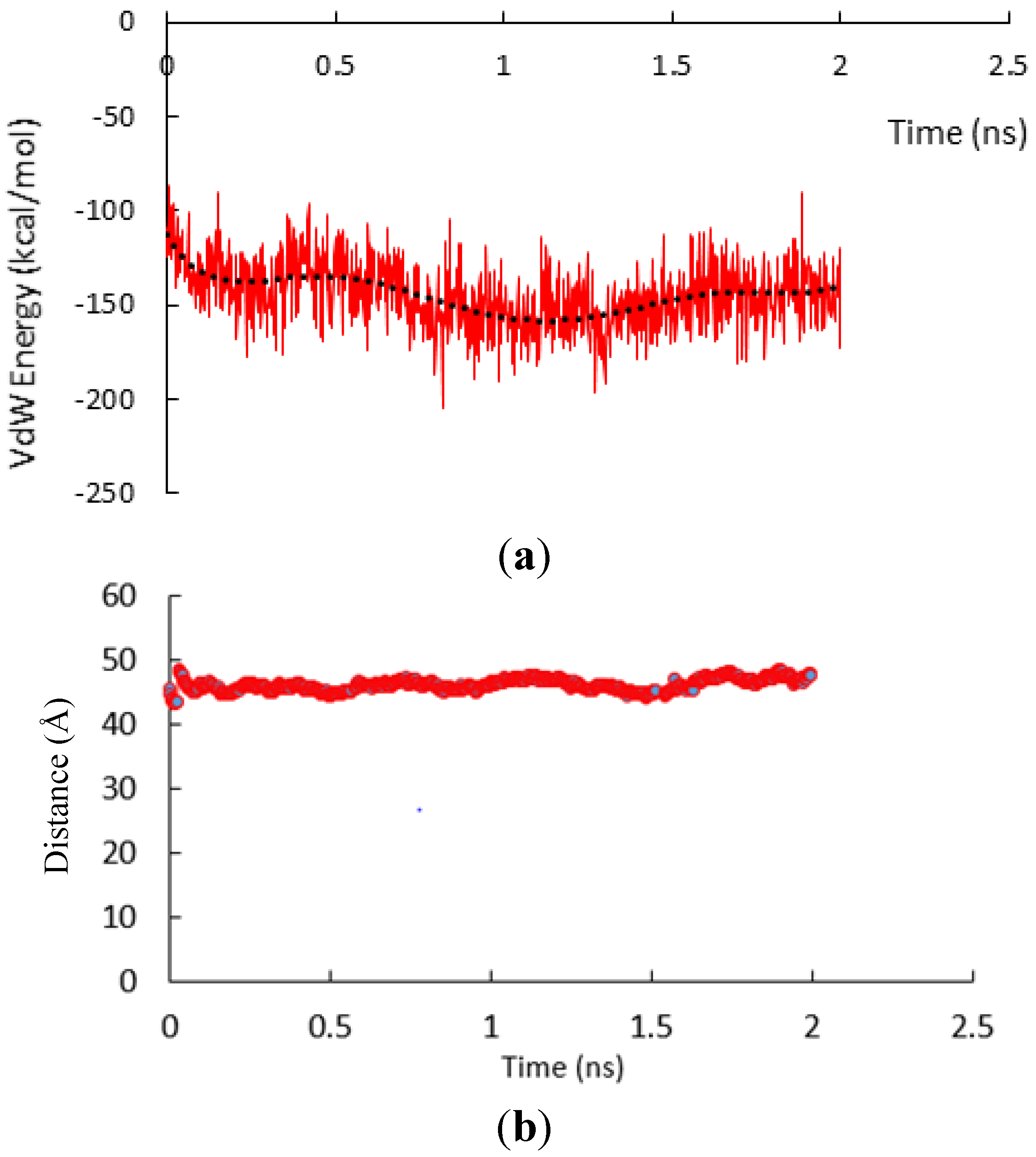
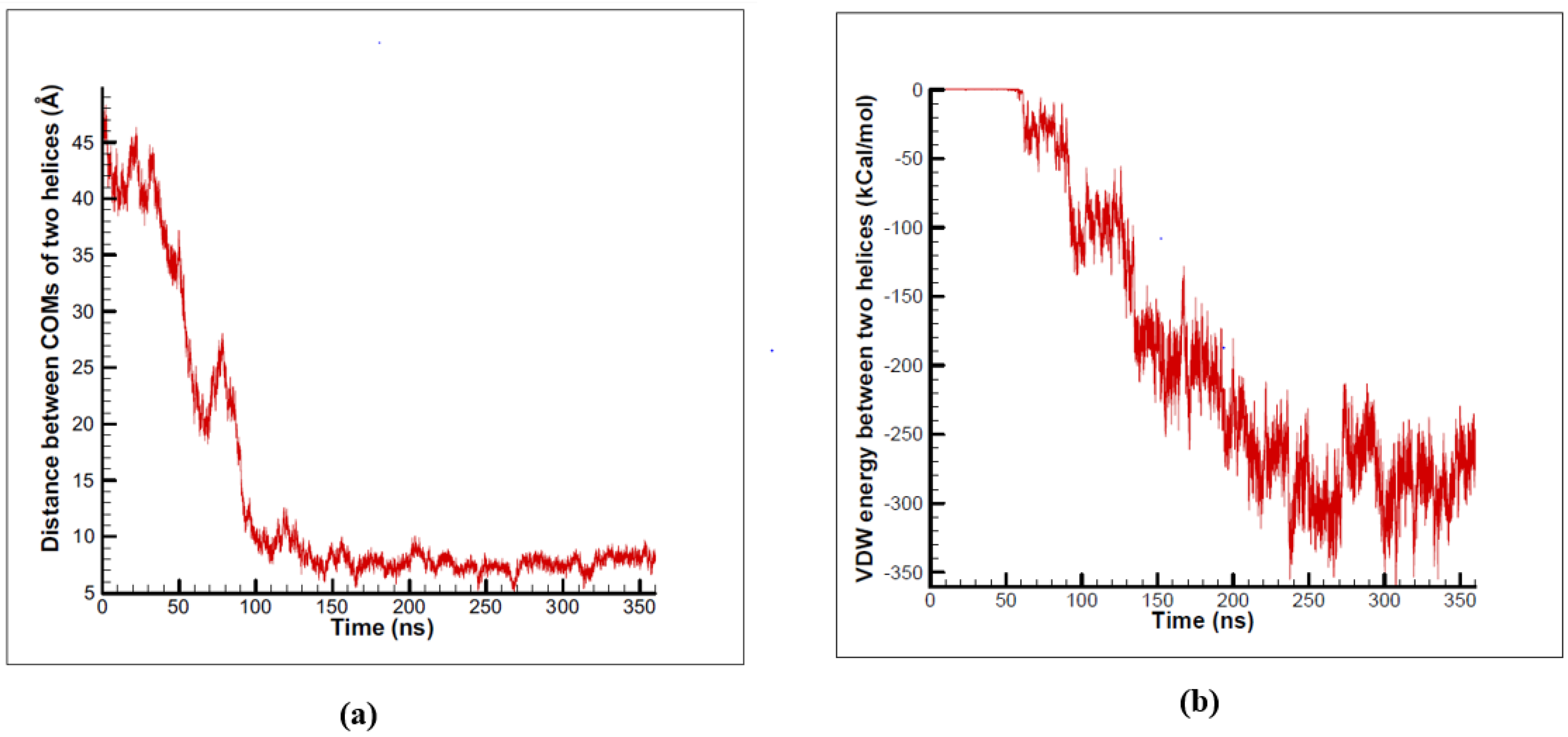
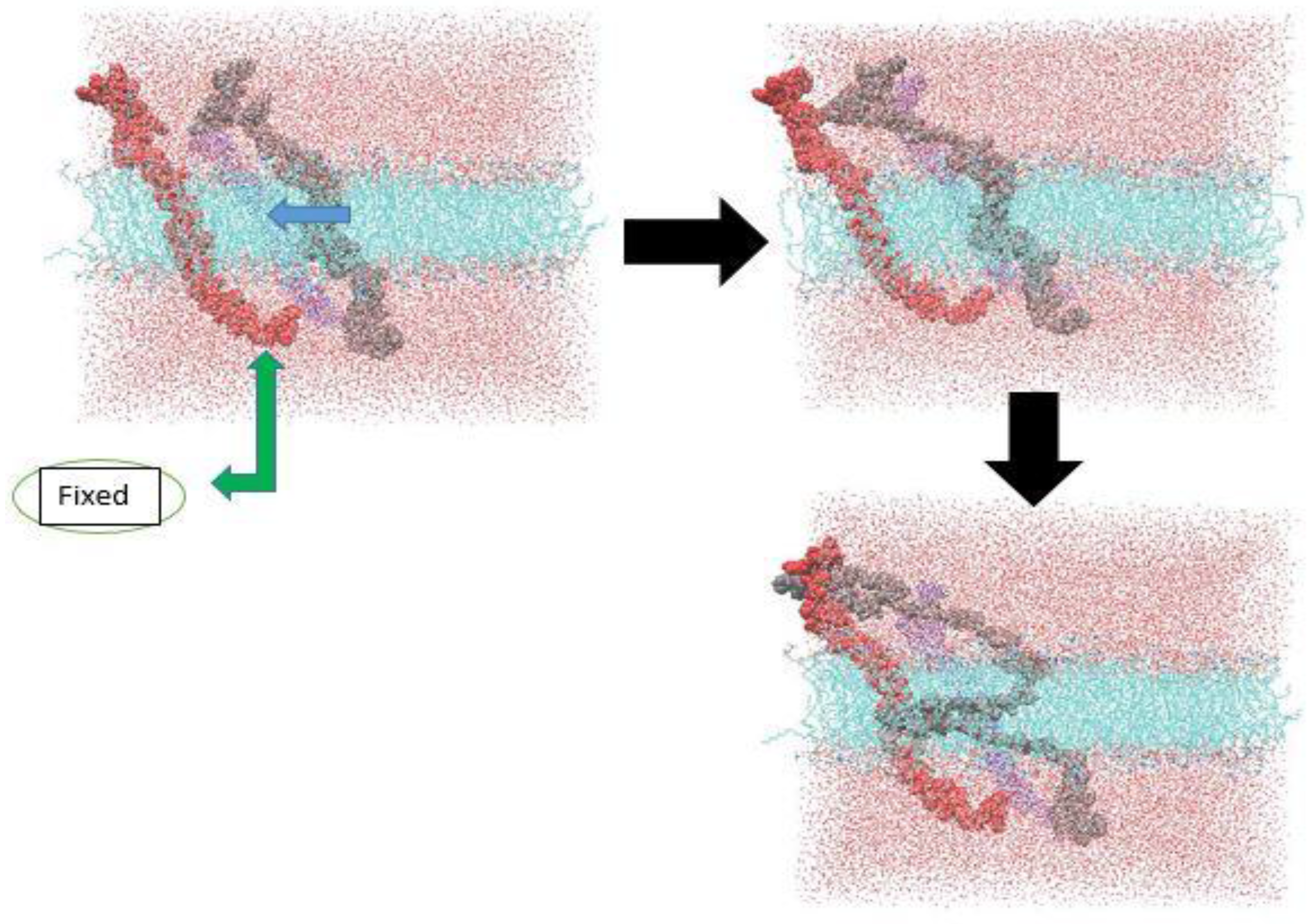
3.1. α-Subunit Homo-Oligomerization Simulations
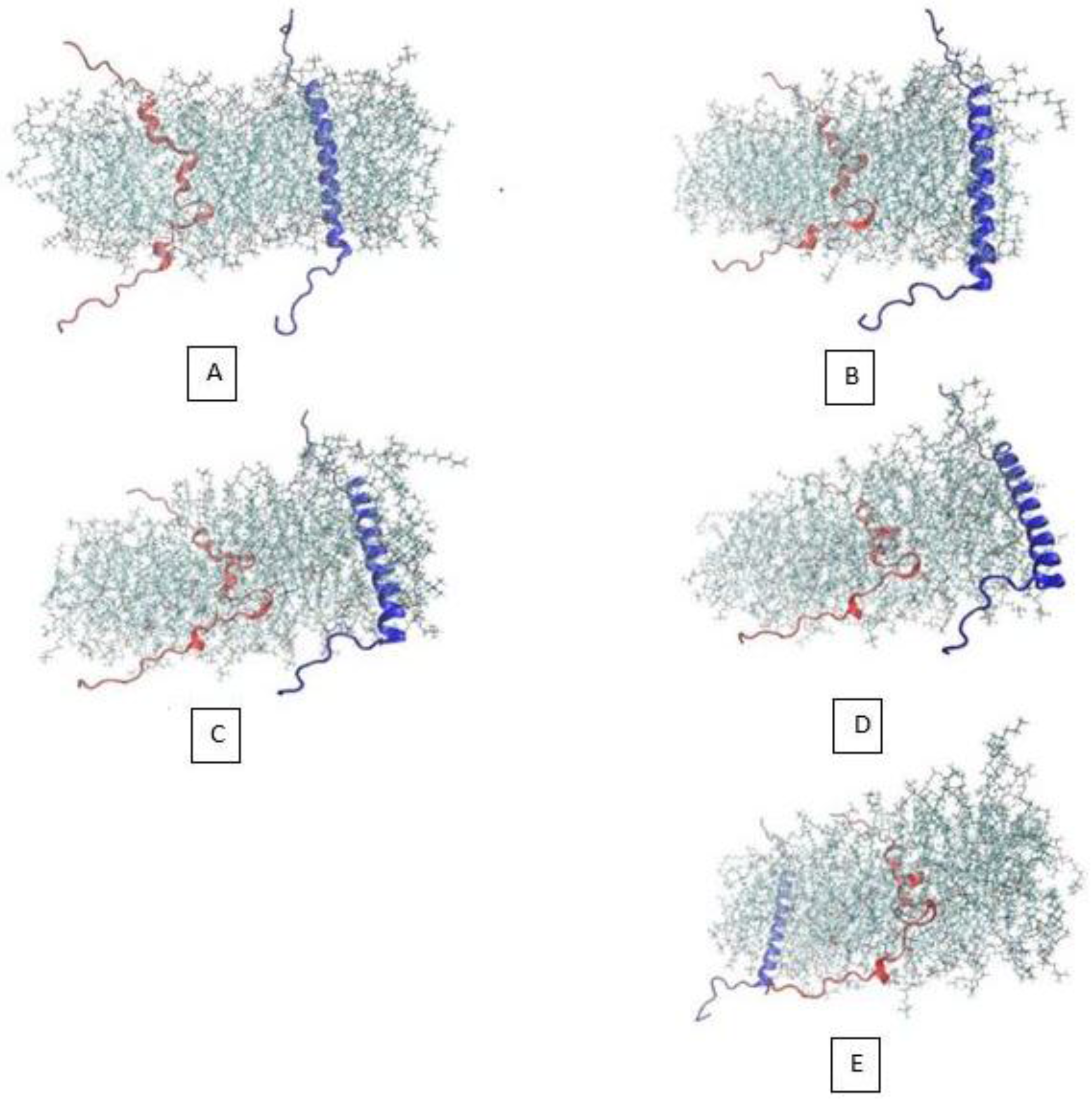
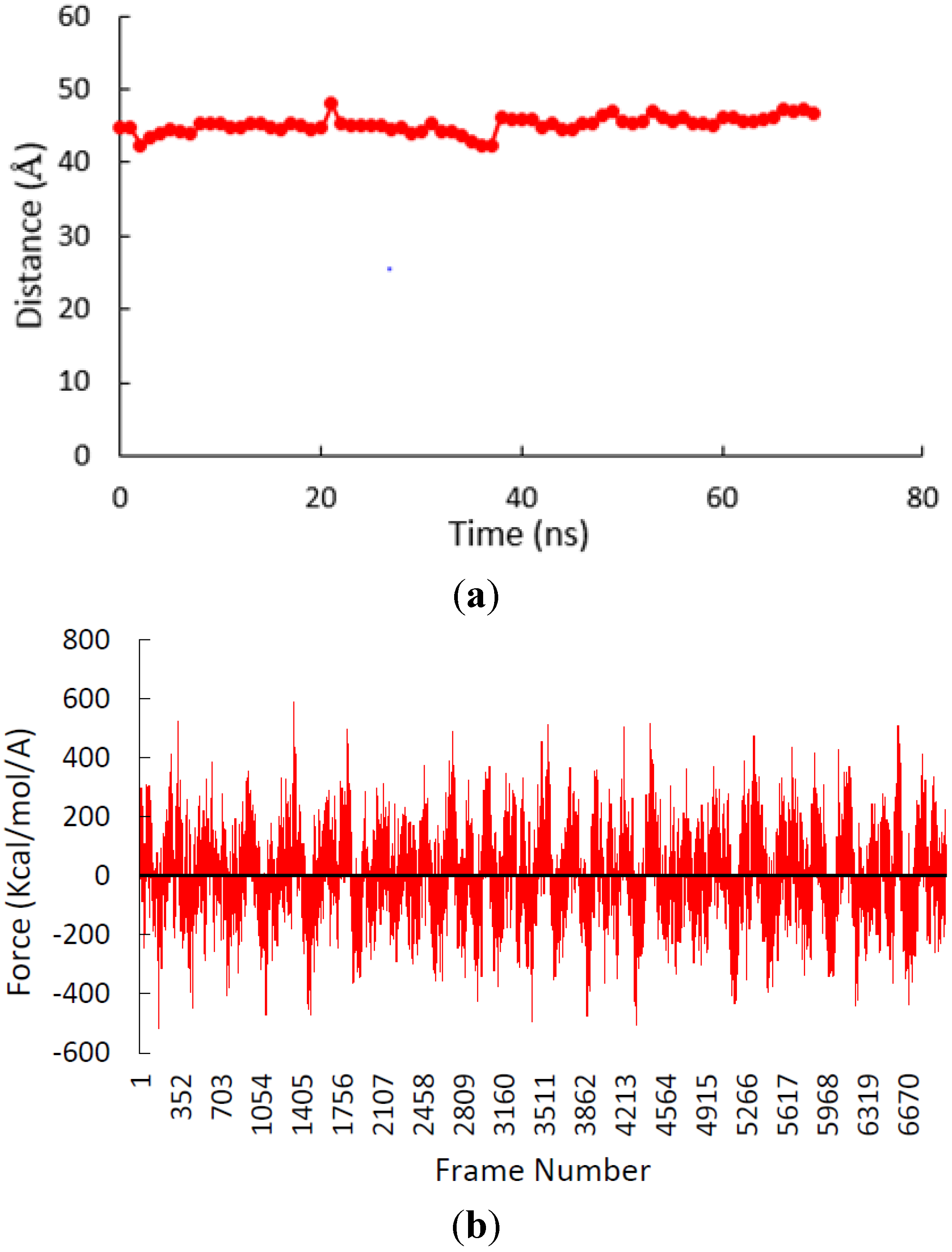
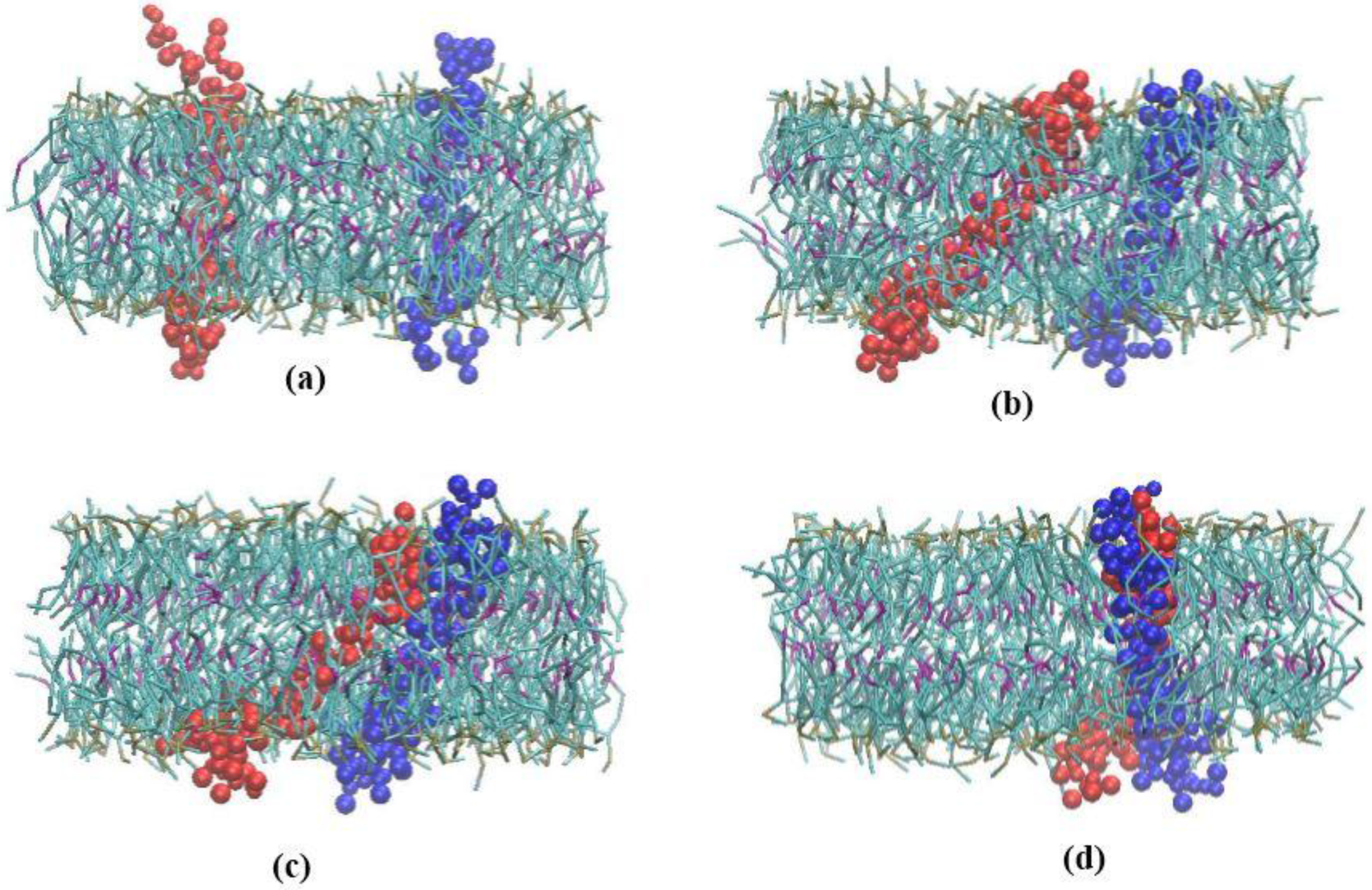
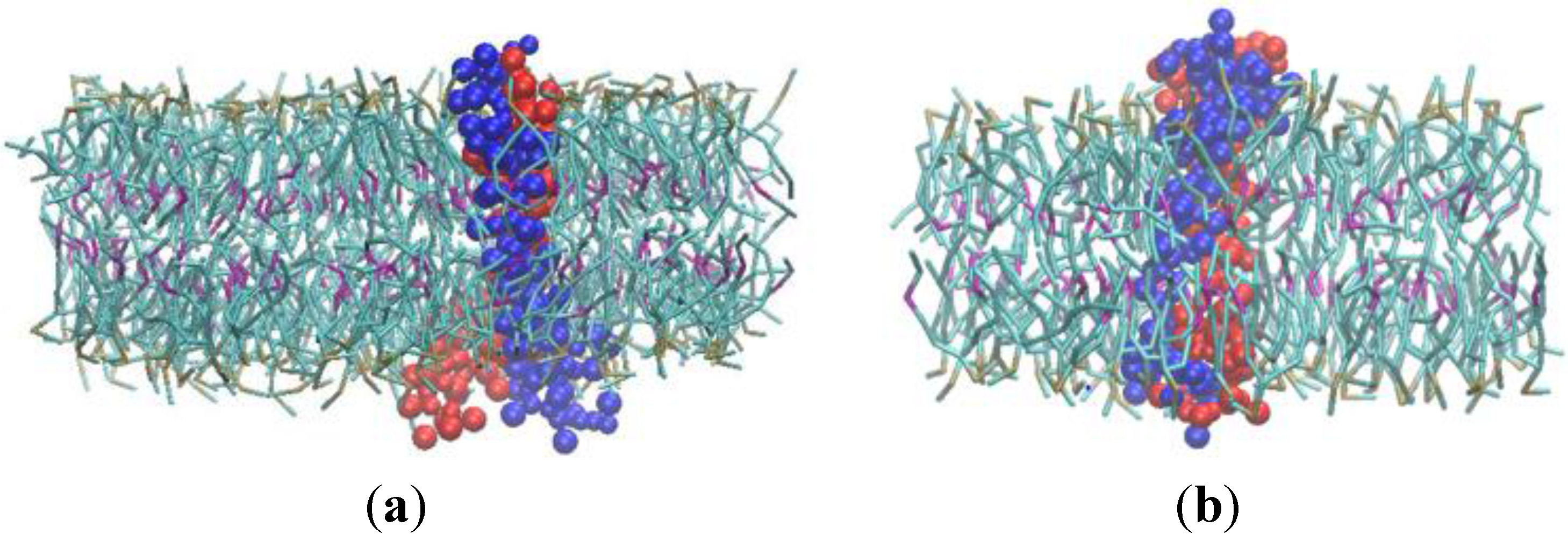
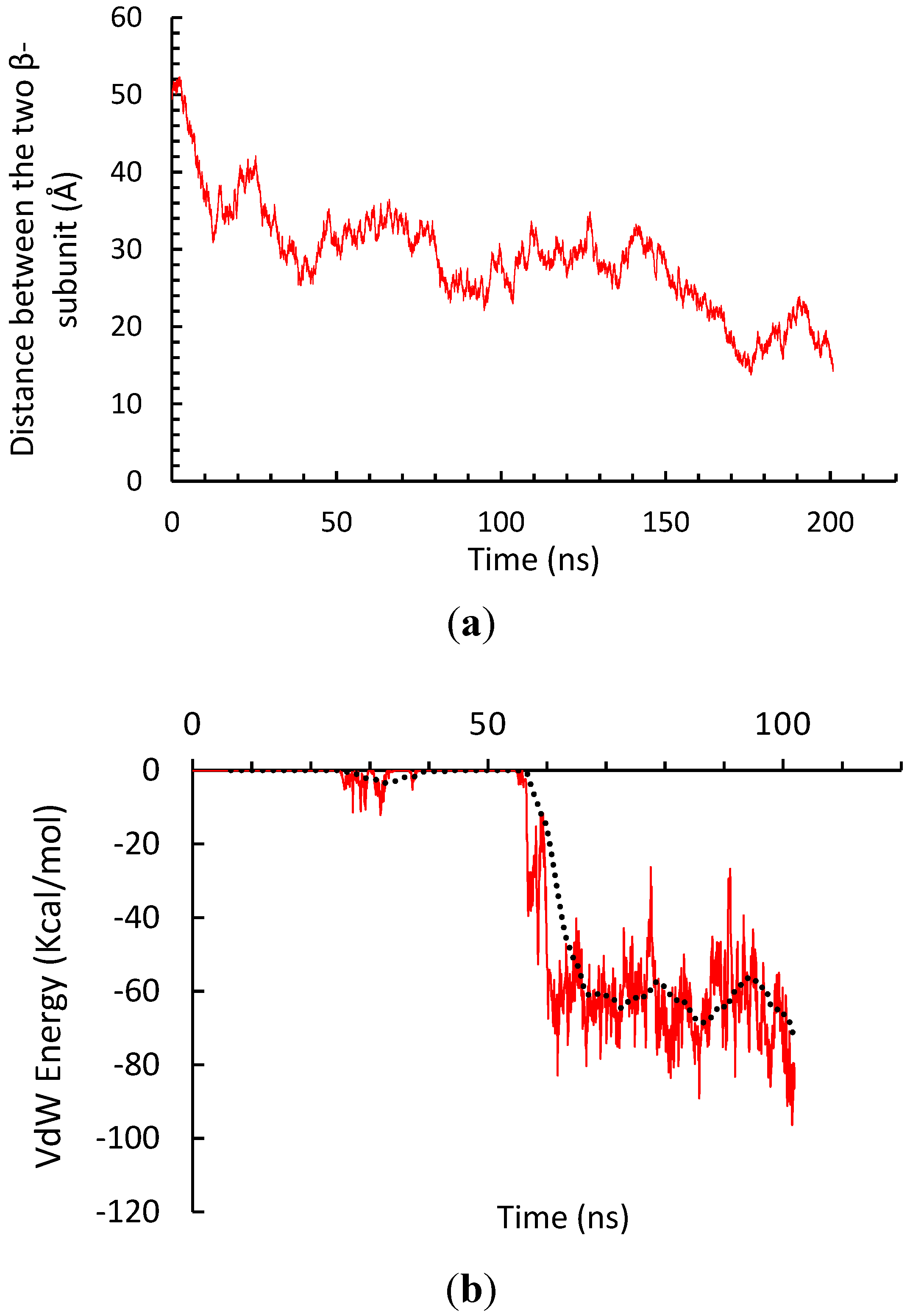
3.2. β-Subunit Homo-Oligomerization Simulations


4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Paszek, M.J.; Boettiger, D.; Weaver, V.M.; Hammer, D.A. Integrin Clustering Is Driven by Mechanical Resistance from the Glycocalyx and the Substrate. PLoS Comput. Biol. 2009. [Google Scholar] [CrossRef] [PubMed]
- Schneider, D.; Engelman, D.M. Involvement of transmembrane domain interactions in signal transduction by α/β integrins. J. Biol. Chem. 2004, 279, 9840–9846. [Google Scholar] [CrossRef] [PubMed]
- Alberts, B.; Bray, D.; Lewis, J.; Raff, M.; Roberts, K.; Watson, J.D. Molecular Biology of the Cell; Garland Publishing: New York, NY, USA, 1994; pp. 139–194. [Google Scholar]
- Ginsberg, M.H.; Partridge, A.; Shattil, S.J. Integrin regulation. Curr. Opin. Cell Biol. 2005, 17, 509–516. [Google Scholar] [CrossRef] [PubMed]
- Kim, C.; Kim, M.-C. Differences in α–β transmembrane domain interactions among integrins enable diverging integrin signaling. Biochem. Biophys. Res. Commun. 2013, 436, 406–412. [Google Scholar] [CrossRef] [PubMed]
- Srichai, M.B.; Zent, R. Integrin structure and function. In Cell-Extracellular Matrix Interactions in Cancer; Springer: New York, NY, USA, 2010; pp. 19–41. [Google Scholar]
- Shamloo, A.; Nikbin, E.; Mehboudi, N.; Damirchi, B. Homo-oligomerization of transmembrane α-domain of integrin. In Proceedings of the 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Chicago, IL, USA, 26–30 August 2014.
- Nelson, D.L.; Lehninger, A.L.; Cox, M.M. Lehninger Principles of Biochemistry; Macmillan: New York, NY, USA, 2008. [Google Scholar]
- Zilly, F.E.; Halemani, N.D.; Walrafen, D.; Spitta, L.; Schreiber, A.; Jahn, R.; Lang, T. Ca2+ induces clustering of membrane proteins in the plasma membrane via electrostatic interactions. EMBO J. 2011, 30, 1209–1220. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Zhu, J.; Springer, T.A.; Luo, B.H. Tests of integrin transmembrane domain homo-oligomerization during integrin ligand binding and signaling. J. Biol. Chem. 2011, 286, 1860–1867. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Babu, C.R.; Lear, J.D.; Wand, A.J.; Bennett, J.S.; DeGrado, W.F. Oligomerization of the integrin αIIbβ3: Roles of the transmembrane and cytoplasmic domains. Proc. Natl. Acad. Sci. USA 2001, 98, 12462–12467. [Google Scholar] [CrossRef] [PubMed]
- Mehrbod, M.; Mofrad, M.R. Localized lipid packing of transmembrane domains impedes integrin clustering. PLoS Comput. Biol. 2013, 9. [Google Scholar] [CrossRef] [PubMed]
- Kalli, A.C.; Hall, B.A.; Campbell, I.D.; Sansom, M.S. A helix heterodimer in a lipid bilayer: Prediction of the structure of an integrin transmembrane domain via multiscale simulations. Structure 2011, 19, 1477–1484. [Google Scholar] [CrossRef] [PubMed]
- Chng, C.-P.; Yang, L.-W. Coarse-grained models reveal functional dynamics–II. molecular dynamics simulation at the coarse-grained level–theories and biological applications. Bioinform. Biol. Insights 2008, 2, 171–185. [Google Scholar] [PubMed]
- Chng, C.P.; Tan, S.M. Leukocyte integrin αLβ2 transmembrane association dynamics revealed by coarse-grained molecular dynamics simulations. Proteins Struct. Funct. Bioinform. 2011, 79, 2203–2213. [Google Scholar] [CrossRef] [PubMed]
- Marrink, S.J.; Risselada, H.J.; Yefi mov, S.; Tieleman, D.P.; de Vries, A.H. The MARTINI force-field: Coarse grained model for biomolecular simulations. J. Phys. Chem. B 2007, 111, 7812–7824. [Google Scholar] [CrossRef] [PubMed]
- Voth, G.A. Coarse-Graining of Condensed Phase and Biomolecular Systems; CRC Press/Taylor and Francis Group: Boca Raton, FL, USA, 2009. [Google Scholar]
- Marrink, S.J.; de Vries, A.H.; Mark, A.E. Coarse grained model for semiquantitative lipid simulations. J. Phys. Chem. 2004, 108, 750–760. [Google Scholar] [CrossRef]
- Brouillette, C.; Anantharamaiah, G. Structural models of human apolipoprotein A-I. Biochim. Biophys. Acta 1995, 1256, 103–129. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD—Visual Molecular Dynamics. J. Mol. Graphics 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Lodish, H. Molecular Cell Biology; Macmillan: New York, NY, USA, 2008. [Google Scholar]
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kale, L.; Schulten, K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shamloo, A.; Golgoon, A.; Zadeh, E.G. Role of α and β Transmembrane Domains in Integrin Clustering. Actuators 2015, 4, 267-280. https://doi.org/10.3390/act4040267
Shamloo A, Golgoon A, Zadeh EG. Role of α and β Transmembrane Domains in Integrin Clustering. Actuators. 2015; 4(4):267-280. https://doi.org/10.3390/act4040267
Chicago/Turabian StyleShamloo, Amir, Ashkan Golgoon, and Ebrahim Ghafar Zadeh. 2015. "Role of α and β Transmembrane Domains in Integrin Clustering" Actuators 4, no. 4: 267-280. https://doi.org/10.3390/act4040267
APA StyleShamloo, A., Golgoon, A., & Zadeh, E. G. (2015). Role of α and β Transmembrane Domains in Integrin Clustering. Actuators, 4(4), 267-280. https://doi.org/10.3390/act4040267






