Nonlinear Dynamic Modeling of Langevin-Type Piezoelectric Transducers †
Abstract
:1. Introduction

2. Theoretical Background
2.1. Nonlinear Constitutive Equations
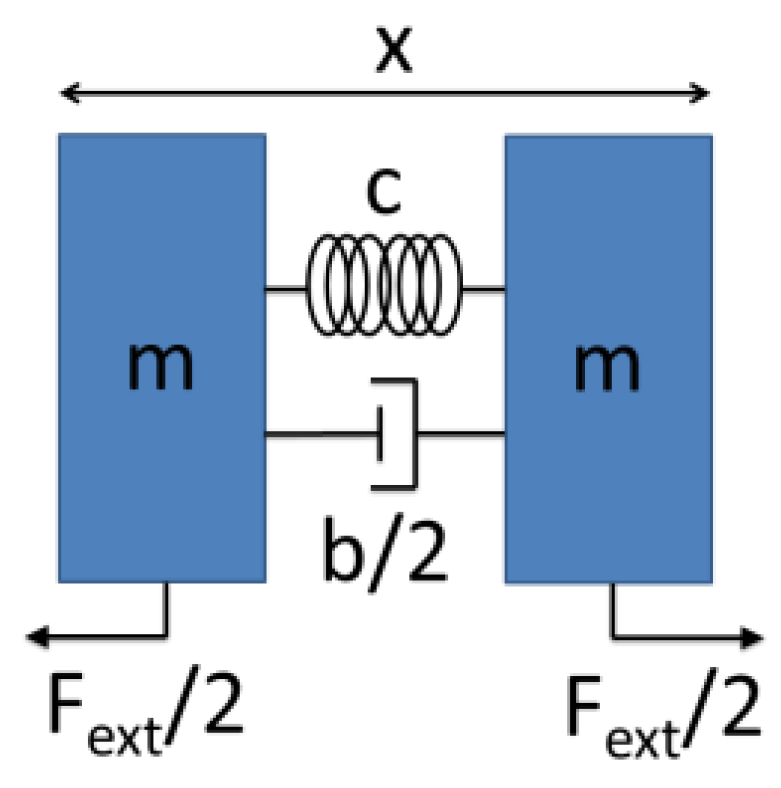
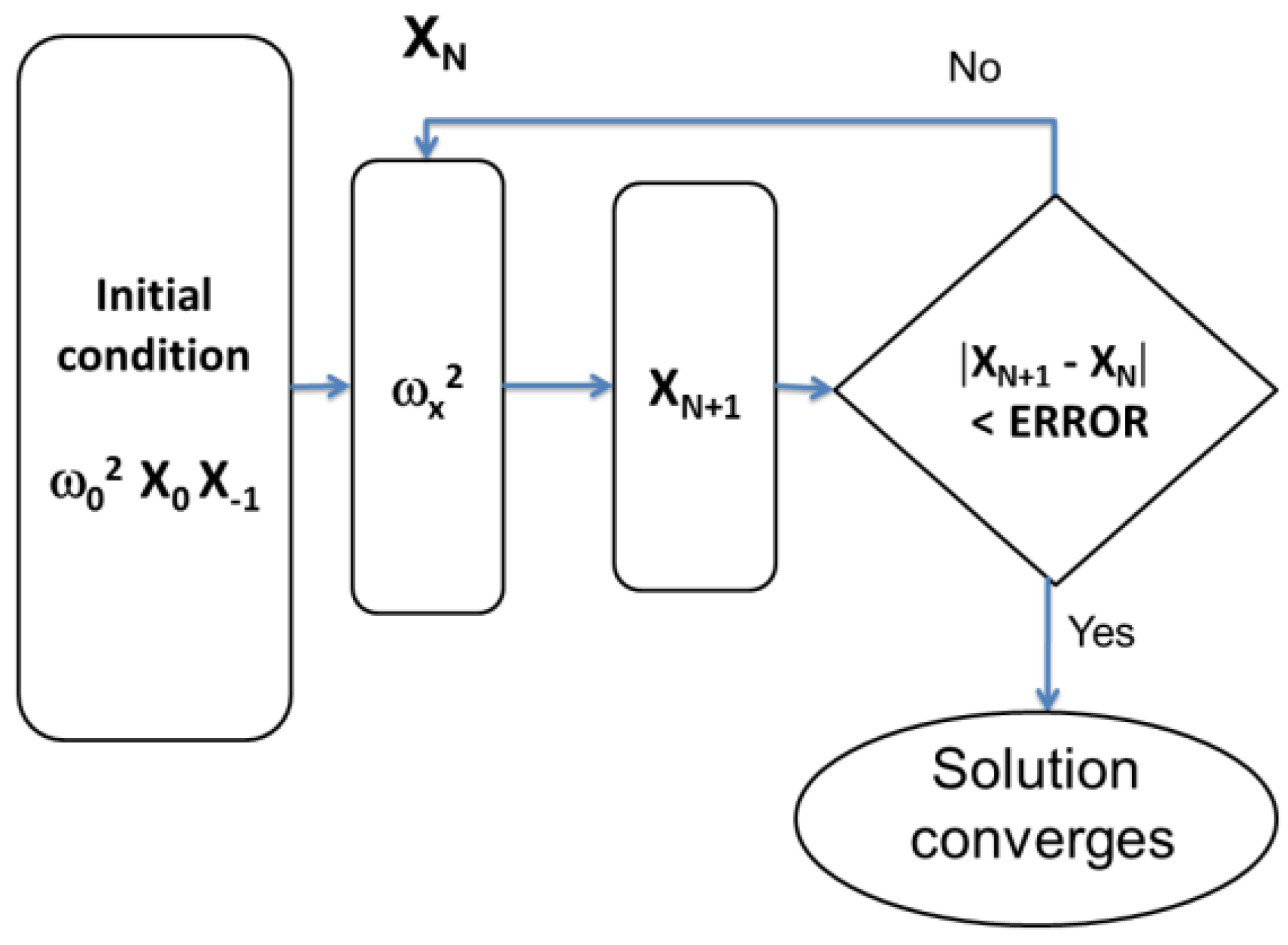
2.2. Nonlinear Model of the Langevin Transducer
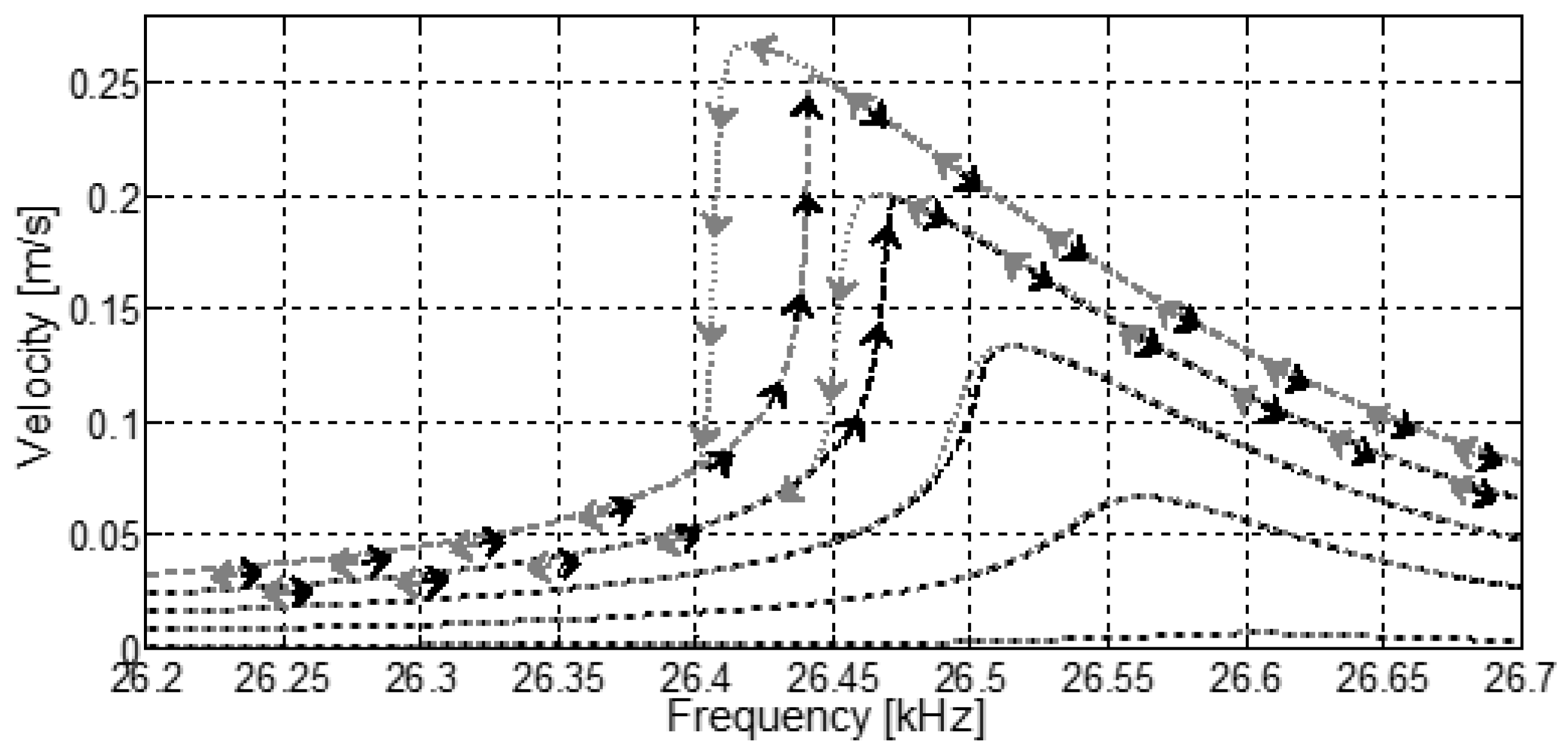
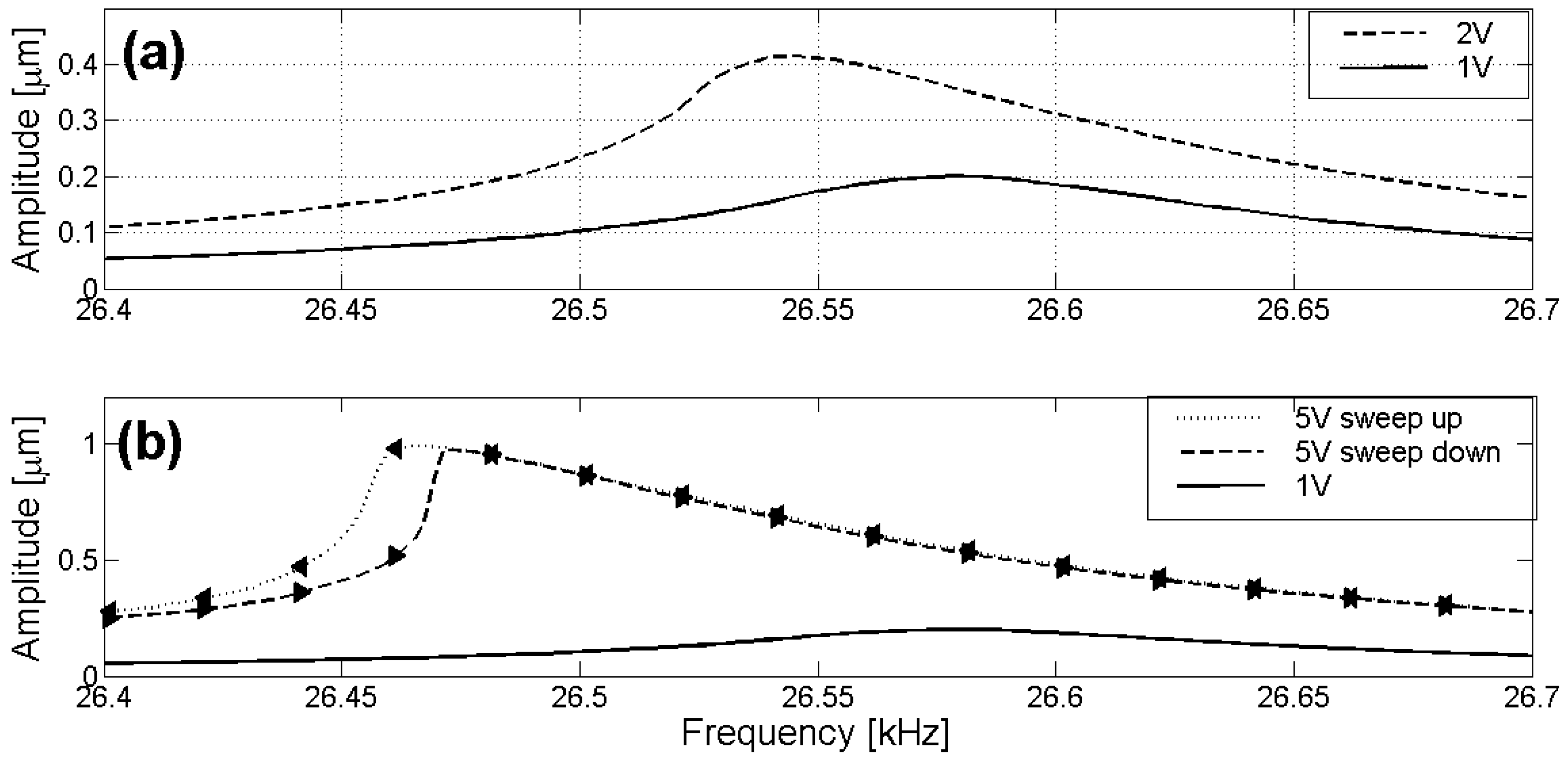
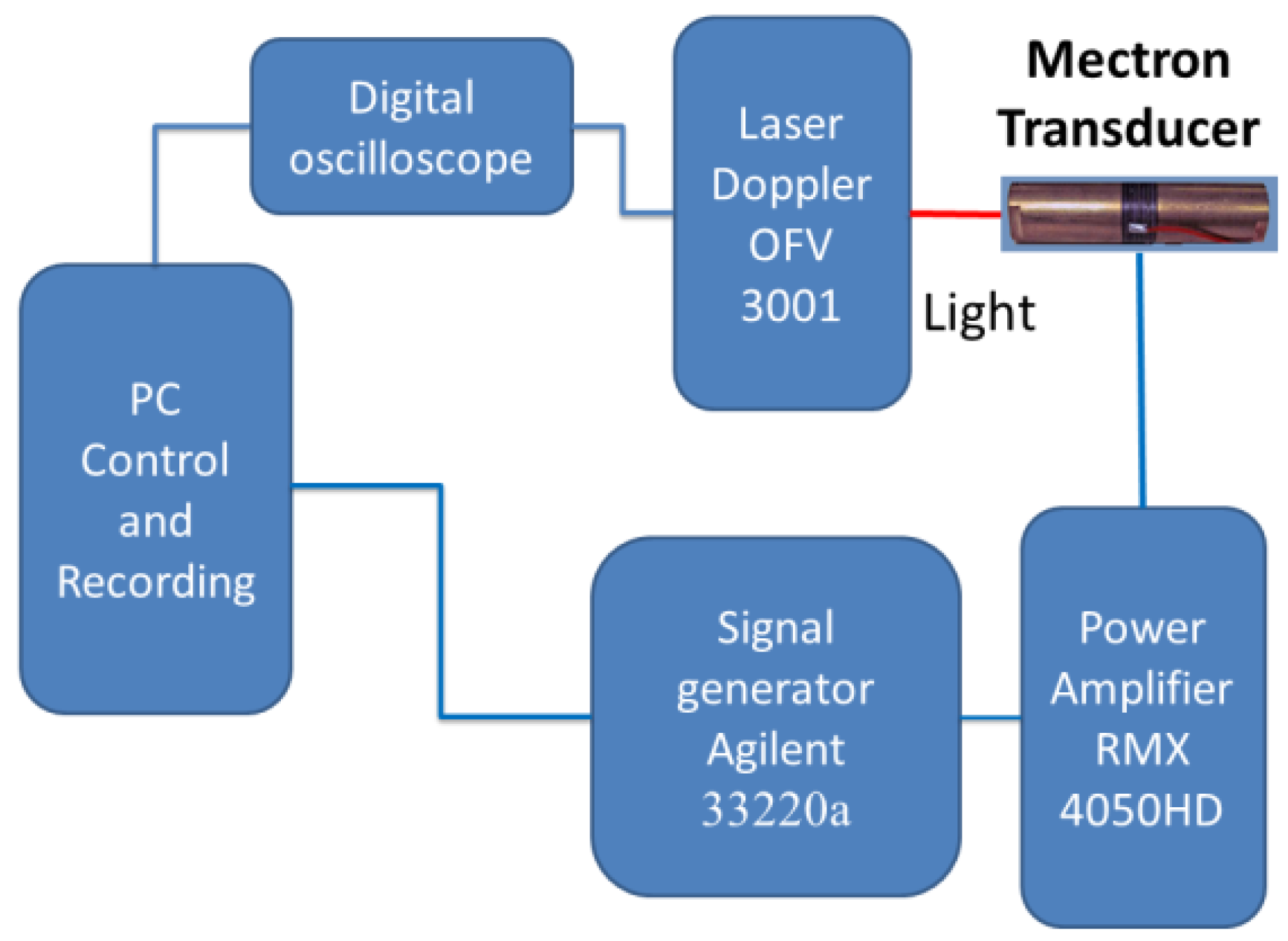
3. Experimental Results
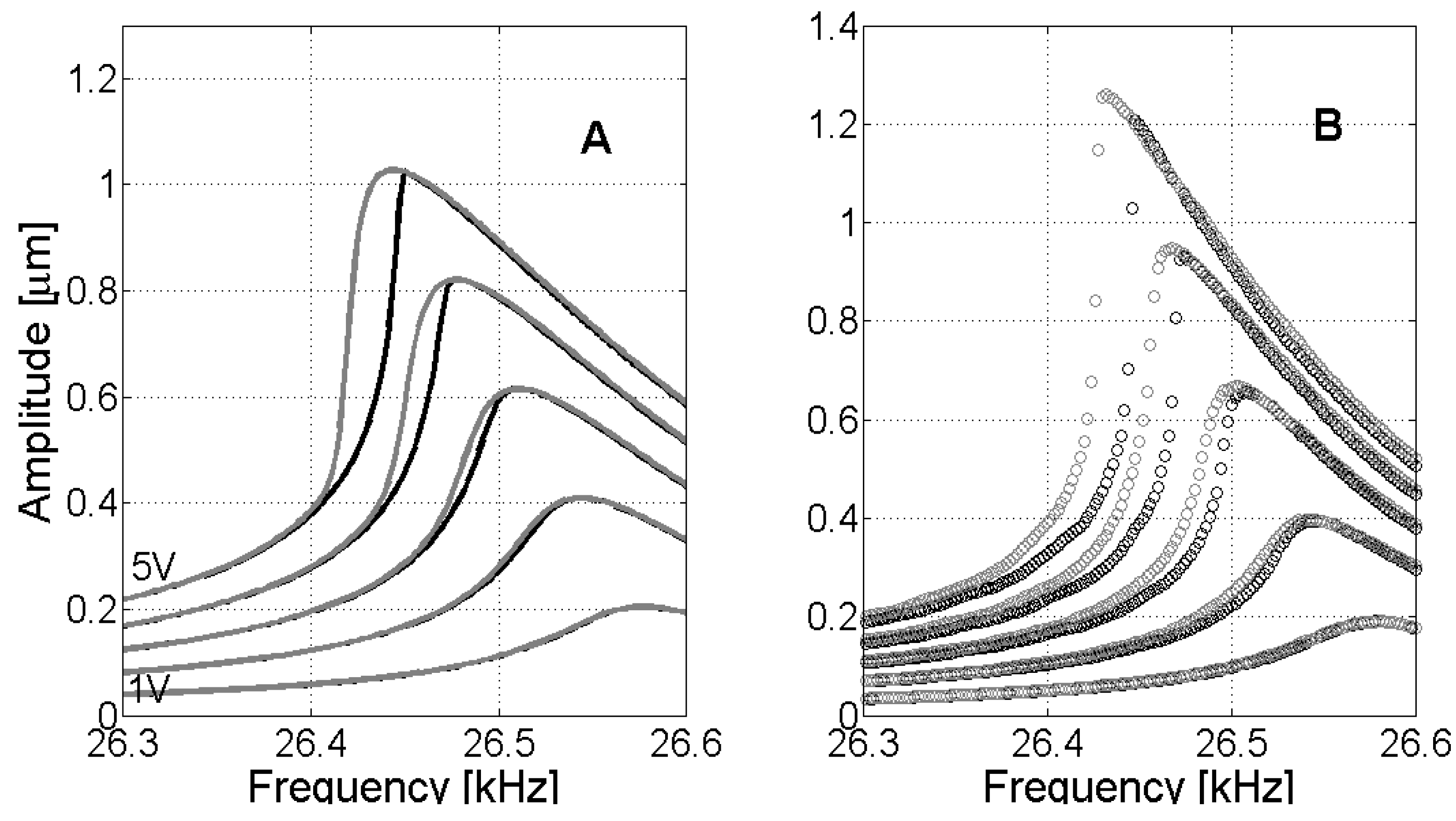
| Experimental | Numerical | |||||
|---|---|---|---|---|---|---|
| Voltage [V] | Maximum Displacement Amplitude [μm] | Frequency of Maximum Displacement [kHz] | Hysteresis [Hz] | Frequency of Maximum Displacement [kHz] | Maximum Displacement Amplitude [μm] | Hysteresis [Hz] |
| 1 | 0.19 | 26.580 | 0.25 | 26.577 | 0.20 | 1 |
| 2 | 0.40 | 26.544 | 7 | 26.543 | 0.41 | 3 |
| 3 | 0.67 | 26.502 | 12 | 26.510 | 0.61 | 7 |
| 4 | 0.95 | 26.467 | 15 | 26.477 | 0.82 | 14 |
| 5 | 1.26 | 26.431 | 20 | 26.444 | 1.03 | 20 |
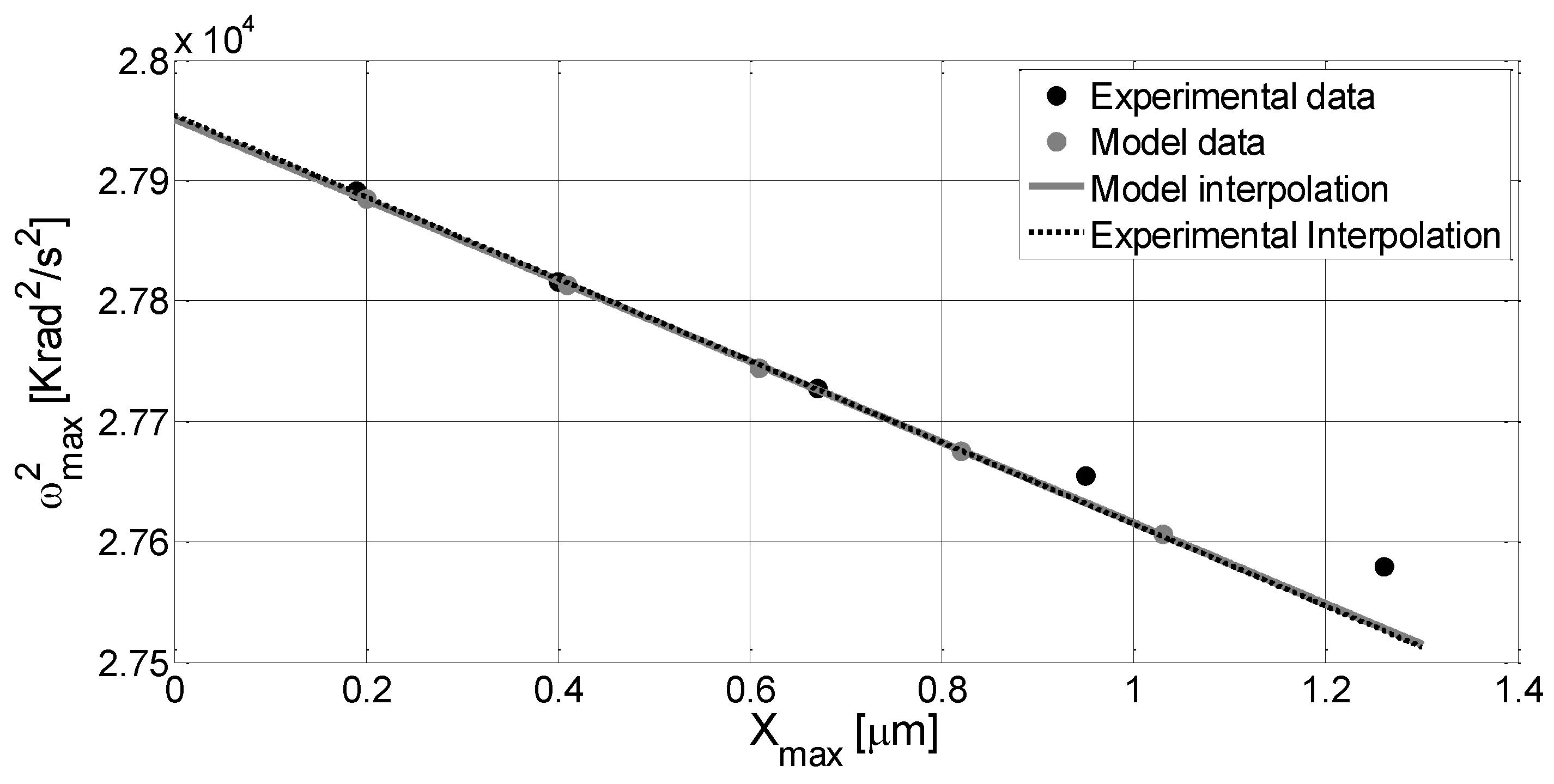
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Iula, A.; Lamberti, N.; Pappalardo, M. An approximated 3-D model of cylinder-shaped piezoceramic elements for transducer design. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 1998, 45, 1056–1064. [Google Scholar] [CrossRef] [PubMed]
- Lasky, M. Review of undersea acoustics to 1950. J. Acoust. Soc. Am. 1977, 61, 283–297. [Google Scholar] [CrossRef]
- Gallego-Juárez, J.A.; Rodriguez, G.; Acosta, V.; Riera, E. Power ultrasonic transducers with extensive radiators for industrial processing. Ultrason. Sonochem. 2010, 6, 953–964. [Google Scholar] [CrossRef] [PubMed]
- Iula, A.; Parenti, L.; Fabrizi, F.; Pappalardo, M. A high displacement ultrasonic actuator based on a flexural mechanical amplifier. Sens. Actuators A Phys. 2006, 135, 118–123. [Google Scholar] [CrossRef]
- Alvareda, A.; Pérez, R.; Casals, J.A.; García, J.E.; Ochoa, D. Optimization of elastic nonlinear behavior measurements of ceramic piezoelectric resonators with burst excitation. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2007, 54, 2175–2188. [Google Scholar] [CrossRef]
- Umeda, M.; Nakamura, K.; Takahashi, S.; Ueha, S. An Analysis of Jumping and Dropping Phenomena of Piezoelectric Transducers using the Electrical Equivalent Circuit Constants at High Vibration Amplitude Levels. Jpn. J. Appl. Phys. 2000, 39, 5623–5628. [Google Scholar] [CrossRef]
- Guyomar, D.; Aurelle, N.; Eyraud, L. Piezoelectric Ceramics Nonlinear Behavior. Application to Langevin Transducer. J. Phys. III 1997, 7, 1197–1208. [Google Scholar] [CrossRef]
- Guyomar, D.; Aurelle, N.; Richard, C.; Gonnard, P.; Eyraud, L. Nonlinear behaviour of an ultrasonic transducer. Ultrasonics 1996, 34, 187–191. [Google Scholar]
- Hall, D.A. Nonlinearity in piezoelectric ceramics. J. Mater. Sci. 2001, 36, 4575–4601. [Google Scholar] [CrossRef]
- Blackburn, J.; Cain, M. Nonlinear piezoelectric resonance: A theoretically rigorous approach to constant I−V measurements. J. Appl. Phys. 2006, 100. [Google Scholar] [CrossRef]
- Blackburn, J.; Cain, M. Non-linear piezoelectric resonance analysis using burst mode: A rigorous solution. J. Phys. D Appl. Phys. 2006, 40, 227–233. [Google Scholar] [CrossRef]
- Guyomar, D.; Ducharne, B.; Sebald, G. High nonlinearities in Langevin transducer: A comprehensive model. Ultrasonics 2011, 51, 1006–1013. [Google Scholar] [CrossRef] [PubMed]
- Pérez, N.; Franceschetti, N.; Adamowski, J.C. Effects of Nonlinearities in Power Ultrasonic Transducers Using Time Reversal Focalization. Phys. Proc. 2010, 3, 161–167. [Google Scholar] [CrossRef]
- Pérez, N.; Franceschetti, N.; Buiochi, F.; Adamowski, J.C. Short pulse characterization of nonlinearities in power ultrasound transducers. ABCM Symp. Ser. Mechatron. 2010, 4, 793–801. [Google Scholar]
- Pérez, N.; Andrade, M.A.B.; Buiochi, F.; Adamowski, J.C. Nonlinear Iterative Model for Langevin Ultrasonic Transducers. In Proceedings of the Internoise, Lisboa, Portugal, 13–15 June 2010.
- Merkeer, T. Standards on Piezoelectricity 176–1987. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1996, 43, 717–772. [Google Scholar]
- Rayleigh, L. On the behavior of iron and steel under the operation of feeble magnetic forces. Phil. Mag. 1887, 23, 225–245. [Google Scholar] [CrossRef]
- Damjanovic, D.; Demartin, M. The Rayleigh law in piezoelectric ceramics. J. Phys. D Appl. Phys. 1996, 29, 2057–2060. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A simplex-method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alvarez, N.P.; Cardoni, A.; Cerisola, N.; Riera, E.; Andrade, M.A.B.; Adamowski, J.C. Nonlinear Dynamic Modeling of Langevin-Type Piezoelectric Transducers. Actuators 2015, 4, 255-266. https://doi.org/10.3390/act4040255
Alvarez NP, Cardoni A, Cerisola N, Riera E, Andrade MAB, Adamowski JC. Nonlinear Dynamic Modeling of Langevin-Type Piezoelectric Transducers. Actuators. 2015; 4(4):255-266. https://doi.org/10.3390/act4040255
Chicago/Turabian StyleAlvarez, Nicolás Peréz, Andrea Cardoni, Niccolo Cerisola, Enrique Riera, Marco Aurélio Brizzotti Andrade, and Julio Cezar Adamowski. 2015. "Nonlinear Dynamic Modeling of Langevin-Type Piezoelectric Transducers" Actuators 4, no. 4: 255-266. https://doi.org/10.3390/act4040255
APA StyleAlvarez, N. P., Cardoni, A., Cerisola, N., Riera, E., Andrade, M. A. B., & Adamowski, J. C. (2015). Nonlinear Dynamic Modeling of Langevin-Type Piezoelectric Transducers. Actuators, 4(4), 255-266. https://doi.org/10.3390/act4040255







