Force-Sensing Actuator with a Compliant Flexure-Type Joint for a Robotic Manipulator
Abstract
:1. Introduction
- High-performance mechanics improve the level of dexterity related to the mechanical structure; control-wise and minimum friction leads to an enhanced stability and fine manipulation capability [16].
- Joint torques are transmitted back as a resistive torque to the DC motor shaft, which can be measured by current sensing [17]. This permits one to estimate external forces exploiting the actuators as sensors, thus improving the dexterity related to the sensory apparatus.
- The resulting mathematical model of the physical behavior of the finger enables alternative strategies to control the mechanical compliance of the finger.
- As additional advantages of the self-sensing approach, the absence of force sensors means wiring simplification, avoidance of sensor drift and reduction of the number of components.
2. Design Rationale

- the set of directions along which a force applied to the finger can be balanced by the cables (working only under tensile strength and not compression);
- plus, for each of those directions, the maximum value of external force that can be balanced taking into account the output of the actuators used to pull the cables.
3. Motor-to-Joint Transmission
3.1. Tendon-Driven Actuation Principle
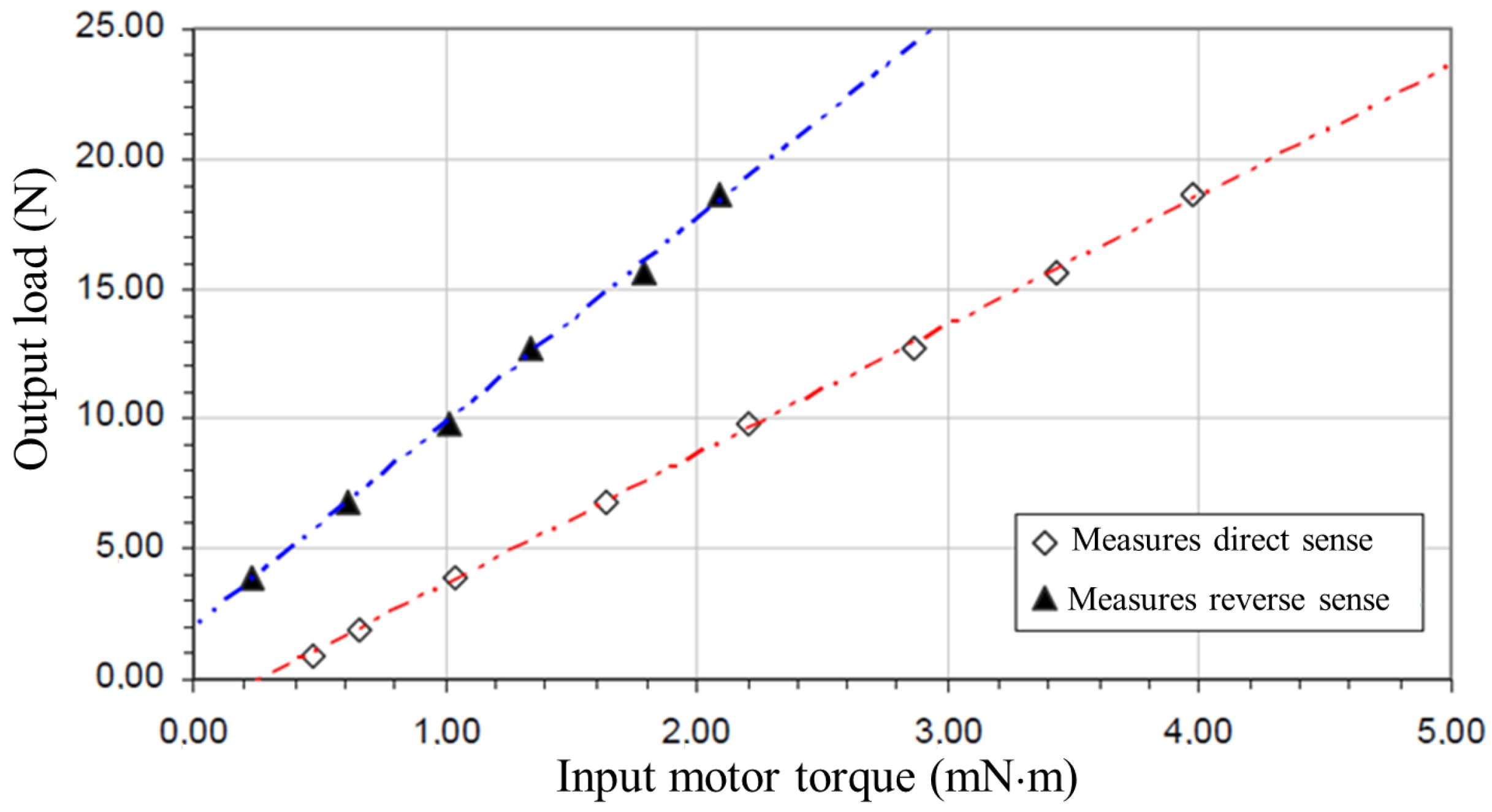
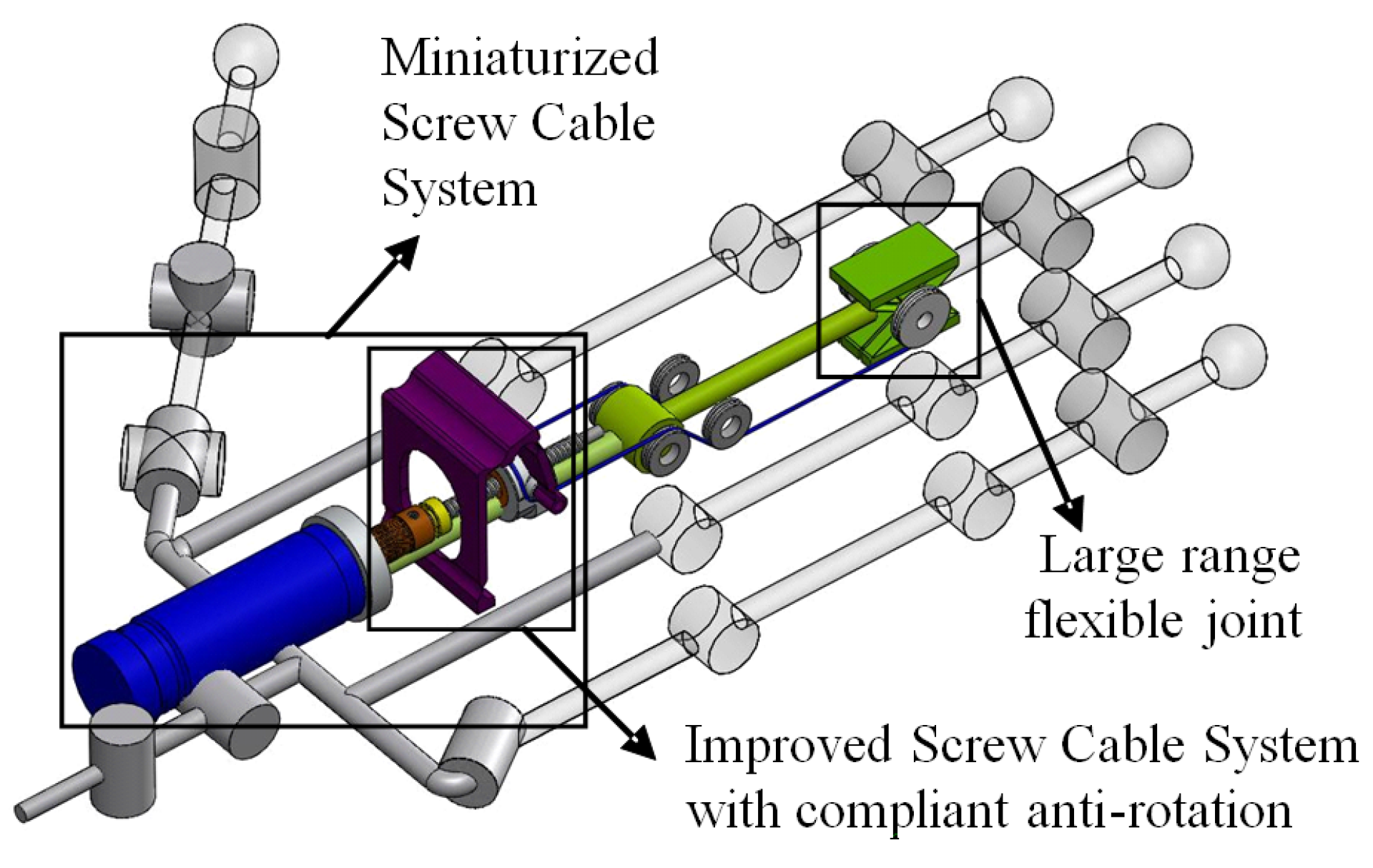
3.2. Monolithic Frictionless Anti-Rotation System
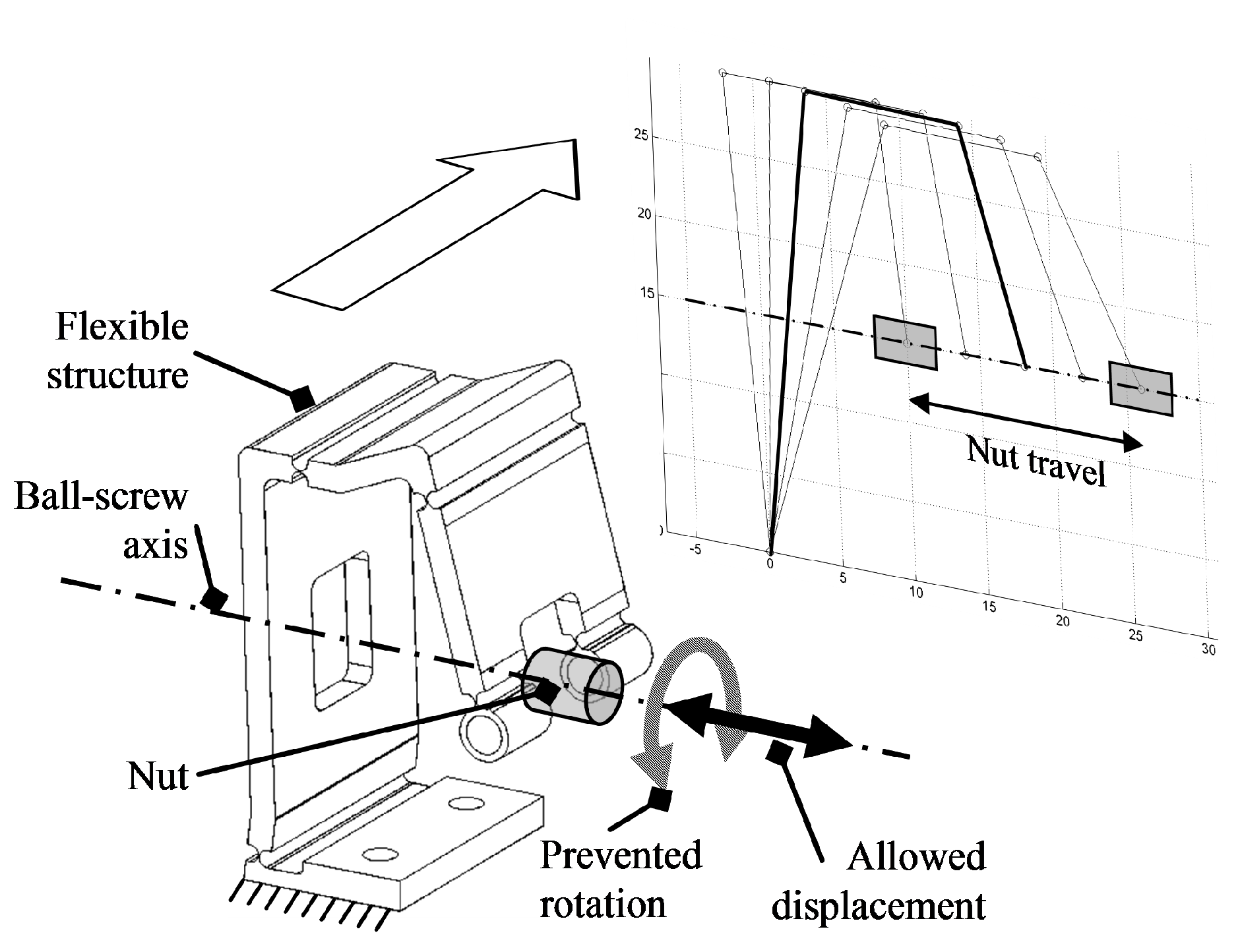
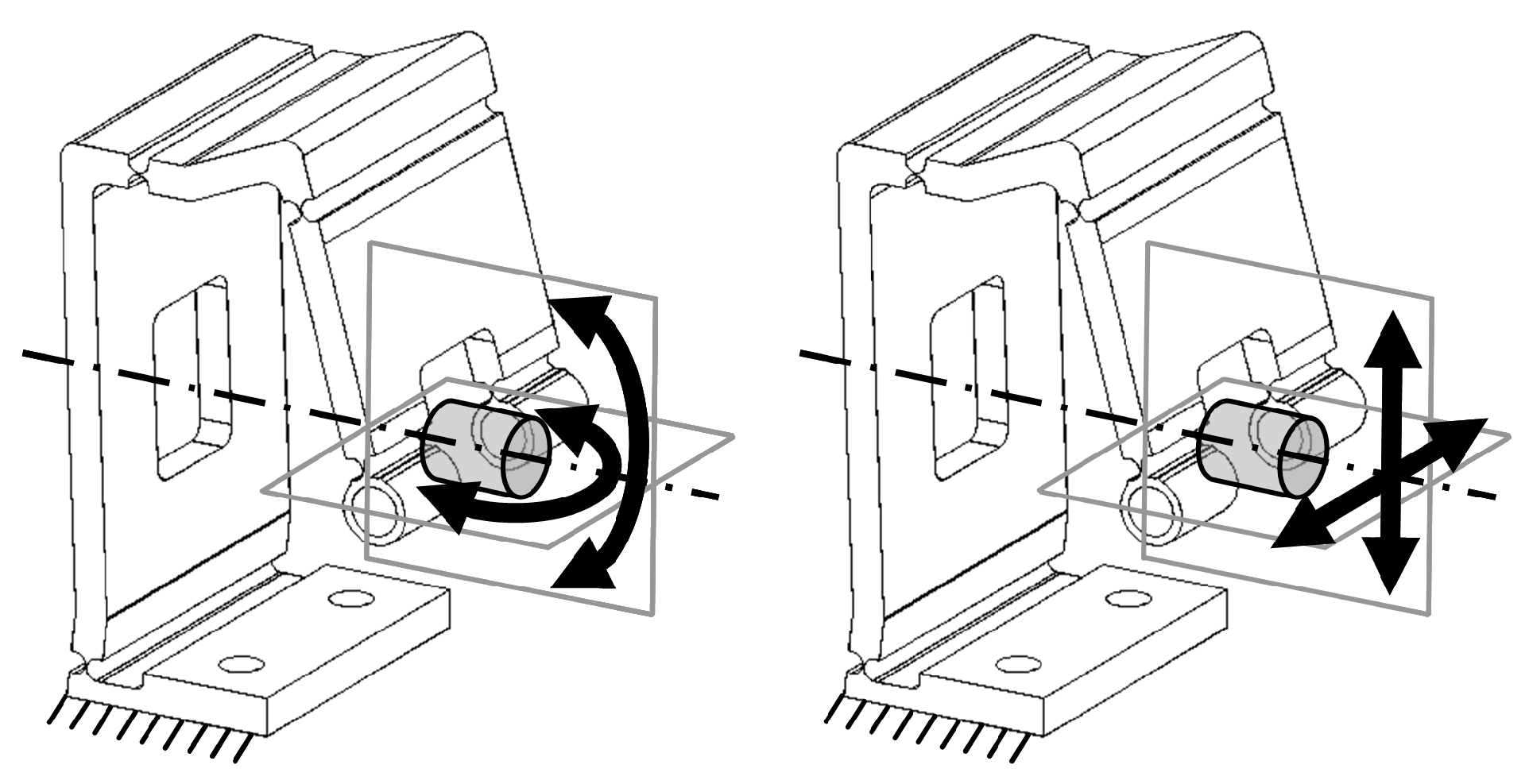
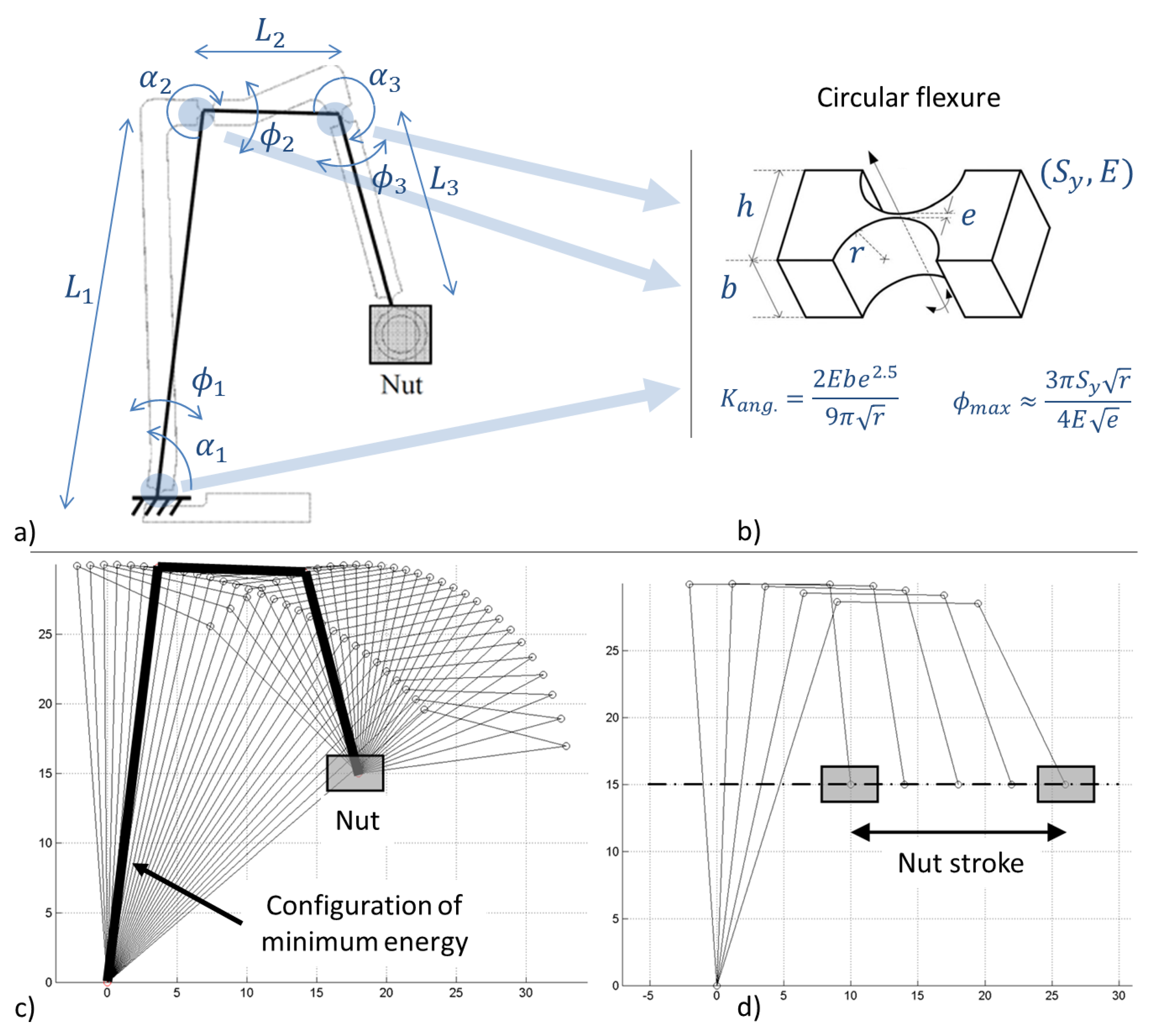
- For each position of the nut in the ball-screw axis, the theoretical configuration of minimum elastic energy of the structure is calculated (Figure 5c);
- For the complete travel of the nut along the ball-screw axis, the previous step permits one to find the successive mechanism configurations, and the total angular displacement of each notch joint is calculated (Figure 5d);
- Parameter values ( and for ) minimizing the largest angular displacement among the three joints () are chosen;
- Once the angular displacements in the articulations are minimized and known, the parameters of the notch joint (Figure 5b) and the material selection (through its Young’s modulus E and its yield strength ) are specified, taking into account practical criteria regarding the integration of the actuator in a minimum package.

4. Inter-Phalangeal Rotational Joint
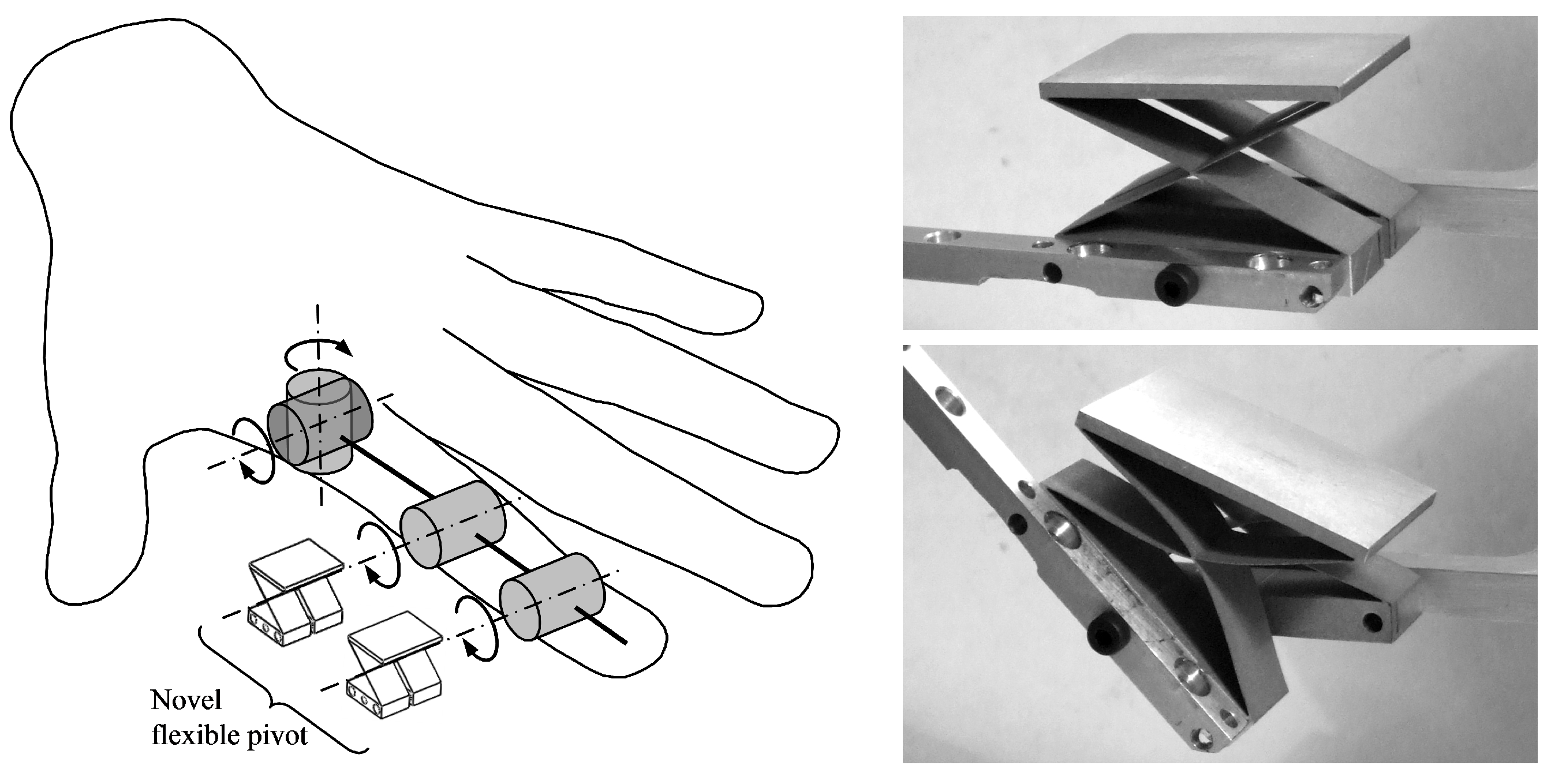
4.1. Concept
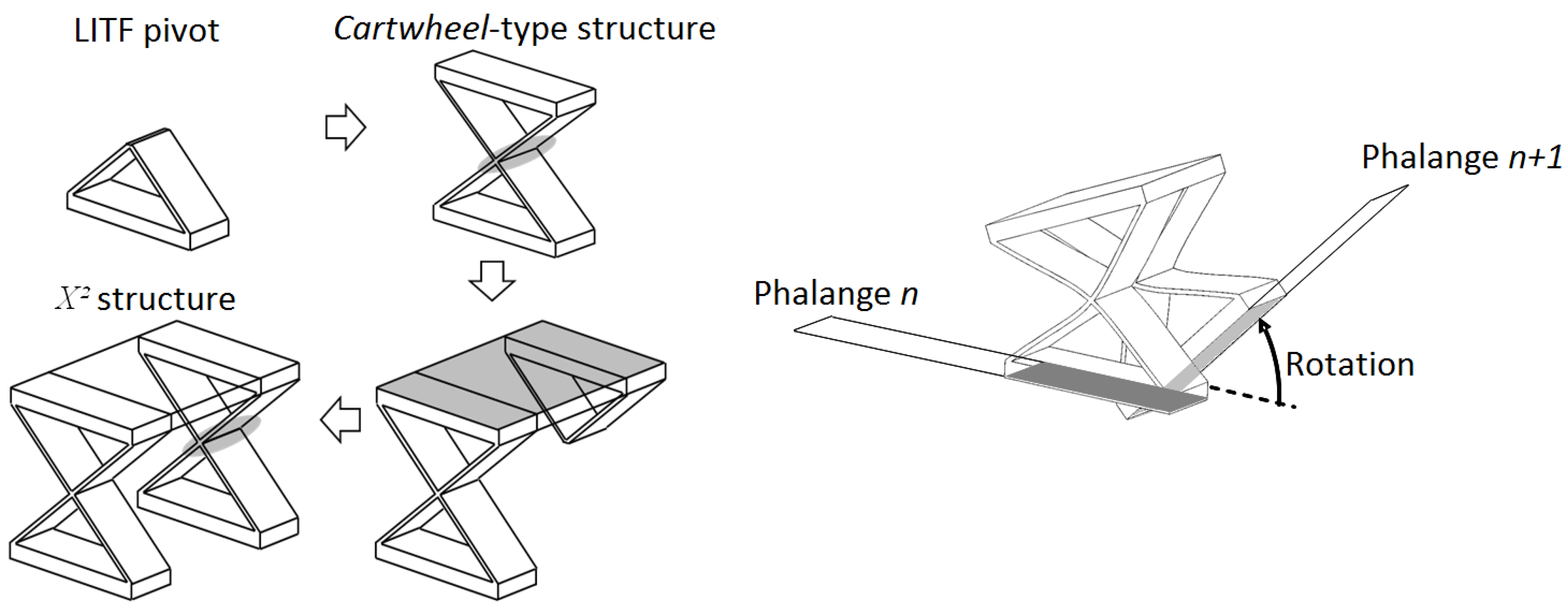
4.2. Design Optimization
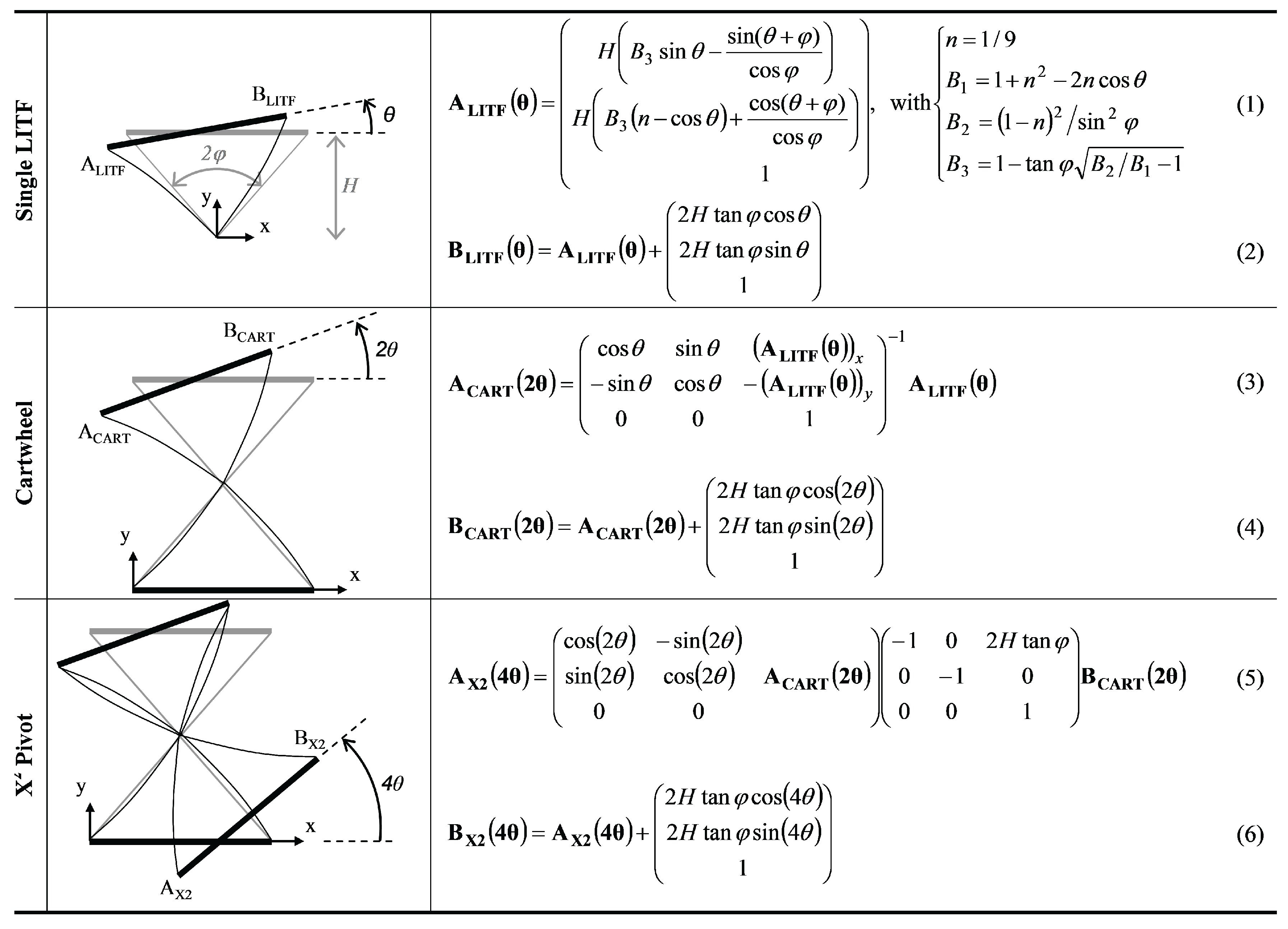
- the two cartwheels that constitute the joint are arranged in a manner that makes their two respective center shift vectors compensate for one another;
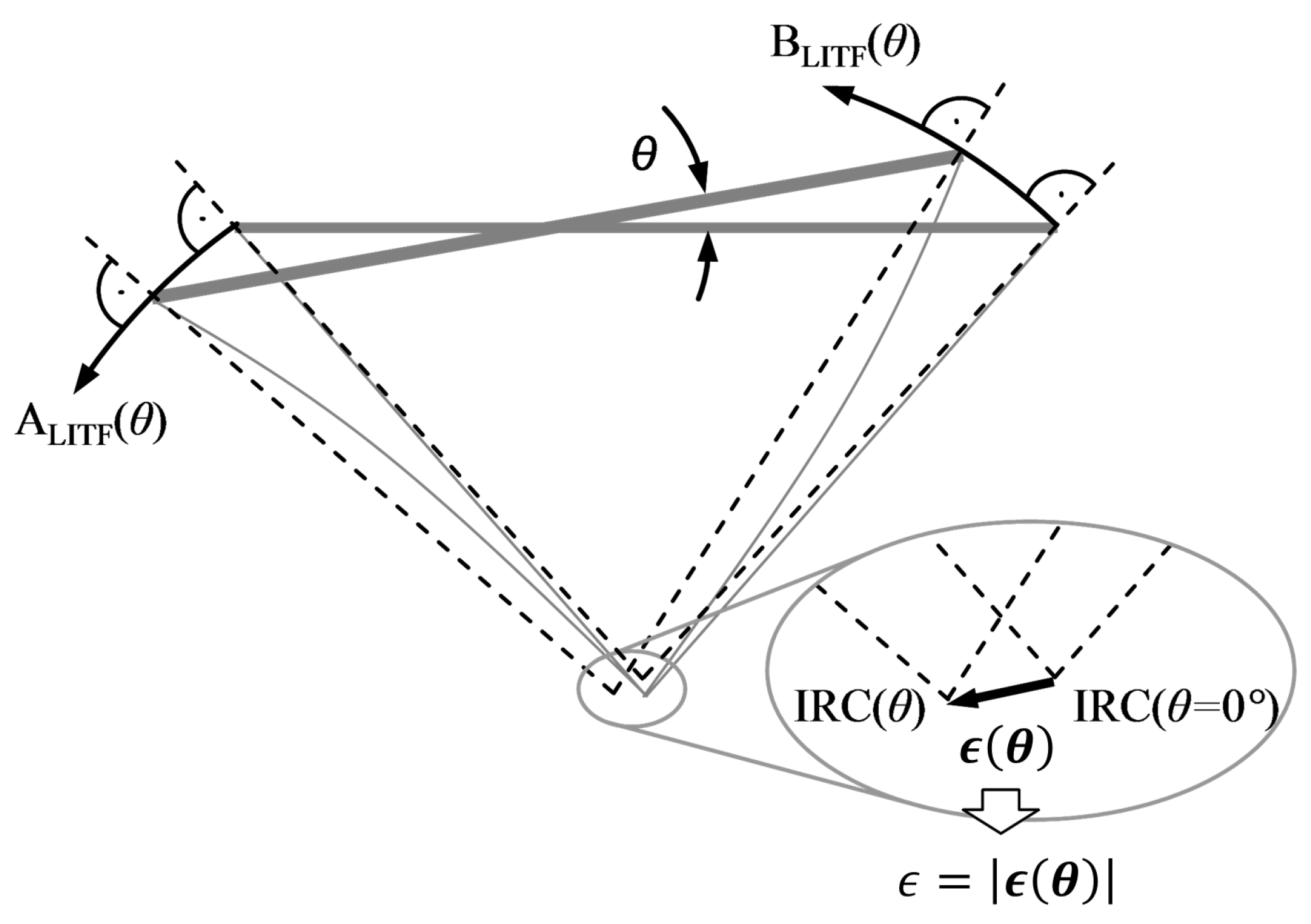
- for a flexible pivot, the value of ϵ increases rapidly with the angular displacement θ; therefore, as the overall displacement θ is distributed into smaller displacements over the two cartwheels, a large reduction of the center shift is achieved for each one.
| Geometry | Performances | ||
|---|---|---|---|
| H | 7 mm | ||
| φ | m | ||
| t | 0.15 mm | m | |
| w | 9 mm | 0.02 Nm/rad | |
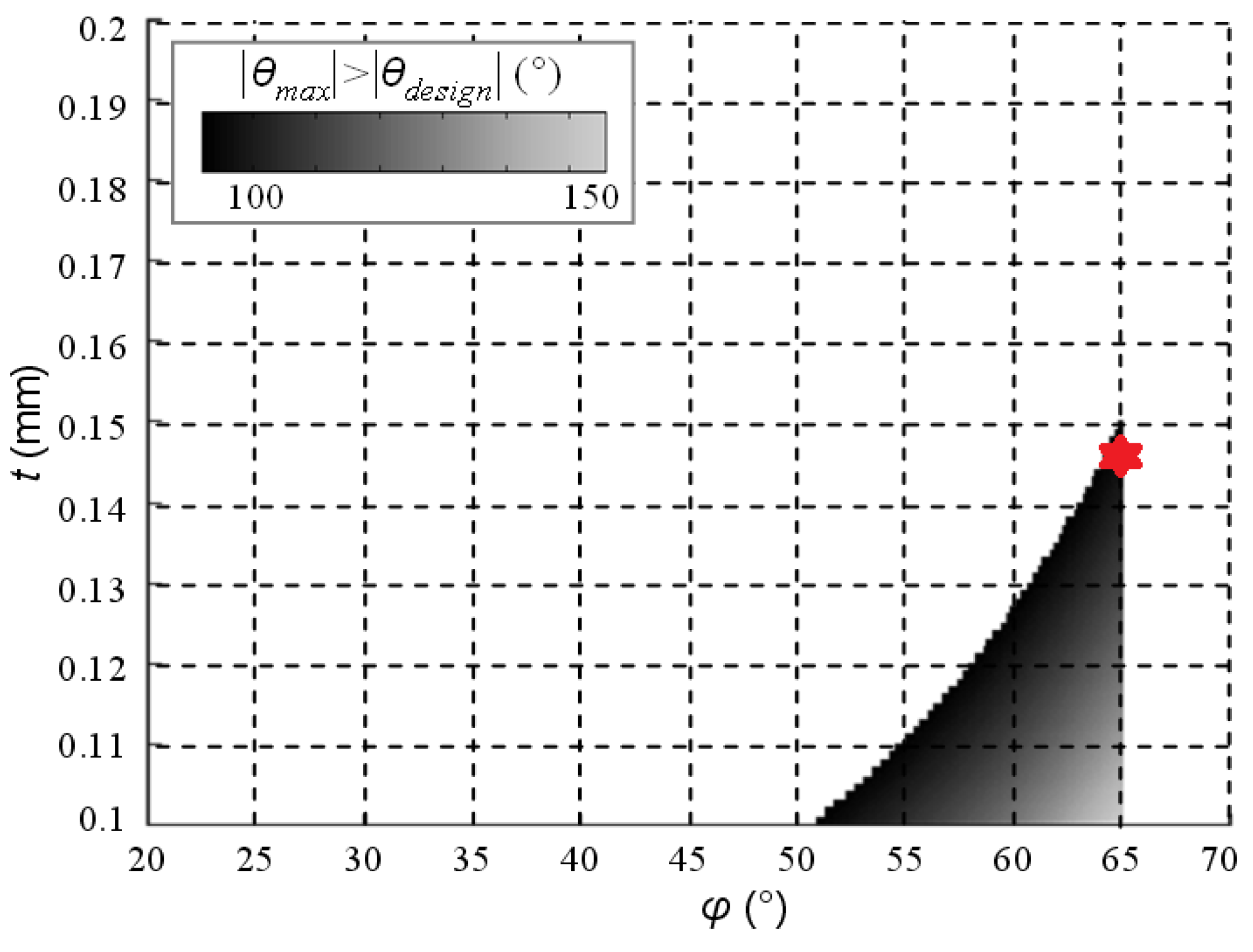
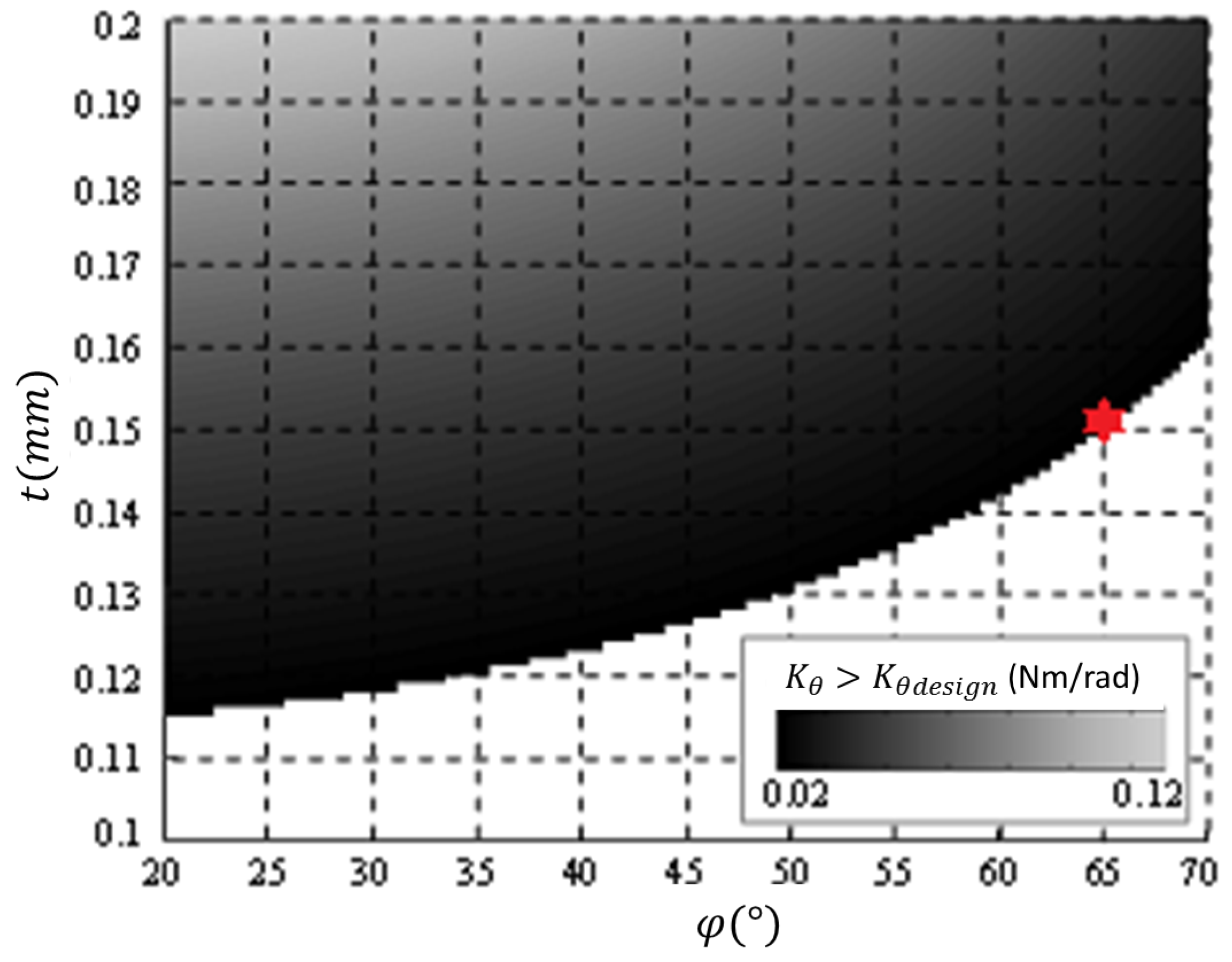
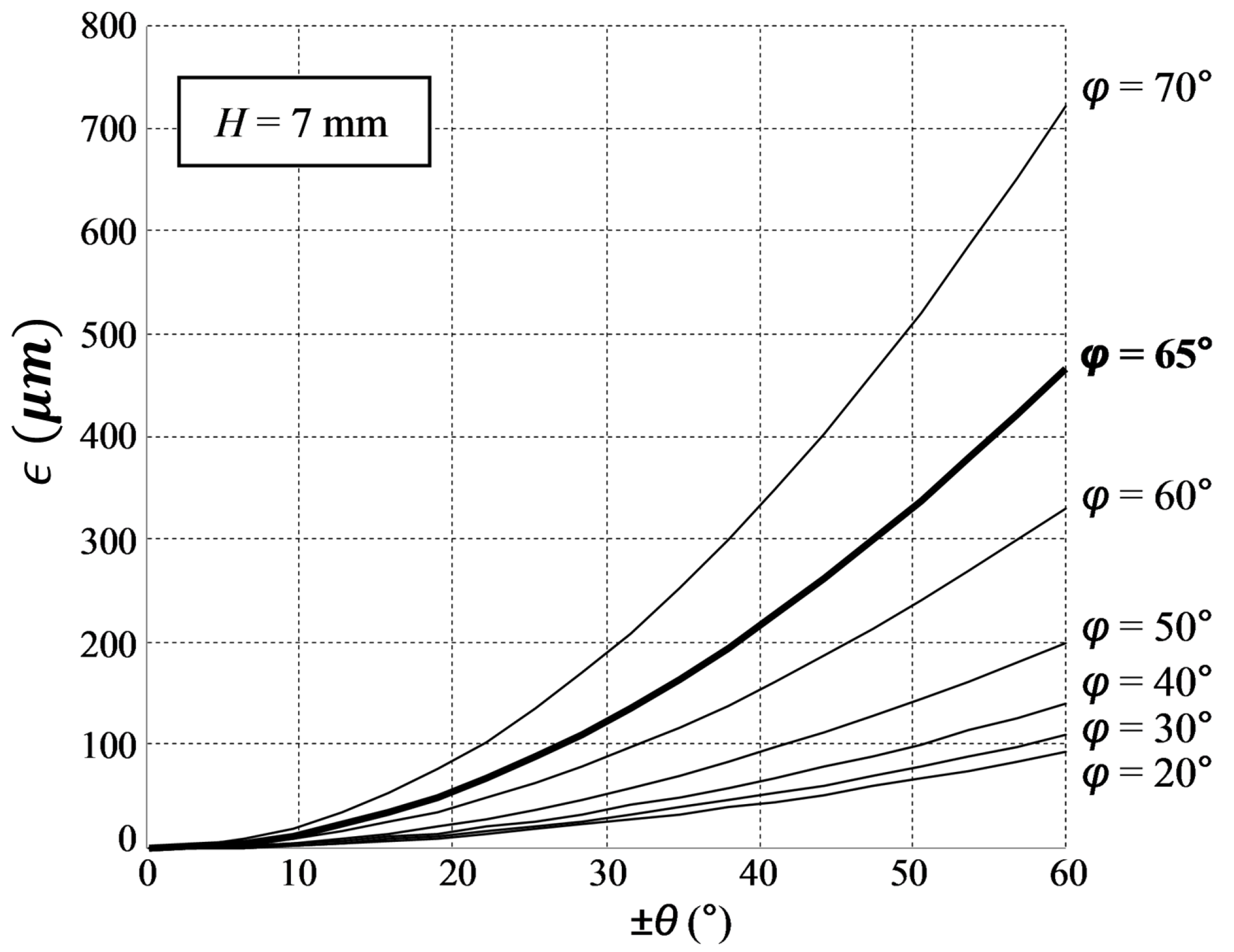
4.3. Experimental Performances
4.3.1. Accuracy of Motion
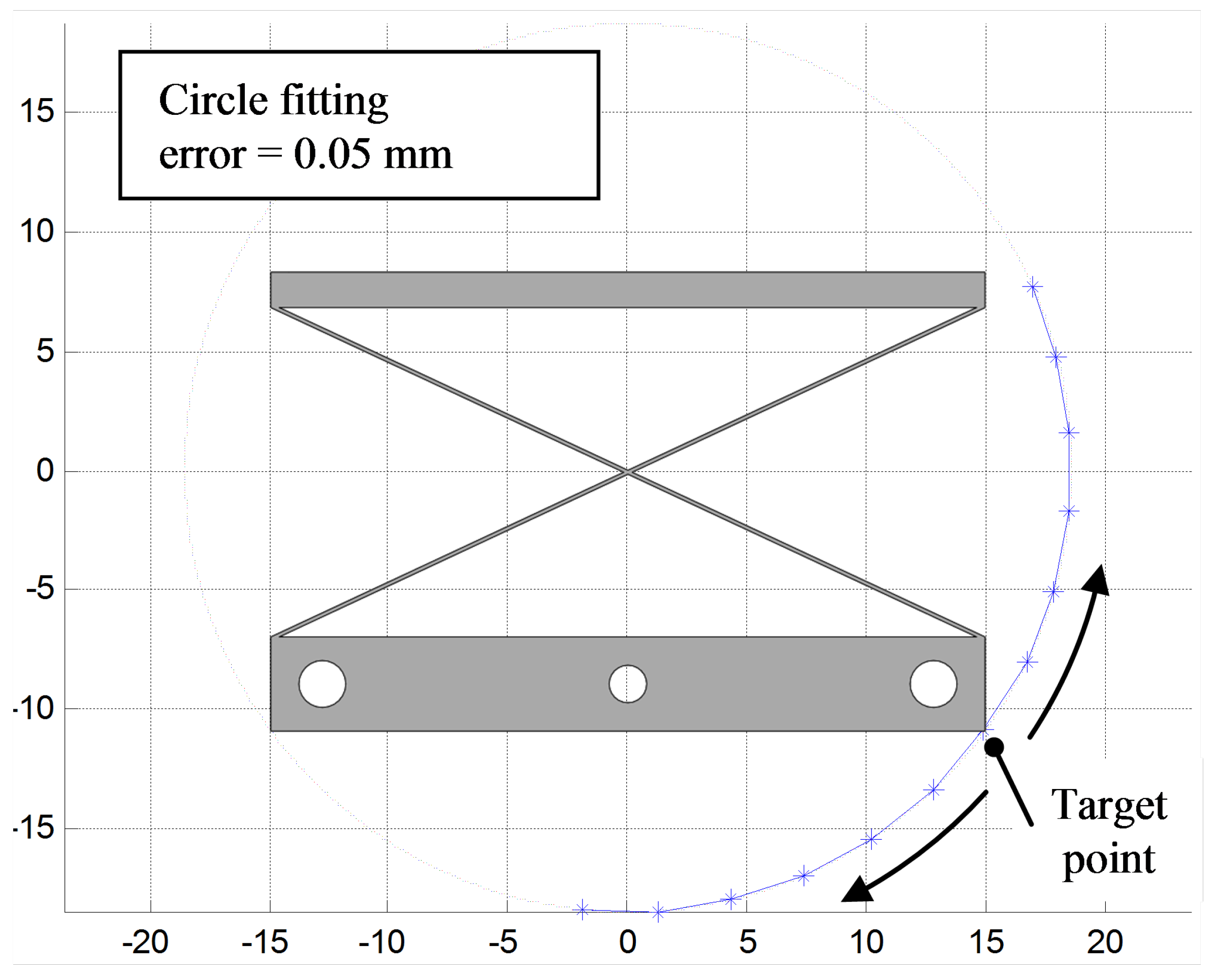
4.3.2. Identification of Pivot Stiffness
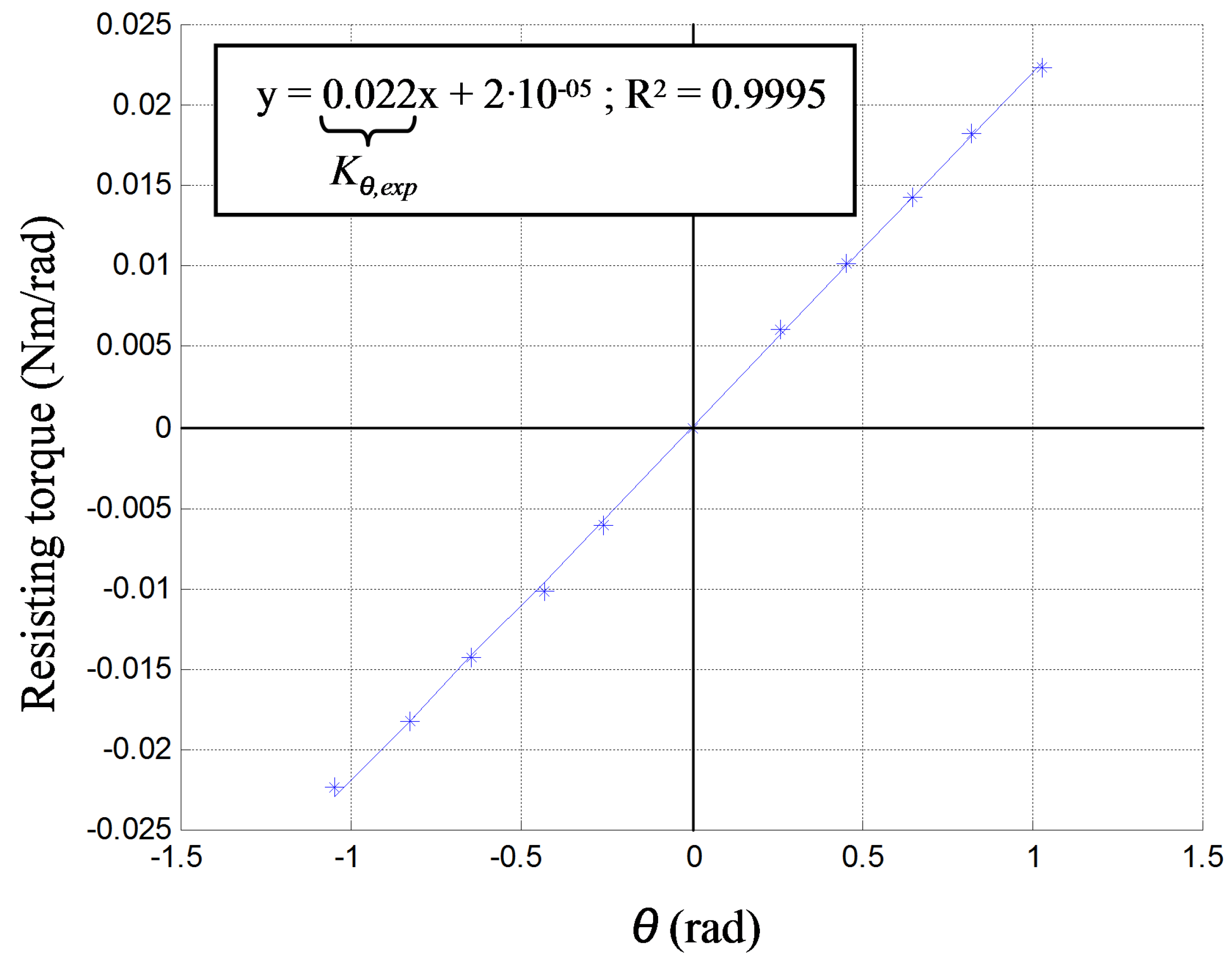
5. Modeling and Self-Sensing Strategy
5.1. Modeling of the Tendon-Based Actuation Principle
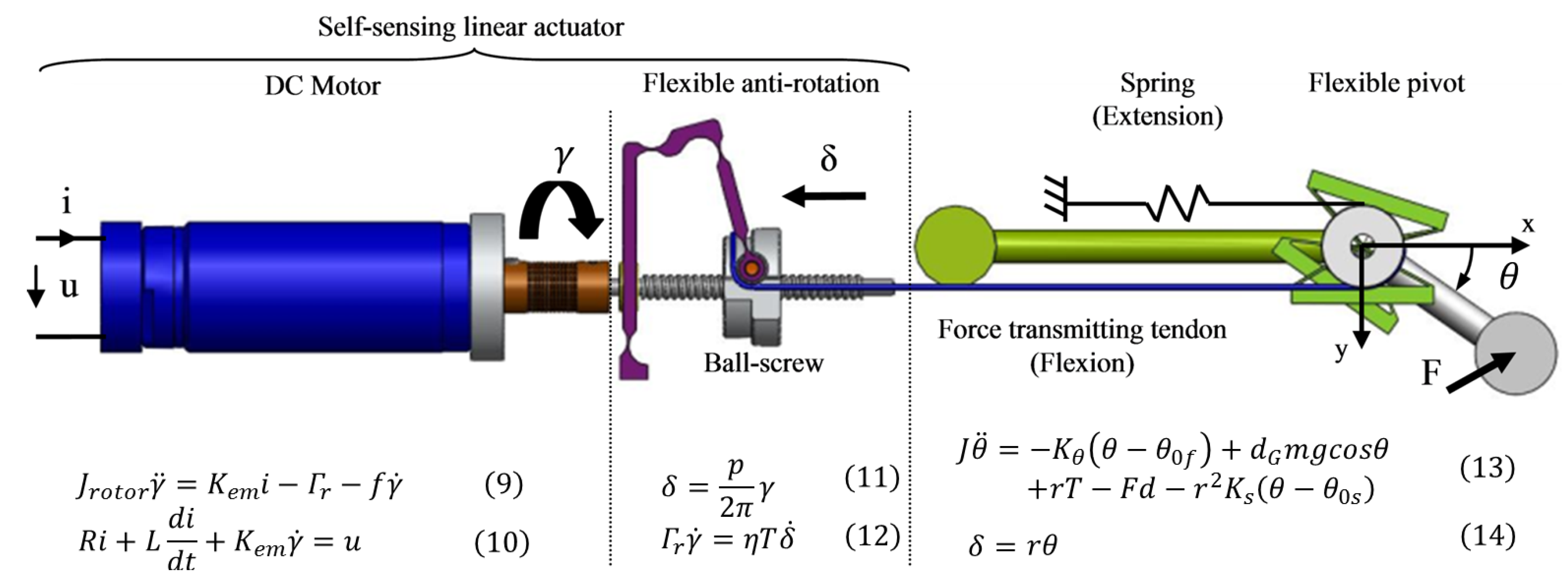
| Parameters | Description |
|---|---|
| Joint angle for relaxed flexible pivot | |
| Joint angle for relaxed extension spring | |
| J | Inertia of flexible pivot and finger |
| m | Mass of flexible pivot and finger |
| g | Gravitational acceleration |
| r | Normal distance between tendon and pivot center |
| Distance between the gravity center and pivot center | |
| d | Distance between the effort application (F) and pivot center |
| Flexible pivot stiffness | |
| Antagonist spring stiffness | |
| p | Screw pitch |
| η | Ball-screw efficiency |
| R | DC motor resistance |
| L | DC motor inductance |
| DC motor constant | |
| DC motor inertia | |
| f | DC motor viscous friction |
5.2. Self-Sensing of External Forces Applied to the Finger

6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Martin Amezaga, J.; Grossard, M. Mechanical flexibility and the design of versatile and dexterous grippers. In Flexible Robotics—Aplications to Multiscale Manipulations; Grossard, M., Regnier, S., Chaillet, N., Eds.; ISTE WILEY: London, UK, 2013; pp. 145–180. [Google Scholar]
- Salisbury, J.K.; Craig, J.J. Articulated Hands: Force Control and Kinematic Issues. Int. J. Robot. Res. 1982, 1, 4–17. [Google Scholar] [CrossRef]
- Hanafusa, H.; Asada, H. Stable Prehension by a Robot Hand with Elastic Fingers. In Proceedings of the 7th International Symposium on Industrial Robots, Tokyo, Japan, 19–21 October 1997; pp. 361–368.
- Soto Martell, J.W.; Gini, G. Robotic hands: Design review and proposal of new design process. Int. J. Appl. Math. Comput. Sci. 2007, 4, 587–592. [Google Scholar]
- Chalon, M.; Grebenstein, M.; Wimbock, T.; Hirzinger, G. The thumb: Guidelines for a robotic design. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 5886–5893.
- Ueda, J.; Kondo, M.; Ogasawara, T. The multi-fingered NAIST hand system for robot in-hand manipulation. Mech. Mach. Theory 2010, 45, 224–238. [Google Scholar] [CrossRef]
- Ambrose, R.O.; Aldridge, H.; Scott Askew, R.; Burridge, R.R.; Bluethmann, W.; Diftler, M.; Lovchik, C.; Magruder, D.; Rehnmark, F. Robonaut: NASA’s Space Humanoid. IEEE Intell. Syst. 2000, 15, 57–63. [Google Scholar] [CrossRef]
- Liu, H.; Wu, K.; Meusel, P.; Seitz, N.; Hirzinger, G.; Jin, M.H. Multisensory Five-Finger Dexterous Hand: The DLR/HIT Hand II. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 3692–3697.
- Gazeau, J.P.; Zeghloul, S.; Arsicault, M.; Lallemand, J.P. The LMS Hand: Force and position controls in the aim of the fine manipulation of objects. In Proceedings of the IEEE/RSJ International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2001; pp. 2642–2648.
- Dollar, A.M.; Howe, R.D. The Highly Adaptive SDM Hand: Design and Performance Evaluation. Int. J. Robot. Res. 2010, 29, 585–597. [Google Scholar] [CrossRef]
- Martin Amezaga, J.; Grossard, M. Design of a fully modular and backdrivable dexterous hand. Int. J. Robot. Res. 2014, 33, 783–798. [Google Scholar] [CrossRef]
- Bicchi, A. Hands for Dexterous Manipulation and Robust Grasping: A Difficult Road toward Simplicity. IEEE Trans. Robot. Autom. 2000, 16, 652–662. [Google Scholar] [CrossRef]
- Murray, R.M.; Sastry, S.S.; Zexiang, L. A Mathematical Introduction to Robotic Manipulation, 1st ed.; CRC Press Inc.: Boca Raton, FL, USA, 1994. [Google Scholar]
- Smith, S.T. Flexures: Elements of Elastic Mechanisms; Taylor & Francis: Abingdon, UK, 2000. [Google Scholar]
- Balasubramanian, R.; Santos, V.J. The Human Hand as an Inspiration for Robot Hand Development; Springer Publishing Company Inc.: Berlin, Germany, 2014. [Google Scholar]
- Cutkosky, M.R.; Kao, I. Computing and controlling the compliance of a robotic hand. IEEE Trans. Robot. Autom. 1989, 5, 151–165. [Google Scholar] [CrossRef]
- Jarrasse, N.; Robertson, J.; Garrec, P.; Paik, J.; Pasqui, V.; Perrot, Y.; Roby-Brami, A.; Wang, D.; Morel, G. Design and acceptability assessment of a new reversible orthosis. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 1933–1939.
- Lotti, F.; Vassura, G. A Novel Approach to Mechanical Design of Articulated Fingers for Robotic Hands. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Lausanne, Switzerland, 30 September–5 October 2002; pp. 1687–1692.
- Garrec, P. Cable Transmission Using Ball-Screw. US Patent AD 479/INPI 03 50046, 2003. [Google Scholar]
- Ouyang, B.; Shang, W. A new computation method for the force-closure workspace of cable-driven parallel manipulators. Robotica 2015, 33, 537–547. [Google Scholar] [CrossRef]
- Gouttefarde, M.; Daney, D.; Merlet, J.P. Interval-analysis-based determination of the wrench-feasible workspace of parallel cable-driven robots. IEEE Trans. Robot. 2011, 27, 1–12. [Google Scholar] [CrossRef]
- Melchiorri, C.; Kaneko, M. Robot Hands. In Springer Handbook of Robotics; Siciliano, B., Khatib, O., Eds.; Springer-Verlag: Berlin, Germany, 2008; pp. 345–360. [Google Scholar]
- Kammerer, N.; Garrec, P. Dry friction modeling in dynamic identification for robot manipulators: Theory and experiments. In Proceedings of the IEEE International Conference on Mechatronics (ICM), Vicenza, Italy, 27 February–1 March 2013; pp. 422–429.
- Henein, S.; Spanoudakis, P.; Droz, S.; Myklebust, L.I.; Onillon, E. Flexure Pivot for Aerospace Mechanisms. In Proceedings of the 10th European Space Mechanisms and Tribology Symposium, San Sebastian, Spain, 24–26 September 2003.
- Pei, X.; Yu, J.; Zong, G.; Bi, S.; Yu, Z. Analysis of rotational precision for an isosceles-trapezoidal flexural pivot. ASME J. Mech. Des. 2008, 130. [Google Scholar] [CrossRef]
- Shang, W.W.; Cong, S. Dexterity and adaptive control of planar parallel manipulators with and without redundant actuation. ASME J. Comput. Nonlinear Dyn. 2015, 10. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grossard, M.; Martin, J.; Huard, B. Force-Sensing Actuator with a Compliant Flexure-Type Joint for a Robotic Manipulator. Actuators 2015, 4, 281-300. https://doi.org/10.3390/act4040281
Grossard M, Martin J, Huard B. Force-Sensing Actuator with a Compliant Flexure-Type Joint for a Robotic Manipulator. Actuators. 2015; 4(4):281-300. https://doi.org/10.3390/act4040281
Chicago/Turabian StyleGrossard, Mathieu, Javier Martin, and Benoît Huard. 2015. "Force-Sensing Actuator with a Compliant Flexure-Type Joint for a Robotic Manipulator" Actuators 4, no. 4: 281-300. https://doi.org/10.3390/act4040281
APA StyleGrossard, M., Martin, J., & Huard, B. (2015). Force-Sensing Actuator with a Compliant Flexure-Type Joint for a Robotic Manipulator. Actuators, 4(4), 281-300. https://doi.org/10.3390/act4040281





