Hybrid Fuzzy-SMC Controller with PSO for Autonomous Underwater Vehicle

Abstract

This paper proposes a fuzzy sliding mode controller optimized using particle swarm optimization (FSMC-PSO) for trajectory tracking of an autonomous underwater vehicle (AUV). Conventional sliding mode control (SMC) is well known for its robustness against external disturbances, unmodeled dynamics, and parameter uncertainties, ensuring stability under challenging operating conditions. In the proposed FSMC-PSO approach, fuzzy logic adaptively tunes the SMC parameters, while PSO optimizes the fuzzy output membership functions offline to improve tuning accuracy and overall control performance. During online operation, the optimized fuzzy system adaptively adjusts the SMC parameters with minimal computational cost. The effectiveness of the proposed method is evaluated through numerical simulations in the presence of random noise. Performance is assessed using standard tracking indices, including IAE, ITAE, ISE, ITSE, and RMSE. Comparative results show that FSMC-PSO achieves higher trajectory tracking accuracy, reduces steady-state and transient errors, and minimizes chattering compared to conventional SMC and SMC-PSO, as well as the super-twisting algorithm-based PSO (STA-PSO) controller.FSMC-PSO achieves up to an 86.58% reduction in ITAE and a 73.53% reduction in ITSE compared to classical SMC while also outperforming SMC-PSO and STA-PSO across all motion states (X, Y, and $\psi$). These results demonstrate the effectiveness of FSMC-PSO for high-precision and disturbance-resilient AUV trajectory tracking within the simulated scenarios.

1. Introduction

1.1. Motivations

Autonomous underwater vehicles (AUVs) have become vital tools in ocean exploration, environmental monitoring, seabed mapping, and defense systems due to their ability to function independently without immediate human intervention. In comparison to tethered systems such as remotely operated vehicles (ROVs), AUVs allow for the advantages of mobility, power efficiency, and the ability to navigate complex underwater terrain independently. Autonomy allows them to operate in high-risk or deep-sea regions that are otherwise hazardous or inaccessible to human divers. Motivated by technological improvements in robotics, control systems, and sensors, AUVs are being built with higher levels of intelligence and adaptability to perform complex missions. However, despite such improvements, constrained communication, power limitation, dynamic underwater currents, and uncertainty in navigation continue to hinder large-scale deployment of AUVs in practice. Such difficulties are treated with robust control methodologies, efficient path planning, and fault-tolerant adaptive control systems. Current research has focused on developing sophisticated algorithms for real-time location, obstacle avoidance, and energy-efficient navigation to increase the range of operation of AUVs [1,2,3]. As the need for autonomous underwater operations grows even more, AUVs are poised to play a key role in underwater exploration in the future.

1.2. State of the Art

Achieving accurate trajectory tracking for AUVs is a central challenge in the fields of ocean engineering and control systems. This difficulty arises due to the complex nature of underwater environments, where AUVs must operate under nonlinear dynamics, uncertain hydrodynamic parameters, and various external disturbances [4,5]. Classical controllers, such as PID, have been widely applied in AUV control due to their simplicity, smooth control action, and ease of implementation. For instance, Bayusari et al. [6] implemented a PID controller to manage the surge, heave, and yaw motions of an AUV. Their simulations demonstrated that the controller could achieve stable trajectory tracking and rapidly reach the desired setpoints. However, despite its effectiveness in minimizing steady-state errors, a fixed-gain PID controller often struggles when the system is subject to parameter uncertainties, external disturbances, or nonlinear dynamics, necessitating frequent manual tuning. Other classical control techniques, such as linear quadratic regulators (LQRs), have been explored to enhance performance under specific operating conditions. In this context, Bae et al. [7] designed an LQR-based controller for waypoint navigation of an AUV, employing separate controllers for depth and steering while accounting for variations in surge speed. The simulation results conducted in MATLAB/Simulink R2023b indicated that the approach maintained tracking errors within approximately 1 m, outperforming conventional state-feedback methods. However, the method still relies on accurate system modeling and exhibits limitations when handling strong nonlinearities and parameter variations.

In order to overcome the limitations of classical controllers, sliding mode control (SMC) has been extensively investigated due to its strong robustness against external disturbances and modeling uncertainties. Recent advances have further enhanced SMC performance by incorporating disturbance observers, higher-order sliding mode controllers (HOSMCs), and adaptive mechanisms, enabling improved tracking accuracy, reduced chattering, and guaranteed stability in the presence of uncertainties [8,9]. For example, Yan et al. [10] developed a trajectory tracking controller for AUVs that accounts for both state and input quantization, incorporating quantization error bounds into the switching term and using a finite-time disturbance observer to estimate unknown disturbances. Their analysis and simulations demonstrated asymptotic stability and accurate trajectory tracking. In addition, HOSMCs have been proposed to enhance tracking precision and reduce the chattering effect associated with conventional SMC. Alibani et al. [11] introduced two super-twisting algorithm (STA)-based controllers for intervention AUV positioning and trajectory tracking and benchmarked them against a dual-loop PID controller. Their method was calibrated using actual AUV parameters and evaluated using six-degree-of-freedom (6-DoF) simulations under disturbance conditions. Adaptive control strategies have also been proposed to manage uncertainties, parameter fluctuations, and unknown dynamics. Zhang et al. [12] developed an adaptive nonlinear high-order sliding mode controller (AHOSMC) to enhance path-following capabilities in AUVs, effectively mitigating nonlinearities and external disturbances. Their controller reduced chattering and improved trajectory tracking performance, achieving faster and smoother responses compared to linear and PID-based control schemes. Guerrero et al. [13] developed an adaptive disturbance observer grounded in the STA to enhance the performance of traditional PD controllers used in underwater vehicles. Their method effectively mitigates the impact of parametric uncertainties and external perturbations. Drawing inspiration from the extended state observer (ESO) framework, the proposed approach is supported by Lyapunov-based stability analysis and verified through real-time experimental results.

Model predictive control (MPC) has attracted attention in AUV applications due to its capability to manage multi-variable dynamics while explicitly handling system constraints. For instance, Yan et al. [14] developed a double closed-loop MPC scheme for 3D trajectory tracking, in which the outer loop generates desired velocities and the inner loop computes control inputs that satisfy system constraints. Lyapunov-based analysis confirmed the stability of the closed-loop system, and simulation results demonstrated accurate trajectory tracking. Despite its advantages in managing multi-variable interactions and constraints, MPC typically requires precise system models and significant computational resources, which may limit its real-time applicability for AUVs. In another contribution, Heshmati et al. [15] proposed a robust nonlinear MPC (NMPC) framework tailored for underactuated AUVs equipped with surge, heave, and yaw actuators. Their approach enabled accurate 3D trajectory tracking while respecting input and state constraints, avoiding obstacles, and adapting to dynamic marine environments. The controller leveraged onboard sensors to dynamically update the operational workspace and compute collision-free real-time trajectories, even in the presence of model uncertainties and external disturbances. The simulation results validated the robustness and efficiency of the proposed method. Lastly, Gong et al. [16] introduced a Lyapunov-based MPC (LMPC) scheme tailored for AUV trajectory tracking in dynamically varying marine environments. Their method integrates nonlinear backstepping control to guarantee stability and explicitly accounts for actuator limitations. Theoretical analysis confirms recursive feasibility, closed-loop stability, and a defined region of attraction, while simulation studies highlight the robustness and effectiveness of the proposed framework.

Hybrid control strategies that combine multiple methodologies have been proposed to exploit the complementary advantages of each approach. Kumar et al. [17] proposed a hybrid control strategy for trajectory tracking in AUVs that merges model-based and model-free techniques in order to address system uncertainties effectively. The approach utilizes a radial basis function, NN, to estimate unknown dynamics and an adaptive compensator to manage disturbances. Lyapunov theory is employed to ensure system stability and error convergence, with simulation results on a four-degree-of-freedom AUV demonstrating improved performance relative to conventional controllers. Basil et al. [18] presented a novel methodology for selecting suitable optimization algorithms for AUV motion control tasks. Their framework uses the full-width zero-importance criteria (FWZIC) for assigning weights to decision criteria and the fuzzy decision optimized selection method (FDOSM) for algorithm selection. The study focuses on optimizing three control motions, yaw, pitch (theta), and depth, concluding that the arithmetic optimization algorithm (AOA) is most suitable for depth and theta, while the Cuckoo algorithm performs best for yaw. Sensitivity analysis further validates the method’s reliability. On the other hand, Herman [19] addressed the problem of trajectory tracking for AUVs under parameter uncertainties and external disturbances. The control strategy combines backstepping, adaptive integral SMC (BAISMC), and velocity transformation from inertia matrix decomposition. Unlike symmetric models, the formulation accounts for center-of-mass displacement and reveals the effects of neglecting dynamic couplings. Simulation results on a 5-DOF vehicle confirm the robustness and effectiveness of the proposed controller. Londhe et al. [20] proposed a robust and adaptive tracking control for a nonlinear AUV using an adaptive fuzzy SMC (AFSMC) scheme. Fuzzy rules are derived via a Lyapunov function to reduce chattering, and an adaptive law adjusts the fuzzy parameters to enhance system stability. Simulations show that the AFSMC model eliminates chattering, reduces steady-state errors, and adapts effectively to unknown uncertainties in the vehicle dynamics.

Recent developments in machine learning have opened new avenues for neural network (NN)- and reinforcement learning-based control (RLC) of AUVs. For example, Seok et al. [21] proposed a neural network-based control (NNC) strategy to manage model uncertainties in AUV systems. Their approach utilized a virtual control input combined with an approach angle strategy to enhance trajectory tracking, while neural networks compensated for unknown variations in hydrodynamic damping. The controller was implemented using the dynamic surface control framework, and Lyapunov-based analysis confirmed system stability. Simulation results demonstrated effective trajectory tracking under uncertain conditions. More recently, Chu et al. [22] introduced a model-free adaptive reinforcement learning method, ARSPPO, to improve AUV docking performance under challenging conditions, including ocean currents and nonlinear dynamics. By incorporating a novel Markov decision process (MDP) framework and a parallel simulation environment, their approach achieved improved robustness, efficiency, and adaptability, which were validated through both simulation and experimental studies.

1.3. Contributions

In this paper, a fuzzy sliding mode controller optimized using particle swarm optimization (FSMC-PSO) is proposed for precise trajectory tracking of an AUV. The main contributions of the proposed FSMC-PSO scheme are summarized as follows:

• A novel FSMC-PSO structure that combines the robustness of sliding mode control with the adaptability of fuzzy logic to effectively reduce chattering and enhance control performance is developed.
• The fuzzy logic system adaptively tunes the SMC parameters in real time, while PSO optimizes the fuzzy membership functions to achieve accurate and efficient tuning.
• The proposed control approach improves disturbance rejection capability and tracking precision under random noise and parameter uncertainties.
• The adaptive fuzzy mechanism contributes to stabilizing control gains, suppressing high-frequency oscillations, and improving reliability in practical AUV applications.

The proposed FSMC-PSO model achieves notable improvements in trajectory tracking accuracy, control smoothness, disturbance rejection, and energy efficiency, with substantial reductions in the IAE, ITAE, ISE, ITSE, and RMSE performance metrics.

1.4. Structure Overview

This paper is structured as follows: Section 2 presents an in-depth analysis of the dynamic modeling of the AUV system. Section 3 outlines the proposed control strategies and their implementation. Section 4 discusses the simulation results. Finally, Section 5 highlights the main findings and contributions of the study.

2. AUV Kinematic and Dynamic Model

As shown in Figure 1, the horizontal motion of an AUV is usually described by three degrees of freedom: surge, sway, and yaw. Movements along the vertical axis, such as velocity, roll, and pitch, are typically small and therefore are often neglected in 2D planar motion analysis [23].

The AUV’s motion was considered in the horizontal plane only (surge, sway, and yaw), while vertical movements such as heave, roll, and pitch are neglected. This simplification limits the direct applicability to 2D planar operations and represents an assumption made in this study. In real-world scenarios, the controller may need adaptation for full 3D motion by considering additional degrees of freedom and coupled dynamics. The kinematic model defines the relationship between the AUV’s velocities in its body-fixed frame and its position and orientation in the inertial (earth-fixed) frame. In particular, the vehicle’s changes in global position and heading are determined by its surge, sway, and yaw velocities [24]. On the other hand, the dynamic model considers the forces and torques acting on the vehicle, including hydrodynamic effects such as added mass and drag, as well as gravitational, buoyant, and actuator-generated forces [25]. Together, these kinematic and dynamic formulations form the essential basis for designing control strategies that achieve precise trajectory tracking and maintain stability during underwater operations. Based on these simplifications, the motion of the AUV, under the above assumptions, encompasses both kinematic and dynamic aspects and can be represented by the following mathematical model [26]. These assumptions imply that the proposed controller is validated in a horizontal-plane context, and its performance under full 3D maneuvers may require further analysis or adjustment.

$$\dot{\zeta }=J\left(\psi \right)v$$

(1)

$$M\dot{v}=-C\left(v\right)v-D\left(v\right)v+\tau +E\left(t\right)$$

(2)

where M represents the mass matrix, which accounts for both the rigid-body inertia of the AUV and the added mass effects from the surrounding fluid. The velocity vector expressed in the body-fixed frame is $v={[u,\nu ,r]}^T$, where u, $\nu$, and r correspond to the surge, sway, and yaw rates, respectively. The Coriolis and centripetal contributions are captured by the matrix $C\left(v\right)$, while $D\left(v\right)$ denotes the hydrodynamic damping matrix. The input vector for the control signal is given by $\tau =u={[{\tau }_1,{\tau }_2,{\tau }_3]}^T$, which includes the forces and moments produced by the thrusters or control surfaces. The position and orientation of the AUV in the earth-fixed frame are described by $\zeta ={[x,y,\psi ]}^T$, with x and y representing the horizontal coordinates and $\psi \in [0,2\pi ]$ indicating the vehicle’s heading angle [27]. External disturbances are modeled using $E\left(t\right)={[E_1\left(t\right),E_2\left(t\right),E_3\left(t\right)]}^T$, where $E_1\left(t\right)$ and $E_2\left(t\right)$ represent the surge and sway forces and $E_3\left(t\right)$ corresponds to a yaw moment. In this study, the full six-degree-of-freedom (6-DOF) equations are reduced to a three-degree-of-freedom (3-DOF) model that focuses on horizontal-plane motion (surge, sway, and yaw), which is appropriate for most AUV trajectory tracking applications [28]. The associated rotation matrix is defined as follows [10]:

$$J\left(\psi \right)=\left[\begin{array}{ccc}cos\psi & -sin\psi & 0\\ sin\psi & cos\psi & 0\\ 0& 0& 1\end{array}\right]$$

(3)

It is worth mentioning that the rotation matrix J satisfies $\parallel J\parallel =1$, where $\parallel ·\parallel$ denotes the Euclidean (two-norm) of a matrix or vector. The term $C\left(v\right)$ accounts for the contributions Coriolis and centripetal, while $D\left(v\right)$ captures the restoring forces acting on the system. Specifically,

$$C\left(\nu \right)=\left[\begin{array}{ccc}0& 0& -m_{\nu }\nu \\ 0& 0& m_{u}u\\ m_{\nu }\nu & -m_{u}u& 0\end{array}\right]$$

(4)

The damping matrix is defined as $D\left(v\right)=\mathrm{diag}\{d_u,d_{\nu },d_r\}$, where the individual damping terms are given by $d_u=-X_u-X_{\left|u\right|u}\left|u\right|$, $d_{\nu }=-Y_{\nu }-Y_{\left|\nu \right|\nu }\left|\nu \right|$, and $d_r=-N_r-N_{\left|r\right|r}\left|r\right|$. The inertia matrix is represented as $M=\mathrm{diag}\{m_u,m_v,m_r\}$, with components $m_u=m-{\dot{X}}_u$, $m_{\nu }=m-{\dot{Y}}_{\nu }$, and $m_r=I_z-{\dot{N}}_r$. Here, m denotes the vehicle’s mass, while $I_z$ represents the moment of inertia about the vertical axis. The terms $X(·)$, $Y(·)$, and $N(·)$ refer to the respective hydrodynamic derivatives, while $d(·)$ represents the damping effects induced by the surrounding fluid. Furthermore, $X_u$, $Y_{\nu }$, and $N_r$ denote the linear hydrodynamic derivatives (i.e., the partial derivatives of surge, sway, and yaw forces/moments with respect to their corresponding velocities), whereas $X_{\left|u\right|u}$, $Y_{\left|\nu \right|\nu }$, and $N_{\left|r\right|r}$ represent the quadratic damping coefficients associated with the nonlinear drag terms $\left|u\right|u$, $\left|\nu \right|\nu$, and $\left|r\right|r$. Similarly, the terms ${\dot{X}}_u$, ${\dot{Y}}_{\nu }$, and ${\dot{N}}_r$ correspond to the added-mass coefficients related to the acceleration components. This notation differentiates the linear, quadratic, and added-mass hydrodynamic effects acting on the AUV [28]. By differentiating Equation (1) and substituting it into Equation (2), the dynamic behavior of the system is obtained as follows [28]:

$$\begin{array}{cc}\hfill \ddot{\zeta }& =\dot{J}\left(\psi \right)v-M^{-1}J\left(\psi \right)C\left(v\right)v-M^{-1}J\left(\psi \right)D\left(v\right)v\hfill \\ \hfill & +M^{-1}J\left(\psi \right)u+M^{-1}J\left(\psi \right)E\left(t\right)\hfill \end{array}$$

(5)

Substituting $v=J^{-1}\left(\psi \right)\dot{\zeta }$ from Equation (1) into Equation (5) leads to the following reformulated expression:

$$\begin{array}{cc}\hfill \ddot{\zeta }& =\left(J^{-1}\left(\psi \right)\dot{J}\left(\psi \right)-M^{-1}C\left(v\right)-M^{-1}D\left(v\right)\right)\dot{\zeta }\hfill \\ \hfill & +M^{-1}J\left(\psi \right)u+M^{-1}J\left(\psi \right)E\left(t\right)\hfill \end{array}$$

(6)

A more compact representation of Equation (6) is given as follows:

$$\ddot{\zeta }=\alpha \dot{\zeta }+\beta u+\beta E\left(t\right)$$

(7)

where $\alpha =\left(J^{-1}\left(\psi \right)\dot{J}\left(\psi \right)-M^{-1}C\left(v\right)-M^{-1}D\left(v\right)\right)$ and $\beta =M^{-1}J\left(\psi \right)$. Using these definitions, the equation can be further rewritten as follows:

$$\ddot{\zeta }=\alpha \dot{\zeta }+\beta u+d\left(t\right)$$

(8)

where, $\beta E\left(t\right)=d\left(t\right)$.

3. Methodology

This section presents a robust control scheme for the autonomous AUV, designed to ensure precise trajectory tracking and strong resilience against external disturbances. The strategy is based on the conventional SMC framework, which is recognized for its ability to handle system nonlinearities and unpredictable environmental effects [29]. However, traditional SMC often suffers from control chattering and limited adaptability in dynamic conditions. This major shortcoming is mainly attributed to the discontinuous switching nature of the SMC control law, which can excite high-frequency dynamics and lead to undesirable oscillations in the control signal, as widely discussed in the literature, including advanced nonlinear control strategies based on differentiator- and observer-based feedback linearization [30]. To overcome these challenges, a fuzzy SMC framework with memberships optimized via particle swarm optimization (FSMC-PSO) is employed. In this approach, the PSO algorithm is used to minimize a predefined objective function and adjust the fuzzy membership functions, which then adaptively tune the SMC parameters, including the sliding surface parameter $\lambda$ and gain k. Importantly, PSO is performed offline; the resulting optimized output fuzzy membership functions are then used online to adaptively tune $\lambda$ and k. The input membership functions of s and $\dot{s}$ are predefined and remain fixed throughout operation. This hierarchical adaptation enhances both responsiveness and stability while effectively reducing chattering. The overall structure of the control system is illustrated in Figure 2.

3.1. Sliding Mode Control

The well-known SMC is a robust nonlinear control technique commonly employed to achieve high-precision tracking and effective disturbance rejection in uncertain dynamic systems [31]. The key idea behind SMC is to design a control law that forces the system’s state to reach and remain on a predefined sliding surface, which guarantees the desired system behavior. The SMC operation is generally divided into two phases: the reaching phase and the sliding phase. During the reaching phase, the control law drives the system states toward the predefined sliding surface despite uncertainties and disturbances. Once the sliding surface is reached, the system enters the sliding phase, where the closed-loop dynamics become insensitive to matched disturbances and parameter variations, ensuring robust tracking performance. The control input u in SMC is typically decomposed into two components: equivalent control $u_{eq}$, which maintains the trajectory of the system on the sliding surface, and switching control $u_{sw}$, which drives the system states toward the surface. Mathematically, the SMC law is expressed as follows [32]:

$$u=u_{eq}+u_{sw}$$

(9)

Equivalent control $u_{eq}$ is derived by setting the sliding surface derivative to zero and solving for nominal dynamics. In contrast, switching control introduces a discontinuous action to overcome model uncertainties and external disturbances. The proposed $u_{sw}$ is defined as follows [32]:

$$u_{sw}=-{\beta }^{-1}k·sign\left(s\right)$$

(10)

where $k=\mathrm{diag}\{k_1,k_2,k_3\}$ is a diagonal positive gain matrix and s is the sliding surface vector. This structure ensures finite-time convergence to the sliding manifold and robustness against matched uncertainties. In order to implement the SMC for the AUV system, a sliding surface is proposed as follows:

$$s=\dot{e}+\lambda {\int }_0^{t}e.dt$$

(11)

where $e=\zeta -{\zeta }_d$ and $\lambda =\mathrm{diag}\left\{{\lambda }_1,{\lambda }_2,{\lambda }_3\right\}$ represent the vector tracking error and the diagonal positive matrix, respectively. To calculate $u_{eq}$, it is necessary to set the sliding surface derivative $\dot{s}$ to zero and solve for the control input of Equation (8) as follows:

$$\begin{array}{c}\dot{s}=\ddot{e}+\lambda e\hfill \\ =\ddot{\zeta }-{\ddot{\zeta }}_d+\lambda e\hfill \\ =\alpha \dot{\zeta }+\beta u+d\left(t\right)-{\ddot{\zeta }}_d+\lambda e\hfill \end{array}$$

(12)

By neglecting the disturbance, the equivalent control is deduced as follows [33]:

$$\dot{s}=0⟹u_{eq}={\beta }^{-1}\left[-\alpha \dot{\zeta }+{\ddot{\zeta }}_d-\lambda e\right]$$

(13)

Using Equations (9), (10) and (13), the embodiment of the switching control law by means of SMC yields the following expression:

$$u={\beta }^{-1}\left[-\alpha \dot{\zeta }+{\ddot{\zeta }}_d-\lambda e\right]-{\beta }^{-1}ksign\left(s\right)$$

(14)

Assumption 1. 

1. 

Fuzzy adaptation ensures that the sliding surface parameters (${\lambda }_i\left(t\right)$) and the switching gains ($k_i\left(t\right)$) remain positive and bounded: $0<k_{min}\le k_i\left(t\right)\le k_{max}$, $0<{\lambda }_{min}\le {\lambda }_i\left(t\right)\le {\lambda }_{max}$.

2. 

The disturbances acting on the AUV, $d\left(t\right)$, are bounded, with $\parallel d\left(t\right)\parallel \le d_{max}$.

3. 

The fuzzy inference system is designed to provide smooth adaptation of the parameters, avoiding abrupt changes in control gains.

Stability Proof. 

In order to establish the stability of the AUV system under SMC, a Lyapunov candidate positive function is defined as follows [34,35]:

$$V\left(s\right)={\displaystyle \frac{1}{2}}{s}^{\top }s$$

(15)

Substituting Equation (9), Equation (12) and Equation (14) into the time derivative of $V\left(s\right)$ yields

$$\begin{array}{ccc}\hfill \dot{V}\left(s\right)& =& s^{\top }\dot{s}\hfill \\ & =& s^{\top }\left[\ddot{e}+\lambda e\right]\hfill \\ & =& s^{\top }\left[\ddot{\zeta }-{\ddot{\zeta }}_d+\lambda e\right]\hfill \\ & =& s^{\top }\left[\alpha \dot{\zeta }+\beta u+d\left(t\right)-{\ddot{\zeta }}_d+\lambda e\right]\hfill \\ & =& s^{\top }\left[\alpha \dot{\zeta }+\beta (u_{eq}+u_{sw})+d\left(t\right)-{\ddot{\zeta }}_d+\lambda e\right]\hfill \\ & =& s^{\top }\left[\alpha \dot{\zeta }+\beta u_{eq}+\beta u_{sw}+d\left(t\right)-{\ddot{\zeta }}_d+\lambda e\right]\hfill \end{array}$$

(16)

Since the equivalent control $u_{eq}$ eliminates the corresponding terms in $\dot{s}$, Equation (16) simplifies to the following equation:

$$\dot{V}\left(s\right)=s^T\dot{s}=s^{\top }\left[-ksign\left(s\right)+d\left(t\right)\right]$$

(17)

where $k\left(t\right)$ is a diagonal positive matrix representing the switching gains, which are adaptively tuned by the fuzzy inference system. The diagonal switching gain matrix is selected such that $k_i\left(t\right)>\left|E_i\left(t\right)\right|$ for all $i=1,2,3$, where $E_i\left(t\right)$ denotes the i-th component of the disturbance vector $E\left(t\right)$. The fuzzy adaptation ensures that both $k_i\left(t\right)$ and the sliding surface coefficients (${\lambda }_i\left(t\right)$) remain positive and bounded within predefined ranges. Under these conditions, the time derivative of the Lyapunov candidate remains negative semi-definite, and the sliding surface is reached in finite time. Consequently, the closed-loop system’s trajectories are uniformly ultimately bounded (UUB), ensuring robustness of the FSMC-PSO controller against disturbances and time-varying gains. □

3.2. Particle Swarm Optimization (PSO)

The PSO is a population-based optimization technique inspired by the collective behavior of bird flocks and fish schools. A swarm of particles is distributed in a multidimensional search space, where each particle represents a candidate solution characterized by its position and velocity [36]. These particles are iteratively updated using three components: inertia, which preserves the previous motion; the cognitive term, which attracts the particle toward its best personal position ($B_{\mathrm{best}}$); and the social term, which guides it toward the global best position ($G_{\mathrm{best}}$). The velocity update rule (Equation (20)) combines these influences, while the position update rule (Equation (21)) determines the new position of the particle. The updates of $p_{\mathrm{best}}$ and $G_{\mathrm{best}}$, given in Equations (18) and (19), ensure a balance between exploration and exploitation, allowing the swarm to converge efficiently toward optimal solutions. This makes PSO particularly suitable for tuning fuzzy membership functions and control parameters. In PSO, each particle updates its best personal position and the best global position as follows [36]:

$$pbes{t}_i(k+1)=\left\{\begin{array}{cc}{x}_i(k+1),\hfill & \mathrm{if}f\left(x_i(k+1)\right)<f\left(pbes{t}_i\left(k\right)\right)\hfill \\ pbes{t}_i\left(k\right),\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(18)

$$gbest(k+1)=\left\{\begin{array}{cc}pbes{t}_j(k+1),\hfill & \mathrm{if}f\left(pbes{t}_j(k+1)\right)<f\left(gbest\left(k\right)\right),\exists j\hfill \\ gbest\left(k\right),\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(19)

The velocity of the particle i is updated according to

$$v_i(k+1)=\eta v_i\left(k\right)+c_1{r}_1\left(k\right)\left(pbes{t}_i\left(k\right)-x_i\left(k\right)\right)+c_2{r}_2\left(k\right)\left(gbest\left(k\right)-x_i\left(k\right)\right)$$

(20)

where $\eta$ is the inertia weight, $c_1$ and $c_2$ are positive acceleration coefficients, and $r_1\left(k\right),r_2\left(k\right)\sim U(0,1)$ are uniformly distributed random numbers in $[0,1]$. The velocity is constrained within predefined bounds: $v_{min}\le v_i\left(k\right)\le v_{max}$. Finally, the position of each particle is updated as follows:

$$x_i(k+1)=x_i\left(k\right)+v_i(k+1)$$

(21)

where $x_i\left(k\right)$ denotes the position of particle i at iteration k. The search process for PSO, as described above, is illustrated in Figure 3. Applications of PSO to optimize fuzzy systems have been widely reported in the literature [37,38].

3.3. Problem Statement

In the proposed AUV control framework, an SMC is enhanced with fuzzy logic adaptation. The fuzzy system is divided into two subsystems: one adjusts the sliding surface coefficients (${\lambda }_x,{\lambda }_y,$ and ${\lambda }_{\psi }$), and the other adjusts the switching gains ($k_x,k_y,$ and $k_{\psi }$). For each subsystem, triangular membership functions (Low, Medium, and High) are used for the input tracking error and its rate, which are normalized within predefined ranges according to actuator limits. Each fuzzy output subsystem has nine tunable parameters, resulting in a total of 18 optimization variables:

$$\Theta =\left[{\lambda }_x^L,{\lambda }_x^M,{\lambda }_x^H,{\lambda }_y^L,{\lambda }_y^M,{\lambda }_y^H,{\lambda }_{\psi }^L,{\lambda }_{\psi }^M,{\lambda }_{\psi }^H,k_x^L,k_x^M,k_x^H,k_y^L,k_y^M,k_y^H,k_{\psi }^L,k_{\psi }^M,k_{\psi }^H\right],$$

(22)

where the superscripts $L,M,$ and H denote the Low, Medium, and High levels of the output parameters. In the FSMC-PSO framework, the fuzzy system’s inputs are the sliding surface s and its derivative $\dot{s}$. Their membership functions are predefined by the designer using simple triangular shapes, as shown in Figure 4, and remain fixed during operation. It should be emphasized that PSO is applied exclusively to optimize the output fuzzy membership function’s parameters associated with $\lambda$ and k. In addition, two separate fuzzy subsystems are employed to independently tune the sliding surface coefficients (${\lambda }_x,{\lambda }_y,$ and ${\lambda }_{\psi }$) and the switching gains ($k_x,k_y,$ and $k_{\psi }$). This design reduces the complexity of the fuzzy rule base, improves interpretability, and allows more efficient offline PSO. Combining both into a single multi-output fuzzy system would significantly increase the number of rules and complicate tuning.

The fuzzy rule base, shown in

Table 1. Fuzzy rule base applied to each control channel ($i\in \{x,y,\psi \}$), thus defining the relationship between the normalized absolute error $|s_i|$, its rate $|{\dot{s}}_i|$, and the corresponding output fuzzy parameters ($k_i$ and ${\lambda }_i$).

$|{\mathit{s}}_{\mathit{i}}|$	$|{\dot{\mathit{s}}}_{\mathit{i}}|$	Rule	${\mathit{k}}_{\mathit{i}}$ (Linguistic Value)	${\mathit{\lambda }}_{\mathit{i}}$ (Linguistic Value)
Low	Low	R1	Low	Low
Low	Med	R2	Low	Low
Low	High	R3	Med	Med
Med	Low	R4	Med	Med
Med	Med	R5	Med	Med
Med	High	R6	High	High
High	Low	R7	High	High
High	Med	R8	High	High
High	High	R9	High	High

, defines the mapping between the absolute sliding surface $|s_i|$, its rate $|{\dot{s}}_i|$, and the corresponding output parameters ($k_i$ and ${\lambda }_i$) for each control channel ($i\in \{x,y,\psi \}$). Rules increase $k_i$ and ${\lambda }_i$ when errors are large to improve responsiveness and robustness and decrease them when errors are small to reduce control effort and mitigate chattering. The Mamdani fuzzy inference mechanism is used: The crisp inputs s and $\dot{s}$ are fuzzified. The rules are evaluated using the min operator for AND. Outputs are aggregated via the max operator, and the centroid method is used for defuzzification. This ensures smooth and continuous control actions while preserving interpretability.

The objective function to be minimized in order to obtain the FSMC-PSO fuzzy membership functions of the output and the SMC-PSO parameters is defined as follows:

$$O=ITA{E}_x+ITA{E}_y+ITA{E}_{\psi },$$

(23)

where $ITA{E}_x$, $ITA{E}_y$, and $ITA{E}_{\psi }$ correspond to the integral of time-weighted absolute errors for the responses x, y, and $\psi$ (yaw), respectively. In FSMC-PSO, the PSO algorithm only optimizes the output fuzzy membership function’s parameters, which then adaptively tune the SMC parameters, including the sliding surface coefficient $\lambda$ and the gain k. Similarly, in SMC-PSO, the PSO algorithm directly tunes the SMC parameters. For the baseline SMC controller, the parameters are obtained through a trial-and-error procedure.

4. Results and Analysis

In this section, all simulations were performed in MATLAB/Simulink R2023b on a personal computer equipped with an Intel Core i7-10700KF CPU (3.80 GHz) and 32 GB of RAM while running a 64-bit Windows 11 operating system. A fixed-step Runge–Kutta (ode4) solver with a time step of 0.001 s was used to integrate the AUV dynamic model. The control algorithms and performance evaluation indices (IAE, ITAE, ISE, ITSE, and RMSE) were implemented and analyzed within the MATLAB environment.

In order to ensure a fair and reproducible comparison, all controllers (SMC, SMC-PSO, FSMC-PSO, and STA-PSO) were tested under identical simulation conditions. The hydrodynamic parameters used in the AUV model are listed in

Table 2. The AUV model parameters.

$m=185$ kg	$I_z=50$ kg·m2	${\dot{X}}_u=-30$ kg
${\dot{Y}}_{\nu }=-80$ kg	${\dot{N}}_r=-30$ kg·m2	$X_u=-70$ kg/s
$Y_{\nu }=-100$ kg/s	$N_r=-50$ kg·m2/s	$X_{\left|u\right|u}=-100$ kg/m
$Y_{\left|\nu \right|\nu }=-200$ kg/m	$N_{\left|r\right|r}=-100$ kg·m2

, following the benchmark AUV formulation presented in [10].

Table 3. PSO parameters, control gain bounds, and final controller parameters.

Parameter	Lower Bound	Upper Bound
PSO parameters
Swarm size ($nPop$)	50
Iterations ($MaxIt$)	100
Inertia weight (w)	0.72
Cognitive coefficient ($c_1$)	1.5
Social coefficient ($c_2$)	1.5
SMC-PSO gain bounds
$\lambda$	$\mathrm{diag}\left(\right[0,0,0\left]\right)$	$\mathrm{diag}\left(\right[3,8,3\left]\right)$
k	$\mathrm{diag}\left(\right[0,0,0\left]\right)$	$\mathrm{diag}\left(\right[10,70,150\left]\right)$
STA-PSO control gain bounds
$\lambda$	$\mathrm{diag}\left(\right[0.1,0.1,0.1\left]\right)$	$\mathrm{diag}\left(\right[10,10,10\left]\right)$
$k_1$	$\mathrm{diag}\left(\right[0.1,0.1,0.1\left]\right)$	$\mathrm{diag}\left(\right[100,100,100\left]\right)$
$k_2$	$\mathrm{diag}\left(\right[0.1,0.1,0.1\left]\right)$	$\mathrm{diag}\left(\right[100,100,100\left]\right)$
Final controller parameters
Baseline SMC
$\lambda$	$\mathrm{diag}\left(\right[3,3,2\left]\right)$
k	$\mathrm{diag}\left(\right[5,40,3\left]\right)$
SMC-PSO
$\lambda$	$\mathrm{diag}\left(\right[1.7273,3.5297,8.0039\left]\right)$
k	$\mathrm{diag}\left(\right[1.7522,50.0000,8.2599\left]\right)$
STA-PSO-optimal parameters
$\lambda$	$\mathrm{diag}\left(\right[7.9688,8.1531,4.1587\left]\right)$
$k_1$	$\mathrm{diag}\left(\right[134.0524,121.8453,13.9245\left]\right)$
$k_2$	$\mathrm{diag}\left(\right[29.4296,12.2544,7.2159\left]\right)$

presents the PSO parameters, control gain bounds, and final controller parameters.

In addition, to evaluate robustness, six levels of random disturbances ($d_1$–$d_6$) were applied to the system, generated as $d=\mathrm{randn}\times (1,1)$ to emulate stochastic perturbations. All controllers were tested with the same initial conditions and reference trajectory. Performance indices (IAE, ITAE, ISE, ITSE, and RMSE) were computed over the full 40 s simulation to ensure a consistent comparison across all controllers.

The performance of the proposed FSMC-PSO strategy is evaluated through numerical simulations of the AUV system. The initial conditions of the AUV are set to ${\zeta }_0={[1,9,0.5]}^T$ for position and heading, with the initial velocity $v_0={[1,1,0.1]}^T$. The desired trajectory is defined as ${\zeta }_d={[2t,3sin\left(0.5t\right),0.3]}^T$, with its first and second derivatives given by ${\dot{\zeta }}_d={[2,1.5cos\left(0.5t\right),0]}^T$ and ${\ddot{\zeta }}_d={[0,-0.75sin\left(0.5t\right),0]}^T$, respectively, following the formulation in [10].

Figure 5 illustrates the convergence behavior of the PSO algorithm when applied to adjust the FSMC-PSO, STA-PSO, and SMC-PSO controllers. For the FSMC-PSO controller, the cost function decreases rapidly during the initial iterations, falling from approximately 51 to about 36 within the first 10 iterations. After this point, the convergence stabilizes, and the cost remains nearly constant, indicating fast and stable convergence behavior.

In the FSMC-PSO framework, a total of 18 output fuzzy membership function parameters are optimized offline, while the input membership functions of s and $\dot{s}$ remain fixed. This design limits the dimensionality of the search space and contributes to the observed rapid convergence. A swarm size of 50 particles with 100 iterations is sufficient to achieve convergence with moderate computational requirements. During online operation, only the fuzzy inference mechanism is executed to adapt the sliding surface coefficients $\lambda$ and switching gains k, resulting in negligible computational overhead.

For the STA-PSO controller, the cost function exhibits a very fast convergence behavior. The cost decreases sharply from an initial value of approximately 15 to below 2 within the first few iterations. After around 10 iterations, the optimization process reaches a steady state, and the cost remains nearly constant with negligible fluctuations. This rapid convergence demonstrates the effectiveness of PSO in tuning the super-twisting algorithm’s parameters and its ability to quickly identify a near-optimal solution.

Furthermore, the smooth and monotonic convergence profile of STA-PSO indicates reduced sensitivity to parameter oscillations during optimization. Compared to FSMC-PSO and SMC-PSO, STA-PSO achieves the lowest final cost value with fewer iterations, highlighting its superior convergence speed and robustness while maintaining high control performance.

For the SMC-PSO controller, the cost function decreases more gradually, starting from approximately 13 and converging to a final value near $3.5$. Compared to FSMC-PSO and STA-PSO, the convergence process is slower and characterized by multiple stages of gradual reduction before stabilization, indicating higher sensitivity and computational effort during optimization.

Overall, although SMC-PSO achieves a lower final cost than FSMC-PSO, the STA-PSO controller demonstrates the fastest convergence and the lowest cost value, while FSMC-PSO provides a favorable balance between convergence speed, robustness, and computational efficiency.

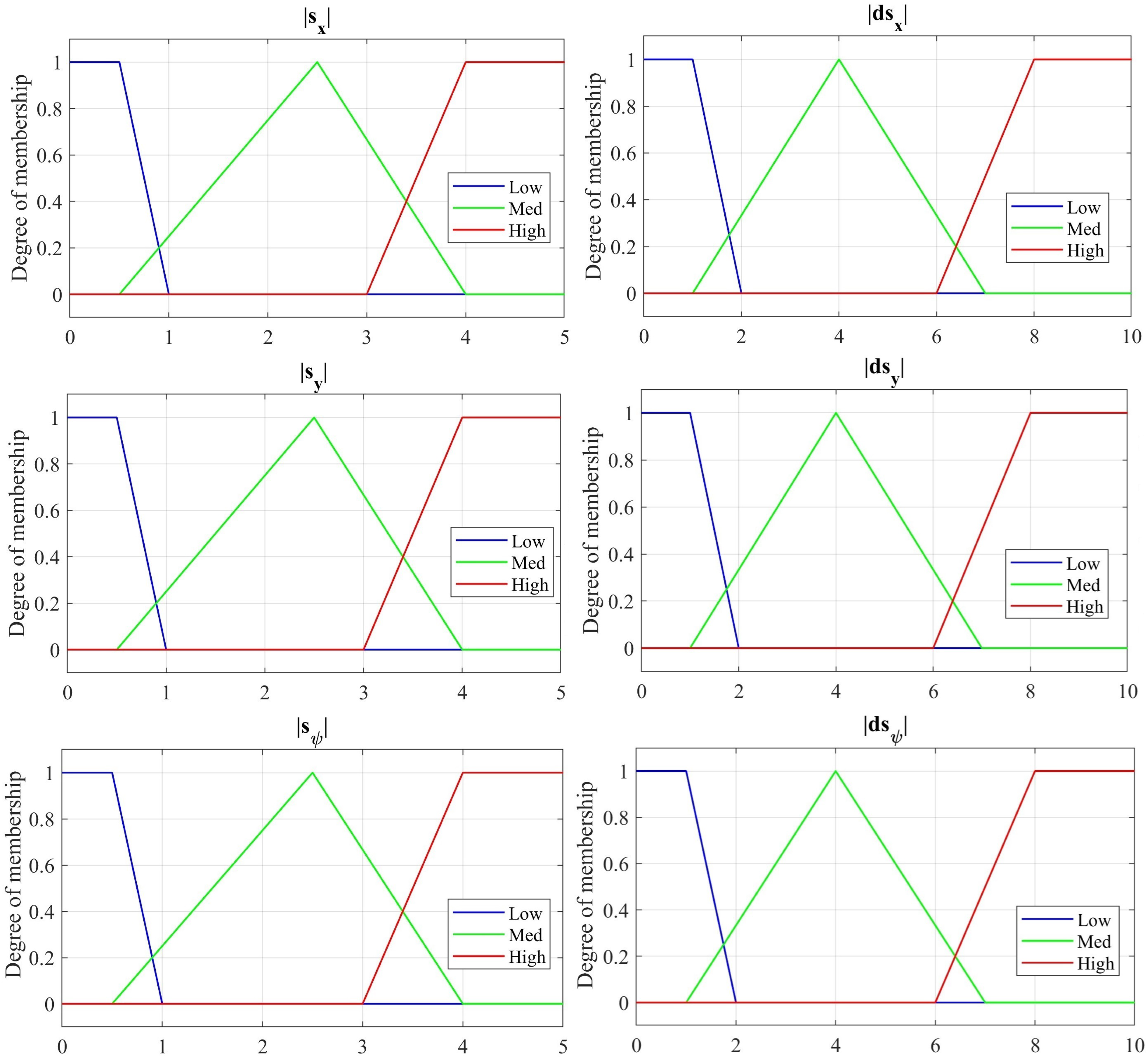
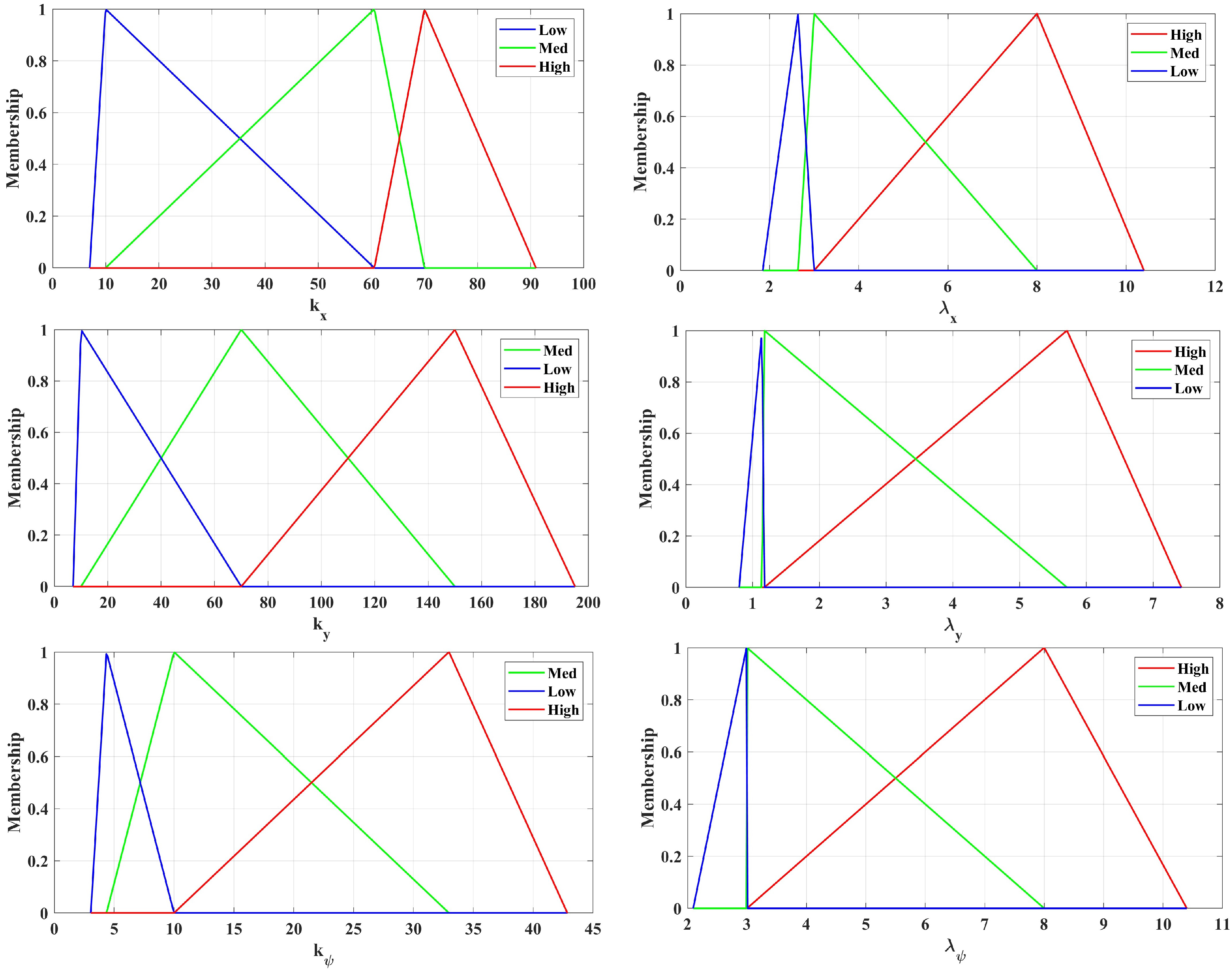
Figure 6 presents the optimized output membership functions associated with the fuzzy parameters k and $\lambda$, which exhibit a well-structured and heterogeneous partitioning of their respective universes of discourse.

The switching gains $k_x$, $k_y$, and $k_{\psi }$ are defined over relatively wide intervals using three triangular membership functions (Low, Medium, and High), allowing smooth transitions between low-switching actions for reduced chattering and high-switching actions for improved robustness against disturbances.

In contrast, the membership functions of ${\lambda }_x$, ${\lambda }_y$, and ${\lambda }_{\psi }$ are distributed over narrower ranges, reflecting their role in fine-tuning the slope of the sliding surface. Lower values of $\lambda$ yield smoother responses with reduced control effort, whereas higher values lead to faster convergence.

This heterogeneous distribution prevents redundancy among fuzzy sets and ensures smooth interpolation during inference while maintaining interpretability.

Overall, the optimized membership function design achieves a suitable balance between robustness and convergence speed.

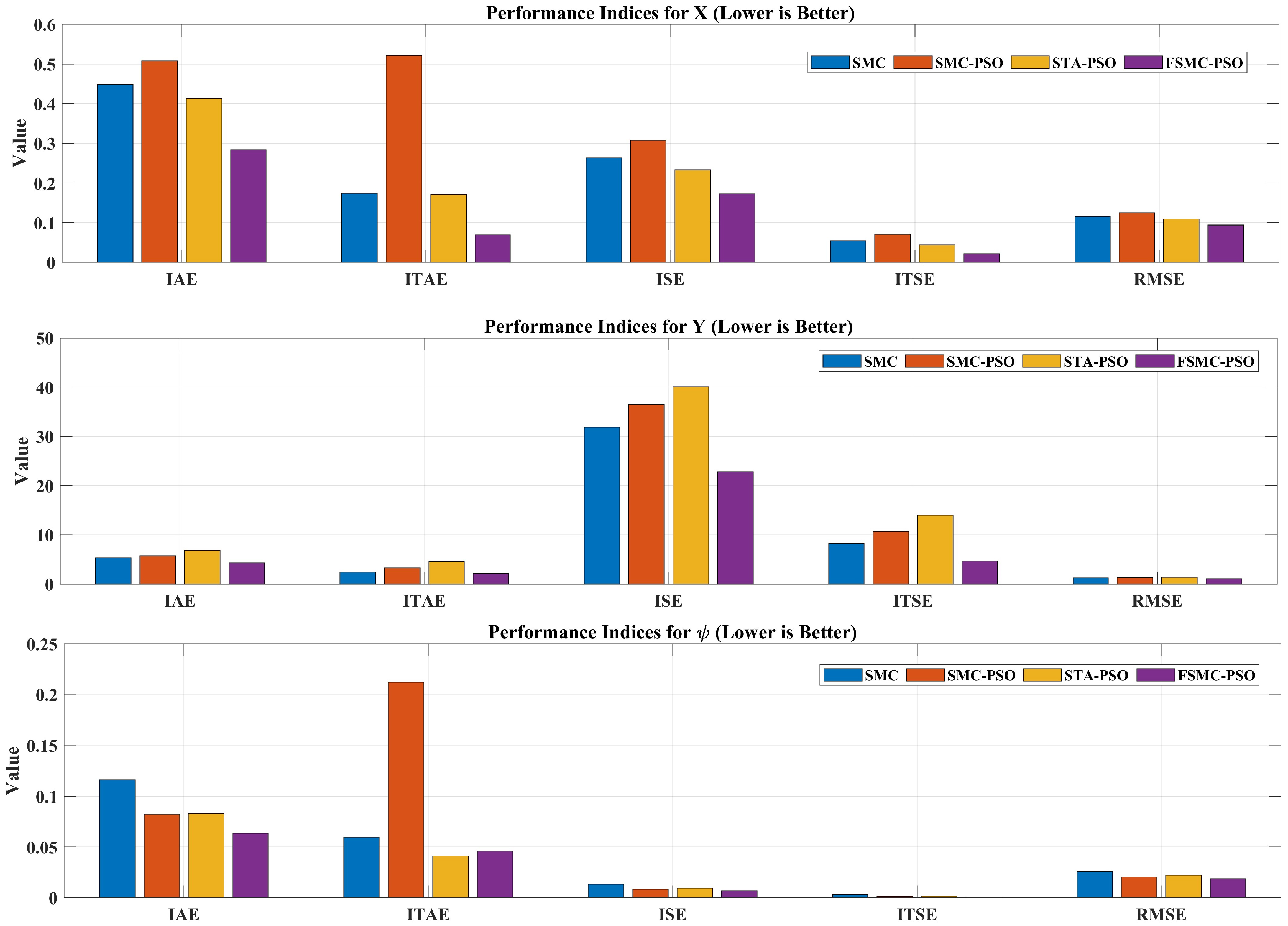
The effectiveness of this optimized structure is further confirmed by the quantitative performance indices reported in

Table 4. Performance indices of controllers and improvement percentages of FSMC-PSO.

Index	SMC			SMC-PSO			STA-PSO			FSMC-PSO
	X	Y	$\mathit{\psi }$	X	Y	$\mathit{\psi }$	X	Y	$\mathit{\psi }$	X	Y	$\mathit{\psi }$
IAE	0.4480	5.3281	0.1162	0.5080	5.8118	0.0825	0.4136	6.8097	0.0831	0.2842	4.3236	0.0636
ITAE	0.1737	2.4283	0.0597	0.5210	3.3024	0.2120	0.1707	4.5590	0.0410	0.0699	2.1873	0.0461
ISE	0.2632	31.9065	0.0131	0.3073	36.4517	0.0083	0.2333	40.0409	0.0095	0.1727	22.8158	0.0069
ITSE	0.0541	8.2822	0.0034	0.0709	10.6877	0.0013	0.0444	13.9462	0.0017	0.0216	4.6677	0.0009
RMSE	0.1158	1.2707	0.0258	0.1249	1.3572	0.0206	0.1091	1.4217	0.0220	0.0942	1.0772	0.0189
Index	FSMC-PSO Improvement vs. SMC (%)				FSMC-PSO Improvement vs. SMC-PSO (%)				FSMC-PSO Improvement vs. STA-PSO (%)
	X	Y	$\mathit{\psi }$		X	Y	$\mathit{\psi }$		X	Y	$\mathit{\psi }$
IAE	36.56	18.87	45.27		44.05	25.59	22.91		31.3	36.5	23.5
ITAE	59.75	9.91	22.77		86.58	33.76	78.25		59.0	52.0	−12.4
ISE	34.39	28.47	47.33		43.78	37.39	16.87		26.0	43.0	27.4
ITSE	60.07	43.64	73.53		69.54	56.31	30.77		51.4	66.5	47.1
RMSE	18.66	15.21	26.74		24.63	20.64	8.25		13.6	24.2	14.1

and illustrated in Figure 7.

FSMC-PSO consistently achieves the lowest values across all error indices (IAE, ITAE, ISE, ITSE, and RMSE) for the X, Y, and $\psi$ states, demonstrating superior tracking accuracy and disturbance rejection.

In summary, FSMC-PSO outperforms both SMC and SMC-PSO in terms of accuracy, robustness, and convergence behavior.

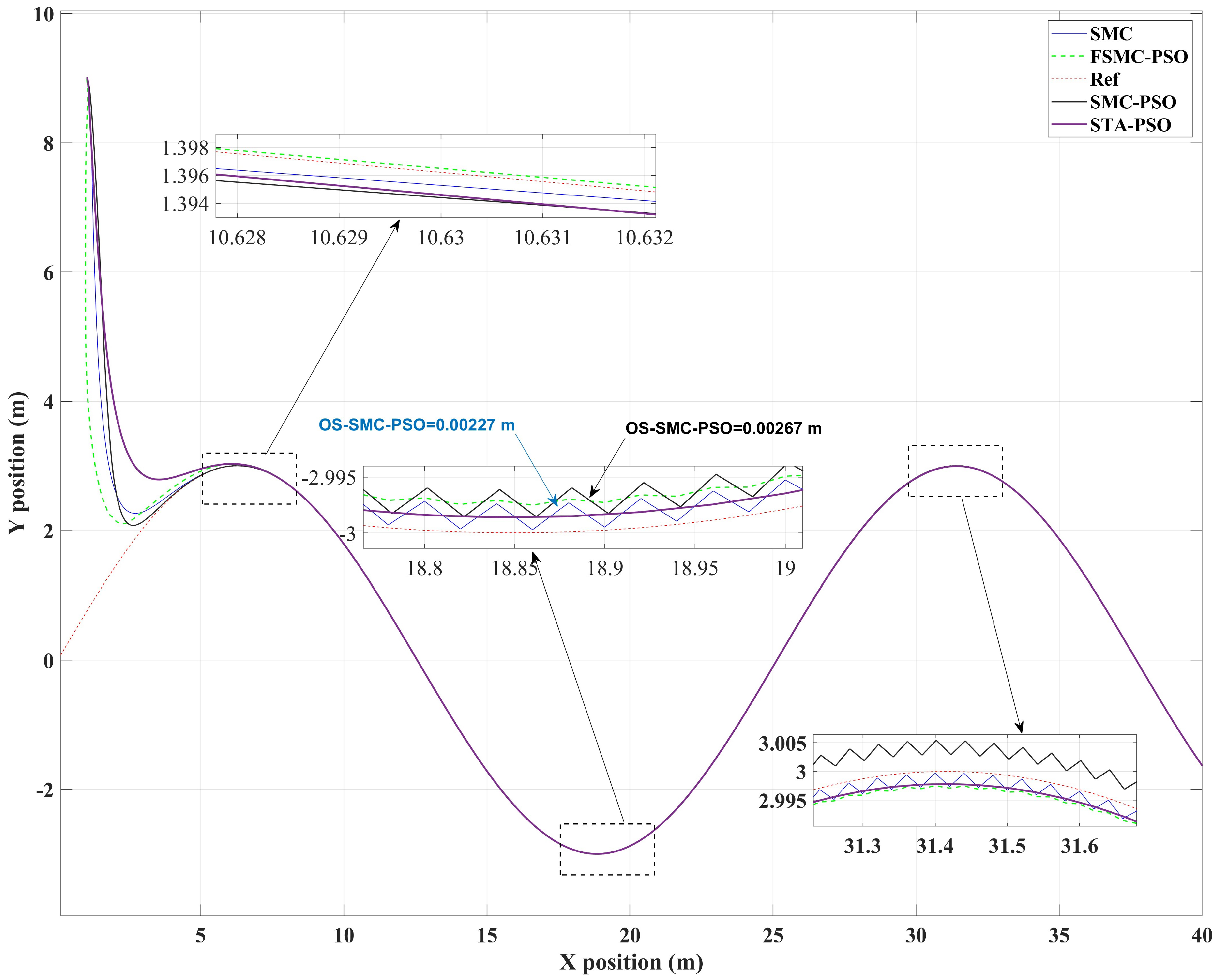
Figure 8 compares the planar motion of the AUV under FSMC-PSO, SMC-PSO, STA-PSO, and conventional SMC against the reference trajectory. The reference trajectory is a smooth nonlinear path with varying curvature and amplitude. Although all controllers are capable of following the desired path, noticeable differences in their dynamic responses can be observed.

During the transient phase (0–5 s), the conventional SMC exhibits a longer settling time accompanied by overshoot and oscillations, mainly due to the use of fixed switching gains. The SMC-PSO controller provides a moderate improvement by optimizing these gains offline, resulting in faster convergence toward the reference path. In contrast, the proposed FSMC-PSO controller achieves the fastest transient response, characterized by smooth convergence and minimal overshoot, and reaches steady-state tracking earlier than the other control strategies.

In the steady-state regime, FSMC-PSO demonstrates superior tracking accuracy and visibly reduced chattering compared to both SMC-PSO and conventional SMC. The zoomed views further highlight these improvements, where FSMC-PSO achieves a smaller overshoot ($OS=0.00227$ m) compared to SMC ($OS=0.00267$ m) and maintains smoother position regulation with negligible high-frequency oscillations.

At the valley near $x\approx 19$ m and the crest around $x\approx 31$–32 m, the magnified windows show that FSMC-PSO remains closest to the reference envelope with minimal under- and overshoot, whereas SMC exhibits wider deviations, while SMC-PSO presents noticeable high-frequency ripples.

These ripples effectively increase the path length and introduce micro-limit cycles that degrade local tracking precision. Across the entire trajectory, the chattering amplitude follows a consistent order: SMC-PSO exhibits the largest high-frequency oscillations. SMC shows moderate ripples, and FSMC-PSO achieves the strongest attenuation of switching artifacts.

This behavior aligns with the intended effect of fuzzy adaptation, where lower gains are applied for small values of $\left|s\right|$ and $|\dot{s}|$, while higher gains are only activated for larger deviations, thereby smoothing the control action while preserving robustness. In contrast, direct PSO tuning of SMC tends to favor aggressive gain values, which improve nominal tracking accuracy but amplify switching activity and noise sensitivity.

The STA-PSO controller exhibits a different compromise between smoothness and tracking accuracy. STA-PSO significantly suppresses classical chattering and ensures a continuous control action. However, in regions with high curvature, such as near the valley at $x\approx 19$ m and the crest around $x\approx 31$–32 m, STA-PSO shows a slight phase lag and a larger envelope deviation compared to FSMC-PSO. Although its steady-state response is smoother than conventional SMC, the absence of fuzzy gain adaptation limits its ability to simultaneously achieve fast transient convergence and tight steady-state tracking.

Overall, FSMC-PSO provides the best trade-off between accuracy, smoothness, and robustness, achieving faster transient convergence, smaller steady-state tracking errors, and significantly reduced chattering. These qualitative observations are consistent with the quantitative results reported in Table 4, where FSMC-PSO achieves lower IAE, ITAE, ISE, ITSE, and RMSE values in x, y, and $\psi$.

Figure 9 shows the time evolution of the SMC gains ($k_x$, $k_y$, and $k_{\psi }$) and the sliding surface parameters (${\lambda }_x$, ${\lambda }_y$, and ${\lambda }_{\psi }$) as adjusted online by the proposed FSMC-PSO controller. In all channels, the parameters exhibit a rapid transient adaptation phase during the first few seconds, followed by convergence to nearly constant steady-state values.

This behavior confirms that the PSO-optimized fuzzy rules effectively tune the controller parameters online, delivering strong corrective action during initial error regulation and stabilizing thereafter to avoid excessive switching activity.

For the surge and sway channels, the gains $k_x$ and $k_y$ initially reach relatively high peak values (approximately 60 and 150, respectively) to enforce rapid error convergence under large initial deviations.

These gains then decay rapidly to small steady-state levels once the tracking errors are reduced, indicating that the fuzzy adaptation mechanism suppresses unnecessary control effort after transient correction.

In contrast, the yaw gain $k_{\psi }$ converges to a moderate constant value around 10 with limited overshoot, reflecting the need for sustained corrective authority due to the AUV’s slower rotational dynamics.

The sliding surface parameters ${\lambda }_x$, ${\lambda }_y$, and ${\lambda }_{\psi }$ exhibit a similar fast convergence behavior.

After an initial adjustment period of approximately 2–3 s, the parameters stabilize at constant values (${\lambda }_x\approx 2.5$, ${\lambda }_y\approx 1.2$, ${\lambda }_{\psi }\approx 4$), forming well-conditioned sliding manifolds that balance convergence speed and robustness.

The absence of significant oscillations after convergence confirms that the FSMC–PSO scheme effectively avoids gain chattering and parameter drift, ensuring consistent closed-loop performance.

Overall, these results indicate that FSMC–PSO provides aggressive transient tuning in the presence of large errors, followed by smooth parameter stabilization during steady-state operation.

This adaptive behavior enhances trajectory precision while mitigating chattering, which is consistent with the reduced ripple observed in the trajectory plots and the superior performance indices reported in Table 4.

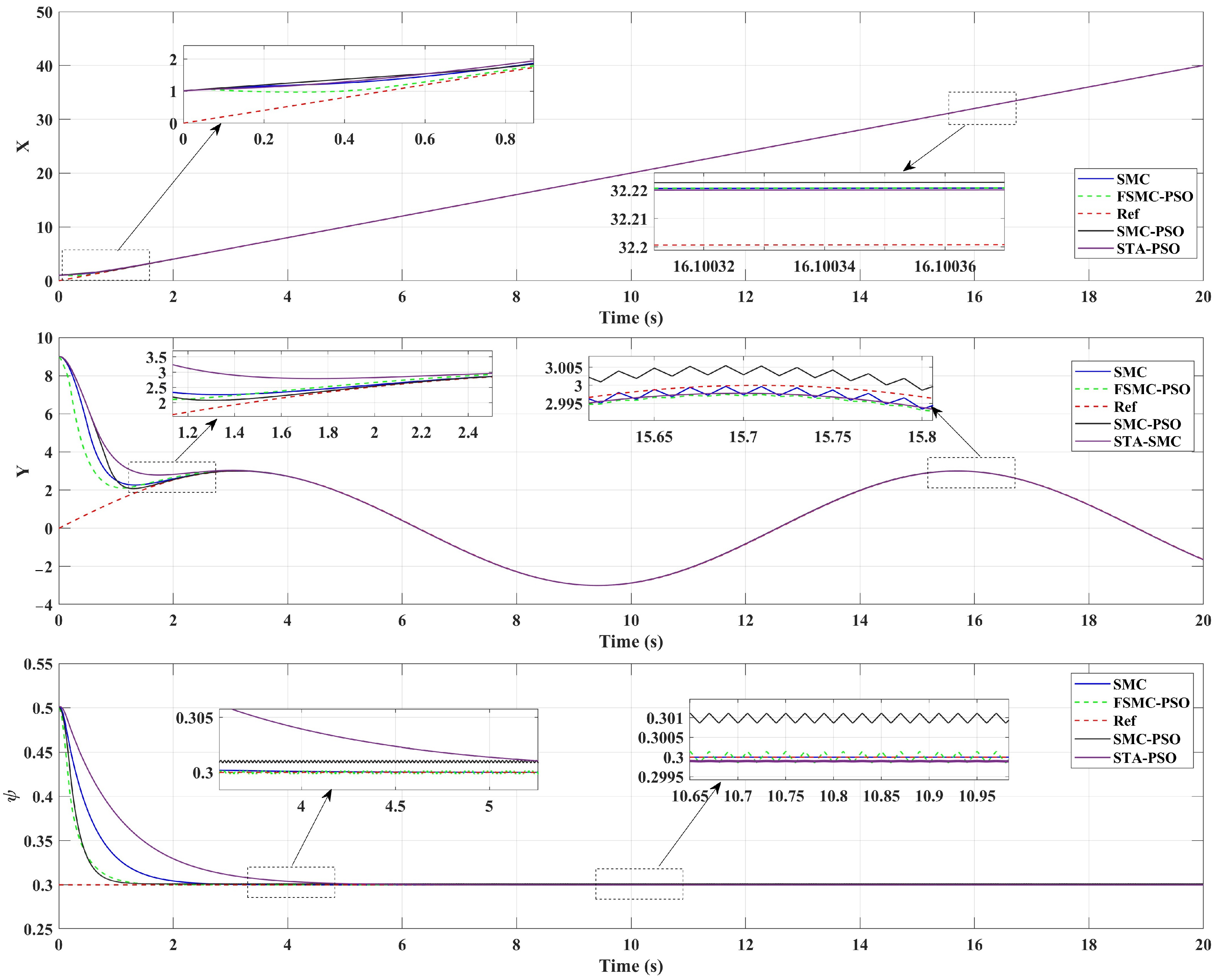
Figure 10 compares the position tracking performance of the x, y, and $\psi$ coordinates under four control strategies: classical SMC, SMC tuned by PSO, STA-PSO, and the proposed FSMC-PSO approach. Although all controllers are able to follow the reference trajectory, noticeable differences arise in terms of the transient response, smoothness, and tracking precision.

For the surge motion (x trajectory), all controllers exhibit nearly identical tracking behavior, with the vehicle rapidly aligning with the desired linear reference. The tracking error converges within the first few seconds, indicating that the surge dynamics are relatively easy to regulate and require only limited enhancement from adaptive tuning strategies. The STA-PSO controller follows the reference accurately with smooth transient behavior, offering performance comparable to SMC-PSO and FSMC-PSO in the surge direction.

In contrast, for the sway motion (y trajectory), the benefits of adaptive tuning become more pronounced. The classical SMC exhibits a larger initial overshoot due to its fixed-gain structure, while SMC–PSO and FSMC-PSO significantly reduce this transient deviation through optimized parameter tuning. The STA-PSO controller also reduces the initial overshoot and provides a smoother response compared to classical SMC, although its convergence speed is slightly slower than that of FSMC-PSO. Among the four methods, FSMC-PSO achieves the smoothest convergence with minimal oscillations, reflecting its ability to adapt the sliding gains online and avoid over-aggressive control actions. Overall, both FSMC-PSO and STA-PSO enhance lateral tracking accuracy while maintaining improved motion smoothness.

For the yaw angle ($\psi$), all controllers converge to the reference heading of approximately $0.3$ rad within about 2 s. FSMC-PSO demonstrates the fastest and smoothest settling behavior with minimal chattering, while STA-PSO also exhibits a smooth rotational response due to the super-twisting mechanism. In contrast, classical SMC shows higher steady-state oscillations caused by its discontinuous control action.

Overall, FSMC-PSO effectively combines the offline global optimization capability of PSO with the online local adaptability of fuzzy logic, resulting in a transient response that is both faster and smoother than classical SMC, SMC-PSO, and STA-PSO. These improvements are reflected in reduced tracking errors, improved disturbance rejection, and enhanced robustness during dynamic maneuvers.

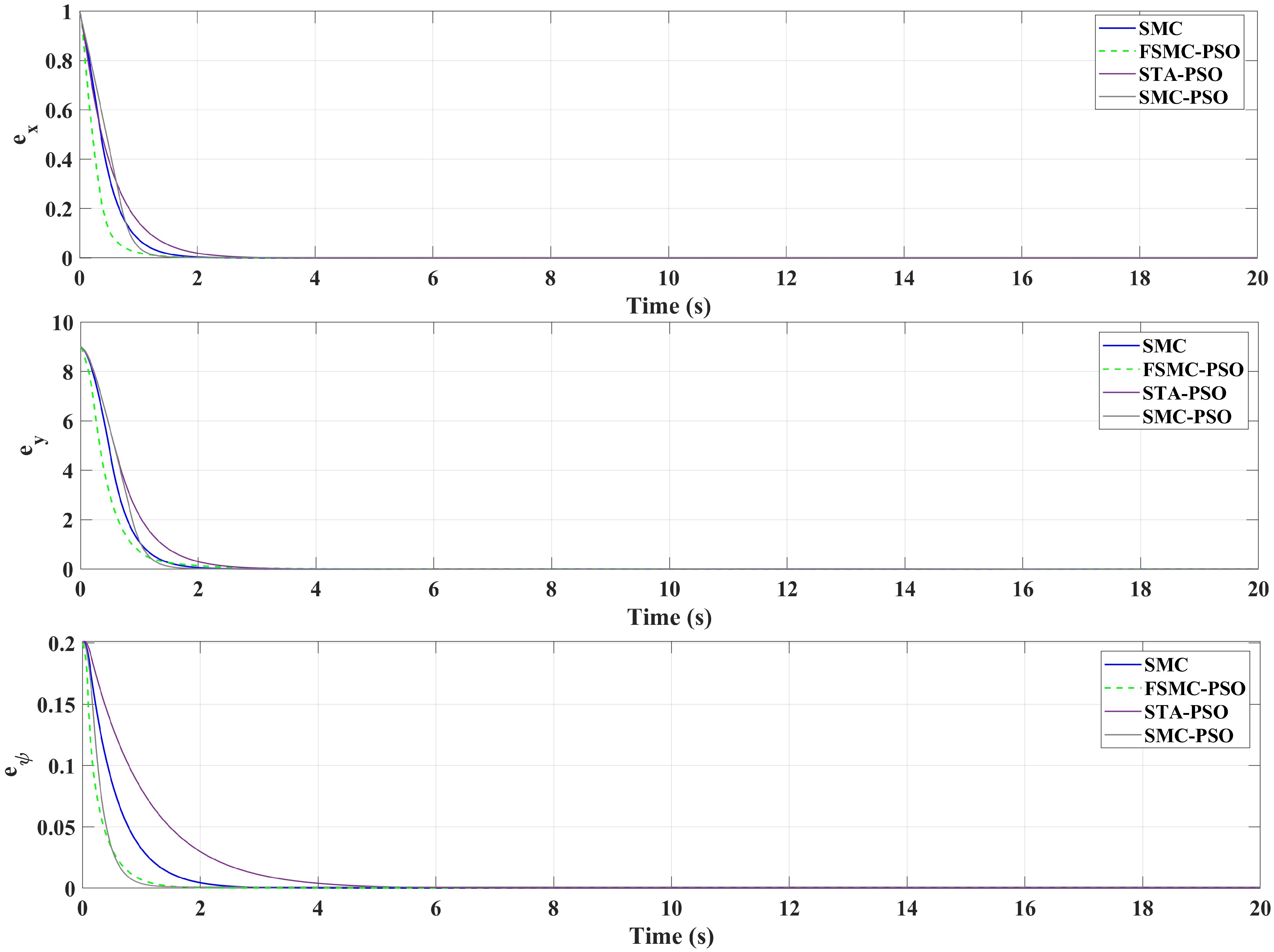
Figure 11 illustrates the tracking errors $e_x$, $e_y$, and $e_{\psi }$ for the four controllers: FSMC-PSO, STA-PSO, SMC-PSO, and classical SMC. For all control strategies, the tracking errors converge rapidly toward zero, confirming the global stability of the closed-loop system. Nevertheless, noticeable differences are observed in the transient performance among the control schemes.

In the surge direction ($e_x$), all controllers exhibit a fast exponential decay rate. FSMC-PSO achieves the fastest convergence, followed closely by SMC-PSO, while STA-PSO ensures stable convergence with a slightly slower decay rate but still outperforms the classical SMC. The adaptive approaches reduce the peak error and shorten the settling time to less than $1.5$ s, compared to approximately 2 s for the classical SMC.

In the sway direction ($e_y$), the improvement offered by adaptive control is more pronounced. The classical SMC exhibits a higher initial deviation and slower error attenuation due to its fixed-gain structure. In contrast, FSMC-PSO and SMC-PSO provide steeper error decay and significantly reduced overshoot, while STA-PSO presents a smoother transient response with moderate convergence speed. All adaptive strategies, including STA-PSO, achieve near-zero error within approximately $1.8$ s, demonstrating superior lateral tracking precision compared to classical SMC.

For the yaw angle ($e_{\psi }$), all controllers ensure rapid alignment with the desired heading. FSMC-PSO produces the smoothest transient response with minimal oscillations and reduced chattering. The STA-PSO controller also exhibits improved smoothness due to the super-twisting mechanism, whereas classical SMC shows more aggressive switching behavior.

Overall, these results validate that adaptive gain tuning through PSO and higher-order sliding mode techniques enhances the transient response, reduces peak tracking errors, and improves trajectory precision without compromising system stability. Among the evaluated strategies, FSMC-PSO achieves the best trade-off between convergence speed and smoothness, while STA-PSO provides a robust and smooth response with reduced chattering, and SMC-PSO offers a clear improvement over the baseline classical SMC.

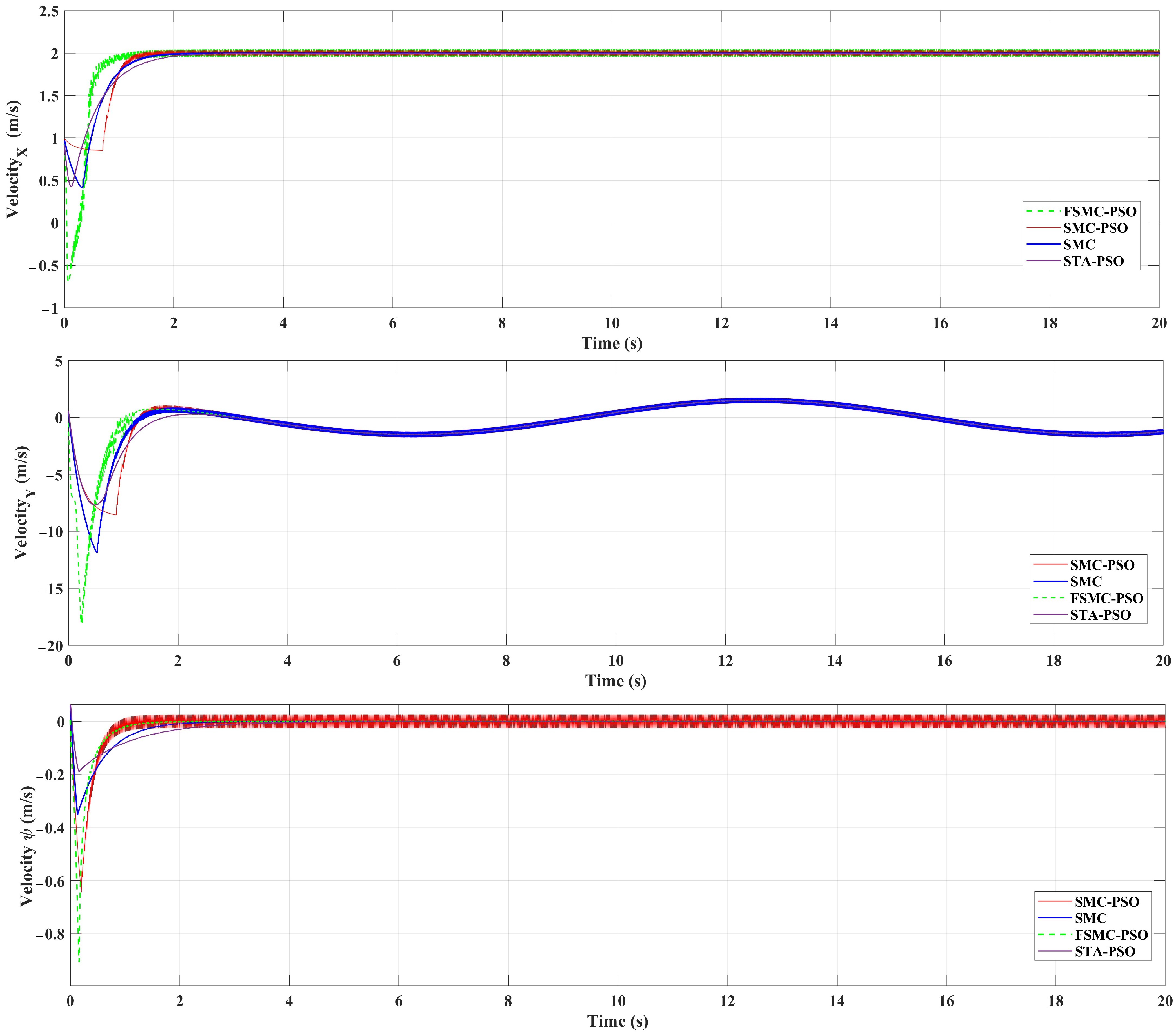
Figure 12 presents the velocity tracking performance of the AUV under four control schemes: FSMC-PSO, SMC-PSO, STA-PSO, and SMC. The responses correspond to the surge velocity u (top), sway velocity v (middle), and yaw rate r (bottom), respectively. For the surge velocity u, all controllers converge to the desired reference; however, clear differences appear in the transient behavior.

The adaptive scheme (FSMC-PSO) exhibits faster error attenuation and reduced initial overshoot compared to the classical SMC. In particular, FSMC-PSO achieves the shortest settling time (below $1.5$ s), followed by STA-PSO and SMC-PSO, whereas the classical SMC requires approximately 2 s to reach steady state, indicating slower transient convergence.

The sway velocity’s (v) response clearly highlights the advantage of adaptive and optimization-based control strategies. Classical SMC exhibits larger initial oscillations and a slower damping rate due to its fixed-gain structure and higher sensitivity to disturbances. In contrast, FSMC-PSO, SMC-PSO, and STA-PSO produce significantly smoother transients, with FSMC-PSO achieving the lowest peak deviation and the fastest stabilization, while STA-PSO shows improved damping compared to SMC-PSO but slightly slower convergence than FSMC-PSO. These improvements directly translate into enhanced lateral trajectory precision and reduced cross-track error during maneuvering.

For the yaw rate r, all four controllers demonstrate convergence with negligible steady-state error; however, their transient smoothness differs noticeably. FSMC-PSO achieves the most uniform transient response, effectively minimizing chattering and excessive switching activity typically associated with conventional SMC. STA-PSO also significantly attenuates chattering due to its continuous super-twisting structure, although slightly larger transient fluctuations are observed compared to FSMC-PSO.

Overall, these results demonstrate that integrating optimization-based tuning and fuzzy adaptation into the SMC framework substantially improves the transient response, reduces velocity tracking errors, and enhances motion smoothness without compromising closed-loop stability.

Among the evaluated controllers, FSMC-PSO provides the most favorable trade-off between convergence speed, overshoot suppression, chattering reduction, and control smoothness, making it particularly suitable for high-precision AUV velocity tracking tasks.

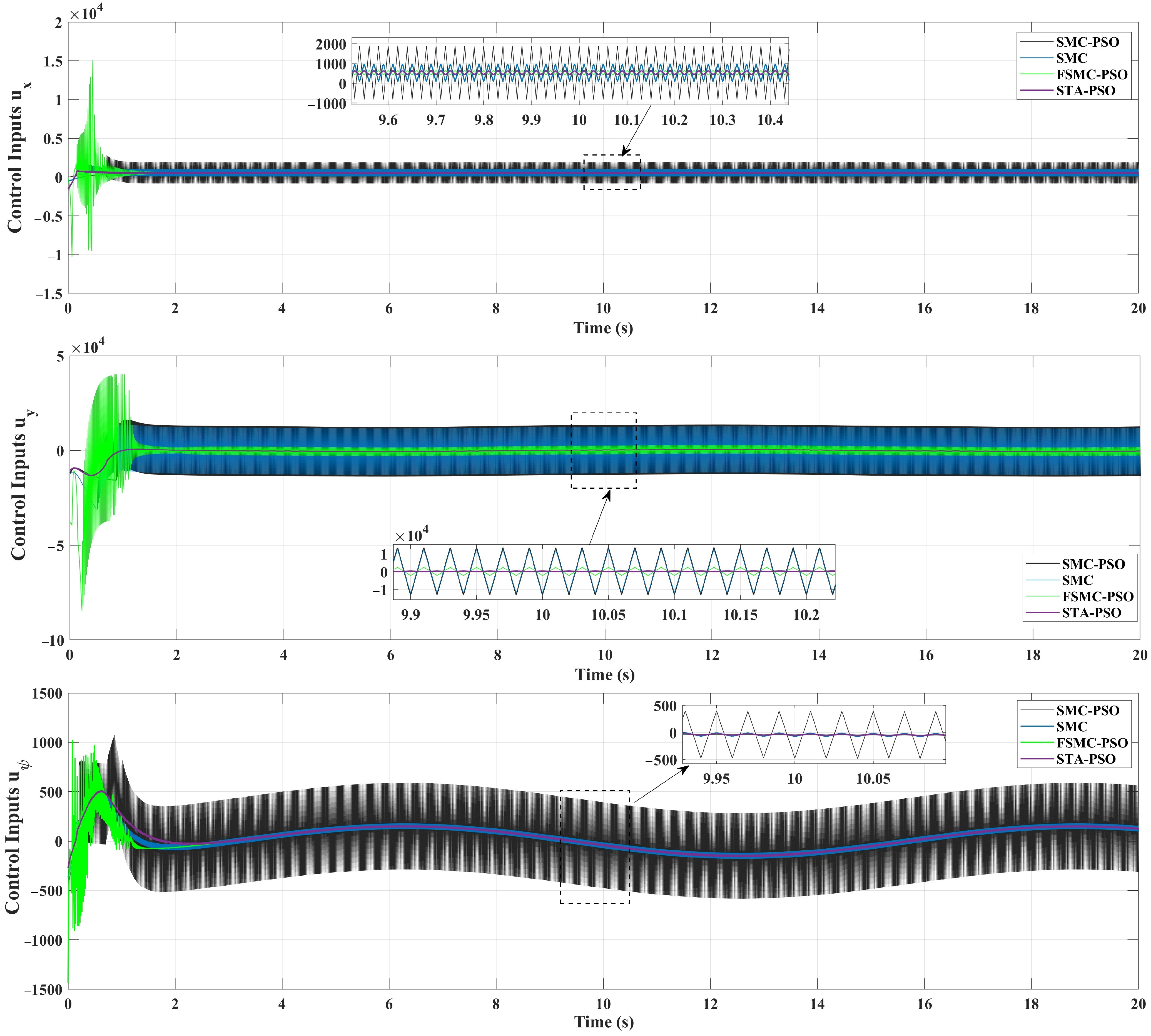
Figure 13 illustrates the control input signals generated under four different control strategies: FSMC-PSO, SMC-PSO, STA-PSO, and conventional SMC. For the FSMC-PSO strategy (top subplot), the control inputs initially exhibit a relatively high magnitude with noticeable oscillations during the transient phase (0–2 s). These oscillations are rapidly attenuated, and the control action converges to a smooth and stable profile with significantly reduced fluctuations after approximately 3 s. This behavior indicates that the combination of fuzzy adaptation and offline PSO tuning enhances robustness and effectively mitigates chattering.

For the classical SMC (middle subplot), the control inputs exhibit persistent oscillatory behavior throughout the entire simulation horizon. The control effort remains relatively large and does not fully settle, reflecting the well-known drawback of SMC, namely chattering caused by the discontinuous switching control law. Although closed-loop stability is achieved, the high-frequency oscillations imply increased actuator stress and reduced control efficiency.

The SMC-PSO strategy (bottom subplot) shows an improvement over classical SMC, with oscillations of lower amplitude and a smoother response, particularly after the transient phase. Nevertheless, residual chattering remains more pronounced than in FSMC-PSO, suggesting that PSO-based parameter optimization alone is insufficient to fully suppress the inherent switching effects of SMC.

The STA-PSO controller exhibits a markedly smoother control profile due to the continuous nature of the super-twisting algorithm. As observed in all three control channels, STA-PSO significantly reduces high-frequency oscillations compared to both SMC and SMC-PSO, resulting in bounded and continuous control inputs after the transient phase. However, during the initial response, the control effort of STA-PSO remains slightly higher than that of FSMC-PSO, and its convergence toward low-amplitude steady-state signals is comparatively slower. This behavior reflects the fixed-gain structure of STA-PSO, which, although effective in chattering suppression, lacks adaptive gain scheduling to further minimize control effort under small tracking errors.

Overall, the comparative results highlight that FSMC-PSO yields the most favorable control performance, achieving faster stabilization, lower control effort, and significant chattering suppression. By contrast, classical SMC suffers from sustained high-frequency oscillations, while SMC-PSO provides only moderate improvements and still lags behind both FSMC-PSO and STA-PSO in terms of control smoothness and efficiency.

Robustness  Study

Figure 14 illustrates the position tracking performance of the proposed controllers under different levels of random noise disturbances. The desired trajectory is shown as a dashed red curve, while the actual tracking responses under various disturbance intensities ($d_1$ to $d_6$) are represented by solid lines. In subplot (a), corresponding to the classical SMC, the trajectory tracking performance degrades noticeably as the noise intensity increases. Large deviations and oscillations are observed, particularly during transient phases and in the mid-trajectory region, indicating the high sensitivity of conventional SMC to stochastic disturbances.

In subplot (b), illustrating the performance of the SMC-PSO controller, moderate deviations from the desired trajectory are observed under high noise levels. The PSO-based optimization method improves robustness relative to classical SMC; however, residual tracking errors persist, especially in the mid-trajectory region, indicating limited noise rejection capability under severe disturbances.

In subplot (c), corresponding to the STA-PSO controller, improved tracking performance is achieved compared to SMC and SMC-PSO. The STA contributes to smoother trajectories and reduced chattering; however, noticeable deviations from the desired path still appear under high noise levels, especially during transient periods.

Subplot (d) illustrates the performance of the proposed FSMC-PSO controller. Trajectory tracking remains close to the desired path even in the presence of severe noise disturbances. Minor transient deviations are observed, but the controller effectively compensates for uncertainties and maintains accurate tracking, demonstrating superior robustness compared to the other control strategies.

Overall, the comparative results clearly indicate that FSMC-PSO achieves the highest tracking accuracy and robustness across all considered noise levels in the simulation. STA-PSO provides improved smoothness and disturbance rejection compared to SMC and SMC-PSO but remains less effective than FSMC-PSO in suppressing noise-induced deviations. Classical SMC exhibits the weakest disturbance rejection capability under stochastic disturbances.

These results are solely based on numerical simulations. Real-world factors, including ocean currents, actuator saturation, sensor noise, and communication delays, were not modeled. In addition, FSMC-PSO requires higher computational resources than SMC, SMC-PSO, and STA-PSO, which may impact real-time implementation. The applied random noise disturbances may also not fully represent realistic underwater conditions.

A comparative analysis is presented between the proposed FSMC-PSO controller and related control strategies reported in the literature, such as classical SMC, SMC-PSO, and STA-PSO. The FSMC-PSO controller offers several advantages: (1) the integration of conventional SMC, fuzzy logic, and PSO enhances overall trajectory tracking accuracy and robustness; (2) chattering is effectively suppressed through continuous adaptation of the switching gain k and sliding surface parameter $\lambda$ based on the real-time tracking error; (3) the controller demonstrates improved disturbance rejection capability compared with conventional approaches; and (4) performance indices (IAE, ITAE, ISE, ITSE, and RMSE) are consistently reduced across all motion states, contributing to smoother control signals and increased actuator longevity.

Despite these advantages, several limitations are acknowledged: (1) The inclusion of the PSO process increases computational complexity compared with conventional SMC, particularly when online optimization is considered, thus requiring higher processing capacity or offline optimization. (2) The fuzzy inference system introduces additional design parameters that must be carefully tuned to maintain stability and performance. (3) Variations in external disturbances can lead to variations in the adaptive fuzzy outputs, which consequently alter the adaptive parameters k and $\lambda$. Such variations may increase sensitivity, complicate real-time tuning, and potentially degrade stability if not properly bounded. (4) The present validation strategy is based solely on numerical simulations, and experimental implementation is still required to confirm practical applicability.

Overall, the FSMC-PSO controller achieves a favorable balance between accuracy, robustness, and smoothness, making it a promising control strategy for high-precision AUV trajectory tracking within the considered simulation framework. In order to illustrate the disturbance rejection capability, the controllers’ tracking performance was evaluated under the representative disturbance of $d_4=60·$ randn(1,1), which is the level at which the baseline SMC begins to exhibit noticeable deviations. Figure 14 shows the trajectories of all four controllers under this disturbance. It can be seen that FSMC-PSO maintains the closest tracking accuracy to the reference trajectory with minimal chattering, while SMC-PSO shows moderate deviations, and classical SMC exhibits significant tracking errors. This representative scenario highlights the superior robustness of the proposed FSMC-PSO controller. 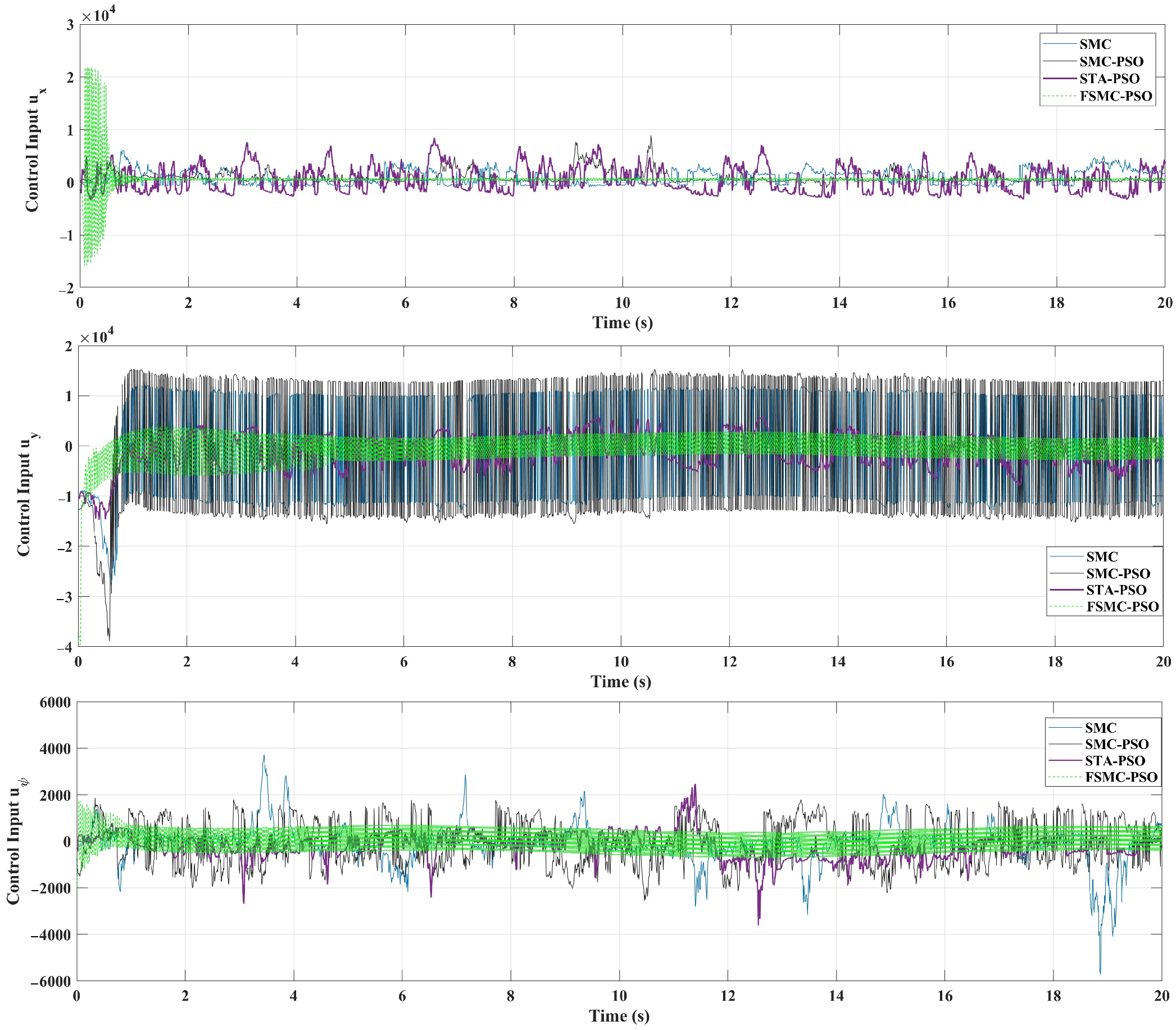Figure 15 shows the control signals for FSMC-PSO, STA-PSO, SMC-PSO, and classical SMC under the representative the random disturbance of $d_4=60·$ randn(1,1). The FSMC-PSO controller exhibits smooth and robust control with minimal chattering, while SMC-PSO displays moderate fluctuations, and classical SMC shows significant oscillations. This illustrates the superior disturbance rejection capability of the proposed FSMC-PSO controller.

5. Conclusions

This study presented a fuzzy sliding mode controller optimized using particle swarm optimization (FSMC-PSO) for trajectory tracking of an AUV. The proposed controller integrates the robustness of SMC, the adaptability of fuzzy logic, and the global optimization capability of PSO to achieve accurate trajectory tracking with reduced chattering.

Comparative simulations were conducted against conventional SMC, SMC-PSO, and STA-PSO under identical operating conditions and in the presence of random noise disturbances. Performance was evaluated using standard tracking indices (IAE, ITAE, ISE, ITSE, and RMSE). The results demonstrated that FSMC-PSO consistently outperformed the benchmark controllers, achieving up to an 86.58% reduction in ITAE and a 73.53% reduction in ITSE while maintaining robust performance across all motion states (X, Y, and $\psi$).

In addition to improved tracking accuracy, FSMC-PSO significantly reduced the chattering effect compared to conventional SMC and SMC-PSO. The adaptive fuzzy tuning of the switching gain and sliding coefficients contributed to smoother control actions, enhanced actuator efficiency, and increased overall system reliability. These improvements highlight the effectiveness of FSMC-PSO in achieving precise and disturbance-resilient trajectory tracking within the considered simulation framework.

The proposed FSMC-PSO control approach is inherently scalable. Its design allows extension to AUVs with different sizes and dynamic characteristics, as well as multi-AUV systems for coordinated operations. The fuzzy adaptation and PSO-optimized parameters can be adjusted to accommodate varying vehicle dynamics and mission requirements, ensuring consistent performance without fundamental changes to the control architecture.

Real-world implementation of FSMC-PSO on an actual AUV may face several challenges. These include sensor noise and delays, actuator saturation and bandwidth limitations, unmodeled hydrodynamic effects, and communication constraints in multi-AUV systems. Ensuring robustness under these practical conditions requires careful calibration of the fuzzy adaptation rules and PSO parameters, as well as real-time monitoring of system performance. Addressing these challenges is crucial to successfully translate the proposed controller from simulations to field deployment.

Although the present study is limited to numerical simulations, future work will focus on experimental validation using real AUV platforms under realistic environmental disturbances, including ocean currents, actuator limitations, and sensor noise. In addition, the FSMC-PSO framework will be extended to cooperative multi-AUV systems for coordinated motion and formation control. Further efforts will also aim to optimize computational efficiency to support real-time implementation.