Magnetic Equivalent Circuit-Based Performance Evaluation of Modular PCB AFPM Motor for Electric Water Pumps

Abstract

Electric Water Pumps (EWPs) are being adopted more widely to improve thermal management in internal combustion engines and electrified powertrain systems. In this context, the drive motor must deliver high efficiency and reliability despite a strict volume constraint. This paper addresses a key drawback of coreless printed circuit board (PCB) stator axial-flux permanent-magnet machines for EWP use: the PCB traces are directly exposed to the magnet flux, which increases AC loss, while the required phase resistance also leads to non-negligible DC copper loss. To mitigate both loss components within the same conductor design space, a pyramid trace concept is introduced. A magnetic equivalent circuit (MEC) based model is first used to estimate the baseline performance as the number of PCB stator modules changes, and the resulting scalability is examined in terms of module commonality. The final design then applies the pyramid trace layout with a layer-dependent trace width that is narrower on the layers closer to the magnets and wider on the layers farther away—the trade-off between AC loss and DC loss is optimized using 3D finite element analysis. Torque predictions from the simplified MEC model are cross-checked against 3D finite element analysis (FEA), and finally, a prototype is built to validate the analysis with experimental measurements; for the final selected model, the torque prediction error is 2.37% compared with the validation result.

1. Introduction

Electric Water Pumps (EWPs) can actively regulate coolant flow according to operating demand. This reduces parasitic power in the thermal management system and improves overall powertrain efficiency. Unlike mechanically driven pumps, EWP speed is decoupled from engine speed. This enables control strategies that maintain cooling performance while avoiding unnecessary pumping power [1]. In practical driving cycles, electric coolant pumps can reduce pump energy consumption and allow a reduction in radiator size [2]. In multi-loop smart thermal management systems, EWPs also improve responsiveness to heat-source variations and suppress overcooling, providing system-level energy benefits [3]. As EWP adoption expands from fuel-economy improvement in internal combustion engines to comprehensive thermal management of batteries, inverters, and motors in HEVs and EVs, pump drive motors must be designed to operate reliably under prolonged continuous operation and wide speed variability [4].

Wide-speed operation changes the loss composition and tends to increase AC loss in the high-speed region. For EWP use, the motor must deliver sufficient torque to satisfy the required flow head conditions within a limited installation volume. As higher speeds and smaller sizes become more common, winding temperature rise becomes a direct performance limit. Therefore, the design objective extends beyond peak efficiency and focuses on maintaining a thermally acceptable current density at the rated current.

Coreless structures that minimize or eliminate ferromagnetic cores have recently gained attention. They can offer advantages in high-speed efficiency and dynamic response. Axial-flux permanent-magnet motors (AFPM) are suitable for integrated pump configurations because they provide high torque density with short axial length. In particular, a PCB stator enables winding patterns to be manufactured with repeatable precision using standard PCB processes. This reduces fabrication variability and supports mass production [5]. Prior studies on PCB motors highlight the geometric flexibility of PCB windings, including deliberate control of cross-sectional areas and parallel paths. They also note that high-frequency copper loss and thermal design can become key bottlenecks [6].

Many PCB stator motors operate in a near-coreless configuration. In this case, airgap flux penetrates the winding region directly. Conductor loss is then not explained by DC copper loss alone, because the conductors experience time-varying magnetic fields. High-speed case studies of coreless AFPM machines with PCB windings identify winding loss and thermal management as central design issues [7]. Electromagnetic design and modeling of a two-phase AFPM PCB motor also show that PCB winding modeling is feasible. At the same time, loss components induced by airgap flux can influence design outcomes if not treated appropriately [8].

PCB winding losses include resistive loss due to RMS current, frequency-dependent AC copper loss driven by skin and proximity effects, and additional losses caused by circulating currents in multilayer and parallel paths. Multiphysics investigations on high-speed AFPM machines with multilayer PCB windings show that these mechanisms can make the overall loss behavior complex [9]. Experimental and numerical studies on open circuit losses of PCB stators in coreless AFPM machines further report that eddy current components inside PCB traces depend strongly on waveform characteristics, flux asymmetry, and conductor geometry [10]. For these reasons, final validation of PCB stator designs often requires 3D FEA.

Accordingly, recent PCB motor research increasingly targets loss mitigation structures, more accurate modeling, and integrated electro-thermal design. For example, conductor slits have been investigated to segment eddy current paths and reduce loss, with quantitative analysis of how slit configurations affect eddy current and supply current loss components [11]. However, slit designs can also introduce design risk. Depending on operating conditions and geometry, certain configurations may trigger localized transient eddy currents and sharply increase AC loss. Under identical AFPM conditions, resistance and loss characteristics have also been shown to vary with PCB winding patterns such as wave, spiral, and segmented designs. This confirms that winding-pattern selection can dominate performance [12]. Disk-type PMSM with PCB windings likewise demonstrates feasibility while emphasizing the importance of loss modeling for high-speed operation [13].

The geometric flexibility of PCB windings also enables loss-oriented optimization. Increasing the trace cross-section reduces DC resistance and thus DC copper loss. In regions with strong flux exposure, however, a larger trace can enlarge eddy current paths and increase AC loss. This opposing influence creates a trade-off between DC and AC losses that directly affects efficiency [14]. Because proximity effect loss depends on the local magnetic field distribution and the non-uniformity of current density, a larger cross-section does not necessarily reduce total loss, as also indicated by modeling and loss analysis studies [15]. Classical analyses of AC loss in multilayer thin traces similarly show that the frequency-dependent resistance increase must be considered in the design process. They also suggest that segmentation and multilayer strategies can reduce AC copper loss [16].

In PCB motor designs, flux exposure is strongly dependent on layer position. Layers closer to the magnets experience higher flux density and larger dB/dt. When identical trace width and thickness are applied across all layers, copper loss can become concentrated in the most strongly exposed layers. In addition, within a given layer, tangential speed and flux distribution vary with radius, leading to radius-dependent sensitivity of AC copper loss. Nevertheless, uniform-width traces are frequently used to maintain geometric symmetry and consistent current sharing, which restricts layer and radius-specific allocation of conductor area based on loss sensitivity.

To address this limitation, researchers have investigated windings with nonuniform trace width. Unequal-width PCB windings have been reported for AFPM generators to enhance electromagnetic performance; however, most prior studies have emphasized output characteristics and flux coupling rather than the deliberate spatial allocation of frequency-dependent copper loss, which becomes dominant in high-speed continuous duty operation such as EWP drives [17]. Separately, current crowding in PCB vias has been identified as a major source of copper loss, and multi-via interconnections have been proposed to reduce this contribution [18]. These findings suggest that effective PCB motor design should be treated as an integrated problem that includes winding geometry, current path design, and thermal pathways.

Accordingly, AFPM research has placed increasing emphasis on model-based design. Recent review papers highlight the growing adoption of coreless topologies and underscore the need for design criteria that simultaneously account for loss mechanisms, thermal constraints, and manufacturing limitations [19]. To enable rapid design iterations, MEC models have been widely used due to their low computational cost and suitability for sensitivity studies, and the literature reports that MEC-based approaches can reduce reliance on computationally intensive 3D analysis [20]. Moreover, MEC formulations have been applied to nonconventional winding configurations, including ring windings, indicating that the approach remains applicable even under winding topology variations [21]. In this work, a simplified but refined MEC formulation is adopted, and its torque prediction error is quantitatively evaluated against three-dimensional FEA.

The main contribution of this paper is a copper loss reduction concept based on layer-dependent PCB winding design, supported by an evaluation framework enabled by the modular PCB stator configuration. A pyramid trace concept is introduced, in which trace width is varied stepwise across layers and along the radial direction. Trace width is reduced in layers near the magnets to limit AC copper loss in regions of high flux exposure, whereas it is increased in layers farther from the magnets to reduce phase resistance and DC copper loss under RMS current. Consequently, the conductor area is not increased uniformly; instead, it is redistributed from regions with high AC loss sensitivity toward regions with lower sensitivity. This provides a practical design rule that explicitly reflects airgap flux exposure in coreless PCB motors [22].

The torque capability of baseline designs is first estimated using the MEC model, and accuracy is assessed by comparison with 3D FEA. The design tendency is further examined by combining MEC-based flux estimation with a leakage-factor formulation for airgap flux. Finally, efficiency and current-density maps are analyzed over the full EWP operating region, and thermal stability is validated through temperature tests on a prototype. The prediction errors of the MEC model and the 3D FEA model are also evaluated through prototype testing by comparing measured results with the analysis outcomes.

2. Characteristics

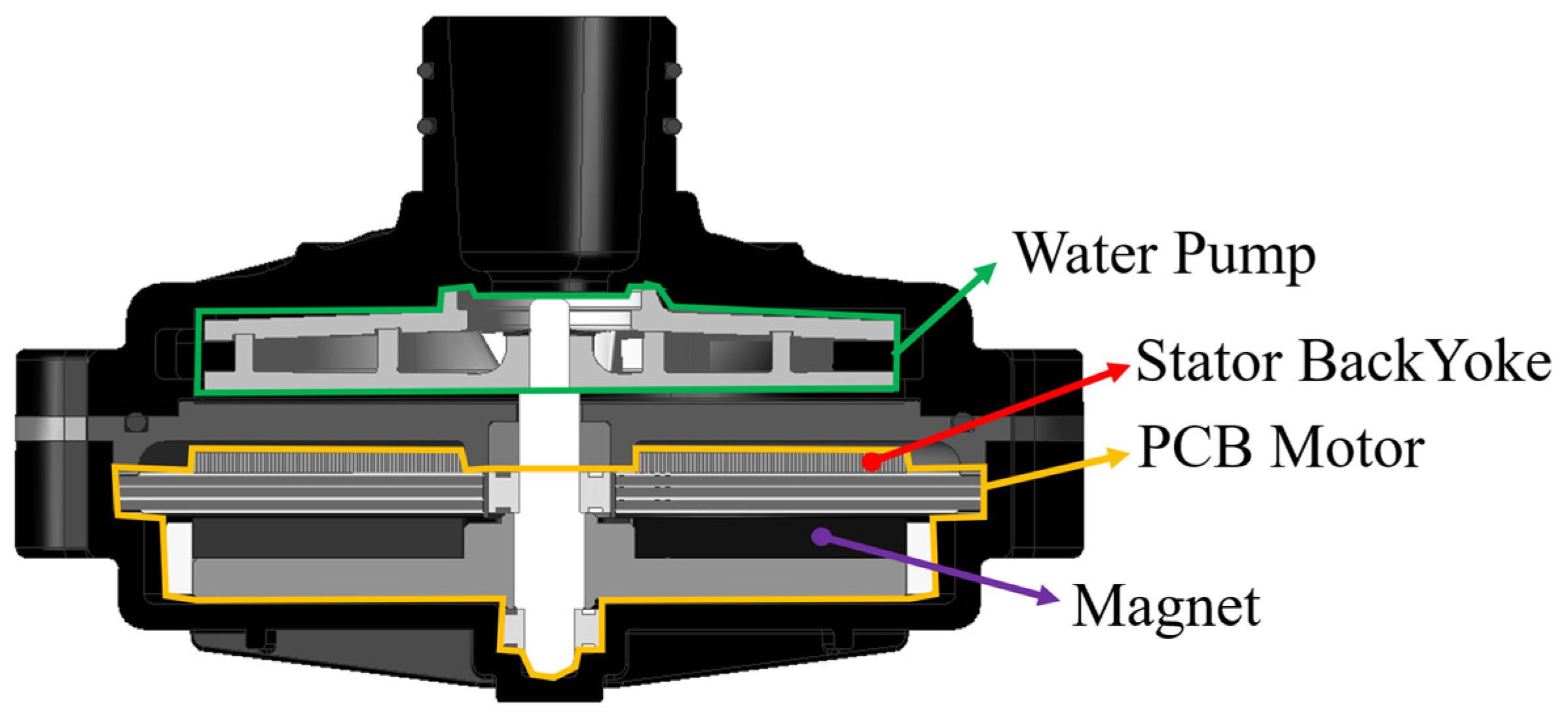
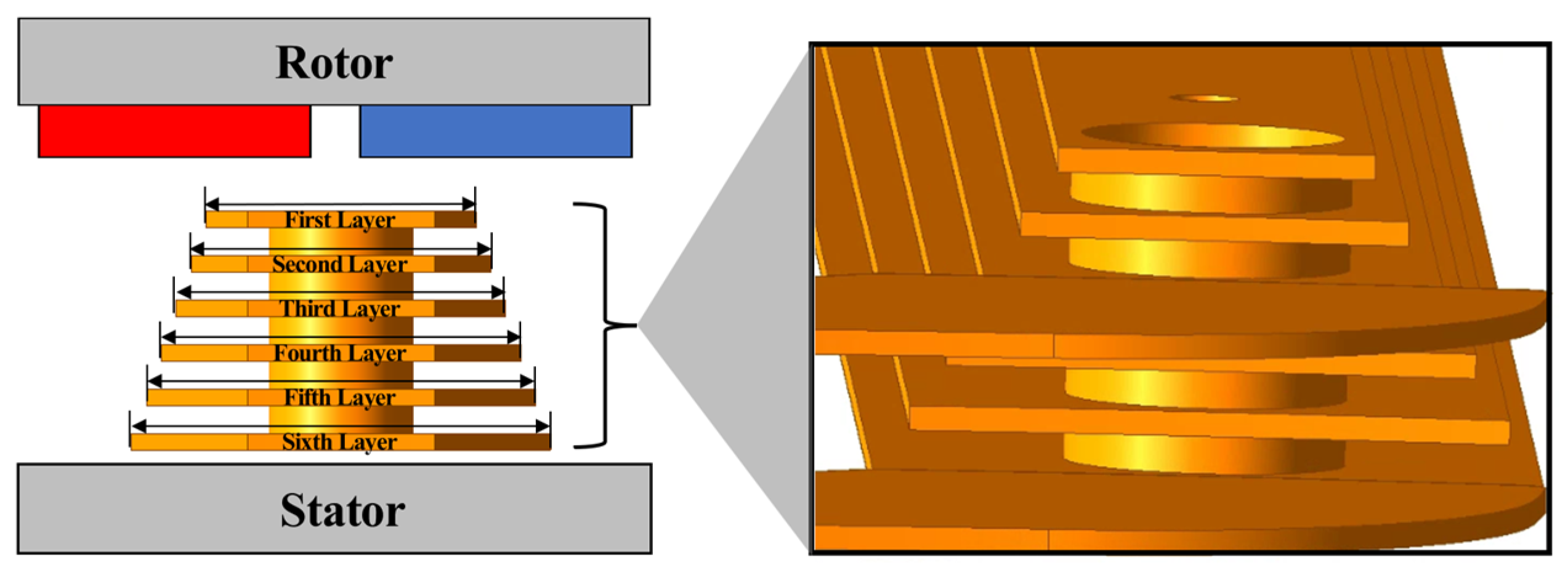
2.1. Machine Structure for EWP System

Figure 1 shows the axial-flux permanent-magnet configuration proposed in this paper, where the motor is integrated inside the EWP housing. Although the integrated motor–pump layout can reduce the axial length, it imposes strict constraints on the outer diameter, stack length, and airgap length. Because the impeller geometry of an EWP is limited by hydraulic resistance and cavitation margin, the available design space for the motor is also restricted. Therefore, the motor must secure sufficient torque within a limited outer diameter. In addition, the pump coolant can be utilized as a heat sink to remove motor heat, but insulation and leakage considerations are required. In the proposed EWP architecture using a PCB stator, the coolant does not directly enter the motor region; instead, the water-pump section and the motor section are separated by a partition wall. In this structure, the stator back yoke of the PCB stator is in direct contact with the partition wall, providing an efficient heat-transfer path and favorable thermal performance. This configuration also enables a design with a minimized airgap length.

Table 1. Design specifications for EWP PCB motor.

Parameter	Value	Unit
Pole/Slot	10/30	-
PCB Stator Inner Diameter	80	mm
PCB Stator Outer Diameter	17.7	mm
Stack length (Active)	14.4	mm
Trace Copper Thickness	2	oz
Trace Layer (Parallel)	6	-
Core	35PN300	-
Magnet	N45UH	-
PCB Prepreg	FR-4	-
Coil	Copper	-

shows the specifications of the PCB motor designed for the EWP application. The motor has an active part outer diameter of 80 mm. The PCB uses 2oz copper and a 6-layer structure. The total axial length of the active part is 14.4 mm. The 3D FEA was conducted using Ansys Maxwell Release 2025R2.

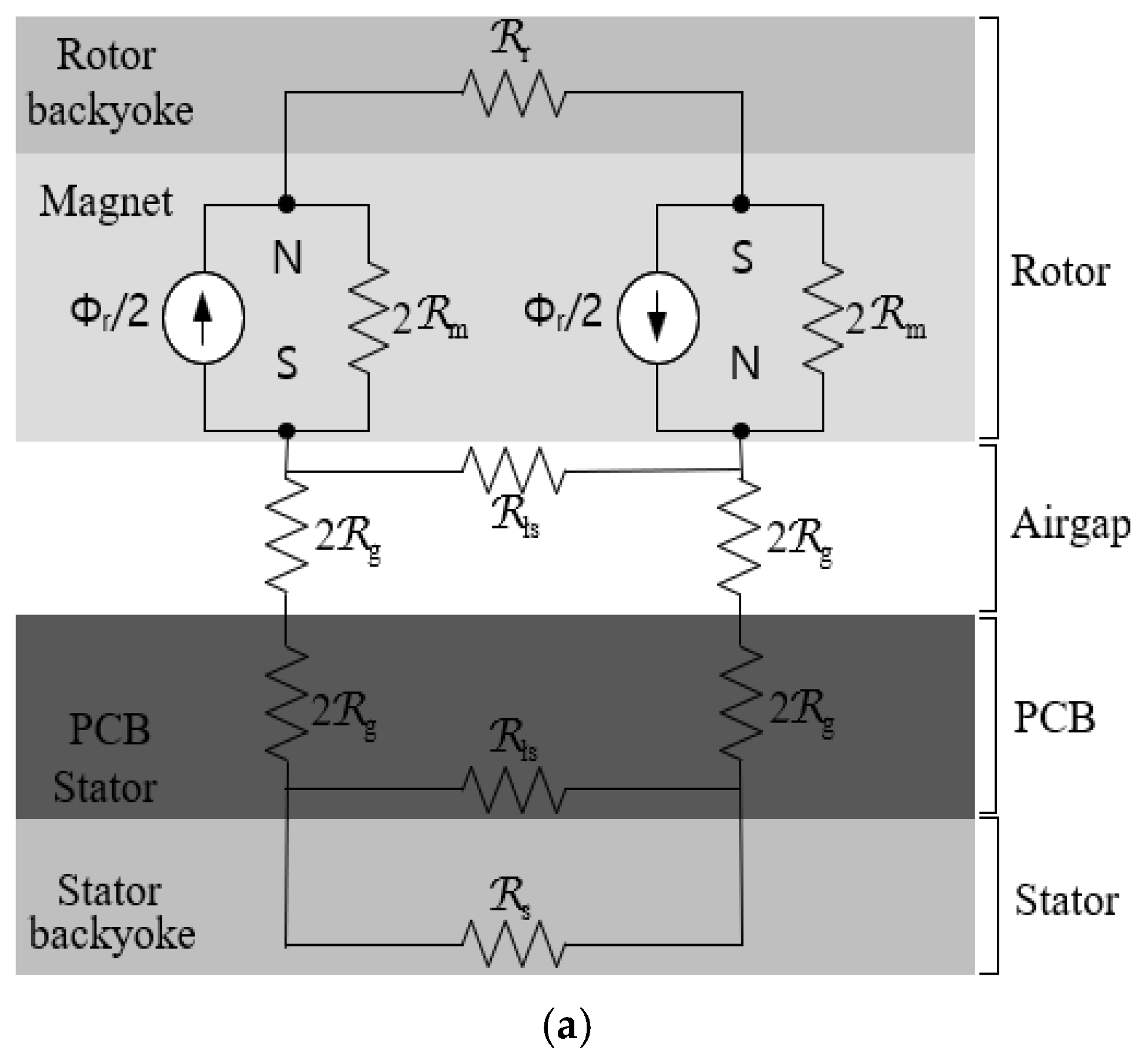
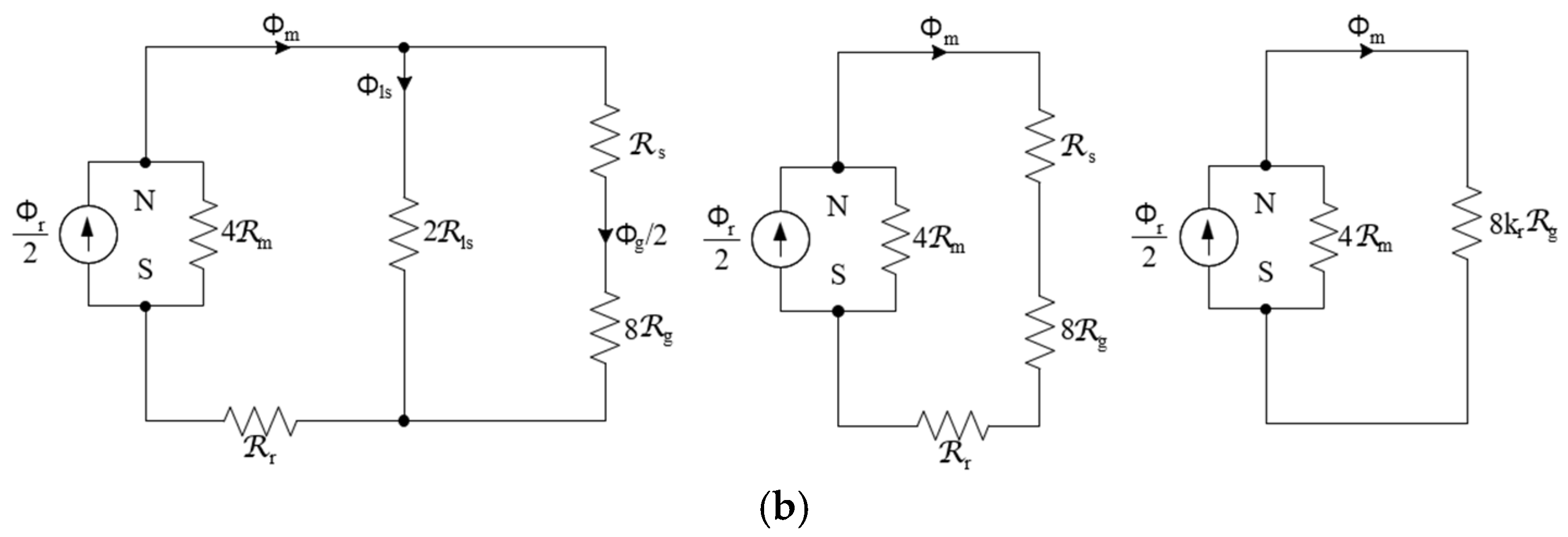
2.2. Magnetic Equivalent Circuit Model of PCB AFPM

Equations (1) and (2) present the torque expressions for the RFPM and the AFPM, respectively. In Equation (1), T_RFM denotes the torque of the radial-flux motor. The winding factor is represented by k_w, and B_g1 indicates the airgap flux density per pole. In (1), the airgap term ac represents the average airgap flux per unit area, which can be expressed as the average airgap flux density. The angle $\beta$ denotes the electrical angle between the current vector and the airgap flux vector; therefore, cos($\beta$) captures their phase alignment. The geometric parameters D_g and L_stk indicate the rotor outer diameter and the active axial stack length, respectively. Equation (2) expresses the electromagnetic torque of the axial-flux machine, T_AFM. The winding factor k_w1 is defined for the fundamental component so that torque capability can be discussed in terms of the dominant harmonic while limiting the influence of higher-order harmonics. Using the average airgap flux density B_avg and the torque coefficient K_d, the formulation also reflects how non-ideal effects reduce torque; a larger K_d corresponds to a larger torque drop. The diameter term D_out denotes the rotor outer diameter, which is equivalent to the overall machine diameter in this study. These definitions allow a clear interpretation of torque scaling. For a radial-flux machine operated at comparable magnetic loading and electric loading, torque scales approximately with D_g²L_stk, meaning that shortening the stack length directly reduces torque and output. In contrast, the axial-flux topology exhibits a stronger dependence on diameter, with torque scaling dominated by the rotor diameter term. This is the main reason that axial-flux machines are attractive for applications requiring a short axial length, where torque is preferably increased by utilizing a larger effective airgap area rather than extending L_stk. This scaling viewpoint is used in the following sections to motivate the module-stacking strategy and its impact on torque capability.

$$T_{RFM}=\left({\displaystyle \frac{\pi }{4}}{k}_w{B}_{g1}ac cos\beta \right)D_g^2{L}_{stk}$$

(1)

$$T_{AFM}=\left\{\left({\displaystyle \frac{1}{8}}ac\pi k_{w1}{B}_{avg}\right)\left(1-K_d^2\right)\right\}{D}_{out}^3$$

(2)

Figure 2a shows the MEC model of the AFPM motor using a PCB stator. Since the MEC model in this paper is intended for rapid, equation-based torque calculation, the circuit is simplified as shown in Figure 2b.

Since a magnetic equivalent circuit must account for the magnetic reluctance of each material along the flux path, R_m represents the magnetic reluctance of the permanent magnet, R_pcb represents the magnetic reluctance of the PCB substrate, and R_g represents the magnetic reluctance of the mechanical airgap. These reluctances are calculated using Equations (3)–(5).

$${\mathrm{R}}_{\mathrm{m}}={\displaystyle \frac{{\mathrm{L}}_{\mathrm{m}}}{{\mathsf{\mu }}_0{\mathsf{\mu }}_{\mathrm{p}\mathrm{m}}{\mathrm{A}}_{\mathrm{m}}}}$$

(3)

$${\mathrm{R}}_{\mathrm{p}\mathrm{c}\mathrm{b}}={\displaystyle \frac{{\mathrm{g}}_{\mathrm{p}\mathrm{c}\mathrm{b}}}{{\mathsf{\mu }}_0{\mathrm{A}}_{\mathrm{p}\mathrm{c}\mathrm{b}}}}$$

(4)

$${\mathrm{R}}_{\mathrm{g}}={\displaystyle \frac{\mathrm{g}\mathrm{’}}{{\mathsf{\mu }}_0{\mathrm{A}}_{\mathrm{g}}}}$$

(5)

The A_m of the PCB AFPM can be expressed as follows in Equation (6),

$${\mathrm{A}}_{\mathrm{m}}={\displaystyle \frac{\left\{\left(\mathsf{\pi }{{\mathrm{R}}_{\mathrm{o}\mathrm{u}\mathrm{t}}}^2-\mathsf{\pi }{{\mathrm{R}}_{\mathrm{i}\mathrm{n}}}^2\right)\left({\mathsf{\alpha }}_{\mathrm{m}}\right)\right\}}{{\mathrm{N}}_{\mathrm{p}\mathrm{o}\mathrm{l}\mathrm{e}\mathrm{s}}}}$$

(6)

α_m is the pole arc coefficient of the permanent magnet. R_s is the magnetic reluctance of the stator, where S_T is the stator thickness, μ_{rec_s} is the relative permeability of the stator, and A_s represents the stator’s cross-sectional area. Similarly, for the rotor, R_r is defined with R_T as the rotor thickness, μ_{rec_r} as the relative permeability of the rotor, and A_r as the rotor’s cross-sectional area.

$${\mathrm{R}}_{\mathrm{s}}={\displaystyle \frac{{\mathrm{S}}_{\mathrm{T}}}{{\mathsf{\mu }}_0{\mathsf{\mu }}_{\mathrm{r}\mathrm{e}{\mathrm{c}}_{\mathrm{s}}}{\mathrm{A}}_{\mathrm{s}}}}$$

(7)

$${\mathrm{R}}_{\mathrm{r}}={\displaystyle \frac{{\mathrm{R}}_{\mathrm{T}}}{{\mathsf{\mu }}_0{\mathsf{\mu }}_{\mathrm{r}\mathrm{e}{\mathrm{c}}_{\mathrm{r}}}{\mathrm{A}}_{\mathrm{r}}}}$$

(8)

${\mathsf{\phi }}_{\mathrm{r}}$ is the ideal flux value of a single pole of the permanent magnet, and

$${\mathsf{\phi }}_{\mathrm{r}}={\mathrm{B}}_{\mathrm{r}}{\mathrm{A}}_{\mathrm{m}}$$

(9)

${\mathsf{\phi }}_{\mathrm{m}}$ is the flux emanating from the permanent magnet as calculated by the magnetic equivalent circuit.

$${\mathsf{\phi }}_{\mathrm{m}}={\displaystyle \frac{4R_m}{\left(4R_m\right)+(R_s+4R_g+4R_p+R_r)}}{\displaystyle \frac{{\mathsf{\phi }}_{\mathrm{r}}}{2}}$$

(10)

To eliminate leakage reluctance, the leakage coefficient K_ls is defined as

$${\mathrm{K}}_{\mathrm{l}\mathrm{s}}={\displaystyle \frac{{\mathsf{\phi }}_{\mathrm{g}}}{2{\mathsf{\phi }}_{\mathrm{m}}}}$$

(11)

The airgap flux, ${\mathsf{\phi }}_g$ is

$${\mathsf{\phi }}_{\mathrm{g}}=2{\mathrm{K}}_{\mathrm{l}\mathrm{s}}{\mathsf{\phi }}_{\mathrm{m}}$$

(12)

If the flux ${\mathsf{\phi }}_{\mathrm{m}}$ is simplified by integrating the low-reluctance core into the reluctance coefficient K_r through the equivalent circuit simplification process shown in Figure 2b, then

$${\mathsf{\phi }}_{\mathrm{m}}={\displaystyle \frac{4{\mathrm{R}}_{\mathrm{m}}}{4{\mathrm{R}}_{\mathrm{m}}+8{{\mathrm{K}}_{\mathrm{r}}\mathrm{R}}_{\mathrm{g}}}}{\displaystyle \frac{{\mathsf{\phi }}_{\mathrm{r}}}{2}}={\displaystyle \frac{1}{1+{2\mathrm{K}}_{\mathrm{r}}\frac{{\mathrm{R}}_{\mathrm{g}}}{{\mathrm{R}}_{\mathrm{m}}}}}={\displaystyle \frac{{\mathsf{\phi }}_{\mathrm{r}}}{2}}$$

(13)

If the leakage coefficient K_ls is determined, then

$${\mathsf{\phi }}_{\mathrm{g}}=2{\mathrm{K}}_{\mathrm{l}\mathrm{s}}{\mathsf{\phi }}_{\mathrm{m}}={\displaystyle \frac{2{\mathrm{K}}_{\mathrm{l}\mathrm{s}}}{1+{2\mathrm{K}}_{\mathrm{r}}\frac{{\mathrm{R}}_{\mathrm{g}}}{{\mathrm{R}}_{\mathrm{m}}}}}={\displaystyle \frac{{\mathsf{\phi }}_{\mathrm{r}}}{2}}$$

(14)

$${\mathsf{\phi }}_{\mathrm{g}}={\displaystyle \frac{2{\mathrm{K}}_{\mathrm{l}\mathrm{s}}}{1+{\mathrm{K}}_{\mathrm{r}}\frac{\mathrm{g}\mathrm{’}{\mathsf{\mu }}_{\mathrm{r}}}{{\mathrm{L}}_{\mathrm{m}}}\frac{{\mathrm{A}}_{\mathrm{m}}}{{\mathrm{A}}_{\mathrm{g}}}}}={\displaystyle \frac{{\mathsf{\phi }}_{\mathrm{r}}}{2}}$$

(15)

Equation (16) is used to calculate the airgap leakage coefficient as a function of the number of PCB modules. In this paper, up to 6-layer stator modules with 2oz copper thickness are considered; therefore, Equation (16) provides a correction for the leakage coefficient to account for the effective increase in the magnetic air gap caused by stacking additional modules.

$$\left\{\begin{array}{c}\mathrm{a}{{\mathrm{g}}_1}^2+\mathrm{b}{\mathrm{g}}_1+\mathrm{c}={\mathrm{K}}_{ls1}\\ \mathrm{a}{{\mathrm{g}}_2}^2+\mathrm{b}{\mathrm{g}}_2+\mathrm{c}={\mathrm{K}}_{ls2}\\ \mathrm{a}{{\mathrm{g}}_3}^2+\mathrm{b}{\mathrm{g}}_3+\mathrm{c}={\mathrm{K}}_{ls3}\end{array}\right.$$

(16)

Accordingly, K_ls(g) is computed using Equation (17).

$${\mathrm{K}}_{\mathrm{ls}}\left(\mathrm{g}\right)=0.028{\mathrm{g}}^2-0.36\mathrm{g}+1.69$$

(17)

The fundamental airgap flux density, B_g1, is

$$B_{g1}={\displaystyle \frac{4}{\pi }}{B}_g\sin \left(\pi {\displaystyle \frac{{\alpha }_m}{2}}\right)$$

(18)

The fundamental component of the air gap flux is

$${\phi }_{g1}=B_{g1}{A}_m$$

(19)

Therefore, the permanent magnet flux λ_pm, considering the winding factor and the number of phases, is

$${\lambda }_{pm}=K_w{N}_{ph}{\phi }_{g1}$$

(20)

Moreover, for a 10-pole, 30-slot machine, the winding factor is 1. Therefore, if the torque equation is derived using ${\lambda }_{pm}$,

$$I_a^{*}={\displaystyle \frac{T}{\frac{3}{2}{\lambda }_{pm}}}$$

(21)

In other words,

$$T={\displaystyle \frac{3}{2}}{I}_a^{*}{\lambda }_{pm}$$

(22)

Ultimately, the torque is calculated using Equation (22).

2.3. Torque Analysis of Magnetic Equivalent Circuit (MEC) Modeling

Figure 3 shows the relationship between the number of PCB stators and the total layer count. Each PCB stator is designed as a 6-layer copper structure, meaning that one PCB contains 6 copper layers. Accordingly, these 6 layers correspond to a single stator, 12 layers correspond to two stators, and 18 layers correspond to three stators. The individual PCBs are stacked and bonded using insulating paper between the boards, and the windings are connected in series.

Figure 4 shows the torque data calculated using the MEC model equations described in Section 2.2 as a function of the number of PCB stator modules. The results are evaluated with respect to the permanent-magnet thickness. With an applied current of 10 A_rms, the torque increment decreases as the magnet becomes thicker, because the effective magnetic airgap increases with magnet thickness.

3. Basic 3D FEA Model Design and Loss-Reduction Trace Design

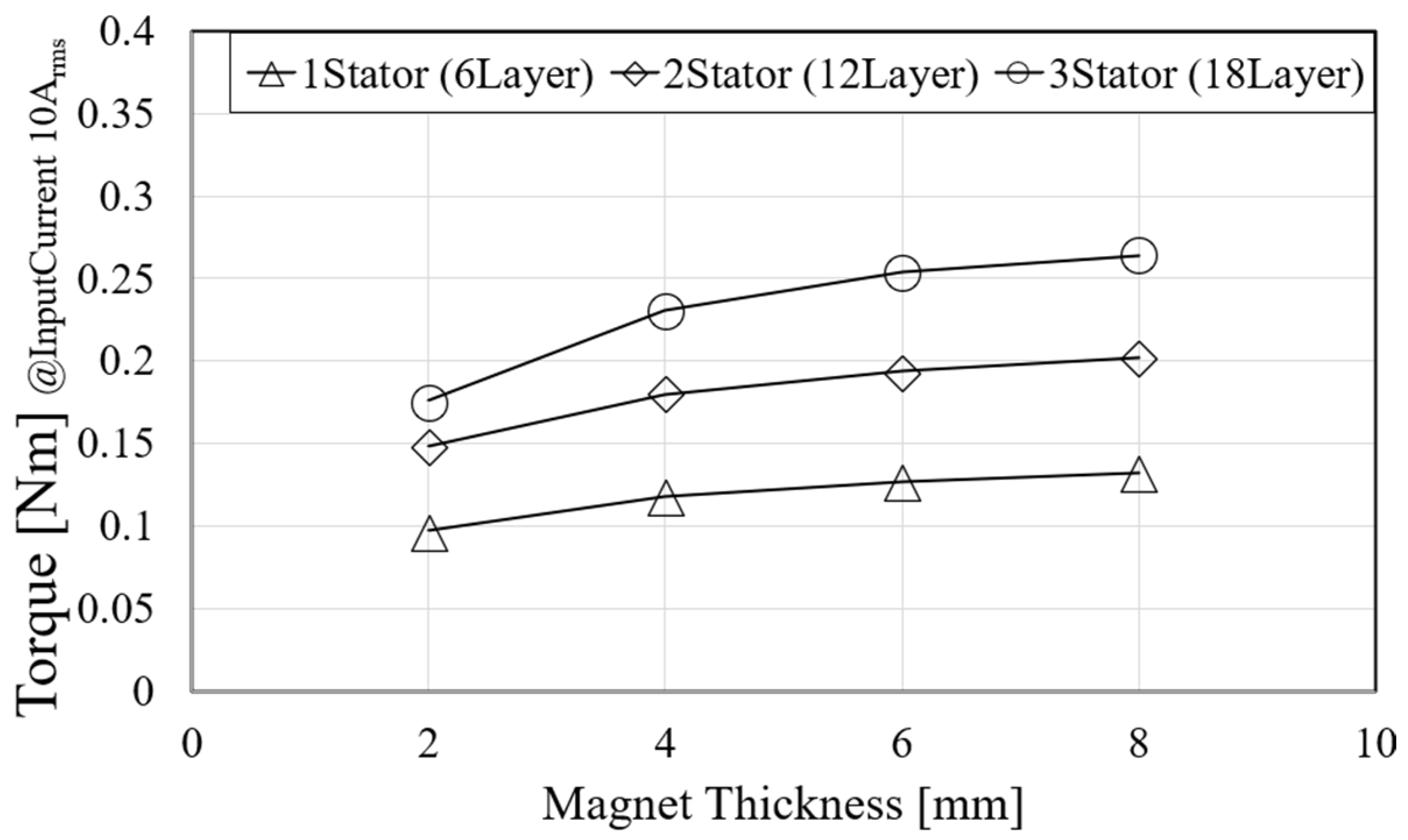
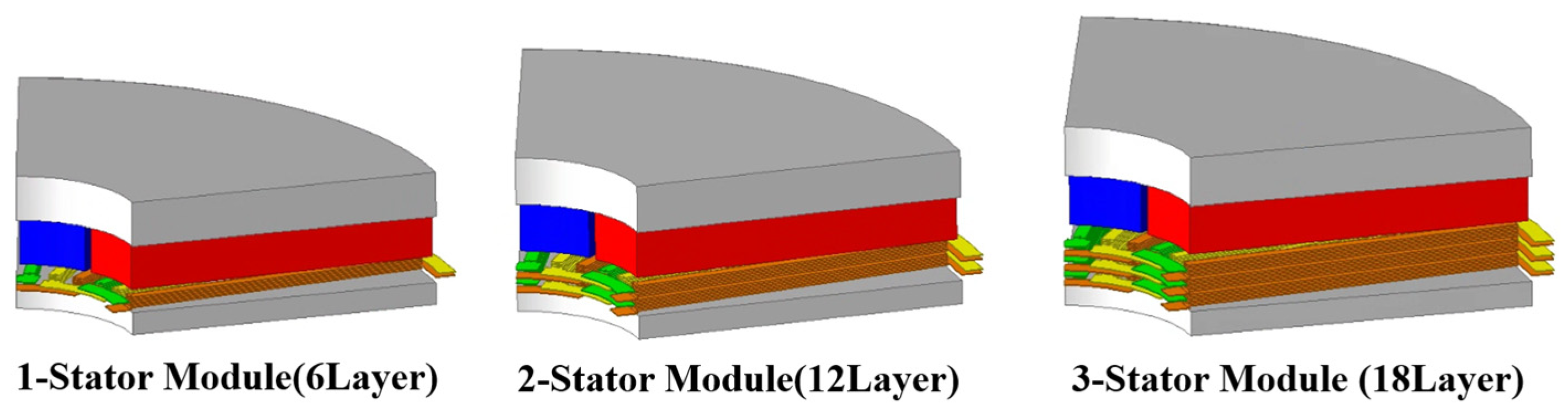
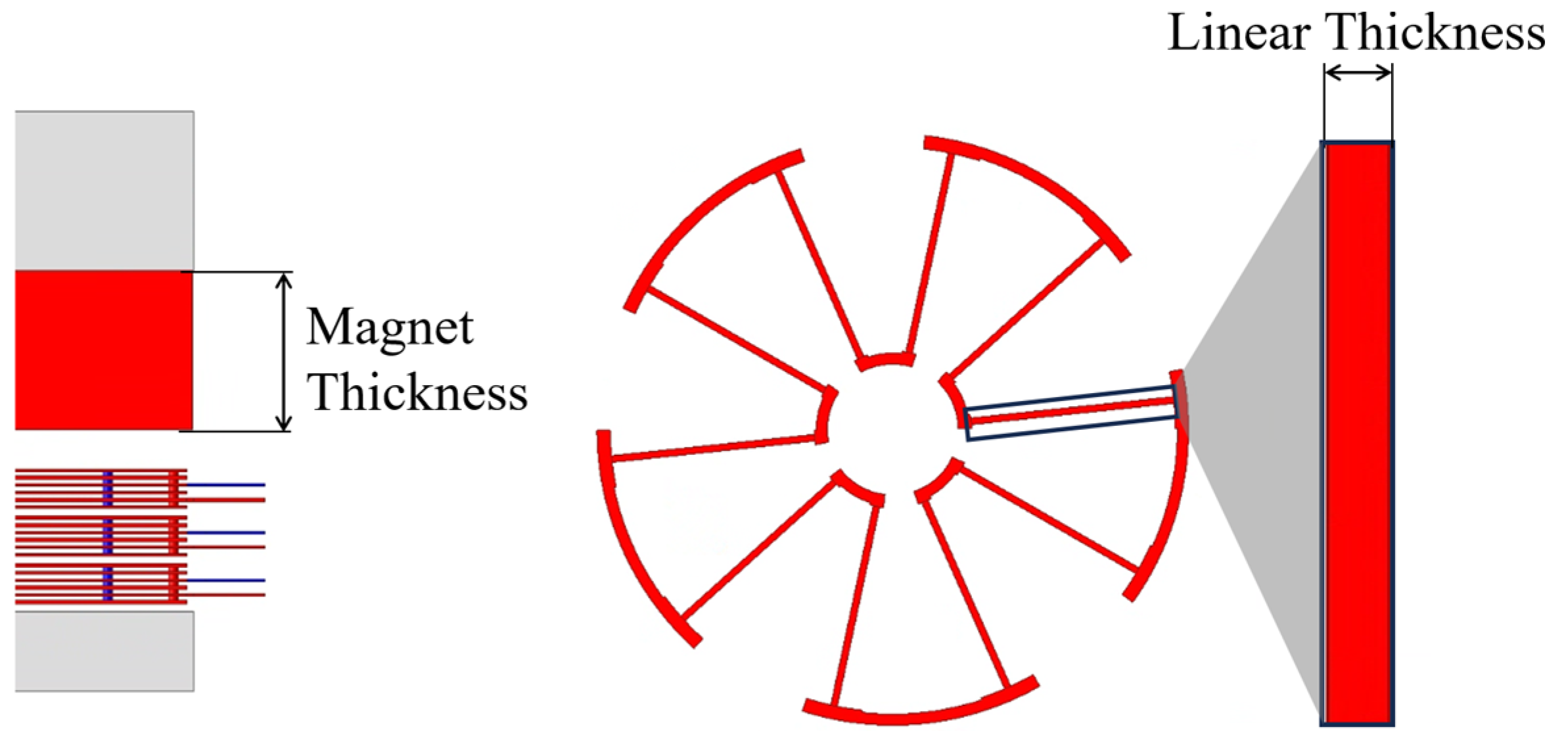
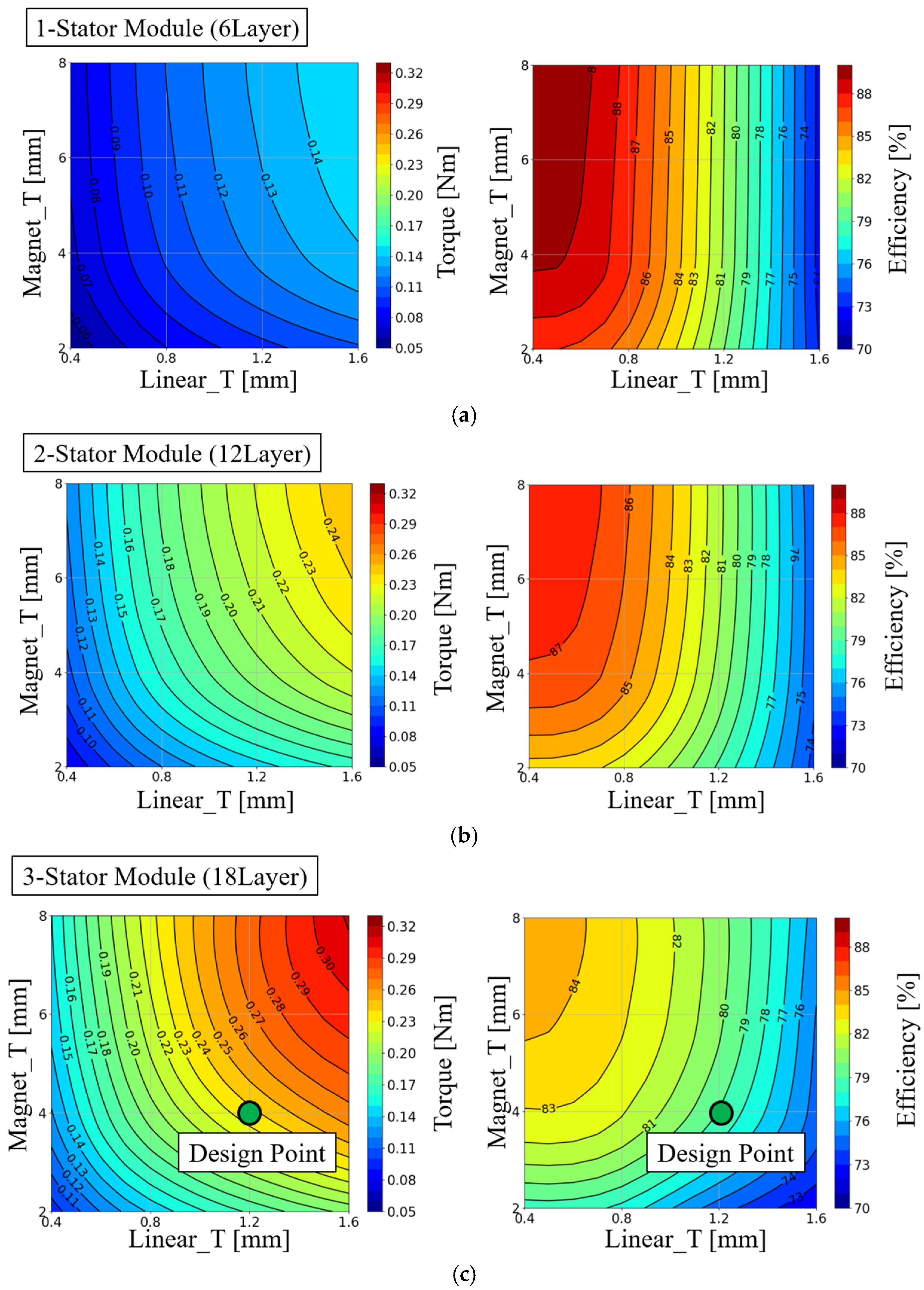
3.1. Description and Specifications of the Basic 3D FEA Model According to the Number of Stator Modules

Figure 5 shows the basic 3D FEA models according to the number of stator modules. In this paper, configurations up to three stator modules are investigated. A four-module configuration is not considered because, in a coreless motor, the permanent-magnet thickness and the PCB stator thickness effectively constitute the magnetic airgap length. As the number of PCB stator modules increases, the magnetic air gap becomes larger and the flux leakage increases excessive; therefore, the study is limited to a maximum of three modules.

Figure 6 summarizes the essential design variables that should be considered in the basic design stage of a PCB AFPM motor. First, the end-turn thickness is examined at the minimum feasible value to maximize the permanent-magnet usage and to clearly observe the design trends. The permanent-magnet thickness is directly related to magnet usage; however, increasing the magnet thickness also increases the effective magnetic airgap and enlarges the amount of leakage flux, so the back-EMF does not necessarily increase linearly with magnet thickness. In addition, the thickness of the effective conductor that contributes to the useful torque component is defined as the linear thickness, which is closely related to the phase resistance and AC copper loss. Increasing the conductor thickness reduces the phase resistance, but it can increase AC loss and consequently degrade the efficiency. Therefore, trend analysis of these design variables is essential at the basic model stage.

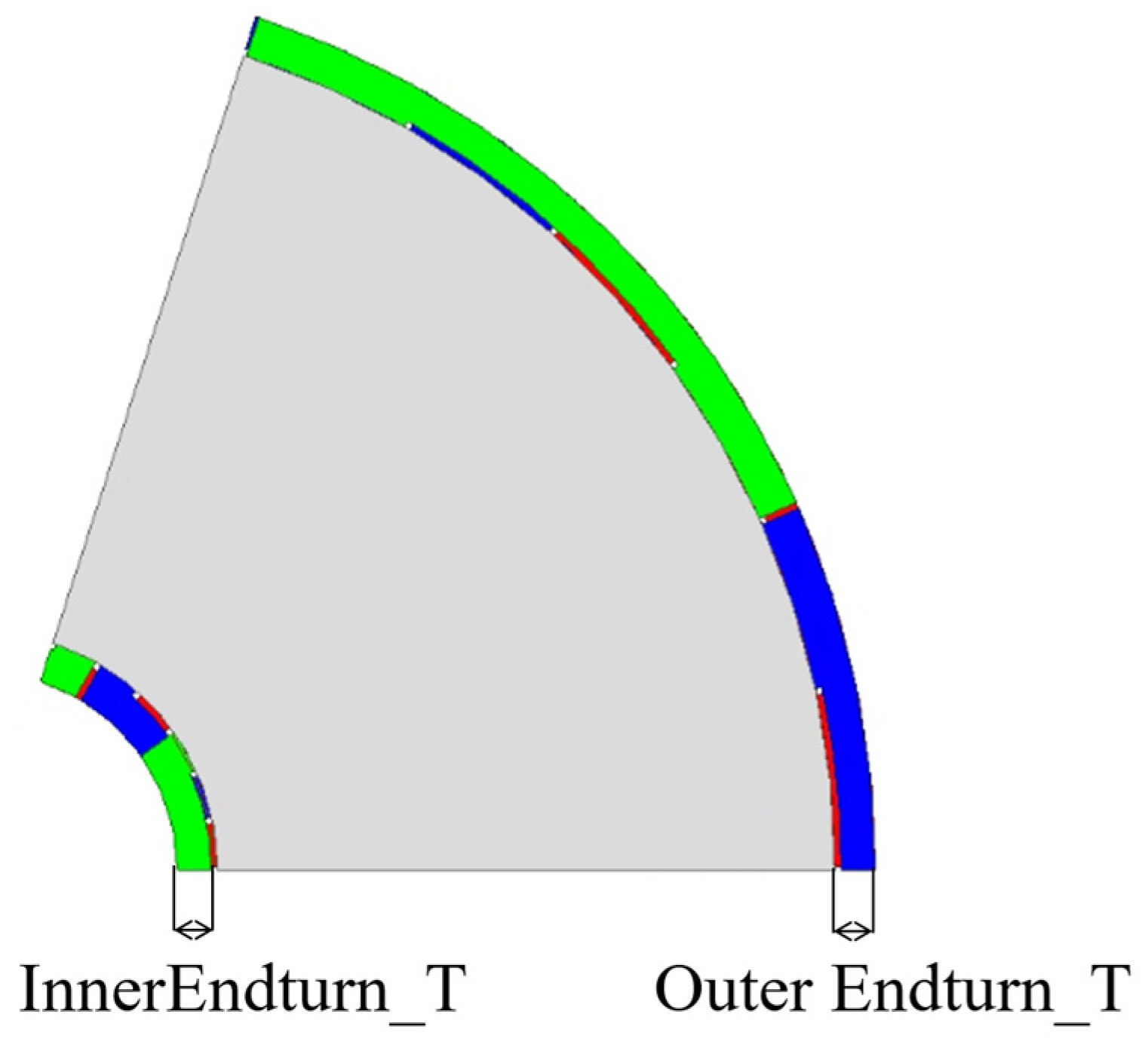
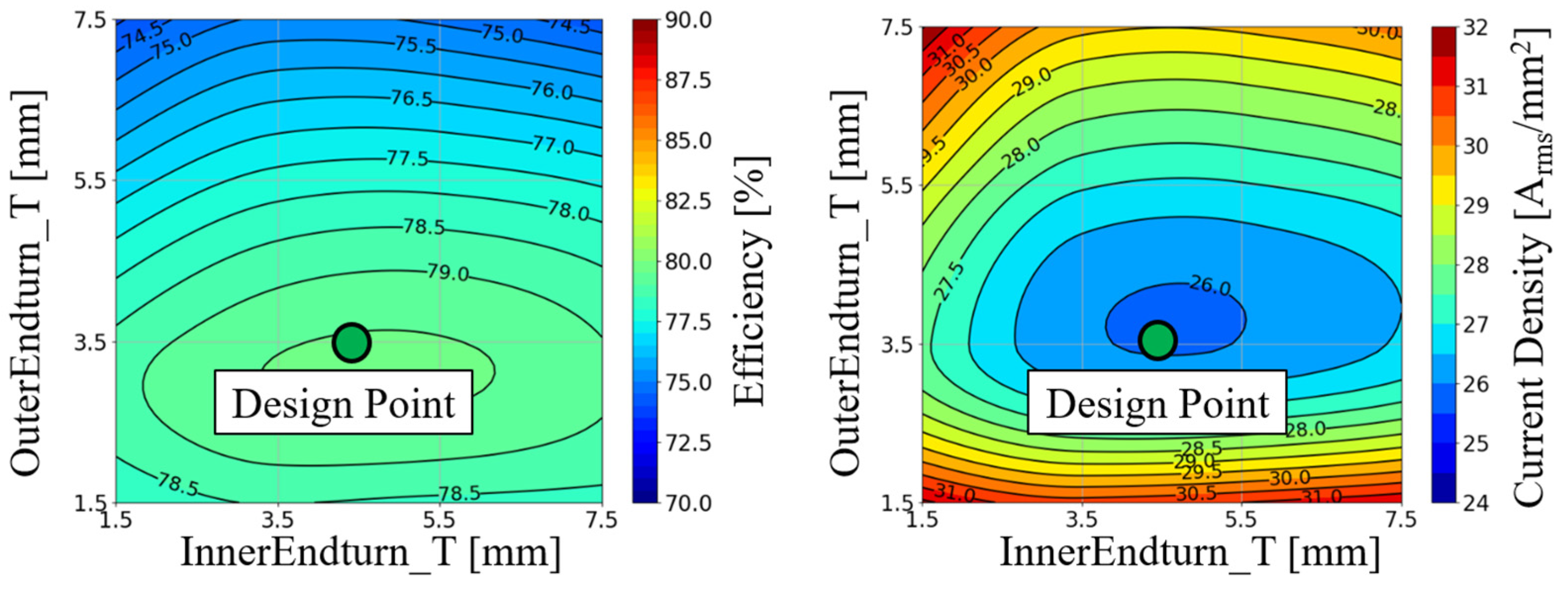
3.2. End-Turn Optimization Design of the 3D FEA Model

Figure 7 illustrates the geometries of the inner and outer end turns of the PCB stator. For compact motors such as the EWP PCB motor, the end-turn thickness has a significant impact on performance. Increasing the end-turn thickness can be beneficial for reducing the phase resistance because it allows a larger conductor cross-sectional area along the current path. However, a thicker end turn reduces the inner and outer diameters of the permanent magnets, thereby decreasing the magnet volume. This reduction in magnet usage leads to a lower back-EMF, which in turn requires a higher current to achieve the target torque. Therefore, optimization analysis of the efficiency and current density with respect to the inner and outer end-turn thicknesses is essential.

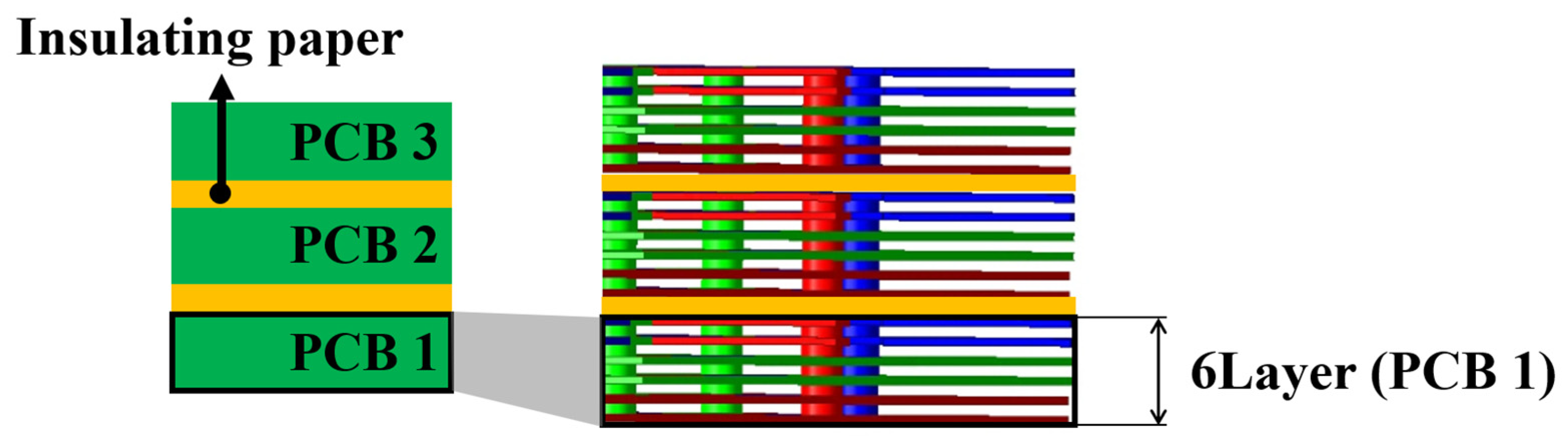
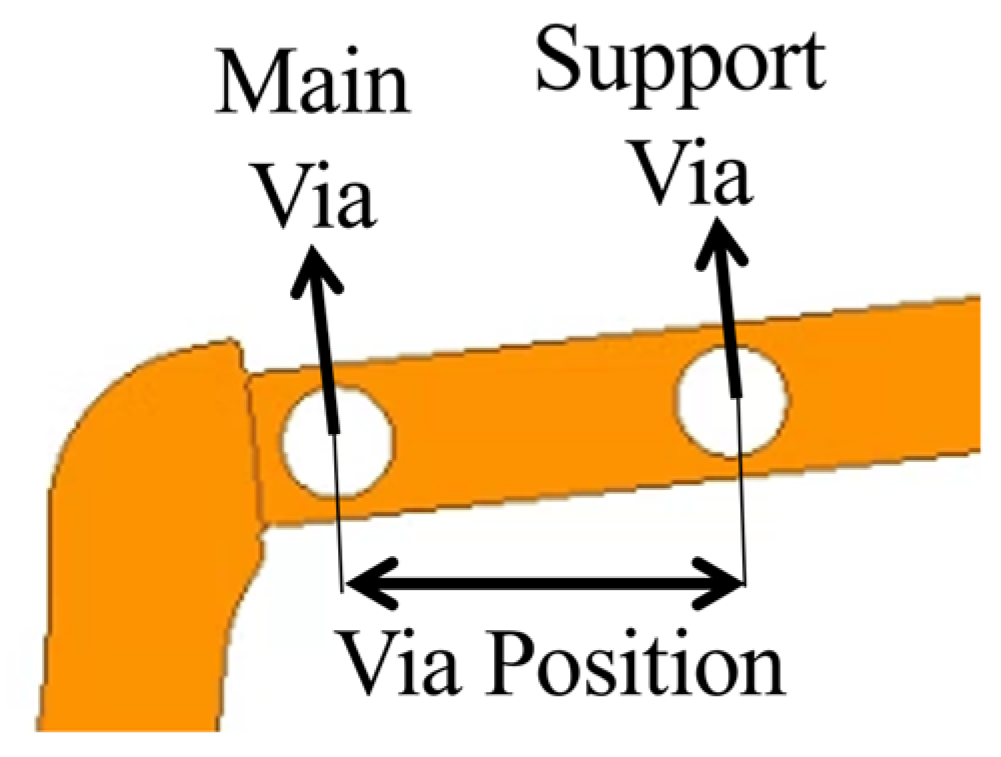
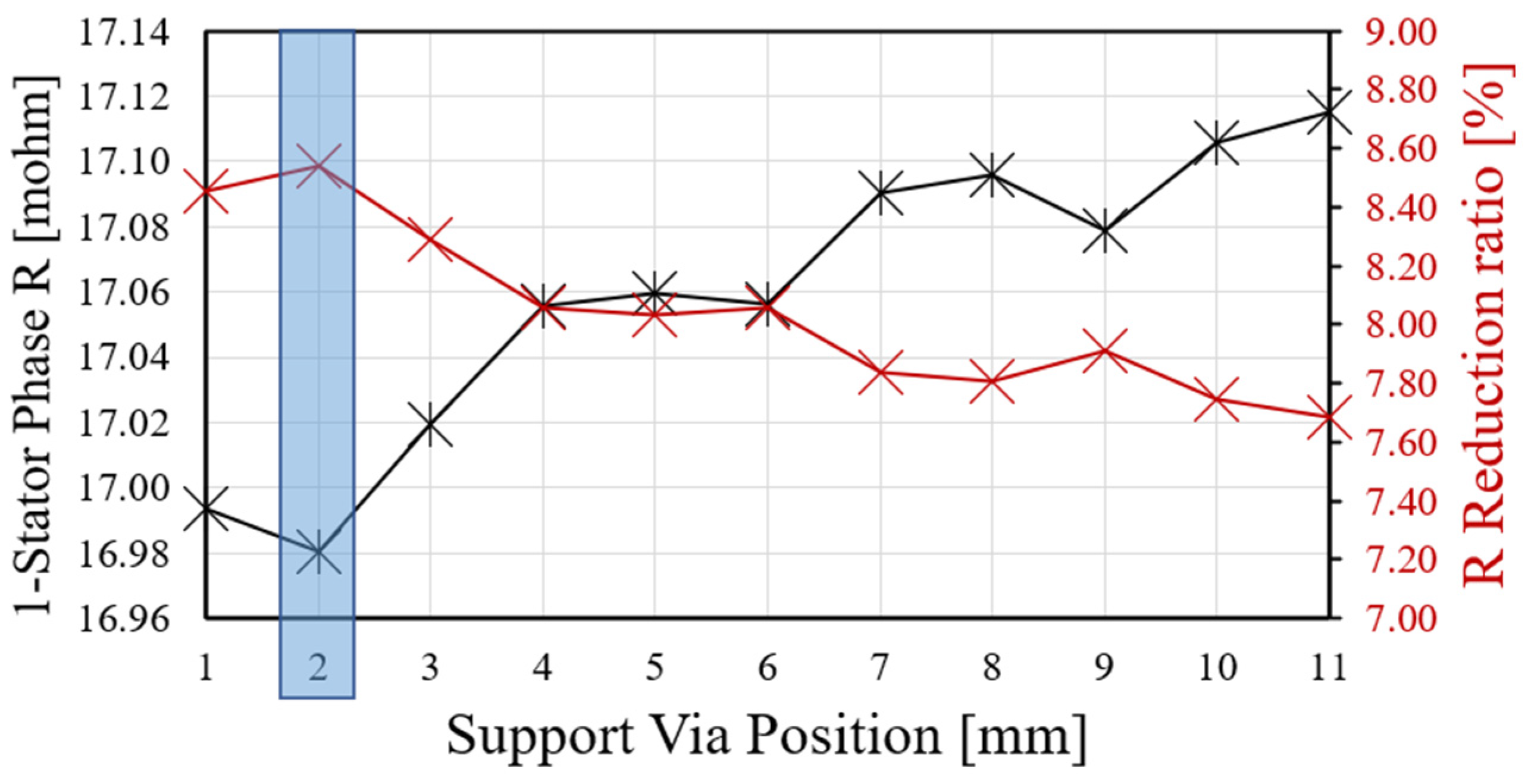
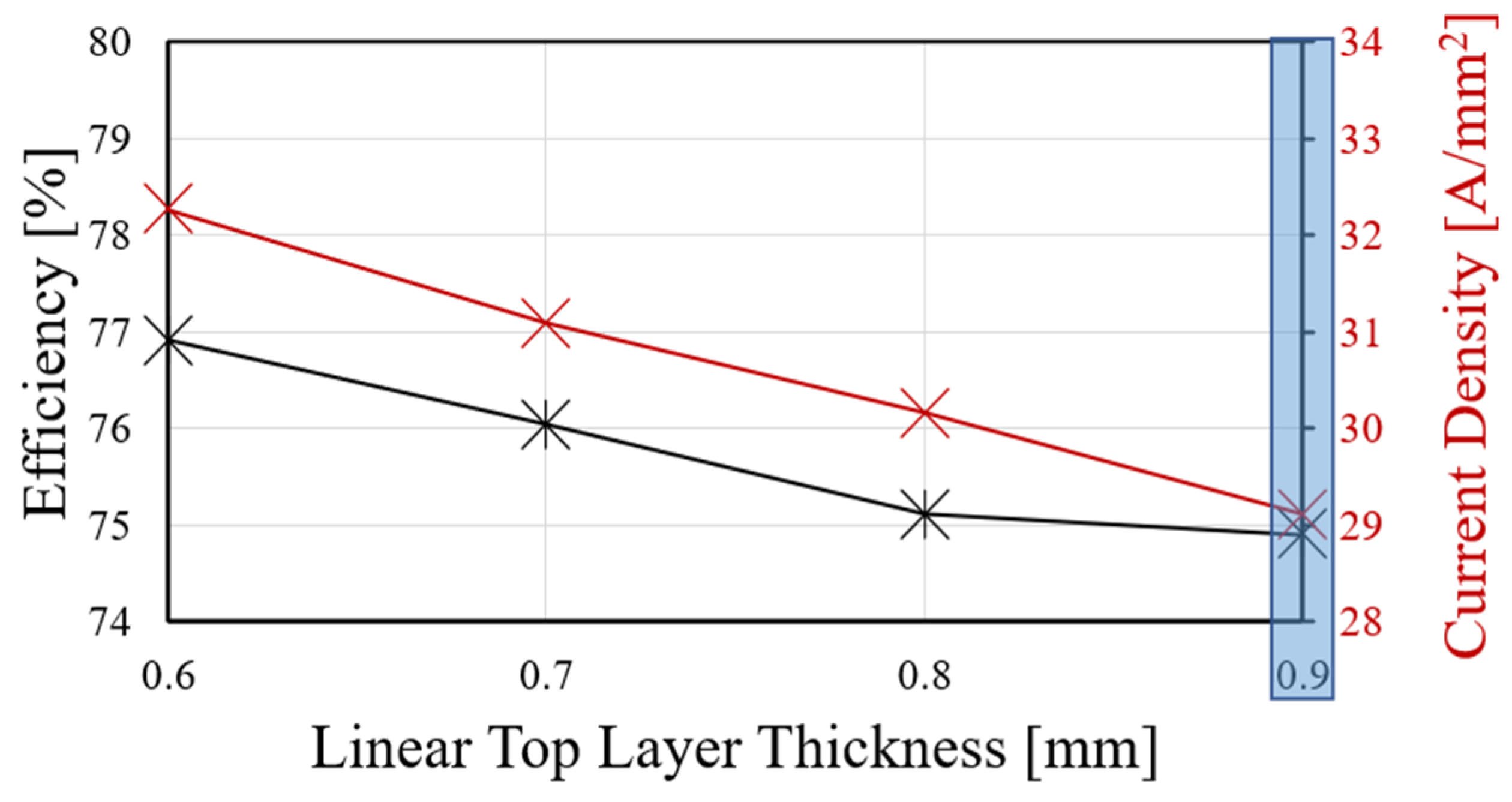
3.3. Via Design and Pyramid Trace of the 3D FEA Model for Loss Reduction

Figure 8 presents the via-hole design. For compact, low-current PCB motors, many vias are not necessarily required. However, relying on a single via is disadvantageous in terms of current density; thus, an additional support via is introduced to reduce the phase resistance. Since manufacturing costs generally increase with the number of via-holes, the design aims to minimize the via count while maximizing loss reduction.

Figure 9 shows the 3D FEA model geometry incorporating the pyramid trace design. Since AC copper loss becomes more severe in the layers closer to the permanent magnet, the trace width is reduced in those layers to minimize the loss. Because PCB circuits are fabricated through a chemical etching process, changing the trace width does not require additional manufacturing steps. Therefore, the proposed approach provides a clear advantage in that efficiency can be improved through width redistribution alone, without adding process complexity.

4. Derivation of the Final 3D FEA Model, Proto-Type Test and Validation

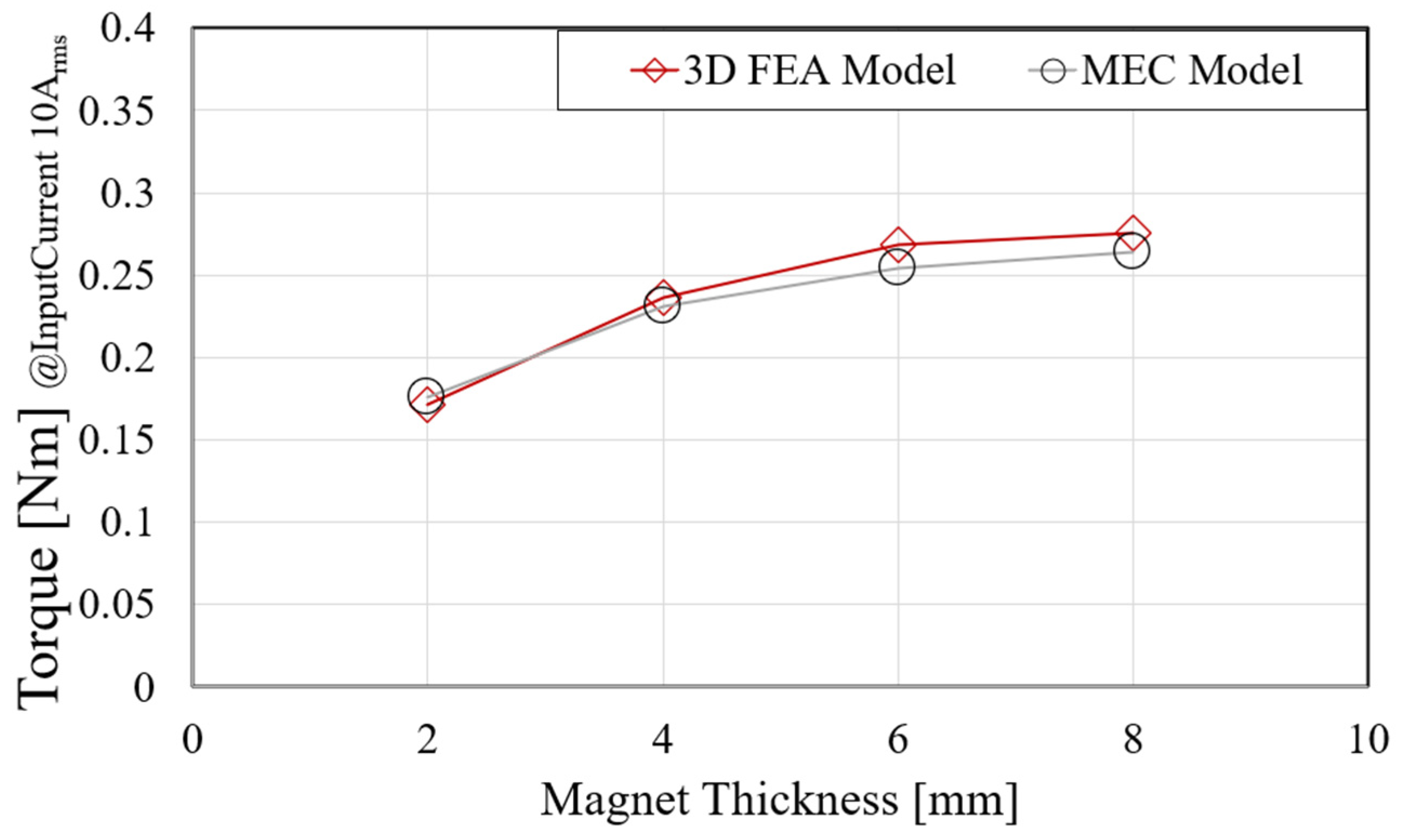
4.1. Derivation Process of the Final 3D FEA Model and Data Comparison with the MEC Model

Figure 10 presents the torque and efficiency performance maps as a function of the number of PCB stator modules. The maps evaluate the resulting torque and efficiency at a current density of 30 A_rms/mm² for each module configuration. This modular stator concept enables a wide range of power ratings to be realized using the same PCB design by simply varying the number of stator modules. In this study, the final model is selected based on the configurations with up to three modules. To satisfy the target performance, a design point providing a torque of 0.22 N·m or higher was selected. The permanent magnet thickness was selected as the minimum value that satisfies the target torque, because increasing the magnet thickness increases the overall axial length and the associated active material cost.

Figure 11 compares the torque results obtained from the MEC model with those from the 3D FEA model to evaluate their agreement. The discrepancy is within approximately −3% to 5%, indicating that the simplified MEC formulation can be used for rapid trend evaluation during the design process.

Figure 12 presents the efficiency and current-density maps obtained from the end-turn optimization of the basic PCB motor model under an ideal PCB fabrication assumption. Because these two metrics can vary in opposite directions, the design point was determined based on a consistent trade-off criterion that prioritizes both electrical performance and thermal loading. Specifically, the selected point corresponds to the region where the efficiency reaches its maximum while the current density is simultaneously minimized. This selection emphasizes reducing copper-loss-related thermal stress without sacrificing efficiency, and it provides a clear reference for the subsequent evaluation stages in which practical manufacturing effects are additionally considered.

Figure 13 shows the trend of the phase resistance and the corresponding resistance reduction ratio as a function of the support via’s position presented in Figure 8. The analysis is performed by varying the distance of the support via with respect to the main via’s location, which is used as the reference. The design point is determined at the condition where the resistance reduction ratio is maximized while the phase resistance is minimized.

When the PCB etching process is considered, the phase resistance increases slightly, which leads to an increase in current density. Even after applying the via-design approach, it was difficult to satisfy the target current density of 30 A_rms/mm². Therefore, a pyramid trace design was introduced, in which the trace width was varied by layer, and its performance was evaluated. Figure 14 presents the results as a function of the trace width of the topmost layer. Based on these results, the trace width that satisfies the current-density requirement (within 30 A_rms/mm²) while providing the highest efficiency was selected. By applying the pyramid trace design, the AC loss can be partially reduced while maintaining the same phase resistance, resulting in an efficiency improvement of approximately 0.4%.

4.2. Photographs of the Prototype and Test Environment

Figure 15 shows the fabricated prototype. The active part of the PCB motor consists of four main components. The rotor is composed of the rotor back yoke and the permanent magnets, while the stator is composed of the PCB stator and the stator back yoke. The proposed machine is a single-rotor AFPM configuration. In conventional single-rotor AFPM machines with teeth, stator manufacturing can be challenging because slot geometries must be formed to accommodate wound coils. In contrast, the PCB stator does not require teeth or slots for coil winding, resulting in a simple structure with excellent manufacturability. This configuration is also well suited for mass production.

Figure 16 shows the experimental test setup, including the EWP PCB motor and the torque meter. During the test, the torque was measured as a function of the applied current under the target output condition, and the motor housing temperature was monitored simultaneously.

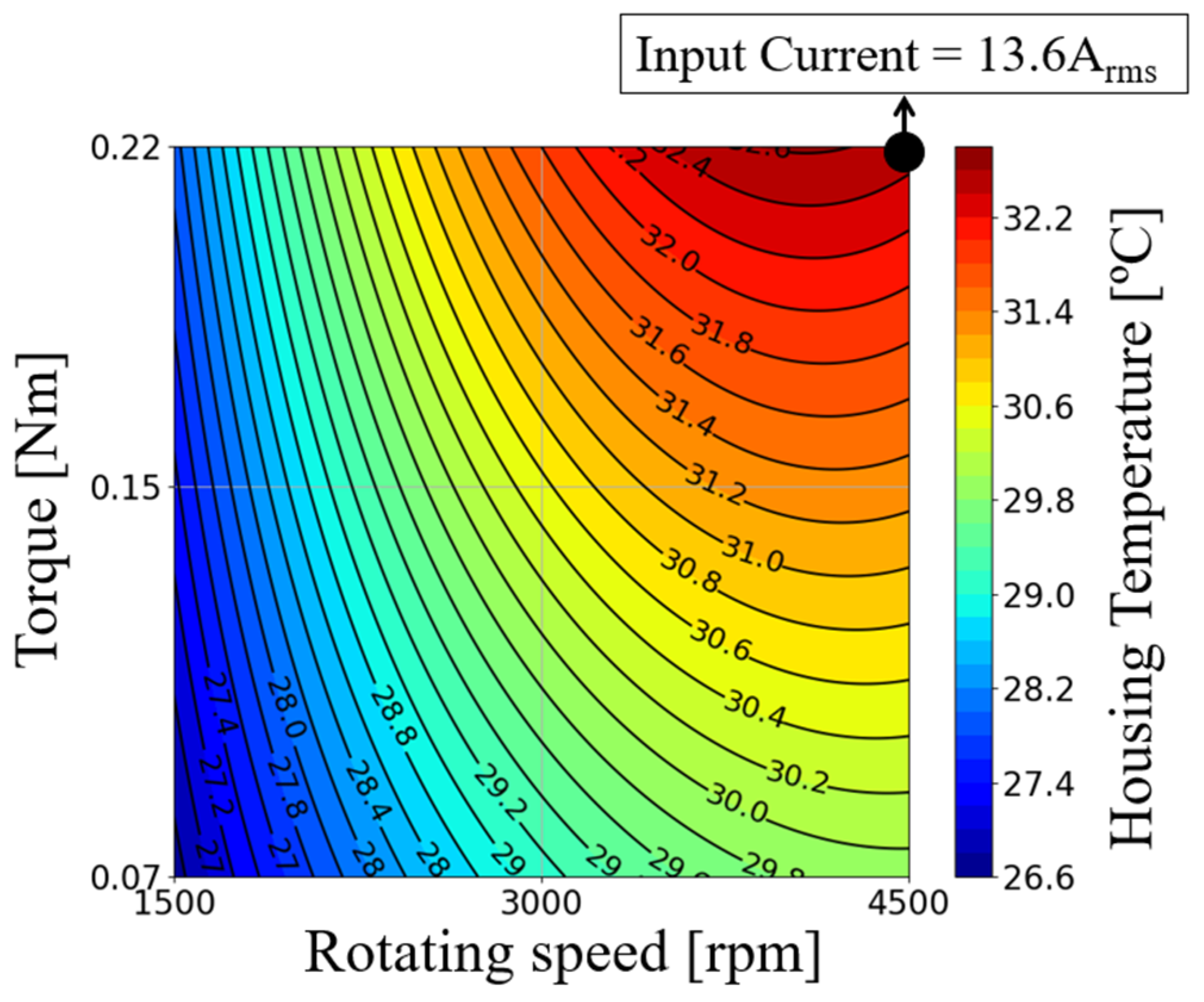
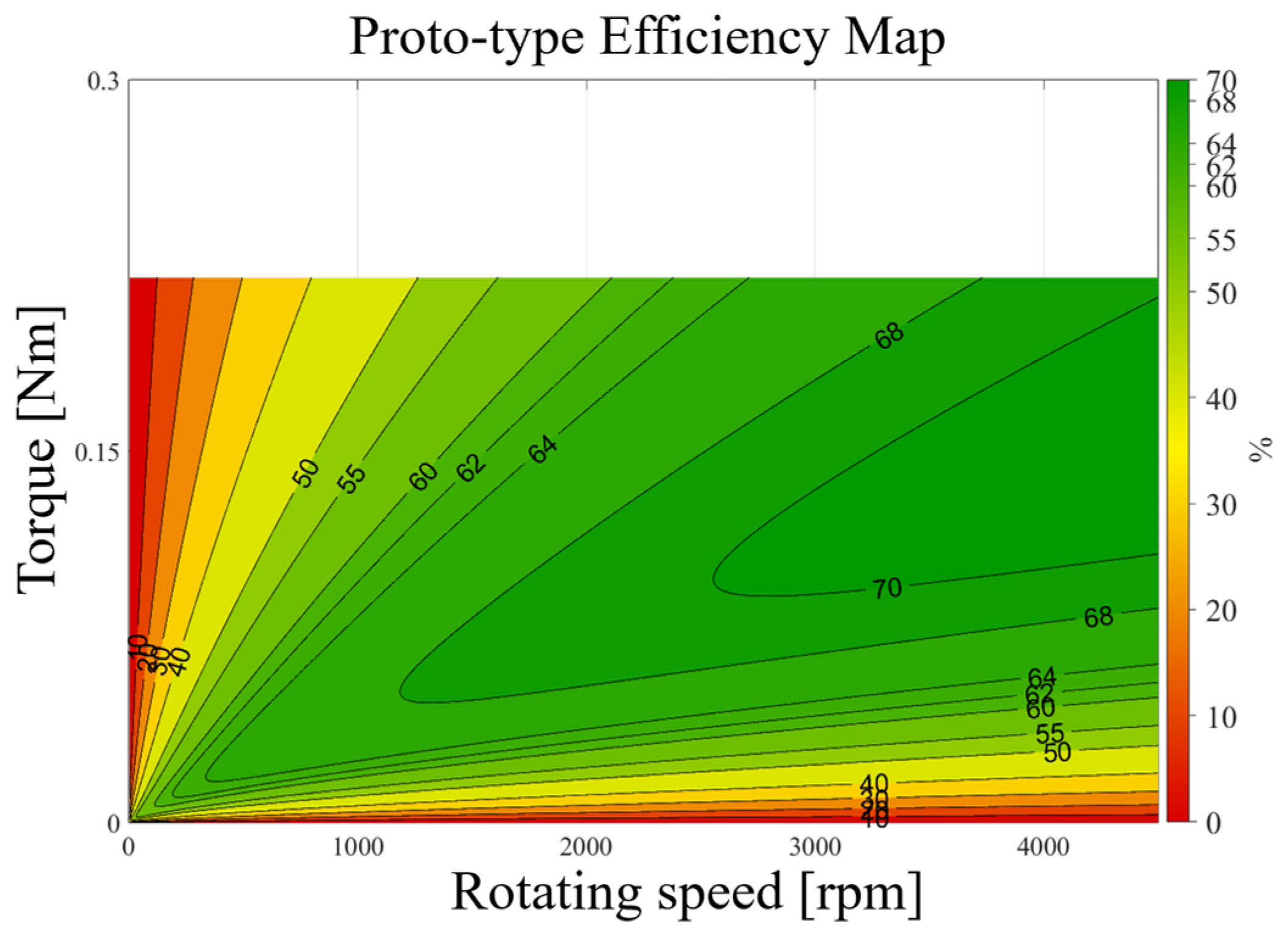
4.3. Prototype Test Results and Comparison

Figure 17 presents a performance map of the measured motor housing temperature under load conditions. The housing temperature was measured at the hottest spot on the housing using a laser temperature meter (non-contact infrared thermometer). At the maximum load point of 0.22 N·m at 4500 rpm, the applied current density was 13.6 A_rms/mm² and the measured peak housing temperature was 32.5 °C. Since this test was conducted under air-cooling conditions rather than in an actual water-pump installation, the housing temperature is expected to be lower in the real application where coolant flow directly cools the housing. Therefore, the results indicate that the motor can be operated without thermal issues under the target operating conditions.

Figure 18 shows the measured efficiency map over the operating region under load-test conditions. Because the test was conducted under air-cooling conditions, the phase resistance increased, resulting in a higher applied current than the simulated value. In addition, the test was performed with a switching frequency of 100 kHz, and the corresponding switching losses were reflected in the measured efficiency reduction. In an actual water-pump application, the operating temperature is expected to be lower; nevertheless, the prototype achieved an efficiency of approximately 70% or higher at the maximum load point.

5. Conclusions

This paper presents a PCB AFPM motor for automotive EWP drives and demonstrates a compact, scalable stator concept together with a rapid MEC based design framework. A MEC model formulation is developed for fast torque prediction and is validated by 3D FEA and prototype measurements, showing agreement within approximately 5%. To address winding copper losses in the coreless PCB motor, a pyramid trace concept is proposed by redistributing trace width across layers according to flux exposure, with the design objective of optimizing the balance between AC and DC copper losses while maintaining operation within the targeted current density guideline of approximately 30 A_rms/mm². Based on this approach, the final EWP PCB motor is realized with an overall axial length of 14.4 mm, corresponding to an approximately 40% reduction compared with a typical 100 W-class EWP motor, which is advantageous for packaging where axial length reduction is critical. Prototype testing further confirms stable thermal operation at operating points that meet the target torque of 0.22 N·m or higher, as verified by housing temperature measurements. Finally, the modular PCB stator architecture enables output scalability by adjusting the number of stacked modules while retaining the same PCB design, supporting product-line expansion and manufacturability.