Design and Investigation of Powertrain with In-Wheel Motor for Permanent Magnet Electrodynamic Suspension Maglev Car

Abstract

A new type of transportation vehicle, the maglev car, is gaining attention in the automotive and maglev industries due to its potential to meet personalized urban mobility and future travel needs. To optimize the chassis layout of maglev cars, this paper proposes a compact powertrain integrating electrodynamic suspension with in-wheel motor technology, in which a permanent magnet electrodynamic in-wheel motor (PMEIM) enables integrated propulsion and levitation. First, the PMEIM external magnetic field distribution is characterized by analytical and finite element (FEM) approaches, revealing the magnetic field distortion of the contactless powertrain. Subsequently, the steady-state electromagnetic force is modeled and the operating states of the PMEIM powertrain are calculated and determined. Next, the PMEIM electromagnetic design is conducted, and its electromagnetic structure rationality is verified through magnetic circuit and parametric analysis. Finally, an equivalent prototype is constructed, and the non-contact electromagnetic forces of the PMESM are measured in bench testing. Results indicate that the PMEIM powertrain performs propulsion and levitation functions, demonstrating 14.2 N propulsion force and 45.8 N levitation force under the rated condition, with a levitation–weight ratio of 2.52, which hold promise as a compact and flexible drivetrain solution for maglev cars.

1. Introduction

Electrical machines are integrated with intermediate transmission mechanisms (e.g., chains, rack-and-pinion systems, or lead screws) to form an electric powertrain for power transmission. However, these powertrains typically suffer from mechanical contact and induced wear and tear [1,2]. To address such limitations in conventional mechanical powertrains, research on non-contact transmission technologies has attracted substantial attention, including linear motors, magnetic bearings, and maglev systems [3,4].

Linear motors can directly generate thrust without additional transmission systems. Specifically, linear induction motors (LIMs) exhibit structural simplicity and operational flexibility, owing to the lack of fixed magnetic poles on the secondary, and thus have been widely adopted in maglev transportation [5]. In the high-temperature superconducting (HTS) maglev ring test line of “Super-Maglev” developed by Southwest Jiaotong University (SWJTU), a LIM of 3 m in length is adopted, which is composed of on-board armature and guideway conductive plates. This configuration enables the maglev vehicle to operate stably at 50 km/h through cyclic acceleration [6]. The working principle of LIMs is as follows. A time-varying magnetic field acting on a conductive plate or closed coil induces currents within the conductors, which interact with the magnetic field to generate electromagnetic force for contactless thrust transmission. In the maglev system, this mechanism is typically associated with electrodynamic suspension (EDS) [7].

Although LIMs are technically mature, relying on multiphase windings to generate a traveling wave magnetic field for propulsion, they require an independent suspension system to achieve simultaneous levitation and propulsion. In addition, LIMs suffer from the end effects, where excitation current rises rapidly with increasing velocity, thereby degrading the power factor and operational efficiency [8]. Inspired by permanent magnet (PM) EDS (PMEDS), a time-varying magnetic field for addressing this issue is generated via PMs movement, leveraging the high remanence. Regarding PMs’ arrangement, PMEDS include linear and wheel types [9,10]. The linear type is limited by motion form and low-speed magnetic resistance, typically serving as a passive suspension system, damping device, or eddy current brake in high-speed maglev systems [11,12,13]. The wheel type, termed the electrodynamic wheel (EDW), produces a continuous rotational magnetic field by rotating annular PMs around a fixed axis, and the field frequency is directly proportional to the PMs rotational speed, enabling active control of levitation and propulsion.

Fujii et al. [14,15] pioneered the first EDW system. Constructed by arranging axially magnetized arc-shaped PMs in an alternating magnetic pole configuration, it has laid a foundation for subsequent research. Bird et al. [16,17] conducted a systematic study on the EDW scheme where PMs are radially magnetized and arranged in a Halbach array, involving magnetic field modeling, electromagnetic force calculation, and parameter optimization. Notably, the radially magnetized EDW generates tangential thrust in addition to normal force, enabling levitation–propulsion integration. It has been innovatively applied to the automotive industry, leading to the development of maglev cars.

Maglev cars abandon the traditional wheel-driven mode, utilizing the normal force of EDW for vehicle support and tangential force for propulsion to achieve integrated levitation and propulsion. It eliminates tire–road contact, enabling driving performance independent of the road adhesion coefficient. It aligns with the development requirements for enhancing automotive quality, riding comfort, and driving experience [18,19]. Currently, a multi-degree-of-freedom prototype developed at SWJTU has achieved static levitation and low-speed operation [20]. Meanwhile, Deng et al. [21] developed a full-scale vehicle based on linear PMEDS and completed the first dynamic levitation test, advancing the research on maglev cars significantly. They further expanded the EDW application by symmetrically arranging it on both sides of the HTS maglev [22,23], where the normal force provides guidance, while the tangential force serves as traction, enhancing the HTS maglev guiding force and offering an economical propulsion solution. Subsequently, Lu et al. [24] experimentally verified the feasibility of an EDW-based propulsion and guidance system for HTS maglev, with lateral dynamical performance analyzed in Ref. [25]. Based on a 165 m long HTS maglev engineering prototype test line in SWJTU, the first EDW-driven HTS maglev prototype was constructed, achieving stable operation at 10 km/h with curb weight 1.2 t, demonstrating the EDW potential in maglev applications [26].

To date, research on EDW-based maglev cars has focused primarily on the structural design, analytical modeling, and parametric analysis of EDW itself. However, the rotational power of the EDW is typically derived from electric motors, with the EDW essentially acting as a medium for transmitting forces or torques from the prime movers. In practice, due to assembly space constraints, adjustments to the transmission path between the motor and EDW require an intermediate commutation device, which introduces additional mechanical contact and wear in the powertrain while also complicating the vehicle chassis layout. To avoid this issue, this paper proposes an integrated hub motor design for maglev car powertrains, termed the PM electrodynamic in-wheel motor (PMEIM). By integrating the EDW with in-wheel motor technology, the PMEIM provides a compact and flexible driving solution for maglev cars.

This paper is organized as follows: Section 2 outlines the overall structure and operating principle of the maglev car and the onboard PMEIM. Section 3 models the magnetic field, electromagnetic force, and operational states of the PMEIM. Subsequently, Section 4 presents the PMEIM integrated design in light of the powertrain mechanical characteristics and analyzed its electromagnetic performance. Section 5 implements prototype experiments for the PMEIM powertrain. Finally, Section 6 draws conclusions.

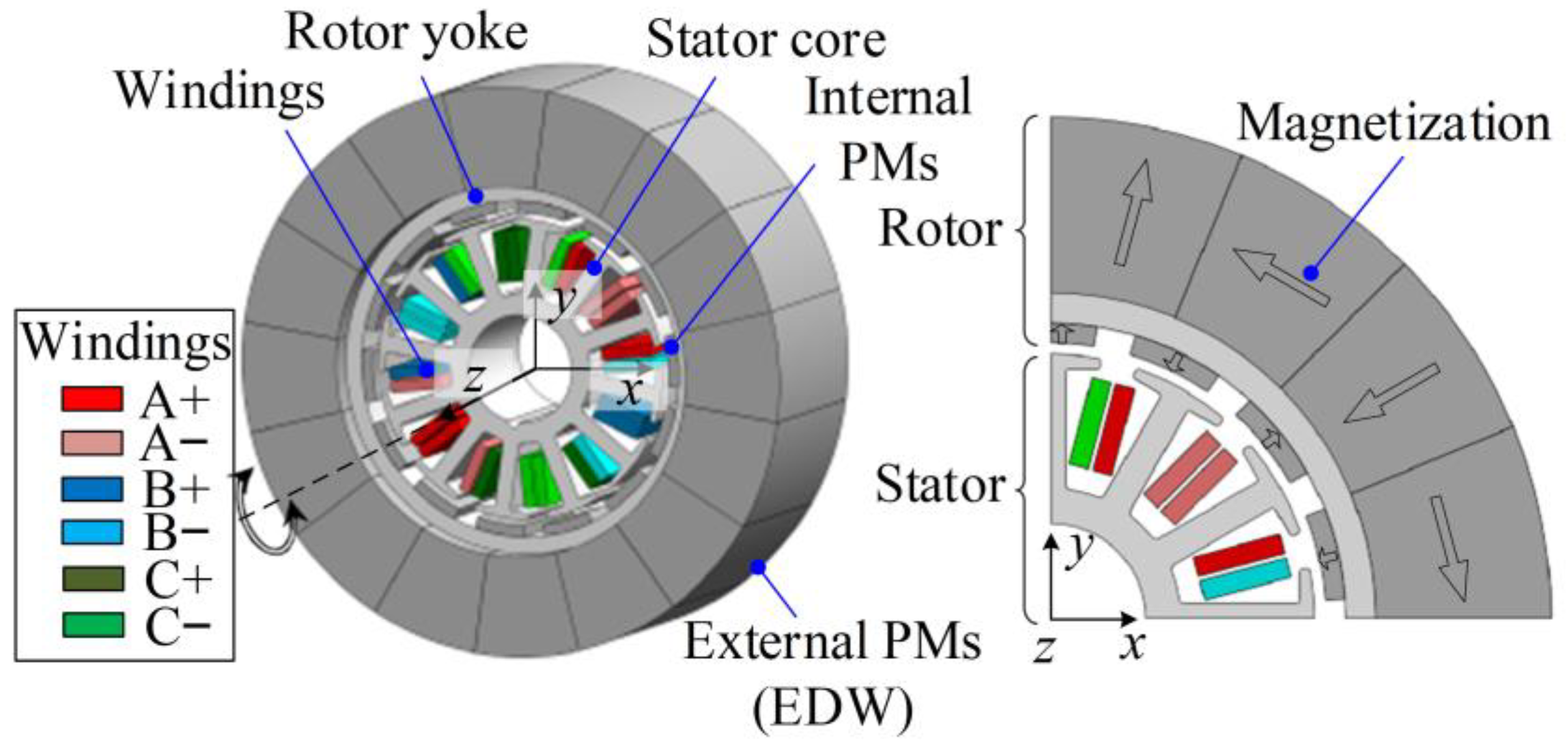
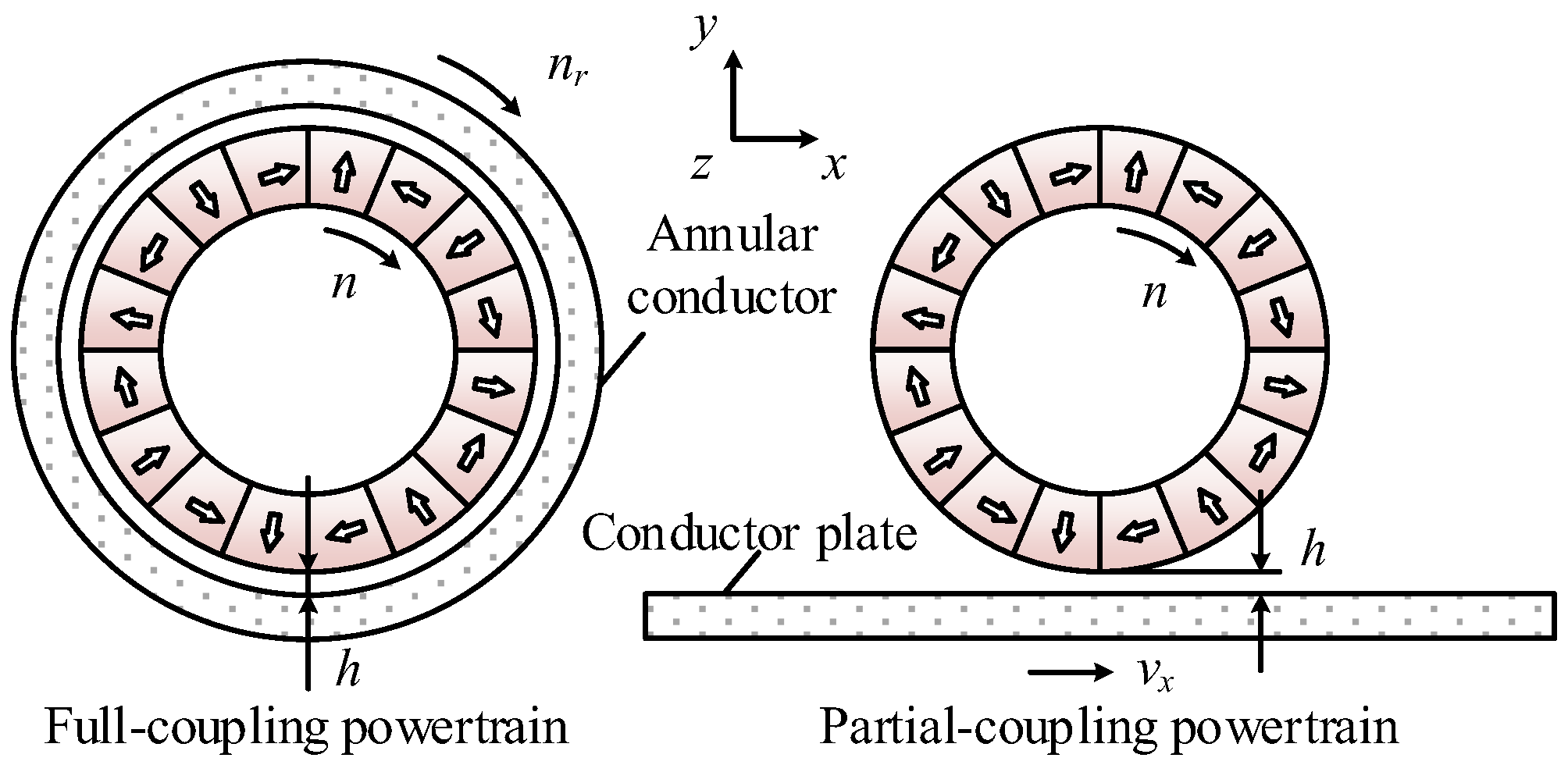
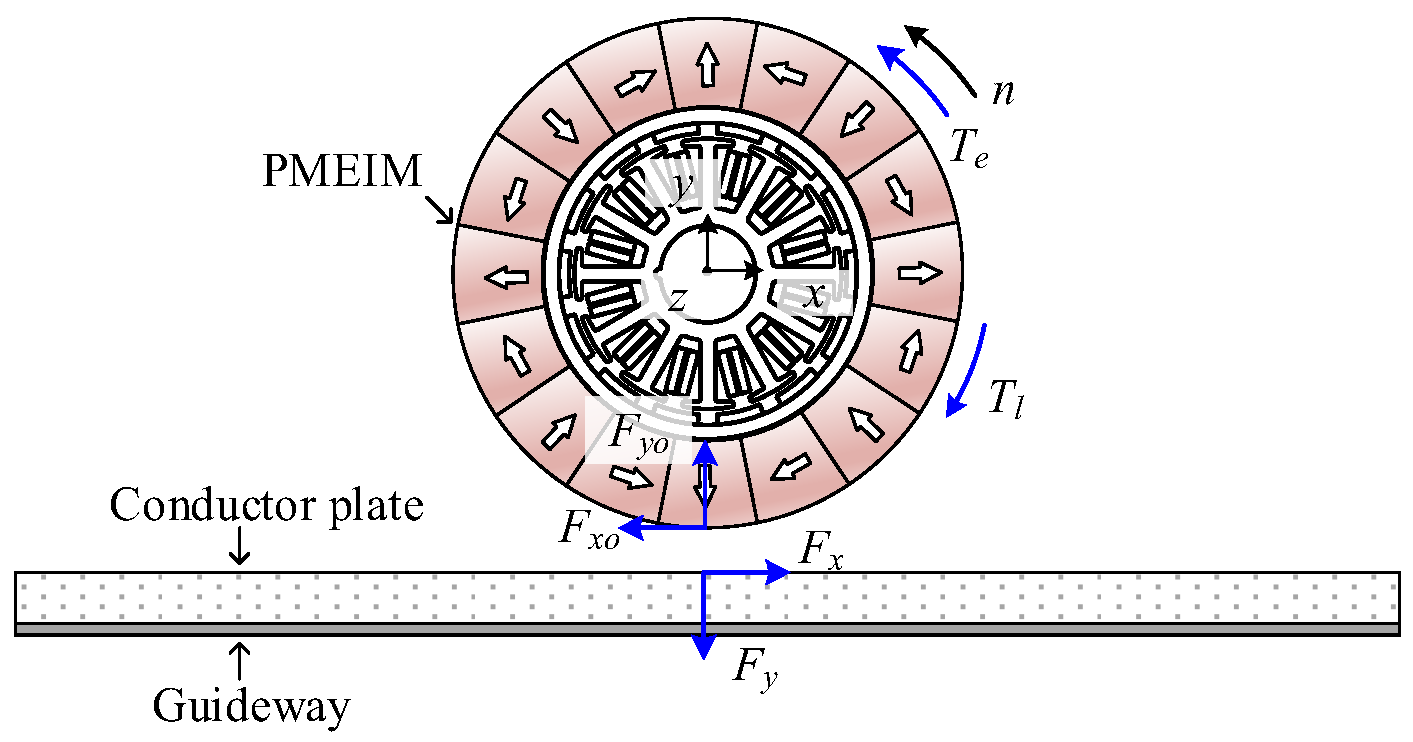
2. Description of PMEIM

The magnetic car system comprises a maglev vehicle and its dedicated lane. The vehicle shares a similar body structure with electric vehicles, differing in being equipped with radially magnetized EDWs. The lane is constructed with non-ferromagnetic conductive plates, e.g., copper, aluminum, as the base structure, laid on high-speed road surfaces as a dedicated track. As illustrated in Figure 1, when the EDWs rotate relative to the lane, the rotating magnetic field generated at its outer edge induces eddy currents in the lane conductor. These eddy currents interact with the rotating magnetic field to produce electromagnetic force, which can be decomposed into a normal force perpendicular to the lane and a tangential force (parallel to the lane). The repulsive normal force enables vehicle levitation, while the tangential force, opposite to PMEIM rotation direction and analogous to the road-wheel friction in traditional wheeled drive, serves as the propulsion force for vehicle movement.

Based on Figure 1a, the operating principle of the maglev car is as follows:

(i)

Static levitation: Front and rear wheels rotate in opposite directions at the same speed, where tangential forces cancel each other out while normal forces superimpose to enable static vehicle levitation.

(ii)

Propulsion and braking: Front and rear wheels rotate at different speeds, where the resulting speed difference generates a net tangential force for vehicle propulsion or braking, with normal forces remaining superimposed.

(iii)

Steering: The speed difference between left and right wheels produces differential tangential forces, creating a yaw moment to facilitate vehicle steering.

Considering the structure and functional requirements of the maglev car in Figure 1, the PMEIM powertrain consists of the onboard PMEIM and the lane conductive plate. Unlike conventional PM motors, the PMEIM rotor integrates double-sided PMs. As illustrated in Figure 2, the outer PMs adopt Halbach array magnetization to provide a source magnetic field interacting with the conductive plate, while the inner PMs use N-S alternating magnetization to form a closed magnetic flux between the stator and rotor. The PMEIM enables direct contactless conversion of rotational motion to linear motion, enhancing the compactness of the propulsion system and optimizing the chassis layout.

3. Mechanical Characteristic of PMEIM Powertrain

The output of the PMEIM depends on the load, and its initial design parameters are determined based on the performance indicators of the operating conditions. Since the energy conversion and transmission of the PMEIM are achieved through electromagnetic induction, with the PMs outside the rotor as the source magnetic field, analytical modeling of the powertrain is performed to determine its mechanical characteristics, thereby providing a basis for the PMEIM design. The positioning schematic of the PMEIM powertrain is shown in Figure 3, and the demonstration parameters are listed in

Table 1. Dimensions of the PMEIM powertrain.

Parameters	Symbols	Nominal Values
Pole pairs	p	4
Inner radius	Ri	32.5 mm
Outer radius	Ro	50 mm
Wheel width	Wm	35 mm
Conductor plate width	Wp	100 mm
Conductor plate thickness	d	10 mm
PMs remanence	Bre	1.23 T
Conductor plate conductivity	σ	5.8 × 107 S/m

.

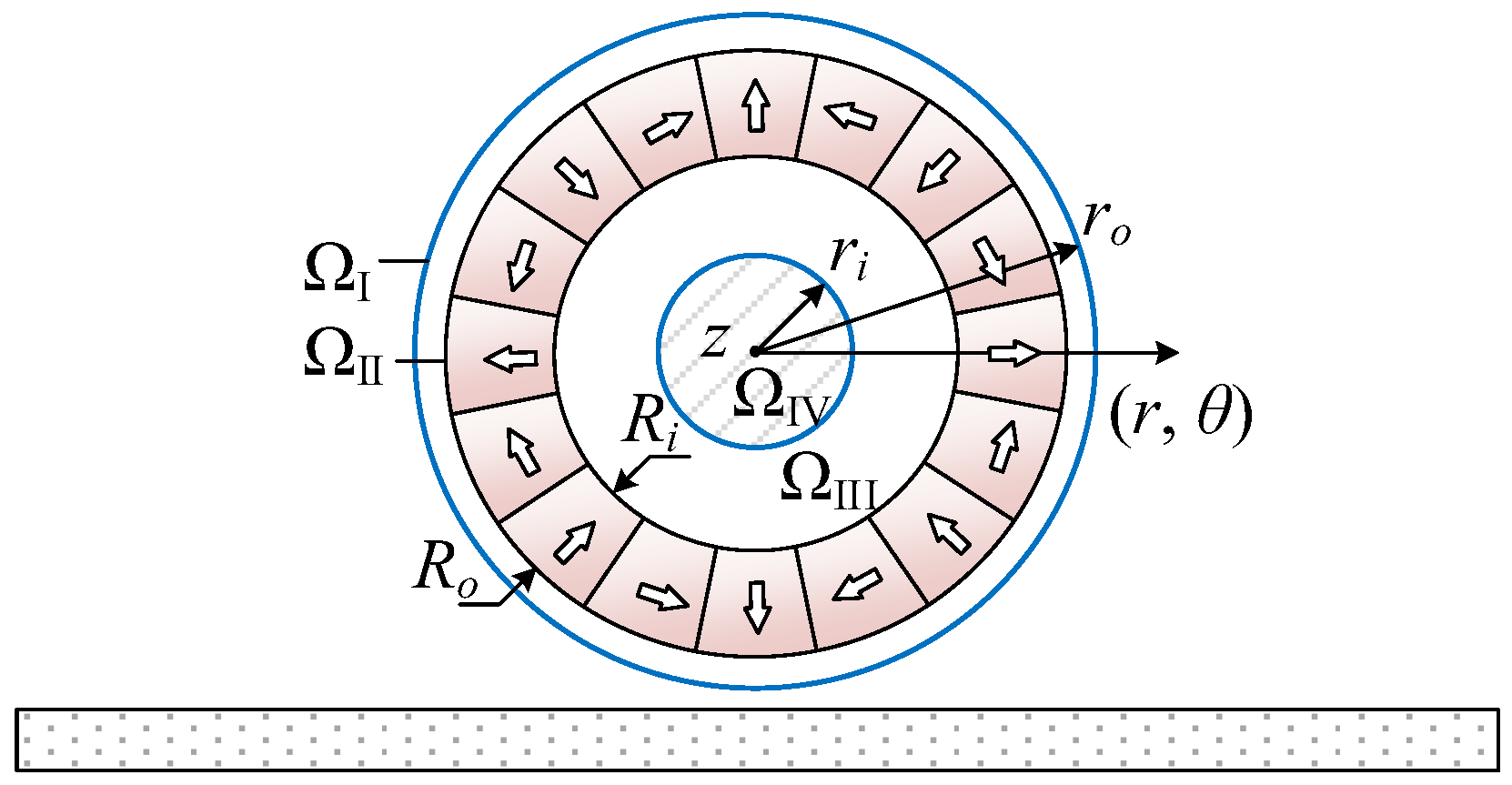
3.1. Magnetic Field

To investigate the source magnetic field distribution on the conductor plate, an analytical model for the PMs outside the PMEIM rotor is established (Figure 4). Divided into four regions in decreasing order of radius, the model is defined as follows: Ω_I (R_o < r < r_o) denotes the outer air region, Ω_II (R_i < r < R_o) the PMs array, Ω_III (r_i < r < R_i) the inner air region, and Ω_IV (r < r_i) the rotor yoke. The model relies on the following assumptions [27].

(i)

A cylindrical coordinate system r-θ-z is established at the geometric center of the PMEIM.

(ii)

The z-axis is infinitely long, and the magnetic flux density is uniformly distributed along the z-axis, without attenuation due to the transverse end effect.

(iii)

The magnetic yoke is infinitely permeable.

In the analytical model, the field vectors B and H satisfy

$$B={\mu }_{0}H, \mathrm{in} {\Omega }_{\mathrm{I}}, {\Omega }_{\mathrm{III}}$$

(1)

$$B={\mu }_0{\mu }_{r}H+{\mu }_{0}M, \mathrm{in} {\Omega }_{\mathrm{II}}$$

(2)

where μ₀ is the vacuum permeability, μ_r the relative permeability of the permanent magnet, H the magnetic field intensity, B the magnetic flux density, and M the magnetization.

The outer PMs of the PMEIM are arranged in a Halbach array. In the cylindrical coordinate system, the magnetization intensity is given by Equation (3).

$$M=M_r{e}_r+M_{\theta }{e}_{\theta }=M \cos (p\theta )e_r-M \sin (p\theta )e_{\theta }$$

(3)

where M_r and M_θ denote the radial and tangential magnetization components, as well as e_r and e_θ the radial and tangential unit vectors.

The scalar magnetic potential φ is introduced, with H expressed as

$$H_r=-{\displaystyle \frac{\partial \phi }{\partial r}}, H_{\theta }=-{\displaystyle \frac{1}{r}}{\displaystyle \frac{\partial \phi }{\partial \theta }}$$

(4)

From the fundamental equation $\nabla \cdot B=0$ and Equations (1) and (2), the governing equations are obtained.

$${\displaystyle \frac{{\partial }^2{\phi }_i}{\partial r^2}}+{\displaystyle \frac{1}{r}}{\displaystyle \frac{\partial {\phi }_i}{\partial r}}+{\displaystyle \frac{1}{r^2}}{\displaystyle \frac{{\partial }^2{\phi }_i}{\partial {\theta }^2}}=0, i = \mathrm{I},\mathrm{III}$$

(5)

$${\displaystyle \frac{{\partial }^2{\phi }_{\mathrm{II}}}{\partial r^2}}+{\displaystyle \frac{1}{r}}{\displaystyle \frac{\partial {\phi }_{\mathrm{II}}}{\partial r}}+{\displaystyle \frac{1}{r^2}}{\displaystyle \frac{{\partial }^2{\phi }_{\mathrm{II}}}{\partial {\theta }^2}}={\displaystyle \frac{1}{{\mu }_r}}(\nabla \cdot M)$$

(6)

By the separation of variables and combined with the boundary conditions, the magnetic flux density B of the Halbach PM array is derived as

$$B_r^s={\displaystyle \frac{2B_{re}p}{(1+p)r^{p+1}}}\cdot {\displaystyle \frac{(R_o^{p+1}-R_i^{p+1})R_o^{2p}\cos (p\theta )}{(1+{\mu }_r)R_o^{2p}-(1-{\mu }_r)R_i^{2p}}}$$

(7)

$$B_{\theta }^s={\displaystyle \frac{2B_{re}p}{(1+p)r^{p+1}}}\cdot {\displaystyle \frac{(R_o^{p+1}-R_i^{p+1})R_o^{2p}\sin (p\theta )}{(1+{\mu }_r)R_o^{2p}-(1-{\mu }_r)R_i^{2p}}}$$

(8)

where the superscript of “s” denotes the source magnetic field.

The magnetic flux density distribution at radius r = 60 mm is analyzed. As shown in Figure 5, the amplitude of B_rs and B_θs is 0.295 T for analytical calculations and 0.294 T for finite element (FEM) simulations. Curves from both methods agree well, showing four peaks and peaks and troughs in a four-pole-pair distribution, which matches the Halbach PM array configuration. Moreover, B_rs and B_θs exhibit a 90-degree phase difference.

Although the outer PMs on the PMEIM rotor form an annular structure with four pole pairs magnetized in the Halbach configuration, the conductor plate, i.e., maglev lane, is planar. Due to inherent geometric constraints, the conductor plate cannot achieve full coupling with all poles of the Halbach PM array. To quantify the coupling degree between the Halbach PM array and the conductor plate, the powertrain is categorized into a full-coupling model and a partial-coupling model. As shown in Figure 6, the full-coupling model can be equivalent to a rotating induction motor, where three-phase windings are replaced by mechanically rotating PMs to generate a high-quality sinusoidal magnetic field. In the partial-coupling model, the powertrain directly converts rotational motion into linear motion, consistent with the operating principle of conventional vehicle wheels. Here, v_x denotes the relative velocity between the PMEIM and conductor plate, equivalent to the maglev car traveling speed. Notably, in the partial-coupling model, the non-uniform air gap between the Halbach PM array and the conductor plate complicates the source magnetic field distribution on the conductor plate’s upper surface.

In the partial-coupling configuration, to obtain the source magnetic field distribution on the conductor plate’s upper surface, the analytical magnetic field model is transformed from the cylindrical to the Cartesian coordinate system. According to the fundamental electromagnetic field equations, B and A are coupled via

$$\nabla \cdot B=0, B=\nabla \times A$$

(9)

where A is the vector magnetic potential.

Solving Equations (7) and (8) simultaneously gives

$$A_z={\displaystyle \frac{C}{p}}{\displaystyle \frac{\sin p\theta }{r^p}}$$

(10)

where $C={\displaystyle \frac{2B_{re}p}{1+p}}{\displaystyle \frac{(R_o^{p+1}-R_i^{p+1})R_o^{2p}}{{(1+{\mu }_r)}^2{R}_o^{2p}-{(1-{\mu }_r)}^2{R}_i^{2p}}}$.

Expressed in complex form, A_z in the Cartesian coordinate system is given by Equation (11) after coordinate system transformation.

$$A_z=\mathrm{Im}[{\displaystyle \frac{C}{p}}{\displaystyle \frac{1}{{\left(x-jy\right)}^p}}]$$

(11)

From Equation (9), the component form of B^s in the Cartesian coordinate system is derived as

$$B_x^s=\mathrm{Im}[{\displaystyle \frac{jC}{{(x-jy)}^{p+1}}}], B_y^s=\mathrm{Im}[{\displaystyle \frac{C}{{(x-jy)}^{p+1}}}]$$

(12)

According to Equation (12), three field points are selected on the conductor plate upper surface (as shown in Figure 3b): P₁ (−60, −60), P₂ (0, −60), and P₃ (60, 60). The magnetic flux density B at these points is calculated. As presented in Figure 7, when the rotation speed is 3000 rpm, the x- and y-axis components of B vary sinusoidally with time, exhibiting a 90-degree phase difference and a 5 ms period. For analytical calculations and FEM simulations, the B amplitudes at P₁, P₂, and P₃ are 0.052 T, 0.295 T, 0.052 T and 0.053 T, 0.296 T, 0.053 T, respectively. The results have a high degree of consistency.

Figure 8 presents the magnetic flux density B distribution on the conductor plate upper surface over one electrical period. Standing waves at different instants exhibit non-sinusoidal characteristics, with a maximum amplitude of 0.295 T occurring at x = 0. The source magnetic field follows an amplitude-modulated periodic distribution. Herein, all points along the x-axis share the same period while their amplitudes vary with position, a behavior described by Equation (20).

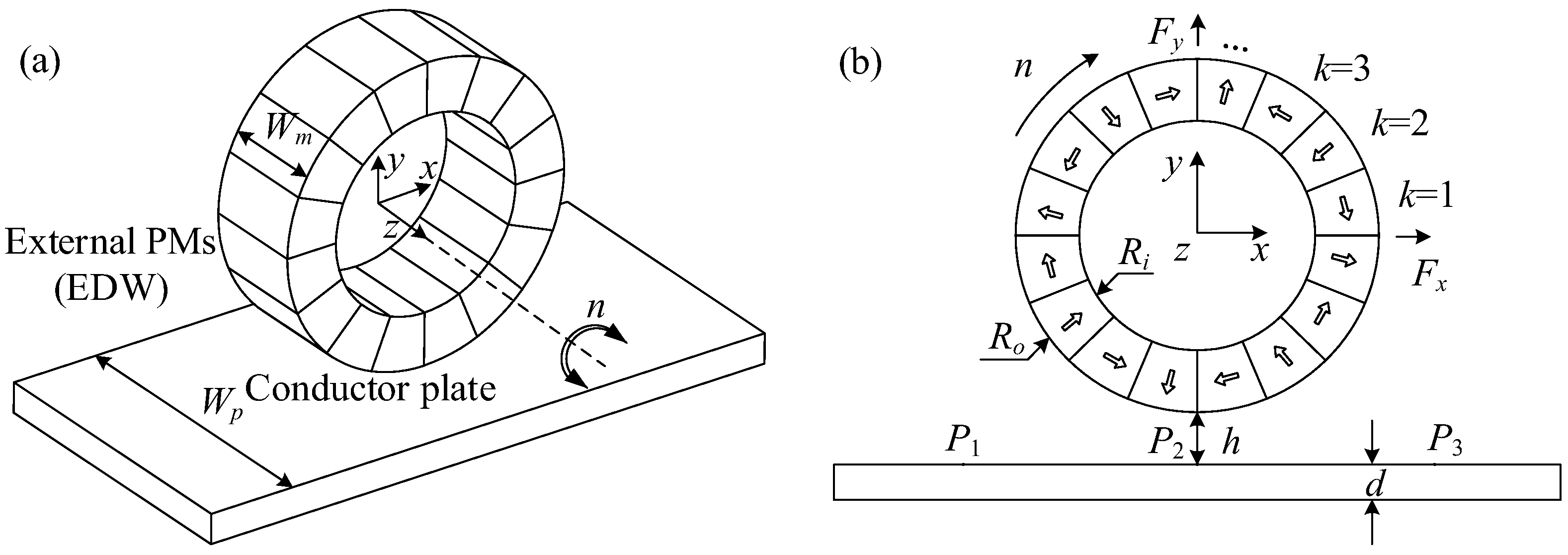
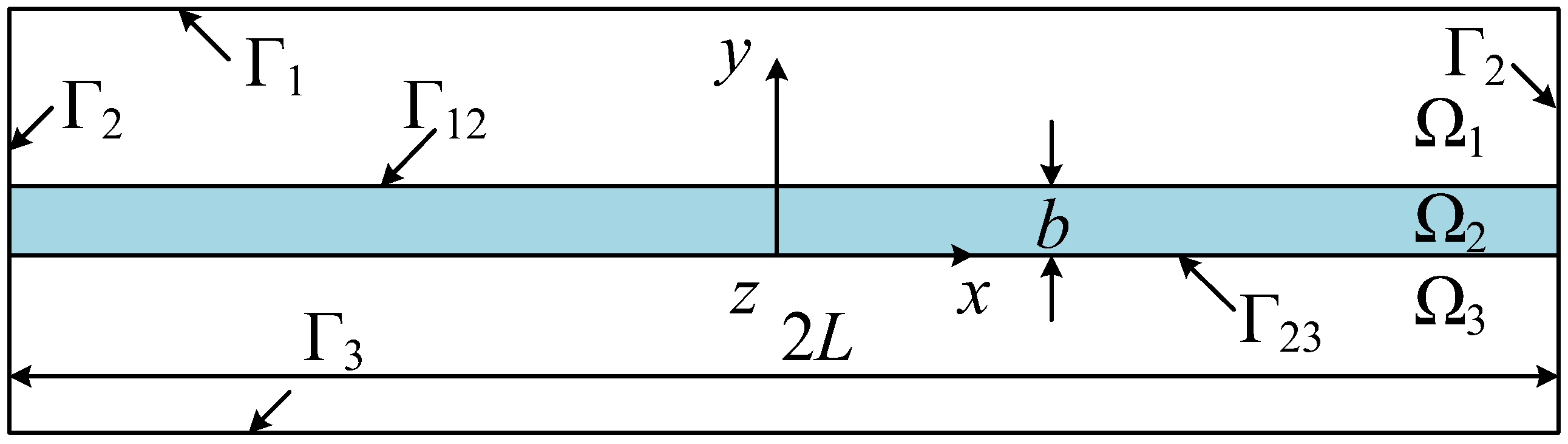
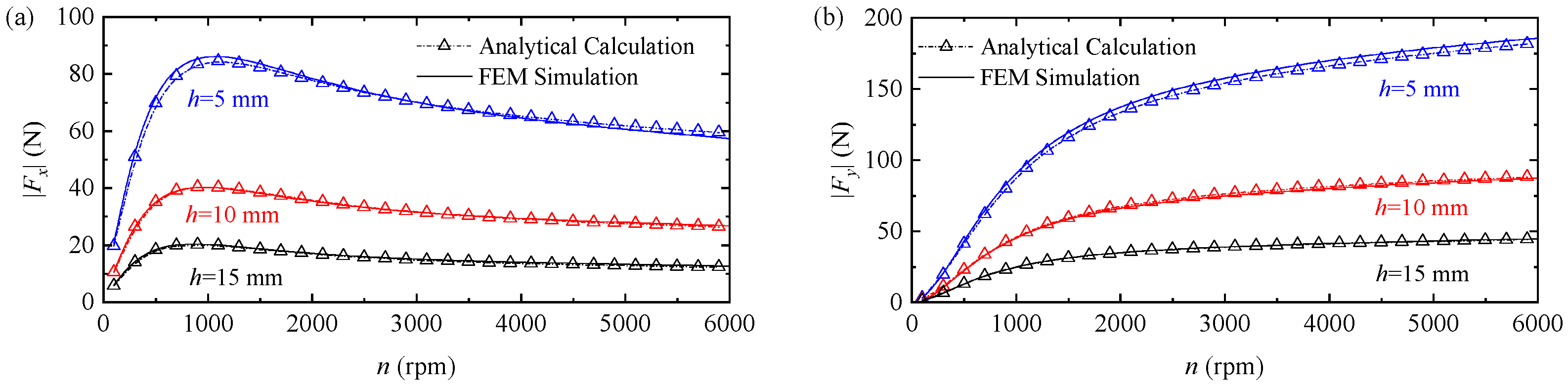
3.2. Electromagnetic Force

Figure 7 and Figure 8 illustrate the distortion characteristics of the source magnetic field on the conductor plate’s upper surface from the temporal and spatial perspectives, respectively. This distortion leads to significant differences in the electromagnetic force analysis between the PMEIM powertrain and other mechanisms, e.g., LIMs and flat PMEDS. Relative motion occurs between the maglev car and the lane, resulting in velocities v_x and v_y between the source magnetic field and the conductor plate, which further increases the complexity of the source magnetic field on the conductor plate surface. To investigate the electromagnetic force characteristics of the PMEIM powertrain, the conductor plate eddy current model is shown in Figure 9, which follows the following assumptions [28].

(i)

A Cartesian coordinate system x-y-z is established, with its origin at the geometric center of the conductor plate’s lower surface.

(ii)

The magnetic flux density is uniformly distributed axially, free from attenuation due to the transverse end effect.

(iii)

The conductor plate is isotropic and homogeneous, with its dimensions greatly exceeding the coverage range of the source magnetic field.

As depicted in Figure 9, the analytical model comprises three regions: air region Ω₁, conductor region Ω₂, and air region Ω₃. In Ω₁ and Ω₃, the scalar magnetic potential ϕ is introduced, with H expressed as negative gradient of ϕ. The governing equations for Ω₁ and Ω₃ are derived as

$${\displaystyle \frac{{\partial }^2{\varphi }_m}{\partial x^2}}+{\displaystyle \frac{{\partial }^2{\varphi }_m}{\partial y^2}}=0, \mathrm{in} {\Omega }_{\mathrm{m}}, m = 1, 3$$

(13)

In Ω₂, the steady-state differential equation for A is derived as

$${\displaystyle \frac{{\partial }^2{A}_z}{\partial x^2}}+{\displaystyle \frac{{\partial }^2{A}_z}{\partial y^2}}={\mu }_0\sigma (j{\omega }_e{A}_z+v_x{\displaystyle \frac{\partial A_z}{\partial x}}+v_y{\displaystyle \frac{\partial A_z}{\partial y}}), \mathrm{in} {\Omega }_2$$

(14)

where ω_e denotes angular frequency of the source magnetic field. v_x and v_y denote the relative velocity between the source magnetic field and the conductor plate.

To solve the governing Equations (13) and (14), the Fourier transform (FT) of A_z and ϕ_m is applied with respect to x, resulting in the FT governing equations.

$${\displaystyle \frac{{\partial }^2{\varphi }_m(\xi ,y)}{\partial y^2}}-{\xi }^2{\varphi }_m(\xi ,y)=0, {\displaystyle \frac{{\partial }^2{A}_z(\xi ,y)}{\partial y^2}}-2\lambda {\displaystyle \frac{\partial A_z(\xi ,y)}{\partial y}}-{\gamma }^2{A}_z(\xi ,y)=0$$

(15)

where ξ denotes spatial frequency, $\lambda ={\displaystyle \frac{{\mu }_0\sigma v_y}{2}}$, and $\gamma =\sqrt{{\xi }^2+j\mu \sigma ({\omega }_e+\xi v_x)}$.

By solving the general solution of Equation (15) and combining with the boundary conditions, A_z is derived as follows.

$$A_z(\xi ,y)=T(\xi ,y)B^s(\xi ,b)$$

(16)

where $T(\xi ,y)={\displaystyle \frac{({\beta }_2-\xi )e^{{\beta }_{1}y}-({\beta }_1-\xi )e^{{\beta }_{2}y}}{({\beta }_2-\xi )({\beta }_1+\xi )e^{{\beta }_{1}b}-({\beta }_1-\xi )({\beta }_2+\xi )e^{{\beta }_{2}b}}}$ and ${\beta }_{1,2}=\lambda \pm \sqrt{{\lambda }^2+{\gamma }^2}$.

From the second equation of Equation (9), the Fourier form of the magnetic flux density inside the Ω₁ is derived.

$$B_x(\xi ,y)={\displaystyle \frac{\partial T(\xi ,y)}{\partial y}}{B}^s(\xi ,b), B_y(\xi ,y)=-j\xi T(\xi ,y)B^s(\xi ,b)$$

(17)

The magnetic flux density B^r of the reflected field is expressed in component form as

$$B_x^r(\xi ,y)=j\left[B_y^s(\xi ,b)+j\xi T(\xi ,b)B^s(\xi ,b)\right]e^{\xi (b-y)}$$

(18)

$$B_y^r(\xi ,y)=-\left[B_y^s(\xi ,b)+j\xi T(\xi ,b)B^s(\xi ,b)\right]e^{\xi (b-y)}$$

(19)

Equation (17) as well as Equations (18) and (19) are the analytical models for the magnetic flux densities of the eddy current field and reflected field, respectively. The electromagnetic force of the PMEIM powertrain can be calculated by applying the Maxwell stress tensor on the conductor plate upper surface. Then, through FT and subsequent collation and simplification, the analytical model of the electromagnetic force can be derived.

$$F_x={\displaystyle \frac{W_m}{8\pi {\mu }_0}}\mathrm{Im}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\left[2\xi T(\xi ,b)-1\right]|B^s(\xi ,b){|}^{2}d\xi }$$

(20)

$$F_y={\displaystyle \frac{W_m}{8\pi {\mu }_0}}\mathrm{Re}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\left[2\xi T(\xi ,b)-1\right]|B^s(\xi ,b){|}^{2}d\xi }$$

(21)

Based on the electromagnetic force model, the propulsion and levitation forces generated by the PMEIM powertrain vary with rotational speed under the condition of no relative motion, as shown in Figure 10. The propulsion force first increases and then decreases with increasing rotational speed, peaking at 1000 rpm. The levitation force is repulsive and acts on the conductor plate along the negative y-axis, which increases with rotational speed and tends to saturate. Both forces decrease as the suspension height increases. Overall, the curves from analytical calculation and the FEM simulation show consistent trends. The maximum errors of the propulsion force are 3.22% (h = 5 mm), 0.77% (h = 10 mm), and 0.77% (h = 15 mm), respectively. The maximum errors of the levitation force are 0.18% (h = 5 mm), 1.94% (h = 10 mm), and 0.42% (h = 15 mm), respectively.

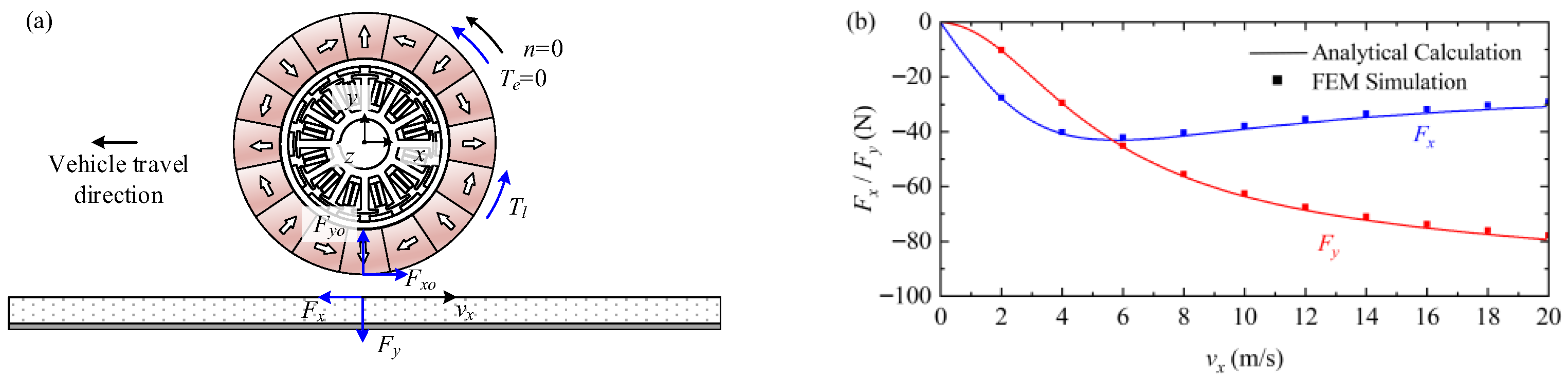
3.3. Operating State

During the operation of a maglev car, its magnetic wheels move relative to the lane at a longitudinal speed. This results in a slip between PMEIM and the conductor plate. To analyze the slip and simplify subsequent derivations, it assumes that the conductor plate moves relative to the PMEIM at a speed v_x. Herein, the slip ratio is defined as

$$s=(v_s-v_x)/v_s$$

(22)

where v_s is the velocity of the source magnetic field at the conductor plate, referred to as the synchronous speed, and depends on the rotational speed of the PMEIM.

According to Figure 11, the propulsion principle of the PMEIM powertrain is described as follows: The PMEIM generated an electromagnetic torque, T_e. Driven by T_e, the rotor exerts a force F_x on the conductor plate, while the conductor exerts a reaction force F_xo on the PMEIM, serving as the propulsion force. F_x, F_xo, F_y, and F_yo are the respective interaction forces acting between the PMEIM and the conductor plate.

Therefore, under a steady state, the force–torque relationship holds

$$T_l=F_{xo}{R}_o, T_e=T_l$$

(23)

where T_e and T_l denote the electromagnetic torque and the load torque of the PMEIM, respectively. R_o denotes the PMEIM outer diameter.

3.3.1. Motor Operation

As presented in Figure 12a, the PMEIM rotates counterclockwise, and the synchronous velocity v_s is directed along the positive x-axis. When the conductor plate velocity v_x satisfies 0 < v_x < v_s (i.e., 0 < s < 1), v_x is also oriented along the positive x-axis. The corresponding electromagnetic forces are shown in Figure 12b,c.

As shown in Figure 12b, the directions of F_x and v_x are identical, indicating that the PMEIM powertrain is operating in the motor state.

3.3.2. Braking Operation

The PMEIM powertrain has three braking modes. By analogy to LIMs, these are classified into regenerative braking, plugging braking, and dynamic braking. All modes share a common characteristic, where the propulsion force exerted on the PMEIM is opposite to the vehicle travel velocity.

(i)

Regenerative braking

As presented in Figure 13, the PMEIM rotates counterclockwise, and the synchronous velocity v_s is directed along the positive x-axis. When the conductor plate velocity v_x satisfies v_x > v_s (i.e., s < 0), v_x is also oriented along the positive x-axis. The corresponding electromagnetic forces are shown in Figure 13b,c. As shown in Figure 13b, the directions of F_x and v_x are opposite, which indicates that the PMEIM powertrain is operating in the braking state.

When the input current of the PMEIM is controlled to zero, it no longer delivers electromagnetic torque (T_e = 0). Conversely, it operates in the generator model. Driven by the load torque T_l, an inductive electromotive force (EMF) is induced in the armature of the PMEIM. When the circuit is closed, this induced EMF can feed the electrical energy back to the storage device.

(ii)

Plugging braking

When s > 1, the velocity relationship is as follows:

$$s={\displaystyle \frac{v_s-(-v_x)}{v_s}}={\displaystyle \frac{v_s+v_x}{v_s}}>1$$

(24)

$$s={\displaystyle \frac{-v_s-v_x}{-v_s}}={\displaystyle \frac{v_s+v_x}{v_s}}>1$$

(25)

As presented in Figure 14a, the PMEIM rotates counterclockwise, and the synchronous velocity v_s is directed along the positive x-axis. When the conductor plate velocity v_x satisfies Equation (24), v_x is oriented along the negative x-axis. The corresponding electromagnetic forces are shown in Figure 14b,c. As shown in Figure 14b, the directions of F_x and v_x are opposite, which indicates that the PMEIM powertrain is operating in the braking state.

As presented in Figure 15, the directions of all quantities of the PMEIM powertrain are opposite to those illustrated in Figure 14a. Essentially, however, their motion states are identical. Therefore, the characteristics of the electro-magnetic force are similar, which will not be reiterated here.

(iii)

Dynamic braking

As presented in Figure 16a, when the PMEIM is switched off and its rotor is locked (n = 0, T_e = 0), a static source magnetic field is generated. The conductor plate moves relative to the PMEIM along the positive x-axis at a velocity of v_x. Herein, the slip ratio is s = 1, and the PMEIM powertrain is equal to a permanent magnet eddy current brake. The corresponding electromagnetic forces are shown in Figure 16b. The directions of F_x and v_x are opposite, which indicates that the PMEIM powertrain is operating in the braking state.

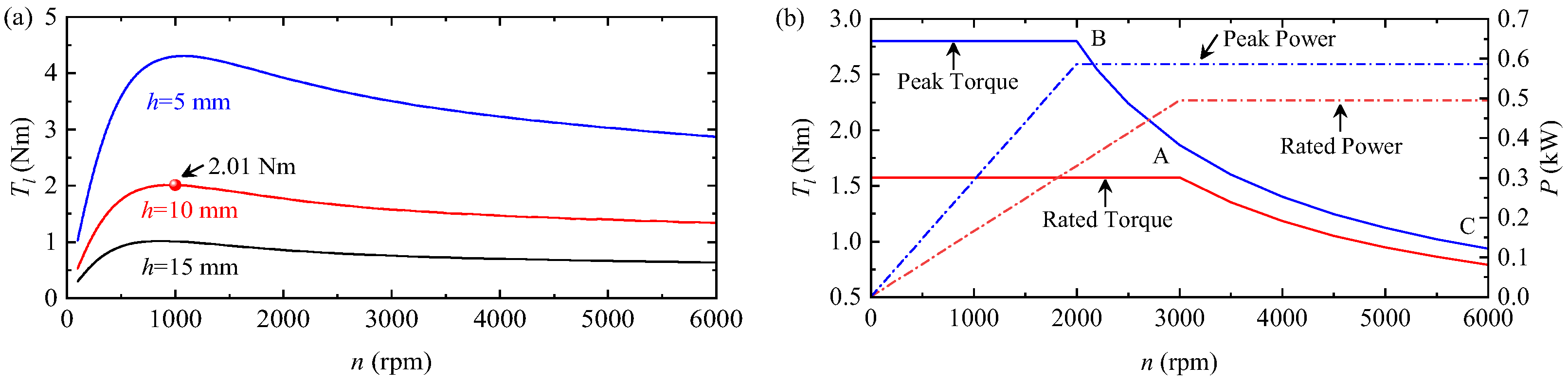
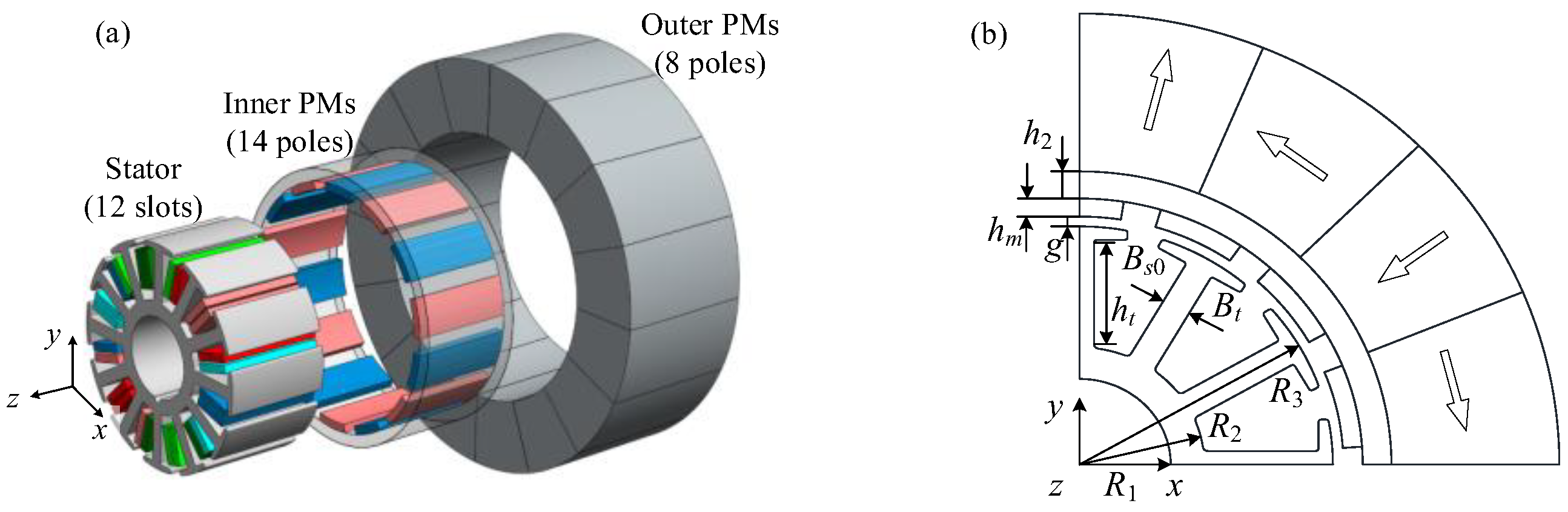
4. Integrated Design of PMEIM

4.1. Electromagnetic Model

Based on the mechanical characteristics of the PMEIM powertrain shown in Figure 10, its propulsion force is converted to the PMEIM load torque, as illustrated in Figure 17a. For the PMEIM design, the load curve at a suspension height of 10 mm is adopted as the reference, where the maximum load torque is 2.01 Nm at 1000 rpm. Accounting for overload operation, the peak torque is set to 2.8 Nm, with the PMEIM-specific initial design parameters summarized in

Table 2. Initial design data of the PMEIM.

Parameters	Symbols	Nominal Values	Parameters	Symbols	Nominal Values
Rated speed	nN	3000 rpm	Peak speed	np	6000 rpm
Rated torque	TN	1.57 Nm	Peak torque	Tp	2.80 Nm
Rated power	PN	495 W	Peak power	Pp	586 W

. Using Equation (26), the external characteristic curve of the PMEIM is plotted, as shown in Figure 17b, where three typical operating conditions are highlighted: A (rated condition), B (peak torque condition), and C (peak rotational speed condition).

$$P=T\cdot n/9550$$

(26)

where P denotes the mechanical power.

According to the dimensions of the Halbach PM array on the rotor’s outer side, the stator armature adopts a fractional-slot concentrated winding structure to enhance structural compactness. Together with the PMs on the inner side of the rotor, it forms a 12-slot and 14-pole configuration, as illustrated in Figure 18a. The armature winding factor is 0.933. Figure 18b presents the structural parameters of the PMEIM quarter-model, with detailed values listed in

Table 3. Structure parameters of the PMEIM.

Parameters	Symbols	Values	Parameters	Symbols	Values
Inner radial	R1	9.5 mm	Pole arc coefficient	αp	0.7
Middle radial	R2	13 mm	Thickness of rotor yoke	h2	3 mm
Outer radial	R3	26.4 mm	Slots and poles	z/2p	12/14
Axial length	Lef	25 mm	Pitch	y	1
Tooth depth	ht	11.25 mm	Conductors per slot	Ns	14
Tooth width	Bt	3 mm	Parallel strands	n	1
Slot width	Bs0	3.5 mm	Parallel branches	a1	1
Airgap	g	1.1 mm	PMs type	Bre	1.23 T
Thickness of PM	hm	2 mm	Winding type	σ	5.8 × 107 S/m

.

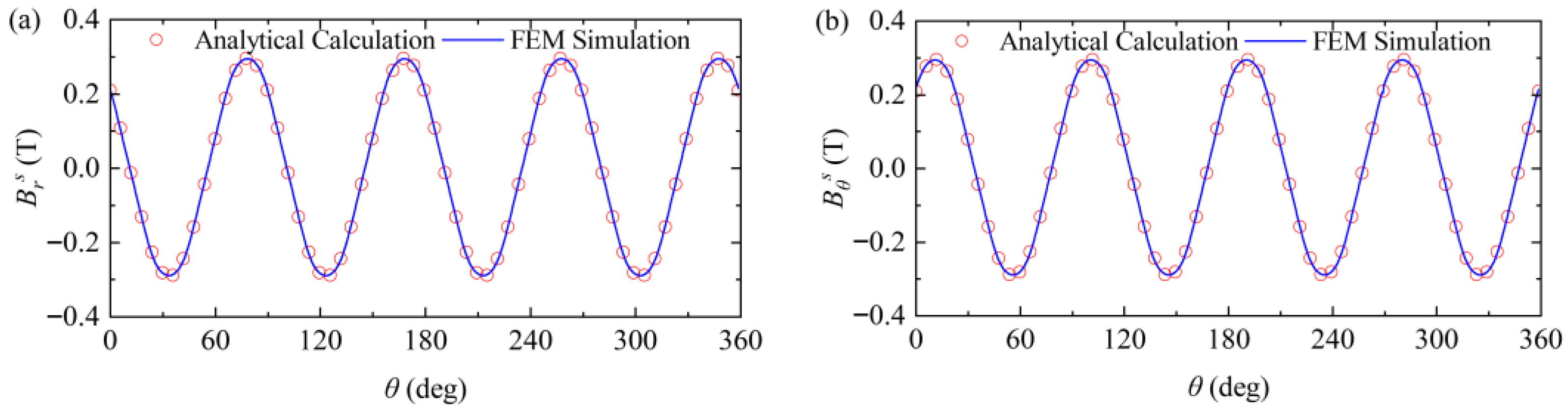
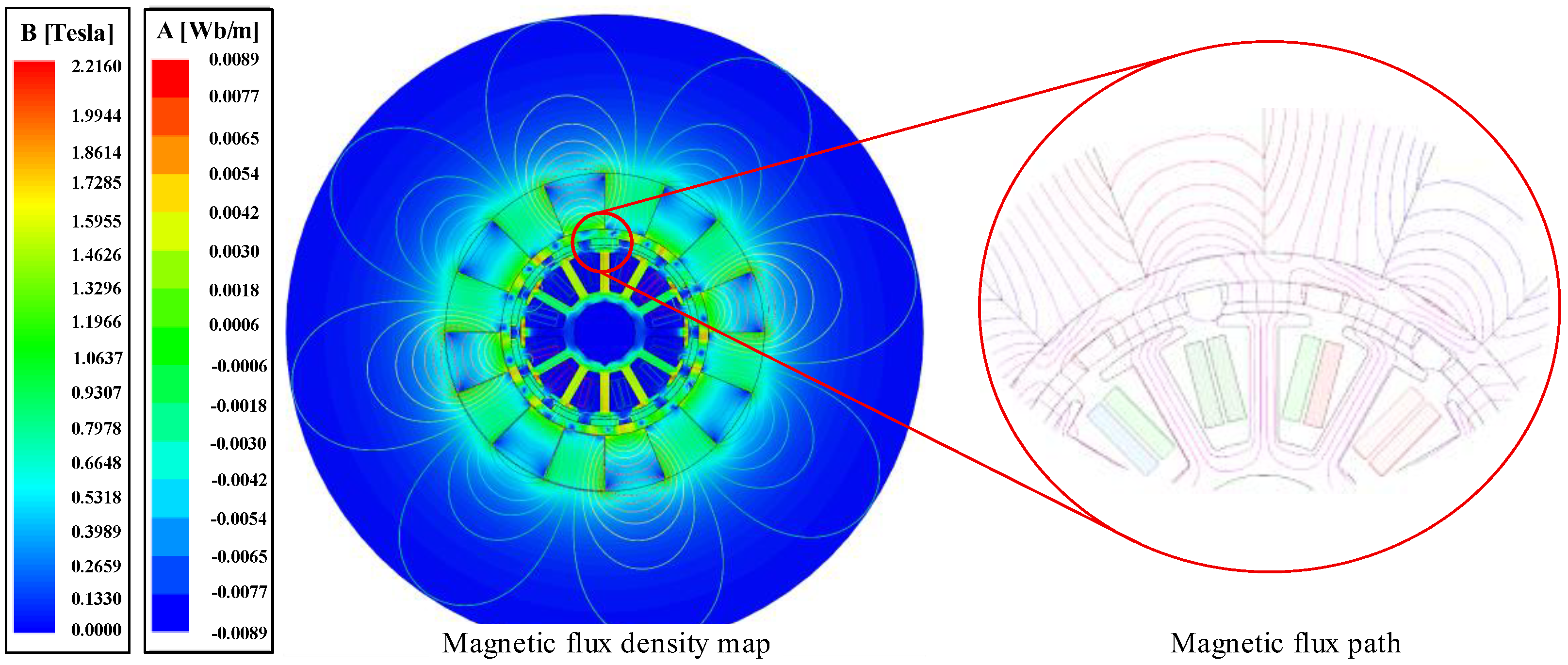
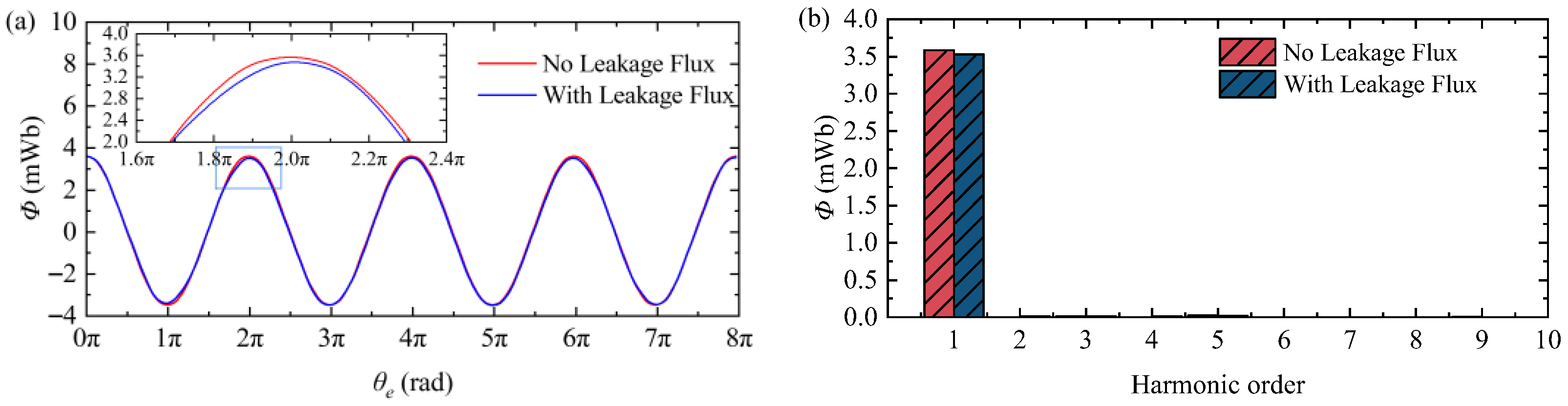
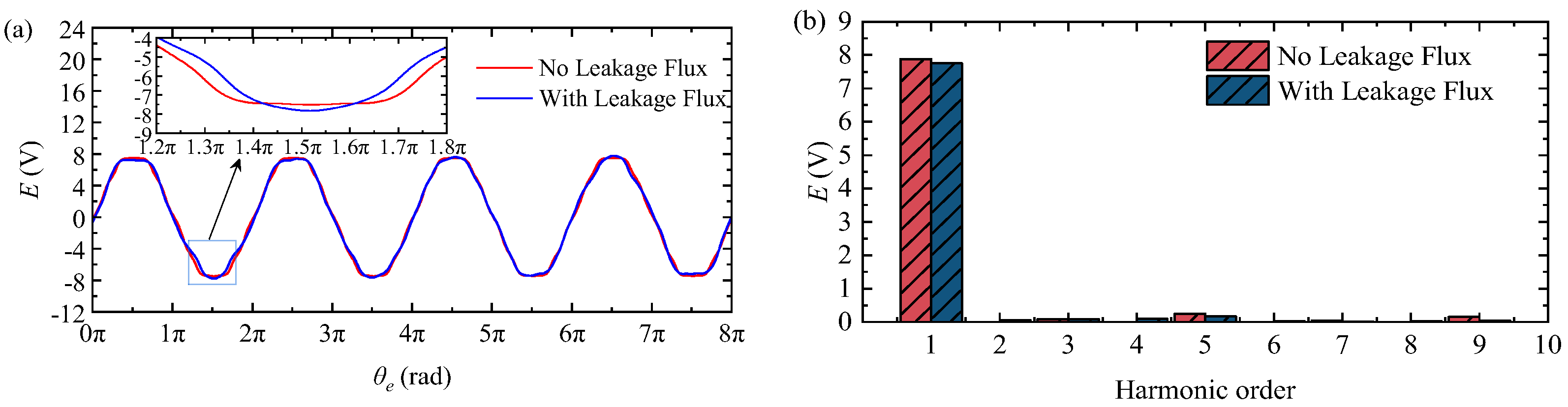
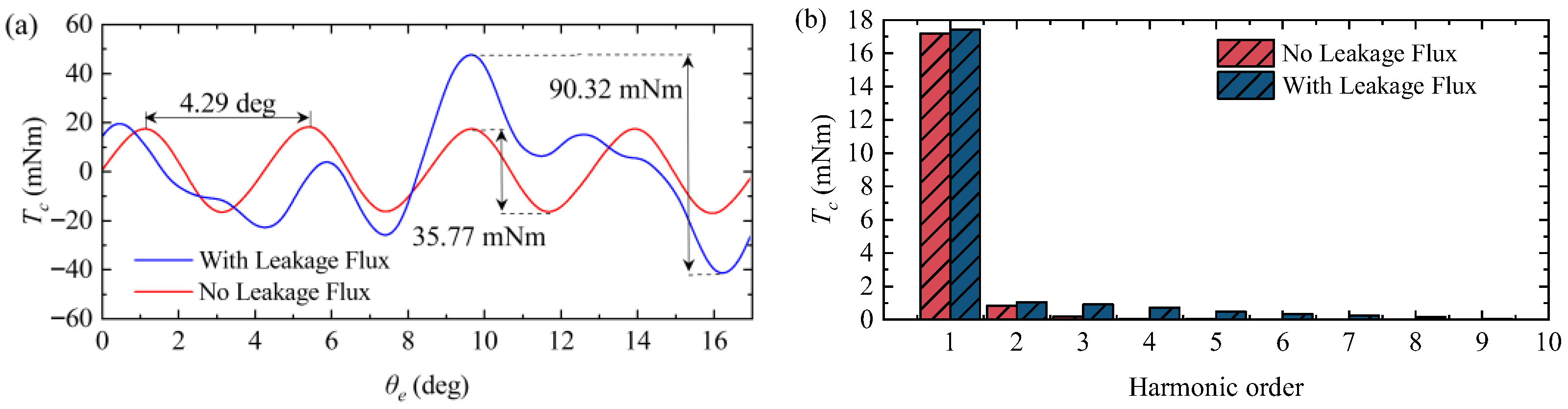
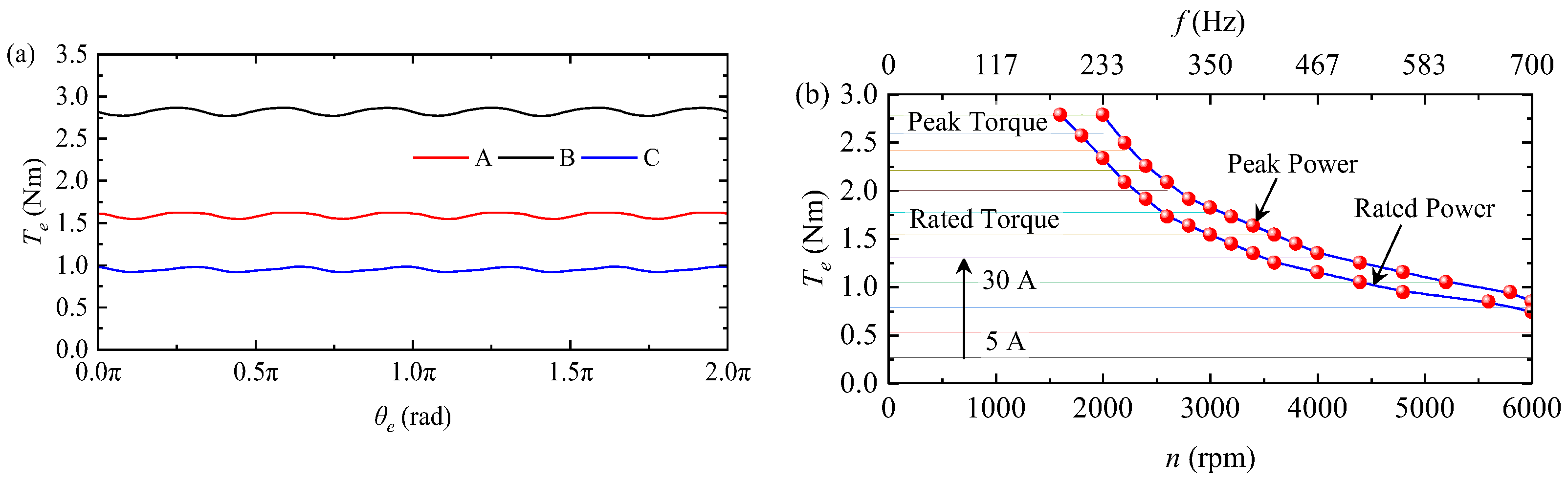
4.2. Electromagnetic Analysis

In the integrated configuration, PMs are mounted on both sides of the rotor. To minimize the stator-rotor magnetic reluctance, the rotor middle yoke is fabricated from a high-permeability material. Although the outer PMs are arranged in a Halbach array, concentrating magnetic flux on the outer side, leakage flux still exists on the inner side. As illustrated in Figure 19, this leakage flux couples with the inner PMs via the rotor yoke. The resulting magnetic flux passes through the air gap to the stator teeth, travels to adjacent teeth via the stator yoke, and finally returns to the adjacent PM through the air gap, forming a closed magnetic field.

To evaluate the impact of the inner leakage flux of the Halbach PM array, the no-load operating condition at a rotor rotational speed of 3000 rpm is analyzed. Figure 20 illustrates the air gap flux. The waveforms under the two conditions (with and without leakage flux) are nearly identical and exhibit a sinusoidal distribution, with fundamental amplitudes of 3.28 mWb and 3.53 mWb, respectively. The EMF is shown in Figure 21, where both waveforms present a flat-top profile with fundamental amplitudes of 7.88 V and 7.54 V, respectively. Furthermore, Figure 22 depicts the PMEIM cogging torque T_c. Without the outer rotator Halbach PM array, the machine cogging torque exhibits a sinusoidal waveform with a peak-to-peak value of 35.77 mNm and a period of 4.29 degrees. In contrast, leakage flux distorts the cogging torque distribution, increasing the peak-to-peak value to 90.31 mNm. Specifically, leakage flux increases the fundamental harmonic amplitude of the cogging torque and enhances the presence of higher-order harmonics.

From the results, it is concluded that the leakage flux of the outer Halbach PM array couples with the internal flux, affecting the PMEIM electromagnetic performance. However, this influence is relatively weak, as the maximum cogging torque only accounts for 3.05% of the rated torque.

For the load conditions, the PMEIM performance at operating points A, B, and C, shown in Figure 23a, is analyzed. The RMS values of the three-phase current required for these three operating points are 15.5 A, 30.5 A, and 9 A, with corresponding current frequencies of 350 Hz, 233 Hz, and 700 Hz. The average electromagnetic torque T_e values are 1.59 Nm, 2.82 Nm, and 0.947 Nm, exhibiting respective errors of 1.27%, 0.71%, and 1.50% compared with the target of performance requirements. Furthermore, a parametric analysis of the PMEIM is conducted with discrete armature currents (5–30 A, step 5 A) and rotational speeds (1000–6000 rpm, step 500 rpm). As observed in Figure 22b, the torque remains stable across different rotational speeds and currents, meeting the application requirements of the PMEIM powertrain. With the increasing armature current, the torque increases and the output power rises accordingly, with the power curves forming the envelope of the torque curves at the corresponding operating points.

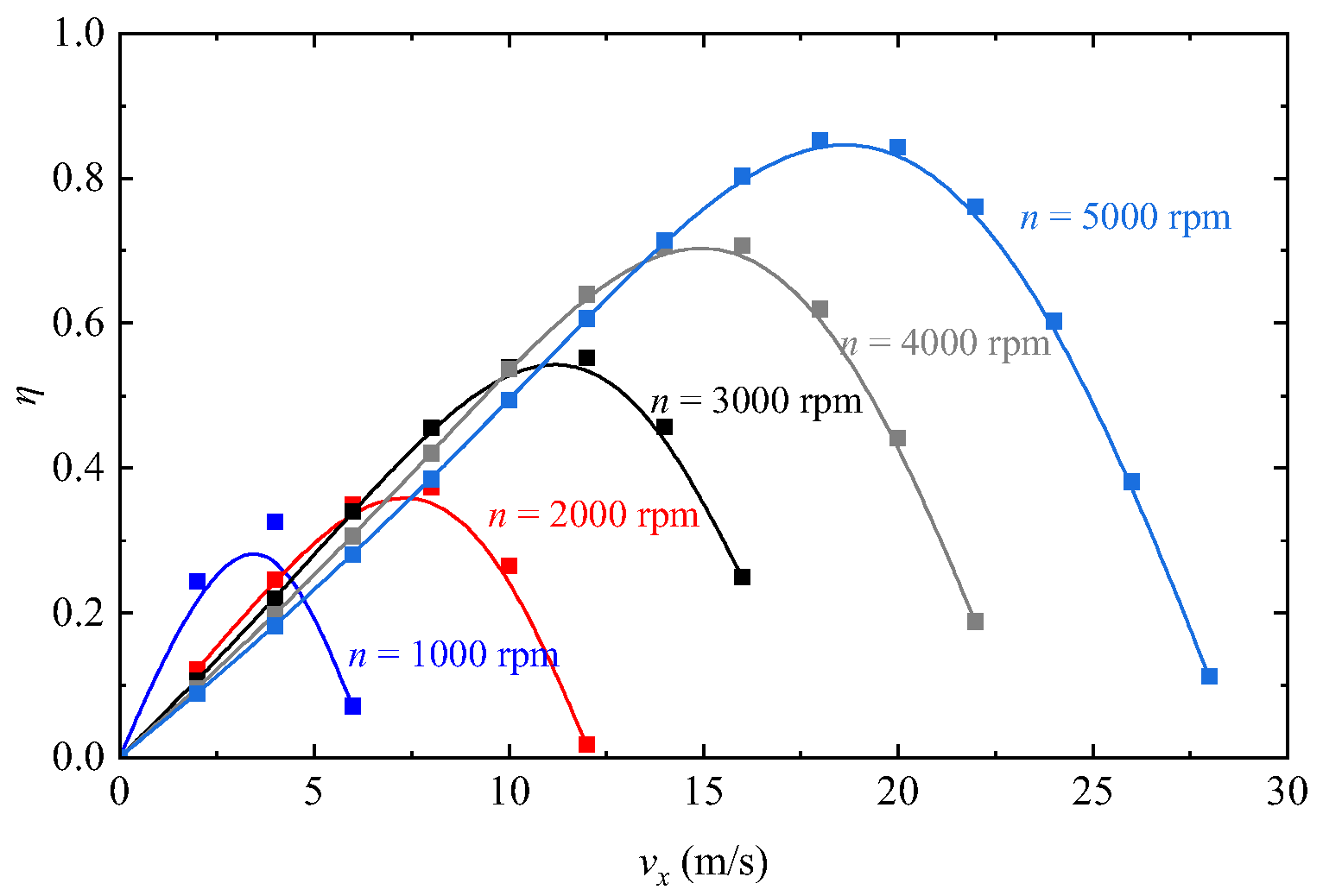
4.3. Efficiency Evaluation

In the PMEIM powertrain, the PMEIM acts as the prime mover, which converts rotational motion into linear motion in a contactless manner via electromagnetic induction. Based on this transmission mechanism, propulsion efficiency η is discussed in accordance with Equation (27).

$$\eta =9.55{\displaystyle \frac{F_x{v}_x}{T_{e}n}}$$

(27)

Figure 24 shows the efficiency estimation results of the PMEIM powertrain at a suspension height of 10 mm. At a constant rotational speed, efficiency exhibits a variation trend of first increasing and then decreasing with the increase in linear velocity. The higher the rotational speed, the greater the peak efficiency. At a rotational speed of 5000 rpm and a linear velocity of 18 m/s, the maximum efficiency of 85% is achieved.

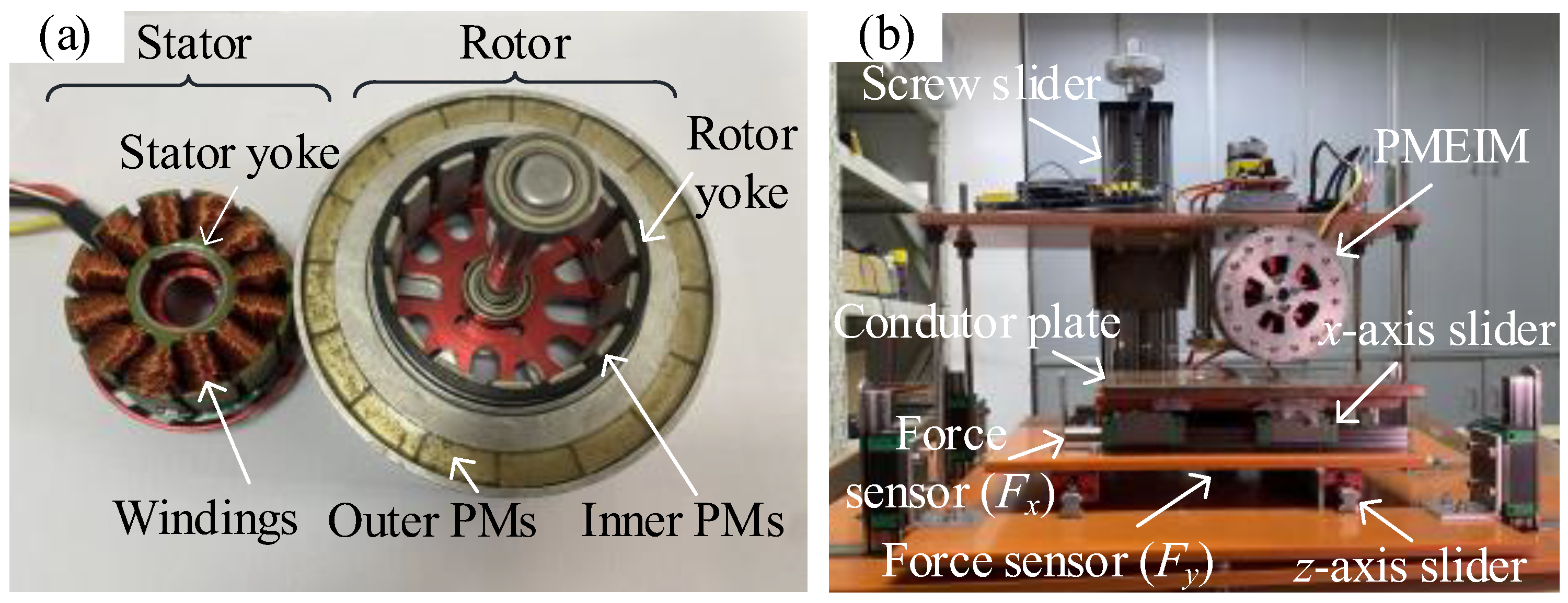
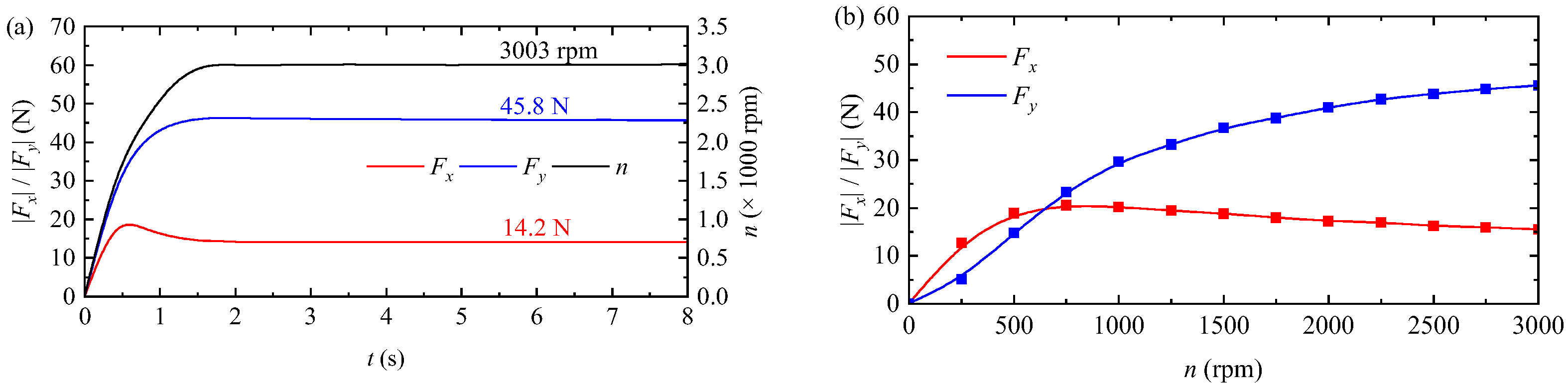
5. Prototype Experiment of PMEIM

Experimental investigations were performed to evaluate the PMEIM, with a small-scale prototype and test platform established (Figure 25). Figure 25a shows the PMEIM prototype, consisting of a stator and a composite rotor. The external Halbach-array PMs are encapsulated in an aluminum alloy shell for mechanical protection. Figure 25b presents the experimental setup: the epoxy resin supports minimize the magnetic interference, the stator end cover is bolted to the bracket, and an adjustable copper plate (screw-driven slider) maintains a 10 mm air gap under the rotor. Force measurement uses a dual-axis sliding rail system, with horizontal and vertical slides transmitting propulsion and levitation forces to calibrated sensors.

Figure 26a shows the measurement results of electromagnetic forces at a rotation speed of 3000 rpm, with a suspension gap of 10 mm. During the acceleration of the PMEIM to 3000 rpm, the propulsion force initially increases and then decreases. In contrast, the levitation force gradually increases, reflecting the mechanical characteristics of the EDW powertrain. At a steady state, the propulsion and levitation forces are 14.2 N and 45.8 N, respectively. Figure 26b further illustrates the steady-state electromagnetic forces under different rotational speeds, showing the stable values of propulsion and levitation force measured at various speeds. Influenced by structure and vibration, the maximum testing speed is set to 3000 rpm.

Notably, the following assumptions are adopted in analytical calculations and FEM simulations: The magnetic field is uniformly distributed along the z-axis and is not affected by the attenuation induced by the transverse end effect. However, in practice, owing to the transverse end effect arising from the finite axial length along the z-axis, the source magnetic field gradually decays from the center of the z-axis to its two axial ends. Consequently, the experimentally measured electromagnetic forces are smaller than the theoretical prediction, while the variation trend remains consistent.

To clarify the relationship between mass and levitation, the indicator of the levitation–weight ratio for a single PMEIM unit is adopted.

$$\lambda ={\displaystyle \frac{F_y}{G}}$$

(28)

where F_y denotes the levitation force, G denotes the weight of the single PMEIM, and λ denotes the levitation–weight ratio.

The mass of the PMEIM is measured to be 1.845 kg. According to Equation (28), the levitation–weight ratio curve is plotted as shown in Figure 27. Similarly to the characteristics of the levitation force, the levitation–weight ratio increases with rising rotational speed. At 750 rpm, the levitation–weight ratio reaches 1.29, enabling the PMEIM to achieve levitation. At 3000 rpm, the generated levitation force can reach 2.52 times the self-weight of the PMEIM.

6. Conclusions

In this study, a PMEIM configuration is proposed by integrating PMEDS with in-wheel motor technology to provide a compact and flexible propulsion and levitation solution for maglev car powertrains. The main conclusions are as follows:

(1)

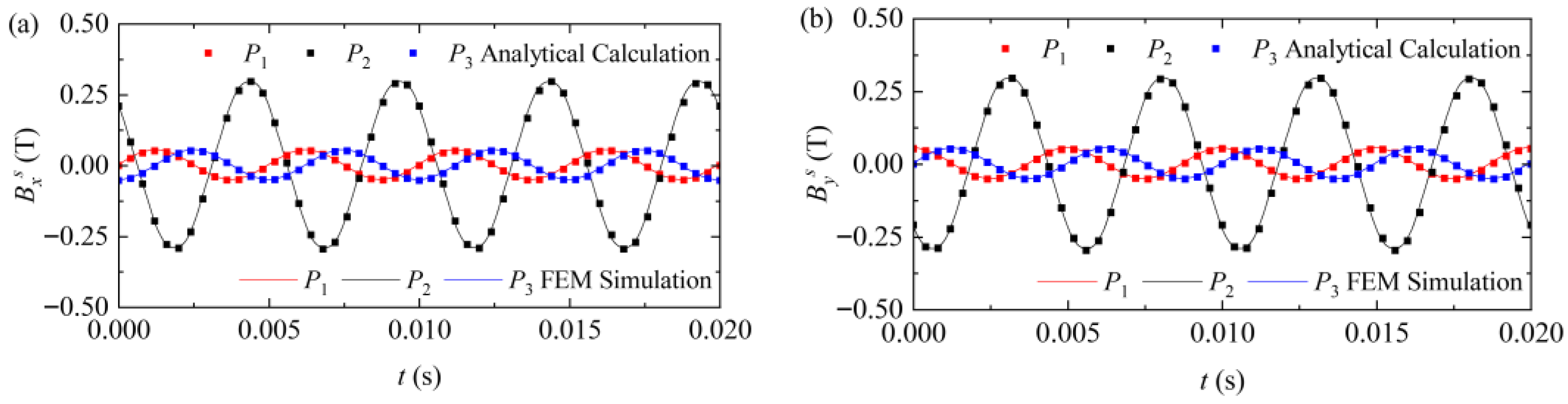
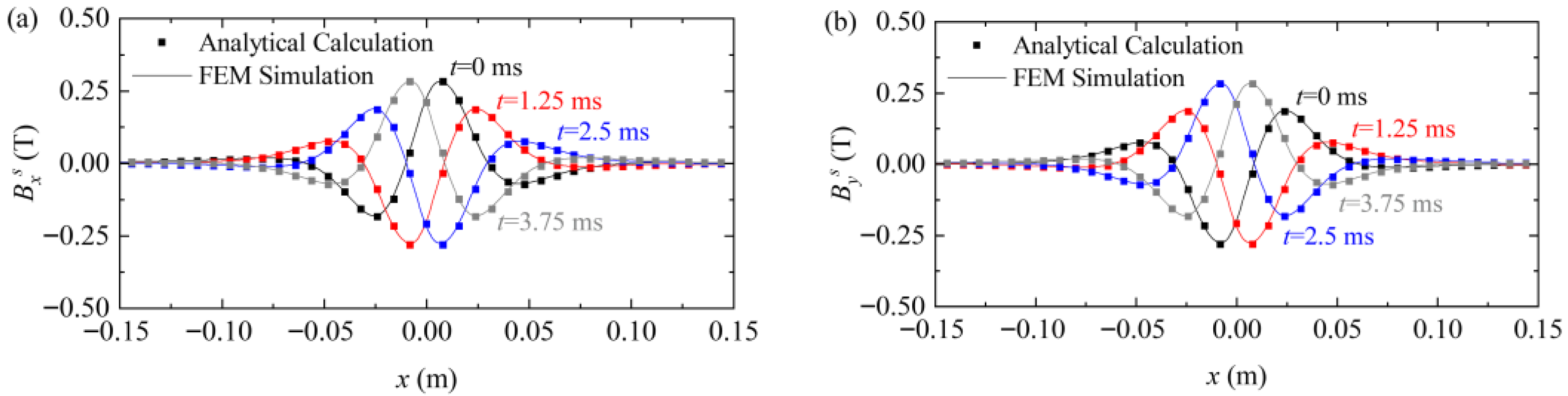
The external magnetic field distribution of the PMEIM is characterized by analytical and FEM approaches. Results indicate that despite the powertrain adopting a Halbach PM array, non-uniformity of the suspension gap causes magnetic field distortion, which presents amplitude-modulated periodic waves on the conductor plate.

(2)

The electromagnetic force characteristics of the PMEIM powertrain are analyzed via analytical and FEM methods. The powertrain operating states (motor operation, regenerative braking, plugging braking, and dynamic braking) are calculated and determined.

(3)

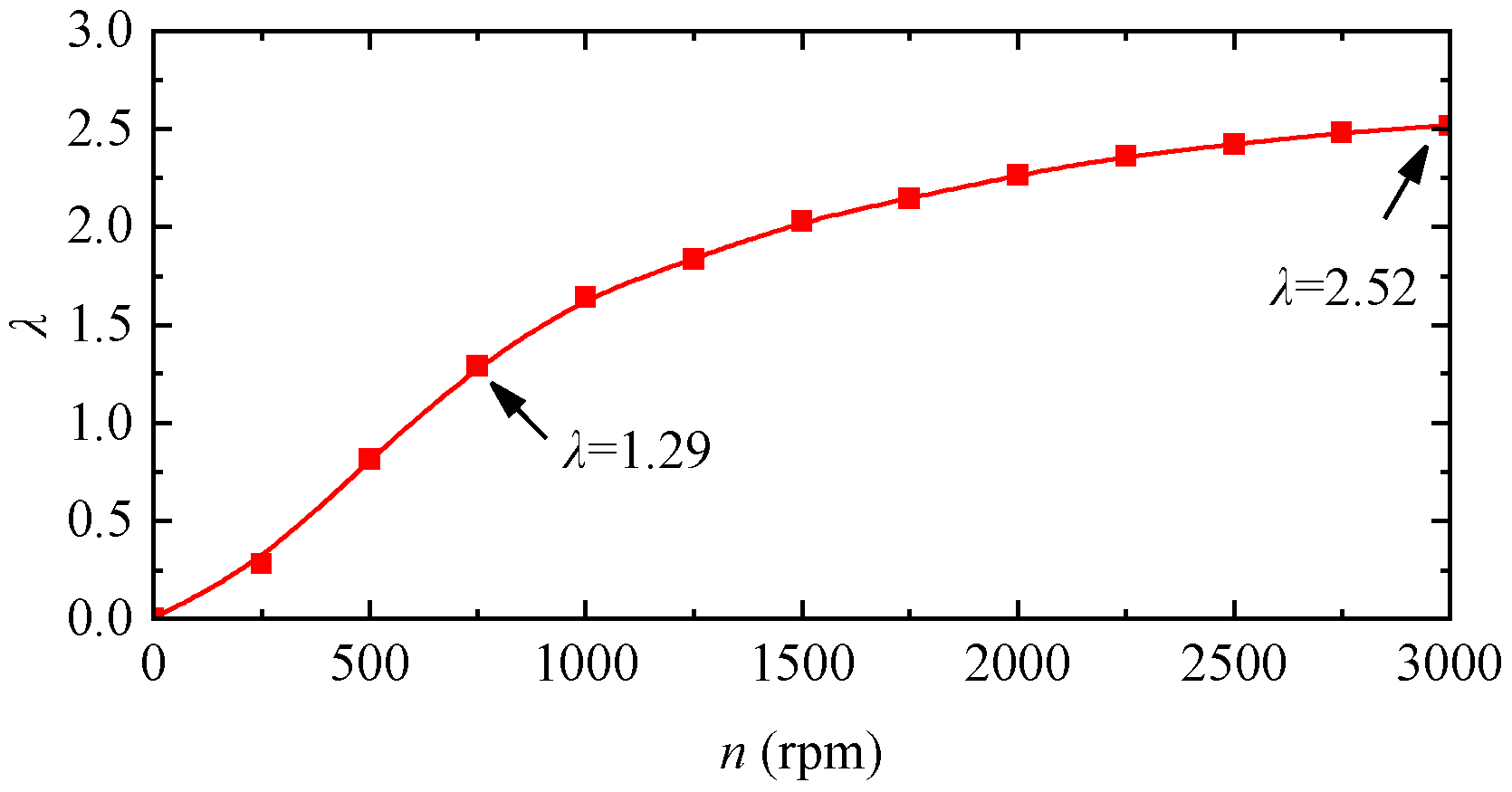
The PMEIM electromagnetic design is conducted on a small-scale PMEIM prototype. Results confirm that, under rated conditions, the measured thrust force and guidance force of the prototype are 14.2 N and 45.8 N, respectively, with a levitation–weight ratio of 2.52. The PMEIM powertrain exhibits integrated levitation and propulsion functions.

Future research will focus on more rigorous 3D analytical modeling to account for the influence of axial finite dimensions, followed by the fabrication of maglev car prototypes and experimental research.