RBF-NN Supervisory Integral Sliding Mode Control for Motor Position Tracking with Reduced Switching Gain

Abstract

Integral Sliding Mode Control (ISMC) is widely employed in motor position control systems due to its robustness against uncertainties. However, its control performance is critically dependent on the selection of the switching gain. Although Disturbance Observer-Based Control (DOBC) is commonly adopted as an effective alternative for uncertainty compensation, it may exhibit limitations when high gains are required, potentially leading to system instability. To address these issues, this study proposes a Radial Basis Function Neural Network (RBF-NN)-based supervisory learning approach designed to minimize switching gain requirements. The effectiveness of the proposed scheme is validated through comparative simulations and laboratory experiments, specifically under scenarios involving system parameter uncertainties and sinusoidal disturbances with unknown offsets. Both simulation and experimental results demonstrate the superior performance of the proposed RBF-NN approach in terms of switching gain reduction and tracking error norms compared to a conventional ISMC and a DOBC-based cascade P–PI controller.

1. Introduction

The control of electric motor position systems under uncertainty remains a challenging problem in modern industrial applications [1,2,3,4]. Precision position control is critical across diverse domains, including factory automation, robotics, and autonomous vehicles. Various sources of uncertainty, including parameter variations, external load disturbances, and nonlinear friction dynamics, can significantly degrade the positioning accuracy and overall system performance. To address these challenges, various control strategies have been developed and investigated, including adaptive control [5,6], disturbance observer-based control [7,8], and sliding mode control [9,10], each offering distinct advantages in handling different types of uncertainties. As industrial automation systems demand increasingly stringent performance requirements, the development of robust control strategies capable of maintaining nominal performance despite these uncertainties has become essential.

Among robust control techniques, sliding mode control (SMC) has been widely recognized as one of the most effective approaches for systems operating under uncertainties [9,10]. The inherent robustness of SMC stems from its insensitivity to matched uncertainties once the system trajectory reaches the sliding surface. However, classical SMC suffers from the reaching phase problem, during which the system is vulnerable to uncertainties before reaching the sliding surface. To eliminate this vulnerability, integral sliding mode control (ISMC) has been developed, which incorporates an integral action into the sliding surface design [11]. By ensuring that the system trajectory starts on the sliding surface from the initial time, ISMC provides robustness throughout the entire control process and eliminates steady-state errors. Despite these advantages, both SMC and ISMC face a fundamental challenge: the chattering phenomenon caused by the discontinuous switching control input. The switching gain must be sufficiently large to overcome uncertainties, but excessive switching gains lead to high-frequency oscillations that can excite unmodeled dynamics, cause actuator wear, and degrade control performance. This trade-off between robustness and chattering has motivated extensive research on chattering reduction techniques.

Numerous approaches have been proposed to alleviate the chattering problem in sliding mode control. One common strategy involves replacing the discontinuous sign function with continuous approximations, such as saturation functions or smooth sigmoid functions [9]. While this approach reduces chattering, it compromises the robustness properties of SMC and may result in bounded tracking errors. An alternative method integrates the output of the sign function to smooth the switching control input, thereby reducing high-frequency oscillations [12]. Sliding mode reaching laws have also been developed to provide a systematic way to balance the convergence rate and chattering level [13]. Time-delay-based approximations of the sign function offer another means of chattering reduction by exploiting the system’s time-delay characteristics [14]. More recently, time-varying gain approaches have been proposed, where the switching gain is adaptively adjusted based on the system state or uncertainty estimates [15]. Higher-order sliding mode control techniques extend the basic SMC framework by acting on higher derivatives of the sliding variable, thereby enabling discontinuous control to appear only in higher control derivatives and resulting in continuous actual control inputs [16]. Although these methods demonstrate various degrees of success in reducing chattering, they often require careful tuning, may introduce conservatism in the control design, or add significant complexity to the implementation.

In parallel to sliding mode control approaches, disturbance observer-based control (DOBC) has emerged as another highly effective robust control strategy for handling uncertainties in motor control systems [7,8]. The fundamental principle of DOBC is to estimate the lumped disturbance (which includes model uncertainties, parameter variations, and external disturbances) using an observer and then compensate for it through feedforward control. Unlike SMC, which relies on high-gain switching action to reject uncertainties, DOBC achieves robustness through accurate disturbance estimation and compensation. The disturbance observer provides feedforward compensation that counteracts the estimated disturbances, enabling the baseline controller to maintain nominal performance even in the presence of significant uncertainties. This estimation-based approach has demonstrated its versatility by being successfully applied to various control structures. Cascade P–PI controllers, which are widely used in industrial motor drives due to their intuitive structure and ease of implementation, represent one such application where observer-based disturbance compensation has proven particularly effective [2]. By incorporating the estimated disturbances into the feedforward path of cascade controllers, both tracking performance and disturbance rejection capabilities can be substantially improved, making DOBC an attractive solution for practical industrial applications [17].

Despite the effectiveness of observer-based approaches in various control configurations, they encounter significant limitations in certain scenarios. The estimation accuracy of disturbance observers depends critically on the observer gain: higher gains provide faster disturbance tracking and better estimation accuracy, but may lead to amplification of measurement noise and increased sensitivity to unmodeled high-frequency dynamics. When high observer gains are required to achieve desired performance through accurate disturbance estimation, stability issues can arise, particularly in systems with fast dynamics or significant measurement noise. Furthermore, disturbance observers typically rely on nominal system models, and their performance may degrade when the actual system dynamics deviate significantly from the assumed model. The need for high observer gains often indicates the presence of large uncertainties or fast-varying disturbances, which are precisely the conditions under which observer stability becomes questionable [18]. These fundamental limitations of observer-based methods, whether applied to cascade controllers or other control structures, motivate the exploration of alternative compensation approaches that can handle large uncertainties without relying on high-gain observers or precise system models.

In recent years, neural network-based approaches have gained considerable attention as promising alternatives to model-based compensation methods. Among various neural network architectures, Radial Basis Function Neural Networks (RBF-NNs) have attracted particular interest in control applications due to their universal approximation capability and relatively simple structure compared to multi-layer perceptron networks [19,20]. The theoretical foundation for using RBF-NNs in control lies in their ability to approximate any continuous function over a compact set to arbitrary accuracy, provided that a sufficient number of hidden neurons are used. This property makes RBF-NNs particularly well-suited for learning and compensating complex nonlinear dynamics without requiring explicit mathematical models. Moreover, the local representation property of RBF-NNs, where each basis function is activated only in a localized region of the input space, facilitates faster learning and better generalization compared to global approximators.

The application of RBF-NNs in various control systems has demonstrated significant success across multiple domains [20]. In magnetic levitation vehicle control systems, RBF-NNs have been integrated to improve robustness against nonlinearities and achieve better tracking performance [21]. For bilateral teleoperation of robotic systems, RBF-NN-based controllers have successfully addressed challenges posed by time delays and external disturbances, ensuring stable and transparent teleoperation [22]. In permanent magnet synchronous motor control, RBF-NNs have been employed to reduce torque ripple and current fluctuations caused by time-varying parameters and nonlinear characteristics [23]. Furthermore, real-time learning RBF-NN compensators have been combined with disturbance rejection algorithms to suppress harmonic disturbances in high-precision motion control systems [24]. These successful applications demonstrate the versatility and effectiveness of RBF-NN-based approaches in handling various types of uncertainties and nonlinearities.

Building upon these insights, this study proposes a novel approach that integrates an RBF-NN supervisory controller with integral sliding mode control for electric motor position systems. The key innovation lies in using the sliding function itself as the training signal for the RBF-NN, creating a direct connection between the learning objective and the control goal. The RBF-NN learns to approximate the equivalent disturbance, which represents the combined effect of all uncertainties and nonlinearities in the system. As the neural network progressively learns this equivalent disturbance through online adaptation, it provides increasingly accurate compensation that reduces the burden on the ISMC. Consequently, the required switching gain can be significantly reduced without sacrificing robustness, effectively addressing the chattering problem while maintaining strong disturbance rejection capabilities. Unlike observer-based methods, this learning-based approach does not require precise system models, can handle highly nonlinear and unstructured uncertainties, and avoids the high-gain instability issues that plague observer-based techniques. The proposed method combines the guaranteed robustness of ISMC with the adaptive learning capability of RBF-NNs, offering a synergistic solution to robust motor position control.

Extensive studies have explored the combination of SMC with RBF-NNs [25,26,27,28]. These existing works can be generally categorized based on the type of sliding surface employed—such as standard [25,26], integral [27,28] or high-order sliding surfaces [28]—and the input vectors for the RBF network, which typically consist of reference inputs, system states, control errors, and their derivatives. For instance, studies [25,26] are grounded in standard SMC, with [26] notably utilizing a dual-RBF structure that incorporates additional state information. The approach in [27] integrates a PID controller with a feedforward term and ISMC, using reference inputs, errors, and derivatives for the RBF inputs. Furthermore, ref. [28] proposes a super-twisting controller that combines an adaptive high-order ISMC with an RBF network, where a high-order sliding function is required even for the weight update law.

In contrast to these works, which often employ complex input vectors or auxiliary controllers, this study focuses on a streamlined ISMC framework designed for practical simplicity. Unlike the aforementioned methods, our approach utilizes a single RBF network that takes only the reference input to estimate the equivalent disturbance, and derives the weight update law exclusively from the integral sliding variable. This distinct design strategy avoids the complexity of high-order terms while effectively reducing the switching gain.

Consequently, the main contributions of this paper are summarized as follows:

• A systematic method is proposed for reducing the switching gain of an ISMC via a simplified RBF-NN structure that utilizes only the reference input, with the sliding variable serving as the training signal.
• The proposed control architecture enables the RBF-NN to learn the equivalent disturbance online without requiring explicit disturbance models or high-gain observers, thereby addressing potential instability issues.
• Comprehensive validation is performed through comparative simulations and laboratory experiments against two baseline approaches: a conventional ISMC and a DOBC-based cascade P–PI controller.
• Experimental results demonstrate the superior performance of the proposed method in terms of tracking accuracy, disturbance rejection, and switching gain reduction, particularly under scenarios involving parameter uncertainties and time-varying disturbances.

The remainder of this paper is organized as follows. Section 2 presents the problem formulation for electric motor position control and reviews the baseline control approaches, including the integral sliding mode controller and the cascade P–PI controller with observer-based compensation. Section 3 introduces the RBF-NN supervisory learning scheme, describes the overall control architecture, and provides the design procedure for the proposed controller. Section 4 provides comprehensive performance analysis through comparative simulations and laboratory experiments against both baseline controllers under various scenarios. Finally, Section 5 concludes the paper with a summary of key findings and suggestions for future research directions.

2. Problem Formulation

2.1. System Description

This paper deals with the position control problem of a DC motor system described as follows:

$$\begin{array}{cc}\hfill {\displaystyle \frac{d{\theta }_m}{dt}}& ={\omega }_m,\hfill \end{array}$$

(1a)

$$\begin{array}{cc}\hfill {\displaystyle \frac{d{\omega }_m}{dt}}& =-{\displaystyle \frac{B_m}{J_m}}{\omega }_m+{\displaystyle \frac{K_t}{J_m}}{i}_a-F+\mathrm{\Delta },\hfill \end{array}$$

(1b)

$$\begin{array}{cc}\hfill {\displaystyle \frac{d{i}_a}{dt}}& =-{\displaystyle \frac{K_b}{L_a}}{\omega }_m-{\displaystyle \frac{R_a}{L_a}}{i}_a+{\displaystyle \frac{1}{L_a}}{e}_a.\hfill \end{array}$$

(1c)

In the above equations, ${\theta }_m,{\omega }_m$ and $i_a$ denote the rotor position, rotational speed, and armature current, respectively; $B_m$ is the friction coefficient, $J_m$ is the moment of inertia, $K_t$ is the torque constant, $K_b$ is the back-EMF constant, $L_a$ is the armature inductance, $R_a$ is the armature resistance, $e_a$ is the input voltage, F represents the unknown friction force, and $\mathrm{\Delta }$ represents the uncertainty including model parameter variations and external time-varying disturbance $d_s$.

By defining the system states as $x_1={\theta }_m$ and $x_2={\omega }_m$, the friction force F is described by the LuGre dynamic friction model [29].

$$\begin{array}{cc}\hfill F& ={\sigma }_{0}z+{\sigma }_1\dot{z}+{\sigma }_2{x}_2,\hfill \\ \hfill \dot{z}& =x_2-{\displaystyle \frac{|x_2|}{g\left(x_2\right)}}z,\hfill \\ \hfill g\left(x_2\right)& =F_c+(F_s-F_c)e^{-{\left(x_2/v_s\right)}^2}\hfill \end{array}$$

(2)

where z denotes the internal state representing the average bristle deflection, and ${\sigma }_0,{\sigma }_1,$ and ${\sigma }_2$ are the unknown parameters of the friction model. The function $g\left(x_2\right)$ captures the Stribeck effect, with $F_c,F_s,$ and $v_s$ representing the Coulomb friction, static friction, and Stribeck velocity, respectively. This model enables the representation of dynamic friction effects that cannot be captured by classical memoryless models.

The external disturbance $d_s$ is assumed to be a biased sinusoidal one represented by

$$d_s\left(t\right)=d_0+d_1\sin ({\omega }_{0}t+{\varphi }_d)$$

(3)

where $d_0,d_1,{\omega }_0$, and ${\varphi }_d$ are unknown constants.

Since the electrical dynamics is much faster than the mechanical dynamics in actual motor systems, a reduced–order model obtained by assuming $L_a=0$ in (1c) is frequently considered in position control problems [6].

$$\begin{array}{cc}\hfill {\dot{x}}_1& =x_2,\hfill \end{array}$$

(4a)

$$\begin{array}{cc}\hfill {\dot{x}}_2& =-a{x}_2+bu+\psi \hfill \end{array}$$

(4b)

where the input is defined as $u=e_a$, the two positive constants as $a=(B_m{R}_a+K_t{K}_b/\left(J_m{R}_a\right)$, $b=K_t/\left(J_m{R}_a\right)$, and the uncertainties as $\psi =-F+\mathrm{\Delta }$. The output of the system is $y=x_1$.

To consider the case where parameter uncertainties are present, the nominal parameters $a_n$ and $b_n$ are used instead of a and b as follows.

$$\begin{array}{cc}\hfill {\dot{x}}_1& =x_2,\hfill \end{array}$$

(5a)

$$\begin{array}{cc}\hfill {\dot{x}}_2& =-a_n{x}_2+b_n(u+d_e),\hfill \end{array}$$

(5b)

$$\begin{array}{cc}\hfill d_e& =b_n^{-1}\left(-\tilde{a}{x}_2+\tilde{b}u+\psi \right)\hfill \end{array}$$

(5c)

where $\tilde{a}=a-a_n,\tilde{b}=b-b_n$ and $d_e$ is referred to as the equivalent disturbance. Both a and b are also positive constants.

Before presenting the proposed controller design, a conventional Integral Sliding Mode Control (ISMC) is briefly reviewed in the next.

2.2. Integral Sliding Mode Control (ISMC)

From (5), consider the following error equation

$$\begin{array}{cc}\hfill {\dot{e}}_1& =e_2,\hfill \\ \hfill {\dot{e}}_2& =-a_n{x}_2+b_n\left(u+d_e\right)-\ddot{r}\hfill \end{array}$$

(6)

where the controlled error $e_1:=x_1-r$ with a reference signal r, and $e_2:={\dot{e}}_1=x_2-\dot{r}$.

To handle the equivalent disturbance $d_e$ including model uncertainties and external time–varying disturbances, integral sliding mode controllers are commonly used [30,31].

The sliding function s considered in this paper is given by

$$s=z+k_2\int zdt,z=k_1{e}_1+e_2$$

(7)

where $k_1$ and $k_2$ are positive design parameters.

On the sliding surface $s=0$, the control error is obtained as

$$\dot{z}=-k_{2}z,{\dot{e}}_1=-k_1{e}_1.$$

(8)

From (7) and (8), it can be shown that the control error converges sequentially to zero on the sliding surface $s=0$. First, z converges to zero with a rate proportional to $k_2$ and, subsequently, $e_1$ converges to zero at a rate proportional to $k_1$. Therefore, to achieve desirable control performance, $k_2$ is chosen to be sufficiently larger than $k_1$.

To derive the control input u that ensures the convergence of s to zero, the time derivative of the Lyapunov function $V=\frac{1}{2}{s}^2$ is given by

$$\begin{array}{cc}\hfill \dot{V}& =s\dot{s}=s(\dot{z}+k_{2}z)=s(k_{2}z+k_1{e}_2+{\dot{e}}_2)\hfill \\ \hfill & =s\left(k_{2}z+k_1{e}_2-a_n{x}_2+b_n(u+d_e)-\ddot{r}\right).\hfill \end{array}$$

(9)

For the design of the sliding mode controller, it is a standard assumption that the absolute value of the disturbance $d_e$ is bounded; i.e.,

$$|d_e\left(t\right)|\le D$$

(10)

where D is a known positive constant. From the above equation, the following ISMC input $u_1$ can be obtained to ensure $\dot{V}<0$ when $s\ne 0$.

$$\begin{array}{cc}\hfill u_c& =b_n^{-1}\left(\ddot{r}-k_{2}z-k_1{e}_2+a_n{x}_2-\varphi s\right),\hfill \end{array}$$

(11a)

$$\begin{array}{cc}\hfill u_s& =-\overline{D}\mathrm{sgn}\left(s\right),\hfill \end{array}$$

(11b)

$$\begin{array}{cc}\hfill u& =u_c+u_s=:u_1\hfill \end{array}$$

(11c)

where the gain $\varphi$ of $u_c$ is positive, and the switching gain $\overline{D}$ is designed to be larger than the magnitude of the equivalent disturbance such that $\overline{D}-D=:{\nu }_1>0$. Substituting (11) into (9) yields the following result:

$$\begin{array}{cc}\hfill \dot{V}& =-\varphi s^2-b_n\overline{D}\left|s\right|+b_n{d}_{e}s\hfill \\ \hfill & \le -\varphi s^2-b_n(\overline{D}-D)\left|s\right|\hfill \\ \hfill & \le -\varphi s^2-b_n{\nu }_1\left|s\right|\hfill \\ \hfill & \le -b_n{\nu }_1\sqrt{2V}.\hfill \end{array}$$

(12)

From the above equation, it can be seen that the control objective is achieved as s converges to zero within finite time.

Before introducing the proposed ISMC with a supervisory RBF term, the baseline ISMC is first examined to clarify its inherent behavior. To illustrate the performance of the ISMC controller (11), simulation results obtained using the system parameters given in Section 4 are shown in Figure 1 and Figure 2.

Figure 1 and Figure 2 correspond to the non-RBF case and present the tracking error and control input of the ISMC under different switching gains. As the switching gain $\overline{D}$ is increased to mitigate the effect of the equivalent disturbance, the tracking error decreases for $\overline{D}=8$ compared to $\overline{D}=2$. However, an increased switching gain is expected to induce severe chattering in the control input and aggravate vibration and noise as shown in Figure 2, which motivates the introduction of the proposed RBF-based ISMC controller in the subsequent section to overcome these limitations.

2.3. PIO–Based P–PI Cascade Control

To compare the performance with the proposed method, a DOBC-based P–PI cascade controller was implemented as shown in Figure 3. Using the nominal system model, a cascade controller can be designed to track the position reference input r.

For the P–PI controller design, the outer loop computes the position error ${\overline{e}}_1=-e_1=r-x_1$ and uses the reference derivative $\dot{r}$ as a feed-forward term to generate the inner-loop reference $x_2^{*}=\dot{r}+k_{p1}{\overline{e}}_1$. The inner-loop error is then given by ${\overline{e}}_2=x_2^{*}-x_2$, and the control input is constructed as follows.

$$\begin{array}{cc}\hfill u_{cas}& =k_{p2}{\overline{e}}_2+k_i\int {\overline{e}}_{2}dt.\hfill \end{array}$$

(13)

Since the controller is designed based on nominal parameters, performance degradation may occur due to modeling uncertainties and external time-varying disturbances. To mitigate the effect of the equivalent disturbance, a proportional–integral observer (PIO) is employed to estimate the equivalent disturbance and compensate it in the control input. The full-order PIO was adopted as the baseline observer to ensure high-precision control by leveraging its noise robustness and its ability to mitigate steady-state estimation offsets via integral action. Although designed under a constant disturbance assumption, the PIO can effectively compensate for slowly time-varying nonlinearities within its observer bandwidth, thereby providing a robust and high-fidelity benchmark for performance evaluation [2,18].

To design the observer the system (5) is rewritten as follows:

$$\begin{array}{c}\hfill \dot{x}=Ax+B\left(u+d_e\right),y=Cx,\end{array}$$

(14a)

$$\begin{array}{c}\hfill A=\left[\begin{array}{cc}0& 1\\ 0& -a_n\end{array}\right],B=\left[\begin{array}{c}0\\ b_n\end{array}\right],C=\left[\begin{array}{cc}1& 0\end{array}\right].\end{array}$$

(14b)

Assuming ${\dot{d}}_e=0$, the PIO is designed to estimate the equivalent disturbance and states.

$$\begin{array}{cc}\hfill \dot{\widehat{x}}& =A\widehat{x}+Bu+B{\widehat{d}}_e+\left[\begin{array}{c}{l}_1\\ l_2\end{array}\right]\left(y-\widehat{y}\right),\widehat{y}=C\widehat{x},\hfill \end{array}$$

(15a)

$$\begin{array}{cc}\hfill {\dot{\widehat{d}}}_e& =l_3\left(y-\widehat{y}\right)\hfill \end{array}$$

(15b)

where the observer gain $L={\left[\begin{array}{ccc}{l}_1& l_2& l_3\end{array}\right]}^T$ is chosen such that the observer poles are at least five times faster than those of the inner loop.

The estimated equivalent disturbance is then compensated in the control input as follows:

$$\begin{array}{c}\hfill u=u_{cas}-{\widehat{d}}_e=:u_2\end{array}$$

(16)

where $u_{cas}$ denotes the output of the P–PI cascade controller in Figure 3.

With the control system model and baseline controllers introduced, Section 3 proceeds to the design of the proposed control scheme.

3. Design of the Proposed RBF–NN–Based Controller

As a robust control method against model uncertainties and disturbances, the RBF neural network-based supervisory control system shown in Figure 4 has been widely utilized [20]. By combining the controller output $u_p$ with RBF output $u_n$, the control input u is generated to drive the tracking error to zero. In this case, the RBF neural network is employed to approximate a feed-forward compensation function that reduces errors caused by uncertainties and various disturbances. Unlike conventional supervisory control approaches, this study proposes a method to improve the control performance of the ISMC (11).

The output of the RBF neural network block in Figure 4 is expressed as follows:

$$u_n=h_1{w}_1+h_2{w}_2+\cdots +h_m{w}_m=:w^{T}h\left(r\right)$$

(17)

where r represents the reference input and m denotes the number of nodes in the hidden layer of the neural network. The RBF parameter vectors are defined as $w={[w_1,\dots ,w_m]}^T$, $c={[c_1,\dots ,c_m]}^T$, and $b={[b_1,\dots ,b_m]}^T$, which denote the weights, centers, and widths of the Gaussian basis functions, respectively. The hidden layer output function $h_j\left(r\right)$ is defined as

$$h_j\left(r\right)=\exp \left(-{\displaystyle \frac{{∥r-c_j∥}^2}{2b_j^2}}\right),1\le j\le m,$$

(18)

where the notation ${\parallel v\parallel }^2$ denotes $v^{T}v$ for a vector v.

It is known that the approximation error with respect to the ideal function can be reduced arbitrarily as the number of basis functions m increases [19]. In conventional RBF supervisory control methods, the cost function J for learning is defined as follows, and the gradient descent method is employed to update $w_j$, $b_j$, and $c_j$. The learning rate $\eta$ is bounded between 0 and 1 [20].

$$\begin{array}{cc}\hfill J& ={\displaystyle \frac{1}{2}}{(u_n-u)}^2,\hfill \end{array}$$

(19a)

$$\begin{array}{cc}\hfill \mathrm{\Delta }{w}_j& =-\eta {\displaystyle \frac{\partial J}{\partial w_j}}=-\eta (u_n-u)h_j,\hfill \end{array}$$

(19b)

$$\begin{array}{cc}\hfill \mathrm{\Delta }{b}_j& =-\eta (u_n-u)w_j{h}_j{\displaystyle \frac{{(r-c_j)}^2}{b_j^3}},\hfill \end{array}$$

(19c)

$$\begin{array}{cc}\hfill \mathrm{\Delta }{c}_j& =\eta (u_n-u)w_j{h}_j{\displaystyle \frac{(r-c_j)}{b_j^2}}.\hfill \end{array}$$

(19d)

The performance of the control input $u=u_p+u_n$ obtained as in Figure 4 and the RBF neural network learning process are largely affected by the design of the feedback controller $u_p$. In this paper, $u_p$ is designed to have a zero steady-state value such that the control objective (i.e., $e=0$) is achieved when the learning progresses and the objective function (19a) ultimately converges to zero. To devise a method for reducing the switching gain of the integral sliding mode controller (11), $u_p$ is chosen as follows:

$$u_p=-k_{d}s,k_d>0.$$

(20)

In this case, if $s\to 0$, then $u_p\to 0$ and hence $u\to u_n$ from the structure in Figure 4. Here, unlike the conventional supervisory controller ($u=u_n+u_p$), the proposed controller does not make ‘$u-u_p$’ depend solely on neural network learning. Instead, the RBF neural network is trained to approximate the equivalent disturbance $d_e$; that is, an RBF neural network that minimizes the following objective function is considered.

$$\begin{array}{c}J={\displaystyle \frac{1}{2}}{\left(u_{ns}-u\right)}^2,\end{array}$$

(21a)

$$\begin{array}{c}{u}_{ns}=u_c-w^{T}h\left(r\right),\end{array}$$

(21b)

$$\begin{array}{c}{u}_c=b_n^{-1}\left(\ddot{r}-k_{2}z-k_1{e}_2+a_n{x}_2-\varphi s\right)\end{array}$$

(21c)

where $u_c$ is the same as the one in ISMC (11). For the input $u=u_n+u_p$ in Figure 4, $u_{ns}$ is employed in the above equation so that $u_n$ plays a role similar to that of the ISMC in both the transient and steady-state responses of $u_p$.

For the closed-loop stability analysis of the proposed control scheme, we consider the scenario where the RBF neural network has been sufficiently trained, allowing the equivalent disturbance to be approximated as follows:

$$\left|d_e-w^{\mathrm{T}}h\left(r\right)\right|<\delta$$

(22)

where the positive constant $\delta$ denotes the approximation error.

The bound in (22) is interpreted over the practical operating range of the learning signal, rather than over the entire real line. By the universal approximation property of RBF networks on compact sets [19], the approximation error can be made sufficiently small over such an operating region with appropriate choices of centers and widths. In our implementation, the centers are chosen to cover the predefined operating range and the widths are set uniformly to provide consistent overlap, while the residual mismatch due to a finite number of nodes is captured by the constant $\delta$. The learning rate mainly affects the speed and smoothness of online weight adaptation and thus influences transient behavior.

From (20) and (21), the control input proposed in this paper is given as follows:

$$\begin{array}{cc}\hfill u& =u_{ns}+u_p=:u_3,\hfill \\ \hfill u_{ns}& =u_c-w^{T}h-\overline{\delta }\mathrm{sgn}\left(s\right)\hfill \end{array}$$

(23)

where the switching gain $\overline{\delta }$ of $u_{ns}$ is designed to be larger than $\delta$ in (22) such that $\overline{\delta }-\delta >{\nu }_2>0$. The term $w^{\mathrm{T}}h\left(r\right)$ represents the RBF neural network estimation of the equivalent disturbance $d_e$ defined in (5c) and is introduced to compensate for $d_e$, thereby reducing the disturbance component that must be counteracted by the switching term.

Substituting (23) into (9), which is obtained by the time derivative of the Lyapunov function $V=\frac{1}{2}{s}^2$, yields the following:

$$\begin{array}{cc}\hfill \dot{V}& =-(\varphi +k_d)s^2-b_n\overline{\delta }\left|s\right|+b_n\left(d_e-w^{T}h\left(r\right)\right)s\hfill \\ \hfill & \le -(\varphi +k_d)s^2-b_n\overline{\delta }\left|s\right|+b_n\delta \left|s\right|\hfill \\ \hfill & \le -(\varphi +k_d)s^2-b_n{\nu }_2\left|s\right|\hfill \\ \hfill & \le -b_n{\nu }_2\sqrt{2V}.\hfill \end{array}$$

(24)

From the above equation, it can be seen that the control objective is achieved as s converges to zero in finite time. Therefore, the RBF neural network reduces the effective bound of the equivalent disturbance in the Lyapunov analysis, enabling the use of a smaller switching gain than conventional ISMC and consequently alleviating chattering. Overall, the proposed RBF-assisted ISMC effectively compensates for the equivalent disturbance $d_e$, including parameter uncertainties and external disturbances, while preserving stability with a reduced switching gain.

In the next section, simulation and experimental results are compared among the PIO-based P–PI controller, the ISMC without the RBF, and the proposed controller to validate the performance of the proposed controller.

4. Performance Evaluation

The controller parameters used in this Section are summarized in

Table 1. Controller Gains and RBF Neural Network Parameters.

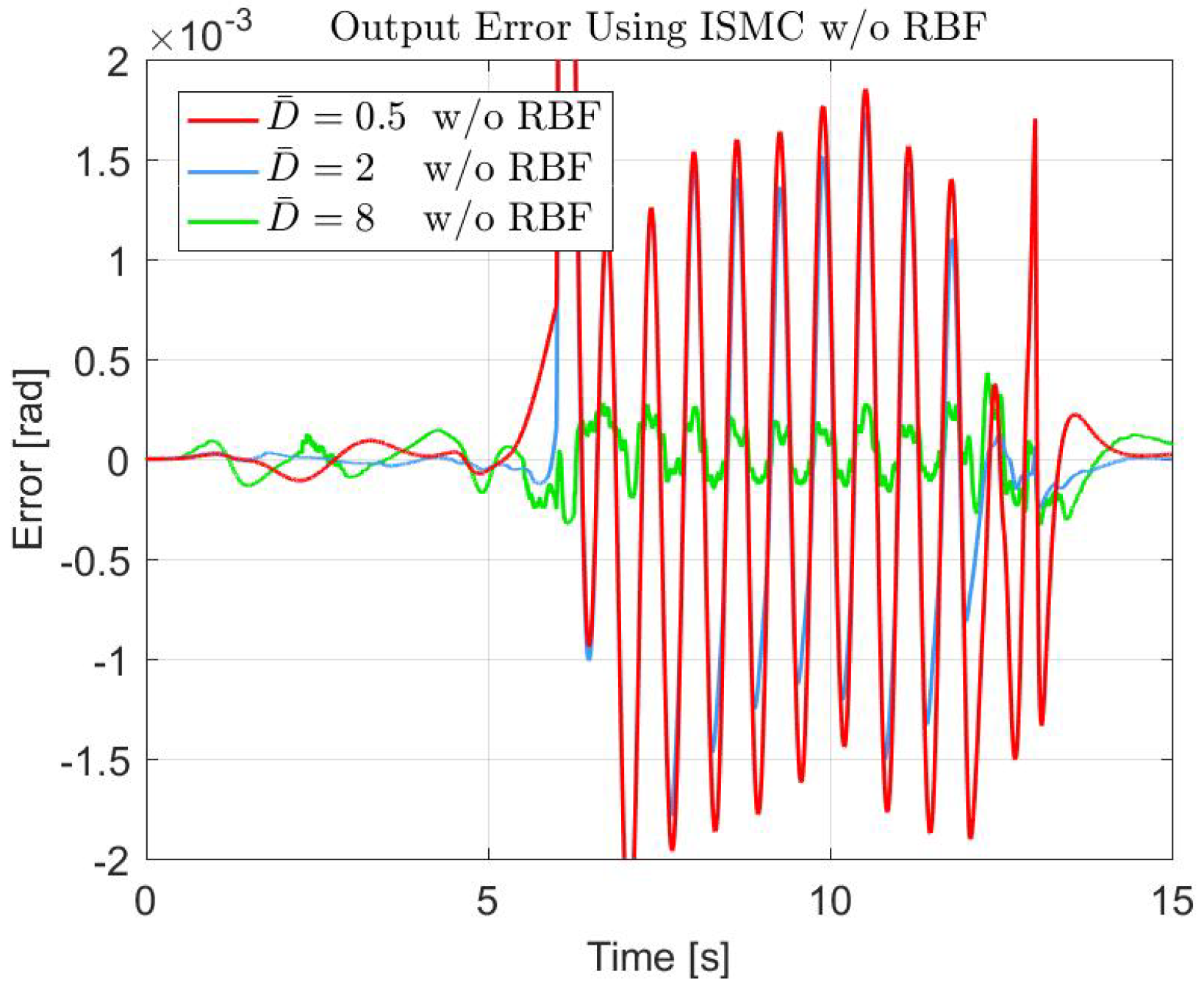
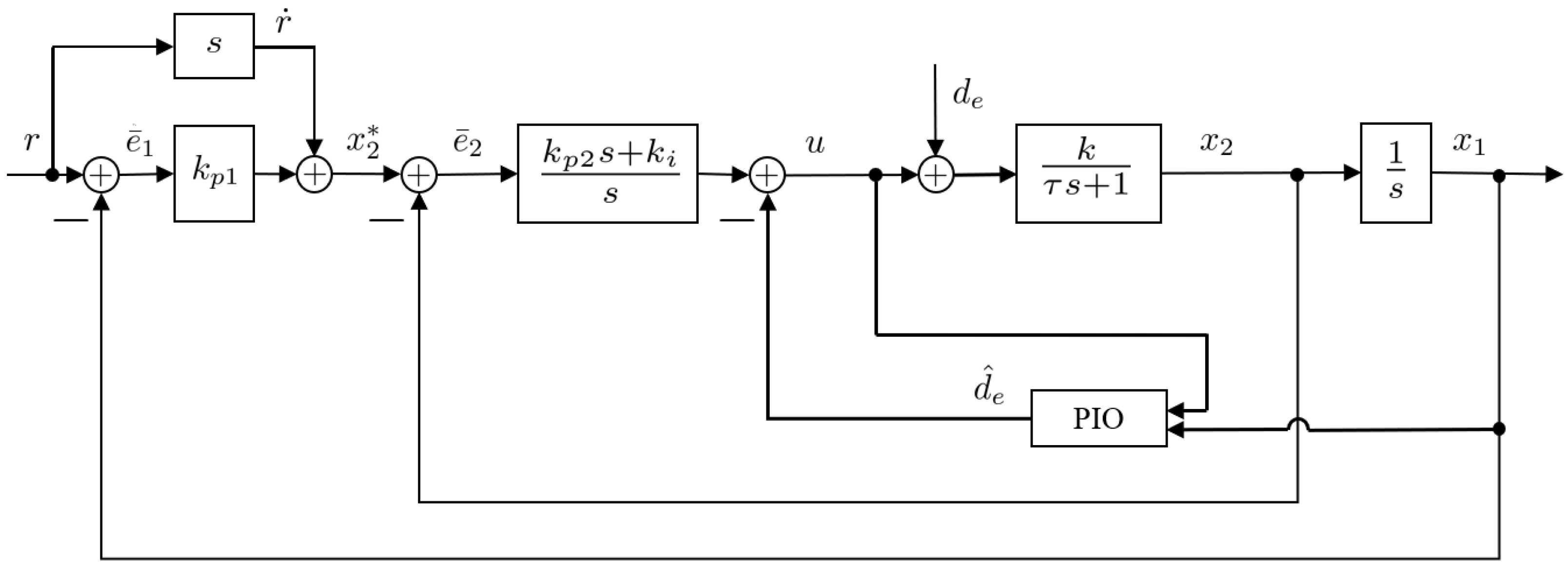
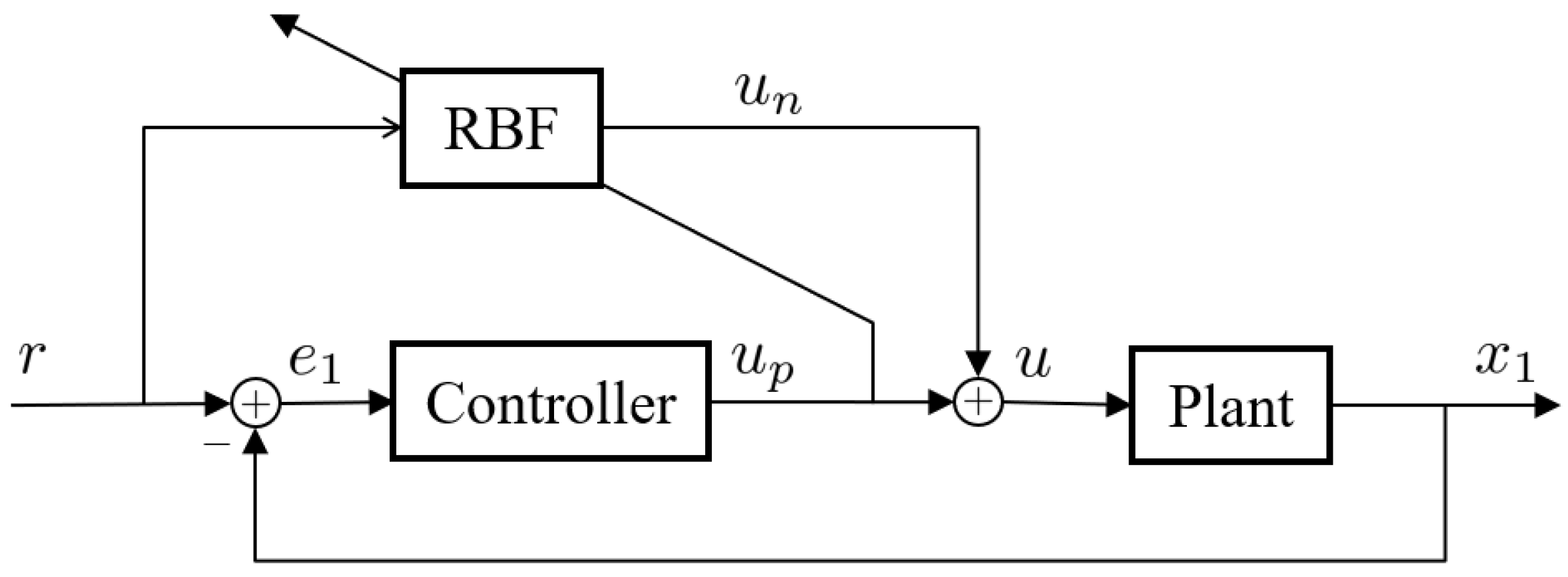
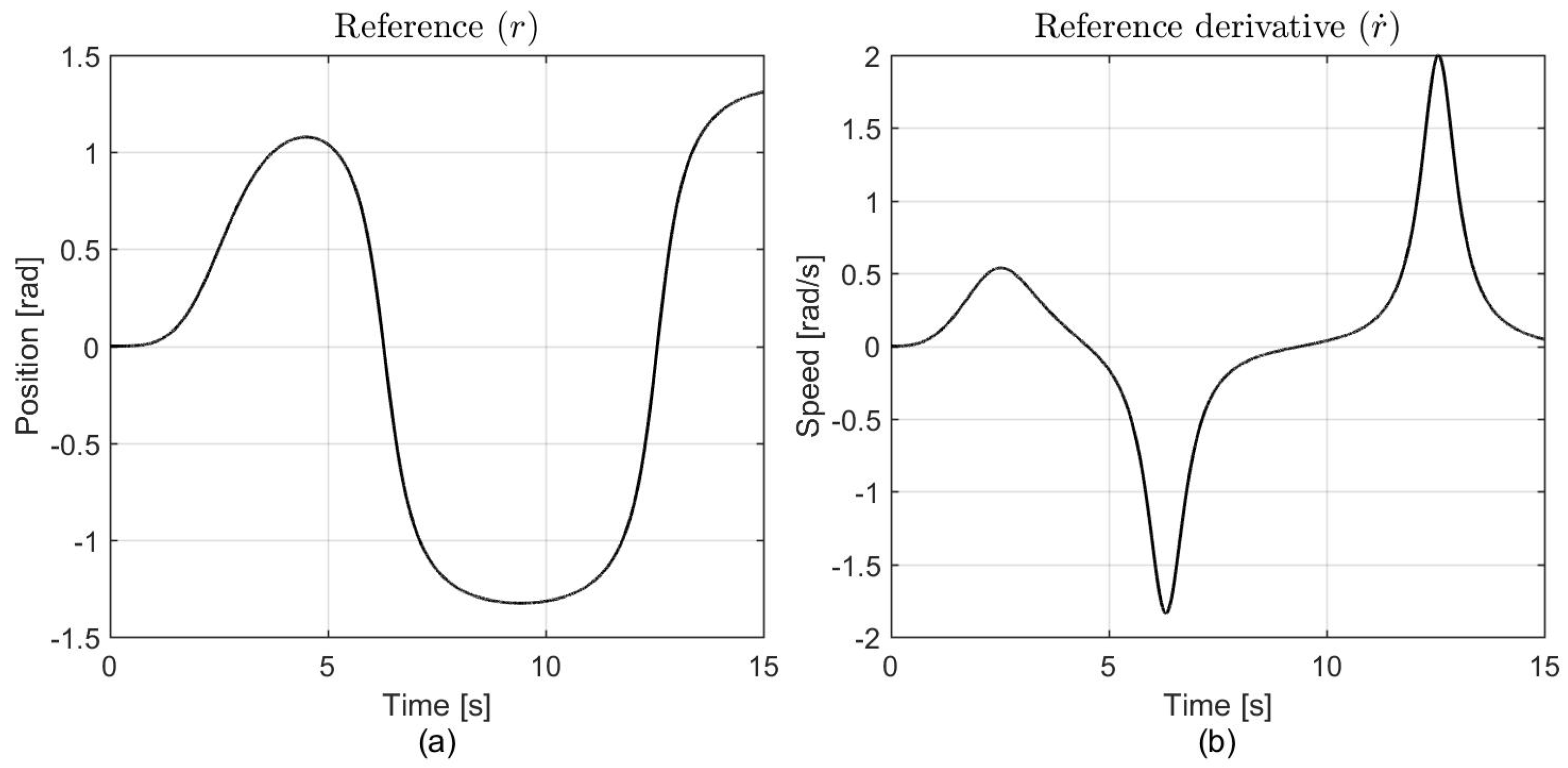
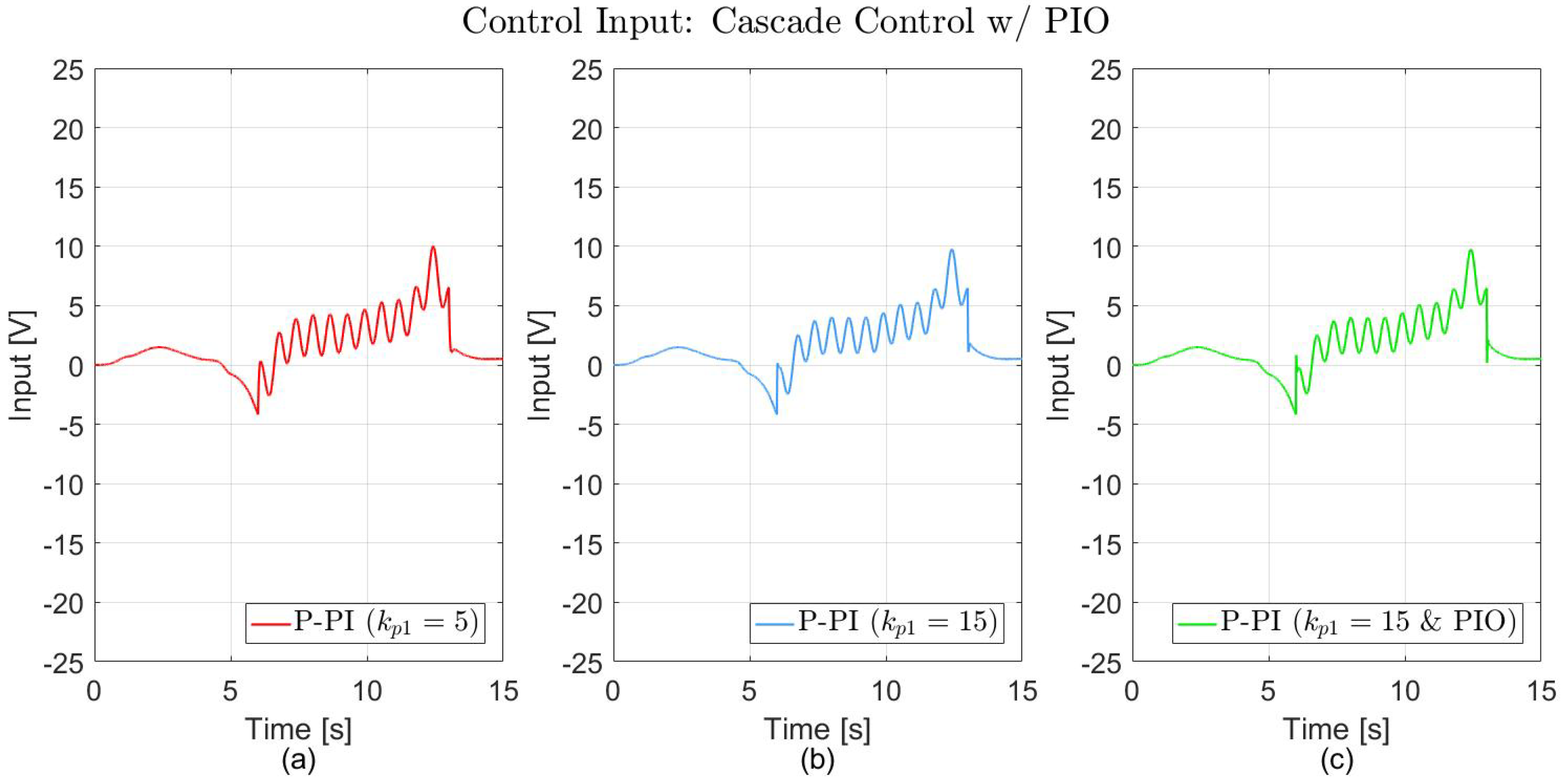
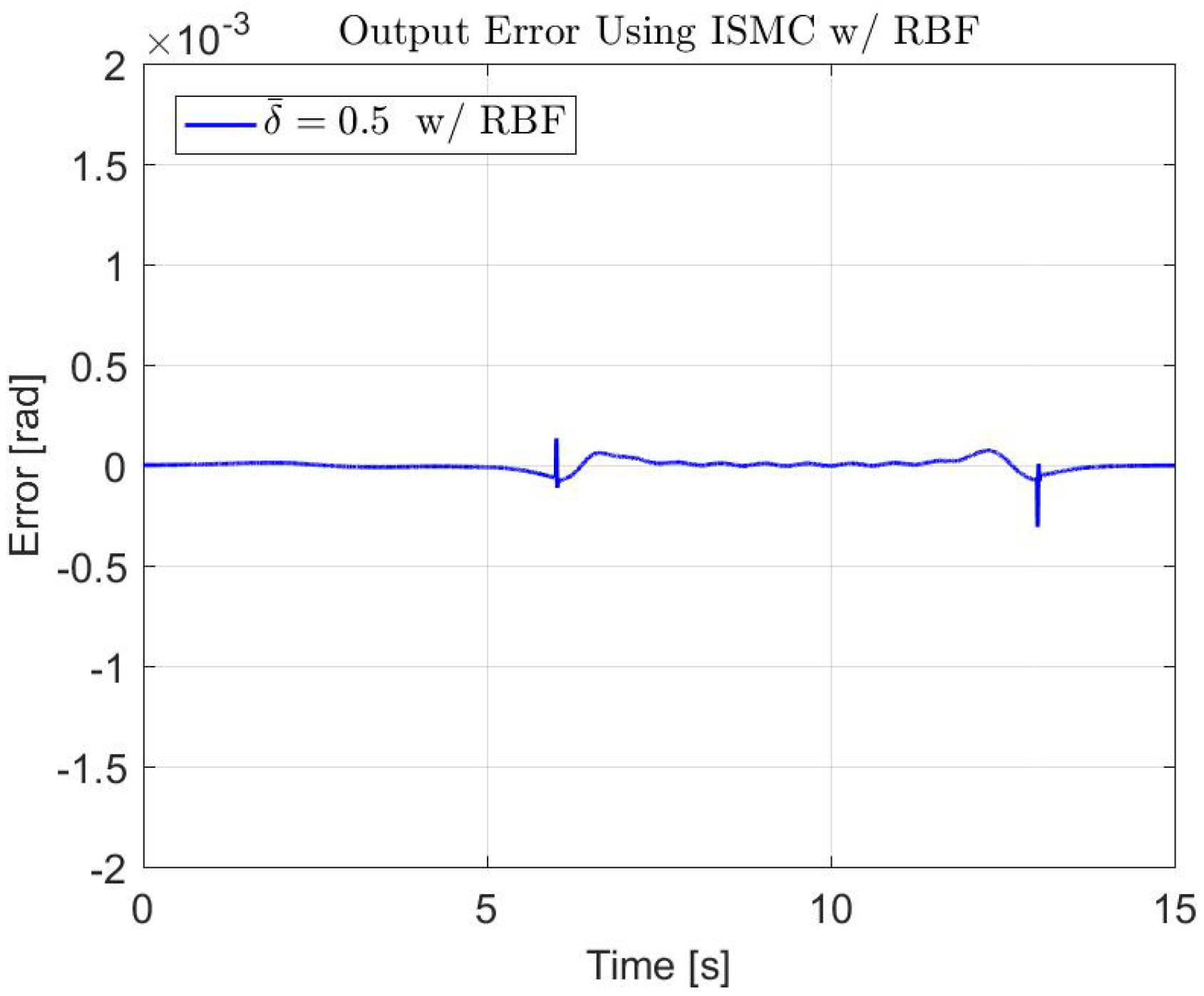
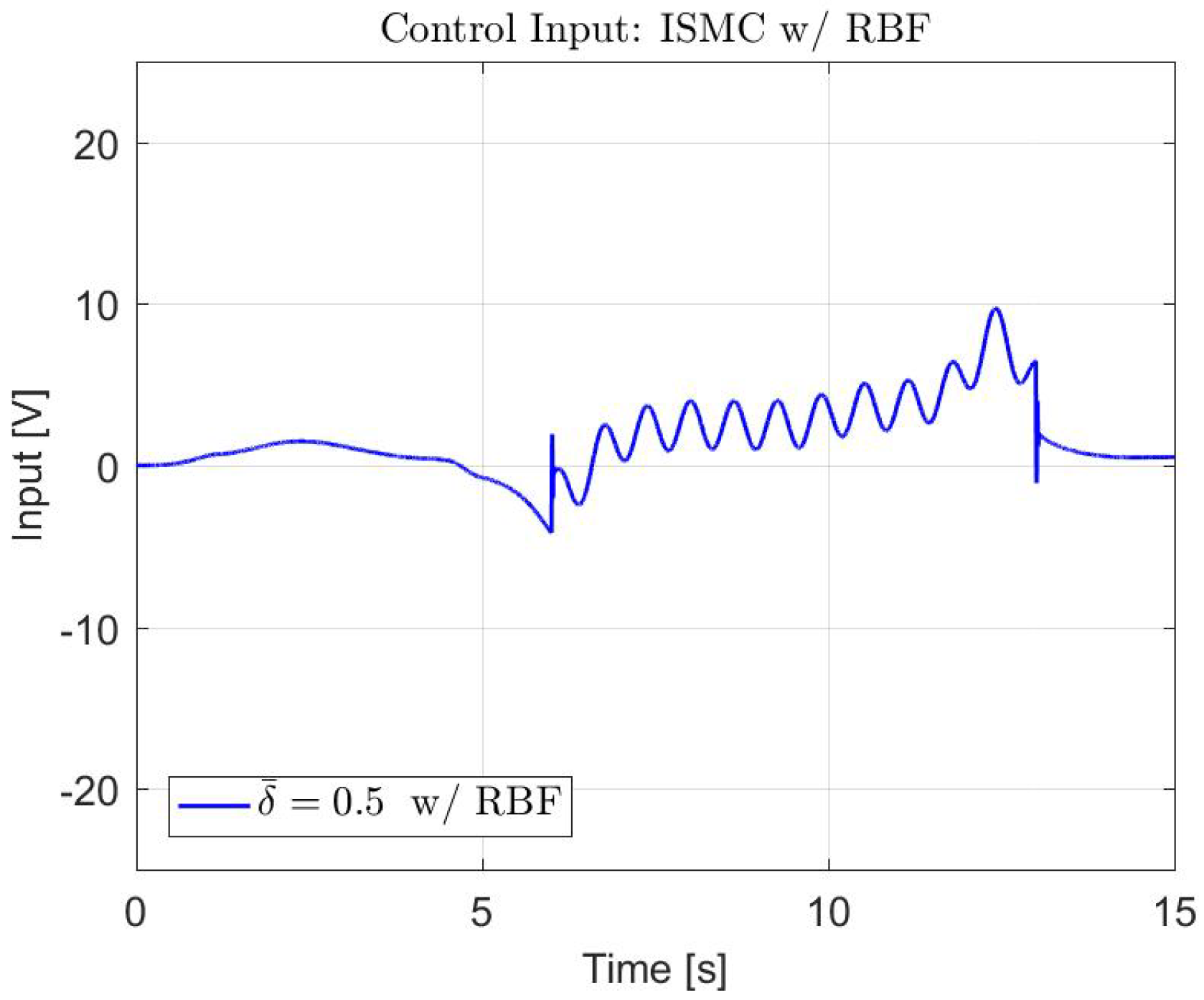
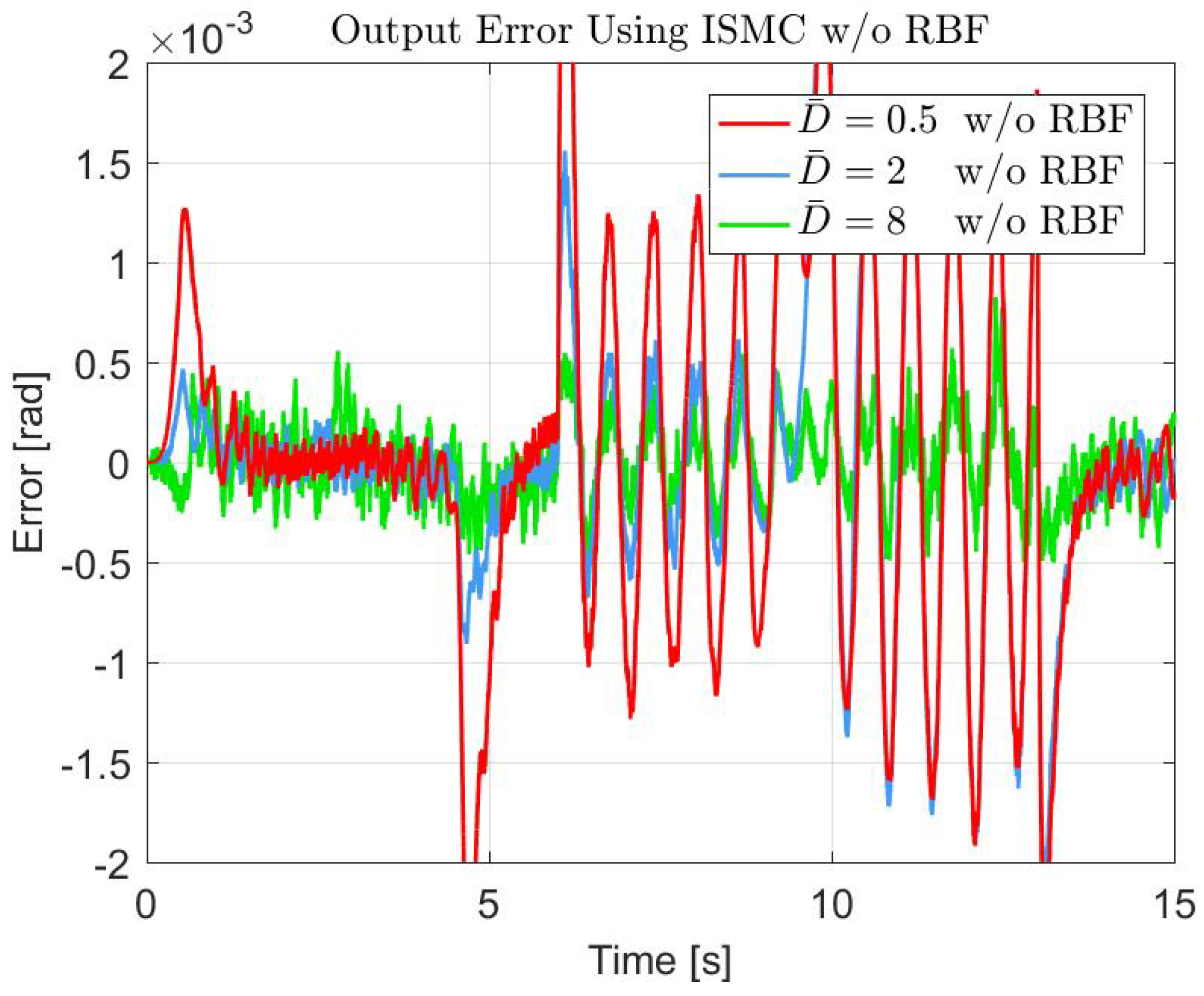
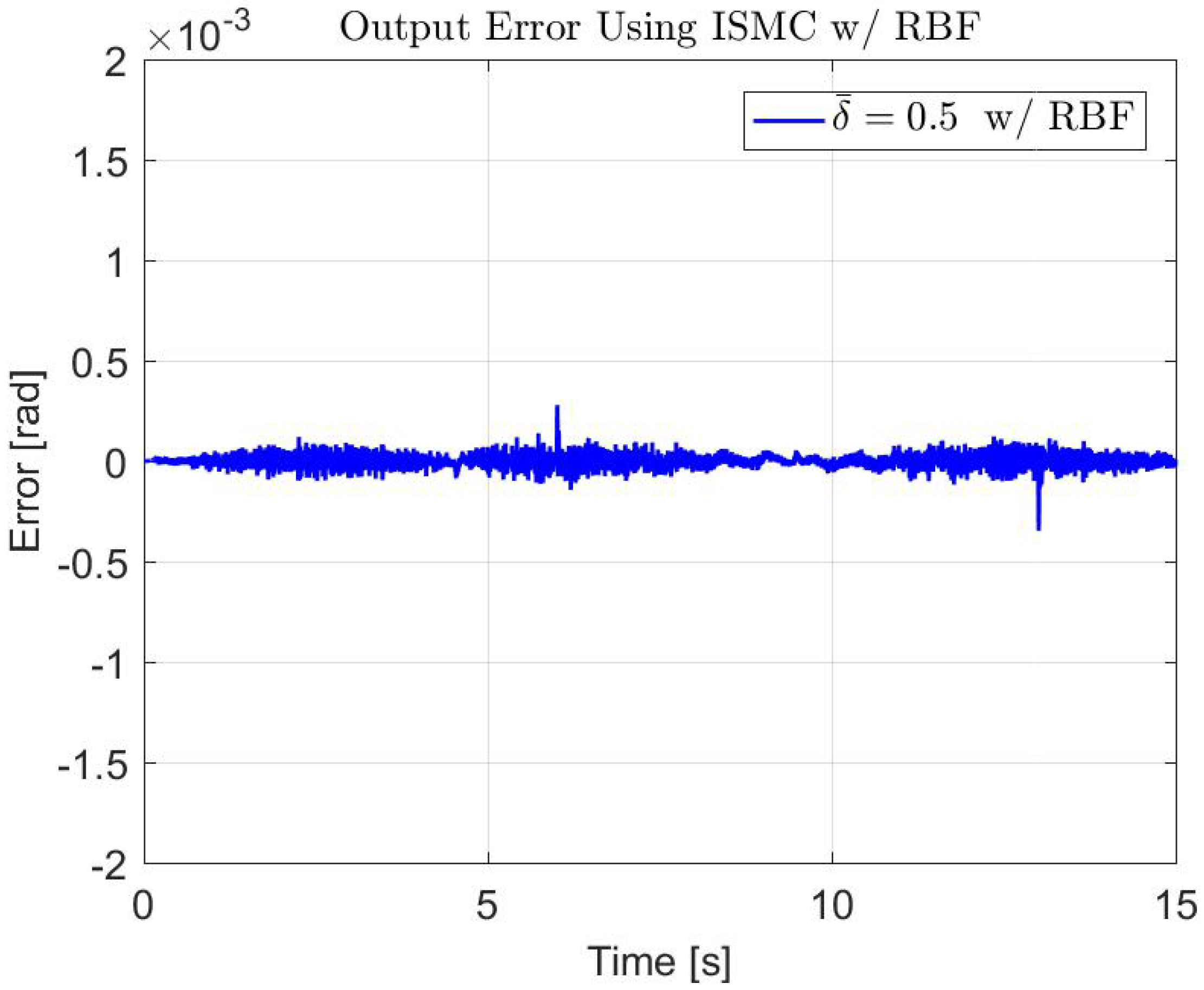
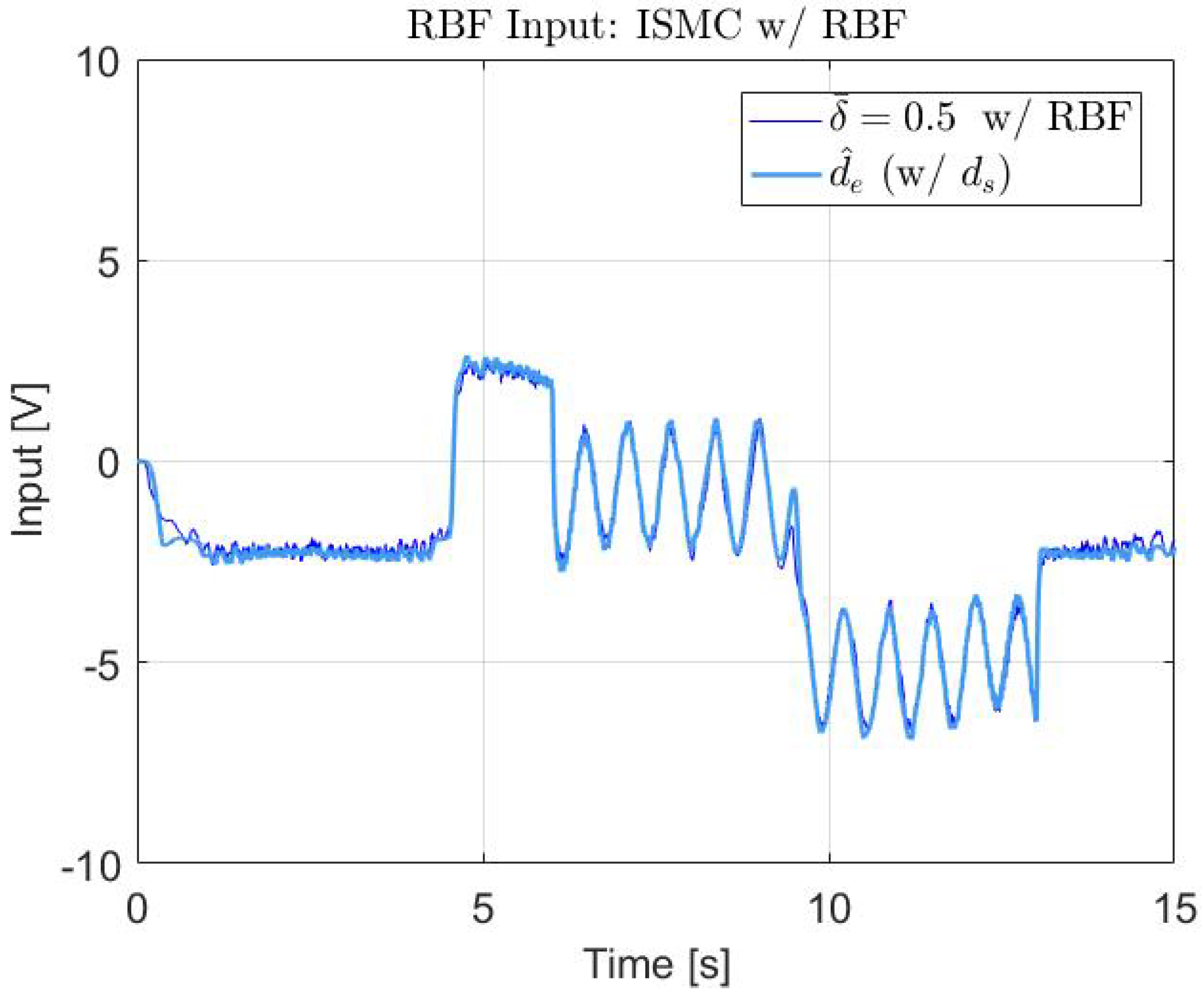
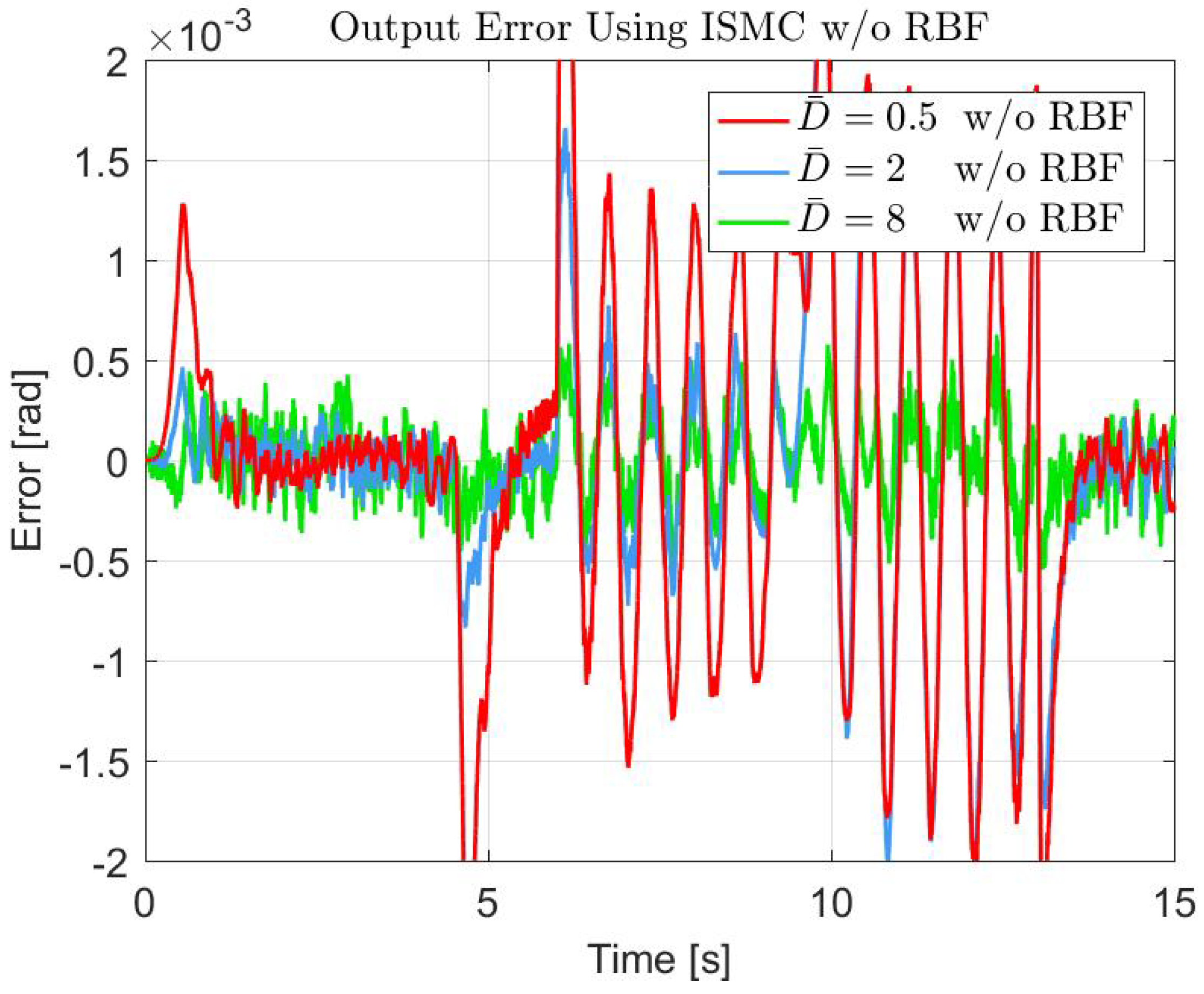
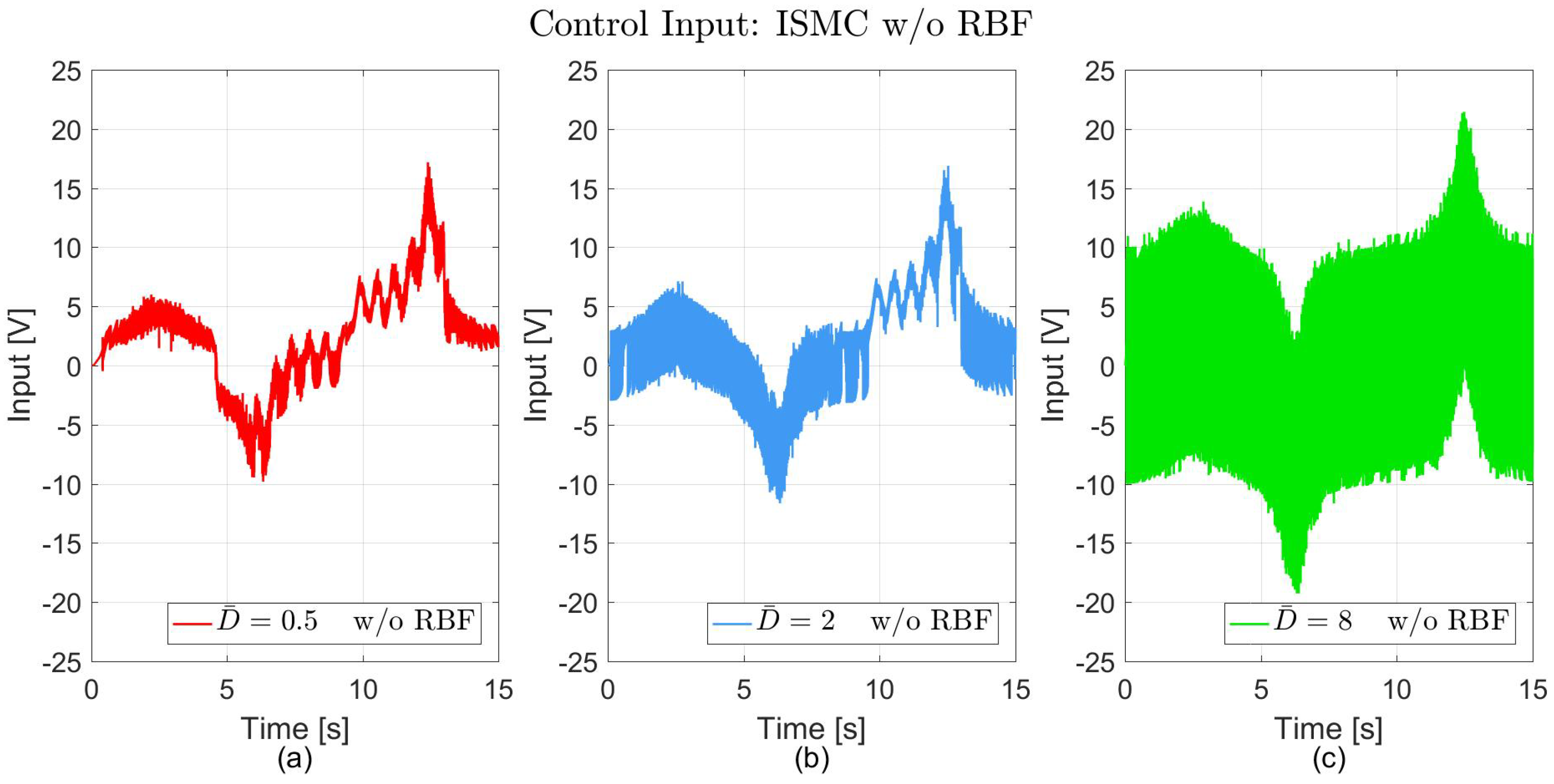
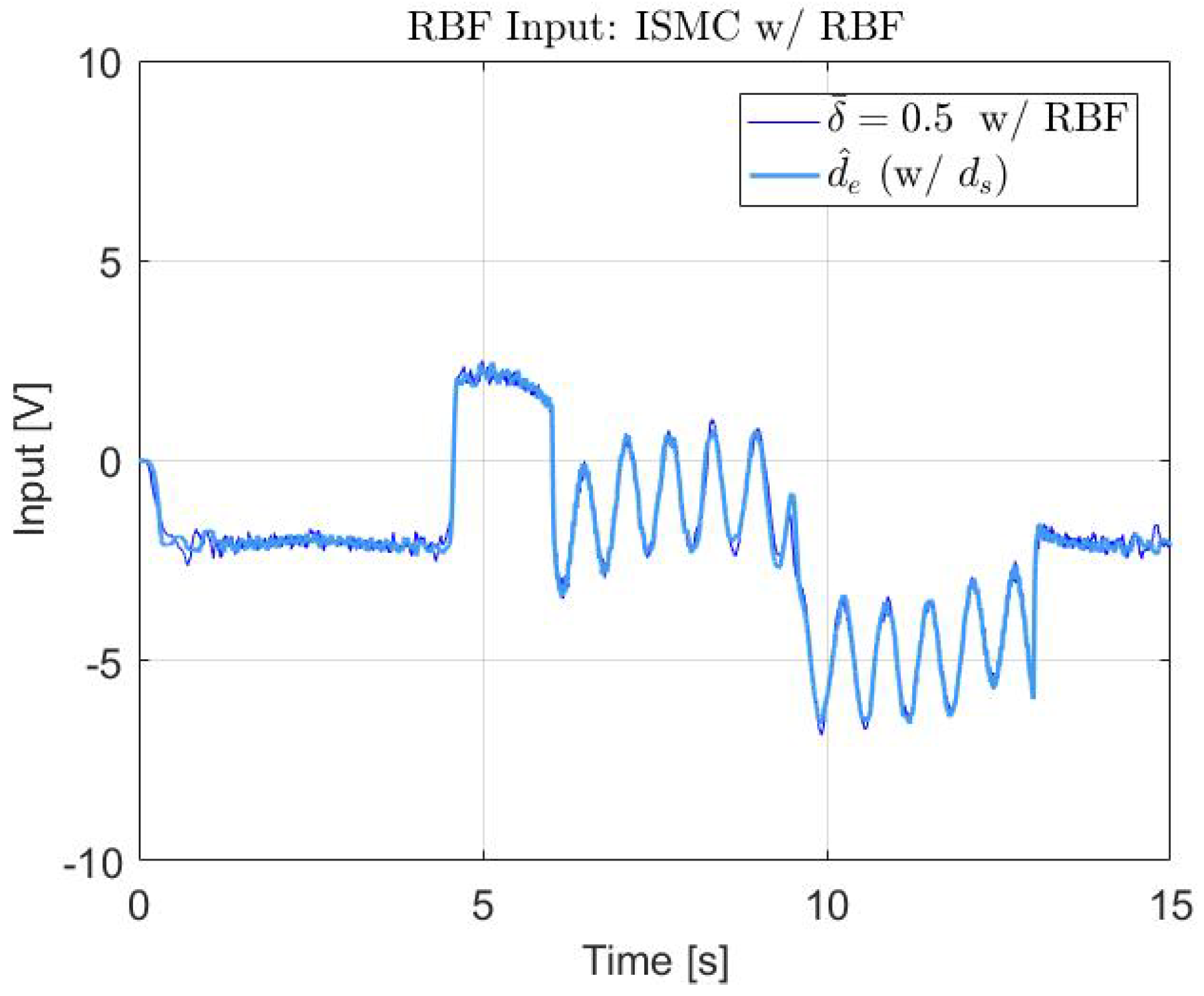
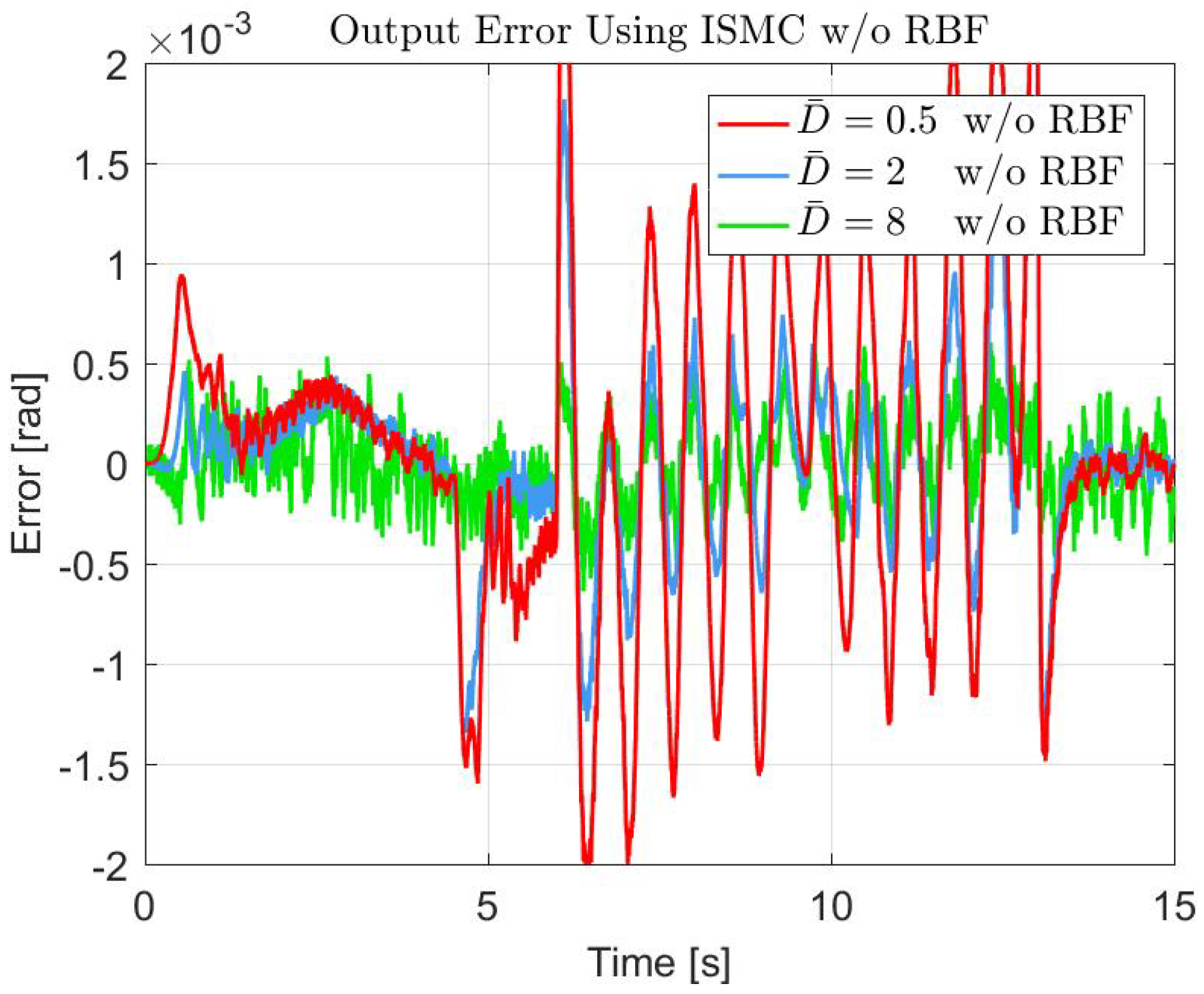
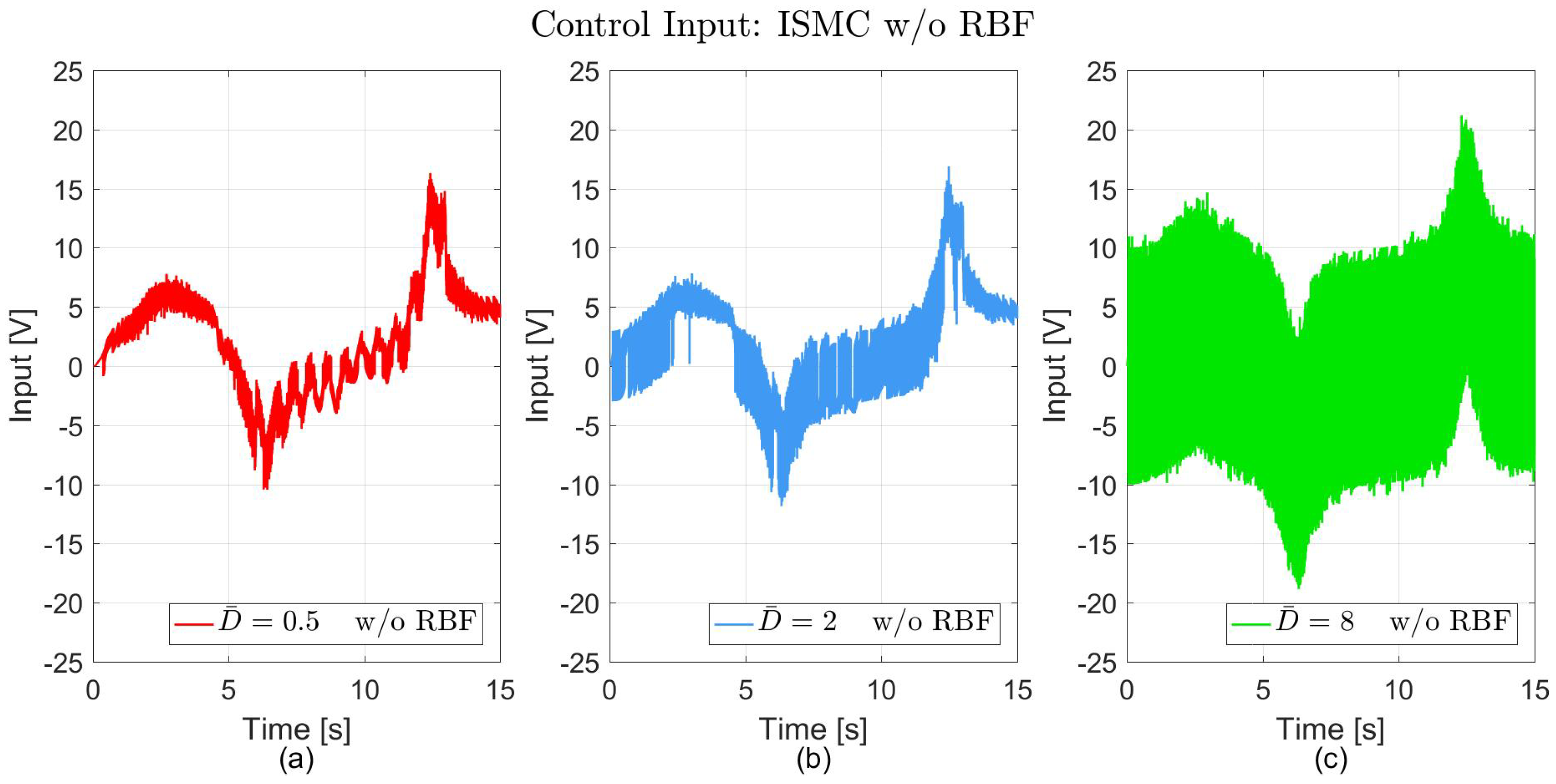
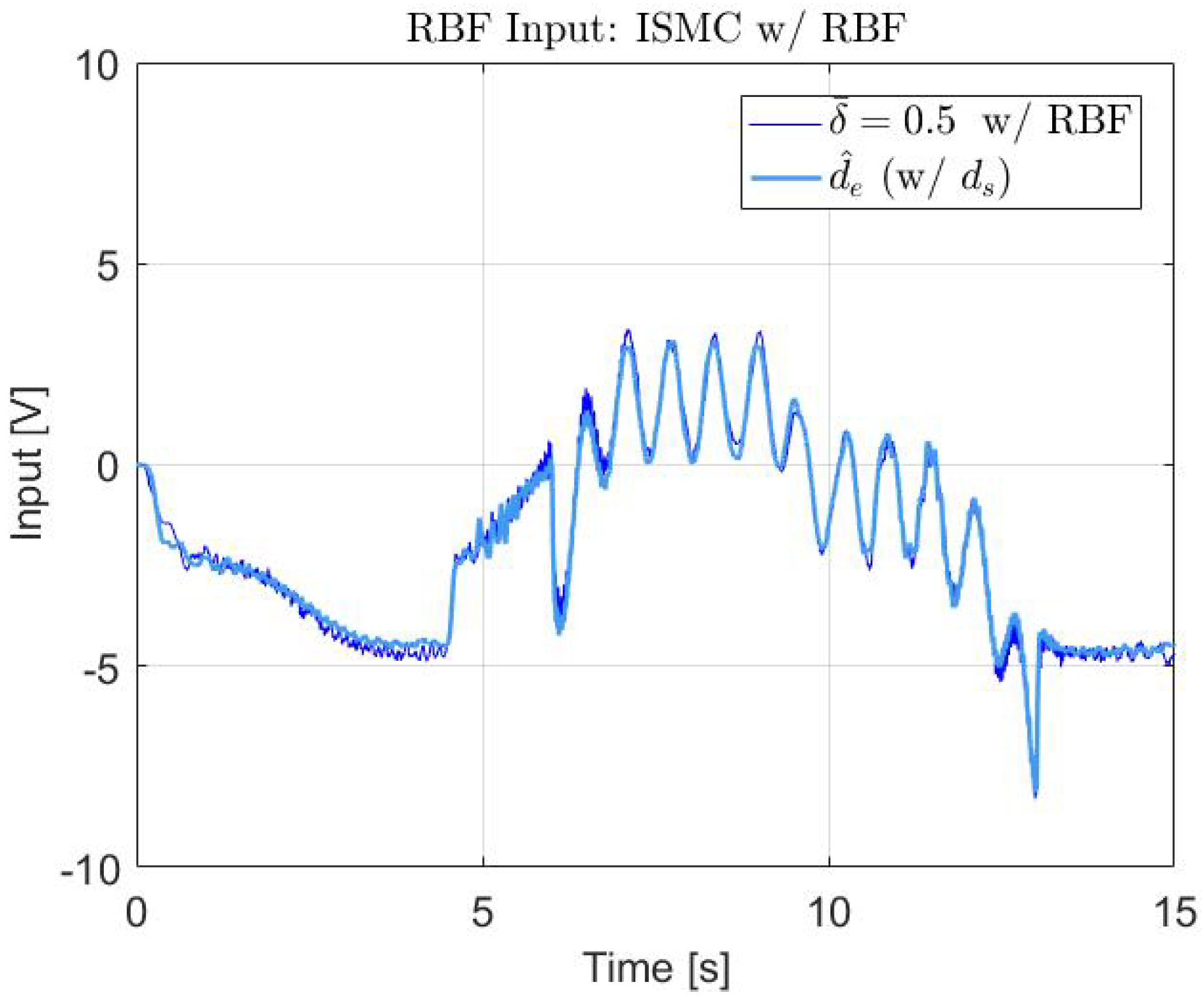
Controller	Parameter	Value
P–PI	$k_{p1}$	5 → 15
	$k_{p2}$	11.3560 → 43.0981
	$k_i$	198.3888 → 1785.4990
PIO	$l_1$	$3.6078\times {10}^2$
	$l_2$	$4.1743\times {10}^4$
	$l_3$	$6.1996\times {10}^5$
ISMC	$k_1$	5
	$k_2$	15
	$\varphi$	85
	$\overline{D}$	0.5, 2, 8
	$\overline{\delta }$	0.5
RBF	c	$[-5-4-3-2-1012345]$
	b	$\left[11111111111\right]$
	$k_d$	10
	$\eta$	$0.99$

. For the design of controllers and observer the nominal motor parameters $a_n=14.2243$ and $b_n=3.1504$ were experimentally identified by using the step response in Section 4.2.

To avoid case-by-case tuning, the RBF centers were uniformly and symmetrically distributed over the predefined input range as listed in Table 1, with identical widths. In simulation, it is observed that increasing the number of nodes reduces the approximation error mainly at low node counts, while the error reduction becomes marginal once the number of nodes reaches 9 (i.e., further improvements are negligible). Based on this trend, we conservatively selected $m=11$ to ensure sufficient coverage of the predefined operating range without requiring additional tuning. This suggests that the proposed method is not highly sensitive to the exact grid density once the operating range is sufficiently covered [28].

In addition to the above configuration choices, practical robustness was further enhanced at the implementation level. To avoid excessive adaptation, saturation limits were applied to both the RBF weight update law and the network output in all simulations and experiments. This implementation-level measure improves numerical robustness and prevents over-adaptation, while preserving the nominal learning behavior of the proposed controller.

4.1. Simulation Results

In this subsection the performance of the proposed controller is verified through simulations. The reference signal for the control objective is as follows [32]:

$$r\left(t\right)=\arctan \left(4\sin \left(0.5t\right)\left(1-e^{-0.01t^3}\right)\right).$$

(25)

For the analysis of the tracking controllers Figure 5 shows both the reference signal and its time derivative.

Table 2. Friction Parameters and External Disturbance used in Simulations.

Uncertainty Component	Symbol	Value	Note
LuGre Model	${\sigma }_0$	0.1	bristle stiffness
	${\sigma }_1$	0.001	bristle damping
	${\sigma }_2$	$1.33\times {10}^{-4}$	viscous friction coefficient
	$F_c$	$7.78\times {10}^{-3}$	Coulomb friction level
	$F_s$	0.022	stiction friction force
	$v_s$	0.1	Stribeck velocity
External Disturbance	$d_s\left(t\right)$	$-3+1.5\sin \left(10t\right)$	$6\le t<13$

lists the LuGre friction model parameters [33] and the external disturbance $d_s$ used in the simulations. All the controllers and the PIO used in both simulation and experiments are implemented as discrete-time systems with a sampling period of 1 ms.

It is noted that, with the observer designed in Section 2.3, the estimated disturbance corresponds to $d_e$ rather than the external disturbance $d_s$ in Figure 6a. Since $d_e$ also includes the effects of the friction and modeling errors, the estimated disturbance obtained in simulation differs from the external disturbance, as shown in Figure 6b. However, defining ${\widehat{d}}_a$ as the estimate ${\widehat{d}}_e$ when $d_s=0$ and ${\widehat{d}}_b$ as the estimate when $d_s\ne 0$ is applied as in Table 2, the difference ${\widehat{d}}_b-{\widehat{d}}_a$ becomes similar to $d_s$. This indicates that the external disturbance is also properly estimated as shown in Figure 6a.

Figure 7 shows simulation results obtained using the P–PI controller with the PIO designed in Equation (15). As the controller gains ($k_{p1},k_{p2}$) increase, the tracking error decreases, and the smallest error is achieved when the estimation ${\widehat{d}}_e$ is compensated. The corresponding control inputs for the three cases are shown in Figure 8, where similar input magnitudes are observed. These results indicate that the inner-loop PI controller is functioning properly and that even small differences in control input are critical to position control performance.

Figure 9 and Figure 10 present simulation results demonstrating the superior performance of the conventional ISMC in Figure 1 and Figure 2 compared to a simpler SMC scheme, justifying the selection of ISMC as the baseline controller in this study. The sliding surface s and corresponding control input of the SMC are defined as follows:

$$\begin{array}{cc}\hfill s& =k_1{e}_1+e_2,\hfill \\ \hfill u_c& =b_n^{-1}\left(-k_1{e}_2+a_n{x}_2+\ddot{r}-\varphi s\right),\hfill \\ \hfill u_s& =-\overline{D}\mathrm{sgn}\left(s\right),\hfill \\ \hfill u& =u_c+u_s=:u_4.\hfill \end{array}$$

(26)

In Figure 9 it is observed that the error magnitude is larger than that of the ISMC. The corresponding control input is presented in Figure 10. These results suggest that the ISMC provides improved control performance compared with the conventional SMC.

The simulation results of the proposed controller given in (24) are presented in Figure 11 and Figure 12. When employing the RBF function, the tracking error can be reduced with a small switching gain $\overline{\delta }=0.5$. Compared to the ISMC with $\overline{D}=8$ shown in Figure 2, the reduced switching gain $\overline{\delta }=0.5$ effectively reduces chattering in the control input. The simulation results show that the RBF-based term compensates for the equivalent disturbance. The RBF input $u_n$ is explained in the experimental results.

4.2. Experimental Setup

This section details the experimental setup and the identification of system transfer function through an open-loop speed step–response experiment. The setup is shown in Figure 13 with its specifications listed in

Table 3. Experimental Setup Specifications.

Components	Specification	Value
Motor (Maxon RE-35)	Power	90 W
	Nominal voltage	24 V
	Nominal current	3.81 A
	Nominal speed	6970 rpm
Encoder (Encoder MR, Type L)	CPR	2000
	Number of channels	3
	Max. operating frequency	200 kHz
Motor Driver (L298N motor driver)	Nominal operating voltage	24 V
	Output current	2 A
	Max. PWM frequency	40 kHz
Control Board (Nucleo F767ZI)	MCU type	32-bit ARM Cortex-M7
	Operating voltage	3.3 V
	Clock speed	216 MHz

. The payload mass in the figure is for the additional load experiments in Section 4.3.3.

DC power supply provides electrical power to the motor driver, which converts it into the input voltage required to drive the motor. The Nucleo-F767ZI board used in the experiments processes the encoder pulses, generates PWM control signals, and delivers them to the motor driver. For this experiment, an L298N motor driver, a Maxon RE-35 motor, and an Encoder MR Type L (500 PPR, three channels, with a line driver) were used [34]. The key specifications are summarized in Table 3. The nominal transfer function of the system composed of the motor and motor driver was identified through an open-loop step–response experiment. The open-loop step–response result is shown in Figure 14. For an input of $u=12$ V, the steady-state motor speed is approximately $2.6577$ rad/s. Therefore, by applying the final value theorem, the gain k is obtained as follows:

$$\begin{array}{cc}\hfill {\omega }_{ss}& =\underset{t\to \infty }{\lim }\omega \left(t\right)=\underset{s\to 0}{\lim }s\mathrm{\Omega }\left(s\right)\hfill \\ \hfill & =\underset{s\to 0}{\lim }s\times {\displaystyle \frac{k}{\tau s+1}}\times {\displaystyle \frac{12}{s}}=2.6577k.\hfill \end{array}$$

(27)

$$k={\displaystyle \frac{{\omega }_{ss}}{12}}={\displaystyle \frac{2.6577}{12}}=0.221478.$$

(28)

The time constant $\tau$ is defined as the time required for the response to reach $63\%$ of the steady-state value. Since $63\%$ of $2.6577$ rad/s is approximately $1.6744$ rad/s, and the experimentally measured time to reach this speed is about $0.070302\mathrm{s}$, the time constant is identified as $\tau \approx 0.070302\mathrm{s}$. Consequently, the nominal parameters $a_n$ and $b_n$ are obtained by setting the equivalent disturbance to $d_e=0$ in (5b) and rewriting it into the transfer function form yielding $a_n=1/\tau =14.2243$ and $b_n=k/\tau =3.1504$.

4.3. Experimental Results

This section presents the experimental validation results, organized into three parts: baseline experiments without a payload mass, horizontal rotation experiments with a payload, and vertical rotation experiments with a payload for robustness validation.

4.3.1. Baseline Experiments Without Payload Mass

The experiments were conducted under the same conditions as the simulations using the parameters listed in Section 4.1. For the P–PI controller, the tracking errors shown in Figure 15 and Figure 16 are similar to those observed in the simulations. As the controller gains increase, the tracking error decreases. Moreover, introducing the PIO and compensating the estimated disturbance further reduces the tracking error. The disturbance estimated by the PIO is presented in Figure 17.

Figure 17 shows the disturbance ${\widehat{d}}_e$ estimated using the PIO. As in the simulations, two cases were compared: with (a) $d_s=0$ and with (b) $d_s$ in Table 2 applied to the input. When $d_s$ is applied, the estimated disturbance ${\widehat{d}}_b$ differs from the external disturbance defined in Table 2 due to the modeling error including the unknown friction. On the other hand, the estimated disturbance in the case $d_s=0$, denoted by ${\widehat{d}}_a$, corresponds to the equivalent disturbance. By subtracting ${\widehat{d}}_a$ from ${\widehat{d}}_b$, i.e., ${\widehat{d}}_b-{\widehat{d}}_a$, the remaining component is observed to be similar to $d_s$ closely. Therefore, compensating ${\widehat{d}}_e$ estimated by PIO could mitigate not only the external disturbance but also the modeling error, resulting in improved tracking performance for the same controller gains as shown in Figure 15 and Figure 16.

Figure 18 and Figure 19 evaluate the experimental results with the ISMC. As the switching gain $\overline{D}$ increases, the error magnitude decreases. However, the error becomes more affected by switching action. In addition, the chattering in the control input increases, which leads to increased noise and vibration.

Finally, the performance of the proposed controller is verified. Figure 20 and Figure 21 show the tracking error and control input of the proposed controller, respectively. For performance comparison, the switching gain was set to $\overline{\delta }=0.5$, which is relatively small compared with the ISMC case with $\overline{D}=8$ shown in Figure 18. It is observed that the proposed controller achieves the smallest tracking error among the tested controllers even with the low switching gain. In addition, by setting $\overline{\delta }$ to a small value, the chattering in the control input is reduced, thereby alleviating noise and vibration. To further support this observation,

Table 4. Quantitative Comparison of the Compared Controllers (Exp.): RMS of Control Input and Normed Error.

Controller	Switching Gain	RMS of u	Normed Error $\parallel \mathit{e}\parallel$
P–PI w/ PIO	–	5.0721	$2.18\times {10}^{-2}$
ISMC w/o RBF	$\overline{D}$ = 0.5	5.1745	$1.133\times {10}^{-1}$
ISMC w/o RBF	$\overline{D}$ = 2	5.3086	$8.60\times {10}^{-2}$
ISMC w/o RBF	$\overline{D}$ = 8	9.7831	$2.42\times {10}^{-2}$
ISMC w/ RBF (Proposed)	$\overline{\delta }$ = 0.5	5.0831	$3.8\times {10}^{-3}$

summarizes the RMS values of the control input voltage and the normed tracking errors ($\parallel e\parallel$), providing a quantitative comparison of both chattering and tracking performance. This shows that, the proposed controller reduced the tracking error to approximately one-sixth of that of the best-performing P–PI (with PIO) and conventional ISMC without RBF compensation.

Figure 22 compares the RBF-generated input $u_n$ with the PIO-estimated disturbance ${\widehat{d}}_b$ in Figure 17b. Based on Table 4, although the proposed method performs a role similar to the PIO as in the figure, it exhibits significantly superior performance.

4.3.2. Horizontal Rotation Experiment with Payload Mass

To further validate robustness under physical load variations, additional experiments were conducted by attaching a 1 kg weight plate to the motor shaft via a rigid link. In the horizontal rotation configuration, the added load primarily increases the equivalent moment of inertia of the plant and thus acts mainly as a parameter variation. This experiment evaluates whether the proposed controller maintains stable tracking performance and consistent compensation behavior under significant inertia changes. Figure 23, Figure 24, Figure 25 and Figure 26 present the tracking errors and control inputs of the baseline ISMC cases and the proposed method under the horizontal rotation load condition. In addition, Figure 27 compares the RBF input with the PIO-based disturbance estimate.

Table 5. Quantitative Comparison of the Compared Controllers (Experimental results of payload horizontal rotation): RMS of Control Input and Normed Error.

Controller	Switching Gain	RMS of u	Normed Error $\parallel \mathit{e}\parallel$
ISMC w/o RBF	$\overline{D}$ = 0.5	4.8227	$1.161\times {10}^{-1}$
ISMC w/o RBF	$\overline{D}$ = 2	4.9918	$8.52\times {10}^{-2}$
ISMC w/o RBF	$\overline{D}$ = 8	9.6867	$2.37\times {10}^{-2}$
ISMC w/ RBF (Proposed)	$\overline{\delta }$ = 0.5	4.8412	$4.8\times {10}^{-3}$

summarizes a quantitative comparison under the horizontal rotation load condition in terms of the RMS of the control input and the normed tracking error. Compared with the best-performing baseline ISMC case ($\overline{D}=8$), the proposed ISMC with RBF compensation reduces the normed tracking error to approximately one-fifth of the baseline value.

Figure 23, Figure 24, Figure 25 and Figure 26 and Table 5 show that the proposed ISMC with RBF compensation achieves the smallest normed tracking error under the horizontal rotation load condition, while keeping the RMS of the control input comparable to the baseline ISMC cases. Moreover, Figure 27 indicates that the learned RBF compensation exhibits a similar trend to the PIO-based disturbance estimate, supporting that the proposed method effectively compensates the load-induced equivalent disturbance.

4.3.3. Vertical Rotation Experiment with Payload Mass

To further validate robustness against a state-dependent disturbance, additional vertical rotation experiments were conducted with a 1 kg weight plate by reorienting the motor assembly to enable vertical rotation of the payload as shown in Figure 13. In this configuration, the gravity-induced torque varies with the rotational state, yielding a nonlinear time-varying disturbance. Figure 28, Figure 29, Figure 30 and Figure 31 show the tracking errors and control inputs of the baseline ISMC cases and the proposed method, and Figure 32 compares the RBF-generated compensation input with the PIO-based disturbance estimate.

Table 6. Quantitative Comparison of the Compared Controllers (Experimental results of payload vertical rotation): RMS of Control Input and Normed Error.

Controller	Switching Gain	RMS of u	Normed Error $\parallel \mathit{e}\parallel$
ISMC w/o RBF	$\overline{D}$ = 0.5	4.9237	$1.053\times {10}^{-1}$
ISMC w/o RBF	$\overline{D}$ = 2	4.9812	$6.18\times {10}^{-2}$
ISMC w/o RBF	$\overline{D}$ = 8	9.8205	$2.46\times {10}^{-2}$
ISMC w/ RBF (Proposed)	$\overline{\delta }$ = 0.5	5.1465	$5.6\times {10}^{-3}$

summarizes a quantitative comparison under the vertical rotation load condition in terms of the RMS of the control input and the normed tracking error. Compared with the best-performing baseline ISMC case ($\overline{D}=8$), the proposed ISMC with RBF compensation reduces the normed tracking error to about one-fourth of the baseline value.

In conclusion, while the conventional ISMC is robust against uncertainties, augmenting it with the RBF could further improve the control performance and achieve satisfactory tracking even with a relatively small switching gain.

5. Conclusions

This study presented a novel RBF-NN supervisory learning scheme designed to enhance the performance of Integral Sliding Mode Control (ISMC) for motor position tracking. The primary objective was to overcome the inherent limitations of conventional high-gain controllers and Disturbance Observer-Based Control (DOBC) methods, which often suffer from instability or excessive chattering under large uncertainties.

The proposed control architecture utilizes the sliding variable as a training signal, enabling the RBF-NN to estimate the equivalent disturbance online without the need for precise system models or high-gain observers. By adaptively compensating for lumped disturbances, the proposed method significantly reduces the required switching gain of the ISMC.

Comprehensive validation was performed through both simulations and laboratory experiments. The proposed RBF-NN-based ISMC was compared against two baseline controllers: a conventional ISMC and a DOBC-based cascade P–PI controller. The experimental results demonstrated that the proposed scheme achieves superior tracking accuracy and robustness, particularly under challenging scenarios involving parameter uncertainties and sinusoidal disturbances with unknown offsets. Quantitative analysis confirmed that the proposed approach yields lower tracking error norms and reduced RMS values of the control input voltage, while effectively alleviating chattering compared to the baseline methods.

In conclusion, the proposed method provides a systematic and effective solution for high-precision motor position control, successfully reconciling the trade-off between robustness and switching gain magnitude. Future work will focus on optimizing the RBF network structure, specifically the selection of centers, widths, and learning rates, potentially leveraging reinforcement learning algorithms for autonomous tuning. Additionally, we plan to extend the proposed scheme to multi-axis motion control systems to verify its robustness under diverse and complex load variations.