Temperature Estimation of Thin Shape Memory Alloy Springs in a Small-Scale Hip Exoskeleton with System Identification and Adaptive Control

Abstract

This study presents a small-scale hip exoskeleton incorporating bi-directional artificial muscles constructed with springs of Shape Memory Alloy (SMA). The prototype can effectively support hip motion in both extension and flexion, spanning an angular range of $-{20}^{°}$ to ${200}^{°}$. Experiments for thermo-mechanical characterization were executed to assess the performance of the SMA muscles throughout the entire motion range. The outcomes not only confirmed the suitability of the SMA muscles for the designed exoskeleton but also provided valuable insights into their behavior and capabilities. System identification experiments were carried out to establish an accurate transfer function, guiding the tuning of Proportional-Integral-Derivative (PID) controllers for enhanced motion-control effectiveness. The safety of the SMA system was addressed with a focus on preventing overheating. Challenges in accurately measuring the temperature of a thin spring were overcome by utilizing two thermocouples for each SMA springs group. Additionally, conventional SMA temperature measurement methods, such as infrared and resistance-based techniques, are limited by high cost, nonlinearity, and small range. This study presents a model-based temperature estimation algorithm that integrates a heat transfer model, electrical input data, and thermocouple data to enable accurate and real-time SMA temperature estimation without additional sensors, offering a cost-effective and reliable alternative. To evaluate the small hip prototype and its controller capabilities, control experiments were executed for both stepping and sinusoidal trajectories. The exoskeleton successfully tracked the desired trajectories, showing its precision. Moreover, system performance under adaptive control was further investigated, revealing an RMSE of $0.{94}^{°}$ in sinusoidal trajectory experiments, indicating reliable disturbance rejection in the angle measurements.

1. Introduction

During mobility and maintaining the body’s weight, the hip joint is prone to injury and pain. The World-Health Organization (WHO) has reported that around 190 million people mostly with hand or leg disabilities experience difficulties with mobility. The challenges are likely to increase with global aging and conflicts [1]. Wearable devices known as exoskeletons and orthoses can provide the affixed body part external support and force. Essentially, they can be classified into two different categories: (1) elastic parts, like bands or springs, which are capable of storing and releasing energy, and (2) electromechanical components, like actuators, which transform electrical energy into mechanical energy [2,3]. The compliance and softness needed for wearable electronics, however, are absent from conventional electrical actuators.

Researchers are looking for effective materials that can overcome this challenge by delivering the required force and stroke while yet being lightweight and flexible [4,5]. A revolutionary soft elbow exoskeleton based on the actuation of an SMA spring is developed in [6], where a high-elastic rubber band and active deformation material SMA are used in a bionic fashion. The exoskeleton mimics the contraction and relaxation of the elbow flexor and extensor muscles. In [7], the researchers developed a flexible SMA-based actuator for exoskeletons utilized in upper limb rehabilitation. A fast-response magnetorheological elastomer–SMA artificial muscle and a controllable magnetorheological fluid (MRF) exoskeleton developed in [8] effectively address issues such as limited load holding capacity owing to their softness and slow response due to prolonged cooling time. SMAs are utilized as a variable stiffness driving element in [9], which intends to eliminate the conventional premise of utilizing motors as the dominant driving sources, simplify the exoskeleton’s structure, and lower the exoskeleton’s complexity. The researchers in [10] developed an active and passive SMA-driven control system for a knee exoskeleton with variable stiffness. SMA wires perform the stiffness adjustment function to improve the knee exoskeleton’s mobility.

Shape Memory Alloys (SMAs), particularly nickel–titanium (NiTi) alloys, have emerged as promising actuators due to their high power-to-weight ratio, silent operation, and ability to produce large stresses under compact form factors. These unique characteristics have positioned SMA actuators as attractive alternatives to traditional electromagnetic or pneumatic systems in wearable robotics and exoskeleton applications [11,12,13]. However, despite their advantages, SMA-based actuators face critical challenges such as limited displacement, slow cooling dynamics, nonlinear hysteresis, and strong dependency on temperature conditions [14,15]. Due to their capacity to produce appropriate displacements and forces, SMAs offer significant potential for the research and development of soft actuators. A phenomenon known the shape memory effect happens when SMAs are heated above the transitional temperature and can regain their trained shape [16]. SMAs’ flexibility allows for the fabrication of a wide range of configurations and shapes, which makes them appropriate for a variety of uses, including wearable technology [17]. SMAs have several applications when used as actuators, such as compliance, compact size, silent operation, and a substantial force-to-weight ratio [18]. The common shapes for SMAs are wire and and spring [19]. Since SMA wires have multiple activation methods, a high power density, and flexibility, they have been extensively utilized in the construction of therapeutic equipment. For example, Park et al. used single and double diamond-shaped structures built of SMA to fabricate an artificial muscle for a robotic elbow joint [20].

The accurate temperature estimation of SMA is essential for reliable actuation. Since SMA phase transformation is thermally driven, temperature sensing or indirect estimation via resistance feedback is often employed to achieve closed-loop control. Studies have demonstrated the feasibility of resistance-based feedback for the real-time monitoring of SMA actuators [21], while review articles emphasize that self-sensing methods and predictive control strategies are key enablers for stable performance in robotics and wearable systems [15,22]. These approaches mitigate the drawbacks of external temperature sensors and enhance actuator bandwidth. Temperature measurement and temperature estimation have been conducted for various systems including SMAs in various approaches [23,24]. However, obtaining the temperature of thin SMA wire or spring is challenging.

SMA wires have been controlled using a variety of adaptive controller approaches. Kannan et al. [25] proposed a direct linear adaptive control law for a robotic arm actuated by a single SMA wire. Pan et al. [26] used a neural network to build an observer-based output feedback control in an indirect adaptive manner. Using a DNN, a direct adaptive inverse model-based controller for SMA actuator has been implemented [27]. Tai and Ahn [28] suggested a unique PID-tuned adaptive sliding mode control technique designed especially for SMA actuators. An adaptive PID controller for controlling an experimental model of an AAFO system actuated by SMAs’ was implemented [29]. In the context of wearable robotics, SMA actuators have been successfully integrated into exoskeletons and assistive devices. For instance, lightweight exo-gloves powered by SMA wires have been proposed for telerehabilitation, demonstrating effective control of finger joints with compact integration [30]. Similarly, SMA-based soft exosuits for pediatric gait rehabilitation have shown potential in reproducing natural motion patterns, offering new opportunities for clinical applications [31]. Innovative actuator designs such as hoist-based SMA modules [32] and flexural configurations [12] further expand the displacement range and functional applicability of SMA systems, making them increasingly viable for human–machine interaction.

Our previous work [33,34] aimed to utilize SMA actuators with an arc configuration to make a finger-like mechanism. In addition to this, we also employed SMA springs demonstrated as a two degrees-of-freedom actuator [35,36], a caterpillar robot [37], and bi-directional SMA muscles [38]. Similarly, in our work [39], we developed a small-scale prototype knee exoskeleton utilizing SMA springs and refined the design process, system identification, and control. Then, we utilized the SMA wire and the SMA springs in hexagonal architecture to build compact bio-inspired SMA muscles [38,40,41].

This paper addresses these challenges by focusing on SMA actuators with particular emphasis on temperature measurement and estimation strategies and their role in exoskeleton applications. In this work, using SMA springs, a small scale hip exoskeleton that mimics and supports the hip muscles is developed and characterized. Our main goal is to build and control this prototype to evaluate the design before constructing a full-scale model. To evaluate the system’s performance, thermomechanical characterization studies were carried out. The transfer functions of the system were identified with the MATLAB R2021a, System Identification Toolbox, yielding a fitness accuracy greater than $95\%$, enabling PID controller tuning. Moreover, an Adaptive PID controller was tuned using an inertial measurement unit (IMU) and a Kalman filter to regulate the hip angle. Additionally, thermocouples were used to monitor the temperature of the SMA and prevent overheating. Furthermore, accurate temperature measurement of SMA is essential for precise control of their phase transformation and actuation performance. However, existing techniques, such as infrared imaging and resistance-based sensing, face practical limitations. Infrared methods, though accurate, are costly and unsuitable for compact or embedded applications. Resistance-based methods, while low-cost, suffer from nonlinear resistance–temperature characteristics and limited measurement ranges, leading to poor estimation accuracy. To address these limitations, this study develops a temperature estimation algorithm that combines heat transfer modeling with measured electrical inputs (voltage and current) and thermocouple-calibrated parameters. The proposed method enables the real-time temperature estimation of SMA actuators without requiring additional temperature sensors. This approach offers a cost-effective, accurate, and easily integrable solution for SMA-based systems, representing a significant improvement over traditional measurement techniques. By bridging the actuator design aspects with sensing and adaptive control, this work aims to advance the state of the art in SMA-powered wearable robotics.

This paper is organized as follows: Section 2 describes the system architecture. Section 3 shows the mathematical models. Section 4 explains the control algorithm, while Section 5 provides details of the system identification and temperature estimation. Finally, the characterization and the control experiments are discussed in Section 6.

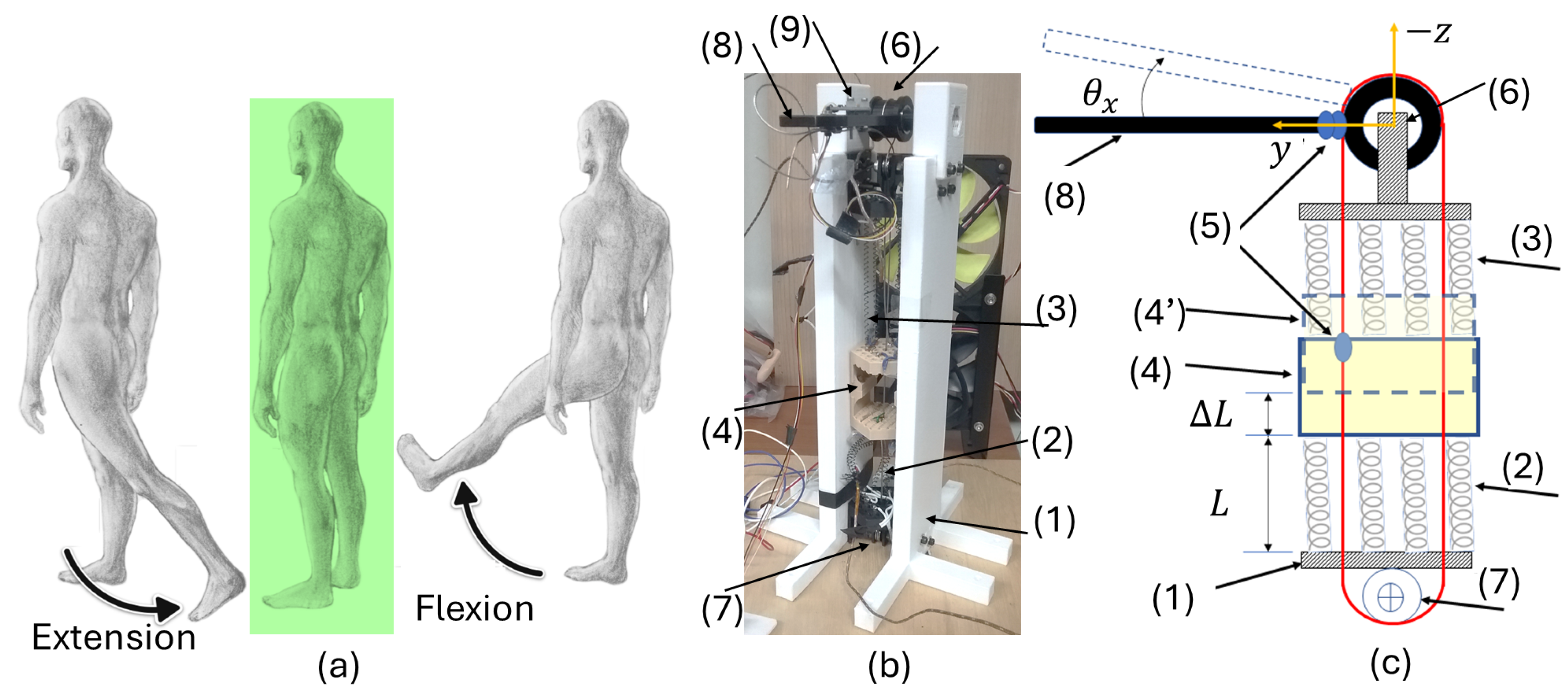
2. Architecture of the System

Drawing inspiration from the architecture of human muscles, we have developed a hexagonal arrangement of two antagonistic SMA springs bundles, composing an SMA muscle in bi-directions [38,41]. Our ambition is to utilize this bi-directional muscle in a small-scale hip exoskeleton.

The fundamental concept of our design is based on the thermo-mechanical characteristics of SMA. When heated, the deformed material transforms from Martensite to Austenite, restoring the original contracted spring shape. Upon cooling, it reverts to the Martensite phase while retaining its recovered shape, thereby exhibiting the one-way memory phenomenon, as shown in Figure 1. The SMA spring has wire diameter d = $0.5$ mm; spring outer diameter Dout = $3.5$ mm; number of coils n = 25 turns.

In Figure 2a, we provide a representation of the human hip’s motion with extension–flexion range ($-{15}^{°}$ to ${120}^{°}$). In addition, Figure 2b illustrates the architecture of the SMA-based bidirectional artificial muscle. Figure 2c, describes the system kinematics, where (1) reference structure and hexagonal bases; (2) 6 SMA springs (group A); (3) 6 Antagonistic SMA springs (group B); (4) the actuated part driven by groups A and B of springs; (4’) position of the actuated part when group B is activated (contracted); (5) fixation points of the steel transmission wires for converting linear motion into link rotation; (6) joint of rotation ${\theta }_x$; (7) lower pulley; (8) rotating link; (9) an IMU sensor measures the link angle ${\theta }_x$.

We used an IMU to measure the angular velocity, and hence, the angle is estimated using the Kalman filter. A comparative study of various Kalman filters is investigated in [42]. We also used two thermocouples to measure the temperature of the wire in two places. It should be noted that the temperature of the SMA springs can rise to 100 °C or higher. Therefore, designing for safety is essential to protect human skin by using heat-resistant fabrics or materials. For more comprehensive details on the system architecture, please refer to our previous publications [38,41].

3. Mathematical Modeling

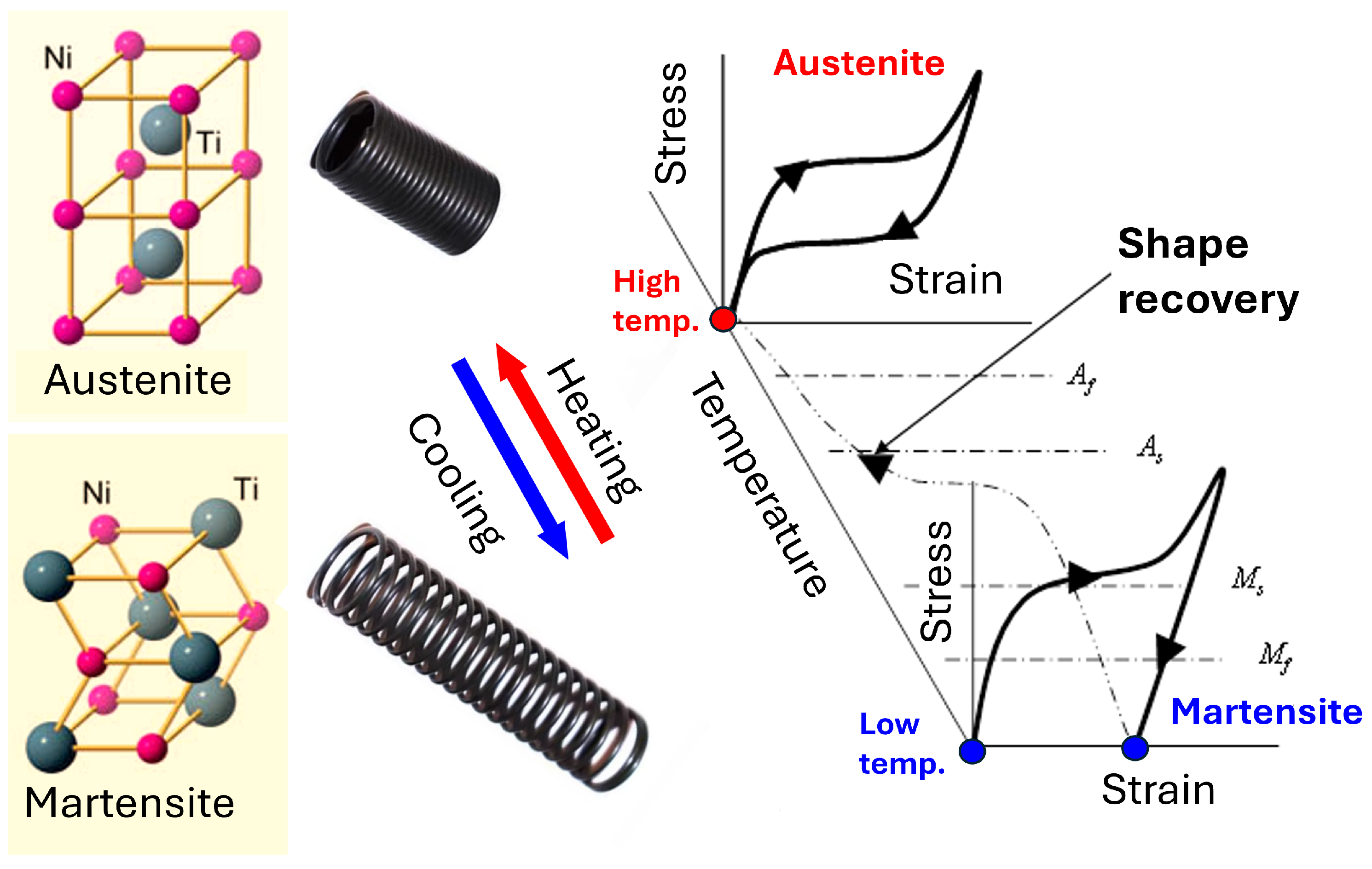
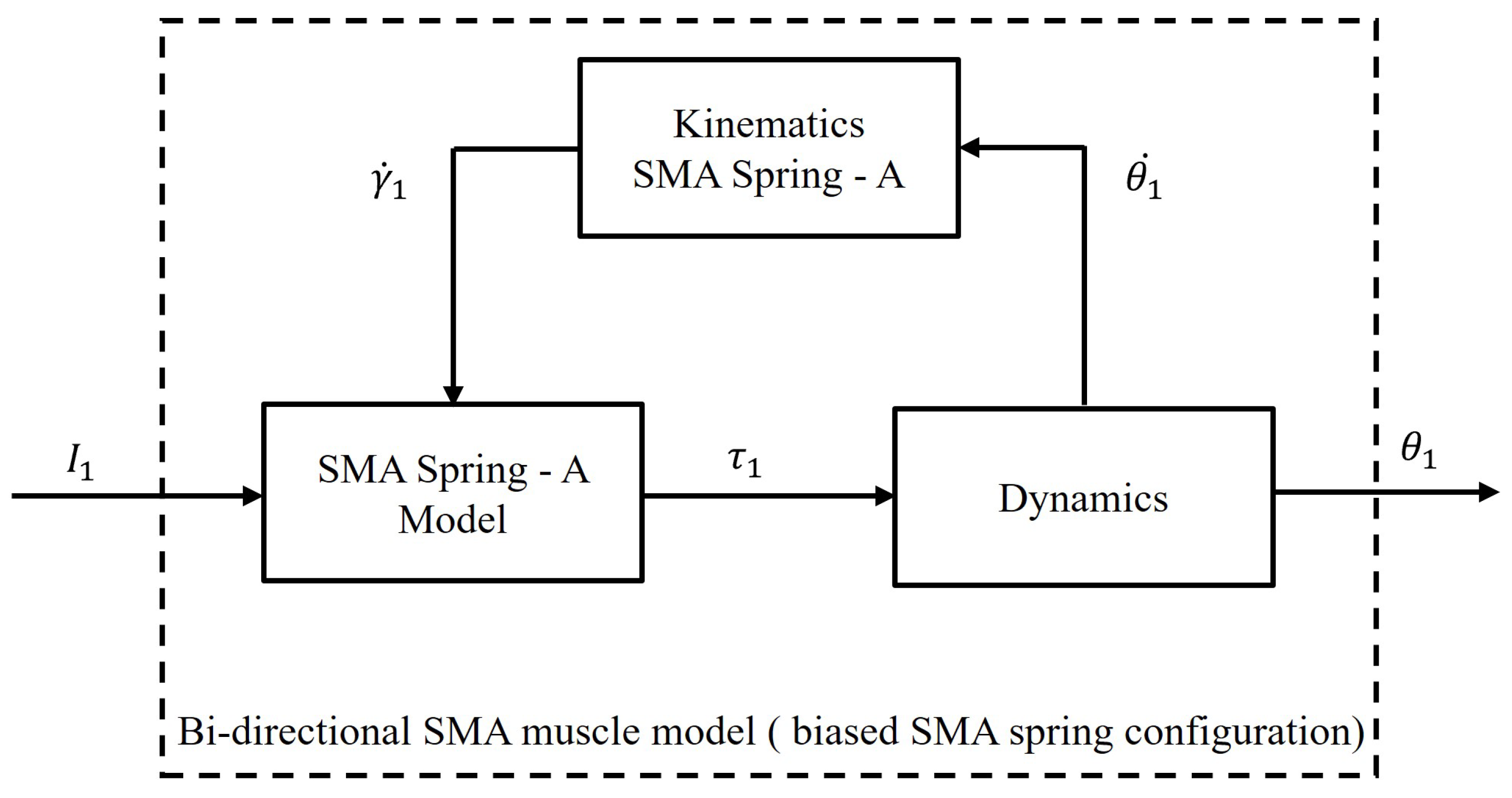
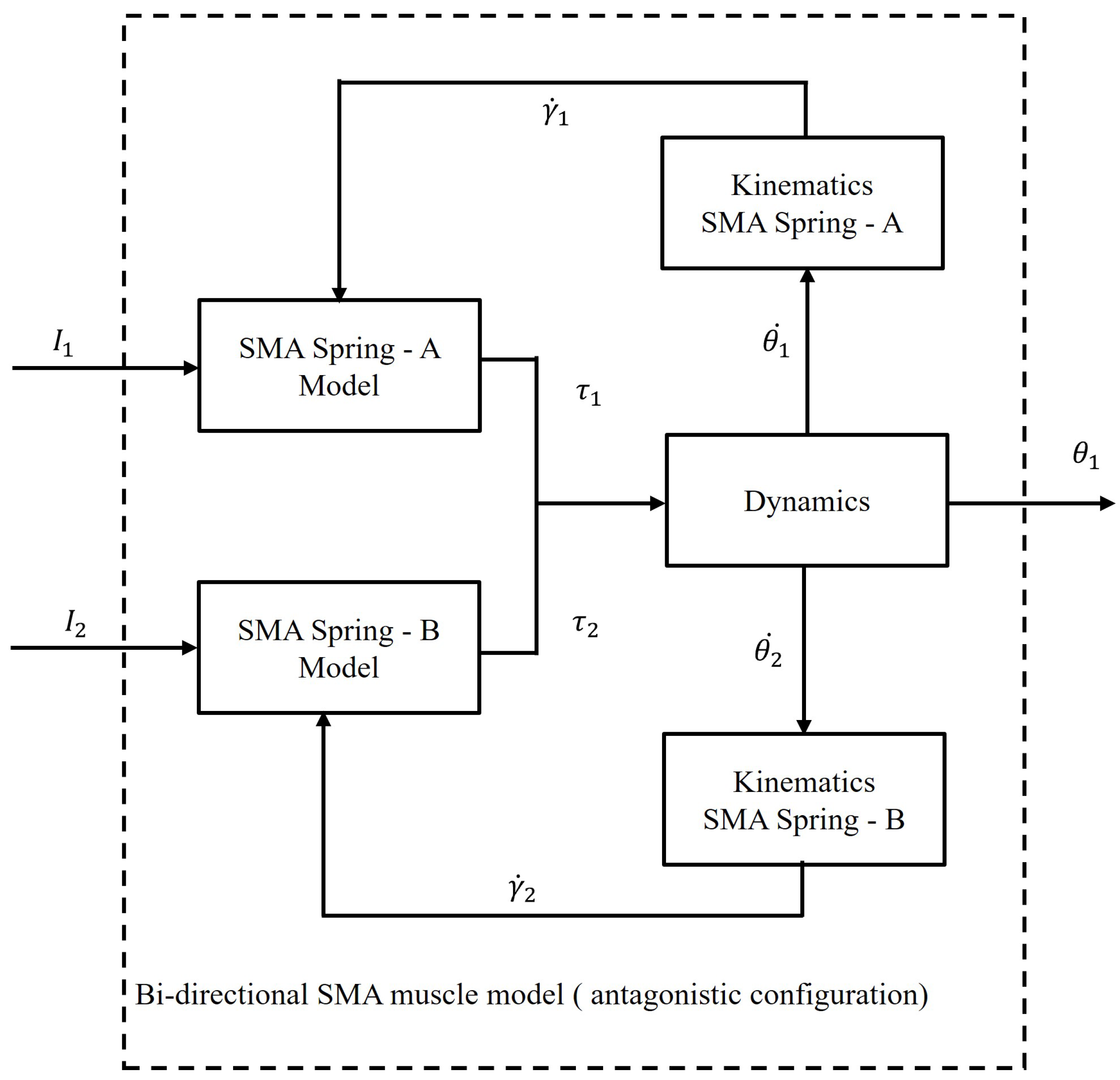
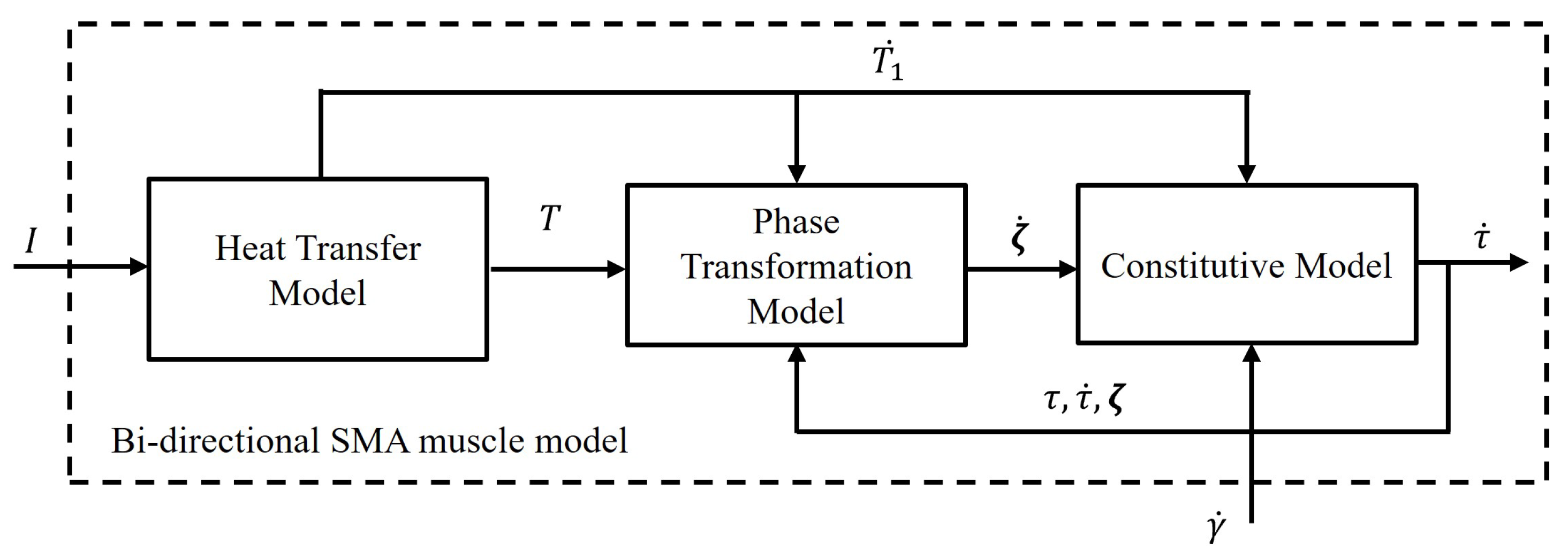
3.1. Model of the Bi-Directional SMA Muscle

This section provides a block diagram representation of the mathematical model for the bi-directional SMA muscle, encompassing both configurations. Figure 3 represents the spring SMA biased configuration, while Figure 4 shows the antagonistic configuration. The model of the bi-directional SMA muscle comprises two primary subsystems: (1) the SMA spring model and (2) the kinematic and dynamic model. The diagram in Figure 5 depicts the schematic model of the bi-directional SMA muscle subsystem. This particular subsystem is described by a mathematical model proposed by Elahinia and Ahmadian [43]. The model can be subdivided into three distinct subsystems: thermal dynamics, heat transformation, and constitutive model. The interrelationships and interactions between the variables of each subsystem within the SMA spring model are visually represented in Figure 5.

3.2. SMA Spring Mathematical Model

The length of the SMA spring can be contracted by applying electrical energy (current and voltage), and it is also dependent on the loading force, which causes shear stress and shear strain. The constitutive model of an SMA spring is based on the Tanaka model [44], Hisaaki model [45], and Elahinia model [43]. This model can be presented as a time derivative relation between torsional stress $\tau$, and three states: temperature T, shear strain $\gamma$, and martensite fraction $\xi$ as

$$\dot{\tau }=G\dot{\gamma }+\Omega \dot{\xi }+\Theta \dot{T},$$

(1)

where G is the shear modulus, $\Omega$ is a transformation tensor, and $\Theta$ is a thermoelastic tensor. The martensite fraction $\xi$ has hysteresis between the martensite state and austenite state. It is important to note that $\xi =1$ indicates that the SMA is fully in the martensite phase (cold state), while $\xi =0$ corresponds to the SMA being entirely in the austenite phase (hot state). The transformation from martensite to austenite generates internal stresses within the SMA, which in turn produce the desired force and motion, as illustrated in Figure 1.

3.3. Heat Transfer Model

The heat transfer model of the SMA can be expressed by the rate of changing the temperature (°C/s) as

$$\dot{T}={\displaystyle \frac{I\times V-h_c{A}_{s}p(T-T_{amb})}{m_{sp}{C}_p}},$$

(2)

where V and I denote the input voltage and current supplied to the SMA spring, $m_{sp}$ is the mass of the SMA spring, $C_p$ is the specific heat capacity, and $T_{amb}$ represents the ambient room temperature 25 °C. $A_{sp}$ is the surface area (that has heat exchange) of the SMA spring. $h_c$ is the heat convection coefficient, which is not usually a constant or even linear. It can be defined as

$$h_c=h_o+h_2{T}^n,$$

(3)

where $A_{sp}=\pi dL$, with L denoting the length of the SMA spring wire and d its diameter. $h_2,h_o,\mathrm{and}n$ are unknowns, and they can be evaluated imperially, as we will investigate in Section 5.

3.4. Kinematic Model

As shown in Figure 2c, when energizing the SMA springs group B (3), the moving part (4) starts upward motion to the position (4’); this moving part is connected to the rotating link (8) using the transmission wire (6). The direction of motion can be reversed by energizing the antagonistic SMA springs group A (2). The rotation angle can be formulated as

$${\theta }_x={\displaystyle \frac{\Delta L}{r_{pulley}}},$$

(4)

where $\Delta L$ is the linear movement of part (4) caused by the SMA springs, and $r_{pulley}$ is the radius of the pulley.

For the detailed design of the desired stroke and other design parameters, please refer to our previous publication [38] and the manufacturer datasheet on [19].

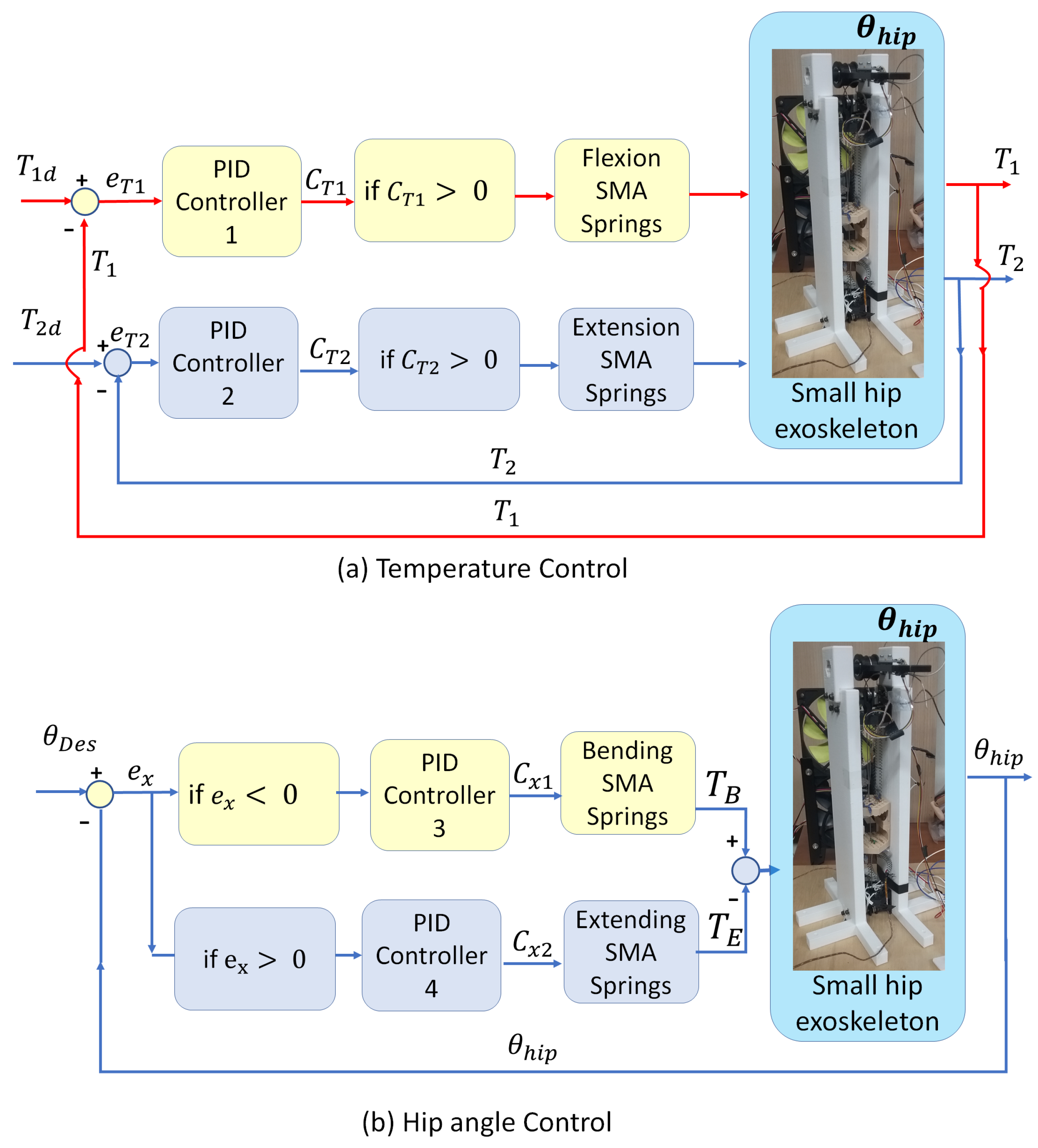
4. Control Algorithm

The control algorithm employed in our system relies on two key measurements: the temperature and hip angle. The temperature is measured using four thermocouples, with two dedicated to monitoring the temperature of the hip flexion SMA springs and the other two for the hip extension SMA springs. The hip angle rate is measured using an IMU, and then the hip angle is estimated using the Kalman filter.

To achieve reliable control of the SMA bi-directional muscles, four PID controllers were implemented. The first two controllers regulate the temperatures of the SMA springs: $T_1$ for hip flexion and $T_2$ for hip extension. Conversely, for hip angle regulation, we employ the third and fourth adaptive PID controllers. The sampling time is 50 ms, corresponding to a control frequency of 20 Hz.

4.1. SMA Temperature Control

The PID controllers of the temperature of the SMA springs can be formulated by the following equations:

$$e_T=T_m-T_d,$$

(5)

$$C_{T1,T2}=K_{pT}{e}_T+K_{iT}\int e_{T}dt+K_{dT}\left(d{e}_T\right)/dt,$$

(6)

where, $T_d$ denotes the reference temperature, $T_m$ represents the thermocouple-measured temperatures for $T_1$ (of the hip flexion SMA springs) and $T_2$ (of the hip extension SMA springs), $e_T$ denotes the error, $K_{PT}$, $K_{iT}$, and $K_{dT}$ are the PID gains, and $C_{T1}$ and $C_{T2}$ are the corresponding control inputs. It should be emphasized that those two controllers operate exclusively in the heating phase, whereas cooling relies solely on ambient conditions. Hence, the control logic is conditional: it is activated only when $C_{T1}>0$ or $C_{T2}>0$, as shown in Figure 6a.

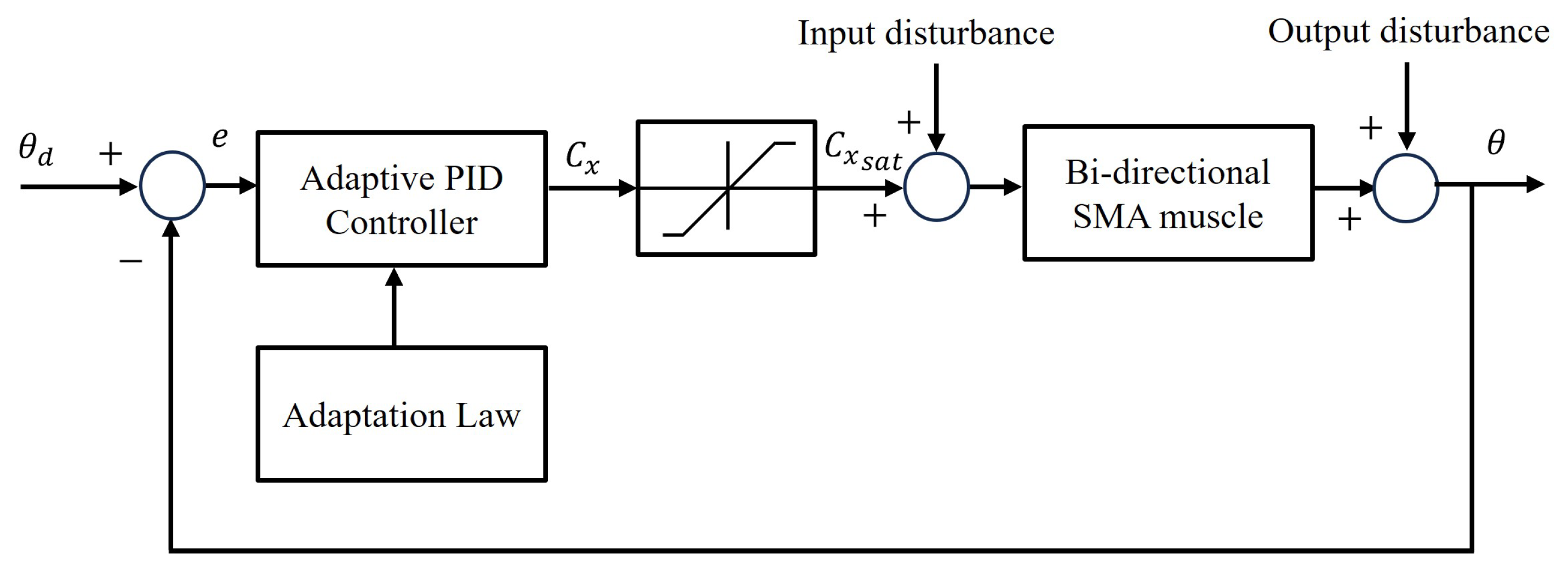
4.2. Adaptive PID Controller

On the other hand, to control the hip angle we utilize third and fourth adaptive PID controllers, as illustrated in Figure 7. The adaptive control approach encompasses a variety of techniques that offer a systematic and automated means of adjusting the control parameters in real time. Its purpose is to ensure the desired performance is consistently maintained despite uncertainties in parameters and models [46]. The field of adaptive control techniques has been categorized into two main types: direct adaptive and indirect adaptive. Similarly, ref. [47] simplified the classification by distinguishing between adaptive control techniques for linear systems and nonlinear systems. Additionally, adaptive techniques can be further classified as either adaptive linear control or adaptive nonlinear control. The control law for the PID controller is expressed as follows:

$$C_{x1,x2}\left(t\right)=K_{P}e\left(t\right)+K_I{\int }_0^{t}e\left(t\right)dt+K_D{\displaystyle \frac{d}{dt}}e\left(t\right),$$

(7)

$$e_x={\theta }_{hip}-{\theta }_{Des}.$$

(8)

The proportional ($K_P$), integral ($K_I$), and derivative ($K_D$) gains correspond to the PID parameters. The tracking error is represented by $e_x\left(t\right)$, and the control signal is denoted as $C_{x1}\left(t\right)$ for the SMA springs group A and $C_{x2}\left(t\right)$ for the SMA springs group B. In this study, we employed adaptation laws for updating the values of $K_P$, $K_I$, and $K_D$ as follows:

$$K_P(n+1)=K_P\left(n\right)+{\gamma }_1{e}_x\left(t\right),$$

(9)

$$K_I(n+1)=K_I\left(n\right)+{\gamma }_2{K}_I{\int }_0^t{e}_x\left(t\right)dt,$$

(10)

$$K_D(n+1)=K_D\left(n\right)+{\gamma }_3{K}_D{\displaystyle \frac{d}{dt}}{e}_x\left(t\right).$$

(11)

In the given control law, ${\gamma }_1$, ${\gamma }_2$, and ${\gamma }_3$ (where ${\gamma }_1>0$, ${\gamma }_2>0$, and ${\gamma }_3>0$) represent the learning rates. The learning rate is a critical factor in the adaptation process. The learning rates and initial PID gains were determined experimentally through iterative tuning during system identification, aiming to minimize the overshoot and steady-state error while maintaining stable operation. It should be emphasized that inappropriate choices of the learning rates or initial PID gain values may lead the controller to drive the system states away from the desired behavior. Therefore, careful selection of these parameters is essential to ensure stable and effective control performance.

The simulation results of the adaptive PID controller are shown in Figure 8. The temporal variations of the adaptive control gains $K_p$, $K_i$, and $K_d$ are illustrated in Figure 9.

5. Estimation and System Identification

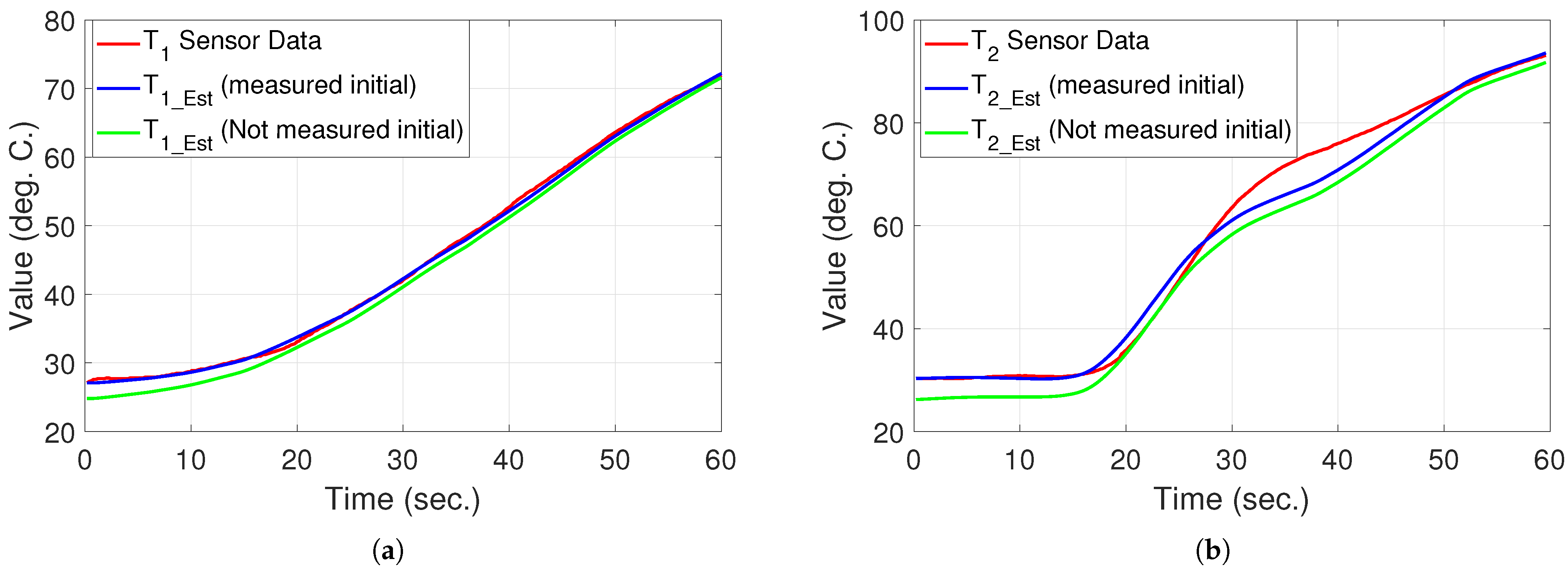
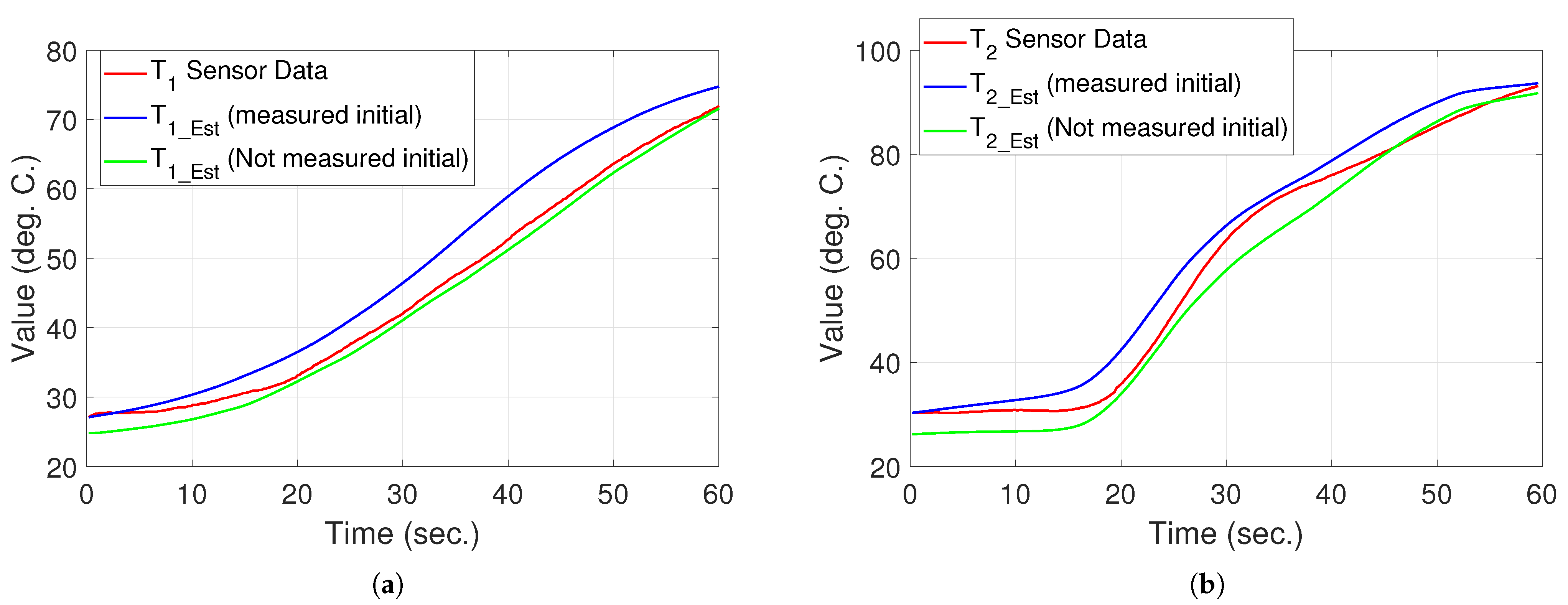
5.1. Temperature Estimation

The temperature measurement of the SMA wire is a very important task while making any control. This uses the temperature measurement as an indicator and alarm to prevent the overheating of the SMA wire, which would cause the shape memory effect to be lost or at least degraded. However, attaching a thermocouple to an SMA wire is not easy. We should attach the thermocouple tip (the sensing point) to the SMA adequately (which means good and eclectically isolated mechanical contact to prevent electrical noise on the measurement signal). For these reasons, we used polyimide tape to make good electrical isolation and nylon wire (fishing wire) to make a strong tie; hence, stable measurement can be compare to the thermal camera. A good measurement can be acquired using this method, but measurement failure can happen at any time, because it is a small tip attached to a wire. For this reason, we used two thermocouples at each SMA springs group to obtain the temperature and to guarantee that at least one of them will work properly. To further ensure the knowledge of these critical temperatures: $T_1$ of SMA springs group A and $T_2$ of SMA springs group A, another approach was applied, a computational approach to estimate the temperature based on other easier and more trusted measurements like the current and voltage and the knowledge of the heating and cooling dynamics.

As given in the heat transfer model in Equation (3) and considering that

$$T_e=T-T_{amb},$$

(12)

$$\dot{T_e}=a_{1}VI+a_2{T}_e^n,$$

(13)

where $T_e$ is the difference between the temperature of the SMA spring T and the ambient temperature $T_{amb}$, the coefficients $a_1$ and $a_2$ can be numerically calculated based on the experimental data.

Assuming $n=1$, and letting $Z=\dot{T_e}$, $X=VI$, and $Y=Te$, which are all vector from real experimental data, we can rewrite the equation in the following form:

$$\left[\begin{array}{c}Z\end{array}\right]=\left[\begin{array}{cc}X& Y\end{array}\right]\left[\begin{array}{c}{a}_1\\ a_2\end{array}\right],$$

(14)

where Z, X, and Y are vectors of the sampled data. Then, we can find the values of the coefficients $a_1$, and $a_2$, as follows:

$$\left[\begin{array}{c}{a}_1\\ a_2\end{array}\right]={\left[\begin{array}{cc}X& Y\end{array}\right]}^{-1}\left[\begin{array}{c}Z\end{array}\right],$$

(15)

where ${\left[XY\right]}^{-1}$ is the pseudo inverse of the non-square matrix (‘pinv’, as in matlab, for example). Figure 10 shows the estimation results for the first order assumption indicating the RMSE.

Then, we assumed that $n=2$ and $n=3$ and conducted the same computations two more times to select the acceptable RMSE, as shown in the figures below. Moreover, for each model, we compared between two cases:

• The first case: the initial temperature is measured and trusted.
• The second case: the initial temperature is not measured, and hence, we assumed the initial temperature equals $T_{amb}$.

Figure 11 shows the estimation results for the second order assumption indicating the RMSE in both cases of the initial temperature (known, unknown (assumed to be the same as $T_{amb}$)).

Figure 12 shows the estimation results for the third order assumption indicating the RMSE in both cases of the initial temperature (known, unknown (assumed to be the same as $T_{amb}$)). From all these, we can conclude the following: For the experimental estimation data, the first order estimation has a lower RMSE ($0.{40}^{°}$, $1.{53}^{°}$) in the case of $T_1$ data, and the second order estimation has a lower RMSE ($3.{78}^{°}$, $3.{51}^{°}$) in the case of $T_2$ data. The maximum observed temperature during the experiments was below ${100}^{°}$, which is well within the safe working range for SMA Nitinol (typically below ${120}^{°}$). The RMSE values obtained in Figure 10, Figure 11 and Figure 12 indicate that the temperature estimation error remains within $\pm 2^{°}$, which is sufficiently low to ensure safe operation. Therefore, the estimation accuracy is adequate for maintaining the SMA below damaging thermal thresholds.

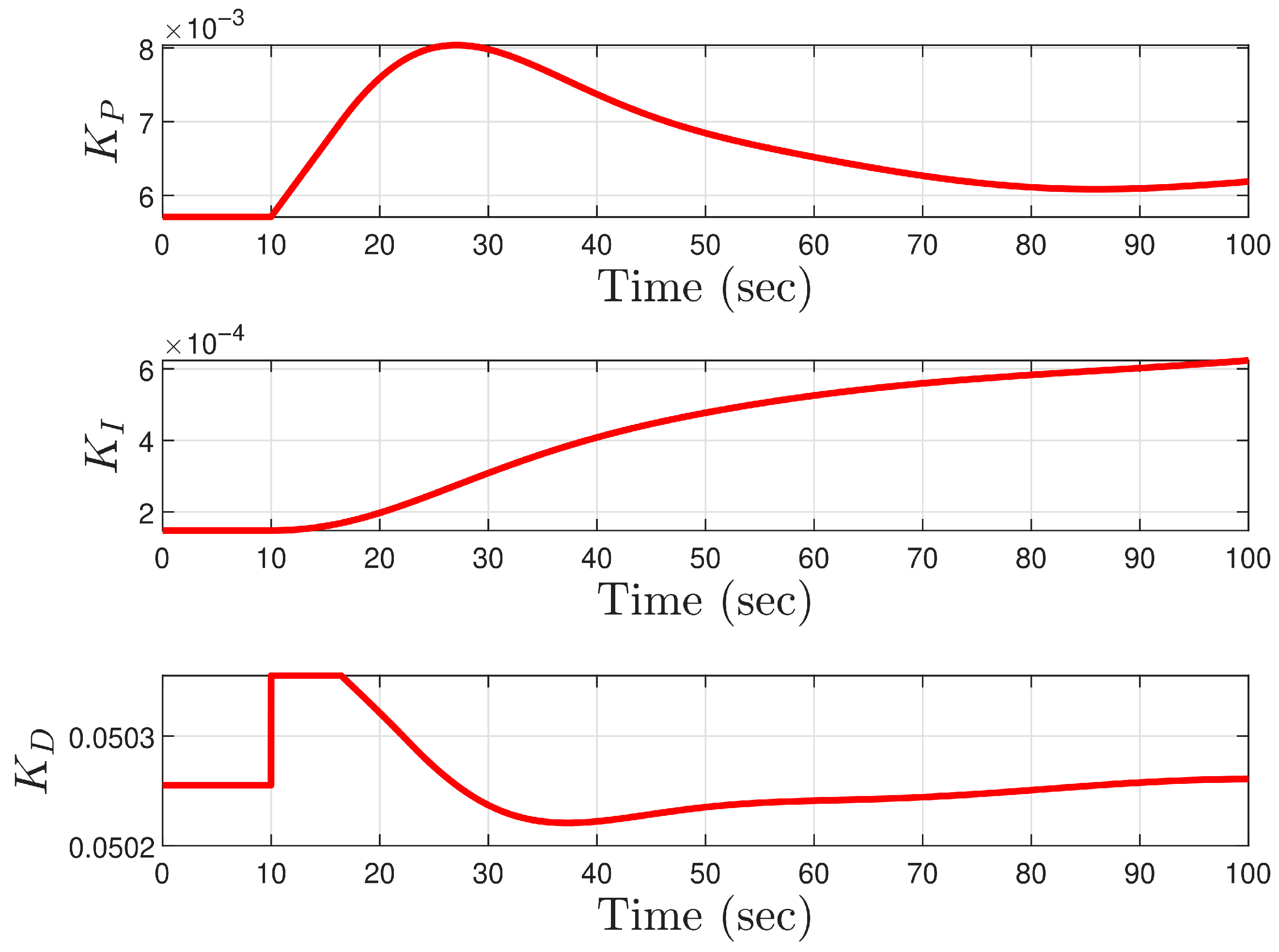
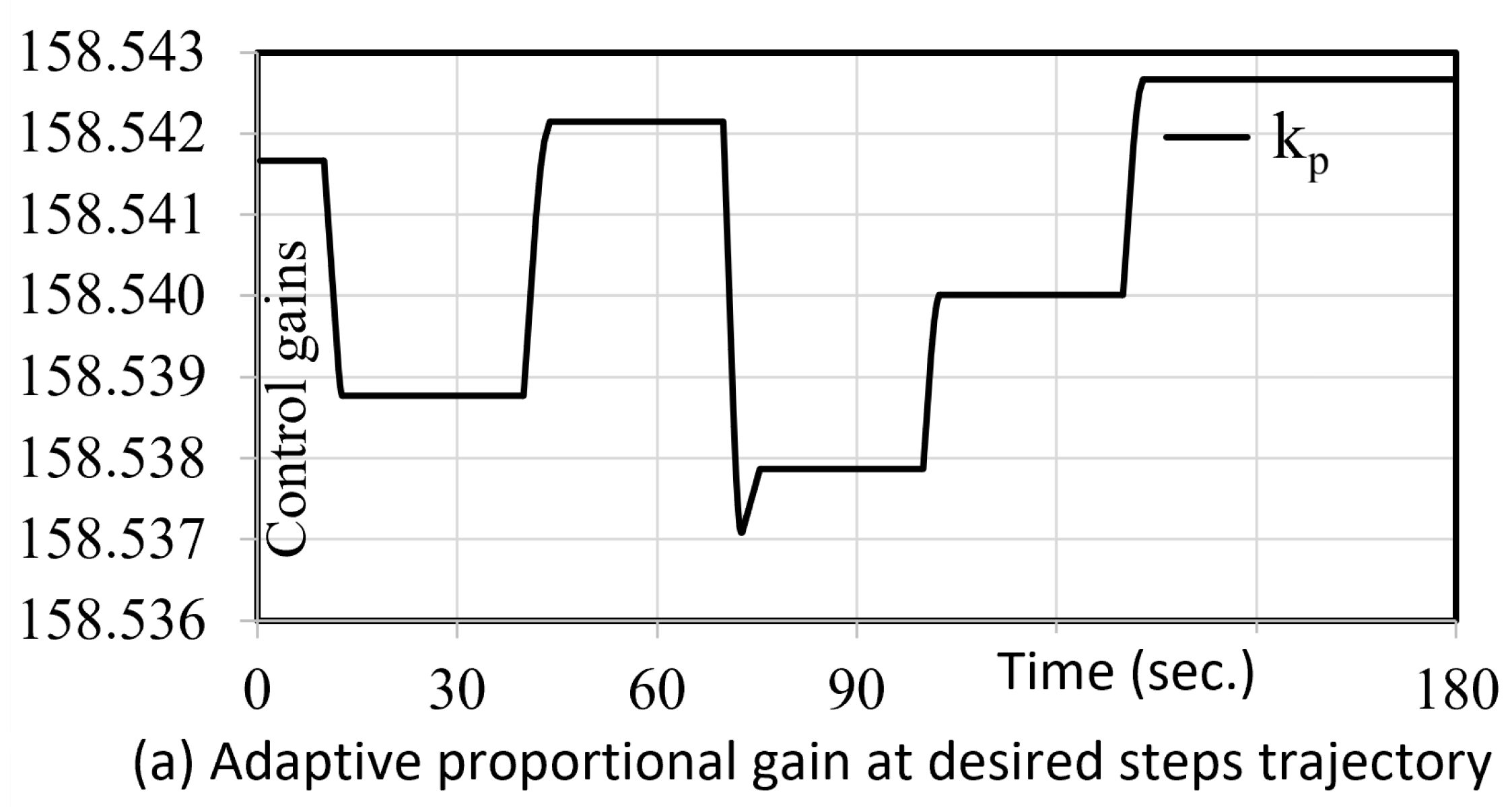
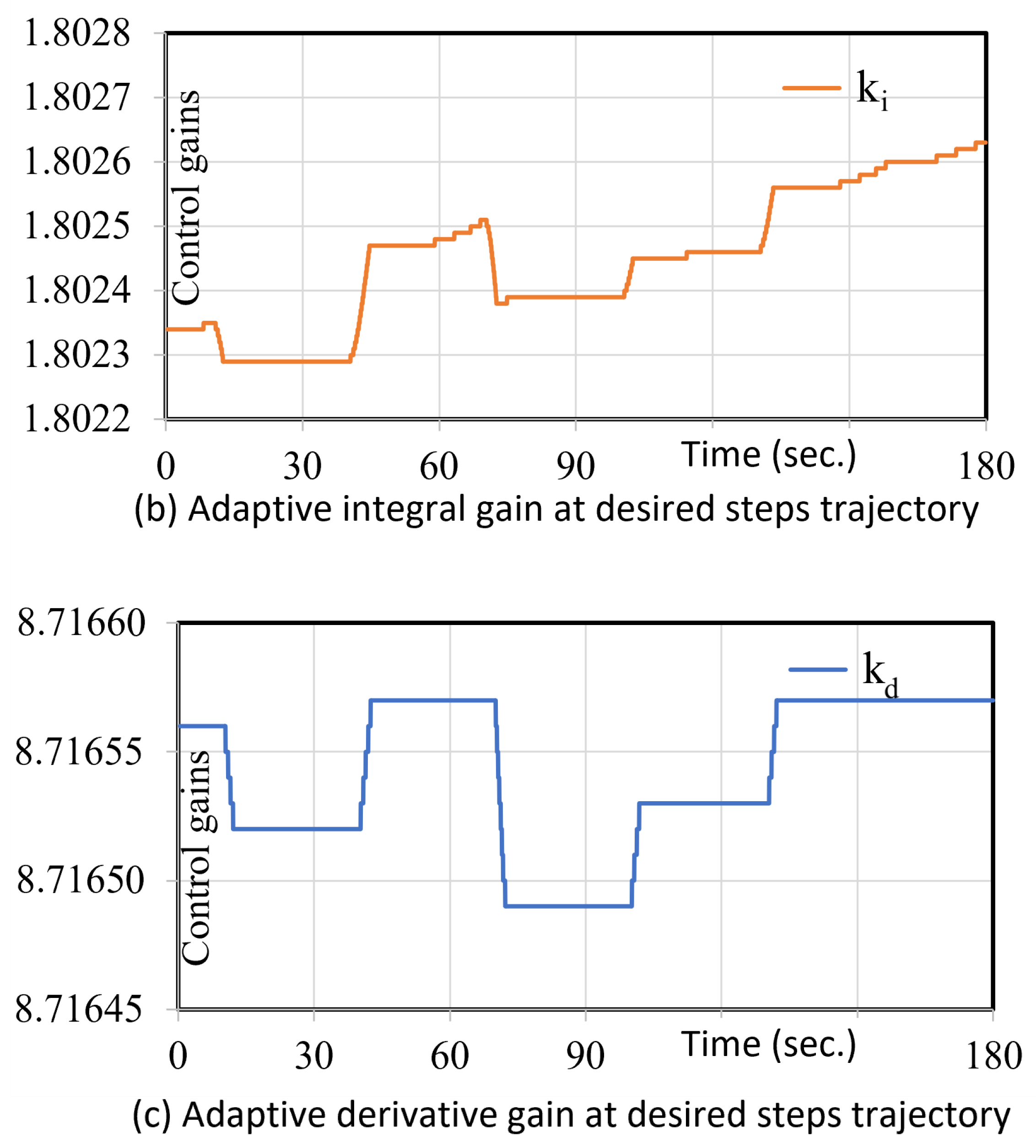
5.2. System Identification with Controller Tuning

In this section, the hip actuation system is characterized using transfer functions obtained through the MATLAB System Identification Toolbox.

Subsequently, the identified transfer functions serve to tune the PID controllers using MATLAB’s PID Tuning Toolbox. The procedure can be described as follows:

1.

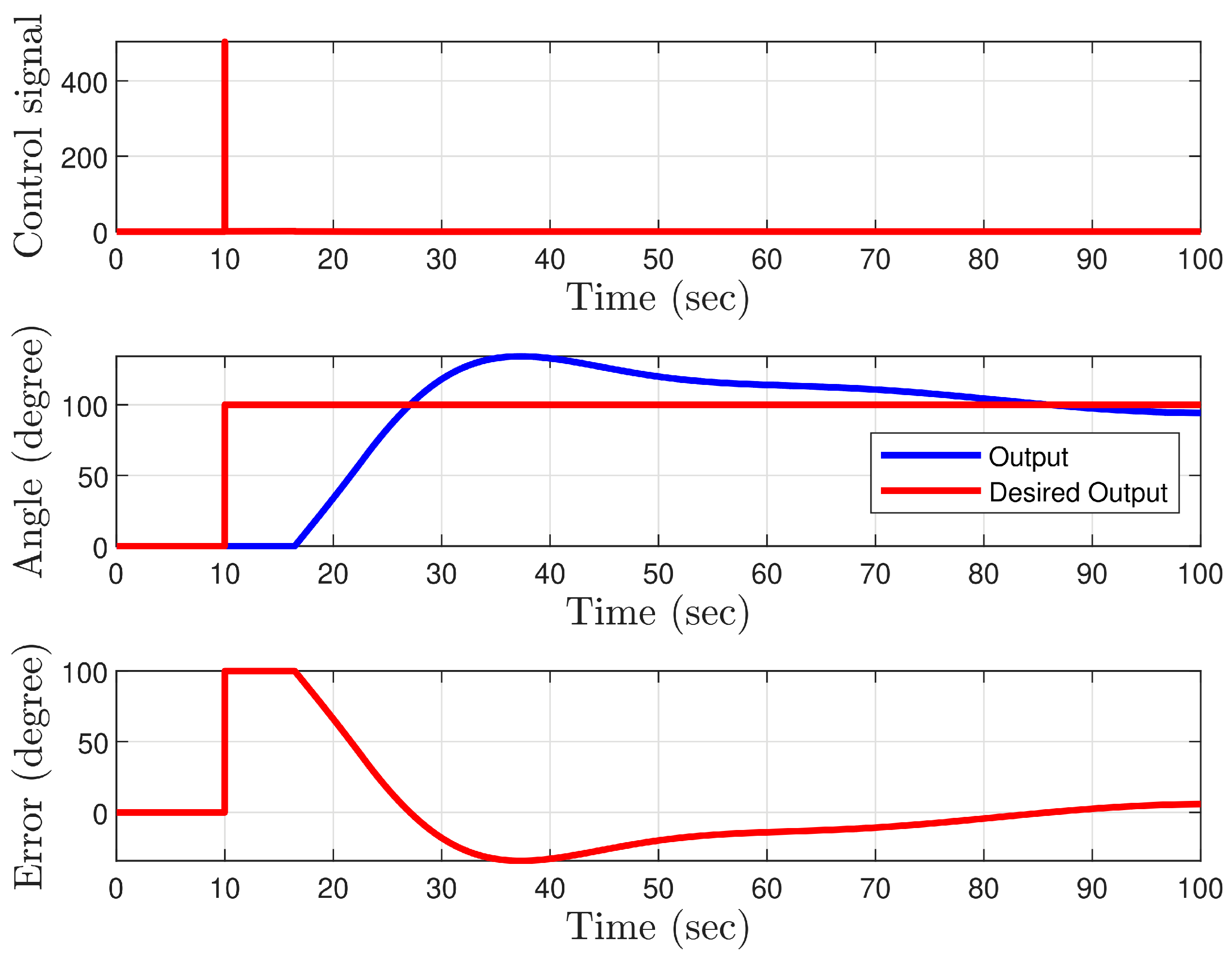
Initially, a step input was applied, causing the desired hip angle to shift from $0^{°}$ to ${100}^{°}$.

2.

Subsequently, with the flexion operation data (SMA springs group B active), we tested several transfer function structures using the System Identification Toolbox and compared the estimation fitness and prediction errors, as summarized in

Table 1. Hip flexion system identification.

Transfer Function Form	Fitness	Error
One pole with delay	81.4%	26.35
Two poles with delay	95.15%	1.08
Underdamped pair with delay	96.51%	0.93
Underdamped pair, real pole, delay	93.73%	3.04

.

3.

After several trials, the system was best represented by a transfer function with two poles and a time delay, achieving a fitness of $95.15\%$, which can be represented as follows:

$${\displaystyle \frac{648.2}{348.8s^2+37.35s+1}}\times e^{-6.46s}.$$

(16)

4.

Using this transfer function, we further fine-tuned the PID controller to enhance the system’s response time and transient behavior. The chosen PID gains for the controller were as follows: Proportional Gain ($K_p$) = 0.00518, Integral Gain ($K_i$) = 0.00001, Derivative Gain ($K_d$) = 0.05697. The simulation results with these PID gains yielded a rise time of $8.7$ s, a settling time of $56.8$ s, and an overshoot of $6.9\%$. These findings demonstrate the effectiveness of the tuned PID controller in achieving improved performance for the hip exoskeleton system.

5.

Then, with the extension operation data (SMA springs group A is active), we tested several transfer functions structure using the System Identification Toolbox and compared the estimation fitness and prediction errors, as summarized in

Table 2. Hip extension system identification.

Transfer Function Form	Fitness	Error
One pole with delay	47.13%	392.56
Two poles with delay	52.42%	319.52
Underdamped pair with delay	88.1%	19.99
Underdamped pair, real pole, delay	55.73%	282.086

.

6.

We chose the transfer function that had an underdamped pair and delay, with $88.1\%$ fitness:

$${\displaystyle \frac{0.003174}{281.2s^2+15.33s+1}}\times e^{-22.4s}.$$

(17)

7.

Accordingly, we tuned the PID controller to enhance both the system’s response time and the transient characteristics of the system. We used the PID gains: $K_p=120.3254$, $K_i=5.7343$, $K_d=631.2162$, and the simulation results: rise time = $39.3$ s, settling time 290 s, overshoot $8.15\%$.

8.

Then, we executed the control experiments, as described in the next section.

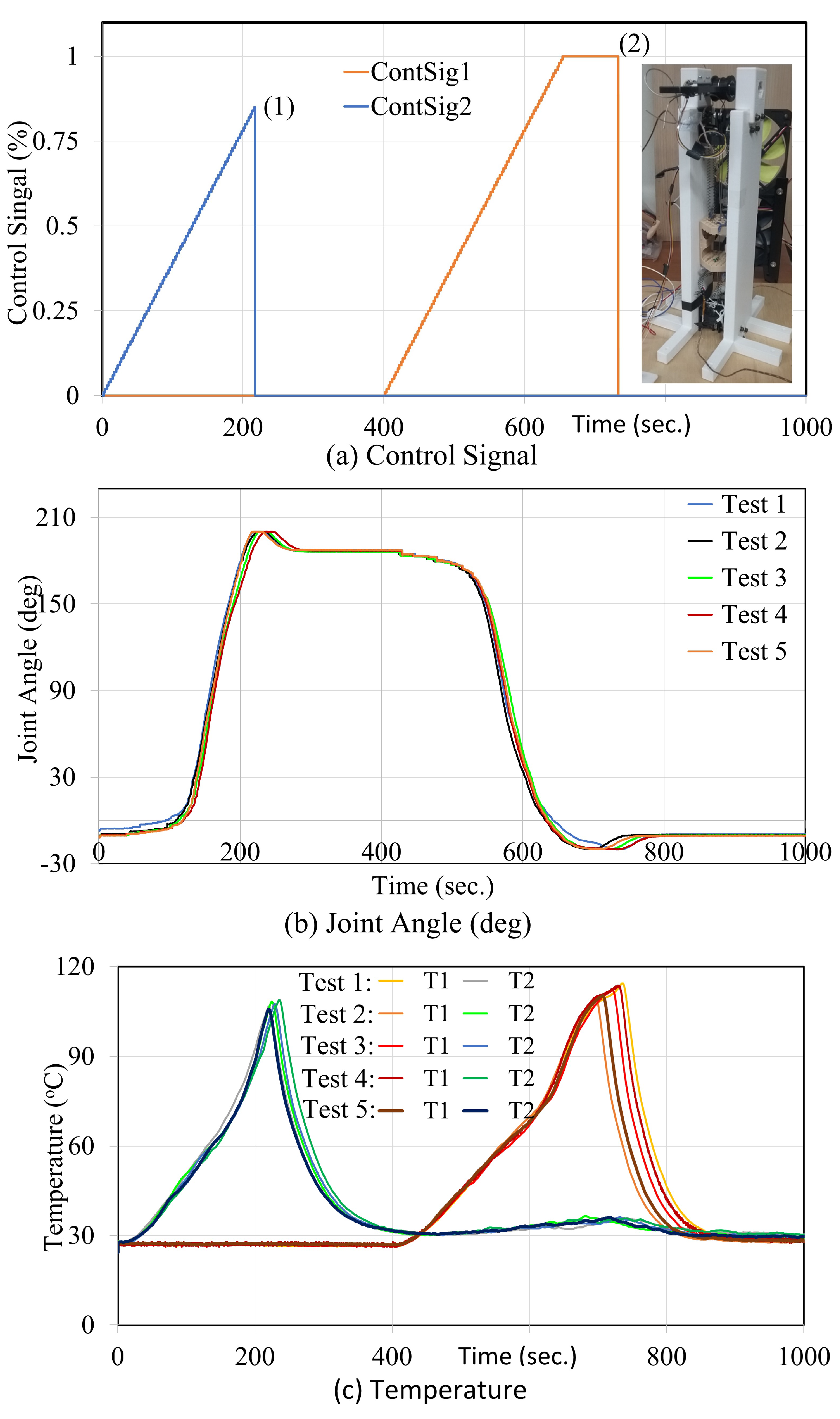
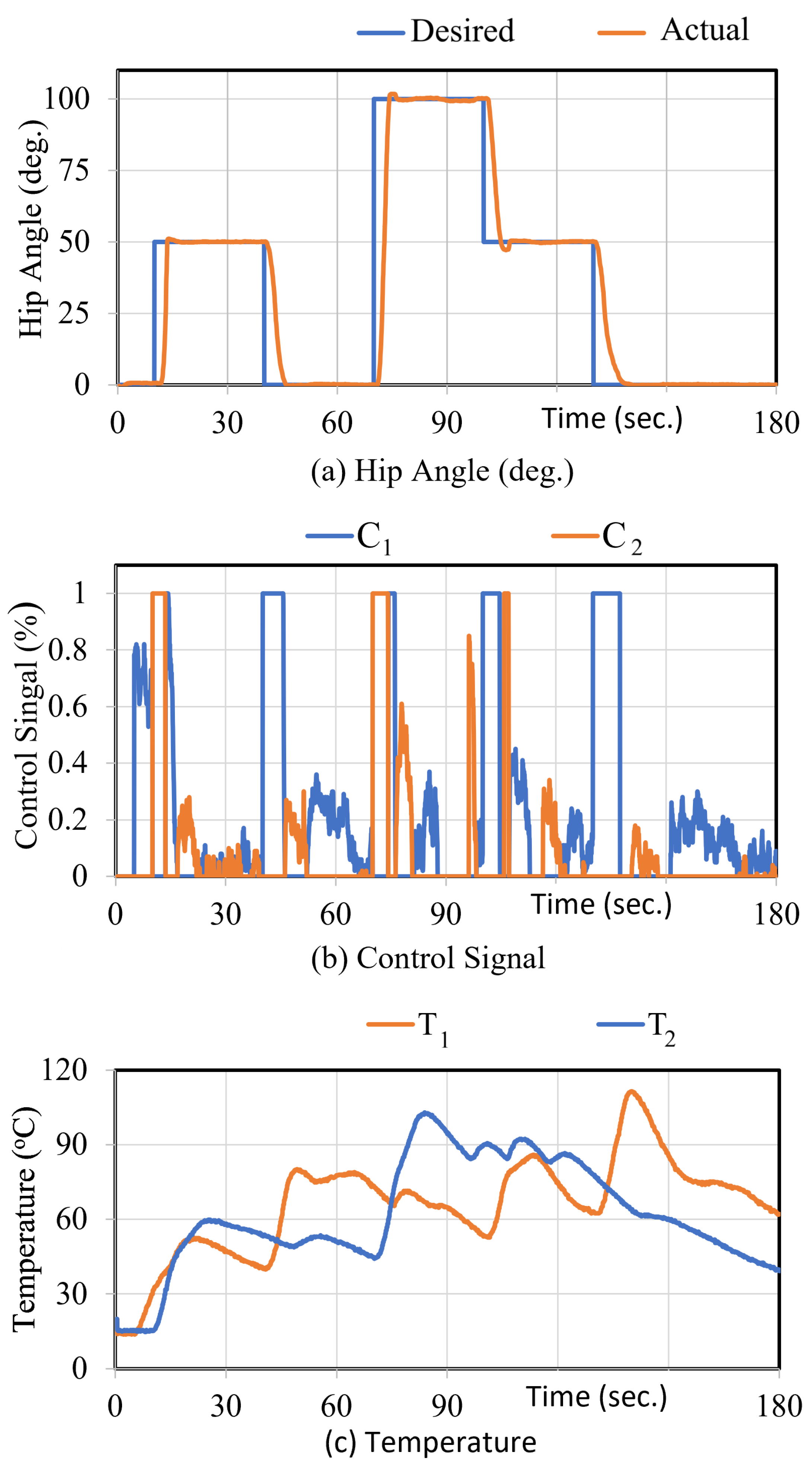
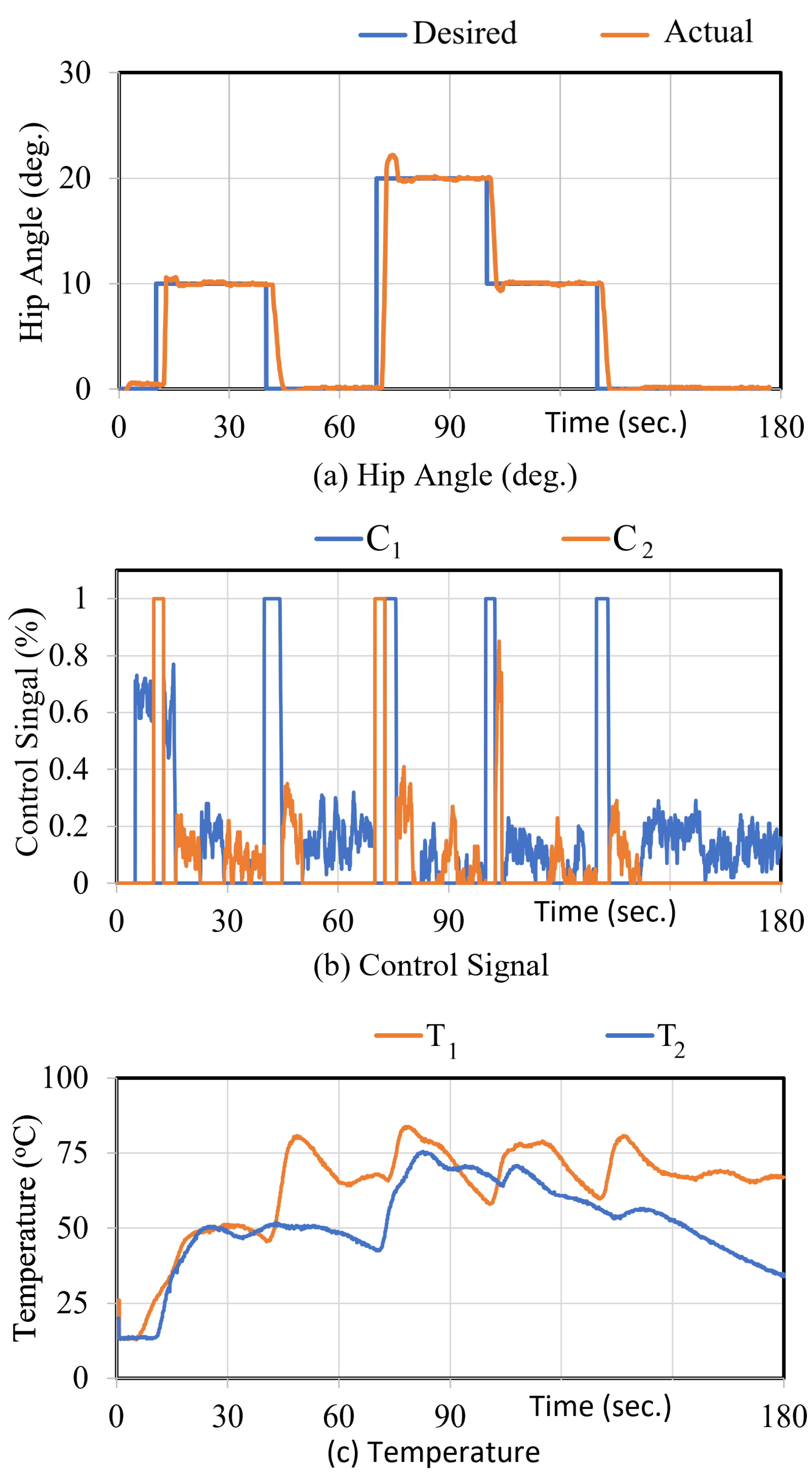
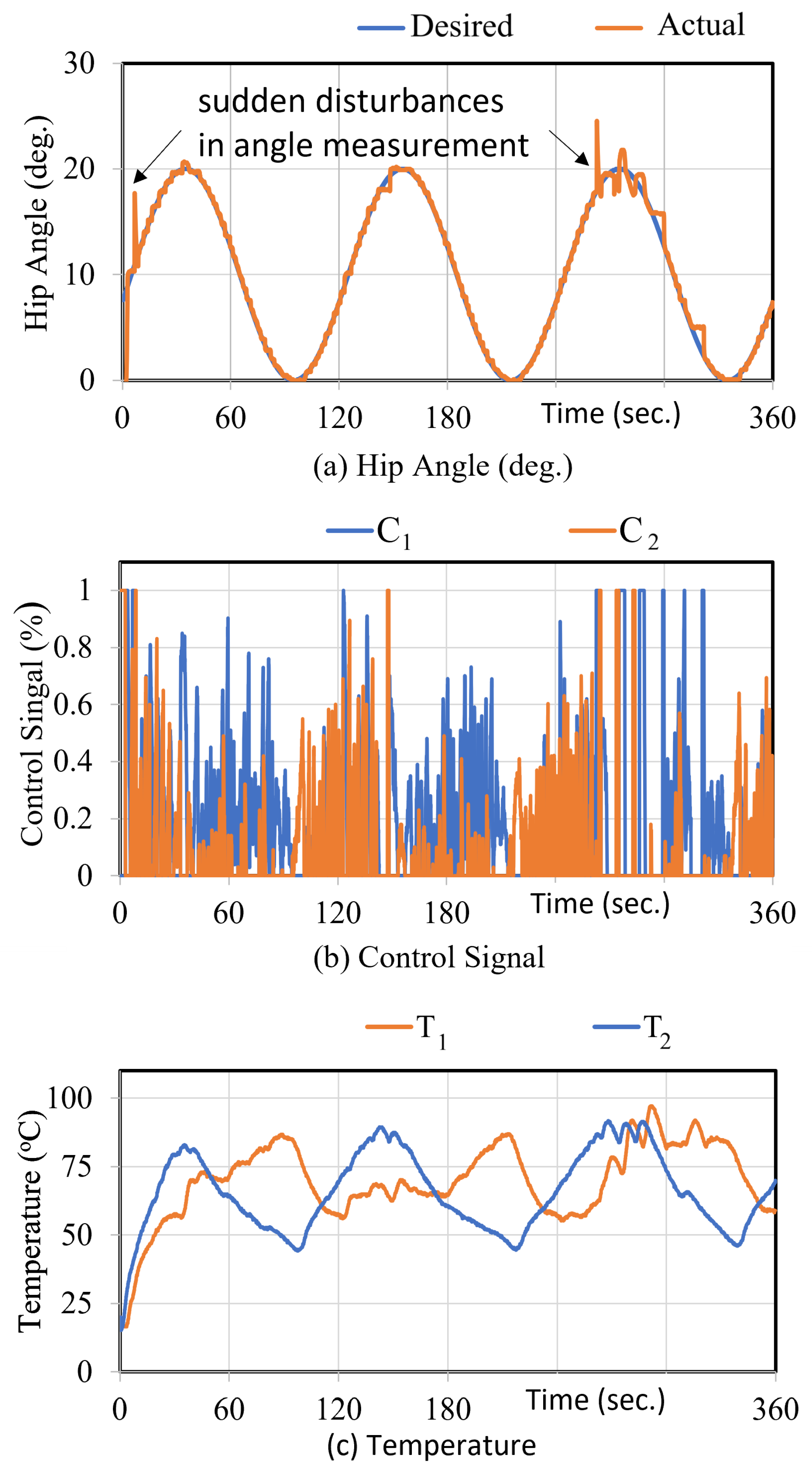
6. Experimental Results

6.1. Artificial Muscle Characterization

This subsection presents the thermo-mechanical experiments conducted to characterize the SMA springs, acting as bidirectional artificial muscles for the small-scale hip. The main target is to gain a clear understanding of the actuator’s capabilities, limitations, and performance.

The link angle is estimated by applying a Kalman filter that acquired the angle rate of change, as measured by the IMU. In addition, four thermocouples are attached on the SMA springs in both group A and group B using polyimide tape and fishing wire. These thermocouples have an important function in preventing overheating by monitoring the actuator’s thermal behavior. Moreover, a temperature estimation algorithm is presented in Section 5 in order to be utilized in case of thermocouple measurement failure.

In Figure 13, we depict the characterization experiments with gradual heating. These begin by applying a DC voltage of 10 V to the SMA springs: group B for flexion motion. Slowly, the average current is raised by increasing the Pulse Width Modulation (PWM). The current moving through the SMA springs causes heating. Hence, the temperature of the SMA springs gradually increases until it reaches a critical point of 120 °C (also the joint angle change). At this temperature, the joule heating stage is stopped, initiating the stage of ambient cooling. We monitor the temperature as it steadily decreases until it almost saturates at a time of 400 s.

After the characterization of group B, we proceed to group A, which consists of the extension SMA springs. The action is similar: we apply 10 V of voltage and incrementally adjust the PWM to achieve the electrical currents. Once again, we observe the temperature rise until it reaches 120 °C, after which, we stop the joule heating process. The ambient cooling stage allows the temperature to gradually return to a stable state, which happens at almost at 733 s. The heating and cooling cycles occurred in both SMA groups: B and A, resulting in the flexion and extension of the link angle. We repeated these experiments five times to ensure the consistency and reliability of the experimental findings.

Figure 13a shows the control signal as a slowly increasing input. Figure 13b shows the temperature of the SMA springs “group B” and “group A”, respectively, against time during the joule heating and ambient cooling, illustrating the actuator’s thermal behavior. Finally, Figure 13c shows the flexion and extension of the hip angle, increasing smoothly to the maximum flexion angle at 200° and returning again to the maximum extension angle at −20°.

6.2. Control Experimental Results

This section presents the experimental evaluation of the SMA-spring-based artificial muscles designed with a hexagonal architecture. The system performance is investigated applying an adaptive PID controller with both steps and sin wave trajectories as the input.

In a comparison between the PID control experiments, executed 10 months earlier [41], and Figure 14 (this work), more heating is required to reach the similar angle stroke. The temperature had to be higher to reach the same angle, which is unacceptable because it risks the SMA’s ability to retain its training characteristics, which are evaluated in Section 2 and Figure 13. To reduce the risk of SMA damage or more degradation (due to the problem of overheating, which reduces the SMA springs’ shape memorization and, hence, reduces the actuator stroke), we had to reduce the stroke range to ${20}^{°}$ in our further experiments and to tune the adaptive controller experimentally.

Figure 15 shows the experimental results of the adaptive controller, which start from the same gains ($k_p=0.621732\ast 255$, $k_i=0.007068\ast 255$, $k_d=0.0341826\ast 255$) and (${\gamma }_1=6.0\times {10}^{-6}$, ${\gamma }_2={10}^{-7}$, and ${\gamma }_3=5\times {10}^{-9}$). Figure 16 shows the adaptive gain changes through the experiments.

Then, we applied the sin trajectory as the desired input, as shown in Figure 17. It is noticed that the adaptive control can overcome disturbances in the angle measurements and the resulting root mean square error (RMSE) = $0.{94}^{°}$. Figure 18 shows the adaptive gains changes through the sin wave experiment.

To prevent overheating and ensure safe operation, the stroke range was intentionally reduced during the experiments. The excessive heating of Nitinol wires accelerates phase transformation fatigue, leading to microstructural degradation and reduced actuation lifespan. This limitation is particularly critical in wearable applications, where user safety and long-term reliability are essential. Maintaining the SMA temperature within a safe range (<100 °C) helps to preserve its shape memory properties and minimizes irreversible deformation. Future work will focus on enhancing thermal management through strategies such as active cooling and real-time temperature feedback to balance the stroke range, response speed, and durability.

7. Conclusions

A bi-directional artificial muscle was designed and fabricated using Shape Memory Alloy (SMA) springs to create a small-scale hip. The compact prototype can effectively support hip motion in both extension and flexion, with an angle range from $-{20}^{°}$ to ${200}^{°}$. Subsequently, thermo-mechanical characterization experiments were conducted to assess the performance of the SMA muscle in the entire motion range. These experiments yielded valuable insights into the behavior and capabilities of the SMA muscle, confirming its suitability for our exoskeleton design. System identification experiments were also carried out to determine an accurate transfer function, guiding the tuning of PID controllers for enhanced performance.

To ensure the safety of the SMA system, overheating should be prevented. Accurately measuring the temperature of a thin wire poses challenges, which we addressed by electrically isolating the thermocouple, attaching it to the thin SMA spring and utilizing two thermocouples to ensure reliable readings. Additionally, we developed a temperature estimation algorithm for the SMA spring, incorporating the heat transfer laws, as well as the measurement of the applied voltage and current.

To evaluate the controller capabilities, control experiments were executed for both stepping and sinusoidal trajectories. The exoskeleton successfully tracked the desired trajectory, showing its precision. In the stepping experiments, the delay time was $2.09$ s, the rise time was $2.51$ s, and the overshoot was $10.5\%$. Furthermore, system performance under adaptive control was investigated, revealing an RMSE of $0.94$ in the sinusoidal trajectory experiments. The adaptive control results indicate reliable disturbance rejection in the angle measurements.

The key contributions include (i) a dual antagonistic SMA spring design for hip actuation, (ii) a temperature estimation algorithm enhancing thermal safety, and (iii) adaptive PID control achieving accurate motion tracking. Although stroke reduction due to heating remains a limitation, these results provide a strong foundation for safe efficient SMA-based wearable systems. Future work will focus on forced cooling and long-term durability assessment.