A Framework of Designing Multi-Coil Electromagnetic System for 6-DOF Manipulation of Magnetic Miniature Robot

Abstract

Precise and programmable magnetic field control is essential for the reliable actuation of magnetic miniature robots in biomedical applications. However, the workspace of existing systems often relies on empirical designs and lacks a clear framework to define an entire workspace with independently controllable magnetic field strength, as well as precisely specified volume, shape, and position. Here, we present a rational design framework that systematically elucidates the fundamental principles governing the generation of uniform and gradient magnetic fields using spherically distributed magnetic coil arrays (SDMCAs). We first identify the eight independent parameters that fully define the magnetic field. Using both analytical and numerical methods, we demonstrate that the control of the magnetic field strength and gradient can be decoupled. This concept is then extended to three dimensions through the development of a finite element analysis (FEA) model, which accurately simulates the spatial magnetic field distribution of complex coil geometries. The simulation results are validated experimentally, showing excellent agreement. Finally, we propose a step-by-step SDMCA design workflow that enables precise control over the magnetic field parameters within a target workspace. This framework provides a practical and scalable approach for the development of high-performance magnetic actuation systems for miniature robots.

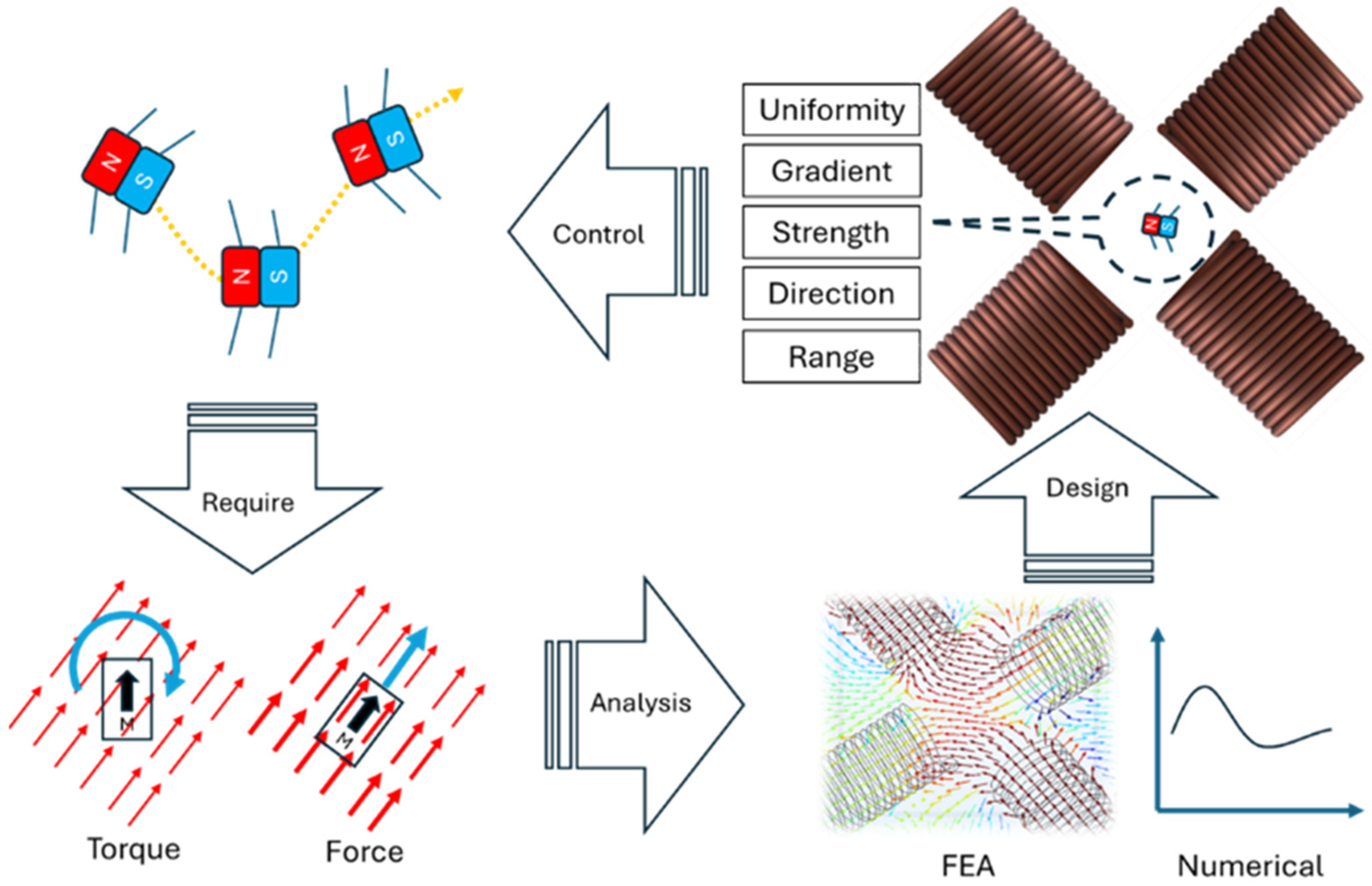
1. Introduction

Miniature robots, ranging from nanometers to sub-millimeters, have attracted significant attention across various research fields in recent years due to their unique ability to conduct tasks in complex or confined environments that are inaccessible to conventional large-scale robots [1,2,3]. This feature is particularly useful for biomedical applications such as non-invasive surgeries [4], in vivo diagnostics [5], drug delivery [6], and micro-implants [7], where tasks involve navigation through the intricate internal space of the human body. Micro-implants, in particular, enable localized and long-term therapeutic or sensing functions by integrating miniaturized structures with wireless actuation, power delivery, or signal transmission, thereby supporting chronic monitoring and site-specific intervention while minimizing surgical trauma and patient burden. Compared to traditional large-scale robots, the delicate maneuver of miniature robots reduces the risk of wound infection and tissue damage resulting from operations, thereby enhancing patient safety and comfort. A diverse range of actuation mechanisms have been employed to actuate these robots nowadays, typically including pneumatic [8], piezoelectric [9], thermal [10,11], and electrochemical actuation strategies. Pneumatic actuation employs pressurized air to inflate and deflate air chambers embedded in movable parts of the robot, thereby inducing deformation for locomotion; however, it requires complicated air pathways with airtight sealings and an external pressure source, posing challenges for the design, fabrication, and miniaturization, especially at sub-millimeter scales. The piezoelectric effect refers to the ability of a material to deform when subjected to an electric field, causing vibration, bending, and other motions well-suited for miniature robot actuation. However, piezoelectric robots often require relatively high driving voltages and substantial energy input, which typically necessitates a tethered external power supply and limits untethered operation. Although onboard batteries can be integrated, the operating duration is usually short and the added power electronics and packaging increase the overall size of the robot, making miniaturization more challenging. Thermal actuation exploits a temperature-induced shape-memory effect to actuate miniature robots. Although effective, the process usually suffers from a slow and irreversible response, necessitating an additional process to reset the shape. Electrochemical actuation leverages ion transport and redox-driven volume/strain changes in electroactive materials to generate bending or contraction under a low driving voltage [12]. By controlling ion insertion/extraction and associated osmotic swelling, electrochemical actuators can produce relatively large deformation with compliant, lightweight structures, which are attractive for soft miniature robots and potentially biocompatible applications. However, the actuation performance is strongly coupled to the electrochemical environment: it typically requires an electrolyte (liquid or gel) and stable electrode interfaces, and the response speed is often limited by ion diffusion and charge transport, especially as the device thickness increases. In addition, long-term operation may suffer from dehydration, electrochemical side reactions, and material fatigue, which can degrade the repeatability and lifetime.

The aforementioned actuation strategies often suffer from a slow response, low energy efficiency, or limited degree of freedom. Additionally, the actuators are usually embedded or adhered to the main body of the robot, resulting in relatively bulky designs that hinder their ability to navigate tight or tortuous environments such as blood vessels and bronchial branches. To address these limitations, magnetic actuation has emerged as a promising alternative approach. A magnetic field offers several distinct advantages that make it well-suited for manipulating miniature robots, especially inside complex and dynamic human body environments [13,14,15]. Most notably, a magnetic field allows the remote control of miniature robots without the need for physical contact, enabling deep tissue penetration and long-term operation inside the human body.

Magnetically responsive miniature robots are usually fabricated from polymers embedded with magnetic particles [16,17,18]. In typical designs, the robot body itself serves as an actuator, enabling the seamless integration of structures and functions within a highly compact design [5,19,20]. Additionally, a magnetic field can be precisely modulated in terms of the strength, direction, and gradient that allows 6 degrees of freedom (6-DOF) in robot control [21,22], enabling diverse locomotion such as the crawling, rotation, swimming, and manipulation of micro objects [6,23,24]. These capabilities of magnetic miniature robots are valuable for medical procedures requiring rapid and adaptive control, such as targeted drug delivery in physiological environments [25,26].

Despite these advantages, it remains a significant challenge to achieve the precise and predictable magnetic control of miniature robots. Existing magnetic control systems heavily rely on heuristic design and empirical tuning, resulting in suboptimal configuration with limited spatial control accuracy. Fundamentally, the motion of magnetic miniature robots is governed by the spatial and temporal characteristics of magnetic fields, which are commonly achieved by using either an electromagnetic system or a permanent magnet-based system [27,28]. A Helmholtz coil is a typical electromagnetic system widely used to produce a highly uniform magnetic field in the central region between two parallelly placed coils [29]. This uniform magnetic field is useful for inducing shape morphing-based locomotion, such as crawling through an inching mechanism [30,31]. However, the deformation induced by a uniform magnetic field is often unable to generate a strong enough force for magnetic miniature robots to overcome resistance in confined or obstructed regions of the body. In such scenarios, non-uniform magnetic fields with a well-defined gradient magnetic field are essential. Typically achieved using a multi-magnetic coil system, a gradient magnetic field generates sufficient actuation force to propel magnetic robots through complex environments or across biological barriers [32,33]. Electromagnetic multi-coil systems offer tunable magnetic fields by modulating the current inputs and coil configurations [34,35]. Although several coil systems have demonstrated systematic approaches to electromagnet configuration and control [36,37,38], these efforts typically focus on achieving the desired field characteristics at a single point within the workspace. In most cases, the exact position, shape, and volume of such a workspace are still defined through heuristic or trial-and-error methods. As a result, the generated magnetic field across the workspace often lacks consistent and well-characterized strength and direction. This highlights an unmet need for a comprehensive and systematic design methodology that enables the construction of workspaces with precise control over both the magnetic field strength and direction throughout the entire workspace.

In this study, we propose a comprehensive design framework for the rational design and implementation of an electromagnetic coil system tailored for the 6-DOF manipulation of a magnetic miniature robot (Figure 1). This study begins by elucidating the underlying principles governing the magnetic actuation of a magnetic miniature robot by identifying the key parameters critical for effective interactions between the magnetic field and the miniature robots. Next, both analytical and numerical methods are employed to characterize and visualize the distribution of the magnetic field, with a focus on field coupling and gradient control. Finally, we present the rational design framework by demonstrating how to design and optimize a magnetic workspace meeting specific operational requirements. This design framework provides a robust and intuitive guideline for designing electromagnetic coil-based actuation systems. In contrast to prior multi-coil electromagnetic systems that are often configured empirically or tuned via case-specific numerical optimization, this work establishes a requirement-driven and physically constrained design framework that explicitly links robot actuation objectives to the coil-generated magnetic environment. The key novelty lies in identifying a minimal set of independent magnetic field descriptors (three flux density components and five independent gradient components) and using them as the design and control targets, thereby enabling systematic workspace definition and decoupled regulation of the field magnitude and gradient. This transforms coil system development from an experience-based process into a reproducible methodology with clear design variables, constraints, and performance metrics. We believe this strategy offers valuable insights into the future development of next-generation magnetic miniature robots for a diverse range of high-precision biomedical and engineering applications.

2. Results and Discussion

Magnetic fields generated by electromagnetic coils are highly nonlinear, posing a significant challenge for the predictable and precise control of magnetic miniature robots, a prerequisite for achieving accurate deformation and locomotion in complex, confined, and dynamic environments. Therefore, a deep understanding of how magnetic fields interact with magnetic miniature robots is crucial to identifying the key parameters governing the actuation and robotic operation.

The defining characteristics of a magnetic field include its direction, magnitude, and spatial gradient. In a multi-coil electromagnetic system, the superposition and directional cancellation of magnetic fields play a significant role in defining these parameters. Additionally, factors specific to coil-based systems, such as coil geometric configuration and the magnitude of the input current, must also be taken into consideration when modulating the field characteristics. By mastering these parameters and their interactions, the magnetic field within a target workspace can be fully defined and accurately tailored to specific requirements.

Therefore, in this section, we first present a mathematic framework that fully defines the magnetic field and its gradients generated by electromagnetic coils, forming the theoretical foundation for the control of the magnetic field of a multi-coil system. We then employ both analytical and numerical methods to elucidate how specific electromagnetic coil configurations and input currents modulate uniform as well as gradient magnetic fields. This mathematical framework offers a powerful tool for the rational design and optimization of an electromagnetic coil-based miniature robotic actuation system.

2.1. Spherically Distributed Magnetic Coil Array

Generally, the magnetic field at a given point in three-dimensional space can be expressed as follows:

$$\mathit{B}=[B_x{,B}_y,B_z]$$

(1)

The magnetic gradient tensor B_gra is defined as follows:

$${\mathit{B}}_{\mathit{g}\mathit{r}\mathit{a}}=\left[\begin{array}{ccc}{\displaystyle \frac{\partial B_x}{\partial x}}& {\displaystyle \frac{\partial B_x}{\partial y}}& {\displaystyle \frac{\partial B_x}{\partial z}}\\ {\displaystyle \frac{\partial B_y}{\partial x}}& {\displaystyle \frac{\partial B_y}{\partial y}}& {\displaystyle \frac{\partial B_z}{\partial z}}\\ {\displaystyle \frac{\partial B_x}{\partial x}}& {\displaystyle \frac{\partial B_y}{\partial y}}& {\displaystyle \frac{\partial B_z}{\partial z}}\end{array}\right]$$

(2)

According to Maxwell equations, the magnetic field must satisfy the following:

$$\mathbf{\nabla }·\mathit{B}=\mathbf{0}$$

(3)

$$\nabla \times \mathit{B}={\mu }_0(\mathit{J}+{ϵ}_0{\displaystyle \frac{\mathbf{\partial }\mathit{E}}{\partial t}})$$

(4)

where μ₀ is the permeability of free space, ϵ₀ is the permittivity of free space, J is the current density, and ∂E/∂t is the time derivative of the electric field. These constraints imply that the magnetic environment at a point can be fully characterized by eight independent parameters: the three components of the magnetic flux density and five independent components of its spatial gradient. Together, these eight parameters are sufficient to describe the local magnetic field required for precise force and torque control in electromagnetic coil systems for magnetic miniature robotic manipulation. More details of the derivation can be found in Supplementary Material S1.

In nature, a magnetic field arises from a single permanent magnet or moving charges that typically exhibit highly nonlinear spatial distribution. Such nonlinearity is unsuitable for the actuation of magnetic miniature robots where precise and controllable magnetic fields are essential. To address this issue, tailored magnetic fields, either a uniform field or a field with a defined gradient, are generated by integrating multiple single-source magnetic fields arranged in specific spatial configurations.

An ideal uniform magnetic field maintains constant magnitude and direction across a designed workspace. In this case, the gradient of the uniform magnetic field is thus 0, with magnetic field lines aligning in parallel and equally spaced. In contrast, a gradient magnetic field exhibits a linear variation in magnitude along a specific direction, enabling controllable magnetic force generation. Both uniform and gradient magnetic fields are fundamental in various applications, such as charged particle dynamics, sensor calibration, and magnetic manipulation.

The two most widely used systems for generating controllable magnetic fields are the Helmholtz coil and a spherically distributed magnetic coil array (SDMCA). A Helmholtz coil consists of two identical coils placed symmetrically along a common axis, with a separation distance equal to the radius of the coil, a condition that ensures the generation of highly uniform magnetic fields. This configuration not only enhances the strength of the magnetic field but also cancels directional bias. While the Helmholtz coil provides a simple and effective way of generating uniform magnetic fields, it is highly sensitive to the separation distance between the coils, which limits the number of turns of the magnetic coil and the flux density to <10 mT. Additionally, due to the identical current input, a Helmholtz coil is unable to generate a magnetic gradient. Furthermore, due to the large coil size and compact configuration, the workspace of a Helmholtz coil is significantly limited. In contrast, an SDMCA consists of a set of coils distributed on a notional spherical surface surrounding the workspace. The superposition of magnetic fields from all the coils enables the generation of both uniform and gradient magnetic fields. The SDMCA can achieve customizable gradients, including zero-gradient uniform fields, by appropriately modulating the input current of each coil, thereby minimizing directional bias and offering a larger workspace. Notably, the Helmholtz coil is essentially a special case of an SDMCA, where the gradient of the magnetic field maintains zero due to the paired coil design.

To elucidate the control principle of an SDMCA, here, we consider a circular coil in a cartesian coordinate system (Figure 2a) and examine the magnetic field strength—magnetic flux density B_p at an arbitrary point along the center lines (X-axis) according to the Biot–Savart law:

$${\mathit{B}}_{\mathit{p}}={\displaystyle \frac{{\mu }_0}{4\pi }}{\int }_C{\displaystyle \frac{I{\mathit{d}}_{\mathit{l}}\times \mathit{r}}{{\left|\mathit{r}\right|}^3}}$$

(5)

where I is the current flowing through the coil, d_l is a vector along the current path C with its magnitude being the length of the differential element of the wire, and r is the displacement vector from the wire element to the observation point. The distribution of the magnetic flux density is mapped in the cartesian coordinates, and the origin of the X-axis is at the center between the paired coils. Therefore, along the X-axis, Equation (5) is simplified to the following:

$${\mathit{B}}_{\mathit{p}}={\displaystyle \frac{{\mu }_{0}NI{R}^2}{2{(x^2+R^2)}^{3/2}}}{\mathit{x}}_{\mathit{e}}$$

(6)

where N is the number of turns of the magnetic coil, R is the radius of the coil, and x is the position along the X-axis. Due to the symmetry of magnetic fields about the X-axis (Figure 2a), the gradient of the magnetic flux density is given by the first derivative of (6) the following:

$${\displaystyle \frac{{\mathit{d}\mathit{B}}_{\mathit{p}}}{{\mathit{d}}_{\mathit{x}}}}={\displaystyle \frac{-3{\mu }_0{NIR}^{2}x}{2{(x^2+R^2)}^{5/2}}}{\mathit{x}}_{\mathit{e}}$$

(7)

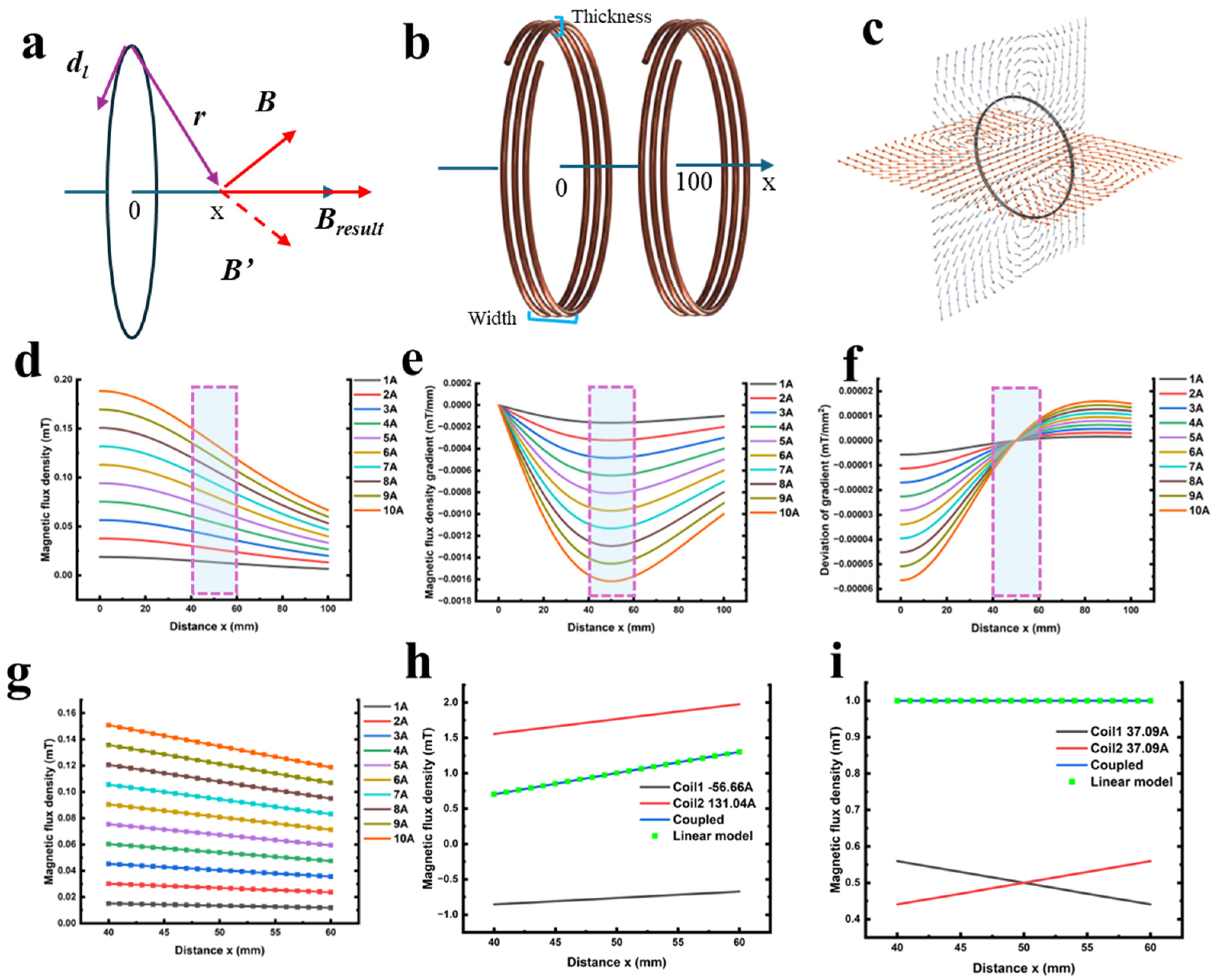
2.1.1. Generation of Gradient Magnetic Field

The magnetic field gradient arises from spatial variations in magnetic field strength. It governs magnetic forces acting on magnetic dipoles and charged particles, and is crucial for the magnetic actuation of miniature robots. Here, we consider a simplified example to illustrate the principle of magnetic field gradient generation by an SDMCA. The diameter of the coil is set to 200 mm with three turns to minimize the effect of the thickness and width (Figure 2b). Equations (6) and (7) are plotted for various input currents (Figure 2d,e). A transition region is observed where the gradient remains nearly constant around x = 50 mm, verified by analyzing the second derivative of Equation (6) (Figure 2f). Within x $\in$ [40, 60], the maximum deviation of the second derivative is <1.3 × 10⁻⁵ mT/mm², resulting in a linear region with a linearity coefficient of determination R² > 0.95. This region exhibits a nearly linear variation in magnetic flux density, and hence a constant magnetic gradient. Therefore, a second derivative <1.3 × 10⁻⁵ mT/mm² is set as the threshold that guarantees strong linearity. The magnetic gradient within this approximately linear region can be considered a constant regardless of the position x, and Equation (7) is simplified to the following:

$${\displaystyle \frac{{d\mathit{B}}_{\mathit{p}}}{d_x}}=CI{\mathit{x}}_{\mathit{e}} (x\in \mathrm{R})$$

(8)

Accordingly, the flux density described in Equation (6) can be approximated by the following:

$${\mathit{B}}_{\mathit{p}}=\left(CIx+b\right){\mathit{x}}_{\mathit{e}} (x\in \mathrm{R})$$

(9)

where C is the gradient at the center of the region R, and b is an integration constant determined at a reference point in workspace R. The magnetic flux density predicted by Equation (9) is shown as dots in Figure 2g. This linear approximation is verified by the theoretical values, with a goodness-of-fit R² > 0.99 across all the current inputs. Equation (8) indicates the magnetic gradient can be tuned by varying the input current. Nevertheless, the magnetic flux density is simultaneously determined by the current, meaning that the magnetic flux density and gradient cannot be decoupled with a single coil. To enable independent tuning of these two parameters, a second magnetic coil is placed along the X-axis (Figure 2b). The superimposed magnetic flux density and gradient are given by the following:

$${\mathit{B}}_{\mathit{c}\mathit{o}\mathit{u}\mathit{p}\mathit{l}\mathit{e}}={\displaystyle \frac{{\mu }_{0}N{R}^2}{2}}\left({\displaystyle \frac{I_1}{{\left(x^2+R^2\right)}^{\frac{3}{2}}}}+{\displaystyle \frac{I_2}{{({\left(0.1-x\right)}^2+R^2)}^{\frac{3}{2}}}}\right){\mathit{x}}_{\mathit{e}} (x\in \mathrm{R})$$

(10)

$${\displaystyle \frac{{d\mathit{B}}_{\mathit{c}\mathit{o}\mathit{u}\mathit{p}\mathit{l}\mathit{e}}}{d_x}}={(C}_1{I}_1+C_2{I}_2){\mathit{x}}_{\mathit{e}} (x\in \mathrm{R})$$

(11)

With two target values (magnetic flux density and its gradient) and two unknowns (I₁ and I₂) in the system formed by Equations (10) and (11), the system is fully solvable. The center position of workspace R is usually selected for easy calibration and control. Once I₁ and I₂ are determined, the resulting superimposed magnetic field is simplified to the following:

$${\mathit{B}}_{\mathit{c}\mathit{o}\mathit{u}\mathit{p}\mathit{l}\mathit{e}}=[\left(C_1{I}_1+C_2{I}_2\right)x+(b_1+b_2\left)\right]{\mathit{x}}_{\mathit{e}}$$

(12)

An example (Figure 2h) demonstrates this decoupled control of the magnetic flux density and gradient for the SDMCA configuration shown in Figure 2b. A magnetic gradient value of 0.03 mT/mm and a magnetic flux density of 1 mT at the center of the workspace R are achieved. The predicted profile given by Equation (12) matches well with the analytical results given by Equation (10), validating the decoupled control of the magnetic flux density and gradient via the linear approximation. For the special case of a uniform magnetic field wherein ${\displaystyle \frac{{d\mathit{B}}_{\mathit{p}}}{d_x}}=0$, the magnetic flux density calculated by Equation (10) is shown in Figure 2i, exhibiting a nearly constant value of 1 mT in the workspace R.

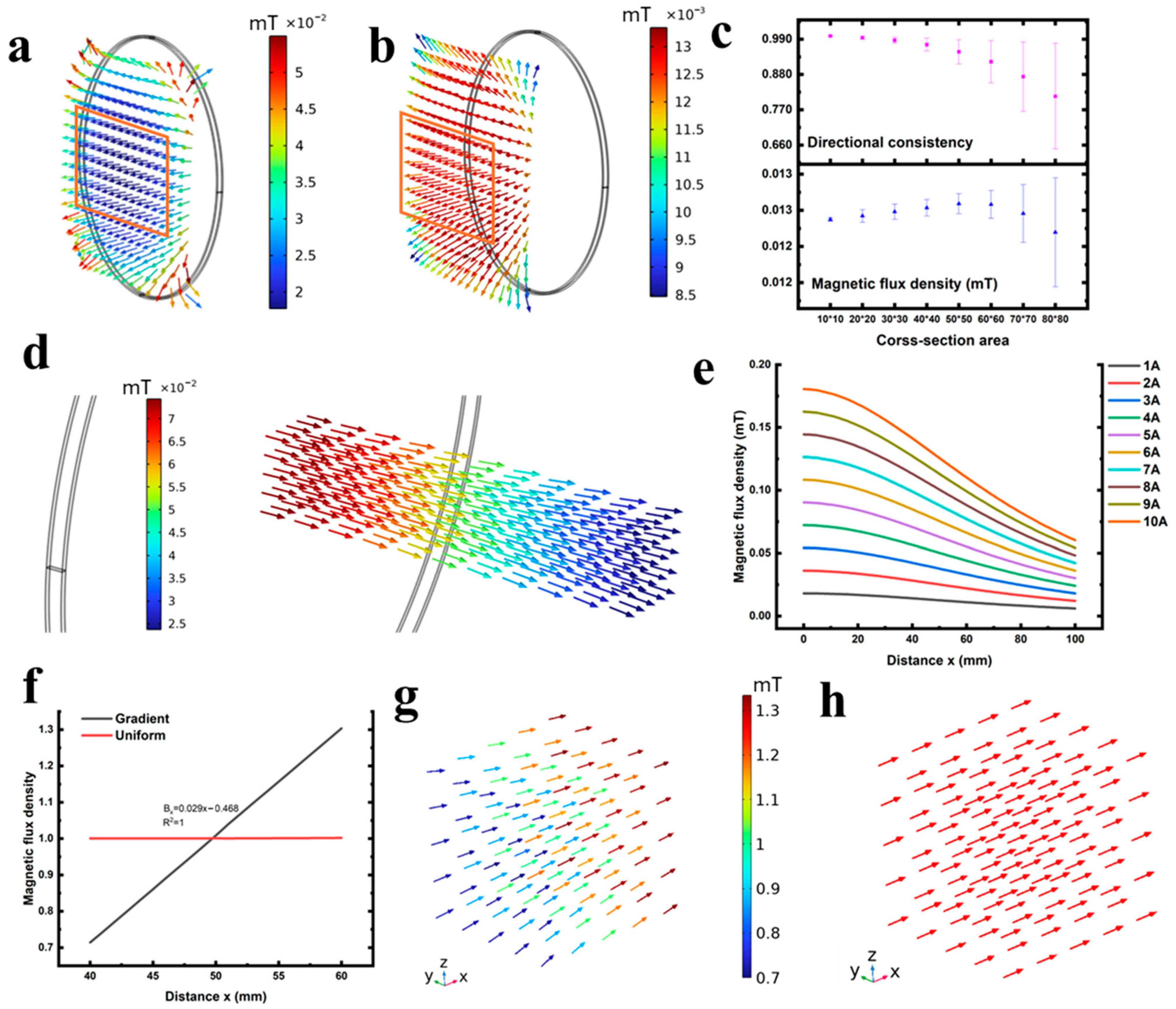
2.1.2. FEA Model

In Section 2.1.1, a simplified one-dimensional case was examined to elucidate the principle of the decoupled control of the magnetic flux density and its gradient along the X-axis. However, magnetic fields in a realistic system are more complex with three-dimensional vector components along the three principal axes of the cartesian coordinate system. Consequently, it is challenging to determine the magnetic flux density at arbitrary points by the analytical method presented above, especially for multi-coil configurations. To address this limitation, a finite element analysis (FEA) model was built by using COMSOL Multiphysics 6.0 to numerically compute the spatial distribution of the 3D magnetic field. The FEA model not only computes the magnitude of the magnetic flux intensity but also the direction, offering a comprehensive understanding of magnetic control by multi-coil systems. The static FEA model is based on the Equation (3) with the magnetic flux density B constrained by

$$\nabla ·(\mathit{H}+\mathit{M})=\mathbf{0}$$

(13)

H can be decomposed into external and internal components. The external component H_ext is induced by the electric current flowing through the coil, while the internal component H_int results from magnetic potential in response to the external magnetic field, also referred to as the intrinsic magnetization of the magnetic material, which can be expressed as ${\mathit{H}}_{\mathit{i}\mathit{n}\mathit{t}}=-\nabla \phi$, where φ is the potential function. Substituting into Equation (13) gives the following:

$$\nabla ·\left({\mathit{H}}_{\mathit{e}\mathit{x}\mathit{t}}-\nabla \phi +\mathit{M}\right)=0$$

(14)

In our model, the boundary conditions are given by specifying H_ext and M, where $\mathit{M}=\mathbf{0}$ in the absence of iron core of the electromagnetic coil, and H_ext is defined by the following:

$${\mathit{H}}_{\mathit{e}\mathit{x}\mathit{t}}={\displaystyle \frac{NI}{L}}\mathit{Z}$$

(15)

where N is the number of turns of the magnetic coil, I is the current flowing through the coil, L is the length of the coil, and z is the unit vector along the axis of the coil. Solving Equation (14) numerically by the Newton–Raphson method, we obtain H_int and further compute the distribution of magnetic flux density B according to Equation (13). Figure 2c shows the FEA results of a single coil, confirming the expected closed magnetic flux loops predicted by Equation (5). The cross-sectional views of the magnetic coil (Figure 3a,b) reveal a central region where both the direction and magnitude of the magnetic flux density remain nearly uniform. In contrast, regions further from the center show increasing distortion. In practical magnetic control systems for magnetic miniature robot actuation, it is usually challenging to achieve a perfect uniform magnetic field. Magnetic field strength is typically applied in discrete steps, e.g., 1 mT, 3 mT, or 10 mT, with limited precision beyond the first decimal. Based on this practice, we define a magnetic field as uniform if its local deviation from the target value does not exceed ±0.5 mT. For example, if the target magnetic field is 10 mT, a field ranging from 9.5 mT to 10.5 mT is considered to have acceptable uniformity, consistent with the practical resolution and control tolerance of typical systems. Another important characteristic of a uniform magnetic field is directional consistency, which is defined by the three components (X, Y, Z) of the unit vector at each point. To evaluate the consistency of the magnetic field direction within a target workspace, we compute the dot product between the unit vector of the magnetic field at each point and a predefined target direction vector. A dot product of 1 indicates perfect alignment with the target direction, while lower values imply angular deviation. In this study, we define directional uniformity as having an average product greater than 0.985. This threshold ensures that the maximum directional deviation falls within 10° relative to the target direction. The choice of this threshold is set based on an acceptable lag angle—the angular discrepancy between the magnetic moment of a miniature robot and the applied actuation magnetic field. A lag angle below 10° generally does not result in sufficient torque to significantly affect the control of robots, especially for robots with small magnetic moments. According to the above criterion, the uniformity of the magnetic field across the cross-sectional area along the coil’s long axis is validated (Figure 3c). For the coils used in this study, the uniform region is approximately 20 × 20 mm², with a directional consistency of 0.994 and an average magnetic flux density of 0.012 mT. The magnetic flux density around the central axis of the coil (Figure 3d,e) closely matches the theoretical analysis shown in Figure 2d. Following the decoupling strategy discussed in Section 2.1.1, a gradient magnetic field (0.03 mT/mm) and uniform magnetic field (1 mT) using a paired coil configuration are predicted (Figure 3f). The results obtained from the analytical method (Figure 2h,i) and FEA (Figure 3f) with the same current input show excellent agreement, further confirming the robustness and accuracy of both models. Additionally, the FEA results forecast a workspace with a highly consistent magnetic gradient around the center region (X ∈ [40 mm, 60 mm], Y ∈ [−10 mm, 10 mm], Z ∈ [−10 mm, 10 mm]) between the coils (Figure 3g,h).

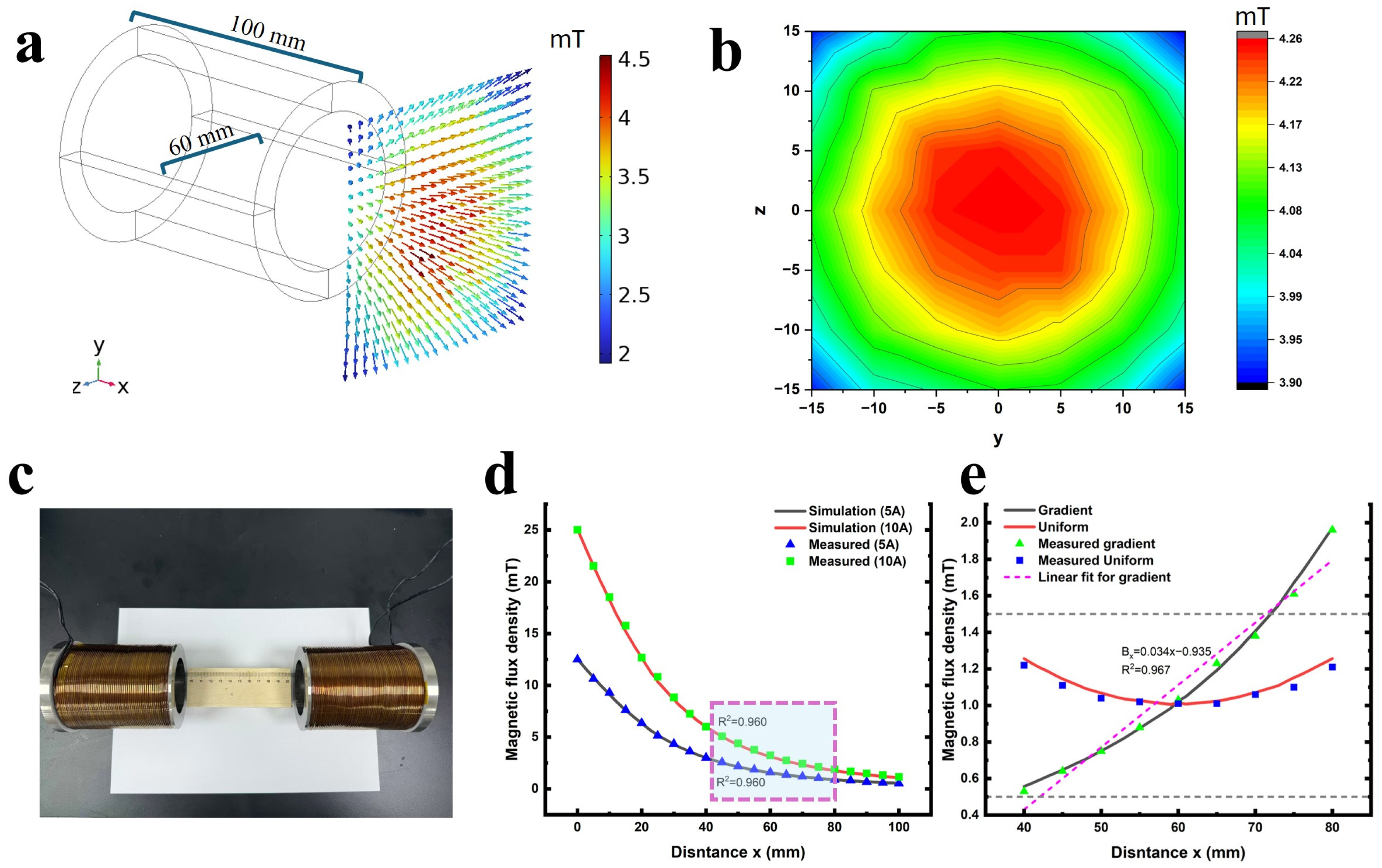
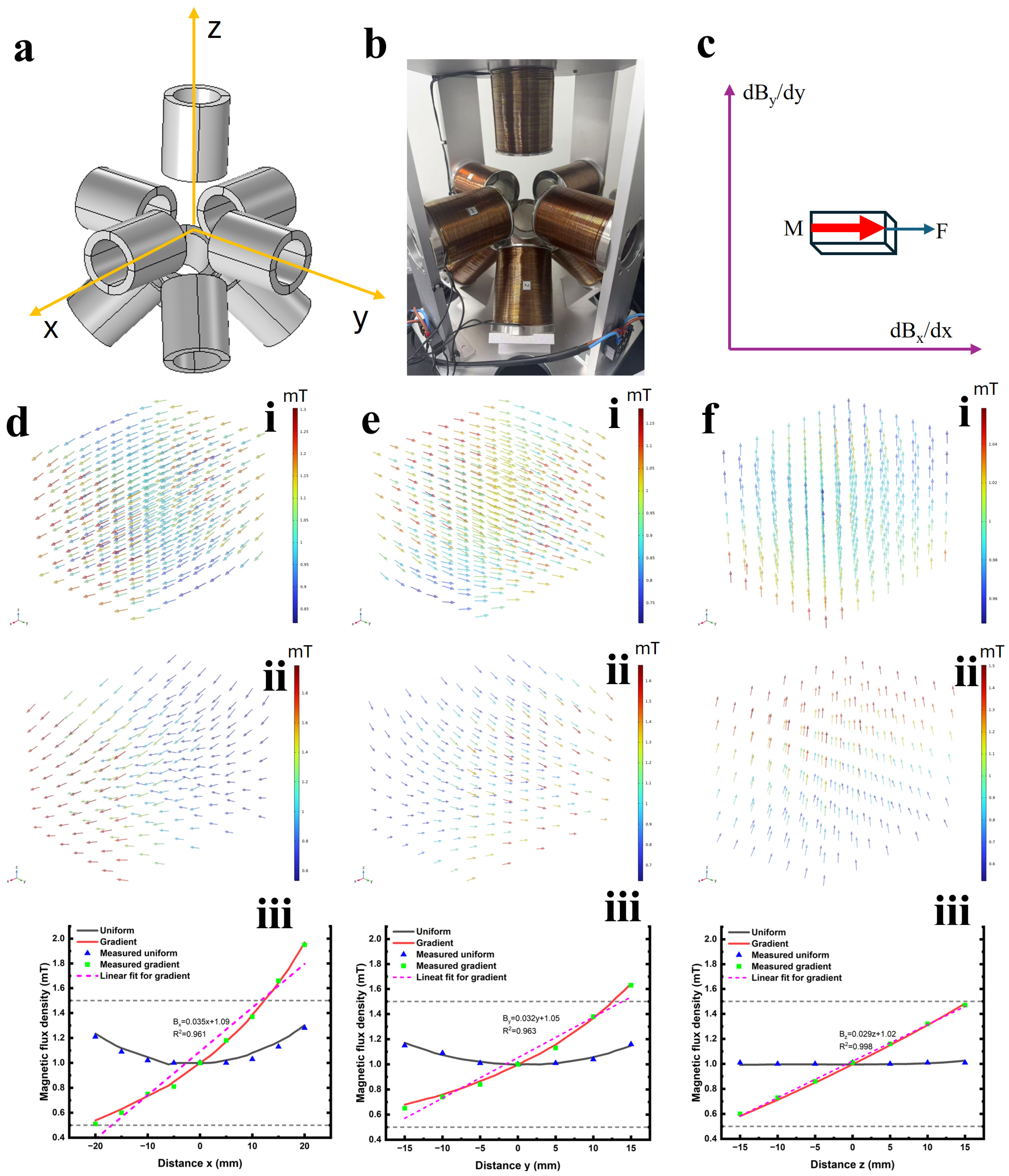
2.2. Validation

While a simplified coil with only three turns was used in Section 2.1 to elucidate the underlying principle of magnetic field control, practical applications typical employ coils with a significantly larger number of turns to generate stronger field strength and larger spatial coverage (Figure 4c). To validate the applicability of the analytical framework and FEA model proposed above under realistic conditions, we simulated and experimentally verified the magnetic field distribution of a coil with 430 turns, 100 mm width, 60 mm inner diameter, and 1.5 mm wire diameter. The FEA simulation of a cross-section at a distance of 50 mm perpendicular to the coil axis (Figure 4a) reveals a region of a nearly uniform magnetic field, consistent with the analytical prediction discussed in Section 2.1.1. The experimental measurements (Figure 4b) agree closely with the simulation results within the region at x = 50 mm, Y ∈ [–15 mm, 15 mm], and Z ∈ [–15 mm, 15 mm]. Further comparison between the simulated and measured results in the same region under various input currents (Figure 4d) reveals that both exhibit a nearly constant magnetic field gradient within the region X ∈ [40 mm, 80 mm], with a linear coefficient of determination R² is 0.96 in both cases.

Using the two-coil configuration shown in Figure 4c, we successfully generated a gradient magnetic field (0.03 mT/mm) and a uniform magnetic field (1 mT) (Figure 4e) based on the methods described in Section 2.1.1. Compared to the simplified case with only three turns (Figure 3f), the real-world high-turn coil shows slightly more distortion due to the complex geometric configuration. Nevertheless, the overall magnetic field profile still closely matches the theoretical expectations, validating the feasibility and robustness of the proposed design framework for an SDMCA.

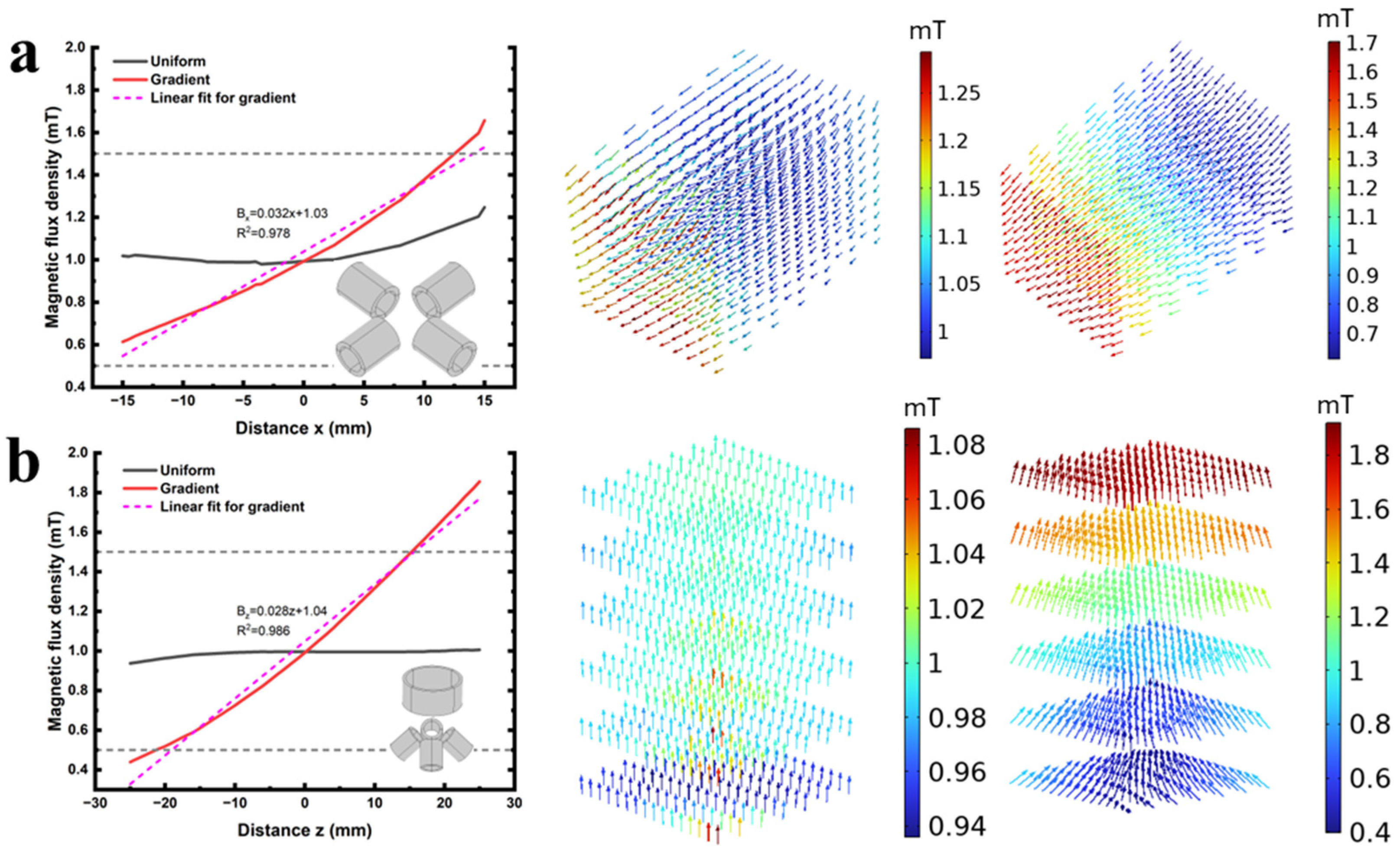
2.3. Generalization in Multi-Dimensional Space

In previous sections, we have successfully demonstrated the one-dimensional independent control of both the magnetic flux density and its gradient (B_x and ∂Bx/∂x) using a two-coil system. As discussed in Section 2.1, a total of eight parameters are required to fully define a magnetic field in three-dimensional space. And therefore, a minimum of eight independently controlled coils are required for full-field control. According to Equations (10) and (11), tuning the magnetic field and its gradient at the central point of the workspace R is sufficient to control the magnetic field within the entire workspace. So, Equations (10) and (11) can be expressed in matrix form as follows:

$$\left[\begin{array}{c}{\mathit{B}}_{\mathit{c}\mathit{o}\mathit{u}\mathit{p}\mathit{l}\mathit{e}}\\ {\displaystyle \frac{{\mathit{d}\mathit{B}}_{\mathit{c}\mathit{o}\mathit{u}\mathit{p}\mathit{l}\mathit{e}}}{{\mathit{d}}_{\mathit{x}}}}\end{array}\right]=\left[\begin{array}{cc}{A}_1& A_2\\ C_1& C_2\end{array}\right]\left[\begin{array}{c}{I}_1\\ I_2\end{array}\right]$$

(16)

In a more generalized three-dimensional case with eight parameters, Equation (16) can be extended to the following:

$$\left[\begin{array}{c}{\mathit{B}}_{\mathit{x}}\\ {\mathit{B}}_{\mathit{y}}\\ \begin{array}{c}{\mathit{B}}_{\mathit{z}}\\ {\displaystyle \frac{\mathbf{\partial }{\mathit{B}}_{\mathit{x}}}{\mathbf{\partial }\mathit{x}}}\\ \begin{array}{c}{\displaystyle \frac{\mathbf{\partial }{\mathit{B}}_{\mathit{y}}}{\mathbf{\partial }\mathit{y}}}\\ {\displaystyle \frac{\mathbf{\partial }{\mathit{B}}_{\mathit{z}}}{\mathbf{\partial }\mathit{y}}}\\ \begin{array}{c}{\displaystyle \frac{\mathbf{\partial }{\mathit{B}}_{\mathit{x}}}{\mathbf{\partial }\mathit{z}}}\\ {\displaystyle \frac{\mathbf{\partial }{\mathit{B}}_{\mathit{y}}}{\mathbf{\partial }\mathit{x}}}\end{array}\end{array}\end{array}\end{array}\right]=\left[\begin{array}{cccccccc}{A}_{11}& A_{12}& A_{13}& A_{14}& A_{15}& A_{16}& A_{17}& A_{18}\\ A_{21}& A_{22}& A_{23}& A_{24}& A_{25}& A_{26}& A_{27}& A_{28}\\ A_{31}& A_{32}& A_{33}& A_{34}& A_{35}& A_{36}& A_{37}& A_{38}\\ C_{11}& C_{12}& C_{13}& C_{14}& C_{15}& C_{16}& C_{17}& C_{18}\\ C_{21}& C_{22}& C_{23}& C_{24}& C_{25}& C_{26}& C_{27}& C_{28}\\ C_{31}& C_{32}& C_{33}& C_{34}& C_{35}& C_{36}& C_{37}& C_{38}\\ C_{41}& C_{42}& C_{43}& C_{44}& C_{45}& C_{46}& C_{47}& C_{48}\\ C_{51}& C_{52}& C_{53}& C_{54}& C_{55}& C_{56}& C_{57}& C_{58}\end{array}\right]\left[\begin{array}{c}{I}_1\\ I_2\\ \begin{array}{c}{I}_3\\ I_4\\ \begin{array}{c}{I}_5\\ I_6\\ \begin{array}{c}{I}_7\\ I_8\end{array}\end{array}\end{array}\end{array}\right]$$

(17)

Once the coil configuration is fixed, matrices [A] and [C] can be calibrated experimentally by sequentially setting the current of each coil to 1 A and measuring the corresponding magnetic flux density and gradient at the center of the workspace R. Once a desired magnetic field [B] in the left side of Equation (17) is specified, the input currents for each coil can be determined by solving the matrix equation. SDMCA systems typically employ more than eight coils forming an underdetermined system that prevents excessive current in any coil. By solving this system using the pseudo-inverse method, the overall coil currents are minimized, which reduces spatial variation to enhance magnetic field uniformity and gradient linearity within the workspace. The additional coils simply expand the dimension of the matrix in (17), resulting in an underdetermined system with enhanced control precision and robustness.

2.4. Workflow for Designing SDMCA with a Specified Workspace

Despite the wide adoption of SDMCAs for the manipulation of magnetic miniature robots, few studies have systematically designed the coil system to precisely define the effective workspace of SDMCAs. Conventional designs often rely on trial and error, leading to uncertainties in key parameters such as the number of coil turns, coil diameter, and overall spatial configuration. This heuristic design approach requires iterative adjustment and frequently leads to suboptimal magnetic field characteristics, thereby compromising control accuracy. In contrast, the design strategy proposed in this study enables the systematic optimization of coil parameters and spatial configurations, with the capability of visualizing the magnetic field within the effective workspace. The design workflow consists of the following key steps:

a.

Definition of the target workspace

The first step involves specifying the spatial dimensions of the target workspace (height × length × width) and defining the required magnetic field parameters, including the acceptable range of the field magnitude and gradient, to ensure the reliable and precise actuation of a magnetic miniature robot.

b.

Design of individual electromagnetic coil

Using the FEA model for a single coil developed in Section 2.1, coil parameters such as inner and outer diameters, number of turns, and wire diameter are swept to identify configurations that produce a region with a nearly constant field gradient that matches the target workspace. The key design objective is to maximize the field uniformity and gradient linearity while minimizing the current to reduce Joule heating.

c.

Optimization of the coil array configuration

The full coil array is then analyzed with the FEA model by placing multiple coils on a notional spherical surface surrounding the workspace. The orientations and spatial locations of the coils are adjusted to maximize the uniformity and gradient linearity within the workspace. Practical constraints, such as hardware limitations and available space, are incorporated into this optimization process.

d.

Calibration of the coil system

Once the SDMCA configuration is finalized, each coil is energized sequentially with a 1-A current. The resulting magnetic flux density and gradient at the center of the workspace are measured to experimentally calibrate the characteristic matrices [A] and [C] introduced in (23), which are required for the real-time decoupled control of the magnetic field and gradient.

2.5. Demonstration of a Nine-Coil SDMCA for Full-Field Control

Following the design workflow, we constructed a nine-coil SDMCA enclosing a 30 × 30 × 40 mm³ workspace (Figure 5a,b) with a maximum uniform field of 40 mT and a magnetic gradient of 1 mT/mm. Each coil has 430 turns, a width of 100 mm, an inner diameter of 60 mm, and is wound using 1.5 mm wire. The coils are mounted on a notional spherical shell with a diameter of 120 mm, and each coil is independently powered by a custom-built current regulation system capable of supplying currents between −20 A and 20 A that enables simultaneous current control across all coils. Figure 5d–f(i) show the FEA simulations of a 1 mT uniform magnetic field along the x-, y-, and z-axes, with directional consistency exceeding 0.985 across all sampled points. Experimental measurements using the same input currents confirm strong agreement with the simulations (Figure 5d–f(iii)). The maximum absolute difference between the simulated and measured magnetic flux density/gradient at the sampled points is 0.04 mT, which is sufficiently small that the simulated and experimental curves largely overlap. In addition, the linear fitting of the measured gradients along the x, y, and z directions yields R² values exceeding 0.96, indicating good linearity. Collectively, these results validate the accuracy and robustness of the design framework.

As the coil current approaches 20 A, active cooling becomes necessary to mitigate Joule heating. Therefore, a forced-air cooling system is employed, and the corresponding continuous-operation limits and duty cycle constraints are specified to ensure safe and reliable operation. In our setup, each coil is equipped with a high-speed fan to enhance convective heat dissipation, and each programmable DC power supply is rated to sustain up to 30 A with an embedded cooling system. Based on thermal monitoring during operation, the system can operate continuously at 15 A per coil with active cooling while maintaining the coil temperature below 80 °C. For operating conditions requiring higher currents (>15 A per coil), we limit continuous operation to within 5 min to prevent excessive Joule heating and potential insulation degradation. In addition, the coils are air core; therefore, magnetic saturation of the coil itself is not a limiting factor.

To demonstrate precise field control, a rigid magnetic block magnetized along its long axis (Figure 6a(i)) was actuated within the workspace. Under a 30 mT uniform magnetic field generated by the nine-coil SDMCA, precise control of the block’s rotation about the z-axis was realized (Figure 6a), with the full rotational motion about the principal axes shown in Supplementary Video S1. Additionally, the SDMCA enabled the locomotion of a magnetic soft miniature robot along a specific direction (Figure 6b,c, and Supplementary Video S2). The proposed SDMCA also generated a gradient field of 0.03 mT/mm along each axis (Figure 5d–f(ii)) with a direction consistency slightly below the uniformity threshold of 0.985. This limitation arises from the fact that the magnetic field gradient along a given direction cannot be independently controlled according to (8). However, if the magnetic moment of the object is constrained along a specific direction (Figure 5c), only unidirectional force is exerted on the object, and any residual torque is mitigated by reducing the magnetic field strength in the orthogonal directions, thereby suppressing rotational motion due to magnetic lag. Again, the simulation and experimental results of the magnetic gradient are well matched (Figure 5d–f(iii)). Thus, we can achieve the precise translational control of the object in all directions (Figure 6d,e and Supplementary Video S3).

Figure 5 and Figure 6a–e demonstrate the full 6-DOF control of magnetic miniature robots within the workspace. The magnetic miniature robot was fabricated via 3D printing following our previous work [16]. The printed material consists of 15% magnetic particles (SrFe₁₂O₁₉) and 85% polymer. After printing, the robot was magnetized under a 1 T magnetic field to achieve the desired magnetization profile for precise locomotion. The consistency between the simulated results and experimental data across the entire workspace validates the accuracy of the FEA model and the proposed SDMCA design framework.

Finally, we designed two additional SDMCA configurations tailored for enhanced performance in the following two scenarios. In the first scenario, the configuration is designed to enhance the magnetic strength and direction consistency within the horizontal XY-plane (Figure 7a), making the design suitable for planar actuation tasks. In another scenario, the configuration is optimized to achieve high field uniformity and gradient linearity along the Z-axis (Figure 7b), making it suitable for tasks involving vertical translation or lifting. These configurations offer larger effective workspaces and require lower current input. Additionally, these designs relax the constraint that all coils must be identical, allowing for greater flexibility in design and performance optimization.

Existing electromagnetic actuation platforms often achieve strong performance for a specific geometry or task; however, they seldom provide a general methodology for constructing a coil system with a well-defined workspace in which both B and ∇B can be independently prescribed under explicit physical constraints. By enforcing Maxwell-consistent parameter independence and validating an FEA-based predictive model against the experimental measurements, the proposed framework provides not only a practical hardware realization but also a transferable design logic that can be extended to different coil geometries, workspace sizes, and robotic requirements without relying on empirical tuning.

3. Conclusions

Precise control of the magnetic field is essential for the reliable actuation of magnetic miniature robots. However, there remains a lack of systematic methodology for constructing an electromagnetic system with a well-defined workspace in which both the magnetic field strength and gradient can be independently modulated. The current lack of a systematic design methodology makes it difficult to scale magnetic actuation from benchtop demonstrations to autonomous operation over larger areas, because the field strength and gradient cannot be predictably maintained across an expanded workspace. This limitation can lead to reduced manipulation accuracy and robustness, increased calibration burden, and higher dependence on frequent re-tuning or dense sensing/feedback, thereby constraining the development of future autonomous magnetic miniature robots intended for long-range navigation and task execution in large or complex environments. In this work, we first identify the twelve physical parameters required to fully describe the magnetic field and its spatial derivatives at a point, and show that only eight of these parameters are independent based on Maxwell’s equations. We then demonstrate one-dimensional magnetic field control using a pair of simple coils, each capable of producing a nearly constant magnetic field gradient near the coil. Through the superposition of fields from two coils, we achieve the precise and independent regulation of both the magnetic field magnitude and gradient within a designated workspace. To extend this analysis to practical applications, we develop an FEA model that accurately simulates the three-dimensional magnetic field of real coil geometries and configurations. The FEA results are validated through experimental measurements, showing excellent agreement and confirming the accuracy of the model. Finally, we outline a step-by-step workflow for the systematic design of SDMCA systems with user-specified uniform and gradient magnetic fields.

This work also provides three key technical contributions toward reliable magnetic field actuation for miniature soft robots. We introduce a visualization-based analytical model that clarifies the underlying field–gradient control mechanism and enables coil system design through magnetic field predictions that closely match realistic spatial distributions. A streamlined control architecture is established in which a customized software interface synchronously commands coil currents, reducing dependence on complicated amplification or conversion stages and improving robustness and operational simplicity. Finally, the coil system design is formulated in a requirement-driven manner guided by robot actuation needs, replacing experience-based configurations with a systematic mapping from control objectives to coil geometry and operating conditions, thereby improving the precision, repeatability, and practicality of magnetic manipulation for biomedical robotic applications.

Altogether, our design framework not only clarifies the fundamental principles governing the generation of a uniform and gradient magnetic field but also provides a practical guideline for the design and control of soft miniature robots, facilitating the development of highly functional, versatile, and cost-effective magnetic actuation systems that empower biomedical applications of magnetic miniature robots.