A Fast Response, High Flow Rate, Low Power Consumption Pneumatic Proportional Valve for Medical Ventilators Driven by a Piezoelectric Bimorph
Abstract
1. Introduction
2. Materials and Methods
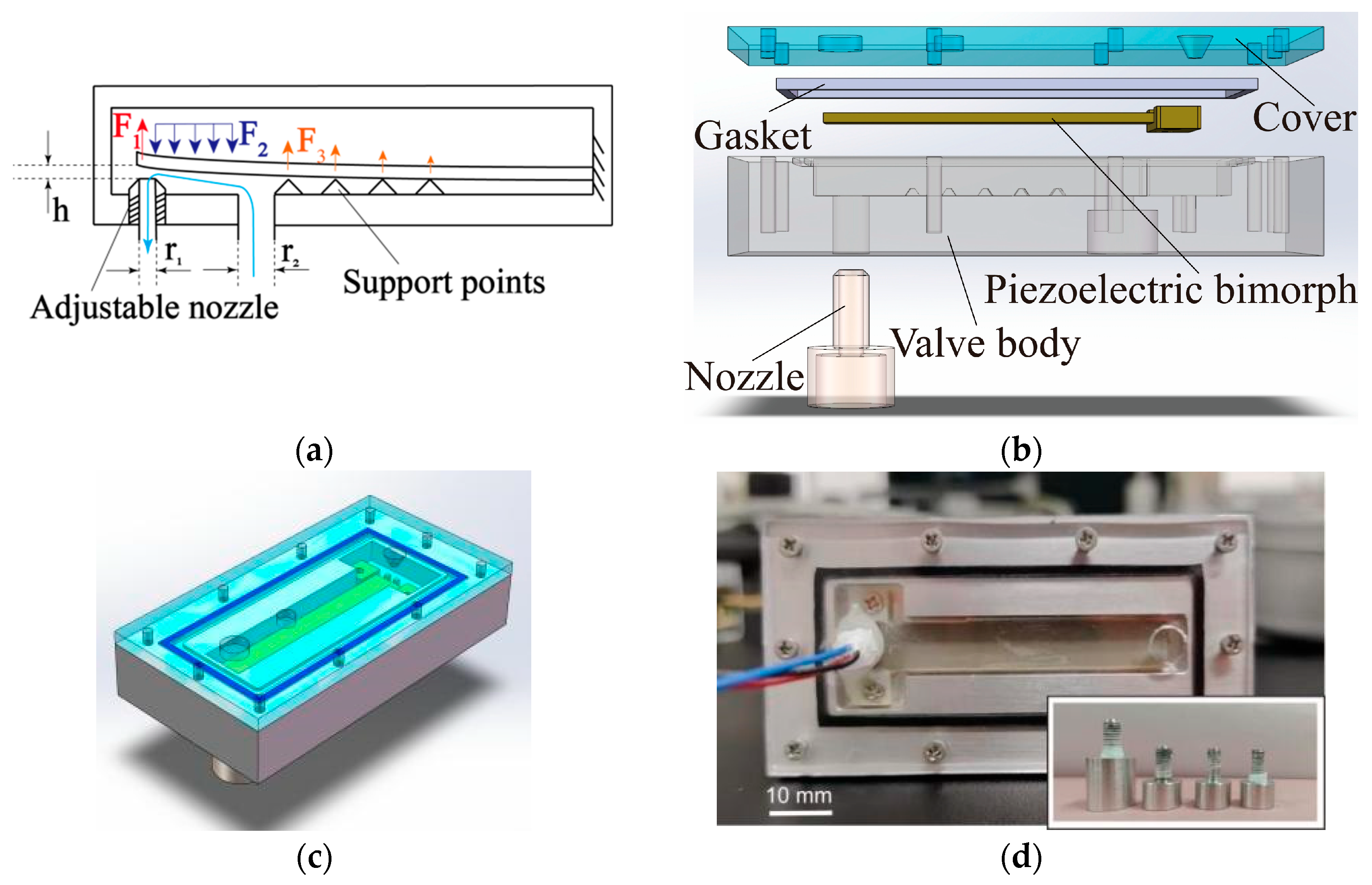
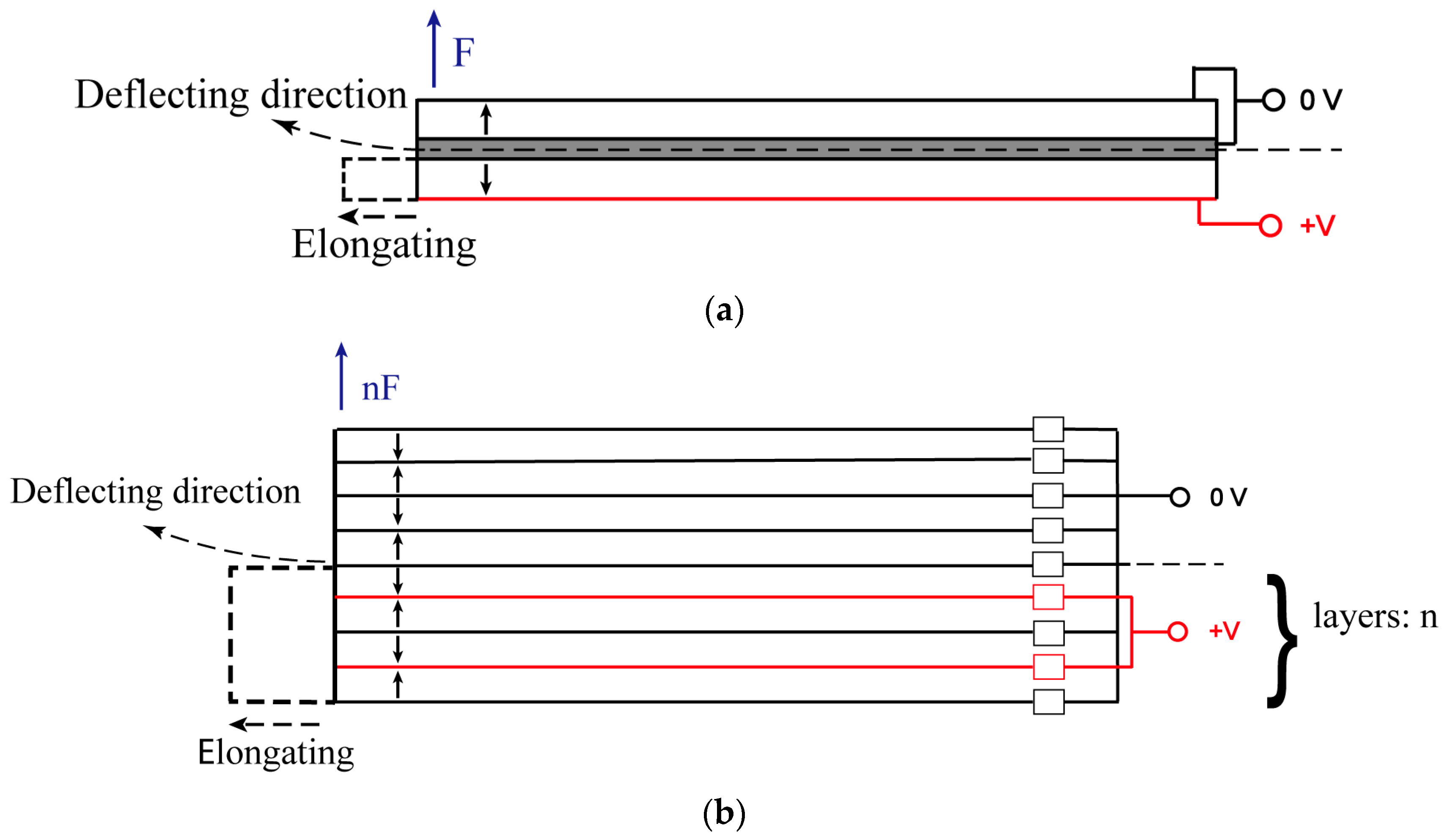
2.1. Working Principle and Structural Design
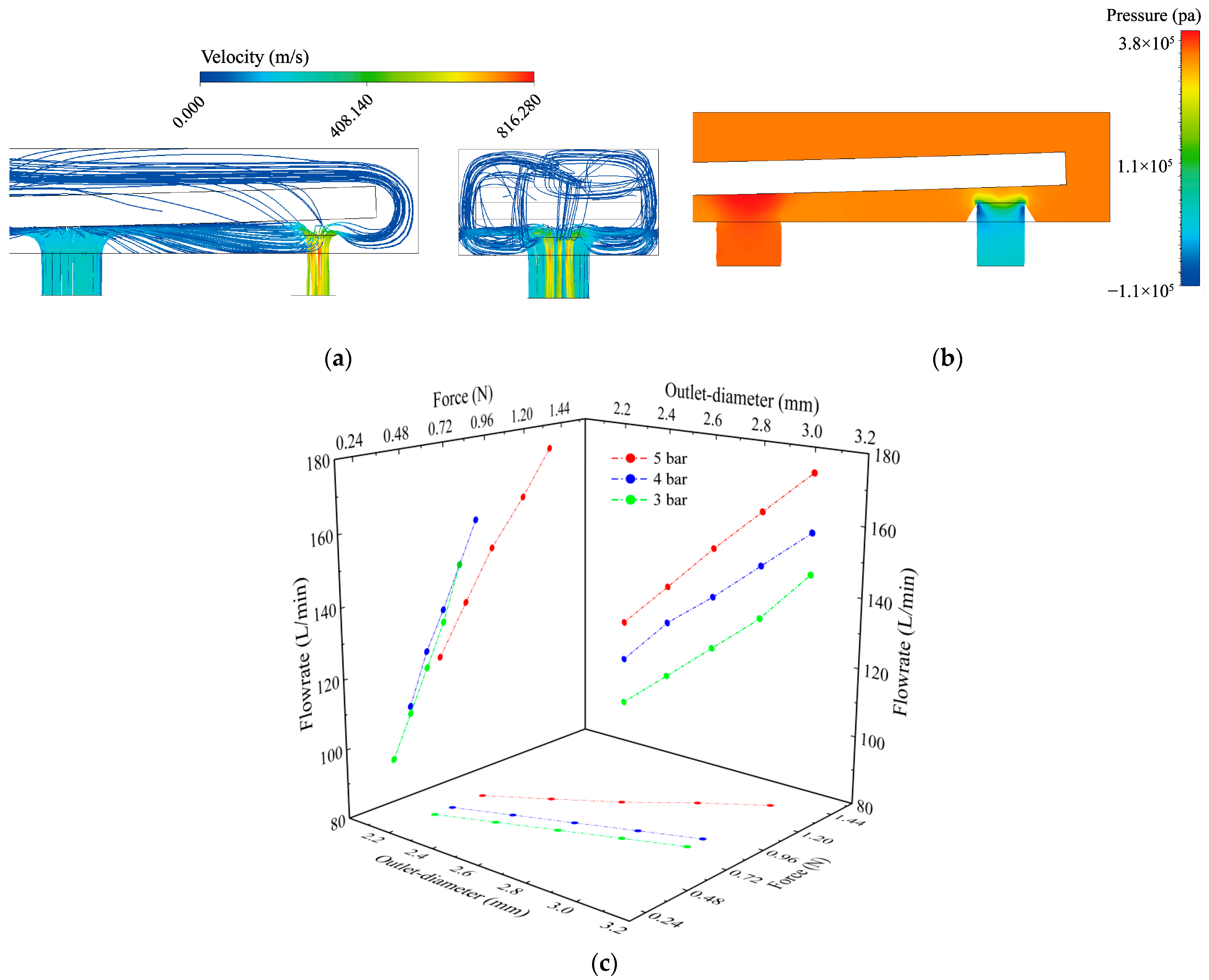
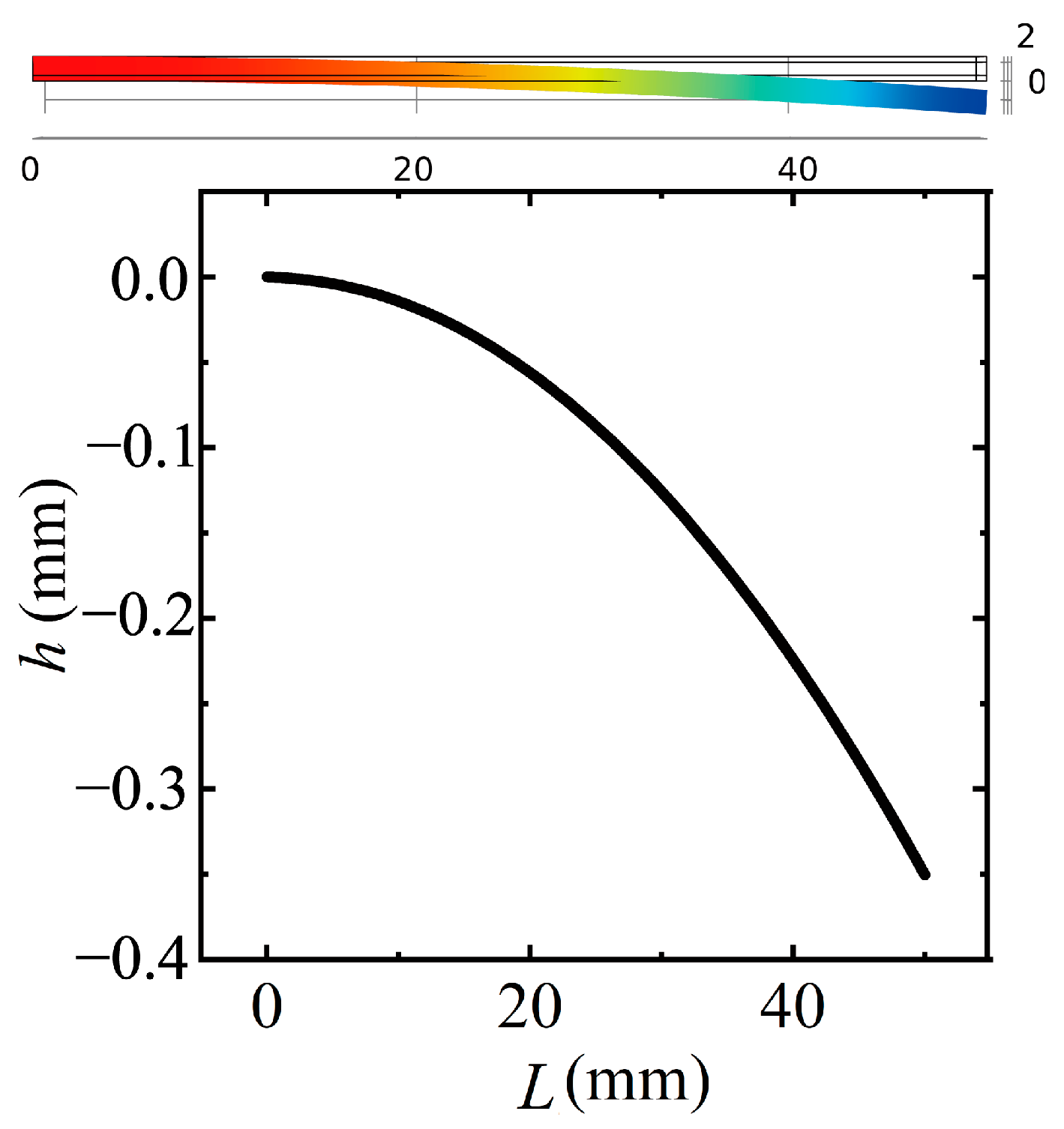
2.2. Determination of Key Parameters
3. Experimental Results and Discussion
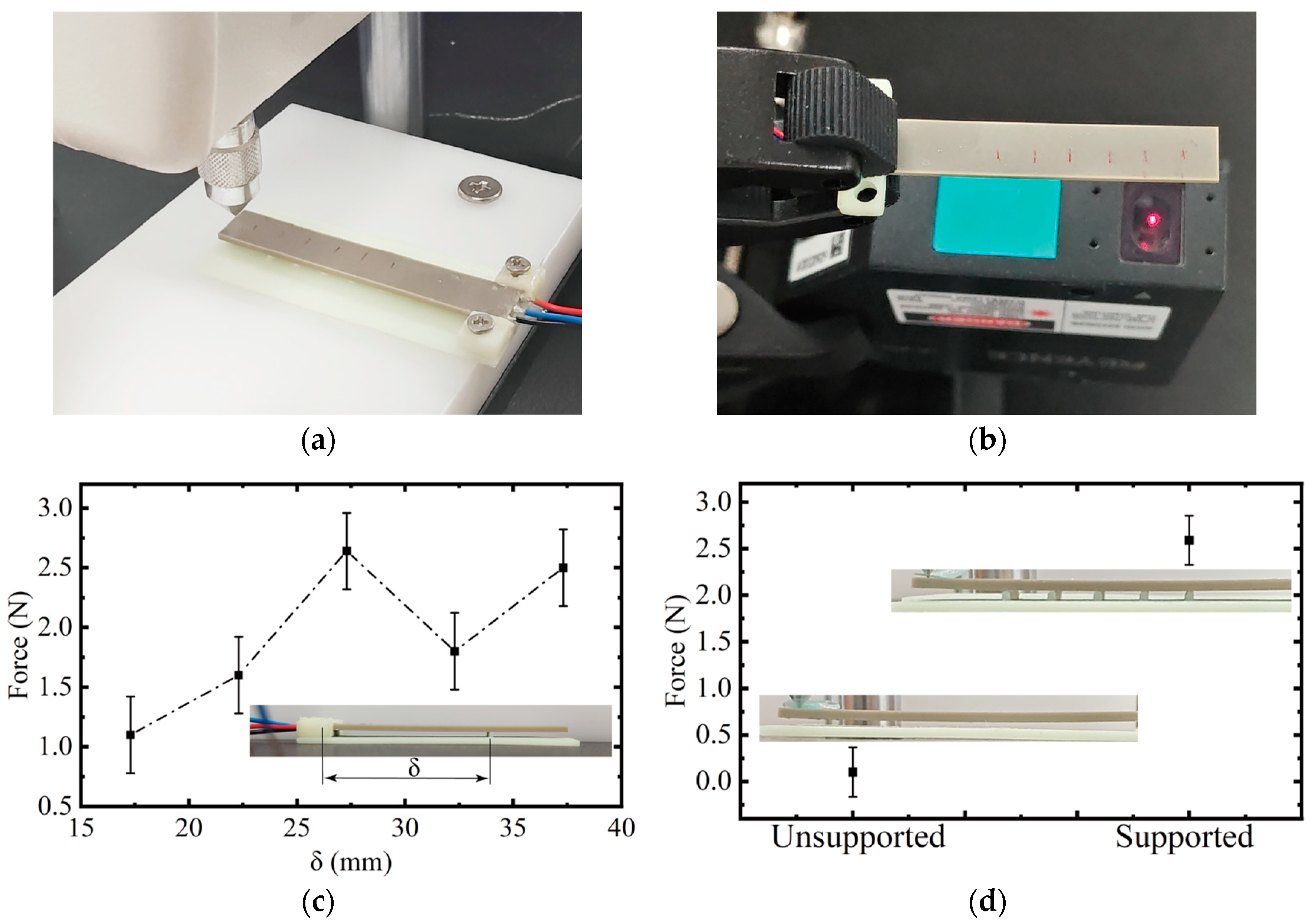
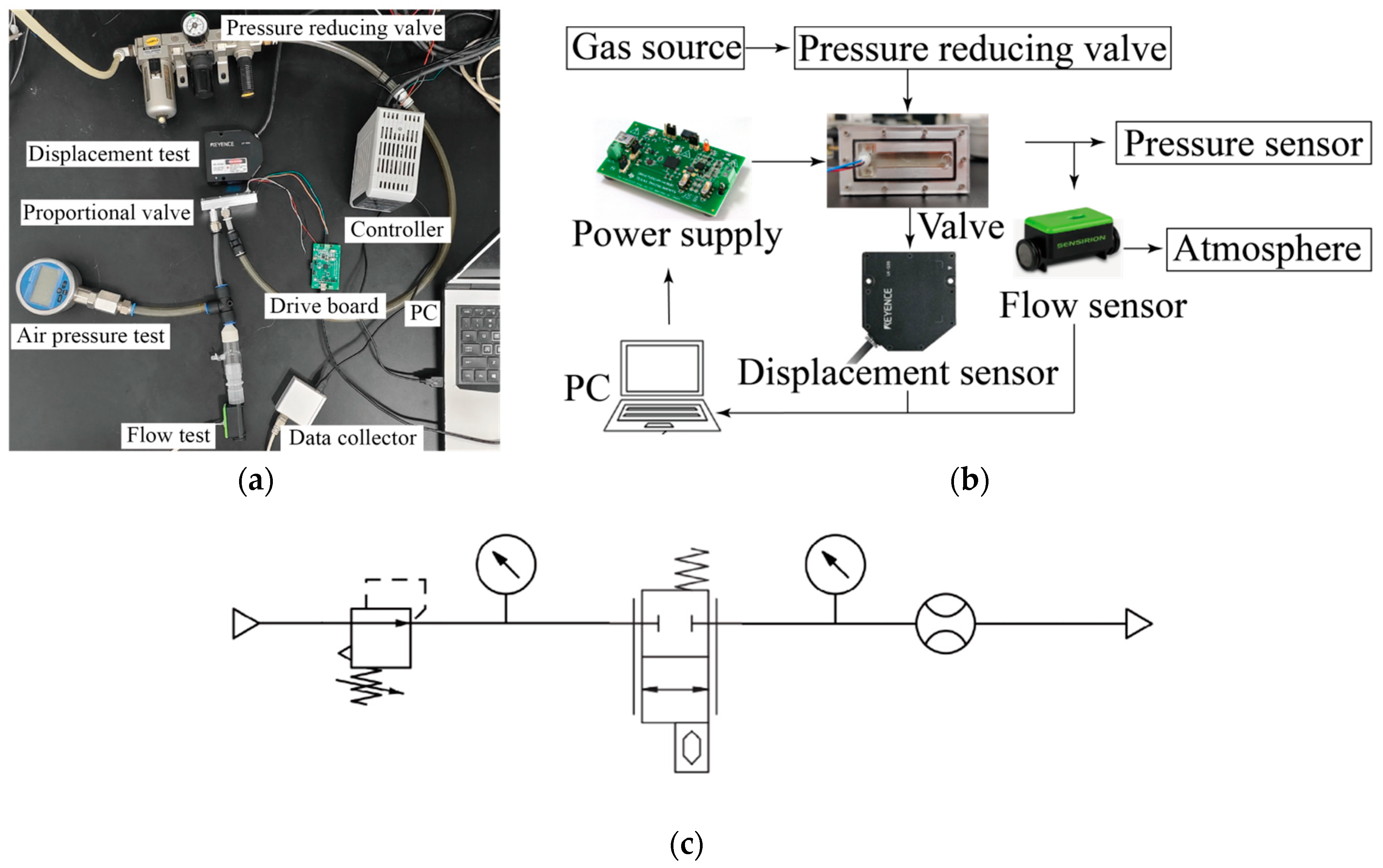
3.1. Preparation Experiment and Experimental Platform Construction
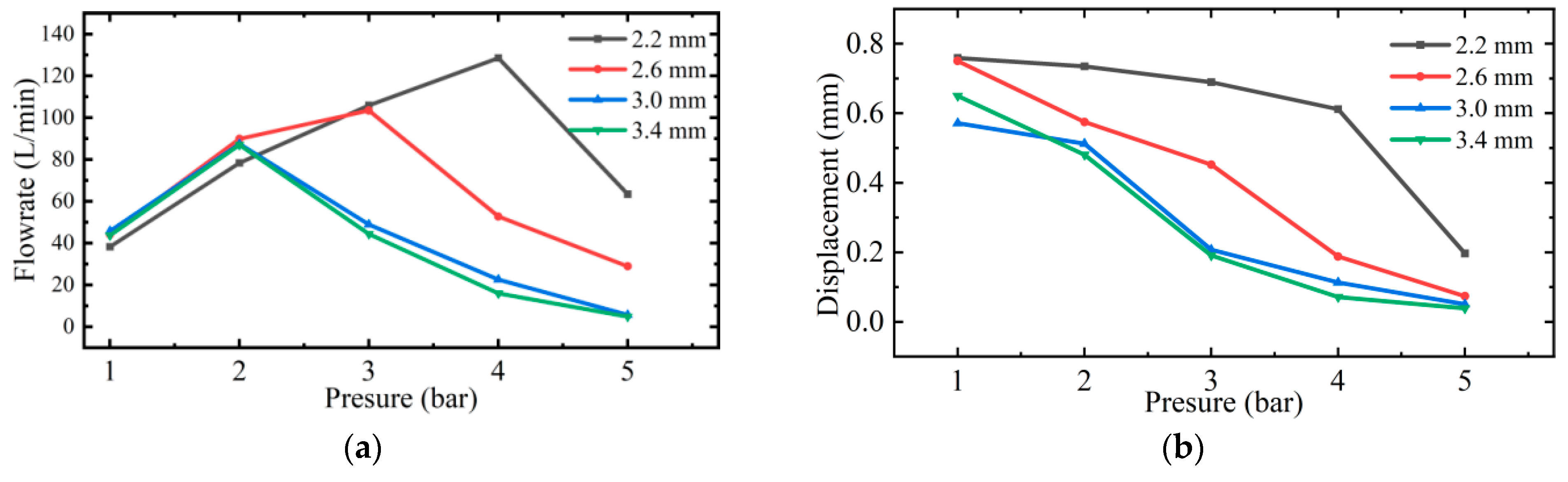
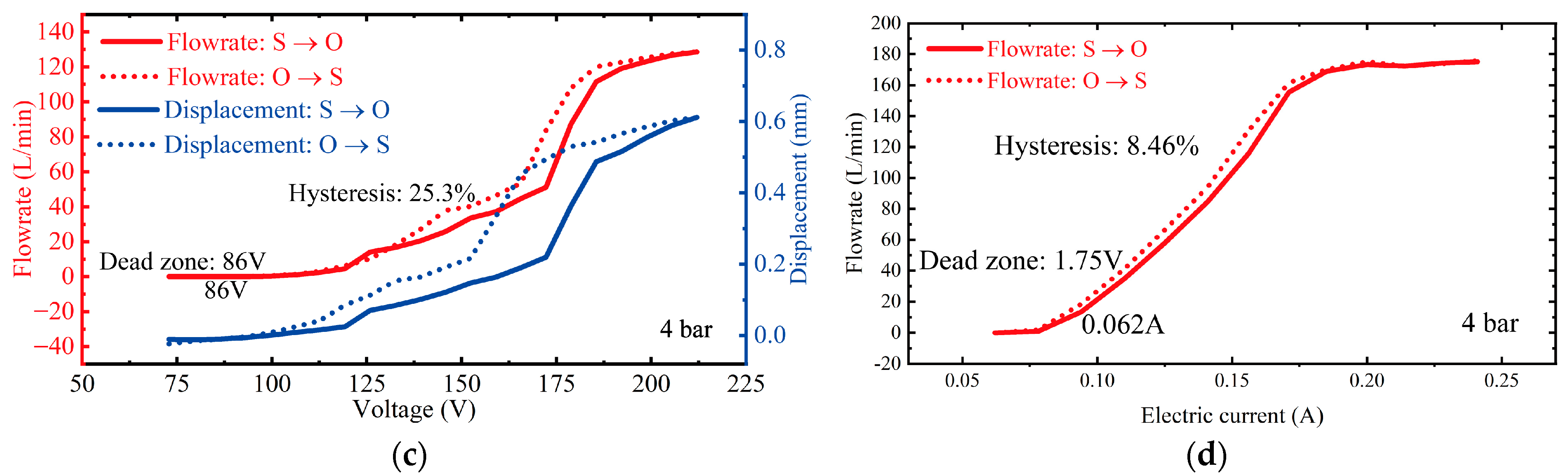
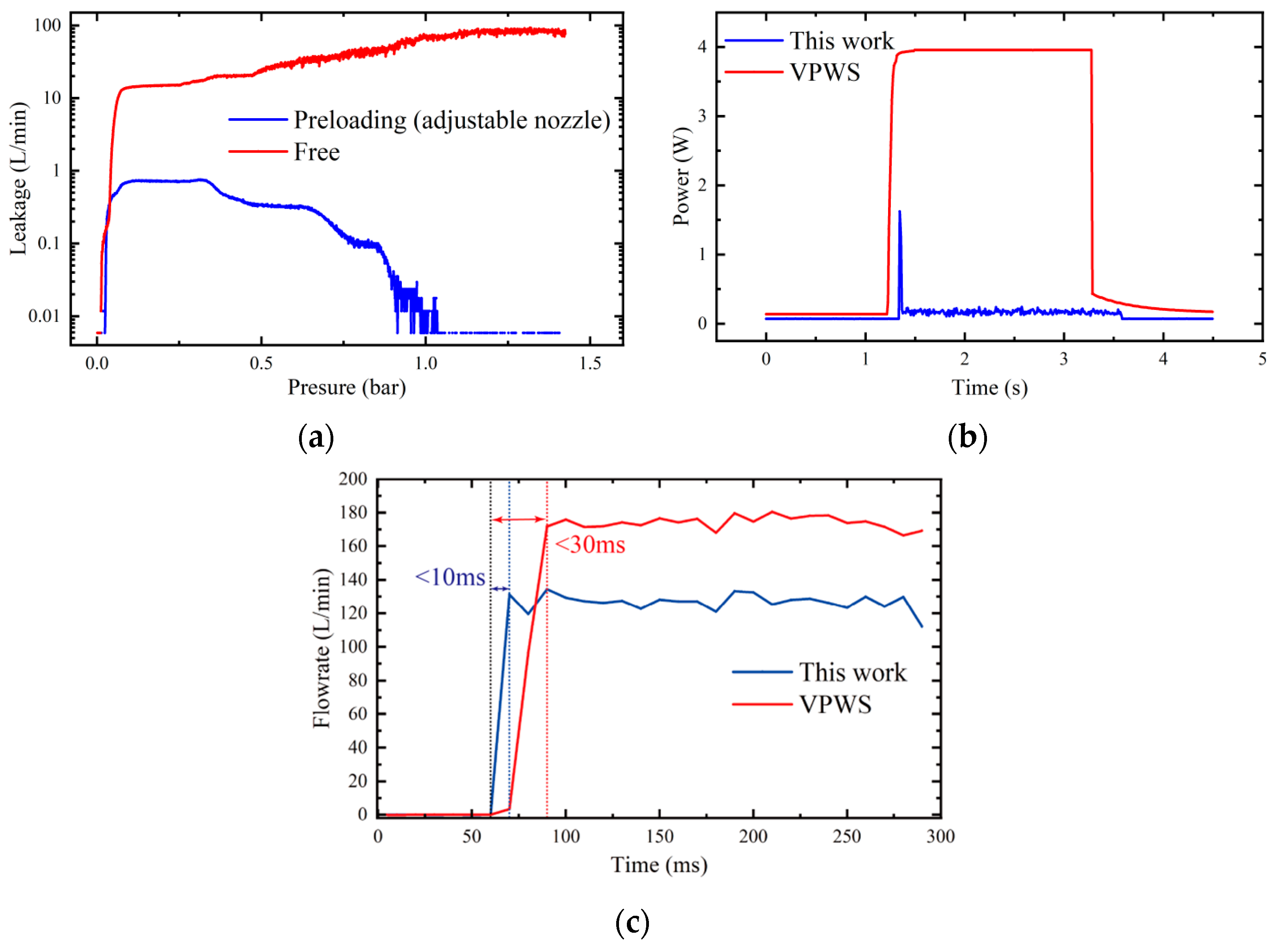
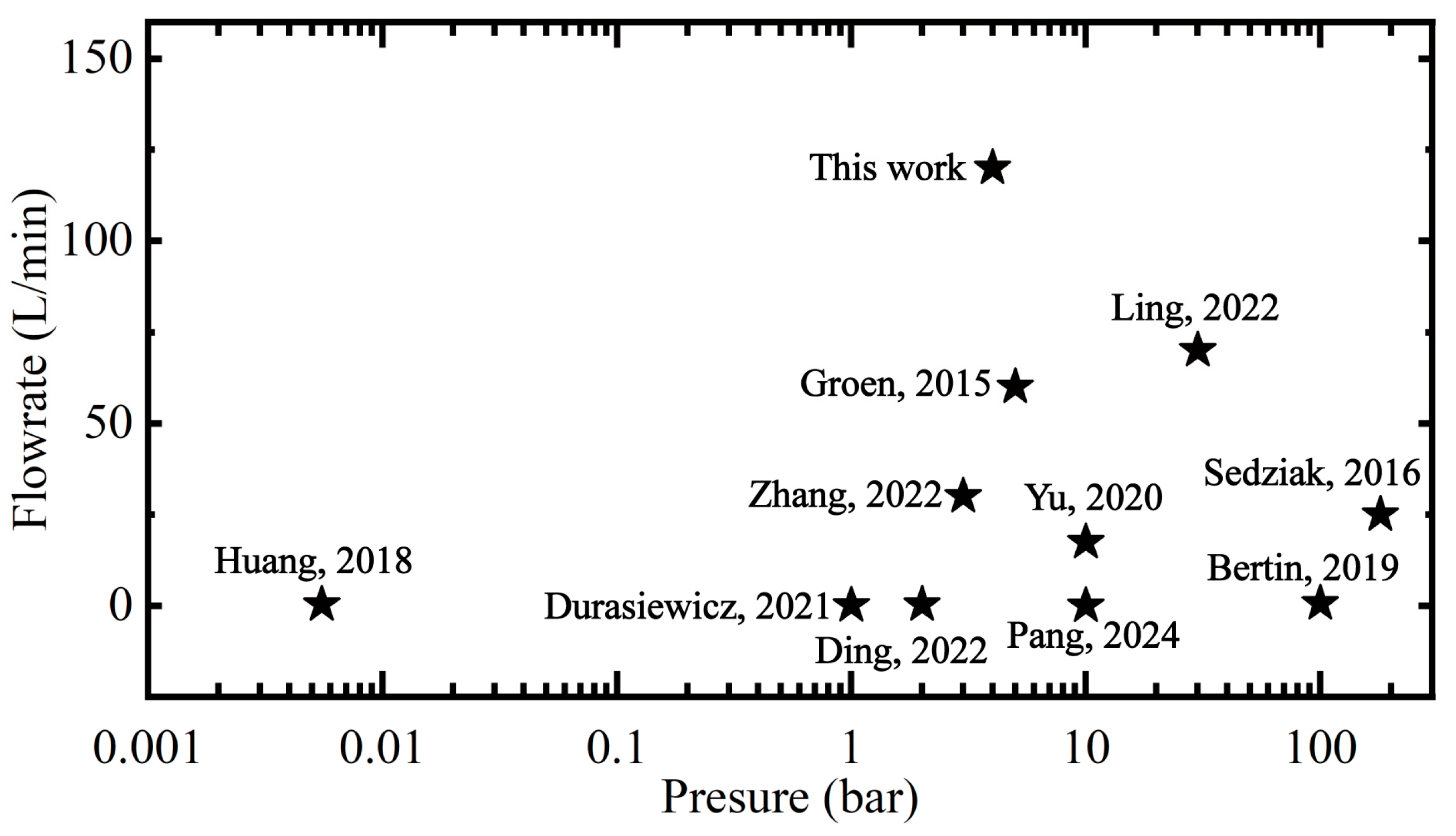
3.2. Experimental Verification and Result Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kacmarek, R.M. The mechanical ventilator: Past, present, and future. Respir. Care 2011, 56, 1170–1180. [Google Scholar] [CrossRef]
- Wallace, C.L.; Sanborn, W.G.; Arnett, D.; Butterbrodt, J.; Ferguson, H.L. Ventilator Breath Display and Graphic User Interface. U.S. Patent US5881723A, 16 March 1999. [Google Scholar]
- Zhang, Y.; Li, K.; Cai, M.; Wei, F.; Gong, S.; Li, S.; Lv, B. Establishment and experimental verification of a nonlinear position servo system model for a magnetically coupled rodless cylinder. Actuators 2022, 11, 50. [Google Scholar] [CrossRef]
- Zhu, J.; Han, P.; Qi, C.; Gong, G.; Yang, H.; Shinshi, T.; Han, D. A single-coil-driven tristable electromagnetic mini valve with multiple working states. Sens. Actuators A Phys. 2024, 377, 115699. [Google Scholar] [CrossRef]
- Pradeep, A.; Raj S., V.; Stanley, J.; Nair, B.G.; Babu, T.S. Automated and programmable electromagnetically actuated valves for microfluidic applications. Sens. Actuators A Phys. 2018, 283, 79–86. [Google Scholar] [CrossRef]
- Zak, A.K.; Yazdi, S.T.; Abrishami, M.E.; Hashim, A.M. A review on piezoelectric ceramics and nanostructures: Fundamentals and fabrications. J. Aust. Ceram. Soc. 2024, 60, 723–753. [Google Scholar] [CrossRef]
- Pang, Y.-J.; Wang, L.; Jin, J.-M. Design and Experimental Research of a High-Precision Piezoelectric Control Valve. In Proceedings of the 2022 16th Symposium on Piezoelectricity, Acoustic Waves, and Device Applications (SPAWDA), Nanjing, China, 10–14 October 2022. [Google Scholar]
- Brusa, E.; Carrera, A.; Delprete, C. A review of piezoelectric energy harvesting: Materials, design, and readout circuits. Actuators 2023, 12, 457. [Google Scholar] [CrossRef]
- Jones, N.A.; Clark, J. Analytical Modeling and Simulation of S-Drive Piezoelectric Actuators. Actuators 2021, 10, 87. [Google Scholar] [CrossRef]
- Morita, K.; Fujii, F.; Hosoda, K. Modeling and Compensation of a Bimorph Type Piezoelectric Actuator Exhibiting Odd-Harmonic Oscillation and Frequency-Dependent, Interleaved Hysteresis. Actuators 2020, 9, 36. [Google Scholar]
- Ling, M.; He, X.; Wu, M.; Cao, L. Dynamic design of a novel high-speed piezoelectric flow control valve based on compliant mechanism. IEEE/ASME Trans. Mechatron. 2022, 27, 4942–4950. [Google Scholar] [CrossRef]
- Bera, B.; Sarkar, M.D. Piezoelectric effect, piezotronics and piezophototronics: A review. Imp. J. Interdiscip. Res. IJIR 2016, 2, 1407–1410. [Google Scholar]
- Li, H.; Liu, Y.; Li, K.; Deng, J.; Feng, Y.; Liu, J. A resonant piezoelectric proportional valve for high-flowrate regulation operated by a bending sandwich actuator. Sens. Actuators A Phys. 2021, 331, 112971. [Google Scholar]
- Vilarinho, P.M.; Ribeiro, T.; Laranjeira, R.; Pinho, J.; Kingon, A.I.; Costa, M.E. Performance of piezoelectric actuators in gas microvalves: An engineering case study. Sens. Actuators A Phys. 2022, 344, 113703. [Google Scholar] [CrossRef]
- Chakraborty, I.; Tang, W.; Bame, D.; Tang, T. MEMS micro-valve for space applications. Sens. Actuators A Phys. 2000, 83, 188–193. [Google Scholar] [CrossRef]
- Bertin, M.; Plummer, A.; Bowen, C.; Johnston, N.; Griffiths, M.; Bickley, D. A dual lane piezoelectric ring bender actuated nozzle-flapper servo valve for aero engine fuel metering. Smart Mater. Struct. 2019, 28, 115015. [Google Scholar] [CrossRef]
- Geipel, A.; Doll, A.; Goldschmidtboing, F.; Jantscheff, P.; Esser, N.; Massing, U.; Woias, P. Pressure-independent micropump with piezoelectric valves for low flow drug delivery systems. In Proceedings of the 19th IEEE International Conference on Micro Electro Mechanical Systems, Istanbul, Turkey, 22–26 January 2006. [Google Scholar]
- Han, P.; Lu, F.; Gong, G.; Yang, H.; Han, D. A Bistable Four-Working-States Electromagnetic Mini Valve Based on Flexible Magnets for Pneumatic Soft Actuators. IEEE Trans. Ind. Electron. 2023, 71, 11061–11071. [Google Scholar]
- Takefumi, K.; Kou, H.; Yuma, M.; Yusuke, O.; Shuichi, W.; Daisuke, Y.; Koichi, S.; Hiroyuki, N. A Flow Control Valve using Piezoelectric Vibrator for Hydraulic Soft Actuators. In Proceedings of the ACTUATOR 2024—International Conference and Exhibition on New Actuator Systems and Applications, Wiesbaden, Germany, 13–14 June 2024; pp. 182–183. [Google Scholar]
- Wu, M.-X.; Ling, M.-X.; Deng, L.-S. Dynamic Modeling and Experimental Verification of A Piezoelectric Valve Based on Compliant Mechanisms. In Proceedings of the 2020 15th Symposium on Piezoelectrcity, Acoustic Waves and Device Applications (SPAWDA), Zhengzhou, China, 16–19 April 2021. [Google Scholar]
- Fazal, I.; Elwenspoek, M.C. Design and analysis of a high pressure piezoelectric actuated microvalve. J. Micromech. Microeng. 2007, 17, 2366–2379. [Google Scholar] [CrossRef]
- Park, J.M.; Evans, A.T.; Rasmussen, K.; Brosten, T.R.; Nellis, G.F.; Klein, S.A.; Gianchandani, Y.B. A microvalve with integrated sensors and customizable normal state for low-temperature operation. J. Microelectromech. Syst. 2009, 18, 868–877. [Google Scholar] [CrossRef]
- Debin, W.; Ma, X.; Liu, W. Simulation and analysis of piezoelectric actuator under weft insertion. In Proceedings of the 2020 5th International Conference on Electromechanical Control Technology and Transportation (ICECTT), Nanchang, China, 15–17 May 2020. [Google Scholar]
- Ling, M.; Cao, J.; Jiang, Z.; Lin, J. Theoretical modeling of attenuated displacement amplification for multistage compliant mechanism and its application. Sens. Actuators A: Phys. 2016, 249, 15–22. [Google Scholar]
- Groen, M.S.; Brouwer, D.M.; Lötters, J.C.; Wiegerink, R.J. Miniature proportional control valve with top-mounted piezo bimorph actuator with millisecond response time. J. Micromech. Microeng. 2015, 25, 105008. [Google Scholar] [CrossRef]
- Yun, S.; Lee, K.; Kim, H.; So, H. Development of the pneumatic valve with bimorph type PZT actuator. Mater. Chem. Phys. 2006, 97, 1–4. [Google Scholar] [CrossRef]
- Dong, S.; Du, X.-H.; Bouchilloux, P.; Uchino, K. Piezoelectric ring-morph actuators for valve application. J. Electroceram. 2002, 8, 155–161. [Google Scholar] [CrossRef]
- Cai, M.L. Modern theory and practice of pneumatic technology, lecture 1: Characteristic of pneumatic elements. Hydraul. Pneum. Seals 2007, 27, 44–48. [Google Scholar]
- Chen, J.; Ren, S.; Ren, J.; Wang, T. A Flow Control Algorithm for Piezoelectric Proportional Valves Based on Active Disturbance Rejection Control. In Proceedings of the 2024 43rd Chinese Control Conference (CCC), Kunming, China, 28–31 July 2024. [Google Scholar]
- Huang, C.; Hsu, Y.-H.; Lee, C.-K. Piezoelectric gas flow controller based on dual-bimorph actuators. In Active and Passive Smart Structures and Integrated Systems XII; SPIE: Pune, India, 2018; Volume 10595. [Google Scholar]
- Sedziak, D.; Minorowicz, B.; Stefanski, F.; Regulski, R. Modelling and investigations of piezobender used in control of electrohydraulic servovalve. In Proceedings of the 2016 17th International Carpathian Control Conference (ICCC), High Tatras, Slovakia, 29 May–1 June 2016. [Google Scholar]
- Pang, Y.; Wang, L.; Jin, J. Design, modeling and experimental research of a multi-mode, fast-response piezoelectric control valve. Mechatronics 2023, 97, 103113. [Google Scholar] [CrossRef]
- Durasiewicz, C.P.; Güntner, S.T.; Maier, P.K.; Hölzl, W.; Schrag, G. Piezoelectric normally open microvalve with multiple valve seat trenches for medical applications. Appl. Sci. 2021, 11, 9252. [Google Scholar] [CrossRef]
- Zhang, Q.; Sun, Z.; Huang, X. Research on Pneumatic High Speed On-Off Valve Based on Piezoelectric Bimorph. Piezoelectr. Acoustoopt. 2022, 44, 758. [Google Scholar]
- Ding, Y.; Cai, Y.; Li, Y. Continuously adjustable micro valve based on a piezoelectric actuator for high-precision flow rate control. Electronics 2022, 11, 1689. [Google Scholar] [CrossRef]
- Yu, J.; Jiao, Z.; Wu, S. Design, simulation and test of high-flow high-speed on/off valve driven by piezoelectric. J. Mech. Eng. 2020, 56, 226–234. [Google Scholar]
| Symbols | Parameters | Values | Units |
|---|---|---|---|
| L | Length | 50 (±1) | mm |
| b | Width | 7.8 | mm |
| T | Height | 1.3 | mm |
| Driving Voltage | 200 | V | |
| Displacement | ±1000 | μm | |
| Blocked Force | 2.6 (With the help of supporting structures) | N |
| Parameters | Values: This Work | Values: VPWS | Values: VEAE | Units |
|---|---|---|---|---|
| Maximum flow rate (4 bar) | 130 | 180 | 64 | L/min |
| Hysteresis rate | 25.3% | 8.5% | 35.9% | |
| Power consumption | 0.07 | 3.96 | 0.1 (5 Hz) | W |
| Frequency response | <20 | 18 | 11 | Hz |
| Response time | <10 | <30 | <40 | ms |
| Weight (entirety) | 145 | 140 | 10 | g |
| Weight (actuator) | <1 | 23 | <1 | g |
| Volume | 78 × 41 × 13 | 44 × 25 × 42 (Includes manifold block) | 63 × 17 × 8 | mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, S.; Chen, J.; Wang, T.; Ma, B. A Fast Response, High Flow Rate, Low Power Consumption Pneumatic Proportional Valve for Medical Ventilators Driven by a Piezoelectric Bimorph. Actuators 2025, 14, 463. https://doi.org/10.3390/act14090463
Ren S, Chen J, Wang T, Ma B. A Fast Response, High Flow Rate, Low Power Consumption Pneumatic Proportional Valve for Medical Ventilators Driven by a Piezoelectric Bimorph. Actuators. 2025; 14(9):463. https://doi.org/10.3390/act14090463
Chicago/Turabian StyleRen, Shuai, Junling Chen, Tao Wang, and Bingbing Ma. 2025. "A Fast Response, High Flow Rate, Low Power Consumption Pneumatic Proportional Valve for Medical Ventilators Driven by a Piezoelectric Bimorph" Actuators 14, no. 9: 463. https://doi.org/10.3390/act14090463
APA StyleRen, S., Chen, J., Wang, T., & Ma, B. (2025). A Fast Response, High Flow Rate, Low Power Consumption Pneumatic Proportional Valve for Medical Ventilators Driven by a Piezoelectric Bimorph. Actuators, 14(9), 463. https://doi.org/10.3390/act14090463







