An Adaptive Estimation Model for the States and Loads in Electro-Hydraulic Actuation Systems

Abstract

In this study, we introduce an advanced framework for state estimation in electro-hydraulic systems, utilizing a structurally adapted Kalman filter. The proposed model was designed to enhance estimation accuracy and robustness under dynamic load variations and evolving measurement conditions. A notable feature of the approach is the algebraic resolution of one system state during each iteration, enabling the seamless inclusion of variables that are otherwise difficult to measure, without disrupting the model’s linear formulation. In addition, the dynamics of the load torque are empirically characterized through a regression-based model derived from experimental observations. The framework integrates adaptive mechanisms for updating the model and measurement error covariance matrices, facilitating the real-time accommodation of system nonlinearities and environmental changes. Experimental results are presented in different operating modes, reflecting characteristic dynamic movements. They show that the method reduced the root mean square error (RMSE) when estimating angular velocity between five and more than six times, depending on the mode. When evaluating the load torque, even in modes with a sharply changing load, the RMSE value remains stable below 0.05 Nm, which indicates the absence of systematic drift and high stability of the estimates. This confirms the stable operation of the algorithm in dynamic conditions and its applicability in real systems.

1. Introduction

Electro-hydraulic systems play an important role in modern industrial applications that require large force management in a confined space, high dynamics, and reliability [1]. Their ability to combine high energy density with flexible electronic control makes them particularly suitable in complex engineering solutions, especially those involving variable loads and unstable external influences [2,3].

Despite their advantages, electro-hydraulic systems have several inherent limitations. These include pronounced nonlinear behavior, energy losses due to hydraulic resistance, temperature fluctuations, and dynamic oscillations of the components [4]. Moreover, the electronic control of such systems is often closely tied to the specific configuration of the end-actuated object. Consequently, the control algorithms must be carefully tailored to the application’s specific requirements, necessitating flexibility and the ability to customize both the static and dynamic characteristics of the hydraulic module [5,6].

In a number of modern engineering applications where precise positioning is required, electro-hydraulic systems play an important role [7]. Among them, CNC machines with high load capacity, positioning platforms, hexapod systems, industrial robots, test benches for aerospace and automotive equipment, as well as specialized precision actuators stand out [8]. These systems require not only the transmission of significant power but also extremely high positioning accuracy, motion stability, and repeatability [9,10,11]. A similar need for high accuracy and reliability has been emphasized in other high-energy and precision engineering applications [12].

Such applications place additional demands on electro-hydraulic systems that go beyond traditional parameters, such as power and speed [13,14]. This requires the use of modern approaches for dynamic error compensation, increasing stability and improving control accuracy in conditions of changing loads and external interference [15]. Among the main disadvantages are the difficulty in modeling certain states, the dependence on static parameter assessments, and the sensitivity of the system to discrepancies between its real behavior and the dynamics described by the model—problems that require the application of adaptive and structurally flexible approaches [16,17,18].

The development of microprocessor technology, embedded computing systems, and real-time control methods provides opportunities for intelligent algorithms that compensate for nonlinearities, increase accuracy, and adapt the behavior of electro-hydraulic systems. They are classified into four groups: stochastic methods (Kalman filters and Bayesian estimates), adaptive techniques (recursive identification and self-adjusting models), artificial intelligence algorithms (neural networks and fuzzy logic), and hybrid structures. The choice depends on the application, the availability of measurements, and the dynamic characteristics of the system.

The adaptive Kalman filter (AKF) is widely used in environments with uncertainties and variable loads, as it allows for dynamic updating of noise covariance matrices to current conditions [19,20]. However, its classic implementations often rely on preset windows or stationary assumptions, which limits its effectiveness in sharply changing dynamic modes. This requires the development of advanced methods for determining covariance matrices that better reflect real-world conditions. In systems with highly nonlinear dynamics, extended (EKF), advanced (UKF), and ensemble Kalman filters (EnKF) are widely used, as well as Bayesian approaches to integrate advance information [21,22,23,24,25].

The structure-adaptive Kalman filter proposed in this study differs from these classical implementations by the inclusion of algebraic determination of one of the states and hybrid adaptive procedures for updating covariance matrices. This achieves higher accuracy and stability in dynamic modes, while maintaining computational efficiency and real-time realization.

Adaptive techniques that change the parameters of the model or regulator according to current conditions, including recursive identification and self-adjusting models, are also widely used [16]. Artificial intelligence algorithms—neural networks and fuzzy logic—are increasingly used to model and control systems with nonlinearities and uncertainties [26,27]. In recent years, hybrid structures have also been developed, combining classical controllers and intelligent methods to increase adaptability and resilience [28].

Despite the proven effectiveness of these methods in the control and assessment of conditions, in real electro-hydraulic systems, they often encounter significant challenges. Many of the classic algorithms rely on preset models and fixed parameters that do not always reflect the real dynamics of the system. Contrastingly, some smart and hybrid approaches require complex setups or significant computing resources, which limits their practical applicability in environments with limited computing power or with requirements for rapid real-time adaptation. In addition, sensitivity to parametric inconsistencies, temporary delays, and poor measurement accessibility limits the ability to maintain high accuracy under variable operating conditions.

This article proposes an adapted model built on the structure of the Kalman filter but differing from the classical approach by structural modification. The main focus is reliable tracking and forecasting of an external load, which allows for active adaptation of control actions to real conditions. In the model, one of the states is determined algebraically at each step of the algorithm, and the dynamics of the load are described by empirical modeling based on experimental data. This ensures a better match between the model and the actual operation of the system.

Within the framework of the developed model, an adaptive mechanism was implemented for updating the covariance matrices that characterize the errors in the model and in measurement. Unlike traditional fixed-value approaches, here, variances were calculated in real time by analyzing the differences between measured and predicted state changes. This made it possible to automatically adapt the filter to nonlinearities, external influences, and changes in system dynamics. Additionally, a hybrid algorithm is introduced that adaptively determines the covariance matrix of measurement errors, combining exponential smoothing and local regression. This approach allowed for the timely detection of changes in the characteristics of the sensors and ensured a stable response of the filter to short-term disturbances and fluctuations in the measuring environment.

2. A Description of the Electro-Hydraulic System

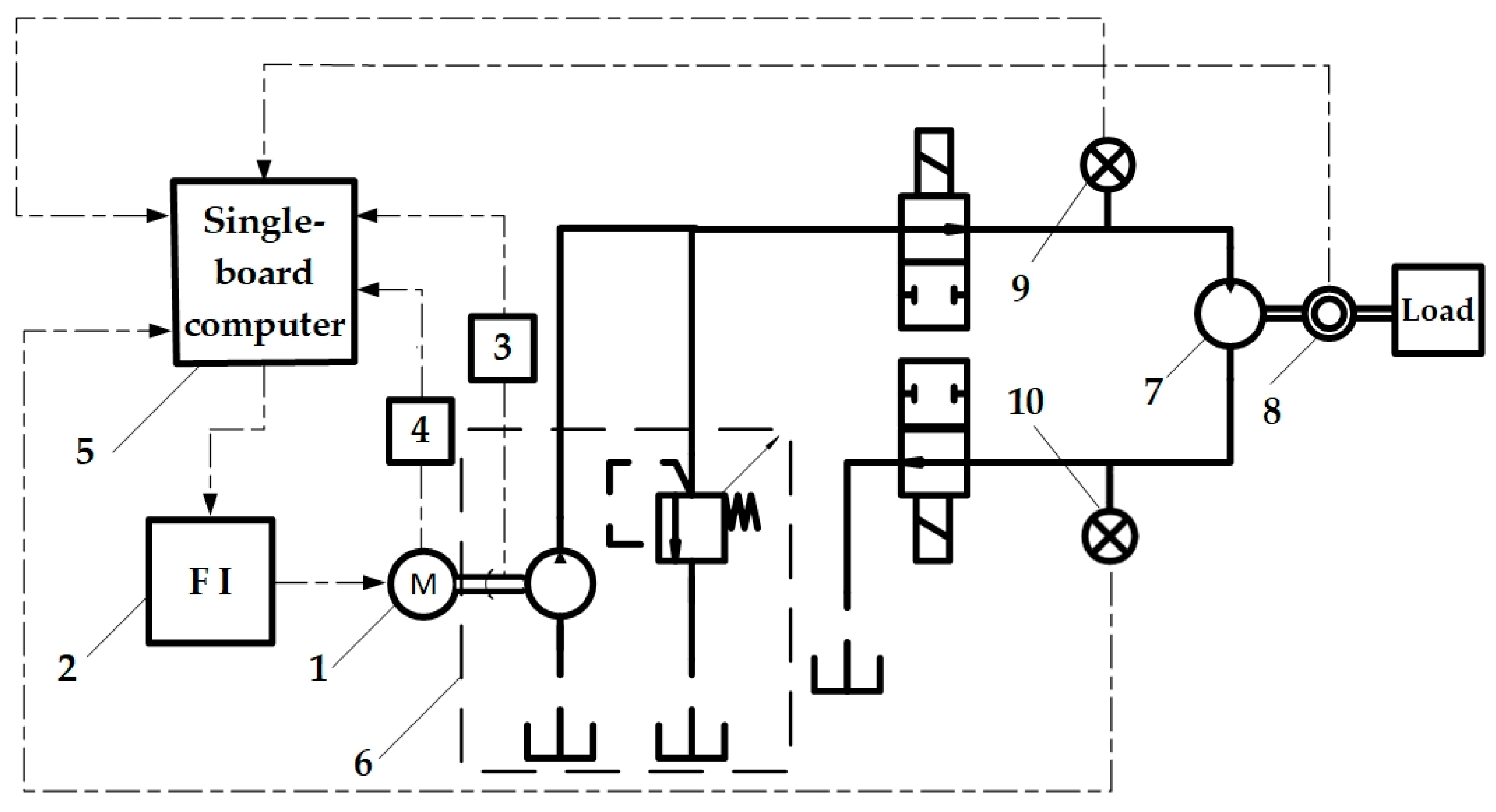
An illustration of the structure of the electro-hydraulic system under study is shown in Figure 1. The system included electromechanical and hydraulic modules, measuring transducers, and a built-in computer unit for processing and control.

The electromechanical module consisted of an asynchronous electric motor, controlled by a frequency inverter. An incremental encoder was installed on the shaft of the electric motor to measure the angular velocity, along with a Hall-type current sensor to measure the current proportionally to the generated electromagnetic moment. The built-in computing module received both the signal from the angular velocity encoder and the measured current value from the Hall sensor used to calculate the electromagnetic moment.

The electric motor drove a hydraulic pump, which supplied hydraulic energy to the hydraulic motor. On the shaft of the hydraulic motor, there was a tachogenerator that measured its angular velocity. In addition, there were two pressure sensors located at the inlet and outlet of the hydraulic motor, which registered the corresponding values.

All measurement signals were processed by the built-in computing module, implemented through a single-board computer platform. The module provided the necessary computing capacity to execute algorithms for evaluating system states and parameters, as well as applying real-time filtering algorithms. It integrated measurements, mathematical models, and error correction procedures, and, based on the received ratings, a control signal was formed, which was fed back to the frequency control, closing the control loop.

3. Development of the Kalman Filter

The purpose of applying the Kalman filter in the present study was to provide an optimal estimation of the hidden states of the electro-hydraulic system based on available measured quantities that were subject to noise and uncertainties. In this particular case, basic variables, such as the angular velocity of the hydraulic motor shaft and its corresponding acceleration and external load, were evaluated, based on data obtained from the integrated current and angular velocity sensors on the electric motor, as well as the measured values of the angular velocity and the pressure difference at the inlet and outlet of the hydraulic motor.

The Kalman filter played a dual role—predicting the next state of the system based on the mathematical model and updating the forecast through real measurements, thus minimizing the impact of noise and data errors. Although the version of the filter used here was a linear model, which at first glance might seem like a limitation, given the characteristic nonlinearity of electro-hydraulic systems, the proposed adaptive strategy for dynamically updating the covariance matrices of the model and the measurement allowed the filter to adapt to the current operating conditions. This combination of classical structure and adaptive behavior allowed for increased accuracy and stability in assessing states under conditions of nonlinear dynamics and unpredictable load disturbances. At the same time, the direct measurement of both the angular velocity of the electric motor and the hydraulic motor, as well as the difference in pressures at the inlet and outlet of the hydraulic module, allowed for a more reliable update of the filter, thus ensuring a more accurate recovery of hard-to-measure quantities, such as the external load.

In this model, a functional approach was adopted, in which the dynamics of the electro-hydraulic system were described by the input–output mechanical variables, without directly entering the internal hydrodynamic parameters, such as flow rate, pressure, or other quantities characteristic of the internal flows in the system. This decision was motivated by the need for the model to be appropriately simplified and suitable for implementation using a linear Kalman filter, while still preserving the essential relationships between the control inputs and the observed variables.

Instead of building a full-scale hydraulic model, the influence of internal processes was accounted for by empirically determined coefficients in the load variation equation. These coefficients—$k_t$, $k_d$, and $k_p$—were determined experimentally based on real measurements and were used to calculate the dynamic characteristics of the system under variable loads and dynamic conditions. In this way, a necessary balance was achieved between computational efficiency, algorithm robustness, and sufficient accuracy in real-time state assessment. In addition, this model structure allows for easy adaptation to other real electro-hydraulic systems with different types of motors, pumps, and actuators, and, if necessary, it is possible to readjust its parameters by re-identification.

In order to ensure the monitoring and prediction of conditions, it was necessary to formulate the dynamics of the moment acting on the shaft of the hydraulic motor. This moment included both internal inertial and frictional forces, as well as the external impact of the load. The balance of moments applied to the shaft is expressed by the following equation:

$$T_{hid}\left(t\right)=J_m·{\dot{\omega }}_m\left(t\right)+B_m·{\omega }_m\left(t\right)+T_{load}\left(t\right)$$

(1)

where $T_{hid}\left(t\right)$ is the moment that actually reaches the shaft of the hydraulic motor; $J_m$ is the inertial moment of the hydraulic motor shaft; $B_m$ is the coefficient of friction in the hydraulic motor; ${\omega }_m\left(t\right)$ is the angular velocity of the hydraulic motor shaft; and ${\dot{\omega }}_m\left(t\right)$ is the angular acceleration of the hydraulic motor.

It is necessary to take into account that the moment, $T_{hid}\left(t\right)$, which acts on the shaft of the hydraulic motor is not equal to the moment generated by the electric motor. In the process of converting from electrical to hydraulic energy, part of the supplied torque is lost due to hydraulic and mechanical losses in the pump and connecting elements. Thus, it is appropriate to introduce into the equations a torque conversion coefficient, ${\eta }_{pump}$, which describes the transmission efficiency between the electric motor and the hydraulic module:

$$T_{hid}\left(t\right)={\eta }_{pump}·T_{motor}\left(t\right)$$

(2)

where $T_{hid}\left(t\right)$ is the moment that actually drives the hydraulic motor; $T_{motor}\left(t\right)$ is the control input torque supplied by the electric motor; and ${\eta }_{pump}$ is a conversion factor reflecting losses in the system and pump efficiency.

The coefficient ${\eta }_{pump}$ should not be considered as a classic efficiency but rather as a parameter uniting loss from different origins—hydraulic, mechanical, temperature, and structural. The inclusion of ${\eta }_{pump}$ allows for more accurate modeling of the real energy connection between the electric motor and the hydraulic actuator. The practical use of the instantaneous balance equation requires the introduction of a real estimate of the losses that occur when energy is converted from electrical to hydraulic. These losses are due to a number of factors, such as friction in the internal components of the pump, hydraulic resistance, fluid heating, and fluid compressibility. Instead of modeling each of these effects individually, their total impact is accounted for using the momentum conversion factor, ${\eta }_{pump}$, which is defined as the ratio between the actually transmitted torque to the hydraulic motor and the torque generated by the electric motor.

In the present work, the value of ${\eta }_{pump}$ was determined experimentally using measured values of the angular velocity and pressures of the hydraulic motor. By applying the equation of dynamic balance and applied load, the value of the real hydraulic torque could be calculated, which was subsequently compared with the input torque from the electric motor. This approach avoids the need for a complex multi-parameter loss model by introducing a single correction factor that reflects the actual operating conditions of the specific system. If necessary, the value of ${\eta }_{pump}$ can be adapted to other systems with a similar structure through a new experimental calibration. As a result of the experimental calculations carried out, within the framework of the developed prototype, the value of the coefficient was accepted as ${\eta }_{pump}=0.85$. More detailed information on the determination of ${\eta }_{pump}$ are presented in Section 3.2.

In order to fully describe the dynamics of the electro-hydraulic system, it is necessary to take into account the internal torque equilibrium in the electric motor. The electromagnetic torque, $T_{el}\left(t\right)$, applied to the shaft of the electric motor, compensates for the inertial forces and the friction losses in the motor, as well as the load torque, $T_{motor}\left(t\right)$, transmitted to the hydraulic pump. The instantaneous balance in an electric motor is described by the following equation:

$$J_e·{\dot{\omega }}_{motor}\left(t\right)+B_e·{\omega }_{motor}\left(t\right)=T_{el}\left(t\right)-T_{motor}\left(t\right)$$

(3)

where $J_e$ is the moment of inertia of the electric motor; $B_e$ is the coefficient of friction in the electric motor; $T_{el}\left(t\right)$ is the electromagnetic moment measured by a Hall-type current sensor mounted to the power line of the electric motor; $T_{motor}\left(t\right)$ is the moment that the electric motor transmits to the pump; and ${\omega }_{motor}\left(t\right)$ is the angular velocity of the electric motor shaft.

After substituting Equation (1) for the moment transmitted to the hydraulic system in the expression [Equation (3)] for the internal moment balance of the electric motor and performing the necessary conversions, a generalized differential equation is obtained that describes the dynamics of the system from the controlling electromagnetic moment to the output of the hydraulic motor:

$$J_e·{\dot{\omega }}_{motor}\left(t\right)+B_e·{\omega }_{motor}\left(t\right)=T_{el}\left(t\right)-{\displaystyle \frac{1}{{\eta }_{pump}}}·\left(J_m·{\dot{\omega }}_m\left(t\right)+B_m·{\omega }_m\left(t\right)+T_{load}\left(t\right)\right)$$

(4)

The dynamic model of the electro-hydraulic system can be represented in the following form:

$$\dot{x}\left(t\right)=A·x\left(t\right)+B·u\left(t\right)+w\left(t\right)$$

(5)

where $x\left(t\right)$ is a state vector describing the current internal state of the system; $A$ is a state matrix describing the dynamics of the system; $B$ is the input matrix describing how the control effect affects the state; $u\left(t\right)$ is a vector of the control inputs, which includes parameters related to the electromagnetic moment (determined from the current measured by a Hall-type sensor) and the angular velocity of the electric motor (measured using an incremental encoder); and $w\left(t\right)$ is a vector that takes into account the noise in the model caused by uncertainties, nonlinear effects, and external disturbances.

Based on the accepted concept of the structure of the Kalman filter, the state vector is determined by the following:

$$x\left(t\right)=\left[\begin{array}{c}{\omega }_m\left(t\right)\\ {\dot{\omega }}_m\left(t\right)\\ T_{load}\left(t\right)\end{array}\right]$$

(6)

and the control vector will be the following:

$$u\left(t\right)=\left[\begin{array}{c}{T}_{el}\left(t\right)\\ {\omega }_{motor}\left(t\right)\end{array}\right]$$

(7)

Based on the selected states and control variables, the equations describe the dynamics of each of the components in $x\left(t\right)$. For this purpose, Equation (4) is transformed into the following form:

$$\begin{gathered} {\dot{\omega }}_m\left(t\right)=-{\displaystyle \frac{B_m}{J_m}}·{\omega }_m\left(t\right)-{\displaystyle \frac{1}{J_m}}·T_{load}\left(t\right)+{\displaystyle \frac{{\eta }_{pump}}{J_m}}·T_{el}\left(t\right)-{\displaystyle \frac{{\eta }_{pump}·B_e}{J_m}}·{\omega }_{motor}\left(t\right) \\ -{\displaystyle \frac{{\eta }_{pump}·J_e}{J_m}}·{\dot{\omega }}_{motor}\left(t\right) \end{gathered}$$

(8)

Based on the selected states and control variables, the system can be written as a set of three simple differential equations corresponding to each component of the vector $x\left(t\right)$:

$${\dot{x}}_1\left(t\right)={\displaystyle \frac{d}{dt}}{\omega }_m\left(t\right)=x_2\left(t\right)$$

(9)

$$x_2\left(t\right)={\dot{\omega }}_m\left(t\right)=-{\displaystyle \frac{B_m}{J_m}}·x_1\left(t\right)-{\displaystyle \frac{1}{J_m}}·x_3\left(t\right)+{\displaystyle \frac{{\eta }_{pump}}{J_m}}·u_1\left(t\right)-{\displaystyle \frac{{\eta }_{pump}·B_e}{J_m}}·u_2\left(t\right)$$

(10)

$${\dot{x}}_3\left(t\right)={\displaystyle \frac{d}{dt}}{T}_{load}\left(t\right)$$

(11)

Although Equation (10) formally uses a notation in the form of a simple first-order differential equation, it should be clarified that this equation does not express the derivative of ${\dot{\omega }}_m\left(t\right)$ [i.e., ${\ddot{\omega }}_m\left(t\right)$] and is essentially an algebraic model for calculating ${\dot{\omega }}_m\left(t\right)$ based on the current state of the system and the control impacts. This means that in the specific implementation of the Kalman filter, the second state, $x_2\left(t\right)={\dot{\omega }}_m\left(t\right)$, is not integrated through its own dynamics but is calculated directly in real time using the values of ${\omega }_m\left(t\right)$, $T_{load}\left(t\right)$, and the input values $T_{el}\left(t\right)$ and ${\omega }_{motor}\left(t\right)$. A detailed description of this approach is presented in Section 3.1.

In the process of constructing the state model within the Kalman filter, it is necessary to develop the dynamics of the external load, $T_{load}\left(t\right)$, which is generally a time-varying quantity. Equation (11), which describes the variation in the load over time, does not provide sufficient information about this change. In order to represent this behavior more accurately, an approximate differential model is used, which takes into account both external influences and internal interactions in the system:

$${\dot{T}}_{load}\left(t\right)=-k_t·\left[{\omega }_m\left(t\right)-{\omega }_{motor}\left(t\right)\right]-k_d·T_{load}\left(t\right)+k_p·\left[P_{in}\left(t\right)-P_{out}\left(t\right)\right]$$

(12)

where $k_t$ is the load sensitivity coefficient, which characterizes the influence of the difference between the angular velocity of the hydraulic motor, ${\omega }_m\left(t\right)$, and that of the electric motor, ${\omega }_{motor}\left(t\right)$, on the rate of change of the load; $k_d$ is the dissipation coefficient, which models the natural tendency to reduce the impact of the load over time; $k_p$ is the pressure correction factor; $P_{in}\left(t\right)$ is the measured value of the hydraulic motor inlet pressure; and $P_{out}\left(t\right)$ is the measured value of the pressure at the outlet of the hydraulic motor.

A more detailed analysis of this model, including the methodology for identifying the coefficients $k_t$, $k_d$, and $k_p$, is presented in Section 3.2.

Following Equation (12), the relationship between the change in load and the states and inputs of the system is described as follows:

$${\dot{x}}_3\left(t\right)=-k_t·x_1\left(t\right)+k_t·u_2\left(t\right)-k_d·x_3\left(t\right)$$

(13)

where $x_1\left(t\right)={\omega }_m\left(t\right)$; $x_3\left(t\right)=T_{load}\left(t\right)$; and $u_2\left(t\right)={\omega }_{motor}\left(t\right)$.

Equation (13) does not include the component determining the load correction based on the difference between the measured pressures because this is not a function of either the states or the control inputs, rather serving as an external corrective signal. For this reason, it is not involved in structuring matrices A and B but is used at a later stage in estimating the change in torque created by the load. It is included to compensate for deviations between the set values of the load and the actual realized moment due to hydraulic, electromagnetic, and inertial influences that are not fully reflected in the basic regression model.

It follows that the values of $k_t$ and $k_d$, respectively, define the elements $A_{31}=-k_t$ and $A_{33}=-k_d$ of matrix A and $B_{32}=k_t$ of matrix B.

Because the second state, $x_2\left(t\right)={\dot{\omega }}_m\left(t\right)$, is calculated in real time using an algebraic model, it does not have its own differential dynamics and cannot be described by an equation of the form ${\dot{x}}_2\left(t\right)=A_{2\ast }·x\left(t\right)+B_{2\ast }·u\left(t\right)$. Therefore, when formulating the dynamics of the system in a form compatible with the classical Kalman filter, its matrices refer only to those states for which differential equations exist [here, the lines for ${\omega }_m\left(t\right)$ and $T_{load}\left(t\right)$], while the value of ${\dot{\omega }}_m\left(t\right)$ is updated algebraically in each iteration. This requires a structural “separation” of the predictive step through the combined use of dynamic prediction and algebraic renewal, according to the formulation of Equation (8).

To preserve the overall structure and index sequence of states in the model, the matrices $A$ and $B$ are presented in full size ($3\times 3$ and $3\times 2$, respectively), with their second lines containing zeros. This is determined by the fact that the state of ${\dot{\omega }}_m\left(t\right)$ does not have its own differential dynamics but is calculated algebraically after the predictive step. This achieves full compatibility with the implementation of the Kalman filter, without violating the order and size of the matrix operations.

Thus, matrix A will be as follows:

$$A=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 0\\ -k_t& 0& -k_d\end{array}\right]$$

(14)

and matrix B, as follows:

$$B=\left[\begin{array}{cc}0& 0\\ 0& 0\\ 0& k_t\end{array}\right]$$

(15)

The algebraic calculation of $x_2\left(t\right)$ is carried out after each iteration, according to Equation (25).

The measurement model for the application of the Kalman filter is presented in the following general linear form:

$$z\left(t\right)=C·x\left(t\right)+v\left(t\right)$$

(16)

where $z\left(t\right)$ is the measurement vector; $C$ is the measuring matrix, describing the relationship between the measured quantities and the states vector; and $v\left(t\right)$ is the vector determining the noise and measurement errors.

The measurement vector will be as follows:

$$z\left(t\right)=\left[\begin{array}{c}{\omega }_m\left(t\right)\\ ∆P\left(t\right)\end{array}\right]$$

(17)

where $∆P\left(t\right)$ is the pressure difference at the inlet and outlet of the hydraulic motor. Both quantities in $z\left(t\right)$ are measured using sensors located based on the configuration of the system described in Section 2.

The relationship between the measured pressure and the internal state of the system is derived from the equation for the balance of moments in the hydraulic motor:

$$T_{hid}\left(t\right)={\displaystyle \frac{V_d}{2\pi }}·∆P\left(t\right)$$

(18)

where $V_d$ is the displacement of the hydraulic motor.

After substituting Equation (18) into Equation (1), the following expression is obtained for the applied load:

$$T_{load}\left(t\right)={\displaystyle \frac{V_d}{2\pi }}·∆P\left(t\right)-J_m·{\dot{\omega }}_m\left(t\right)-B_m·{\omega }_m\left(t\right)$$

(19)

From Equation (19), the expression for $∆P\left(t\right)$ follows as a linear combination of the states:

$$∆P\left(t\right)={\displaystyle \frac{2\pi }{V_d}}·J_m·{\dot{\omega }}_m\left(t\right)+{\displaystyle \frac{2\pi }{V_d}}·B_m·{\omega }_m\left(t\right)+{\displaystyle \frac{2\pi }{V_d}}·T_{load}\left(t\right)$$

(20)

Equation (20) determines the measured pressure difference, $∆P\left(t\right)$, as a linear function of the states of the system, ${\omega }_m\left(t\right)$, ${\dot{\omega }}_m\left(t\right)$, and $T_{load}\left(t\right)$. This ratio is important for the operation of the Kalman filter because it allows it to integrate pressure information into the process of evaluating hidden states. For example, under a fixed load, the filter “expects” a certain level of pressure for a given speed and acceleration, which increases the accuracy of the prediction and control of the system. In addition, the model allows for timely detection of deviations due to load changes or malfunctions in the hydraulic part.

At the output of the measuring matrix, $C$, it is taken into account that the only directly measured magnitude of the state vector is angular velocity, ${\omega }_m\left(t\right)$, with the pressure, $∆P\left(t\right)$, expressed as a linear combination of the states, according to Equation (20), in which the full form of the measuring matrix, $C$, will be as follows:

$$C=\left[\begin{array}{ccc}1& 0& 0\\ {\displaystyle \frac{2\pi }{V_d}}·B_m& {\displaystyle \frac{2\pi }{V_d}}·J_m& {\displaystyle \frac{2\pi }{V_d}}\end{array}\right]$$

(21)

The following then follows from Equations (16) and (21):

$$z\left(t\right)=\left[\begin{array}{ccc}1& 0& 0\\ {\displaystyle \frac{2\pi }{V_d}}·B_m& {\displaystyle \frac{2\pi }{V_d}}·J_m& {\displaystyle \frac{2\pi }{V_d}}\end{array}\right]·\left[\begin{array}{c}{\omega }_m\left(t\right)\\ {\dot{\omega }}_m\left(t\right)\\ T_{load}\left(t\right)\end{array}\right]+v\left(t\right)$$

(22)

Matrix $C$ defines the linear relationship between the measured values and the states in the system, allowing the Kalman filter to make corrections based on real sensor data, reflecting both the kinematics of the hydraulic motor and its load.

3.1. Algebraic State Determination and Structural Adaptation of the Kalman Filter

As mentioned above, in the presented model of the electro-hydraulic system, a structural adaptation of the Kalman filter was applied, in which one of the states in the vector $x\left(t\right)$—the angular acceleration of the hydraulic motor shaft, ${\dot{\omega }}_m\left(t\right)$—was not modeled by a differential equation but was calculated algebraically in each iteration of the algorithm’s predictive step.

After the values are predicted,

$${\widehat{x}}_1\left[k|k-1\right]={\widehat{\omega }}_m\left[k|k-1\right]; {\widehat{x}}_3\left[k|k-1\right]={\widehat{T}}_{load}\left[k|k-1\right]$$

(23)

and the control inputs are known,

$$u_1\left[k-1\right]=T_{el}\left[k-1\right]; u_2\left[k-1\right]={\omega }_{motor}\left[k-1\right]$$

(24)

the second state is calculated using the following algebraic expression:

$$\begin{gathered} {\widehat{x}}_2\left[k|k-1\right]=-{\displaystyle \frac{B_m}{J_m}}·{\widehat{x}}_1\left[k|k-1\right]-{\displaystyle \frac{1}{J_m}}·{\widehat{x}}_3\left[k|k-1\right]+{\displaystyle \frac{{\eta }_{pump}}{J_m}}·u_1\left[k-1\right] \\ -{\displaystyle \frac{{\eta }_{pump}·B_e}{J_m}}·u_2\left[k-1\right] \end{gathered}$$

(25)

where ${\widehat{\omega }}_m\left[k|k-1\right]$ is the estimated value of the angular velocity of the hydraulic motor, determined based on the information in the $k-1$ iteration; and ${\widehat{T}}_{load}\left[k|k-1\right]$ is the estimated value of the moment of the external load, determined based on the $k-1$ iteration.

This approach allows for the storage of ${\dot{\omega }}_m\left(t\right)$ in the state vector, which is essential for the accuracy of the estimates, this quantity being directly involved in the expressions for the measured values (particularly in the pressure model) without requiring the introduction of a second derivative. In this way, a combination is achieved between the formal structure of a linear system and the algebraically defined states, which is fully compatible with the classical Kalman linear filter and provides high computational efficiency and accuracy of real-time estimates.

An additional advantage of this approach is that it avoids the need for the numerical integration of signals with superimposed noise, which often leads to the accumulation of errors in real data. Instead, the acceleration value is calculated algebraically using current states and input quantities, which improves the robustness of the estimates under dynamic load modes. This creates a structure in which some of the states are defined dynamically and others analytically, without disturbing the sequence of matrix operations in the filter. This expands the possibilities for applying the method to real systems with internal variables that are not subject to direct measurement or that are measured with high uncertainty, such as the electro-hydraulic system in the present study. Due to its flexibility and compatibility with the algorithms of the classical Kalman filter, the proposed structure has the potential for application in other technical systems, in which some of the states cannot be measured directly but are subject to algebraic calculation based on available measurements and input effects.

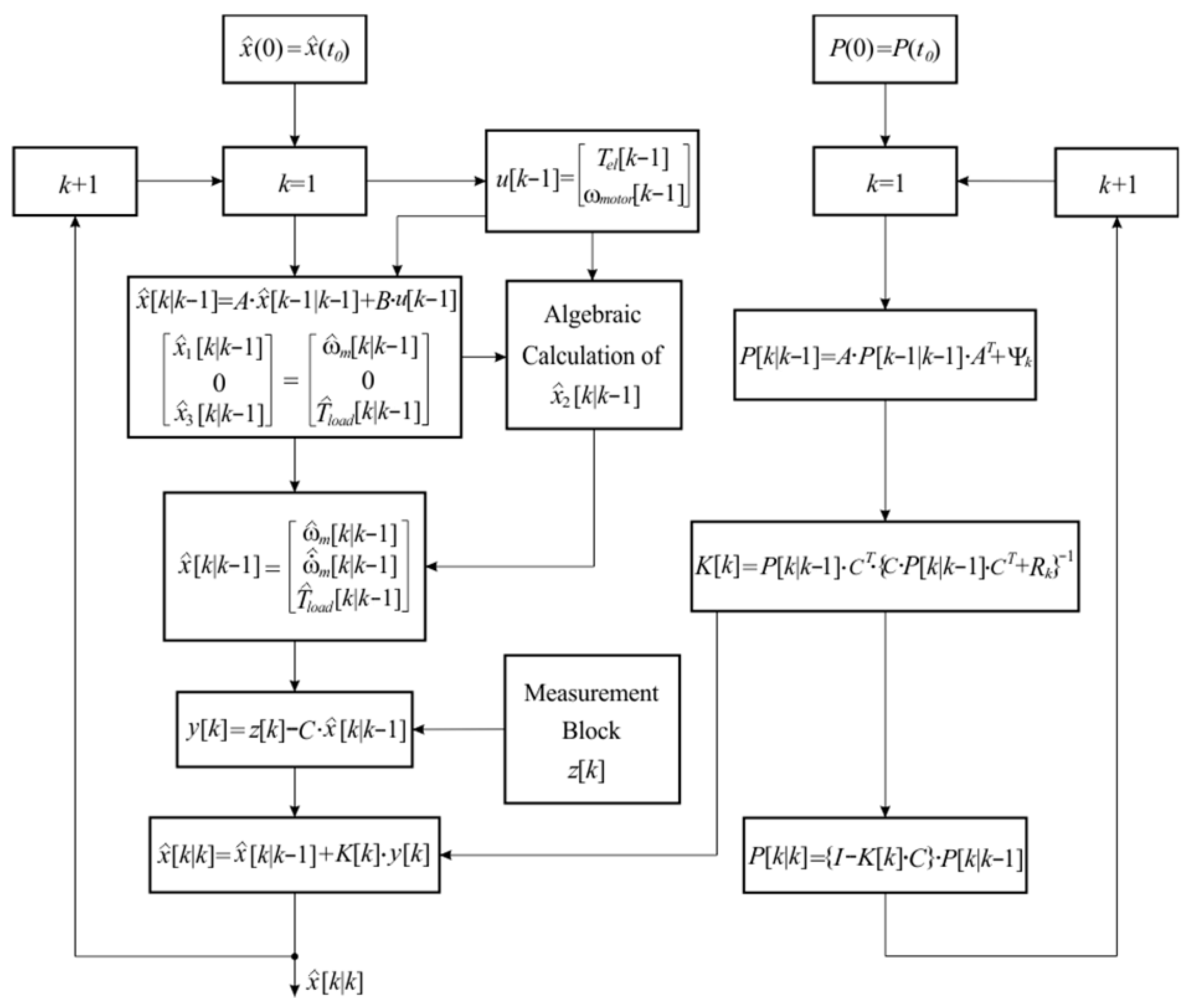
The principles for the development of the Kalman filter outlined above are graphically illustrated in the block diagram in Figure 2. The structure was developed in two parallel circuits––one for estimation of the states, $\widehat{x}\left[k|k\right]$, the other for the dynamic computation of the covariance matrices, $P\left[k|k-1\right]$ and $P\left[k|k\right]$, and the Kalman gain, $K\left[k\right]$, which determine the forecast error covariance, the updated estimate covariance, and the weighting factor for the state correction, respectively. The calculation of these quantities was based on the dynamic and measurement patterns shown in the algorithm. The first circuit covered the prediction of states, the algebraic determination of angular acceleration, and the updating of estimates using innovation. In this part of the scheme, the load was considered as a dynamic variable identified by empirical modeling based on experimental data and numerical analysis, as detailed in Section 3.2. The second circuit calculated and updated the covariance matrices and the coefficient $K\left[k\right]$ based on the dynamic and measurement models presented in the algorithm, thus taking into account the influence of nonlinearities and noises in each iteration. This chain includes an adaptive mechanism for updating the covariance matrix of errors in the model, as discussed in detail in Section 4, and a hybrid algorithm for determining the correlation matrix of measurement errors, as described in Section 5.

3.2. Empirical Modeling and Identification of External Load Dynamics

As shown in Equation (12), the dynamics of the external load, $T_{load}\left(t\right)$, are described by an approximate differential model that takes into account both external influences and internal dissipation mechanisms in the system. In order for this dependence to be integrated into the structure of the Kalman filter, it was necessary to quantify $k_t$, $k_d$, and $k_p$ based on experimental data. The methodology used to numerically determine the coefficients $k_t$ and $k_d$ and the pressure correction factor, $k_p$, involved regression analysis, based on experimental data on the control inputs and measured quantities. To limit the effect of measurement noise and increase the robustness of the regression model, the measured values of angular velocity and pressure difference were smoothed using the Savitzky–Golay filter [29]. This provides more reliable input data for the identification of external load dynamics.

The selection of a regression model to describe the dynamics of the external load was driven by the need for a clear, physically justified, and structurally unambiguous approach that would enable seamless integration into the Kalman filter structure. While there were other methods with higher computational complexity, they usually require a significantly larger amount of training data, specific settings, and subsequent validation of the results obtained. By contrast, the proposed regression methodology provides good accuracy, noise resistance, and a direct relationship to the physical characteristics of the system, which is essential in engineering applications with a limited set of experimental data.

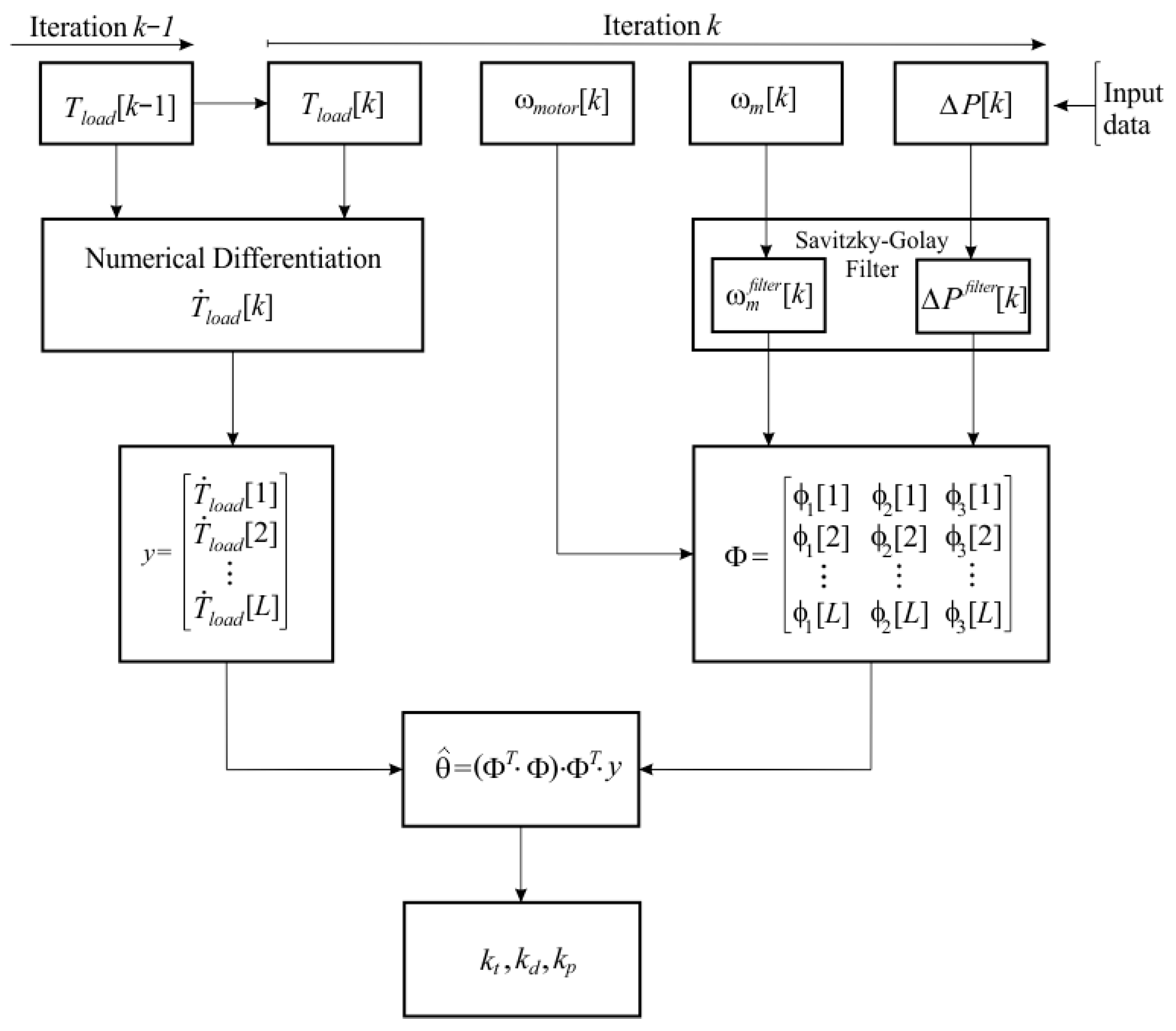
The generalized algorithm for identifying the coefficients is presented in Figure 3. The input data include the measured values of the angular velocity of the hydraulic motor, ${\omega }_m\left(t\right)$, the control angular velocity, ${\omega }_{motor}\left(t\right)$, and the pressure difference at the inlet and outlet of the hydraulic system, $∆P\left(t\right)=P_{in}\left(t\right)-P_{out}\left(t\right)$. To limit the influence of noise, the Savitzky–Golay filter was applied to selected signals. The derivative of the load value was calculated by numerical differentiation. The obtained values were used to form a vector of the observed values and a regression matrix, to which an optimization procedure for evaluating the parameters $k_t$, $k_d$, and $k_p$ was applied.

It should be clarified that in the context under consideration, $T_{load}\left(t\right)$ was not interpreted as a constant physical mass or external mechanical object but as a dynamic variable reflecting the instantaneous response of the load on the system. Even when the load itself, as a physical object, remains unchanged, its torque on the system can change as a result of internal processes. This dynamic change is modeled by $-k_d·T_{load}\left(t\right)$. The coefficient $k_d$ determines the internal mechanisms of energy dissipation in the system which lead to a gradual attenuation of the load response. These mechanisms include the following: viscous hydraulic losses, with internal friction of the working fluid leading to conversion of part of the energy into heat; friction in the mechanical elements, with bearing units, pistons, seals, and other moving parts helping reduce the effective load; and elastic deformations and vibrations at the micro-scale in the components attenuating over time, with part of the energy being lost in the form of mechanical vibrations, sound, or heat.

All these effects were summed and modeled empirically by the coefficient $k_d$. It determined how quickly the impact of the load on the system faded, even when the external load, such as the mass, remained constant. Thus, the model allows for an adequate description of the real behavior of the electro-hydraulic system under dynamic conditions. Along with this, the coefficient $k_t$ characterized the transmission of the moment from the input angular velocity of the electric motor to the response of the load. It describes the proportional relationship between the control effect and the dynamic change of the load, including the influence of inertial effects and resistances along the mechanical path of energy transfer.

The coefficients $k_t$, $k_d$, and $k_p$ were determined experimentally by means of sequences of experimental data, including the measured values of ${\omega }_m\left(t\right)$, $∆P\left(t\right)$, and ${\omega }_{motor}\left(t\right)$ and the known-in-advance values of $T_{load}\left(t\right)$. The latter values were set by simulated load effects in a controlled experimental setup in which the reference values of $T_{load}\left(t\right)$ were known in advance, allowing for the tracking of its dynamic response. In order to ensure wider applicability of the identified coefficients, the experiments were carried out under a variety of load modes that reproduced the different dynamic characteristics encountered under real operating conditions. Because the derivative ${\dot{T}}_{load}\left(t\right)$ was not directly measurable, it was approximated using the central finite differences method:

$${\dot{T}}_{load}\left[k\right]={\displaystyle \frac{T_{load}\left[k\right]-T_{load}\left[k-1\right]}{∆t}}$$

(26)

where $T_{load}\left[k\right]$ is the value of the load in the kth iteration; $T_{load}\left[k-1\right]$ is the value of the load in the (k − 1)th iteration; and $∆t$ is the time interval between two measurements.

When setting the experimental impact with predetermined load torque values, their exact reproduction in the real system was not always achieved, and so an additional correction component, based on the measured pressure difference, was included in the model. This adjustment, defined by the coefficient $k_p$, aimed to compensate for possible discrepancies due to dynamic losses, nonlinearities, or inertial effects that could result in deviations between the reference load and the actual realized load. This provided higher reliability in estimating the actual dynamics of the load and improved the correspondence between the model and the behavior of the system.

The resulting approximation is used to build a regression model with two input variables:

$${\dot{T}}_{load}\left[k\right]=-k_t·\left\{{\omega }_m\left[k\right]-{\omega }_{motor}\left[k\right]\right\}-k_d·T_{load}\left[k\right]+k_p·∆P\left[k\right]$$

(27)

In regression matrix form, this is as follows:

$$y\left[k\right]=\left[\begin{array}{ccc}{\omega }_m\left[k\right]-{\omega }_{motor}\left[k\right]& T_{load}\left[k\right]& ∆P\left[k\right]\end{array}\right]·\left[\begin{array}{c}-k_t\\ -k_d\\ k_p\end{array}\right]$$

(28)

Once they accumulate L per number of measurements, the regression matrix and the observation vector are presented as follows:

$$\mathsf{\Phi }=\left[\begin{array}{ccc}{\varphi }_1\left[1\right]& {\varphi }_2\left[1\right]& {\varphi }_3\left[1\right]\\ {\varphi }_1\left[2\right]& {\varphi }_2\left[2\right]& {\varphi }_3\left[2\right]\\ ⋮& ⋮& ⋮\\ {\varphi }_1\left[L\right]& {\varphi }_2\left[L\right]& {\varphi }_3\left[L\right]\end{array}\right]=\left[\begin{array}{ccc}{\omega }_m\left[1\right]-{\omega }_{motor}\left[1\right]& T_{load}\left[1\right]& ∆P\left[1\right]\\ {\omega }_m\left[2\right]-{\omega }_{motor}\left[2\right]& T_{load}\left[2\right]& ∆P\left[2\right]\\ ⋮& ⋮& ⋮\\ {\omega }_m\left[L\right]-{\omega }_{motor}\left[L\right]& T_{load}\left[L\right]& ∆P\left[L\right]\end{array}\right]$$

(29)

$$y=\left[\begin{array}{c}{\dot{T}}_{load}\left[1\right]\\ {\dot{T}}_{load}\left[2\right]\\ ⋮\\ {\dot{T}}_{load}\left[L\right]\end{array}\right]$$

(30)

The method of least squares is applied, with the estimation of the parameters being obtained from the following [30]:

$$\widehat{\theta }={\left({\mathsf{\Phi }}^T·\mathsf{\Phi }\right)}^{-1}·{\mathsf{\Phi }}^T·y$$

(31)

And the following, respectively:

$$\widehat{\theta }=\left[\begin{array}{c}{\widehat{\theta }}_1\\ {\widehat{\theta }}_2\\ {\widehat{\theta }}_3\end{array}\right]=\left[\begin{array}{c}-k_t\\ -k_d\\ k_p\end{array}\right]$$

(32)

The quantification of the coefficients $k_t$, $k_d$ and $k_p$ was carried out through a series of characteristic operating modes, including the three experimental studies discussed in Section 6: with a linear increasing load, with a stepwise change in the torque load, and with an asymmetrical sawtooth load. Each of these modes is implemented at different values of the parameters characterizing the respective load, which allows for the coverage of a wider range of dynamic behavior of the system.

The values of the coefficients are determined automatically based on the algorithm illustrated in Figure 3. The input data for this algorithm are the simultaneously measured quantities—the angular velocity of the hydraulic motor, ${\omega }_m\left(t\right)$, the control angular velocity, ${\omega }_{motor}\left(t\right)$, and the pressure difference at the inlet and outlet of the hydraulic system $∆P\left(t\right)=P_{in}\left(t\right)-P_{out}\left(t\right)$—that form the regression matrix, $\mathsf{\Phi }$, as well as the values of the set load moment, $T_{load}$, that determine the vector of observations. In this way, the identification process takes place completely automatically, and the data from the experiment are directly fed into the software implementation of the algorithm. The algorithm is executed in increments, $∆t=0.02 \mathrm{s}$, at a sample rate of 50 Hz and a total number of 500 measurement points. This choice is consistent with both the dynamics of the electro-hydraulic system and the capabilities of the measuring instruments used.

After the identification procedure for each operating mode has been completed, r, a trio of odds scores is obtained:

$${\widehat{\theta }}_r=\left[\begin{array}{c}{\widehat{k}}_{t,r}\\ {\widehat{k}}_{d,r}\\ {\widehat{k}}_{p,r}\end{array}\right], r=1, 2, \dots ,R$$

(33)

As different modes are characterized by different dynamics and different degrees of correspondence of the model with real data, direct arithmetic averaging of estimates would lead to significant distortions. Therefore, a weighting procedure is applied, whereby each triplet of assessments is taken into account according to the quality of the relevant regime.

The quality of compliance is assessed by two criteria—Mean Square Error (MSE) and the coefficient of determination, $R^2$, calculated according to the following formulas:

$${MSE}_r={\displaystyle \frac{1}{L}}·\sum _{i=1}^L{\left(y_i-{\widehat{y}}_{i,r}\right)}^2$$

(34)

$$R_r^2=1-{\displaystyle \frac{\sum _{i=1}^L{\left(y_i-{\widehat{y}}_{i,r}\right)}^2}{\sum _{i=1}^L{\left(y_i-\overline{y}\right)}^2}}$$

(35)

where $y_i$—measured values; ${\widehat{y}}_{i,r}$—calculated by the model; and $\overline{y}$—average value.

For each mode, a weight factor, $w_r,$ is formed, which is inversely proportional to the error and/or directly proportional to the determination, as in, for example, the following:

$$w_r={\displaystyle \frac{R_r^2}{{MSE}_r}}$$

(36)

The final odds estimates are calculated as a weighted average:

$${\widehat{\theta }}_r=\left[\begin{array}{c}{\widehat{k}}_{t,r}\\ {\widehat{k}}_{d,r}\\ {\widehat{k}}_{p,r}\end{array}\right]={\displaystyle \frac{\sum _{r=1}^R{w}_r·{\widehat{\theta }}_r}{\sum _{r=1}^R{w}_r}}$$

(37)

Thus, in the calculation of the final values, those modes in which the model provides a better correspondence with the experimental data, while the influence of weaker modes is reduced, have greater weight. This approach eliminates the influence of random distortions characteristic of individual modes and provides more stable final estimates of the coefficients.

As a result of this procedure, the following final assessments were obtained: $k_t=0.649 \mathrm{N}\mathrm{m}·{\displaystyle \frac{\mathrm{s}}{\mathrm{r}\mathrm{a}\mathrm{d}}}$, $k_d=0.052 {\mathrm{s}}^{-1}$, and $k_p=0.081 {\displaystyle \frac{{\mathrm{m}}^2}{\mathrm{s}}}$.

Along with the identification of the coefficients $k_t$, $k_d$ and $k_p$, in the model, it is necessary to experimentally determine the conversion factor, ${\eta }_{pump}$, which ensures the correct coordination between the input torque from the electric motor and the actual torque transmitted to the hydraulic module. In this paper, it is determined according to an analogous procedure and precedes the evaluation of the other coefficients in order to ensure the physical consistency of the input data.

The determination of ${\eta }_{pump}$ is performed automatically by an algorithm similar to that presented in Figure 3, used for the identification of the coefficients $k_t$, $k_d$ and $k_p$. The algorithm is applied in all experimental modes considered in the identification process, and for each mode, r, a separate value is calculated, ${\eta }_{pump,r}$.

The obtained values, ${\eta }_{pump,r}$, for each experimental mode are not averaged directly but combined by weighted generalization, where the contribution of each assessment depends on the quality of the correspondence between the model and the real data. This quality is evaluated through two established criteria, MSE and the coefficient of determination, $R^2$, similar to the procedure used for the identification of the coefficients $k_t$, $k_d$ and $k_p$. Thus, estimates from those modes in which the model provides a lower error and a better explanation of the variation in the data are given more weight in the final value of ${\eta }_{pump}$.

The final value is calculated using formulas identical to 33 ÷ 37, used to combine the results of the other coefficients, which ensures full methodological consistency within the model.

In this sense, the identification of ${\eta }_{pump}$ provides basic calibration of the model, ensuring the correct conversion of the input torque from the electric motor to the hydraulic module. Subsequently, the coefficients identified, $k_t$, $k_d$ and $k_p$, further specify and refine the dynamic description of the system, taking into account the internal dissipation mechanisms and the influence of pressure. Thus, the three coefficients can be considered as building parameters that adapt the model to real conditions and guarantee its reliability under different load modes.

The proposed methodology extends the classical approach to the formation of states in the Kalman filter by introducing an experimentally identified differential model of the external load. By combining the Savitzky–Golay pretreatment filter with a regression procedure for numerical parameterization, it provides reliable tracking of the load status in the filter and increases the accuracy of variable mode estimations.

4. Development of an Adaptive Method for Determining the Covariance Matrix of Errors in the Theoretical Model

In accordance with Equation (5), to describe the dynamics of the system, it was also necessary to define the model of random deviations, $w\left(t\right)$, which determined the impact of errors, nonlinear effects, and external interference on the behavior of the electro-hydraulic system. The statistical characteristics of this noise are given by the covariance matrix, $\mathbf{\Psi }$, whose correct setting is important for the effectiveness of the Kalman filter.

Because the real system was characterized by pronounced nonlinearities, dynamic changes in the operating conditions, and the presence of noise, static determination of the matrix, $\mathbf{\Psi }$, would lead to a decrease in the accuracy of the estimates. Therefore, in this work, the variances in the covariance matrix, $\mathbf{\Psi }$, were determined based on the successive differences calculated in the iterative procedure. These differences formed between the actual changes in the parameters determining the state of the system, calculated on the basis of their derivatives, and the forecast changes in the same parameters, determined by the linear model of the dynamics of the system.

The utilization of parameter derivatives rather than their discrete values at the iteration points was driven by the need to enhance the filter’s accuracy and adaptability in dynamic environments. Derivatives capture the rate of parameter change, which is critical for systems exposed to rapidly varying operational conditions. This enables the model to respond and adjust in real time to evolving system behaviors. Moreover, derivative-based measurements exhibit greater resilience to the noise and deviations typically present in direct parameter observations, thereby reducing reliance on the absolute accuracy of the sensors. Computation of the derivatives further facilitates improved state prediction by emphasizing temporal trends rather than isolated static values. Incorporating derivatives into the model also reflects the physical essence of the system processes, such as variations in pressure or acceleration, that are essential for effective control and adaptation.

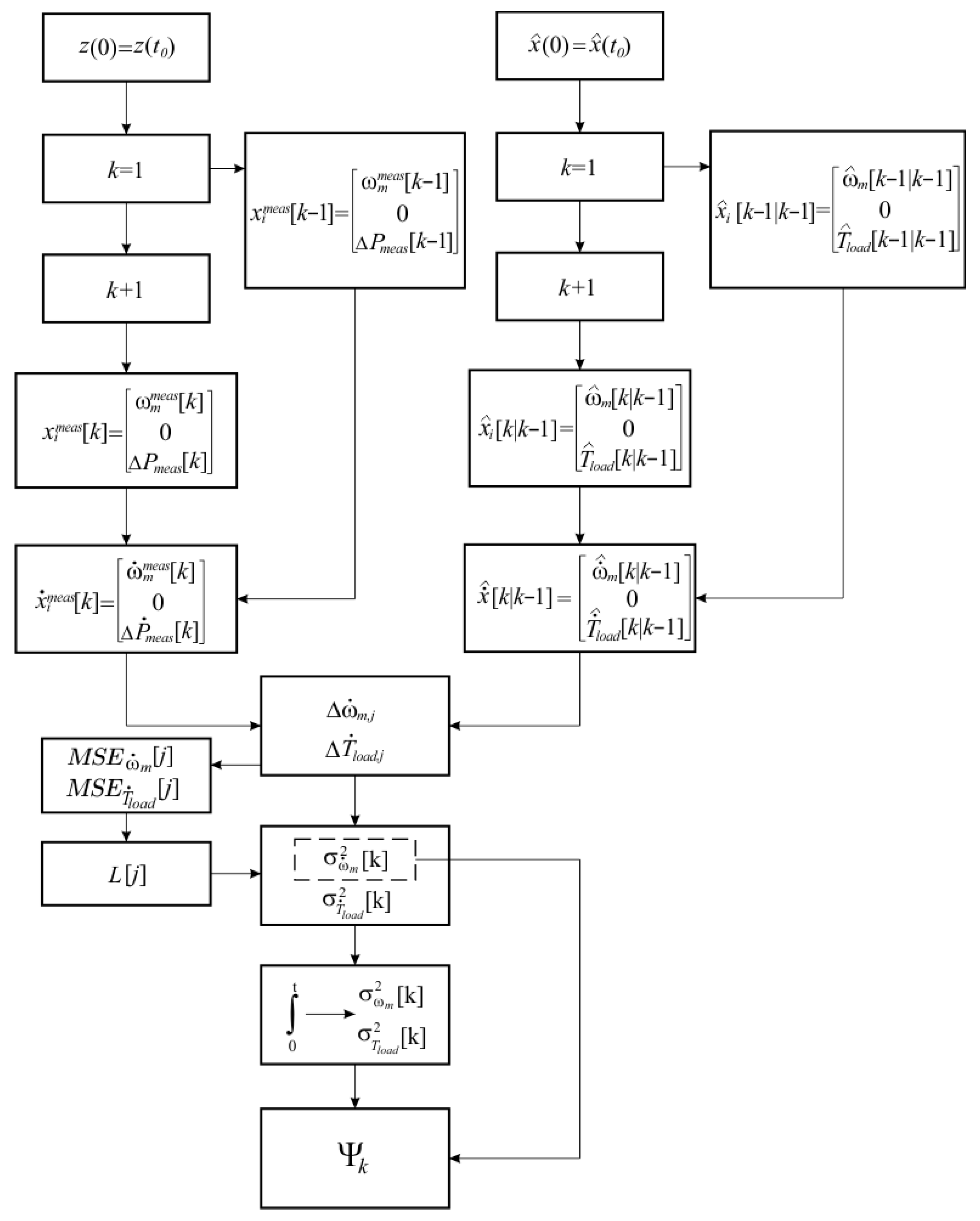
The goal of this approach was to ensure the adaptability of the Kalman filter so that it could accommodate the current nonlinearities and noises in the system. This ensured more accurate assessments of the state of the system and optimal control of the electro-hydraulic motor. The procedure for adaptive determination of the elements in the matrix, $\mathbf{\Psi }$, is summarized in Figure 4, where the steps for calculating the variances of model errors and updating the parameters are presented.

The calculation of variances in the covariance matrix, $\mathbf{\Psi }$, was based on determining the differences between the actual parameter changes and the estimated values calculated by the linear filter model. The real changes were determined based on the derivatives of the parameters, and for each iteration, they were calculated by the difference between the measured values of the parameter at the beginning and end of the time interval, divided by the duration of this interval:

$${\dot{x}}_i^{meas}\left(t\right)={\displaystyle \frac{x_i^{meas}\left(t\right)-x_i^{meas}\left(t-\Delta t\right)}{\Delta t}}$$

(38)

where $i=1, 2, 3$; $\left(1\equiv {\omega }_m\left(t\right);2\equiv {\dot{\omega }}_m\left(t\right);3\equiv T_{load}\left(t\right)\right)$; and $∆t$ is the time between two iterations.

The estimates of the derivatives in the Kalman filter are calculated in a similar way but based on the estimated values of the model:

$${\widehat{\dot{x}}}_i\left(t\right)={\displaystyle \frac{{\widehat{x}}_i\left(t\right)-{\widehat{x}}_i\left(t-∆t\right)}{∆t}}$$

(39)

The differences between the measured and forecast values for each parameter of the state vector, $x\left(t\right)$, are as follows:

$$∆{\dot{x}}_i\left(t\right)={\dot{x}}_i^{meas}\left(t\right)-{\widehat{\dot{x}}}_i\left(t\right)$$

(40)

According to the structure of the Kalman filter, it is necessary to switch to discrete time, where k is the current moment of the iterative process, and k − 1 is the moment in the previous iteration. Because angular velocity is a measured quantity and is reported directly by the system, it follows that its derivative in discrete time will be as follows:

$${\dot{\omega }}_m^{meas}\left[k\right]={\displaystyle \frac{{\omega }_m^{meas}\left[k\right]-{\omega }_m^{meas}\left[k-1\right]}{∆t}}$$

(41)

where ${\omega }_m^{meas}\left[k\right]$ is the measured value of the angular velocity at a moment in time corresponding to step $k$; and ${\omega }_m^{meas}\left[k-1\right]$ is the measured value of the angular velocity at a point in time corresponding to the previous step, $k-1$.

The angular acceleration prediction in the Kalman filter is expressed by the difference between the predicted values of ${\omega }_m\left(t\right)$ at the current and previous moments:

$${\widehat{\dot{\omega }}}_m\left[k|k-1\right]={\displaystyle \frac{{\widehat{\omega }}_m\left[k|k-1\right]-{\widehat{\omega }}_m\left[k-1|k-1\right]}{∆t}}$$

(42)

where ${\widehat{\dot{\omega }}}_m\left[k|k-1\right]$ is the estimated value of the parameter ${\dot{\omega }}_m\left(t\right)$ at the time corresponding to step $k$; ${\widehat{\omega }}_m\left[k|k-1\right]$ is the estimated value of the parameter ${\omega }_m\left(t\right)$ at the time corresponding to step $k$, based on the current state, $k-1$; and ${\widehat{\omega }}_m\left[k-1|k-1\right]$ is the posterior estimate of the value of the parameter ${\omega }_m\left(t\right)$ at the time corresponding to step $k-1$, taking into account all the measurements so far.

Angular acceleration, ${\dot{\omega }}_m\left(t\right)$, is not measured directly by the system, but the covariance matrix, $\mathbf{\Psi }$, and dispersion, ${\sigma }_{{\dot{\omega }}_m}^2$, can be determined by the measurement and calculation procedure for ${\omega }_m\left(t\right)$.

Determining the loading moment, $T_{load}\left(t\right)$, is carried out indirectly, based on data from the measured pressure, which, in the structure of the Kalman filter, is a directly measured parameter. Determining the derivative of the pressure in the kth iteration uses the measured pressure values from the initial, $∆P_{meas}\left[k-1\right]$, and end, $∆P_{meas}\left[k\right]$, points of each successive iteration––that is,

$$∆\dot{P}\left[k\right]={\displaystyle \frac{∆P_{meas}\left[k\right]-{∆P}_{meas}\left[k-1\right]}{∆t}}$$

(43)

From this, the derivative of $T_{load}\left(t\right)$, determined based on current measurements, will be as follows:

$${\dot{T}}_{load}\left[k\right]={\displaystyle \frac{D_m}{2·\pi }}·∆\dot{P}\left[k\right]$$

(44)

The predictive estimate of the derivative of the load on the hydraulic motor, $T_{load}\left(t\right)$, is calculated based on the difference between the obtained forecast values for the current and previous time:

$${\widehat{\dot{T}}}_{load}\left[k|k-1\right]={\displaystyle \frac{{\widehat{T}}_{load}\left[k|k-1\right]-{\widehat{T}}_{load}\left[k-1|k-1\right]}{∆t}}$$

(45)

where ${\widehat{\dot{T}}}_{load}\left[k|k-1\right]$ is the predictive estimate of the load derivative on the hydraulic motor; ${\widehat{T}}_{load}\left[k|k-1\right]$ is the estimated load moment in the current iteration; and ${\widehat{T}}_{load}\left[k-1|k-1\right]$ is the posterior estimate of the loading moment in the previous iteration.

Based on Equation (40), the differences between the derivatives of the state vector parameters, $x\left(t\right)$, can be calculated based on the direct and indirect measurements in N per number of iterations and those from the estimates calculated during the operation of the Kalman filter. These differences are used to determine the variances in the matrix, $\mathbf{\Psi }$, by considering N number of successive iterations, as denoted by the index, j:

$$∆{\dot{\omega }}_{m,j}={\dot{\omega }}_{m,j}^{meas}-{\widehat{\dot{\omega }}}_{m,j|k-1}$$

(46)

$$∆{\dot{T}}_{load,j}={\dot{T}}_{load,j}-{\widehat{\dot{T}}}_{load,j|k-1}$$

(47)

where $∆{\dot{\omega }}_{m,j},∆{\dot{T}}_{load,j}$ are the differences between the derivatives of the parameters of the state vector, $x\left(t\right)$, determined from the direct and indirect measurements in the jth iteration, and the corresponding estimated values calculated by the Kalman filter; ${\dot{\omega }}_{m,j}^{meas}, {\dot{T}}_{load,j}$ are the derivatives derived from the direct or indirect measurements in the jth iteration; and ${\widehat{\dot{\omega }}}_{m,j|k-1},{\widehat{\dot{T}}}_{load,j|k-1}$ are the estimates of the derivatives of the state vector parameters, $x\left(t\right)$, in the jth iteration that are predicted in the filter based on the information available so far, $k-1$.

Then, the variances of the differences determined by Equations (46) and (47) will be as follows:

$$\begin{gathered} {\sigma }_{{\dot{\omega }}_m}^2\left[k\right]={\displaystyle \frac{1}{N-1}}·\sum _{j=1}^N{\left(∆{\dot{\omega }}_{m,j}-∆{\overline{\dot{\omega }}}_m\right)}^2 \\ {\sigma }_{{\dot{T}}_{load}}^2\left[k\right]={\displaystyle \frac{1}{N-1}}·\sum _{j=1}^N{\left(∆{\dot{T}}_{load,j}-∆{\overline{\dot{T}}}_{load}\right)}^2 \end{gathered}$$

(48)

where ${\sigma }_{{\dot{\omega }}_m}^2\left[k\right]$ and ${\sigma }_{{\dot{T}}_{load}}^2\left[k\right]$ are the variances of the derivatives calculated for the current iteration.

Because the variances in Equation (48) refer to the derivatives of the quantities that determine the state vector, and the matrix, $\mathbf{\Psi }$, defines the variances of random errors in the model of the quantities themselves, it is necessary to convert the variances from the derivatives to the corresponding quantities, taking into account the time interval between the iterations and the accumulation of errors over time. For this purpose, the following integral transformation was used [31]:

$$D\left[x\left(t\right)\right]=\underset{0}{\overset{t}{\int }}D\left[\dot{x}\left(\tau \right)\right]·d{\tau }^2$$

(49)

where $\tau$ is the time variable in the integration range, reflecting the accumulation of variance over the time interval $0$ to $t$; $D\left[\dot{x}\left(\tau \right)\right]$ is the variance of the derivative $\dot{x}\left(\tau \right)$ at moment $\tau$; and $D\left[x\left(t\right)\right]$ is the variance of the quantity $x\left(t\right)$, calculated by integrating the variance of the derivative, $\dot{x}\left(\tau \right)$, in time.

In discrete time, and in accordance with the structure of the Kalman filter, the variances of the quantities, $x\left(t\right)$, are calculated based on the variances of their derivatives, taking into account the time interval between successive iterations, $∆t$. That is,

$${\sigma }_{{\omega }_m}^2\left[k\right]={\sigma }_{{\dot{\omega }}_m}^2\left[k\right]·{\left(∆t\right)}^2; {\sigma }_{T_{load}}^2\left[k\right]={\sigma }_{{\dot{T}}_{load}}^2\left[k\right]·{\left(∆t\right)}^2$$

(50)

where ${\sigma }_{{\omega }_m}^2\left[k\right]$, ${\sigma }_{{\dot{\omega }}_m}^2\left[k\right]$, and ${\sigma }_{T_{load}}^2\left[k\right]$ are the variances defined by the correlation matrix, $\mathbf{\Psi }$, in the kth iteration.

These variances determine the deviations between the linear theoretical model and the actual behavior of the system. They also characterize the influence of nonlinearities arising as a result of changes in the operating conditions, such as the pressure, temperature, and external loads, as well as the effects of random noise, which can significantly affect the accuracy of the model, in which the full form of the correlation matrix, $\mathbf{\Psi }$, in the kth iteration will be as follows:

$${\mathbf{\Psi }}_k=\left[\begin{array}{ccc}{\sigma }_{{\omega }_m}^2\left[k\right]& 0& 0\\ 0& {\sigma }_{{\dot{\omega }}_m}^2\left[k\right]& 0\\ 0& 0& {\sigma }_{T_{load}}^2\left[k\right]\end{array}\right]$$

(51)

The covariance matrix, ${\mathbf{\Psi }}_k$, is a variable, and its values are updated adaptively in each step of the iteration procedure. Errors in the linear model determined by this matrix are primarily due to nonlinearities, noises, and other deviations caused by changes in the pressure, temperature, and external loads. These deviations lead to a decrease in the accuracy of the model, but the Kalman filter allows the adaptive nature of the matrix, ${\mathbf{\Psi }}_k$, to adjust to the current state of the system and the dynamic changes in the operating conditions, thus improving the condition ratings.

To ensure adaptive matrix determination, ${\mathbf{\Psi }}_k$, it was necessary to define a method to update its parameters, including the number of iterations, the values of which were used to calculate variances.

In order to avoid unstable or distorted estimates of variances caused by too few values, a two-step formulation is used. The general calculation window is set with the parameter N, which determines the maximum number of iterations on which the differences between real and forecast derivatives are calculated. Within this window, the effective number of values L is selected, which is a dynamic subset of N and is defined adaptively depending on current errors. To avoid unstable or skewed variance estimates at small values, a minimum limit of $L_{min}=10$ shall be introduced. If the calculated value in an iteration, $L\left[j\right]$, is less than $L_{min}$, $L\left[j\right]=L_{min}$ is assumed.

The adaptive definition of $L\left[j\right]$ was based on the analysis of the differences between the measured and predicted values of the derivatives of the state vector parameters defined in Equations (46) and (47). In each iteration, the mean square error (MSE) was calculated based on the differences between the measured and estimated values of the derivatives obtained from the sequential $L\left[j\right]$ iteration.

$${MSE}_{{\dot{\omega }}_m}\left[j\right]={\displaystyle \frac{1}{L\left[j\right]}}·\sum _{j=1}^N∆{{\dot{\omega }}_{m,j}}^2; {MSE}_{{\dot{T}}_{load}}\left[j\right]={\displaystyle \frac{1}{L\left[j\right]}}·\sum _{j=1}^N∆{{\dot{T}}_{load,j}}^2$$

(52)

where ${MSE}_{{\dot{\omega }}_m}\left[j\right]$ and ${MSE}_{{\dot{T}}_{load}}\left[j\right]$ are the MSEs of the predictions for the derivatives of the angular velocity, ${\dot{\omega }}_m\left(t\right)$, in the jth iteration, calculated based on the differences between the measured and estimated values.

When determining the optimal number of points, L, for the calculation of variances in the covariance matrix, ${\mathbf{\Psi }}_k$, an adaptive approach was used based on the ratio between the current MSE, $MSE\left[j\right]$, for the jth and maximum error values defined within the boundaries of the same iteration, ${MSE}_{max}\left[j\right]$. The current value of L for each iteration j is determined by the following expression:

$$L\left[j\right]=L_{min}+\left(L_{max}\left[j\right]+L_{min}\right)·\left(1-{\displaystyle \frac{MSE\left[j\right]}{{MSE}_{max}\left[j\right]}}\right)$$

(53)

The maximum value of the MSE, ${MSE}_{max}\left[j\right]$, for the current iteration j is calculated as the highest value of $MSE\left[\lambda \right]$ in the latter, M, iteration:

$${MSE}_{max}\left[j\right]=\underset{\lambda \in \left[j-M,j\right]}{\max }MSE\left[\lambda \right]$$

(54)

where M is a predefined parameter equal to 10; and λ is an internal index modified by the current variable j, which denotes a subset of successive iterations in the interval $\left[j-M,j\right]$.

5. Development of an Adaptive Method for Determining the Covariance Matrix of Measurement Errors

The covariance matrix of measurement errors, ${\mathbf{R}}_k$, was also determined based on an adaptive update approach that allowed for the compensation of nonlinearity and external interference effects. An accurate estimate of this matrix was essential for the effectiveness of the Kalman filter because it determines the weight of the measured values relative to those predicted in each iteration. The summarized structure of the algorithm for estimating, ${\mathbf{R}}_k$, is illustrated in Figure 5.

As shown in Equation (28), two measured signals were used in the system—the angular velocity of the hydraulic motor, ${\omega }_m\left[k\right]$, and the pressure difference, $∆P\left[k\right]$. In this case, ${\omega }_m\left[k\right]$ was the angular velocity value measured in the current iteration, and $∆P\left[k\right]$ was the difference between the inlet and outlet pressure of the hydraulic motor, also measured at time k.

Both signals were affected by noise, temperature drifts, and dynamic fluctuations in the system, among other factors that can reduce measurement accuracy over time. Therefore, a hybrid method was applied in the model to adaptively determine the variances in the matrix, ${\mathbf{R}}_k$, which combined the ability to predict the filter using an independent analysis of the accuracy of the measurements themselves.

The structural diagram of the algorithm for adaptive determination of the correlation matrix, ${\mathbf{R}}_k$, presented in Figure 5, includes two parallel procedures for estimating the variances of the measurement signals, the first based on exponential smoothing of the error between the measurement and the prediction and the second based on the local regression of previous values to obtain a reference estimate.

Depending on the ratio between the current and reference estimates, the algorithm went through one of two adaptive logics. For limited deviations, a sensitivity correction coefficient was applied, while for more significant differences, the variance was updated with the value obtained from the regression analysis.

The updated estimates were used to form the matrix, ${\mathbf{R}}_k$, which was updated in each iteration. This structure ensured stable and sensitive algorithm behavior in a dynamically changing measurement environment.

The basic iteration procedure is based on the difference between the actual measured values and their predictions from the model:

$$\epsilon \left[k\right]=z\left[k\right]-C·\widehat{x}\left[k|k-1\right]$$

(55)

where $\widehat{x}\left[k|k-1\right]$ is the estimated value of the state vector in the current iteration.

The difference from Equation (55) is used to determine the current estimate of variances in the matrix, ${\mathbf{R}}_k$, by exponential smoothing (exponential moving average) from the following type:

$${\sigma }_{{\omega }_m,meas}^2\left[k\right]=\alpha ·{\epsilon }^2\left[k\right]+\left(1-\alpha \right)·{\sigma }_{{\omega }_m,meas}^2\left[k-1\right]$$

(56)

$${\sigma }_{∆P,meas}^2\left[k\right]=\alpha ·{\epsilon }^2\left[k\right]+\left(1-\alpha \right)·{\sigma }_{∆P,meas}^2\left[k-1\right]$$

(57)

where ${\sigma }_{{\omega }_m,meas}^2\left[k\right]$ and ${\sigma }_{∆P,meas}^2\left[k\right]$ are the current estimates of measurement error variances, allowed, respectively, in the measurement of angular velocity and the pressure difference in iteration, k; and $\alpha \in \left(0, 1\right)$ is an adaptation coefficient.

The values

$${\sigma }_{meas}^2\left[k-1\right]=\left[\begin{array}{c}{\sigma }_{{\omega }_m,meas}^2\left[k-1\right]\\ {\sigma }_{∆P,meas}^2\left[k-1\right]\end{array}\right]$$

(58)

represent the variances accumulated in the previous iteration using the same recursive formula. The procedure for calculating variances by exponential smoothing was performed after each iteration, so that the matrix, ${\mathbf{R}}_k$, was dynamically adapted to the last state of the measurement error.

In contrast to the classical estimation of variance, based on a sample of a fixed number of values and a difference from an average, the current model used adaptive exponential estimation. This was implemented by recursively smoothing out the squares of errors, $\epsilon \left[k\right]$, with a preset coefficient, $\alpha$, which provided sensitivity to the new values and stability to random fluctuations.

The algorithm in the present paper worked with the value of the coefficient, $\alpha =0.11$, that was determined empirically based on a preliminary analysis of the dynamics of the measurements. This value allowed the filter to monitor the current trends in the evolution of the measurement errors while providing smoothing, which was necessary to prevent instabilities in the adaptation of the matrix, ${\mathbf{R}}_k$.

At the same time, in each jth iteration, the accuracy of the calculated variances was evaluated. For this purpose, a reference value was constructed based on local regression applied to a sequence of previous measurements. The reference variances were estimated by the following expressions:

$${\sigma }_{{\omega }_m,ref}^2\left[k\right]={\displaystyle \frac{1}{G}}·\sum _{j=k-G+1}^k{\left[z_{{\omega }_m}\left(j\right)-{\widehat{z}}_{{\omega }_m}^{ref}\left(j\right)\right]}^2$$

(59)

$${\sigma }_{∆P,ref}^2\left[k\right]={\displaystyle \frac{1}{G}}·\sum _{j=k-G+1}^k{\left[z_{∆P}\left(j\right)-{\widehat{z}}_{∆P}^{ref}\left(j\right)\right]}^2$$

(60)

where $z_{{\omega }_m}\left(j\right)$ and $z_{∆P}\left(j\right)$ are the measured respective values of angular velocity and pressure difference in the respective iteration, $j$; and ${\widehat{z}}_{{\omega }_m}^{ref}\left(j\right)$ and ${\widehat{z}}_{∆P}^{ref}\left(j\right)$ are values obtained from the regression analysis of measurements in a range of steps, $G$.

In order to facilitate the mathematical notation in the following expressions, as well as in the structural diagram of the algorithm from Figure 5, the values of the reference variances are represented in the following vector form:

$${\sigma }_{ref}^2\left[k\right]=\left[\begin{array}{c}{\sigma }_{{\omega }_m,ref}^2\left[k\right]\\ {\sigma }_{∆P,ref}^2\left[k\right]\end{array}\right]$$

(61)

In each iteration, the matrix, ${\mathbf{R}}_k$, is initially formed based on current estimates of measurement variances calculated by exponential smoothing—accordingly, ${\sigma }_{{\omega }_m,meas}^2\left[k\right]$ and ${\sigma }_{∆P,meas}^2\left[k\right]$. When there is a difference between the current estimates of variance, ${\sigma }_{{\omega }_m,meas}^2\left[k\right]$ and ${\sigma }_{∆P,meas}^2\left[k\right]$, and their respective reference values, ${\sigma }_{{\omega }_m,ref}^2\left[k\right]$ and ${\sigma }_{∆P,ref}^2\left[k\right]$, an adaptive adjustment is applied, the value of which is determined depending on the degree of deviation between them.

For relatively small differences, where the condition is met,

$$1<{\displaystyle \frac{{\sigma }_{ref}^2\left[k\right]}{{\sigma }_{meas}^2\left[k\right]}}<\delta$$

(62)

The current value of the variance, ${\sigma }_{meas}^2\left[k\right]$, is corrected by multiplying it by a sensitivity factor, $\gamma \left[k\right]$, determined by the following formula:

$$\gamma \left[k\right]=1+\left\{{\displaystyle \frac{{\sigma }_{ref}^2\left[k\right]}{{\sigma }_{meas}^2\left[k\right]}}-1\right\}·\eta$$

(63)

This procedure results in the renewal of the variances in accordance with the following expressions:

$${\sigma }_{{\omega }_m,R}^2\left[k\right]={\gamma }_{\omega }\left[k\right]·{\sigma }_{{\omega }_m,meas}^2\left[k\right]$$

(64)

$${\sigma }_{∆P,R}^2\left[k\right]={\gamma }_{∆P}\left[k\right]·{\sigma }_{∆P,meas}^2\left[k\right]$$

(65)

where ${\gamma }_{\omega }\left[k\right]$ and ${\gamma }_{∆P}\left[k\right]$ are adaptive sensitivity coefficients calculated for the angular velocity and pressure difference, respectively, based on the current ratio between the reference and measured variances.

The coefficients ${\gamma }_{\omega }\left[k\right]$ and ${\gamma }_{∆P}\left[k\right]$ provide a differentiated adaptation of each measurement channel, taking into account individual changes in the characteristics of the respective sensors.

In this work, a value of $\eta =0.5$ was used to ensure a smooth response, from a minimal correction for small differences to a more substantial increase in the estimated variance when the value approaches the threshold.

In the presence of a significant deviation satisfying the condition

$${\sigma }_{ref}^2\left[k\right]>\delta ·{\sigma }_{meas}^2\left[k\right]$$

(66)

the current estimate of variance is updated with the reference value ${\sigma }_{ref}^2\left[k\right]$. This ensures rapid adaptation in case of a sharp deterioration of the measuring environment when the correction by the coefficient $\gamma \left[k\right]$ is insufficient.

In the developed algorithm, a value of $\delta =1.5$ was used, with adaptation being activated when the reference variance exceeds the current estimate by more than 50%. This threshold provided a balance between sensitivity to significant changes and resilience to short-term deviations.

The developed algorithm was based on local regression, in which a polynomial model was built on a sequence of measurements of length, $G$. The degree of the polynomial was determined adaptively, depending on the nature of the dynamics of the measured quantity, with the algorithm applying a model of the first degree for smooth and monotonous changes and, for more complex but regular changes, a model of the second degree. The goal was to provide a reference value that adequately determined the overall direction of signal development, while minimizing the impact of random fluctuations and local interference.

Based on the current variances, ${\sigma }_{{\omega }_m,R}^2\left[k\right]$ and ${\sigma }_{∆P,R}^2\left[k\right]$, the covariance matrix of the measurements is formed as follows:

$${\mathbf{R}}_k=\left[\begin{array}{cc}{\sigma }_{{\omega }_m,R}^2\left[k\right]& 0\\ 0& {\sigma }_{∆P,R}^2\left[k\right]\end{array}\right]$$

(67)

This matrix is updated in each iteration and determines the current state of the measurement circuit. This achieves a higher sensitivity to real changes in sensor characteristics and ensures stability and adaptability of the Kalman filter ratings under real operating conditions.

6. Experimental Study and Results

The experimental setup was based on the electro-hydraulic system described in detail in Section 2, where the operation of the individual modules is presented. In the specific implementation, an asynchronous electric motor was used, ELPROM TROYAN Ltd., 5600 Troyan, Bulgaria (2.2 kW, 3000 min⁻¹), with a frequency inverter, ELDI V-B, 3 HP (2.2 kW; Output Freq, 0.5–400 Hz); with a Power Unit with a built-in gear pump, M+S HYDRAULIC; and with a constant flow rate of 4.5 cm³/rev, a nominal pressure of 200 bar, and a maximum speed of 3500 rpm (Gerotor hydraulic motor M + S HYDRAULIC, maximum speed, 1550 rev/min. and flow rate, 12.5 cm³/rev; tachogenerator DYNAMO TG5—1/1000 V/min⁻¹; incremental encoder ZGPU GRUP FRP-7 KPP; Hall current sensor ZGPU GRUP SH-M12 and two pressure sensors COMECO PSPR—060—Q23 F-X). The computing module was implemented through an SBC platform Jetson Nano b01 16 GB eMMC 5.1. For the purposes of the experiments, an additional induction motor was added (ELPROM; 2.2 kW, 3000 min⁻¹) with frequency control (ELDI V-B, 3 HP—2.2 kW), operating in braking mode and acting as an external load. By means of preset control signals, various load profiles with adjustable parameters were reproduced from this control, which serve as reference inputs for testing the algorithms. In Figure 6, photographic material of the experimental setup is presented, on which the main components are marked.

The values set by the frequency control were reference load moments, while the actual torque exerted on the hydraulic shaft may have deviated from these as a result of electromagnetic, inertial, and hydraulic influences. These deviations, although not directly measured, had an impact on the estimate obtained by the algorithm, manifesting as differences from the set profiles.

However, the ratio between the error obtained during the direct measurement of the set parameters and the error in their evaluation by the algorithm was perceived as a sufficiently accurate criterion, from a metrological point of view, for the effectiveness of the algorithm. This approach allowed for a comparative assessment between the direct measurement and the adaptive signal evaluation, provided that a single reference profile was used as the basis for comparison. The resulting ratio between the RMSE values, with and without the use of the algorithm, served as a criterion for improving the accuracy in evaluating the parameters. For parameters for which there was no direct measurement information (e.g., load torque), the estimate was based solely on the absolute error relative to the reference value.

The experimental studies were carried out under different types of dynamic modes, defined by variations in the parameters of the load profiles. The analysis presented below is based on three characteristic modes—linearly increasing, stepped, and asymmetrical sawtooth load moments, which determine the basic properties of the system.

The first mode was characterized by a smooth increase in the torque applied to the hydraulic motor shaft. The load was applied by controlling the second induction electric motor, operating in braking mode, by means of a preset frequency profile. This provided a controlled measuring environment in which the angular velocity—although not directly set as an input value—formed as a result of the interaction between the set load and the inertial and hydraulic characteristics of the system.

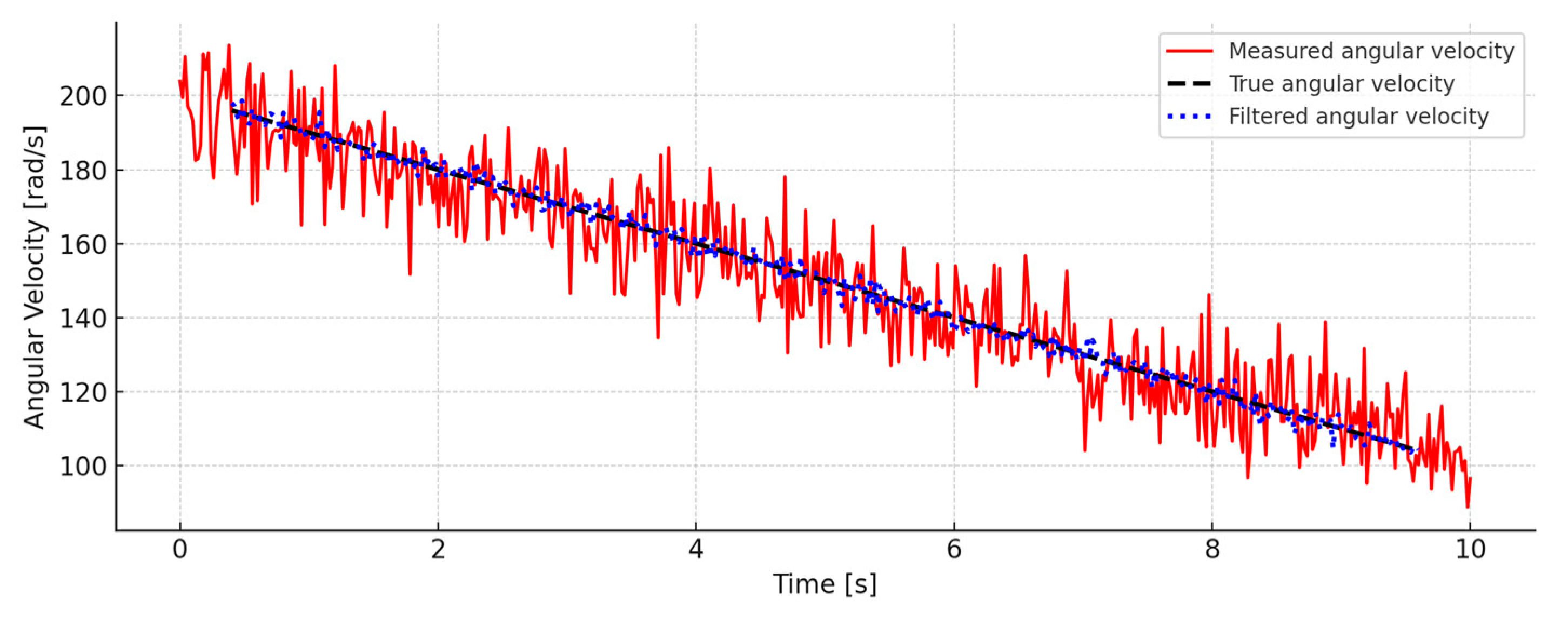
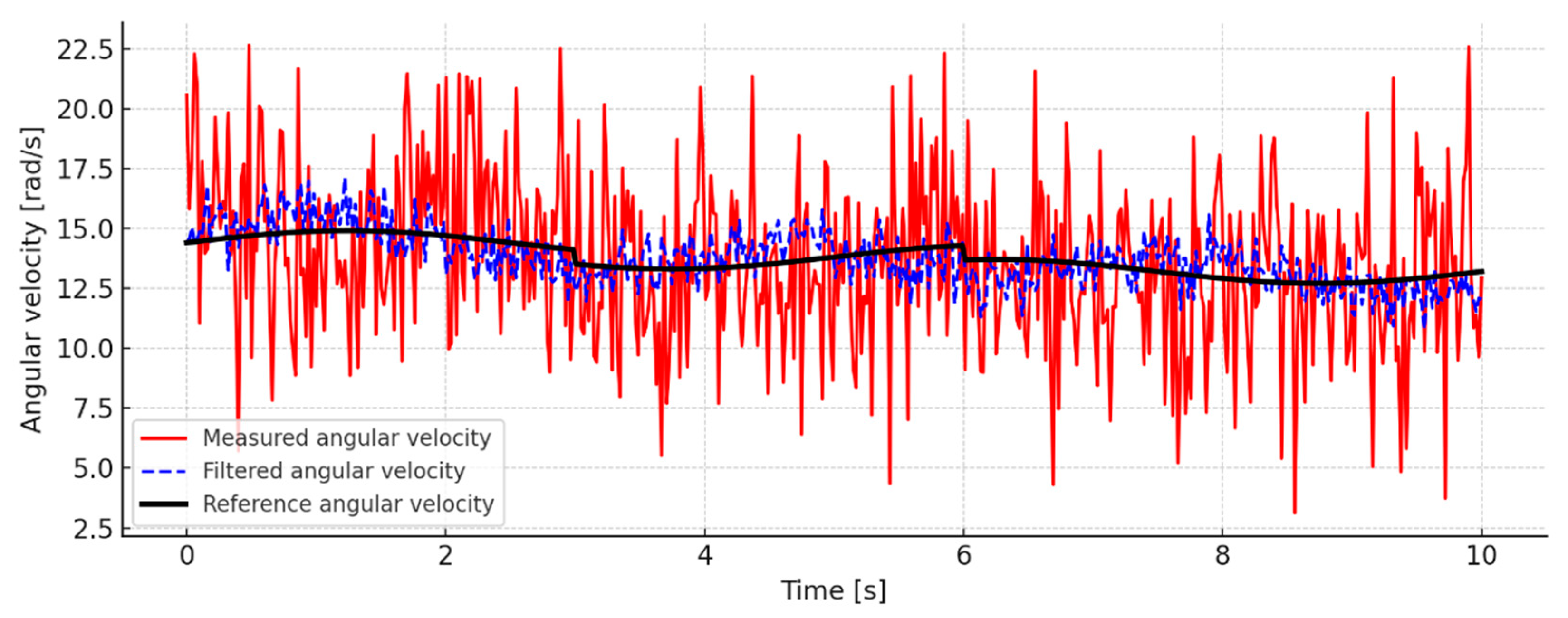
Figure 7 presents the results of the measurement and evaluation of the angular velocity. The graph includes the signal measured from the tachogenerator (containing measuring noise), the evaluated signal received by the algorithm, and the preset reference profile of the angular velocity used as the basis for evaluating the accuracy. The graph shows that the adaptive filter significantly reduced the noise in the measurements and provided an assessment that followed the set signal dynamics with high accuracy.

For this study and analysis, the time interval was assumed to be 10 s at a sample rate of 50 Hz. This corresponded to 500 measurement points, with a discrete time interval, $∆t=0.02 \mathrm{s}$. The sampling rate was consistent with the dynamics of the electro-hydraulic system and the capabilities of the measuring instruments used.

The reference values used to evaluate the accuracy were preset time functions for angular velocity and load torque realized by the interaction between the hydraulic and electric load motors. Measurements and evaluations were carried out synchronously within this time base.

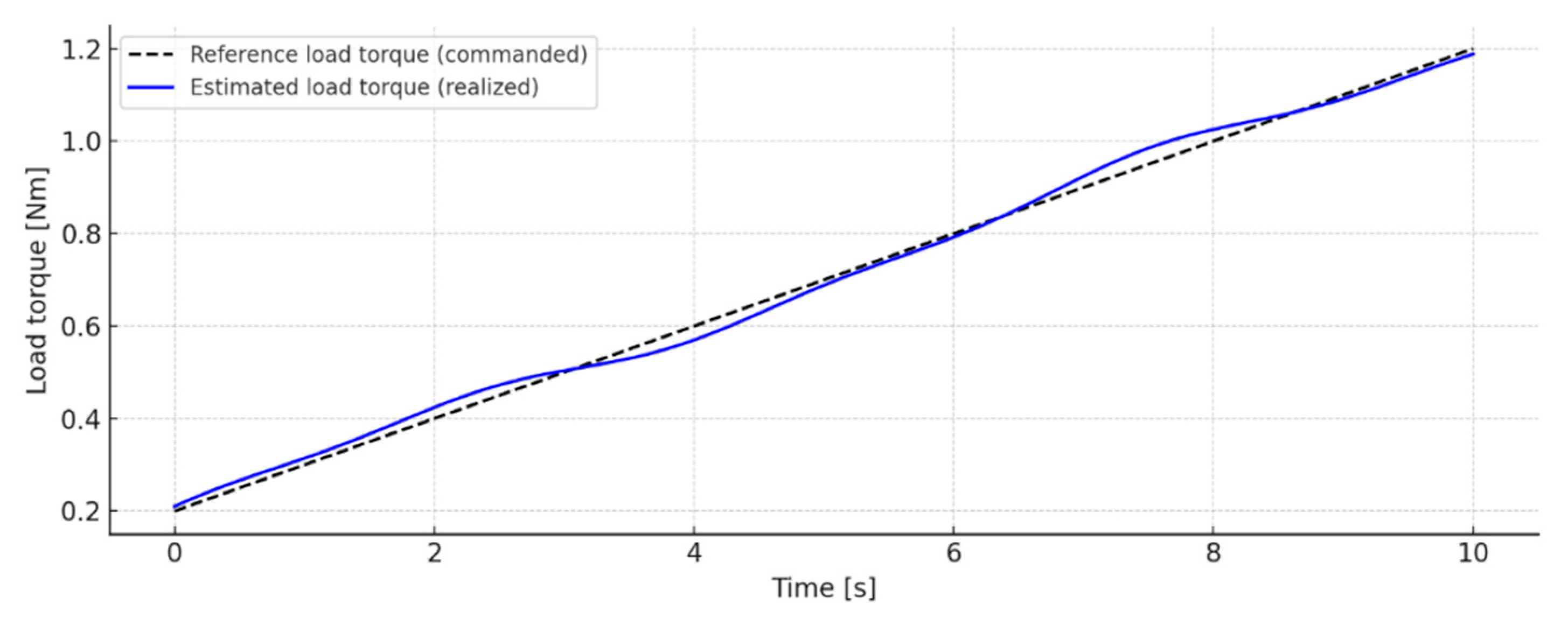
The behavior of the load torque is shown in Figure 8 by comparing the reference profile set by the frequency management and the estimated value of the algorithm. Unlike angular velocity, which is measured directly and subjected to noise, the load torque is determined indirectly based on a dynamic pattern and the difference between the inlet and outlet pressures. The resulting estimate fluctuates symmetrically around the set profile, without systematic drift, and the included deviations are smooth and reflect the real dynamics of the system. This behavior confirms the robustness and metrological validity of the adaptive algorithm, in which the covariance matrices are updated in real time, providing a reliable estimate of the applied load.

The resulting graphical results are complemented by a quantitative assessment of the algorithm’s performance carried out by calculating the RMS errors in two cases—without the Kalman filter (direct use of measured values) and with the Kalman filter. The formulas for calculating the RMS errors in both cases are as follows:

$${RMSE}_{{\omega }_m}^{meas}=\sqrt{{\displaystyle \frac{1}{H}}·\sum _{k=1}^H{\left\{{\omega }_m^{meas}\left[k\right]-{\omega }_m^{ref}\left[k\right]\right\}}^2}$$

(68)

$${RMSE}_{{\omega }_m}^{filt}=\sqrt{{\displaystyle \frac{1}{H}}·\sum _{k=1}^H{\left\{{\omega }_m^{filt}\left[k\right]-{\omega }_m^{ref}\left[k\right]\right\}}^2}$$

(69)

where ${\omega }_m^{meas}\left[k\right]$ is the measured value of the angular velocity in the discrete step k, received from a tachogenerator; ${\omega }_m^{filt}\left[k\right]$ is the estimated angular velocity value calculated by the Kalman filter; ${\omega }_m^{ref}\left[k\right]$ is the reference (preset) value of the angular velocity used for comparison; and $H$ is the total number of discrete steps in the measurement interval.

The values of the error in estimating the angular velocity are presented graphically in Figure 9, where a comparison is made between the error when using the measured signal directly and the error after applying the adaptive Kalman filter.

The calculated RMSE value when using the directly measured signal is ${RMSE}_{{\omega }_m}^{meas}=10.08 \mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}$. When using the filter rating, the value decreases to ${RMSE}_{{\omega }_m}^{filt}=1.51 \mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}$. The efficiency of the filter can be evaluated by the following attitude:

$${\displaystyle \frac{{RMSE}_{{\omega }_m}^{meas}}{{RMSE}_{{\omega }_m}^{filt}}}=6.67$$

This ratio indicates the algorithm’s ability to reduce the measurement error by more than six times, providing a significant improvement in the accuracy and reliability of the estimate.

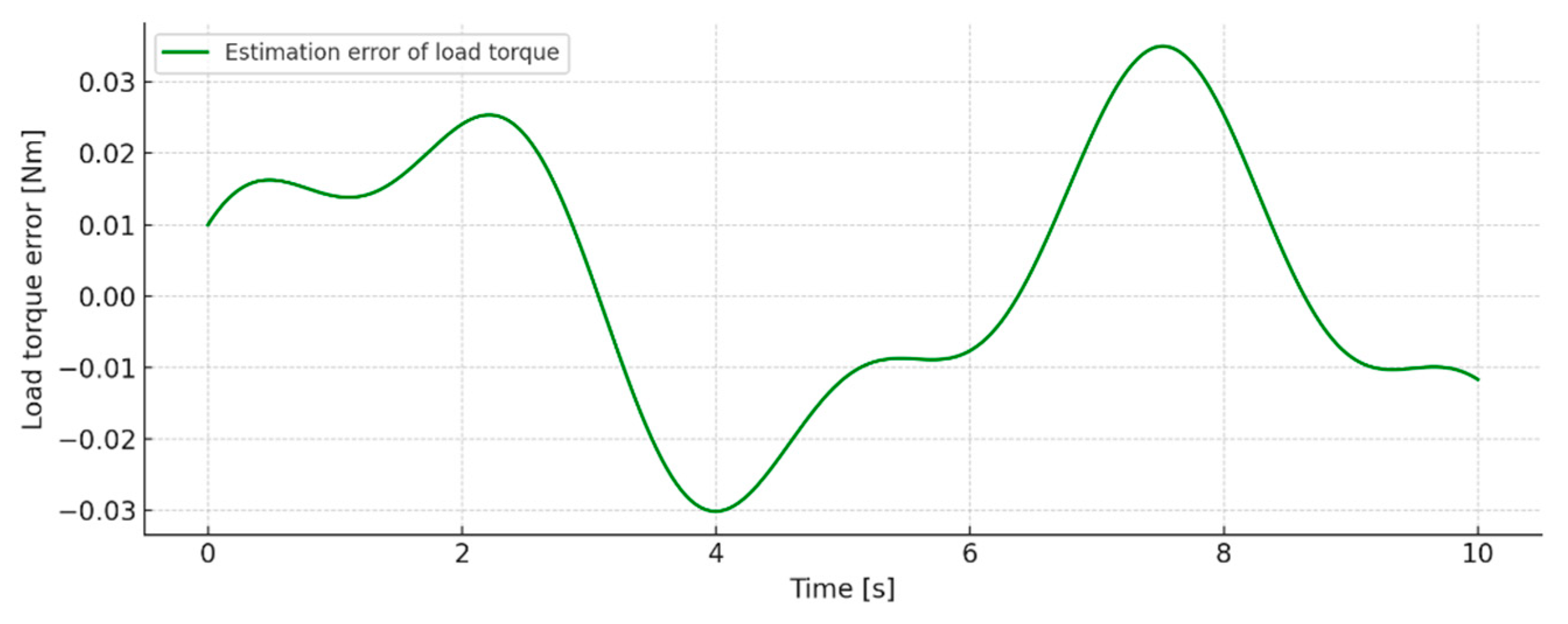
The error in estimating the load moment is graphically represented in Figure 10. Due to the lack of direct measurement, the accuracy of the value calculated by the filter was evaluated by comparison with the preset load torque value accepted as a reference. The RMSE was calculated according to the following expression:

$${RMSE}_{T_{load}}^{filt}=\sqrt{{\displaystyle \frac{1}{H}}·\sum _{k=1}^H{\left\{T_{load}^{filt}\left[k\right]-T_{load}^{ref}\left[k\right]\right\}}^2}$$

(70)

where $T_{load}^{filt}\left[k\right]$ is the value estimated by the Kalman filter; and $T_{load}^{ref}\left[k\right]$ is the reference value set by the frequency changer.

The resulting value of ${RMSE}_{T_{load}}^{filt}=0.018 \mathrm{N}\mathrm{m}$ confirms the high accuracy of the adaptive algorithm in restoring parameters that were not directly measured. As can be seen in Figure 10, the load estimation error oscillates symmetrically around zero, with no signs of drift or accumulation over time, which corresponds to the analysis carried out based on Figure 8. Fluctuations in the estimation resulted from physical deviations in the actual reproduction of the load moment and are of small amplitude and physically justified dynamic character.

The results obtained for linear loads show that the accuracy of the estimates depends to a large extent on the way in which the variable ${\dot{\omega }}_m\left(t\right)$ is included in the filter structure. In the present study, it is not obtained by numerical differentiation, which would amplify noise, but is calculated algebraically based on current states and input effects. This way ${\dot{\omega }}_m\left(t\right)$ remains part of the state vector, while maintaining the linear structure compatible with the classical Kalman filter. This prevents the accumulation of errors in real data, improves stability in dynamic modes, and ensures high computational efficiency.

The introduced computational structure has a direct impact on the accuracy of the theoretical model, and this effect is expressed in the covariance matrix of the model, given by Equation (47). As can be seen from this matrix, the variances of individual states—angular velocity, ${\omega }_m\left(t\right)$, angular acceleration, ${\dot{\omega }}_m\left(t\right)$, and external load, $T_{load}\left(t\right)$—are interconnected and depend on how acceleration is introduced into the filter structure. The nature of these processes is shown in Figure 11 and Figure 12, where the error distribution curves in the states are presented. Figure 11 shows the results using an algorithm for algebraic calculation of ${\dot{\omega }}_m\left(t\right)$, while Figure 12 shows the results in the absence of this algorithm and with the classical approach based on numerical differentiation.

The presentation of the two figures is essential not only for visualizing the results but also from the point of view of the metrological correctness of the estimates. Figure 11 also includes the distribution of errors in determining ${\dot{\omega }}_m\left(t\right)$, which is possible only thanks to the algebraic approach to calculating this variable. This provides a complete and internally consistent state vector at which the interdependence between the constituent variances can be realistically estimated. The absence of such a structural element in Figure 12, where acceleration is not derived algebraically, leads to incomplete information about error distributions and limits the possibilities for full metrological traceability of variables. This has a direct impact on the adequacy of the covariance matrix and its ability to reflect the real stochastic properties of the system.

To quantify the effect on the accuracy of the estimates, we introduce a normalized combined error, $e_{comb}\left(k\right)$, calculated on each iteration, k, through the following expression:

$$e_{comb}\left(k\right)={\epsilon \left(k\right)}^T·{\mathbf{\Psi }}^{-1}·\epsilon \left(k\right); \epsilon \left(k\right)=\left[\begin{array}{c}{\epsilon }_{{\omega }_m}\left(k\right)\\ {\epsilon }_{{\dot{\omega }}_m}\left(k\right)\\ {\epsilon }_{T_{load}}\left(k\right)\end{array}\right]$$

(71)

where ${\epsilon }_{{\omega }_m}\left(k\right)$, ${\epsilon }_{{\dot{\omega }}_m}\left(k\right)$, and ${\epsilon }_{T_{load}}\left(k\right)$ are the errors in step k that are allowed when estimating angular velocity, angular acceleration, and external load relative to their respective reference values.

Since the covariance matrix, $\mathbf{\Psi }$, is diagonal in the form $\Psi =diag\left({\sigma }_{{\omega }_m}^2,{\sigma }_{{\dot{\omega }}_m}^2,{\sigma }_{T_{load}}^2 \right)$, the expression for the normalized combined error takes the form

$$e_{comb}\left(k\right)=\sqrt{{\displaystyle \frac{{\epsilon }_{{\omega }_m}^2\left(k\right)}{{\sigma }_{{\omega }_m}^2}}+{\displaystyle \frac{{\epsilon }_{{\dot{\omega }}_m}^2}{{\sigma }_{{\dot{\omega }}_m}^2}}+{\displaystyle \frac{{\epsilon }_{T_{load}}^2}{{\sigma }_{T_{load}}^2}}}$$

(72)

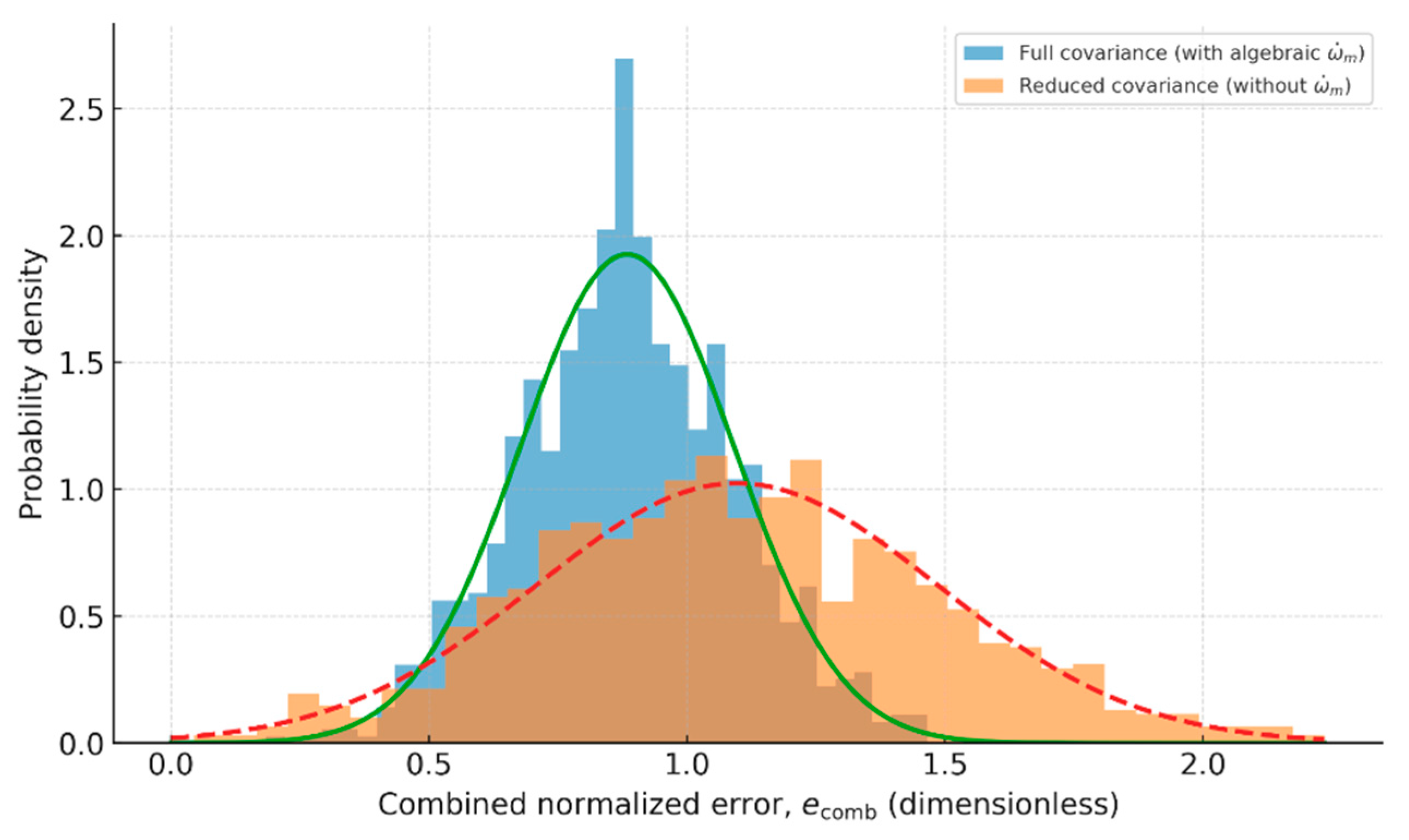
In Figure 13, histograms of multiple values, ${\left\{e_{comb}\left(k\right)\right\}}_{k=1}^Y$, are presented, where Y is the number of discrete steps in the experimental record under consideration. For each of the two cases—in the presence of an algebraic calculation of ${\dot{\omega }}_m\left(t\right)$, and in its absence—the corresponding metric values are calculated. On the abscissa axis, the dimensionless error values, $e_{comb}$, are plotted, obtained by normalization with the covariance matrix, $\mathbf{\Psi }$, so that each composite error participates in the metric in proportion to its own variance. Normal approximations are imposed on histograms, from which approximate sample estimates of the mean and standard deviation are derived. In the first case, we obtain ${\overline{e}}_{comb}=0.88$ and a standard deviation of ${\sigma }_{comb}=0.21$, while in the second—respectively, ${\overline{e}}_{comb}=1.10$ and ${\sigma }_{comb}=0.3$.

The results clearly show that the proposed structure with algebraic determination of acceleration leads to a simultaneous decrease in the mean (reduction in systematic error) and in the range of the distribution (reduction in the random component), i.e., to increased accuracy and repeatability of estimates.

The second experimental mode is implemented with a stepwise change in the load moment, which allows for analysis of transients and the stability of the algorithm in case of sudden changes. Figure 14 shows the measured angular velocity, the evaluation through the adaptive filter, and the reference profile. As expected, as the load torque increases, and the angular velocity decreases, with the stepped nature of the load determining the discrete appearance of the reference profile used to evaluate the algorithm.

The measured signal received by the tachogenerator contained significant high-frequency interference that led to deviations from the set reference value. After processing through the adaptive filter, the resulting assessment approached the reference profile and reproduced its basic shape. Also, during the transitions between the steps, the assessment reacted with a characteristic delay and smooth adaptation to the new level. This behavior is characteristic of adaptive algorithms, where the covariance matrices of the model and measurements are adjusted in real time and limit abrupt changes in estimates, thus providing stability and protection against sudden fluctuations due to noise or transition states in the system.

The stepwise variation in the load torque mode creates characteristic dynamic conditions that make it particularly suitable for experimental validation of the efficiency of the combined application of the algorithms for an adaptive update of the covariance matrix of the model and hybrid correction of the covariance matrix of measurement errors.

For this purpose, studies have been carried out based on a comparison between three approaches to assessing the condition. The first uses the classic Kalman filter with predefined and fixed covariance matrices of the model and measurements. This approach does not take into account dynamic changes in the system and does not adapt its assessments to changing conditions. The second approach is an adaptive version of the Kalman filter, in which covariance matrices are modified in real time by empirical dependencies based on the behavior of observed errors. Refresh is usually realized through adaptive factors or preset dependencies, with no real estimation of noise dispersions. The third approach is the one developed in the current study, which introduces simultaneous adaptation of both covariance matrices through a combination of current statistical estimates and reference values.

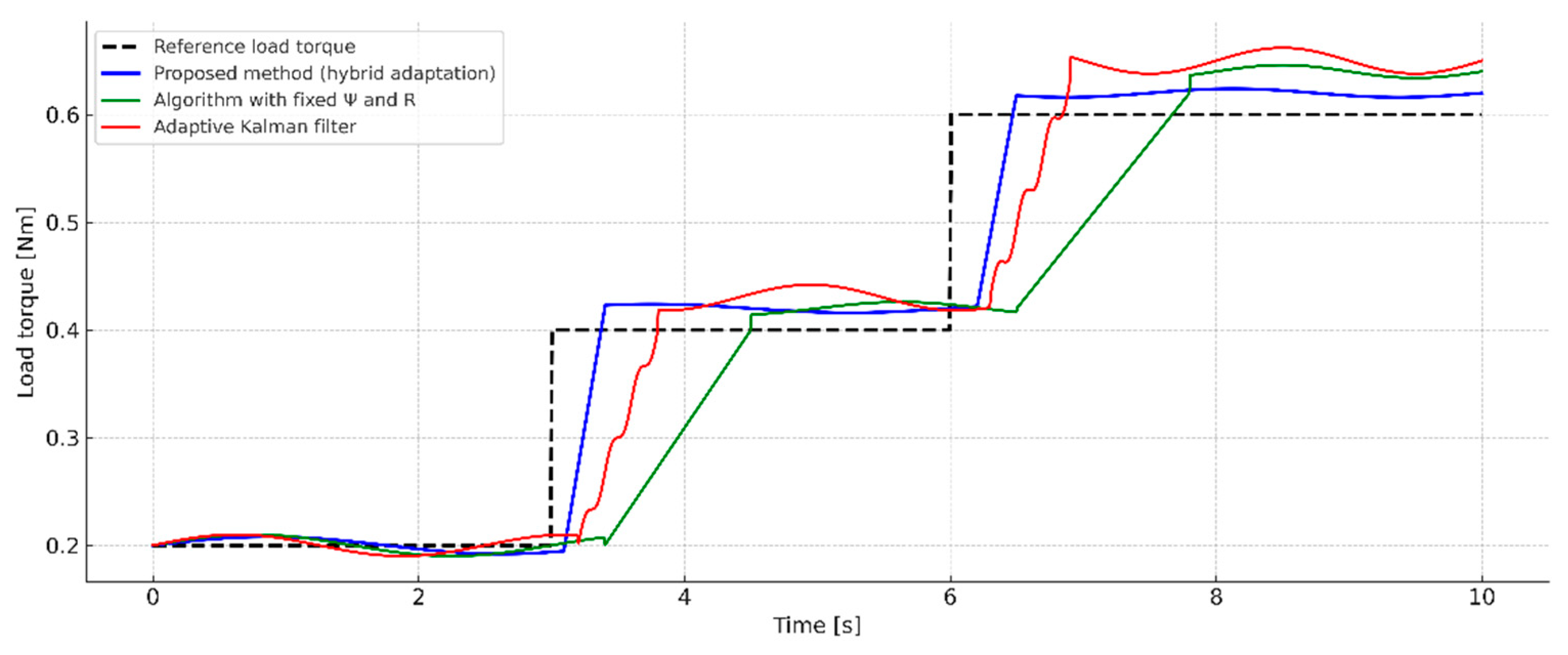
The differences in the behavior of the three algorithms in stepped loading mode are illustrated in Figure 15. It clearly shows that the hybrid adaptation method achieves the fastest and most precise tracking of the reference load torque without introducing fluctuations after sudden changes in load.

In the classic filter with fixed covariance matrices, there is a significant lag and smoothing in the transition sections, which is due to the lack of adaptability to changing conditions. For its part, the fixed-adaptation coefficient algorithm demonstrates a faster response but leads to significant deviations and instability, especially after the second and third changes in the load torque. This underlines not only the need for adaptability but also the crucial importance of combining different update mechanisms, as implemented in the proposed approach.

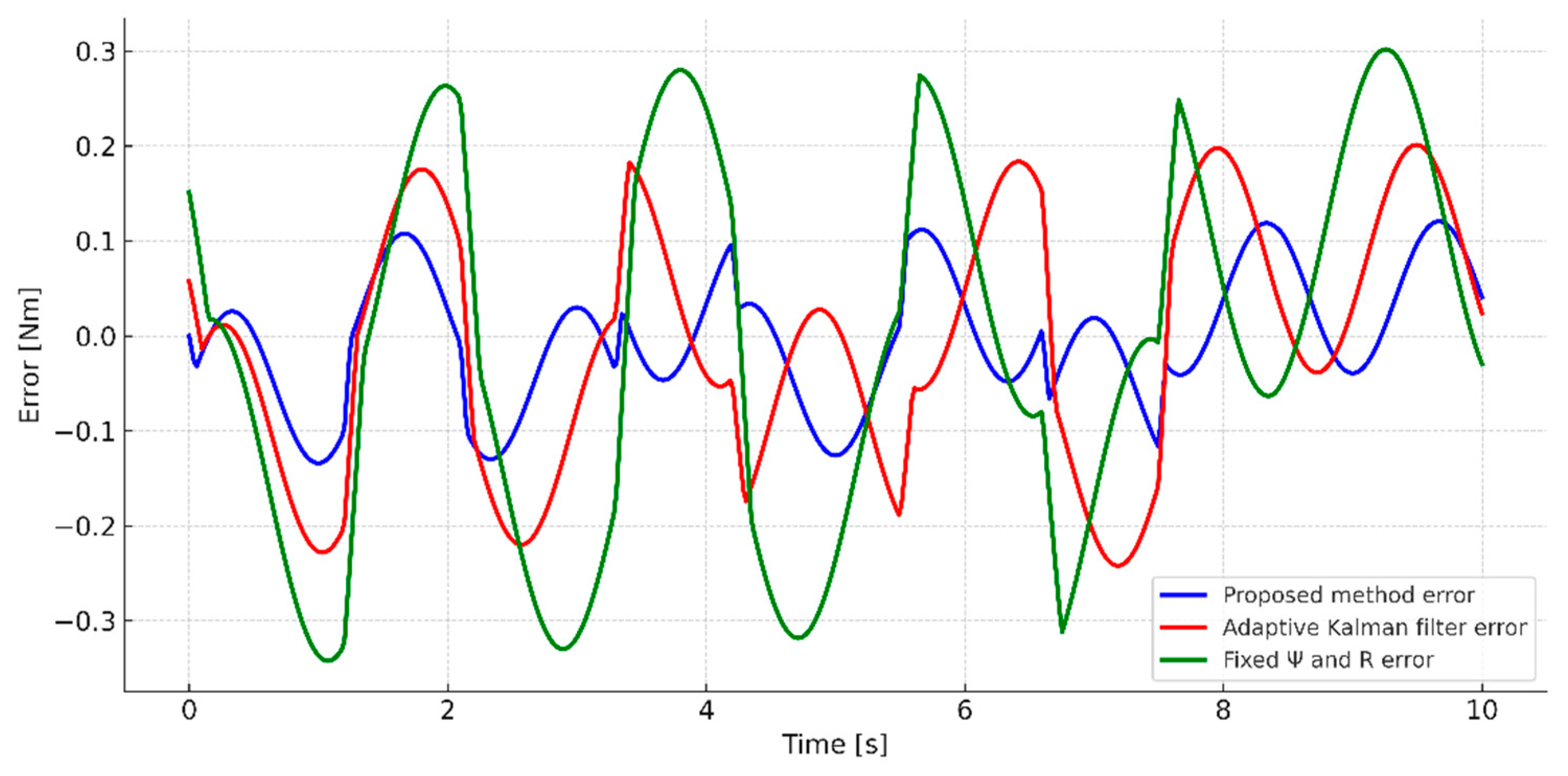
All this is confirmed by the graphical representation of errors in the load torque estimate shown in Figure 16. With the combined algorithm for adaptive determination of the covariance matrices of the model and measurement proposed in this paper, a rapid adaptation of the filter to the abrupt changes in the dynamics of the system is observed, in contrast to the other two algorithms.

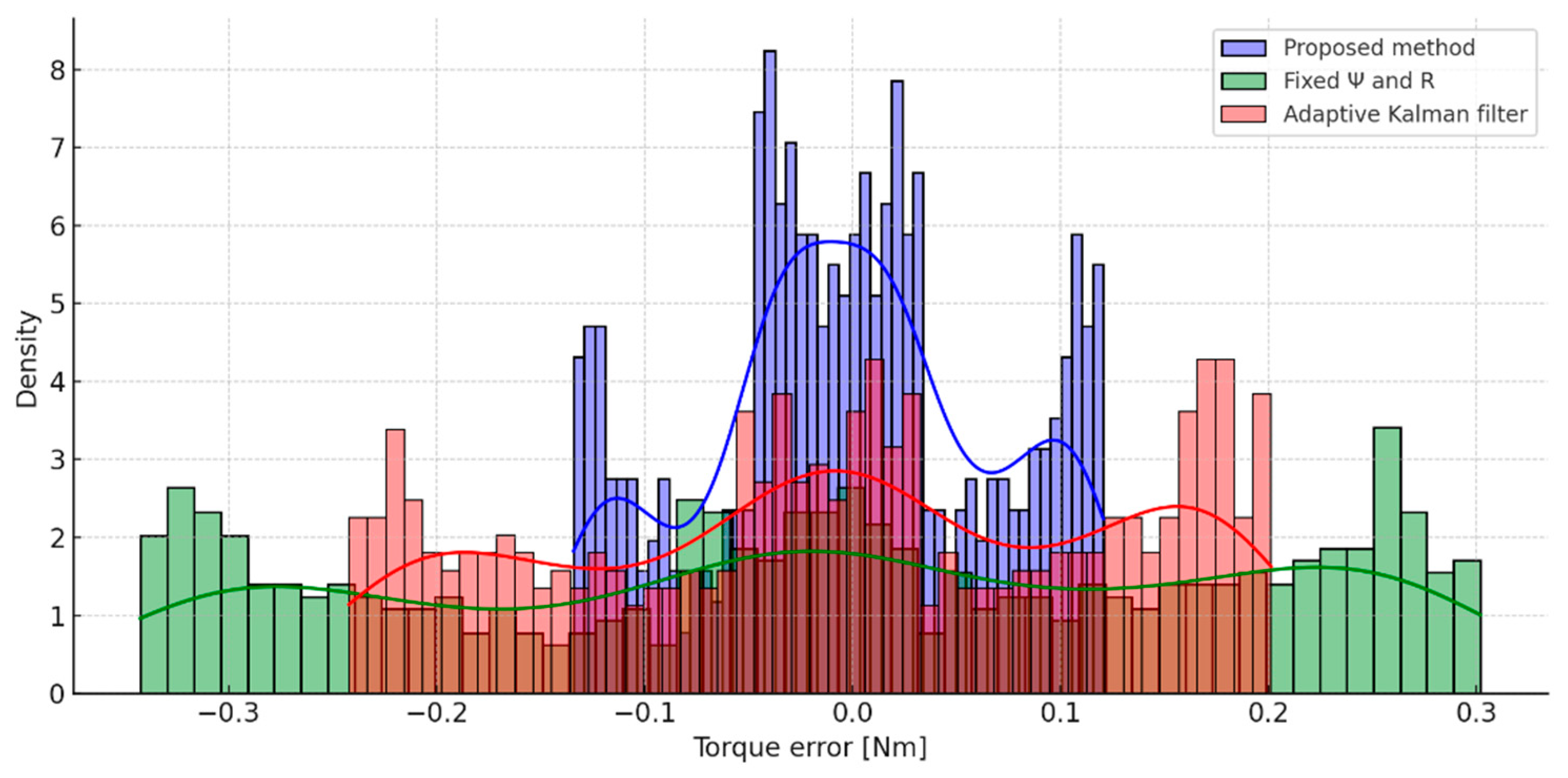
A graphical representation of the error distribution in the load moment estimation is illustrated in Figure 17 by histograms and continuous probability density estimation functions obtained by the Kernel Density Estimation (KDE) method. All approximation curves demonstrate two pronounced extremes, reflecting the characteristic dynamics of the system.

The first, lower extremum, occurs on the left side of the graph and is due to the inertial reaction of the system to sudden stepwise changes in the load moment. The second, higher extremum, is located near zero error and reflects the behavior of the system in a fixed driving mode. It is in this interval that most of the error values for all three approximation distributions are concentrated.

In these two characteristic areas, the proposed method clearly stands out with the highest density around its extremum and the least dispersion around it, which is a reliable indicator of lower random errors. This behavior meets the requirements for high repeatability and robustness of evaluations, especially in transient modes where classical structures show greater scattering. A table presents the quantitative estimates of the statistical characteristics of the errors, calculated based on empirical histogram distributions.

From the results presented in the table, it is found that the proposed method achieves the lowest value of the systematic error, estimated by the deviation of the mean from zero. In addition, it is characterized by the smallest variance of errors relative to the mean, which is directly related to a reduced influence of random components and shows high repeatability of estimates under dynamic load conditions. The shape of the resulting distribution is also closest to symmetrical and consistent with the normal distribution law, without pronounced deformations, which further confirms the metrological reliability and stability of the estimates obtained by the proposed method. These conclusions are also confirmed by the values in

Table 1. Statistical characteristics of the errors in the estimation of a stepwise varying load torque.

Method	Average Value [Nm]	Standard Deviation [Nm]	Asymmetry	Excesses
Algorithm with the proposed method	0.0104	0.0150	0.08	−0.16
With fixation Ψ and R	0.0142	0.0200	0.19	−0.51
Kalman adaptive filter	0.0171	0.0288	−0.15	−0.33

for asymmetry and excess, which further characterize the shape of the error distribution. The asymmetry coefficient of the proposed method is close to zero, which is a characteristic of good symmetry of the distribution relative to the mean and the absence of systematic deviations in a certain direction.

At the same time, the least negative value of the excess coefficient (−0.16) compared to the other methods indicates a better concentration of values around the center of the distribution and a lower degree of scattering, which is an important conclusion for metrological stability and normal distribution of errors.

In addition to the data in Table 1, the effectiveness of the proposed algorithm can also be evaluated by calculating the RMSE and its relative value relative to that obtained by directly using the measured values, without using the Kalman filter. The calculated RMS error value when using the measured signal is ${RMSE}_{{\omega }_m}^{meas}=4.99 \mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}$, and with the filtered score, it decreases to ${RMSE}_{{\omega }_m}^{filt}=0.98 \mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}$. This results in a more than 5-fold reduction in error, which is evidenced by the ratio

$${\displaystyle \frac{{RMSE}_{{\omega }_m}^{meas}}{{RMSE}_{{\omega }_m}^{filt}}}=5.11$$

which shows the efficiency of the filter in modes with a sharp change in the input load.

The maximum error observed in the assessment of the load torque reaches values of up to 0.20 Nm, but this is typical for the short transition moments associated with sudden changes in the set load.

At all other time intervals, the error remains significantly smaller and varies around 0.02–0.03 Nm, which confirms that the behavior of the adaptive algorithm is stable and does not lead to a divergent departure from the reference profile.

The error remains limited and stable over time, with no tendency to accumulate, which confirms the stable operation of the algorithm in dynamic conditions. The calculated RMS value is ${RMSE}_{T_{load}}^{filt}=0.044 \mathrm{N}\mathrm{m}$.

For a more complete picture of the capabilities of the proposed method and for assessing its stability in conditions of more complex dynamics, the study was extended with an analysis of a non-symmetric sawtooth-shaped load. This type of impact is characterized by smooth transitions and irregular intervals of variation, which leads to a more complex spectral composition and places additional requirements on the capabilities for accurate tracking and filtering. This analysis aimed to examine the extent to which different methods can adapt to such dynamic conditions without a significant increase in errors.

In order to validate the characteristics of the proposed method in conditions close to real operating modes with smoothly changing dynamics, Figure 18 presents the results of the operation of the three considered algorithms under reference influence of an asymmetrically varying sawtooth load (black dashed line). The blue line depicts the reaction of the proposed method, the red line depicts the reaction of an adaptive Kalman filter with varying parameters, and the green line depicts the reaction of a filter with fixed values of the covariance matrices.

A clearer picture of the accuracy of each of the methods considered can be obtained by analyzing the load torque recovery errors presented in Figure 19. The graph illustrates the deviations between the estimated and reference values over the entire exposure interval. The results show that in the proposed method, the errors remain within narrow limits, with a symmetrical distribution around the zero line, which indicates good compensation of the dynamic components and the absence of systematic bias. With the adaptive Kalman filter, the deviations are more noticeable, especially in areas with a sharp change in load, while with the fixed-die filter, significant systematic errors and a wider range of fluctuations are observed.

A graphical interpretation of the error distributions in the load torque estimation is presented in Figure 20 by histograms and the corresponding approximation curves. All three distributions show three distinct maximums, and in the proposed method, these maxima are located in the narrowest range around the zero value. This indicates the lowest systematic error and high accuracy of assessments. At the same time, the shape and width of the distributions show that the proposed method has the smallest error scattering, which means better repeatability and lower sensitivity to random interference compared to the other two approaches.

All of this is confirmed by the quantitative results presented in

Table 2. Statistical error characteristics under a non-symmetric sawtooth load.

Method	Average Value [Nm]	Standard Deviation [Nm]	Asymmetry	Excesses
The proposed method	0.0091	0.0143	0.04	−0.12
With fixation Ψ and R	0.0164	0.0221	0.21	−0.44
Kalman adaptive filter	0.0183	0.0312	−0.17	−0.29

, which summarize the main statistical characteristics of the load torque estimation errors for the three approaches considered.

From the data in the table, it can be established that the proposed method achieves the lowest average deviation from the reference load moment and is characterized by the lowest dispersion, which is a clear indicator of high metrological reliability and repeatability. The asymmetry is close to zero, and the excess value indicates that the distribution is close to normal, with no significant deformations or tails. All of this confirms the effectiveness of the proposed combined adaptation in dynamically changing load mode.

7. Discussion

In real operating modes, electro-hydraulic systems face significant difficulties that limit the accuracy of their control and the assessment of their states. The main factors that hinder or complicate the operation of these systems include the presence of strong nonlinearity, internal losses of a hydraulic and mechanical nature, sensitivity to external disturbances, changes in pressure and temperature, and limited possibilities for the direct measurement of essential quantities, such as load torque. These impacts lead to a discrepancy between the actual behavior of the system and its mathematical model, which limits the effectiveness of classical algorithms for controlling and evaluating states.

The model proposed in this work was aimed at minimizing the above limitations by introducing structurally adaptive solutions based on the Kalman filter, which allowed for the reliable tracking and timely forecasting of load changes, thus ensuring the active adaptation of control actions to real working conditions. The proposed Kalman adaptive filter structure demonstrated efficiency in overcoming some of the most common difficulties experienced in electro-hydraulic systems. One of the essential contributions was the algebraic determination of angular acceleration, which allowed for the inclusion of this quantity in the state vector without the need to use second-order derivatives or numerical integration of signals with a high level of noise and errors. This solution increased the accuracy and stability of the estimates, especially in transitional modes where classical approaches showed instability.

Another important aspect was the empirical modeling of the load torque through a regression relationship based on the measured angular velocity and pressure difference. This allowed for better synchronization with the real dynamics of the system and increased adaptability of the filter. From a metrological point of view, the application of this model led to a significant reduction in the probability of large-amplitude errors. Analysis of the experimental results (Figure 14) showed that the probability of the load torque estimate deviating by a maximum value from the reference trajectory was less than 3% of the total probability of an error. This is directly related to the improved metrological reliability of the estimates and a reduction in the contribution of the dynamic component to the total error of the system.

The adaptive update of the covariance matrix of the model, $\mathbf{\Psi }$, based on analysis of the differences between the predicted and measured values of the derivatives, allowed the algorithm to detect moments of greater dynamic deviation and adjust its sensitivity to deviations in real time. This is essential for sudden changes in pressure, temperature fluctuations, or transitions between different load modes.

Similarly, the hybrid strategy for updating the covariance matrix of measurement errors, ${\mathbf{R}}_k$, by combining exponential smoothing and local regression, provided an effective compromise between adaptability and sustainability. Thus, the filter remained sensitive to systematic fluctuations in the data, while limiting the influence of statistically isolated deviations. This approach is particularly important from a metrological point of view because it allows for the adaptive management of weighting factors under conditions of dynamically changing uncertainty.

As a result, the overall model not only preserved the theoretical sequence of the classical Kalman filter but also extended it with practically applicable mechanisms, allowing operation with limited measurement information, the presence of noise, and nonlinear dynamics. This makes it suitable for implementation in real industrial systems, where the accuracy of assessments and the ability to adapt have a direct impact on the quality of management.

The experimental results obtained confirm the effectiveness of the developed model under different dynamic load modes. By applying the algorithm for the algebraic determination of angular acceleration and empirical load modeling, a significant improvement in the accuracy of the estimates was observed, especially in those transients with linearly increasing or pulse-applied loads.

With a linearly increasing load torque, the efficiency of the system is manifested by reducing the RMS angular velocity error by 6.67 times compared to the direct measurement, while the load torque estimate reproduces the profile without drift and with acceptable symmetrical fluctuations. In step mode, the filter adapts quickly to sudden changes, as the angular velocity error is reduced by more than 5 times, and at the load torque, the deviations in the transitions reach 0.20 Nm, while in an established state, they remain within the limits of 0.02–0.03 Nm. The results confirm the metrological robustness and reliability of the adaptive algorithm under dynamically changing modes.

In modes with sudden load changes, where traditional algorithms often exhibit instability and delays, the proposed adaptive model provides stable operation through regression modeling of the load and dynamic adaptation of covariance matrices. With a sharp change, the variances temporarily increase, which reduces the dependence on predictions and increases the flexibility of the filter, and after stabilization, they are normalized, restoring sensitivity to measurements. Additional resilience is ensured by exponential smoothing and local regression, which limits the impact of noise and interference and increases the accuracy of estimates.

The proposed method shows high efficiency in assessing conditions and load impacts in real conditions and is applicable in a wide range of tasks. Its linear structure provides computational efficiency and robustness, compensating for its limitations by adaptive mechanisms for updating covariance matrices and algebraically defined states. Potential future extensions include the use of neural networks to identify the load pattern and adaptive training of covariance matrices, which would increase accuracy and robustness in nonlinear and non-stationary processes.

8. Conclusions

The method presented here was based on the structural implementation of the Kalman filter, designed for a more precise and stable assessment of the states in electro-hydraulic systems operating under conditions of dynamic loads and an unstable measuring environment. The developed approach was aimed at providing reliable tracking and forecasting of changes in the external load in order to adapt the control actions to the real operating conditions.

The proposed solution was based on a structural adaptation of the algorithm, in which one of the states was determined algebraically at each step, allowing the integration of quantities that were difficult to measure but significant for the dynamics of the system, without disturbing the linear structure of the rest of the model. The dynamic behavior of the load torque was modeled using a regression approach based on experimental data, rather than using a fixed or preset value. In this way, adequate correspondence between the model and the actual operation of the system was ensured.

An essential element of the methodology was the adaptive calculation of the covariance variances that characterized the model and measurement errors. The use of real-time estimation based on the differences between the predicted and measured values, as well as the combination of exponential smoothing with local regression, contributed to the resilience of the estimates to short-term disturbances and variable conditions.

Experimental studies conducted in a laboratory environment with a real electro-hydraulic installation confirmed the effectiveness of the developed model. The results obtained demonstrate high accuracy and stability of the estimates under different load modes, and the calculated values of the RMSE indicate significantly improved consistency between the model and the measured data.