Design and Evaluation of a Torque-Controlled Ankle Exoskeleton Using the Small-Scale Hydrostatic Actuator: miniHydrA
Abstract
1. Introduction
2. Exoskeleton Design
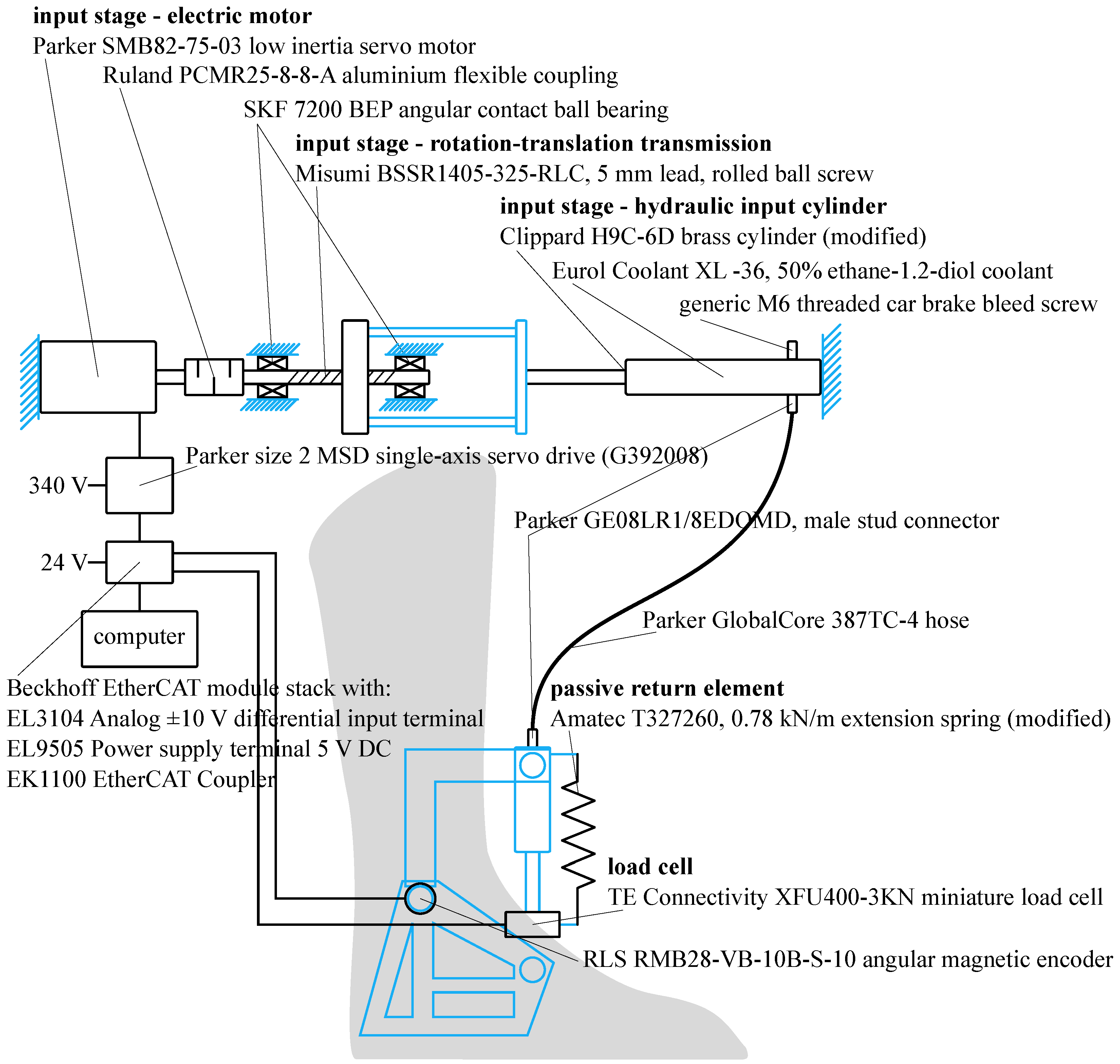
3. miniHydrA Design
3.1. Input Stage
3.2. Hose
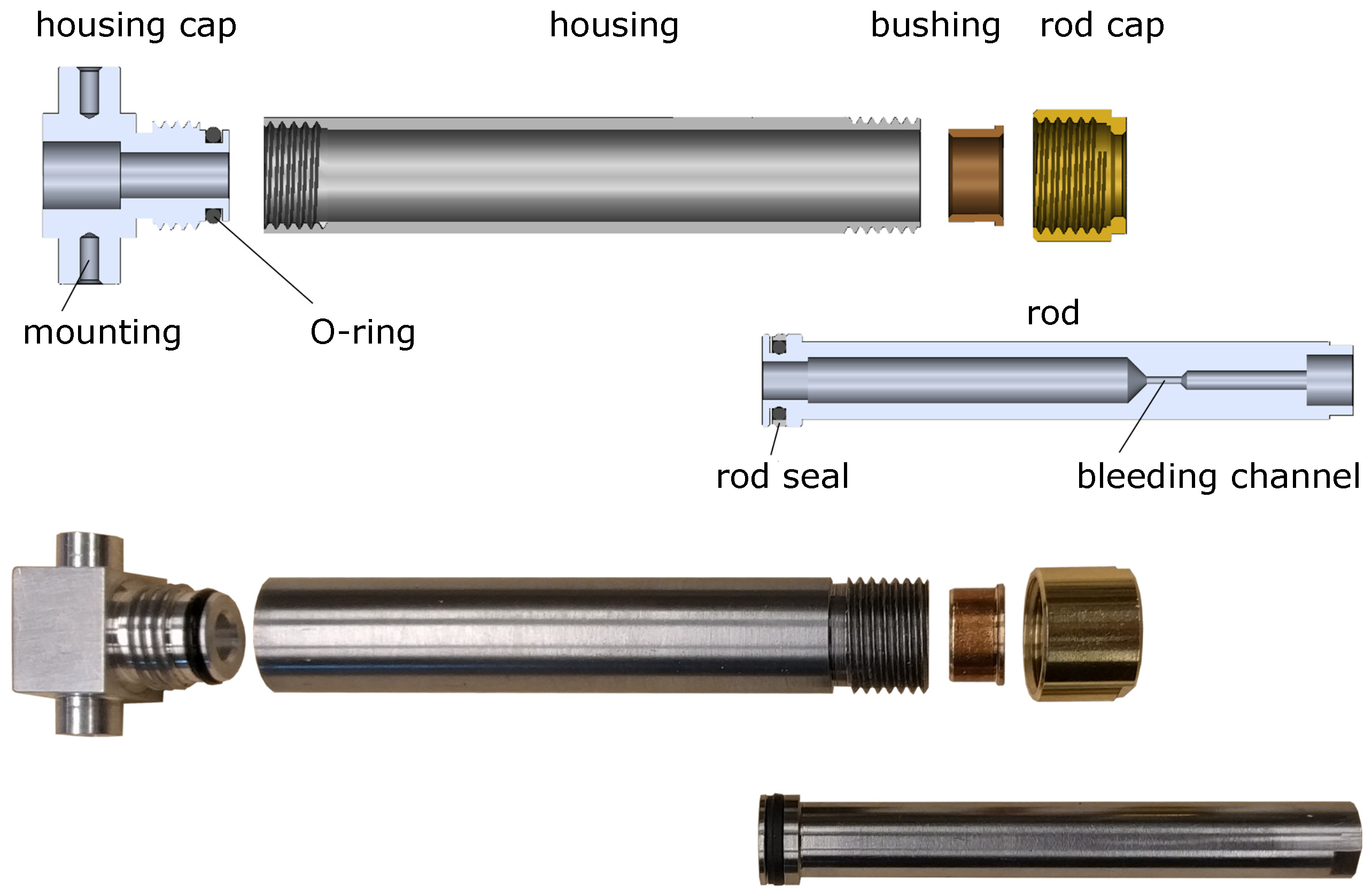
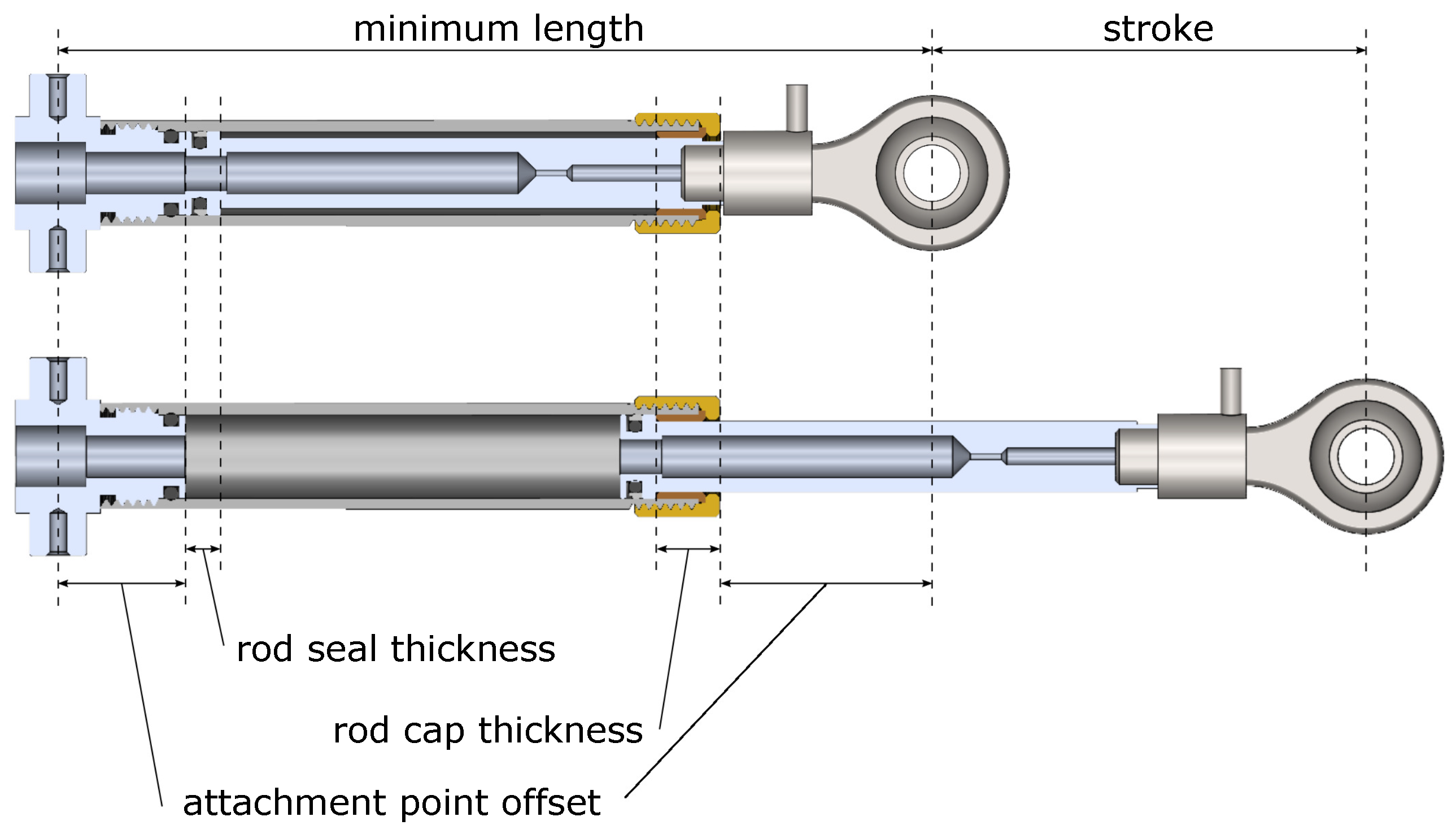
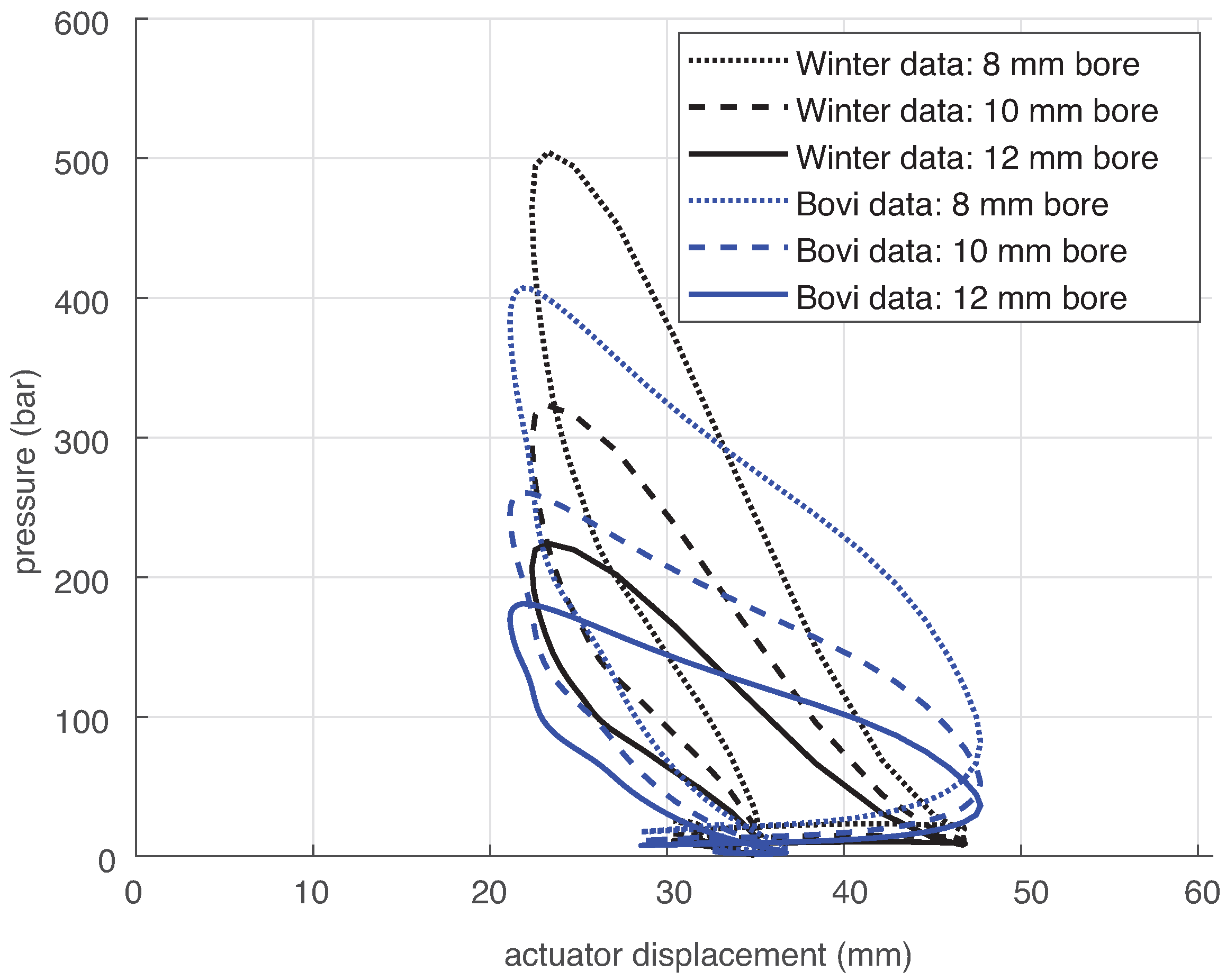
3.3. Output Cylinder
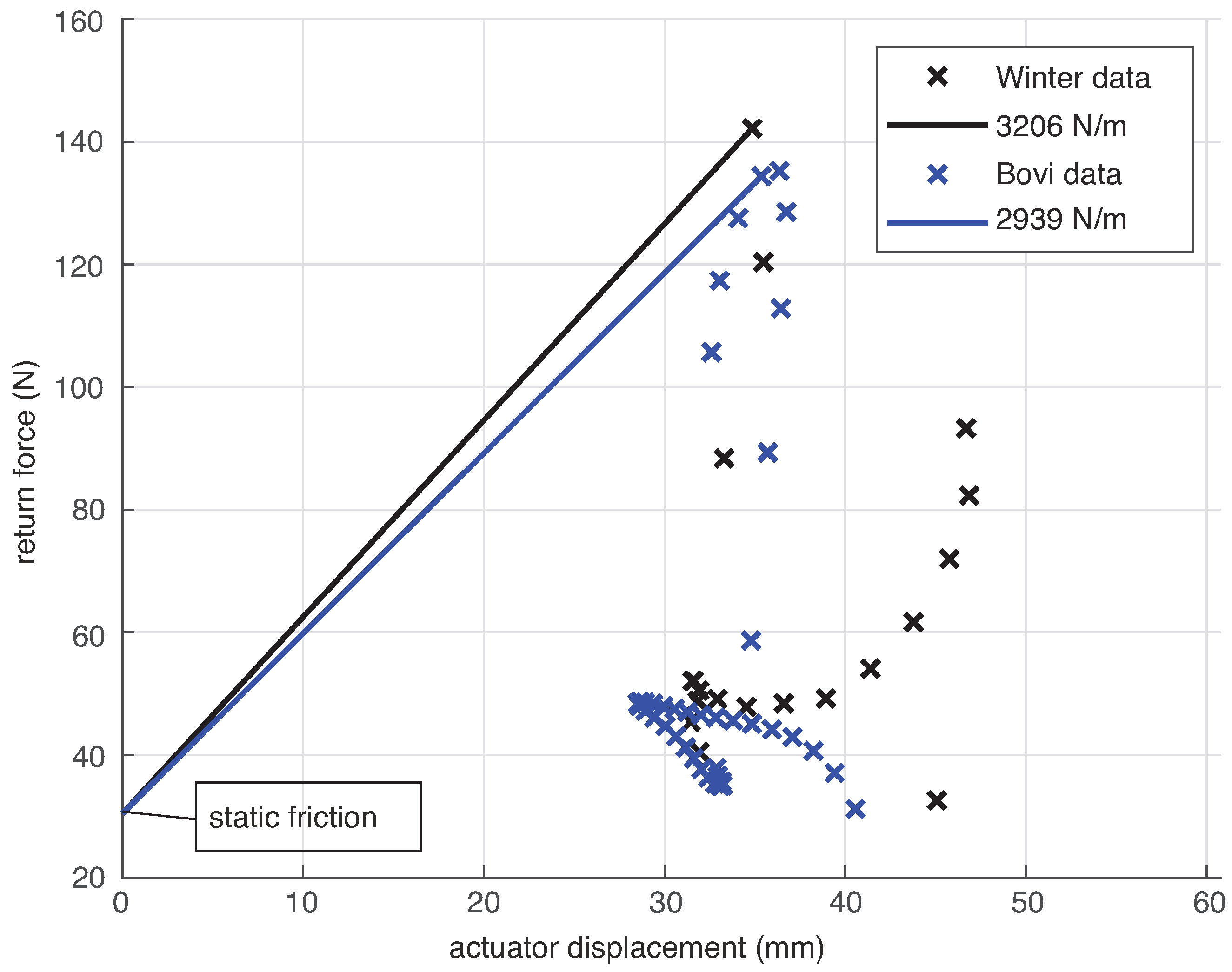
3.4. Passive Return Element
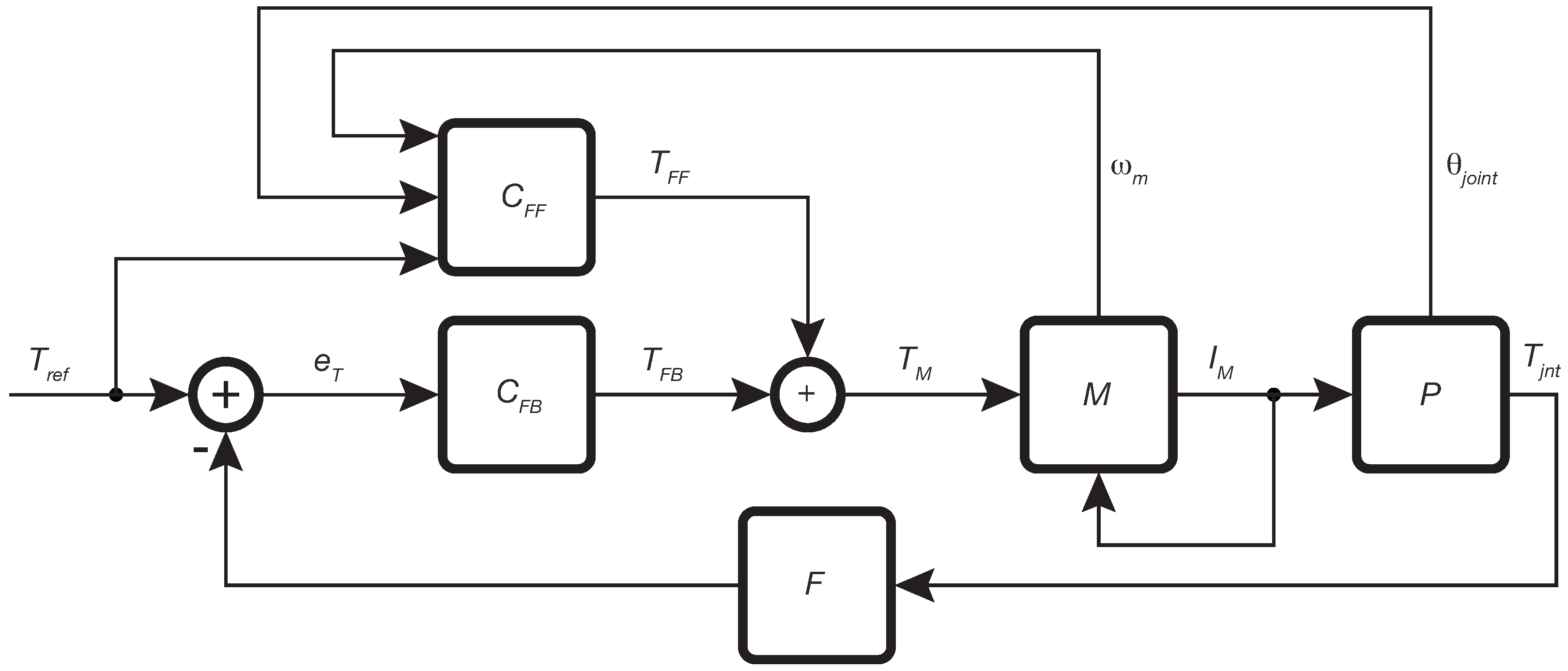
4. Control
4.1. Feedforward
4.2. Feedback
5. Results
5.1. Leakage
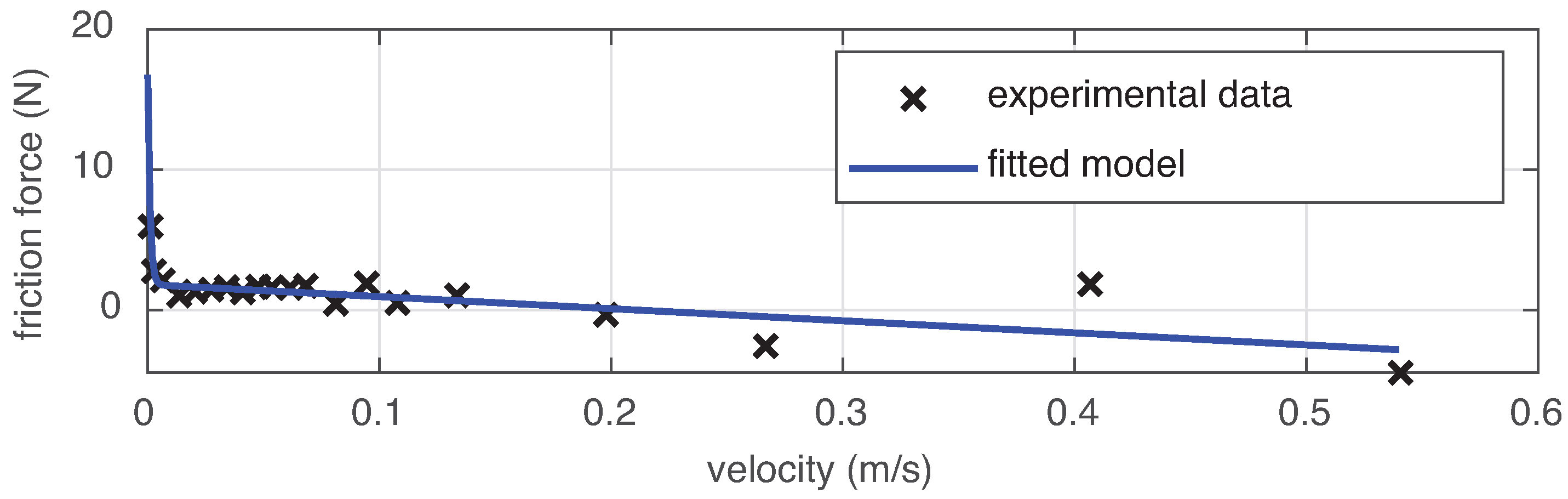
5.2. Friction Identification
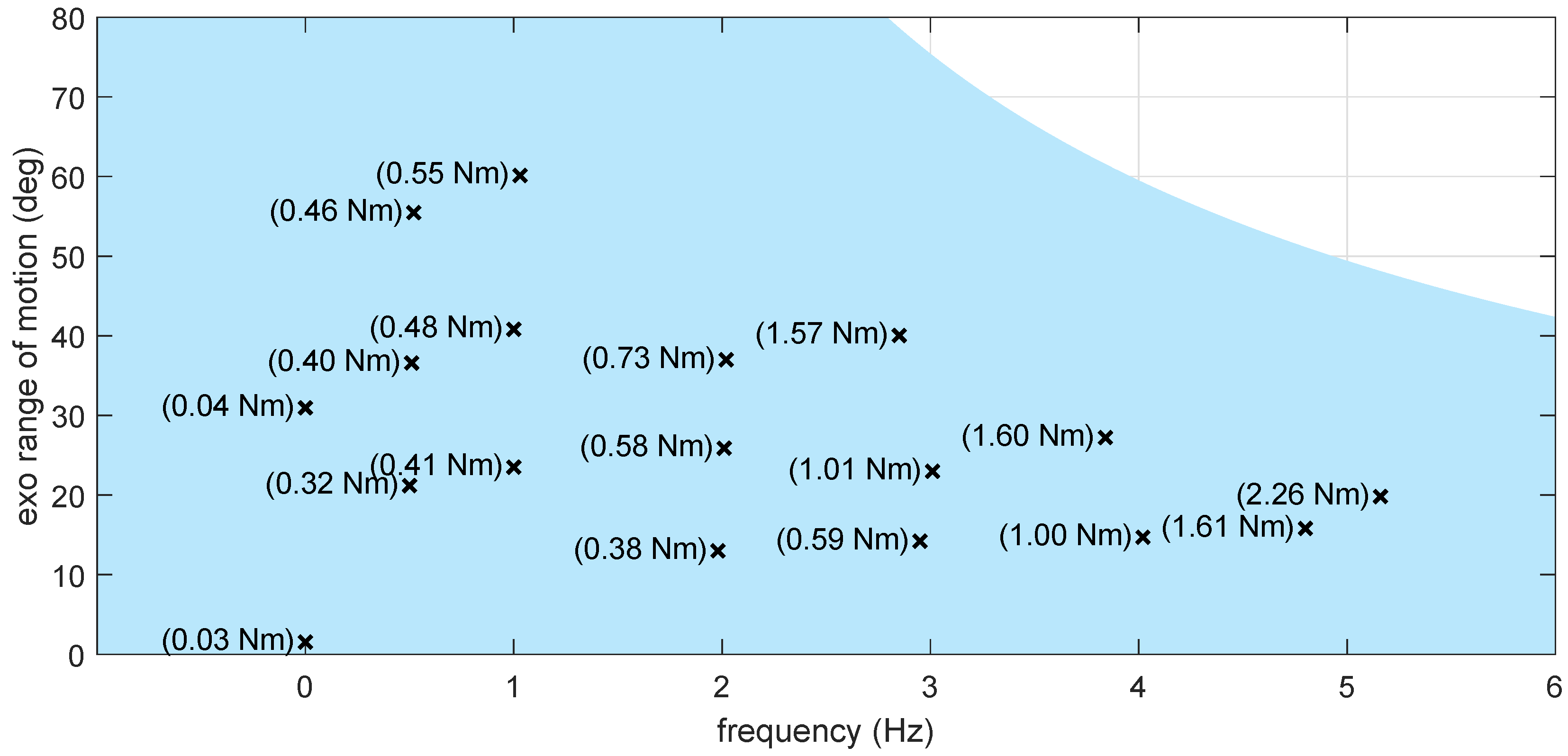
5.3. Benchtop Torque Tracking
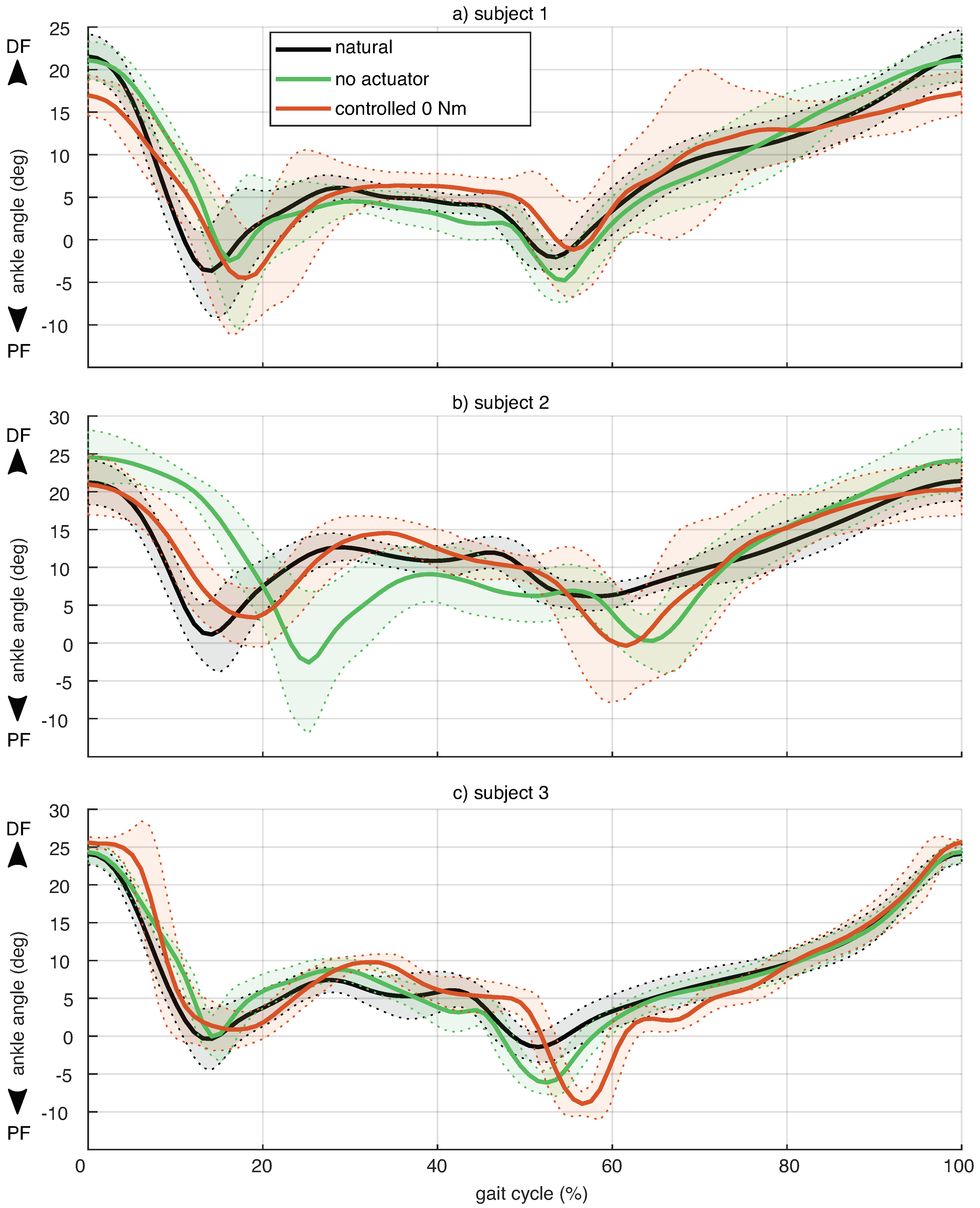
5.4. Treadmill Walking
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Choi, J.; Na, B.; Jung, P.G.; Rha, D.w.; Kong, K. WalkON suit: A medalist in the powered exoskeleton race of Cybathlon 2016. IEEE Robot. Autom. Mag. 2017, 24, 75–86. [Google Scholar] [CrossRef]
- Esquenazi, A.; Talaty, M.; Packel, A.; Saulino, M. The ReWalk powered exoskeleton to restore ambulatory function to individuals with thoracic-level motor-complete spinal cord injury. Amer. J. Phys. Med. Rehabil. 2012, 91, 911–921. [Google Scholar] [CrossRef]
- Zoss, A.B.; Kazerooni, H.; Chu, A. Biomechanical design of the Berkeley lower extremity exoskeleton (BLEEX). IEEE Trans. Mechatronics 2006, 11, 128–138. [Google Scholar] [CrossRef]
- Galle, S.; Malcolm, P.; Collins, S.H.; De Clercq, D. Reducing the metabolic cost of walking with an ankle exoskeleton: Interaction between actuation timing and power. J. Neuroeng. Rehabil. 2017, 14, 35. [Google Scholar] [CrossRef]
- Witte, K.A.; Zhang, J.; Jackson, R.W.; Collins, S.H. Design of two lightweight, high-bandwidth torque-controlled ankle exoskeletons. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1223–1228. [Google Scholar]
- Blaya, J.A.; Herr, H. Adaptive control of a variable-impedance ankle-foot orthosis to assist drop-foot gait. IEEE Trans. Neural Syst. Rehabil. Eng. 2004, 12, 24–31. [Google Scholar] [CrossRef] [PubMed]
- dos Santos, W.M.; Caurin, G.A.; Siqueira, A.A. Design and control of an active knee orthosis driven by a rotary series elastic actuator. Control Eng. Pract. 2017, 58, 307–318. [Google Scholar] [CrossRef]
- Saccares, L.; Sarakoglou, I.; Tsagarakis, N.G. iT-Knee: An exoskeleton with ideal torque transmission interface for ergonomic power augmentation. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 780–786. [Google Scholar]
- Pratt, J.E.; Morse, C.J.; Collins, S.H. The RoboKnee: An exoskeleton for enhancing strength and endurance during walking. In Proceedings of the IEEE International Conference on Robotics and Automation, New Orleans, LA, USA, 26 April–1 May 2004; IEEE: Piscataway, NJ, USA, 2004. [Google Scholar]
- Yang, C.; Yu, L.; Xu, L.; Yan, Z.; Hu, D.; Zhang, S.; Yang, W. Current developments of robotic hip exoskeleton toward sensing, decision, and actuation: A review. Wearable Technol. 2022, 3, e15. [Google Scholar] [CrossRef]
- Ishmael, M.K.; Archangeli, D.; Lenzi, T. A Powered Hip Exoskeleton with High Torque Density for Walking, Running, and Stair Ascent. IEEE/ASME Trans. Mechatron. 2022, 27, 4561–4572. [Google Scholar] [CrossRef]
- Zhang, T.; Ning, C.; Li, Y.; Wang, M. Design and Validation of a Lightweight Hip Exoskeleton Driven by Series Elastic Actuator With Two-Motor Variable Speed Transmission. IEEE Trans. Neural Syst. Rehabil. Eng. 2022, 30, 2456–2466. [Google Scholar] [CrossRef]
- Browning, R.C.; Modica, J.R.; Kram, R.; Goswami, A. The effects of adding mass to the legs on the energetics and biomechanics of walking. Med. Sci. Sports Exerc. 2007, 39, 515–525. [Google Scholar] [CrossRef]
- Meuleman, J.; Terpstra, W.; van Asseldonk, E.H.; van der Kooij, H. Effect of added inertia on the pelvis on gait. In Proceedings of the 2011 IEEE International Conference on Rehabilitation Robotics, Zurich, Switzerland, 29 June–1 July 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1–6. [Google Scholar]
- Staman, K.; Veale, A.J.; van der Kooij, H. Design, control and evaluation of the electro-hydrostatic actuator, PREHydrA, for gait restoration exoskeleton technology. IEEE Trans. Med Robot. Bionics 2020, 3, 156–165. [Google Scholar] [CrossRef]
- Veneman, J.F.; Ekkelenkamp, R.; Kruidhof, R.; van der Helm, F.C.; van der Kooij, H. A series elastic-and Bowden-cable-based actuation system for use as torque actuator in exoskeleton-type robots. Int. J. Robot. Res. 2006, 25, 261–281. [Google Scholar] [CrossRef]
- Asbeck, A.T.; De Rossi, S.M.; Holt, K.G.; Walsh, C.J. A biologically inspired soft exosuit for walking assistance. Int. J. Robot. Res. 2015, 34, 744–762. [Google Scholar] [CrossRef]
- Williams, J.R.; Cuddeback, C.F.; Fang, S.; Colley, D.; Enlow, N.; Cox, P.; Pridham, P.; Lerner, Z.F. OpenExo: An open-source modular exoskeleton to augment human function. Sci. Robot. 2025, 10, eadt1591. [Google Scholar] [CrossRef]
- Su, Q.; Pei, Z.; Tang, Z. Analysis of dynamic characteristics of hydraulic driven system for weight bearing lower limb exoskeleton. J. Phys. Conf. Ser. 2022, 2365, 012011. [Google Scholar] [CrossRef]
- Chen, D.; Yun, Y.; Deshpande, A.D. Experimental characterization of Bowden cable friction. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 5927–5933. [Google Scholar]
- Kim, H.; Seo, C.; Shin, Y.J.; Kim, J.; Kang, Y.S. Locomotion control strategy of hydraulic lower extremity exoskeleton robot. In Proceedings of the 2015 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Busan, Republic of Korea, 7–11 July 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 577–582. [Google Scholar]
- Zhu, J.; Wang, Y.; Jiang, J.; Sun, B.; Cao, H. Unidirectional variable stiffness hydraulic actuator for load-carrying knee exoskeleton. Int. J. Adv. Robot. Syst. 2017, 14, 1–12. [Google Scholar] [CrossRef]
- Khazoom, C.; Véronneau, C.; Bigué, J.P.L.; Grenier, J.; Girard, A.; Plante, J.S. Design and control of a multifunctional ankle exoskeleton powered by magnetorheological actuators to assist walking, jumping, and landing. IEEE Robot. Autom. Lett. 2019, 4, 3083–3090. [Google Scholar] [CrossRef]
- Yu, T.; Plummer, A.R.; Iravani, P.; Bhatti, J.; Zahedi, S.; Moser, D. The design, control, and testing of an integrated electrohydrostatic powered ankle prosthesis. IEEE/ASME Trans. Mechatron. 2019, 24, 1011–1022. [Google Scholar] [CrossRef]
- Neubauer, B.; Durfee, W. Preliminary design and engineering evaluation of a hydraulic ankle–foot orthosis. J. Med. Devices 2016, 10, 041002. [Google Scholar] [CrossRef]
- Soo, C.H.; Donelan, J.M. Mechanics and energetics of step-to-step transitions isolated from human walking. J. Exp. Biol. 2010, 213, 4265–4271. [Google Scholar] [CrossRef] [PubMed]
- Vlutters, M.; van Asseldonk, E.H.; van der Kooij, H. Lower extremity joint-level responses to pelvis perturbation during human walking. Sci. Rep. 2018, 8, 14621. [Google Scholar] [CrossRef]
- Bovi, G.; Rabuffetti, M.; Mazzoleni, P.; Ferrarin, M. A multiple-task gait analysis approach: Kinematic, kinetic and EMG reference data for healthy young and adult subjects. Gait Posture 2011, 33, 6–13. [Google Scholar] [CrossRef] [PubMed]
- Winter, D.A. Biomechanics and Motor Control of Human Movement; John Wiley & Sons: Hoboken, NJ, USA, 1990. [Google Scholar]
- Siegler, S.; Chen, J.; Schneck, C. The three-dimensional kinematics and flexibility characteristics of the human ankle and subtalar joints—Part I: Kinematics. J. Biomech. Eng. 1988, 110, 364–373. [Google Scholar] [CrossRef] [PubMed]
- Baud, R.; Manzoori, A.R.; Ijspeert, A.; Bouri, M. Review of control strategies for lower-limb exoskeletons to assist gait. J. Neuroeng. Rehabil. 2021, 18, 119. [Google Scholar] [CrossRef] [PubMed]
- Staman, K.; Veale, A.J.; van der Kooij, H. The PREHydrA: A passive return, high force density, electro-hydrostatic actuator concept for wearable robotics. IEEE Robot. Autom. Lett. 2018, 3, 3569–3574. [Google Scholar] [CrossRef]
- Schepers, M.; Giuberti, M.; Bellusci, G. Xsens MVN: Consistent Tracking of Human Motion Using Inertial Sensing; Xsens Technologies B.V.: Enschede, The Netherlands, 2018. [Google Scholar] [CrossRef]
- Zhang, J.; Fiers, P.; Witte, K.A.; Jackson, R.W.; Poggensee, K.L.; Atkeson, C.G.; Collins, S.H. Human-in-the-loop optimization of exoskeleton assistance during walking. Science 2017, 356, 1280–1284. [Google Scholar] [CrossRef]
- Huber, J.; Fleck, N.; Ashby, M. The selection of mechanical actuators based on performance indices. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1997, 453, 2185–2205. [Google Scholar] [CrossRef]
- Wang, T.-m.; Pei, X.; Hou, T.-g.; Fan, Y.-b.; Yang, X.; Herr, H.M.; Yang, X.-b. An untethered cable-driven ankle exoskeleton with plantarflexion-dorsiflexion bidirectional movement assistance. Front. Inf. Tech. Electron. Eng. 2020, 21, 723–739. [Google Scholar] [CrossRef]
- Rampeltshammer, W.; Keemink, A.; Sytsma, M.; van Asseldonk, E.; Kooij, H. Evaluation and Comparison of SEA Torque Controllers in a Unified Framework. Actuators 2023, 12, 303. [Google Scholar] [CrossRef]
- Yu, S.; Huang, T.H.; Wang, D.; Lynn, B.; Sayd, D.; Silivanov, V.; Park, Y.S.; Tian, Y.; Su, H. Design and control of a high-torque and highly backdrivable hybrid soft exoskeleton for knee injury prevention during squatting. IEEE Robot. Autom. Lett. 2019, 4, 4579–4586. [Google Scholar] [CrossRef]
- Azocar, A.F.; Rouse, E.J. Characterization of Open-loop Impedance Control and Efficiency in Wearable Robots. IEEE Robot. Autom. Lett. 2022, 7, 4313–4320. [Google Scholar] [CrossRef]
- Yu, S.; Huang, T.H.; Yang, X.; Jiao, C.; Yang, J.; Chen, Y.; Yi, J.; Su, H. Quasi-Direct Drive Actuation for a Lightweight Hip Exoskeleton With High Backdrivability and High Bandwidth. IEEE/ASME Trans. Mechatron. 2020, 25, 1794–1802. [Google Scholar] [CrossRef] [PubMed]
- Ma, Z.; Wang, Y.; Zhang, T.; Liu, J. Reconfigurable Exomuscle System Employing Parameter Tuning to Assist Hip Flexion or Ankle Plantarflexion. IEEE/ASME Trans. Mechatron. 2025, 1–12. [Google Scholar] [CrossRef]
- Zhang, J.; Cheah, C.C.; Collins, S.H. Experimental comparison of torque control methods on an ankle exoskeleton during human walking. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 5584–5589. [Google Scholar] [CrossRef]
- Tessari, F.; Galluzzi, R.; Tonoli, A.; Amati, N.; De Michieli, L.; Laffranchi, M. Knee prosthesis powered by a fully integrated and highly back-drivable electro-hydrostatic actuator. Mechatronics 2023, 91, 102972. [Google Scholar] [CrossRef]

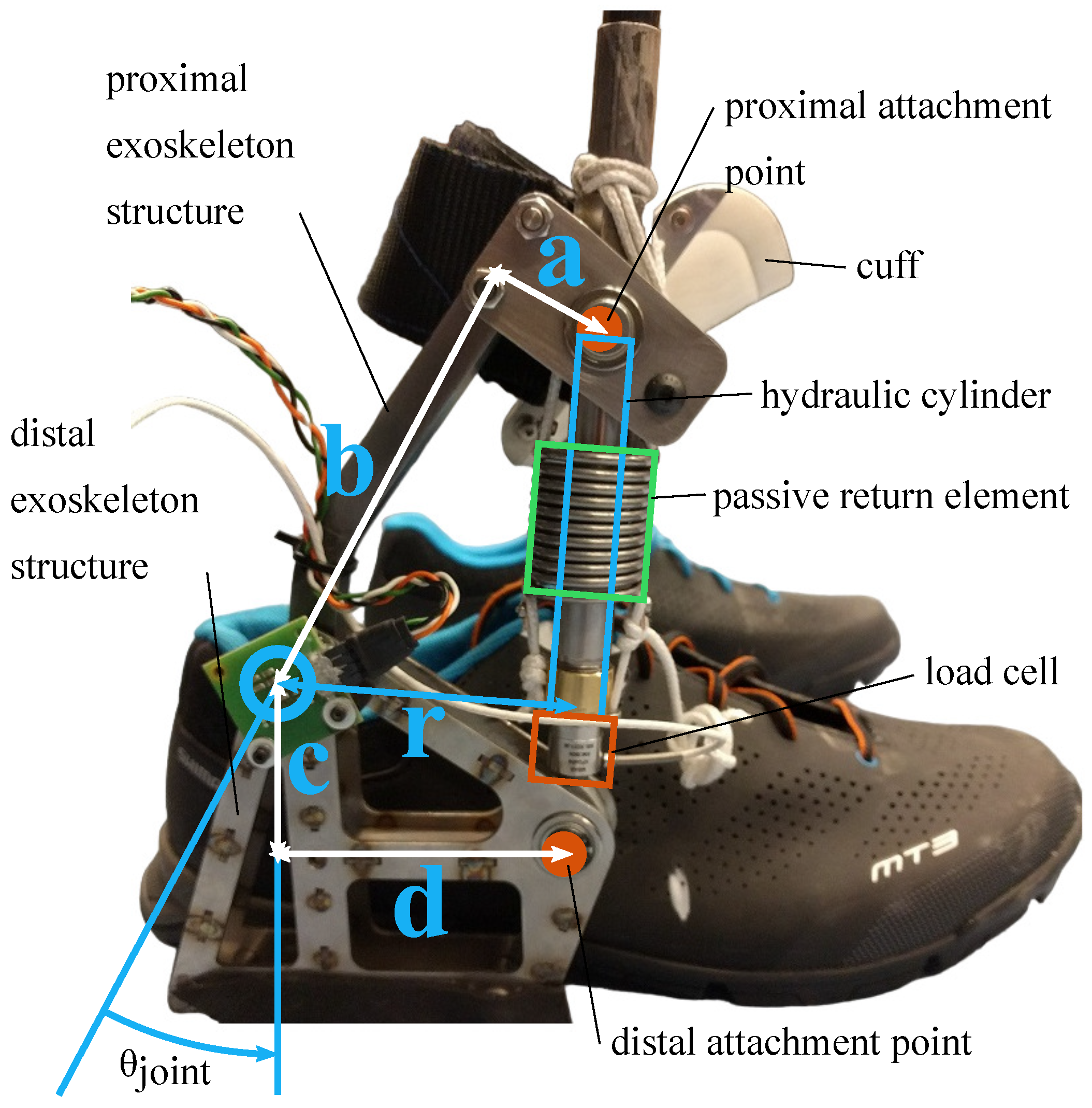


| Parameter | Value |
|---|---|
| proximal attachment distance, a | 25 mm |
| proximal attachment distance, b | 105 mm |
| distal attachment distance, c | 45 mm |
| distal attachment distance, d | 65 mm |
| moment arm, r | 15 to 68 mm |
| actuator minimum length (including load cell) | 120 mm (of which 62 mm dead length) |
| output cylinder stroke | 61.7 mm |
| output cylinder inner diameter | 12 mm |
| output cylinder forces | 31 to 2618 N |
| output cylinder pressures | 3 to 232 bar |
| return element stiffness | 3 N/m |
| Parameter | Commercial Input Cylinder (Standard Deviation) | miniHydrA Output Cylinder (Standard Deviation) |
|---|---|---|
| c | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Staman, K.; van der Kooij, H. Design and Evaluation of a Torque-Controlled Ankle Exoskeleton Using the Small-Scale Hydrostatic Actuator: miniHydrA. Actuators 2025, 14, 443. https://doi.org/10.3390/act14090443
Staman K, van der Kooij H. Design and Evaluation of a Torque-Controlled Ankle Exoskeleton Using the Small-Scale Hydrostatic Actuator: miniHydrA. Actuators. 2025; 14(9):443. https://doi.org/10.3390/act14090443
Chicago/Turabian StyleStaman, Kyrian, and Herman van der Kooij. 2025. "Design and Evaluation of a Torque-Controlled Ankle Exoskeleton Using the Small-Scale Hydrostatic Actuator: miniHydrA" Actuators 14, no. 9: 443. https://doi.org/10.3390/act14090443
APA StyleStaman, K., & van der Kooij, H. (2025). Design and Evaluation of a Torque-Controlled Ankle Exoskeleton Using the Small-Scale Hydrostatic Actuator: miniHydrA. Actuators, 14(9), 443. https://doi.org/10.3390/act14090443






