Multibody Dynamics Simulation of Upper Extremity Rehabilitation Exoskeleton During Task-Oriented Exercises
Abstract
1. Introduction
2. Methodology
- The torque values required to achieve the desired dynamics during the execution of planned movements;
- The actual internal loads within the joints of the structure.
- Recording real-life ADLs, used in the simulations as the input trajectories (described in the complementary paper [13]);
- Constructing a rigid multibody model that reflects the designed structure;
- Performing simulations to compute the outputs;
- Selecting extreme combinations of loads in the structures and extreme driving torques;
- Preparing “.rom” (Reduced Order Model) files and meshes for key structural elements, which enable the deformations in these elements within the motion to be computed;
- Constructing a flexible multibody model for selected components and analyzing the impact of deformations on the mechanical structure.
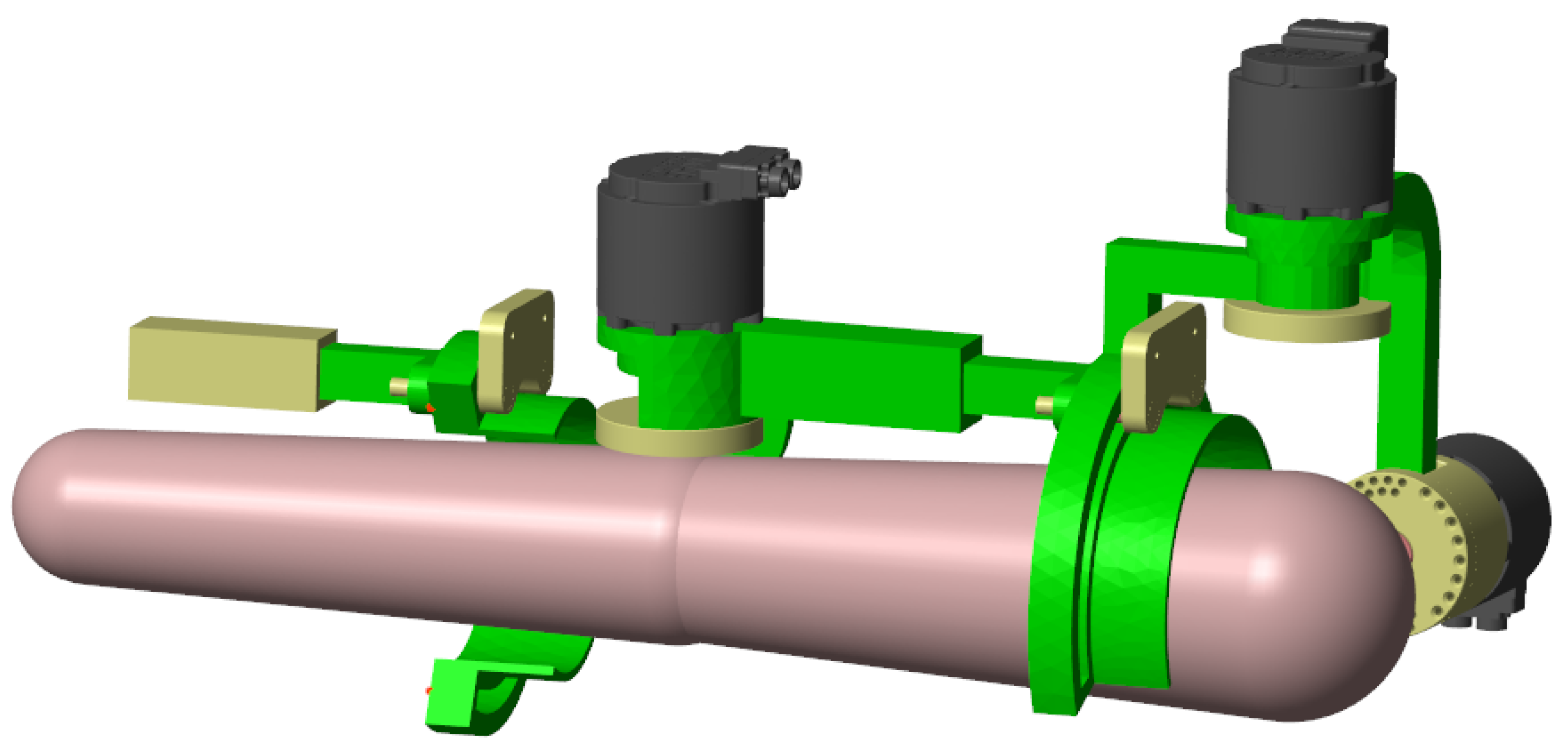
2.1. The Exoskeleton
2.2. Tools
- Movella DOT—Measurement units and software used for data collection;
- Autodesk Inventor 2021—CAD software for preparing the exoskeleton design;
- Matlab 2024a—Engineering software used to create the simulation model;
- Simulink—The block diagram environment for model-based design within MATLAB;
- Simscape—A tool for modeling and simulating physical systems;
- Simscape Multibody—A specialized toolbox within Simscape, designed for modeling and simulating the mechanics of 3D systems;
- Signal Processing Toolbox—A package that provides tools for analyzing, designing, and simulating signal processing systems;
- Robotic System Toolbox—Enables the design, simulation, and control of robotics systems;
- Partial Differential Equation Toolbox—Provides functions for solving partial differential equations, utilized for “.rom” file generation.
3. The Model
3.1. Model Inputs
3.2. Model Initialization
- A script that enables the selection of a recorded trajectory from each patient to be used in the simulation.
- A script importing a mechanical model—the paths to the files representing the mechanical components are automatically adjusted to the location of the main folder where the simulation file “.slx” and all other data regarding the 43 solid models of all of the exoskeleton design subcomponents are stored.
- A script that processes and loads the trajectories as the input to the system. First, the trajectory is read from the “.csv” file, followed by splitting it into appropriate vectors and matrices to ensure dimensional consistency of the variables for the correct operation of the model with each trajectory used. The variable defining the duration of the simulation is also defined here by reading the maximum value from the time column.
- An optional script used for deformable simulations, which assigns the deformable elements to the model.
3.3. Model Configuration
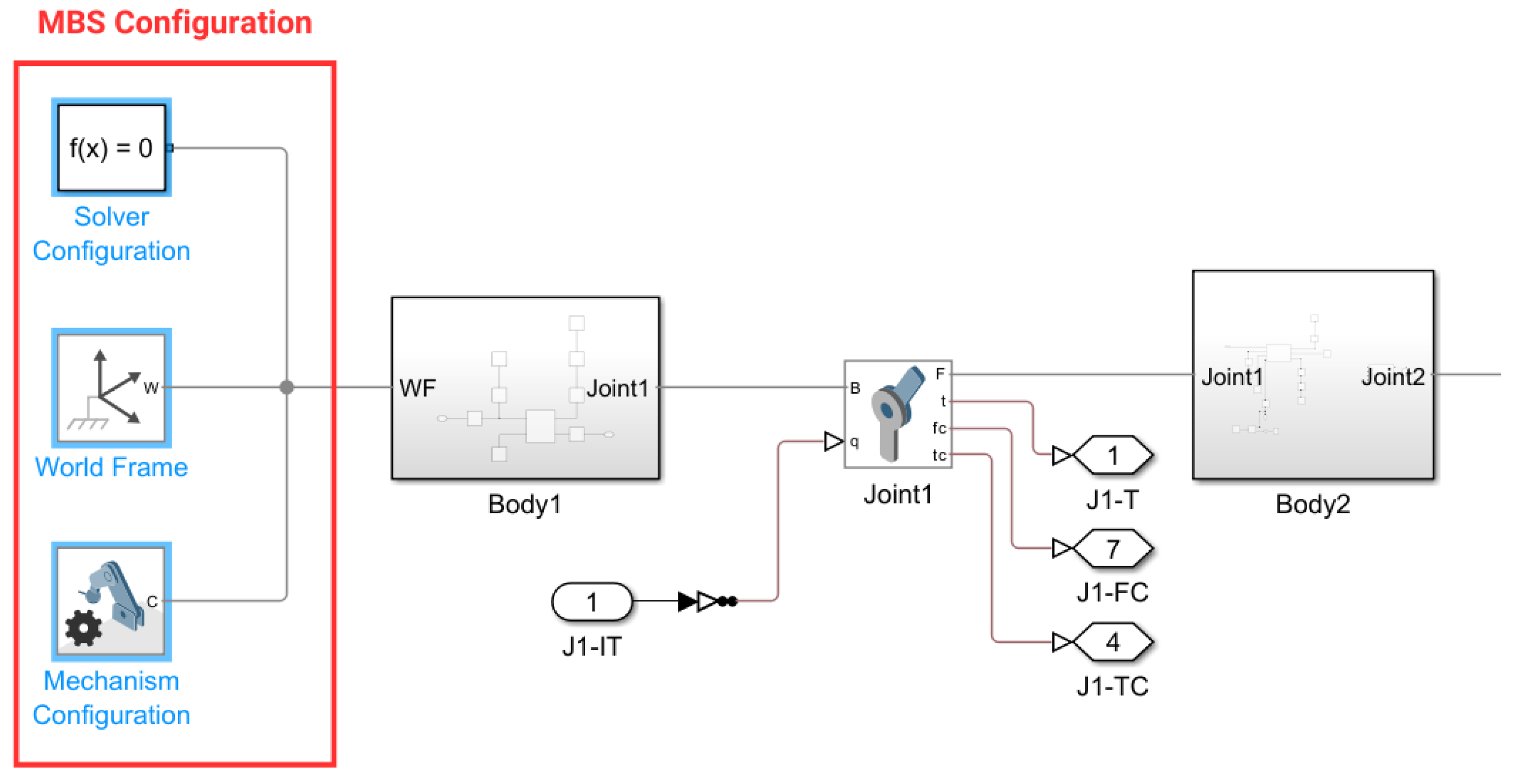
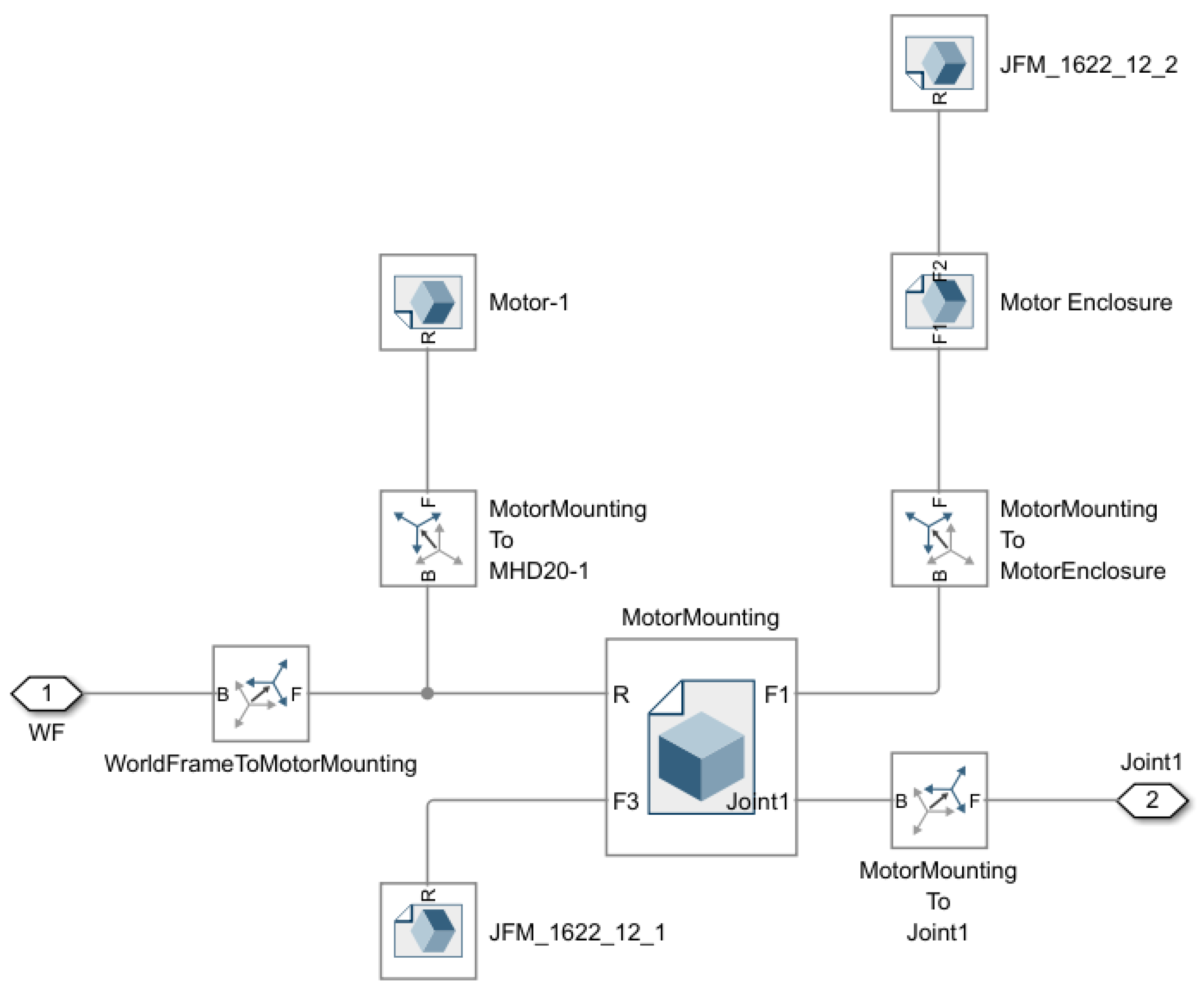
3.4. The Subsystem Structure
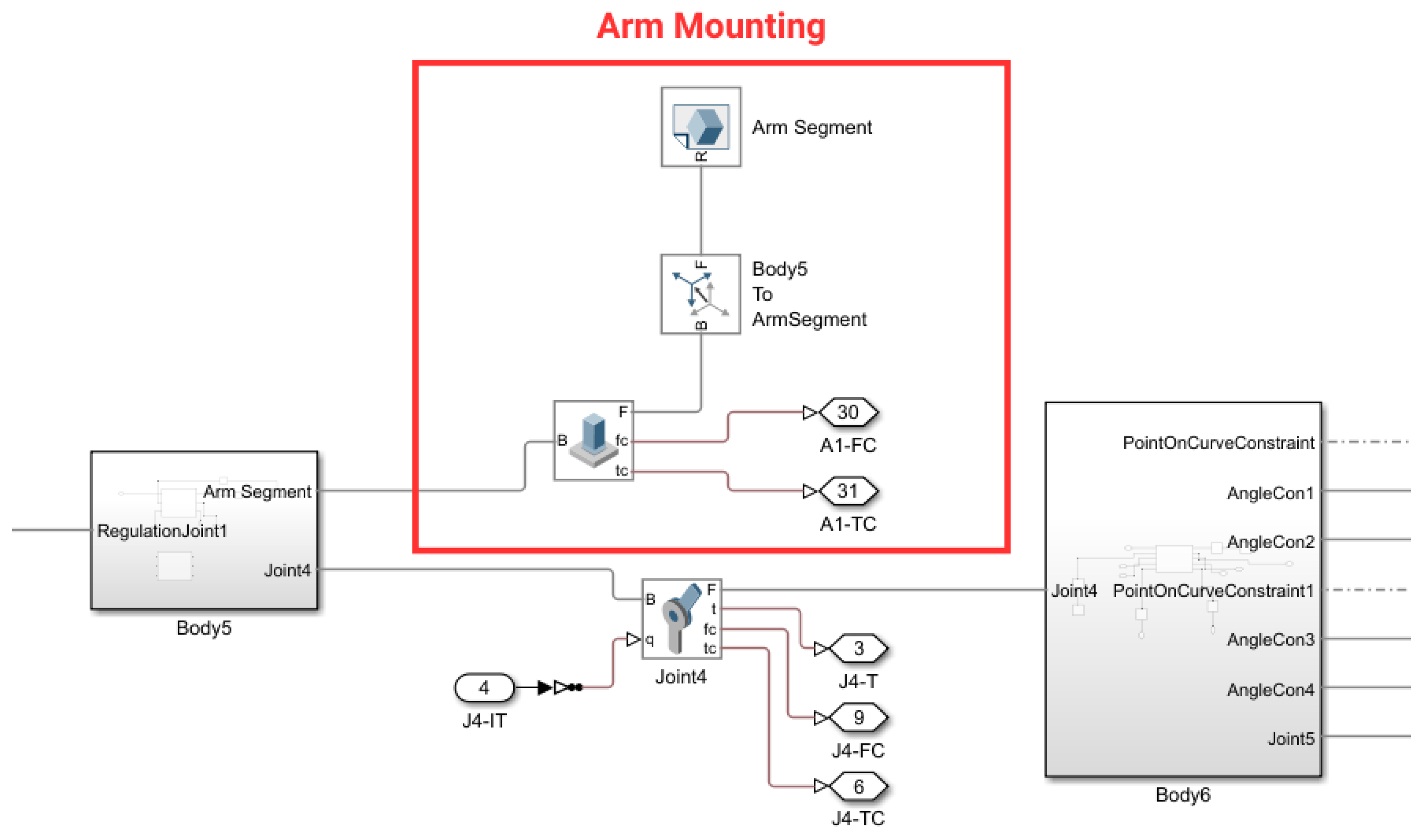
3.5. Joint Structure
3.5.1. Extremity Attachment
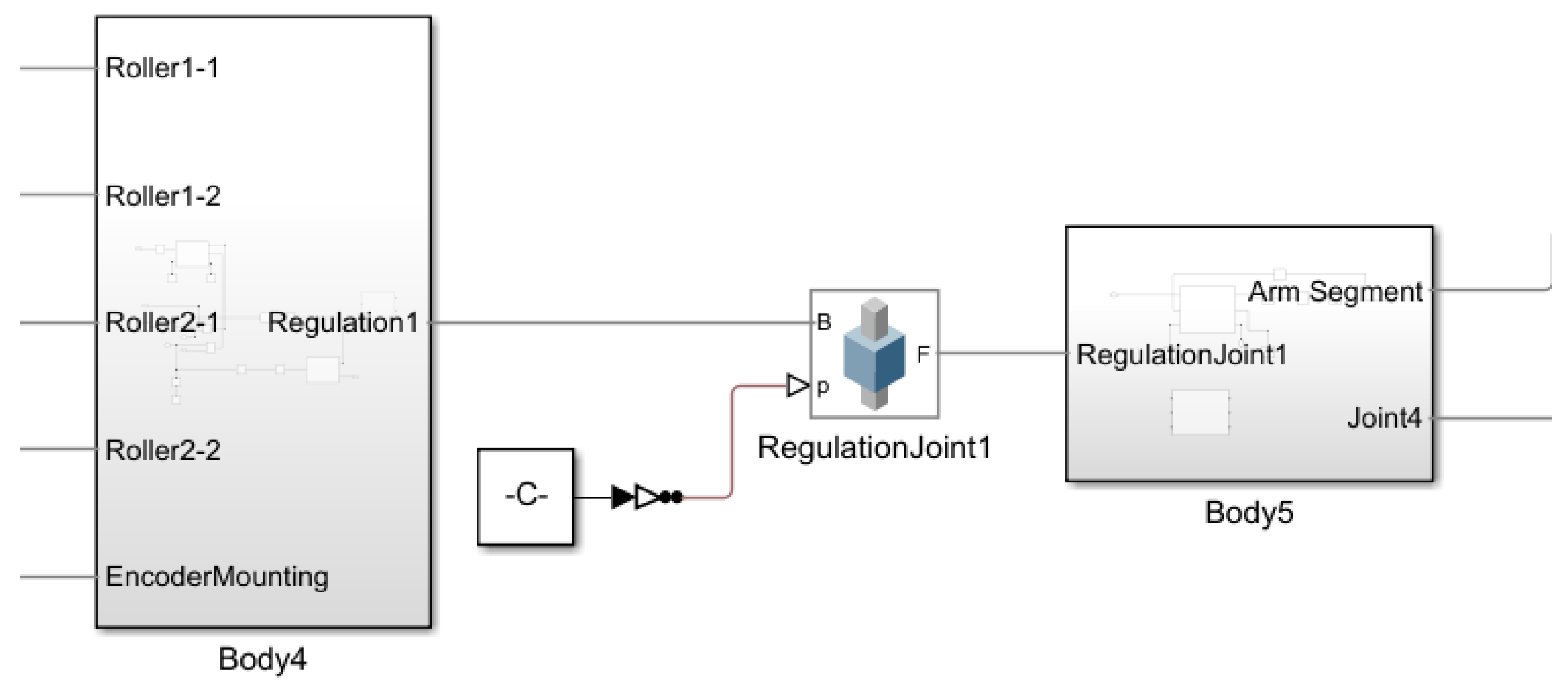
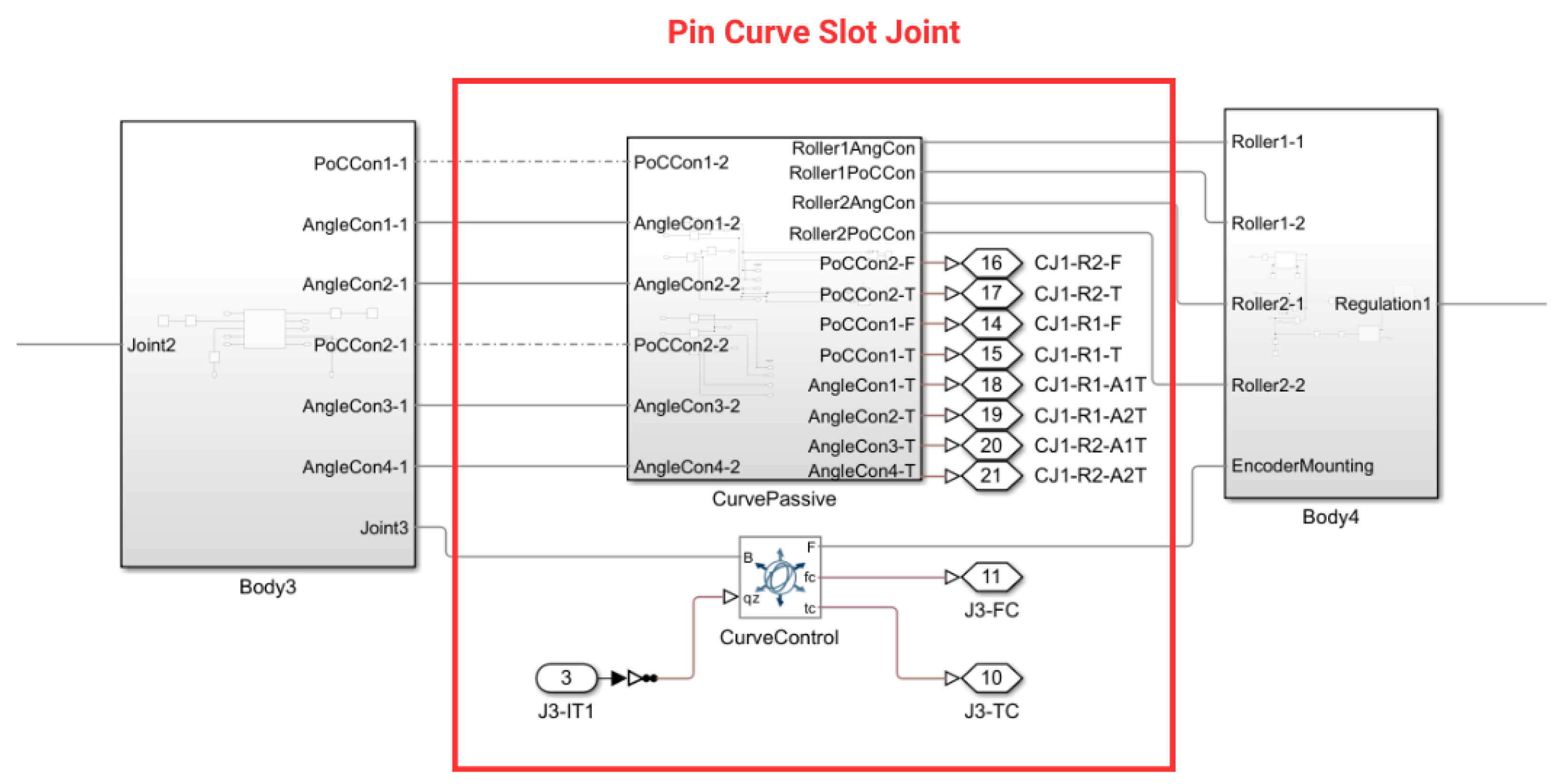
3.5.2. Free Sliding Bearings
- PointOnCurveConstraint—This enforces the movement of the assigned coordinate system of the roller along the curve. The forces and reaction torques resulting from maintaining the specified point on the defined curve are measured.
- Angle Constraint 1—This enforces the maintenance of a particular angle within the range of degrees between the Z-axes of the base and the follower coordinate systems. In this case, the movement around the X-axis of the coordinate system is restricted, and the angle is set to 90 degrees. The only value measured is the reaction torque resulting from the applied constraint.
- Angle Constraint 2—Similarly, this enforces the maintenance of the angle value between the Z-axes. In this case, the movement around the Y-axis of the coordinate system is restricted. The measured quantity is the same as that in Angle Constraint 1, but the reaction torque is measured around a different axis.
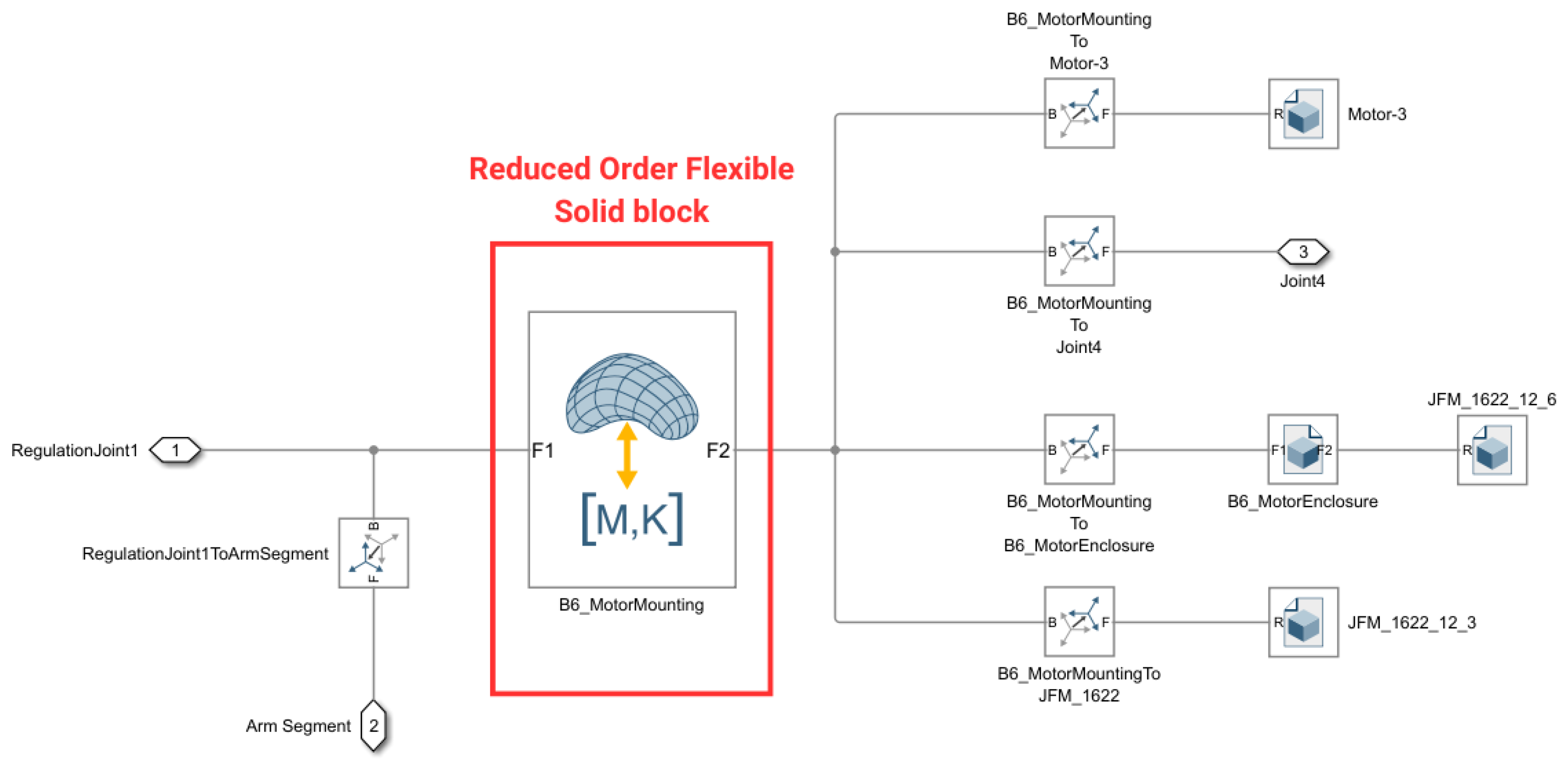
3.6. Deformable Bodies
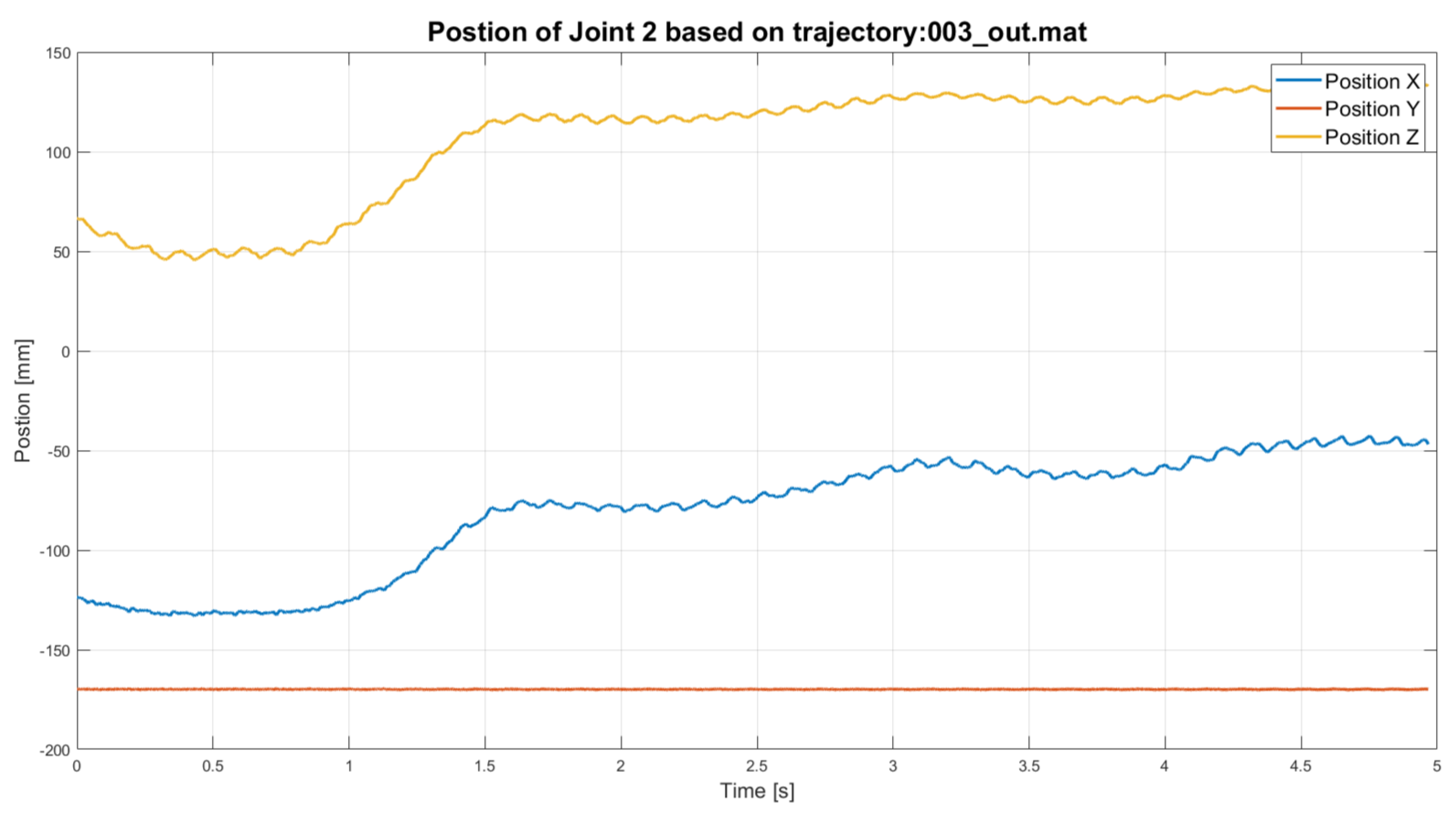
3.7. Model Outputs
- The required drive torques for all three active joints;
- The reaction forces and torques at all five joints;
- The reaction forces and torques at two points of attachment of the extremity;
- The reaction forces and torques at two length adjustments.
4. Results and Discussion
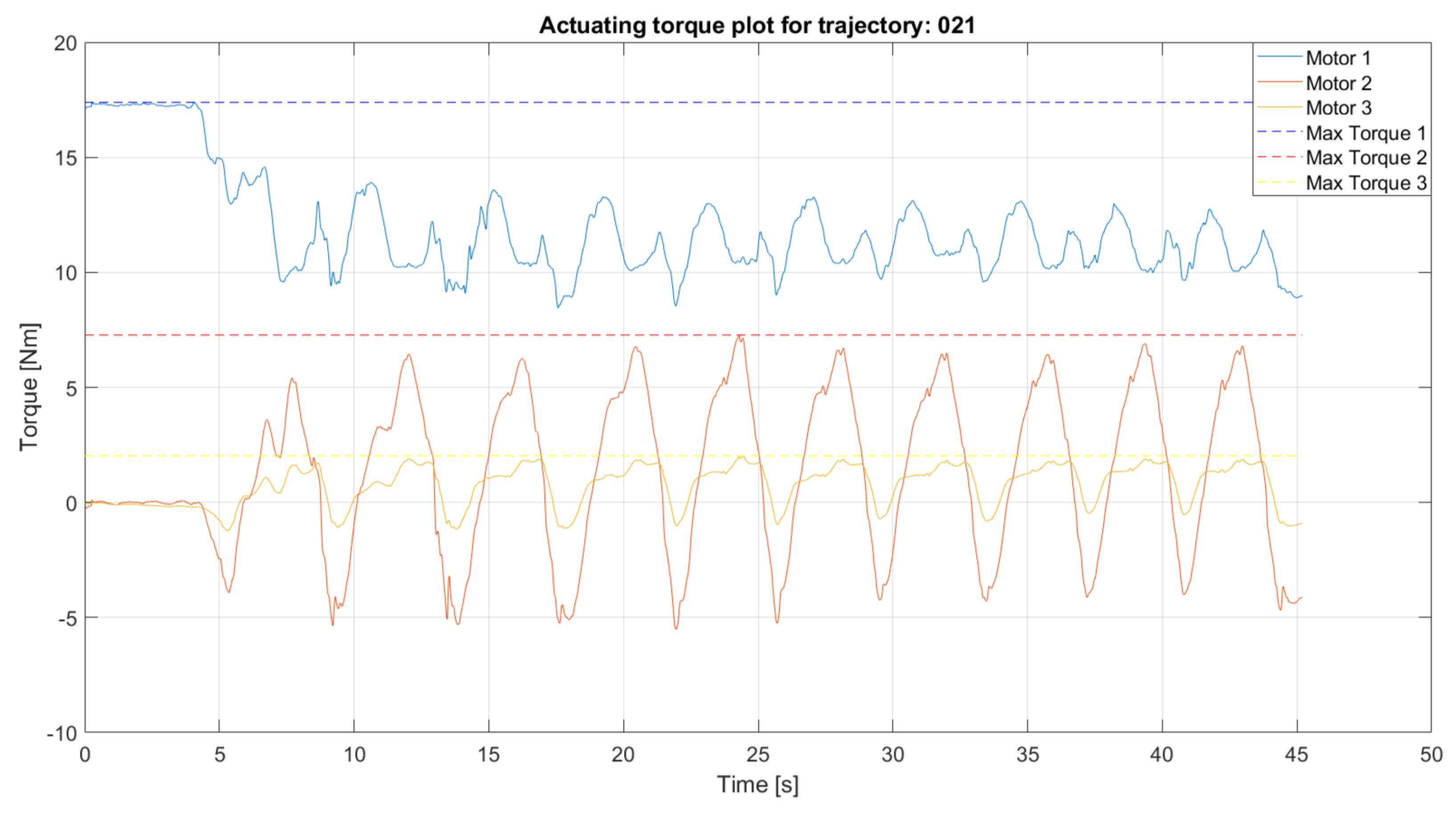
4.1. The Required Actuating Torques
4.2. Critical Reaction Loads
4.3. Deformability
5. Conclusions
6. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- United Nations Department of Economic and Social Affairs. World Social Report: Leaving No One Behind in an Ageing World; United Nations: New York, NY, USA, 2023. [Google Scholar]
- de Meijer, C.; Wouterse, B.; Polder, J.; Koopmanschap, M. The effect of population aging on health expenditure growth: A critical review. Eur. J. Ageing 2013, 10, 353–361. [Google Scholar] [CrossRef]
- Kovner, C.T.; Mezey, M.; Harrington, C. Who cares for older adults? Workforce implications of an aging society. Health Aff. 2002, 21, 78–89. [Google Scholar] [CrossRef]
- World Health Organization; World Trade Organization. Promoting Access to Medical Technologies and Innovation: Intersections Between Public Health, Intellectual Property and Trade; World Health Organization and World Trade Organization: Geneva, Switzerland, 2020. [Google Scholar]
- Li, X.; You, K. Real-time tracking and detection of patient conditions in the intelligent m-Health monitoring system. Front. Public Health 2022, 10, 922718. [Google Scholar] [CrossRef]
- Payedimarri, A.B.; Ratti, M.; Rescinito, R.; Vanhaecht, K.; Panella, M. Effectiveness of Platform-Based Robot-Assisted Rehabilitation for Musculoskeletal or Neurologic Injuries: A Systematic Review. Bioengineering 2022, 9, 129. [Google Scholar] [CrossRef]
- Desmond, D.; Layton, N.; Bentley, J.; Boot, F.H.; Borg, J.; Dhungana, B.M.; Gallagher, P.; Gitlow, L.; Gowran, R.J.; Groce, N.; et al. Assistive technology and people: A position paper from the first global research, innovation and education on assistive technology (GREAT) summit. Disabil. Rehabil. Assist. Technol. 2018, 13, 437–444. [Google Scholar] [CrossRef] [PubMed]
- Olatunji, S.A.; Nguyen, V.; Cakmak, M.; Edsinger, A.; Kemp, C.C.; Rogers, W.A.; Mahajan, H.P. Immersive participatory design of assistive robots to support older adults. Ergonomics 2024, 67, 717–731. [Google Scholar] [CrossRef] [PubMed]
- Thøgersen, M.; Gull, M.A.; Kobbelgaard, F.V.; Mohammadi, M.; Bengtson, S.H.; Struijk, L.N.A. Exotic-a discreet user-based 5 dof upper-limb exoskeleton for individuals with tetraplegia. In Proceedings of the 2020 3rd International Conference on Mechatronics, Robotics and Automation (ICMRA), Shanghai, China, 16–18 October 2020; pp. 79–83. [Google Scholar]
- Huang, J.; Ji, J.R.; Liang, C.; Zhang, Y.Z.; Sun, H.C.; Yan, Y.H.; Xing, X.B. Effects of physical therapy-based rehabilitation on recovery of upper limb motor function after stroke in adults: A systematic review and meta-analysis of randomized controlled trials. Ann. Palliat. Med. 2022, 11, 521–531. [Google Scholar] [CrossRef] [PubMed]
- Eraifej, J.; Clark, W.; France, B.; Desando, S.; Moore, D. Effectiveness of upper limb functional electrical stimulation after stroke for the improvement of activities of daily living and motor function: A systematic review and meta-analysis. Syst. Rev. 2017, 6, 40. [Google Scholar] [CrossRef]
- Osiak, T.; Osiak, N.; Falkowksi, P.; Aktan, M.E.; Czerechowicz, P.; Ömürlü, V.E. Literature-based analysis of lower extremity kinematics and dynamics during task-oriented physiotherapy for rehabilitation robot design. In Lecture Notes in Networks and Systems; Springer: Berlin/Heidelberg, Germany, 2024. [Google Scholar]
- Falkowski, P.; Pikuliński, M.; Osiak, T.; Jeznach, K.; Zawalski, K.; Kołodziejski, P.; Zakręcki, A.; Oleksiuk, J.; Śliż, D.; Osiak, N. Similarity Analysis of Upper Extremity’s Trajectories in Activities of Daily Living for Use in an Intelligent Control System of a Rehabilitation Exoskeleton. Actuators 2025, 14, 324. [Google Scholar] [CrossRef]
- Alsubiheen, A.M.; Choi, W.; Yu, W.; Lee, H. The effect of task-oriented activities training on upper-limb function, daily activities, and quality of life in chronic stroke patients: A randomized controlled trial. Int. J. Environ. Res. Public Health 2022, 19, 14125. [Google Scholar] [CrossRef]
- Falkowski, P.; Rzymkowski, C.; Pilat, Z. Analysis of rehabilitation systems in regards to requirements towards remote home rehabilitation devices. J. Autom. Mob. Robot. Intell. Syst. 2023, 17, 61–73. [Google Scholar] [CrossRef]
- Falkowski, P.; Zawalski, K.; Oleksiuk, J.; Leczkowski, B.; Pilat, Z.; Aktan, M.E.; Akdogan, E.; Niedbalski, P.; Ömürlü, V.E.; Jarek, M.; et al. Systematic review of mechanical designs of rehabilitation exoskeletons for lower-extremity. Arch. Mech. Eng. 2024, 71, 621–644. [Google Scholar] [CrossRef]
- Fareh, R.; Elsabe, A.; Baziyad, M.; Kawser, T.; Brahmi, B.; Rahman, M.H. Will your next therapist be a robot?—A review of the advancements in robotic upper extremity rehabilitation. Sensors 2023, 23, 5054. [Google Scholar] [CrossRef]
- Coremans, M.; Carmeli, E.; De Bauw, I.; Essers, B.; Lemmens, R.; Verheyden, G. Error Enhancement for Upper Limb Rehabilitation in the Chronic Phase after Stroke: A 5-Day Pre-Post Intervention Study. Sensors 2024, 24, 471. [Google Scholar] [CrossRef]
- Borghi, B.; Aghamohammadi, N.R.; Cancrini, A.; Ramirez, A.; Celian, C.; Patton, J. Personalized robotic training on a planar reaching task. In Proceedings of the 2025 International Conference On Rehabilitation Robotics (ICORR), Chicago, IL, USA, 12–16 May 2025; pp. 1493–1499. [Google Scholar]
- Moulaei, K.; Bahaadinbeigy, K.; Haghdoostd, A.A.; Nezhad, M.S.; Sheikhtaheri, A. Overview of the role of robots in upper limb disabilities rehabilitation: A scoping review. Arch. Public Health 2023, 81, 84. [Google Scholar] [CrossRef]
- Hasan, S.K.; Bhujel, S.B.; Niemiec, G.S. Emerging trends in human upper extremity rehabilitation robot. Cogn. Robot. 2024, 4, 174–190. [Google Scholar] [CrossRef]
- Khalid, S.; Alnajjar, F.; Gochoo, M.; Renawi, A.; Shimoda, S. Robotic assistive and rehabilitation devices leading to motor recovery in upper limb: A systematic review. Disabil. Rehabil. Assist. Technol. 2023, 18, 658–672. [Google Scholar] [CrossRef]
- Falkowski, P.; Mohammadi, M.; Andreasen Struijk, L.N.; Rzymkowski, C.; Pilat, Z. Optimising a driving mechanism mechanical design of EXOTIC exoskeleton—A review on upper limb exoskeletons driving systems and a case study. Multibody Syst. Dyn. 2025, 1–24. [Google Scholar] [CrossRef]
- Calafiore, D.; Negrini, F.; Tottoli, N.; Ferraro, F.; Ozyemisci-Taskiran, O.; de Sire, A. Efficacy of robotic exoskeleton for gait rehabilitation in patients with subacute stroke: A systematic review. Eur. J. Phys. Rehabil. Med. 2022, 58, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Rose, C.G.; Deshpande, A.D.; Carducci, J.; Brown, J.D. The road forward for upper-extremity rehabilitation robotics. Curr. Opin. Biomed. Eng. 2021, 19, 100291. [Google Scholar] [CrossRef]
- Kapsalyamov, A.; Hussain, S.; Jamwal, P.K. State-of-the-art assistive powered upper limb exoskeletons for elderly. IEEE Access 2020, 8, 178991–179001. [Google Scholar] [CrossRef]
- Siviy, C.; Baker, L.M.; Quinlivan, B.T.; Porciuncula, F.; Swaminathan, K.; Awad, L.N.; Walsh, C.J. Opportunities and challenges in the development of exoskeletons for locomotor assistance. Nat. Biomed. Eng. 2023, 7, 456–472. [Google Scholar] [CrossRef]
- Falkowski, P. A numerical algorithm for optimal selection of the driving mechanisms for ExoReha exoskeleton. In Proceedings of the 2024 10th International Conference on Mechatronics and Robotics Engineering (ICMRE), Milan, Italy, 27–29 February 2024; pp. 149–154. [Google Scholar]
- Firouzi, V.; Seyfarth, A.; Song, S.; von Stryk, O.; Ahmad Sharbafi, M. Biomechanical models in the lower-limb exoskeletons development: A review. J. NeuroEng. Rehabil. 2025, 22, 12. [Google Scholar] [CrossRef]
- Ren, B.; Liu, J.; Chen, J. Simulating human–machine coupled model for gait trajectory optimization of the lower limb exoskeleton system based on genetic algorithm. Int. J. Adv. Robot. Syst. 2020, 17, 1729881419893493. [Google Scholar] [CrossRef]
- Fregly, B.J. Design of Optimal Treatments for Neuromusculoskeletal Disorders using Patient-Specific Multibody Dynamic Models. Int. J. Comput. Vis. Biomech. 2009, 2, 145–155. [Google Scholar]
- Gedliczka, A.; Pochopień, P. Atlas Miar Człowieka: Dane do Projektowania i Oceny Ergonomicznej: Antropometria, Biomechanika, Przestrzeń Pracy, Wymiary Bezpieczeństwa; CIOP: Warsaw, Poland, 2001. [Google Scholar]
- Falkowski, P. Predicting dynamics of a rehabilitation exoskeleton with free degrees of freedom. In Proceedings of the Conference on Automation; Springer: Berlin/Heidelberg, Germany, 2022; pp. 223–232. [Google Scholar]
- McConville, J.T. Anthropometric Relationships of Body and Body Segment Moments of Inertia; Air Force Aerospace Medical Research Laboratory, Aerospace Medical Division: Dayton, OH, USA, 1981; Volume 32.
- Torzo, G.; Paolo, P. The real pendulum: Theory, simulation, experiment. Lat.-Am. J. Phys. Educ. 2009, 3, 221–228. [Google Scholar]
- Park, G.; Kim, C.; Lee, M.; Choi, C. Building geometry simplification for improving mesh quality of numerical analysis model. Appl. Sci. 2020, 10, 5425. [Google Scholar] [CrossRef]
- Rong, B.; Rui, X.; Tao, L.; Wang, G. Theoretical modeling and numerical solution methods for flexible multibody system dynamics. Nonlinear Dyn. 2019, 98, 1519–1553. [Google Scholar] [CrossRef]
- Vande Wouwer, A.; Saucez, P.; Vilas, C. Simulation of ODE/PDE Models with MATLAB®, OCTAVE and SCILAB. In Scientific and Engineering Applications; Springer International Publishing: Cham, Switzerland, 2014. [Google Scholar]
- Zahedi Khameneh, A.; Kilicman, A. Some construction methods of aggregation operators in decision-making problems: An overview. Symmetry 2020, 12, 694. [Google Scholar] [CrossRef]
- Falkowski, P.; Jeznach, K. Simulation of a control method for active kinesiotherapy with an upper extremity rehabilitation exoskeleton without force sensor. J. NeuroEng. Rehabil. 2024, 21, 22. [Google Scholar] [CrossRef] [PubMed]
- Falkowski, P. Light exoskeleton design with topology optimisation and fem simulations for fff technology. J. Autom. Mob. Robot. Intell. Syst. 2021, 15, 14–19. [Google Scholar] [CrossRef]



| Joint | Anatomical Range of Motion |
|---|---|
| 1 | – |
| 2 | −– |
| 3 | −– |
| 4 | – |
| 5 | −– |
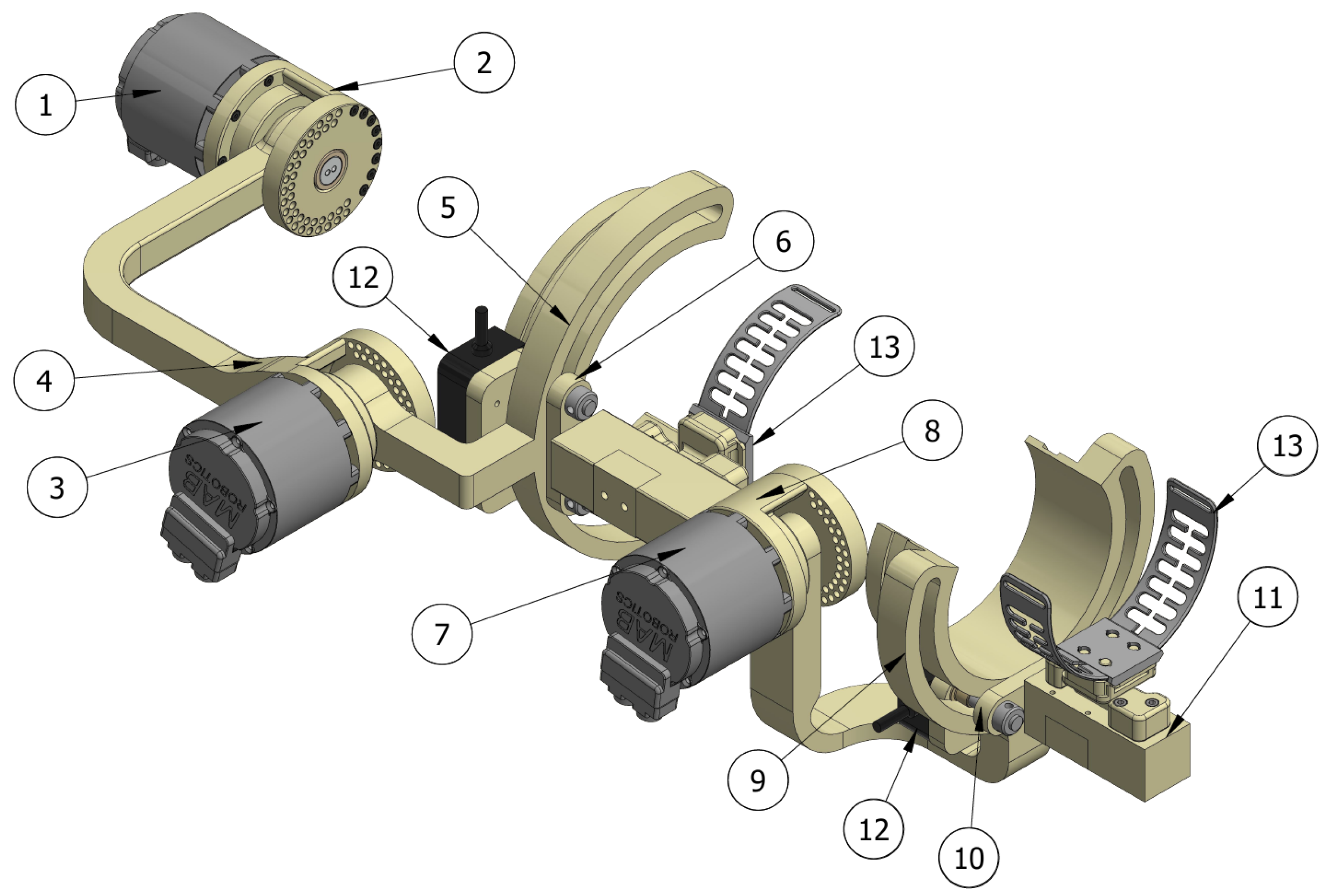
| No. | Part of the Exoskeleton |
|---|---|
| 1 | Motor 1 |
| 2 | Body 1 |
| 3 | Motor 2 |
| 4 | Body 2 |
| 5 | Body 3/passive shoulder joint |
| 6 | Body 4 with linear adjustment |
| 7 | Motor 3 |
| 8 | Body 5 |
| 9 | Body 6 |
| 10 | Body 7 with linear adjustment |
| 11 | Body 8 |
| 12 | Magnetic encoders |
| 13 | Extremity mounting elastic straps |
| No. | Parts | Mass [kg] |
|---|---|---|
| 1 | Body 1 + Motor 1 | 1.18 |
| 2 | Body 2 + Motor 2 | 1.54 |
| 3 | Body 3 | 0.95 |
| 4 | Body 4 | 0.16 |
| 5 | Body 5 + Motor 3 | 1.42 |
| 6 | Body 6 | 1.08 |
| 7 | Body 7 | 0.13 |
| 8 | Body 8 | 0.14 |
| 9 | Arm | 3.15 |
| 10 | Forearm + hand | 2.1 |
| Motor | Max. Torque [Nm] |
|---|---|
| 1 | 29.44 |
| 2 | 30.83 |
| 3 | 9.94 |
| Load Point | Constraint Force [N] | Constraint Torque [Nm] | ||||
|---|---|---|---|---|---|---|
| X | Y | Z | X | Y | Z | |
| AJ 1 | −500.18 | −472.41 | −329.70 | −243.31 | 160.21 | 0.00 |
| AJ 2 | 345.29 | 475.38 | −516.26 | −94.39 | −143.73 | 0.00 |
| AJ 3 | 79.86 | 32.57 | −7.55 | −2.15 | −4.32 | 0.00 |
| PJ 1 Roller 1 | 1058.88 | −369.57 | −68.79 | −71.51 | −64.22 | 0.00 |
| PJ 1 Roller 2 | −250.20 | 716.81 | −68.44 | −67.26 | −61.57 | 0.00 |
| PJ 2 Roller 1 | −52.88 | 22.89 | −3.90 | −0.23 | 1.45 | 0.00 |
| PJ 2 Roller 2 | −23.95 | 55.32 | −30.15 | −0.72 | 1.22 | 0.00 |
| EM 1 | 30.85 | 6.68 | 17.64 | −0.36 | 3.03 | 0.04 |
| EM 2 | 57.25 | −4.09 | 22.88 | −2.54 | 1.64 | 4.62 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Falkowski, P.; Zawalski, K. Multibody Dynamics Simulation of Upper Extremity Rehabilitation Exoskeleton During Task-Oriented Exercises. Actuators 2025, 14, 426. https://doi.org/10.3390/act14090426
Falkowski P, Zawalski K. Multibody Dynamics Simulation of Upper Extremity Rehabilitation Exoskeleton During Task-Oriented Exercises. Actuators. 2025; 14(9):426. https://doi.org/10.3390/act14090426
Chicago/Turabian StyleFalkowski, Piotr, and Krzysztof Zawalski. 2025. "Multibody Dynamics Simulation of Upper Extremity Rehabilitation Exoskeleton During Task-Oriented Exercises" Actuators 14, no. 9: 426. https://doi.org/10.3390/act14090426
APA StyleFalkowski, P., & Zawalski, K. (2025). Multibody Dynamics Simulation of Upper Extremity Rehabilitation Exoskeleton During Task-Oriented Exercises. Actuators, 14(9), 426. https://doi.org/10.3390/act14090426






