Decentralized Sliding Mode Control for Large-Scale Systems with Actuator Failures Using Dynamic Event-Triggered Adaptive Dynamic Programming

Abstract

This study develops a new integral sliding mode-based method to address the decentralized adaptive fault-tolerant guaranteed cost control (GCC) problem via a dynamic event-triggered (DET) adaptive dynamic programming (ADP) approach. Firstly, integral sliding mode control technology is applied to eliminate the influence of actuator faults, which can guarantee that the large-scale system states stay on the sliding mode surface. Secondly, the ADP algorithm based on DET mode is employed to improve the control performance for equivalent sliding mode surface and reduce computational and communication overhead. Meanwhile, the GCC method is introduced to ensure that the performance cost function is less than an upper bound while maintaining system stability. Then, through Lyapunov stability analysis, it is proven that the presented DET-GCC method based on ADP algorithm can guarantee that all signals are uniformly ultimately bounded. Finally, the validity of the developed approach is confirmed through the simulation results.

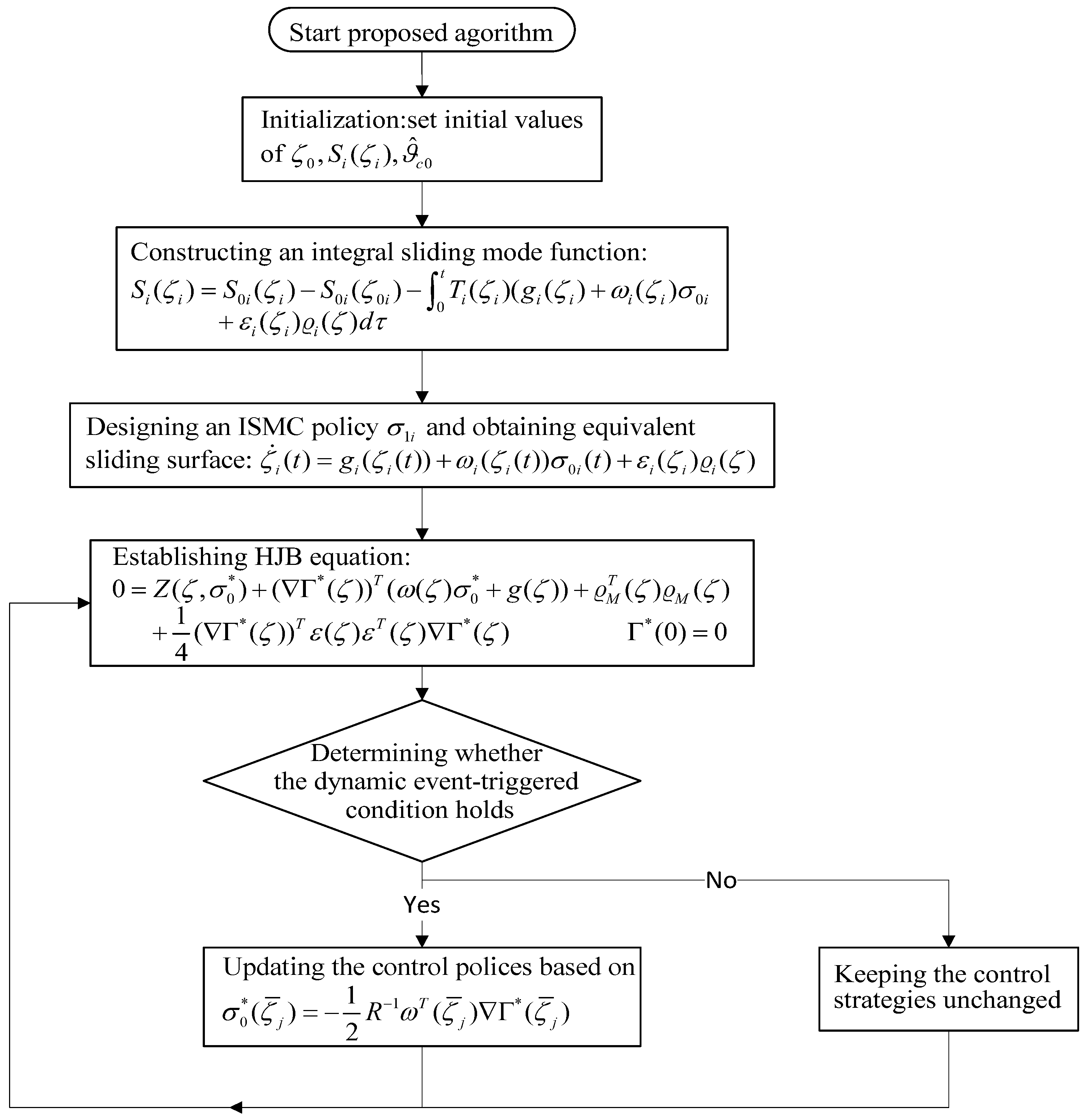
1. Introduction

Over the past few years, large-scale (LS) system models have been widely studied in unmanned aerial vehicle (UAV) systems, smart transportation, microgrid systems and other fields [1,2,3]. These systems are usually composed of multiple low-dimensional subsystems with complex dynamic coupling relationships. However, the traditional centralized control method cannot effectively deal with the interaction between subsystems, which threatens the stability of the whole system [4]. Consequently, decentralized control approaches have been widely concerned, which mainly use local state information for control design, rather than relying on the global state information of the whole system [5]. In [6], a decentralized robust optimal control (OC) method was used for LS systems subject to constrained structural variations, and its superior performance was proved in power systems. In [7], a neural network (NN)-based decentralized adaptive control approach is put forward to tackle the control issue of nonlinear large-scale (NLS) systems. In [8], a novel decentralized control approach for discrete-time LS systems was presented, which ensures the passivity properties of subsystems by locally solving semi-definite programs, thereby achieving asymptotic stability for the entire system.

The OC strategy for LS systems optimizes multiple performance indicators by adjusting control parameters [9,10]. Different from the adaptive control strategy [11,12], the adaptive dynamic programming (ADP) method, which learned future optimal strategies based on current states and actions, was introduced to solve OC problems [13,14,15]. In [16], a novel ADP approach was designed to address the OC issue of unknown LS systems with application to the fuel control system for turbofan engines. In [17], a decentralized ADP-based OC approach was developed to address the control issue for multi-agent systems. In [18], for the nonlinear system with state constraints, the authors presented a new ADP approach for tackling OC issues. In recent years, the ADP algorithm has effectively handled uncertainties in NLS systems with matched and unmatched interconnections while offering an approach for tackling decentralized OC issues. In [19], ADP methodology was employed to address the decentralized OC issue in NLS systems subject to unknown time delays and mismatched interconnections, for which a novel cost function was developed for converting decentralized control issues into an OC problem. In [20], by solving a series of Hamilton–Jacobi–Bellman equations for auxiliary subsystems, a decentralized NN control scheme was proposed via the ADP algorithm. In [21], a synchronous value iteration algorithm based on the ADP method was formulated for the restricted optimization issue of uncertain NLS systems.

On the other hand, researchers have utilized an ADP-based sliding mode control (SMC) scheme to address the fault-tolerant control (FTC) issue, which can not only eliminate the impact of actuator faults, but also guarantee OC performance of sliding-mode dynamics (SMD) [22,23,24,25]. In [22], a comprehensive control method combining ADP algorithm and global SMC was formulated to resolve the orientation control issue for flexible spacecraft subject to actuator failure. In [23], a novel off-line optimal SMC method based on an ADP algorithm was presented to handle the FTC problem for cascade nonlinear systems with mismatched uncertainties. In [24], an ADP-based sliding mode FTC method was proposed with an optimizer for OC parameters. The integral SMC in this method adds an integral term to traditional SMC to improve anti-interference. In [25], a FTC method combining fuzzy integral nonsingular terminal SMC and ADP was proposed to enhance launch vehicle flight safety in the event of actuator failure. However, the control methods in these studies have limitations in guaranteeing control performance when the system is under complex fault scenarios. To enhance the robustness for the system against uncertainty, guaranteed cost control (GCC) has been introduced in [26], with the goal of strictly ensuring that the performance cost index does not exceed the upper bound while satisfying system stability. Over recent years, the GCC strategy has been further utilized with more complex system models and scenarios such as the study in [27] on the finite-time GCC for LS singular systems subject to interconnected state lags. In [28], a quantitative guaranteed cost FTC approach was developed for addressing the control issue of unknown multi-input systems with actuator failures.

An event-triggered control (ETC) method can reduce communication and computing resource consumption compared to traditional time-triggered control mode [29,30,31], as it updates the controller strategies only when preset conditions are violated. Static ETC approach optimizes resources for decentralized control of NLS systems by using fixed triggering conditions. In [32], a hierarchical sliding mode surface (SMS)-based ADP algorithm combined with the ETC approach was designed to tackle the OC issue for switched nonlinear systems. In [33], a decentralized ETC strategy according to the ADP method was proposed for NLS systems to reduce communication costs and computing burden. However, compared with static ETC, dynamic ETC has higher resource utilization efficiency and lower communication and computing burden. In [34], a novel ADP method under dynamic ETC mode was developed by using only agent interaction information without needing model dynamics, thus addressing the problem of resolving algebraic Riccati equations. Reference [35] presented a new decentralized control scheme for certain continuous-time interconnected NLS systems with interconnection terms and unmodeled internal dynamics by integrating the dynamic ETC and ADP method. However, these systems do not contain failures when the operating system operates normally.

Inspired by the above discussions, this paper presents an SMC strategy based on the dynamic event-triggered ADP method for LS systems with actuator faults. The main innovations are as follows:

1.

This article proposes an FTC scheme for NLS systems with actuator faults using integral sliding mode control (ISMC) technology, which eliminates the effect of actuator faults and achieves stable SMD.

2.

This article presents a GCC approach based on the ADP algorithm, which ensures that the motion trajectories of the system stay on the SMS, while the overall performance index is less than a certain upper bound.

3.

Different from the ETC methods in [31,32,33], to improve the utilization of communication resources of the equivalent SMD, a decentralized dynamic ETC approach combined with the ADP method is designed to optimize the control performance of NLS systems.

The subsequent sections of this article is arranged as follows. Section 2 presents the issue description. Section 3 develops an FTC approach utilizing ISMC methodology. Section 4 develops a dynamic ETC scheme based on GCC via the ADP method. Section 5 proposes a simulation example for the corresponding subsystem to verify the strategy’s performance. Section 6 presents a conclusion of the present study.

2. Problem Statement

The uncertain NLS systems are as follows:

$$\begin{array}{c}\hfill {\dot{\xi }}_i=g_i\left({\xi }_i\right)+{\omega }_i\left({\xi }_i\right)\left[{\sigma }_i\left(t\right)+{\beta }_i(t-t_T)f_{s_i}\left(t\right)\right]+{\epsilon }_i\left({\xi }_i\right){\varrho }_i\left(\xi \right),\end{array}$$

(1)

where the control input is denoted as ${\sigma }_i\left(t\right)\in {\mathbb{R}}^{m_i}$ for the ith subsystem, ${\xi }_i\in {\mathbb{R}}^{n_i}$ represents the system state vector, the actuator abrupt fault occurring at time $t_T$ is represented by ${\beta }_i(t-t_T)f_{s_i}\left(t\right)$. Here, ${\beta }_i(t-t_T)=1$ for $t\ge t_T$ and ${\beta }_i(t-t_T)=0$ for $t<t_T$. Assume that $f_{s_i}\left(t\right)$ is continuous with ${\dot{f}}_{s_i}\left(t\right)$ being bounded by $∥{\dot{f}}_{s_i}\left(t\right)∥\le b_F$, $g_i\left({\xi }_i\right)\in {\mathbb{R}}^{n_i}$ and ${\omega }_i\left({\xi }_i\right)\in {\mathbb{R}}^{n_i\times m_i}$ denote system functions that satisfy local Lipschitz continuity on ${\Omega }_i\in {\mathbb{R}}^{n_i}$, ${\omega }_i\left({\xi }_i\right)$ is a smooth known function, which is different from $g_i\left({\xi }_i\right)$. Moreover, ${\varrho }_i\left(\xi \right)\in {\mathbb{R}}^{r_i}$ is the uncertain interconnection and ${\epsilon }_i\left({\xi }_i\right)\in {\mathbb{R}}^{n_i\times r_i}$ is a disturbance function that shows the architecture of the uncertain term, where $\xi ={[{\xi }_1^T,{\xi }_2^T,\dots ,{\xi }_N^T]}^T\in {\mathbb{R}}^n$ denotes the state for NLS systems (1), with $n={\sum }_{i=1}^N{n}_i$.

Further, the nominal version of system (1) is

$$\begin{array}{c}\hfill {\dot{\xi }}_i\left(t\right)={\omega }_i\left({\xi }_i\left(t\right)\right){\sigma }_i\left(t\right)+g_i\left({\xi }_i\left(t\right)\right).\end{array}$$

(2)

Assumption 1.

Assume that $g_i+{\omega }_i[{\sigma }_i+{\beta }_i(t-t_T)f_{s_i}]$ satisfies the Lipschitz continuity condition within a domain $\Omega \in {\mathbb{R}}^{n_i}$ and suppose that system (2) is controllable.

Here, the matched uncertain term ${\epsilon }_i\left({\xi }_i\right){\varrho }_i\left(\xi \right)$ satisfies

$$\begin{array}{c}\hfill {\varrho }_i^T\left(\xi \right){\varrho }_i\left(\xi \right)\le {\varrho }_{iM}^T\left(\xi \right){\varrho }_{iM}\left(\xi \right).\end{array}$$

(3)

Here, ${\varrho }_i(·)\in {\mathbb{R}}^{r_i}$, $i=1,2,\dots ,N$ is an uncertain function with ${\varrho }_i\left(0\right)=0$, and ${\varrho }_{iM}(·)\in {\mathbb{R}}^{r_i}$ represents a known constrained function where ${\varrho }_{iM}\left(0\right)=0$.

This research aims to construct an adaptive control strategy that enables the NLS systems to remain stable when actuator faults occur, and there exists an upper bound of the performance index for the system dynamics on the SMS. Additionally, a dynamic ETC mechanism is developed to enhance communication resource utilization efficiency.

3. Design of FTC Strategy Approach Based on ISMC Technique

To eliminate the influence of time-varying faults in NLS systems (1), we develop a SMC approach as follows:

$$\begin{array}{c}\hfill {\sigma }_i={\sigma }_{0i}+{\sigma }_{1i}\end{array}$$

(4)

with ${\sigma }_{0i}$ being the nominal control for guaranteed dynamic ETC performance, and ${\sigma }_{1i}$ being the control law for fault accommodation, which is utilized to eliminate the influence of actuator failures.

Assumption 2.

The system functions $\omega \left(\xi \right)$ and ${\epsilon }_i\left({\xi }_i\right)$ are bounded by $\left|\right|\omega \left(\xi \right)\left|\right|\le {\omega }_{max}$ and $\parallel {\epsilon }_i\left({\xi }_i\right)\parallel \le {\epsilon }_{max}$, where ${\epsilon }_{max}$ and ${\omega }_{max}$ are positive constants. Additionally, ${\omega }_i\left({\xi }_i\right)$ represents a full column rank matrix.

Remark 1.

The guaranteed cost controller the under dynamic ETC method takes the form ${\sigma }_i^{*}={\sigma }_{0i}^{*}+{\sigma }_{1i}$, ensuring that nonlinear system (1) achieves stability while simultaneously optimizing the adjusted cost functional during sliding mode operation.

The ISMC function is formulated as

$$\begin{array}{cc}\hfill S_i\left({\xi }_i\right)=& S_{0i}\left({\xi }_i\right)-S_{0i}\left({\xi }_{0i}\right)\hfill \\ \hfill & -{\int }_0^t{T}_i\left({\xi }_i\right)(g_i\left({\xi }_i\right)+{\omega }_i\left({\xi }_i\right){\sigma }_{0i}+{\epsilon }_i\left({\xi }_i\right){\varrho }_i\left(\xi \right)d\tau .\hfill \end{array}$$

(5)

where $S_{0i}\left({\xi }_i\right)\in {\mathbb{R}}^{m\times 1}$ and $T_i\left({\xi }_i\right)=\left(\partial S_{0i}\left({\xi }_i\right)/\partial {\xi }_i\right)$.

In light of (5), it has

$$\begin{array}{c}\hfill {\dot{S}}_i\left({\xi }_i\right)=T_i\left({\xi }_i\right){\omega }_i\left({\xi }_i\right)({\sigma }_{1i}+{\beta }_i(t-t_T)f_{si}\left(t\right)).\end{array}$$

(6)

To ensure the system states remain on the SMS $S_i({\xi }_i,t)=0$, ${\sigma }_{1i}$ is designed as

$$\begin{array}{c}\hfill {\sigma }_{1i}=-\alpha \mathrm{sgn}\left({\omega }_i^T\left({\xi }_i\right)T_i^T\left({\xi }_i\right)S_i\left({\xi }_i\right)\right)\end{array}$$

(7)

where $\alpha$ and $sgn(·)$ represent a gain and a symbolic function, respectively.

$$\begin{array}{c}\hfill \mathrm{sgn}\left({\mho }_i\right)=\left\{\begin{array}{cc}1\hfill & {\mho }_i>0\hfill \\ 0\hfill & {\mho }_i=0\hfill \\ -1\hfill & {\mho }_i<0.\hfill \end{array}\right.\end{array}$$

(8)

where $\mathrm{sgn}\left({\mho }_i\right)={\left[\mathrm{sgn}\left({\mho }_{i1}\right),\dots ,\mathrm{sgn}\left({\mho }_{i{m}_i}\right)\right]}^{\top }\in {\mathbb{R}}^{m_i}$, and ${\mho }_i={\omega }_i^T\left({\xi }_i\right)T_i^T\left({\xi }_i\right)S_i\left({\xi }_i\right)$.

Theorem 1.

With regard to system (1), when the SMC law is designed based on (6) and $\alpha >{\overline{\beta }}_i\left|\right|f_{si}\left(t\right)\left|\right|$, $S_i\left({\xi }_i\right)=0$ is achievable from the beginning, where ${\overline{\beta }}_i$ denotes the upper bound of ${\beta }_i(t-t_T)$.

Proof. 

Define the Lyapunov candidate:

$$\begin{array}{c}\hfill L_{s_i}={\displaystyle \frac{1}{2}}{S}_i{\left({\xi }_i\right)}^T\left({\xi }_i\right)S_i\left({\xi }_i\right).\end{array}$$

(9)

According to (6), we have

$$\begin{array}{c}\hfill {\dot{L}}_{si}=S_i{\left({\xi }_i\right)}^T{T}_i\left({\xi }_i\right){\omega }_i\left({\xi }_i\right)[{\sigma }_{1i}+{\beta }_i(t-t_T)f_{si}\left(t\right)].\end{array}$$

(10)

According to the control rule (7) and (8), we have

$$\begin{array}{cc}\hfill {\dot{L}}_{si}=& S_i{\left({\xi }_i\right)}^T{T}_i\left({\xi }_i\right){\omega }_i\left({\xi }_i\right)[-\alpha \mathrm{sgn}\left({\omega }_i^T\left({\xi }_i\right)T_i^T\left({\xi }_i\right)S_i\left({\xi }_i\right)\right)+{\beta }_i(t-t_T)f_{si}\left(t\right)]\hfill \\ \hfill =& -\alpha {∥S_i^T\left(\xi \right)T_i\left({\xi }_i\right){\omega }_i\left({\xi }_i\right)∥}_1+S_i^T\left({\xi }_i\right)T_i\left({\xi }_i\right){\omega }_i\left({\xi }_i\right){\beta }_i(t-t_T)f_{si}\left(t\right)\hfill \\ \hfill \le & -\alpha {∥S_i^T\left({\xi }_i\right)T_i\left({\xi }_i\right){\omega }_i\left({\xi }_i\right)∥}_1+{\overline{\beta }}_i\left|\right|f_{si}\left(t\right)\left|\right|{∥S_i^T\left({\xi }_i\right)T_i\left({\xi }_i\right){\omega }_i\left({\xi }_i\right)∥}_1\hfill \\ \hfill =& -(\alpha -{\overline{\beta }}_i\left|\right|f_{si}\left(t\right)\left|\right|){∥S_i^T\left({\xi }_i\right)T_i\left({\xi }_i\right){\omega }_i\left({\xi }_i\right)∥}_1\hfill \end{array}$$

(11)

where ${\beta }_i(t-t_T)f_{si}\left(t\right)\le {\overline{\beta }}_i\left|\right|f_{si}\left(t\right)\left|\right|$, and if the condition $\alpha >{\overline{\beta }}_i\left|\right|f_{si}\left(t\right)\left|\right|$ is satisfied, and ${\dot{L}}_{si}\left(t\right)\le 0$ for any $S_i\left({\xi }_i\right)\ne 0$. Hence, the SMS $S_i\left({\xi }_i\right)=0$ achieves asymptotic stability.

The proof is completed. □

The objective of employing ISMC methodology is to ensure that ${\dot{S}}_i\left({\xi }_i\right)=0$, hence the equivalent control input takes the form ${\sigma }_{1eqi}=-{\beta }_i(t-t_T)f_{si}\left(t\right)$. Substituting ${\sigma }_{1eqi}=-{\beta }_i(t-t_T)f_{si}\left(t\right)$ to (1), the SMD is

$$\begin{array}{c}\hfill {\dot{\xi }}_i\left(t\right)=g_i\left({\xi }_i\left(t\right)\right)+{\omega }_i\left({\xi }_i\left(t\right)\right){\sigma }_{0i}\left(t\right)+{\epsilon }_i\left({\xi }_i\right){\varrho }_i\left(\xi \right).\end{array}$$

(12)

The nominal form of uncertain SMD (12) is

$$\begin{array}{c}\hfill {\dot{\xi }}_i\left(t\right)={\omega }_i\left({\xi }_i\left(t\right)\right){\sigma }_{0i}\left(t\right)+g_i\left({\xi }_i\left(t\right)\right).\end{array}$$

(13)

Denote ${\xi }_i\left(0\right)={\xi }_{i0}$. The control input is $\sigma ={[{\sigma }_1^{\top },{\sigma }_2^{\top },\dots ,{\sigma }_N^{\top }]}^{\top }$. Define the cost function as

$$\begin{array}{c}\hfill \overline{\mathrm{\Gamma }}({\xi }_0,{\sigma }_{0i})=\sum _{i=1}^N{\int }_t^{\infty }{Z}_i({\xi }_i\left(\tau \right),{\sigma }_{0i}\left(\tau \right))\mathrm{d}\tau \end{array}$$

(14)

with ${\xi }_0={[{\xi }_{10}^{\top },{\xi }_{20}^{\top },\dots ,{\xi }_{N0}^{\top }]}^{\top }$, $Z_i({\xi }_i,{\sigma }_{0i})={\xi }_i^{\top }{Q}_i{\xi }_i+{\sigma }_{0i}^{\top }{R}_i{\sigma }_{0i}$, $R_i^{\top }=R_i>0$ and $Q_i^{\top }=Q_i>0$ being constant matrices.

To address the decentralized cost-constrained control issue, a feedback control law is denoted by ${\sigma }_0\left(\xi \right)={[{\sigma }_{01}^{\top }\left({\xi }_1\right),{\sigma }_{02}^{\top }\left({\xi }_2\right),\dots ,{\sigma }_{0N}^{\top }\left({\xi }_N\right)]}^{\top }$ and obtained a bounded cost functional $\mathcal{J}\left(\sigma \right)$, i.e., satisfying $\mathcal{J}\left(\sigma \right)\le {\mathcal{J}}_M<+\infty$, where ${\mathcal{J}}_M$ represents a positive number that guarantees the stability of the system, and the cost function (14) satisfies the constraint $\overline{\mathrm{\Gamma }}\le \mathcal{J}$.

It should be noted that the control system allows for a more concise representation. To offer a clearer illustration for the system, we have listed the following formula

$$\begin{array}{cc}\hfill g\left(\xi \right)& ={[g_1^{\top }\left({\xi }_1\right),g_2^{\top }\left({\xi }_2\right),\dots ,g_N^{\top }\left({\xi }_N\right)]}^{\top },\hfill \\ \hfill \omega \left(\xi \right)& =\mathrm{diag}\{{\omega }_1\left({\xi }_1\right),{\omega }_2\left({\xi }_2\right),\dots ,{\omega }_N\left({\xi }_N\right)\},\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill \varrho \left(\xi \right)& ={\left[{\varrho }_1^T\left(\xi \right),{\varrho }_2^T\left(\xi \right),\dots ,{\varrho }_N^T\left(\xi \right))\right]}^{\top },\hfill \\ \hfill \epsilon \left(\xi \right)& =\mathrm{diag}\{{\epsilon }_1\left({\xi }_1\right),{\epsilon }_2\left({\xi }_2\right),\dots ,{\epsilon }_N\left({\xi }_n\right)\},\hfill \\ \hfill {\varrho }_M\left(\xi \right)& ={\left[{\varrho }_{1M}^T\left(\xi \right),{\varrho }_{2M}^T\left(\xi \right),\dots ,{\varrho }_{NM}^T\left(\xi \right))\right]}^{\top }.\hfill \end{array}$$

Thus, the nonlinear system (12) becomes

$$\begin{array}{c}\hfill \dot{\xi }\left(t\right)=\omega \left(\xi \right){\sigma }_0+\epsilon \left(\xi \right)\varrho \left(\xi \right)+g\left(\xi \right)\end{array}$$

(15)

where ${\sigma }_0$ is the control for guaranteed dynamic ETC performance.

The nominal version of system (15) is

$$\begin{array}{c}\hfill \dot{\xi }=\omega \left(\xi \right){\sigma }_0+g\left(\xi \right)\end{array}$$

(16)

The cost function (14) becomes

$$\begin{array}{c}\hfill \overline{\mathrm{\Gamma }}({\xi }_0,{\sigma }_0)={\int }_0^{\infty }Z(\xi \left(\tau \right),{\sigma }_0\left(\tau \right))\mathrm{d}\tau \end{array}$$

(17)

where $Z(\xi ,{\sigma }_0)={\xi }^{\top }Q\xi +{\sigma }_0^{\top }R{\sigma }_0$, with the diagonal matrix $R=\mathrm{diag}\{R_1,R_2,\dots ,R_N\}$ and $Q=\mathrm{diag}\{Q_1,Q_2,\dots ,Q_N\}$ being constant matrices.

4. Dynamic Event-Triggered Guaranteed Cost Control Using ADP

Here, we present the innovation of a control law ${\sigma }_0$, which is designed by using the ADP algorithm under the dynamic ETC approach to achieve near-optimal control strategies.

Lemma 1 is introduced to demonstrate that the cost function for the NLS system (15) can be well-defined, with its proof provided in [36].

Lemma 1.

Suppose there exist a bounded positive function $J\left(\xi \right)$, a cost function $\mathcal{V}\left(\xi \right)$ with $\mathcal{V}\left(\xi \right)>0$, and a control input ${\sigma }_0\left(\xi \right)$, so that

$$\begin{array}{cc}\hfill & {(\nabla \mathcal{V}\left(\xi \right))}^T\epsilon \left(\xi \right)\varrho \left(\xi \right)\le J\left(\xi \right);\hfill \\ \hfill & Z(\xi ,{\sigma }_0)+{(\nabla \mathcal{V}\left(\xi \right))}^T(\omega \left(\xi \right){\sigma }_0+g\left(\xi \right))+J\left(\xi \right)=0,\hfill \end{array}$$

(18)

with $\nabla \mathcal{V}\triangleq \partial \mathcal{V}/\partial \xi$. Therefore, the local asymptotic stability of system (16) can be verified within a specific domain around the origin. Furthermore, it follows that $\overline{\mathrm{\Gamma }}({\xi }_0,{\sigma }_0)\le \mathcal{V}({\xi }_0,{\sigma }_0)=\mathrm{\Gamma }({\xi }_0,{\sigma }_0)$, with $\mathrm{\Gamma }({\xi }_0,{\sigma }_0)$ representing the adjusted cost function for system (16), is given by

$$\begin{array}{c}\hfill \mathrm{\Gamma }({\xi }_0,{\sigma }_0)={\int }_0^{\infty }\{Z(\xi ,{\sigma }_0\left(\xi \right))+J\left(\xi \right)\}d\tau .\end{array}$$

(19)

Remark 2.

Referring to [37,38,39], the bounded function $J\left(\xi \right)$ is

$$\begin{array}{c}\hfill J\left(\xi \right)={\displaystyle \frac{1}{4}}{(\nabla \mathcal{V}\left(\xi \right))}^T\epsilon \left(\xi \right){\epsilon }^T\left(\xi \right)\nabla \mathcal{V}\left(\xi \right)+{\varrho }_M^T\left(\xi \right){\varrho }_M\left(\xi \right),\end{array}$$

(20)

where $J\left(\xi \right)$ is designed to handle the coupling and uncertain terms of the system.

Considering system (16), the adjusted cost function is defined as

$$\begin{array}{c}\hfill \mathcal{V}\left({\xi }_0\right)={\int }_0^{\infty }\{Z(\xi ,{\sigma }_0)+J\left(\xi \right)\}d\tau .\end{array}$$

(21)

Based on (21) for system (16), the Hamiltonian function is

$$\begin{array}{c}\hfill H(\xi ,{\sigma }_0,\nabla \mathcal{V}\left(\xi \right))=Z(\xi ,{\sigma }_0)+{(\nabla \mathcal{V}\left(\xi \right))}^T(\omega \left(\xi \right){\sigma }_0+g\left(\xi \right))+J\left(\xi \right).\end{array}$$

(22)

Moreover, the optimal guaranteed cost for the NLS system (16) is ${\mathrm{\Gamma }}^{*}\left({\xi }_0\right)={min}_{{\sigma }_0\in \mathcal{A}(\Omega )}$ $\mathrm{\Gamma }({\xi }_0,{\sigma }_0)$, where $\mathrm{\Gamma }({\xi }_0,{\sigma }_0)$ is provided in (19) and $\mathcal{A}(\Omega )$ represents the admissible control set. In the OC design, ${\mathrm{\Gamma }}^{*}\left(\xi \right)$ satisfies the HJB equation

$$\begin{array}{c}\hfill 0=\underset{d_0\in \mathcal{A}(\Omega )}{min}H(\xi ,{\sigma }_0,\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right)).\end{array}$$

(23)

According to the equilibrium conditions, the OC policy is derived as

$$\begin{array}{c}\hfill {\sigma }_0^{*}\left(\xi \right)=-{\displaystyle \frac{1}{2}}{R}^{-1}{\omega }^T\left(\xi \right)\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right).\end{array}$$

(24)

The modified HJB equation is formulated as

$$\begin{array}{cc}\hfill 0=& Z(\xi ,{\sigma }_0^{*})+{(\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right))}^T(\omega \left(\xi \right){\sigma }_0^{*}+g\left(\xi \right))+{\varrho }_M^T\left(\xi \right){\varrho }_M\left(\xi \right)\hfill \\ \hfill & +{\displaystyle \frac{1}{4}}{(\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right))}^T\epsilon \left(\xi \right){\epsilon }^T\left(\xi \right)\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right),{\mathrm{\Gamma }}^{*}\left(0\right)=0.\hfill \end{array}$$

(25)

According to (24) and (25), we have

$$\begin{array}{cc}\hfill 0=& -{\xi }^{T}Q\xi +{\displaystyle \frac{1}{4}}{\left(\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right)\right)}^T\omega \left(\xi \right)R^{-1}{\omega }^T\left(\xi \right)\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right)-{\left(\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right)\right)}^{T}g\left(\xi \right)\hfill \\ \hfill & -{\varrho }_M^T\left(\xi \right){\varrho }_M\left(\xi \right)-{\displaystyle \frac{1}{4}}{\left(\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right)\right)}^T\epsilon \left(\xi \right){\epsilon }^T\left(\xi \right)\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right).\hfill \end{array}$$

(26)

Consider the NLS system (15) with the modified index (17), and assume that the solution to the HJB equation (25) exists and is continuous. Denote this solution as ${\mathrm{\Gamma }}^{*}\left(\xi \right)$. Therefore, the optimal guaranteed cost is determined when ${\sigma }_0={\sigma }_0^{*}$, i.e., $J\left({\sigma }_0^{*}\right)={\mathrm{\Gamma }}^{*}\left({\xi }_0\right)$. Consequently, it follows that $J^{*}={min}_{{\sigma }_0}J\left({\sigma }_0\right)={\mathrm{\Gamma }}^{*}\left({\xi }_0\right)$ and ${\overline{{\sigma }_0}}^{*}=arg{min}_{{\sigma }_0}J\left({\sigma }_0\right)={\sigma }_0^{*}$. Therefore, the optimal GCC of the original NLS system (15) can be transformed into solving an OC issue for the nominal system.

4.1. Dynamic ETC-Based ADP Method Design

Initially, establish a strictly monotonically increasing sequence ${\left\{t_j\right\}}_{j=0}^{\infty }$ where $j\in \mathbb{N}$ and $t_0=0$, comprising the activation times $t_j$. For any $t\in [t_j,t_{j+1})$, denote the system state as ${\overline{\xi }}_j=\xi \left(t_j\right)$.

The triggering error is given by

$$\begin{array}{c}\hfill e_j\left(t\right)={\overline{\xi }}_j-\xi \left(t\right).\end{array}$$

(27)

The corresponding control is described by

$$\begin{array}{c}\hfill {\sigma }_0\left(t\right)={\sigma }_0\left({\overline{\xi }}_j\right).\end{array}$$

According to (27), the dynamic ETC strategy is expressed as

$$\begin{array}{c}\hfill {\sigma }_0\left({\overline{\xi }}_j\right)={\sigma }_0(e_j\left(t\right)+\xi \left(t\right)).\end{array}$$

(28)

Based on (24), the optimal dynamic ETC strategy is obtained as

$$\begin{array}{c}\hfill {\sigma }_0^{*}\left({\overline{\xi }}_j\right)=-{\displaystyle \frac{1}{2}}{R}^{-1}{\omega }^T\left({\overline{\xi }}_j\right)\nabla {\mathrm{\Gamma }}^{*}\left({\overline{\xi }}_j\right),\forall t\in [t_j,t_{j+1})\end{array}$$

(29)

where $\nabla {\mathrm{\Gamma }}^{*}\left({\overline{\xi }}_j\right)={\left.{\displaystyle \frac{\partial {\mathrm{\Gamma }}^{*}\left(\xi \right)}{\partial \xi }}\right|}_{\xi ={\overline{\xi }}_j}$.

Subsequently, the HJB equation (25) can be rewritten as

$$\begin{array}{cc}\hfill H(\xi ,{\sigma }_0^{*}\left({\overline{\xi }}_j\right),\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right))=& {\xi }^{T}Q\xi +{\displaystyle \frac{1}{4}}{(\nabla {\mathrm{\Gamma }}^{*}\left({\overline{\xi }}_j\right))}^T\omega \left({\overline{\xi }}_j\right)R^{-1}{\omega }^T\left({\overline{\xi }}_j\right)\nabla {\mathrm{\Gamma }}^{*}\left({\overline{\xi }}_j\right)\hfill \\ \hfill & +\nabla {\mathrm{\Gamma }}^{*}{\left(\xi \right))}^{T}g\left(\xi \right)-{\displaystyle \frac{1}{2}}{(\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right))}^T\omega \left(\xi \right)R^{-1}{\omega }^T\left({\overline{\xi }}_j\right)\nabla {\mathrm{\Gamma }}^{*}\left({\overline{\xi }}_j\right)\hfill \\ \hfill & +{\varrho }_M^T\left(\xi \right){\varrho }_M\left(\xi \right)+{\displaystyle \frac{1}{4}}{(\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right))}^T\epsilon \left(\xi \right){\epsilon }^T\left(\xi \right)\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right).\hfill \end{array}$$

(30)

Assumption 3.

Suppose that the Lipschitz condition holds for ${\sigma }_0^{*}\left(\xi \right)$ such that $\rho \parallel e_j\left(t\right)\parallel \ge \parallel {\sigma }_0\left(\xi \left(t\right)\right)-{\sigma }_0\left({\overline{\xi }}_j\right)\parallel$, where ρ represents a positive constant.

Assumption 4.

The cost function ${\mathrm{\Gamma }}^{*}\left(\xi \right)$ is bounded by ${\mathrm{\Gamma }}_M$ in the compact set $\mathrm{\Xi }\subset \mathbb{R}$. Moreover, $\parallel \nabla {\mathrm{\Gamma }}^{*}\left(\xi \right)\parallel \le {\mathrm{\Gamma }}_{CM}$ holds with ${\mathrm{\Gamma }}_{CM}$ as a positive constant.

Theorem 2.

Considering the NLS system (15) and (16), if Assumptions 3 and 4 hold and the solution of the HJB equation (23) exists, the dynamic ETC near-OC signal is designed as (29) when the triggering condition is presented as

$$\begin{array}{c}\hfill \parallel e_j{\parallel }^2\le {\displaystyle \frac{{\beta }_1{\breve{\sigma }}_1-{\eta }^2{\lambda }_{min}\left(Q\right){∥\xi ∥}^2}{\mathfrak{r}{\rho }^2}}\triangleq e_T,\end{array}$$

(31)

where $0<\eta <1$, ${\beta }_1>0$, $\mathfrak{r}$ denotes the largest singular value for matrix R and $e_T$ is the triggering threshold. The dynamics of internal signal ${\breve{\sigma }}_1$ are denoted as

$$\begin{array}{c}\hfill {\dot{\breve{\sigma }}}_1=-{\beta }_1{\breve{\sigma }}_1+{\lambda }_{min}\left(Q\right){∥\xi ∥}^2\end{array}$$

(32)

Proof. 

For system (15), the optimal cost function ${\mathrm{\Gamma }}^{*}\left(\xi \left(t\right)\right)$ is positive definite, while ${\sigma }_0^{*}\left({\overline{\xi }}_j\right)$ denotes the dynamic ETC strategy. According to (15), selecting $V\left(t\right)=V_1+V_2={\mathrm{\Gamma }}^{*}\left(\xi \left(t\right)\right)+{\breve{\sigma }}_j$ as the Lyapunov function, it obtains

$$\begin{array}{cc}\hfill \dot{V}\left(\xi \left(t\right)\right)=& {\dot{\breve{\sigma }}}_1+{(\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right))}^T\left(\omega \left(\xi \right){\sigma }_0^{*}({\overline{\xi }}_j+g\left(\xi \right))\right)+\epsilon \left(\xi \right)\varrho \left(\xi \right).\hfill \end{array}$$

(33)

According to (25), it follows that

$$\begin{array}{cc}\hfill {\left(\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right)\right)}^{T}g\left(\xi \right)=& -{\left({\sigma }_0^{*}\right)}^{T}R{\sigma }_0^{*}-{\xi }^{T}Q\xi +{\displaystyle \frac{1}{2}}{\left(\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right)\right)}^T\omega \left(\xi \right)R^{-1}{\omega }^T\left(\xi \right)\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right)\hfill \\ \hfill & -{\varrho }_M^T\left(\xi \right){\varrho }_M\left(\xi \right)-{\displaystyle \frac{1}{4}}{\left(\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right)\right)}^T\epsilon \left(\xi \right){\epsilon }^T\left(\xi \right)\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right).\hfill \end{array}$$

(34)

Bringing (34) into (33), it yields

$$\begin{array}{cc}\hfill \dot{V}\left(\xi \left(t\right)\right)=& -{\xi }^{T}Q\xi -{\left({\sigma }_0^{*}\left(\xi \right)\right)}^{T}R{\sigma }_0^{*}\left(\xi \right)+{\displaystyle \frac{1}{2}}{(\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right))}^T\omega \left(\xi \right)R^{-1}{\omega }^T\left(\xi \right)\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right)\hfill \\ \hfill & -{\varrho }_M^T\left(\xi \right){\varrho }_M\left(\xi \right)-{\displaystyle \frac{1}{4}}{(\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right))}^T\epsilon \left(\xi \right){\epsilon }^T\left(\xi \right)\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right)+{\dot{\breve{\sigma }}}_1\hfill \\ \hfill & +{(\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right))}^T\omega \left(\xi \right){\sigma }_0^{*}\left({\overline{\xi }}_j\right)+{(\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right))}^T\epsilon \left(\xi \right)\varrho \left(\xi \right).\hfill \end{array}$$

(35)

Using Yang’s inequality, it has

$${(\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right))}^T\epsilon \left(\xi \right)\varrho \left(\xi \right)\le {\displaystyle \frac{1}{4}}{(\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right))}^T\epsilon \left(\xi \right){\epsilon }^T\left(\xi \right)\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right)+{\varrho }^T\left(\xi \right)\varrho \left(\xi \right).$$

(36)

Since ${\varrho }^T\left(\xi \right)\varrho \left(\xi \right)\le {\varrho }_M^T\left(\xi \right){\varrho }_M\left(\xi \right)$ and (24), we have

$$\begin{array}{cc}\hfill \dot{V}\left(\xi \left(t\right)\right)\le & -{\xi }^{T}Q\xi +{\displaystyle \frac{1}{4}}{(\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right))}^T\omega \left(\xi \right)R^{-1}{\omega }^T\left(\xi \right)\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right)\hfill \\ \hfill & +{(\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right))}^T\omega \left(\xi \right){\sigma }_0^{*}\left({\overline{\xi }}_j\right)+{\dot{\breve{\sigma }}}_1\hfill \\ \hfill \le & -{\eta }^2{\lambda }_{min}{\left(Q\right)\parallel \xi \parallel }^2-(1-{\eta }^2){\lambda }_{min}\left(Q\right){\parallel \xi \parallel }^2+{\dot{\breve{\sigma }}}_1\hfill \\ \hfill & +{\displaystyle \frac{1}{4}}{(\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right))}^T\omega \left(\xi \right)R^{-1}{\omega }^T\left(\xi \right)\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right)\hfill \\ \hfill & +{(\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right))}^T\omega \left(\xi \right){\sigma }_0^{*}\left({\overline{\xi }}_j\right).\hfill \end{array}$$

(37)

Based on (37), it has

$$\begin{array}{cc}\hfill \dot{V}\left(\xi \left(t\right)\right)\le & -{\eta }^2{\lambda }_{min}{\left(Q\right)\parallel \xi \parallel }^2-(1-{\eta }^2){\lambda }_{min}\left(Q\right){\parallel \xi \parallel }^2+{\dot{\breve{\sigma }}}_1\hfill \\ \hfill & +{\displaystyle \frac{1}{4}}{(\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right))}^T\omega \left(\xi \right)R^{-1}{\omega }^T\left(\xi \right)\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right)\hfill \\ \hfill & -{\displaystyle \frac{1}{2}}{(\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right))}^T\omega \left(\xi \right)R^{-1}{\omega }^T\left({\overline{\xi }}_j\right)\nabla {\mathrm{\Gamma }}^{*}\left({\overline{\xi }}_j\right)\hfill \\ \hfill & +{\displaystyle \frac{1}{4}}{(\nabla {\mathrm{\Gamma }}^{*}\left({\overline{\xi }}_j\right))}^T\omega \left({\overline{\xi }}_j\right)R^{-1}{\omega }^T\left({\overline{\xi }}_j\right)\nabla {\mathrm{\Gamma }}^{*}\left({\overline{\xi }}_j\right)\hfill \\ \hfill & -{\displaystyle \frac{1}{4}}{(\nabla {\mathrm{\Gamma }}^{*}\left({\overline{\xi }}_j\right))}^T\omega \left({\overline{\xi }}_j\right)R^{-1}{\omega }^T\left({\overline{\xi }}_j\right)\nabla {\mathrm{\Gamma }}^{*}\left({\overline{\xi }}_j\right).\hfill \end{array}$$

(38)

Using (24), (29), and (38), we have

$$\begin{array}{cc}\hfill \dot{V}\left(\xi \right(t\left)\right)\le & -{\eta }^2{\lambda }_{min}{\left(Q\right)\parallel \xi \parallel }^2-(1-{\eta }^2){\lambda }_{min}\left(Q\right){\parallel \xi \parallel }^2+{\dot{\breve{\sigma }}}_1\hfill \\ \hfill & +{({\sigma }_0^{*}\left(\xi \right)-{\sigma }_0^{*}\left({\overline{\xi }}_j\right))}^{T}R({\sigma }_0^{*}\left(\xi \right)-{\sigma }_0^{*}\left({\overline{\xi }}_j\right)).\hfill \end{array}$$

(39)

Based on Assumption 3 and Equation (39), it has

$$\begin{array}{c}\hfill {({\sigma }_0^{*}\left(\xi \right)-{\sigma }_0^{*}\left({\overline{\xi }}_j\right))}^{T}R({\sigma }_0^{*}\left(\xi \right)-{\sigma }_0^{*}\left({\overline{\xi }}_j\right))\le \mathfrak{r}{\rho }^2{\parallel e_j\parallel }^2\end{array}$$

(40)

where $\mathfrak{r}$ denotes the largest singular value for matrix R.

Bringing (40) into (39), it yields

$$\begin{array}{cc}\hfill \dot{V}\left(\xi \left(t\right)\right)\le & -{\eta }^2{\lambda }_{min}{\left(Q\right)\parallel \xi \parallel }^2-(1-{\eta }^2){\lambda }_{min}\left(Q\right){\parallel \xi \parallel }^2+{\dot{\breve{\sigma }}}_1\hfill \\ \hfill & +\mathfrak{r}{\rho }^2{\parallel e_j\parallel }^2.\hfill \end{array}$$

(41)

It is clear that the constraint (31) holds, and it follows that $\dot{V}\left(\xi \left(t\right)\right)\le -{\eta }^2{\lambda }_{min}\left(Q\right){\parallel \xi \parallel }^2<0$ where $\xi \ne 0$.

The proof is finished. □

Theorem 3.

Considering (15) with the cost function (17), assume that a continuously differentiable solution ${\mathrm{\Gamma }}^{*}\left(\xi \right)$ of HJB equation (23) exists. Then, the OC inputted under the dynamic ETC strategy is developed as (24), and the near-optimal guaranteed cost function (17) satisfies

$$\begin{array}{cc}\hfill \overline{\mathrm{\Gamma }}(\xi \left(0\right),{\sigma }_0^{*}\left({\overline{\xi }}_j\right))\le & {\mathrm{\Gamma }}^{*}\left(\xi \left(0\right)\right)\hfill \\ \hfill & +{\int }_0^{\infty }{\left({\sigma }_0^{*}\left({\overline{\xi }}_j\right)-{\sigma }_0^{*}\left(\xi \right)\right)}^{T}R\left({\sigma }_0^{*}\left({\overline{\xi }}_j\right)-{\sigma }_0^{*}\left(\xi \right)\right)d\tau .\hfill \end{array}$$

(42)

Additionally, set ${\sigma }_0^{*}\left(\xi \right)={\sigma }_0^{*}\left({\overline{\xi }}_j\right)$, and one gets

$$\begin{array}{cc}\hfill \overline{\mathrm{\Gamma }}(\xi \left(0\right),{\sigma }_0^{*}\left({\overline{\xi }}_j\right))\le & {\mathrm{\Gamma }}^{*}\left(\xi \left(0\right)\right).\hfill \end{array}$$

(43)

Proof. 

By applying a control input ${\sigma }_0\left(\xi \right)$, it follows that

$$\begin{array}{c}\hfill \overline{\mathrm{\Gamma }}(\xi \left(0\right),{\sigma }_0)={\int }_0^{\infty }\left\{{\xi }^{T}Q\xi +{\sigma }_0^{T}R{\sigma }_0+{\dot{\mathrm{\Gamma }}}^{*}\left(\xi \right)\right\}d\tau +{\mathrm{\Gamma }}^{*}\left(\xi \left(0\right)\right).\end{array}$$

(44)

Based on (15) and (34), we have

$$\begin{array}{cc}\hfill Z(\xi ,{\sigma }_0)+{\dot{\mathrm{\Gamma }}}^{*}\left(\xi \right)=& {\sigma }_0^{T}R{\sigma }_0-{\left({\sigma }_0^{*}\right)}^{T}R{\sigma }_0^{*}-{\displaystyle \frac{1}{4}}{\left(\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right)\right)}^T\epsilon \left(\xi \right){\epsilon }^T\left(\xi \right)\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right)\hfill \\ \hfill & -{\varrho }_M^T\left(\xi \right){\varrho }_M\left(\xi \right)+{\left(\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right)\right)}^T\omega \left(\xi \right)({\sigma }_0-{\sigma }_0^{*})\hfill \\ \hfill & +{\left(\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right)\right)}^T\epsilon \left(\xi \right)\varrho \left(\xi \right)\hfill \end{array}$$

(45)

Due to (36), it obtains

$$\begin{array}{cc}\hfill Z(\xi \left(0\right),{\sigma }_0)+{\dot{\mathrm{\Gamma }}}^{*}\left(\xi \right)\le & {\sigma }_0^{T}R{\sigma }_0-{\left({\sigma }_0^{*}\right)}^{T}R{\sigma }_0^{*}\hfill \\ \hfill & +{\left(\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right)\right)}^T\omega \left(\xi \right)({\sigma }_0-{\sigma }_0^{*}).\hfill \end{array}$$

(46)

According to (24), it has

$$\begin{array}{c}\hfill {\sigma }_0^{T}R{\sigma }_0-{\left({\sigma }_0^{*}\right)}^{T}R{\sigma }_0^{*}={({\sigma }_0-{\sigma }_0^{*})}^{T}R({\sigma }_0-{\sigma }_0^{*})+2{\left({\sigma }_0^{*}\right)}^{T}R({\sigma }_0-{\sigma }_0^{*}).\end{array}$$

(47)

By substituting (47) into (46), we have

$$\begin{array}{c}\hfill Z(\xi \left(0\right),{\sigma }_0)+{\dot{\mathrm{\Gamma }}}^{*}\left(\xi \right)\le {({\sigma }_0-{\sigma }_0^{*})}^{T}R({\sigma }_0-{\sigma }_0^{*}).\end{array}$$

(48)

By invoking (44), (45), and (48), it obtains

$$\begin{array}{cc}\hfill \overline{\mathrm{\Gamma }}({\sigma }_0,\xi \left(0\right))=& {\int }_0^{\infty }\left\{Z(\xi \left(0\right),{\sigma }_0)+{\dot{\mathrm{\Gamma }}}^{*}\left(\xi \right)\right\}d\tau +{\mathrm{\Gamma }}^{*}\left(\xi \left(0\right)\right)\hfill \\ \hfill & \le {\int }_0^{\infty }{({\sigma }_0-{\sigma }_0^{*})}^{T}R({\sigma }_0-{\sigma }_0^{*})d\tau +{\mathrm{\Gamma }}^{*}\left(\xi \left(0\right)\right).\hfill \end{array}$$

(49)

Substituting ${\sigma }_0={\sigma }_0^{*}\left({\overline{\xi }}_j\right)$ results in $\overline{\mathrm{\Gamma }}(\xi \left(0\right),{\sigma }_0^{*}\left({\overline{\xi }}_j\right))\le {\mathrm{\Gamma }}^{*}\left(\xi \left(0\right)\right)+{\int }_0^{\infty }{\left({\sigma }_0^{*}\left({\overline{\xi }}_j\right)-{\sigma }_0^{*}\left(\xi \right)\right)}^T$ $R\left({\sigma }_0^{*}\left({\overline{\xi }}_j\right)-{\sigma }_0^{*}\left(\xi \right)\right)d\tau$.

Therefore, the proof is concluded. □

4.2. Neural Network-Based Realization

According to the universal approximation principle of NNs within a compact region $\Omega$ [40], ${\mathrm{\Gamma }}^{*}\left(\xi \right)$ can be given by

$$\begin{array}{c}\hfill {\mathrm{\Gamma }}^{*}\left(\xi \right)={\delta }_c\left(\xi \right)+{\vartheta }_c^T{\kappa }_c\left(\xi \right)\end{array}$$

(50)

where ${\delta }_c\left(\xi \right)\in \mathbb{R}$ is the estimation error, ${\vartheta }_c\in {\mathbb{R}}^{n_c}$ represents the target weight for the critic NN, ${\kappa }_c\left(\xi \right)\in {\mathbb{R}}^{n_c}$ denotes the activation function, and $n_c$ represents the node number of the hidden layer of the critic NN. For practical scenarios, the cost function is presented as

$$\begin{array}{c}\hfill \widehat{\mathrm{\Gamma }}\left(\xi \right)={\widehat{\vartheta }}_c^T{\kappa }_c\left(\xi \right)\end{array}$$

(51)

with ${\widehat{\vartheta }}_c\in {\mathbb{R}}^{n_c}$ being the real weight for the critic NN.

Assumption 5.

The NN weight vector ${\vartheta }_c$ satisfies $\parallel {\vartheta }_c\parallel \le {\overline{\vartheta }}_c$, and the activation function ${\kappa }_c\left(\xi \left(t\right)\right)$ satisfies $\parallel {\kappa }_c\left(\xi \left(t\right)\right)\parallel <{\kappa }_{cm}$ and $\parallel \partial {\kappa }_c\left(\xi \left(t\right)\right)/\partial \xi \parallel \le {\overline{\kappa }}_{cm}$. The residual approximation errors satisfy $\parallel {\delta }_c\left(\xi \right)\parallel <{\delta }_{cm}$ and $\parallel \partial {\delta }_c\left(\xi \right)/\partial \xi \parallel <{\overline{\delta }}_{cm}$, where ${\kappa }_{cm}$, ${\overline{\kappa }}_{cm}$, ${\overline{\delta }}_{cm}$, and ${\delta }_{cm}$ are positive constants.

Using (50), one has

$$\begin{array}{c}\hfill \nabla {\mathrm{\Gamma }}^{*}\left(\xi \right)={(\nabla {\kappa }_c\left(\xi \right))}^T{\vartheta }_c+\nabla {\delta }_c\left(\xi \right)\end{array}$$

(52)

where $\nabla {\delta }_c\left(\xi \right)=\partial {\delta }_c\left(\xi \right)/\partial \xi$ and $\nabla {\kappa }_c\left(\xi \right)=\partial {\kappa }_c\left(\xi \right)/\partial \xi$.

Furthermore, it obtains

$$\begin{array}{c}\hfill \nabla {\widehat{\mathrm{\Gamma }}}^{*}\left(\xi \right)={(\nabla {\kappa }_c\left(\xi \right))}^T{\widehat{\vartheta }}_c\end{array}$$

(53)

Based on (29) and (52), the dynamic event-triggered OC law is

$$\begin{array}{c}\hfill {\sigma }_0^{*}\left({\overline{\xi }}_j\right)=-{\displaystyle \frac{1}{2}}{R}^{-1}{\omega }^T\left({\overline{\xi }}_j\right)\left(\nabla {\delta }_c\left({\overline{\xi }}_j\right)+{\left(\nabla {\kappa }_c\left({\overline{\xi }}_j\right)\right)}^T{\vartheta }_c\right).\end{array}$$

(54)

Subsequently, the actual control policy is

$$\begin{array}{c}\hfill {\widehat{\sigma }}_0\left({\overline{\xi }}_j\right)=-{\displaystyle \frac{1}{2}}{R}^{-1}{\omega }^T\left({\overline{\xi }}_j\right){\left(\nabla {\kappa }_c\left({\overline{\xi }}_j\right)\right)}^T{\widehat{\vartheta }}_c.\end{array}$$

(55)

From (25) and (29), the approximate Hamiltonian function is

$$\begin{array}{cc}\hfill H\left(\xi ,{\widehat{\sigma }}_0\left({\overline{\xi }}_j\right),{\widehat{\vartheta }}_c\right)=& {\left({(\nabla {\kappa }_c\left(\xi \right))}^T{\widehat{\vartheta }}_c\right)}^T(\omega \left(\xi \right){\widehat{\sigma }}_0\left({\overline{\xi }}_j\right)+g\left(\xi \right))+Z(\xi ,{\widehat{\sigma }}_0\left({\overline{\xi }}_j\right))\hfill \\ \hfill & +{\varrho }_M^T\left(\xi \right){\varrho }_M\left(\xi \right)+{\displaystyle \frac{1}{4}}{(\nabla {\widehat{\mathrm{\Gamma }}}^{*}\left(\xi \right))}^T\epsilon \left(\xi \right){\epsilon }^T\left(\xi \right)(\nabla {\widehat{\mathrm{\Gamma }}}^{*}\left(\xi \right))\hfill \\ \hfill \triangleq & e_c.\hfill \end{array}$$

(56)

The weight adaptation strategy for the critic NN is presented as

$$\begin{array}{c}\hfill {\dot{\widehat{\vartheta }}}_{ctra}=-{\displaystyle \frac{{\alpha }_c\theta }{{\left(1+{\theta }^T\theta \right)}^2}}\left({\widehat{\vartheta }}_c^T\theta +J\left(\xi \right)+Z\left(\xi ,{\widehat{\sigma }}_0\left({\overline{\xi }}_j\right)\right)\right),\end{array}$$

(57)

with $\theta =\nabla {\kappa }_c\left(\xi \right)(g\left(\xi \right)+\omega \left(\xi \right){\widehat{\sigma }}_0\left({\overline{\xi }}_j\right))$ and ${\alpha }_c$ being the update rate of the critic NN. Utilizing (53), one gets

$$\begin{array}{c}\hfill J\left(\xi \right)={\displaystyle \frac{1}{4}}{\widehat{\vartheta }}_c^T\nabla {\kappa }_c\left(\xi \right)\epsilon \left(\xi \right){\epsilon }^T\left(\xi \right)\nabla {\kappa }_c^T\left(\xi \right){\widehat{\vartheta }}_c+{\varrho }_M^T\left(\xi \right){\varrho }_M\left(\xi \right).\end{array}$$

(58)

In the proposed approach, to relax the persistence of excitation condition, an enhanced weight adjustment strategy for the critic NN is

$$\begin{array}{cc}\hfill {\dot{\widehat{\vartheta }}}_c=& -[\left({\alpha }_c\theta \right)/{({\theta }^T\theta +1)}^2][{\widehat{\vartheta }}_c^T\theta +J\left(\xi \right)+Z(\xi ,{\widehat{\sigma }}_0\left({\overline{\xi }}_j\right))]\hfill \\ \hfill & -\sum _{k=1}^{l_c}{\displaystyle \frac{{\alpha }_c{\theta }_{\left(k\right)}}{{(1+{\theta }_{\left(k\right)}^T{\theta }_{\left(k\right)})}^2}}[{\widehat{\vartheta }}_c^T{\theta }_{\left(k\right)}+J\left(\xi \left(t_k\right)\right)+Z(\xi \left(t_k\right),{\widehat{\sigma }}_0\left({\overline{\xi }}_j\right))],\hfill \end{array}$$

(59)

with $k\in \{1,2,\dots ,l_c\}$ being the index of stored data $\xi \left(t_k\right)$, $t_k\in [t_j,t_{j+1}),j\in N$ and ${\theta }_{\left(k\right)}=\nabla {\kappa }_c\left(\xi \left(t_k\right)\right)$ $(g\left(\xi \left(t_k\right)\right)+\omega \left(\xi \left(t_k\right)\right){\widehat{\sigma }}_0\left({\overline{\xi }}_j\right))$, and

$$\begin{array}{cc}\hfill J\left(\xi \left(t_k\right)\right)=& {\displaystyle \frac{1}{4}}{\widehat{\vartheta }}_c^T\nabla {\kappa }_c\left(\xi \left(t_k\right)\right)\epsilon \left(\xi \left(t_k\right)\right){\epsilon }^T\left(\xi \left(t_k\right)\right)\nabla {\kappa }_c^T\left(\xi \left(t_k\right)\right){\widehat{\vartheta }}_c\hfill \\ \hfill & +{\varrho }_M^T\left(\xi \left(t_k\right)\right){\varrho }_M\left(\xi \left(t_k\right)\right).\hfill \end{array}$$

(60)

Define the weights estimation error as

$$\begin{array}{c}\hfill {\tilde{\vartheta }}_c={\vartheta }_c-{\widehat{\vartheta }}_c.\end{array}$$

(61)

Based on (59) and (61), it follows that

$$\begin{array}{cc}\hfill {\dot{\tilde{\vartheta }}}_c=& -{\alpha }_c\left[\psi {\psi }^T+\sum _{k=1}^{l_c}{\psi }_{\left(k\right)}{\psi }_{\left(k\right)}^T\right]{\tilde{\vartheta }}_c+{\displaystyle \frac{{\alpha }_c\psi }{1+{\theta }^T\theta }}{\delta }_H\hfill \\ \hfill & +\sum _{k=1}^{l_c}{\displaystyle \frac{{\alpha }_c{\psi }_{\left(k\right)}}{1+{\theta }_{\left(k\right)}^T{\theta }_{\left(k\right)}}}{\delta }_{H_{\left(k\right)}},t,t_k\in [t_j,t_{j+1})\hfill \end{array}$$

(62)

with ${\delta }_H=-\nabla {\delta }_c^T\left(\xi \right)[g\left(\xi \right)+\omega \left(\xi \right){\widehat{\sigma }}_0\left({\overline{\xi }}_j\right)]$ and ${\delta }_{H_{\left(k\right)}}=-\nabla {\delta }_c^T\left(\xi \left(t_k\right)\right)[g\left(\xi \left(t_k\right)\right)+\omega \left(\xi \left(t_k\right)\right){\widehat{\sigma }}_0\left({\overline{\xi }}_j\right)]$ representing the residual errors, and $\psi =\theta /({\theta }^T\theta +1)$ and ${\psi }_{\left(k\right)}={\theta }_{\left(k\right)}/({\theta }_{\left(k\right)}^T{\theta }_{\left(k\right)}+1)$.

Define the augmented state vector represented by $\chi ={[{\xi }^T,{\overline{\xi }}_j^T,{\tilde{\vartheta }}_c^T]}^T$, incorporating the closed-loop SMD $\dot{\xi }=\omega \left(\xi \right){\widehat{\sigma }}_0\left({\overline{\xi }}_j\right)+g\left(\xi \right)$, and then the hybrid control system becomes

$$\begin{array}{c}\hfill \dot{\chi }\left(t\right)=\left[\begin{array}{c}g\left(\xi \right)+\omega \left(\xi \right){\widehat{\sigma }}_0\left({\overline{\xi }}_j\right)\\ 0\\ -{\alpha }_c\mathrm{\Psi }(\psi ,{\psi }_{\left(k\right)}){\tilde{\vartheta }}_c+\mathrm{\Pi }(\psi ,{\psi }_{\left(k\right)})\end{array}\right],t\in [t_j,t_{j+1})\end{array}$$

(63)

with

$$\begin{array}{cc}\hfill \mathrm{\Psi }(\psi ,{\psi }_{\left(k\right)})=& \psi {\psi }^T+\sum _{k=1}^{l_c}{\psi }_{\left(k\right)}{\psi }_{\left(k\right)}^T\hfill \\ \hfill \mathrm{\Pi }(\psi ,{\psi }_{\left(k\right)})=& \sum _{k=1}^{l_c}{\displaystyle \frac{{\alpha }_c{\psi }_{\left(k\right)}}{1+{\theta }_{\left(k\right)}^T{\theta }_{\left(k\right)}}}{\delta }_{H_{\left(k\right)}}+{\displaystyle \frac{{\alpha }_c\psi }{1+{\theta }^T\theta }}{\delta }_H\hfill \end{array}$$

(64)

and

$$\begin{array}{c}\hfill \chi \left(t\right)=\chi \left(t^{-}\right)+\left[\begin{array}{c}0\\ \xi -{\overline{\xi }}_j\\ 0\end{array}\right],t=t_{j+1}\end{array}$$

(65)

with $\chi \left(t^{-}\right)={lim}_{\epsilon \to 0}\chi (t-\epsilon )$.

Remark 3.

In order to address the FTC problem for NLS systems and improve the communication resource utilization efficiency, an integrated control framework is developed which combines ISMC technology and ADP-based GCC under a dynamic ETC mechanism. The proposed approach weakens the impact of actuator failures on system stability, as well as ensures that the certain limits of the control performance indicators exist under the ETC mode.

Remark 4.

The simulation experiment in this paper is implemented using MATLAB R2021a. To clearly present the designed control scheme, the relevant control block diagram of the proposed control strategy is shown in Figure 1.

4.3. Stability Analysis

Theorem 4.

Consider the NLS system (16), assume that Assumptions 2−5 hold and the control strategy is presented in (55). The critic NN weight updating mechanism is formulated in (59). Hence, the dynamic ETC condition is established as

$$\begin{array}{c}\hfill \parallel e_j{\parallel }^2\le {\displaystyle \frac{{\beta }_2{\breve{\sigma }}_2-{\hslash }^2{\lambda }_{min}\left(Q\right){\parallel \xi \parallel }^2+{\widehat{\sigma }}_0^T\left({\overline{\xi }}_j\right)R{\widehat{\sigma }}_0\left({\overline{\xi }}_j\right)}{2{\mathfrak{r}}^2{\rho }^2}}\triangleq {\overline{e}}_T\end{array}$$

(66)

where ℏ denotes a design parameter within the interval $[0,1]$, ${\overline{e}}_T$ is the triggering threshold and the dynamics of internal signal ${\breve{\sigma }}_2$ are given by

$$\begin{array}{c}\hfill {\dot{\breve{\sigma }}}_2=-{\beta }_2{\breve{\sigma }}_2+{\lambda }_{min}\left(Q\right){\parallel \xi \parallel }^2\end{array}$$

(67)

The parameter approximation error ${\tilde{\vartheta }}_c$ and sliding dynamics (16) both achieve UUB.

Proof. 

The candidate Lyapunov function is

$$\begin{array}{c}\hfill \mathfrak{L}\left(t\right)={\mathfrak{L}}_1\left(t\right)+{\mathfrak{L}}_2\left(t\right)+{\mathfrak{L}}_3\left(t\right)+{\mathfrak{L}}_4\left(t\right)\end{array}$$

(68)

where ${\mathfrak{L}}_1\left(t\right)={\mathrm{\Gamma }}^{*}\left({\overline{\xi }}_j\right)$, ${\mathfrak{L}}_2\left(t\right)={\mathrm{\Gamma }}^{*}\left(\xi \left(t\right)\right)$, ${\mathfrak{L}}_3\left(t\right)={\displaystyle \frac{1}{2}}{\tilde{\vartheta }}_c^T{\tilde{\vartheta }}_c$, and ${\mathfrak{L}}_4\left(t\right)={\breve{\sigma }}_2$. The complete proof involves consideration of two cases.

Case 1: During $\forall t\in [t_j,t_{j+1}),j\in \mathbb{N}$, the events are not triggered. It has

$$\begin{array}{c}\hfill {\dot{\mathfrak{L}}}_1\left(t\right)={\dot{\mathrm{\Gamma }}}^{*}\left({\overline{\xi }}_j\right)=0.\end{array}$$

(69)

Based on ${\mathfrak{L}}_2\left(t\right)={\mathrm{\Gamma }}^{*}\left(\xi \left(t\right)\right)$, and according to $\dot{\xi }=\omega \left(\xi \right){\widehat{\sigma }}_0\left({\overline{\xi }}_j\right)+\epsilon \left(\xi \left(t\right)\right)\varrho \left(\xi \left(t\right)\right)+g\left(\xi \right)$, we have

$$\begin{array}{cc}\hfill {\dot{\mathfrak{L}}}_2\left(t\right)=& {\left(\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right)\right)}^T\dot{\xi }\hfill \\ \hfill =& {(\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right))}^T[g\left(\xi \right)+\epsilon \left(\xi \right)\varrho \left(\xi \right)+\omega \left(\xi \right){\widehat{\sigma }}_0\left({\overline{\xi }}_j\right)]\hfill \\ \hfill =& {(\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right))}^{T}g\left(\xi \right)+{(\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right))}^T\omega \left(\xi \right){\widehat{\sigma }}_0\left({\overline{\xi }}_j\right)+{(\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right))}^T\epsilon \left(\xi \right)\varrho \left(\xi \right).\hfill \end{array}$$

(70)

According to (26), one has

$$\begin{array}{cc}\hfill {\dot{\mathfrak{L}}}_2\left(t\right)\le & -{\xi }^{T}Q\xi +{(\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right))}^{T}h\left(\xi \right)[{\widehat{\sigma }}_0\left({\overline{\xi }}_j\right)-{\sigma }_0^{*}\left(\xi \right)]\hfill \\ \hfill & -{\displaystyle \frac{1}{4}}{(\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right))}^{T}h\left(\xi \right)R^{-1}{\omega }^T\left(\xi \right)\nabla {\mathrm{\Gamma }}^{*}\left(\xi \right)\hfill \\ \hfill \le & -{\xi }^{T}Q\xi +{\left({\sigma }_0^{*}\left(\xi \right)\right)}^{T}R{\sigma }_0^{*}\left(\xi \right)-2{\left({\sigma }_0^{*}\left(\xi \right)\right)}^{T}R{\widehat{\sigma }}_0\left({\overline{\xi }}_j\right).\hfill \end{array}$$

(71)

Based on the fact that $-2a^{T}Rb={(a-b)}^{T}R(a-b)-a^{T}Ra-b^{T}Rb$, it has

$$\begin{array}{cc}\hfill & -2{\left({\sigma }_0^{*}\left(\xi \right)\right)}^{T}R{\widehat{\sigma }}_0\left({\overline{\xi }}_j\right)+{\left({\sigma }_0^{*}\left(\xi \right)\right)}^{T}R{\sigma }_0^{*}\left(\xi \right)\hfill \\ \hfill =& {({\sigma }_0^{*}\left(\xi \right)-{\widehat{\sigma }}_0\left({\overline{\xi }}_j\right))}^{T}R({\sigma }_0^{*}\left(\xi \right)-{\widehat{\sigma }}_0\left({\overline{\xi }}_j\right))-{\widehat{\sigma }}_0^T\left({\overline{\xi }}_j\right)R{\widehat{\sigma }}_0\left({\overline{\xi }}_j\right).\hfill \end{array}$$

(72)

Considering Assumptions 3 and 5, (54), (55), and assuming that ${∥\nabla {\delta }_c\left(\xi \right)∥}^2\le {\overline{\delta }}_{cm}^2$ and ${∥\nabla {\kappa }_c\left(\xi \right)∥}^2\le {\overline{\kappa }}_{cm}^2$, it has

$$\begin{array}{cc}\hfill & {({\sigma }_0^{*}\left(\xi \right)-{\widehat{\sigma }}_0\left({\overline{\xi }}_j\right))}^{T}R({\sigma }_0^{*}\left(\xi \right)-{\widehat{\sigma }}_0\left({\overline{\xi }}_j\right))\hfill \\ \hfill \le & 2{\mathfrak{r}}^2{\rho }^2{\parallel e_j\left(t\right)\parallel }^2+2{\left\{{\displaystyle \frac{1}{2}}∥R^{-1}∥{\omega }_{max}[\nabla {\kappa }_c^T\left({\overline{\xi }}_j\right)∥{\tilde{\vartheta }}_c∥+∥\nabla {\delta }_c\left({\overline{\xi }}_j\right)]∥\right\}}^2\hfill \\ \hfill \le & 2{\mathfrak{r}}^2{\rho }^2{\parallel e_j\left(t\right)\parallel }^2+{\displaystyle \frac{1}{2}}{∥R^{-1}∥}^2{\omega }_{max}^2{\left\{{\overline{\kappa }}_{cm}∥{\tilde{\vartheta }}_c∥+{\overline{\delta }}_{cm}\right\}}^2\hfill \\ \hfill \le & 2{\mathfrak{r}}^2{\rho }^2{\parallel e_j\left(t\right)\parallel }^2+{∥R^{-1}∥}^2{\omega }_{max}^2{\overline{\kappa }}_{cm}^2{∥{\tilde{\vartheta }}_c∥}^2+{∥R^{-1}∥}^2{\omega }_{max}^2{\overline{\delta }}_{cm}^2\hfill \end{array}$$

(73)

Based on Assumption 4, (71), (72), and (73), it follows that

$$\begin{array}{cc}\hfill {\dot{\mathfrak{L}}}_2\left(t\right)\le & -{\hslash }^2{\lambda }_{min}{\left(Q\right)\parallel \xi \parallel }^2-(1-{\hslash }^2){\lambda }_{min}\left(Q\right){\parallel \xi \parallel }^2+2{\mathfrak{r}}^2{\rho }^2{\parallel e_j\left(t\right)\parallel }^2.\hfill \\ \hfill & +{∥R^{-1}∥}^2{\omega }_{max}^2{\overline{\kappa }}_{cm}^2{∥{\tilde{\vartheta }}_c∥}^2+{∥R^{-1}∥}^2{\omega }_{max}^2{\overline{\delta }}_{cm}^2-{\widehat{\sigma }}_0^T\left({\overline{\xi }}_j\right)R{\widehat{\sigma }}_0\left({\overline{\xi }}_j\right)\hfill \end{array}$$

(74)

Furthermore, the derivative of ${\mathfrak{L}}_3\left(t\right)$ is

$$\begin{array}{cc}\hfill {\dot{\mathfrak{L}}}_3\left(t\right)=& -{\alpha }_c{\tilde{\vartheta }}_c^T\left(\psi {\psi }^T+\sum _{k=1}^{l_c}{\psi }_{\left(k\right)}{\psi }_{\left(k\right)}^T\right){\tilde{\vartheta }}_c+{\displaystyle \frac{{\alpha }_c{\tilde{\vartheta }}_c^T\psi }{1+{\theta }^T\theta }}{\delta }_H\hfill \\ \hfill & +\sum _{k=1}^{l_c}{\displaystyle \frac{{\alpha }_c{\tilde{\vartheta }}_c^T{\psi }_{\left(k\right)}}{1+{\theta }_{\left(k\right)}^T{\theta }_{\left(k\right)}}}{\delta }_{H_{\left(k\right)}}.\hfill \end{array}$$

(75)

Based on the fact $a^{T}b\le (1/2)a^{T}a+(1/2)b^{T}b$, it can be derived that

$$\begin{array}{c}\hfill {\displaystyle \frac{{\alpha }_c{\tilde{\vartheta }}_c^T\psi }{1+{\theta }^T\theta }}{\delta }_H\le {\displaystyle \frac{{\alpha }_c}{2}}{\tilde{\vartheta }}_c^T\psi {\psi }^T{\tilde{\vartheta }}_c+{\displaystyle \frac{{\alpha }_c}{2}}{\delta }_H^T{\delta }_H\end{array}$$

(76)

$$\begin{array}{c}\hfill \sum _{k=1}^{l_c}{\displaystyle \frac{{\alpha }_c{\tilde{\vartheta }}_c^T{\psi }_{\left(k\right)}}{1+{\theta }_{\left(k\right)}^T{\theta }_{\left(k\right)}}}{\delta }_{H_{\left(k\right)}}\le {\displaystyle \frac{{\alpha }_c}{2}}\sum _{k=1}^{l_c}{\tilde{\vartheta }}_c^T{\psi }_{\left(k\right)}{\psi }_{\left(k\right)}^T{\tilde{\vartheta }}_c+{\displaystyle \frac{{\alpha }_c}{2}}\sum _{k=1}^{l_c}{\delta }_{H_{\left(k\right)}}^T{\delta }_{H_{\left(k\right)}}\end{array}$$

(77)

with ${\delta }_H$ being the residual error. Suppose that $∥{\delta }_H∥\le b_{{\delta }_H}$. According to (75), (76), and (77), it follows that

$$\begin{array}{c}\hfill {\dot{\mathfrak{L}}}_3\left(t\right)\le -{\displaystyle \frac{{\alpha }_c}{2}}{\lambda }_{min}(\mathrm{\Psi }(\psi ,{\psi }_{\left(k\right)}){∥{\tilde{\vartheta }}_c∥}^2+{\displaystyle \frac{{\alpha }_c(l_c+1)}{2}}{b}_{{\delta }_H}^2.\end{array}$$

(78)

where $\mathrm{\Psi }(\psi ,{\psi }_{\left(k\right)})$ is given in (64).

Based on (69), (74), and (78), we have

$$\begin{array}{cc}\hfill \dot{\mathfrak{L}}\left(t\right)\le & -{\hslash }^2{\lambda }_{min}{\left(Q\right)\parallel \xi \parallel }^2-(1-{\hslash }^2){\lambda }_{min}\left(Q\right){\parallel \xi \parallel }^2+2{\mathfrak{r}}^2{\rho }^2{\parallel e_j\left(t\right)\parallel }^2\hfill \\ \hfill & -{\displaystyle \frac{1}{2}}{\alpha }_c{\lambda }_{min}\left(\mathrm{\Psi }(\psi ,{\psi }_{\left(k\right)})\right){\parallel {\tilde{\vartheta }}_c\parallel }^2+{\dot{\breve{\sigma }}}_2+{\displaystyle \frac{{\alpha }_c(l_c+1)}{2}}{b}_{{\delta }_H}^2\hfill \\ \hfill & +{∥R^{-1}∥}^2{\omega }_{max}^2{\overline{\kappa }}_{cm}^2{∥{\tilde{\vartheta }}_c∥}^2+{∥R^{-1}∥}^2{\omega }_{max}^2{\overline{\delta }}_{cm}^2-{\widehat{\sigma }}_0^T\left({\overline{\xi }}_j\right)R{\widehat{\sigma }}_0\left({\overline{\xi }}_j\right)\hfill \end{array}$$

(79)

The triggering condition, constructed as (66), is activated when one of the following inequalities is satisfied

$$\begin{array}{c}\hfill ∥\xi ∥>{\displaystyle \frac{1}{\hslash }}\sqrt{{\displaystyle \frac{{\alpha }_c\left(l_c+1\right)b_{{\delta }_H}^2+2{∥R^{-1}∥}^2{\omega }_{max}^2{\overline{\delta }}_{cm}^2}{2{\lambda }_{min}\left(Q\right)}}}=D_1\end{array}$$

(80)

$$\begin{array}{c}\hfill ∥\tilde{\vartheta }c∥>\sqrt{{\displaystyle \frac{{\alpha }_c(l_c+1)b_{{\delta }_H}^2+2{∥R^{-1}∥}^2{\omega }_{max}^2{\overline{\delta }}_{cm}^2}{{\alpha }_c{\lambda }_{min}\left(\mathrm{\Psi }(\psi ,{\psi }_{\left(k\right)})\right)-2{∥R^{-1}∥}^2{\omega }_{max}^2{\overline{\kappa }}_{cm}^2}}}=D_2\end{array}$$

(81)

It can obtain that $\dot{\mathfrak{L}}\left(t\right)<0$ under the condition ${\alpha }_c{\lambda }_{min}\left(\mathrm{\Psi }(\psi ,{\psi }_{\left(k\right)})\right)-2{∥R^{-1}∥}^2{\omega }_{max}^2{\overline{\kappa }}_{cm}^2>0$.

This demonstrates that the UUB property holds for both $\xi \left(t\right)$ and ${\tilde{\vartheta }}_c$.

Case 2: During the trigger moment $t=t_j$, the derivative of $\mathfrak{L}\left(t\right)$ is constructed as

$$\begin{array}{cc}\hfill \mathrm{\Delta }\mathfrak{L}\left(t_{j+1}\right)& =\mathfrak{L}\left(t_{j+1}^{+}\right)-\mathfrak{L}\left(t_{j+1}\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}[{\tilde{\vartheta }}_c^T\left(\xi \left(t_j^{+}\right)\right){\tilde{\vartheta }}_c\left(\xi \left(t_j^{+}\right)\right)-{\tilde{\vartheta }}_c^T\left(\xi \left(t_j\right)\right){\tilde{\vartheta }}_c\left(\xi \left(t_j\right)\right)]\hfill \\ \hfill & +[{\breve{\sigma }}_2\left(t_{j+1}^{+}\right)-{\breve{\sigma }}_2\left(t_j\right)]+[{\mathrm{\Gamma }}^{*}\left(\xi \left(t_j^{+}\right)\right)-{\mathrm{\Gamma }}^{*}\left(\xi \left(t_j\right)\right)]\hfill \\ \hfill & +[{\mathrm{\Gamma }}^{*}\left({\overline{\xi }}_{j+1}\right)-{\mathrm{\Gamma }}^{*}\left({\overline{\xi }}_j\right)].\hfill \end{array}$$

(82)

According to case 1, $\mathfrak{L}\left(t\right)$ exhibits continuous and monotonic decrease within $[t_j,t_{j+1})$. Therefore, it follows that

$$\begin{array}{c}\hfill \mathfrak{L}(s+t_j)<\mathfrak{L}\left(t_j\right),\forall s\in (0,t_{j+1}-t_j).\end{array}$$

(83)

Through applying limits on each side of (83) while establishing the definition $\mathfrak{L}\left(t_j^{+}\right)=li{m}_{s\to 0^{+}}L(t_j+s)$, it obtains $\mathfrak{L}\left(t_j^{+}\right)\le \mathfrak{L}\left(t_j\right)$. Then we have

$$\begin{array}{cc}\hfill {\mathrm{\Gamma }}^{*}\left(\xi \left(t_j^{+}\right)\right)+{\breve{\sigma }}_2\left(t_j^{+}\right)+& {\displaystyle \frac{1}{2}}{\tilde{\vartheta }}_c^T\left(\xi \left(t_j^{+}\right)\right){\tilde{\vartheta }}_c\left(\xi \left(t_j^{+}\right)\right)+{\mathrm{\Gamma }}^{*}\left(\overline{\xi }\left(t_j\right)\right)\hfill \\ \hfill & \le {\displaystyle \frac{1}{2}}{\tilde{\vartheta }}_c^T\left(\xi \left(t_j\right)\right){\tilde{\vartheta }}_c\left(\xi \left(t_j\right)\right)+{\mathrm{\Gamma }}^{*}\left({\overline{\xi }}_j\right)+{\breve{\sigma }}_2\left(t_j\right)+{\mathrm{\Gamma }}^{*}\left(\xi \left(t_j\right)\right).\hfill \end{array}$$

(84)

Additionally, ${\mathrm{\Gamma }}^{*}\left(\xi \right)$ is continuous differentiability properties at triggering moments $t_j$. Based on case 1, it obtains

$$\begin{array}{c}\hfill {\mathrm{\Gamma }}^{*}\left(\overline{\xi }\left(t_{j+1}\right)\right)\le {\mathrm{\Gamma }}^{*}\left({\overline{\xi }}_j\right).\end{array}$$

(85)

Considering (84) and (85), it follows that $\mathfrak{L}\left(t\right)\le 0$.

Through the analysis of these two cases, the proof of the theorem is completed. □

5. Simulation

In this section, consider the following NLS systems:

$$\begin{array}{cc}\hfill {\dot{\xi }}_1& =\left[\begin{array}{c}-{\xi }_{11}+{\xi }_{12}cos{\xi }_{11}\\ -0.5({\xi }_{11}+{\xi }_{12})+{sin}^2{\xi }_{11}\end{array}\right]+\left[\begin{array}{c}0\\ 1\end{array}\right]\left[{\sigma }_1\left({\xi }_1\right)+{\beta }_1(t-t_T)f_{s_1}\left(t\right)\right]+\left[\begin{array}{c}-1\\ 0\end{array}\right]{\varrho }_1\left(\xi \right);\hfill \\ \hfill {\dot{\xi }}_2& =\left[\begin{array}{c}-{\xi }_{21}+{\xi }_{22}cos\left(0.5{\xi }_{21}\right)\\ -{\xi }_{21}+{cos}^2\left({\xi }_{21}\right)\end{array}\right]+\left[\begin{array}{c}0\\ 1\end{array}\right]\left[{\sigma }_2\left({\xi }_2\right)+{\beta }_2(t-t_T)f_{s_2}\left(t\right)\right]+\left[\begin{array}{c}-1\\ 0\end{array}\right]{\varrho }_2\left(\xi \right),\hfill \end{array}$$

(86)

where ${\xi }_1={[{\xi }_{11},{\xi }_{12}]}^T\in {\mathbb{R}}^2$ and ${\xi }_2={[{\xi }_{21},{\xi }_{22}]}^T\in {\mathbb{R}}^2$ are the system states, ${\sigma }_1\left({\xi }_1\right)\in \mathbb{R}$ and ${\sigma }_2\left({\xi }_2\right)\in \mathbb{R}$ are the control inputs. The interconnected disturbances is ${\varrho }_1={\mathfrak{p}}_1{\xi }_{11}sin\left({\xi }_{12}{\xi }_{21}\right)$ and ${\varrho }_2={\mathfrak{p}}_2{\xi }_{21}sin\left({\xi }_{12}{\xi }_{21}\right)$ with ${\mathfrak{p}}_{12}\in [-0.5,0.5]$ and ${\mathfrak{p}}_{21}\in [-0.25,0.25]$. Here, we further choose ${\varrho }_{1M}\left(\varsigma \left(\xi \right)\right)=0.5\left|{\xi }_{11}\right|$; ${\varrho }_{2M}\left(\varsigma \left(\xi \right)\right)=0.5\left|{\xi }_{21}\right|$. Assuming that an actuator failure suddenly occurs at $t_T=4s$, the fault dynamics can be represented as

$$\begin{array}{cc}\hfill {\beta }_1(t-t_T)f_{s_1}\left(t\right)& =\left\{\begin{array}{cc}-2sin0.5t,& t\ge 4\\ 0,& t<4\end{array}\right.\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\beta }_2(t-t_T)f_{s_2}\left(t\right)& =\left\{\begin{array}{cc}-2.5cost,& t\ge 4\\ 0,& t<4\end{array}\right.\hfill \end{array}$$

In this simulation, the original states of subsystem 1 and subsystem 2 are selected as ${\xi }_{10}={\xi }_{20}={[1,-1]}^T$ and the relevant parameters are set to $R_1=1$, $R_2=1$,$Q_1=\mathrm{diag}\{1,1\}$, $Q_2=\mathrm{diag}\{1,1\}$. The cost function can be defined as

$$\begin{array}{c}\hfill J\left(\xi \right)={\widehat{\vartheta }}_c^T{\kappa }_c\left(\xi \right)\end{array}$$

where ${\widehat{\vartheta }}_c={\left[{\widehat{\vartheta }}_{c1},{\widehat{\vartheta }}_{c2}\right]}^T$, ${\kappa }_c\left(\xi \right)=\left[{\kappa }_{c1}\left(\xi \right),{\kappa }_{c2}\left(\xi \right)\right]$, ${\kappa }_{c1}\left(\xi \right)=[{\xi }_{11}^2,{\xi }_{11}{\xi }_{12},{\xi }_{12}^2,{\xi }_{11}^4,{\xi }_{11}^3{\xi }_{12},{\xi }_{11}^2{\xi }_{12}^2,$ ${\xi }_{11}{\xi }_{12}^3,{\xi }_{12}^4{]}^T$ and ${\kappa }_{c2}\left(\xi \right)={\left[{\xi }_{21}^2,{\xi }_{21}{\xi }_{22},{\xi }_{22}^2,{\xi }_{21}^4,{\xi }_{21}^3{\xi }_{22},{\xi }_{21}^2{\xi }_{22}^2,{\xi }_{21}{\xi }_{22}^3,{\xi }_{22}^4\right]}^T$. Moreover, the parameters in dynamic triggering conditions are set as $\hslash =0.5$, $\rho =5$, $\mathfrak{r}=1$, ${\beta }_2=0.1$.

Figure 2 and Figure 3 illustrate the state trajectories of the subsystems. It is clear that all state trajectories can ultimately converge to the equilibrium point.

Figure 4 presents the SMC law ${\sigma }_{11}$ for subsystem 1, and the dynamic ETC input ${\sigma }_{01}$ for subsystem 1 is depicted in Figure 5.

Similarly, the SMC rule ${\sigma }_{12}$ for subsystem 2 is shown in Figure 6, while the dynamic ETC input ${\sigma }_{02}$ for subsystem 2 is illustrated in Figure 7.

Figure 8 and Figure 9 demonstrate the convergence behaviors of the critic NNs’ weights for subsystem 1 and subsystem 2. As shown in the figures, the weight vectors of the critic NNs for both subsystems converge within 150 s, indicating that the adaptive learning strategy designed in this article can enable the system to achieve asymptotic stability, thereby validating the UUB property of the control system.

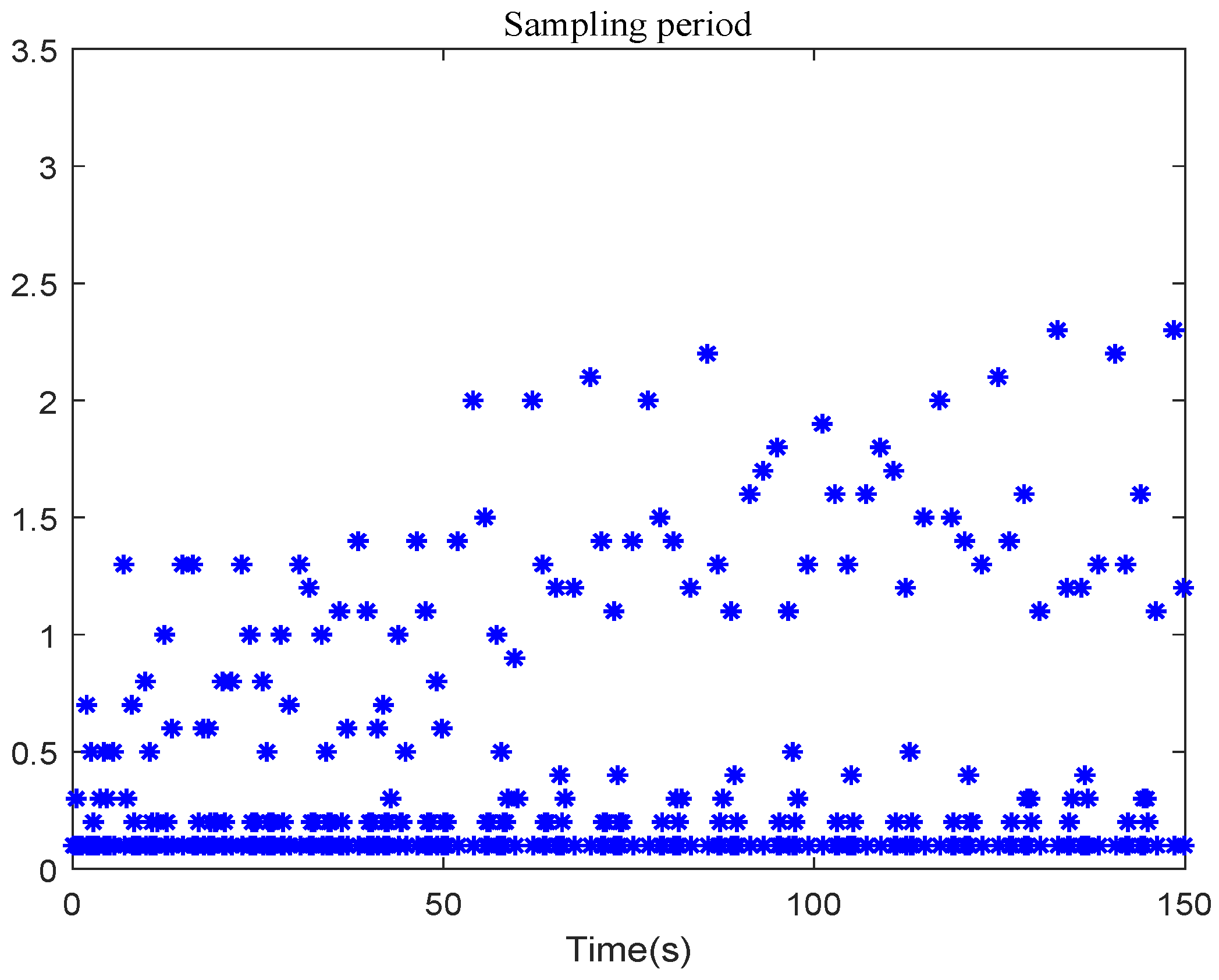
Figure 10 presents the dynamic ETC condition. Figure 11 shows the situation of the sampling period during the learning process, which indicates that the control approach presented in this article can effectively improve the utilization of communication resources.

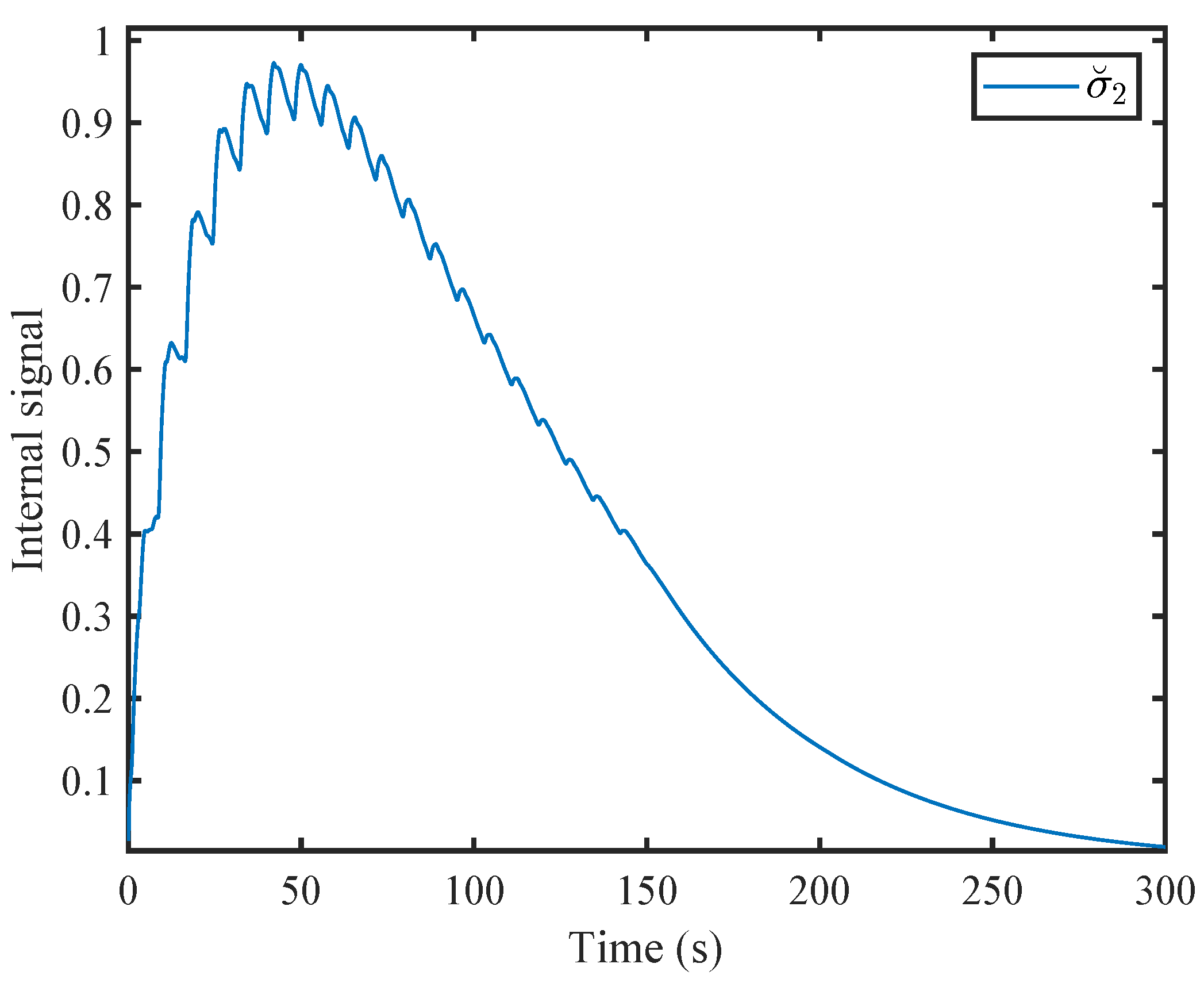
The internal signal evolution of the dynamic ETC method is depicted in Figure 12. It is clear that the internal signal ${\breve{\sigma }}_2$ remains positive at all times.

6. Conclusions

In our research, a new ISMC approach with a dynamic event-triggered mechanism has been designed for NLS systems with actuator faults. Firstly, ISMC technology keeps the motion trajectory of the subsystems on the SMS and eliminates the impact of actuator failures in NLS systems. Secondly, a dynamic event-triggered decentralized GCC scheme has been presented via the ADP method to ensure system stability while also guaranteeing that the cost function of the entire NLS system has an upper bound. In our design, the developed method decreases the consumption of communication resources. Moreover, the system states and the weight values of the critic NN have been proved to be UUB using the Lyapunov stability theorem. Finally, the effectiveness of the presented control strategy has been verified by a simulation example. In future research, the fault-tolerant control problems of more complex systems will be discussed and studied, such as sensor failure problems, control problems with asymmetric input constraints, and so on.