Reliable Neural Network Control for Active Vibration Suppression of Uncertain Structures
Abstract
1. Introduction
- This study presents a reliable MPC approach, which is then approximated by neural networks to establish a reliable NNC. In contrast to existing robust MPC methods, the proposed reliable NNC not only ensures the satisfaction of structural reliability constraints but also significantly reduces the online computational burden, making it more practical for real-time control applications.
- A novel importance sampling strategy is introduced. By leveraging an auxiliary neural network to guide the selection of training samples, this strategy effectively enhances the efficiency of the entire training process to achieve sufficient accuracy. This leads to faster convergence during the training process and better generalization ability of the neural network controller.
- An adaptive nonprobabilistic Kalman filter (ANKF) is proposed. Through the use of acceleration data to set adaptive parameters, the ANKF can accurately estimate the system state variables and delineate their uncertain regions in the presence of external disturbance loads. This method provides a more precise and reliable state estimation solution for systems with nonprobabilistic uncertainties.
2. Dynamic Model of Smart Structures with Nonprobabilistic Uncertainties and Time Delay
3. The Framework of Reliable NNC
3.1. Establishing Reliable MPC
3.2. Approximating Reliable MPC with a Deep Neural Network (DNN)
3.3. Importance Sampling Strategy
3.4. Procedure for Training the Reliable NNC Law
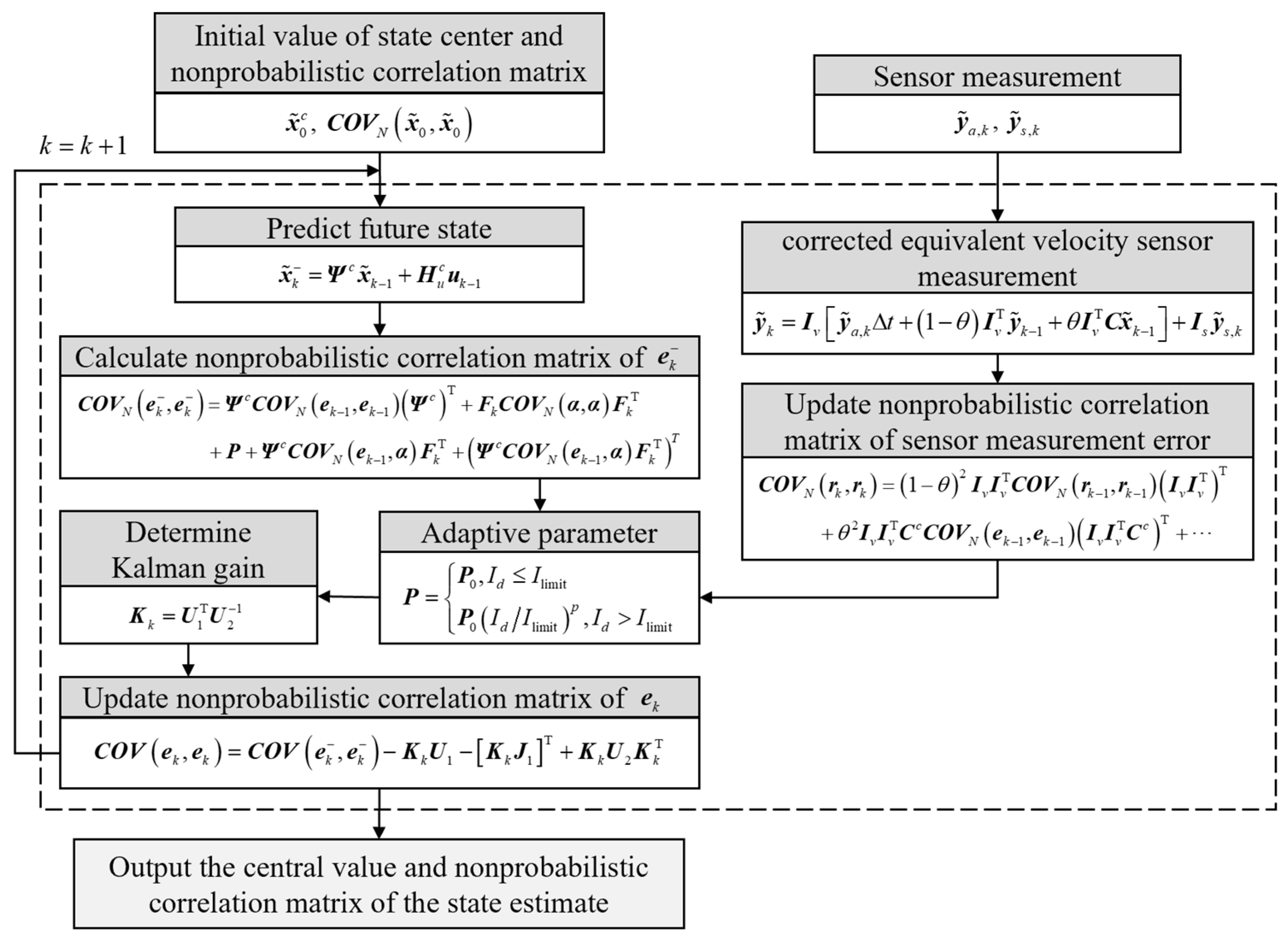
4. Adaptive Nonprobabilistic Kalman Filter for State Estimation
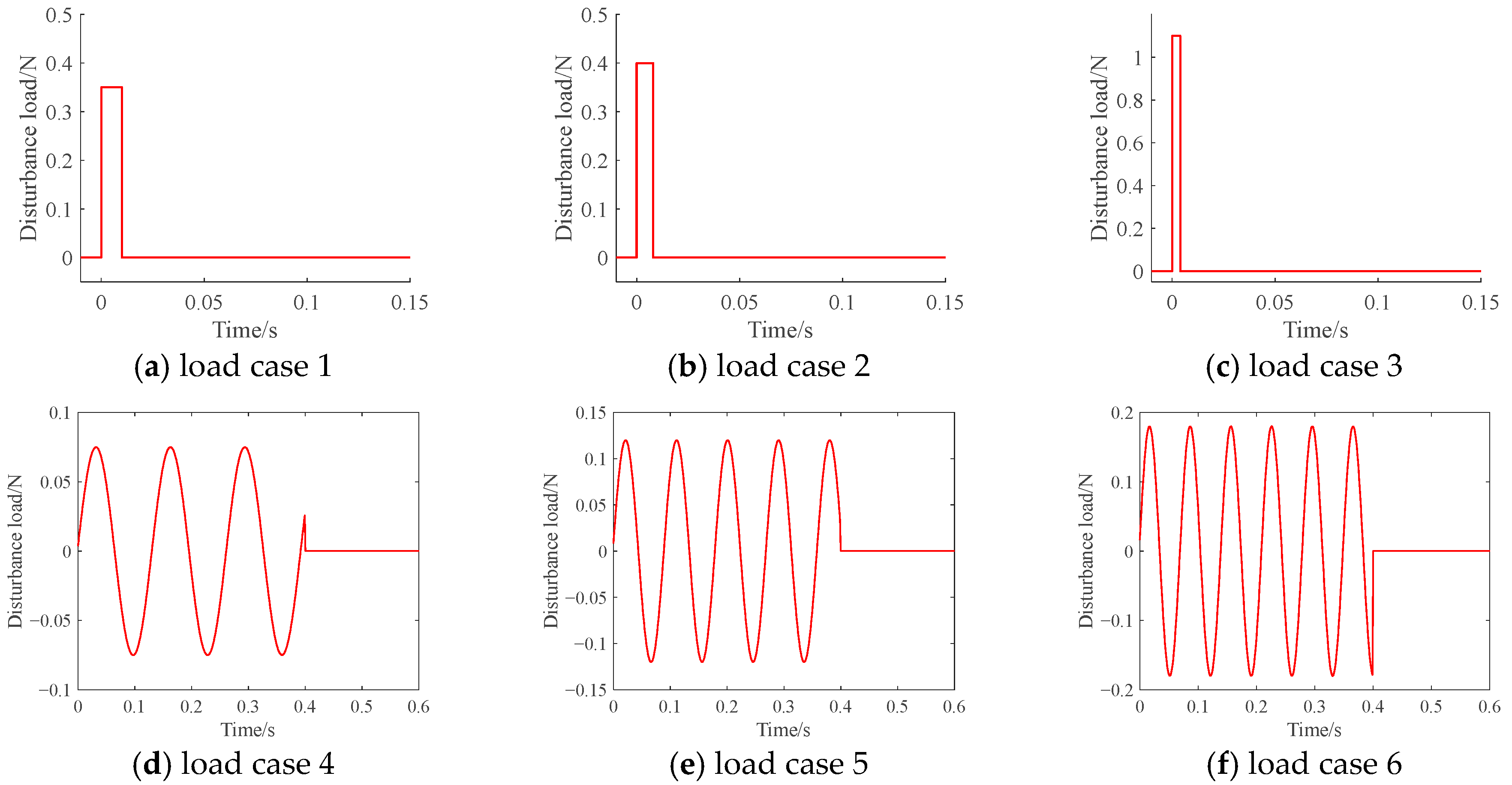
5. Numerical Examples and Experimental Validation
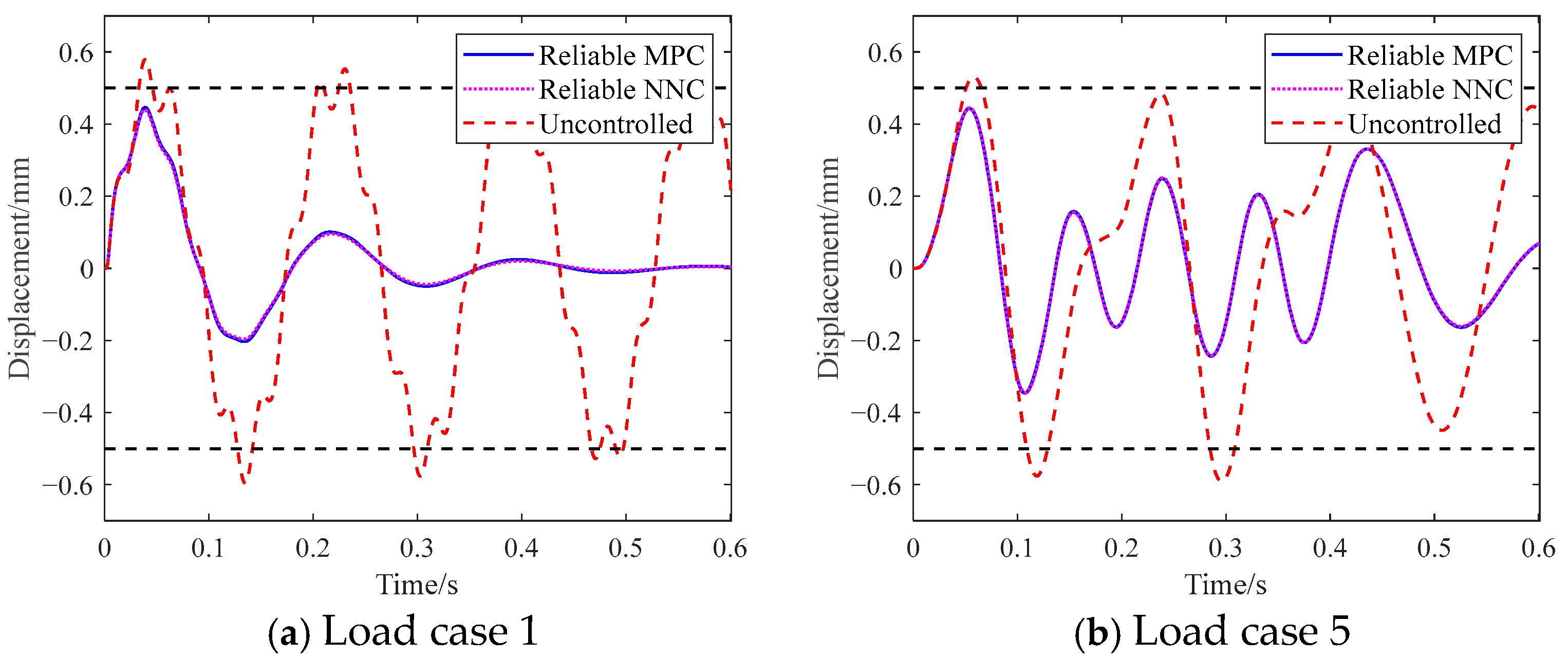
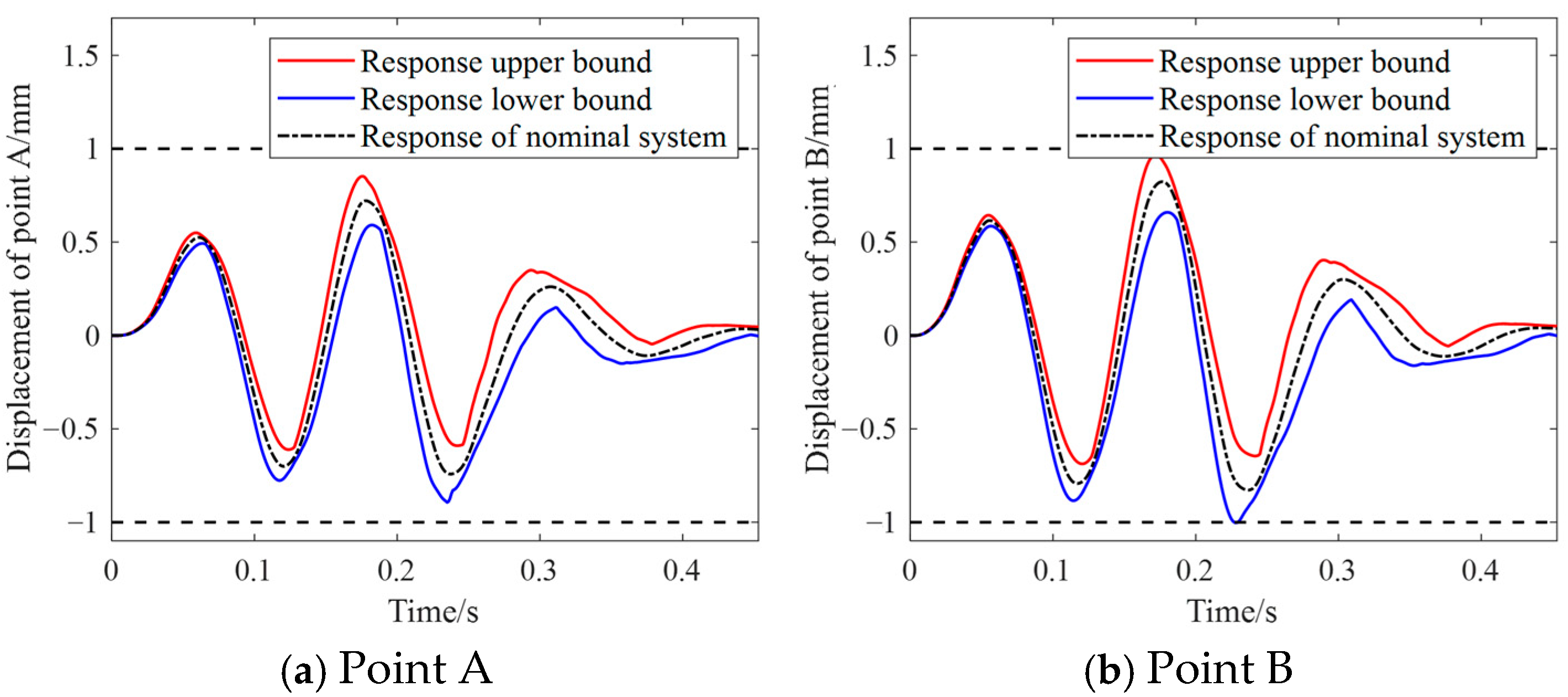
5.1. Numerical Example 1: Cantilever Beam
5.2. Numerical Example 2: Simplified Vertical Tail Structure
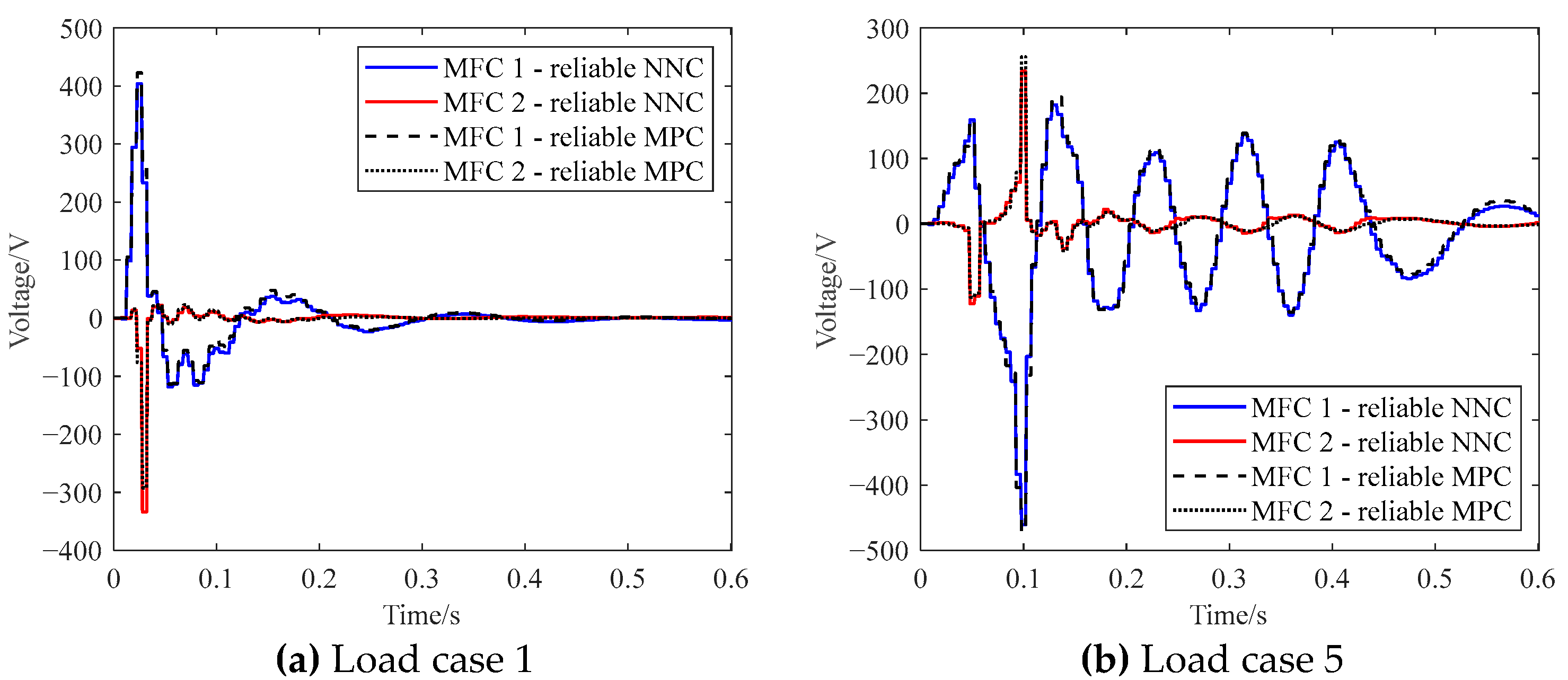
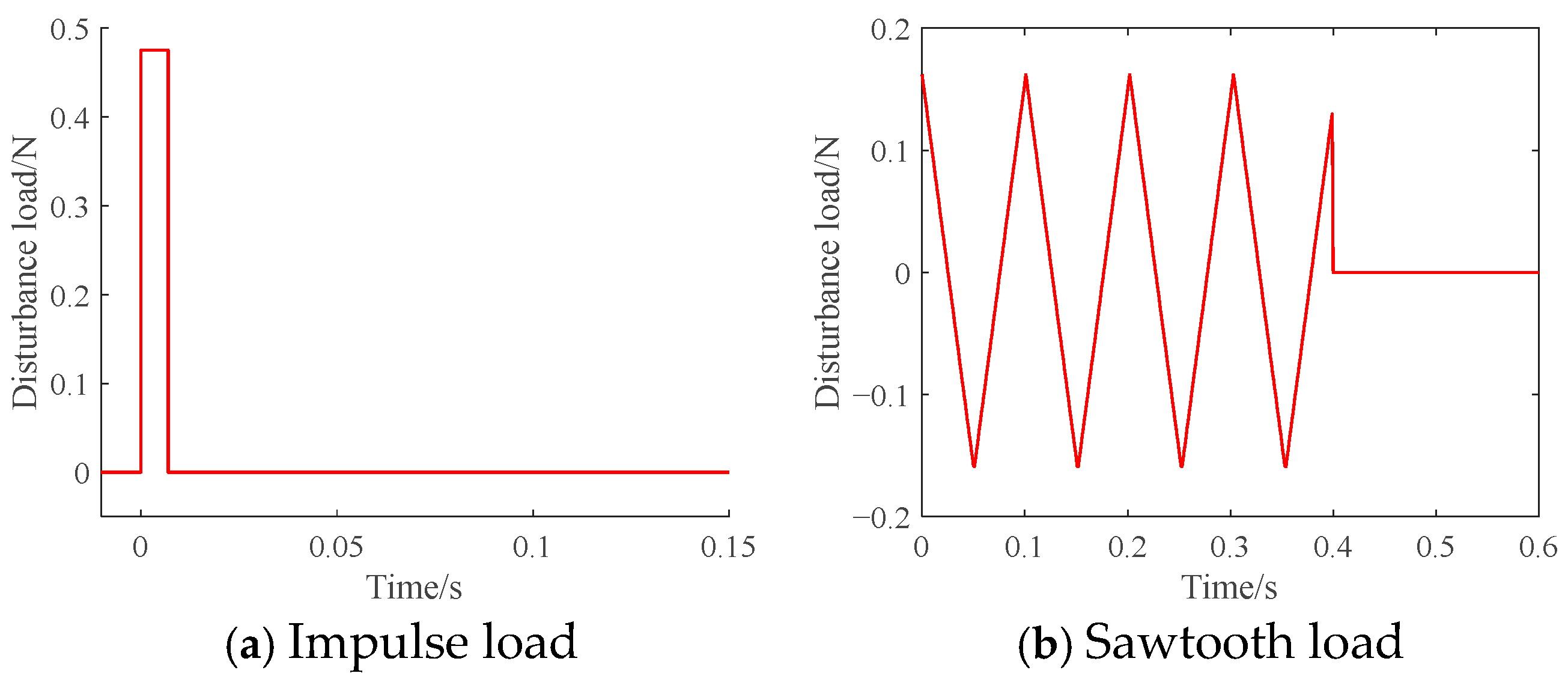
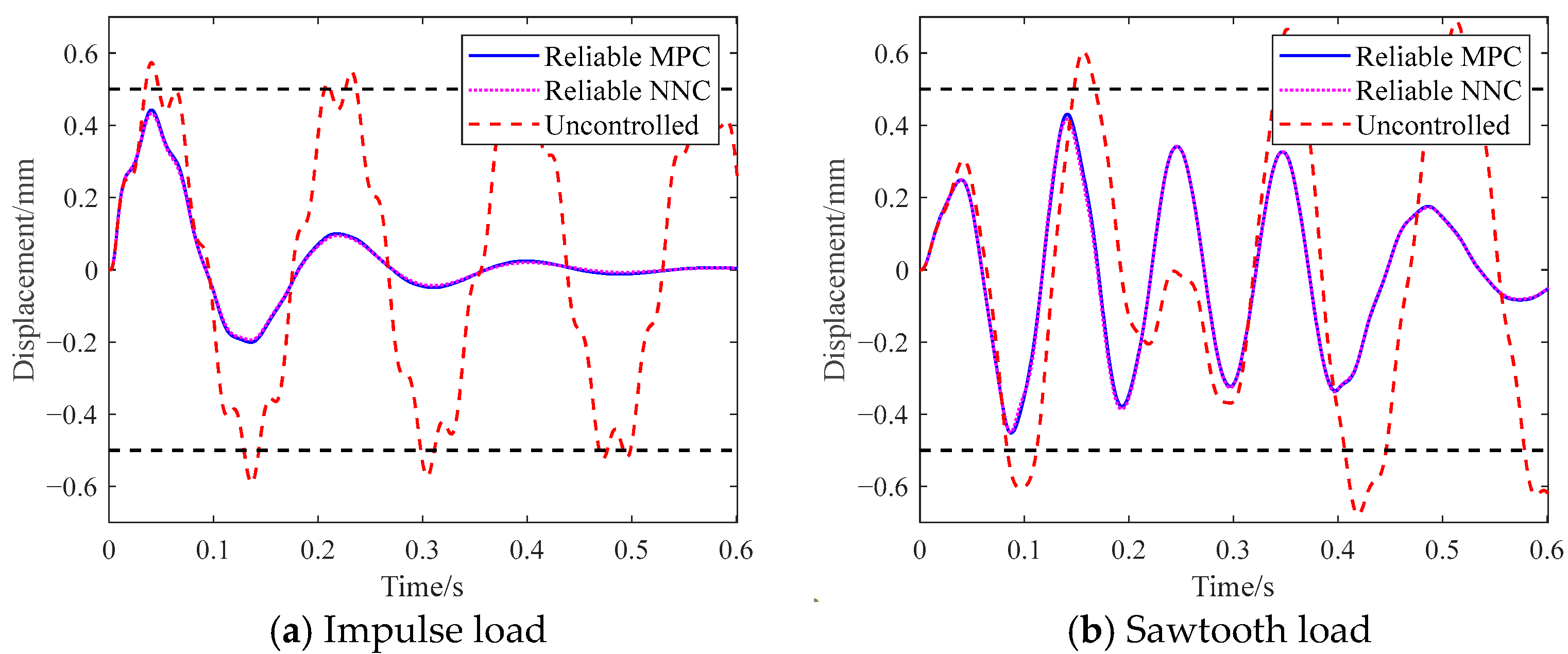
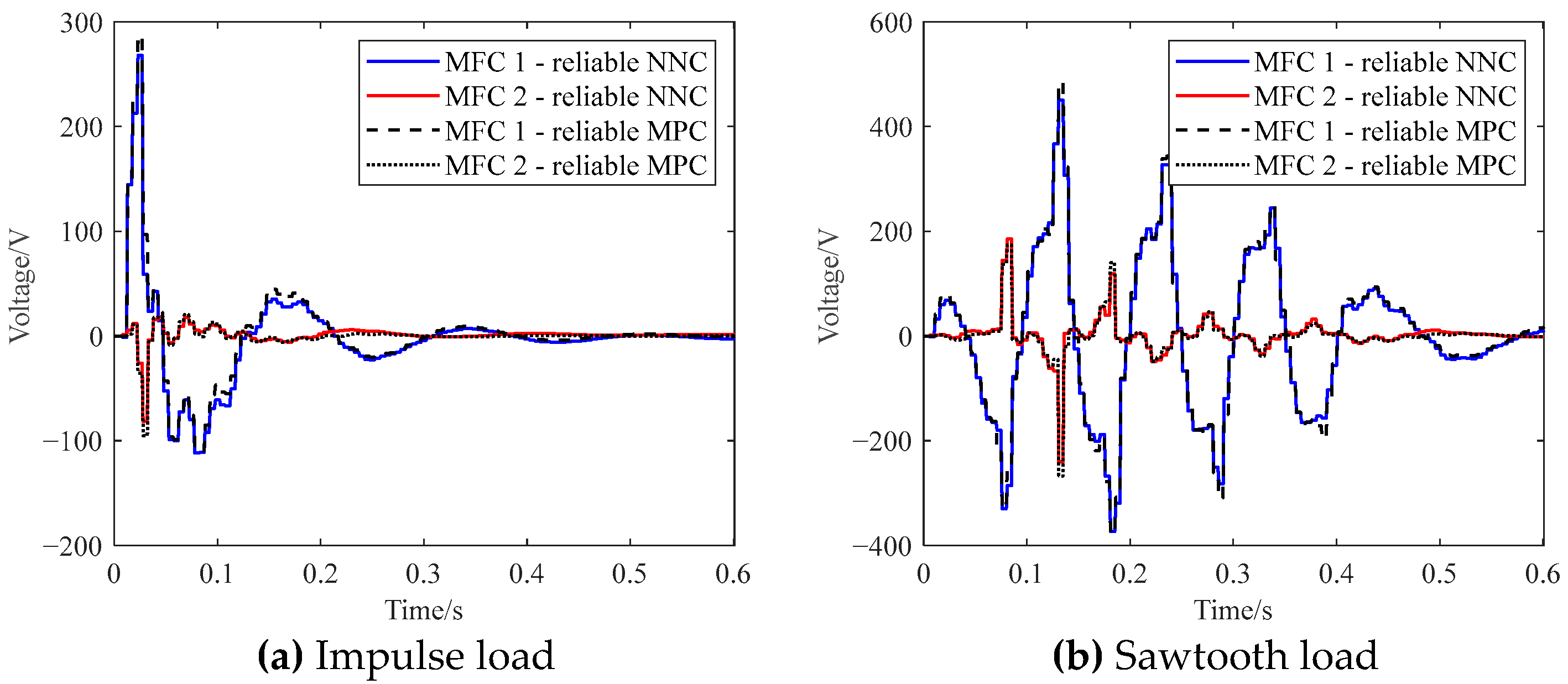
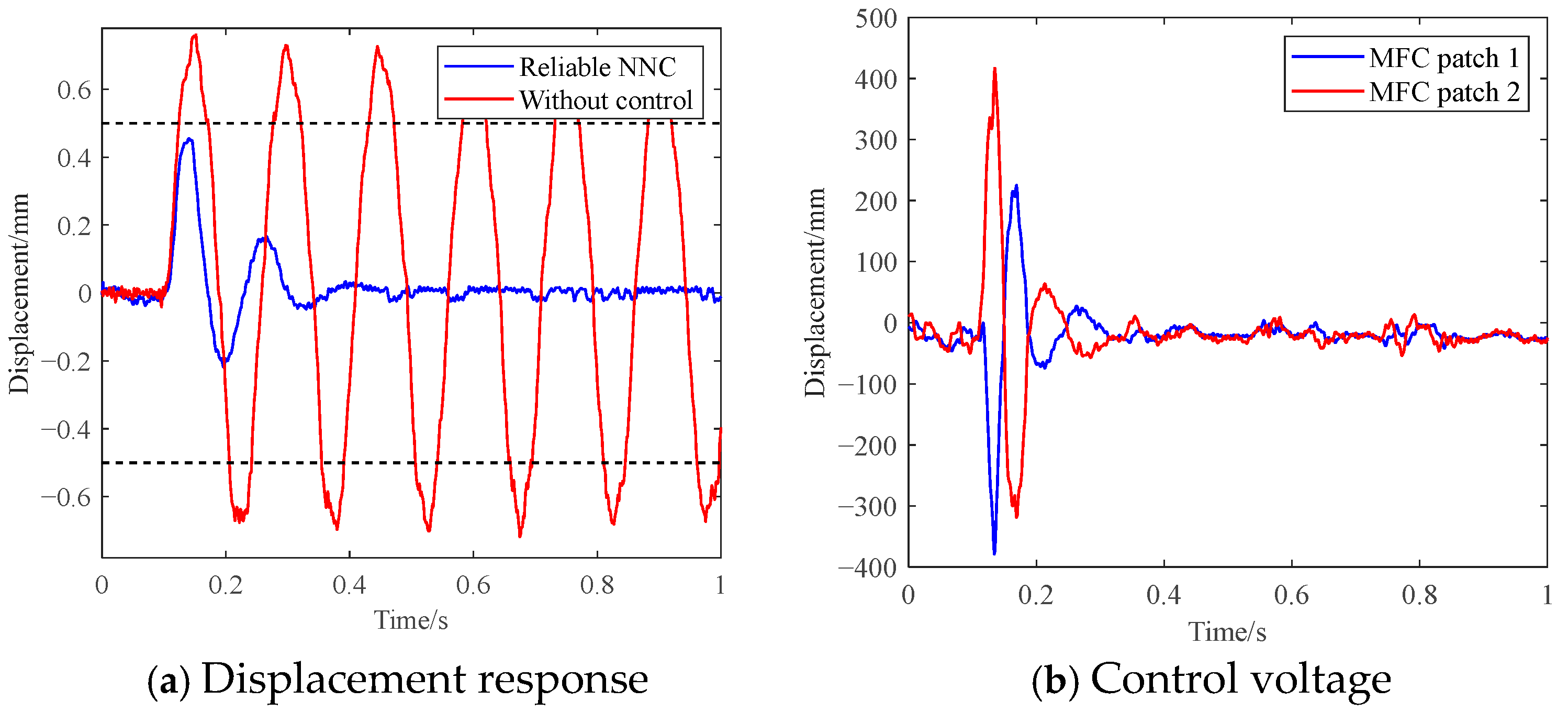
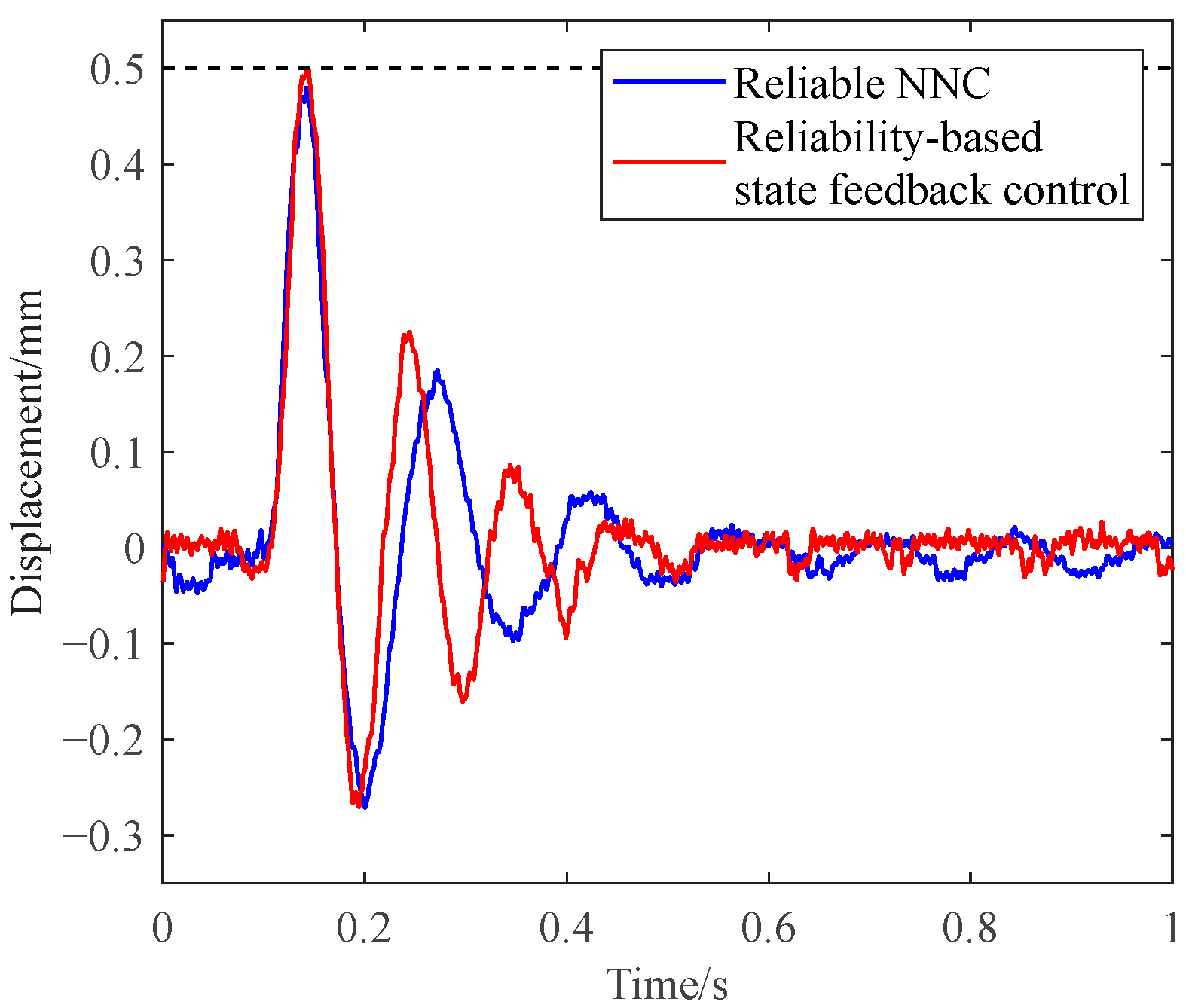
5.3. Experimental Validation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ANKF | Adaptive nonprobabilistic Kalman filter |
| DNN | Deep neural network |
| MFC | Macro fiber composite |
| MPC | Model predictive control |
| NNC | Neural network control |
| RMSE | Root mean square error |
References
- Preumont, A. Vibration Control of Active Structures; Solid Mechanics and Its Applications; Springer International Publishing: Cham, Switzerland, 2018; Volume 246, ISBN 978-3-319-72295-5. [Google Scholar]
- Gardonio, P. Review of Active Techniques for Aerospace Vibro-Acoustic Control. J. Aircr. 2002, 39, 206–214. [Google Scholar] [CrossRef]
- He, W.; Ouyang, Y.; Hong, J. Vibration Control of a Flexible Robotic Manipulator in the Presence of Input Deadzone. IEEE Trans. Ind. Inform. 2017, 13, 48–59. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, R.; Wang, J.; Shi, Y. Robust Finite Frequency Static-Output-Feedback Control with Application to Vibration Active Control of Structural Systems. Mechatronics 2014, 24, 354–366. [Google Scholar] [CrossRef]
- Karkoub, M.; Balas, G.; Tamma, K.; Donath, M. Robust Control of Fexible Manipulators via μ-Synthesis. Control Eng. Pract. 2000, 8, 725–734. [Google Scholar] [CrossRef]
- Chen, Z.; Yao, B.; Wang, Q. μ-Synthesis-Based Adaptive Robust Control of Linear Motor Driven Stages with High-Frequency Dynamics: A Case Study. IEEE ASME Trans. Mechatron. 2015, 20, 1482–1490. [Google Scholar] [CrossRef]
- Brand, Z.; Cole, M.O.T. Mini-Max Optimization of Actuator/Sensor Placement for Flexural Vibration Control of a Rotating Thin-Walled Cylinder over a Range of Speeds. J. Sound Vib. 2021, 506, 116105. [Google Scholar] [CrossRef]
- Choi, D. Min-Max Control for Vibration Suppression of Mobile Manipulator with Active Suspension System. Int. J. Control Autom. Syst. 2022, 20, 618–626. [Google Scholar] [CrossRef]
- Rodriguez, J.; Collet, M.; Chesné, S. Active Vibration Control on a Smart Composite Structure Using Modal-Shaped Sliding Mode Control. J. Vib. Acoust. 2022, 144, 21013. [Google Scholar] [CrossRef]
- Qing-lei Hu; Zidong Wang; Huijun Gao Sliding Mode and Shaped Input Vibration Control of Flexible Systems. IEEE Trans. Aerosp. Electron. Syst. 2008, 44, 503–519. [CrossRef]
- Lu, Q.; Wang, P.; Liu, C. An Analytical and Experimental Study on Adaptive Active Vibration Control of Sandwich Beam. Int. J. Mech. Sci. 2022, 232, 107634. [Google Scholar] [CrossRef]
- Landau, I.D.; Airimițoaie, T.-B.; Castellanos-Silva, A.; Constantinescu, A. Adaptive and Robust Active Vibration Control: Methodology and Tests; Advances in Industrial Control; Springer International Publishing: Cham, Switzerland, 2017; ISBN 978-3-319-41449-2. [Google Scholar]
- Liu, Z.; Liu, J.; He, W. An Adaptive Iterative Learning Algorithm for Boundary Control of a Flexible Manipulator. Int. J. Adapt. Control Signal Process. 2017, 31, 903–916. [Google Scholar] [CrossRef]
- Wang, C.; Zheng, M.; Wang, Z.; Peng, C.; Tomizuka, M. Robust Iterative Learning Control for Vibration Suppression of Industrial Robot Manipulators. J. Dyn. Syst. Meas. Control 2018, 140, 11003. [Google Scholar] [CrossRef]
- Pisarski, D.; Jankowski, Ł. Reinforcement Learning-based Control to Suppress the Transient Vibration of Semi-active Structures Subjected to Unknown Harmonic Excitation. Comput.-Aided Civ. Infrastruct. Eng. 2023, 38, 1605–1621. [Google Scholar] [CrossRef]
- Qiu, Z.; Yang, Y.; Zhang, X. Reinforcement Learning Vibration Control of a Multi-Flexible Beam Coupling System. Aerosp. Sci. Technol. 2022, 129, 107801. [Google Scholar] [CrossRef]
- Crespo, L.G.; Kenny, S.P. Reliability-Based Control Design for Uncertain Systems. J. Guid. Control Dyn. 2005, 28, 649–658. [Google Scholar] [CrossRef]
- Li, Y.; Xu, M.; Chen, J.; Wang, X. Nonprobabilistic Reliable LQR Design Method for Active Vibration Control of Structures with Uncertainties. AIAA J. 2018, 56, 2443–2454. [Google Scholar] [CrossRef]
- Yang, C.; Lu, W.; Xia, Y. Positioning Accuracy Analysis of Industrial Robots Based on Non-Probabilistic Time-Dependent Reliability. IEEE Trans. Reliab. 2024, 73, 608–621. [Google Scholar] [CrossRef]
- Gorla, A.; Serkies, P. Comparative Study of Analytical Model Predictive Control and State Feedback Control for Active Vibration Suppression of Two-Mass Drive. Actuators 2025, 14, 254. [Google Scholar] [CrossRef]
- Li, H.; Shi, Y. Distributed Receding Horizon Control of Large-Scale Nonlinear Systems: Handling Communication Delays and Disturbances. Automatica 2014, 50, 1264–1271. [Google Scholar] [CrossRef]
- Li, H.; Shi, Y. Robust Distributed Model Predictive Control of Constrained Continuous-Time Nonlinear Systems: A Robustness Constraint Approach. IEEE Trans. Autom. Control 2014, 59, 1673–1678. [Google Scholar] [CrossRef]
- Scokaert, P.O.M.; Mayne, D.Q. Min-Max Feedback Model Predictive Control for Constrained Linear Systems. IEEE Trans. Autom. Control 1998, 43, 1136–1142. [Google Scholar] [CrossRef]
- Kerrigan, E.C.; Maciejowski, J.M. Feedback Min-max Model Predictive Control Using a Single Linear Program: Robust Stability and the Explicit Solution. Int. J. Robust Nonlinear Control 2004, 14, 395–413. [Google Scholar] [CrossRef]
- Raković, S.V.; Kouvaritakis, B.; Cannon, M.; Panos, C. Fully Parameterized Tube Model Predictive Control: FULLY PARAMETERIZED TUBE MPC. Int. J. Robust Nonlinear Control 2012, 22, 1330–1361. [Google Scholar] [CrossRef]
- Kohler, J.; Soloperto, R.; Muller, M.A.; Allgower, F. A Computationally Efficient Robust Model Predictive Control Framework for Uncertain Nonlinear Systems. IEEE Trans. Autom. Control 2021, 66, 794–801. [Google Scholar] [CrossRef]
- Mayne, D.Q.; Kerrigan, E.C.; Falugi, P. Robust Model Predictive Control: Advantages and Disadvantages of Tube-Based Methods. IFAC Proc. Vol. 2011, 44, 191–196. [Google Scholar] [CrossRef]
- Hajiloo, A.; Xie, W.F. The Stochastic Robust Model Predictive Control of Shimmy Vibration in Aircraft Landing Gears: The Stochastic Robust Model Predictive Control. Asian J. Control 2015, 17, 476–485. [Google Scholar] [CrossRef]
- Schildbach, G.; Calafiore, G.C.; Fagiano, L.; Morari, M. Randomized Model Predictive Control for Stochastic Linear Systems. In Proceedings of the 2012 American Control Conference (ACC), Montreal, QC, Canada, 27–29 June 2012; IEEE: New York, NY, USA, 2012; pp. 417–422. [Google Scholar]
- Mesbah, A. Stochastic Model Predictive Control: An Overview and Perspectives for Future Research. IEEE Control Syst. 2016, 36, 30–44. [Google Scholar] [CrossRef]
- Dai, L.; Yu, Y.; Zhai, D.-H.; Huang, T.; Xia, Y. Robust Model Predictive Tracking Control for Robot Manipulators with Disturbances. IEEE Trans. Ind. Electron. 2021, 68, 4288–4297. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, S.; Peng, H.; Chen, B.; Zhang, H. A Novel Fast Model Predictive Control for Large-Scale Structures. J. Vib. Control 2017, 23, 2190–2205. [Google Scholar] [CrossRef]
- Wang, E.; Wu, S.; Xun, G.; Liu, Y.; Wu, Z. Active Vibration Suppression for Large Space Structure Assembly: A Distributed Adaptive Model Predictive Control Approach. J. Vib. Control 2021, 27, 365–377. [Google Scholar] [CrossRef]
- Dubay, R.; Hassan, M.; Li, C.; Charest, M. Finite Element Based Model Predictive Control for Active Vibration Suppression of a One-Link Flexible Manipulator. ISA Trans. 2014, 53, 1609–1619. [Google Scholar] [CrossRef] [PubMed]
- Alessio, A.; Bemporad, A. A Survey on Explicit Model Predictive Control. In Nonlinear Model Predictive Control: Towards New Challenging Applications; Magni, L., Raimondo, D.M., Allgöwer, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 345–369. ISBN 978-3-642-01094-1. [Google Scholar]
- Takács, G.; Rohal’-Ilkiv, B. MPC Implementation for Vibration Control. In Model Predictive Vibration Control; Springer: London, UK, 2012; pp. 361–389. ISBN 978-1-4471-2332-3. [Google Scholar]
- Gulan, M.; Takács, G.; Nguyen, N.A.; Olaru, S.; Rodríguez-Ayerbe, P.; Rohal’-Ilkiv, B. Efficient Embedded Model Predictive Vibration Control via Convex Lifting. IEEE Trans. Control Syst. Technol. 2019, 27, 48–62. [Google Scholar] [CrossRef]
- Bemporad, A.; Oliveri, A.; Poggi, T.; Storace, M. Ultra-Fast Stabilizing Model Predictive Control via Canonical Piecewise Affine Approximations. IEEE Trans. Autom. Control 2011, 56, 2883–2897. [Google Scholar] [CrossRef]
- Parisini, T.; Zoppoli, R. A Receding-Horizon Regulator for Nonlinear Systems and a Neural Approximation. Automatica 1995, 31, 1443–1451. [Google Scholar] [CrossRef]
- Aslam, S.; Chak, Y.-C.; Jaffery, M.H.; Varatharajoo, R.; Razoumny, Y. Deep Learning Based Fuzzy-MPC Controller for Satellite Combined Energy and Attitude Control System. Adv. Space Res. 2024, 74, 3234–3255. [Google Scholar] [CrossRef]
- Gómez, P.I.; Gajardo, M.E.L.; Mijatovic, N.; Dragičević, T. Enhanced Imitation Learning of Model Predictive Control through Importance Weighting. IEEE Trans. Ind. Electron. 2024, 72, 4073–4083. [Google Scholar] [CrossRef]
- Wen, C.; Ma, X.; Erik Ydstie, B. Analytical Expression of Explicit MPC Solution via Lattice Piecewise-Affine Function. Automatica 2009, 45, 910–917. [Google Scholar] [CrossRef]
- Cseko, L.H.; Kvasnica, M.; Lantos, B. Explicit MPC-Based RBF Neural Network Controller Design with Discrete-Time Actual Kalman Filter for Semiactive Suspension. IEEE Trans. Control Syst. Technol. 2015, 23, 1736–1753. [Google Scholar] [CrossRef]
- Hertneck, M.; Kohler, J.; Trimpe, S.; Allgower, F. Learning an Approximate Model Predictive Controller with Guarantees. IEEE Control Syst. Lett. 2018, 2, 543–548. [Google Scholar] [CrossRef]
- Li, Y.; Hua, K.; Cao, Y. Using Stochastic Programming to Train Neural Network Approximation of Nonlinear MPC Laws. Automatica 2022, 146, 110665. [Google Scholar] [CrossRef]
- Ben-Haim, Y. A Non-Probabilistic Concept of Reliability. Struct. Saf. 1994, 14, 227–245. [Google Scholar] [CrossRef]
- Jiang, C.; Li, J.W.; Ni, B.Y.; Fang, T. Some Significant Improvements for Interval Process Model and Non-Random Vibration Analysis Method. Comput. Methods Appl. Mech. Eng. 2019, 357, 112565. [Google Scholar] [CrossRef]
- Du, H.; Zhang, N.; Naghdy, F. Actuator Saturation Control of Uncertain Structures with Input Time Delay. J. Sound Vib. 2011, 330, 4399–4412. [Google Scholar] [CrossRef]
- Gong, J.; Wang, X. Reliable Model Predictive Vibration Control for Structures with Nonprobabilistic Uncertainties. Struct. Control Health Monit. 2024, 2024, 7596923. [Google Scholar] [CrossRef]
- Karg, B.; Lucia, S. Reinforced Approximate Robust Nonlinear Model Predictive Control. In Proceedings of the 2021 23rd International Conference on Process Control (PC), Strbske Pleso, Slovakia, 1–4 June 2021; IEEE: New York, NY, USA, 2021; pp. 149–156. [Google Scholar]
- Liu, Z.; Ji, H.; Wu, Y.; Zhang, C.; Tao, C.; Qiu, J. Design of a High-Voltage Miniaturized Control System for Macro Fiber Composites Actuators. Actuators 2024, 13, 509. [Google Scholar] [CrossRef]
- Yang, C. Interval Riccati Equation-Based and Non-Probabilistic Dynamic Reliability-Constrained Multi-Objective Optimal Vibration Control with Multi-Source Uncertainties. J. Sound Vib. 2025, 595, 118742. [Google Scholar] [CrossRef]






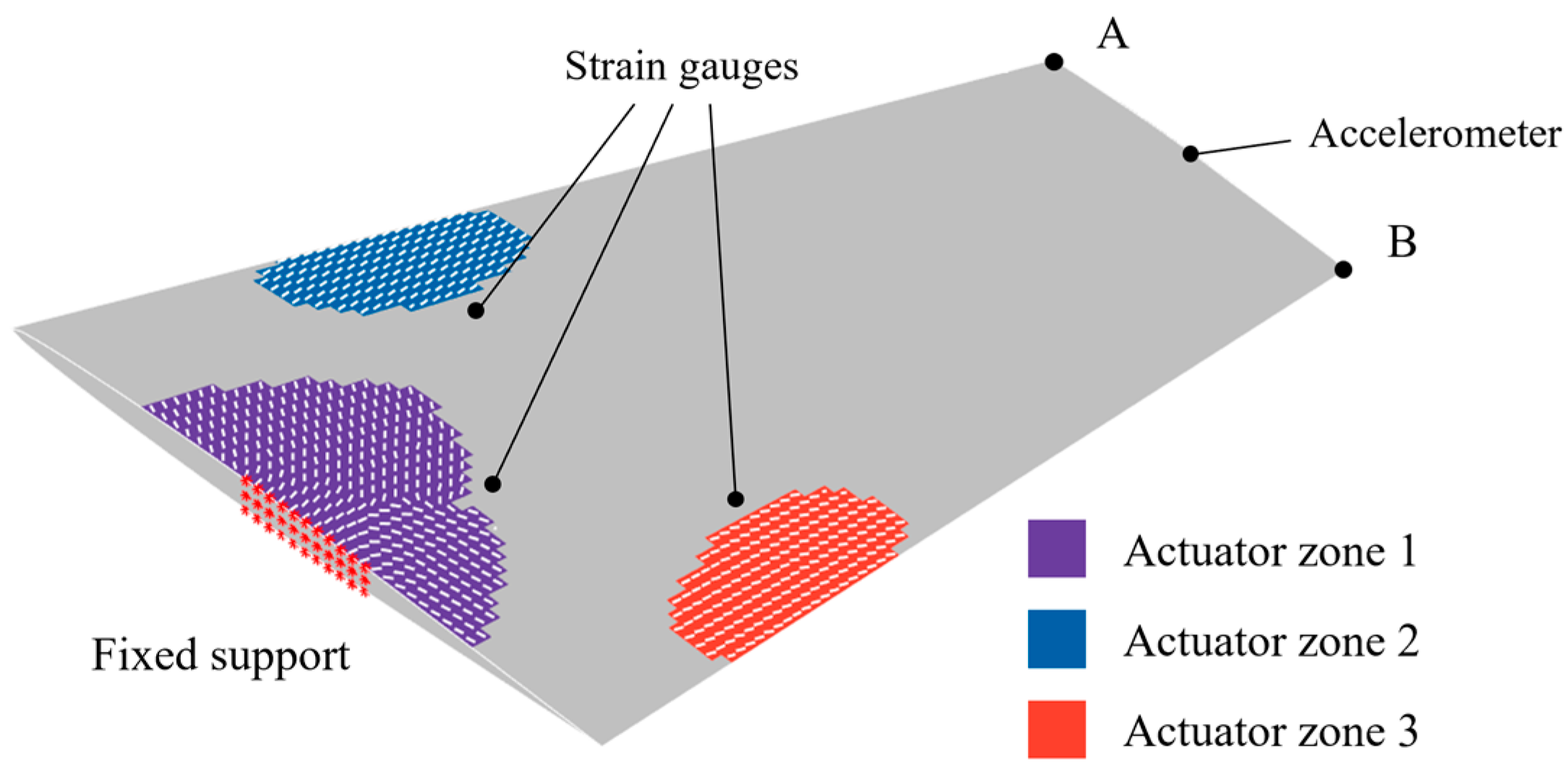
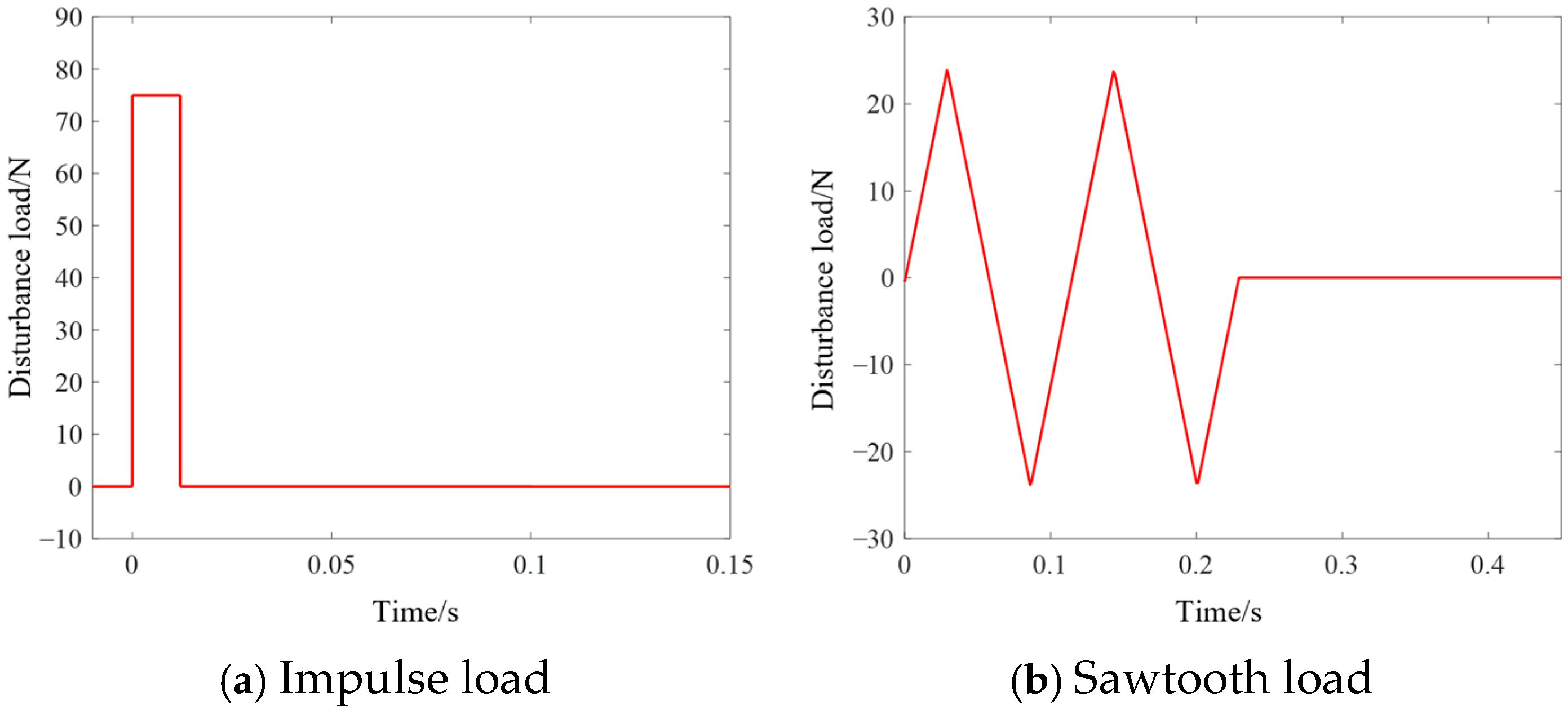
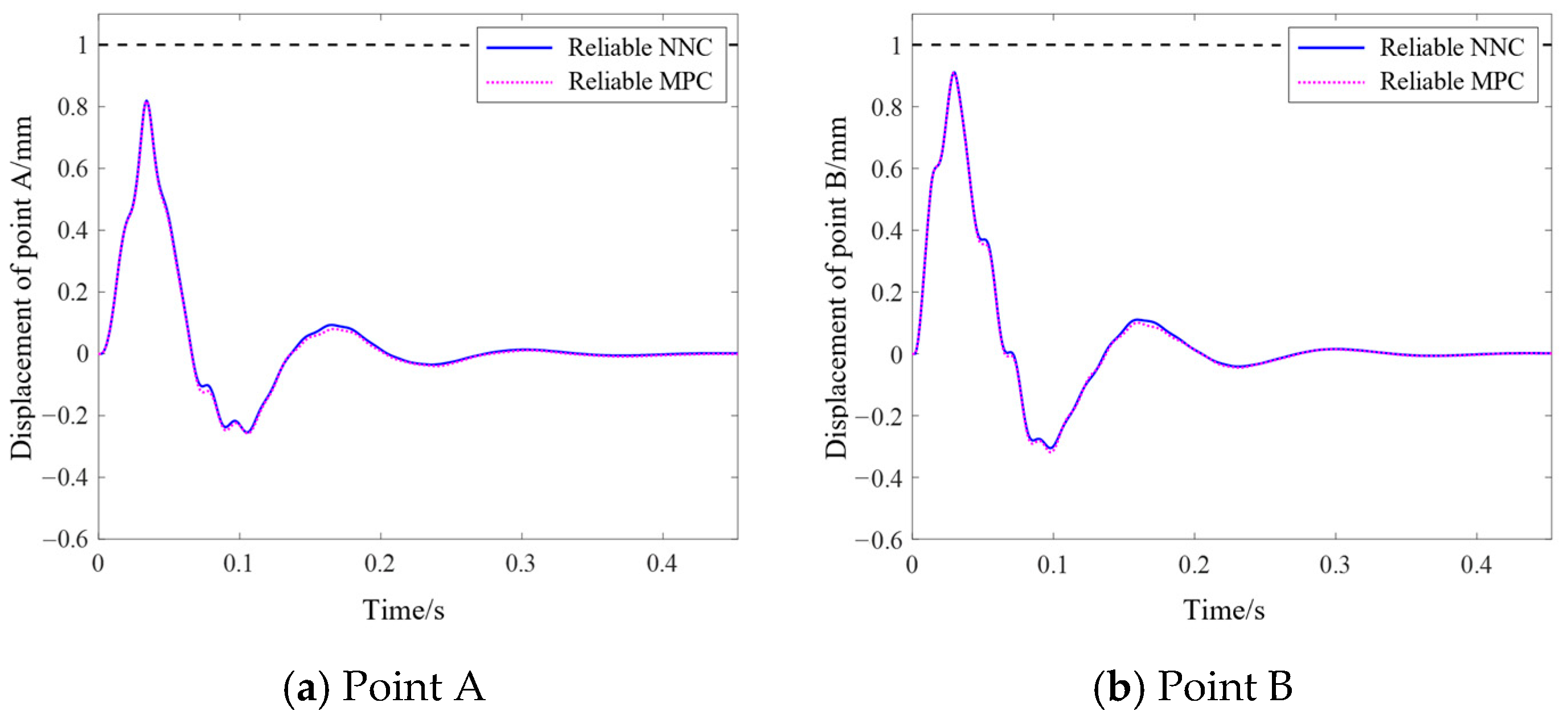
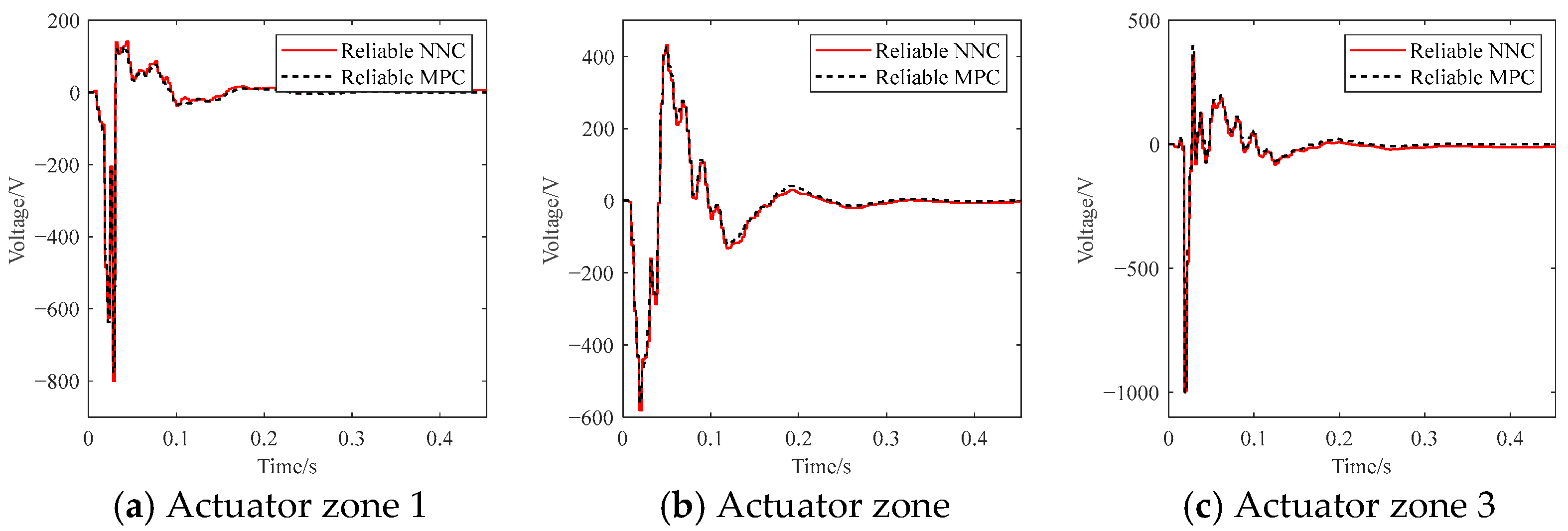
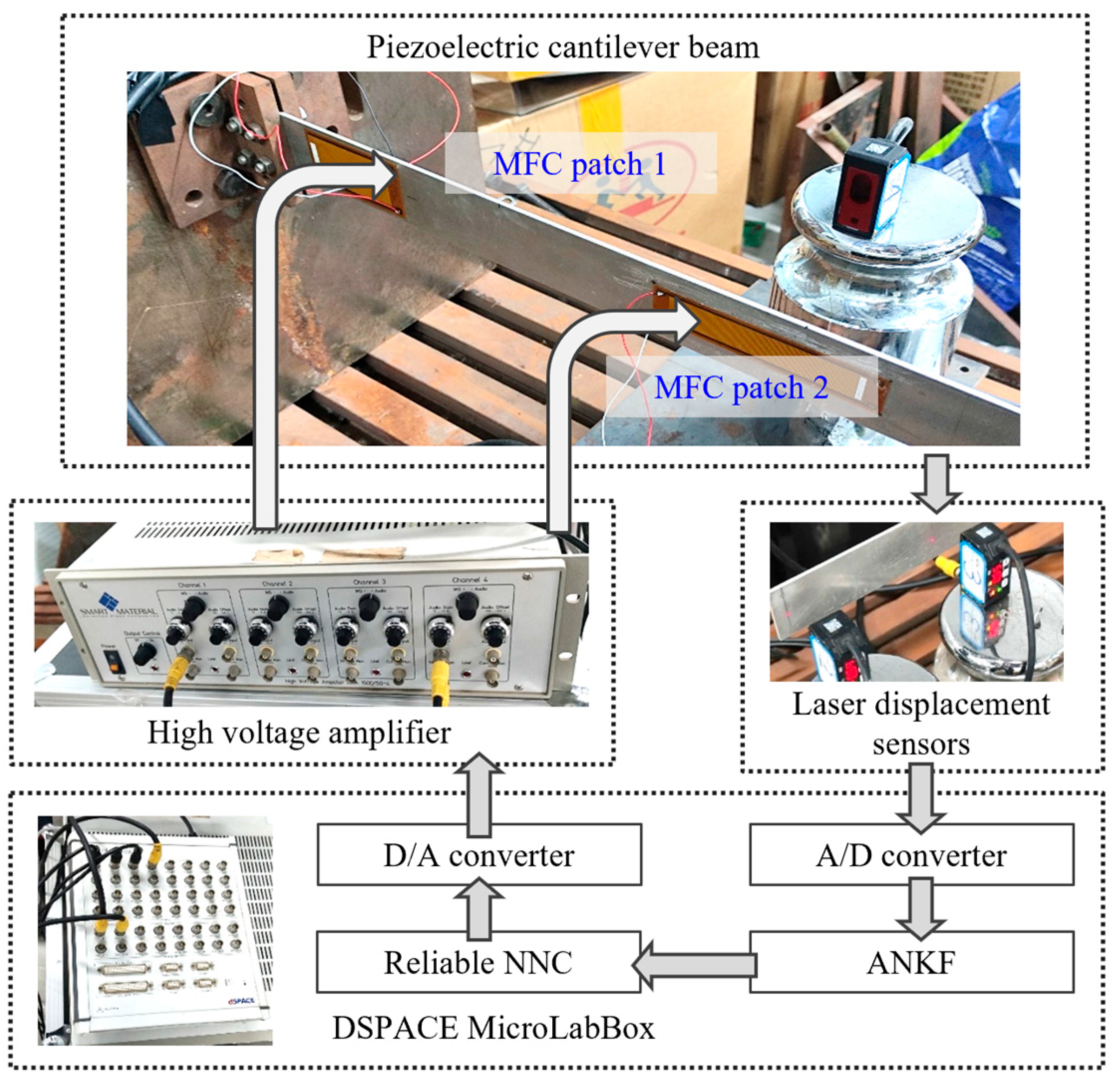

| Length/mm | Width/mm | Thickness/mm | |
|---|---|---|---|
| Host structure | 600 | 40 | 2.5 |
| MFC patch-1 | 56 | 28 | 0.3 |
| MFC patch-2 | 43 | 12 | 0.3 |
| The Number of Neurons per Layer | 20 | 30 | 40 | 50 | 60 |
|---|---|---|---|---|---|
| RMSE | 9.4986 | 7.5063 | 5.6120 | 8.3075 | 10.4610 |
| Amplitude of Impulse Load/N | Nonprobabilistic Reliability | |||
|---|---|---|---|---|
| Reliable NNC | Reliable MPC | Nominal MPC | Reliability-Based State Feedback Control [52] | |
| 0.35 | 1 | 1 | 1 | 1 |
| 0.375 | 1 | 1 | 1 | 1 |
| 0.4 | 1 | 1 | 0.9368 | 0.9804 |
| 0.425 | 1 | 0.9942 | 0.5427 | 0.5410 |
| 0.45 | 1 | 0.9874 | 0.4667 | 0.1710 |
| 0.475 | 0.9934 | 0.9825 | 0.5337 | 0 |
| 0.5 | 0.9862 | 0.9802 | 0.5851 | 0 |
| 0.525 | 0.7567 | 0.5896 | 0.4996 | 0 |
| 0.55 | 0.4658 | 0.3873 | 0.3383 | 0 |
| Method | Online Computation | Offline Computation | Reliability |
|---|---|---|---|
| Reliable NNC | Forward propagation of neural network, fast | None | More conservative than reliable MPC |
| Reliable MPC | Reliability-based optimization, slow | Sample generation and neural network training | Reliability assurance within actuator operational limits |
| Nominal MPC | Deterministic optimization, fast | None | Low reliability |
| Reliability-based state feedback control [52] | Multiply operation, fast | Reliability-based optimization | High-reliability only for design load Case |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, J.; Wang, X. Reliable Neural Network Control for Active Vibration Suppression of Uncertain Structures. Actuators 2025, 14, 402. https://doi.org/10.3390/act14080402
Gong J, Wang X. Reliable Neural Network Control for Active Vibration Suppression of Uncertain Structures. Actuators. 2025; 14(8):402. https://doi.org/10.3390/act14080402
Chicago/Turabian StyleGong, Jinglei, and Xiaojun Wang. 2025. "Reliable Neural Network Control for Active Vibration Suppression of Uncertain Structures" Actuators 14, no. 8: 402. https://doi.org/10.3390/act14080402
APA StyleGong, J., & Wang, X. (2025). Reliable Neural Network Control for Active Vibration Suppression of Uncertain Structures. Actuators, 14(8), 402. https://doi.org/10.3390/act14080402







