A Novel Kinematic Calibration Method for Industrial Robots Based on the Improved Grey Wolf Optimization Algorithm
Abstract
1. Introduction
2. Kinematic Error Parameter Calibration Model
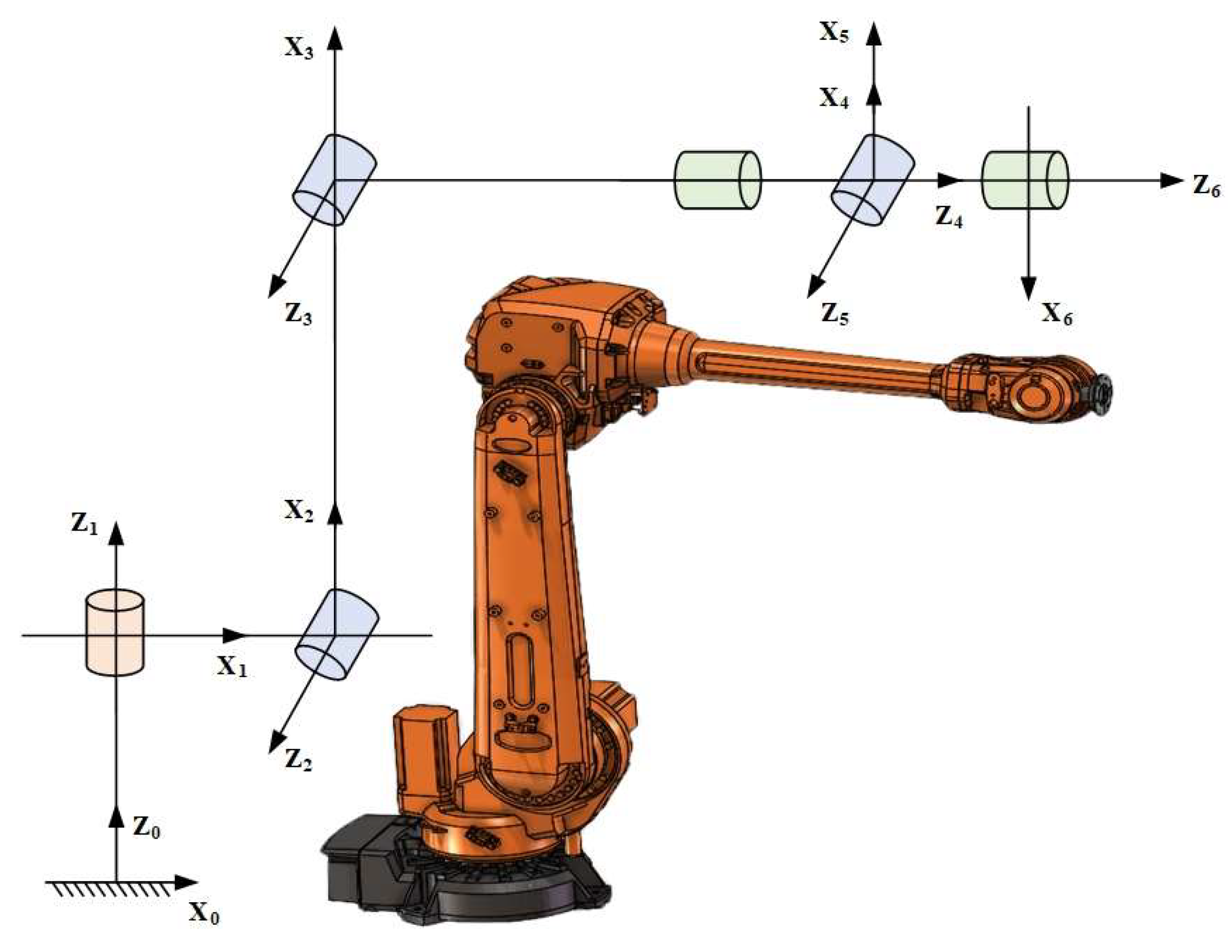
2.1. Kinematic Model of Industrial Robot
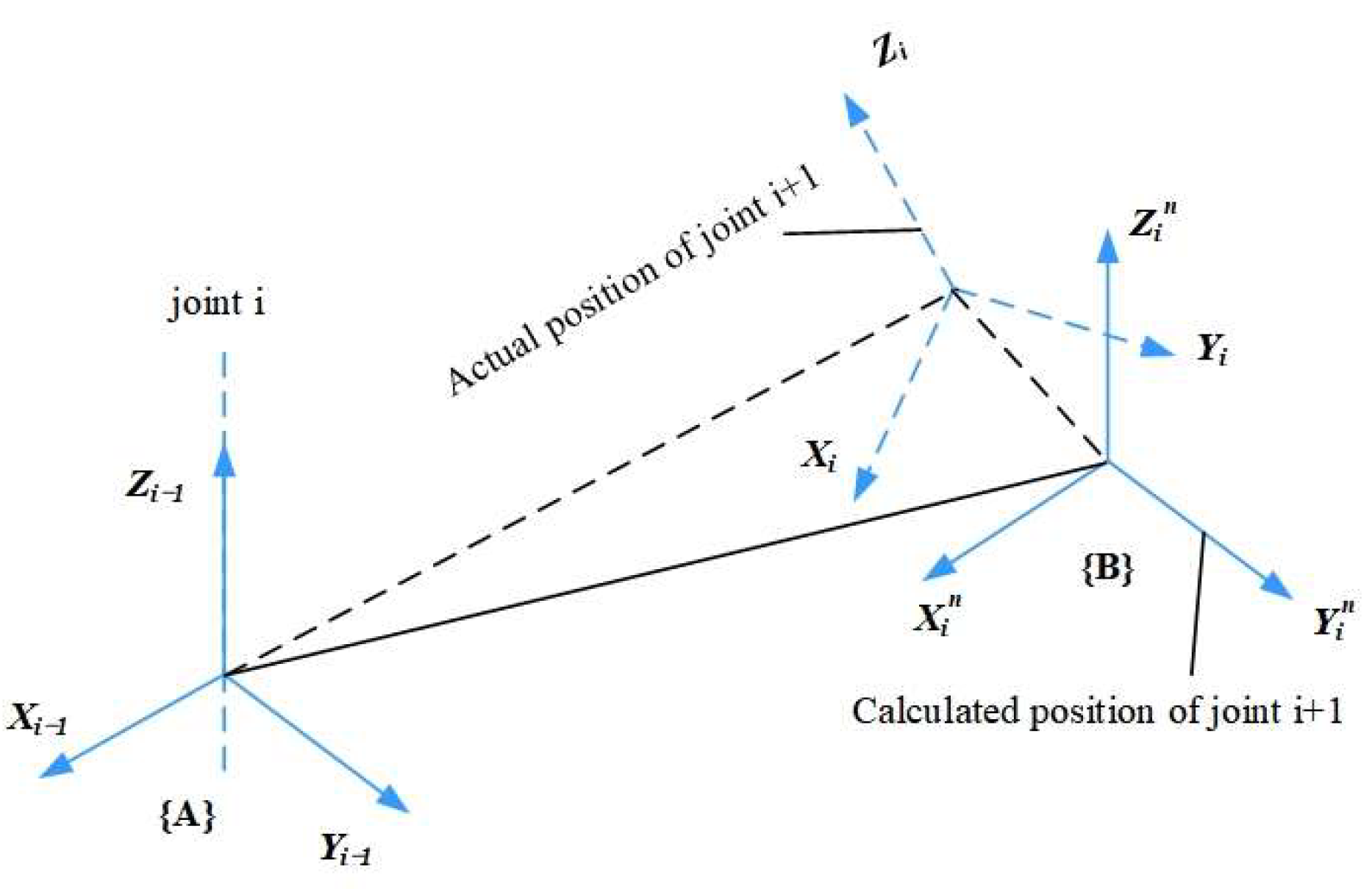
2.2. Error Model
2.3. Optimization Problem and Fitness Function
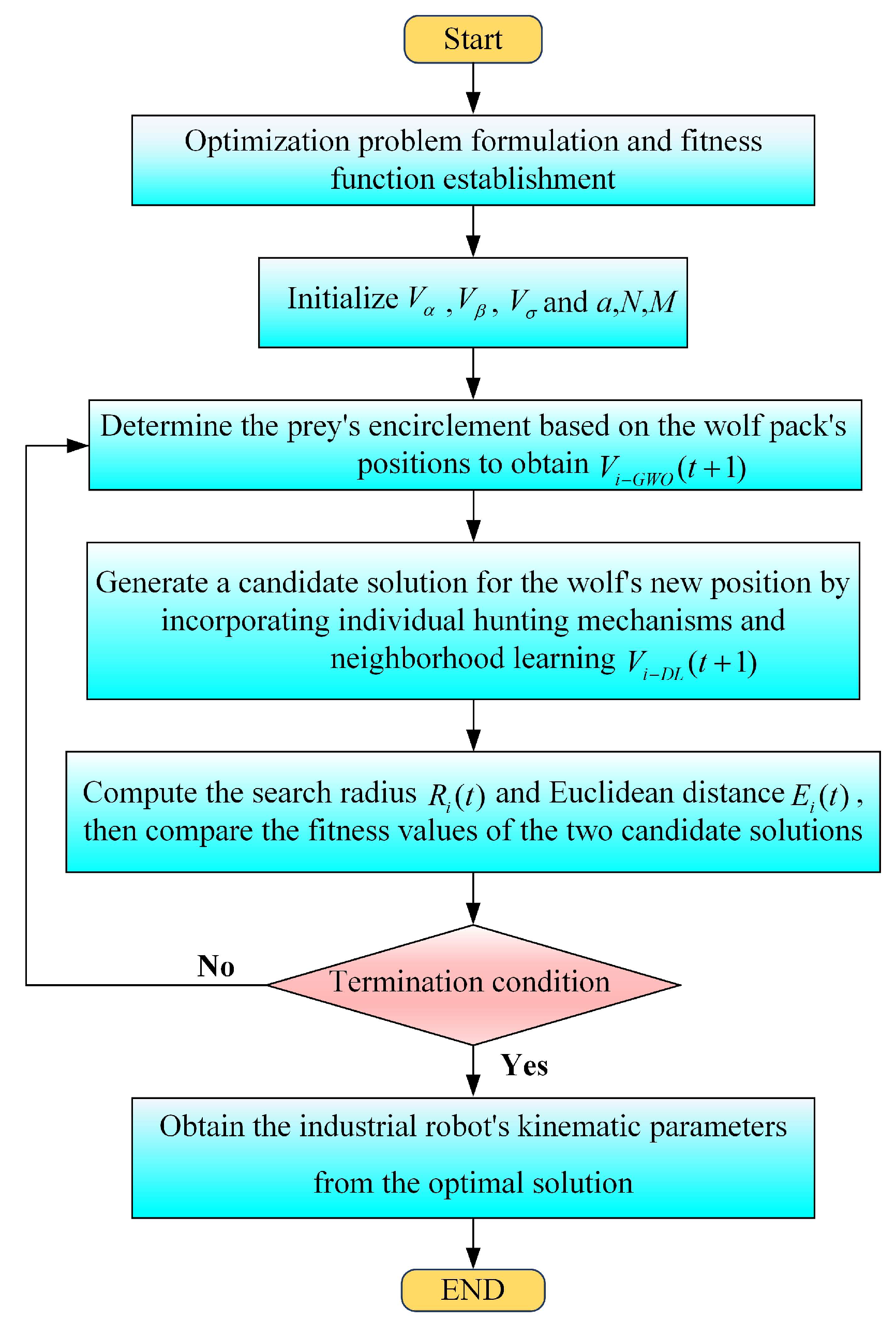
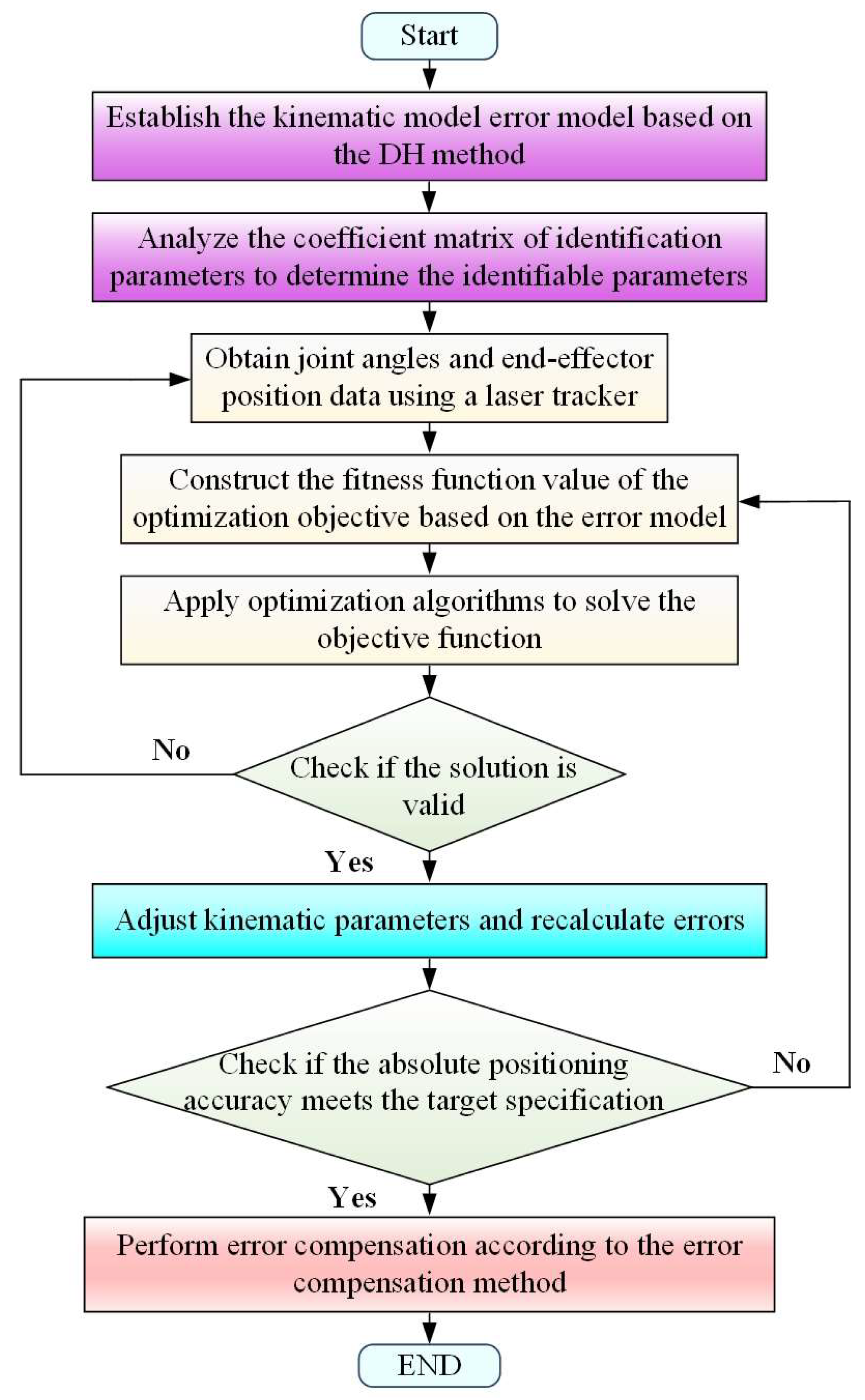
3. Robot Calibration Method Based on IGWO
3.1. Introduction to the GWO Algorithm
3.2. Improvements to GWO for Kinematic Calibration
- (1)
- Improvements to the initialization phase.
- (2)
- Improvements to the boundary-processing strategy.
- (3)
- Improvements to parameters update strategy.
4. Error Compensation Experiment
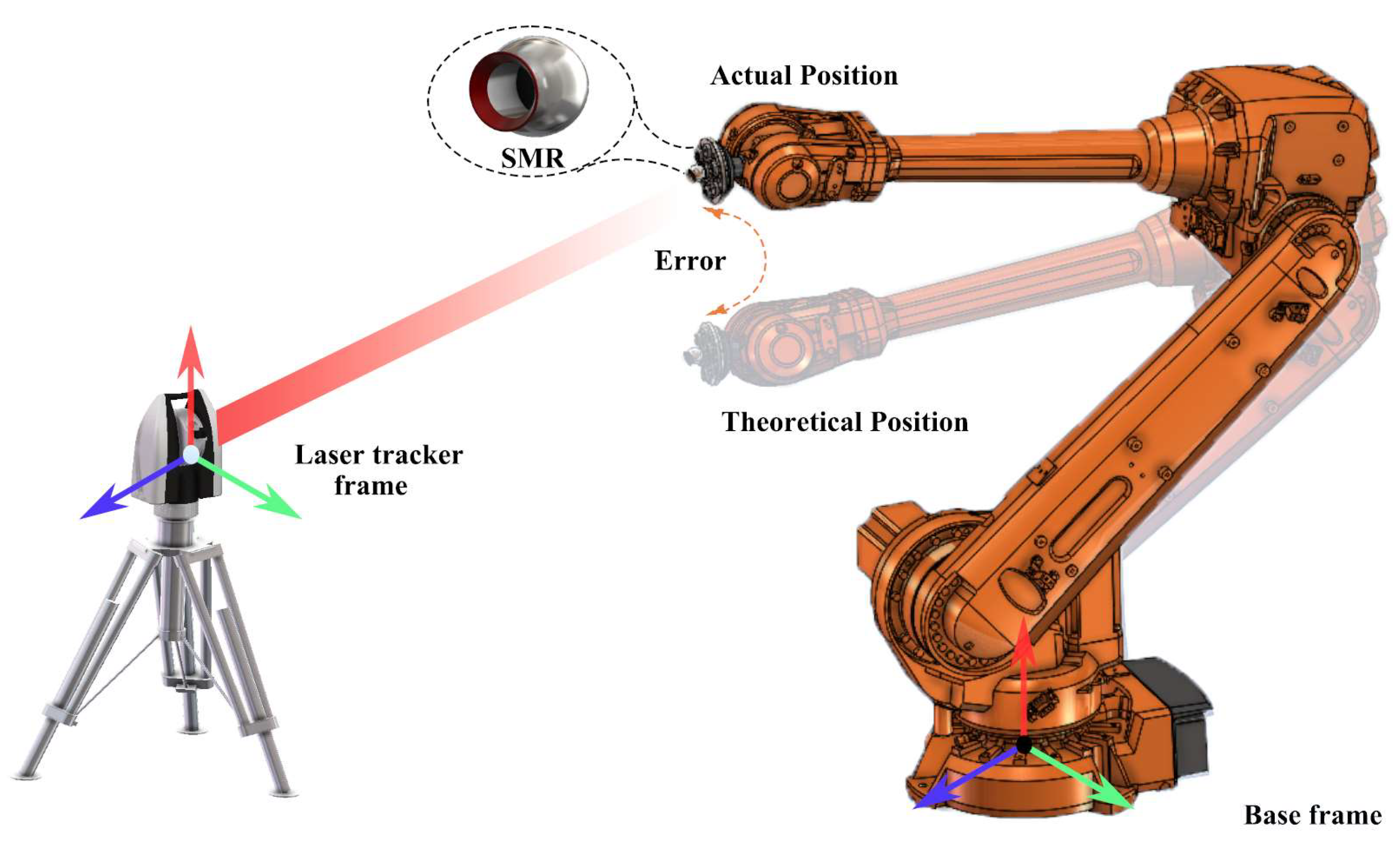
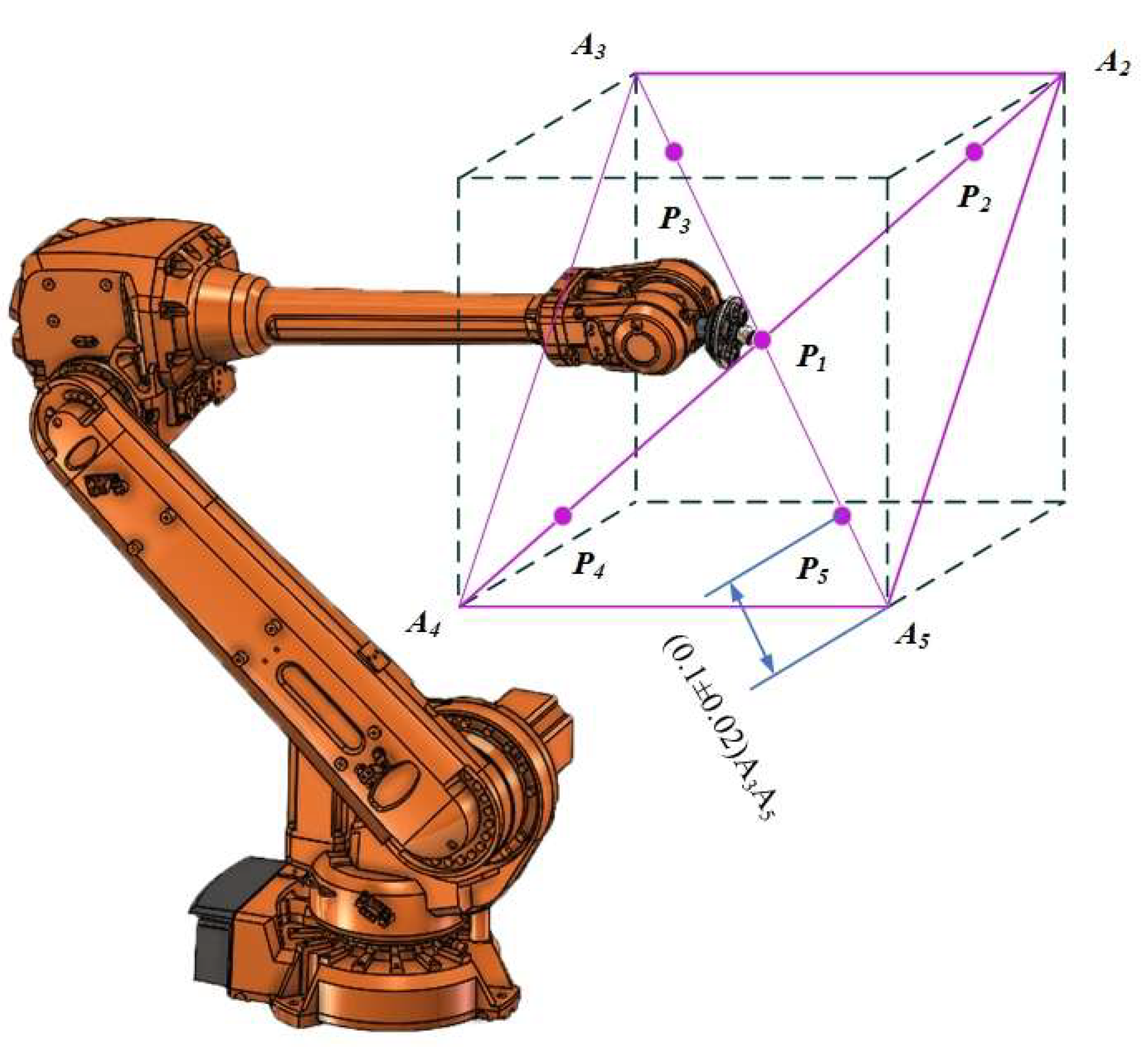
4.1. Experimental Instruments
4.2. Experimental Setup
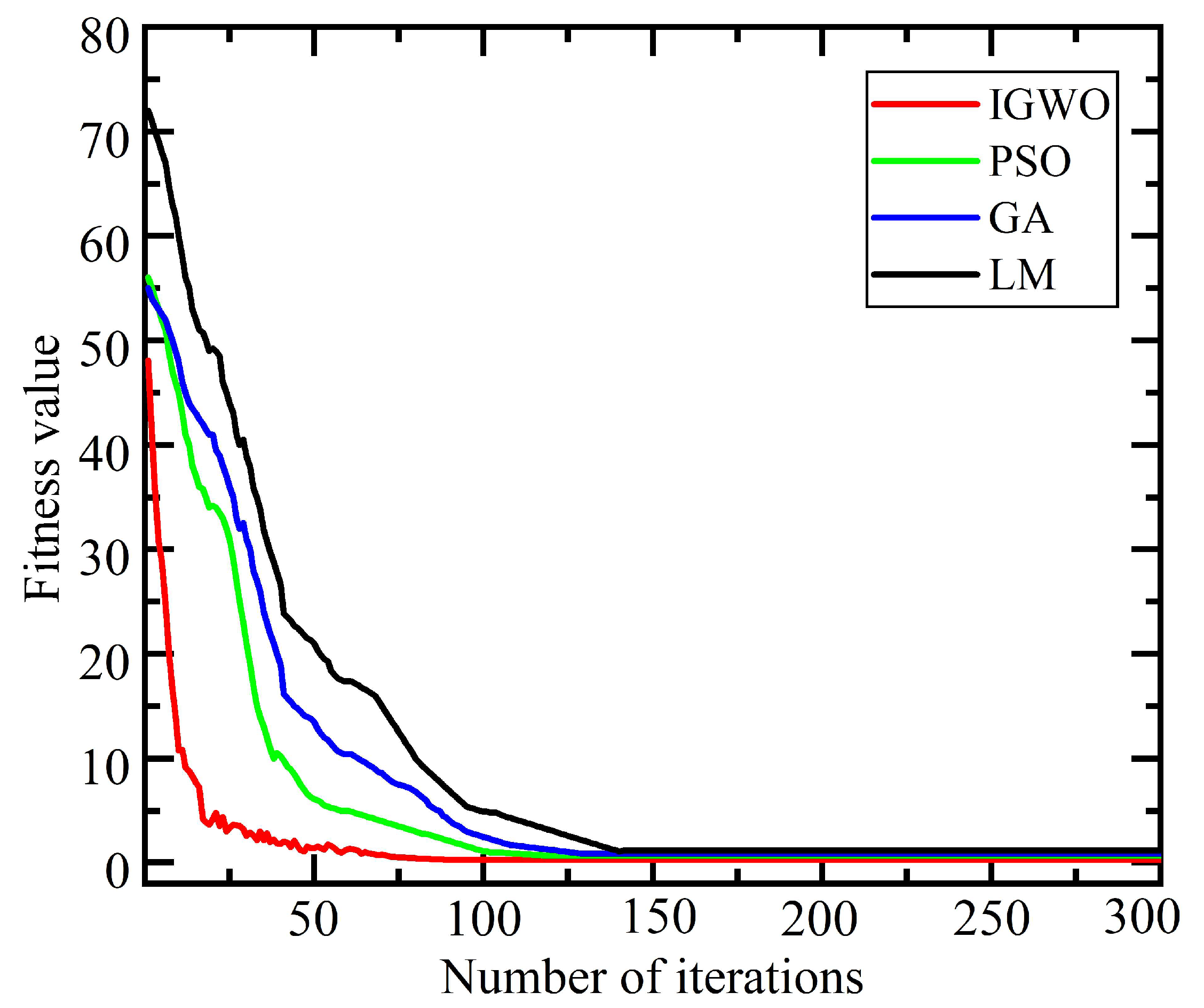
4.3. Parameter Identification
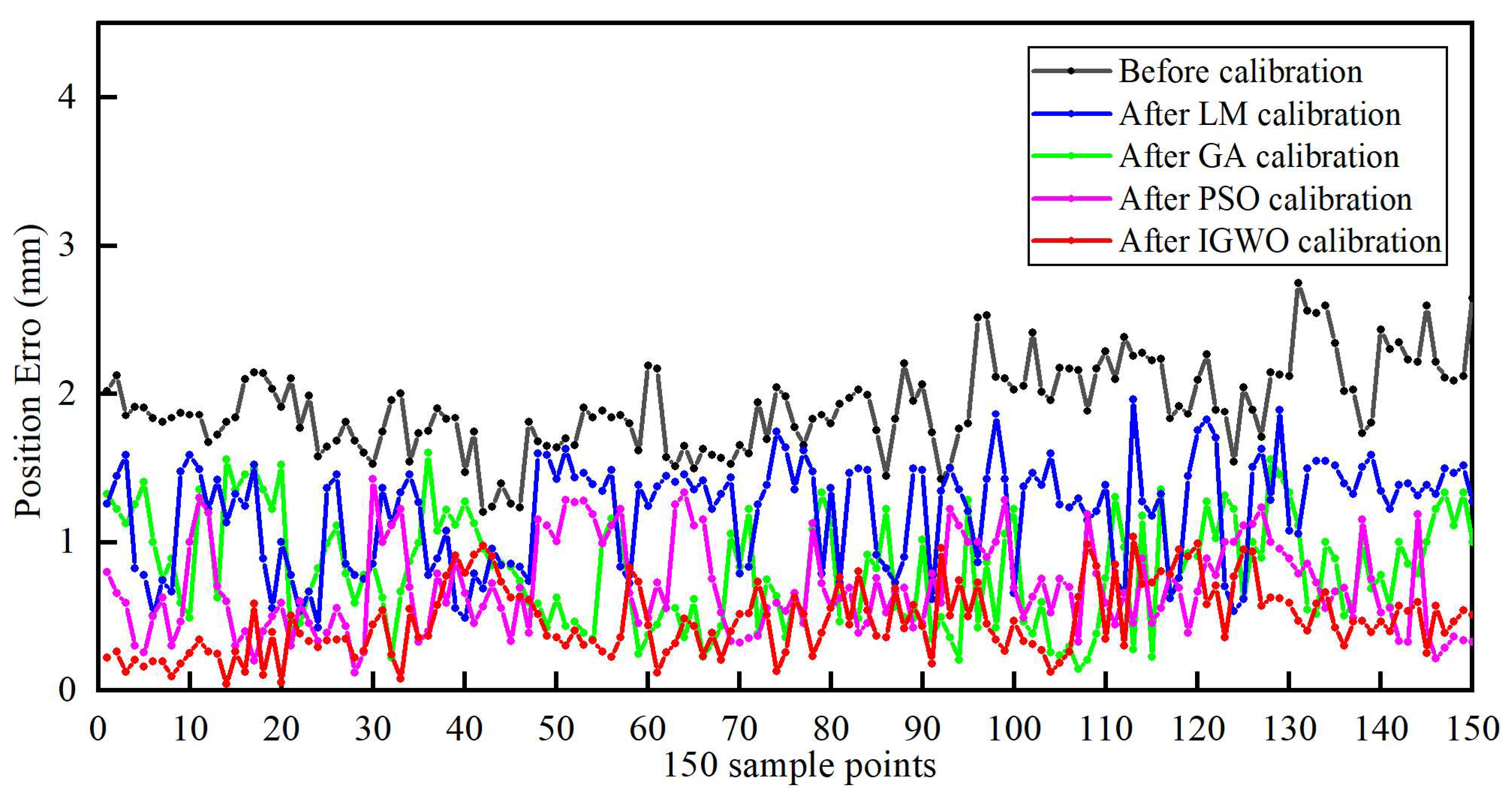
4.4. Error Compensation Verification
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, L.; Gao, W.; Lu, D.; Zeng, D.; Lei, P.; Yu, J.; Tang, M. Robotic simple and fast drilling system for automated aircraft assembly. Int. J. Adv. Manuf. Technol. 2022, 122, 411–426. [Google Scholar] [CrossRef]
- Ma, F.; Cao, W.; Luo, Y.; Qiu, Y. The review of manufacturing technology for aircraft structural part. Procedia CIRP 2016, 56, 594–598. [Google Scholar] [CrossRef][Green Version]
- Frommknecht, A.; Kuehnle, J.; Effenberger, I.; Pidan, S. Multi-sensor measurement system for robotic drilling. Robot. Comput. Integr. Manuf. 2017, 47, 4–10. [Google Scholar] [CrossRef]
- Liu, Y.; Zhuang, Z.; Li, Y. Closed-loop kinematic calibration of robots using a six-point measuring device. IEEE Trans. Instrum. Meas. 2022, 71, 1–12. [Google Scholar] [CrossRef]
- Lin, Y.; Zhao, H.; Ding, H. Spindle configuration analysis and optimization considering the deformation in robotic machining applications. Robot. Comput. Integr. Manuf. 2018, 54, 83–95. [Google Scholar] [CrossRef]
- Olsson, T.; Haage, M.; Kihlman, H.; Johansson, R.; Nilsson, K.; Robertsson, A.; Brogardh, T. Cost-efficient drilling using industrial robots with high-bandwidth force feedback. Robot. Comput. Integr. Manuf. 2010, 26, 24–38. [Google Scholar] [CrossRef]
- Xu, H.; Xue, J.; Guo, G.; Liu, Y.; Liu, M.; Zhang, D. Stiffness optimization of a robotic drilling system for enhanced accuracy in aerospace assembly. Actuators 2025, 14, 86. [Google Scholar] [CrossRef]
- Li, Z.; Tian, W.; Wang, M.; Li, B.; Liao, W. Positioning error compensation of a flexible track hybrid robot for aircraft assembly based on response surface methodology and experimental study. Int. J. Adv. Manuf. Technol. 2022, 119, 1313–1330. [Google Scholar] [CrossRef]
- Ma, S.; Deng, K.; Lu, Y.; Xu, X. Robot error compensation based on incremental extreme learning machines and an improved sparrow search algorithm. Int. J. Adv. Manuf. Technol. 2023, 125, 5431–5443. [Google Scholar] [CrossRef]
- Lattanzi, L.; Cristalli, C.; Massa, D.; Boria, S.; Lépine, P.; Pellicciari, M. Geometrical calibration of a 6-axis robotic arm for high accuracy manufacturing task. Int. J. Adv. Manuf. Technol. 2020, 111, 1813–1829. [Google Scholar] [CrossRef]
- Nubiola, A.; Bonev, I.A. Absolute calibration of an ABB IRB 1600 robot using a laser tracker. Robot. Comput. Integr. Manuf. 2013, 29, 236–245. [Google Scholar] [CrossRef]
- Le, P.N.; Kang, H.J. Robot manipulator calibration using a model based identification technique and a neural network with the teaching learning-based optimization. IEEE Access 2020, 8, 105447–105454. [Google Scholar] [CrossRef]
- Roth, Z.; Mooring, B.; Ravani, B. An overview of robot calibration. IEEE J. Robot. Autom. 2003, 3, 377–385. [Google Scholar] [CrossRef]
- Kim, S.H.; Nam, E.; Ha, T.I.; Hwang, S.H.; Lee, J.H.; Park, S.H.; Min, B.K. Robotic machining: A review of recent progress. Int. J. Precis. Eng. Manuf. 2019, 20, 1629–1642. [Google Scholar] [CrossRef]
- Jiang, Z.; Zhou, W.; Li, H.; Mo, Y.; Ni, W.; Huang, Q. A new kind of accurate calibration method for robotic kinematic parameters based on the extended Kalman and particle filter algorithm. IEEE Trans. Ind. Electron. 2017, 65, 3337–3345. [Google Scholar] [CrossRef]
- Gao, G.; Liu, F.; San, H.; Wu, X.; Wang, W. Hybrid Optimal Kinematic Parameter Identification for an Industrial Robot Based on BPNN-PSO. Complexity 2018, 1, 4258676. [Google Scholar] [CrossRef]
- Luo, G.; Zou, L.; Wang, Z.; Lv, C.; Ou, J.; Huang, Y. A novel kinematic parameters calibration method for industrial robot based on Levenberg-Marquardt and Differential Evolution hybrid algorithm. Robot. Comput. Integr. Manuf. 2021, 71, 102165. [Google Scholar] [CrossRef]
- Zhong, H.; Hu, C.; Li, X.; Gao, L.; Zeng, B.; Dong, H. Kinematic calibration method for a two-segment hydraulic leg based on an improved whale swarm algorithm. Robot. Comput. Integr. Manuf. 2019, 59, 361–372. [Google Scholar] [CrossRef]
- Li, Z.; Li, S.; Luo, X. Using quadratic interpolated beetle antennae search to enhance robot arm calibration accuracy. IEEE Robot. Autom. Lett. 2022, 7, 12046–12053. [Google Scholar] [CrossRef]
- Chen, X.; Zhan, Q. The kinematic calibration of an industrial robot with an improved beetle swarm optimization algorithm. IEEE Robot. Autom. Lett. 2022, 7, 4694–4701. [Google Scholar] [CrossRef]
- Zak, G.; Benhabib, B.; Fenton, R.G.; Saban, I. Application of the weighted least squares parameter estimation method to the robot calibration. J. Mech. Des. 1994, 116, 890–893. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Taghian, S.; Mirjalili, S. An improved grey wolf optimizer for solving engineering problems. Expert Syst. Appl. 2021, 166, 113917. [Google Scholar] [CrossRef]
- Messay, T.; Ordóñez, R.; Marcil, E. Computationally efficient and robust kinematic calibration methodologies and their application to industrial robots. Robot. Comput. Integr. Manuf. 2016, 37, 33–48. [Google Scholar] [CrossRef]
- Theissen, N.A.; Laspas, T.; Archenti, A. Closed-force-loop elastostatic calibration of serial articulated robots. Robot. Comput. Integr. Manuf. 2019, 57, 86–91. [Google Scholar] [CrossRef]
- Dehghani, M.; McKenzie, R.A.; Irani, R.A.; Ahmadi, M. Robot-mounted sensing and local calibration for high-accuracy manufacturing. Robot. Comput. Integr. Manuf. 2023, 79, 102429. [Google Scholar] [CrossRef]
- Nubiola, A.; Slamani, M.; Joubair, A.; Bonev, I.A. Comparison of two calibration methods for a small industrial robot based on an optical CMM and a laser tracker. Robotica 2014, 32, 447–466. [Google Scholar] [CrossRef]
- Du, G.; Liang, Y.; Li, C.; Liu, P.X.; Li, D. Online robot kinematic calibration using hybrid filter with multiple sensors. IEEE Trans. Instrum. Meas. 2020, 69, 7092–7107. [Google Scholar] [CrossRef]
- Zhao, G.; Zhang, P.; Ma, G.; Xiao, W. System identification of the nonlinear residual errors of an industrial robot using massive measurements. Robot. Comput. Integr. Manuf. 2019, 59, 104–114. [Google Scholar] [CrossRef]
- Liu, F.; Gao, G.; Na, J.; Zhang, F. L2-Regularization-Based kinematic parameter identification for industrial robots in limited measurement space. Actuators 2025, 14, 144. [Google Scholar] [CrossRef]
- Sun, Y.; Lu, L.; Wu, F.; Xiao, S.; Sha, J.; Zhang, L. Error analysis of a coordinate measuring machine with a 6-DOF industrial robot holding the probe. Actuators 2023, 12, 173. [Google Scholar] [CrossRef]
- Szabo, R.; Ricman, R.S. Robotic arm position computing method in the 2d and 3d spaces. Actuators 2023, 12, 112. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Emary, E.; Zawbaa, H.M.; Grosan, C. Experienced gray wolf optimization through reinforcement learning and neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2017, 29, 681–694. [Google Scholar] [CrossRef] [PubMed]
- Industrial Robots—Performance Criteria and Related Test Methods. Available online: https://openstd.samr.gov.cn/bzgk/gb/newGbInfo?hcno=713D24CC6BC709694DC90BADA7EE9014 (accessed on 12 November 2013).

| Joint i | αi (°) | ai (mm) | di (mm) | θi (°) |
|---|---|---|---|---|
| 1 | −90 | 175 | 495 | 0 |
| 2 | 0 | 1095 | 0 | −90 |
| 3 | −90 | 175 | 0 | 0 |
| 4 | 90 | 0 | 1270 | 0 |
| 5 | −90 | 0 | 0 | 0 |
| 6 | 0 | 0 | 135 | 0 |
| Joint i | αi (rad) | ai (mm) | di (mm) | θi (rad) |
|---|---|---|---|---|
| 1 | −0.4999 | 174.95 | 494.95 | −0.0001 |
| 2 | 0.0003 | 1094.9628 | −0.0499 | −0.4999 |
| 3 | −0.5001 | 174.9509 | −0.0498 | 0.0002 |
| 4 | 0.4996 | −0.05 | 1269.9501 | 0.0007 |
| 5 | −0.4993 | −0.049 | −0.0489 | 0.0001 |
| 6 | −0.049 | −0.051 | 134.9566 | −0.0476 |
| Position Errors (mm) | Mean | Max | STD | |
|---|---|---|---|---|
| Before calibration | 1.918 | 2.747 | 0.348 | |
| After calibration | LM | 1.194 | 1.965 | 0.286 |
| GA | 0.845 | 1.632 | 0.245 | |
| PSO | 0.672 | 1.423 | 0.197 | |
| IGWO | 0.475 | 1.035 | 0.153 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, B.; Yu, J.; Zhang, Y.; Liu, P.; Zhang, Y.; Sun, H.; Jin, P.; Lin, J.; Wang, L. A Novel Kinematic Calibration Method for Industrial Robots Based on the Improved Grey Wolf Optimization Algorithm. Actuators 2025, 14, 403. https://doi.org/10.3390/act14080403
Cao B, Yu J, Zhang Y, Liu P, Zhang Y, Sun H, Jin P, Lin J, Wang L. A Novel Kinematic Calibration Method for Industrial Robots Based on the Improved Grey Wolf Optimization Algorithm. Actuators. 2025; 14(8):403. https://doi.org/10.3390/act14080403
Chicago/Turabian StyleCao, Bingzhang, Jiuwei Yu, Yi Zhang, Peijun Liu, Yifan Zhang, Hongwei Sun, Peng Jin, Jie Lin, and Lei Wang. 2025. "A Novel Kinematic Calibration Method for Industrial Robots Based on the Improved Grey Wolf Optimization Algorithm" Actuators 14, no. 8: 403. https://doi.org/10.3390/act14080403
APA StyleCao, B., Yu, J., Zhang, Y., Liu, P., Zhang, Y., Sun, H., Jin, P., Lin, J., & Wang, L. (2025). A Novel Kinematic Calibration Method for Industrial Robots Based on the Improved Grey Wolf Optimization Algorithm. Actuators, 14(8), 403. https://doi.org/10.3390/act14080403






