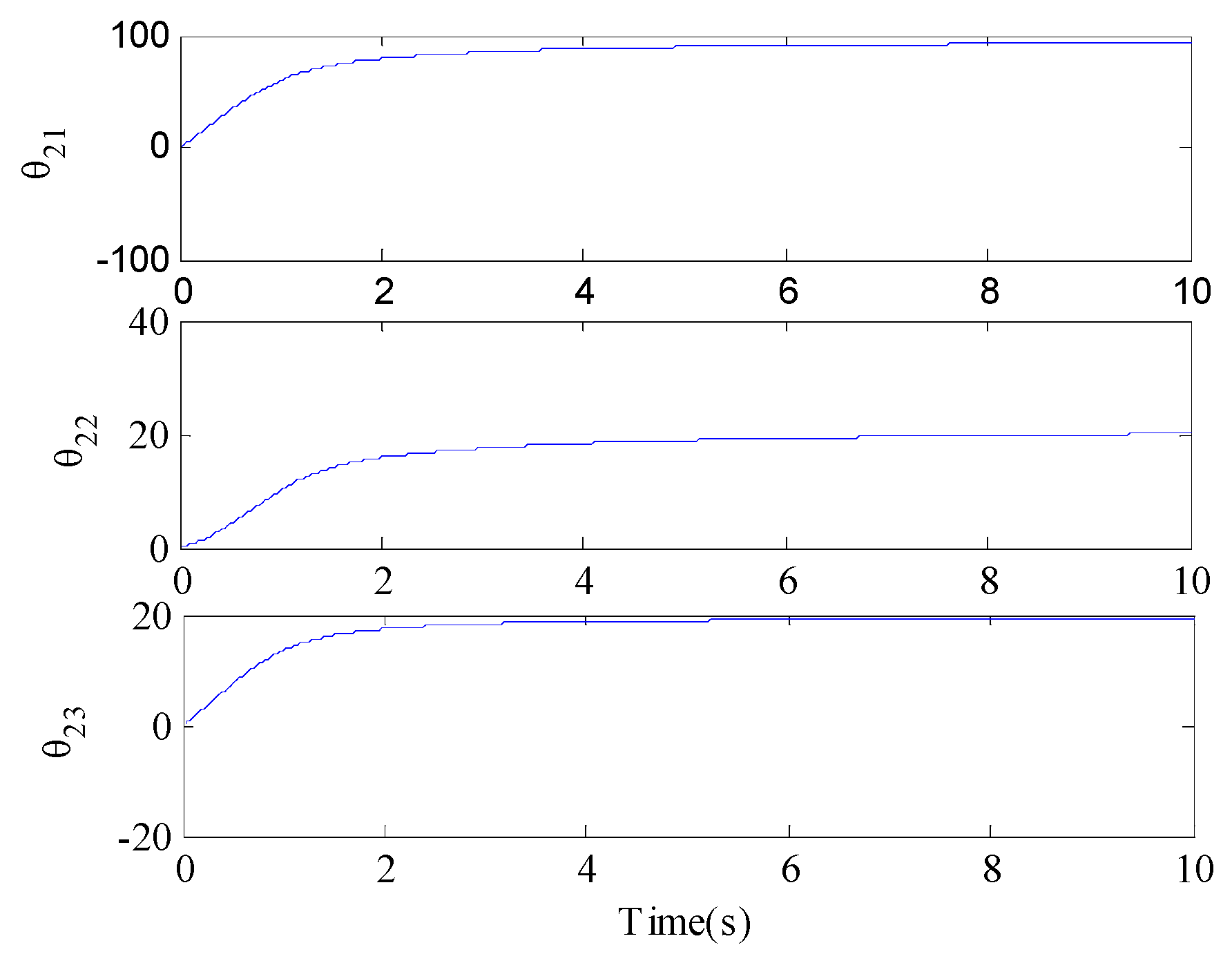Adaptive Robust Stable Tracking Control of Two-Axis Coupled Electromechanical Actuation System Based on Friction Compensation

Abstract

The two-axis coupled electromechanical actuation system (TCEAS) is widely utilized in multiple industrial fields, but its tracking performance and stability are severely hampered by complex nonlinear friction, parameter uncertainties, and strong coupling effects. To address these issues, this paper proposes an adaptive robust stable tracking control (ARSTC) method with friction compensation. First, the friction characteristic of TCEAS is analyzed and a continuously differentiable friction moment function is introduced to accurately describe the nonlinear friction phenomenon. Then, a dynamic analysis model for the system considering friction nonlinearity and model uncertainty is established. Furthermore, the developed ARSTC algorithm leverages adaptive control to estimate and compensate unknown friction parameters (enhancing precision) and robust control to suppress disturbances (ensuring stability). Finally, the superiority is jointly verified by stability analysis and extensive comparative numerical test results. This work demonstrates a practical approach for high-precision control of TCEAS, which has important theoretical significance.

1. Introduction

Two-axis coupled electromechanical actuation systems (TCEAS) have become indispensable components in a wide range of industrial applications, including aerospace, robotics, and weapon aiming [1,2,3]. These systems are responsible for precisely controlling the bidirectional movement and positioning of mechanical components, which directly impacts the overall performance and efficiency of the equipment. For instance, in aerospace applications, accurate control of two-axis actuators ensures the stable operation of aircraft control surfaces and satellite pointing mechanisms [4]; in robotics, they enable robots to perform complex tasks with high precision [5]; in weapon aiming, they can ensure that the firing system maintains precise aiming in terms of orientation and pitch during movement [6]. However, the performance of TCEAS is significantly compromised by several challenges. Complex nonlinear friction within the system, such as static friction, coulomb friction, and viscous friction, leads to tracking errors, limit cycles, and even system instability [7]. Parameter uncertainties, arising from manufacturing tolerances, component wear, and environmental changes, further degrade the control accuracy [8]. Additionally, the strong coupling effects between the two axes lead to the relative complexity of achieving excellent robust control of each axis, posing a significant obstacle to realizing high-performance tracking [9].

Over the years, numerous control strategies have been proposed to address these issues. Traditional control methods, such as PID control, have been extensively applied because of their simplicity and ease of implementation [10]. However, PID controllers often struggle to handle complex nonlinearities and uncertainties, resulting in limited control performance. Advanced control techniques, including sliding mode control [11], backstepping control [12], and model predictive control [13], have shown better adaptability to nonlinear systems. Sliding mode control drives motion trajectory for electromechanical actuation systems to the predetermined sliding surface and keeps it stable. It is used to enhance the robustness, enabling accurate tracking of the given expected motion trajectory even when confronted with external force impacts or load changes [14]. However, sliding mode control not only creates unwanted vibrations, but also causes wear and tear on mechanical components such as gears and bearings. This can reduce the life of the equipment and introduce additional errors in the control system that can affect overall performance and stability. Backstepping control decomposes a complex nonlinear system into a series of simpler subsystems and designs Lyapunov functions for each subsystem, guaranteeing overall stability. In the control of multi-axis servo systems, backstepping control has been successfully used to achieve coordinated control of multiple axes [15]. However, as the complexity and order of the system increase, the design process of backstepping control becomes extremely tedious. The design of the controller is both time-consuming and error-prone due to the need to design multiple Lyapunov functions with an ever-increasing number of intermediate variables and computations. Model predictive control predicts the behavior of the controlled object in future finite time domain by solving an optimization problem at each sampling moment [16]. The electromechanical actuation system based on two-axis coupling achieves better tracking performance by optimizing future control actions [17]. However, its control performance depends on the accuracy of the system model. An inaccurate model may lead to poor control effects. In practical engineering, uncertain factors such as nonlinear friction, component wear, and unmodeled dynamics can all affect the modeling of the system.

Furthermore, in the context of developing various high-performance control strategies, many researchers are dedicated to using friction models to suppress the influence of friction nonlinearity in electromechanical actuation systems [18,19], thereby enhancing the controllability effect. Some studies have employed the Dahl friction model [20], LuGre friction model [21], and Stribeck friction model [22] to describe the friction behavior. Although these models can capture certain characteristics of friction, they may not fully represent the complex friction phenomena in TCEAS. Moreover, most existing control methods either focus on single-axis control or do not adequately consider the strong coupling effects between the two axes, limiting their effectiveness in practical TCEAS.

To bridge these gaps, this paper proposes an adaptive robust stable tracking control (ARSTC) method with friction compensation for TCEAS. We make the following contributions: (1) The smoothness property of the hyperbolic tangent function is employed to construct a continuously differentiable friction dynamic function to improve the characterization of friction nonlinearity. Unlike the LuGre model, which introduces internal state variables that complicate multi-axis extension, the proposed hyperbolic tangent-based model avoids such complexity while retaining key friction characteristics. (2) A mathematical dynamic model of the TCEAS considering friction nonlinearity and model uncertainty is established, providing a more realistic basis for controller design. (3) Unlike prior work, our method explicitly distinguishes adaptive and robust roles: adaptation mitigates parametric uncertainties, while robustness handles unmodeled dynamics. The value of the presented method has been rigorously validated through stability analysis and extensive comparisons of co-simulations.

Furthermore, the proposed method is not a simple extension of single-axis control. For a two-axis coupled system, it combines the coupling dynamic model of the mechanical interaction between the two axes and the cross-axis friction effect. This model is based on multi-body system dynamics rather than a simplified derivation based on a single-axis. Through a unified adaptive robust framework, it is used to estimate the coupling friction parameters and suppress the cross-axis interference, thereby solving the problem of mutual interference between the axes. Finally, the stability analysis of the coupled closed-loop system is conducted to ensure that all signals are bounded under the interaction of the two axes. These contributions are unique to TCEAS and cannot be reduced to the results of a single-axis.

The remainder of this paper is organized as follows: Section 2 develops the complete dynamic model of the electromechanical actuation system, including electrical and mechanical subsystems with friction effects. Section 3 presents the adaptive robust controller design with stability proofs. Section 4 details the co-simulation results and comparative analyses. Section 5 discusses practical implications and concludes with future research directions.

2. Mathematical Modeling of TCEAS

2.1. Mathematical Modeling of Mechanical Dynamics

The TCEAS is shown in Figure 1, which consists of two subsystems in the vertical and horizontal directions, each of which is a set comprising an independent power subsystem and a control subsystem.

From Figure 1, m_h and m_a are the masses of the vertical and horizontal subsystems, q_h is the vertical rotation angle of the vertical subsystem with respect to the body of the vehicle, q_a is the horizontal rotation angle of the horizontal subsystem with respect to the body of the vehicle, L_h is the distance from the center of the trunnion to the center of the mouth of the body tube, and L_a is the distance between the center of the horizontal rotation and the center of the trunnion. In modeling the mechanical dynamics of TCEAS, the horizontal subsystem plane is chosen to be the zero potential energy reference position, so that its potential energy is P_a = 0, and the potential energy of the vertical subsystem P_h = 0.5m_hgL_hsinq_h. Then, the kinetic energy in the vertical subsystem and horizontal subsystem is expressed as follows:

$$E_h={\displaystyle \frac{1}{6}}{m}_h{\dot{q}}_a^2(3L_a^2+3L_a{L}_h\cos q_h+L_h^2{\cos }^2{q}_h)+{\displaystyle \frac{1}{6}}{m}_h{L}_h^2{\dot{q}}_h^2$$

(1)

$$E_a={\displaystyle \frac{1}{4}}{m}_a{L}_a^2{\dot{q}}_a^2$$

(2)

where ${\dot{q}}_h$ and ${\dot{q}}_a$ denote the angular velocity of the vertical subsystem and horizontal subsystem rotation.

Combined with the definition of the Lagrange equation

$$K=E_a+E_h-P_a-P_h$$

(3)

Then, the horizontal and vertical driving torque T_h and T_a of the TCEAS are as follows:

$$\begin{array}{ll}{T}_h& ={\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}{\displaystyle \frac{\partial K}{\partial {\dot{q}}_h}}-{\displaystyle \frac{\partial K}{\partial q_h}}\\ & ={\displaystyle \frac{1}{3}}{m}_h{L}_h^2{\ddot{q}}_h+{\displaystyle \frac{1}{2}}{m}_h{L}_a{L}_h\sin q_h{\dot{q}}_a^2+{\displaystyle \frac{1}{6}}{m}_h{L}_h^2\sin (2q_h){\dot{q}}_a^2+{\displaystyle \frac{1}{2}}{m}_{h}g{L}_h\cos q_h+d_h(t)\end{array}$$

(4)

$$\begin{array}{ll}{T}_a& ={\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}{\displaystyle \frac{\partial K}{\partial {\dot{q}}_a}}-{\displaystyle \frac{\partial K}{\partial q_a}}\\ & =({\displaystyle \frac{1}{2}}{m}_a{L}_a^2+m_h{L}_a^2+m_h{L}_a{L}_h\cos q_h+{\displaystyle \frac{1}{3}}{m}_h{L}_h^2{\cos }^2{q}_h){\ddot{q}}_a\\ & -(m_h{L}_a{L}_h\sin q_h+{\displaystyle \frac{1}{3}}{m}_h{L}_h^2\sin (2q_h)){\dot{q}}_a{\dot{q}}_h+d_a(t)\end{array}$$

(5)

where ${\ddot{q}}_h$ is the angular acceleration of the rotation of the vertical subsystem and ${\ddot{q}}_a$ is the angular acceleration of the rotation of the horizontal subsystem; g is the universal gravitational constant; d_h(t) is the unmodeled disturbance of the vertical subsystem and d_a(t) is the unmodeled disturbance of the horizontal subsystem.

2.2. Mathematical Modeling of Electrical Dynamics

2.2.1. Mathematical Modeling of Electrical Dynamics of Vertical Subsystem

For a vertical subsystem, the electric cylinder is selected as the actuator, which is composed of a ball screw, a servo motor, and a gear mechanism to form a transmission system. The servo motor provides precise power output, the reduction gear set amplifies torque and regulates speed, and the ball screw efficiently converts rotational motion into linear motion. The precise coordination of the three components endows the electric cylinder with significant advantages such as compact structure, convenient installation, and outstanding transmission accuracy. With its high response speed, low friction loss, and excellent load-bearing capacity, the electric cylinder perfectly meets the strict requirements of rapid response and precise positioning for the TCEAS in complex environments.

From the perspective of dynamic research, the dynamic model of the electric cylinder can be deconstructed into two key parts. The primary part is the motor dynamic model, which is of great significance for exploring the power output characteristics and motion control mechanism. The electric dynamical equation in the electric cylinder is expressed as in [23]:

$$\left\{\begin{array}{l}{T}_c-T_{c,s}=J_c{\ddot{\theta }}_c+B_c{\dot{\theta }}_c\\ \hspace{1em}\hspace{1em}\hspace{1em}{T}_c=K_c{u}_h\\ T_{c,s}-T_{c,o}=J_{c,d}{\ddot{\theta }}_c+B_{c,d}{\dot{\theta }}_c\end{array}\right.$$

(6)

where T_c refers the electromagnetic torque, T_c,s represents the output torque, J_c refers the rotational inertia, θ_c refers the rotation angle, B_c refers viscous damping coefficient, K_c represents ratio of the torque amplification coefficient for servo motor and the circuit resistance, u_h represents control input, T_c,o represents output torque from electric cylinder, J_c,d refers rotational inertia from driver, and B_c,d is the viscous damping parameter in driver.

The output torque of the electric cylinder can be calculated as follows:

$$\begin{array}{l}{T}_{c,o}=F_c{L}_c{(2\pi \eta N_c)}^{-1}\\ \Delta R=2\pi N_c{L}_c{\theta }_c^{-1}\end{array}$$

(7)

where L_c characterizes lead of ball screw, F_c characterizes output thrust of telescopic rod, η characterizes transmission parameter, ΔR characterizes output displacement of telescopic rod, and N_c represents transmission ratio in actuator electric cylinder.

Figure 2 presents the spatial installation position relationship between the upper and lower fulcrums in the electric cylinder and barrel and cradle.

In Figure 2, the definitions are as follows: R_a indicates the distance in hinge center of the electric cylinder of horizontal subsystem and the center of the trunnion, which characterizes the spatial position parameter of the upper end hinge point of the electric cylinder relative to the trunnion; R₀ indicates zero marking point of the electric cylinder; R_d indicates the length between the bottom support shaft of the electric cylinder and the barrel return shaft; α indicates the angle formed by the connection lines of the upper and lower hinge points and the rotary shaft; α₀ represents the apex angle value when the electric cylinder is in the zero position. Based on the above geometric parameters, the displacement ΔR for telescopic rod in electric cylinder can be derived through spatial geometric relationships, and its expression is as follows:

$$\begin{array}{ll}\Delta R& ={(R_a^2+R_d^2-2R_a{R}_d\cos (\alpha ))}^{1/2}-R_0\\ & ={(R_a^2+R_d^2-2R_a{R}_d\cos (q_h+{\alpha }_0))}^{1/2}-R_0\end{array}$$

(8)

Combining (7) and (8), we can obtain the following:

$${\theta }_c={\displaystyle \frac{2\pi N_c\Delta R}{L_c}}={\displaystyle \frac{2\pi N_c}{L_c}}\left[{(R_a^2+R_d^2-2R_a{R}_d\cos (q_h+{\alpha }_0))}^{1/2}-R_0\right]$$

(9)

Thus, we have the following:

$$T_{c,o}=K_c{u}_h-(J_c{\ddot{\theta }}_c+B_c{\dot{\theta }}_c)-(J_{c,d}{\ddot{\theta }}_c+B_{c,d}{\dot{\theta }}_c)$$

(10)

Next, from Figure 2, it can be seen that the output torque generated by the electric cylinder is as follows:

$$T_h=F_c{R}_d\sin (C)$$

(11)

where the angle C is the angle between the electric cylinder thrust and the horizontal axis of the vertical subsystem, which is obtained from Figure 2:

$$\sin (C)={\displaystyle \frac{R_a\sin (q_h+{\alpha }_0)}{{(R_a^2+R_d^2-2R_a{R}_d\cos (q_h+{\alpha }_0))}^{1/2}}}$$

(12)

In addition, a continuously differentiable friction function is introduced to accurately simulate the friction behavior in vertical subsystem. It effectively describes the complex nonlinear friction phenomena including static friction, coulomb friction, and viscous friction during its motion. The model smoothly approximates the nonlinear relationship between the friction torque and the motion speed through the continuously derivable mathematical expressions. It avoids the discontinuity problem of the traditional segmented friction model near the velocity zero point, and provides a more accurate theoretical basis for system dynamics modeling and friction compensation control. The specific modeling form can be expressed as follows:

$$T_{fh}({\dot{q}}_h)=f_{s1h}\left[\tanh (f_{s2h}{\dot{q}}_h)-\tanh (f_{s3h}{\dot{q}}_h)\right]+f_{c1h}\tanh (f_{c2h}{\dot{q}}_h)+f_{b1h}{\dot{q}}_h$$

(13)

where f_s1h, f_s2h, f_s3h, f_c1h, f_c2h, and f_b1h denote the coefficient of friction for different characteristics.

Therefore, based on (7) and (10), the input torque for vertical subsystem is given by the following:

$$\begin{array}{ll}{T}_h& =2\pi \eta N_c{R}_d{T}_{c,o}\sin C{L}_c^{-1}\\ & ={\displaystyle \frac{2\pi \eta N_c{R}_d{R}_a\sin (q_h+{\alpha }_0)K_c}{L_c{(R_a^2+R_d^2-2R_a{R}_d\cos (q_h+{\alpha }_0))}^{1/2}}}{u}_h\\ & -{\displaystyle \frac{4{\pi }^2\eta N_c^2{R}_d^2{R}_a^2(J_c+J_{c,d}){\sin }^2(q_h+{\alpha }_0)}{L_c^2(R_a^2+R_d^2-2R_a{R}_d\cos (q_h+{\alpha }_0))}}{\ddot{q}}_h\\ & -{\displaystyle \frac{4{\pi }^2\eta N_c^2{R}_d^2{R}_a^2(B_c+B_{c,d}){\sin }^2(q_h+{\alpha }_0){\dot{q}}_h}{L_c^2(R_a^2+R_d^2-2R_a{R}_d\cos (q_h+{\alpha }_0))}}-T_{fh}\\ & +{\displaystyle \frac{4{\pi }^2\eta N_c^2{R}_d^3{R}_a^3(J_c+J_{c,d}){\sin }^3(q_h+{\alpha }_0){\dot{q}}_h^2}{L_c^2(R_a^2+R_d^2-2R_a{R}_d\cos (q_h+{\alpha }_0))}}+f_c(t)\\ & -{\displaystyle \frac{4{\pi }^2\eta N_c^2{R}_d^2{R}_a^2(J_c+J_{c,d})\cos (q_h+{\alpha }_0)\sin (q_h+{\alpha }_0){\dot{q}}_h^2}{L_c^2(R_a^2+R_d^2-2R_a{R}_d\cos (q_h+{\alpha }_0))}}\end{array}$$

(14)

where f_c(t) denotes the modeling error of the vertical subsystem actuator.

Substituting T_h into (4) yields the mechatronic analytical dynamics model of the vertical subsystem as follows:

$$\begin{array}{ll}{\ddot{q}}_h& ={\left[{\displaystyle \frac{1}{3}}{m}_h{L}_h^2+{\displaystyle \frac{4{\pi }^2\eta N_c^2{R}_d^2{R}_a^2(J_c+J_{c,d}){\sin }^2(q_h+{\alpha }_0)}{L_c^2(R_a^2+R_d^2-2R_a{R}_d\cos (q_h+{\alpha }_0))}}\right]}^{-1}\\ & \left\{{\displaystyle \frac{2\pi \eta N_c{R}_d{R}_a\sin (q_h+{\alpha }_0)K_c}{L_c{(R_a^2+R_d^2-2R_a{R}_d\cos (q_h+{\alpha }_0))}^{1/2}}}{u}_h\right.-T_{fh}\\ & -{\displaystyle \frac{4{\pi }^2\eta N_c^2{R}_d^2{R}_a^2(J_c+J_{c,d})\cos (q_h+{\alpha }_0)\sin (q_h+{\alpha }_0){\dot{q}}_h^2}{L_c^2(R_a^2+R_d^2-2R_a{R}_d\cos (q_h+{\alpha }_0))}}\\ & +{\displaystyle \frac{4{\pi }^2\eta N_c^2{R}_d^3{R}_a^3(J_c+J_{c,d}){\sin }^3(q_h+{\alpha }_0){\dot{q}}_h^2}{L_c^2(R_a^2+R_d^2-2R_a{R}_d\cos (q_h+{\alpha }_0))}}+f_c(t)-d_h(t)\\ & -{\displaystyle \frac{1}{6}}{m}_h{L}_h^2\sin (2q_h){\dot{q}}_a^2-{\displaystyle \frac{1}{2}}{m}_h{L}_a{L}_h\sin q_h{\dot{q}}_a^2-{\displaystyle \frac{1}{2}}{m}_{h}g{L}_h\cos q_h\\ & \left.-{\displaystyle \frac{4{\pi }^2\eta N_c^2{R}_d^2{R}_a^2(B_c+B_{c,d}){\sin }^2(q_h+{\alpha }_0){\dot{q}}_h}{L_c^2(R_a^2+R_d^2-2R_a{R}_d\cos (q_h+{\alpha }_0))}}\right\}\end{array}$$

(15)

2.2.2. Mathematical Modeling of Electrical Dynamics of Horizontal Subsystem

The horizontal subsystem selects the high-precision servo motor specially developed for the scene as the core actuator. The servo motor adopts multi-tooth synchronous meshing technology, which significantly improves the transmission accuracy and efficiency through the mutual compensation mechanism of errors between multi-tooths. Its comprehensive transmission error can be controlled within the range of angular-second precision, which meets the stringent requirements for fast and accurate positioning of horizontal orientation.

In terms of mechanical structure layout, the stator of the servo motor is rigidly fixed to the load base inside the vehicle body through high-strength flange components, forming a stable power input source. From the perspective of dynamic modeling, considering that the armature inductance of the servomotor is much smaller than the armature resistance, its time constant is negligible. Therefore, the armature current dynamic process can be approximated as an instantaneous response. Based on this engineering simplification assumption, the dynamic equations of the horizontal subsystem servo motor can be described as in [24]:

$$J_s{\ddot{\theta }}_s=T_s-B_s{\dot{\theta }}_s-T_{s,i}$$

(16)

$$T_s=K_s{u}_a-K_{s,e}{\dot{\theta }}_s$$

(17)

where J_s represents rotational inertia of actuator motor, θ_s characterizes rotational angle of actuator motor, T_s represents electromagnetic torque of actuator motor, B_s characterizes viscous damping coefficient of actuator motor shaft, T_s,i represents gear input torque, K_s represents ratio of the torque amplification coefficient of actuator motor to the resistance of the circuit, u_a characterizes control input, and K_s,e represents ratio of the electric potential coefficient for the actuator motor to the circuit resistance.

The horizontal subsystem needs to achieve speed reduction through the mechanical reduction transmission device composed of a multistage gear mechanism to match the motion speed requirement of the horizontal subsystem. The gear meshing process is bound to have backlash nonlinearity. To facilitate the controller design, the backlash characteristics between the input torques of the multistage gear mechanism are described using the following model:

$$T_a=N_s{T}_{s,i}+f_s(t)$$

(18)

where N_s is the ratio of the multistage gear mechanism and f_s(t) is the unmodeled error in the transmission process of the multistage gear mechanism.

Then, according to ${\theta }_s=N_s{q}_a$, substituting (17) and (18) into (16), we can obtain the following:

$$J_s{N}_s^2{\ddot{q}}_a=K_s{N}_s{u}_a-B_s{N}_s^2{\dot{q}}_a-T_a+f_s(t)-K_{s,e}{N}_s^2{\dot{q}}_a$$

(19)

In order to accurately describe the frictional nonlinearity of the horizontal subsystem, the modified hyperbolic tangent function continuum model is still used to consider the dynamic effects of static friction, Coulomb friction, viscous friction, and Stribeck effect. Its specific form is shown below:

$$T_{fa}({\dot{q}}_a)=f_{s1a}\left[\tanh (f_{s2a}{\dot{q}}_a)-\tanh (f_{s3a}{\dot{q}}_a)\right]+f_{c1a}\tanh (f_{c2a}{\dot{q}}_a)+f_{b1a}{\dot{q}}_a$$

(20)

where f_s1a, f_s2a, f_s3a, f_c1a, f_c2a, and f_b1a denote the coefficient of friction for different characteristics.

Therefore, the input torque for horizontal subsystem is given by the following:

$$T_a=K_s{N}_s{u}_a-B_s{N}_s^2{\dot{q}}_a-J_s{N}_s^2{\ddot{q}}_a-K_{s,e}{N}_s^2{\dot{q}}_a-T_{fa}+f_s(t)$$

(21)

Substituting T_a into (5) yields the mathematical dynamics equation of the two-axis coupled electromechanical actuator system as follows:

$$\begin{array}{ll}{\ddot{q}}_a=& {\left(m_a{L}_a^2/2+m_h{L}_a^2+m_h{L}_a{L}_h\cos q_h+m_h{L}_h^2{\cos }^2{q}_h/3+J_s{N}_s^2\right)}^{-1}\\ & \left\{\begin{array}{l}{K}_s{N}_s{u}_a-K_{s,e}{N}_s^2{\dot{q}}_a-B_s{N}_s^2{\dot{q}}_a-T_{fa}+f_s(t)-d_a(t)\\ +\left(m_h{L}_a{L}_h\sin q_h+m_h{L}_h^{2}sin(2q_h)/3\right){\dot{q}}_a{\dot{q}}_h\end{array}\right\}\end{array}$$

(22)

2.3. Construction of State Space Equation

For controller design purposes, the system dynamics can be compactly represented in a state-space form. First, combining (15) and (22), the following state variable ${\mathit{x}}_1={\left[x_{1h},x_{1a}\right]}^{\mathrm{T}}={\left[q_h,q_a\right]}^{\mathrm{T}}$ and ${\mathit{x}}_2={\left[x_{2h},x_{2a}\right]}^{\mathrm{T}}={\left[{\dot{q}}_h,{\dot{q}}_a\right]}^{\mathrm{T}}$ are defined. Then, the mathematical equation of the TCEAS, considering friction nonlinearity and other uncertainties, is written as the following state space formulation:

$$\left\{\begin{array}{l}{\dot{\mathit{x}}}_1={\mathit{x}}_2\\ {\dot{\mathit{x}}}_2={\mathit{M}}_1^{-1}({\mathit{x}}_1)\left[{\mathit{K}}_1({\mathit{x}}_1)\mathit{u}-{\mathit{C}}_1({\mathit{x}}_1,{\mathit{x}}_2){\mathit{x}}_2-\mathit{G}({\mathit{x}}_1)-\mathit{F}({\mathit{x}}_2)\right]+\mathit{D}(t)\end{array}\right.$$

(23)

where ${\mathit{M}}_1({\mathit{x}}_1)=\left[\begin{array}{cc}{M}_{11}& M_{12}\\ M_{21}& M_{22}\end{array}\right]$, ${\mathit{K}}_1({\mathit{x}}_1)=\left[\begin{array}{cc}{K}_{11}& K_{12}\\ K_{21}& K_{22}\end{array}\right]$, $\mathit{u}=\left[\begin{array}{c}{u}_h\\ u_a\end{array}\right]$, ${\mathit{C}}_1({\mathit{x}}_1,{\mathit{x}}_2)=\left[\begin{array}{cc}{C}_{11}& C_{12}\\ C_{21}& C_{22}\end{array}\right]$, $\mathit{G}({\mathit{x}}_1)=\left[\begin{array}{c}{G}_1\\ G_2\end{array}\right]$, $\mathit{F}({\mathit{x}}_2)=\left[\begin{array}{c}F(x_{21})\\ F(x_{22})\end{array}\right]$, $\mathit{D}(t)=\left[\begin{array}{c}{D}_1(t)\\ D_2(t)\end{array}\right]$. The specific characterization of each element is as follows:

$$\left\{\begin{array}{l}{M}_{11}={\displaystyle \frac{1}{3}}{m}_h{L}_h^2+(4{\pi }^2\eta N_c^2{R}_d^2{R}_a^2(J_c+J_{c,d}){\sin }^2(q_h+{\alpha }_0))\\ \hspace{1em}\hspace{1em}\hspace{1em}\times {(L_c^2(R_a^2+R_d^2-2R_a{R}_d\cos (q_h+{\alpha }_0)))}^{-1};\\ M_{12}=M_{21}=0;\\ M_{22}={\displaystyle \frac{1}{2}}{m}_a{L}_a^2+m_h{L}_a^2+m_h{L}_a{L}_h\cos q_h+{\displaystyle \frac{1}{3}}{m}_h{L}_h^2{\cos }^2{q}_h+J_s{N}_s^2.\end{array}\right.$$

(24)

$$\left\{\begin{array}{l}{K}_{11}=(2\pi \eta N_c{R}_d{R}_a\sin (q_h+{\alpha }_0)K_c)\\ \hspace{1em}\hspace{1em}\hspace{1em}\times {(L_c{(R_a^2+R_d^2-2R_a{R}_d\cos (q_h+{\alpha }_0))}^{1/2})}^{-1};\\ K_{12}=K_{21}=0;\\ K_{22}=K_s{N}_s.\end{array}\right.$$

(25)

$$\left\{\begin{array}{l}{C}_{11}=(4{\pi }^2\eta N_{\mathrm{c}}^2{R}_{\mathrm{d}}^2{R}_{\mathrm{a}}^2(J_{\mathrm{c}}+J_{\mathrm{c},\mathrm{d}})\sin (q_{\mathrm{h}}+{\alpha }_0)\cos (q_{\mathrm{h}}+{\alpha }_0))\\ \hspace{1em}\hspace{1em}\hspace{1em}\times {(L_{\mathrm{c}}^2(R_{\mathrm{a}}^2+R_{\mathrm{d}}^2-2R_{\mathrm{a}}{R}_{\mathrm{d}}\cos (q_{\mathrm{h}}+{\alpha }_0)))}^{-1}{\dot{q}}_{\mathrm{h}}\\ \hspace{1em}\hspace{1em}-(4{\pi }^2\eta N_{\mathrm{c}}^2{R}_{\mathrm{d}}^3{R}_{\mathrm{a}}^3(J_{\mathrm{c}}+J_{\mathrm{c},\mathrm{d}}){\sin }^3(q_{\mathrm{h}}+{\alpha }_0))\\ \hspace{1em}\hspace{1em}\hspace{1em}\times {(L_{\mathrm{c}}^2{(R_{\mathrm{a}}^2+R_{\mathrm{d}}^2-2R_{\mathrm{a}}{R}_{\mathrm{d}}\cos (q_{\mathrm{h}}+{\alpha }_0))}^2)}^{-1}{\dot{q}}_{\mathrm{h}}\\ \hspace{1em}\hspace{1em}+(4{\pi }^2\eta N_{\mathrm{c}}^2{R}_{\mathrm{d}}^2{R}_{\mathrm{a}}^2(B_{\mathrm{c}}+B_{\mathrm{c},\mathrm{d}}){\sin }^2(q_{\mathrm{h}}+{\alpha }_0))\\ \hspace{1em}\hspace{1em}\hspace{1em}\times {(L_{\mathrm{c}}^2(R_{\mathrm{a}}^2+R_{\mathrm{d}}^2-2R_{\mathrm{a}}{R}_{\mathrm{d}}\cos (q_{\mathrm{h}}+{\alpha }_0)))}^{-1};\\ C_{12}=({\displaystyle \frac{1}{2}}{m}_h{L}_a{L}_h\sin q_h+{\displaystyle \frac{1}{6}}{m}_h{L}_h^2\sin (2q_h)){\dot{q}}_a;\\ C_{21}=-{\displaystyle \frac{1}{3}}{m}_h{L}_h^2\sin (2q_h){\dot{q}}_a;C_{22}=K_{s,e}{N}_s^2+B_s{N}_s^2-m_h{L}_a{L}_h\sin q_h{\dot{q}}_h.\end{array}\right.$$

(26)

$$\left\{\begin{array}{l}{G}_1={\displaystyle \frac{1}{2}}{m}_{h}g{L}_h\cos q_h;\\ G_2=0.\end{array}\right.$$

(27)

$$\left\{\begin{array}{l}F(x_{21})=f_{s1h}\left[\tanh (f_{s2h}{\dot{q}}_h)-\tanh (f_{s3h}{\dot{q}}_h)\right]+f_{c1h}\tanh (f_{c2h}{\dot{q}}_h)+f_{b1h}{\dot{q}}_h;\\ F(x_{22})=f_{s1a}\left[\tanh (f_{s2a}{\dot{q}}_a)-\tanh (f_{s3a}{\dot{q}}_a)\right]+f_{c1a}\tanh (f_{c2a}{\dot{q}}_a)+f_{b1a}{\dot{q}}_a.\end{array}\right.$$

(28)

$$\left\{\begin{array}{l}{D}_1(t)=\left(f_c(t)-d_h(t)\right)/M_{11};\\ D_2(t)=\left(f_s(t)-d_a(t)\right)/M_{22}.\end{array}\right.$$

(29)

To systematically elaborate on the design principle of the ARSTC, this chapter assumes that the friction parameters f_s1h, f_c1h, f_b1h, f_s1a, f_c1a, and f_b1a are unknown quantities. Through the parameter adaptive estimation mechanism, the online identification and compensation of parameter uncertainty are carried out. This method is based on the Lyapunov stability theory to construct the adaptive law, and uses the system signals to update the estimated values of the unknown parameters in real time to ensure the convergence of the parameter estimation error.

By defining the unknown parameter $\mathit{\theta }={\left[{\mathit{\theta }}_1^{\mathrm{T}},{\mathit{\theta }}_2^{\mathrm{T}}\right]}^{\mathrm{T}}$, where ${\mathit{\theta }}_1={\left[{\theta }_{11},{\theta }_{12},{\theta }_{13}\right]}^{\mathrm{T}}=$${\left[f_{s1h},f_{c1h},f_{b1h}\right]}^{\mathrm{T}}$, ${\mathit{\theta }}_2={\left[{\theta }_{21},{\theta }_{22},{\theta }_{23}\right]}^{\mathrm{T}}={\left[f_{s1a},f_{c1a},f_{b1a}\right]}^{\mathrm{T}}$. Let ${\mathit{\phi }}_{\theta 1}=\left[(\tanh (f_{s2h}{\dot{q}}_h)-\right.$$\left.\tanh (f_{s3h}{\dot{q}}_h)),\tanh (f_{c2h}{\dot{q}}_h),{\dot{q}}_h\right]$, ${\mathit{\phi }}_{\theta 2}=[(\tanh (f_{s2a}{\dot{q}}_a)-\tanh (f_{s3a}{\dot{q}}_a)),\tanh (f_{c2a}{\dot{q}}_a),{\dot{q}}_a]$; ${\mathit{\phi }}_{\theta }\mathit{\theta }=\left[\begin{array}{cc}{\mathit{\phi }}_{\theta 1}& \mathbf{0}\\ \mathbf{0}& {\mathit{\phi }}_{\theta 2}\end{array}\right]\left[\begin{array}{c}{\mathit{\theta }}_1\\ {\mathit{\theta }}_2\end{array}\right]$ can be obtained.

Therefore, the state space Equation (23) of the TCEAS can be rewritten as

$$\left\{\begin{array}{l}{\dot{\mathit{x}}}_1={\mathit{x}}_2\\ {\dot{\mathit{x}}}_2={\mathit{M}}_1^{-1}({\mathit{x}}_1)\left[{\mathit{K}}_1({\mathit{x}}_1)\mathit{u}-{\mathit{C}}_1({\mathit{x}}_1,{\mathit{x}}_2){\mathit{x}}_2-\mathit{G}({\mathit{x}}_1)-{\mathit{\phi }}_{\theta }\mathit{\theta }\right]+\mathit{D}(t)\end{array}\right.$$

(30)

3. Adaptive Robust Stable Tracking Controller Design

This section first establishes the control objectives, then develops the parameter adaptation mechanism, followed by the complete controller design and stability analysis.

3.1. Control Objectives

The design objective of the controller for the TCEAS is as follows: Given the system reference motion angle signal q_d(t) = x_1d(t) = [x_1dh(t), x_1da(t)]^T, we design a bounded control input u = [u_h, u_a]^T. We therefore make the attitude output of the system x₁ = [x_1h, x_1a]^T = [q_h, q_a]^T track the reference motion angle signal of the TCEAS as accurately as possible.

To successfully design the proposed control strategy, necessary assumptions consistent with engineering realities are demonstrated in advance.

Assumption 1. 

The given angular command x_1d(t) = [x_1dh(t), x_1da(t)]^T of the TCEAS satisfies x_1dh(t) ∈ C³, x_1da(t) ∈ C³.

Assumption 2. 

The upper and lower thresholds of unknown parameter $\mathit{\theta }$ of the TCEAS is known, i.e., $\mathit{\theta }\in {\mathbf{\Omega }}_{\mathit{\theta }}\triangleq \{\mathit{\theta }:{\mathit{\theta }}_{\min }\le \mathit{\theta }\le {\mathit{\theta }}_{\max }\}$, in which  ${\mathit{\theta }}_{\max }={\left[{\theta }_{11\max },{\theta }_{12\max },{\theta }_{13\max },{\theta }_{21\max },{\theta }_{22\max },{\theta }_{23\max }\right]}^{\mathrm{T}}$, ${\mathit{\theta }}_{\min }={\left[{\theta }_{11\min },{\theta }_{12\min },{\theta }_{13\min },{\theta }_{21\min },{\theta }_{22\min },{\theta }_{23\min }\right]}^{\mathrm{T}}$.

Assumption 3. 

The magnitude and range of the unmodeled disturbance D(t) of the two-axis coupled electromechanical actuation system is known, i.e., $\left|D_1(t)\right|\le {\delta }_1,\left|D_2(t)\right|\le {\delta }_2$, $‖\mathit{D}(t)‖\le \sqrt{{\delta }_1^2+{\delta }_2^2}={\delta }_d$, in which  ${\delta }_d$, ${\delta }_1$, and ${\delta }_2$ are known positive numbers.

3.2. Parameter Adaptive Control Mechanism

The ${\widehat{\mathit{\theta }}}_1$ and ${\widehat{\mathit{\theta }}}_2$ are set as the estimated values of the unknown friction coefficients ${\mathit{\theta }}_1$ and ${\mathit{\theta }}_2$ in the TCEAS, and let ${\tilde{\mathit{\theta }}}_1={\widehat{\mathit{\theta }}}_1-{\mathit{\theta }}_1$ and ${\tilde{\mathit{\theta }}}_2={\widehat{\mathit{\theta }}}_2-{\mathit{\theta }}_2$ denote the estimated errors of uncertain parameters. To achieve effective convergence of the subsequently derived parameter adaptive functions, the following discontinuous mapping mechanism equation is given [25]:

$${\mathrm{Proj}}_{{\widehat{\theta }}_{ji}}({•}_{ji})=\left\{\begin{array}{l}0,\hspace{1em}\mathrm{if} {\widehat{\theta }}_{ji}={\theta }_{ji\max } \mathrm{and} {•}_{ji}>0\\ 0,\hspace{1em}\mathrm{if} {\widehat{\theta }}_{ji}={\theta }_{ji\min } \mathrm{and} {•}_{ji}<0\\ {•}_{ji},\hspace{1em}\mathrm{otherwise}\end{array}\right.$$

(31)

where ${\theta }_{ji\max }$ denotes the maximum value of ${\theta }_{ji}$ and ${\theta }_{ji\min }$ denotes the minimum value of ${\theta }_{ji}$, we have j = 1, 2, i = 1, 2, 3. The following controlled parameter adaptive law is used:

$$\dot{\widehat{\mathit{\theta }}}={\mathrm{Proj}}_{\widehat{\mathit{\theta }}}(\mathbf{\Gamma }\mathit{\tau })\hspace{1em}\widehat{\mathit{\theta }}(0)\in {\mathbf{\Omega }}_{\mathit{\theta }}$$

(32)

where ${\mathrm{Proj}}_{\widehat{\mathit{\theta }}}(•)={[{\mathrm{Proj}}_{{\widehat{\theta }}_{11}}({•}_{11}),\dots ,{\mathrm{Proj}}_{{\widehat{\theta }}_{23}}({•}_{23})]}^{\mathrm{T}}$, $\mathbf{\Gamma }$ is a positive definite diagonal matrix which is the control gain matrix of the parameter adaptive function, and $\mathit{\tau }$ is the parameter adaptive function.

Based on the above action of the discontinuous parameter adaptive mechanism, we have the following lemma: for any adaptive function $\mathit{\tau }$ derived, it possesses the following mathematical properties [25]:

$$\left\{\begin{array}{l}(\mathrm{P}1) \widehat{\mathit{\theta }}\in {\Omega }_{\widehat{\mathit{\theta }}}=\{\widehat{\mathit{\theta }}:{\mathit{\theta }}_{\min }\le \widehat{\mathit{\theta }}\le {\mathit{\theta }}_{\max }\}\\ (\mathrm{P}2) {\tilde{\mathit{\theta }}}^{\mathrm{T}}[{\mathbf{\Gamma }}^{-1}{\mathrm{Proj}}_{\widehat{\mathit{\theta }}}(\mathbf{\Gamma }\mathit{\tau })-\mathit{\tau }]\le 0,\forall \mathit{\tau }\end{array}\right.$$

(33)

In summary, the discontinuous mapping adaptive law (31) ensures parameter estimates are bounded within $\left[{\theta }_{\min },{\theta }_{\max }\right]$ and avoid divergence. For coupled systems like TCEAS, due to cross-axis interactions and disturbances, estimates do not strictly converge to true values but stabilize in an effective range that supports friction compensation—this is sufficient to guarantee the controller’s performance.

3.3. Controller Design

Aiming at the friction nonlinearity, parameter uncertainty, and unmodeled disturbance existing in the TCEAS, the design of an ARSTC strategy is carried out.

First, the error variable function is characterized as follows:

$${\mathit{z}}_1={\mathit{x}}_1-{\mathit{x}}_{1d}$$

(34)

where z₁ = [z_1h, z_1a]^T denotes the tracking error of the TCEAS, which is obtained by taking the derivative of time with respect to z₁:

$${\dot{\mathit{z}}}_1={\dot{\mathit{x}}}_1-{\dot{\mathit{x}}}_{1d}={\mathit{x}}_2-{\dot{\mathit{x}}}_{1d}$$

(35)

Next, by characterizing ${\mathit{z}}_2\triangleq {\mathit{x}}_2-{\mathit{\alpha }}_1={[z_{2h},z_{2a}]}^{\mathrm{T}}$ to represent the deviation between them, where ${\mathit{\alpha }}_1={[{\alpha }_{1h},{\alpha }_{1a}]}^{\mathrm{T}}$ represents virtual control function for state x₂, the following is designed:

$${\mathit{\alpha }}_1={\dot{\mathit{x}}}_{1d}-{\mathit{k}}_1{\mathit{z}}_1$$

(36)

where k₁ = diag{k_1h, k_1a} is the non-negative control gain matrix. Thus, the derivative for z₁ is as follows:

$${\dot{\mathit{z}}}_1={\mathit{z}}_2-{\mathit{k}}_1{\mathit{z}}_1$$

(37)

It can be analyzed from (37) that the transfer function matrices $z_{1h}(s)=G_h(s)z_{2h}(s)$, $G_h(s)=1/(s+k_{1h})$, and $z_{1a}(s)=G_a(s)z_{2a}(s)$, $G_a(s)=1/(s+k_{1a})$ are all asymptotically stable systems. When $z_{2h}$ and $z_{2a}$ approach zero, according to the stability theory, it can be concluded that $z_{1h}$ and $z_{1a}$ must also converge to zero. Further analysis shows that the transfer functions $z_{2h}$ and $z_{2a}$ simultaneously contain the position tracking error vector and the velocity tracking error vector, which are nonlinear mapping functions containing errors and their derivatives. If the control strategy design can ensure that $z_{2h}\to 0$ and $z_{2a}\to 0$, then according to the Lyapunov stability theory, it can be deduced that the position error and velocity error tend to zero, thereby achieving the optimization of the system tracking performance.

Based on the above analysis, the subsequent controller design will take the asymptotic convergence of $z_{2h}$ and $z_{2a}$ as the core optimization objective, and achieve the dynamic global exponential stability of errors by constructing an adaptive robust control law.

From (30) and equation ${\mathit{z}}_2\triangleq {\mathit{x}}_2-{\mathit{\alpha }}_1$, the following can be obtained:

$$\begin{array}{ll}{\dot{\mathit{z}}}_2& ={\dot{\mathit{x}}}_2-{\dot{\mathit{\alpha }}}_1\\ & ={\mathit{M}}_1^{-1}({\mathit{x}}_1){\mathit{K}}_1({\mathit{x}}_1)\mathit{u}+\mathit{D}(t)-{\dot{\mathit{\alpha }}}_1\\ & \hspace{1em}+{\mathit{M}}_1^{-1}({\mathit{x}}_1)\left[-{\mathit{C}}_1({\mathit{x}}_1,{\mathit{x}}_2){\mathit{x}}_2-\mathit{G}({\mathit{x}}_1)-{\mathit{\phi }}_{\theta }\mathit{\theta }\right]\end{array}$$

(38)

Analyzing the structure of (38), we can design the ARSTC input u for the TCEAS as follows:

$$\left\{\begin{array}{l}\mathit{u}={\mathit{u}}_m+{\mathit{u}}_s,\\ {\mathit{u}}_m={\mathit{K}}_1^{-1}({\mathit{x}}_1){\mathit{M}}_1({\mathit{x}}_1)\left[{\dot{\mathit{\alpha }}}_1+{\mathit{M}}_1^{-1}({\mathit{x}}_1)\left({\mathit{C}}_1({\mathit{x}}_1,{\mathit{x}}_2){\mathit{x}}_2+\mathit{G}({\mathit{x}}_1)+{\mathit{\phi }}_{\theta }\widehat{\mathit{\theta }}\right)\right],\\ {\mathit{u}}_s={\mathit{K}}_1^{-1}({\mathit{x}}_1){\mathit{M}}_1({\mathit{x}}_1)\left({\mathit{u}}_{s1}+{\mathit{u}}_{s2}\right),{\mathit{u}}_{s1}=-{\mathit{k}}_2{\mathit{z}}_2\end{array}\right.$$

(39)

where k₂ = diag{k_2h, k_2a} is the positive feedback control gain matrix, u_m = [u_mh, u_ma]^T is the parametric adaptive model feedforward compensation control law to enhance the stability of the two-axis coupled system, u_s refers to the robust control term for a two-axis coupled system, u_s1 = [u_s1h, u_s1a]^T stands for the linear robust term, and u_s2 = [u_s2h, u_s2a]^T stands for the nonlinear robust term used to suppress system uncertainty and unmodeled disturbances.

Substituting (39) into (38) yields the following:

$${\dot{\mathit{z}}}_2=-{\mathit{k}}_2{\mathit{z}}_2+{\mathit{u}}_{s2}+{\mathit{M}}_1^{-1}({\mathit{x}}_1){\mathit{\phi }}_{\theta }\tilde{\mathit{\theta }}+\mathit{D}(t)$$

(40)

In order to further improve the stability of the TCEAS, u_s2 is designed to satisfy the following calming conditions:

$$\left\{\begin{array}{l}{\mathit{z}}_2^{\mathrm{T}}\left[{\mathit{u}}_{s2}+{\mathit{M}}_1^{-1}({\mathit{x}}_1){\mathit{\phi }}_{\theta }\tilde{\mathit{\theta }}+\mathit{D}(t)\right]\le {\epsilon }_1\\ {\mathit{z}}_2^{\mathrm{T}}{\mathit{u}}_{s2}\le 0\end{array}\right.$$

(41)

where ε₁ denotes a positive adjustable value which is capable of being sufficiently small.

Therefore, u_s2 can be designed as follows:

$${\mathit{u}}_{s2}=-{\mathit{k}}_{2s2}{\mathit{z}}_2\triangleq -{\displaystyle \frac{{\Psi }_1}{2{\epsilon }_1}}{\mathit{z}}_2$$

(42)

where the definition of Ψ₁ satisfies ${\Psi }_1\ge {‖{\mathit{\phi }}_{\theta }‖}^2{‖{\mathit{\theta }}_M‖}^2+{\delta }_d^2$, ${\mathit{\theta }}_M={\mathit{\theta }}_{\max }-{\mathit{\theta }}_{\min }$, k_2s2 = diag{k_2sh, k_2sa} is the positive feedback nonlinear control gain matrix.

3.4. Performance Theorem and Stability Analysis

Theorem 1. 

By using the discontinuous mapping adaptive law (31), design an adaptive function and select sufficiently large feedback gains k₁ and k₂ to make the matrix Λ₁, defined below as a positive definite matrix:

$${\mathbf{\Lambda }}_1=\left[\begin{array}{cc}{\mathit{k}}_1& -{\displaystyle \frac{1}{2}}\mathit{I}\\ -{\displaystyle \frac{1}{2}}\mathit{I}& {\mathit{k}}_2\end{array}\right]$$

(43)

Then the presented ARSTC controller (39) from the TCEAS can be guaranteed to have the following performance: all signals in the closed-loop controller are bounded and defined as the following Lyapunov function:

$$V_1={\displaystyle \frac{1}{2}}{\mathit{z}}_1^{\mathrm{T}}{\mathit{z}}_1+{\displaystyle \frac{1}{2}}{\mathit{z}}_2^{\mathrm{T}}{\mathit{z}}_2$$

(44)

this satisfies the following inequality:

$$V_1\le e^{-{\lambda }_{1}t}{V}_1(0)+{\displaystyle \frac{{\epsilon }_1}{{\lambda }_1}}\left(1-e^{-{\lambda }_{1}t}\right)$$

(45)

where ${\lambda }_1=2{\sigma }_{\min }({\Lambda }_1)$, ${\sigma }_{\min }({\Lambda }_1)$ is the minimum eigenvalue of the positive definite matrix.

Specific Proof Process: By combining (37) and (40), the derivative of V₁ can be obtained:

$$\begin{array}{ll}{\dot{V}}_1& ={\mathit{z}}_1^{\mathrm{T}}{\dot{\mathit{z}}}_1+{\mathit{z}}_2^{\mathrm{T}}{\dot{\mathit{z}}}_2\\ & ={\mathit{z}}_1^{\mathrm{T}}({\mathit{z}}_2-{\mathit{k}}_1{\mathit{z}}_1)+{\mathit{z}}_2^{\mathrm{T}}(-{\mathit{k}}_2{\mathit{z}}_2+{\mathit{u}}_{s2}+{\mathit{M}}_1^{-1}({\mathit{x}}_1){\mathit{\phi }}_{\theta }\tilde{\mathit{\theta }}+\mathit{D}(t))\\ & =-{\mathit{k}}_1{\mathit{z}}_1^{\mathrm{T}}{\mathit{z}}_1+{\mathit{z}}_1^{\mathrm{T}}{\mathit{z}}_2-{\mathit{k}}_2{\mathit{z}}_2^{\mathrm{T}}{\mathit{z}}_2+{\mathit{z}}_2^{\mathrm{T}}({\mathit{u}}_{s2}+{\mathit{M}}_1^{-1}({\mathit{x}}_1){\mathit{\phi }}_{\theta }\tilde{\mathit{\theta }}+\mathit{D}(t))\end{array}$$

(46)

From (41) and (43), we have the following:

$${\dot{V}}_1\le -{\mathit{Z}}^{\mathrm{T}}{\mathbf{\Lambda }}_1\mathit{Z}+{\epsilon }_1$$

(47)

where $\mathit{Z}={[{\mathit{z}}_1^{\mathrm{T}},{\mathit{z}}_2^{\mathrm{T}}]}^{\mathrm{T}}$. Since the matrix is positively definite and combined with the definition of ${\lambda }_1$, we can obtain the following:

$${\dot{V}}_1\le -{\sigma }_{\min }({\mathbf{\Lambda }}_1)\left({\mathit{z}}_1^{\mathrm{T}}{\mathit{z}}_1+{\mathit{z}}_2^{\mathrm{T}}{\mathit{z}}_2\right)+{\epsilon }_1\le -{\lambda }_1{V}_1+{\epsilon }_1$$

(48)

By using the principle of contrast [26], the following can be obtained:

$$V_1\le e^{-{\lambda }_{1}t}{V}_1(0)+{\displaystyle \frac{{\epsilon }_1}{{\lambda }_1}}\left(1-e^{-{\lambda }_{1}t}\right)$$

(49)

Analyzing (49) shows that V₁ is globally bounded, i.e., both ${\mathit{z}}_1$ and ${\mathit{z}}_2$ are bounded. Because the expected angle, angular velocity, and angular acceleration of the TCEAS are all bounded, ${\mathit{x}}_1$, ${\mathit{\alpha }}_1$, ${\mathit{x}}_2$, ${\dot{\mathit{\alpha }}}_1$ are also bounded. Combined with (33), the parameter estimation $\widehat{\mathit{\theta }}$ of the TCEAS is bounded, then u_m and u_s1 are bounded. Since ${\mathit{\phi }}_{\theta }$ is bounded, u_s2 is bounded, and ultimately the control input u of the design is known to be bounded. This completes the proof of Theorem 1.

Theorem 2. 

The TCEAS contains only parameter uncertainties, i.e., the unmodeled disturbance $‖\mathit{D}(t)‖=0$. The proposed control strategy not only yields the conclusion of Theorem 1, but also achieves the asymptotically stable tracking performance of the TCEAS, i.e., $\mathit{Z}\to 0$ for $t\to \infty$.

Specific Proof Process: When the TCEAS only has parameter uncertainty, the following Lyapunov function is defined:

$$V_2={\displaystyle \frac{1}{2}}{\mathit{z}}_1^{\mathrm{T}}{\mathit{z}}_1+{\displaystyle \frac{1}{2}}{\mathit{z}}_2^{\mathrm{T}}{\mathit{z}}_2+{\displaystyle \frac{1}{2}}{\tilde{\mathit{\theta }}}^{\mathrm{T}}{\Gamma }^{-1}\tilde{\mathit{\theta }}$$

(50)

Combining (32), (37), (40) and the adaptive function $\mathit{\tau }={\mathit{\phi }}_{\theta }^{\mathrm{T}}{\mathit{M}}_1^{-\mathrm{T}}({\mathit{x}}_1){\mathit{z}}_2$, the derivative of V₂ can be obtained:

$$\begin{array}{ll}{\dot{V}}_2& ={\mathit{z}}_1^{\mathrm{T}}{\dot{\mathit{z}}}_1+{\mathit{z}}_2^{\mathrm{T}}{\dot{\mathit{z}}}_2+{\tilde{\mathit{\theta }}}^{\mathrm{T}}{\Gamma }^{-1}\dot{\widehat{\theta }}\\ & ={\mathit{z}}_1^{\mathrm{T}}({\mathit{z}}_2-{\mathit{k}}_1{\mathit{z}}_1)+{\mathit{z}}_2^{\mathrm{T}}(-{\mathit{k}}_2{\mathit{z}}_2+{\mathit{u}}_{s2}+{\mathit{M}}_1^{-1}({\mathit{x}}_1){\mathit{\phi }}_{\theta }\tilde{\mathit{\theta }})+{\tilde{\mathit{\theta }}}^{\mathrm{T}}{\Gamma }^{-1}\dot{\widehat{\mathit{\theta }}}\\ & =-{\mathit{Z}}^{\mathrm{T}}{\mathbf{\Lambda }}_1\mathit{Z}+{\tilde{\mathit{\theta }}}^{\mathrm{T}}({\mathbf{\Gamma }}^{-1}\dot{\widehat{\mathit{\theta }}}-{\mathit{\phi }}_{\theta }^{\mathrm{T}}{\mathit{M}}_1^{-\mathrm{T}}({\mathit{x}}_1){\mathit{z}}_2)\end{array}$$

(51)

It can be further obtained that

$${\dot{V}}_2\le -{\sigma }_{\min }({\mathbf{\Lambda }}_1)\left({\mathit{z}}_1^{\mathrm{T}}{\mathit{z}}_1+{\mathit{z}}_2^{\mathrm{T}}{\mathit{z}}_2\right)\triangleq -H$$

(52)

where $H\in L_2$, which in combination with the designed ARSTC controller ensures that all signals of the TCEAS are bounded, it can be deduced that $\dot{H}\in L_{\infty }$. Therefore, H is consistently continuous, according to Barbalat’s lemma [27]; when time $t\to \infty$, we have $H\to 0$. Furthermore, the characteristic of $\mathit{Z}\to 0$ when $t\to \infty$ is achieved, and the asymptotic control effect of the TCEAS is obtained. At this point, the derivation of Theorem 2 has been concluded.

4. Comparative Co-Simulation Numerical Calculations

In order to comprehensively verify the effectiveness of the nonlinear ARSTC strategy designed in this paper for a two-axis coupled electromechanical actuation system, an interface between RecurDyn and Matlab/Simulink is applied to realize the data exchange in the control system and two-axis coupled mechanical system to achieve the co-simulation numerical calculation. The mathematical equation of the controller and the motor system are established in Matlab/Simulink software, and the angular displacement and angular velocity from horizontal subsystem and vertical subsystem are read in real time through RecurDyn software, which are fed back to the Matlab/Simulink software to solve the output torque of the motor under the current state to drive the multi-body system model in RecurDyn software. The co-simulation principle of the TCEAS is shown in Figure 3 [28].

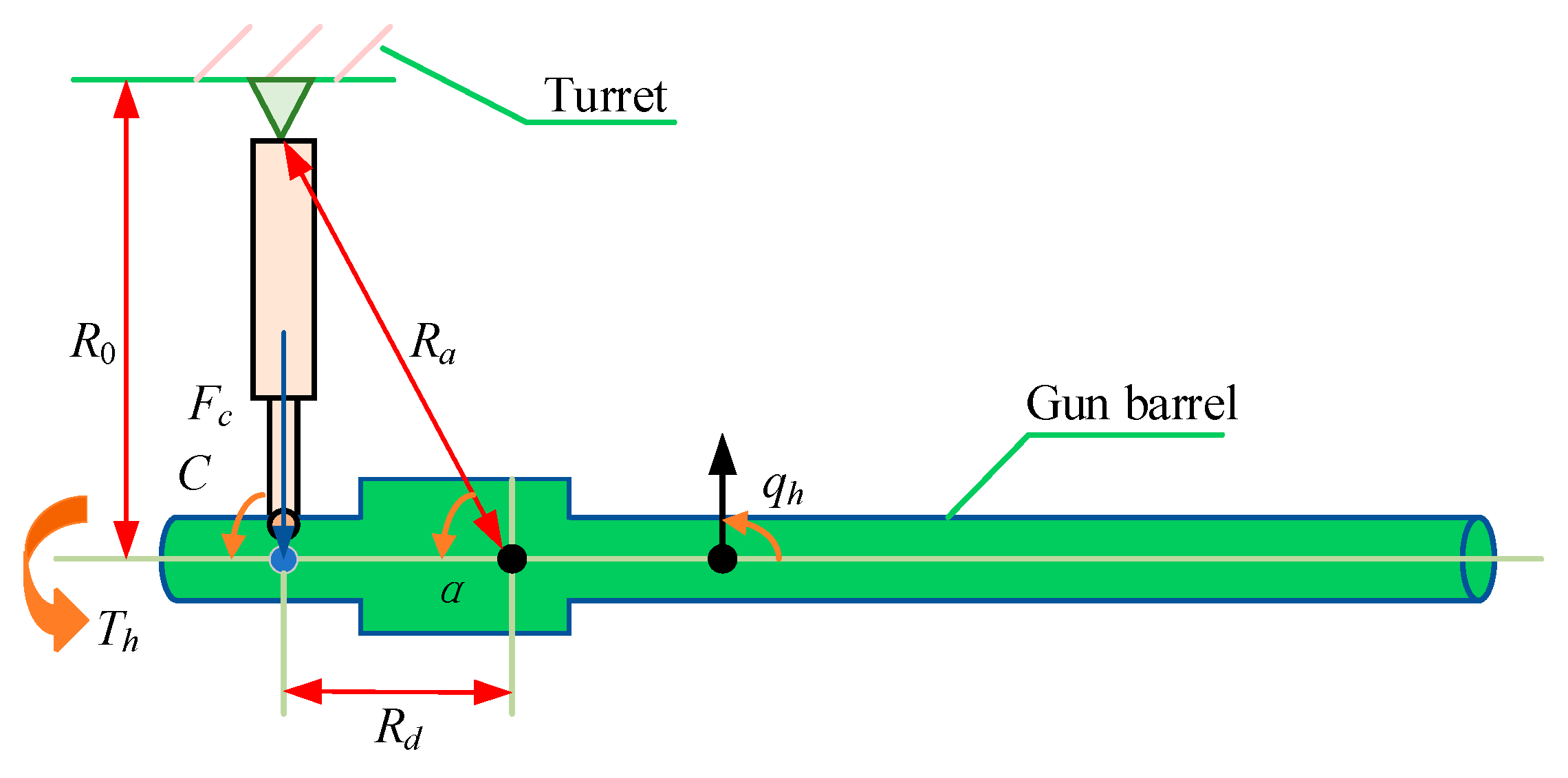
The following system parameters are set for the co-simulation numerical computation process: m_h = 2100.00 kg, L_h = 5.15 m, g = 9.80 m/s², m_a = 5200.00 kg, L_a = 1.15 m, J_c = 0.0505 kg·m², J_c,d = 0.0131 kg·m², B_c = 0.0176 N·m·s/rad, B_c,d = 0.0066 N·m·s/rad, K_c = 3.75 N·m/V, N_c = 3, L_c = 0.02 m, R_a = 0.55 m, R_d = 0.44 m, R₀ = 0.33 m, η = 0.8, α₀ = arcsin(0.65), J_s = 0.022 kg·m², B_s = 0.0088 N·m·s/rad, N_s = 16, K_s = 3.35 N·m/V, K_s,e = 1.81 A·s/rad.

The friction parameters of the vertical subsystem in the co-simulation are set as f_s1h = 42, f_s2h = 110, f_s3h = 0.5, f_c1h = 23, f_c2h = 30, and f_b1h = 12, and the friction parameters of the horizontal subsystem in the co-simulation are set as f_s1a = 90, f_s2a = 300, f_s3a = 85, f_c1a = 20, f_c2a = 160, and f_b1a = 20. The friction parameters are determined based on two considerations: (1) Typical ranges of friction coefficients for electromechanical transmission systems (e.g., ball screws and servo motors) in engineering practice, where static friction-related parameters (e.g., f_s1h, f_s1a) are set to larger values to reflect the initial motion resistance, and viscous friction parameters (e.g., f_b1h, f_b1a) are calibrated to match the velocity-dependent damping characteristics of the transmission components; (2) Consistency with the continuously differentiable friction model structure (Equations (13) and (20)), where parameters such as f_s2h, f_s3h (vertical subsystem) and f_s2a, f_s3a = (horizontal subsystem) are adjusted to simulate the Stribeck effect, ensuring the model captures the transition from static to dynamic friction. These values are validated to induce noticeable friction nonlinearity in the system, which is necessary to test the compensation effectiveness of the ARSTC controller.

In addition, the harmonic superposition method is used to construct a stochastic road surface model as a disturbance to join the co-simulation process in this paper. The simulation adopts the Class E pavement excitation model referenced in [23], which is a typical severe road condition with irregular bumps and vibrations. The driving speed is set to 30 km/h to simulate the dynamic disturbances transmitted to the TCEAS during vehicle movement. The magnitudes of these interferences ensure good consistency with engineering practice. We calibrate the interference range to match the measurement data of the on-board electromechanical system under Class E road conditions, ensuring that the interference can represent the real working environment.

The following three controllers are selected for comparison and validation by the co-simulation process.

(1)

ARSTC: This is an adaptive robust stable tracking controller that considers the friction compensation proposed in this paper. The controller parameters are chosen as k_1h = 5000, k_2h = 1000, and k_2sh = 1200 for the vertical subsystem and k_1a = 8500, k_2a = 1600, and k_2sa = 2000 for the horizontal subsystem. The unknown parameter ranges of the system are θ_max = [500, 200, 200, 1000, 500, 500]^T, θ_min = [0, 0, 0, 0, 0, 0, 0]^T, and the parameter adaptive gain matrix Γ = diag{60, 0.5, 1.5, 110, 6.6, 4}.

(2)

ARSC: This is an adaptive robust stable tracking controller without a friction compensation term. The comparison with this controller can verify the effectiveness of the continuous friction model in the ARSTC controller in compensating the friction nonlinearity of the two-axis coupled electromechanical actuation system. To ensure the fairness of the comparison, the parameters of this controller are consistent with the ARSTC controller.

(3)

ARC: This is a general adaptive controller that does not take into account the role of the nonlinear robust control law, i.e., the parameters k_2sh and k_2sa are set to zero. The strong robustness of the nonlinear robust control law in the ARSTC controller can be verified by comparison with this controller. To ensure the fairness of the comparison, the rest of the control gains are consistent with the ARSTC controller.

The same gain setting ensures a fair comparison of control structures, and theoretical analysis of gain adjustments confirms the following: ARSC and ARC cannot achieve superior performance by simply increasing gains due to chattering and stability risks. ARSTC’s advantages stem from its integrated adaptive-friction and cross-coupling compensation, not gain tuning—strengthening the validity of its core contributions.

To quantitatively assess the tracking effectiveness of three controllers for the TCEAS, the statistical characteristic parameters of the tracking error are used as the evaluation indexes: the maximum value of the absolute value of the tracking error, Me, is selected to represent the deviation limit of the system under the extreme working conditions, the average value, Ae, reflects the average level of the overall tracking accuracy, and the standard deviation, Se, quantifies the degree of dispersion of the error sequence in order to measure the control stability.

Remark 1. 

To guarantee the effective use of the ARSTC controller in TCEAS, there are two methods that can usually be applied to determine the values of the design control parameters. The first approach is to mathematically compute the k₁, k₂, and k_2s values such that the matrix Λ defined by (43) is a positive definite. Although this method is relatively rigorous, it suffers from additional cumbersome mathematical derivations that greatly increase the complexity of control parameter adjustment. This leads to limitations in engineering applications. For an alternative, a practicable method is to directly select larger values of k₁, k₂, and k_2s without considering specific prerequisites. In our manuscript, we adopt the second method, which is convenient for online adjustment of control gain and requires less offline work. In the co-simulation, the control gains k₁, k₂, and k_2s were carefully and cautiously adjusted, and then k₁, k₂, and k_2s were gradually increased to ensure that the TCEAS obtains better stability performance; finally, the value of k₁, k₂, and k_2s were appropriately increased to obtain the most satisfactory control effect.

4.1. Positioning Angle Signal Tracking

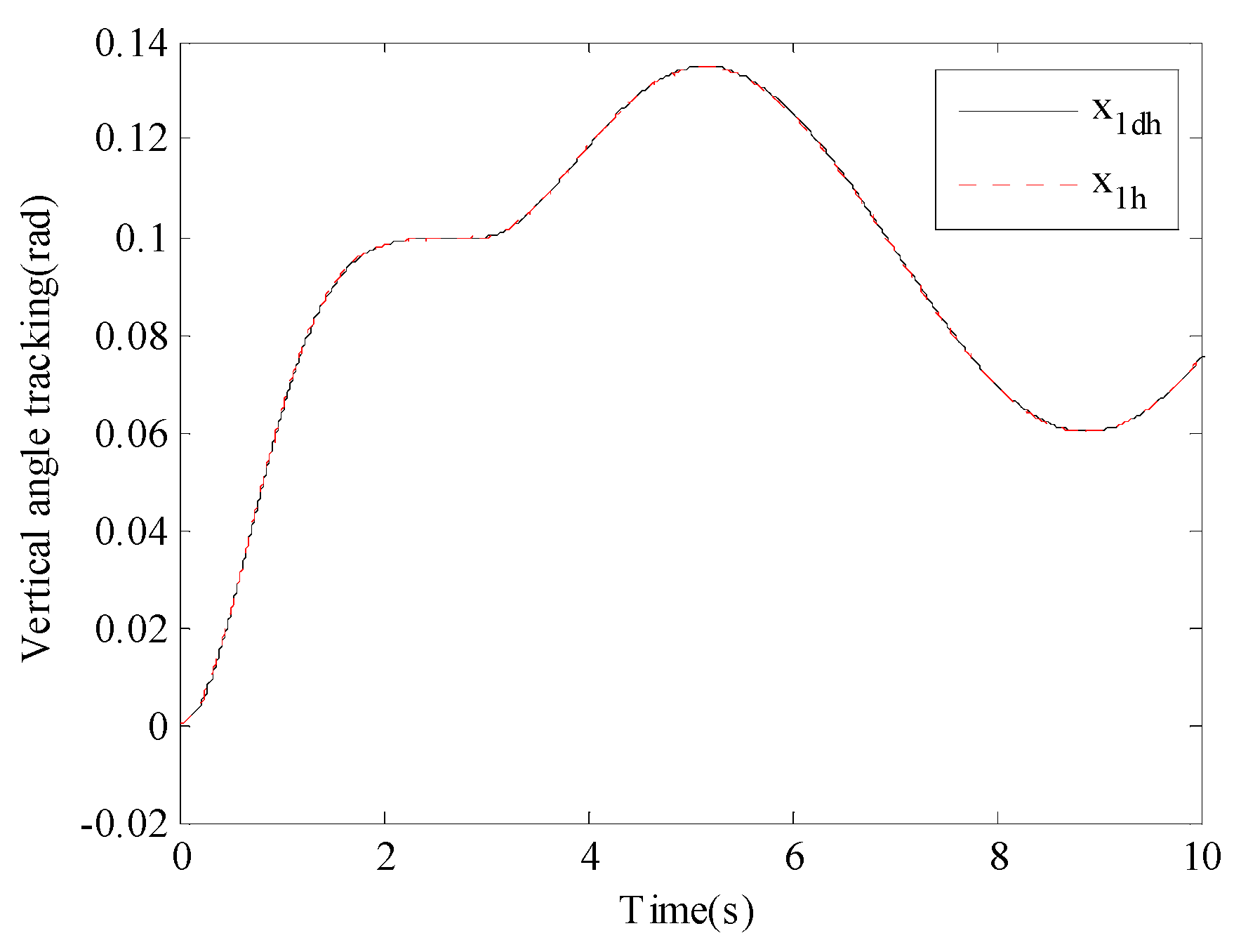
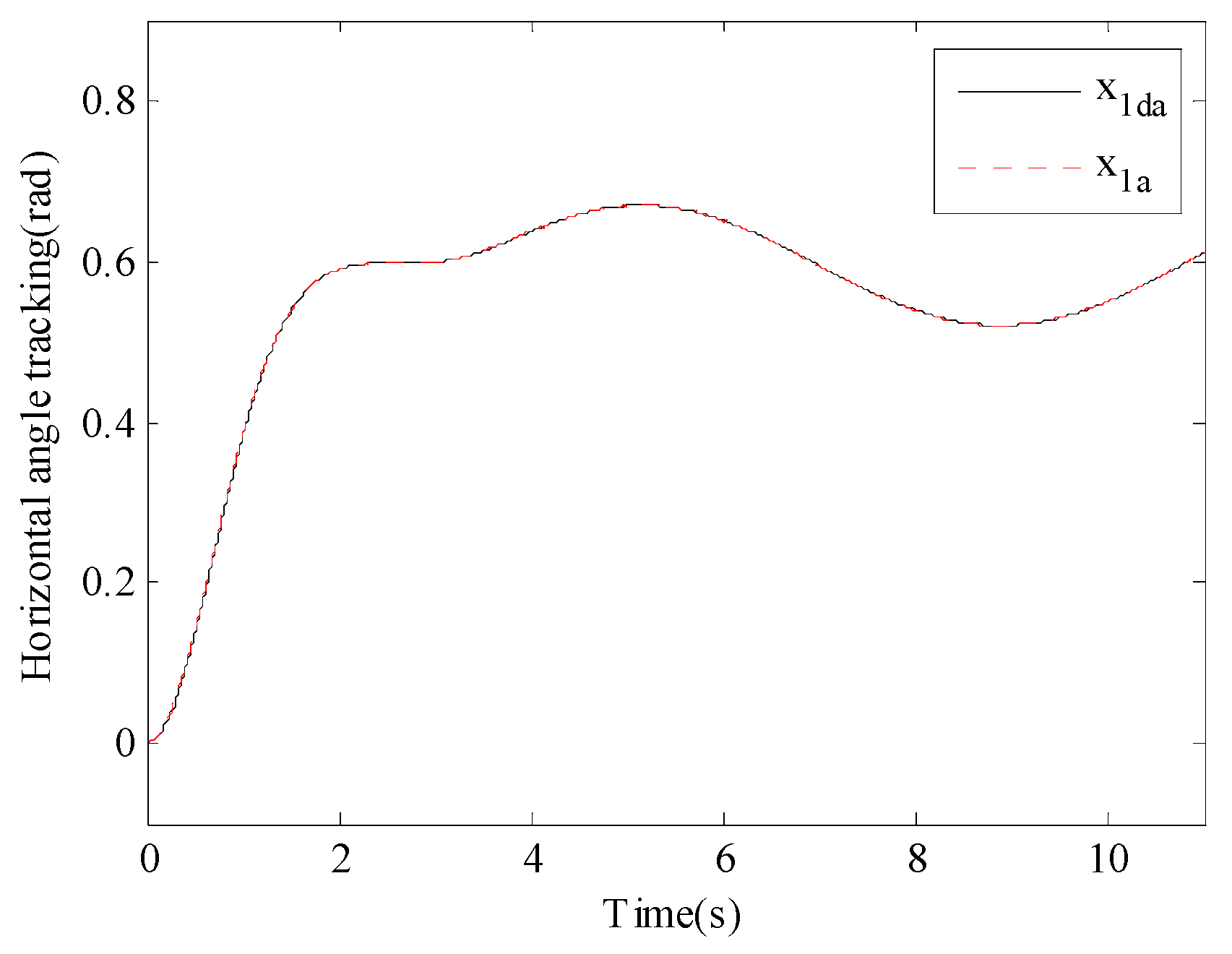
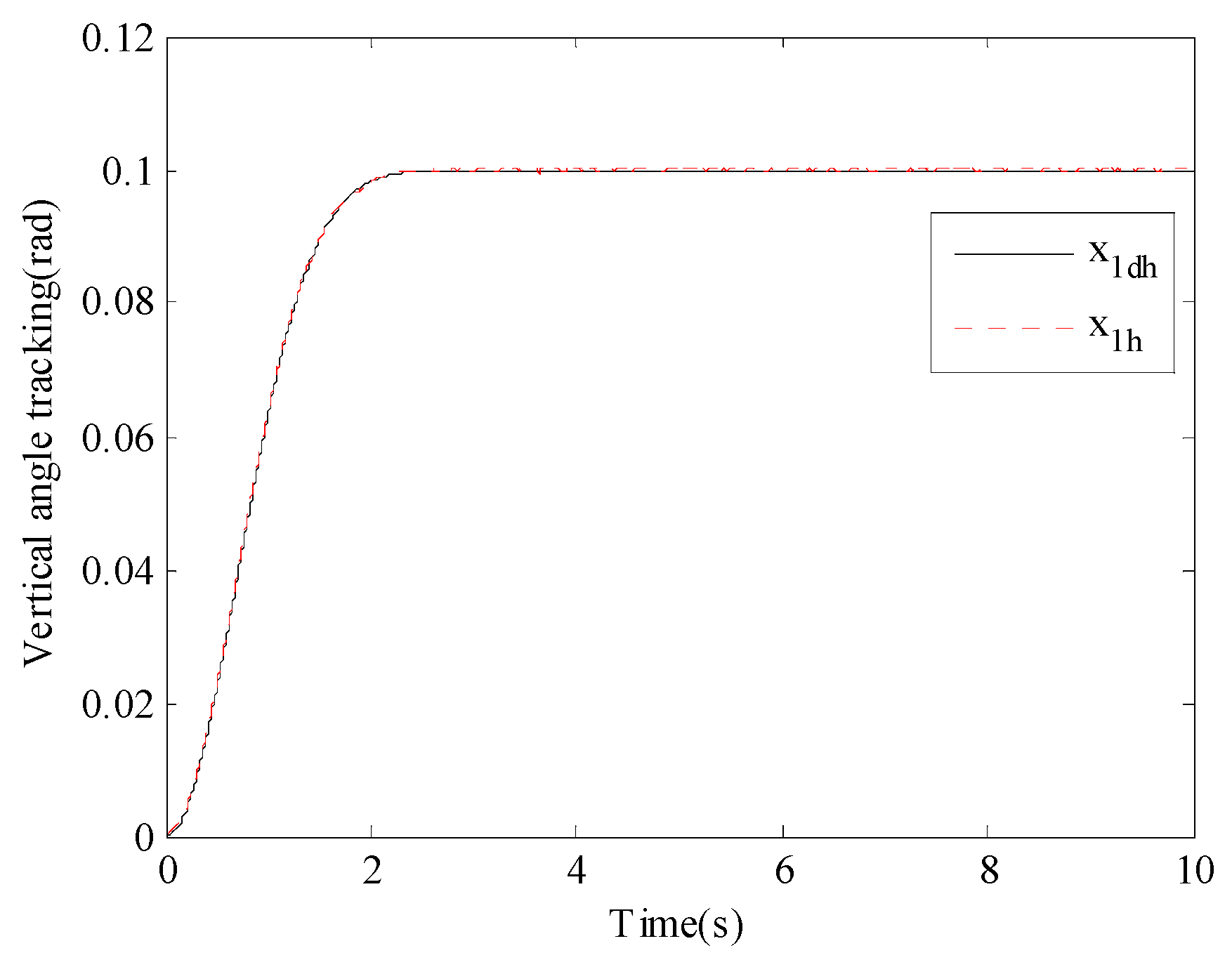
Given the reference motion angle signal of the vertical subsystem $x_{1dh}(t)=0.1(1-e^{-t^2})\mathrm{rad}$, the reference motion angle signal of the horizontal subsystem $x_{1da}(t)=0.6(1-e^{-t^2})\mathrm{rad}$, the simulation time is set to 10 s. This desired tracking signal is able to check the steady state control quality and the positioning accuracy for TCEAS. Figure 4 and Figure 5 show the tracking process of the actual motion angle of the TCEAS to the reference motion angle command under the action of the ARSTC controller. The numerical calculation results show that the coincidence degrees of the tracking trajectories of the vertical subsystem and the horizontal subsystem with the reference curves both exceed 95%, verifying the superiority of the presented controller.

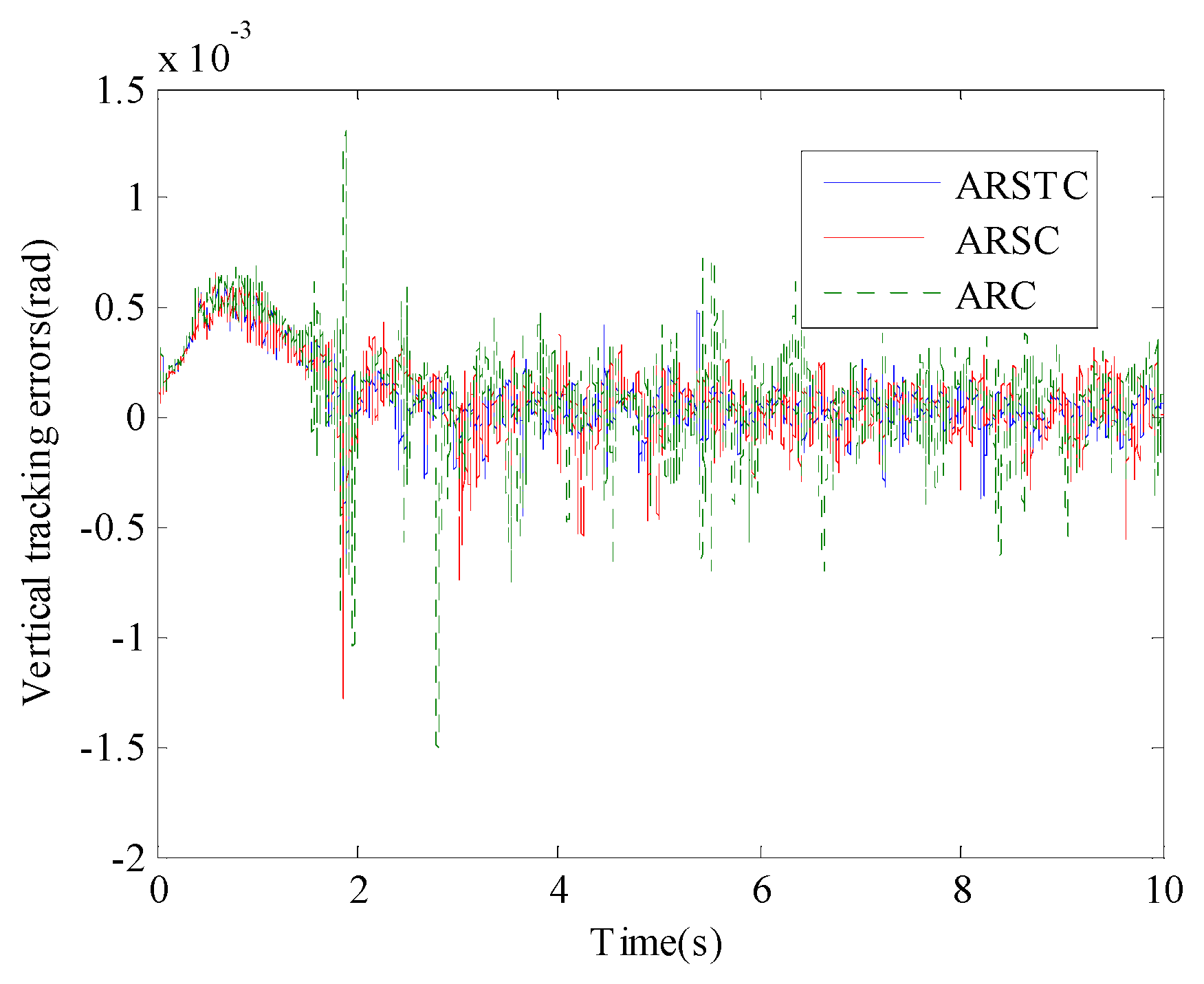
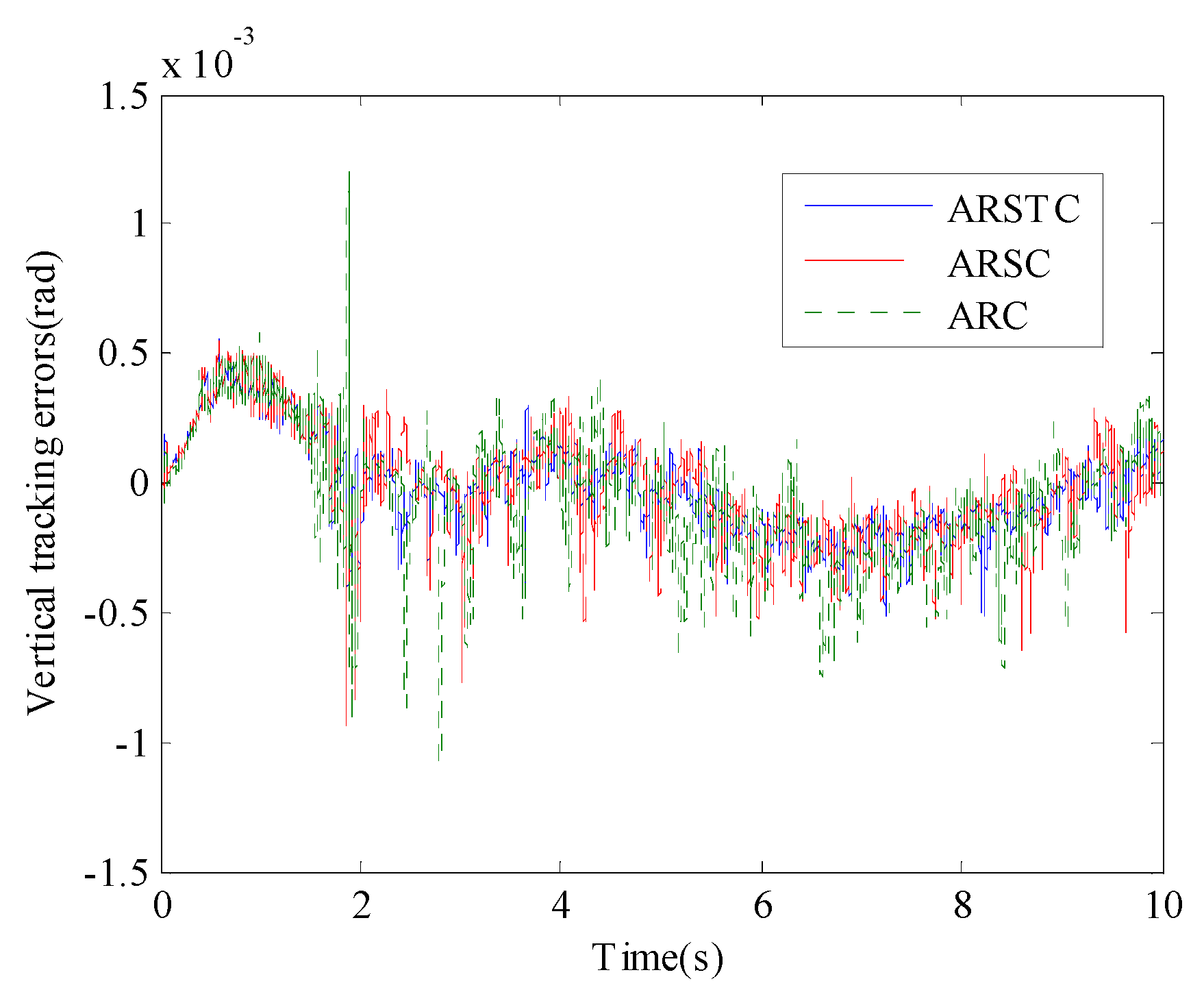
Figure 6 presents the comparison curves of tracking errors of the vertical subsystem under the three controllers of ARSTC, ARSC, and ARC. Even on the E-class road surface at 30 km/h, all three controllers can maintain the stability of the vertical subsystem. The positioning accuracy of the ARSTC controller for the vertical subsystem is better than that of the ARSC and ARC controllers because the ARSTC controller compensates for the unconsidered system friction by means of a smooth friction model in combination with an adaptive method, which greatly reduces the effect of friction nonlinearity and model uncertainty. Meanwhile, comparing with

Table 1. Performance evaluation indicators of the vertical subsystem.

Indexes (mrad)	Me	Ae	Se
ARSTC	0.4892	0.06481	0.07844
ARSC	0.5490	0.09726	0.1171
ARC	0.7249	0.1449	0.1198

, it can also be further found that the positioning accuracy of ARSTC is better than that of ARSC and ARC, which reflects the superiority of feed-forward compensation of friction characteristics and robust suppression of uncertainty.

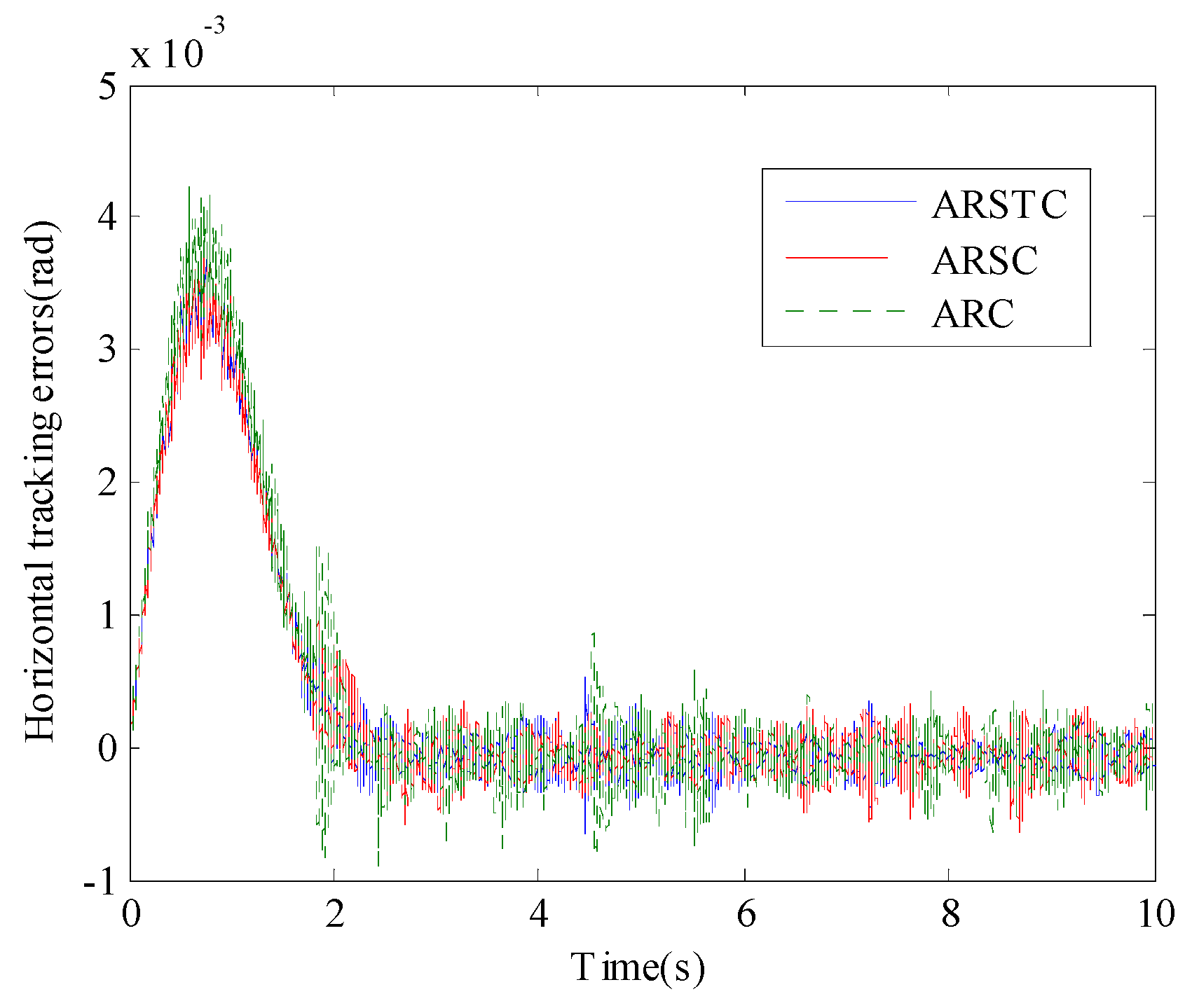
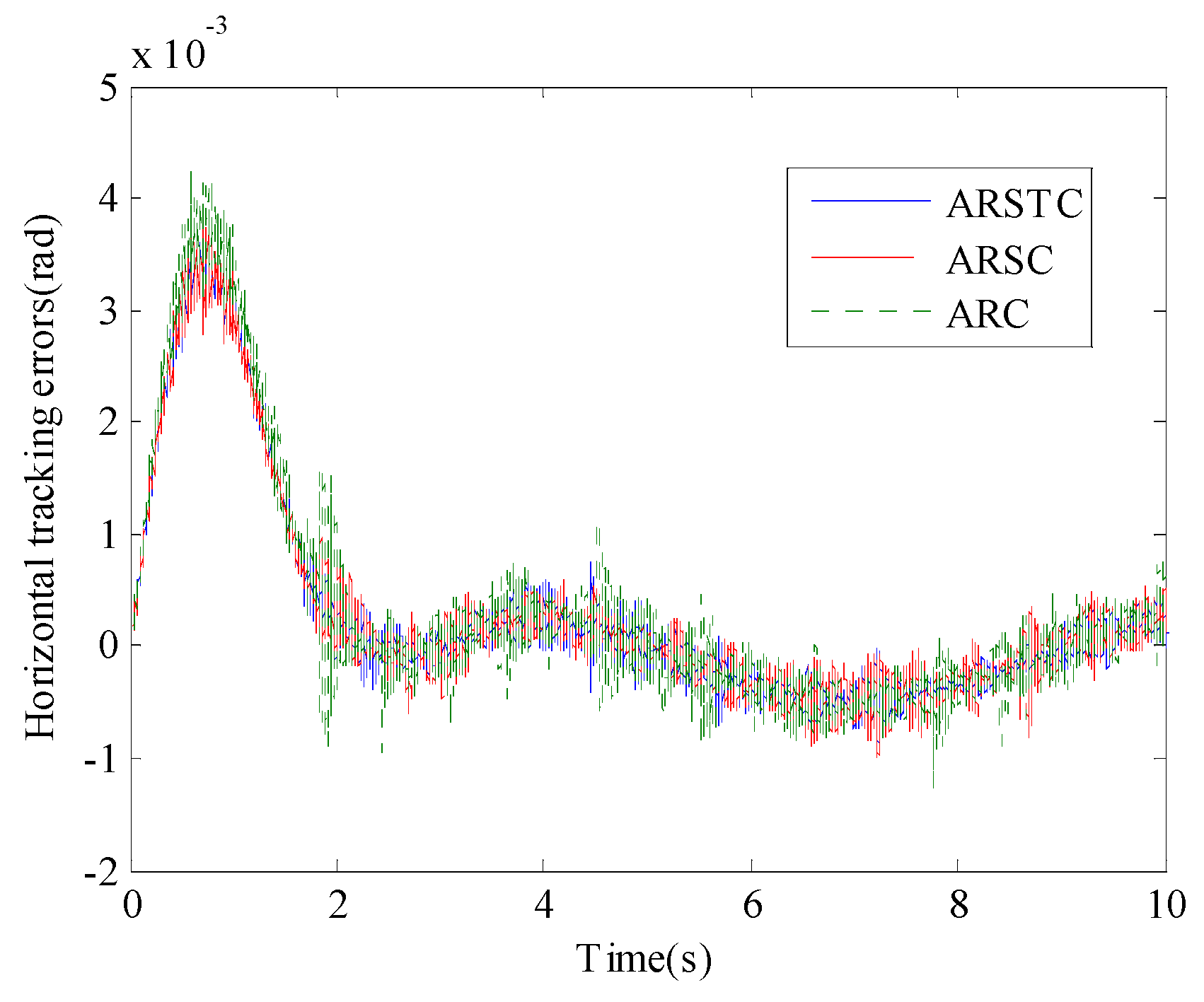
Figure 7 shows the comparative tracking error curves of the horizontal subsystem under the action of the three controllers ARSTC, ARSC, and ARC, and

Table 2. Performance evaluation indicators of the horizontal subsystem.

Indexes (mrad)	Me	Ae	Se
ARSTC	0.4952	0.1020	0.1100
ARSC	0.7288	0.1284	0.1504
ARC	0.7615	0.1400	0.1126

presents the steady-state performance indicators of the three controllers. The ARSTC control method also ensures that the horizontal subsystem achieves the best control result, once again demonstrating the feasibility of friction compensation and adaptive robust stable tracking control. Based on the current working conditions, although the external disturbances are intense, the proposed ARSTC controller can ensure the high-precision angular positioning of the TCEAS.

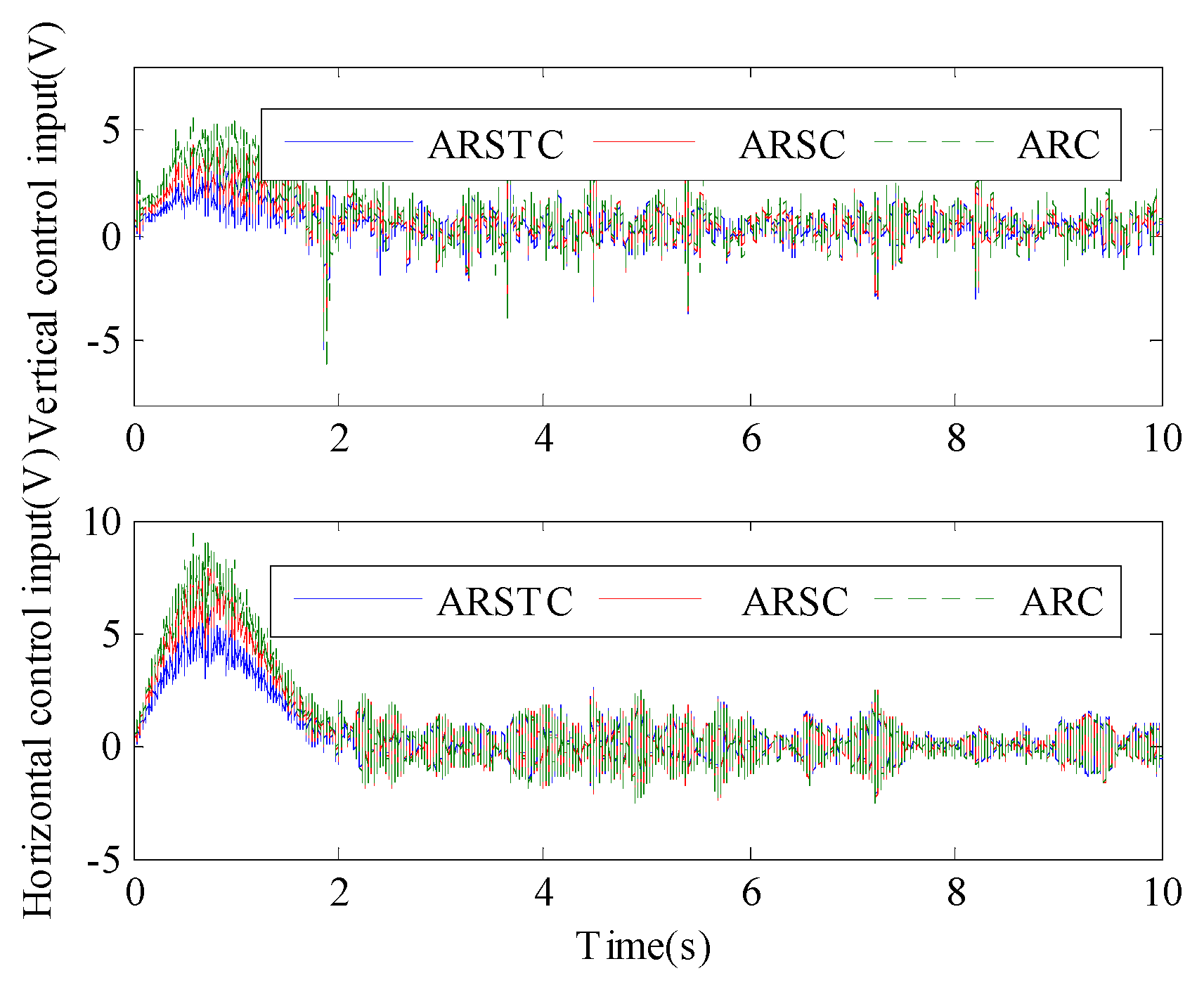
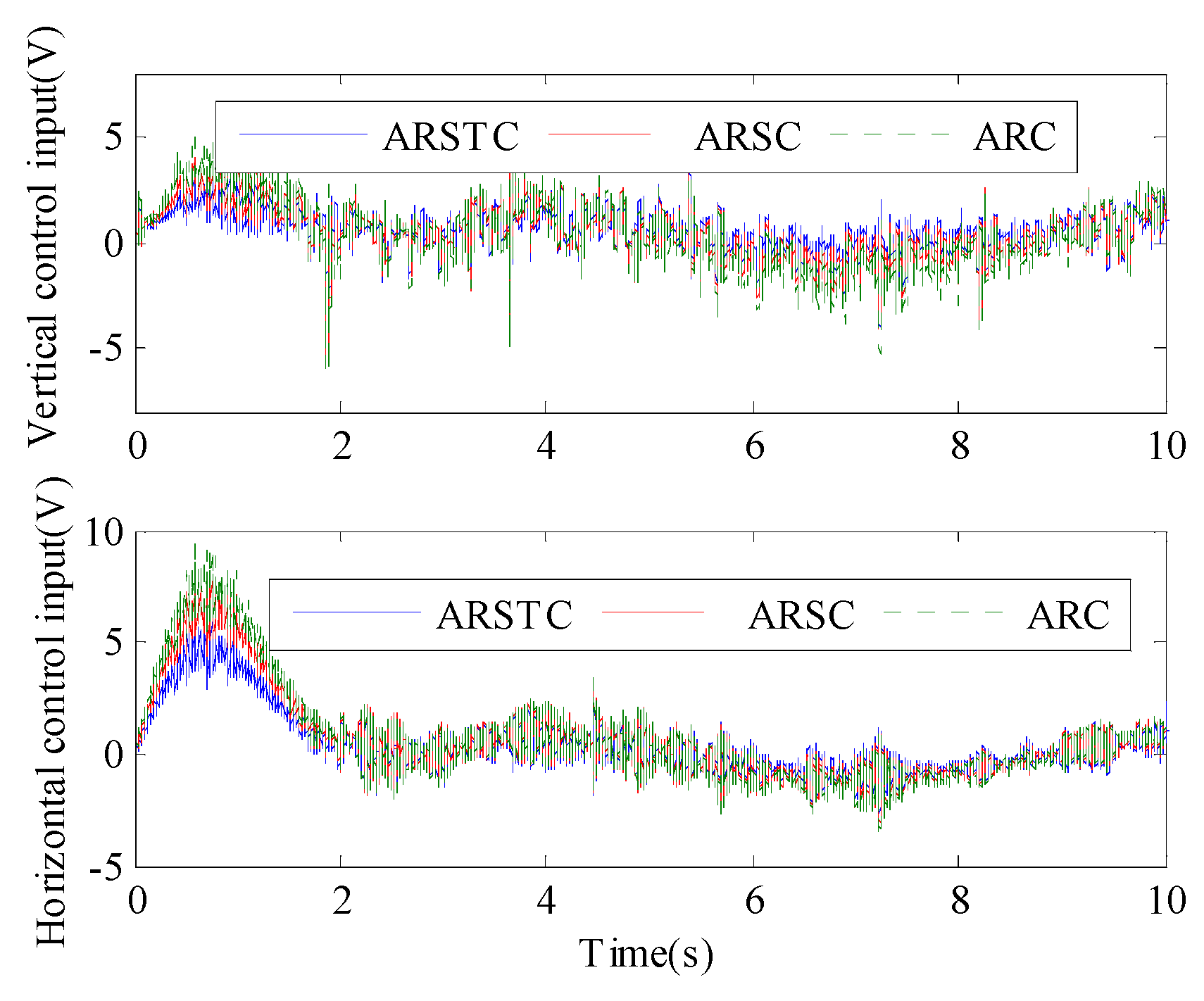
The parameter adaptive curves of the TCEAS under the action of the ARSTC controller are shown in Figure 8 and Figure 9, which prove the reliability for parameter adaptive function derived based on the Lyapunov function. The control input processes are presented in Figure 10, and they are continuously bounded. The results in Figure 10 show that the high frequency chattering of the control inputs of ARSTC is lower than that of ARSC for both vertical and horizontal subsystems, and the amplitude of the control inputs of ARC is the most drastic. This result shows the advantage of integrated friction compensation and nonlinear robustness of the proposed ARSTC controller, which has the lowest control cost.

4.2. Servo Angle Signal Tracking

We further verify the dynamic tracking performance of the TCEAS. Within the time range of 0 to 3 seconds, the reference motion angle signal of the vertical subsystem is $x_{1dh}(t)=0.1(1-e^{-t^2})\mathrm{rad}$, and the reference motion angle signal of the horizontal subsystem is $x_{1da}(t)=0.6(1-e^{-t^2})\mathrm{rad}$. When the time is greater than 3 s, the vertical and horizontal subsystems switch to servo motion angle signals, respectively: $x_{1dh}(t)=0.1(1-e^{-t^2})+0.04\sin \left[0.8(t-3)\right]\left[1-e^{-(t-3)}\right]\mathrm{rad}$ and $x_{1da}(t)=0.6(1-e^{-t^2})+0.08\sin \left[0.8(t-3)\right]\left[1-e^{-(t-3)}\right]\mathrm{rad}$. The simulation time is set to 10 s. This design captures both extreme transitions (t = 3 s) and continuous tracking of the two key operational modes for military electromechanical systems. The given expected tracking angle signal can test the dynamic tracking effect and servo stability accuracy of the proposed control strategy.

From Figure 11 and Figure 12, it is clear that the ARSTC strategy still ensures the best tracking performance for TCEAS. Even when the angular command of follower tracking is completed under highly maneuverable driving environment, the stabilization accuracy of the vertical subsystem can still reach 0.1450 mrad, and the stabilization accuracy of the horizontal subsystem can reach 0.5482 mrad. The various indicators in

Table 3. Performance evaluation indicators of positioning angle tracking of the vertical subsystem.

Indexes (mrad)	Me	Ae	Se
ARSTC	0.5574	0.1450	0.1822
ARSC	0.9365	0.1674	0.2107
ARC	1.2018	0.1973	0.1552

and

Table 4. Performance evaluation indicators of positioning angle tracking of the horizontal subsystem.

Indexes (mrad)	Me	Ae	Se
ARSTC	3.7124	0.5482	0.9239
ARSC	3.8467	0.5651	0.9284
ARC	4.2372	0.6573	0.9196

indicate that the control performance of ARSTC is superior to that of the ARSC controller. Furthermore, the control effect of the ARC controller, without considering the nonlinear robust control law, is still the worst. The above results indicate that in this paper, by combining the methods of friction feedforward compensation and parameter adaptation, the influence of friction in TCEAS is reduced.

By comparing Figure 6, Figure 7, Figure 13 and Figure 14 and Table 1, Table 2, Table 3 and Table 4, with the change in the tracking command, the stability performance of the TCEAS during sinusoidal servo angle tracking has decreased to a certain extent compared with that during positioning angle signal tracking. This indicates that the servo tracking process has a relatively obvious influence on the stability accuracy of the TCEAS, which reflects the importance of a high-performance stable tracking controller from the side. When tracking sinusoidal angle signals, the control inputs of the TCEAS are shown in Figure 15, and they are also continuously bounded.

4.3. Discussion of Engineering Insights

The continuously differentiable friction model avoids discontinuity issues common in traditional piecewise models (e.g., Stribeck effect), making it more suitable for real-time control systems where smooth transitions are critical. The continuous differentiability also distinguishes it from the LuGre model, whose simplified discrete implementations may introduce velocity-dependent discontinuities in coupled systems. To specifically verify the effectiveness of friction compensation, ARSC (without friction compensation) is designed as a contrast. The consistent reduction in tracking errors (Me, Ae, Se) of ARSTC compared to ARSC under both positioning and servo tracking conditions (Table 1, Table 2, Table 3 and Table 4) directly reflects the role of friction compensation in mitigating nonlinear friction effects. Moreover, the smoother control inputs of ARSTC (Figure 10 and Figure 15) indicate that friction compensation reduces unnecessary control adjustments caused by friction disturbances, which is crucial for practical engineering applications. These results collectively confirm that friction compensation is not only a theoretical contribution but also brings measurable performance improvements.

The mathematical design of ARSTC—combining adaptive parameter estimation and robust disturbance suppression—directly addresses two conflicting engineering demands. One of these is the adaptive component: In practical applications, electromechanical systems may encounter the problem of gradual parameter drift, such as the coefficient of friction changing with temperature or component aging. The adaptive law enables the controller to “learn” these changes in real time, thus eliminating the need for frequent manual recalibration. The other is the robust component: Sudden disturbances cannot be predicted by adaptive mechanisms alone. Even under Class E road excitation, the nonlinear robust term limits peak positioning angle tracking errors to less than 0.5 mrad, ensuring that the system remains stable during vehicle movement. The bounded control inputs (Figure 9 and Figure 14) and stable parameter estimates (Figure 7 and Figure 8) confirm that ARSTC is implementable with off-the-shelf hardware. Figure 8 and Figure 9 show that parameter estimates stabilize in a bounded range (rather than diverging), which aligns with (31). Although they do not strictly match the true friction parameters, the significant reduction in tracking errors (compared to ARSC) confirms that these estimates are ‘functionally effective’ for friction compensation—a key practical goal for adaptive control in coupled electromechanical systems.

The mathematical framework is generalizable beyond two-axis systems. For example, the state-space formulation (Equation (30)) can be extended to 3+ axis systems (e.g., CNC machine tool spindles) by adding analogous friction and coupling terms, making the design a modular solution for complex actuation challenges.

5. Conclusions

This study has proposed an adaptive robust stable tracking control method with friction compensation for two-axis coupled electromechanical actuation systems, addressing the critical challenges of nonlinear friction, parameter uncertainties, and strong coupling effects. First, a continuously differentiable friction function approximated by hyperbolic tangent function is introduced to accurately characterize the complex nonlinear friction behaviors in two-axis systems, overcoming the discontinuity issues of traditional piecewise friction models. A dynamic analysis model considering friction nonlinearity and model uncertainty is established, providing a solid theoretical foundation for controller design. Second, the proposed stable tracking control algorithm is capable of estimating and compensating unknown friction parameters in real time using the adaptive component and suppressing external disturbances and model uncertainties through the robust component, which achieves faster convergence via adaptation and disturbance rejection via robustness. Stability analysis proves that the closed-loop system ensures the uniform ultimate boundedness of tracking errors, and the Lyapunov-based adaptive law guarantees the convergence of parameter estimation. Extensive co-simulation results under various working conditions demonstrate the superiority of the proposed method.

Future work focuses on designing targeted control strategies for nonlinearities in actuators of two-axis coupled electromechanical actuation systems and carrying out semi-physical simulation verification. The proposed semi-physical simulation differs from Twin-in-the-Loop or Digital Shadows in that it integrates physical actuators (rather than fully digital replicas) with simulated disturbances, focusing on validating control performance under realistic hardware constraints while controlling the complexity of environmental perturbations.