Modeling and Control for an Aerial Work Quadrotor with a Robotic Arm
Abstract
1. Introduction
2. Dynamic Modeling of the System
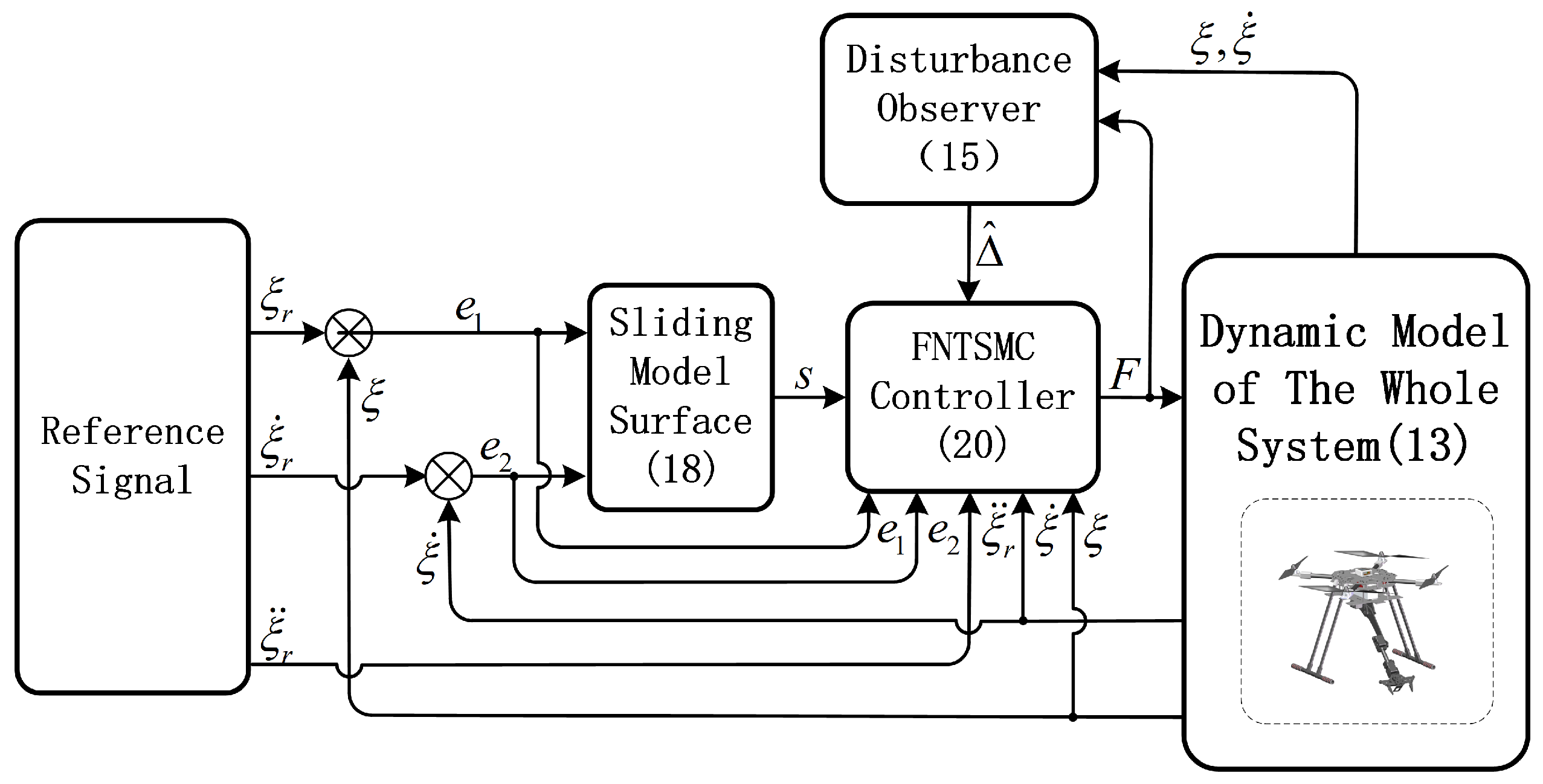
3. Control Design and Analysis
3.1. Design of a Model-Based Lumped Disturbance Observer
3.2. Design of a Composite Finite-Time Tracking Controller
3.3. Closed-Loop System Stability Analysis
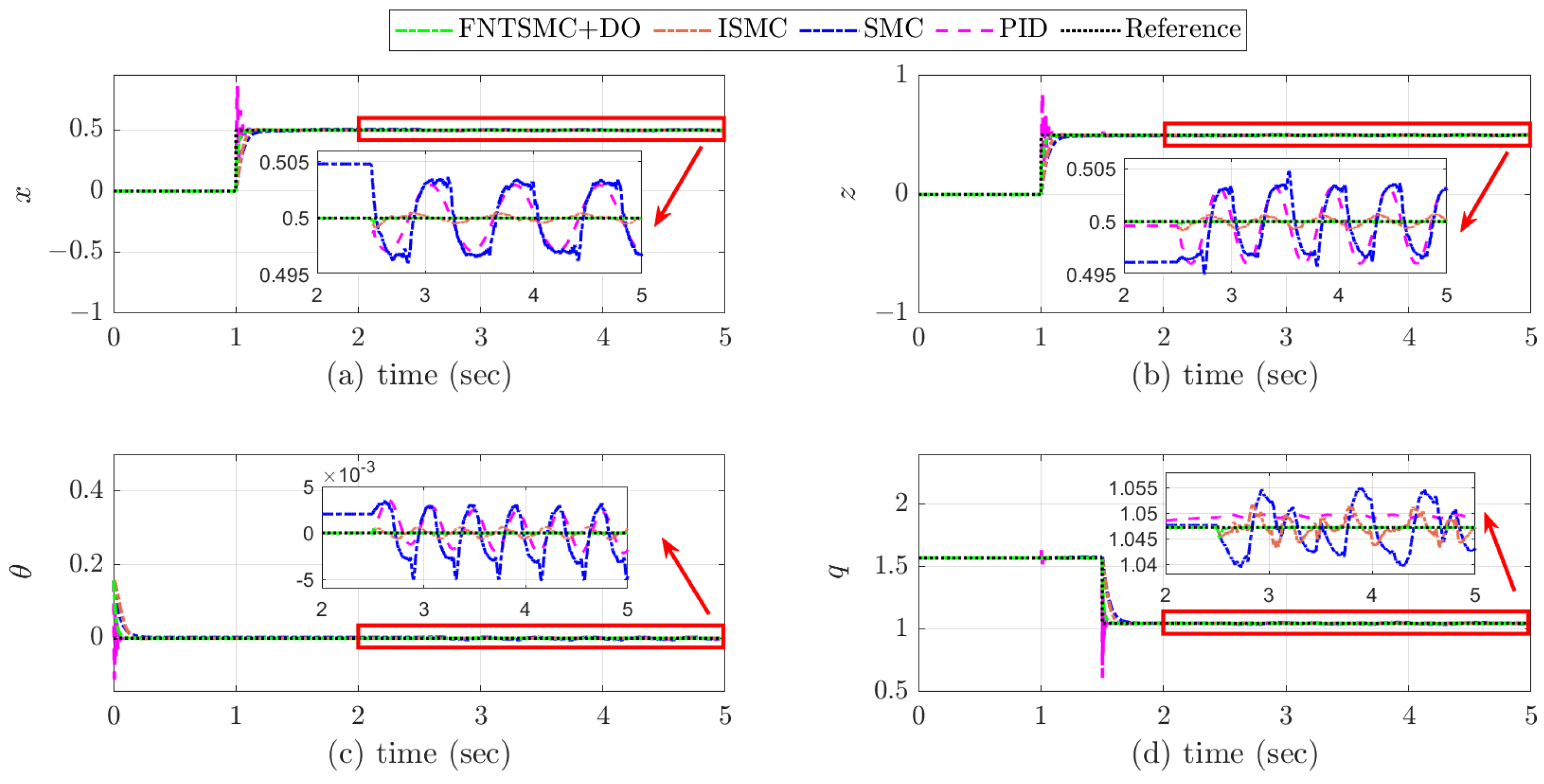
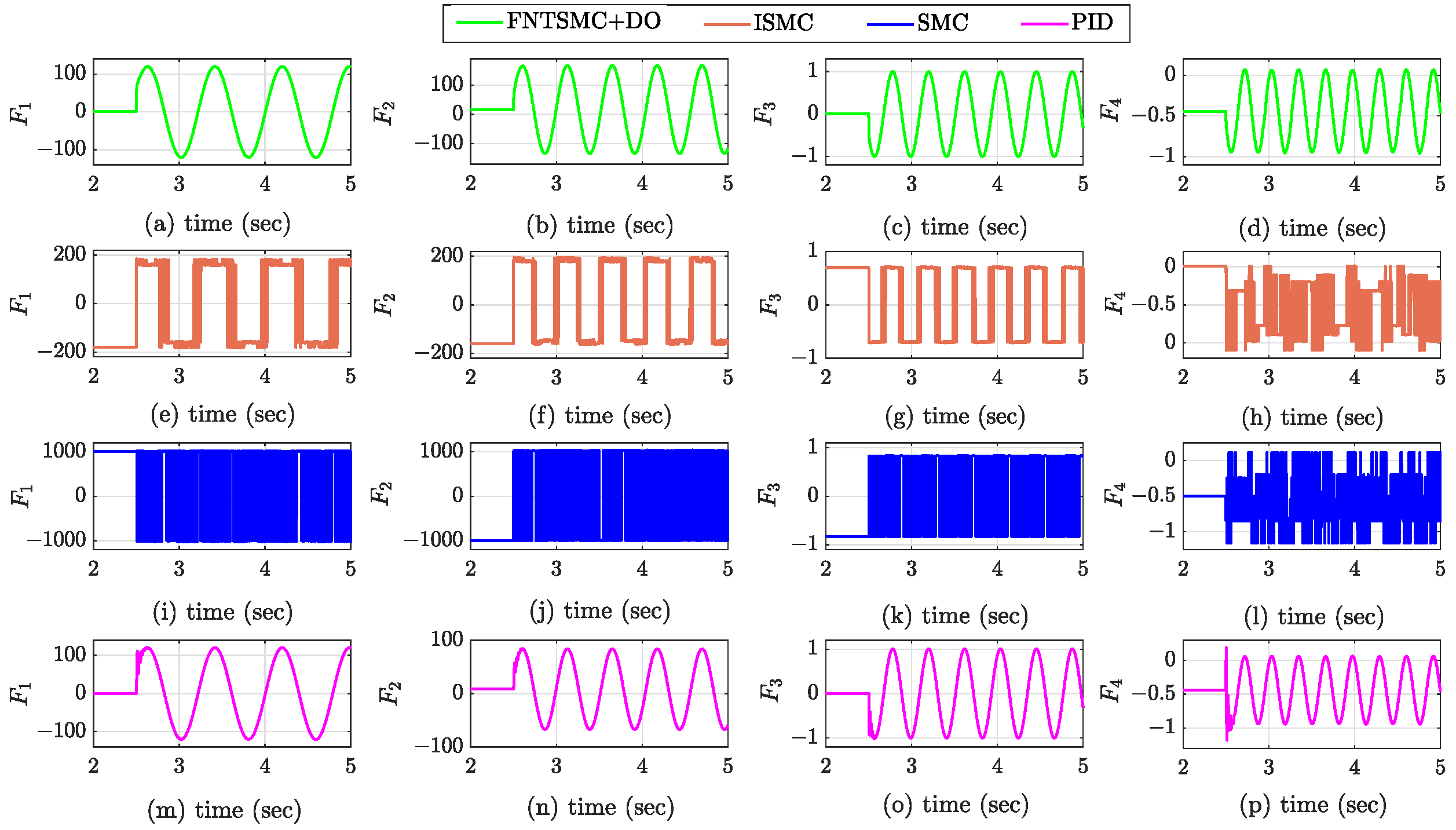
4. Simulation Results and Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ning, B.; Han, Q.; Zuo, Z.; Jin, J.; Zheng, J. Collective behaviors of mobile robots beyond the nearest neighbor rules with switching topology. IEEE Trans. Cybern. 2017, 48, 1577–1590. [Google Scholar] [CrossRef] [PubMed]
- Yu, B.; Du, H.; Wen, G.; Zhou, J.; Zheng, D. A vector-type finite-time output-constrained control algorithm and its application to a mobile robot. Robot. Intell. Autom. 2025, 45, 306–313. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, J.; Li, D.; Wang, D. Vision-Based Anti-UAV Detection and Tracking. IEEE Trans. Intell. Transp. Syst. 2022, 23, 25323–25334. [Google Scholar] [CrossRef]
- Cui, J.; Qin, Y.; Wu, Y.; Shao, C.; Yang, H. Skip Connection YOLO Architecture for Noise Barrier Defect Detection Using UAV-Based Images in High-Speed Railway. IEEE Trans. Intell. Transp. Syst. 2023, 24, 12180–12195. [Google Scholar] [CrossRef]
- Han, L.; Zhou, Z.; Li, M.; Geng, H.; Li, G.; Zhang, M. Energy-Coupling-Based Control for Unmanned Quadrotor Transportation Systems: Exploiting Beneficial State-Coupling Effects. Actuators 2025, 14, 91. [Google Scholar] [CrossRef]
- Zhu, X.; Gao, Y.; Li, Y.; Li, B. Fast Dynamic P-RRT*-Based UAV Path Planning and Trajectory Tracking Control Under Dense Obstacles. Actuators 2025, 14, 211. [Google Scholar] [CrossRef]
- Wang, G.; Chen, Y.; An, P.; Hong, H.; Hu, J. UAV-YOLOv8: A Small-Object-Detection Model Based on Improved YOLOv8 for UAV Aerial Photography Scenarios. Sensors 2023, 23, 7190. [Google Scholar] [CrossRef] [PubMed]
- Jiao, R.; Liu, Y.; He, H.; Ma, X.; Li, Z. A Deep Learning Model for Small-size Defective Components Detection in Power Transmission Tower. IEEE Trans. Power Deliv. 2022, 37, 2551–2561. [Google Scholar] [CrossRef]
- Jeong, J.; Park, S.; Lee, S.; Youn, D.; Kim, M.J. Designing an End-to-End UAV System for Insulator Inspection Under Transmission Tower Environments. In Proceedings of the International Conference on Electronics, Information, and Communication (ICEIC), Taipei, Taiwan, 28–31 January 2024; pp. 1–4. [Google Scholar]
- Zhuo, H.; Yang, Z.; You, Y.; Xu, N.; Liao, L.; Wu, J.; He, J. A Hierarchical Control Method for Trajectory Tracking of Aerial Manipulators Arms. Actuators 2024, 13, 333. [Google Scholar] [CrossRef]
- Ghadiok, V.; Goldin, J.; Ren, W. On the design and development of attitude stabilization, vision-based navigation, and aerial gripping for a low-cost quadrotor. Auton. Robot. 2012, 33, 41–68. [Google Scholar] [CrossRef]
- Fiaz, U.A.; Abdelkader, M.; Shamma, J.S. An intelligent gripper design for autonomous aerial transport with passive magnetic grasping and dual-impulsive release. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Auckland, New Zealand, 9–12 July 2018; pp. 1027–1032. [Google Scholar]
- Chermprayong, P.; Zhang, K.; Xiao, F.; Kovac, M. An integrated delta manipulator for aerial repair: A new aerial robotic system. IEEE Robot. Autom. Mag. 2019, 26, 54–66. [Google Scholar] [CrossRef]
- Qian, L.; Liu, H.H. Path-following control of a quadrotor UAV with a cable-suspended payload under wind disturbances. IEEE Trans. Ind. Electron. 2019, 67, 2021–2029. [Google Scholar] [CrossRef]
- Jafarinasab, M.; Sirouspour, S.; Dyer, E. Model-Based Motion Control of a Robotic Manipulator with a Flying Multirotor Base. IEEE/ASME Trans. Mechatronics 2019, 24, 2328–2340. [Google Scholar] [CrossRef]
- Wang, M.; Lyu, S.; Liu, Q.; Yang, Z.; Guo, K.; Yu, X. Precise End-Effector Control for an Aerial Manipulator Under Composite Disturbances: Theory and Experiments. IEEE Trans. Autom. Sci. Eng. 2024, 22, 4006–4021. [Google Scholar] [CrossRef]
- Li, Z.; Yang, Y.; Yu, X.; Liu, C.; Kaynak, O.; Gao, H. Fixed-Time Control of a Novel Thrust-Vectoring Aerial Manipulator via High-Order Fully Actuated System Approach. IEEE/Asme Trans. Mechatronics 2024, 30, 1084–1095. [Google Scholar] [CrossRef]
- Liang, J.; Chen, Y.; Wu, Y.; Miao, Z.; Zhang, H.; Wang, Y. Adaptive Prescribed Performance Control of Unmanned Aerial Manipulator With Disturbances. IEEE Trans. Autom. Sci. Eng. 2023, 20, 1804–1814. [Google Scholar] [CrossRef]
- Zhu, W.; Du, H. Global Uniform Finite-Time Output Feedback Stabilization for Disturbed Nonlinear Uncertain Systems: Backstepping-like Observer and Nonseparation Principle Design. SIAM J. Control Optim. 2024, 62, 1717–1736. [Google Scholar] [CrossRef]
- Kim, S.; Choi, S.; Kim, H.J. Aerial Manipulation Using a Quadrotor with a Two DOF Robotic Arm. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Tokyo, Japan, 3–7 November 2013; pp. 4990–4995. [Google Scholar]
- Luna, A.L.; Vega, I.C.; Carranza, J.M. Gain-Scheduling and PID Control for an Autonomous Aerial Vehicle with a Robotic Arm. In Proceedings of the IEEE 2nd Colombian Conference on Robotics and Automation (CCRA), Barranquilla, Colombia, 1–3 November 2018; pp. 1–6. [Google Scholar]
- Kim, M.J.; Kondak, K.; Ott, C. A Stabilizing Controller for Regulation of UAV With Manipulator. IEEE Robot. Autom. Lett. 2018, 3, 1719–1726. [Google Scholar] [CrossRef]
- Kim, S.; Seo, H.; Choi, S.; Kim, H.J. Vision-Guided Aerial Manipulation Using a Multirotor With a Robotic Arm. IEEE/ASME Trans. Mechatronics 2016, 21, 1912–1923. [Google Scholar] [CrossRef]
- Ouyang, Z.; Mei, R.; Liu, Z.; Wei, M.; Zhou, Z.; Cheng, H. Control of an Aerial Manipulator Using a Quadrotor with a Replaceable Robotic Arm. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 153–159. [Google Scholar]
- Afifa, R.; Ali, S.; Pervaiz, M.; Iqbal, J. Adaptive Backstepping Integral Sliding Mode Control of a MIMO Separately Excited DC Motor. Robotics 2023, 12, 105. [Google Scholar] [CrossRef]
- Ali, K.; Ulah, S.; Mehmood, A.; Mostafa, H.; Marey, M.; Iqbal, J. Adaptive FIT-SMC Approach for an Anthropomorphic Manipulator With Robust Exact Differentiator and Neural Network-Based Friction Compensation. IEEE Access 2022, 10, 3378–3389. [Google Scholar] [CrossRef]
- Lippiello, V.; Ruggiero, F. Exploiting Redundancy in Cartesian Impedance Control of UAVs Equipped with a Robotic Arm. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 3768–3773. [Google Scholar]
- Nail, M.; Jänne, N.; Ma, O.; Arellano, G.; Atkins, E.; Gillespie, R.B. Simplifying Aerial Manipulation Using Intentional Collisions. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; pp. 5359–5365. [Google Scholar]
- Wang, T.; Umemoto, K.; Endo, T.; Matsuno, F. Modeling and Control of a Quadrotor UAV Equipped With a Flexible Arm in Vertical Plane. IEEE Access 2021, 9, 98476–98489. [Google Scholar] [CrossRef]
- Abhishek, V.; Srivastava, V.; Mukherjee, R. Towards a heterogeneous cable-connected team of UAVs for aerial manipulation. In Proceedings of the American Control Conference (ACC), New Orleans, LA, USA, 25–28 May 2021; pp. 54–59. [Google Scholar]
- Davila, J.; Fridman, L.; Levant, A. Second-Order Sliding-Mode Observer for Mechanical Systems. IEEE Trans. Autom. Control 2005, 50, 1785–1789. [Google Scholar] [CrossRef]


| Parameter | Value |
|---|---|
| Mass of the quadrotor body: | |
| Mass of the robotic arm link: | |
| Length of the robotic arm link: | |
| Inertia tensor of the quadrotor along | |
| the y axis: (kg·m−2) | |
| Inertia tensor of the robotic arm along | |
| the y axis: (kg·m−2) |
| Channel | Algorithm | Adjust Time | Overshoot | IAE | ITAE |
|---|---|---|---|---|---|
| x | FNTSMC | 0.060 s | 0.00% | 0.0083 m·s | 0.0085 m·s2 |
| ISMC | 0.109 s | 1.75% | 0.0224 m·s | 0.0232 m·s2 | |
| SMC | 0.156 s | 0.00% | 0.0331 m·s | 0.0396 m·s2 | |
| PID | 0.088 s | 68.16% | 0.0107 m·s | 0.0111 m·s2 | |
| z | FNTSMC | 0.059 s | 0.00% | 0.0083 m·s | 0.0085 m·s2 |
| ISMC | 0.109 s | 0.87% | 0.0224 m·s | 0.0233 m·s2 | |
| SMC | 0.164 s | 0.00% | 0.0331 m·s | 0.0390 m·s2 | |
| PID | 0.087 s | 71.80% | 0.0118 m·s | 0.0126 m·s2 | |
| FNTSMC | 0.063 s | 0.00% | 0.0033 rad·s | rad·s2 | |
| ISMC | 0.140 s | 0.62% | 0.0103 rad·s | rad·s2 | |
| SMC | 0.168 s | 0.00% | 0.0132 rad·s | 0.0067 rad·s2 | |
| PID | 0.062 s | 71.38% | 0.0021 rad·s | rad·s2 | |
| q | FNTSMC | 0.043 s | 0.00% | 0.0060 rad·s | 0.0091 rad·s2 |
| ISMC | 0.108 s | 0.87% | 0.0236 rad·s | 0.0361 rad·s2 | |
| SMC | 0.154 s | 0.00% | 0.0308 rad·s | 0.0474 rad·s2 | |
| PID | 0.029 s | 83.42% | 0.0062 rad·s | 0.0095 rad·s2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, W.; Wu, F.; Du, H.; Li, L.; Zhang, Y. Modeling and Control for an Aerial Work Quadrotor with a Robotic Arm. Actuators 2025, 14, 357. https://doi.org/10.3390/act14070357
Zhu W, Wu F, Du H, Li L, Zhang Y. Modeling and Control for an Aerial Work Quadrotor with a Robotic Arm. Actuators. 2025; 14(7):357. https://doi.org/10.3390/act14070357
Chicago/Turabian StyleZhu, Wenwu, Fanzeng Wu, Haibo Du, Lei Li, and Yao Zhang. 2025. "Modeling and Control for an Aerial Work Quadrotor with a Robotic Arm" Actuators 14, no. 7: 357. https://doi.org/10.3390/act14070357
APA StyleZhu, W., Wu, F., Du, H., Li, L., & Zhang, Y. (2025). Modeling and Control for an Aerial Work Quadrotor with a Robotic Arm. Actuators, 14(7), 357. https://doi.org/10.3390/act14070357








