Numerical Investigation of the Tribological Performance of Surface-Textured Bushings in External Gear Pumps Under Transient Lubrication Conditions
Abstract
1. Introduction
2. Models
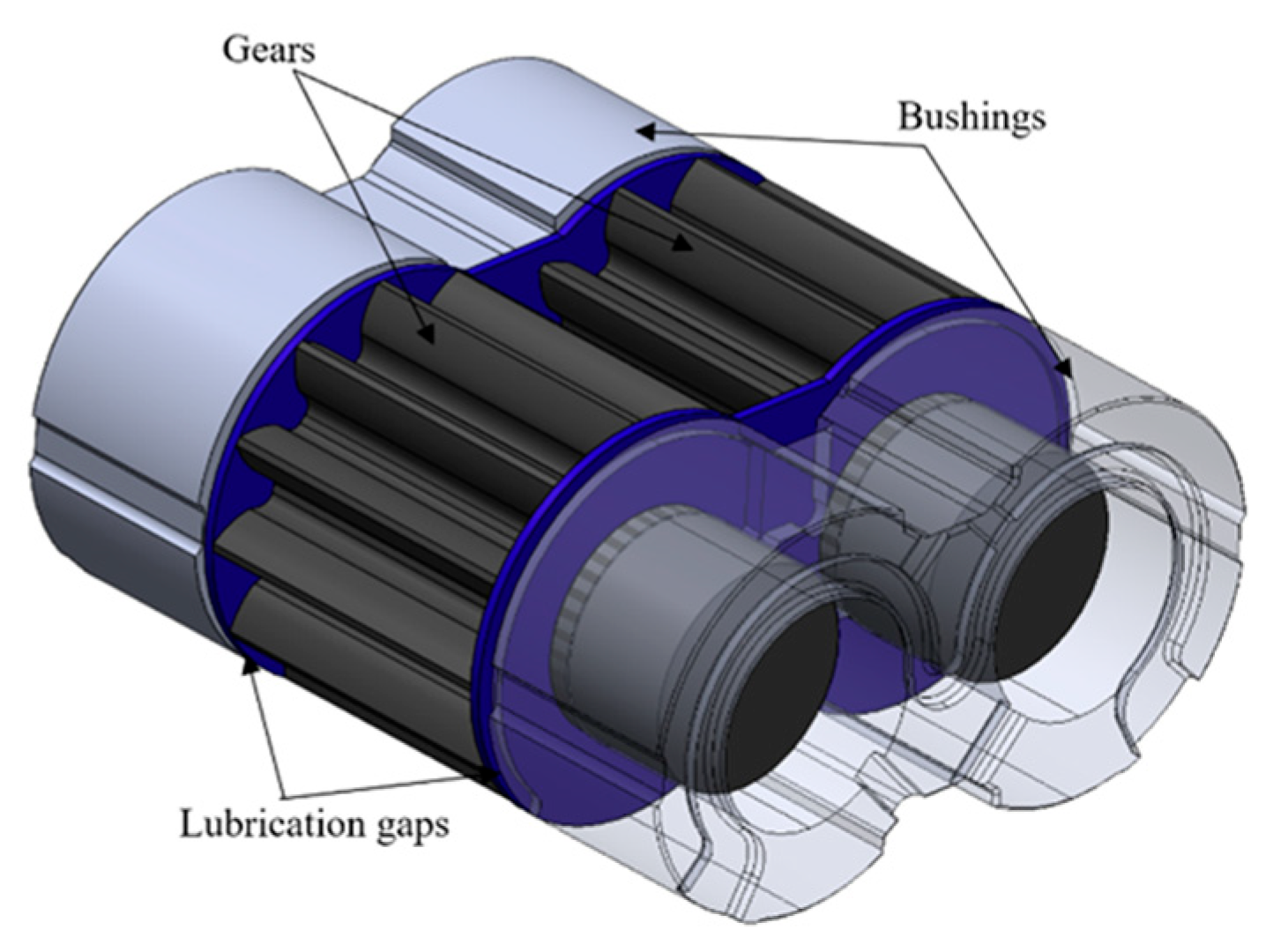
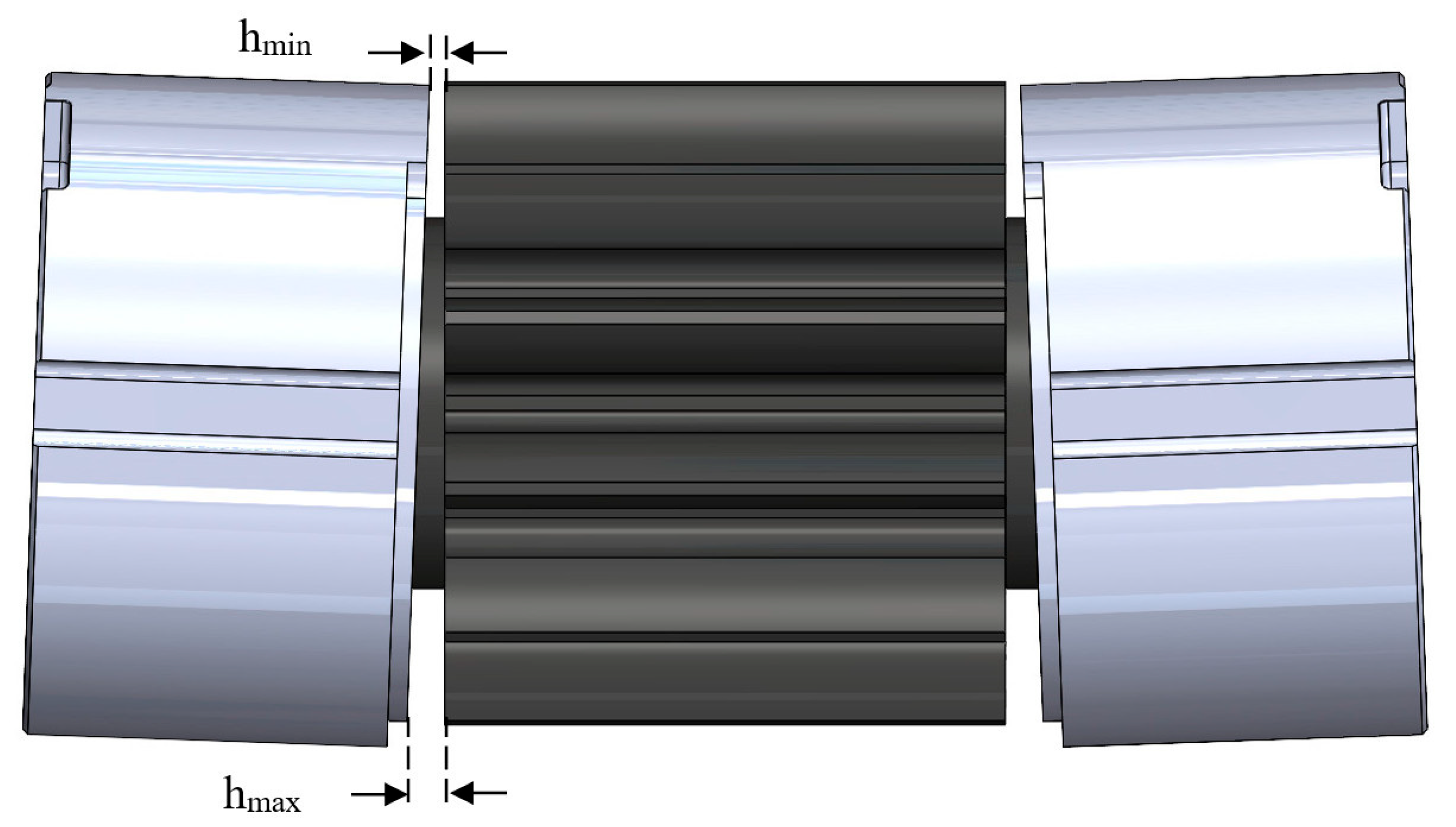
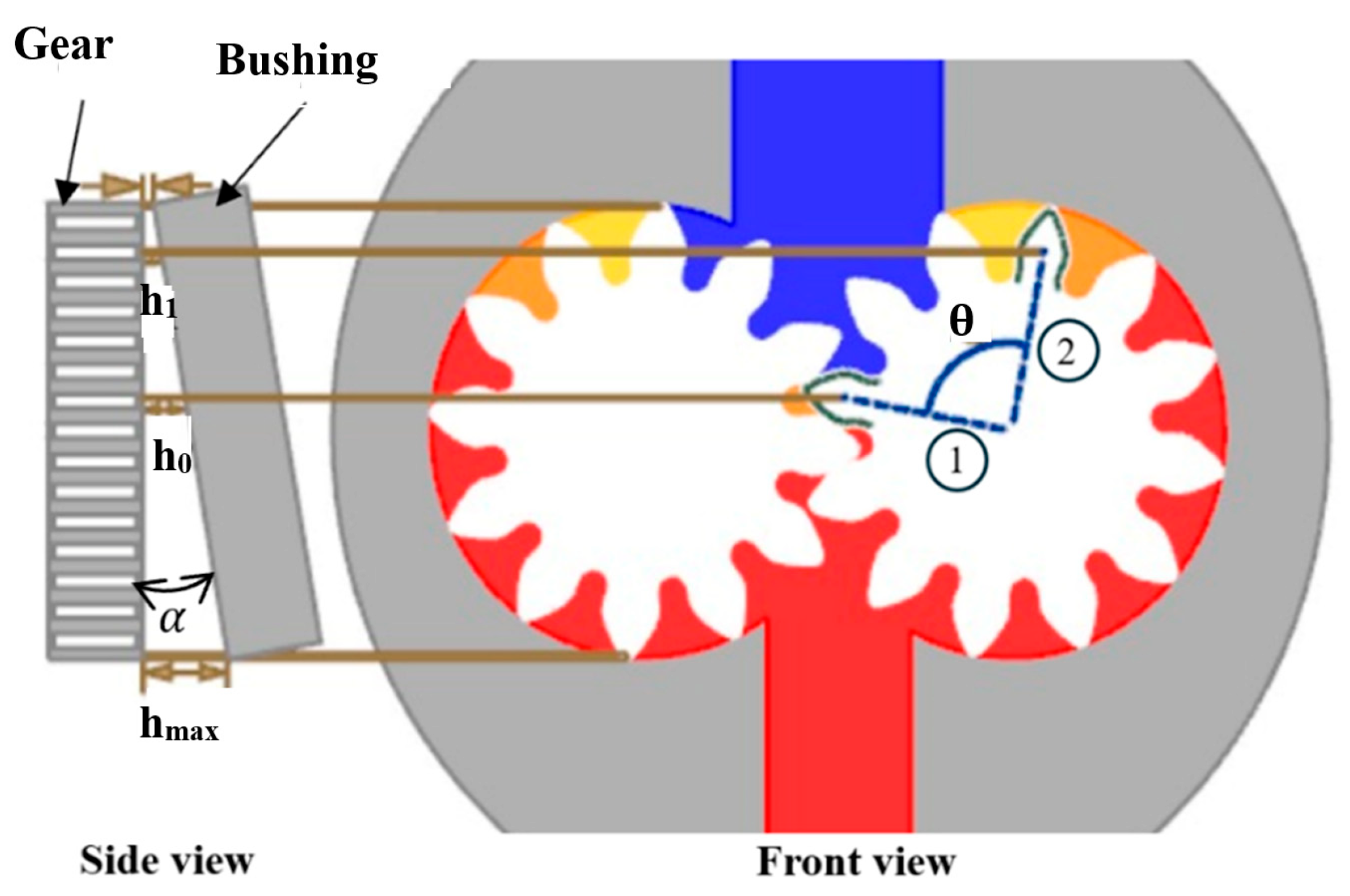
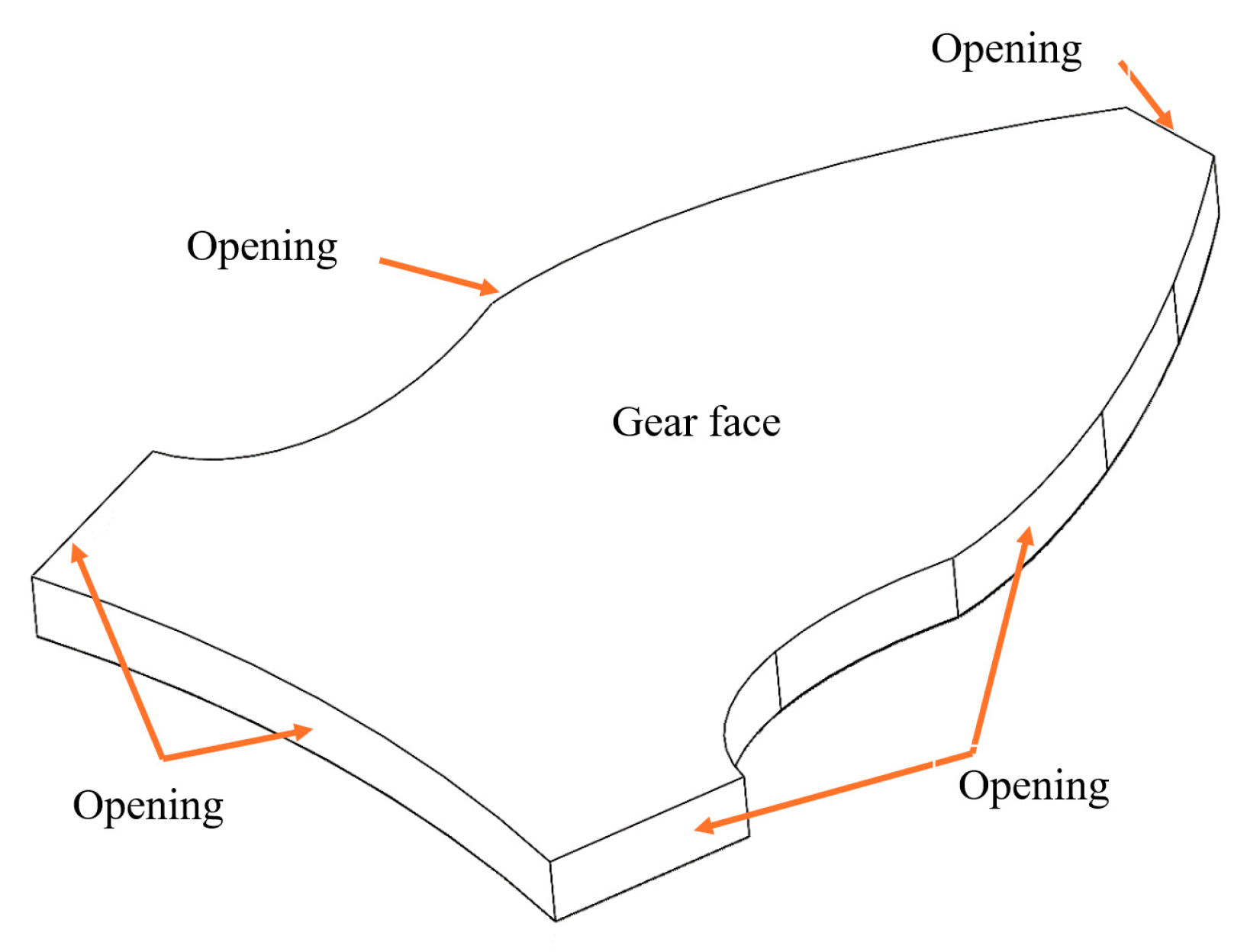
2.1. Bushing–Gear Interaction Model
2.2. Computational Model
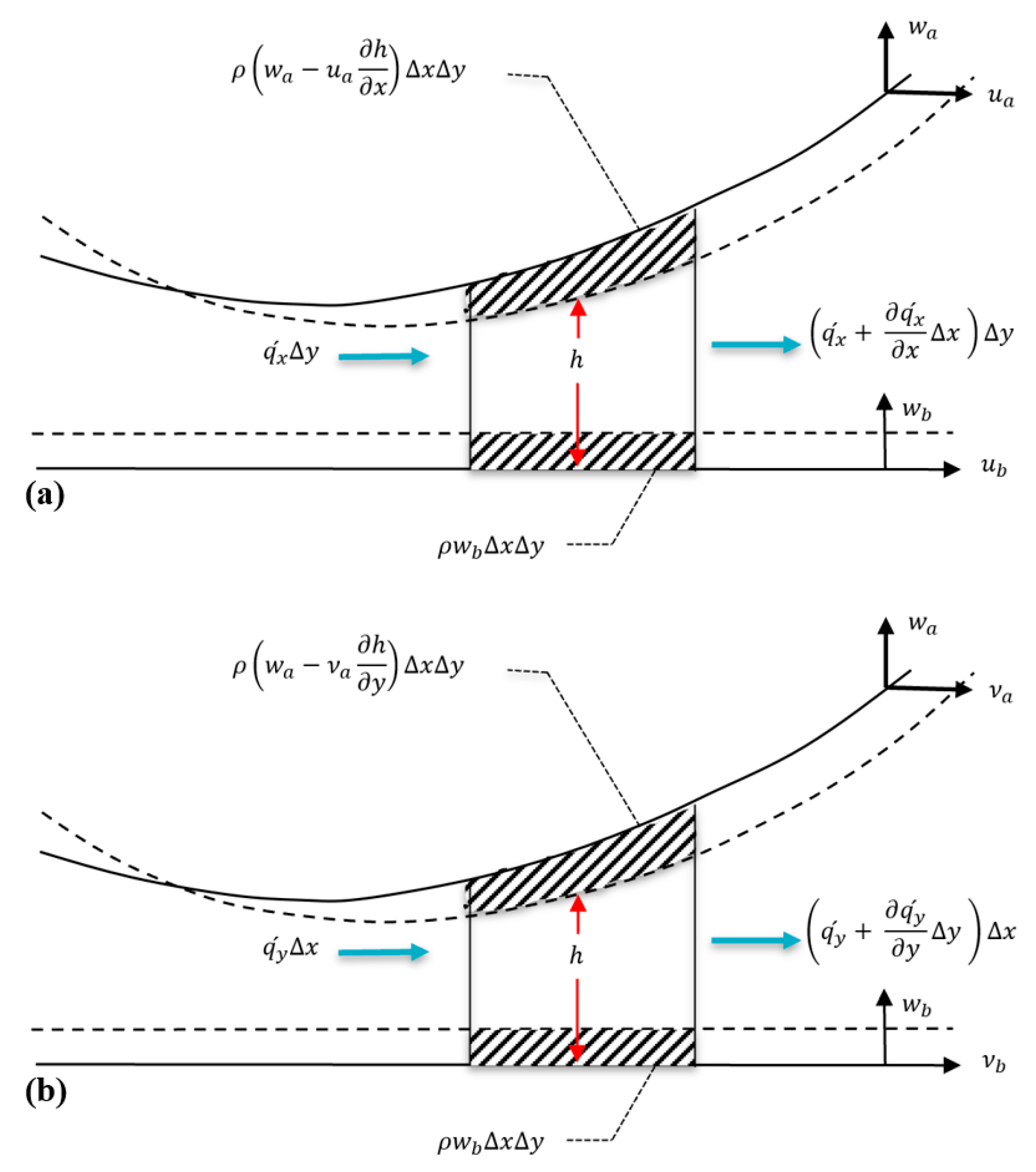
2.3. Governing Equations
2.4. Grid Independence Study
3. Results and Discussion
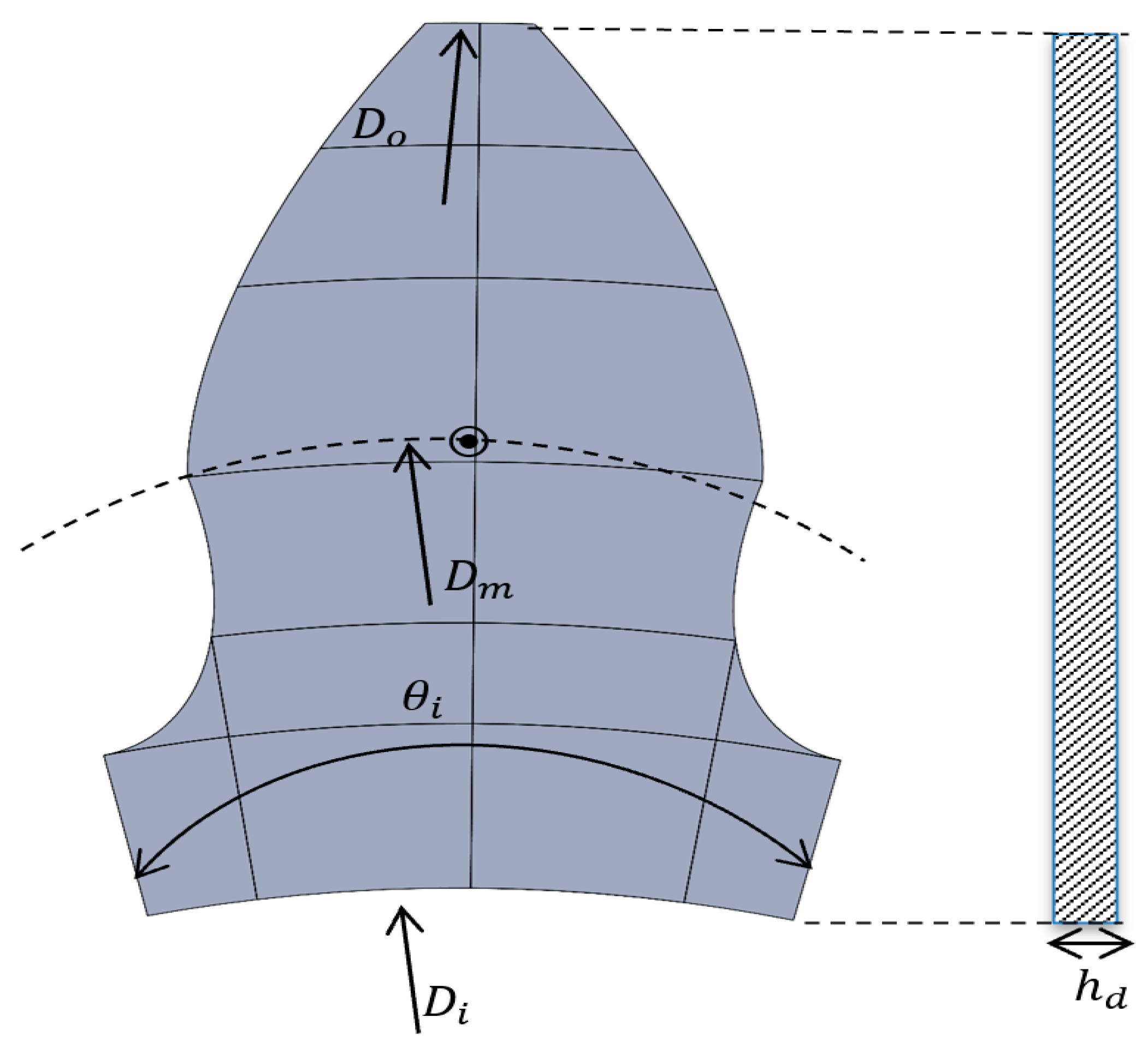
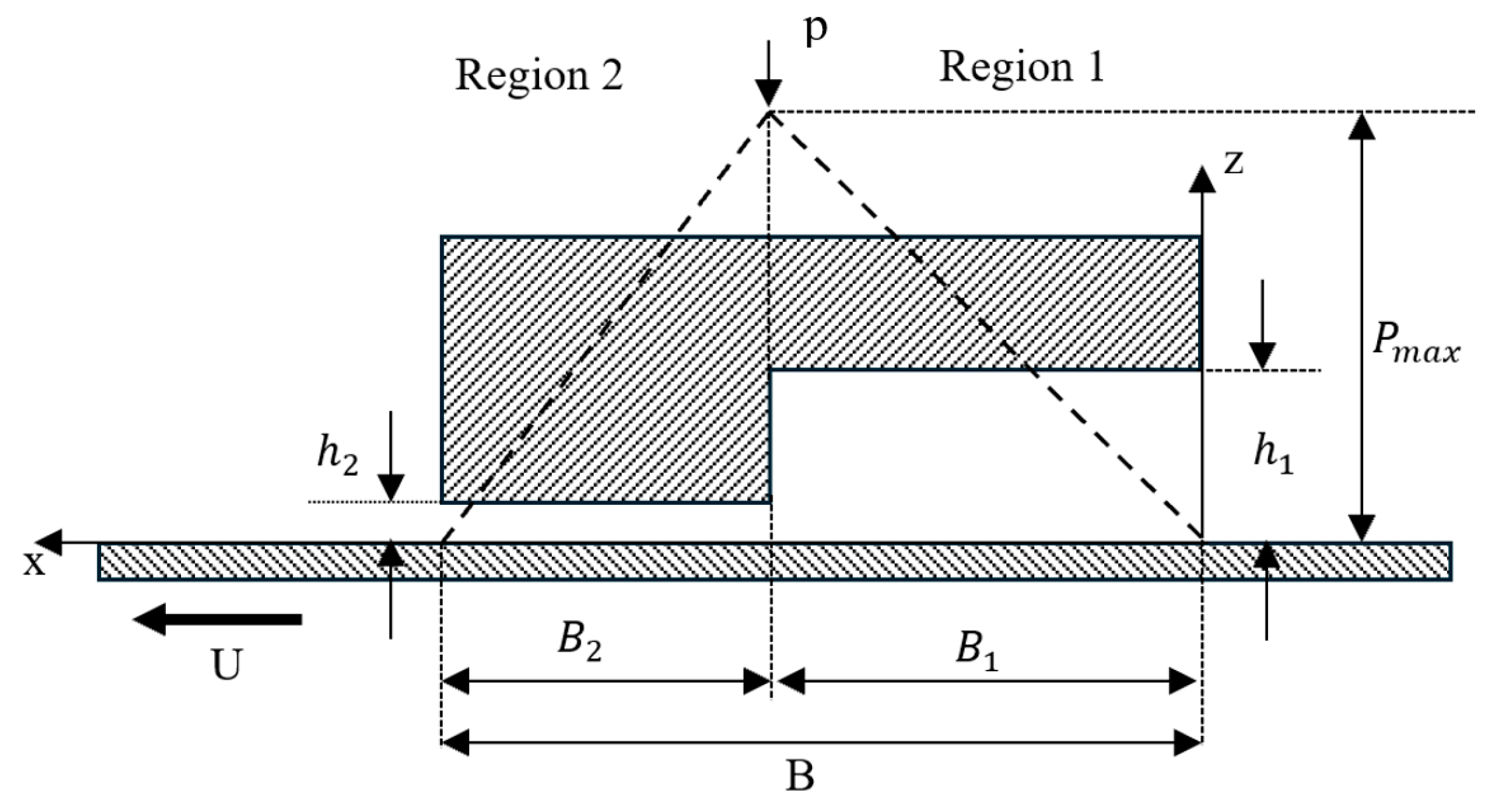
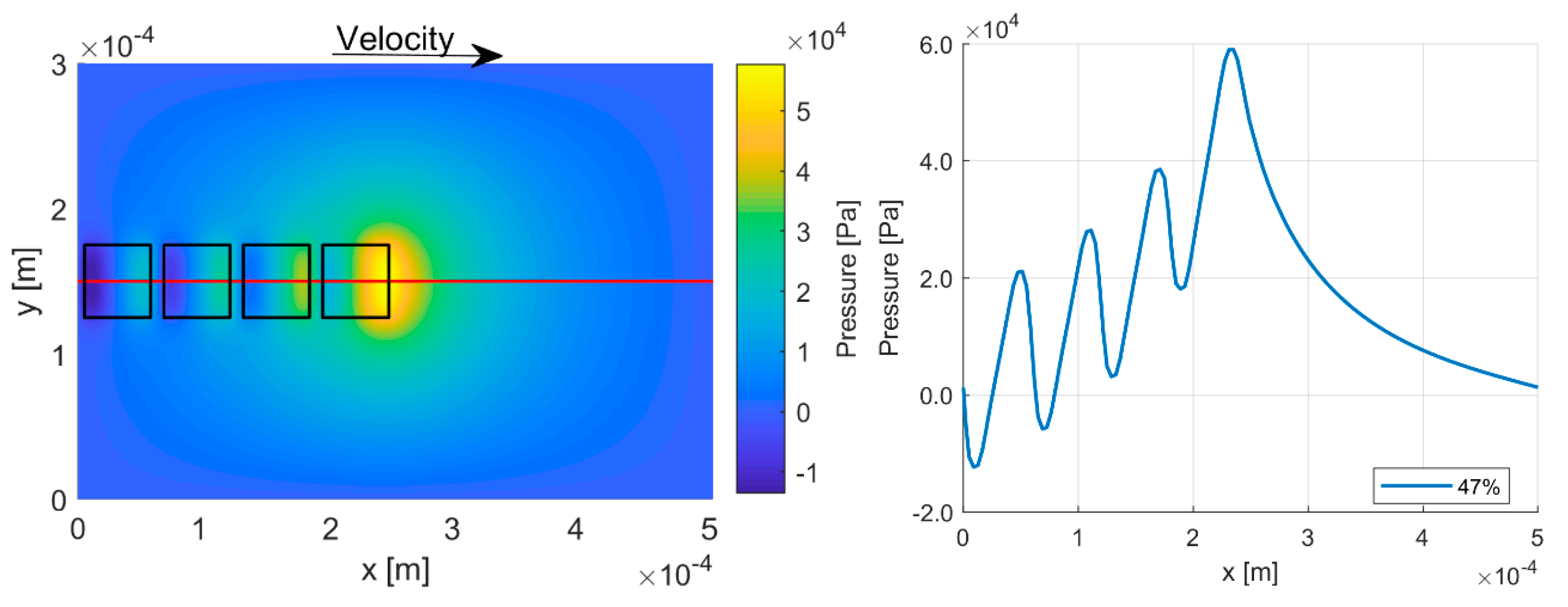
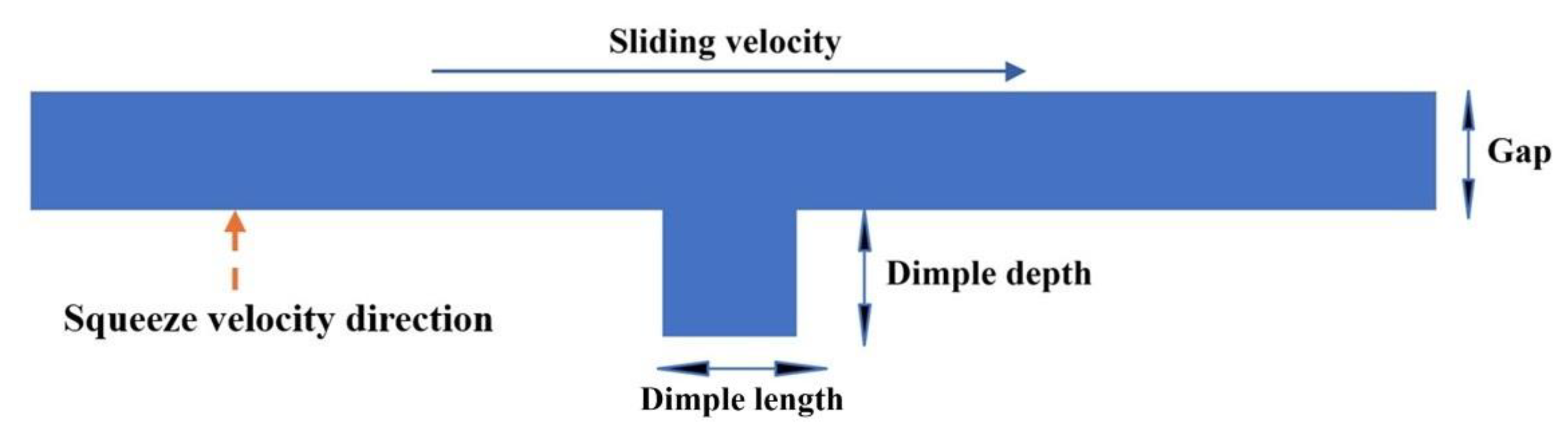
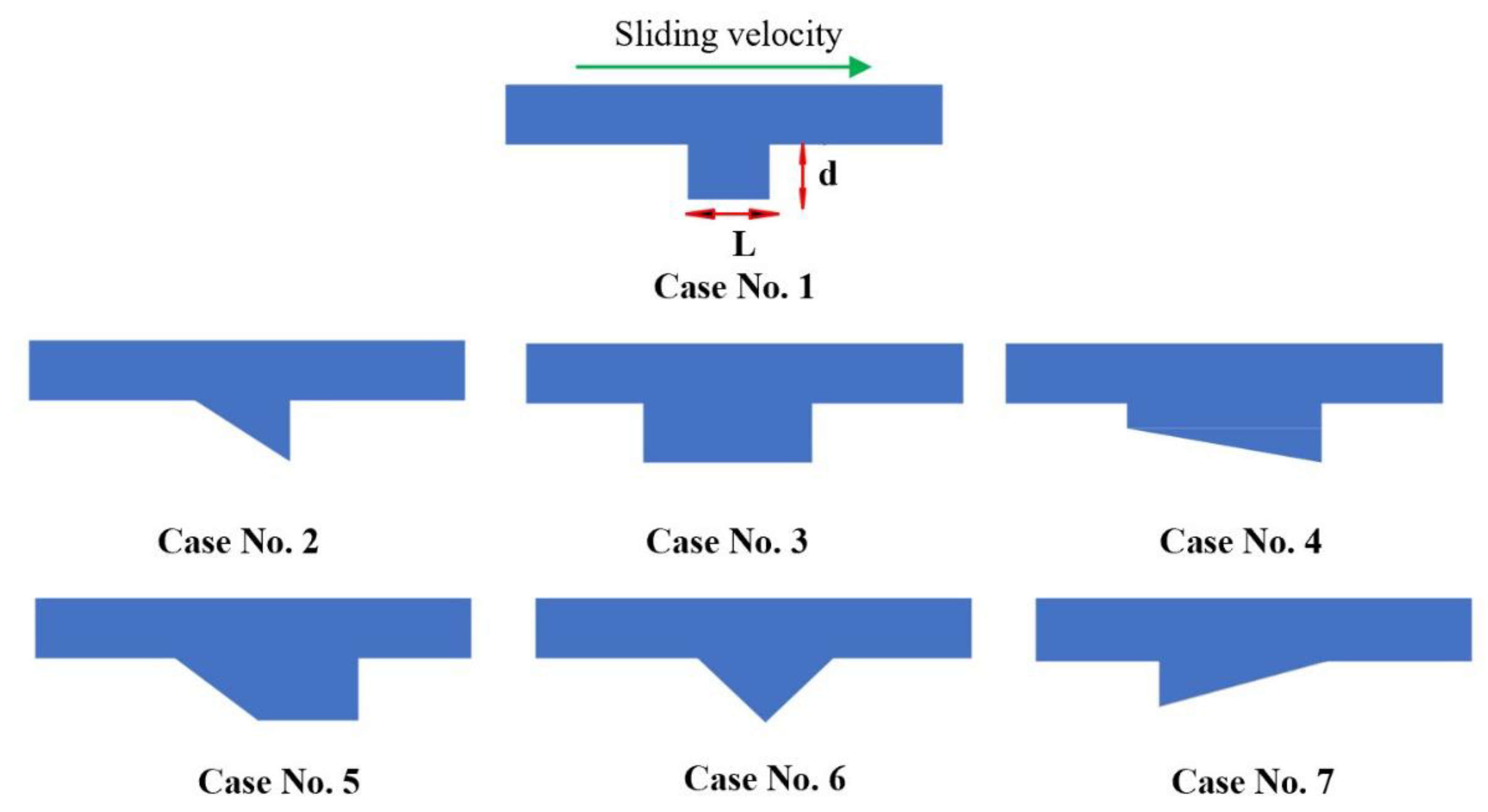
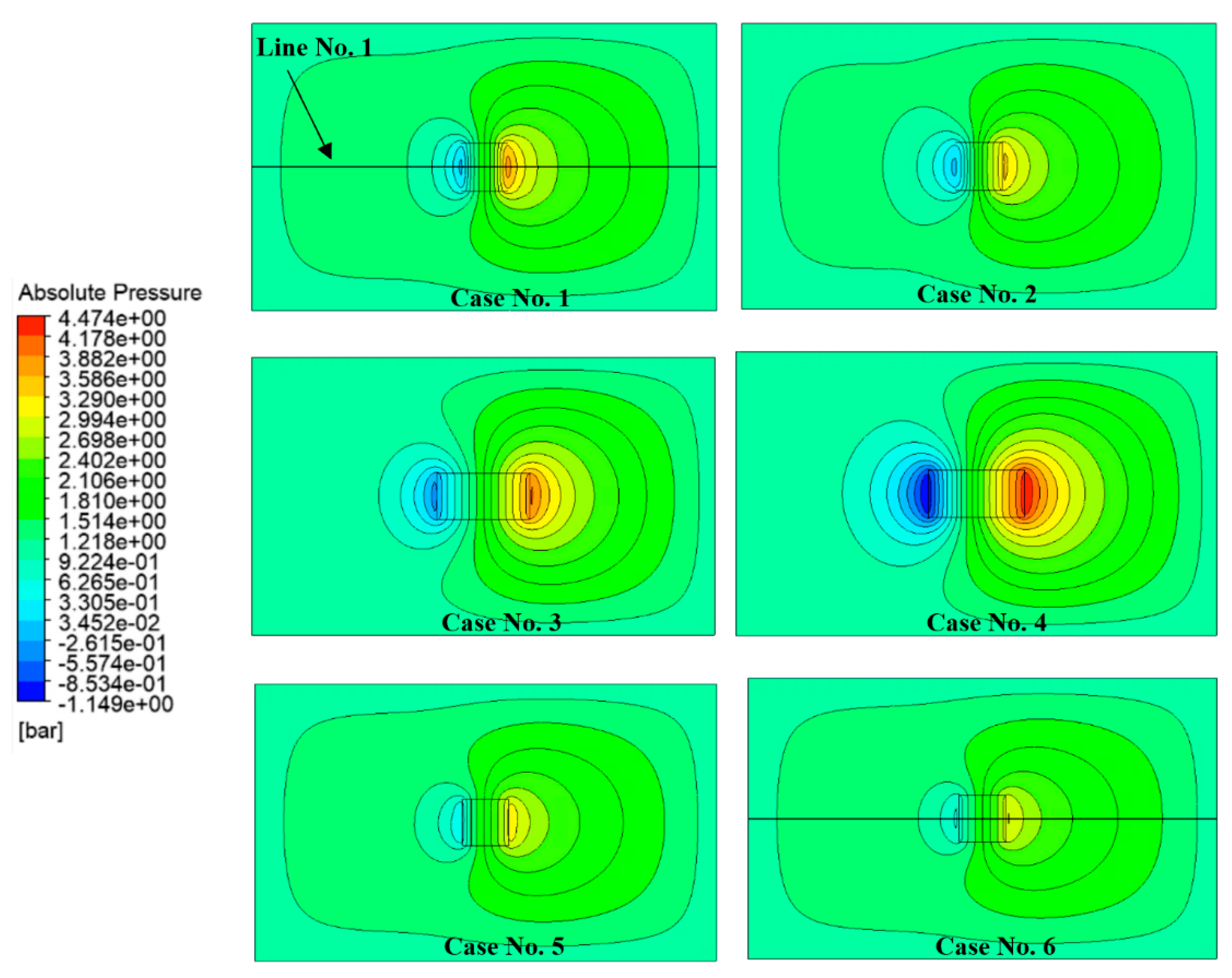
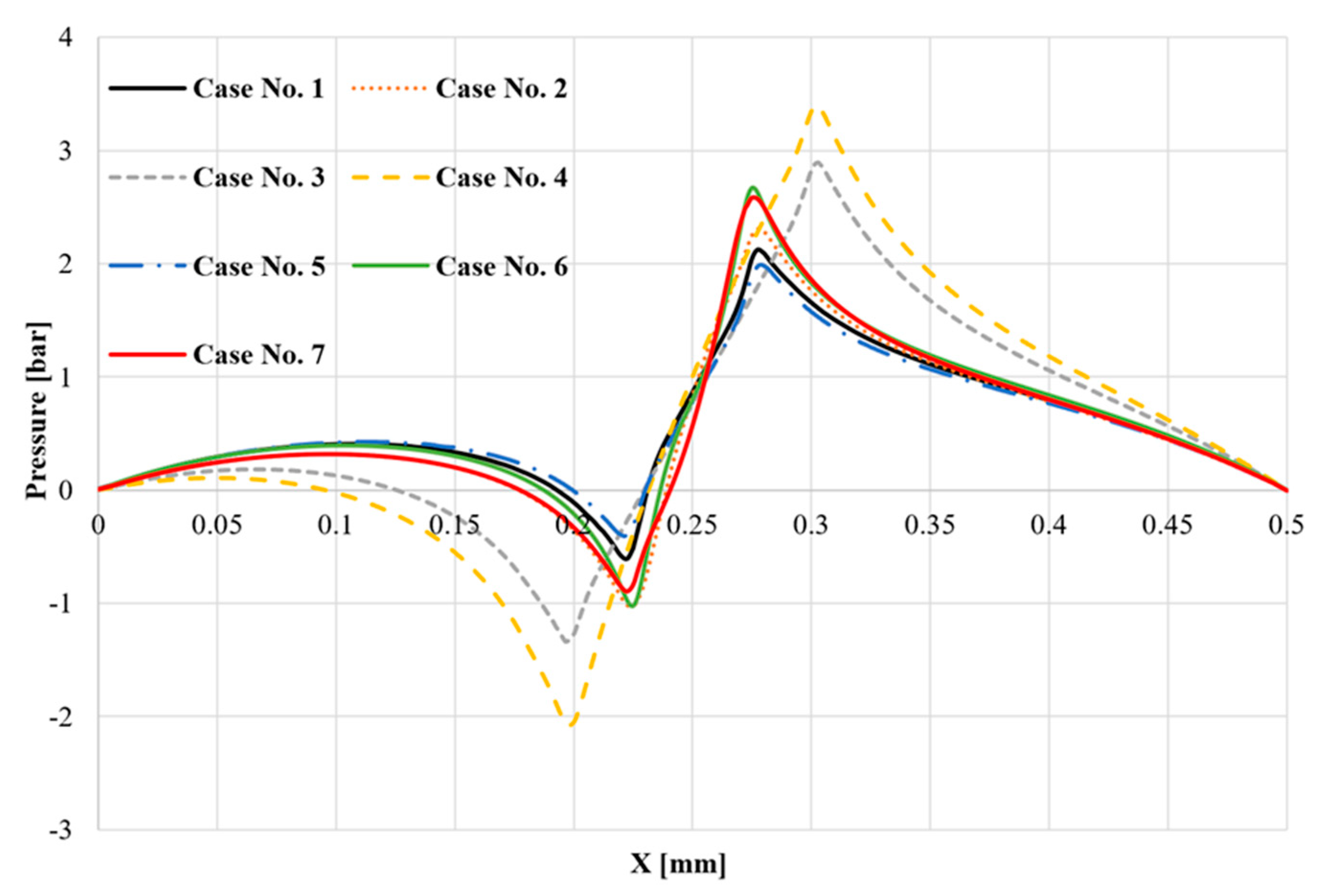
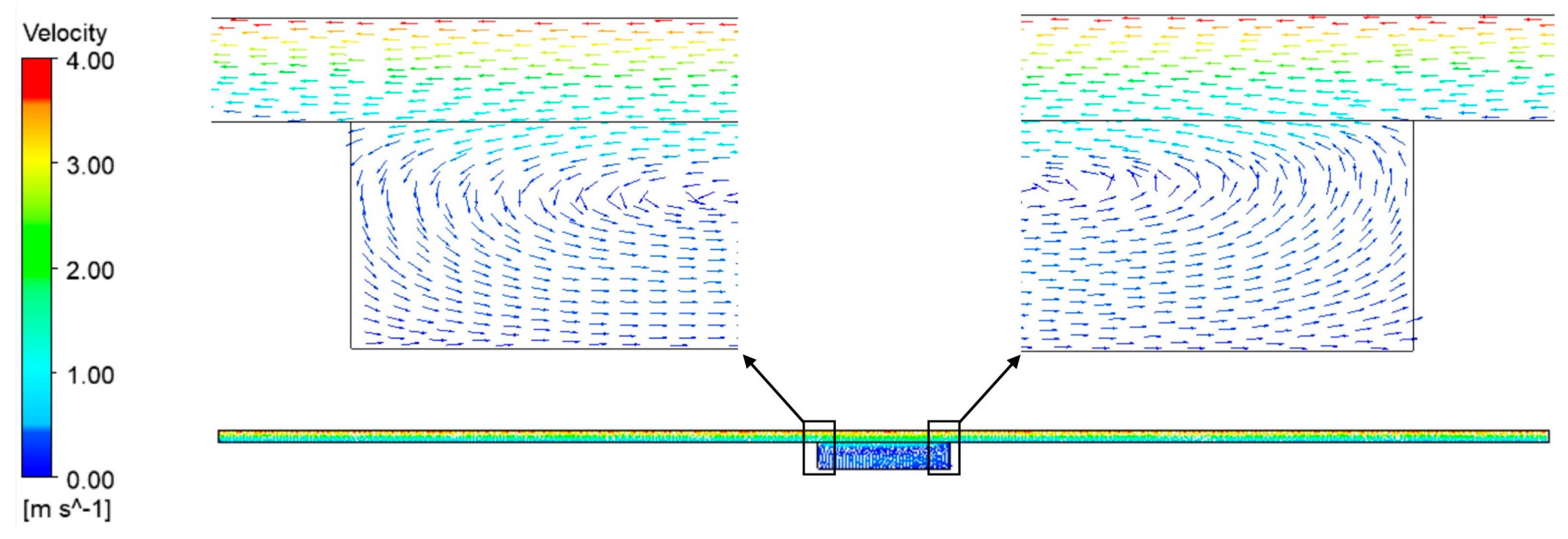
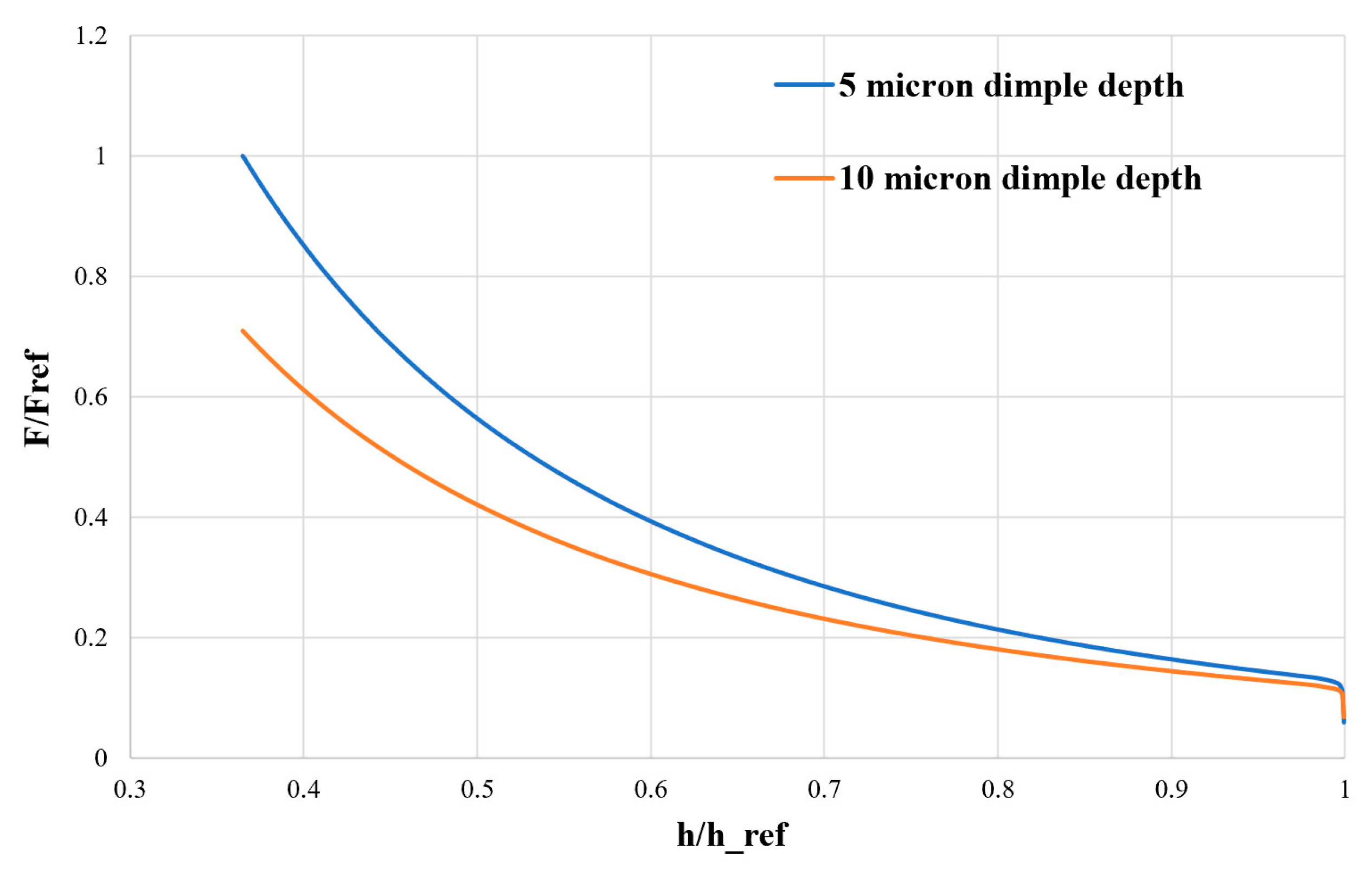
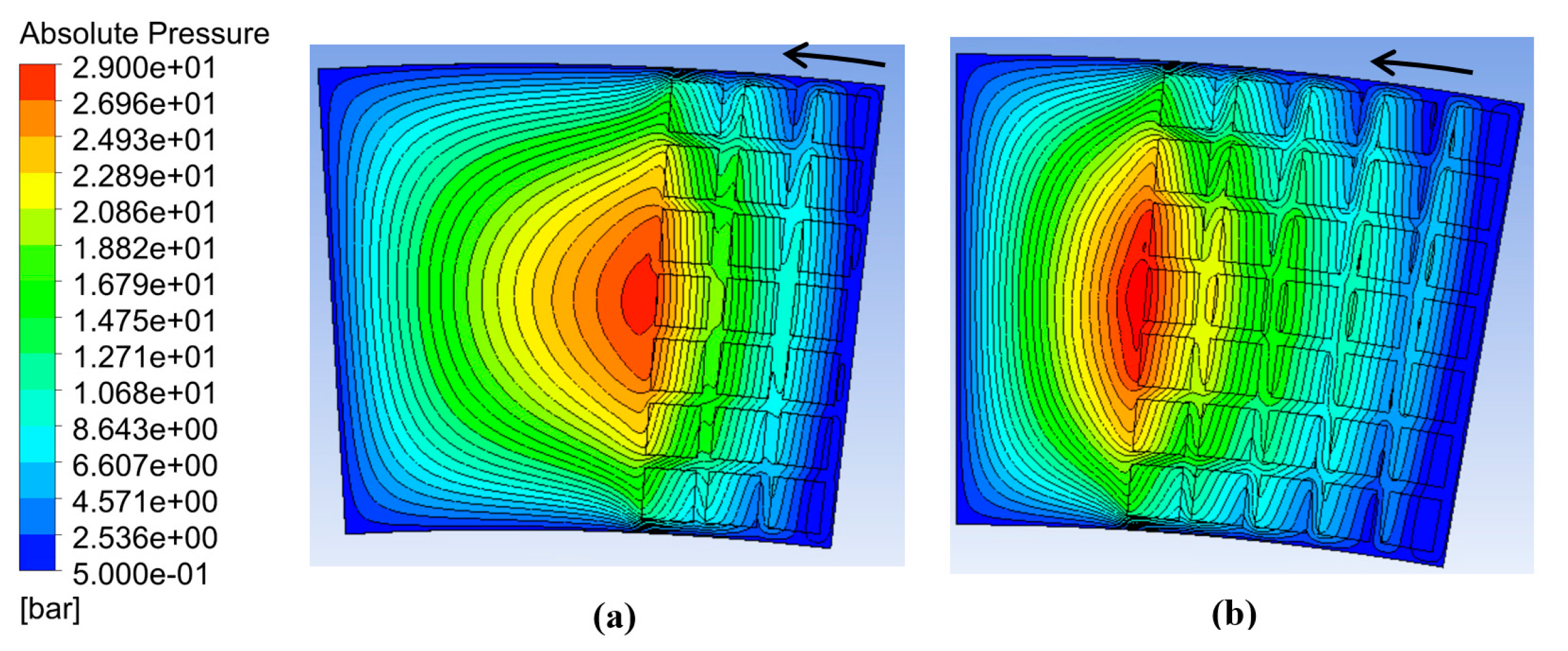
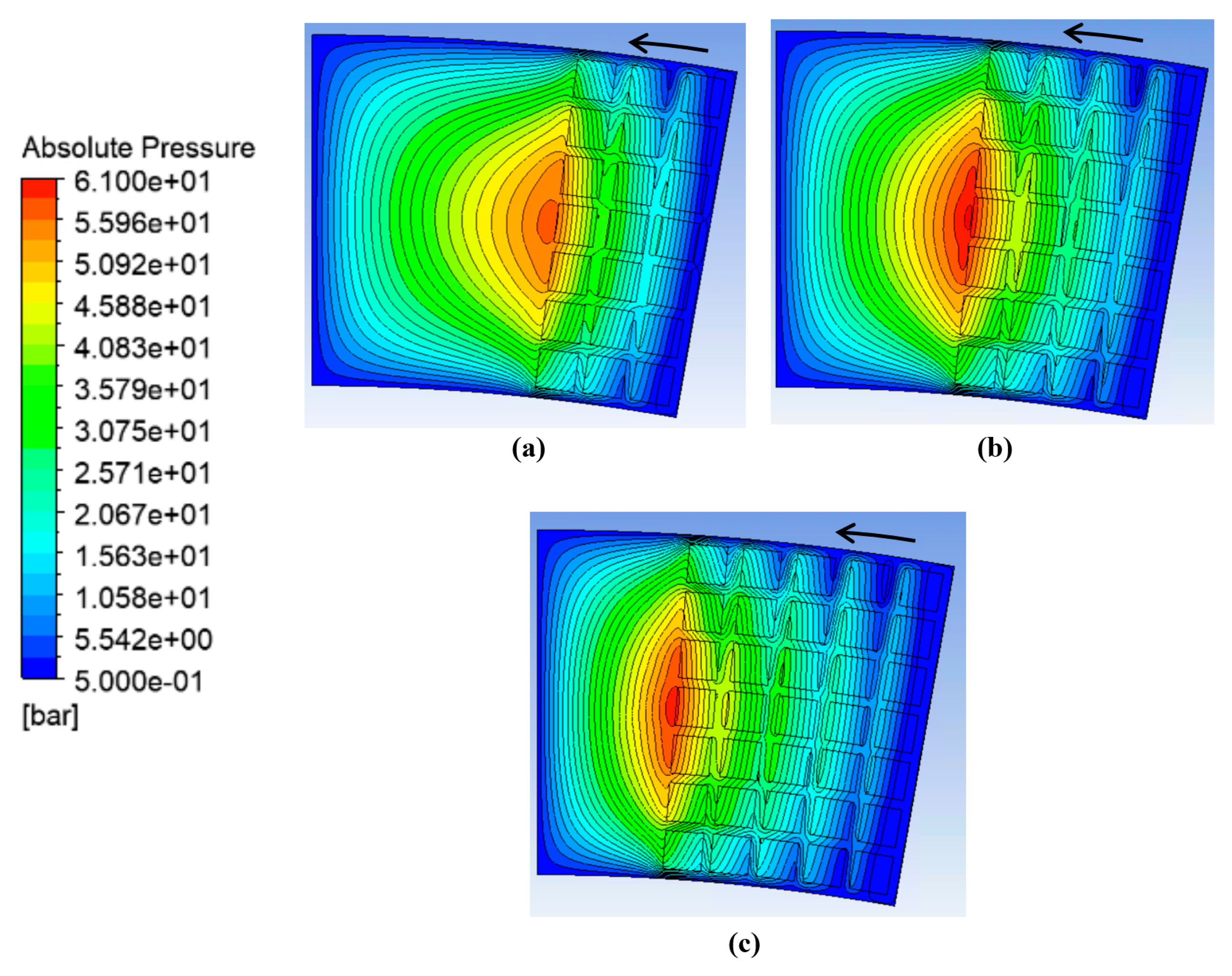
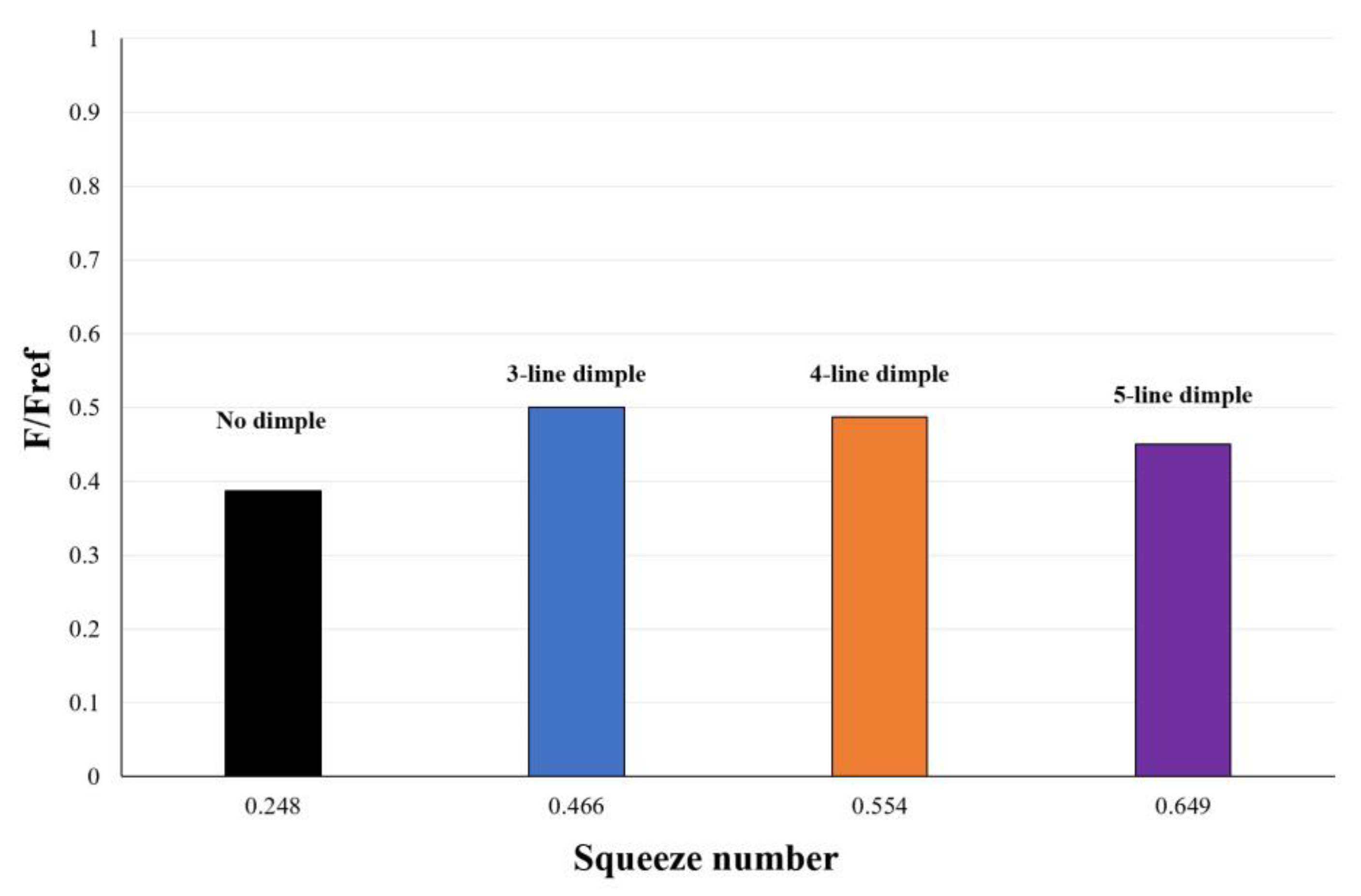
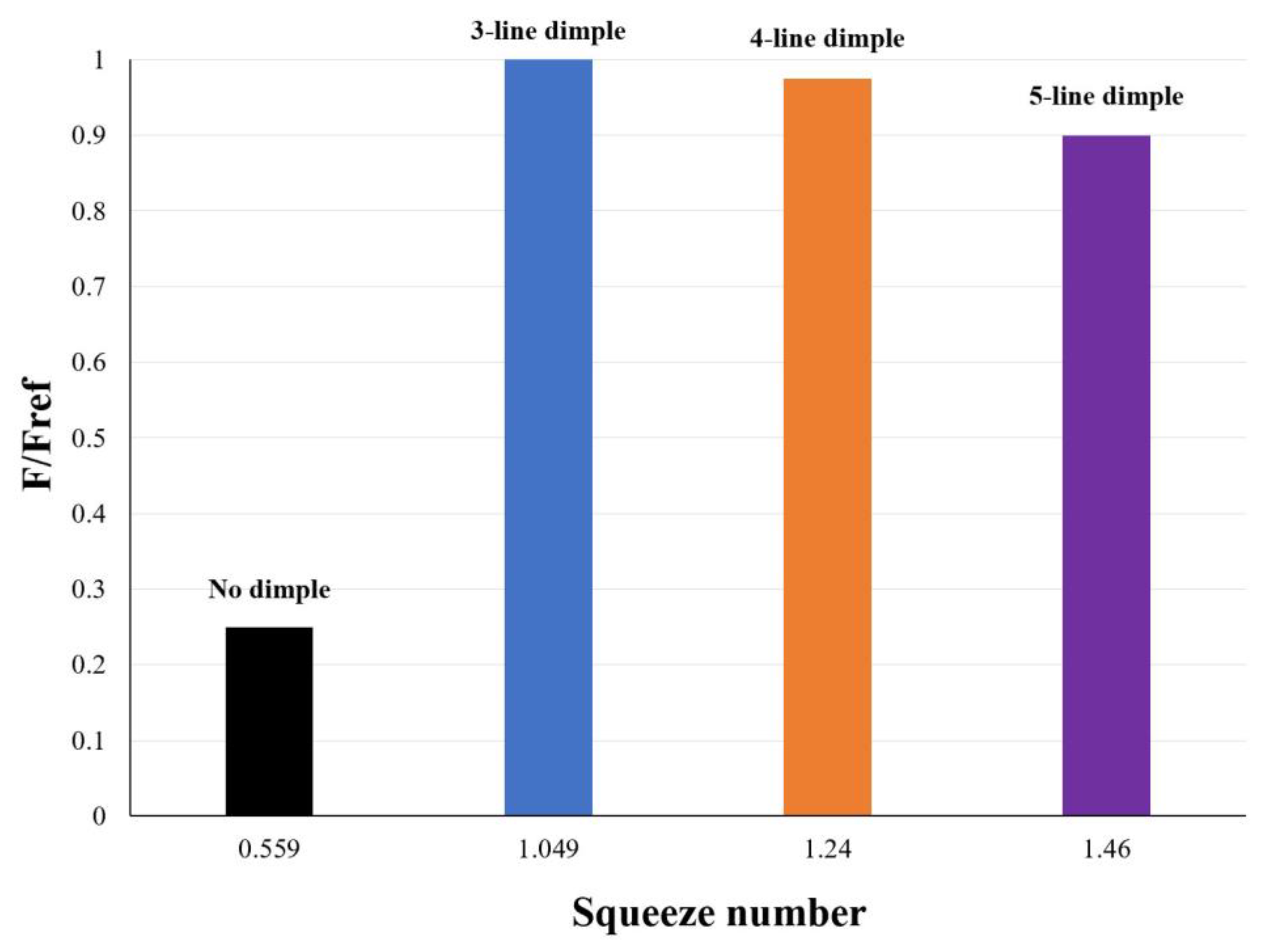
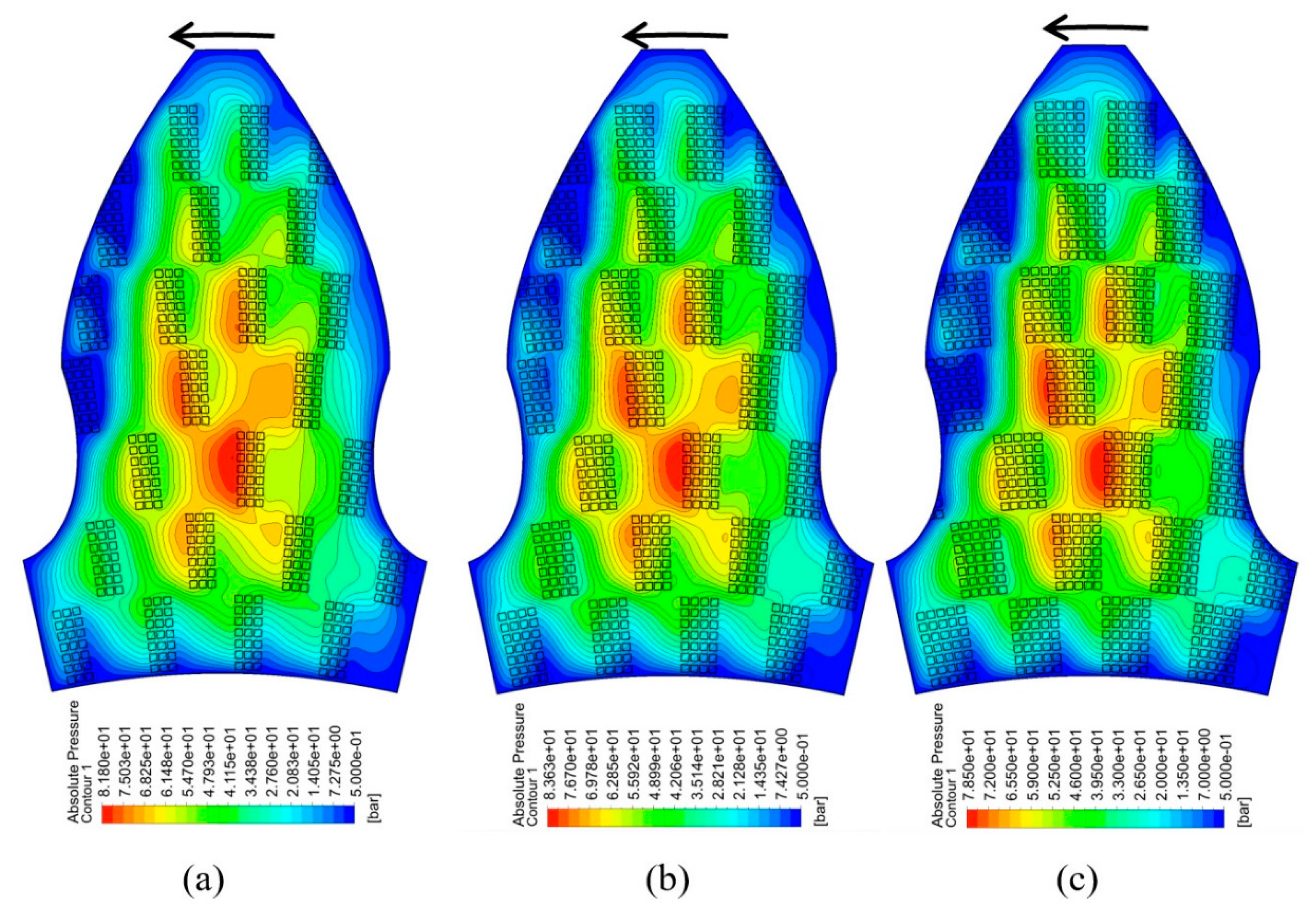
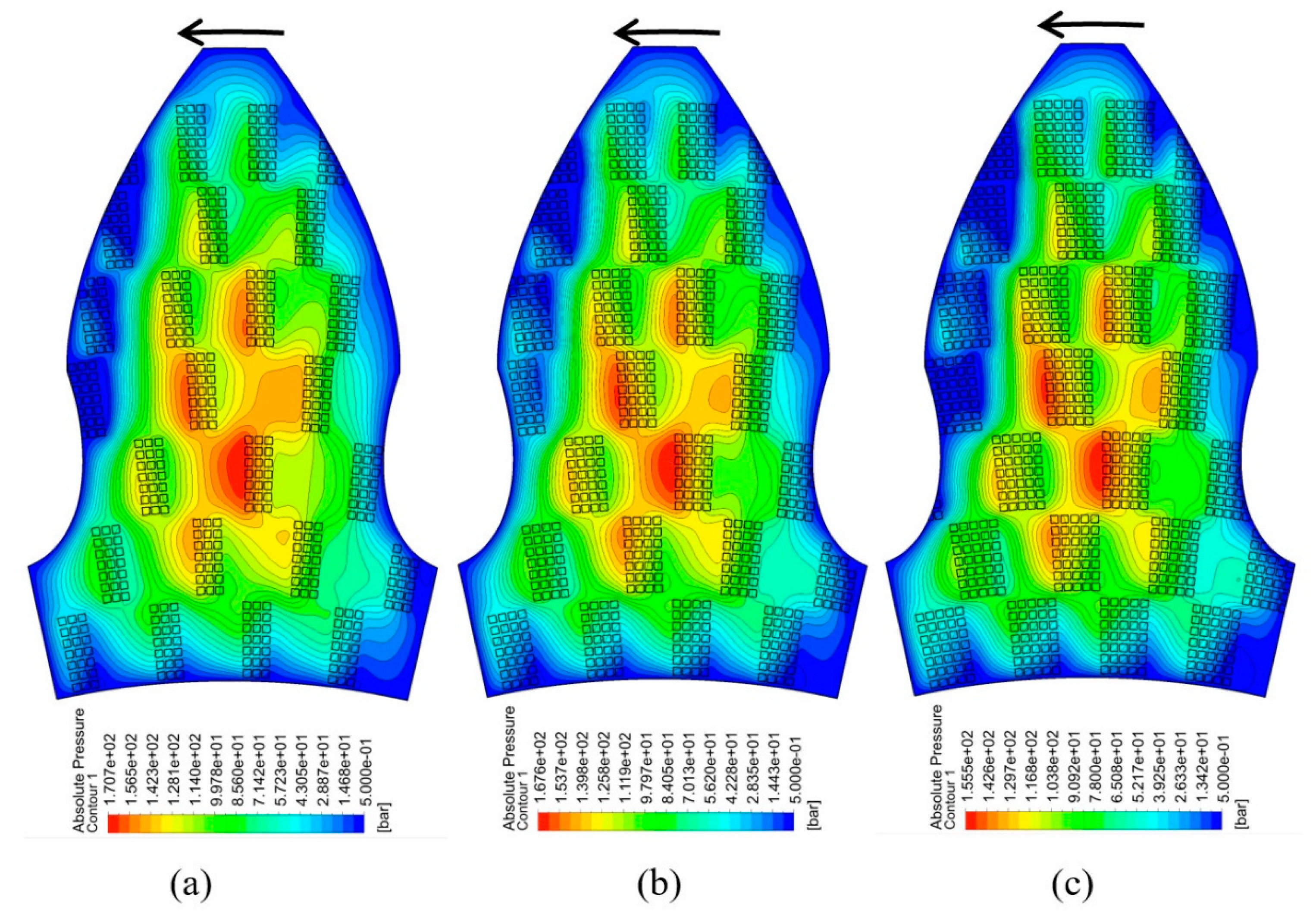
3.1. Optimum Dimple Geometry
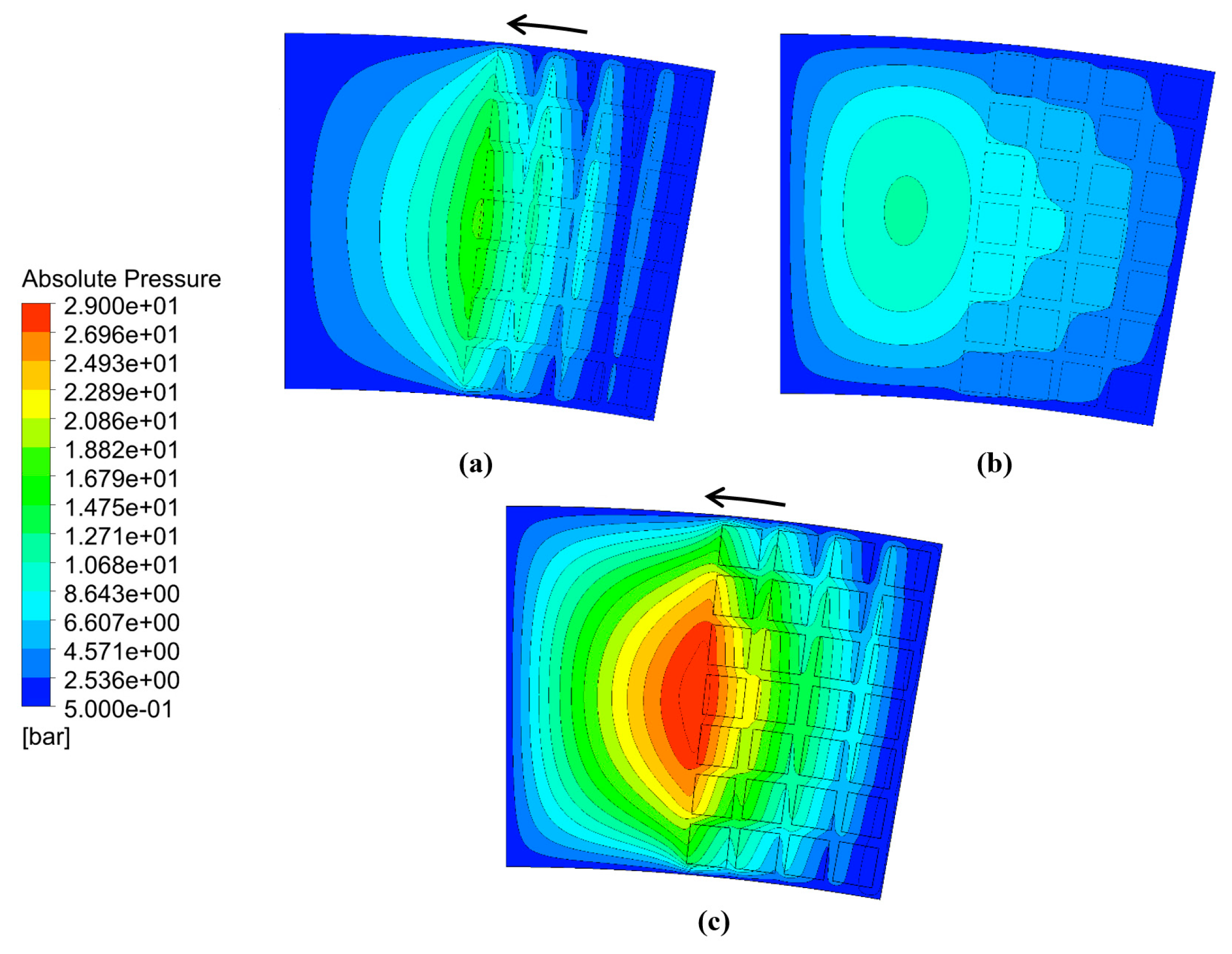
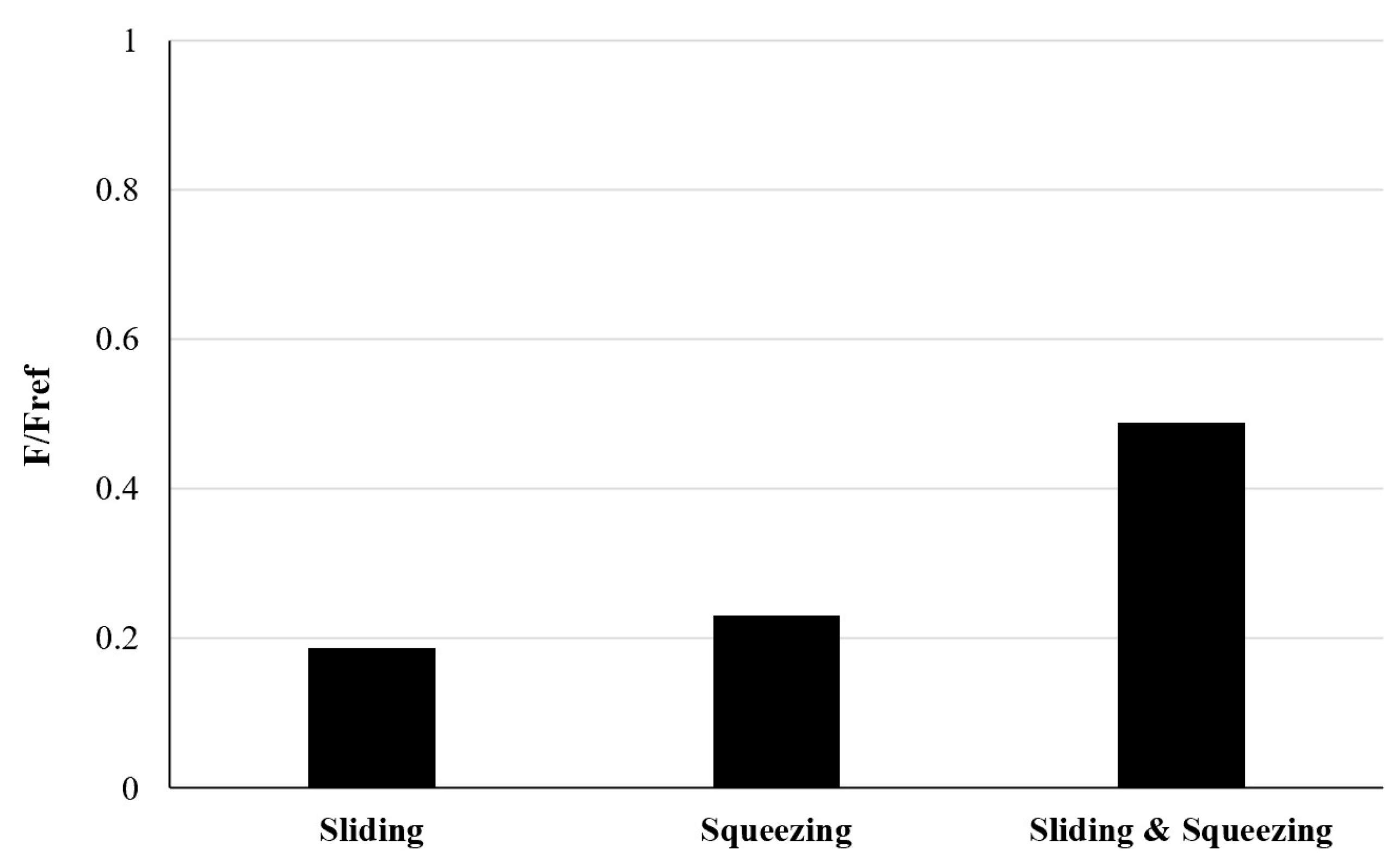
3.2. Texturing of the Surface
3.3. Modeling of the Interaction Between Texturized Bushing and Tooth
4. Uncertainty and Limitations
- Numerical discretization (mesh)
- Temporal discretization (time step)
- Model assumptions
- Model Validation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zardin, B.; Natali, E.; Borghi, M. Evaluation of the Hydro—Mechanical Efficiency of External Gear Pumps. Energies 2019, 12, 2468. [Google Scholar] [CrossRef]
- Koç, E.; Ng, K.; Hooke, C.J. An Analysis of the Lubrication Mechanisms of the Bush-Type Bearings in High Pressure Pumps. Tribol. Int. 1997, 30, 553–560. [Google Scholar] [CrossRef]
- Dhar, S.; Vacca, A. A Fluid Structure Interaction—EHD Model of the Lubricating Gaps in External Gear Machines: Formulation and Validation. Tribol. Int. 2013, 62, 78–90. [Google Scholar] [CrossRef]
- Torrent, M.; Gamez-Montero, P.J.; Codina, E. Model of the Floating Bearing Bushing Movement in an External Gear Pump and the Relation to Its Parameterization. Energies 2021, 14, 8553. [Google Scholar] [CrossRef]
- Torrent, M.; Gamez-Montero, P.J.; Codina, E. Motion Modelling of the Floating Bushing in an External Gear Pump Using Dimensional Analysis. Actuators 2023, 12, 338. [Google Scholar] [CrossRef]
- Corvaglia, A.; Rundo, M.; Casoli, P.; Lettini, A. Evaluation of Tooth Space Pressure and Incomplete Filling in External Gear Pumps by Means of Three-Dimensional CFD Simulations. Energies 2021, 14, 342. [Google Scholar] [CrossRef]
- Dhar, S.; Vacca, A. A Novel CFD—Axial Motion Coupled Model for the Axial Balance of Lateral Bushings in External Gear Machines. Simul. Model. Pract. Theory 2012, 26, 60–76. [Google Scholar] [CrossRef]
- Thiagarajan, D.; Vacca, A.; Watkins, S. On the Lubrication Performance of External Gear Pumps for Aerospace Fuel Delivery Applications. Mech. Syst. Signal Process 2019, 129, 659–676. [Google Scholar] [CrossRef]
- Ren, Q.N.; Hu, H.X.; Zheng, Y.G. Effect of surface microstructure spacing on the cavitation erosion process of stainless steel. Wear 2024, 558–559, 205542. [Google Scholar] [CrossRef]
- Yan, J.; Rong, Y.; Zhang, Y.; Zhou, S.; Huang, J.; Zhao, G.; Liu, Y. Wear and corrosion resistance of textured and functionally particle-enhanced multilayer dual-biomimetic polymer coatings. Tribology Int. 2025, 202, 110335. [Google Scholar] [CrossRef]
- Shen, C.; Khonsari, M.M. Effect of Dimple’s Internal Structure on Hydrodynamic Lubrication. Tribol. Lett. 2013, 52, 415–430. [Google Scholar] [CrossRef]
- Rahmani, R.; Mirzaee, I.; Shirvani, A.; Shirvani, H. An Analytical Approach for Analysis and Optimisation of Slider Bearings with Infinite Width Parallel Textures. Tribol. Int. 2010, 43, 1551–1565. [Google Scholar] [CrossRef]
- Etsion, I.; Halperin, G.; Brizmer, V.; Kligerman, Y. Experimental Investigation of Laser Surface Textured Parallel Thrust Bearings. Tribol. Lett. 2004, 17, 295–300. [Google Scholar] [CrossRef]
- Casoli, P.; Scolari, F.; Rundo, M.; Lettini, A.; Rigosi, M. CFD Analyses of Textured Surfaces for Tribological Improvements in Hydraulic Pumps. Energies 2020, 13, 5799. [Google Scholar] [CrossRef]
- Casoli, P.; Scolari, F.; Vescovini, C.M.; Rossi, C.; Lettini, A. Analyses of Engineered Surfaces for Performance Improvements of External Gear Pumps. In Proceedings of the Global Fluid Power Society PhD Symposium, Naples, Italy, 12–14 October 2022; River Publishers: Alsbjergvej, Denmark, 2024. ISBN 9788770047975. [Google Scholar] [CrossRef]
- Kennedy, F.E. Applied Tribology: Bearing Design and Lubrication. J. Tribol. 2002, 124, 428. [Google Scholar] [CrossRef]




| Item | Value |
|---|---|
| Tooth center diameter Dm (mm) | 31.7 |
| (deg) | 30 |
| Opening pressure (MPa) | 1 |
| Elements Number | Lubrication Gap Layer Number | Gear Force/Fref | |
|---|---|---|---|
| 1 | 532,890 | 5 | 0.82 |
| 2 | 913,146 | 8 | 0.95 |
| 3 | 1,532,631 | 10 | 1 |
| 4 | 1,818,355 | 12 | 1.015 |
| Case No. 1 | Case No. 2 | Case No. 3 | Case No. 4 | Case No. 5 | Case No. 6 | Case No. 7 | |
|---|---|---|---|---|---|---|---|
| L ( | 100 | 100 | 200 | 200 | 100 | 100 | 100 |
| W () | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| d () | 10 | 0–10 | 10 | 5–10 | 10 | 0–10 | 0–10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Casoli, P.; Garousi, M.H.; Rundo, M.; Vescovini, C.M. Numerical Investigation of the Tribological Performance of Surface-Textured Bushings in External Gear Pumps Under Transient Lubrication Conditions. Actuators 2025, 14, 345. https://doi.org/10.3390/act14070345
Casoli P, Garousi MH, Rundo M, Vescovini CM. Numerical Investigation of the Tribological Performance of Surface-Textured Bushings in External Gear Pumps Under Transient Lubrication Conditions. Actuators. 2025; 14(7):345. https://doi.org/10.3390/act14070345
Chicago/Turabian StyleCasoli, Paolo, Masoud Hatami Garousi, Massimo Rundo, and Carlo Maria Vescovini. 2025. "Numerical Investigation of the Tribological Performance of Surface-Textured Bushings in External Gear Pumps Under Transient Lubrication Conditions" Actuators 14, no. 7: 345. https://doi.org/10.3390/act14070345
APA StyleCasoli, P., Garousi, M. H., Rundo, M., & Vescovini, C. M. (2025). Numerical Investigation of the Tribological Performance of Surface-Textured Bushings in External Gear Pumps Under Transient Lubrication Conditions. Actuators, 14(7), 345. https://doi.org/10.3390/act14070345










