Dynamic Study on a Passive Damping Scheme for Permanent Magnet Electrodynamic Suspension Vehicle Utilizing Onboard Magnets End Effects

Abstract

The permanent magnet electrodynamic suspension system (PMEDS) has demonstrated significant advantages in high-speed and ultra-high-speed applications due to its simple structure, low cost, and stable levitation force. However, the weak damping characteristic remains a critical issue limiting its practical implementation. This work investigates a passive damping plate utilizing the end field of onboard magnets, focusing on magnet-damping plate optimization and vehicle dynamics. Firstly, the configuration, operation principles, and electromagnetic parameters of the PMEDS vehicle are elucidated. Secondly, the dependences of magnet-conductive plate specifications on the damping force are examined. An optimization index based on the levitation-to-damping force ratio is proposed to enable collaborative optimization of magnet and conductive plate parameters. Finally, the vehicle dynamic model is developed using Simpack software to investigate payload and speed effects on dynamic responses under random track excitation, validating the effectiveness of the proposed passive damping solution. This study provides technical references for the design, engineering applications, and performance evaluation of passive damping schemes in PMEDS vehicles.

1. Introduction

Magnetic levitation (MAGLEV) technology has emerged as a transformative solution for sustainable transportation systems, with current implementations primarily adopting electromagnetic suspension (EMS), electrodynamic suspension (EDS), and high-temperature superconducting pinning levitation (HTSPL) [1,2,3,4]. Among these, permanent magnet electrodynamic suspension (PMEDS) [5,6] distinguishes itself through structural simplicity, cost efficiency, and levitation stability, as evidenced by the experimental achievement of 1030 km/h operation from Chinese Academy of Sciences in 2022 [7]. Substantial progress has been made globally in recent years, with notable developments including the Magplane, Magpipe, Inductrack [8,9], and vacuum tube maglev transportation [10,11,12]. PMEDS holds wide application prospects in ultra-high-speed ground and vacuum tube transportation. However, it demonstrates inadequate damping and sustained oscillations under disturbances due to insufficient energy dissipation, compromising operation reliability.

Current damping enhancement strategies are composed of active and passive approaches. Active damping implementations, exemplified by Magplane hybrid electromagnetic and permanent magnet arrays, demonstrate controllable stability through real-time suspension force modulation. Subsequent developments [13,14,15] integrating active coils with permanent magnets (PMs) have further refined this type. However, inherent limitations including thermal constraints, electromagnetic interference, and response delay restrict their scalability for ultra-high-speed applications. Therefore, researchers have shifted their focus toward developing passive damping solutions.

The fundamental principle of passive damping lies in utilizing electromagnetic induction between the source magnetic field or air-gap magnetic field within PMEDS and damping structures including damping plates or damping coils [16,17]. This mechanism dissipates vibration energy through eddy current losses in the damping structures, thereby achieving vibration suppression. For superconducting electrodynamic suspension systems, Ohashi et al. [18,19] proposed implementing 8-shaped passive damping coils between superconducting magnets and guideway coils, with dynamic analysis confirming their effectiveness. However, due to the structure compatibility, damping plates demonstrate better adaptation to the PMEDS vehicle.

A prevalent implementation involves generating damping forces through air gap magnetic field interactions between PMs and conductive plates. Zhu et al. [20] pioneered direct damping force measurements as early as 1998, investigating the effects of excitation amplitude, air gap, and frequency, though their work lacked theoretical modeling and simulation validation. In 2024, Luo et al. [21] established a two-dimensional (2D) analytical model for damping plates, yet this advancement remained unsubstantiated by experimental verification or numerical simulations. Furthermore, this configuration exhibits inherent limitations, as its performance heavily depends on air gap magnetic field intensity, which suffers significant attenuation at higher vehicle speeds, thereby constraining vibration suppression effectiveness.

In response to these challenges, researchers have developed passive damping magnet solutions whose performance is independent of vertical vibration speed rather than longitudinal speed-affected air gap fields. Shi et al. [22] proposed lateral damping guidance magnets in the PMEDS line tests, but this configuration lacked experiment validation of free vibration. Zhu et al. [16] and Wu et al. [17] experimentally confirmed the effectiveness of damping magnets. During vertical vibrations, conductive plates cut through the magnetic fields generated by damping magnets, dissipating energy as heat and thereby mitigating vibration. Nevertheless, great damping magnets can introduce mass penalties affecting acceleration performance, while requiring dedicated reaction guideway that increases structural complexity. Liu et al. [23] proposed utilizing longitudinal end magnetic fields generated by onboard PMs interacting with side-mounted damping plates. However, this study remains confined to single PMs array configurations, with critical aspects such as magnet optimization strategies and control methodologies not being addressed, limiting its applicability to full-scale vehicle implementations.

To address these challenges, this work focuses on parameter analysis and optimization of magnet and damping plates, establishing a full-vehicle multibody dynamics model for dynamic analysis and damping solution validation. Section 2 describes the vehicle structure, working principles, and dominating parameters. Section 3 analyzes the relationship between magnet dimensions and damping force to optimize the permanent magnets. Section 4 evaluates the damping performance by developing the multibody dynamics model of PMEDS vehicles. Section 5 concludes this work.

2. Structural Principle and Parameters

2.1. Structural Principle

As illustrated in Figure 1a, the PMEDS vehicle employs a single 27-m-long car incorporating eight bogies, each measuring 2500 mm in length. The distributed arrangement has six levitation units per bogie positioned at front, middle, and rear sections and yields 48 total levitation points per vehicle. It operates on a 2700 mm track gauge with a straddle-type bogie configuration that centrally integrates a linear motor mover for propulsion and braking through electromagnetic interaction with ground coils. According to Lenz’s law, relative motion between onboard magnets and the conductive track plate generates time-varying magnetic fields B, inducing eddy currents J through flux variation. These currents produce counteractive levitation forces to sustain stable suspension against gravitational loads. Lateral stability is enhanced by auxiliary guidance wheels installed on each bogie.

The passive damping configuration, depicted in Figure 1b, incorporates PMs, end damping plates, load-bearing springs, and guide columns. The damping plates are rigidly attached to the bogie, while the magnet array is vertically constrained by guide columns. The levitation force is transmitted to the bogie through springs with tunable stiffness, selected based on operation requirements. During steady-state operation, the levitation force balances the vehicle gravity. Vehicle-induced vibrations trigger relative motion between the PMs and damping plates, causing the electromagnetic interaction between end magnetic fields of onboard PMs and damping plates. This interaction generates an eddy current damping force that attenuates vibrations independent of air gap magnetic field. Notably, this design eliminates the additional magnets or corresponding guideway modifications, ensuring simplicity and practicality. As shown in Figure 1c,d, the integration of passive damping plates converts the original undamped system (with elastic component k₁) into a vibration-suppressed system combining the elastic element k₂ and the damping coefficient c, improving vertical stability.

2.2. Structural Parameters

The levitation and damping forces share a common magnetic source generated by the PMs. The levitation force stems from the interaction between the PMs primary field region and the ground conductive plate, while the damping force results from electromagnetic coupling between the end field of the PMs and lateral damping plates. Payload capacity serves as the critical design constraint, requiring prioritized identification of PMs parameters that meet levitation load demands. A baseline levitation capacity of 2000 kg per PMs array is defined under 10 mm aluminum guideway thickness, 10 mm suspension air gap, and 70 km/h operation speed. Guided by levitation-to-weight and levitation-to-drag ratios, the original PMs specifications are optimized according to previous work by our team [24,25,26], as summarized in

Table 1. Structural parameters of levitation magnet.

Parameters	Value
Length of permanent magnet	40 mm
Width of permanent magnet	240 mm
Thickness of permanent magnet	70 mm
Magnetization angle	45°
Remanent flux density of permanent magnet	1.43 T
Conductor plate thickness	10 mm
Suspension gap	10 mm
Conductivity of conductor plate	3.8 × 107 S/m
Conductor plate thickness	10 mm

.

3. Magnet Specifications Optimization

This section employs the analytical and simulation models proposed in Ref. [24] to analyze the dependence of the length, width, and thickness of PMs, as well as the thickness, conductivity, and temperature of the damping plate, along with the vertical vibration speed and operation gap, on the damping force. Besides, optimization analysis of the structure parameters of the magnet and damping plate is conducted. The investigated ranges of the structure parameters of the PMs are listed in

Table 2. Original discussion ranges of PMs parameters.

Parameters	Value	Unit
Magnet length	10~100	mm
Magnet width	100~240	mm
Magnet thickness	10~100	mm
Damping plate thickness	10	mm
Damping plate width	200	mm
Gap	5	mm
Speed	5	m/s
Conductivity	3.8 × 107	S/m
Magnet remanence density	1.43	T

.

The analytical model can be calculated using the Maxwell stress tensor method based on the spatial magnetic flux density distribution, as expressed in Equation (1). The simulation model captures the interaction between the longitudinal end magnetic fields generated by the onboard permanent magnet arrays and the side-mounted damping plates. The working principle and configuration of the simulation model are illustrated in Figure 2. In Figure 2a, the white arrows indicate the magnetization direction of the PMs.

$$\begin{array}{c}{F}_r={\displaystyle \frac{1}{2{\mathrm{\mu }}_0}}Re\left[{\displaystyle \int {\int }_{T_1}}{B}_{y,x=0}^{II}{\left(B_{x,x=0}^{II}\right)}^{\ast }\mathrm{d}y\mathrm{d}z\right]\\ -{\displaystyle \int {\int }_{T_2}}{B}_{y,x=d}^{II}{\left(B_{x,x=d}^{II}\right)}^{\ast }\mathrm{d}y\mathrm{d}z\\ in B_{i.x=0}^{II}=B_{0^{-}}^{IIs}+B_{0^{-}}^{IIr}i=x,y\end{array}$$

(1)

In the Equation (1), F_r represents the damping force, B^IIs represent the magnetic flux density excited by the PMs inside the induction plate, and B^IIr represents the magnetic flux density generated by the induced eddy current field inner the induction plate.

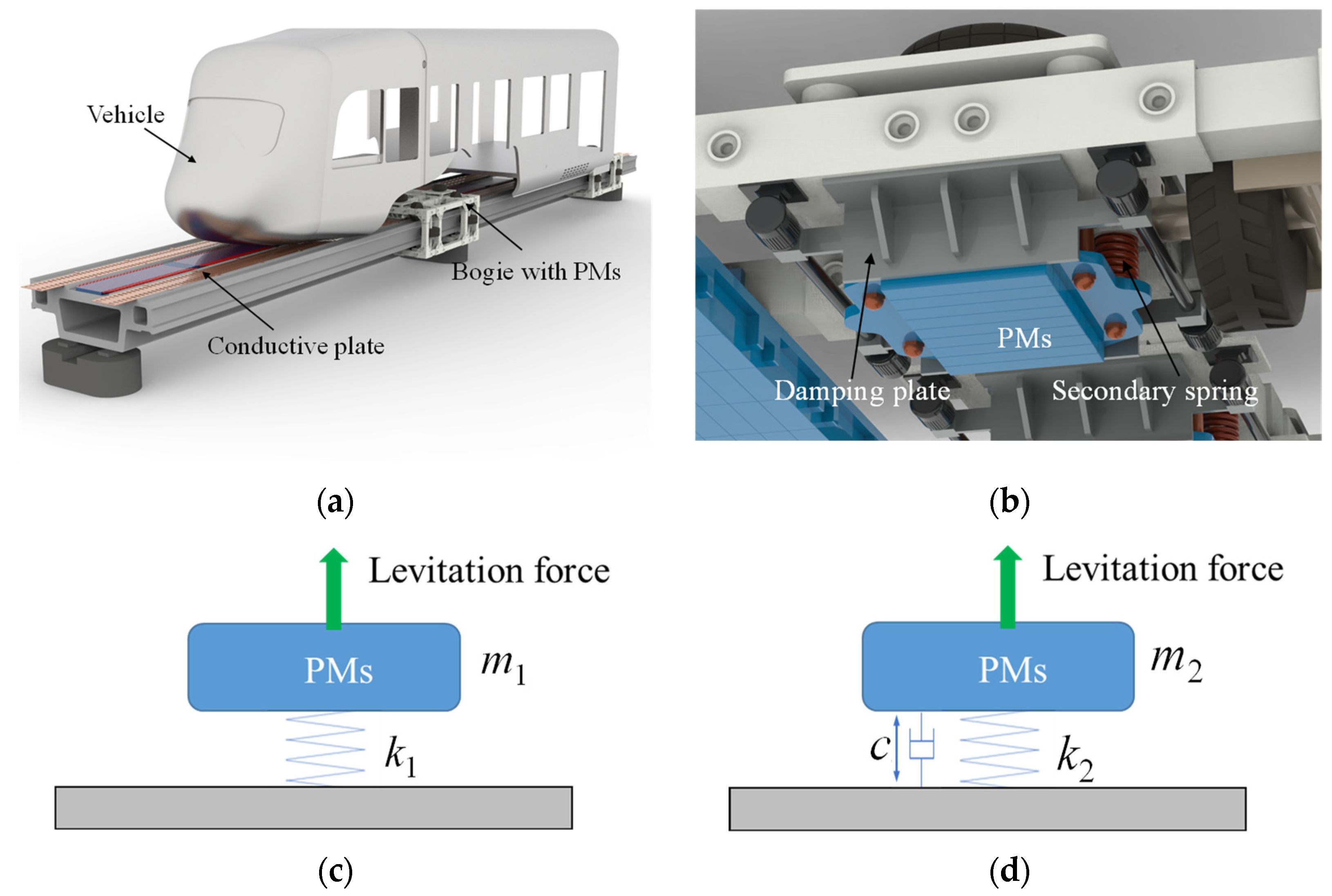
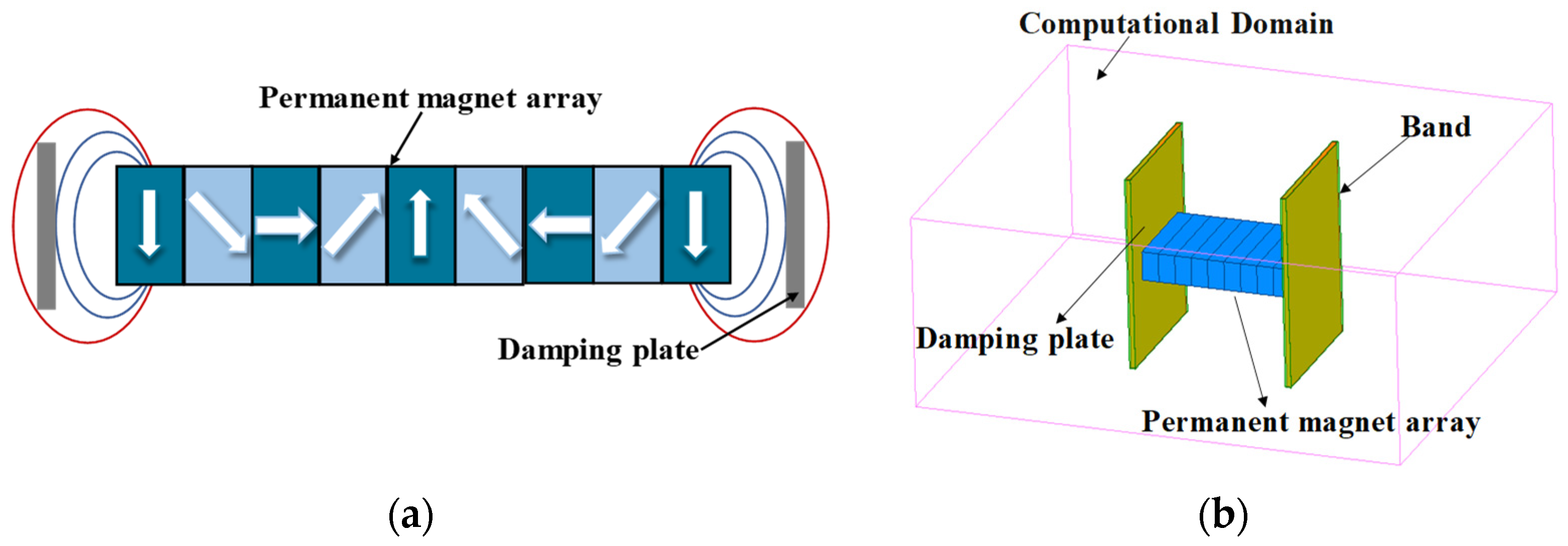
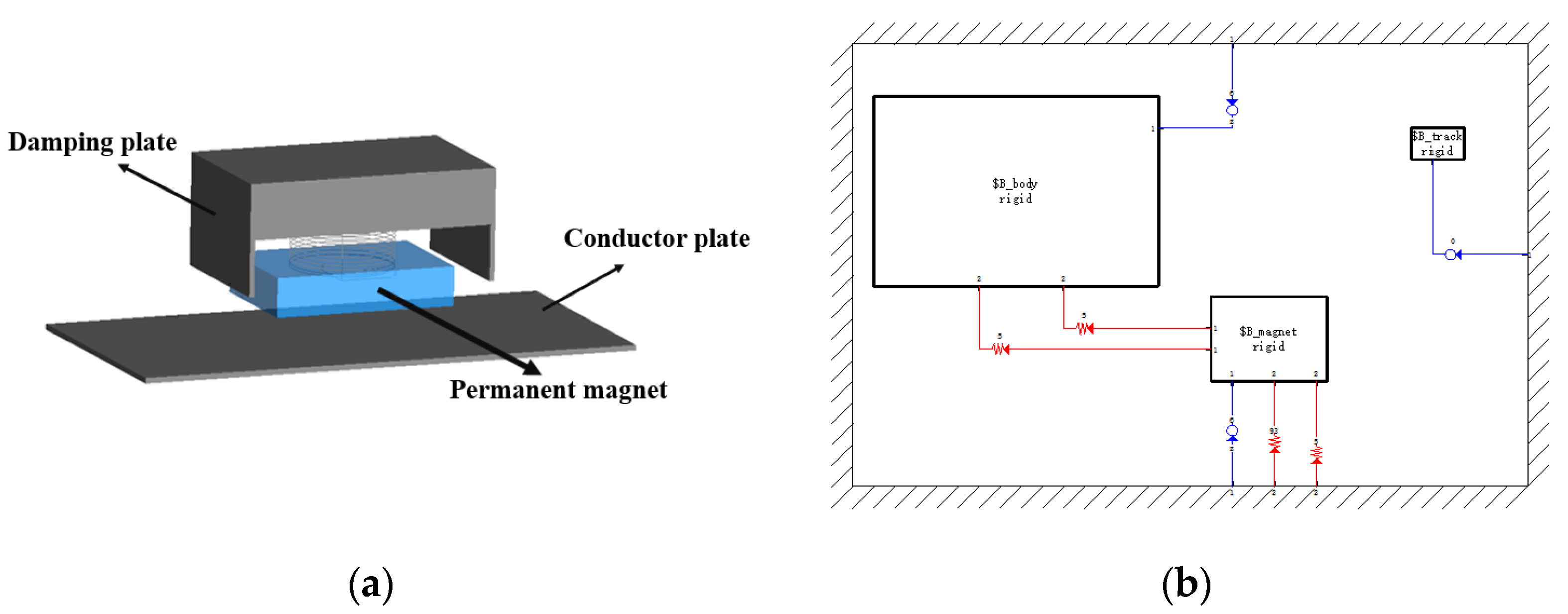
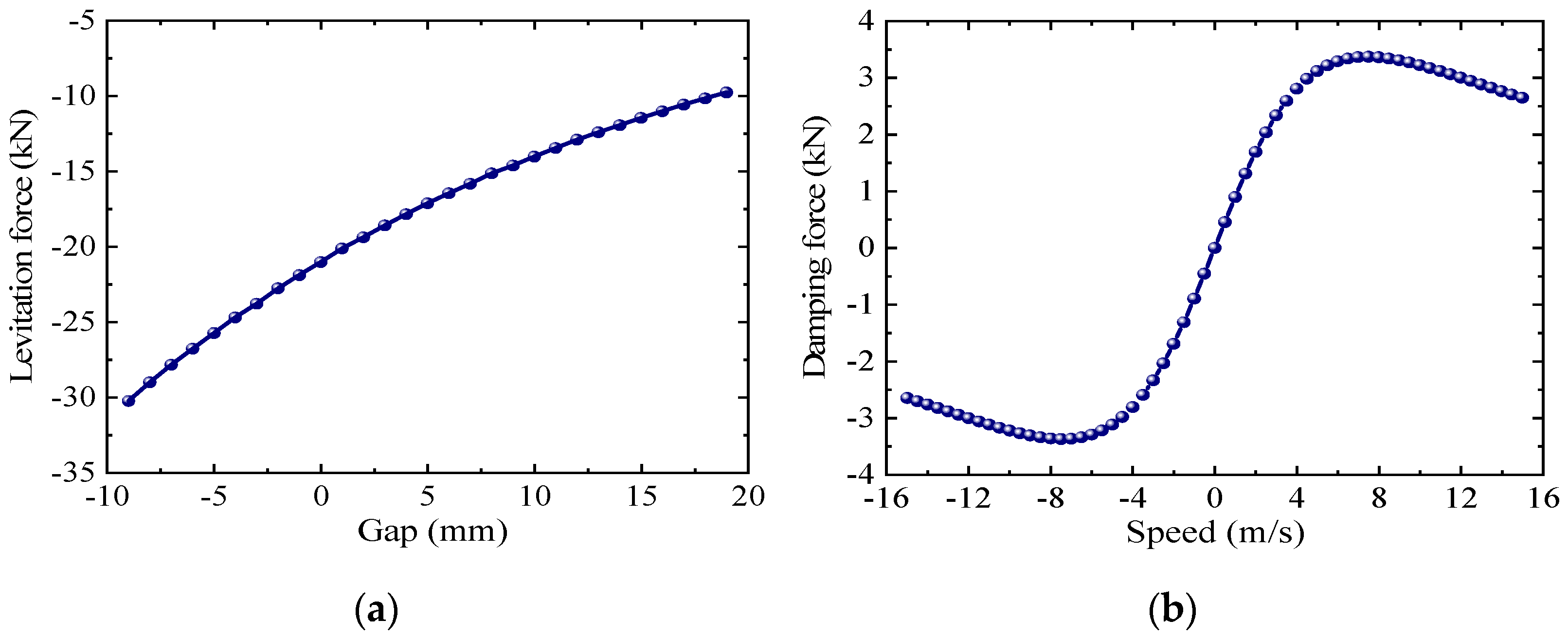
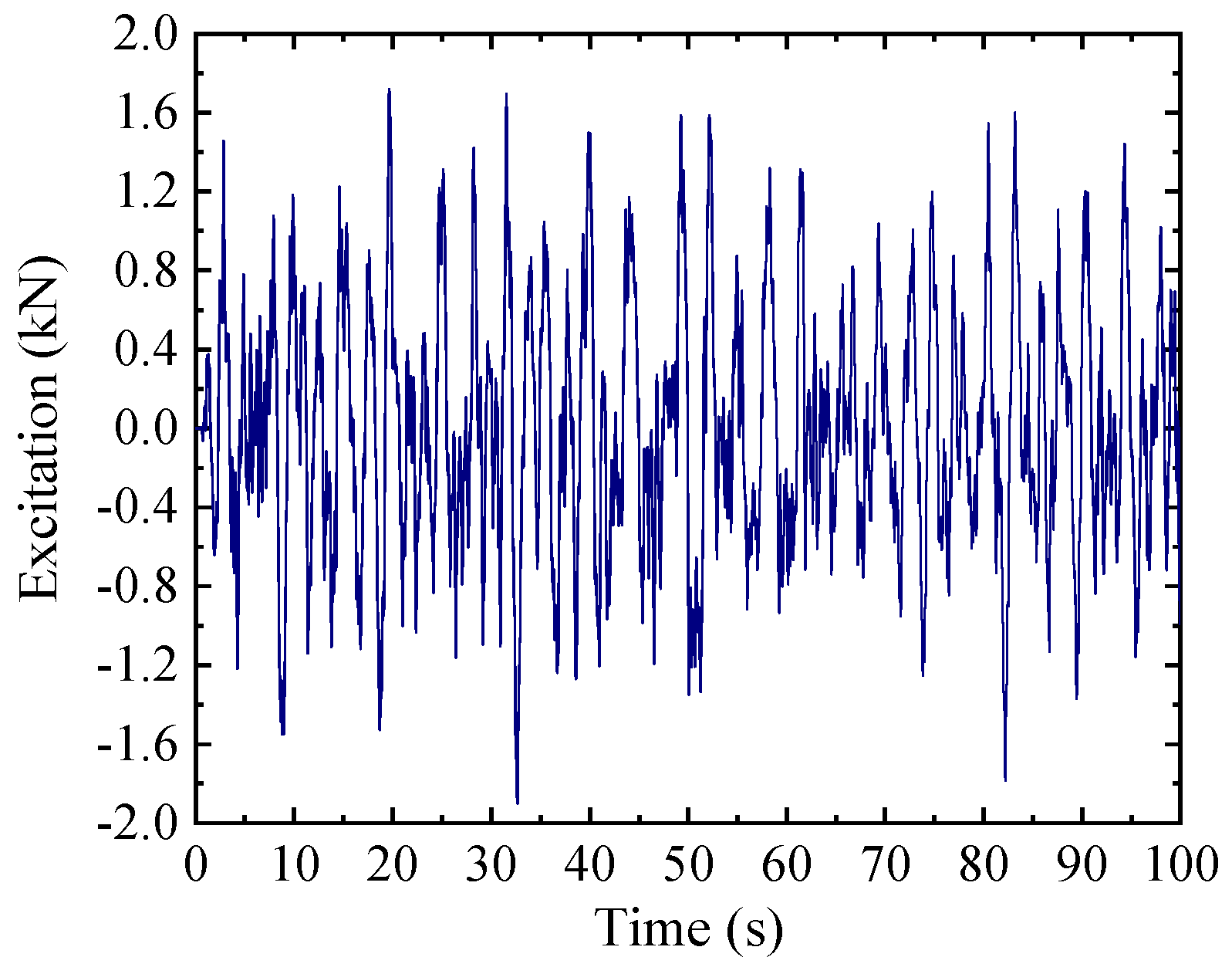
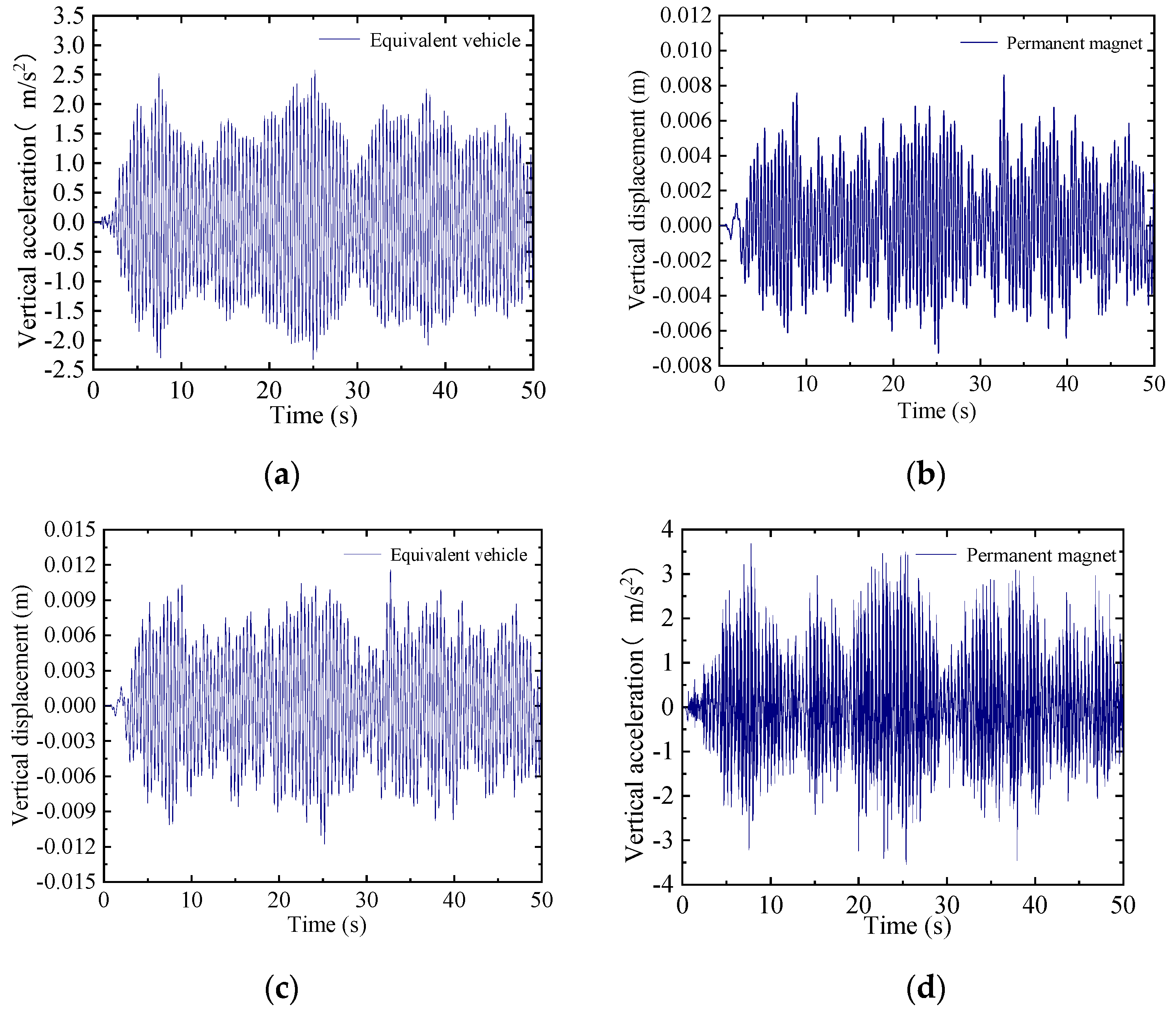
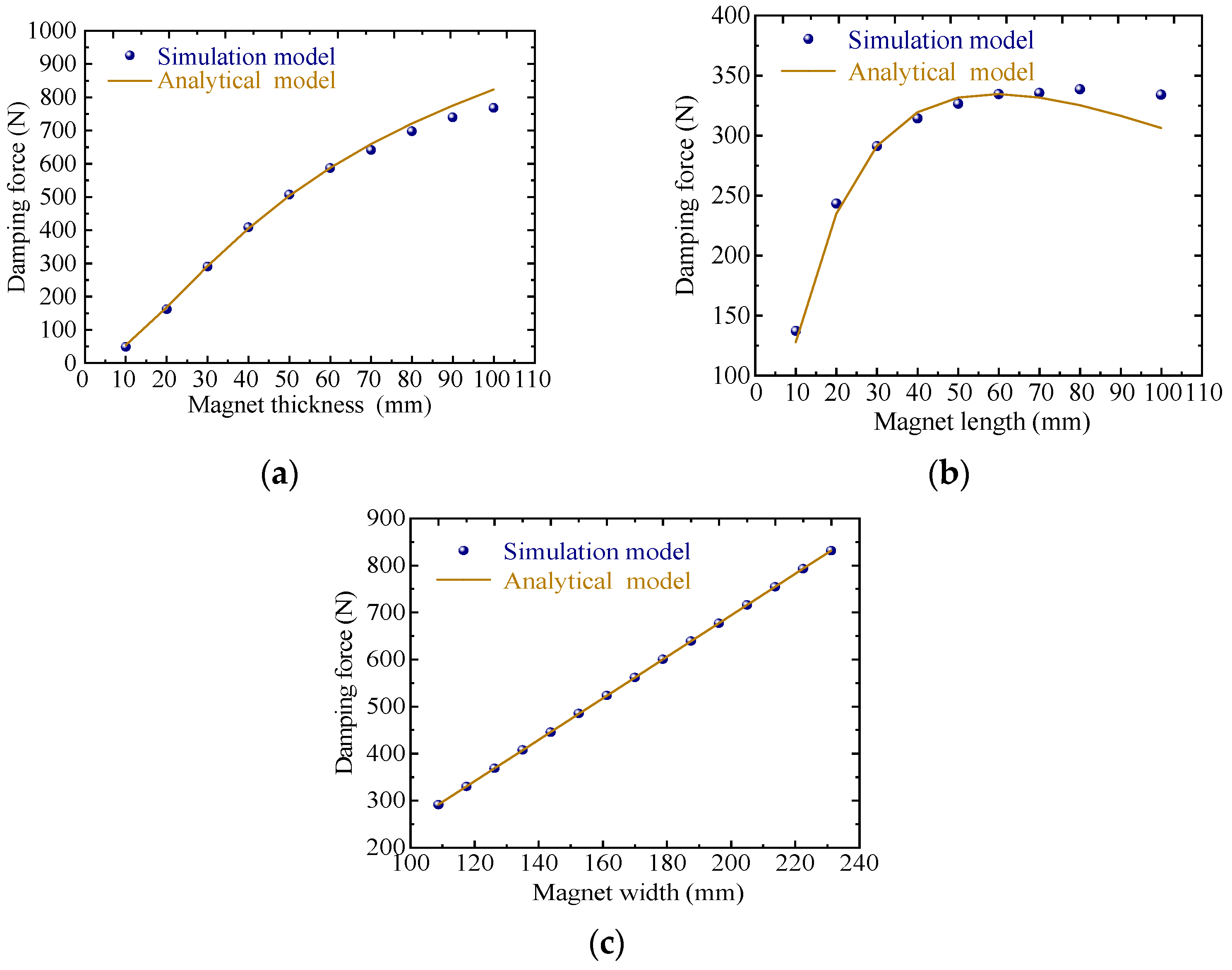
As shown in Figure 3a, the simulation results align well with the analytical predictions, confirming that the damping force exhibits a strong positive correlation with magnet thickness. Across the tested range, the damping force increases sharply with thicker magnets. As observed in Figure 3b, the damping force along the magnet length initially increases and then decreases, with the peak shifting toward greater lengths as thickness increases. As illustrated in Figure 3c, the damping force rises steadily with magnet width, though at a slower rate compared to the thickness dependence. These trends remain consistent under coupled variations of magnet length, thickness, and width. 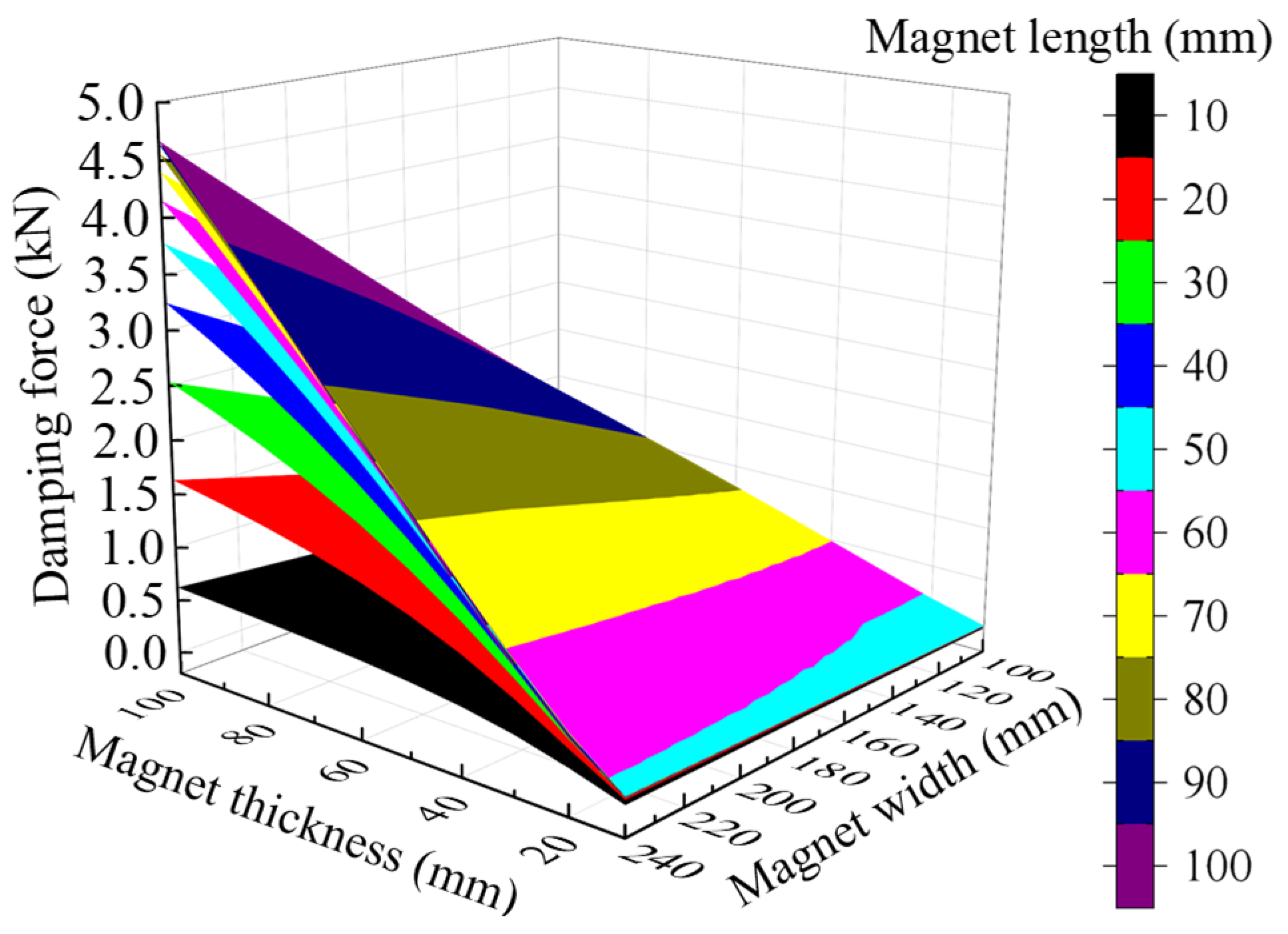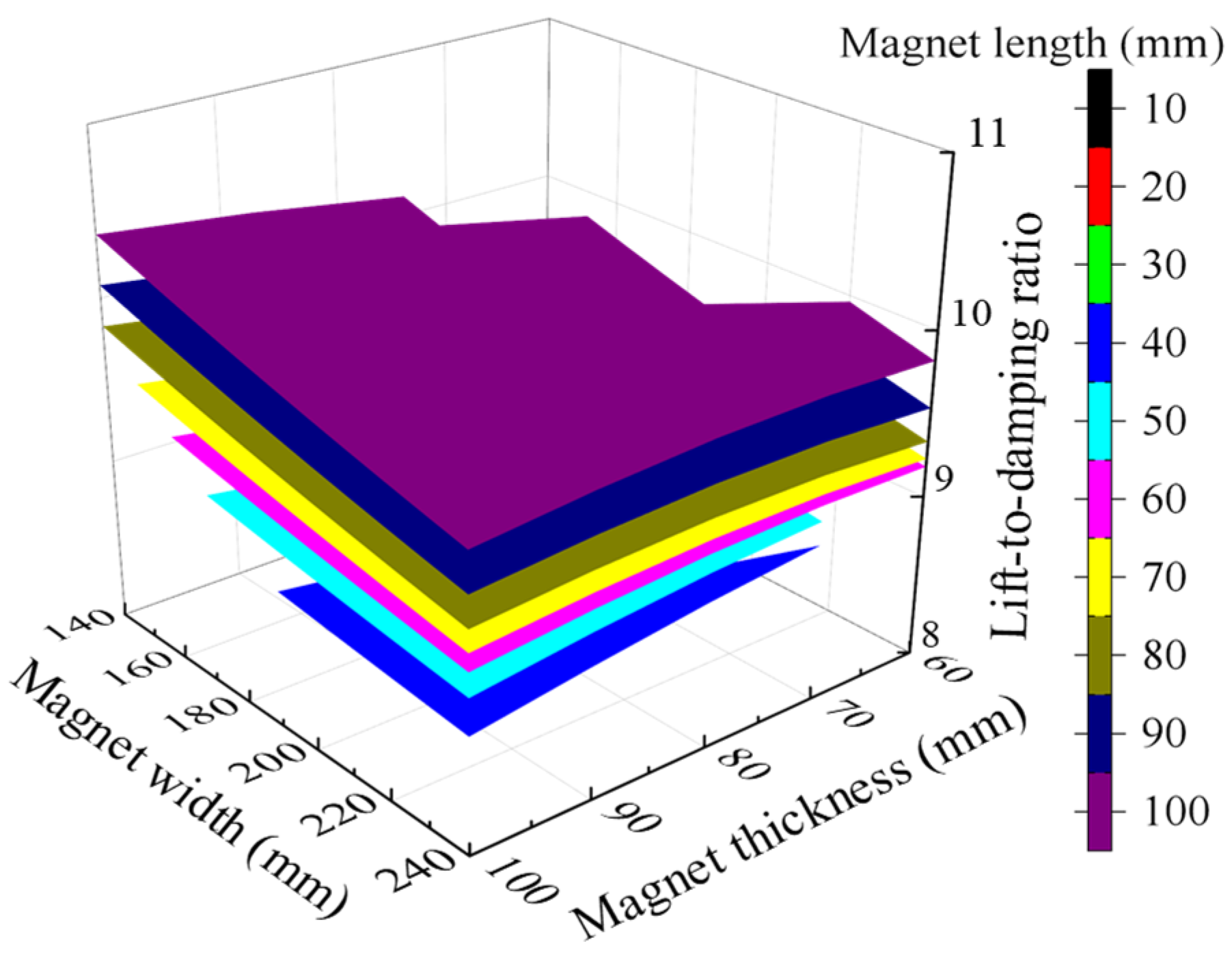Figure 3 presents the three-dimensional parameter space, revealing how synergistic geometric interactions influence damping force generation.

To achieve optimal magnet design that satisfies both levitation and damping requirements, the levitation-to-damping force ratio R_c is considered as the primary optimization criterion, as defined in Equation (2). This defines F_l as the levitation force, F_c as the damping force, and R_c as the levitation-to-damping force ratio. The optimization objective focuses on maximizing the eddy-current-induced damping forces, where lower values of the characteristic ratio R_c indicate superior damping performance.

$$R_c={\displaystyle \frac{F_l}{F_c}}$$

(2)

Figure 3b demonstrates that increasing the magnet length has negligible impact on damping force generation, particularly at larger dimensions. This empirical evidence suggests that damping force remains independent of magnet length variations.

For the levitation magnets that require both minimized levitation-to-damping force ratio R_c and satisfied suspension performance, an optimization objective function is established, as shown in Equation (3), considering the critical influence of magnet dimensions on electromagnetic forces. Based on this objective function and the preceding damping force analysis in Figure 3, Figure 4 and Figure 5, which demonstrates the influences of the magnet dimensions on the levitation-to-damping force ratio. This integrated approach enables the comprehensive evaluation of the geometric dependencies while ensuring optimal suspension performance. In Equation (3), the parameters w₀ and d₀ denote the width and thickness of the magnet, respectively.

$$\begin{array}{l}\min F(w_0,d_0)={\left[R_c\right(w_0,d_0\left)\right]}^{\mathrm{T}}\\ s.t.\left\{\begin{array}{l}10\le d_0\le 100\\ 100\le w_0\le 240\end{array}\right.\end{array}$$

(3)

Figure 5 examines the combined influence of magnet width and thickness on the levitation-to-damping force ratio, while ensuring sufficient levitation force is maintained to overcome the vehicle weight. These findings provide quantitative guidance for optimizing the characteristic ratio R_c to satisfy the diverse operation requirement.

The optimization results presented in Figure 5 identifies a length of 40 mm, a width of 240 mm, and a thickness of 70 mm as the optimal PMs geometry specifications for minimizing the levitation-to-damping force ratio. This configuration maximizes end field damping efficiency and meets the levitation force requirements simultaneously.

Optimal Design of Damping Plate

The damping force is generated through electromagnetic interactions between the end fields of PMs and the conductive damping plate, with its magnitude being highly sensitive to the damping plate. Building upon the optimized PMs dimensions, this subsection evaluates primary damping plate parameters, including vertical vibration speed, thickness, conductivity, temperature rise, and operation gap. The optimal damping plate provides essential input parameters for subsequent vehicle dynamic analysis.

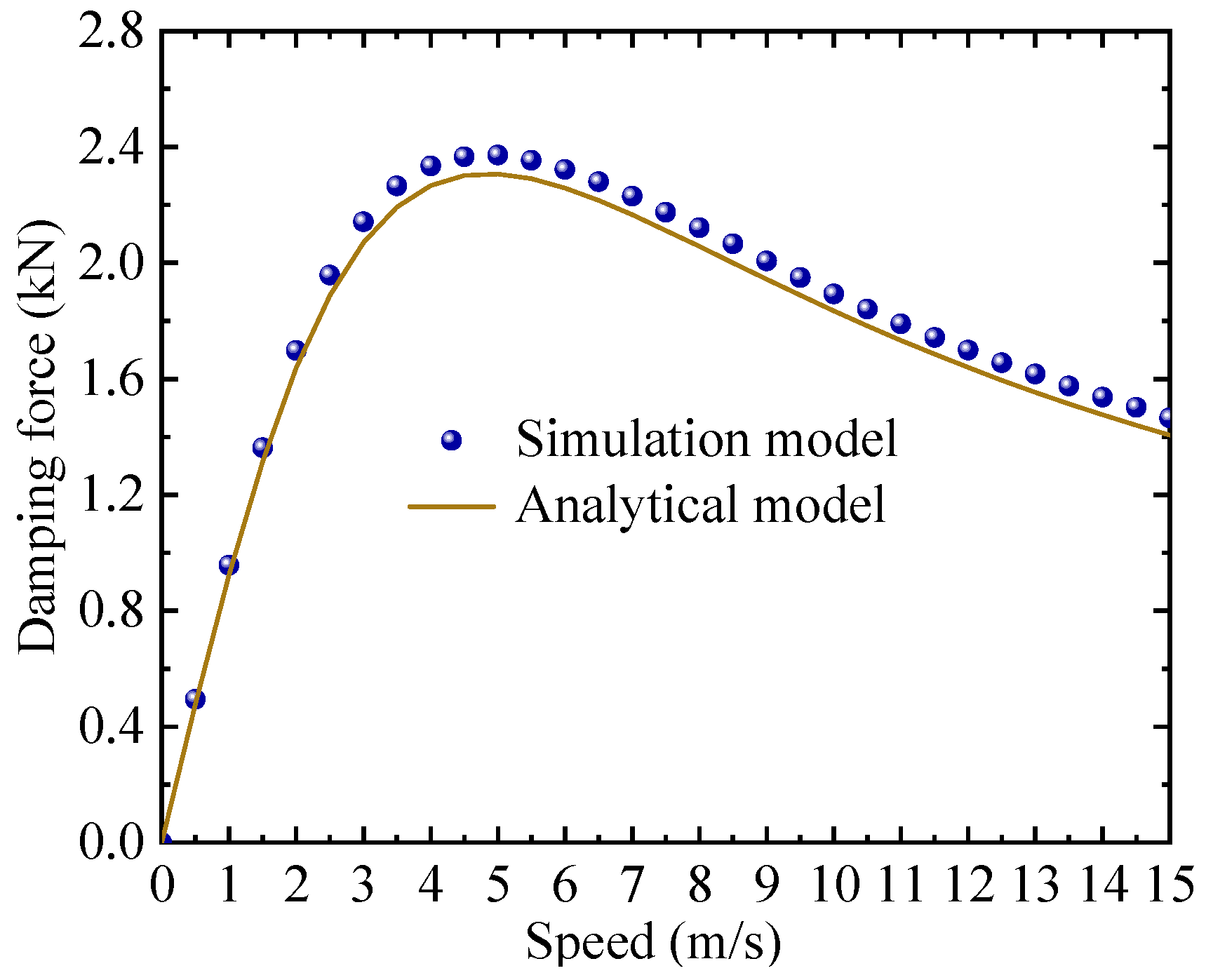
(1) Vertical vibration speed: vertical vibration speed plays a crucial role in damping force generation owing to its speed-dependent constitutive characteristics. Figure 6 demonstrates that for a damping plate configuration with thickness of 10 mm, conductivity of 3.8 × 10⁷ S/m, and air gap of 5 mm, simulation and analytical results consistently show the damping force initially increases then decreases with rising vibration speed. This characteristic evolution resembles the typical drag force–speed relationship.

(2) Damping plate thickness: before discussing the thickness of the damping plate, it is necessary to address the skin effect, a prevalent phenomenon in PMEDS vehicles. The skin effect causes an exponential attenuation of induced eddy current density along the thickness of the conductive plate, with maximum current density occurring at the surface [19]. This phenomenon stems from the surface-biased distribution characteristics of eddy currents induced by impedance gradients [20]. The skin depth δ_d is expressed by Equation (4), where μ_r represents the relative permeability of the conductive plate, μ₀ denotes the vacuum permeability, τ corresponds to the pole pitch of PMs, and σ indicates the conductivity of the conductive plate.

$${\delta }_d=\sqrt{{\displaystyle \frac{\tau }{{\mu }_0{\mu }_r\mathrm{\sigma }\mathrm{\pi }v}}}$$

(4)

Based on the structural parameters in

Table 3. Parameter optimization simulation model structure parameters.

Parameters	Value	Unit
Damping plate thickness	2~40	mm
Gap	5	mm
Speed	0~15	m/s
Conductivity	3.8 × 107	S/m

, a computational model to analyze how damping plate thickness regulates damping force and investigate their relationship.

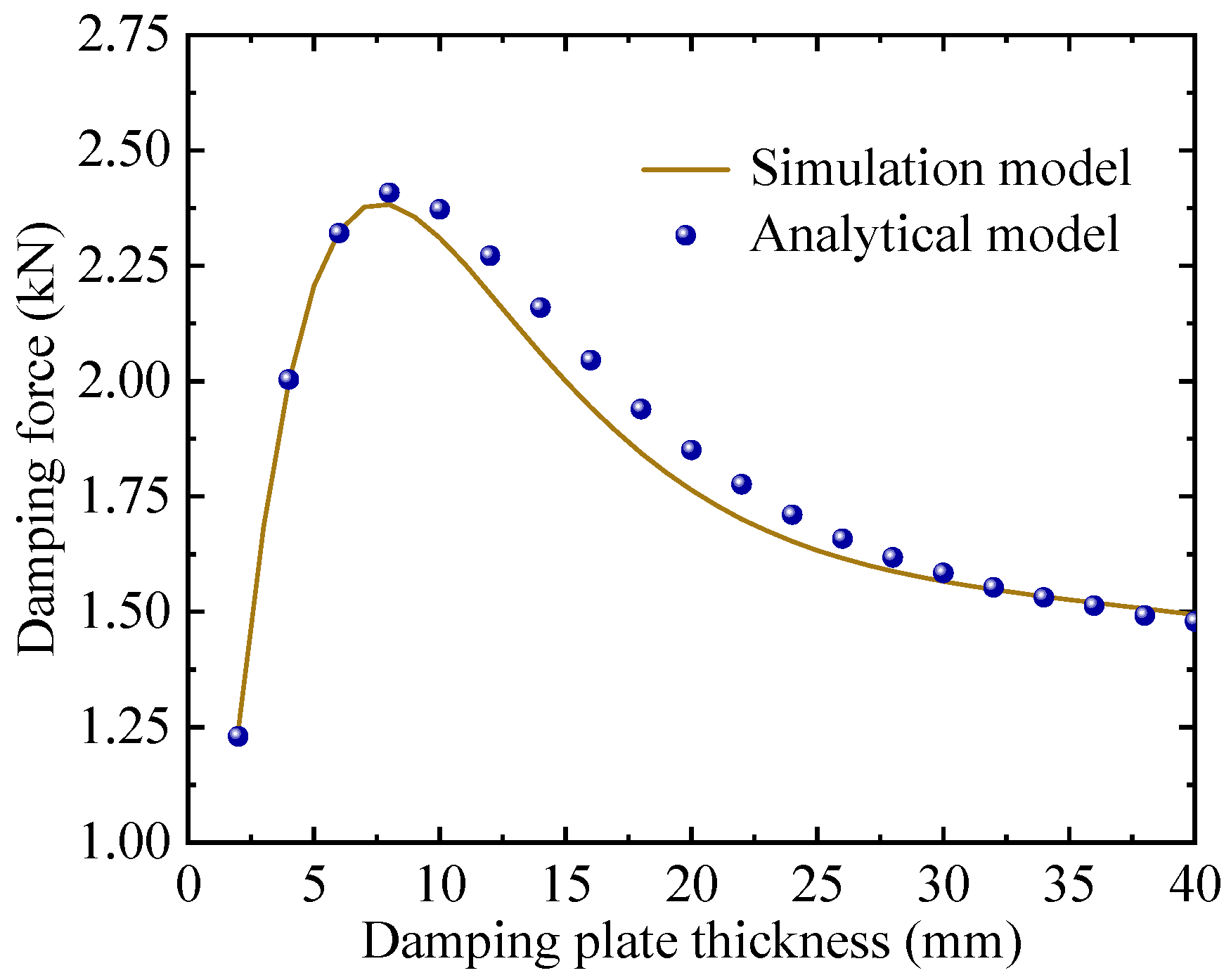
Numerical and simulation analysis presented in Figure 7 reveals a non-monotonic relationship between damping force and plate thickness at vertical speed of 5 m/s. Specifically, the damping force demonstrates an initial ascending trend followed by a subsequent decreasing as plate thickness varies, peaking at an optimal thickness of 8 mm before diminishing returns occur.

Furthermore, during vibration, the relative speed between PMs and the damping plate exhibits time-varying characteristics, necessitating comprehensive analysis of thickness effects on damping force across different speed ranges.

To determine the optimal damping force under coupled speed-thickness conditions, the objective function is established as shown in Equation (5). The approach employs a comprehensive two-stage optimization methodology. First, parametric numerical simulations analyze damping forces across the full operation parameter space. This space includes speeds from 0 to 15 m/s with increments of 1 m/s and thicknesses ranging from 2 to 40 mm with increments of 2 mm. Subsequently, a systematic evaluation using the objective function determines the global optimum. This ensures thorough optimization of damping performance throughout the defined design domain.

$$\begin{array}{l}\max J(v, d_t)={\left[F\right(v, d_t\left)\right]}^{\mathrm{T}}\\ s.t.\left\{\begin{array}{l}0\le v\le 15\\ 2\le d_t\le 40\end{array}\right.\end{array}$$

(5)

In Equation (5), $v$ denotes speed and d_t stands for damping plate thickness.

As illustrated in Figure 8, the damping force demonstrates strong coupled dependence on both thickness and vibration speed, with distinct thickness-dependent trends emerging at different speed ranges. At lower speed of 1 m/s, the damping force exhibits monotonic growth with increasing thickness, attributable to larger skin depths and relatively weaker induced current densities. However, at greater speed such as above 3 m/s, the optimal thickness decreases due to reduced skin depths and intensified eddy current concentration effects. Considering the dynamic vertical speed variations in practical applications, a thickness of 6 mm is recommended to achieve robust damping performance across operation speed ranges.

(3) Temperature rise: damping plates and PMs undergo prolonged reciprocating vibrations, generating induced eddy currents that lead to power loss. This phenomenon heats the damping plate, subsequently altering the conductivity and damping force. Common non-magnetic conductive materials include copper and aluminum, with conductivities of 5.8 × 10⁷ S/m and 3.8 × 10⁷ S/m under ambient temperature, respectively. The temperature-dependent conductivity follows Equation (6). Therein, σ represents material conductivity, T denotes the time-varying temperature, and α is the temperature coefficient. The temperature coefficients for copper and aluminum are 0.0039 and 0.0043, respectively.

$${\mathrm{\sigma }}_t={\displaystyle \frac{{\mathrm{\sigma }}_{22}}{\left(1+\alpha \times \left(T-22\right)\right)}}$$

(6)

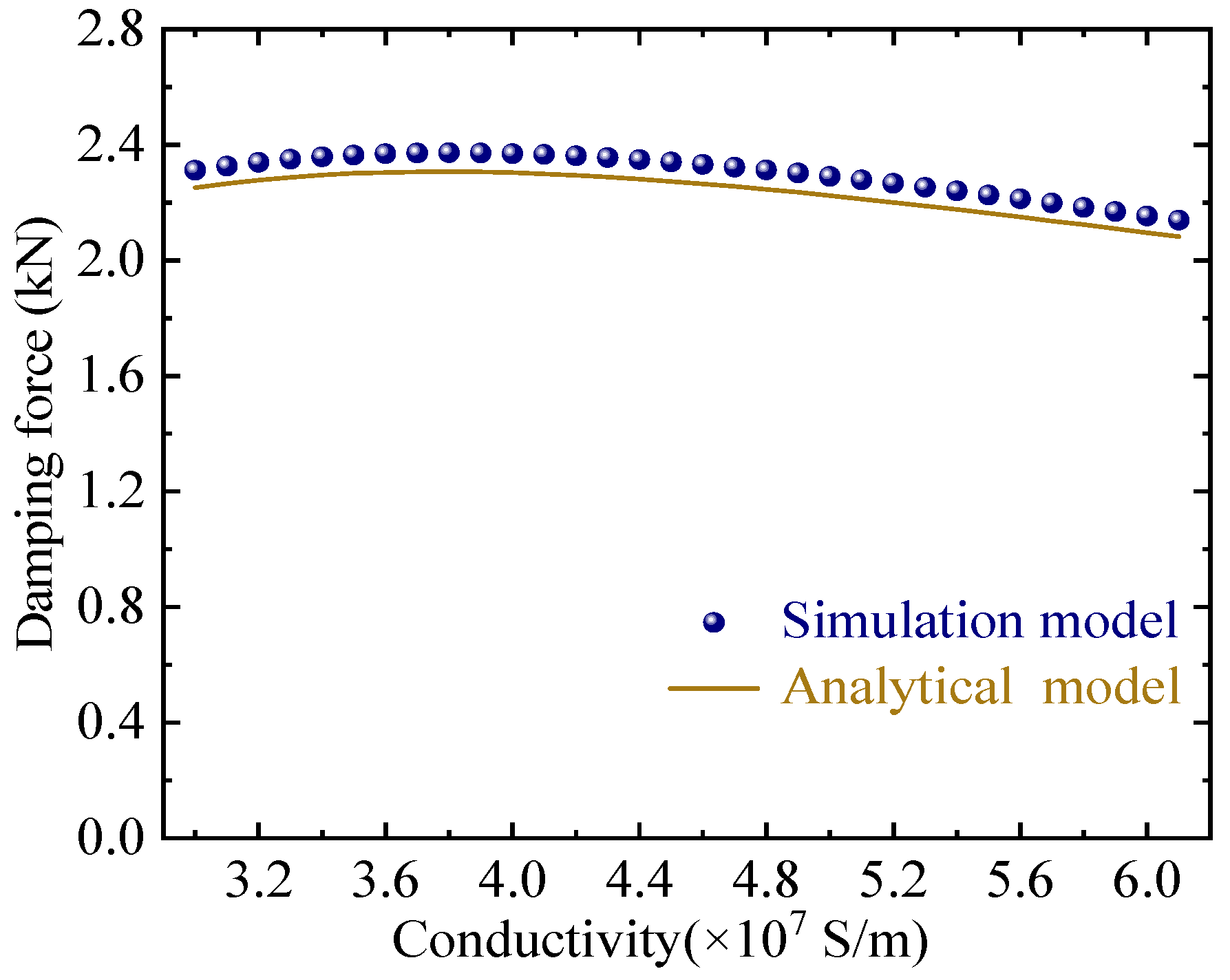
As indicated by Equation (6), the conductivity of the damping plate decreases with increasing temperature. Figure 9 illustrates the relationship between damping force and conductivity at a constant relative speed of 5 m/s. The damping force initially rises with conductivity before reaching a peak and subsequently declining, with all observed variations remaining below 300 N across the tested conductivity ranges.

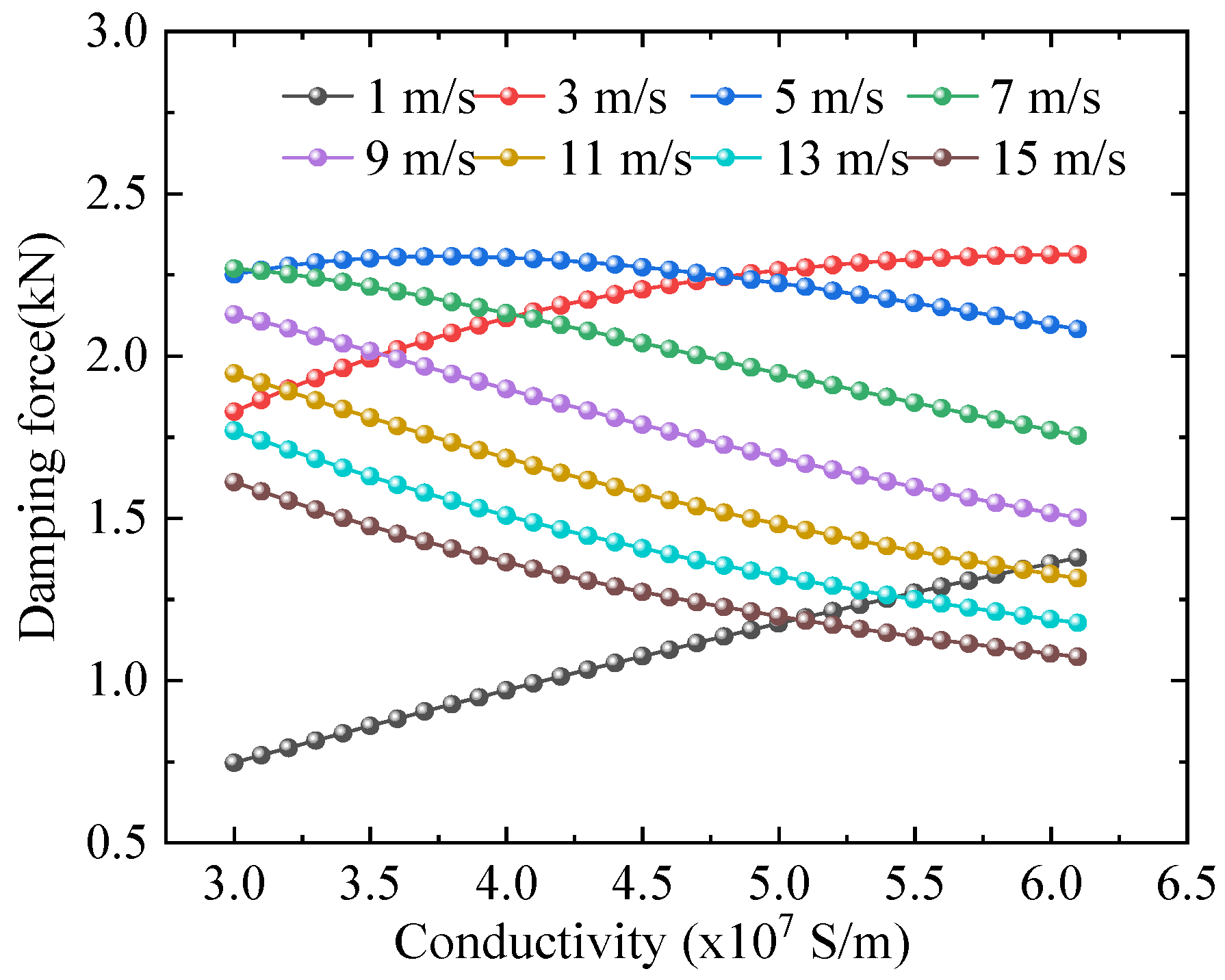
Further analysis is conducted on the damping force under the combined influence of conductivity and speed. The computational results are presented in Figure 10, which reveals that in the low-conductivity region, the damping force exhibits a gradual decline with increasing speed, showing better damping performance. In the high-conductivity range, the attenuation rate increases significantly due to an enhanced skin effect, leading to a more rapid reduction in damping force.

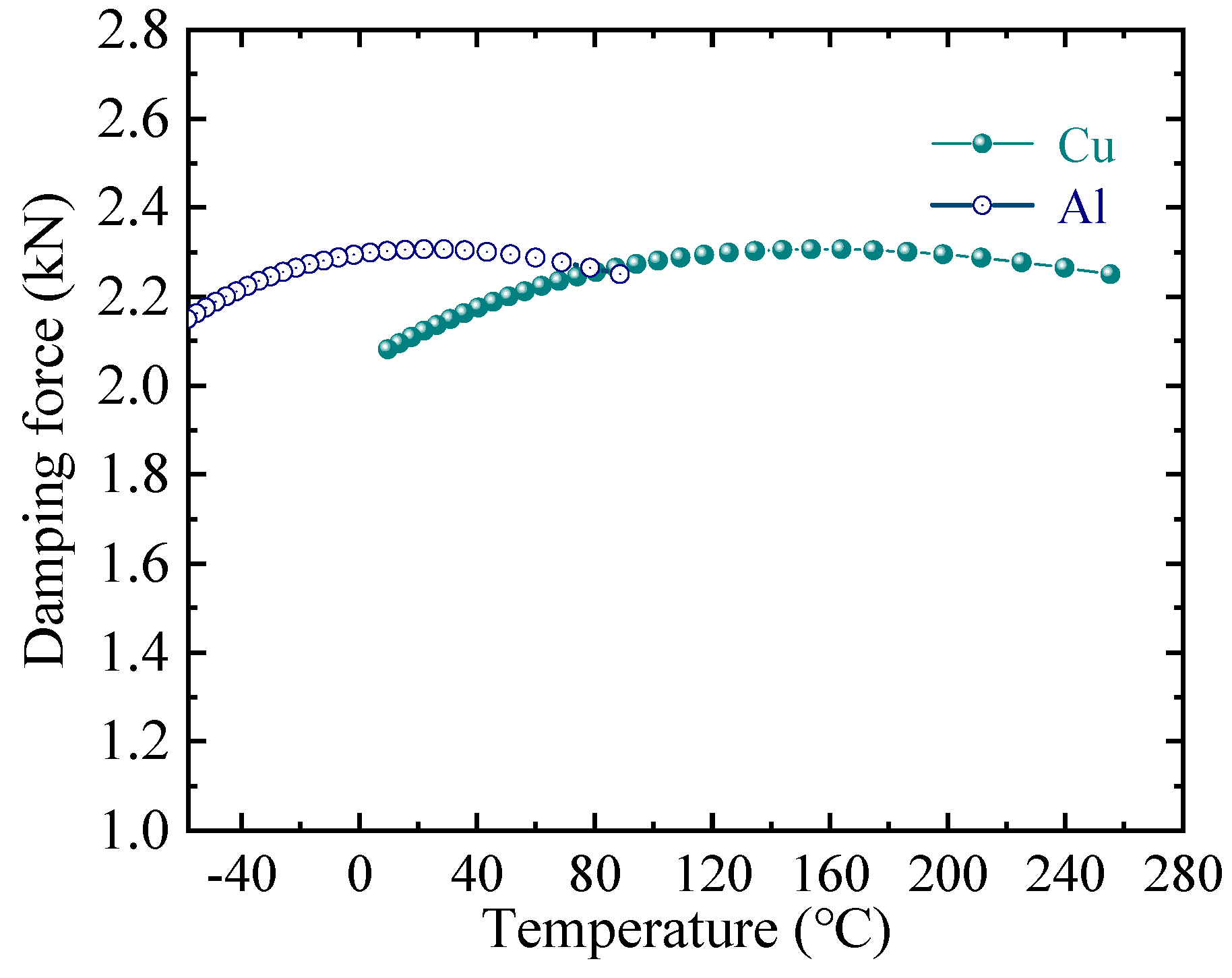
An analysis of the conductivity calculation results in Figure 11 reveals that the copper damping plate demonstrates comparable damping performance across both ambient temperature and elevated-temperature conditions, while the aluminum plate proves more suitable for low-temperature or room-temperature applications. The variation in damping force with temperature remains relatively small within 250 N, while the damping plate exhibits a limited temperature rise. Thus, aluminum emerges as the preferred material choice when damping performance requirements are moderate owing to lower cost.

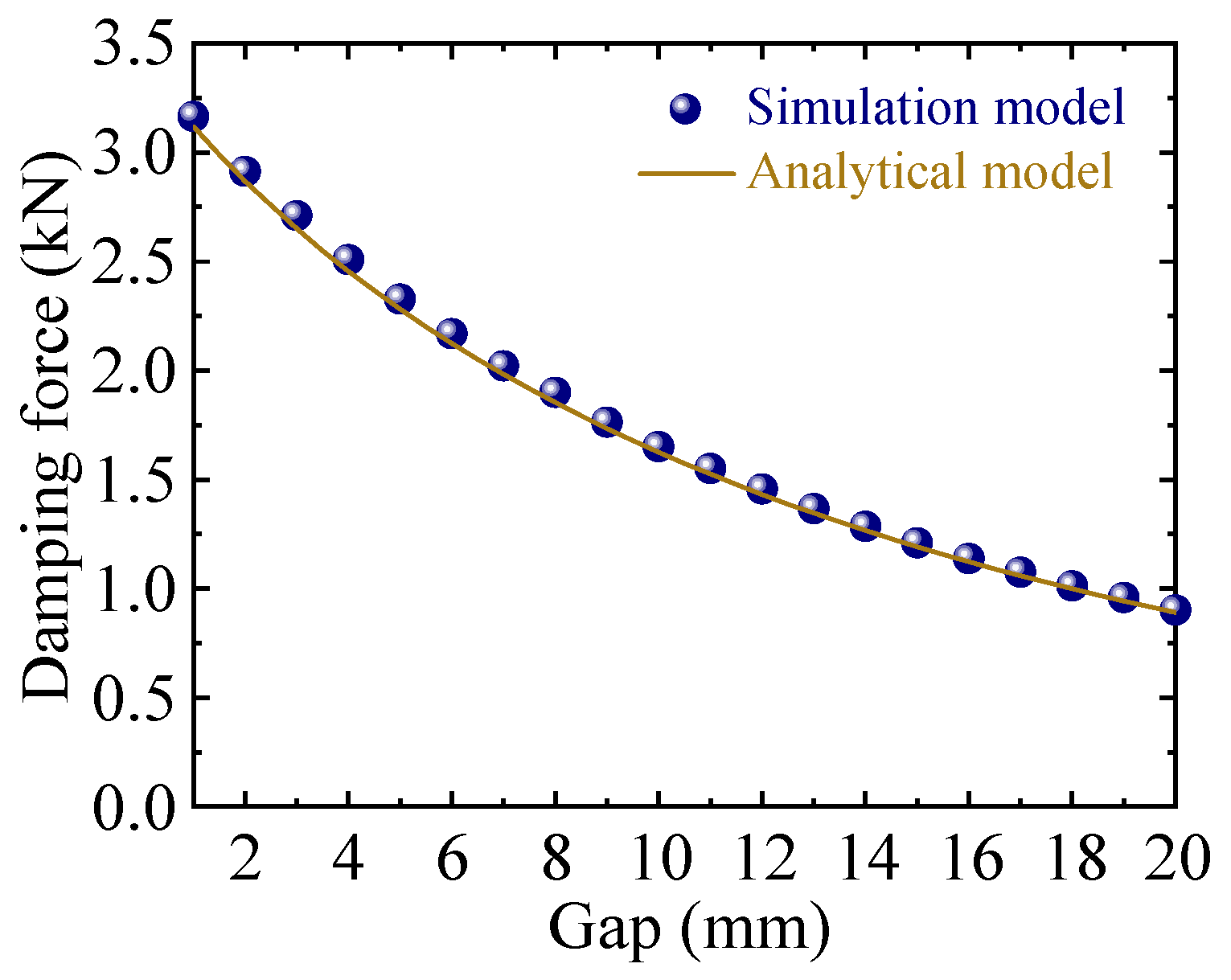
Gap: End field exhibits a gradual decrease with increasing gap, defining the distance of the PMs and damping plate. Consequently, the gap can influence the damping performance. Using the optimized magnet and damping plate, Figure 12 demonstrates the nonlinear decreasing relationship between damping force and increasing gap at a constant speed of 5 m/s. Notably, the damping force progressively diminishes with larger air gaps. For practical applications in which effective damping force needs to be maintained, the working air gap typically varies within a limited range. Under such constrained conditions, the force variation can be reasonably approximated as a linear process.

To determine the optimal gap, a dual-variable damping force objective function is established considering both speed and gap as expressed in Equation (7). Through parametric simulation analysis, the damping force characteristics under various operating speeds and gaps are evaluated, and the optimal gap that satisfies the damping performance requirements is determined.

$$\begin{array}{l}\max J_g(v, d_g)={\left[F\right(v, d_g\left)\right]}^{\mathrm{T}}\\ s.t.\left\{\begin{array}{l}0\le v\le 15\\ 0\le d_g\le 20\end{array}\right.\end{array}$$

(7)

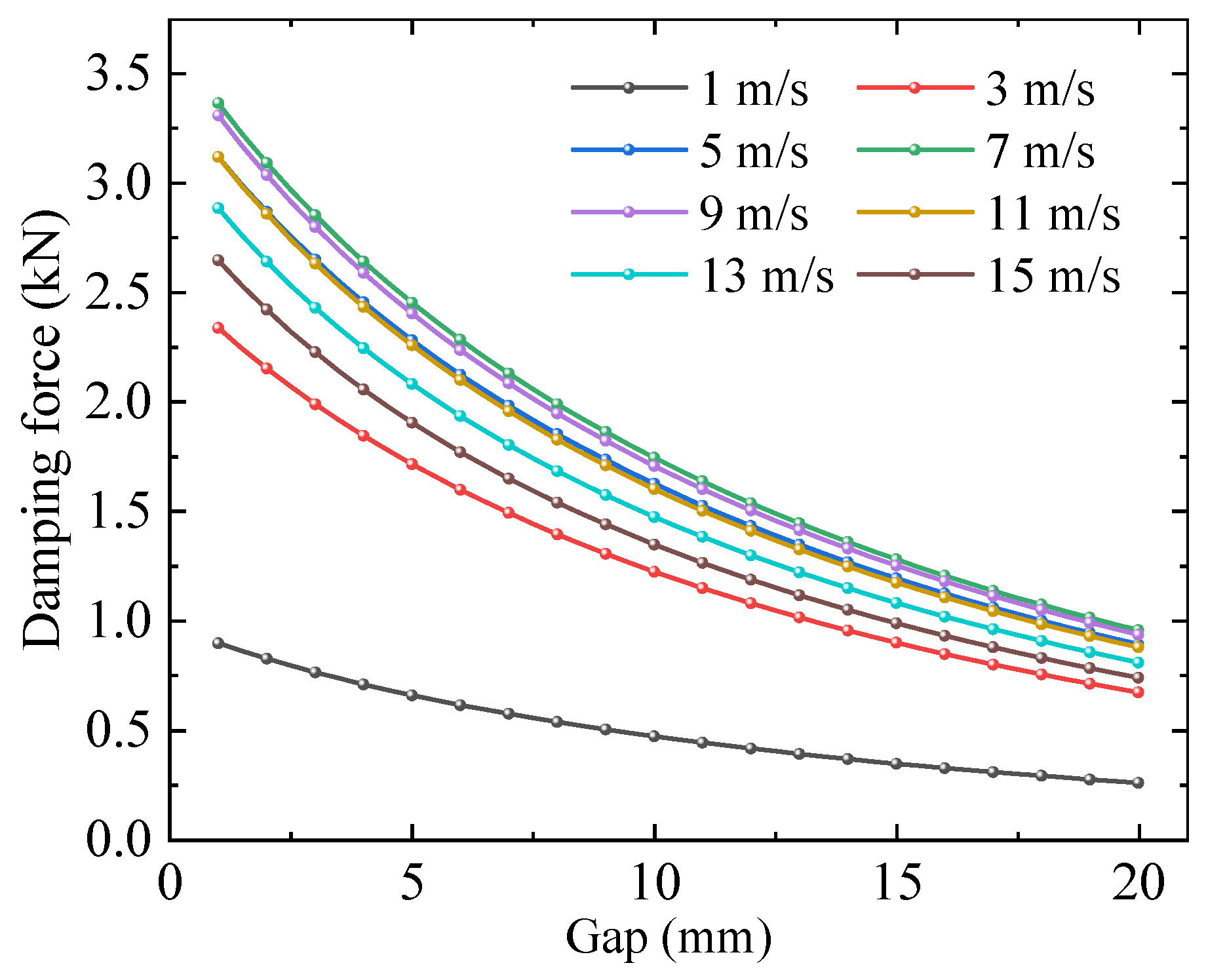
In Equation (7), $\max J\left(v, d_g\right)$ represents the optimization objective function for damping force under coupled speed and gap conditions. $v$ and $d_g$ denote speed and gap.

Figure 13 presents the damping force versus working gap relationship across various operating speeds. The results demonstrate that the damping force exhibits a consistent decreasing trend with increasing gap. The attenuation rate of damping force is speed-dependent, showing significant variation across the tested speed range. These findings indicate that reduced working gaps generally yield enhanced damping performance. For practical implementation, the optimal gap should be determined through careful consideration of guideway operation conditions, structural precision constraints, and required damping performance specifications.

4. Vehicle Dynamic Analysis

4.1. Dynamic Model of Single PMs

Based on the optimized levitation magnet and damping plate derived in Section 3, the structural model can be established in the SIMPACK software. The dominating parameters are listed in

Table 4. Structural parameters of a single PMEDS vehicle.

Parameters	Value	Unit
Length of permanent magnet	40	mm
Width of permanent magnet	240	mm
Thickness of permanent magnet	70	mm
Permanent magnet mass	47	kg
Equivalent vehicle mass	1400	kg

. As shown in Figure 14a, it displays the three-dimensional damping vibration reduction structure and Figure 14b presents the topology diagram of inter-body forces and articulated relationships. The PMs are constrained to vertical degrees of freedom relative to the ground and are coupled through levitation forces, with the input levitation force curve illustrated in Figure 15a.

Similarly, the equivalent car body maintains vertical degrees of freedom with the ground and connects to the PMs via load-bearing springs, while the damper provides damping. The input damping force curve is shown in Figure 15b. Additionally, since the model focuses on vertical motion characteristics, road irregularity excitations can be represented by time-domain varying excitations.

The measured vertical track irregularities are processed into time-domain excitation signals. These signals are then applied to the PMs to further investigate their dynamic response under complex disturbances. The resulting input excitation profile is shown in Figure 16, and the dynamic response is presented in Figure 17.

From the response results of both the equivalent vehicle body and PMs in Figure 17, it can be observed that the maximum acceleration of the equivalent vehicle body reaches 2.56 m/s², while the PMs experience significantly higher peak acceleration of 3.69 m/s². Besides, the maximum vertical displacement measures 11.8 mm for the vehicle body compared to 8.6 mm for the PMs. These results demonstrate that the PMs undergo more severe vibrations than the vehicle body, indicating considerably harsher operation conditions for the magnetic components.

To further demonstrate the performance improvement achieved by the installed damping structure, a comparative simulation is established by constraining the degrees of freedom between the equivalent vehicle body and PMs to represent the vehicle without supplemental damping. The dynamic response under vertical track irregularity excitation is calculated, as shown in Figure 18. The results reveal intensified vehicle body vibrations over time in the single module configuration, and it demonstrates that PMEDS vehicle relying on levitation forces exhibit poor stability and the vertical displacement and acceleration of the equivalent vehicle body exceed those observed in the damped suspension system.

4.2. Dynamic Model of PMEDS Vehicle

This subsection develops a dynamic simulation model for the PMEDS vehicle based on optimized electromagnetic parameters and structural configuration. The dynamic simulation adopts a simplified modeling approach that neglects geometric profile effects while capturing fundamental structure characteristics. The single vehicle model incorporates eight levitation bogies with six groups of PMs, maintaining vertical relative degrees of freedom between bogies and magnets. The car body and bogies are modeled with six degrees of freedom, including heave, sway, pitch, yaw, and roll motions, and are interconnected through secondary suspension spring-damper elements. All components including the vehicle body, bogies, and guideway beams are treated as rigid bodies. The dynamic model configuration and kinematic joint relationships are presented in Figure 19.

Subject to the vertical constraints imposed by non-rotating bogies, the fundamentally continuous electromagnetic forces including levitation, guidance, and damping are represented as equivalent concentrated forces at designated nodal points. Both levitation and guidance forces are assumed to act through the geometric center of each PM unit. The modeled single-car configuration comprises eight bogies, with each bogie incorporating six PMs units, resulting in a total of 48 concentrated force pairs that satisfy established force substitution criteria. The simulation incorporates speed-dependent levitation and guidance force inputs, with track irregularities introduced to replicate realistic operation conditions. The corresponding electromagnetic force distributions and track irregularity power spectral density are presented in Figure 20, while

Table 5. Dynamic simulation model specifications of the PMEDS vehicle.

Parameters	Value	Parameters	Value
PMs mass	47 kg	PMs elastic element stiffness	800 kN/m
Bogie mass	1010 kg	Secondary suspension longitudinal stiffness	150 kN/m
Bogie roll moment of inertia	542 kg·m2	Secondary suspension lateral stiffness	150 kN/m
Bogie pitch moment of inertia	441 kg·m2	Secondary suspension vertical stiffness	450 kN/m
Bogie yaw moment of inertia	967 kg·m2	Secondary suspension longitudinal damping	60 kN·S/m
Vehicle body mass	54,000 kg	Secondary suspension lateral damping	60 kN·S/m
Vehicle body roll moment of inertia	560,000 kg·m2	Secondary suspension vertical damping	80 kN·S/m
Vehicle body pitch moment of inertia	2,000,000 kg·m2	Secondary suspension longitudinal span	1000 mm
Vehicle body yaw moment of inertia	2,000,000 kg·m2	Train center of gravity height	1700 mm

summarizes the key simulation parameters.

4.3. Dynamic Performance Evaluation Metrics

Ride comfort assessment PMEDS vehicle integrates conventional railway evaluation standards with maglev-specific dynamic characteristics due to the absence of commercial operation specifications, employing a comprehensive evaluation framework that combines the Sperling index (W) with component-level vibration analysis to address maglev-specific safety and comfort requirements where the Sperling index is mathematically defined by Equations (8) and (9), with A_i representing vibration acceleration amplitude, f_i denoting bandpass-filtered frequency components, F(f_i) corresponding to frequency-dependent weighting coefficients, and W_i indicating comfort index components at specific frequencies.

$$W_i=3.57\sqrt[10]{{\displaystyle \frac{{A_i}^3}{f_i}}F\left(f_i\right)}$$

(8)

$$W=\sqrt[10]{{\displaystyle \sum _{i=1}^n{W}_i^{10}}}$$

(9)

Vehicle ride stability is categorized into three distinct levels based on the evaluation criteria detailed in

Table 6. Ride comfort evaluation criteria and grades.

Grade	Evaluation	Ride Index
1	Excellent	<2.5
2	Good	2.5 ≤ W < 2.75
3	Qualified	2.75 ≤ W < 3.0

. Ride quality assessment incorporates vertical acceleration measurements of the car body, with established thresholds requiring maximum vertical acceleration below 2.5 m/s² and root mean square (RMS) values to remain below 0.75 m/s². Bogie dynamic performance is evaluated through RMS vertical vibration acceleration measurements, where lower values indicate superior performance. For PMs vibration stability assessment, both RMS values and peak amplitudes of vertical accelerations are implemented.

4.4. Comparative Analysis of Dynamic Performance

(1) Varying Operation Speeds: to investigate the influence of the dampers on train operation performance, this section presents a comparative analysis of vehicle body, levitation bogie, and PMs operation metrics between configurations with dampers considered as original structure and without dampers denoted as optimized structure from 50 to 110 m/s with increments of 10 m/s.

Figure 21 shows that the optimized configuration significantly improves vertical dynamic performance. Compared to the original structure, it achieves superior vertical ride stability indices below 2.5 across all speeds, meeting “excellent” criteria and maintains vertical acceleration RMS values at 0.02 m/s². In contrast to the original structure progressive increase in peak vertical acceleration at elevated speeds, the optimized design effectively suppresses acceleration growth, with mitigation efficiency demonstrating speed-dependent enhancement.

The dynamic behavior of the levitation bogies is a critical monitoring parameter for PMEDS vehicles employing linear motor propulsion, as their operating status directly governs the working air gap between mover and stator. Figure 22 presents vibration performance metrics for bogie No. 1 (leading), No. 4 (trailing), and No. 8 (mid-body) of a single-car configuration. The results reveal a speed-proportional increase in vertical acceleration root mean square (RMS) values across all bogies, with Bogie No. 8 exhibiting the most pronounced oscillations. However, there are minor differences in peak acceleration magnitudes are observed among the three bogies. The optimized configuration demonstrates superior vibration mitigation performance compared to the baseline design, conclusively validating the effectiveness of the passive damping plate optimization strategy.

In addition to vibration analysis, the displacement characteristics of the levitation bogies are computationally evaluated as show in Figure 23. The optimized configuration significantly suppresses vibrational displacement in Bogie No. 1, maintaining lower values than the baseline design. While maximum displacements decrease with increasing velocity in both designs, Bogie No. 8 of the optimized configuration exhibits transient amplification at mid-to-low speeds, followed by rapid attenuation. Critically, all displacements remain below 2.5 mm, confirming the enhanced structure effectiveness in reducing vibrations of the leading bogie while sustaining superior performance across low-and high-speed regions.

(2) Different Load Conditions: vehicle loading constitutes a critical parameter influencing train operation states, prompting a comparative investigation into vibration characteristics across structural components under three distinct loading conditions: empty, overloaded, and rated capacities. Figure 24 presents computational analysis results of vehicular dynamic performance under these loading scenarios. The data reveal that increased payload significantly improves vertical ride stability indices while enhancing overall operation quality, accompanied by progressively reduced peak vertical accelerations. Notably, discrepancies in operation metrics induced by load variations demonstrate diminishing sensitivity to speed escalation.

Figure 25 presents vibration metrics for the leading bogie (No. 1) and trailing bogie (No. 8) under varying load conditions. Reduced vehicle mass correlates with diminished vertical acceleration root mean square (RMS) values for both the leading Bogie No. 1 and trailing Bogie No. 8 across all tested speed conditions, a trend broadly consistent with peak acceleration behavior. This inverse relationship to car body metric variations demonstrates a counteractive correlation between payload effects on bogie vibrations and car body dynamics.

5. Conclusions

This study addresses the technical bottleneck of weak damping in PMEDS vehicles by proposing a passive damping scheme characterized by edge magnetic fields and passive damping plates, focusing on the optimization of magnet-damping plate structure parameters and vehicle dynamics. A passive damping solution utilizing edge effects is proposed, where the PMs and damping structure are optimized through parametric optimization methods. The optimal PMs dimensions are determined as 40 mm in length, 240 mm in width, and 70 mm in thickness, coupled with a 6 mm-thick aluminum damping plate. The effectiveness of the passive damping solution is validated through dynamic analysis of both a single PMs and the PMEDS vehicle under straight-line operating conditions, showing vibration reduction in both the vehicle body and PMs under excitation conditions.

While the optimized damping structure demonstrates appropriate vibration reduction performance, this solution holds significant value as it utilizes neglected edge effects for vertical vibration suppression, removing additional magnetic field assistance or excitation devices, thereby achieving structural simplification. Future research on PMEDS vibration damping will be continued to develop improved solutions and advance PMEDS technology.