Design and Implementation of Flexible Four-Bar-Mechanism-Based Long-Stroke Micro-Gripper
Abstract
1. Introduction
2. Structural Design of Micro-Gripper Based on Flexure Four-Bar Mechanism
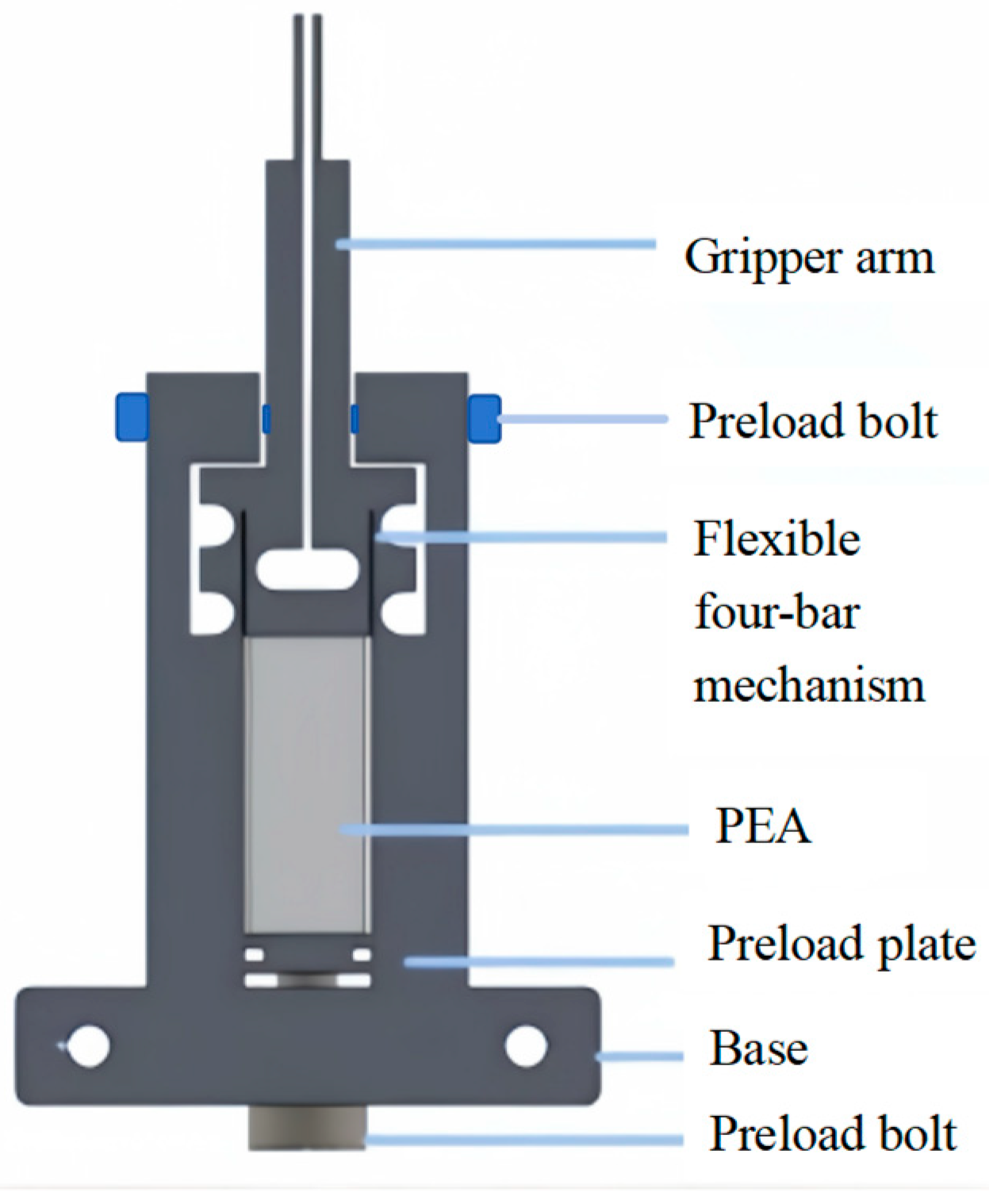
2.1. Structural Design of the Micro-Gripper
2.2. Design of the Flexure Four-Bar Mechanism
3. Kinematic Analysis of the Flexure Four-Bar Mechanism
4. Finite Element Analysis
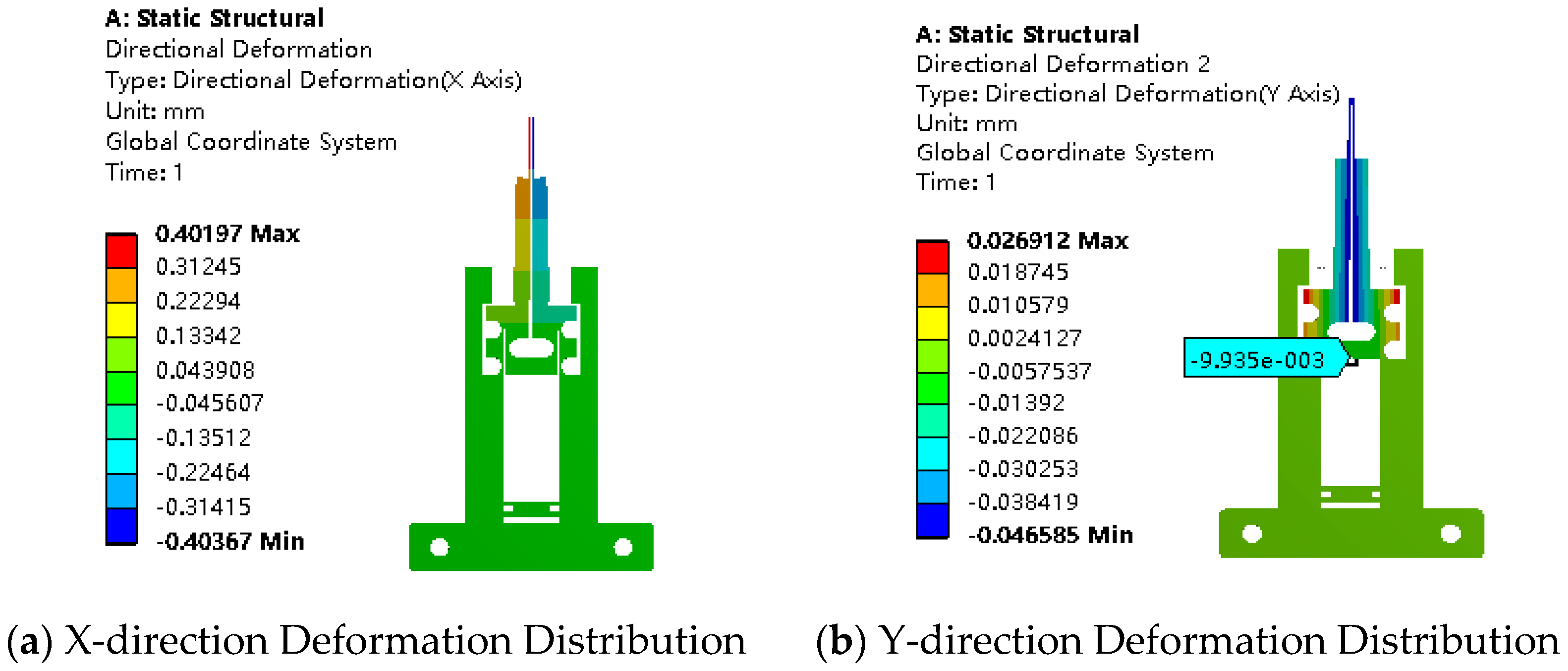
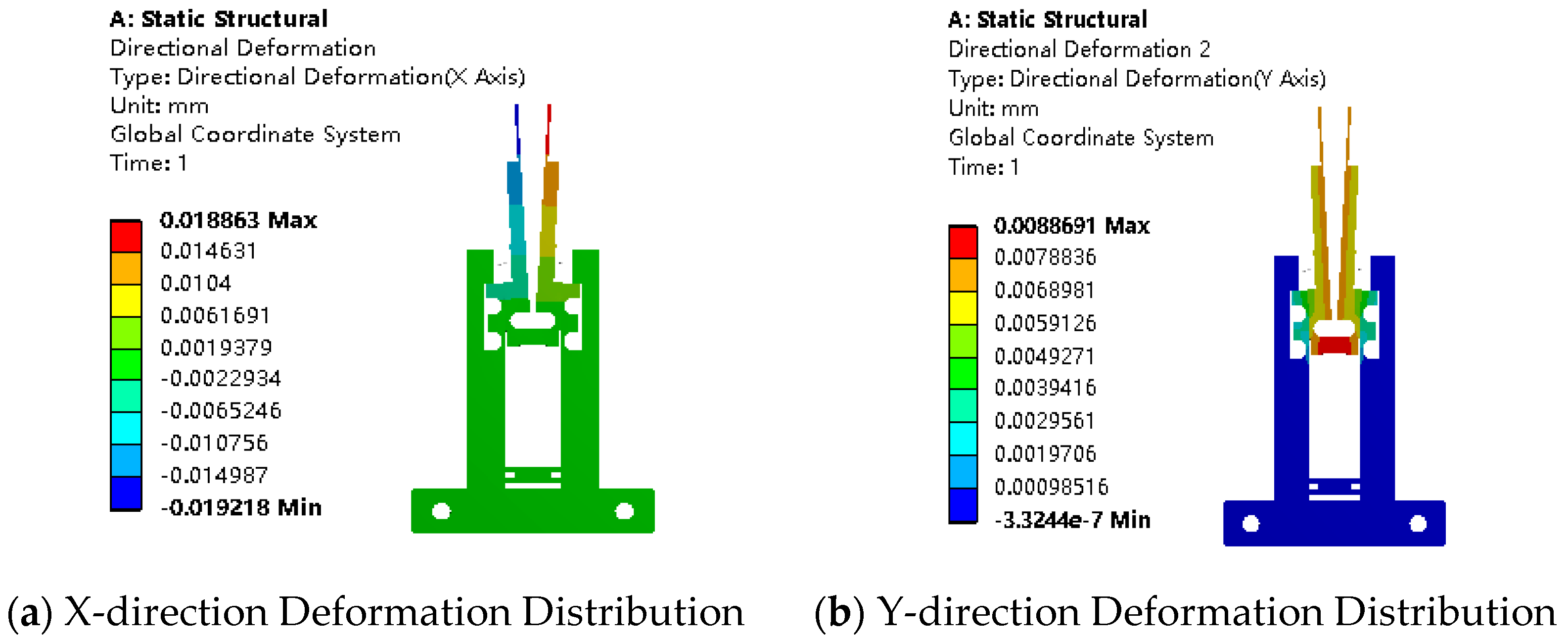
4.1. Analysis of Displacement Amplification Ratio
4.2. Clamping Force and Strain Analysis
4.3. Modal Analysis
5. Experimental Tests
5.1. Building the Experimental Platform
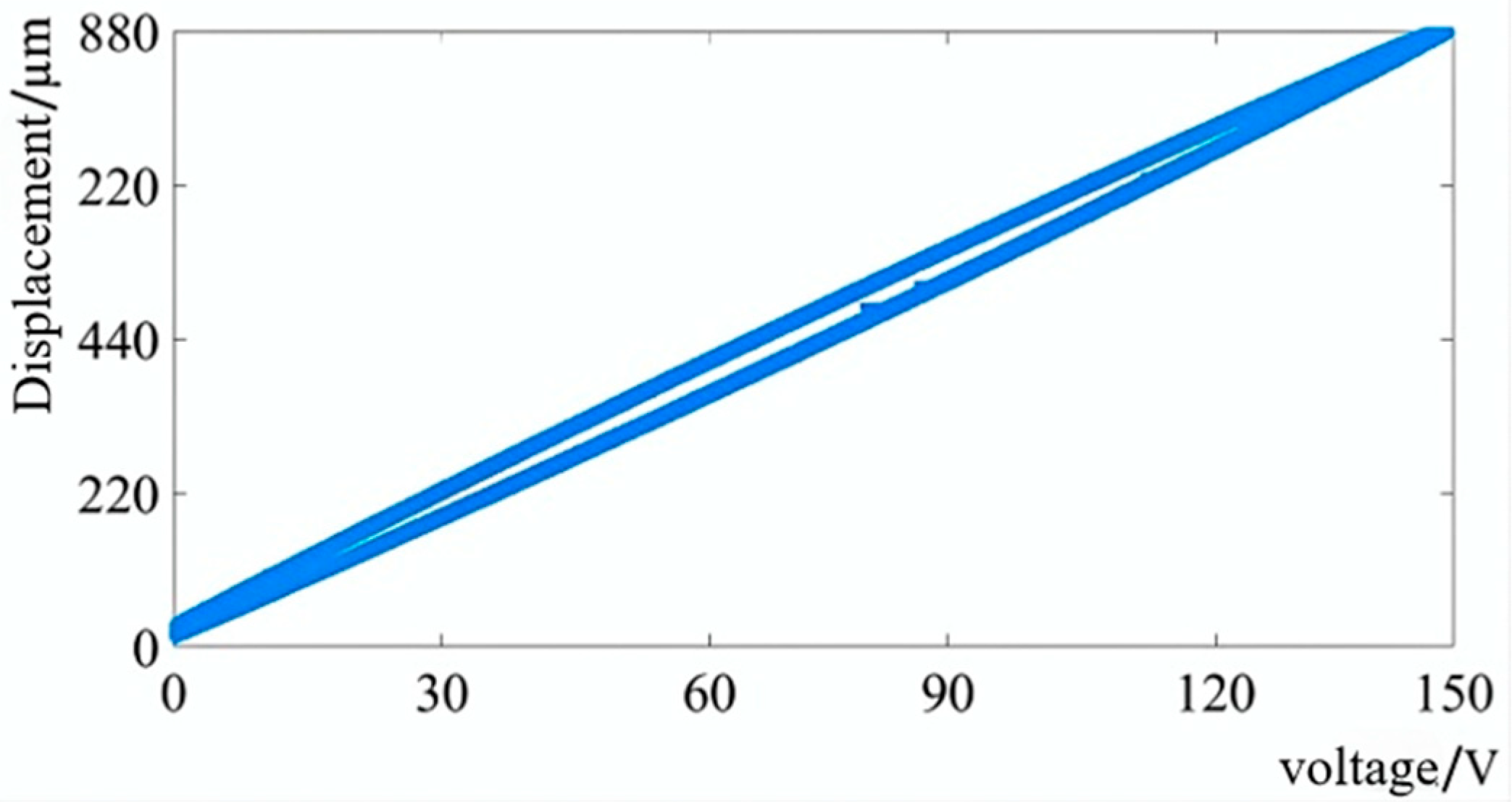
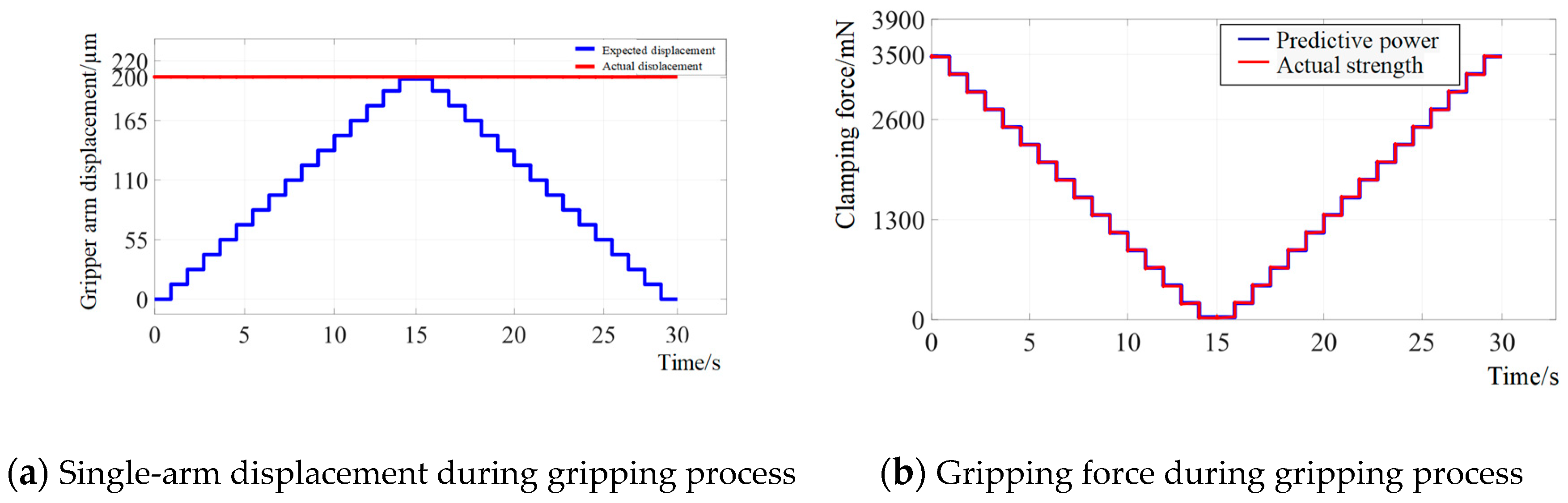
5.2. Displacement Characteristic Experiment
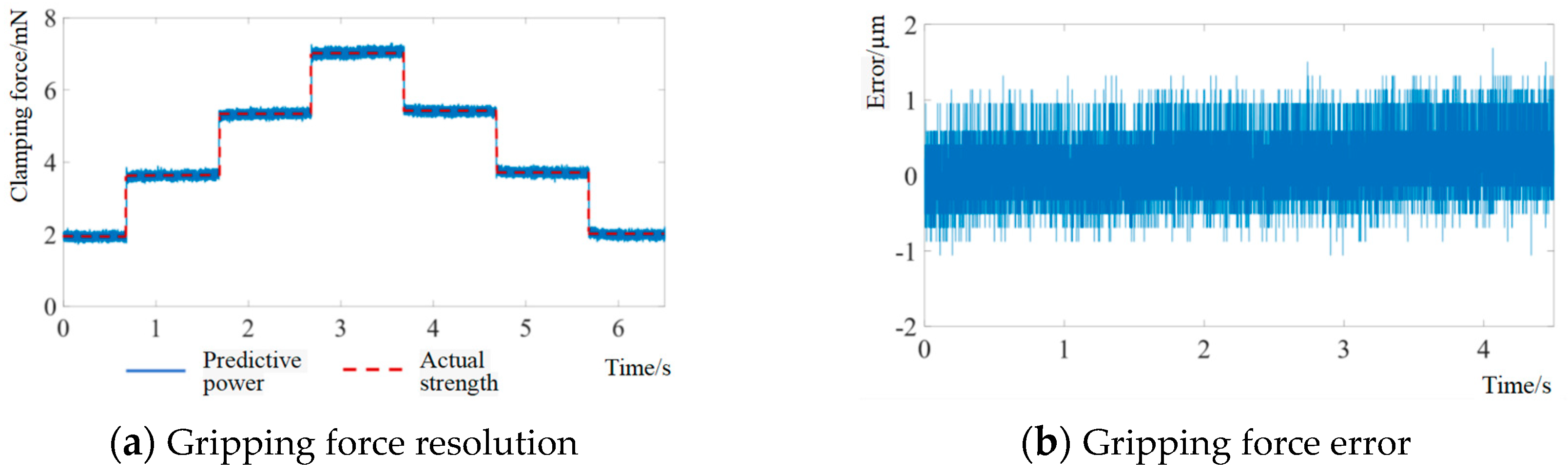
5.3. Gripping Force Test Experiment
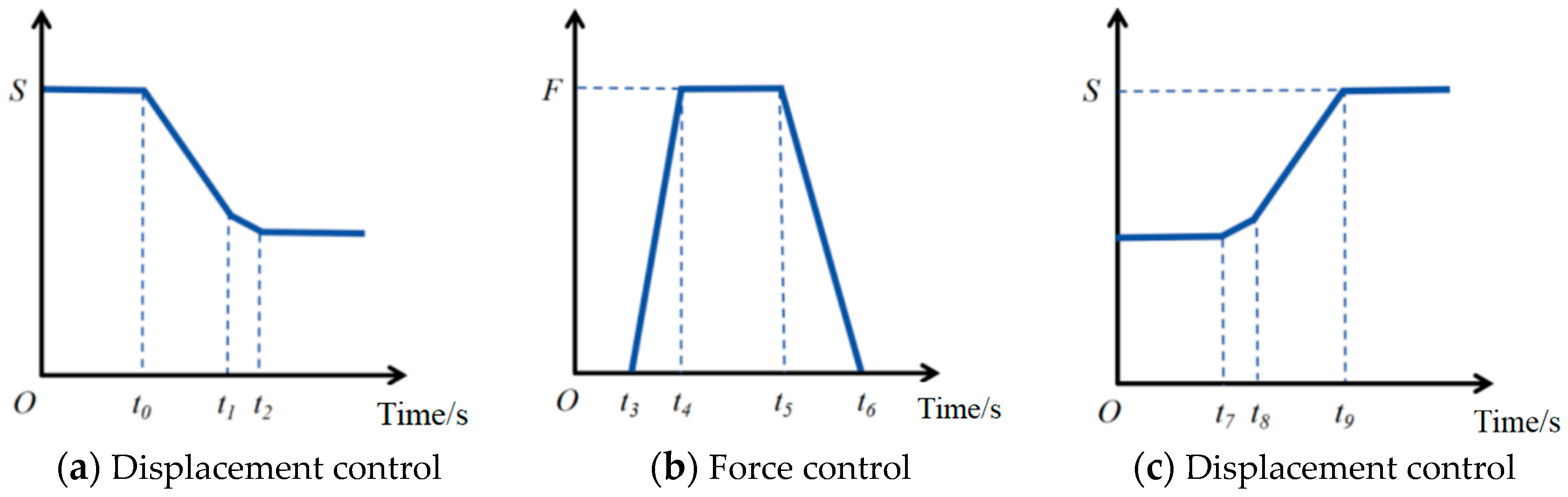
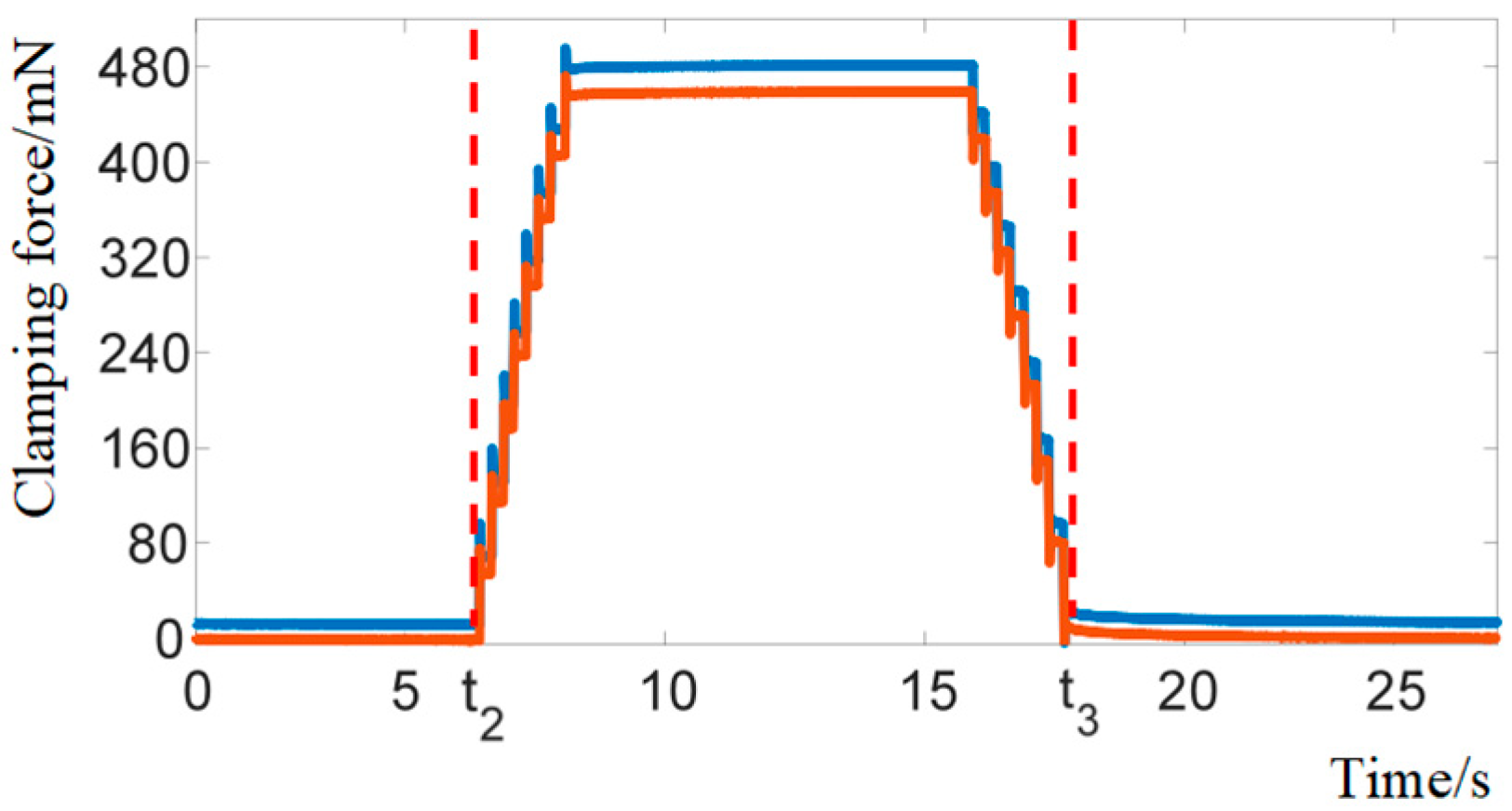
5.4. Gripping Force–Displacement Switching Control
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, F.; Liang, C.; Tian, Y.; Zhao, X.; Zhang, D. Design and control of a compliant microgripper with a large amplification ratio for high-speed micro manipulation. IEEE/ASME Trans. Mechatron. 2016, 21, 1262–1271. [Google Scholar] [CrossRef]
- Lin, M.; Meng, G.; Sheng, Y.; Li, W.; Cao, Y. Analysis and Optimization of a Microgripper with Flexible Structure. J. Donghua Univ. (Nat. Sci.) 2021, 47, 96–104. [Google Scholar] [CrossRef]
- Shi, C.; Dong, X.; Yang, Z. A microgripper with a large magnification ratio and high structural stiffness based on a flexure-enabled mechanism. IEEE/ASME Trans. Mechatron. 2021, 26, 3076–3086. [Google Scholar] [CrossRef]
- Lyu, Z.; Xu, Q. Design and Testing of a New Piezoelectric-Actuated Symmetric Compliant Microgripper. Actuators 2022, 11, 77. [Google Scholar] [CrossRef]
- Qian, J.; Yan, P.; Liu, P. Position/force modeling and analysis of a piezo-driven compliant micro-gripper considering the dynamic impacts of gripping objects. Smart Mater. Struct. 2021, 30, 075036. [Google Scholar] [CrossRef]
- Song, S.; Yang, Y.; Wu, G.; Zhang, S.; Wei, Y. Design and Analysis of a Piezoelectric Compliant XY Microgripper. J. Vib. Shock 2022, 41, 154–161. [Google Scholar] [CrossRef]
- Chen, X.; Xie, Z.; Tai, K.; Tan, H. Design of low parasitic motion microgripper based on symmetrical parallelogram mechanism. Sens. Actuators A 2024, 367, 115072. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, Y.; Chen, M.; Ding, B. Design, analysis, and experimental investigations of an asymmetrical under-actuated micro-gripper. J. Intell. Mater. Syst. Struct. 2024, 35, 960–970. [Google Scholar] [CrossRef]
- Xu, D.; Yang, F.; Yu, S.; Xu, C.; Liu, X.; Zhao, Z.; Zhang, X.; Li, S.; Yang, H.; Lu, Q. A three-stage amplification piezoelectric-actuated micro-gripper with adjustable output displacement: Design, modeling, and experimental evaluation. Smart Mater. Struct. 2023, 32, 095033. [Google Scholar] [CrossRef]
- Guo, Z.; Ma, H.; Li, Q.; Li, Y.; Liu, Z.; Song, Q. Design and analysis of a compliant microgripper with a large amplification ratio. Microcyst. Technol. 2023, 29, 1333–1341. [Google Scholar] [CrossRef]
- Ni, L.; Chen, G.; Hong, K.; Wang, G. Design and development of a compliant piezoelectric microgripper based on three-stage amplification. Microsyst. Technol. 2023, 29, 939–952. [Google Scholar] [CrossRef]
- Chen, F.; Du, Z.J.; Yang, M.; Gao, F.; Dong, W.; Zhang, D. Design and Analysis of a Three-dimensional Bridge-type Mechanism based on the Stiffness Distribution. Precis. Eng. 2018, 51, 48–58. [Google Scholar] [CrossRef]
- Liang, C.; Wang, F.; Shi, B.; Huo, Z.; Zhou, K.; Tian, Y.; Zhang, D. Design and control of a novel asymmetrical piezoelectric actuated microgripper for micromanipulation. Sens. Actuators A 2018, 269, 227–237. [Google Scholar] [CrossRef]







| Reference | Mechanical Size/mm | Amplification Mechanism | Amplification Ratio |
|---|---|---|---|
| [1] | 42 × 25 | Three-stage bridge–lever-type amplifier | 22.8 |
| [12] | 60 × 40 | Scott–Russell mechanism and lever-type mechanism | 16 |
| [13] | 55 × 22 | Bridge–lever amplifier | 13.94 |
| This work | 75 × 40 | Flexible four-bar linkage mechanism | 44.56 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, L.; Zhu, H.; Deng, X.; Chai, Y. Design and Implementation of Flexible Four-Bar-Mechanism-Based Long-Stroke Micro-Gripper. Actuators 2025, 14, 338. https://doi.org/10.3390/act14070338
Cui L, Zhu H, Deng X, Chai Y. Design and Implementation of Flexible Four-Bar-Mechanism-Based Long-Stroke Micro-Gripper. Actuators. 2025; 14(7):338. https://doi.org/10.3390/act14070338
Chicago/Turabian StyleCui, Liangyu, Haonan Zhu, Xiaofan Deng, and Yuanyuan Chai. 2025. "Design and Implementation of Flexible Four-Bar-Mechanism-Based Long-Stroke Micro-Gripper" Actuators 14, no. 7: 338. https://doi.org/10.3390/act14070338
APA StyleCui, L., Zhu, H., Deng, X., & Chai, Y. (2025). Design and Implementation of Flexible Four-Bar-Mechanism-Based Long-Stroke Micro-Gripper. Actuators, 14(7), 338. https://doi.org/10.3390/act14070338





