Distributed Adaptive Angle Rigidity-Based Formation Control of Near-Space Vehicles with Input Constraints
Abstract
1. Introduction
- Unlike previous studies [7,8,18] that have primarily relied on relative position data for formation control, this study presents a novel distributed formation-control strategy for multiple NSVs that relies exclusively on relative attitude angles. By pioneering the application of angle rigidity theory, the proposed method significantly improves the formation stability, robustness, and adaptability.
- In contrast to prior research [34,37,38,39], which has addressed actuator dead zones, saturation, external disturbances, and model uncertainties as isolated problems, this study addresses these interconnected challenges concurrently within the context of multiple NSV formation systems. Specifically, an NN-based adaptive control methodology is proposed that ensures stable and robust system performance in the presence of these combined conditions.
2. Problem Statement
2.1. System Model
2.2. Problem Transformation
3. Graph Theoretical and Angle Rigidity
4. Controller Design
4.1. Control Goal
4.2. Controllers
5. Stability Analysis
6. Simulations
6.1. Attitude Formation Control of NSVs
6.2. Simulation Results
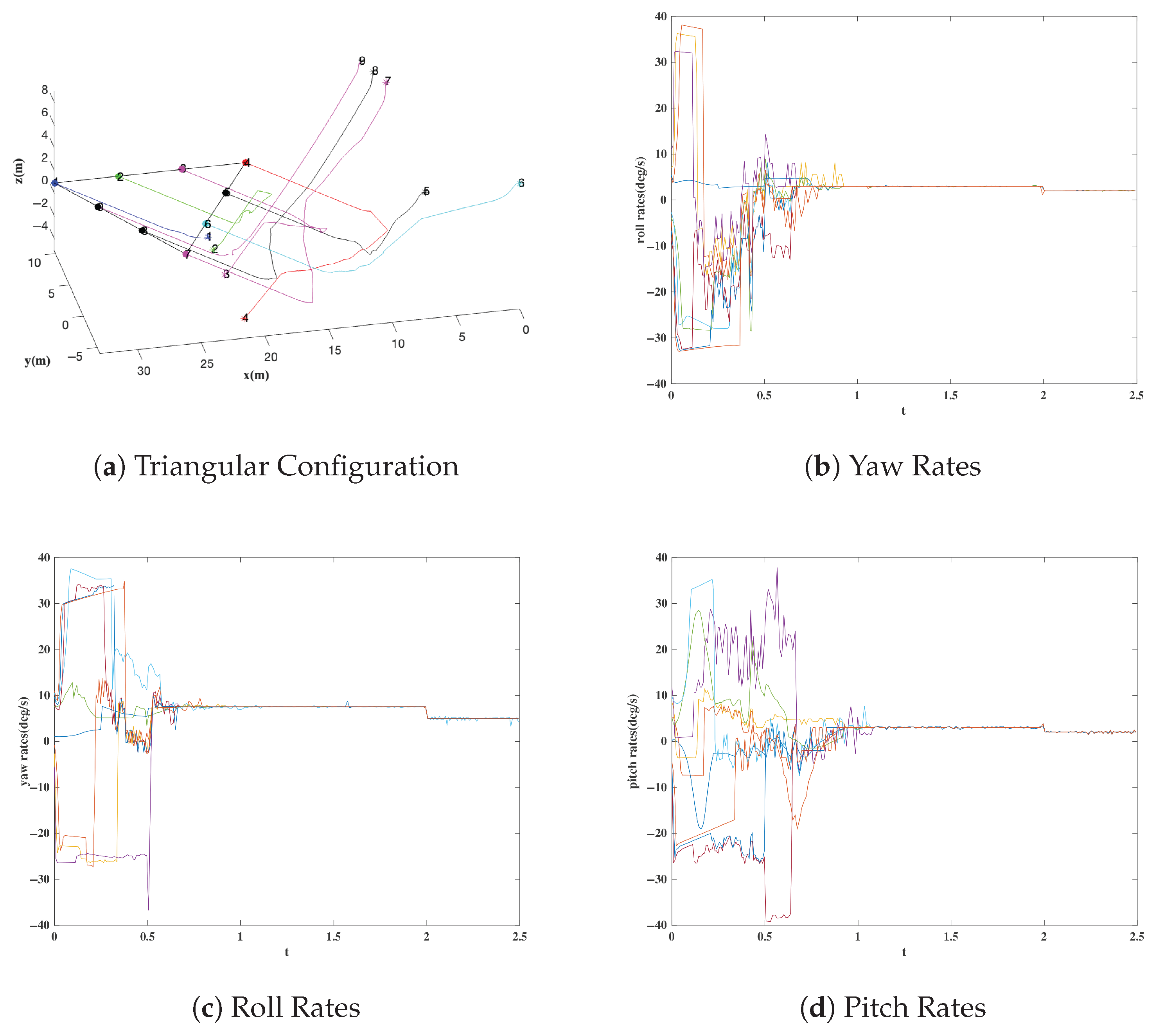
- Case 1: Triangular Configuration Formation
- Case 2: Hexagonal Configuration Formation
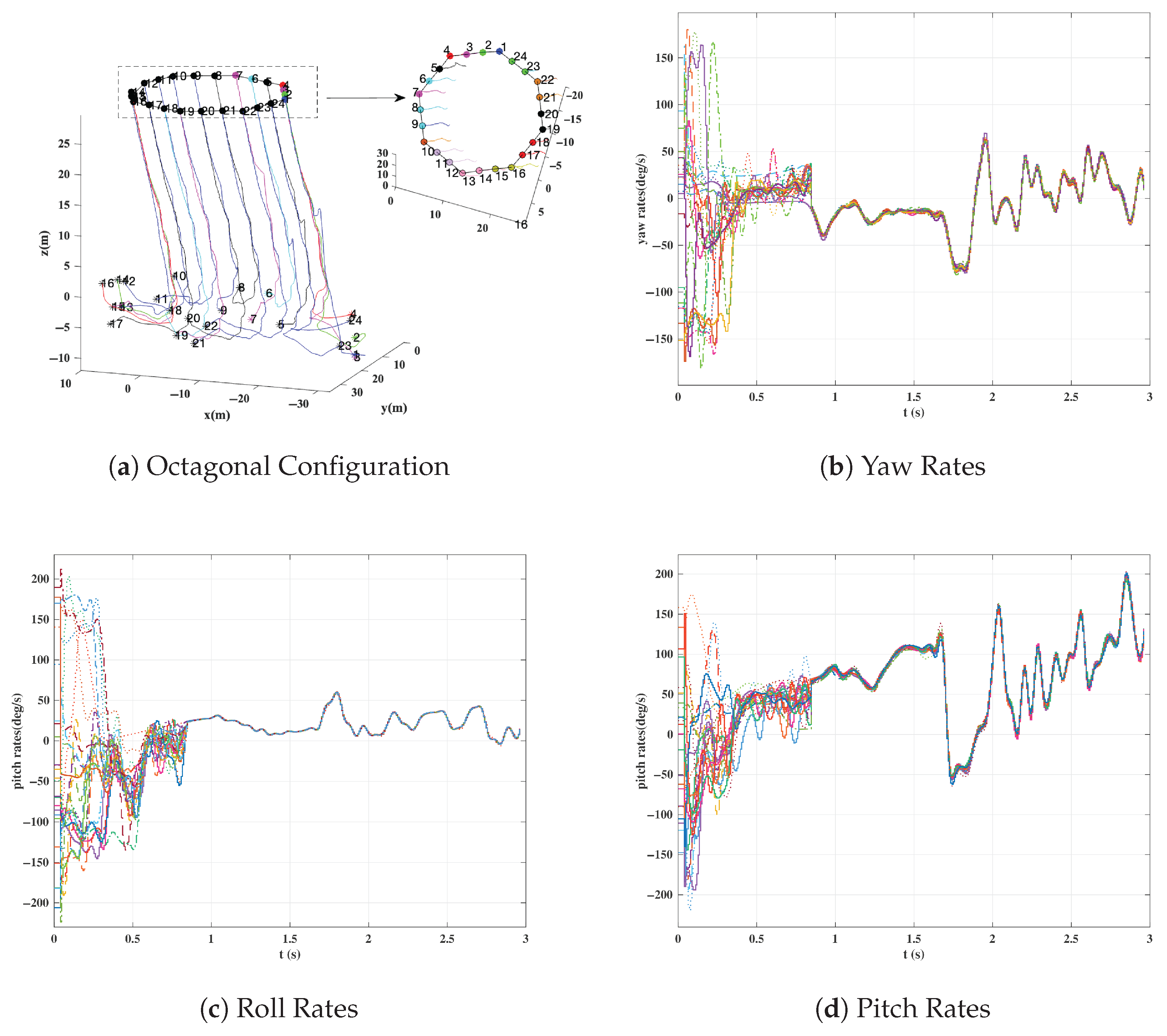
- Case 3: Octagonal Configuration Formation
7. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Acronyms and Notations
| Acronyms | |
| MIMO | Multi-Input Multi-Output |
| NN | Neural Networks |
| NSV | Near-Space Vehicle |
| RBF | Radial Basis Function |
| RBFNN | Radial Basis Function Neural Network |
| Notation | |
| Angle of attack [rad] | |
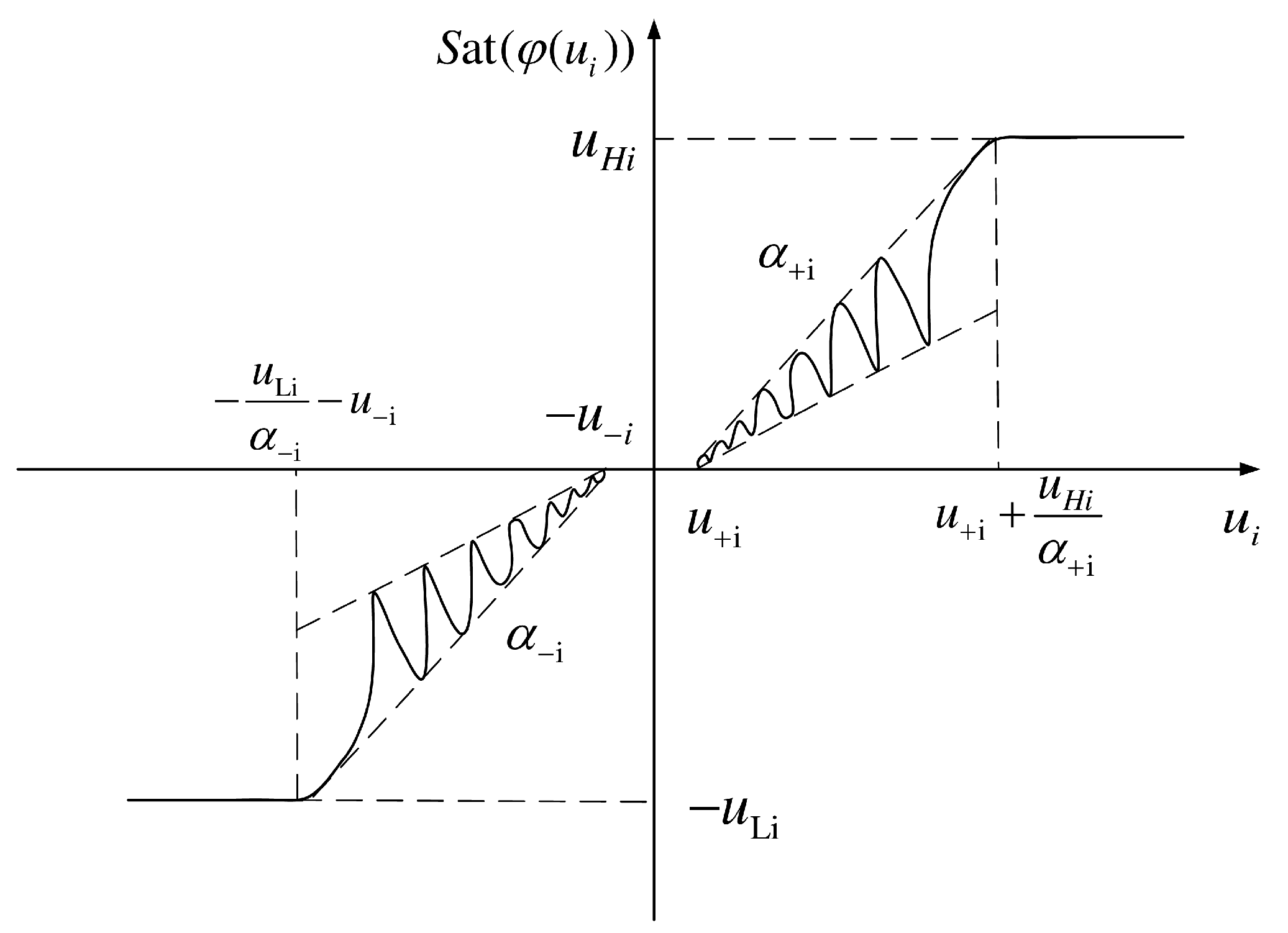
| Saturation slope for l-th component of i-th NSV, | |
| Positive saturation slope for l-th component | |
| Negative saturation slope for l-th component | |
| Sideslip angle [rad] | |
| Spread of ℓ-th RBF [dimensionless] | |
| Lift coefficient derivative w.r.t. angle of attack | |
| Side force coefficient derivative w.r.t. sideslip angle | |
| External disturbance for i-th NSV [rad/s2] | |
| Fast-loop disturbance [rad/s2] | |
| Slow-loop disturbance [rad/s2] | |
| Bound on [rad/s2] | |
| Aileron deflection [rad] | |
| Control deflections, [rad] | |
| Elevator deflection [rad] | |
| RBFNN approximation error [rad/s2] | |
| Bound on [rad/s2] | |
| Rudder deflection [rad] | |
| Saturation error, [rad/s2] | |
| Bound on [rad/s2] | |
| e | Edge vector, [rad] |
| E | Edge set of graph G |
| Nonlinear dynamics for i-th NSV [rad/s2] | |
| Slow-loop dynamics, [rad/s2] | |
| Dynamics for angle of attack [rad/s2] | |
| Dynamics for sideslip angle [rad/s2] | |
| Dynamics for bank angle [rad/s2] | |
| g | Gravitational acceleration [m/s2] |
| Control gain matrix for i-th NSV | |
| Slow-loop gain matrix, | |
| Fast-loop gain matrix, [s2/kg·m2] | |
| Attitude rate coupling matrix | |
| Control effectiveness matrix [rad/s2] | |
| Elevator effect on angle of attack [rad/s2] | |
| Aileron effect on angle of attack [rad/s2] | |
| Rudder effect on angle of attack [rad/s2] | |
| Elevator effect on sideslip angle [rad/s2] | |
| Aileron effect on sideslip angle [rad/s2] | |
| Rudder effect on sideslip angle [rad/s2] | |
| Elevator effect on bank angle [rad/s2] | |
| Aileron effect on bank angle [rad/s2] | |
| Rudder effect on bank angle [rad/s2] | |
| G | Topology graph, |
| Directed topology graph | |
| Disturbance bound [rad/s2] | |
| Estimated disturbance bound [rad/s2] | |
| Dead-zone parameter vector, components [rad/s2] | |
| Disturbance plus error, [rad/s2] | |
| Fast-loop dynamics, [rad/s2] | |
| Slow-loop dynamics, [rad/s2] | |
| Incidence matrix, | |
| Kronecker product, | |
| NSV altitude [m] | |
| identity matrix | |
| Control magnitude for i-th NSV [rad/s2] | |
| K | NSV inertia matrix [kg·m2] |
| 3D standard normal random vector | |
| Adaptive gain for RBFNN weights | |
| Component of | |
| Minimum eigenvalue of | |
| M | NSV mass [kg] |
| Control torque, [N·m] | |
| Bank angle [rad] | |
| Center of l-th RBF [rad] | |
| Neighbor set of i-th NSV | |
| RBF center, [rad] | |
| Adaptive gain for disturbance estimation | |
| Component of | |
| Attitude angles, [rad] | |
| p | Roll rate [rad/s] |
| RBF vector for i-th NSV | |
| Saturation model input [rad/s2] | |
| l-th RBF, | |
| Saturated control, [rad/s2] | |
| q | Pitch rate [rad/s] |
| Dynamic pressure [kg/(m·s2)] | |
| r | Yaw rate [rad/s] |
| Fast-loop input, [N·m] | |
| Slow-loop input, [rad/s] | |
| S | NSV reference area [m2] |
| Spread of l-th RBF [rad] | |
| Saturated control output [rad/s2] | |
| RBFNN optimal weights | |
| Estimated RBFNN weights | |
| Thrust in body x-axis [N] | |
| Thrust in body y-axis [N] | |
| Control input for i-th NSV [rad/s2] | |
| Max dead-zone threshold, [rad/s2] | |
| Positive dead-zone threshold [rad/s2] | |
| Negative dead-zone threshold [rad/s2] | |
| Upper saturation limit [rad/s2] | |
| Lower saturation limit [rad/s2] | |
| V | Node set of graph G |
| NSV airspeed [m/s] | |
| v | Concatenated velocity, [rad/s] |
| Potential energy for i-th NSV [dimensionless] | |
| Potential energy between NSVs i and j | |
| Initial NSV speed [m/s] | |
| Lyapunov function | |
| Attitude angles for i-th NSV [rad] | |
| Fast-loop state, [rad/s] | |
| Slow-loop state, [rad] | |
| Relative attitude, [rad] | |
| Target relative attitude [rad] | |
| RBFNN input vector [rad] | |
| Output of i-th NSV, [rad] | |
| Fast-loop output, [rad/s] | |
| Slow-loop output, [rad] | |
References
- Sun, C.; Mu, C.; Yu, Y. Some Control Problems for Near Space Hypersonic Vehicles. Acta Autom. Sin. 2013, 39, 1901. [Google Scholar] [CrossRef]
- Dong, Z.; Lv, M.; Da, X.; Zhang, Q. Neuro-Adaptive Singularity-Free Fixed-Time Constrained Trajectory Tracking Control of HFVs With Specified Accuracy. Int. J. Robust Nonlinear Control 2025, 35, 3545–3558. [Google Scholar] [CrossRef]
- Dong, Z.; Li, Y.; Lv, M. Adaptive nonsingular fixed-time control for hypersonic flight vehicle considering angle of attack constraints. Int. J. Robust Nonlinear Control 2023, 33, 6754–6777. [Google Scholar] [CrossRef]
- Zhang, S.; Li, X.; Zuo, J.; Qin, J.; Cheng, K.; Feng, Y.; Bao, W. Research progress on active thermal protection for hypersonic vehicles. Prog. Aerosp. Sci. 2020, 119, 100646. [Google Scholar] [CrossRef]
- Aslam, M.S.; Tiwari, P.; Pandey, H.M.; Band, S.S. Robust stability analysis for class of Takagi-Sugeno (T-S) fuzzy with stochastic process for sustainable hypersonic vehicles. Inf. Sci. 2023, 641, 119044. [Google Scholar] [CrossRef]
- Xia, R.; Chen, M.; Wu, Q.; Wang, Y. Neural network based integral sliding mode optimal flight control of near space hypersonic vehicle. Neurocomputing 2020, 379, 41–52. [Google Scholar] [CrossRef]
- Wu, X.; Wei, C.; Chen, T.; Dai, M.Z. On novel distributed fixed-time formation tracking of multiple hypersonic flight vehicles with collision avoidance. Aerosp. Sci. Technol. 2023, 141, 108517. [Google Scholar] [CrossRef]
- Lv, M.; De Schutter, B.; Baldi, S. Nonrecursive Control for Formation-Containment of HFV Swarms With Dynamic Event-Triggered Communication. IEEE Trans. Ind. Inform. 2023, 19, 3188–3197. [Google Scholar] [CrossRef]
- Yi, X.; Yu, H.; Xu, T. Solving multi-objective weapon-target assignment considering reliability by improved MOEA/D-AM2M. Neurocomputing 2024, 563, 126906. [Google Scholar] [CrossRef]
- Liu, Y.; Ma, G.; Lyu, Y.; Wang, P. Neural network-based reinforcement learning control for combined spacecraft attitude tracking maneuvers. Neurocomputing 2022, 484, 67–78. [Google Scholar] [CrossRef]
- Liu, R.; Cao, X.; Liu, M.; Zhu, Y. 6-DOF fixed-time adaptive tracking control for spacecraft formation flying with input quantization. Inf. Sci. 2019, 475, 82–99. [Google Scholar] [CrossRef]
- Feng, J.; Song, W.; Xu, L.; Zhang, J. Formation control of multiagent systems with multileaders through completely distributed intermittent communication strategies. Inf. Sci. 2025, 690, 121555. [Google Scholar] [CrossRef]
- Li, A.; Liu, M.; Cao, X.; Liu, R. Adaptive quantized sliding mode attitude tracking control for flexible spacecraft with input dead-zone via Takagi-Sugeno fuzzy approach. Inf. Sci. 2022, 587, 746–773. [Google Scholar] [CrossRef]
- Dong, H.; Yang, X. Learning-based online optimal sliding-mode control for space circumnavigation missions with input constraints and mismatched uncertainties. Neurocomputing 2022, 484, 13–25. [Google Scholar] [CrossRef]
- Xiao, Y.; Li, Y.; Liu, H.; Chen, Y.; Wang, Y.; Wu, G. Adaptive large neighborhood search algorithm with reinforcement search strategy for solving extended cooperative multi task assignment problem of UAVs. Inf. Sci. 2024, 679, 121068. [Google Scholar] [CrossRef]
- Fabris, M.; Fattore, G.; Cenedese, A. Optimal time-invariant distributed formation tracking for second-order multi-agent systems. Eur. J. Control 2024, 77, 100985. [Google Scholar] [CrossRef]
- Wang, P.-F.; Chang, L.; Yan, B. Development of Near Space Hypersonic Vehicles and Defense Strategies Analysis. Mod. Def. Technol. 2021, 49, 16. [Google Scholar]
- Chen, K.; Pei, S.S.; Zeng, C.Z. SINS/BDS tightly coupled integrated navigation algorithm for hypersonic vehicle. Sci. Rep. 2022, 12, 6144. [Google Scholar] [CrossRef]
- Smith, T.K.; Akagi, J.; Droge, G. Model predictive control for formation flying based on D’Amico relative orbital elements. Astrodynamics 2025, 9, 143–163. [Google Scholar] [CrossRef]
- Xu, B.; Shou, Y.; Shi, Z.; Yan, T. Predefined-Time Hierarchical Coordinated Neural Control for Hypersonic Reentry Vehicle. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 8456–8466. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, C.; Zheng, C.; Kong, X.; Bao, J. Adaptive neural network fault-tolerant control of hypersonic vehicle with immeasurable state and multiple actuator faults. Aerosp. Sci. Technol. 2024, 152, 109378. [Google Scholar] [CrossRef]
- Sun, X.; Wang, Y.; Su, J.; Li, J.; Xu, M.; Bai, S. Relative orbit transfer using constant-vector thrust acceleration. Acta Astronaut. 2025, 229, 715–735. [Google Scholar] [CrossRef]
- Chen, M.; Yu, J. Disturbance observer-based adaptive sliding mode control for near-space vehicles. Nonlinear Dyn. 2015, 82, 1671–1682. [Google Scholar] [CrossRef]
- Cheng, L.; Jiang, C.; Pu, M. Online-SVR-compensated nonlinear generalized predictive control for hypersonic vehicles. Sci. China Inf. Sci. 2011, 54, 551–562. [Google Scholar] [CrossRef]
- Dong, W.; Qi, R.; Jiang, B. Composite fault tolerant control for aerospace vehicles with swing engines and aerodynamic fins. Acta Aeronaut. Astronaut. Sin. 2020, 41, 623850. [Google Scholar]
- Cheng, L.; Wang, Z.; Gong, S. Adaptive control of hypersonic vehicles with unknown dynamics based on dual network architecture. Acta Astronaut. 2022, 193, 197–208. [Google Scholar] [CrossRef]
- Zhao, K.; Song, J.; Ai, S.; Xu, X.; Liu, Y. Active Fault-Tolerant Control for Near-Space Hypersonic Vehicles. Aerospace 2022, 9, 237. [Google Scholar] [CrossRef]
- Zhu, S.; Xu, T.; Wei, C.; Wang, Z. Learning-based adaptive fault tolerant control for hypersonic flight vehicles with abrupt actuator faults and finite time prescribed tracking performance. Eur. J. Control 2021, 58, 17–26. [Google Scholar] [CrossRef]
- Du, Y.; Wu, Q.; Jiang, C.; Wen, J. Adaptive functional link network control of near-space vehicles with dynamical uncertainties. J. Syst. Eng. Electron. 2010, 21, 868–876. [Google Scholar] [CrossRef]
- Yu, J.; Shi, P.; Dong, W.; Lin, C. Adaptive Fuzzy Control of Nonlinear Systems With Unknown Dead Zones Based on Command Filtering. IEEE Trans. Fuzzy Syst. 2018, 26, 46–55. [Google Scholar] [CrossRef]
- Chen, M.; Ren, B.; Wu, Q.; Jiang, C. Anti-disturbance control of hypersonic flight vehicles with input saturation using disturbance observer. Sci. China Inf. Sci. 2015, 58, 1–12. [Google Scholar] [CrossRef]
- Zhao, S.; Zelazo, D. Bearing-based formation maneuvering. In Proceedings of the 2015 IEEE International Symposium on Intelligent Control (ISIC), Sydney, Australia, 21–23 September 2015; pp. 658–663. [Google Scholar]
- Chen, M.; Wu, Q.; Jiang, C.; Jiang, B. Guaranteed transient performance based control with input saturation for near space vehicles. Sci. China Inf. Sci. 2014, 57, 1–12. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, X.; Tang, S. A globally fixed-time solution of distributed formation control for multiple hypersonic gliding vehicles. Aerosp. Sci. Technol. 2020, 98, 105643. [Google Scholar] [CrossRef]
- Zuo, R.; Li, Y.; Lv, M.; Dong, Z. Learning-Based Distributed Containment Control for HFV Swarms Under Event-Triggered Communication. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 568–579. [Google Scholar] [CrossRef]
- Zhou, H.; Jiao, B.; Dang, Z.; Yuan, J. Parametric formation control of multiple nanosatellites for cooperative observation of China Space Station. Astrodynamics 2024, 8, 77–95. [Google Scholar] [CrossRef]
- Zou, A.M.; Kumar, K.D. Neural Network-Based Distributed Attitude Coordination Control for Spacecraft Formation Flying With Input Saturation. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 1155–1162. [Google Scholar]
- Sun, H.J.; Wu, Y.Y.; Zhang, J. A distributed predefined-time attitude coordination control scheme for multiple rigid spacecraft. Aerosp. Sci. Technol. 2023, 133, 108134. [Google Scholar] [CrossRef]
- Zhuang, M.; Tan, L.; Song, S. Fixed-time attitude coordination control for spacecraft with external disturbance. ISA Trans. 2021, 114, 150–170. [Google Scholar] [CrossRef]
- Chen, M.; Jiang, B. Robust attitude control of near space vehicles with time-varying disturbances. Int. J. Control Autom. Syst. 2013, 11, 182–187. [Google Scholar] [CrossRef]
- Guo, Z.; Guo, J.; Zhou, J.; Chang, J. Robust Tracking for Hypersonic Reentry Vehicles via Disturbance Estimation-Triggered Control. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 1279–1289. [Google Scholar] [CrossRef]
- Xia, R.; Bu, C.; Yan, X.; Zhou, T. Finite-horizon optimal trajectory control of near space hypersonic vehicle with multi-constraints. Optim. Control Appl. Methods 2024, 45, 302–320. [Google Scholar] [CrossRef]
- Xi, C.; Dong, J. Adaptive neural network-based control of uncertain nonlinear systems with time-varying full-state constraints and input constraint. Neurocomputing 2019, 357, 108–115. [Google Scholar] [CrossRef]
- Zou, Y.; Zheng, Z. A Robust Adaptive RBFNN Augmenting Backstepping Control Approach for a Model-Scaled Helicopter. IEEE Trans. Control Syst. Technol. 2015, 23, 2344–2352. [Google Scholar] [CrossRef]
- Zhao, S.; Zelazo, D. Bearing Rigidity and Almost Global Bearing-Only Formation Stabilization. IEEE Trans. Autom. Control 2016, 61, 1255–1268. [Google Scholar] [CrossRef]
- Buckley, I.; Egerstedt, M. Infinitesimal Shape-Similarity for Characterization and Control of Bearing-Only Multirobot Formations. IEEE Trans. Robot. 2021, 37, 1921–1935. [Google Scholar] [CrossRef]
- Chen, L.; Cao, M. Angle Rigidity for Multiagent Formations in 3-D. IEEE Trans. Autom. Control 2023, 68, 6130–6145. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Shen, Y.; Yin, H.; Yu, J.; Yi, Y. Distributed Adaptive Angle Rigidity-Based Formation Control of Near-Space Vehicles with Input Constraints. Actuators 2025, 14, 339. https://doi.org/10.3390/act14070339
Wang Q, Shen Y, Yin H, Yu J, Yi Y. Distributed Adaptive Angle Rigidity-Based Formation Control of Near-Space Vehicles with Input Constraints. Actuators. 2025; 14(7):339. https://doi.org/10.3390/act14070339
Chicago/Turabian StyleWang, Qin, Yuhang Shen, Hanyu Yin, Jianjiang Yu, and Yang Yi. 2025. "Distributed Adaptive Angle Rigidity-Based Formation Control of Near-Space Vehicles with Input Constraints" Actuators 14, no. 7: 339. https://doi.org/10.3390/act14070339
APA StyleWang, Q., Shen, Y., Yin, H., Yu, J., & Yi, Y. (2025). Distributed Adaptive Angle Rigidity-Based Formation Control of Near-Space Vehicles with Input Constraints. Actuators, 14(7), 339. https://doi.org/10.3390/act14070339




