Improving the Regenerative Efficiency of the Automobile Powertrain by Optimizing Combined Loss in the Motor and Inverter
Abstract
1. Introduction
2. Losses in Electrical Machine and Inverter
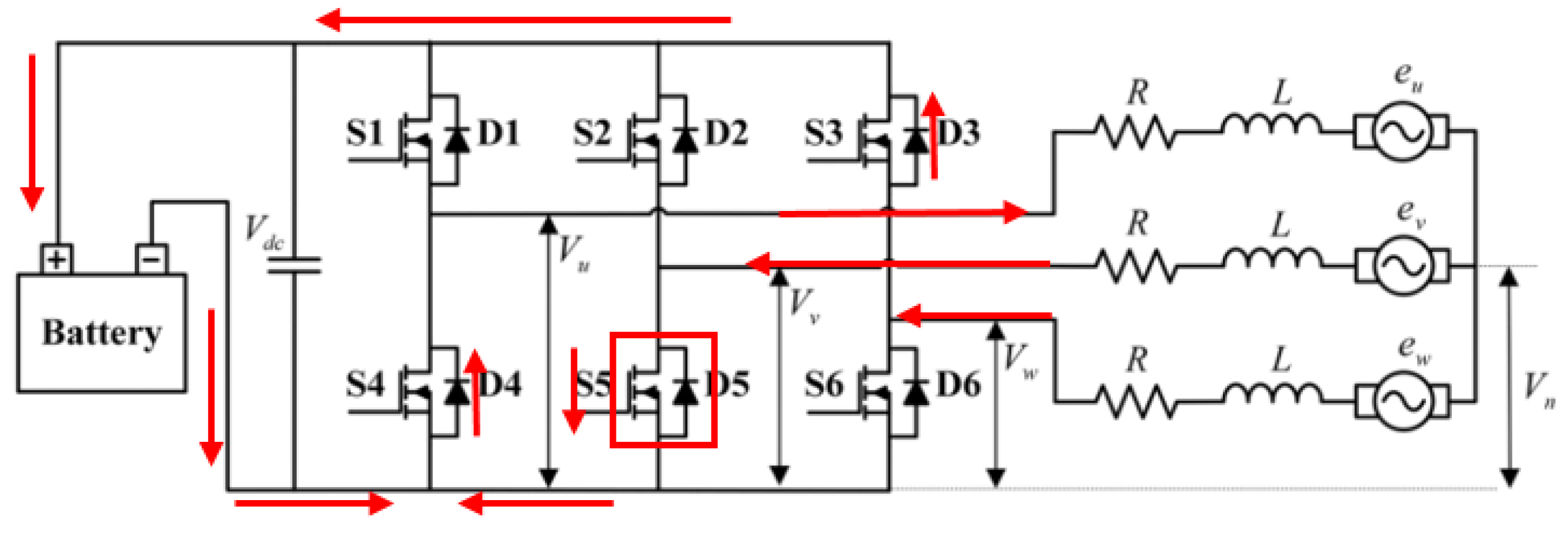
3. Simulation and Analysis
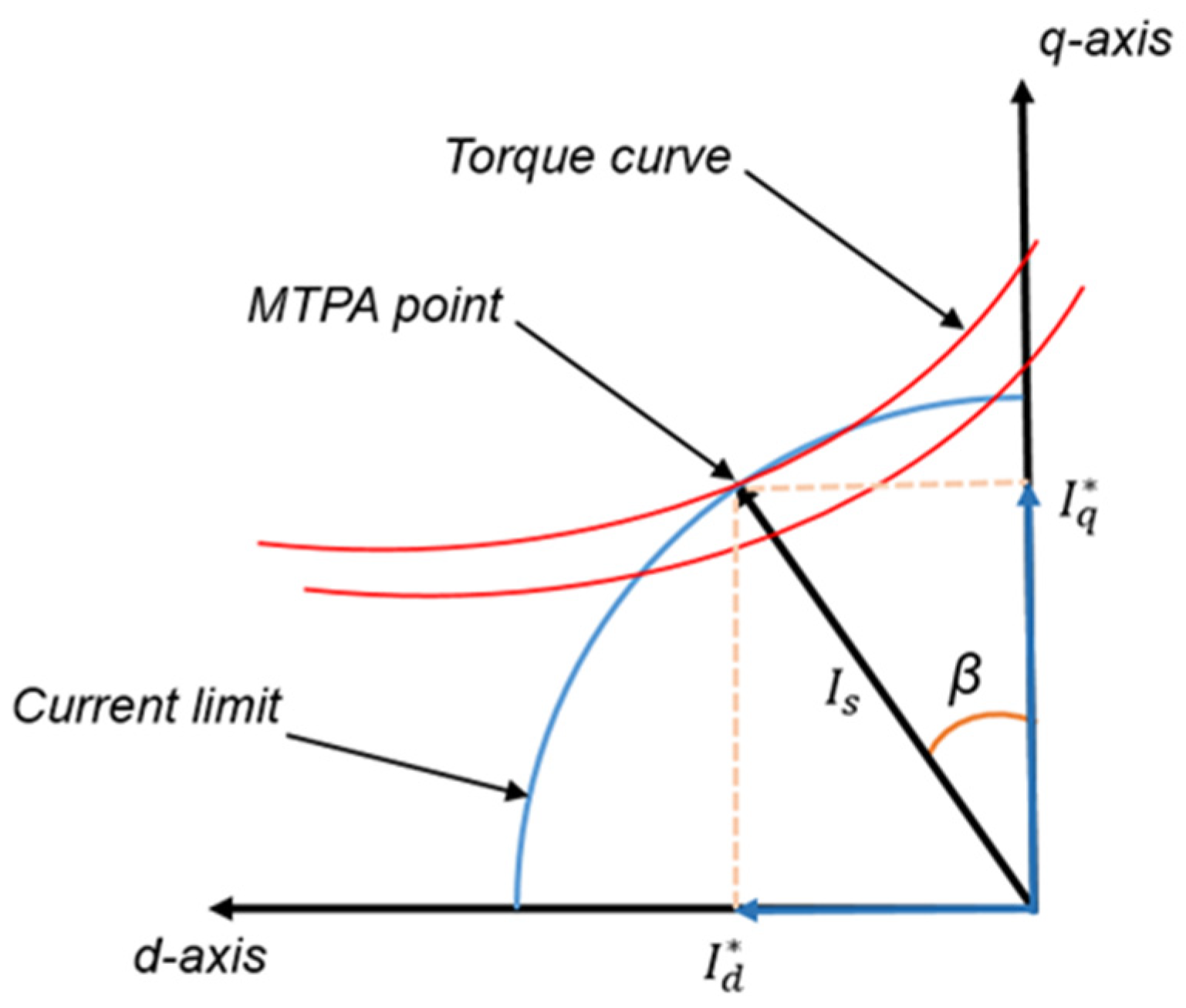
3.1. Simulation of MTPA and TLMM Regenerative Efficiency Under Specific Conditions
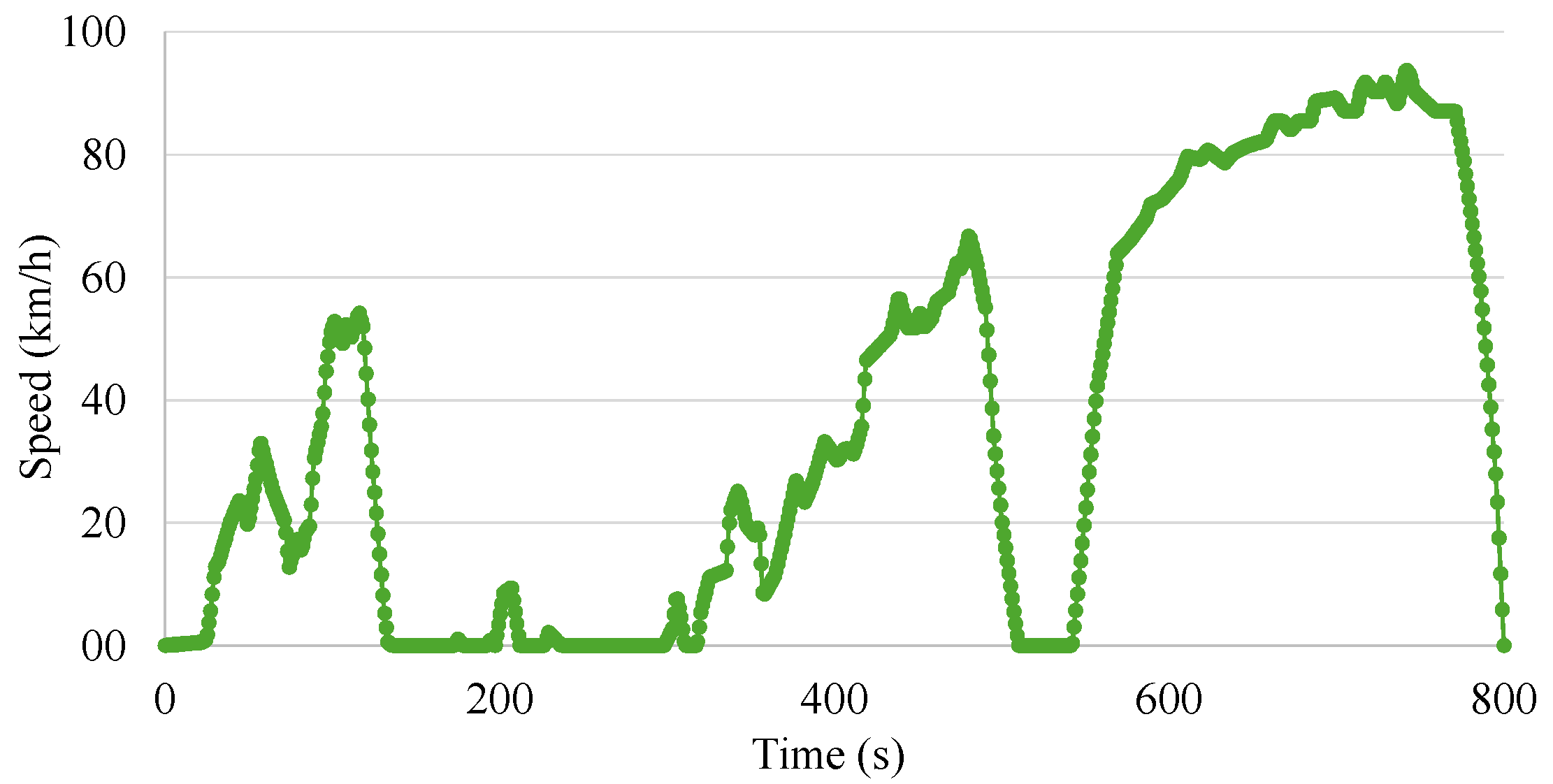
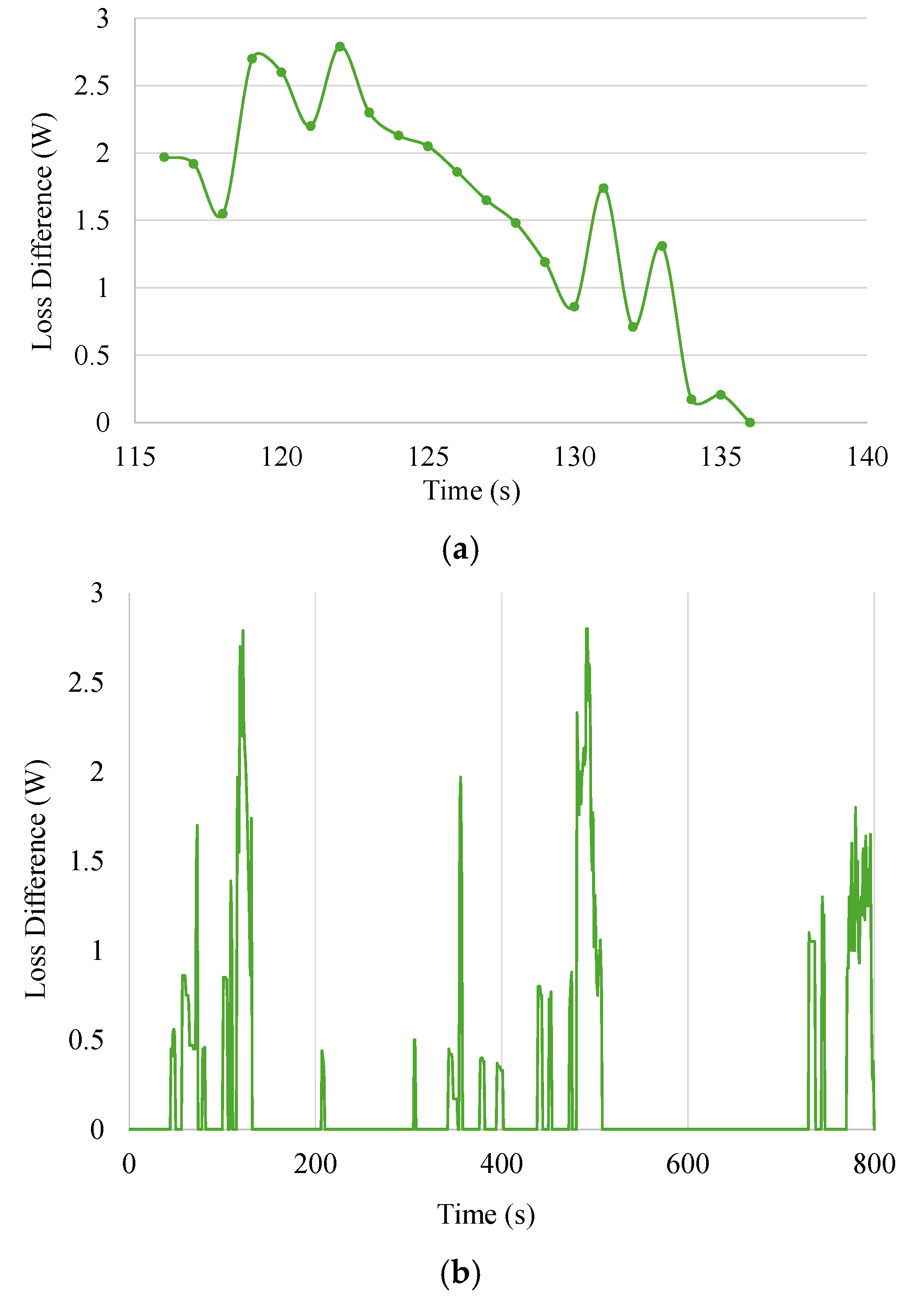
3.2. Comparison of Loss Differences During the UDDS Cycle
4. Experimental Setup and Results
5. Discussion and Experiments
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Al-Ghaili, A.M.; Kasim, H.; Aris, H.; Al-Hada, N.M. Can electric vehicles be an alternative for traditional fossil-fuel cars with the help of renewable energy sources towards energy sustainability achievement? Energy Inform. 2022, 5 (Suppl. 4), 60. [Google Scholar] [CrossRef]
- Li, L.; Liu, Q. Research on IPMSM drive system control technology for electric vehicle energy consumption. IEEE Access 2019, 7, 186201–186210. [Google Scholar] [CrossRef]
- Pinky, K.; Reeba, S.V. Torque improvement in IPMSM for Electric vehicle application. In Proceedings of the 2015 International Conference on Control Communication & Computing India (ICCC), Trivandrum, India, 19–21 November 2015; IEEE: New York, NY, USA, 2015. [Google Scholar] [CrossRef]
- Zhang, K.; Li, J.; Ouyang, M.; Gu, J.; Ma, Y. Electric braking performance analysis of PMSM for electric vehicle applications. In Proceedings of the 2011 International Conference on Electronic & Mechanical Engineering and Information Technology, Harbin, China, 12–14 August 2011; IEEE: New York, NY, USA, 2011; Volume 5. [Google Scholar] [CrossRef]
- U.S. Department of Energy, Energy Requirements for Combined City/Highway Driving—Electric Vehicles. FuelEconomy.Gov. Available online: https://www.fueleconomy.gov/feg/atv.shtml (accessed on 25 May 2025).
- Gupta, U.; Yadav, D.K.; Panchauli, D. Field oriented control of PMSM during regenerative braking. In Proceedings of the 2019 Global Conference for Advancement in Technology (GCAT), Bangalore, India, 18–20 October 2019; IEEE: New York, NY, USA, 2019. [Google Scholar] [CrossRef]
- Ozcira, S.; Bekiroglu, N.; Senol, I. Dynamic performance and analysis of direct torque control method based on DSP for PMSM drives. In Proceedings of the 2012 International Conference on Renewable Energy Research and Applications (ICRERA), Nagasaki, Japan, 11–14 November 2012; IEEE: New York, NY, USA, 2012. [Google Scholar]
- Kim, D.-Y.; Lee, J.-H.; Ko, A.-Y.; Won, C.-Y.; Kim, Y.-R. Braking torque control method of IPMSM for electric vehicle using 2D look-up table. In Proceedings of the 2013 IEEE International Symposium on Industrial Electronics, Taipei, Taiwan, 28–31 May 2013; IEEE: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Won, I.-K.; Hwang, J.-H.; Kim, D.-Y.; Jang, Y.-H.; Won, C.-Y. Performance improvement of IPMSM using finite predictive current control for EV. In Proceedings of the 2015 IEEE 2nd International Future Energy Electronics Conference (IFEEC), Taipei, Taiwan, 1–4 November 2015; IEEE: New York, NY, USA, 2015. [Google Scholar] [CrossRef]
- Mishra, A.; Mahajan, V.; Agarwal, P.; Srivastava, S. Fuzzy logic based speed and current control of vector controlled PMSM drive. In Proceedings of the 2012 2nd International Conference on Power, Control and Embedded Systems, Allahabad, India, 17–19 December 2012; IEEE: New York, NY, USA, 2012. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, D.; Mohammed, S.; Calvi, A. A PMSM fuzzy logic regenerative braking control strategy for electric vehicles. J. Intell. Fuzzy Syst. 2021, 41, 4873–4881. [Google Scholar] [CrossRef]
- Yang, Y.; He, Q.; Chen, Y.; Fu, C. Efficiency optimization and control strategy of regenerative braking system with dual motor. Energies 2020, 13, 711. [Google Scholar] [CrossRef]
- Akatsu, K.; Narita, K.; Sakashita, Y.; Yamada, T. Characteristics comparison between SPMSM and IPMSM under high flux density condition by both experimental and analysis results. In Proceedings of the 2008 International Conference on Electrical Machines and Systems, Wuhan, China, 17–20 October 2008; IEEE: New York, NY, USA, 2008. [Google Scholar]
- Kummerow, A.; Alramlawi, M.; Dirbas, M.; Nicolai, S.; Bretschneider, P. Clark-Park Transformation based Autoencoder for 3-Phase Electrical Signals. In Proceedings of the 2023 IEEE PES Innovative Smart Grid Technologies Europe (ISGT EUROPE), Grenoble, France, 23–26 October 2023; IEEE: New York, NY, USA, 2023. [Google Scholar] [CrossRef]
- Uddin, M.; Radwan, T.; Rahman, M. Performance of interior permanent magnet motor drive over wide speed range. IEEE Trans. Energy Convers. 2002, 17, 79–84. [Google Scholar] [CrossRef]
- Song, L.; Jiang, D.; Cui, S.; Sheng, S. Reluctance torque analysis and reactance calculation of IPM for HEVs based on FEM. In Proceedings of the 2010 IEEE Vehicle Power and Propulsion Conference, Lille, France, 1–3 September 2010; IEEE: New York, NY, USA, 2010. [Google Scholar] [CrossRef]
- Wang, Z.; Yao, X.; Liu, J.; Xu, L.; Tong, H.; Liu, K. Research on IPMSM control based on MTPA. Procedia Comput. Sci. 2022, 208, 635–641. [Google Scholar]
- Hargreaves, P.A.; Mecrow, B.C.; Hall, R. Calculation of iron loss in electrical generators using finite-element analysis. IEEE Trans. Ind. Appl. 2012, 48, 1460–1466. [Google Scholar] [CrossRef]
- Caruso, M.; Di Tommaso, A.; Miceli, R.; Nevoloso, C.; Spataro, C.; Viola, F. Characterization of the parameters of interior permanent magnet synchronous motors for a loss model algorithm. Measurement 2017, 106, 196–202. [Google Scholar] [CrossRef]
- Morimoto, S.; Tong, Y.; Takeda, Y.; Hirasa, T. Loss minimization control of permanent magnet synchronous motor drives. IEEE Trans. Ind. Electron. 1994, 41, 511–517. [Google Scholar] [CrossRef]
- Hang, J.; Wu, H.; Ding, S.; Huang, Y.; Hua, W. Improved loss minimization control for IPMSM using equivalent conversion method. IEEE Trans. Power Electron. 2020, 36, 1931–1940. [Google Scholar] [CrossRef]
- Pou, J.; Osorno, D.; Zaragoza, J.; Jaen, C.; Ceballos, S. Power losses calculation methodology to evaluate inverter efficiency in electrical vehicles. In Proceedings of the 2011 7th International Conference-Workshop Compatibility and Power Electronics (CPE), Tallinn, Estonia, 1–3 June 2011; IEEE: New York, NY, USA, 2011. [Google Scholar]
- Nian, X.; Peng, F.; Zhang, H. Regenerative braking system of electric vehicle driven by brushless DC motor. IEEE Trans. Ind. Electron. 2014, 61, 5798–5808. [Google Scholar] [CrossRef]
- Chen, C.-H.; Chi, W.-C.; Cheng, M.-Y. Regenerative braking control for light electric vehicles. In Proceedings of the 2011 IEEE Ninth International Conference on Power Electronics and Drive Systems, Singapore, 5–8 December 2011; IEEE: New York, NY, USA, 2011. [Google Scholar] [CrossRef]
- Naidu, A.S.; Samanta, S. Analysis of IPMSM motor by using SPWM and SVPWM based vector controller with MTPA control strategy. In Proceedings of the 2022 IEEE 10th Power India International Conference (PIICON), New Delhi, India, 25–27 November 2022; IEEE: New York, NY, USA, 2022. [Google Scholar]


| Number of IGBTs | Number of Diodes | |
|---|---|---|
| Motor mode (SVPWM) | 3 | 3 |
| Generator mode (Single Switch) | 1 | 2 |
| Id (A) | Iq (A) | Total Efficiency | |
|---|---|---|---|
| MTPA | −65.29 | −127.31 | 0.938 |
| TLMM | −65.89 | −126.64 | 0.941 |
| Id (A) | Iq (A) | Total Efficiency | |
|---|---|---|---|
| MTPA | −31.80 | −71.32 | 0.966 |
| TLMM | −32.48 | −70.62 | 0.968 |
| MTPA | TLMM | Difference | |
|---|---|---|---|
| Energy Recovered (J) | 21,746 | 21,944 | 198 |
| Specification | |
|---|---|
| Torque | 440 Nm |
| Nominal Speed | 3473 rpm |
| Maximum Speed | 16,000 rpm |
| Weight | 435 kg |
| J | 0.061 kg·m2 |
| Nominal Load | 160 kW |
| DC Voltage | 700 V |
| Id (A) | Iq (A) | Total Efficiency | ||
|---|---|---|---|---|
| Low Speed | MTPA | −65.91 | −128.6 | 0.920 |
| TLMM | −66.52 | −127.92 | 0.923 | |
| High Speed | MTPA | −32.11 | −72.04 | 0.952 |
| TLMM | −32.82 | −71.33 | 0.954 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shreen, J.; Lee, K.-m. Improving the Regenerative Efficiency of the Automobile Powertrain by Optimizing Combined Loss in the Motor and Inverter. Actuators 2025, 14, 326. https://doi.org/10.3390/act14070326
Shreen J, Lee K-m. Improving the Regenerative Efficiency of the Automobile Powertrain by Optimizing Combined Loss in the Motor and Inverter. Actuators. 2025; 14(7):326. https://doi.org/10.3390/act14070326
Chicago/Turabian StyleShreen, Jayakody, and Kyung-min Lee. 2025. "Improving the Regenerative Efficiency of the Automobile Powertrain by Optimizing Combined Loss in the Motor and Inverter" Actuators 14, no. 7: 326. https://doi.org/10.3390/act14070326
APA StyleShreen, J., & Lee, K.-m. (2025). Improving the Regenerative Efficiency of the Automobile Powertrain by Optimizing Combined Loss in the Motor and Inverter. Actuators, 14(7), 326. https://doi.org/10.3390/act14070326






