Analysis and Optimization Design of a Brushless Power Feedback PM Adjustable Speed Drive with Bilayer Wound Rotor
Abstract
1. Introduction
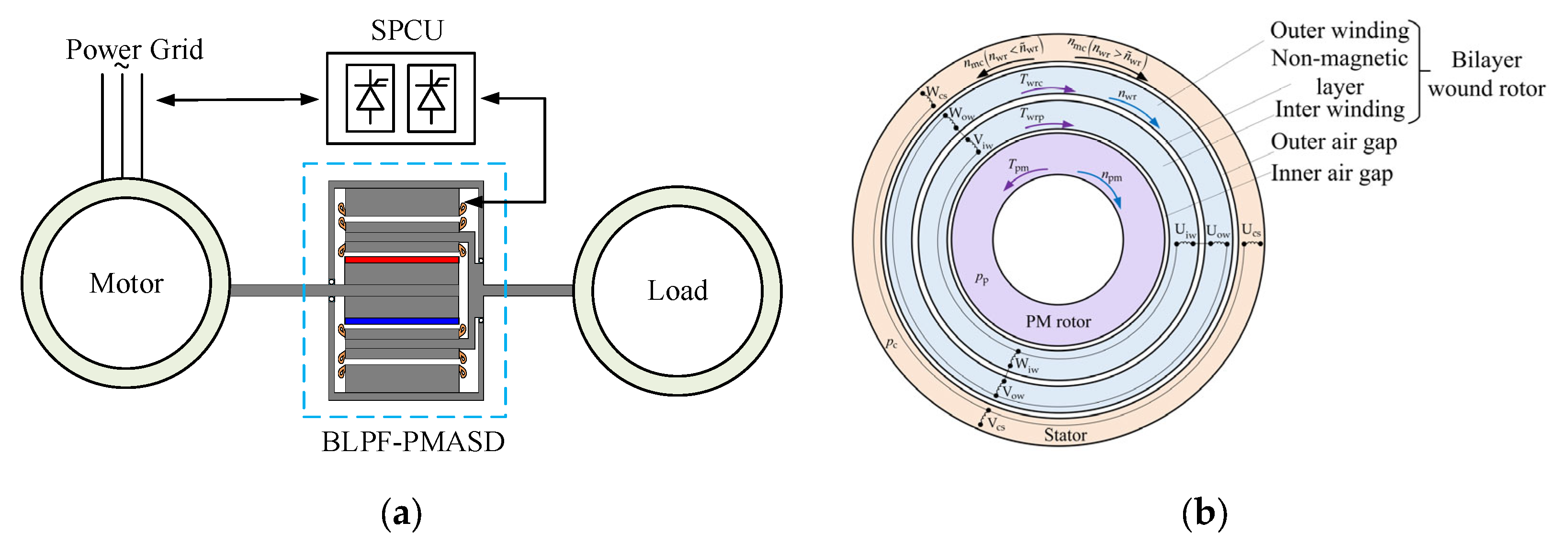
2. Machine Topology, Operating Principle, and Power Feedback Mechanism
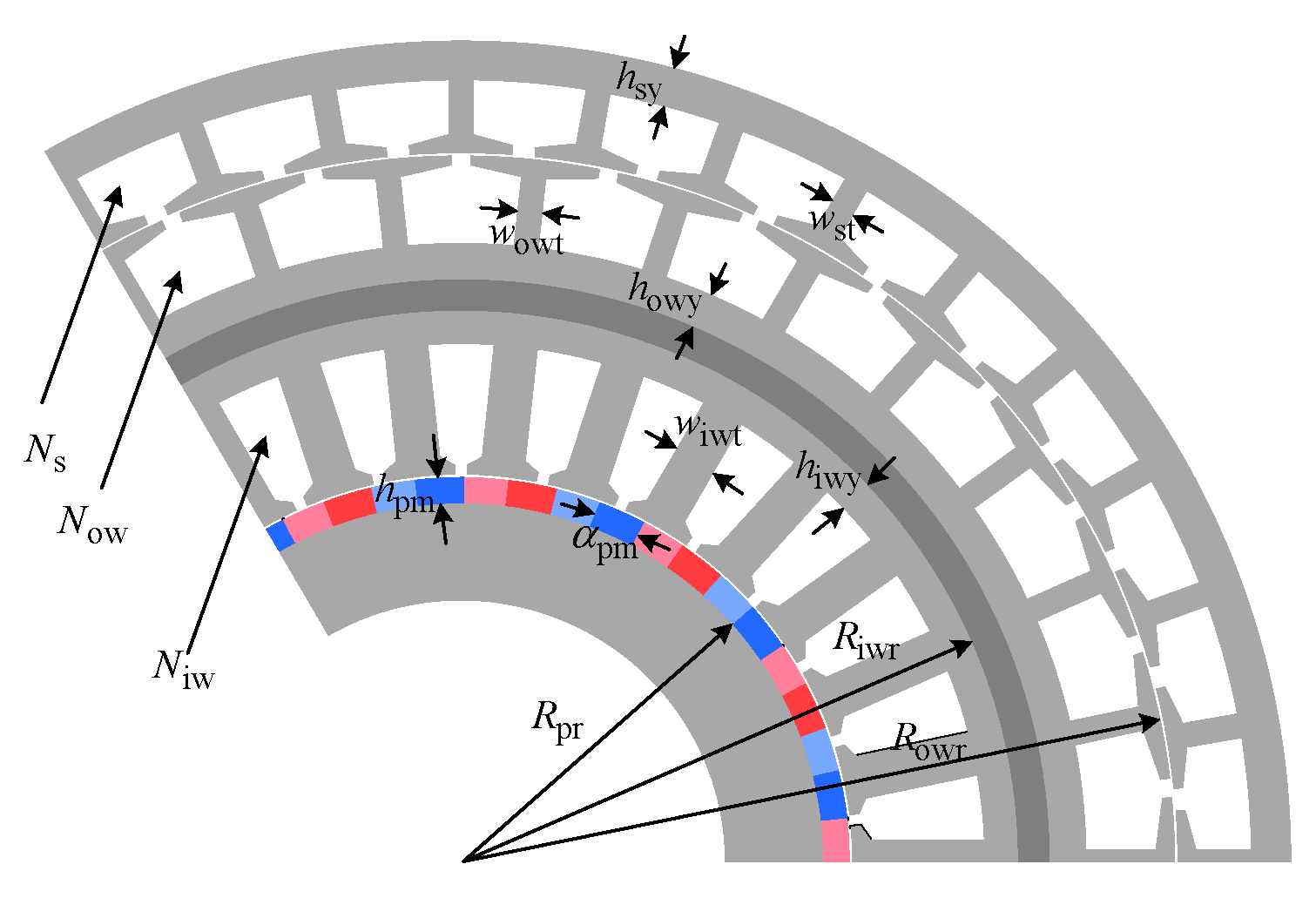
2.1. Machine Topology
2.2. Operating Principle of Speed Regulation
- (1)
- The rotation direction of the PM rotor is defined as the positive direction;
- (2)
- The reference direction for the current at the stator’s electrical terminal is from the external circuit into the stator winding;
- (3)
- The electrical power at the stator’s electrical terminal is considered positive when it is input to the drive and negative when it is output from the drive.
2.3. Mechanism of Power Feedback
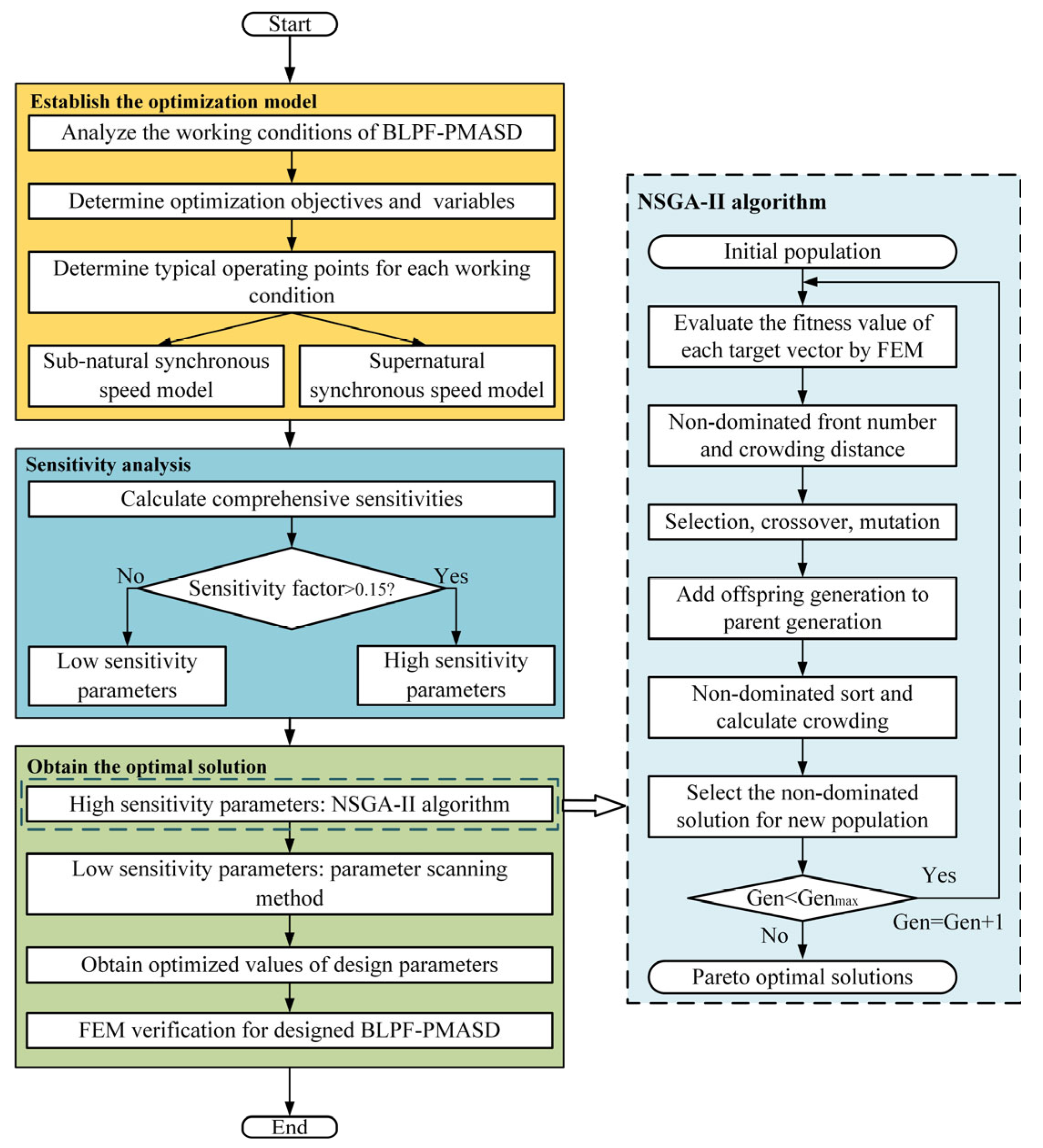
3. Multi-Working Conditions Optimization Design Method
3.1. Determination of Variables and Objectives
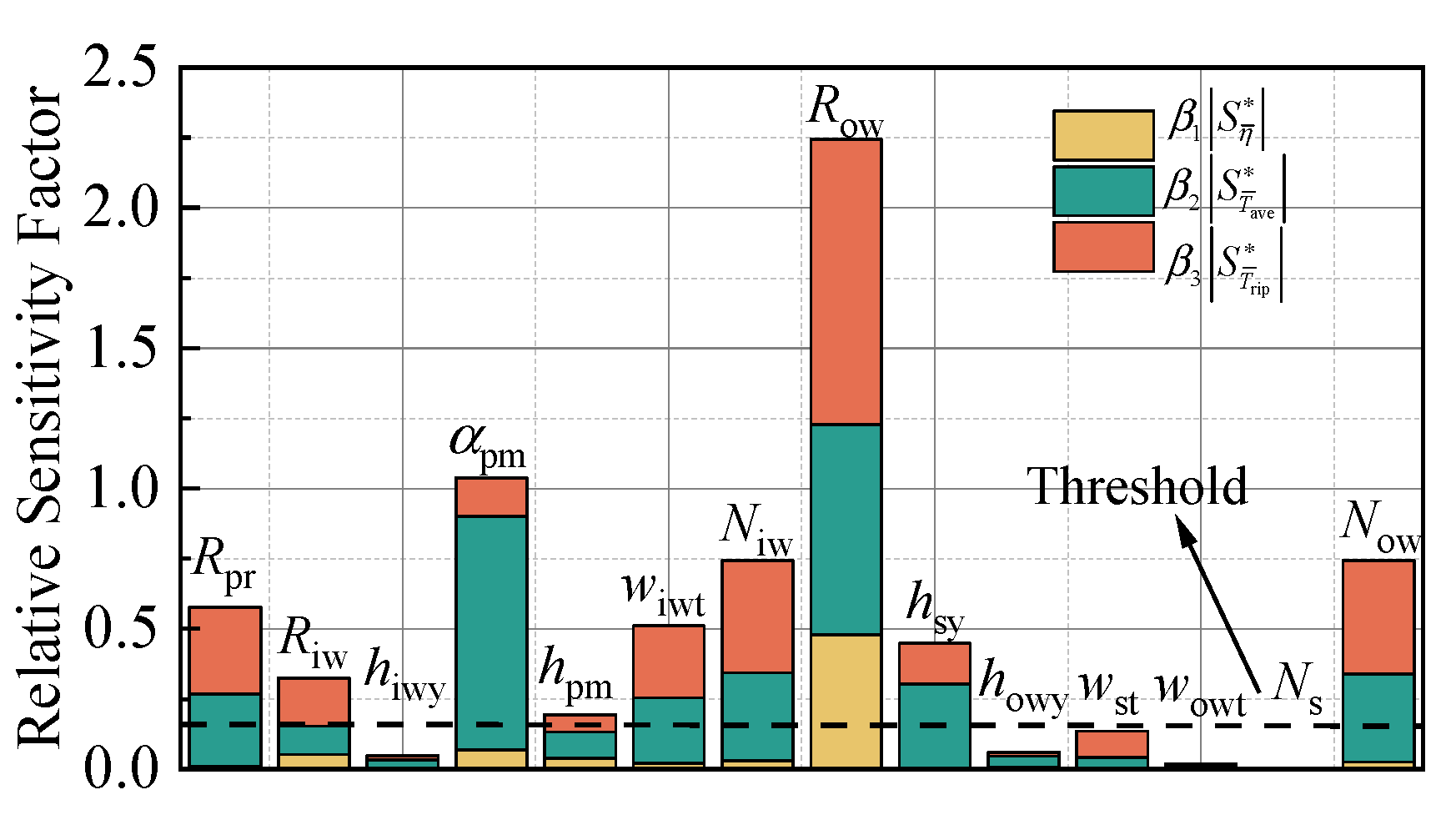
3.2. Sensitivity Analysis
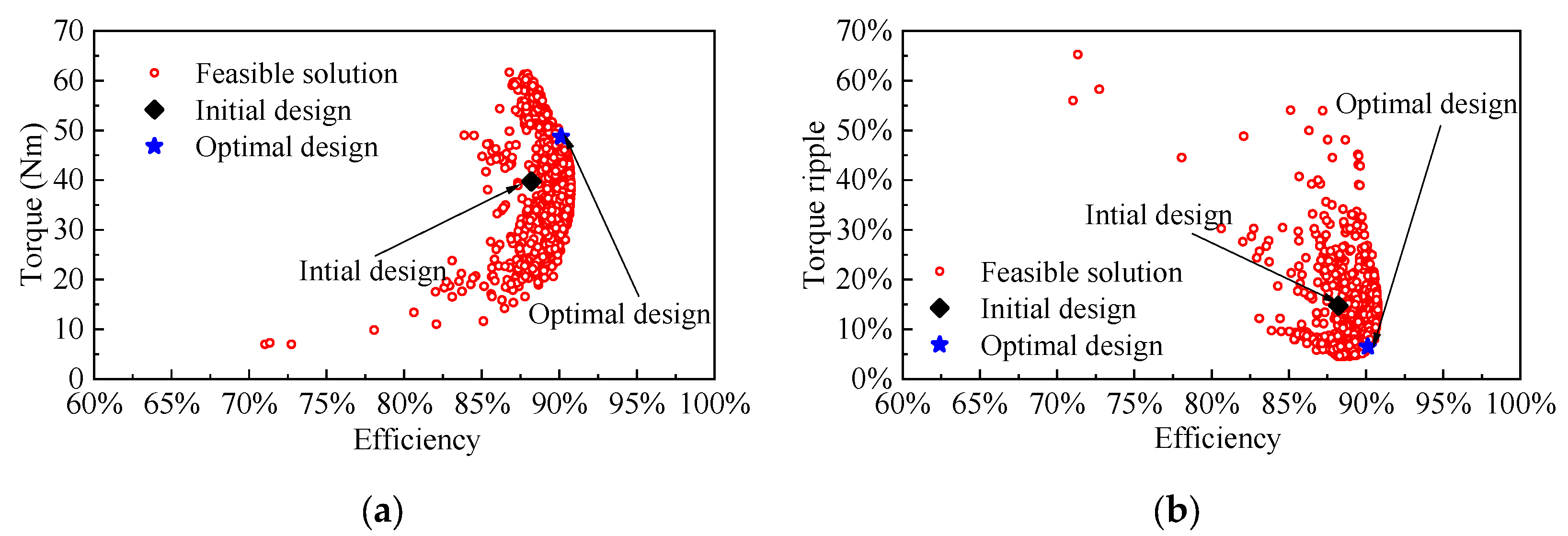
3.3. Optimization Results
4. Machine Performance Analysis
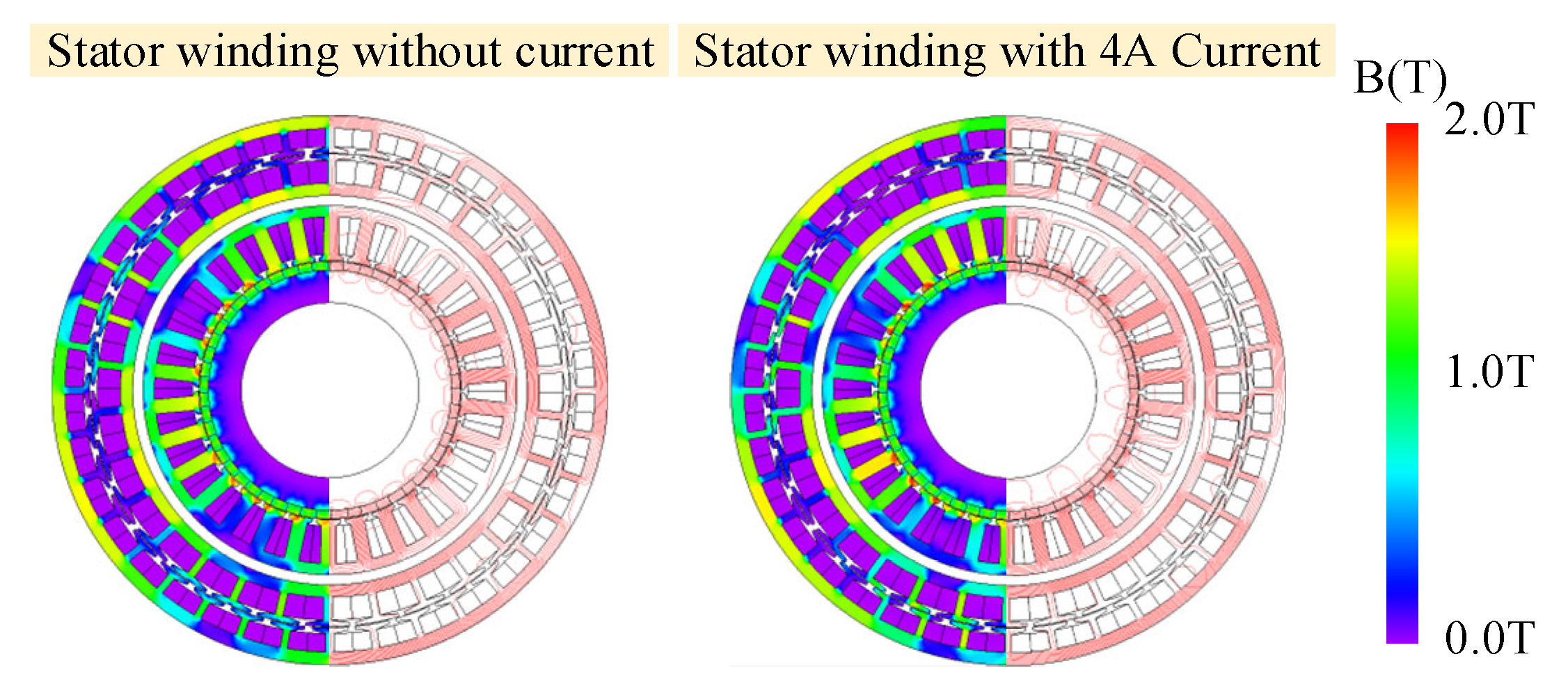
4.1. Magnetic Field Analysis
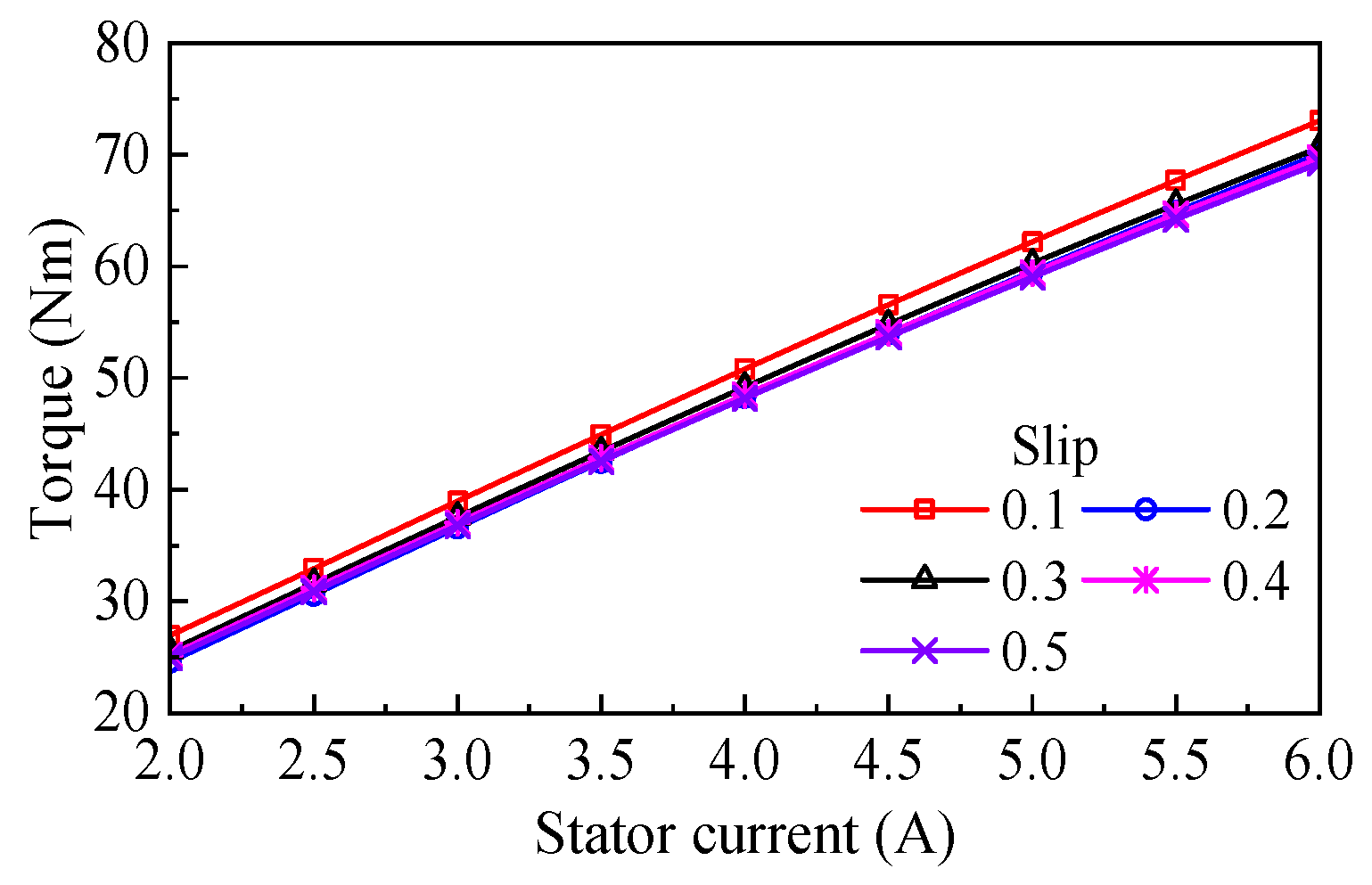
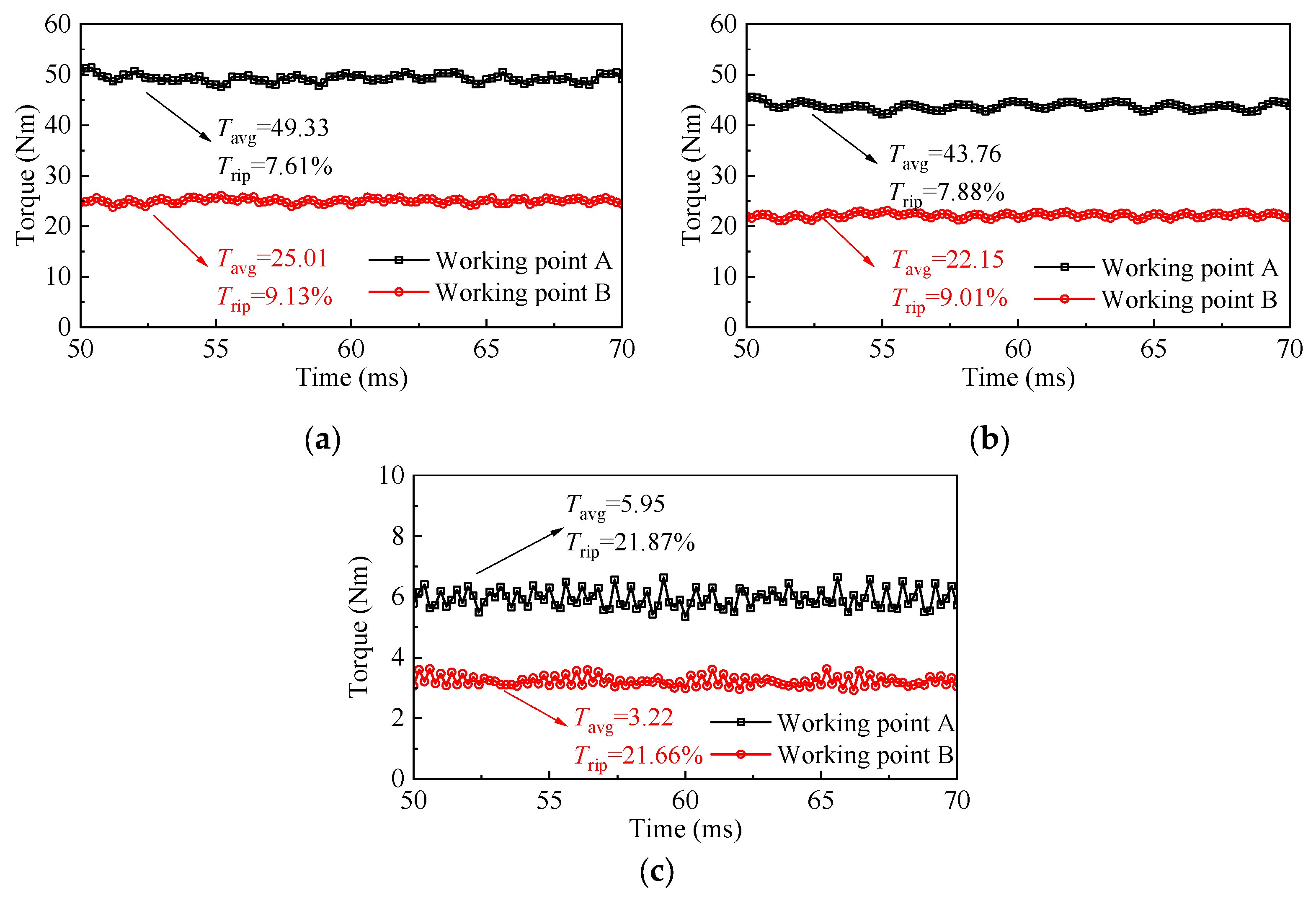
4.2. Torque Characteristics Analysis
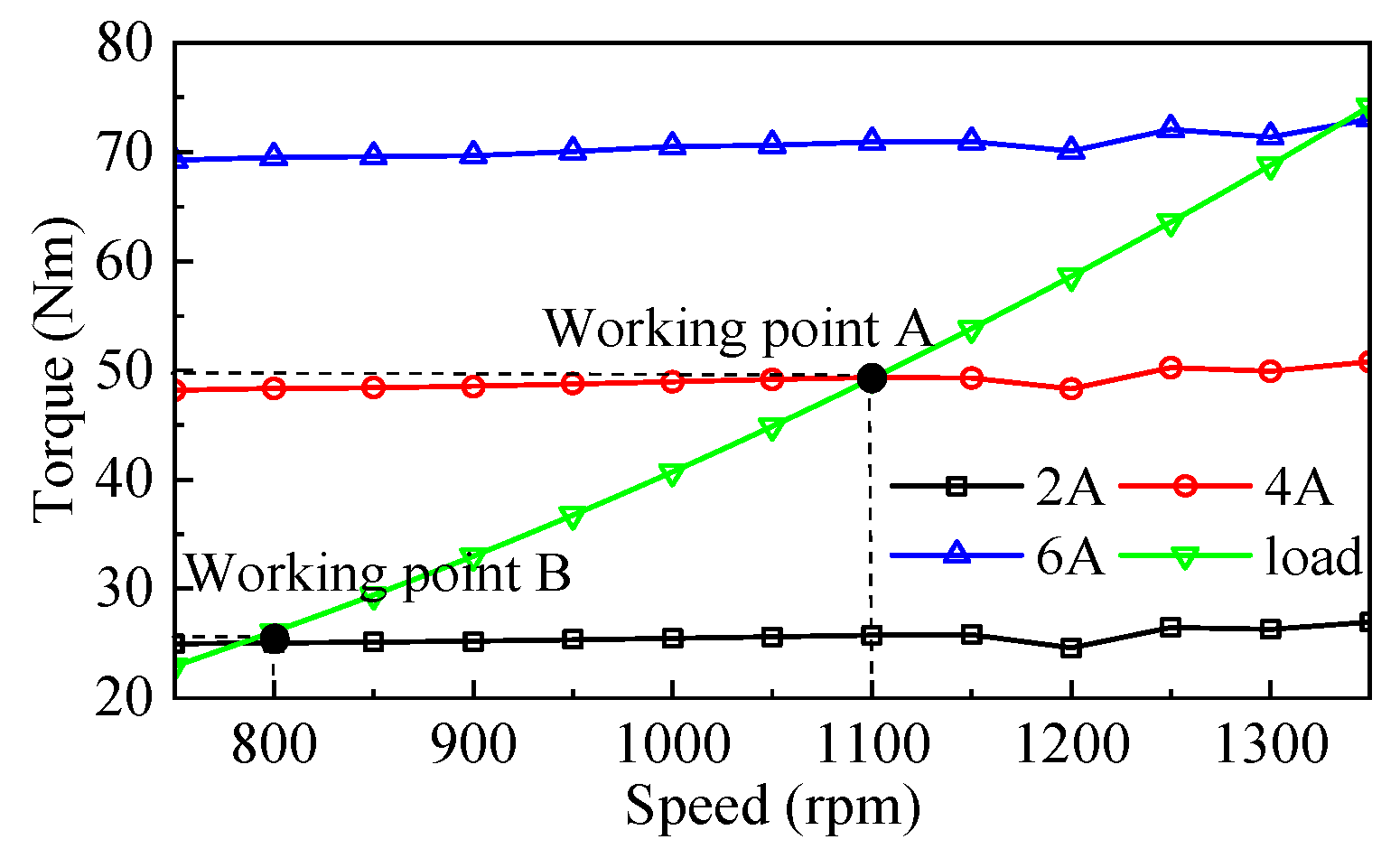
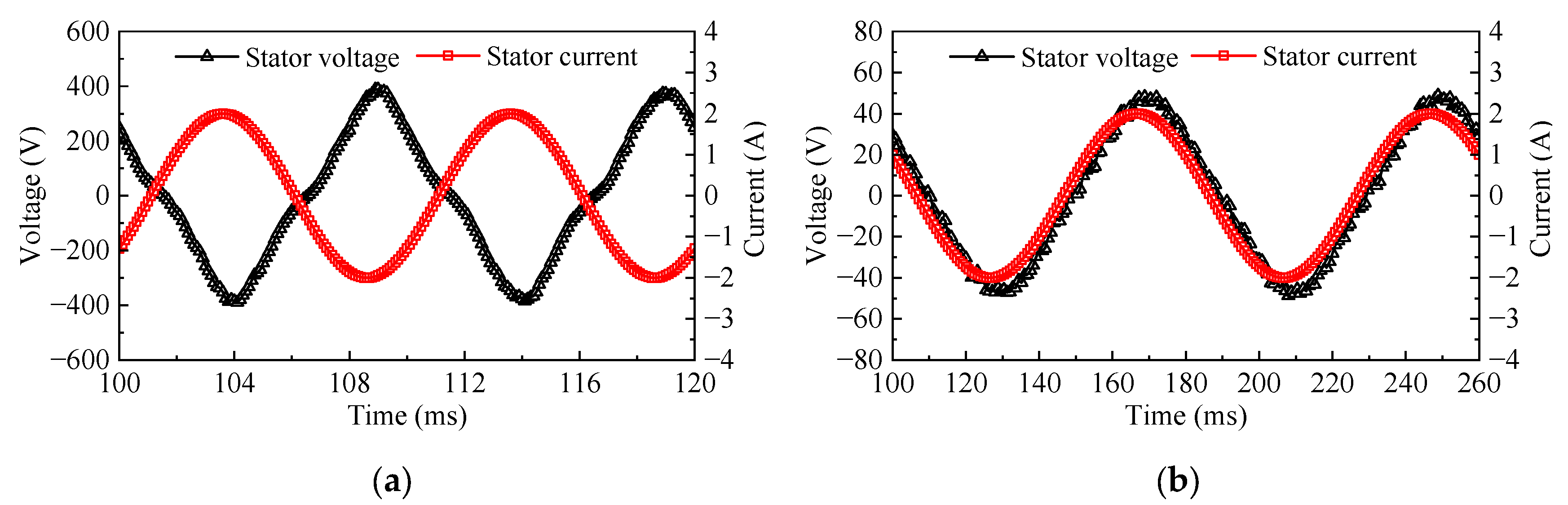
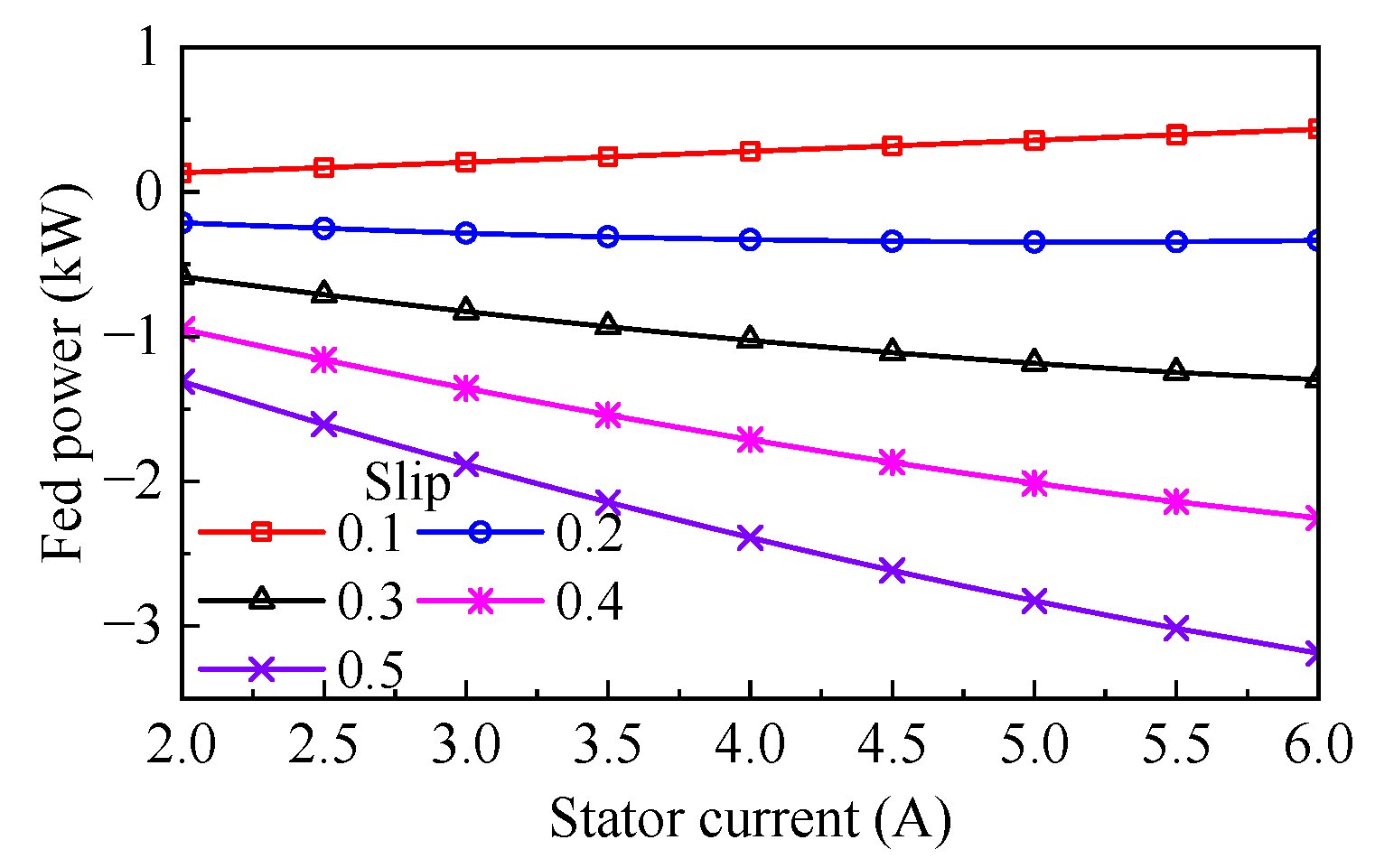
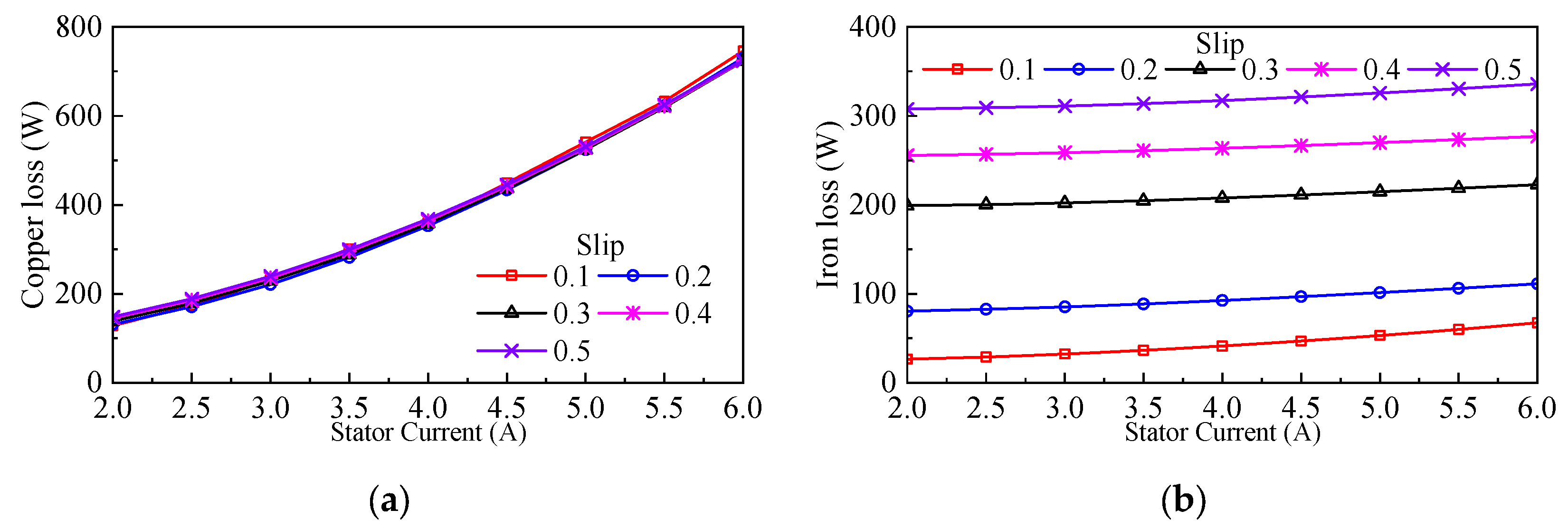
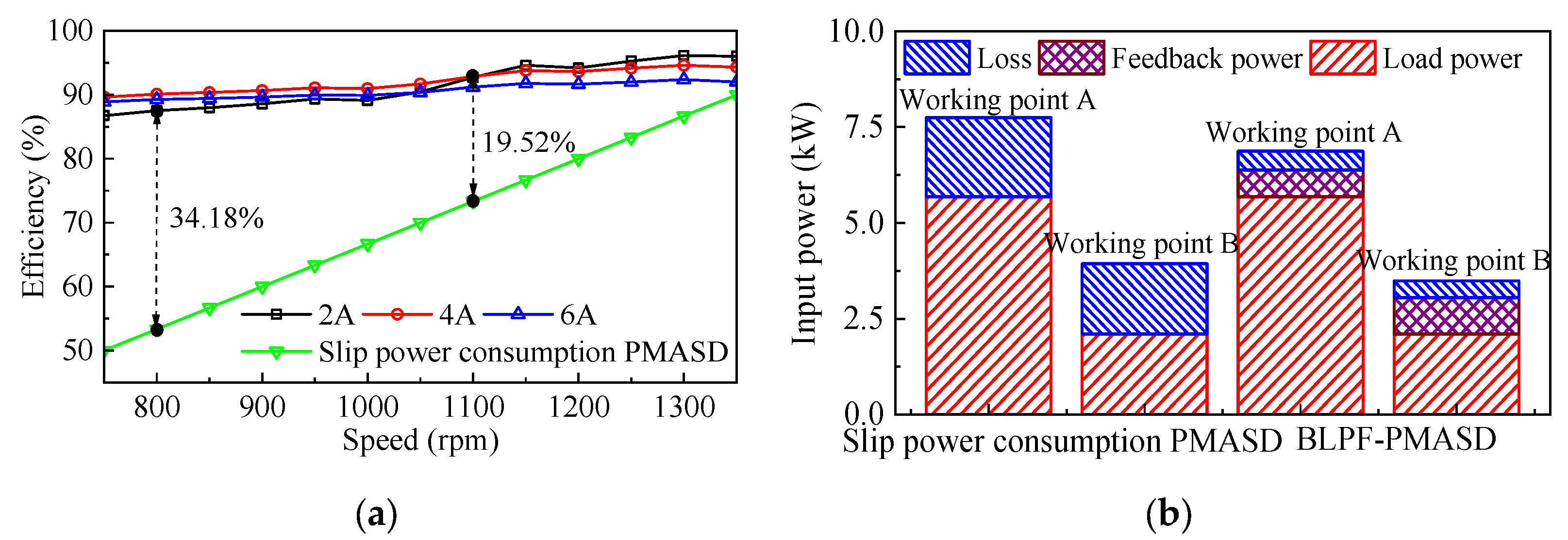
4.3. Power Flow and Efficiency Analysis
5. Conclusions
- (1)
- By analyzing the magnetic field interactions and power flows between the main units, the speed regulation principle and power feedback mechanism of the drive are theoretically elucidated.
- (2)
- A multi-working conditions optimization method is proposed for the electro-magnetic design of the drive. The effectiveness of the optimization method was validated by comparing the electromagnetic performance of the initial and the optimal design schemes. The results indicate that, through optimization, the average torque is increased by 22.62%, the torque ripple is reduced by 56.11%, and the efficiency is improved by 2.17%.
- (3)
- The electromagnetic performance of the designed drive was validated through FEM. The results demonstrate that the proposed drive enables precise adjustment of the output speed and exhibits the advantages of low torque ripple and high efficiency, maintaining an efficiency greater than 85% under all operating conditions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AC | Alternating current |
| VFDs | Variable frequency drives |
| ASDs | Adjustable speed drives |
| PM | Permanent magnet |
| PMASD | Permanent magnet adjustable speed drive |
| PF-PMASD | Power feedback permanent magnet adjustable speed drive |
| BLPF-PMASD | Brushless power feedback permanent magnet adjustable speed drive |
| FEM | Finite element method |
| SPCU | Slip power control unit |
Appendix A
References
- Ferreira, F.J.T.E.; Fong, J.A.C.; Almeida, A.T.d. Ecoanalysis of Variable-Speed Drives for Flow Regulation in Pumping Systems. IEEE Trans. Ind. Electron. 2011, 58, 2117–2125. [Google Scholar] [CrossRef]
- Wang, F.; Stelson, K.A. An Efficient Fan Drive System Based on a Novel Hydraulic Transmission. IEEE/ASME Trans. Mechatron. 2015, 20, 2234–2241. [Google Scholar] [CrossRef]
- Saxena, J.; Choudhury, B.K.; Agra, K.M. Innovations in Variable Frequency Drives and its Implication in Reducing Carbon Footprint. In Encyclopedia of Renewable and Sustainable Materials; Hashmi, S., Choudhury, I.A., Eds.; Elsevier: Oxford, UK, 2020; pp. 534–544. [Google Scholar] [CrossRef]
- Giannoutsos, S.V.; Manias, S.N. A Systematic Power-Quality Assessment and Harmonic Filter Design Methodology for Variable-Frequency Drive Application in Marine Vessels. IEEE Trans. Ind. Appl. 2015, 51, 1909–1919. [Google Scholar] [CrossRef]
- Nassif, A.B. Assessing the Impact of Harmonics and Interharmonics of Top and Mudpump Variable Frequency Drives in Drilling Rigs. IEEE Trans. Ind. Appl. 2019, 55, 5574–5583. [Google Scholar] [CrossRef]
- Moradi, A.; Zare, F.; Kumar, D.; Yaghoobi, J.; Sharma, R.; Kroese, D. Current Harmonics Generated by Multiple Adjustable-Speed Drives in Distribution Networks in the Frequency Range of 2–9 kHz. IEEE Trans. Ind. Appl. 2022, 58, 4744–4757. [Google Scholar] [CrossRef]
- Alshammari, S.; Lazari, P.; Atallah, K. Comparison of Eddy Current Coupling Topologies for High Efficiency Mechanical Power Transmission. IEEE Trans. Energy Convers. 2023, 38, 982–992. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, J. A Simple Method for Performance Prediction of Permanent Magnet Eddy Current Couplings Using a New Magnetic Equivalent Circuit Model. IEEE Trans. Ind. Electron. 2018, 65, 2487–2495. [Google Scholar] [CrossRef]
- Wang, J.X.; Wang, D.Z.; Wang, S.H.; Tong, T.L.; Sun, L.S.; Li, W.H.; Kong, D.S.; Hua, Z.; Sun, G.F. A Review of Recent Developments in Permanent Magnet Eddy Current Couplers Technology. Actuators 2023, 12, 277. [Google Scholar] [CrossRef]
- Bronzeri, R.B.; Chabu, I.E. Concept Validation of an Automotive Variable Flow Water Pump With an Eddy Current Magnetic Coupling. IEEE Trans. Transp. Electrif. 2021, 7, 2939–2950. [Google Scholar] [CrossRef]
- Lubin, T.; Rezzoug, A. 3-D Analytical Model for Axial-Flux Eddy-Current Couplings and Brakes Under Steady-State Conditions. IEEE Trans. Magn. 2015, 51, 8203712. [Google Scholar] [CrossRef]
- Atallah, K.; Wang, J. A Brushless Permanent Magnet Machine With Integrated Differential. IEEE Trans. Magn. 2011, 47, 4246–4249. [Google Scholar] [CrossRef]
- Li, Y.; Lin, H.; Yang, H. A Novel Squirrel-Cage Rotor Permanent Magnet Adjustable Speed Drive With a Non-Rotary Mechanical Flux Adjuster. IEEE Trans. Energy Convers. 2021, 36, 1036–1044. [Google Scholar] [CrossRef]
- Wang, J. A Generic 3-D Analytical Model of Permanent Magnet Eddy-Current Couplings Using a Magnetic Vector Potential Formulation. IEEE Trans. Ind. Electron. 2022, 69, 663–672. [Google Scholar] [CrossRef]
- Aberoomand, V.; Mirsalim, M.; Fesharakifard, R. Design Optimization of Double-Sided Permanent-Magnet Axial Eddy-Current Couplers for Use in Dynamic Applications. IEEE Trans. Energy Convers. 2019, 34, 909–920. [Google Scholar] [CrossRef]
- Xikang, C.; Wei, L.; Yang, Z.; Sitong, L.; Weiqi, L. A Concise Transmitted Torque Calculation Method for Pre-Design of Axial Permanent Magnetic Coupler. IEEE Trans. Energy Convers. 2020, 35, 938–947. [Google Scholar] [CrossRef]
- Jin, P.; Tian, Y.; Lu, Y.; Guo, Y.; Lei, G.; Zhu, J. 3-D Analytical Magnetic Field Analysis of the Eddy Current Coupling With Halbach Magnets. IEEE Trans. Magn. 2020, 56, 7501904. [Google Scholar] [CrossRef]
- Kong, D.S.; Wang, D.Z.; Ni, Y.L.; Song, K.L.; Qi, Y.F.; Li, Y.M. Analytical Analysis of a Novel Flux Adjustable Permanent Magnet Eddy Current Coupling with Double-Sided Conductor. Actuators 2023, 12, 105. [Google Scholar] [CrossRef]
- Wang, D.Z.; Niu, B.W.; Pan, P.Y.; Sun, G.F. Multi-Objective Optimization Design of Permanent Magnet Eddy Current Coupler Based on SCG-BP Neural Network Modeling and the ONDX-NSGA-II Algorithm. Actuators 2023, 12, 367. [Google Scholar] [CrossRef]
- Wang, J.X.; Wang, D.Z.; Wang, S.H.; Li, W.H. Modeling of Permanent Magnet Eddy-Current Coupler Based on Unsupervised Physics-Informed Radial-Based Function Neural Networks. IEEE Trans. Magn. 2025, 61, 4900210. [Google Scholar] [CrossRef]
- Wu, Y.L.; Wang, X.C.; Jiang, H.R.; Li, W.H.; Zhang, X.J.; Zhang, D.; Zhou, D.F.; Zhang, G.M. Study on Magnetic Coupler With Clutch Function Based on Magnetization and Demagnetization Properties of Superconducting Bulks. IEEE Trans. Appl. Supercond. 2025, 35, 6800405. [Google Scholar] [CrossRef]
- Li, Y.; Lin, H.; Huang, H.; Chen, C.; Yang, H. Analysis and Performance Evaluation of an Efficient Power-Fed Permanent Magnet Adjustable Speed Drive. IEEE Trans. Ind. Electron. 2019, 66, 784–794. [Google Scholar] [CrossRef]
- Zhu, X.; Fan, D.; Mo, L.; Chen, Y.; Quan, L. Multiobjective Optimization Design of a Double-Rotor Flux-Switching Permanent Magnet Machine Considering Multimode Operation. IEEE Trans. Ind. Electron. 2019, 66, 641–653. [Google Scholar] [CrossRef]
- Meng, Y.; Fang, S.; Pan, Z.; Liu, W.; Qin, L. Machine Learning Technique Based Multi-Level Optimization Design of a Dual-Stator Flux Modulated Machine With Dual-PM Excitation. IEEE Trans. Transp. Electrif. 2023, 9, 2606–2617. [Google Scholar] [CrossRef]
- Zang, B.; Chen, Y. Multiobjective Optimization and Multiphysics Design of a 5 MW High-Speed IPMSM Used in FESS Based on NSGA-II. IEEE Trans. Energy Convers. 2023, 38, 813–824. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Z.; Han, J. Multiobjective Optimization of High Power Density Outer Rotor PM Starter Generator Considering Electromagnetic and Temperature Characteristics. IEEE Trans. Ind. Electron. 2024, 71, 8339–8350. [Google Scholar] [CrossRef]



| Item | Value |
|---|---|
| Rated load power | 10 kW |
| Driving speed of the prime mover | 1500 rpm |
| Range of slip adjustment | 0.1–0.5 |
| Stator outer radius | 135 mm |
| Active axis length | 90 mm |
| Power subsystem pole pairs | 13 |
| Control subsystem pole pairs | 2 |
| Natural synchronous speed | 1300 rpm |
| Number of stator slots/pitch | 36/8 |
| Number of inter wound rotor slots/pitch | 30/1 |
| Number of outer wound rotor slots/pitch | 30/6 |
| Variable | Initial | Range | Variable | Initial | Range |
|---|---|---|---|---|---|
| Rpr (mm) | 50 | 40–70 | Row (mm) | 110 | 100–120 |
| Riw (mm) | 85 | 75–100 | hsy (mm) | 6 | 4–8 |
| hiwy (mm) | 6 | 4–8 | howy (mm) | 6 | 4–8 |
| αpm (deg) | 9 | 5–11 | wst (mm) | 4 | 2–6 |
| hpm (mm) | 4 | 2–6 | wowt (mm) | 4 | 2–6 |
| wiwt (mm) | 6 | 4–8 | Ns | 300 | 120–480 |
| Niw | 300 | 150–450 | Now | 250 | 150–350 |
| Item | Initial Design | Pareto Point 1 | Pareto Point 2 | Pareto Point 3 | Optimal Design |
|---|---|---|---|---|---|
| Torque (Nm) | 39.73 | 49.59 | 47.85 | 39.48 | 48.72 |
| Torque ripple (%) | 14.78 | 7.57 | 5.51 | 13.21 | 6.49 |
| Efficiency (%) | 88.20 | 89.81 | 89.93 | 90.76 | 90.11 |
| Evaluation index () | 0.246 | 0.117 | 0.121 | 0.191 | 0.114 |
| Variable | Value | Variable | Value | Variable | Value |
|---|---|---|---|---|---|
| Rpr (mm) | 59.0 | wiwt (mm) | 7.1 | wowt (mm) | 3.8 |
| Riw (mm) | 90.7 | Row (mm) | 116.1 | Ns | 300 |
| hiwy (mm) | 5.5 | hsy (mm) | 6.4 | Now | 200 |
| αpm (deg) | 6.4 | howy (mm) | 6.0 | Niw | 390 |
| hpm (mm) | 4.2 | wst (mm) | 3.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, X.; Lin, H.; Li, Y.; Wang, J.; Wen, Q. Analysis and Optimization Design of a Brushless Power Feedback PM Adjustable Speed Drive with Bilayer Wound Rotor. Actuators 2025, 14, 241. https://doi.org/10.3390/act14050241
Zheng X, Lin H, Li Y, Wang J, Wen Q. Analysis and Optimization Design of a Brushless Power Feedback PM Adjustable Speed Drive with Bilayer Wound Rotor. Actuators. 2025; 14(5):241. https://doi.org/10.3390/act14050241
Chicago/Turabian StyleZheng, Xinlei, Heyun Lin, Yibo Li, Jian Wang, and Quanwei Wen. 2025. "Analysis and Optimization Design of a Brushless Power Feedback PM Adjustable Speed Drive with Bilayer Wound Rotor" Actuators 14, no. 5: 241. https://doi.org/10.3390/act14050241
APA StyleZheng, X., Lin, H., Li, Y., Wang, J., & Wen, Q. (2025). Analysis and Optimization Design of a Brushless Power Feedback PM Adjustable Speed Drive with Bilayer Wound Rotor. Actuators, 14(5), 241. https://doi.org/10.3390/act14050241






