Abstract
Effective fault diagnosis in rotating machinery means extracting fault features from complex samples. However, traditional data-driven methods often overly rely on labeled samples and struggle with extracting high-order complex features. To address these issues, a novel Multi-Metric Fusion Hypergraph Neural Network (MMF-HGNN) is proposed for fault diagnosis in rotating machinery. The approach involves constructing hypergraphs for sample vertices using three metrics: instance distance, distribution distance, and spatiotemporal distance. An innovative hypergraph fusion strategy is then applied to integrate these normalized hypergraphs, and a dual-layer hypergraph neural network is utilized for fault diagnosis. Experimental results on three different fault datasets demonstrate that the MMF-HGNN method excels in feature extraction, reduces reliance on labeled samples, achieving a classification accuracy of 0.9965 ± 0.0025 even with only 5% of labeled samples, and shows strong robustness to noise across varying signal-to-noise ratios.
1. Introduction
Rotating machinery is an indispensable component of modern industry, playing a crucial role in areas such as aerospace, marine engineering, wind power generation, and unmanned ground vehicles [1,2,3]. With technological advancements, the scale, integration, and high-speed operation of mechanical equipment have introduced new challenges for rotating machinery [4]. Gears and bearings, as core components, directly impact the operational efficiency and safety of the entire mechanical system [5], and rolling bearings commonly suffer from faults that can degrade system performance and disrupt normal operation [6]. Therefore, fault diagnosis of these critical components is essential. However, the vibration signals of equipment significantly differ from normal conditions. Thus, vibration signal analysis has become a vital approach for fault diagnosis in rotating machinery [7].
Fault diagnosis typically involves three key steps: data acquisition, feature extraction, and fault identification, with feature extraction being particularly crucial [6]. In practical environments, feature extraction is usually faced with two problems, the first is whether the feature extraction is effective or not. From the first perspective, signal analysis techniques such as wavelet transform (WT) and empirical mode decomposition (EMD) are commonly used for effective feature extraction [8]. These features are then analyzed with the help of expert knowledge. However, these techniques often produce features with significant redundant information, which complicates and increases the cost of subsequent processing. Deep learning algorithms, with their end-to-end capabilities, have effectively addressed this issue [9]. Deep learning methods enable automatic feature extraction by integrating methods such as ensemble deep autoencoder (EDAE) [6] and one-dimensional residual convolutional autoencoder (1-DRCAE) [10]. But deep learning models often produce features that are less interpretable [11].
From another perspective, mechanical equipment typically ceases operation immediately upon fault occurrence, making it challenging to collect sufficient actual fault samples. It is usually approached using Synthetic Minority Oversampling Technique (SMOTE) or Transfer Larning (TL) [12], like variational autoencoder (VAE) [13] or Wasserstein gradient penalty-based generative adversarial network (WGAN-GP) [14]. Essentially, these methods aim to expand the sample size or incorporate additional information to reduce reliance on target samples [15]. However, they do not lessen the model’s dependency on labeled samples, requiring engineers to continuously adjust the models for different scenarios to achieve optimal diagnostic performance.
Therefore, diagnosing faults with limited labeled samples has become a crucial focus of current research. One of the solutions is to detect the connections between features. Graph Convolutional Networks (GCNs) are an emerging deep learning algorithm based on graph structures [16]. Unlike traditional methods, GCNs consider both data values and the relationships between data points, providing richer information for the model. Gao et al. [17]. proposed a semi-supervised graph convolutional neural network (SSGCN) method that constructs vibration samples into an undirected weighted k-nearest neighbor graph and uses GCN to adaptively extract fault features, achieving fault diagnosis with limited labeled samples. Wang et al. [18] introduced a residual dual graph neural network (DGNNet) method, which learns sample features from images converted from raw signals through residual modules. Ji et al. [19] presented a soft sensor model based on the GCN and long short-term memory to estimate the effectiveness of hydraulic pumps. This method constructs both sample instances and distribution graphs, using an alternate update policy to propagate label information from labeled to unlabeled samples, enabling fault diagnosis under small sample conditions. However, simple graphs typically assume that relationships between objects exist only in pairs, with each edge connecting only two vertices, making it challenging to fully extract information from data with complex relationships, such as vibration signals. Consequently, hypergraphs have been introduced to address this limitation.
Hypergraphs were first introduced by French mathematician Berge in the 1960s [20]. With ongoing theoretical advancements, hypergraphs have been applied to cutting-edge fields such as social network modeling and biomolecular design. In 2019, Feng et al. from Tsinghua University proposed the Hypergraph Neural Network (HGNN) based on spectral graph theory [21], significantly enhancing the ability of graph-based neural networks to handle complex relational data. Recently, researchers have begun exploring the application of hypergraphs in fault diagnosis. Yan et al. [22]. proposed a Multi-Resolution Hypergraph Neural Network (MrHGNN), resampling the original data at different rates to construct multi-resolution sub-hypergraphs. By concatenating these hypergraphs, they effectively mined latent sample features, achieving efficient fault diagnosis. Ke et al. [23]. introduced a Time-Frequency Hypergraph Neural Network (TFHGNN), combining self-attention mechanisms to extract fault features from both the time and frequency domains of samples, thereby constructing sample hypergraphs. This approach effectively mitigated performance degradation in limited sample and noisy environments. Xia et al. [24]. proposed a Residual Hypergraph Convolutional Network (Res-HGCN), embedding equipment structure and operational mechanisms into the hypergraph model. By integrating residual blocks and multi-sensor data, they improved the interpretability of the diagnostic results.
However, there are several shortcomings in the hypergraph method based research. Firstly, the methods for constructing sample graph structures are often cumbersome and singular, involving complex sample processing to extract fault features and using a single metric to construct the graph structure. This can result in biased measurements of sample similarity, reducing the accuracy of fault diagnosis and hindering the application and promotion of these methods. Secondly, the unweighted hypergraphs constructed are usually sparse and cannot fully capture the complex relationships between vibration signals, making them susceptible to noise and resulting in unstable diagnostic outcomes. Lastly, due to their high dependence on labeled samples, these methods perform poorly when the number of samples is limited.
To address these issues, this paper proposes a Multi-Metric Fusion Hypergraph Neural Network (MMF-HGNN). Specifically, three types of distance metrics are utilized: instance distance, distribution distance, and spatiotemporal distance to construct three types of sample sub-hypergraphs. These normalized sub-hypergraphs are then fused into a weighted hypergraph using a multi-metric fusion strategy, providing a more accurate representation of the similarity relationships among vibration signal samples. Based on this, we construct a dual-layer hypergraph convolution network within the hypergraph neural network framework for fault diagnosis in rotating machinery. The main contributions of this paper are as follows:
- A method for constructing multi-metric fused hypergraphs based on various similarity metrics is proposed. This involves creating a multi-metric weighted hypergraph by integrating instance hypergraphs, distribution hypergraphs, and spatiotemporal hypergraphs, which comprehensively describe the relational features among samples.
- A Multi-Metric Fusion Hypergraph Neural Network (MMF-HGNN) is developed by utilizing a dual-layer hypergraph convolutional network within a hypergraph neural network framework, thereby enhancing the accuracy of fault diagnosis in rotating machinery.
- A thorough analysis of crucial factors for the proposed MMF-HGNN method is conducted and its effectiveness is validated on three benchmark datasets. Additionally, the method’s dependency on labeled samples and its robustness to noise are examined to further assess its performance.
The remainder of this paper is organized as follows: The relevant theory of hypergraphs is introduced in Section 2. The proposed method is presented in Section 3. The effectiveness of the proposed method is validated on benchmark datasets in Section 4. The method’s dependency on labeled samples and its robustness to noise are discussed in Section 5. Finally, Section 6 concludes the paper.
2. Related Work
Hypergraph Neural Networks (HGNNs) were first introduced by Feng et al. [21]. Unlike traditional graphs, the hyperedges can connect multiple vertices. This characteristic enhances the expressive power of hypergraphs in depicting complex relationships between objects, making them more flexible and intuitive [25]. The hypergraph convolution layer is formulated as follows:
In this equation, and represent the input and output of the lth hypergraph convolution layer. The learnable parameter is denoted by . If is not the final layer, is set as the dimension of the hidden layer, as depicted in Figure 1.
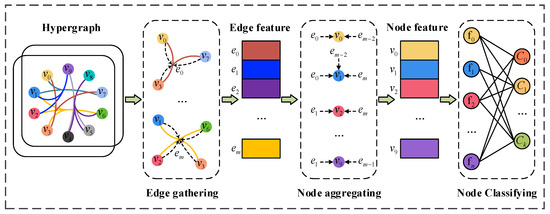
Figure 1.
Hypergraph convolution and node classification.
The input to the HGNN consists of the initialized vertex features and the incidence matrix , where is the dimension of the vertex features. Softmax is utilized as the activation function for the final layer of the HGNN, yielding an output , where represents the number of fault types. Each layer’s hidden dimensions are predefined, and the cross-entropy function is employed as the loss function.
3. The Multi-Metric Hypergraph Neural Network
The HGNN model is constructed with two layers of hypergraph convolution for diagnosing faults in rotating machinery. The Laplacian matrix of the hypergraph, along with the sample vertices, is used as the input, while the fault categories serve as the output. The model is then trained and evaluated to perform fault diagnosis based on the MMF-HGNN framework. The process and basic structure are shown in Figure 2.
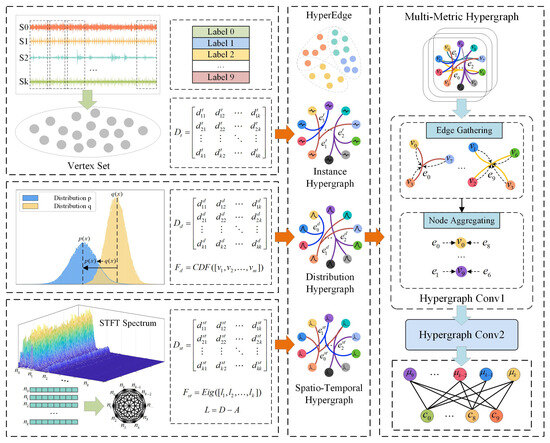
Figure 2.
Overall framework of MMF-HGNN for fault diagnosis.
3.1. Multi-Metric Hypergraph Construction
We frame the fault diagnosis problem as a hypergraph vertex classification task, where fault samples are represented as vertices in the hypergraph. The raw vibration signals are segmented into equal-length segments using a sliding window technique, resulting in fault samples that form the vertex set of the hypergraph.
Since these fault samples are continuous time series without explicit structural relationships, it is essential to measure their similarity and establish connections between vertices. Hyperedges can generally be constructed using one of four methods: distance-based, representation-based, attribute-based, and network-based approaches. In this paper, we utilize a distance-based method for constructing hyperedges.
3.2. Instance Hypergraph Generation
The time-domain data of vibration signals reflect the intensity information of the signals. To measure the time-domain similarity of the samples, Euclidean distance is used to construct the vertex distance matrix, as shown in Equation (2).
While represents the distance of vetrex samples and . Using this formula, the instance distance matrix between sample vertices is calculated. Next, the K-Nearest Neighbors (KNN) method is employed to construct hyperedges. For each vertex sample , the nearest vertices are found in the distance matrix , and these neighboring samples are grouped to form a hyperedge centered on . By iterating over all vertices, an instance hypergraph containing hyperedges is obtained. The algorithm flow is presented in Algorithm 1.
| Algorithm 1: Constructing instance hypergraph from samples |
| Input: , ; Output: ; |
| 1: ; 2: according to Equation (2); 3: using KNN: 4: do 5: ; 6. , ; 7: end for; 8: ; |
3.3. Distribution Hypergraph Generation
The amplitude domain of vibration signals represents the probability distribution across various amplitude ranges and is commonly used in manual fault analysis. To assess the similarity between the amplitude distributions of two samples, this paper employs the Wasserstein distance to construct the vertex distance matrix. As shown in Figure 3.
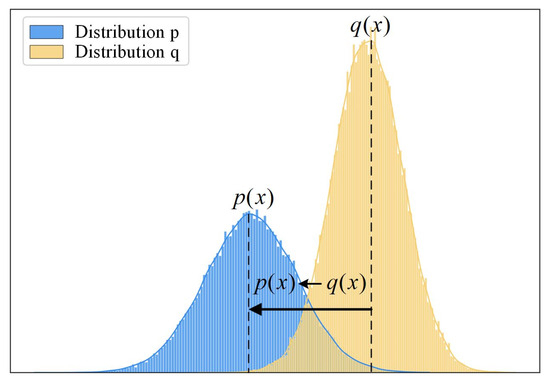
Figure 3.
From distribution to distribution p.
The Wasserstein distance measures the discrepancy between two probability distributions by calculating the minimal cost required to transport one distribution to another. As illustrated in Equation (3), it quantifies this difference by identifying the optimal transport plan.
where represents the set of all joint distributions that can be formed from and . The expectation calculates the average distance between pairs sampled from the joint distribution . The Wasserstein distance is obtained by minimizing this expected distance.
Using this approach, the distribution distance matrix is computed for the sample vertices. The KNN algorithm is then applied to build the hyperedges, resulting in a distribution hypergraph with hyperedges. The algorithm flow is outlined in Algorithm 2:
| Algorithm 2: Constructing distribution hypergraph from samples |
| Input: ; Output: ; |
| 1: to histograms; 2: according to Formula (3); 3: using KNN; 4: do 5: ; 6: , ; 7: end for 8: |
3.4. Spatio-Temporal Hypergraph Generation
The time-frequency domain of vibration signals captures detailed dynamic frequency information. Applying Short-Time Fourier Transform (STFT) to the samples generates time-frequency spectrograms of the vibration signals. Using a spatio-temporal graph is advantageous for effectively extracting the embedded information [26]. Unlike traditional feature extraction methods, the spatio-temporal graph integrates both time-frequency domain and graph structural information, thereby enhancing the discriminative power of the extracted features.
To measure the similarity in the time-frequency domain of vertex samples, this paper constructs the vertex distance matrix based on the spatio-temporal graph distance.
As illustrated in Figure 4, the vibration signal is first processed using STFT to produce a time-frequency spectrogram. Frequencies are treated as vertices, and a fully connected graph—referred to as the spatio-temporal graph—is constructed, with frequencies represented as . Subsequently, the adjacency matrix and degree matrix are computed to derive the graph Laplacian matrix . The eigenvectors of are then used as the features for each sample vertex .
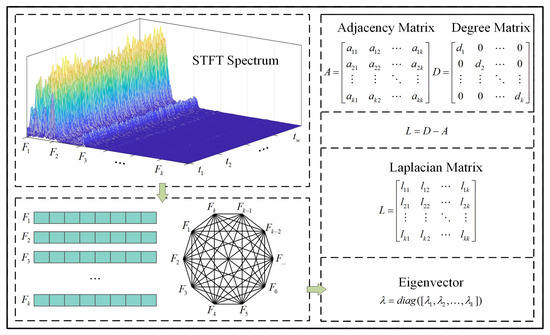
Figure 4.
Construction of spatiotemporal features from STFT.
Based on the spatio-temporal graph features of the vertices, the spatio-temporal distance matrix is computed between sample vertices. Finally, the KNN algorithm is used to construct hyperedges, resulting in a spatio-temporal hypergraph with hyperedges. The algorithm flow is detailed in Algorithm 3.
| Algorithm 3: Constructing spatio-temporal hypergraph from samples |
| Input: ; Output: ; |
| 1: ; 2: , ; 3: as nodes; 4: according to Formula (3); 5: ; 6: according to Formula (2); 7: using KNN; 8: return ; |
3.5. Multi-Metric Hypergraphs Fusion
Instead of conventional hypergraph concatenation, a weighted hypergraph fusion strategy is employed to construct the multi-metric fusion weighted hypergraph. Due to the varying scales of the hypergraphs resulting from different metrics, direct fusion may obscure important information. Therefore, normalization is necessary before fusion, defined as follows in Equation (4):
where is the scaling factor and is the average distance from the center node to the other nodes. The normalization method aims to compute the average distance from the central node to the other nodes and adds a scaling factor to ensure the differentiation of similar samples while suppressing the effect of larger distances on the similarity computation.
In hypergraphs , , , each hyperedge represents the vertices associated with vertex . To accurately represent the similarity relationships between vertices, we combine the vertices associated with vertex from the three hypergraphs into a single hyperedge. After normalization, we calculate the average of the association matrices, resulting in the multi-metric fused hypergraph, as shown in Equation (5).
4. Experimental Analysis
This section evaluates the performance of the proposed MMF-HGNN method using the CWRU bearing dataset [27] as a benchmark. The model is implemented with Python 3.8 and PyTorch 2.0. All experiments are conducted on a system equipped with an Intel Core i9-13900HX CPU, 16 GB of DDR5 RAM, and an NVIDIA RTX 4060 GPU with 8 GB of VRAM. The server device was assembled in-house by Shengbuyun’s lab at Wuhan University of Technology (Wuhan, China). The system runs on [Windows 11/Ubuntu 22.04 LTS]* with CUDA 11.8 and cuDNN 8.9. precision. Timing results may vary with hardware architectures, but relative performance trends remain consistent.
4.1. Dataset Description
The CWRU bearing dataset was obtained from the bearing test rig shown in Figure 5. This platform uses a 2 hp Reliance Electric motor to perform bearing fault tests under load conditions ranging from 0 to 3 hp. Bearing faults are categorized into ball fault (BF), inner race fault (IF), and outer race fault (OF). These faults are single-point defects induced by Electrical Discharge Machining (EDM), with each fault type having three different fault diameters: 7 mils, 14 mils, and 21 mils. Data were collected under various load conditions, including normal bearing data and fault data at 12 kHz and 48 kHz for both drive-end and fan-end faults.

Figure 5.
Platform of CWRU dataset [27]. Note: Case Western Reserve University Bearing Data Center.
For this study, the 48 kHz single-point drive-end fault data recorded under a motor load of 1 hp and an approximate bearing speed of 1772 RPM was selected as the experimental dataset. Detailed descriptions of the specific experimental files are provided in Table 1.

Table 1.
Details of CWRU dataset.
4.2. Experimental Settings
The raw vibration data is loaded from the dataset and segmented into samples using a sliding window with a width and a step size , constructing a vertex set . Subsequently, following the proposed method, three sub-hypergraphs are constructed, resulting in a multi-metric fused hypergraph . The Laplacian matrix of this hypergraph is then calculated and used as input to the model. In this experiment, the sliding window parameters are set to , , and the number of samples , which includes 150 vertices for each of the 10 fault types. The KNN parameter is set to .
Thus, the raw data is transformed into input samples and . A two-layer HGNN model is established with a hidden layer dimension of 128 and an output layer dimension of 10, corresponding to the number of fault types. The ReLU function is used as the nonlinear activation function, and dropout is applied to avoid overfitting with a rate of p = 0.5. During training, the Adam optimizer is used with a learning rate of 0.001, and the loss function is the cross entropy loss function. Training is conducted over 200 epochs with a batch size of 64. The softmax function is employed to generate prediction labels. To ensure the validity of the experiment, 5-fold cross-validation is performed. In 80% of the samples used for training, 70% are randomly selected for the training set and 30% for the validation set. Key metrics, such as accuracy and recall, are recorded for each experiment.
4.3. Results and Analysis
As shown in Figure 6a, the model converges within 30 epochs, achieving a classification accuracy of 99.93 ± 0.13%. Figure 6b presents the confusion matrix, illustrating the model’s predictions versus the actual classifications across different fault types. It is evident that only a few samples are misclassified, demonstrating the method’s excellent diagnostic performance.
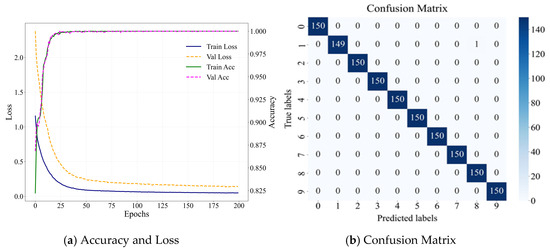
Figure 6.
Basic result for CWRU dataset. (a) is the accuracy and loss curve of the dataset validation; (b) is the confusion matrix of the feature correlation.
To visually analyze the role of the multi-metric hypergraph and the model’s classification performance, t-SNE is utilized to visualize the input hypergraph features and the model’s output features, as shown in Figure 7. In Figure 7a, the Laplacian matrix of the input hypergraph initially separates different vertices based on similarity relationships. After processing these vertices through the HGNN and applying two layers of hypergraph convolution, some previously dispersed samples are effectively distinguished according to their fault categories in Figure 7b. In this paper, Separability Score, average inter distance (avg_inter_dist), and average intra distance (avg_intra_dists) have been introduced as the evaluation of t-SNE. Among them, avg_inter_dist is the average distance between class centers, and the larger it is, the more obvious the interclass distinction. avg_intra_dists is the average distance from intraclass samples to class centers, and the smaller it is, the more obvious the class cohesion. Separability Score, on the other hand, is the avg_inter_dist/avg_intra_dists; the higher the score, the higher the cohesion and the lower the coupling.
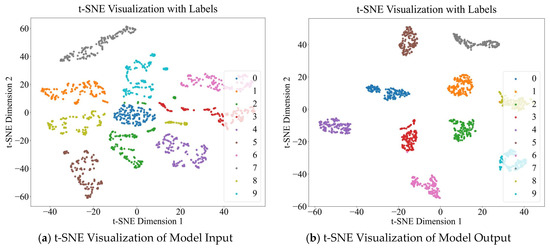
Figure 7.
Comparison of visualizations for input and output features. (a) is the input result and (b) is the output result.
In Figure 7, 0–9 on the right side indicate the different labels provided for categorization. Before the model computation, i.e., in Figure 7a, avg_inter_dist is 46.5396, avg_intra dists is 10.5410, and Separability Score is 4.4151. After computation by the hypergraph neural network model proposed in this paper, the avg_inter_dist is 52.3662 and the avg_intra_dists is 5.2327. The Separability Score is 10.0075, which is comprehensively better than the results without vertex processing and hypergraph convolution. Additionally, the diagnostic performance of the proposed method is significantly influenced by two key parameters: the vertex length in hypergraph construction and the number of associated vertices . The vertex length determines the amount of fault information encapsulated within each vertex, thus affecting the similarity measurement between samples. The number of associated vertices dictates the size of each hyperedge, thereby influencing the relationships between vertices.
To systematically evaluate the impact of these parameters, experiments are conducted by varying from 512 to 9728 and from 2 to 30 independently.
As shown in Figure 8, the diagnostic performance of the model is influenced by both the vertex length and the number of associated vertices . In Figure 8a, as the vertex length W increases, the model’s diagnostic performance improves and then stabilizes. For W values less than 2560, the model’s stability is relatively poor. However, as W exceeds 4096, the performance stabilizes with minor fluctuations due to enhanced similarity judgments from the increased fault information in each vertex. Similarly, in Figure 8b, as the number of associated vertices increases, the model’s diagnostic performance also improves and stabilizes. For values less than 5, the model’s stability is poor. As increases to the range of 5–15, the diagnostic accuracy significantly improves, and further increases in result in minor fluctuations but no significant changes in accuracy. These observations indicate that careful tuning of W and K is crucial for optimizing the model’s diagnostic performance.
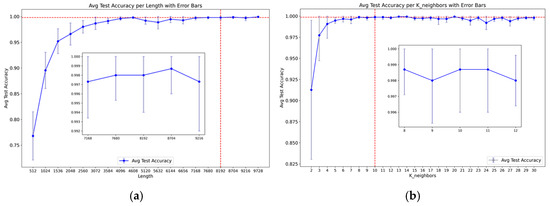
Figure 8.
Key parameter analysis. (a) is the impact of vertex length W, and (b) is the impact of number of associated vertices K.
5. Experimental Validation
This section evaluates the proposed MMF-HGNN method’s dependency on labeled samples and its robustness to noise, using the KAT bearing dataset [28] and the SEU gearbox dataset [12]. Comparative experiments with other state-of-the-art methods are also presented.
5.1. Case 1: Robustness to Sample Ratio
The KAT dataset was collected from the bearing fault experimental platform at Paderborn University in Germany, as shown in Figure 9. This dataset includes bearing data under various operating conditions, including normal, induced faults, and real faults. The real fault data comes from 14 bearings subjected to accelerated life testing, reflecting the degradation conditions of bearings under actual operating circumstances, thereby providing a high reference value.

Figure 9.
Platform of KAT dataset [28]. Note: Konstruktions- und Antriebstechnik Bearing DataCenter. (2016). “Bearing Data Set”. Available online: https://mb.uni-paderborn.de/kat/forschung/kat-datacenter/bearing-datacenter/data-sets-and-download (accessed on 9 May 2025).
To validate the diagnostic effectiveness of the proposed method, experimental data from the N15 M07 F10 condition were selected, where the bearing undergoes accelerated natural degradation. In this condition, the bearing operates at approximately 1500 RPM, with a load torque of 0.7 Nm and a radial force of 1000 N. Detailed experimental files and relevant fault information are provided in Table 2.

Table 2.
KAT dataset setting.
It is worth noting the designation of the bearings used for testing: K003 represents the normal data of bearings at radial force of 1000 N and 1500 rpm; KA04, KA15, KA16 represent the data set of single-point fatigue pitting of the outer ring at different positions; KB23, KB24, KB27 is the data set of fatigue pitting of the inner and outer rings at different positions together; and KI04, KI16, KI21 is the data set of fatigue pitting of the inner ring at different positions together.
The sample vertex length was set to , and the number of associated vertices to , with all other settings remaining consistent with previous experiments. We utilized 5-fold cross-validation, where 80% of the samples were randomly divided into training and validation sets for each fold. The validation set ratio was varied from 30% to 95% in 5% increments. Key metrics, such as accuracy and recall, were recorded for each experiment. The compared methods include the following:
- SVM: Employed 18 common statistical features in the time and frequency domains, which are typically used to assess the state of a device, including average value, standard deviation, root-mean-square, peak value, peak-to-peak value, peak factors, pulse factors, margin factors, waveform factors, skewness, kurtosis, entropy in time domain, and central frequency, average frequency, frequency standard deviation, frequency root-mean-square, frequency variance and signal energy in frequency domain. Training and evaluation provide a baseline for traditional machine learning performance.
- 1DCNN [29]: Used vibration signal samples as input. The network consisted of two convolutional layers (32 and 64 filters, respectively), followed by max-pooling layers, and two fully connected layers (1024 neurons and the number of output classes).
- GCN [30]: Constructed graphs with 12 nodes each, connected by six nearest neighbor (KNN) edges. The network consisted of two graph convolutional layers with 1024 hidden units, followed by batch normalization and fully connected layers with a dropout layer.
- MrHGNN [22]: Resampled vibration signals at different resolutions (1, 0.5, 0.25), and then constructed hypergraphs from the FFT-transformed frequency-domain signals at each resolution. These hypergraphs were concatenated horizontally for input into the two-layer hypergraph convolution network.
- TFHGNN [23]: Integrated both time and frequency domain signals. CNNs were employed to extract features from time and frequency domains separately, and these features were combined using self-attention mechanisms before being input into the two-layer hypergraph convolution network.
All methods were evaluated using the same experimental setup to ensure a fair comparison. The results of these comparisons are presented in Figure 10. To validate the performance of MMF-HGNN and MrHGNN with a minimal number of labeled samples, the training sample ratio was varied from 0.10 to 0.01. As shown in the inner figure from Figure 10, MMF-HGNN consistently demonstrates superior classification accuracy compared to MrHGNN across all sample ratios. Even with an extremely limited labeled sample ratio of 3%, MMF-HGNN maintains a high average classification performance of 0.978 ± 0.026.
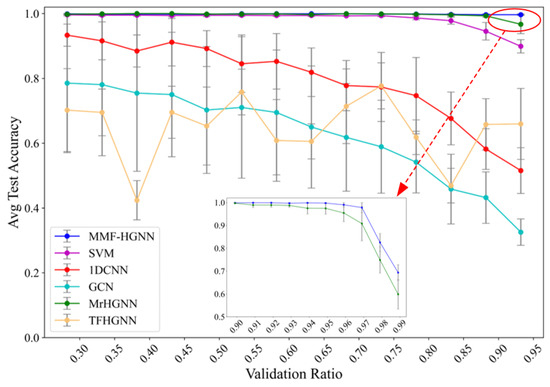
Figure 10.
Comparison of MMF-HGNN and other methods at different ratios. Outer graph is the accuracy in different ratios, while inner graph is the main methods of MMF-HGNN and MrHGNN at ≤10% ratio.
This indicates that traditional deep learning methods are highly dependent on sample labeling, and it is difficult to effectively extract fault features at low sample labeling rates, while hypergraph methods can make full use of unlabeled sample data through structured information modeling and reduce the dependence of model training on labeled samples. Moreover, these results confirm that the proposed method exhibits strong predictive accuracy and robustness in fault diagnosis tasks, even under conditions with very small labeled data sets.
On the KAT dataset, the performance of most algorithms significantly declines as the proportion of training data decreases. In contrast, MMF-HGNN maintains high classification accuracy across all training proportions. As illustrated in Table 3, even with only 5% of the training data, which corresponds to an average of just eight labeled samples per class, MMF-HGNN achieves an accuracy of 99.65 ± 0.25%. This highlights MMF-HGNN’s capability to effectively leverage limited sample data to capture critical features, resulting in a substantial performance advantage over other methods. However, it is worth noting that the computational complexity associated with hypergraph construction makes MMF-HGNN more time-consuming compared to most other methods.

Table 3.
Performance of various methods at 5% training ratio.
5.2. Case 2: Robustness to Random Noise
The SEU gearbox dataset, provided by Southeast University, the dataset contains two subdatasets, including bearing data and gear data, which are both collected from the Dynamic Drive Simulator (DDS). The system operates at speed and load settings of 20 Hz–0 V and 30 Hz–2 V, respectively. The dataset comprises two distinct sets of data: one for the gearbox bearings and one for the gears. Each data file contains eight data channels, which represent eight different sensors in different positions: 1-motor vibration, 2,3,4-vibration of planetary gearbox in three directions (x, y, and z), 5-motor torque, and 6,7,8-vibration of parallel gearbox in three directions (x, y, and z). Signals of rows 2,3,4 are all effective.
In this paper, gear data under the operating condition of 30 Hz–2 V is utilized, encompassing four different gear fault states (Chipped, Miss, Root, Surface) and one healthy state, with 200 samples for each state. To evaluate the robustness of the proposed method against noise, Gaussian white noise is introduced to the data to simulate a noisy environment. The noise level is determined based on the signal-to-noise ratio (SNR), calculated using the formula , where and represent the power of the original signal and the noise.
In this study, gear data under the operating condition of 30 Hz–2 V is utilized, encompassing four different gear fault states (Chipped, Miss, Root, Surface) and one healthy state, with 200 samples for each state. To evaluate the robustness of the proposed method against noise, Gaussian white noise is introduced to the data to simulate a noisy environment. The noise level is determined based on the signal-to-noise ratio (SNR), calculated using the formula , where and represent the power of the original signal and the noise, respectively. The main factors have been shown in Table 4:

Table 4.
SEU dataset setting.
The sample vertex length is set to and the number of associated vertices is set to , with all other parameters kept consistent. Experiments are conducted across a range of SNR values from 10 dB to −10 dB, with increments of 2 dB. Key metrics, including accuracy and recall, are recorded for each SNR setting. The results are then compared with those from other state-of-the-art methods under the same conditions, as illustrated in Figure 11:
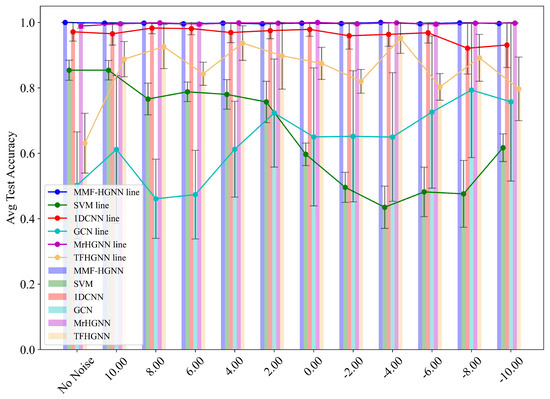
Figure 11.
Hypergraph structure and multi-hypergraph integration.
The classification accuracy of all methods decreases to different degrees as the SNR decreases. However, compared with other methods, MMF-HGNN maintains a more stable classification effect at lower SNR values. When SNR = 5 dB, the classification accuracy of MMF-HGNN decreases only slightly, outperforming the other compared methods. When SNR ≥ 20 dB, the classification accuracy of MMF-HGNN is still higher than other methods, indicating that the diagnostic performance of MMF-HGNN is minimally affected by the additional WGN. In noisy environments, MMF-HGNN suffers less noise interference than other methods and has strong noise robustness.
5.3. Ablation Study
The MMF-HGNN uses three metrics for hypergraph construction as mentioned in Section 3.5. In order to verify the importance of each subhypergraph, ablation experiments have been conducted in this section. The instance hypergraph constructed from the time domain data is denoted as 1, the distribution hypergraph constructed from the magnitude domain data is denoted as 2, and the spatio-temporal hypergraph constructed from the time-frequency domain data is denoted as 3. The experiments are conducted on all datasets, and the results are shown in Table 5.

Table 5.
Ablation experiment on different datasets.
The table compares seven MMF-HGNN variants across performance metrics (Accuracy, Precision, Recall, F1 Score ± standard deviations) and computational efficiency. Because the amount of data was too large to identify accurately, we summarized the above Figure 5 and retained the two core metrics: accuracy and time, as shown in Figure 12.
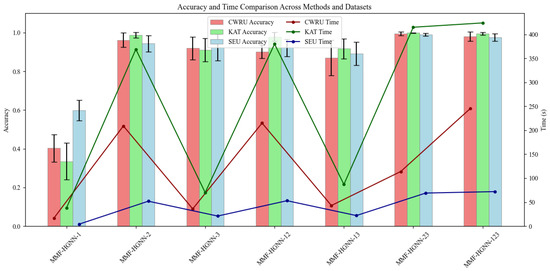
Figure 12.
Ablation Experiment Results.
In Figure 12, the accuracy and time performance of different methods on various datasets have been compared. The datasets are labeled as MMF-HGNN from single metrics like 1, 2, and 3 to three metrics like 123. The accuracy is represented by bars in three colors: red for CWRU dataset Accuracy, green for KAT dataset Accuracy, and blue for SEU dataset Accuracy. The time cost by each method is shown by a darker lines, and error bars indicate the variability in accuracy measurements.
Overall, the MMF-HGNN-23 and MMF-HGNN-123 methods perform very well across multiple datasets, with the other methods slightly worse. The MMF-HGNN-23 and MMF-HGNN-123 methods show superior performance in multiple datasets. High accuracy was achieved in several datasets, which also took less time. The other methods (MMF-HGNN-1, MMF-HGNN-2, MMF-HGNN-3, etc.) show varying degrees of accuracy and time efficiency on different datasets, suggesting that they may not be as universally effective as MMF-HGNN-23 and MMF-HGNN-123. The ablation experiments demonstrate that the MMF-HGNN-123 method can effectively handle the problems we face in the several types of data presented in this paper.
6. Conclusions
This paper introduces a Multi-Metric Fusion Hypergraph Neural Network (MMF-HGNN) for fault diagnosis in rotating machinery. Experiments on three datasets validate its accuracy, high lighting the method’s robustness to noise and dependence on labeled samples. Notably, MMF HGNN achieves a classification accuracy of 0.9965 ± 0.0025 with only 5% labeled samples, outperforming traditional machine learning methods.
The proposed MMF-HGNN offers several key advantages: (1) It employs multiple similarity metrics, including instance, distribution, and spatiotemporal distances, to capture high-order interactions within the data, effectively identifying complex correlations in vibration signals; (2) It introduces an innovative hypergraph fusion strategy, integrating these metrics into a unified multi-metric fusion weighted hypergraph for reliable data feature extraction, enhancing stability and interpretability; (3) It maintains excellent classification performance even with limited labeled samples and in noisy environments, demonstrating strong practical application potential.
Future work could explore additional similarity measurement methods to enhance the construction speed and interpretability of hypergraphs by integrating physical correlations. We will continue to refine MMF-HGNN and investigate its application in other manufacturing and industrial contexts.
Author Contributions
Conceptualization, J.Z. and J.H.; methodology, J.Z.; software, J.H.; validation, J.H.; formal analysis, J.Z.; investigation, J.H.; resources, B.S.; data curation, B.S.; writing—original draft preparation, J.Z and J.H.; writing—review and editing, J.Z and J.H.; visualization, J.H.; supervision, B.S.; project administration, B.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Case Western Reserve University Bearing Data Center. (2009). “Bearing Data Set”. Available online: https://engineering.case.edu/bearingdatacenter (accessed on 9 May 2025). Konstruktions- und Antriebstechnik Bearing DataCenter. (2016). “Bearing Data Set”. Available online: https://mb.uni-paderborn.de/kat/forschung/kat-datacenter/bearing-datacenter/data-sets-and-download (accessed on 9 May 2025).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hou, J.; Lu, X.; Zhong, Y.; He, W.; Zhao, D.; Zhou, F. A comprehensive review of mechanical fault diagnosis methods based on convolutional neural network. J. Vibroeng. 2024, 26, 44–65. [Google Scholar] [CrossRef]
- Misbah, I.; Lee, C.K.M.; Keung, K.L. Fault diagnosis in rotating machines based on transfer learning: Literature review. Knowl.-Based Syst. 2024, 283, 111158. [Google Scholar] [CrossRef]
- An, Y.; Eun, Y. Online Fault Detection for Four Wheeled Skid Steered UGV Using Neural Network. Actuators 2022, 11, 307. [Google Scholar] [CrossRef]
- Xu, X.; Huang, X.; Bian, H.; Wu, J.; Liang, C.; Cong, F. Total process of fault diagnosis for wind turbine gearbox, from the perspective of combination with feature extraction and machine learning: A review. Energy AI 2024, 15, 100318. [Google Scholar] [CrossRef]
- Liu, D.; Cui, L.; Wang, H. Rotating machinery fault diagnosis under time-varying speeds: A review. IEEE Sens. J. 2023, 23, 29969–29990. [Google Scholar] [CrossRef]
- Duan, Z.; Wu, T.; Guo, S.; Shao, T.; Malekian, R.; Li, Z. Development and trend of condition monitoring and fault diagnosis of multi-sensors information fusion for rolling bearings: A review. Int. J. Adv. Manuf. Technol. 2018, 96, 803–819. [Google Scholar] [CrossRef]
- Tiboni, M.; Remino, C.; Bussola, R.; Amici, C. A review on vibration-based condition monitoring of rotating machinery. Appl. Sci. 2022, 12, 972. [Google Scholar] [CrossRef]
- Wei, Y.; Li, Y.; Xu, M.; Huang, W. A review of early fault diagnosis approaches and their applications in rotating machinery. Entropy 2019, 21, 409. [Google Scholar] [CrossRef]
- Li, C.; Zhang, S.; Qin, Y.; Estupinan, E. A systematic review of deep transfer learning for machinery fault diagnosis. Neurocomputing 2020, 407, 121–135. [Google Scholar] [CrossRef]
- Chen, S.; Yu, J.; Wang, S. One-dimensional convolutional neural network-based active feature extraction for fault detection and diagnosis of industrial processes and its understanding via visualization. ISA Trans. 2022, 122, 424–443. [Google Scholar] [CrossRef]
- Li, T.; Sun, C.; Li, S.; Wang, Z.; Chen, X.; Yan, R. Explainable graph wavelet denoising network for intelligent fault diagnosis. IEEE Trans. Neural Netw. Learn. Syst. 2022, 35, 8535–8548. [Google Scholar] [CrossRef] [PubMed]
- Shao, S.; McAleer, S.; Yan, R.; Baldi, P. Highly accurate machine fault diagnosis using deep transfer learning. IEEE Trans. Ind. Inform. 2018, 15, 2446–2455. [Google Scholar] [CrossRef]
- Zhao, D.; Liu, S.; Gu, D.; Sun, X.; Wang, L.; Wei, Y.; Zhang, H. Enhanced data-driven fault diagnosis for machines with small and unbalanced data based on variational auto-encoder. Meas. Sci. Technol. 2019, 31, 035004. [Google Scholar] [CrossRef]
- Gao, X.; Deng, F.; Yue, X. Data augmentation in fault diagnosis based on the Wasserstein generative adversarial network with gradient penalty. Neurocomputing 2020, 396, 487–494. [Google Scholar] [CrossRef]
- Chen, X.; Yang, R.; Xue, Y.; Huang, M.; Ferrero, R.; Wang, Z. Deep transfer learning for bearing fault diagnosis: A systematic review since 2016. IEEE Trans. Instrum. Meas. 2023, 72, 3508221. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Yu, P.S. A comprehensive survey on graph neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 4–24. [Google Scholar] [CrossRef]
- Gao, Y.; Chen, M.; Yu, D. Semi-supervised graph convolutional network and its application in intelligent fault diagnosis of rotating machinery. Measurement 2021, 186, 110084. [Google Scholar] [CrossRef]
- Wang, H.; Wang, J.; Zhao, Y.; Liu, Q.; Liu, M.; Shen, W. Few-shot learning for fault diagnosis with a dual graph neural network. IEEE Trans. Ind. Inform. 2022, 19, 1559–1568. [Google Scholar] [CrossRef]
- Ji, S.; Li, W.; Wang, Y.; Zhang, B.; Ng, S.-K. A Soft Sensor Model for Predicting the Flow of a Hydraulic Pump Based on Graph Convolutional Network–Long Short-Term Memory. Actuators 2024, 13, 38. [Google Scholar] [CrossRef]
- Berge, C. Graphs and Hypergraphs; Elsevier Science Ltd.: Amsterdam, The Netherlands, 1985. [Google Scholar]
- Feng, Y.; You, H.; Zhang, Z.; Ji, R.; Gao, Y. Hypergraph neural networks. In Proceedings of the AAAI’19: AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 3558–3565. [Google Scholar]
- Yan, X.; Liu, Y.; Zhang, C.-A. Multiresolution hypergraph neural network for intelligent fault diagnosis. IEEE Trans. Instrum. Meas. 2022, 71, 3525910. [Google Scholar] [CrossRef]
- Ke, H.; Chen, Z.; Xu, J.; Fan, X.; Yang, C.; Peng, T. Time-frequency Hypergraph Neural Network for Rotating Machinery Fault Diagnosis with Limited Data. In Proceedings of the 2023 IEEE 12th Data Driven Control and Learning Systems Conference (DDCLS), Xiangtan, China, 12–14 May 2023; pp. 1786–1792. [Google Scholar]
- Xia, L.; Liang, Y.; Zheng, P.; Huang, X. Residual-hypergraph convolution network: A model-based and data-driven integrated approach for fault diagnosis in complex equipment. IEEE Trans. Instrum. Meas. 2022, 72, 3501811. [Google Scholar] [CrossRef]
- Bai, S.; Zhang, F.; Torr, P.H.S. Hypergraph convolution and hypergraph attention. Pattern Recognit. 2021, 110, 107637. [Google Scholar] [CrossRef]
- Wang, T.; Liu, Z.; Lu, G.; Liu, J. Temporal-spatio graph based spectrum analysis for bearing fault detection and diagnosis. IEEE Trans. Ind. Electron. 2020, 68, 2598–2607. [Google Scholar] [CrossRef]
- Loparo, K.A. Bearing Vibration Dataset. Available online: https://engineering.case.edu/bearingdatacenter/download-data-file (accessed on 9 May 2025).
- Lessmeier, C.; Kimotho, J.K.; Zimmer, D.; Sextro, W. Condition monitoring of bearing damage in electromechanical drive systems by using motor current signals of electric motors: A benchmark data set for data-driven classification. Phm Soc. Eur. Conf. 2016, 3. [Google Scholar] [CrossRef]
- Yu, J.; Zhou, X. One-dimensional residual convolutional autoencoder based feature learning for gearbox fault diagnosis. IEEE Trans. Ind. Inform. 2020, 16, 6347–6358. [Google Scholar] [CrossRef]
- Li, T.; Zhou, Z.; Li, S.; Sun, C.; Yan, R.; Chen, X. The emerging graph neural networks for intelligent fault diagnostics and prognostics: A guideline and a benchmark study. Mech. Syst. Signal Process. 2022, 168, 108653. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).