Robust Continuous Sliding-Mode-Based Assistive Torque Control for Series Elastic Actuator-Driven Hip Exoskeleton
Abstract
1. Introduction
2. Exoskeleton System
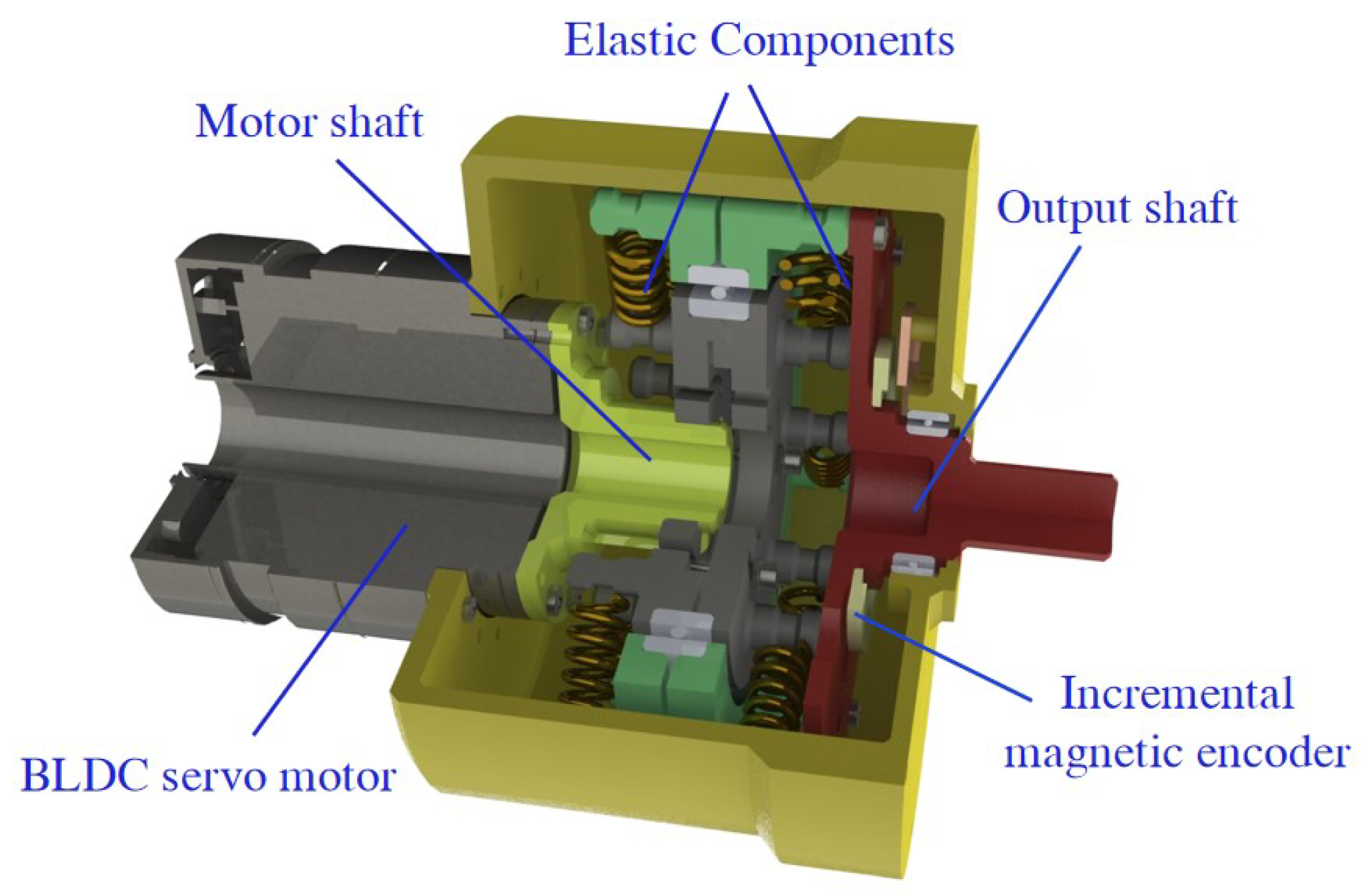
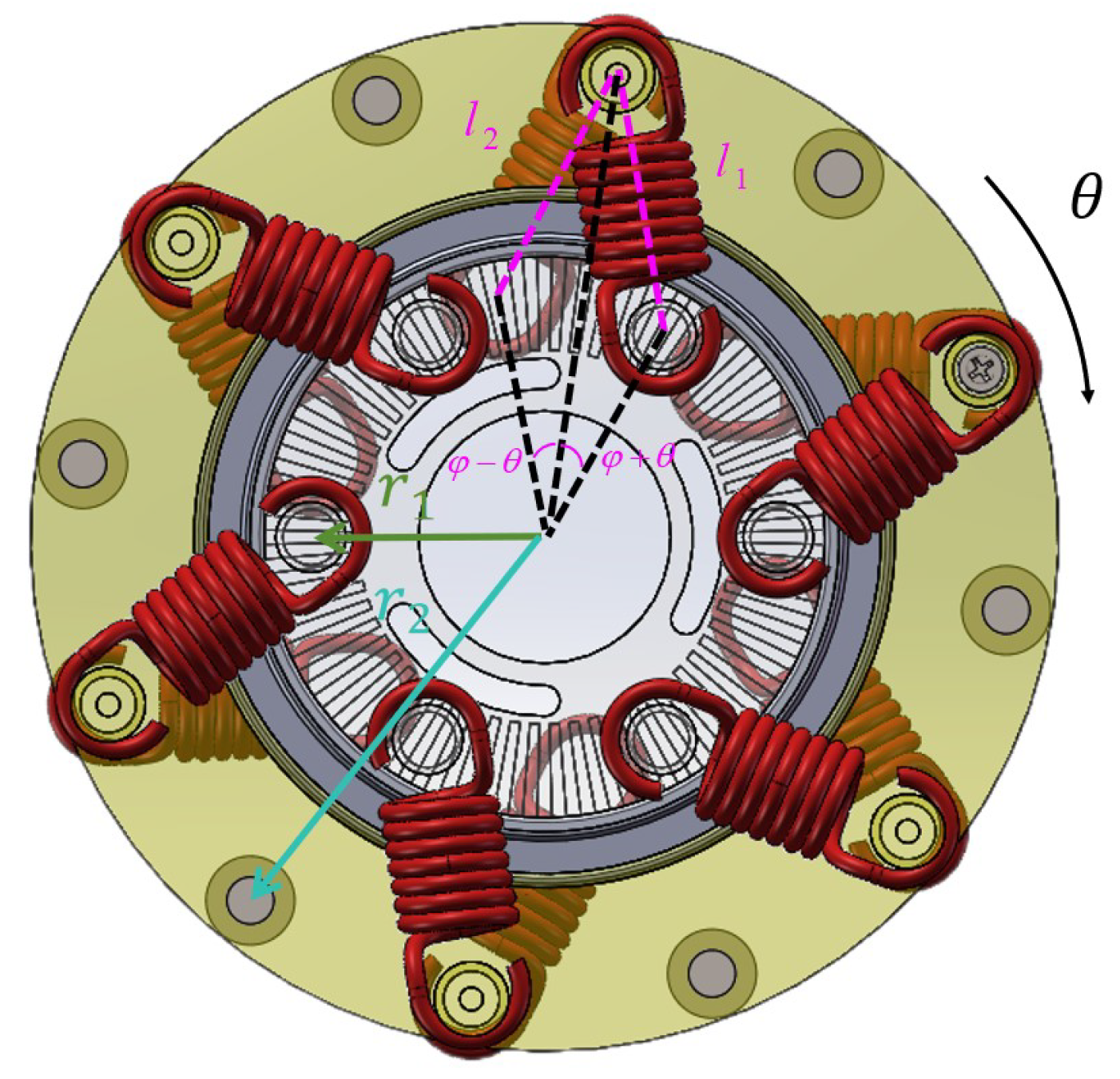
2.1. Design of Series Elastic Actuator
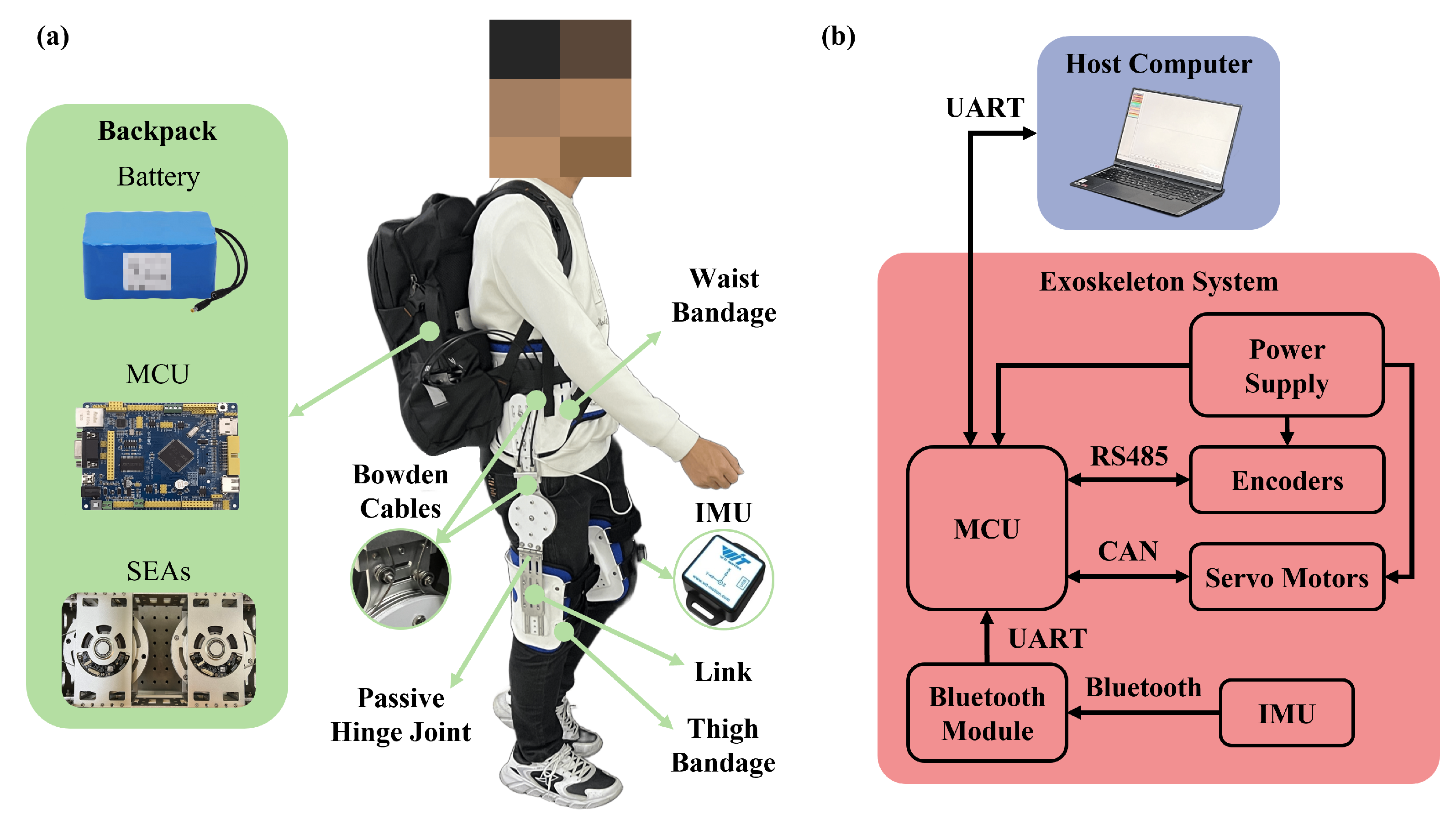
2.2. Exoskeleton System Design
2.3. Electronics and Control Implementation
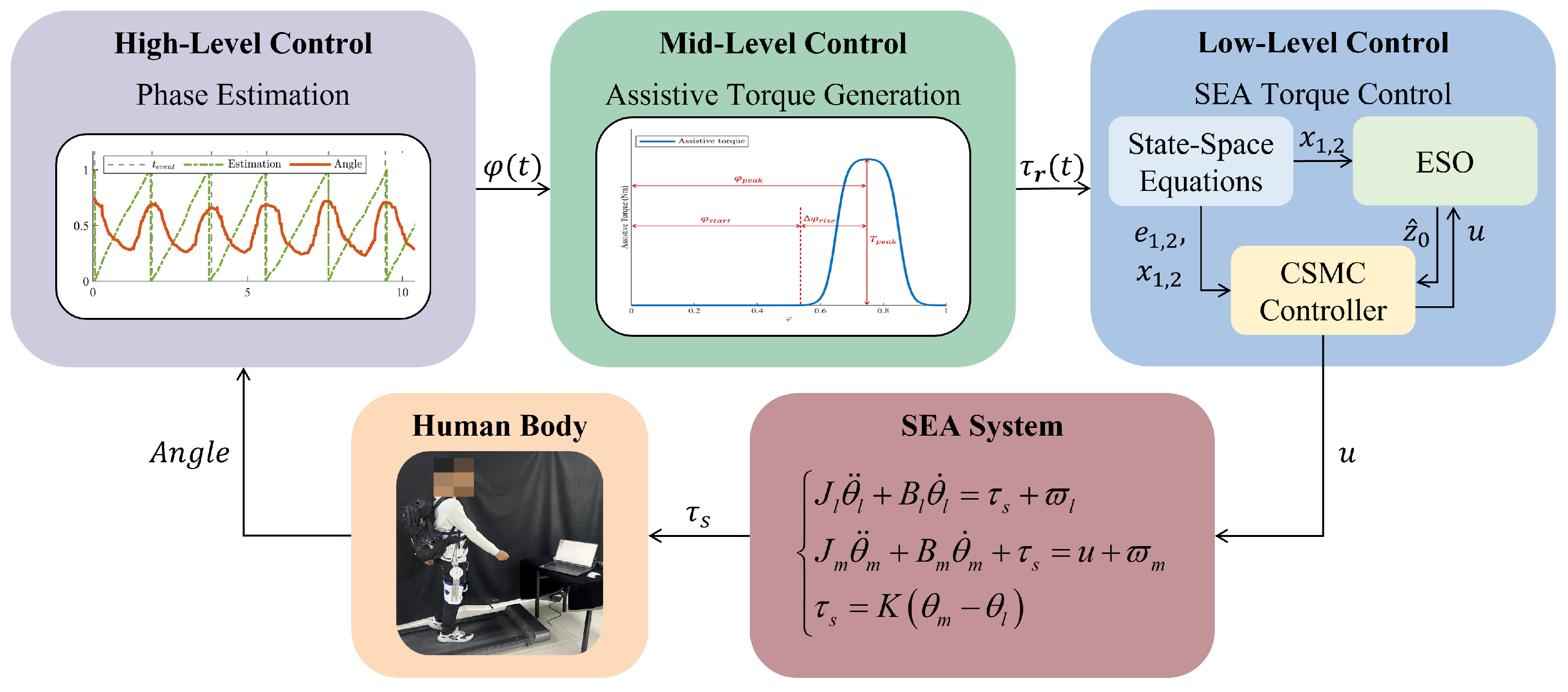
3. Control Strategy
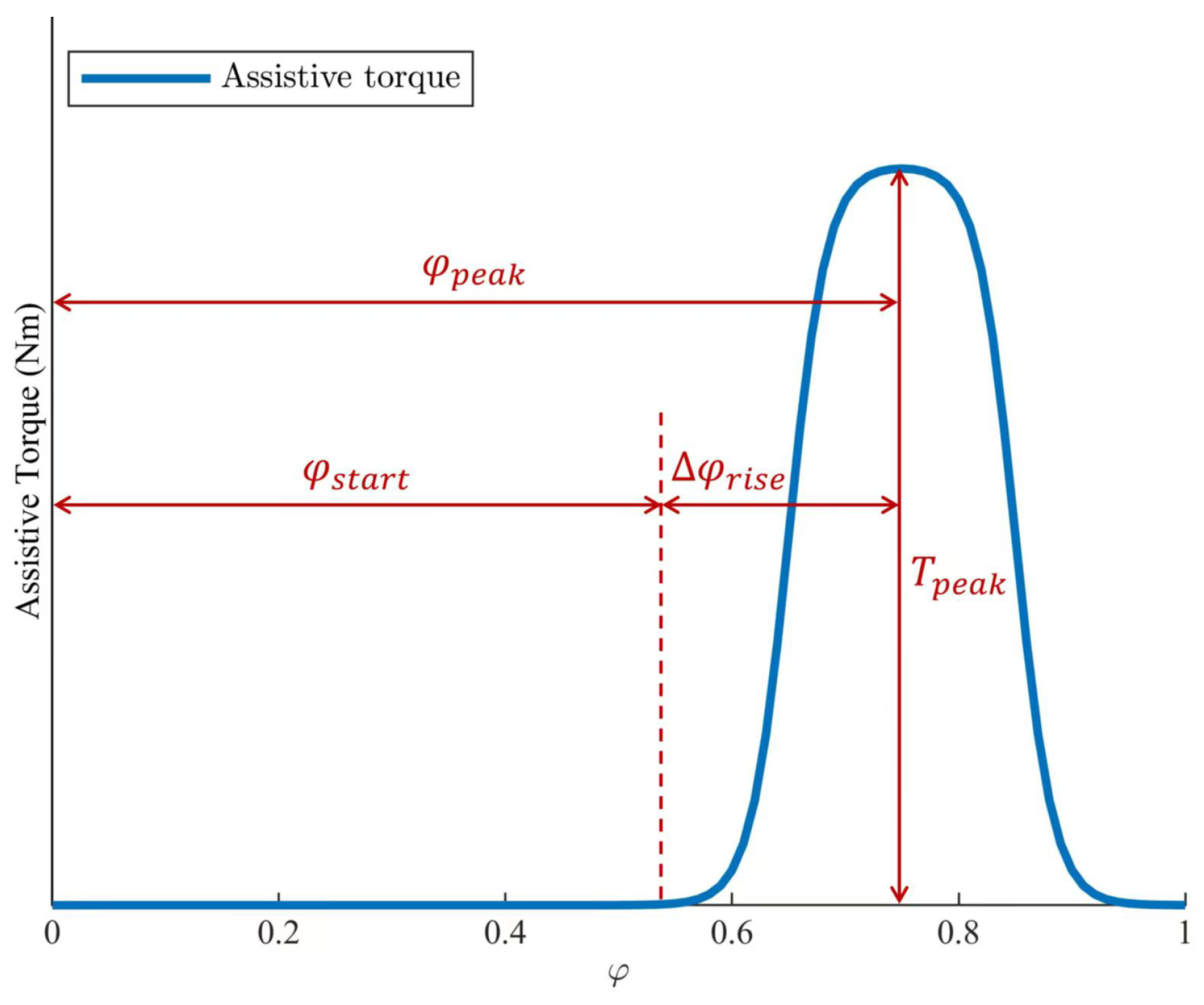
3.1. High-Level Control
3.2. Mid-Level Control
3.3. Low-Level Control
3.3.1. SEA Drive
3.3.2. Extended State Observer
3.3.3. Continuous Sliding-Mode Control
4. Simulation Verification
4.1. Simulation Setup
4.2. Controllers for Comparison
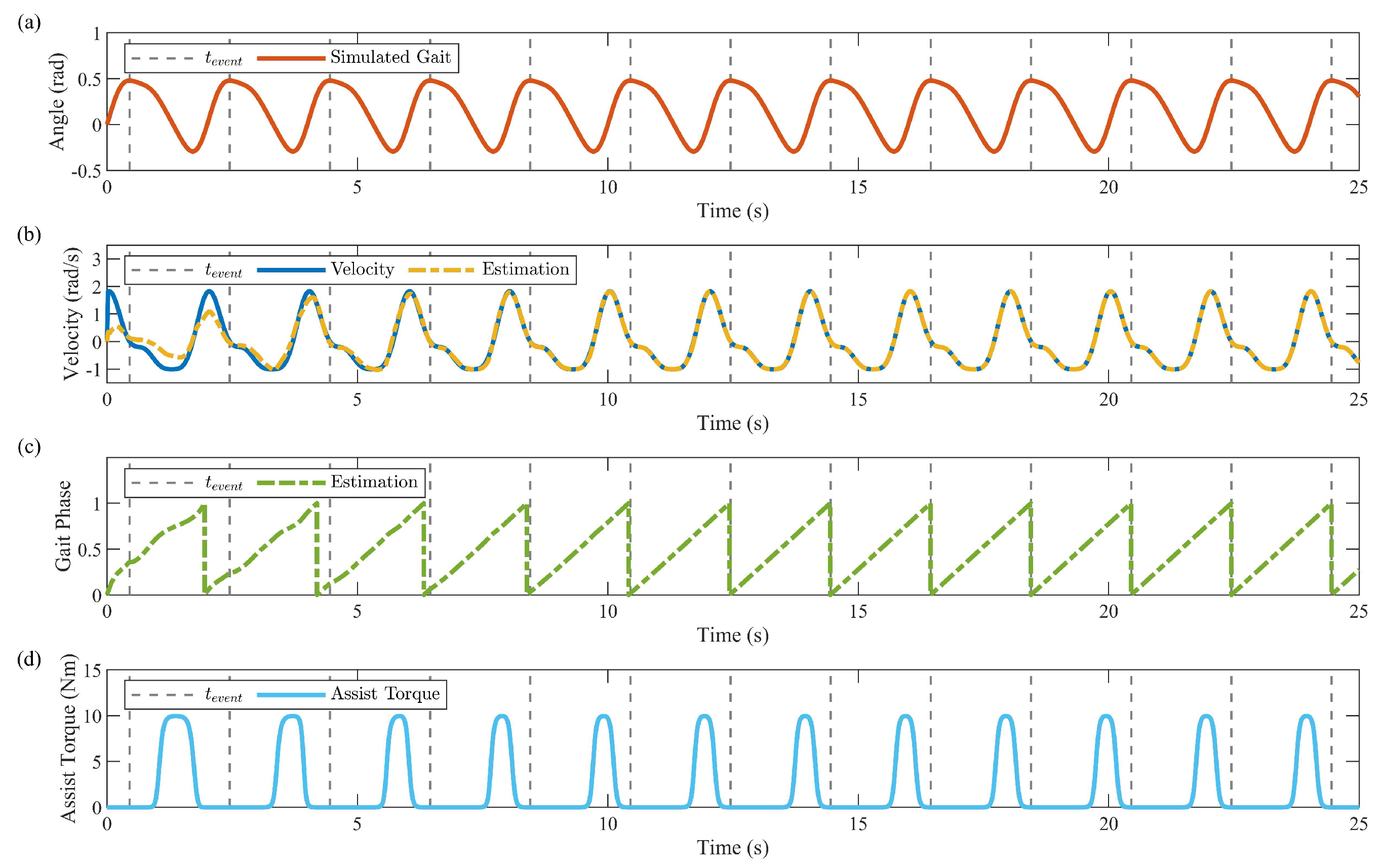
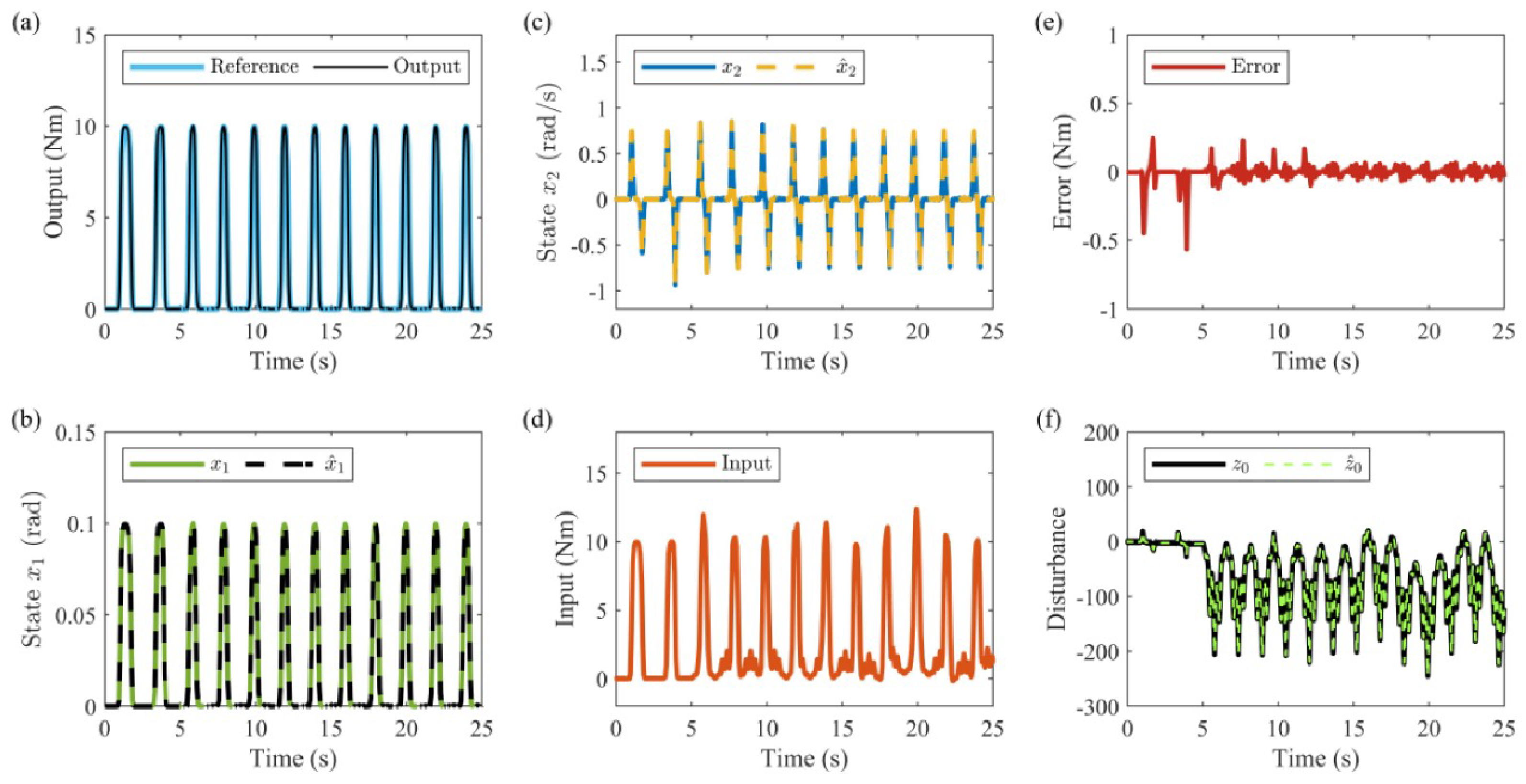
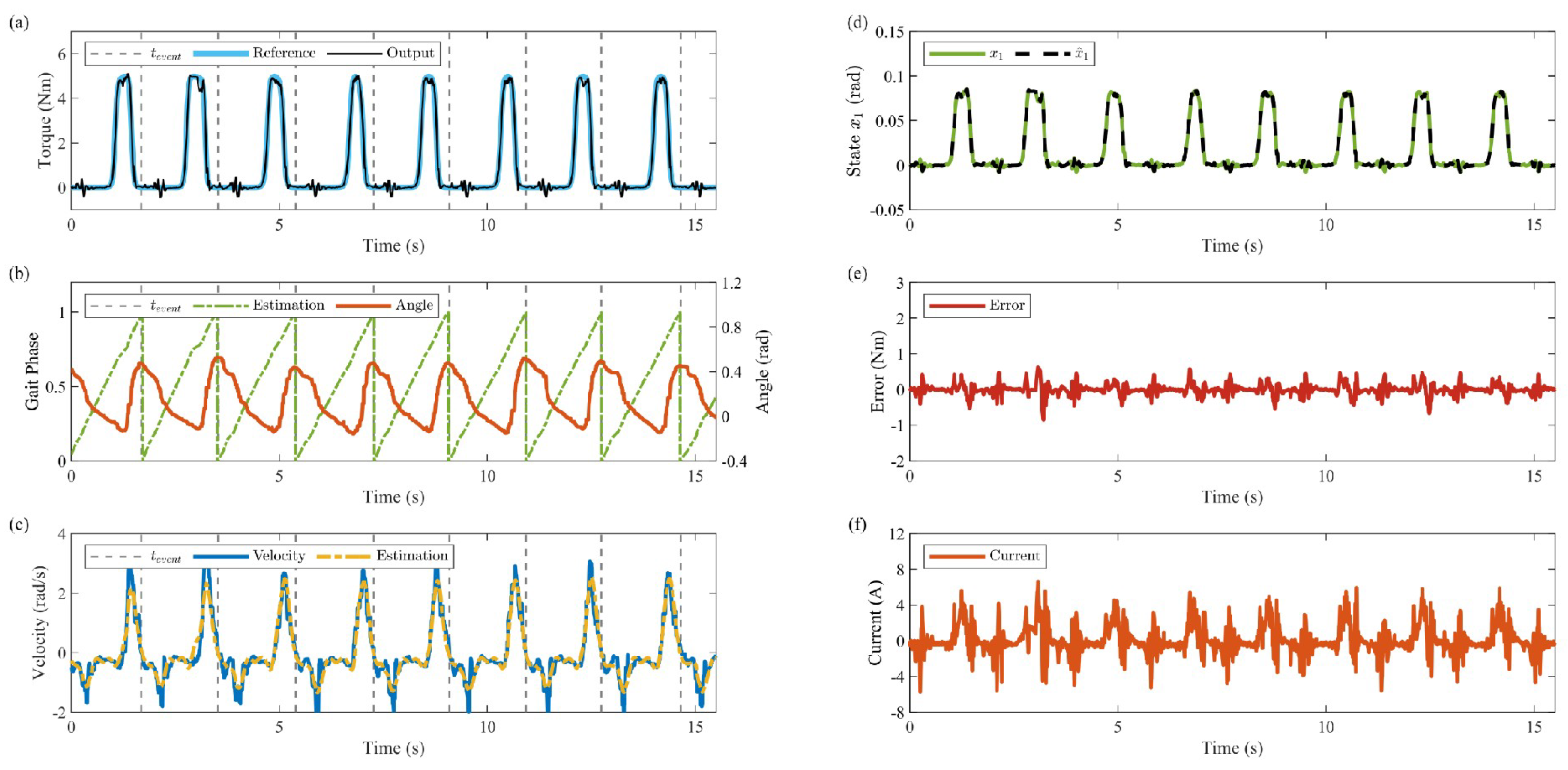
4.3. Results and Analysis
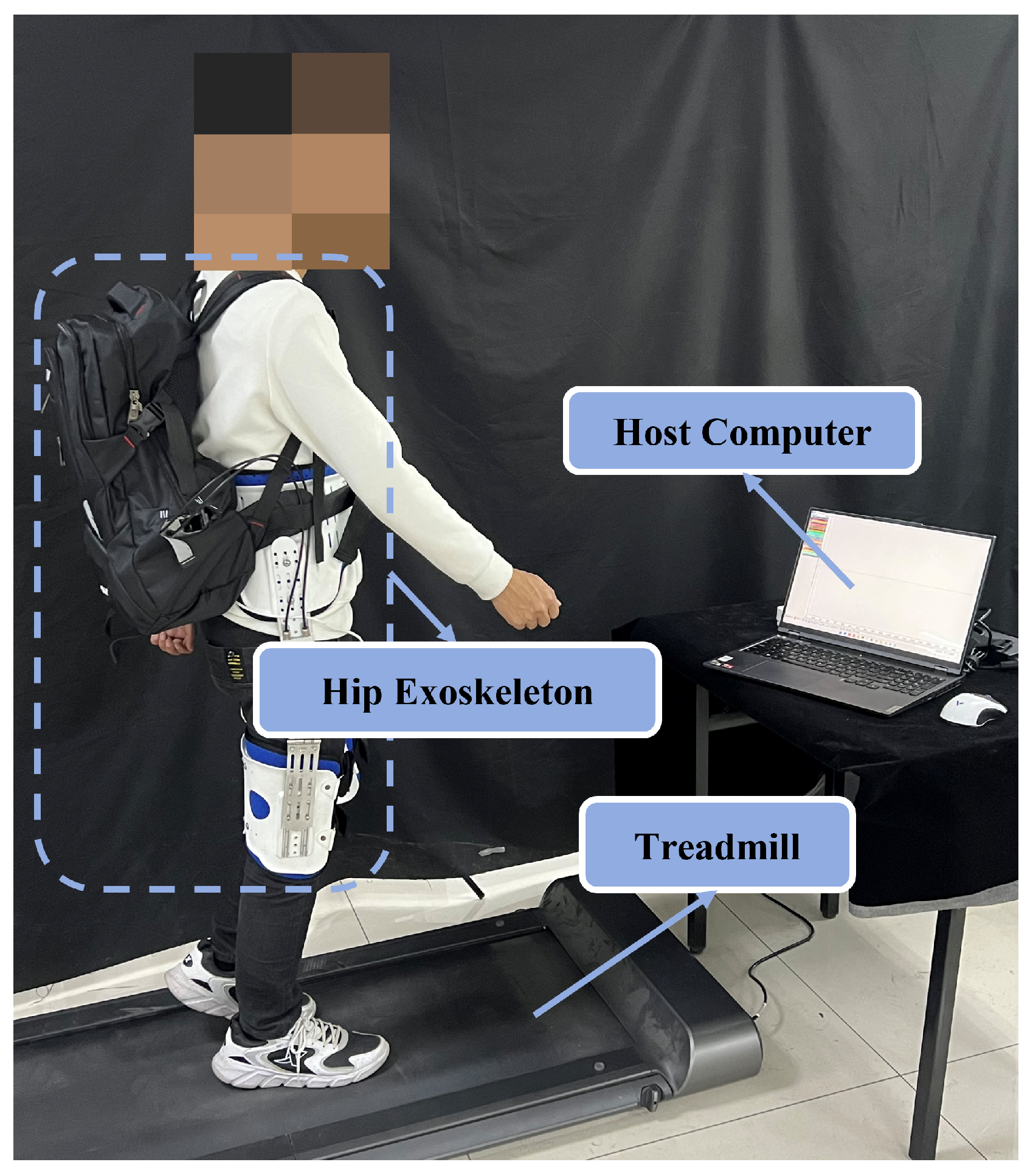
4.4. Experimental Protocol
5. Preliminary Human Subject Experiments
5.1. Controllers for Comparison
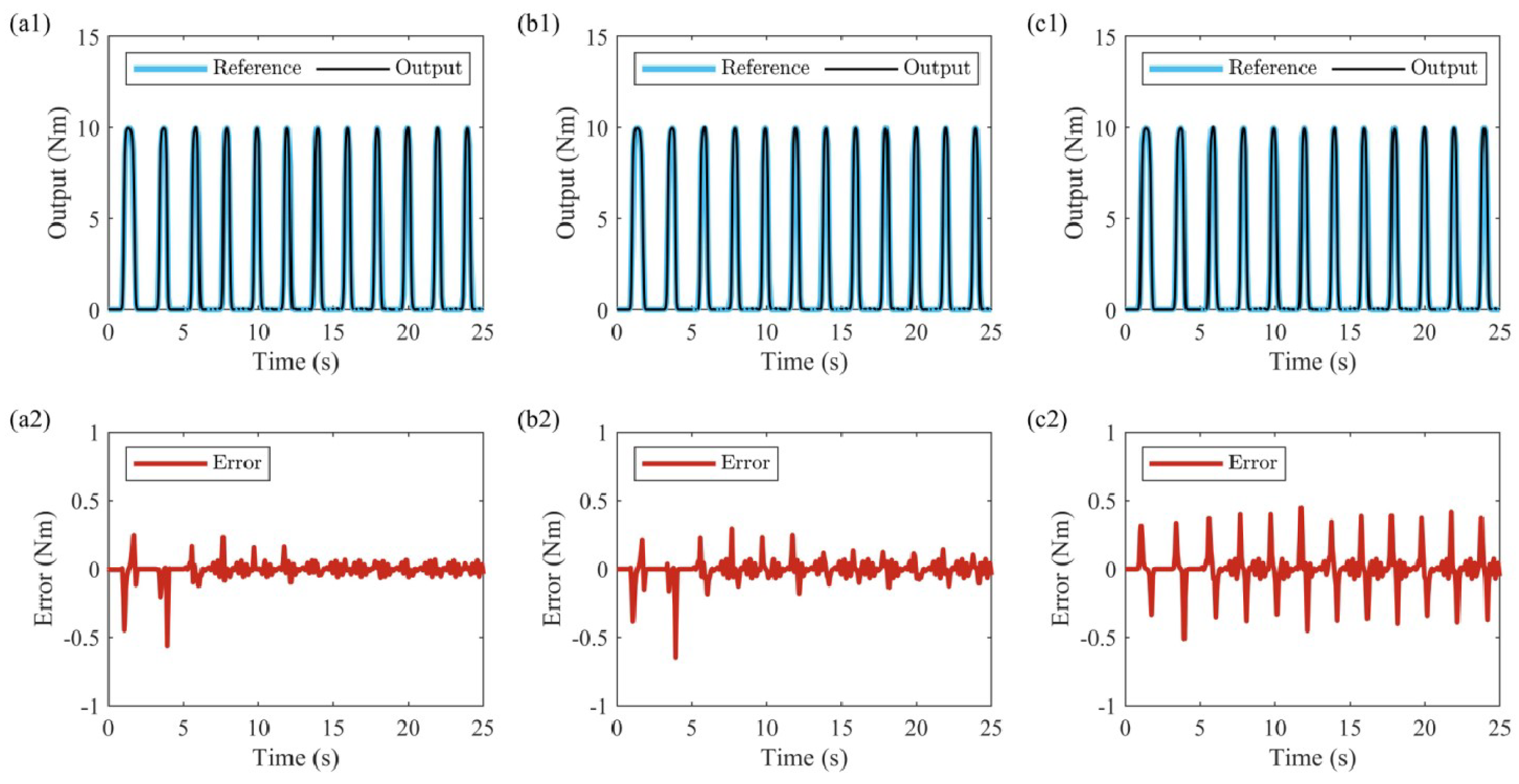
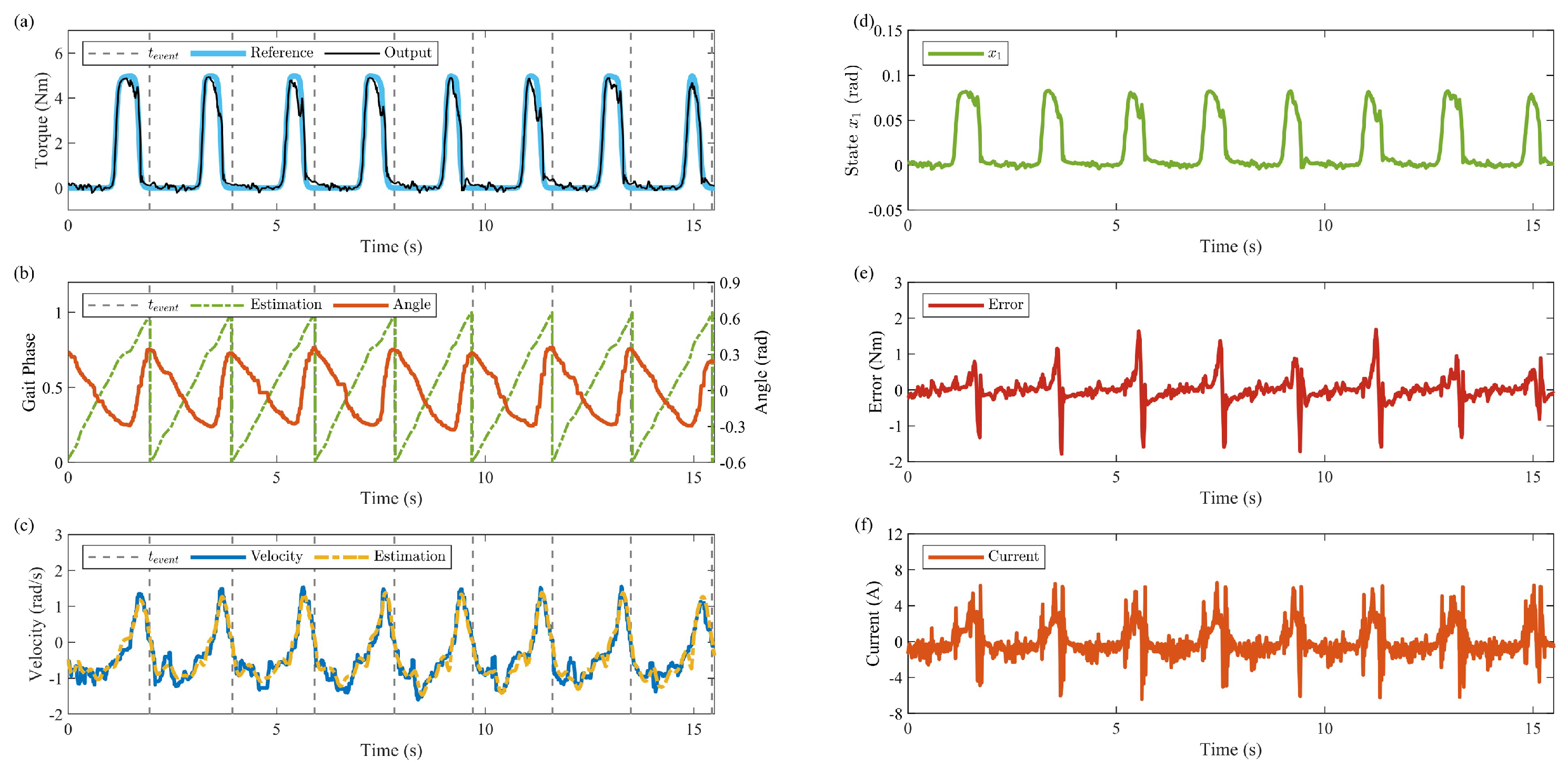
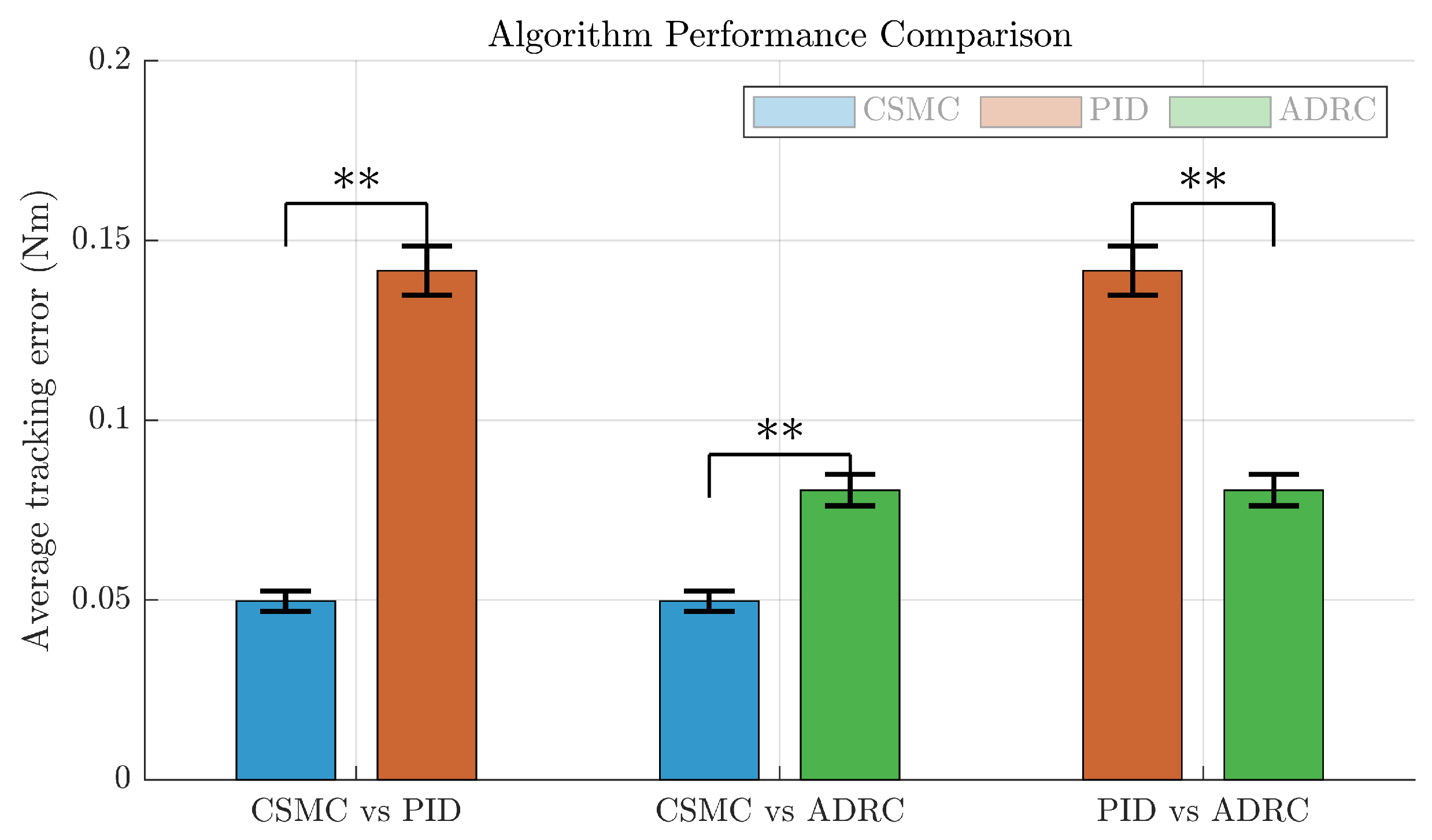
5.2. Results and Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sheng, J.; Ding, R.; Yang, H. Corporate green innovation in an aging population: Evidence from Chinese listed companies. Technol. Forecast. Soc. Chang. 2024, 202, 123307. [Google Scholar] [CrossRef]
- Krahn, G.L. WHO World Report on Disability: A review. Disabil. Health J. 2011, 4, 141–142. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. The Global Burden of Disease: 2004 Update; World Health Organization: Geneva, Switzerland, 2008; Volume 14. [Google Scholar]
- Sun, D.; Ma, J.; Ding, Y.; Luo, D. Human-exoskeleton oscillation model and qualitative analysis of interaction and functional practicality of exoskeletons. Appl. Math. Model. 2023, 120, 40–56. [Google Scholar] [CrossRef]
- Ding, T.J.; Kang, C.C.; Han, W.; Ariannejad, M.; Kang, L.Y.; Ren, C.K. Development trend of robotic exoskeletons. In Proceedings of the 2023 IEEE International Conference on Cybernetics and Intelligent Systems (CIS) and IEEE Conference on Robotics, Automation and Mechatronics (RAM), Penang, Malaysia, 9–12 June 2023; pp. 114–121. [Google Scholar]
- Qiu, S.; Pei, Z.; Wang, C.; Tang, Z. Systematic review on wearable lower extremity robotic exoskeletons for assisted locomotion. J. Bionic Eng. 2023, 20, 436–469. [Google Scholar] [CrossRef]
- Hasan, S.K.; Dhingra, A.K. State of the art technologies for exoskeleton human lower extremity rehabilitation robots. J. Mechatron. Robot. 2020, 4, 211–235. [Google Scholar] [CrossRef]
- Shin, Y.J.; Kim, G.T.; Kim, Y. Optimal design of multi-linked knee joint for lower limb wearable robot. Int. J. Precis. Eng. Manuf. 2023, 24, 967–976. [Google Scholar] [CrossRef]
- Qian, Y.; Han, S.; Wang, Y.; Yu, H.; Fu, C. Toward improving actuation transparency and safety of a hip exoskeleton with a novel nonlinear series elastic actuator. IEEE/ASME Trans. Mechatron. 2022, 28, 417–428. [Google Scholar] [CrossRef]
- Lee, Y.; Kim, Y.J.; Lee, J.; Lee, M.; Choi, B.; Kim, J.; Park, Y.J.; Choi, J. Biomechanical design of a novel flexible exoskeleton for lower extremities. IEEE/ASME Trans. Mechatron. 2017, 22, 2058–2069. [Google Scholar] [CrossRef]
- Zhou, L.; Chen, W.; Wang, J.; Bai, S.; Yu, H.; Zhang, Y. A novel precision measuring parallel mechanism for the closed-loop control of a biologically inspired lower limb exoskeleton. IEEE/ASME Trans. Mechatron. 2018, 23, 2693–2703. [Google Scholar] [CrossRef]
- Xi, R.; Zhu, Z.; Du, F.; Yang, M.; Wang, X.; Wu, Q. Design concept of the quasi-passive energy-efficient power-assisted lower-limb exoskeleton based on the theory of passive dynamic walking. In Proceedings of the 2016 23rd International Conference on Mechatronics and Machine Vision in Practice (M2VIP), Nanjing, China, 28–30 November 2016; pp. 1–5. [Google Scholar]
- Gams, A.; Petrič, T.; Debevec, T.; Babič, J. Effects of robotic knee exoskeleton on human energy expenditure. IEEE Trans. Biomed. Eng. 2013, 60, 1636–1644. [Google Scholar] [CrossRef]
- Arazpour, M.; Chitsazan, A.; Bani, M.A.; Rouhi, G.; Ghomshe, F.T.; Hutchins, S.W. The effect of a knee ankle foot orthosis incorporating an active knee mechanism on gait of a person with poliomyelitis. Prosthet. Orthot. Int. 2013, 37, 411–414. [Google Scholar] [CrossRef] [PubMed]
- Jin, X.; Cui, X.; Agrawal, S.K. Design of a cable-driven active leg exoskeleton (C-ALEX) and gait training experiments with human subjects. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 5578–5583. [Google Scholar]
- Ortiz, J.; Di Natali, C.; Caldwell, D.G. XoSoft-iterative design of a modular soft lower limb exoskeleton. In Proceedings of the International Symposium on Wearable Robotics, Pisa, Italy, 16–20 October 2018; Springer: Cham, Switzerland, 2018; pp. 351–355. [Google Scholar]
- Dingan, S.; Hua, J.; Lia, Y. Research on Assisting Control and Oxygen Metabolism Testing of Rope Driven Flexible Exoskeleton. Mater. Sci. Eng. Appl. 2023, 40, 517–525. [Google Scholar]
- Xu, D.; Liu, X.; Wang, Q. Knee exoskeleton assistive torque control based on real-time gait event detection. IEEE Trans. Med Robot. Bionics 2019, 1, 158–168. [Google Scholar] [CrossRef]
- Li, C.; He, Y.; Chen, T.; Chen, X.; Tian, S. Real-time gait event detection for a lower extremity exoskeleton robot by infrared distance sensors. IEEE Sens. J. 2021, 21, 27116–27123. [Google Scholar] [CrossRef]
- Huang, B.; Chen, M.; Shi, X.; Xu, Y. Gait event detection with intelligent shoes. In Proceedings of the 2007 International Conference on Information Acquisition, Seogwipo, Republic of Korea, 8–11 July 2007; pp. 579–584. [Google Scholar]
- Zhang, J.; Fiers, P.; Witte, K.A.; Jackson, R.W.; Poggensee, K.L.; Atkeson, C.G.; Collins, S.H. Human-in-the-loop optimization of exoskeleton assistance during walking. Science 2017, 356, 1280–1284. [Google Scholar] [CrossRef]
- Wen, Y.; Si, J.; Brandt, A.; Gao, X.; Huang, H.H. Online reinforcement learning control for the personalization of a robotic knee prosthesis. IEEE Trans. Cybern. 2019, 50, 2346–2356. [Google Scholar] [CrossRef]
- Li, M.; Wen, Y.; Gao, X.; Si, J.; Huang, H. Toward expedited impedance tuning of a robotic prosthesis for personalized gait assistance by reinforcement learning control. IEEE Trans. Robot. 2021, 38, 407–420. [Google Scholar] [CrossRef]
- Yang, X.; Fu, Z.; Yi, S.; Qi, B.; Guo, Z. Adaptive Oscillator-Based Gait Event Detection and Trajectory Planning for Lower Limb Exoskeleton. In Proceedings of the 2024 World Rehabilitation Robot Convention (WRRC), Shanghai, China, 23–26 August 2024; pp. 1–6. [Google Scholar]
- Xue, T.; Wang, Z.; Zhang, T.; Zhang, M. Adaptive oscillator-based robust control for flexible hip assistive exoskeleton. IEEE Robot. Autom. Lett. 2019, 4, 3318–3323. [Google Scholar] [CrossRef]
- Qian, Y.; Yu, H.; Fu, C. Adaptive oscillator-based assistive torque control for gait asymmetry correction with a nSEA-driven hip exoskeleton. IEEE Trans. Neural Syst. Rehabil. Eng. 2022, 30, 2906–2915. [Google Scholar] [CrossRef]
- Zhang, T.; Li, Y.; Ning, C.; Zeng, B. Development and adaptive assistance control of the robotic hip exoskeleton to improve gait symmetry and restore normal gait. IEEE Trans. Autom. Sci. Eng. 2022, 21, 799–809. [Google Scholar] [CrossRef]
- Suzuki, K.; Mito, G.; Kawamoto, H.; Hasegawa, Y.; Sankai, Y. Intention-based walking support for paraplegia patients with Robot Suit HAL. Adv. Robot. 2007, 21, 1441–1469. [Google Scholar] [CrossRef]
- Farris, R.J.; Quintero, H.A.; Goldfarb, M. Preliminary evaluation of a powered lower limb orthosis to aid walking in paraplegic individuals. IEEE Trans. Neural Syst. Rehabil. Eng. 2011, 19, 652–659. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Cao, G.; Li, L.; Diao, D. AEKF-based trajectory-error compensation of knee exoskeleton for human–exoskeleton interaction control. Robot. Intell. Autom. 2024, 44, 84–95. [Google Scholar] [CrossRef]
- Chen, Y.; Liang, L.; Wu, M.; Wang, Y.; Liu, C. Experimental verification study on trajectory tracking of a novel rehabilitation exoskeleton shoulder joint. J. Mech. Med. Biol. 2019, 19, 1940037. [Google Scholar] [CrossRef]
- Khan, R.F.A.; Rsetam, K.; Cao, Z.; Man, Z. Singular perturbation-based adaptive integral sliding mode control for flexible joint robots. IEEE Trans. Ind. Electron. 2022, 70, 10516–10525. [Google Scholar] [CrossRef]
- Pan, Y.; Li, X.; Wang, H.; Yu, H. Continuous sliding mode control of compliant robot arms: A singularly perturbed approach. Mechatronics 2018, 52, 127–134. [Google Scholar] [CrossRef]
- Korayem, M.; Nekoo, S.R.; Kazemi, S. Finite-time feedback linearization (FTFL) controller considering optimal gains on mobile mechanical manipulators. J. Intell. Robot. Syst. 2019, 94, 727–744. [Google Scholar] [CrossRef]
- Abdul-Adheem, W.R.; Ibraheem, I.K.; Humaidi, A.J.; Azar, A.T. Model-free active input–output feedback linearization of a single-link flexible joint manipulator: An improved active disturbance rejection control approach. Meas. Control 2021, 54, 856–871. [Google Scholar] [CrossRef]
- Cheng, X.; Zhang, Y.; Liu, H.; Wollherr, D.; Buss, M. Adaptive neural backstepping control for flexible-joint robot manipulator with bounded torque inputs. Neurocomputing 2021, 458, 70–86. [Google Scholar] [CrossRef]
- Chang, W.; Li, Y.; Tong, S. Adaptive fuzzy backstepping tracking control for flexible robotic manipulator. IEEE/CAA J. Autom. Sin. 2018, 8, 1923–1930. [Google Scholar] [CrossRef]
- Gao, H.; He, W.; Zhou, C.; Sun, C. Neural network control of a two-link flexible robotic manipulator using assumed mode method. IEEE Trans. Ind. Inform. 2018, 15, 755–765. [Google Scholar] [CrossRef]
- Diao, S.; Sun, W.; Su, S.F.; Zhao, X.; Xu, N. Novel adaptive control for flexible-joint robots with unknown measurement sensitivity. IEEE Trans. Autom. Sci. Eng. 2023, 21, 1445–1456. [Google Scholar] [CrossRef]
- Tafrishi, S.A.; Hirata, Y. SPIRO: A Compliant Spiral Spring–Damper Joint Actuator With Energy-Based Sliding-Mode Controller. IEEE/ASME Trans. Mechatron. 2024, 29, 947–959. [Google Scholar] [CrossRef]
- Suryawanshi, P.V.; Shendge, P.D.; Phadke, S.B. A boundary layer sliding mode control design for chatter reduction using uncertainty and disturbance estimator. Int. J. Dyn. Control 2016, 4, 456–465. [Google Scholar] [CrossRef]
- Lu, B.; Fang, Y.; Sun, N. Continuous sliding mode control strategy for a class of nonlinear underactuated systems. IEEE Trans. Autom. Control 2018, 63, 3471–3478. [Google Scholar] [CrossRef]
- Ginoya, D.; Shendge, P.; Phadke, S. Sliding mode control for mismatched uncertain systems using an extended disturbance observer. IEEE Trans. Ind. Electron. 2013, 61, 1983–1992. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, Z.; Tang, X.; Zhao, Z.; Yan, Y. Continuous output feedback sliding mode control for underactuated flexible-joint robot. J. Frankl. Inst. 2022, 359, 7847–7865. [Google Scholar] [CrossRef]
- Zaare, S.; Soltanpour, M.R. Continuous fuzzy nonsingular terminal sliding mode control of flexible joints robot manipulators based on nonlinear finite time observer in the presence of matched and mismatched uncertainties. J. Frankl. Inst. 2020, 357, 6539–6570. [Google Scholar] [CrossRef]
- Qian, Y.; Wang, Y.; Chen, C.; Xiong, J.; Leng, Y.; Yu, H.; Fu, C. Predictive locomotion mode recognition and accurate gait phase estimation for hip exoskeleton on various terrains. IEEE Robot. Autom. Lett. 2022, 7, 6439–6446. [Google Scholar] [CrossRef]
- Qian, Y.; Chen, C.; Xiong, J.; Wang, Y.; Leng, Y.; Yu, H.; Fu, C. Terrain-Adaptive Exoskeleton Control With Predictive Gait Mode Recognition: A Pilot Study During Level Walking and Stair Ascent. IEEE Trans. Med. Robot. Bionics 2024, 6, 281–291. [Google Scholar] [CrossRef]
- Chen, C.; Du, Z.; Zhang, H.; Dong, W. Double-mode switching control of a lower limb exoskeleton based on flexible drive joint. Jiqiren/Robot 2021, 43, 513–525. [Google Scholar]


| Control Strategy | ATE | SDE | MAE |
|---|---|---|---|
| 0.0268 | 0.0484 | 0.5642 | |
| 0.0357 | 0.0544 | 0.6461 | |
| 0.0604 | 0.0953 | 0.5115 |
| Control Strategy | ATE | SDE | MAE |
|---|---|---|---|
| 0.0501 | 0.0553 | 0.4735 | |
| 0.0956 | 0.1228 | 0.8468 | |
| 0.1502 | 0.2860 | 0.9496 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, R.; Lin, X.; Yin, C.; Liu, Z.; Zhang, Y.; Liu, W.; Du, F. Robust Continuous Sliding-Mode-Based Assistive Torque Control for Series Elastic Actuator-Driven Hip Exoskeleton. Actuators 2025, 14, 239. https://doi.org/10.3390/act14050239
Wang R, Lin X, Yin C, Liu Z, Zhang Y, Liu W, Du F. Robust Continuous Sliding-Mode-Based Assistive Torque Control for Series Elastic Actuator-Driven Hip Exoskeleton. Actuators. 2025; 14(5):239. https://doi.org/10.3390/act14050239
Chicago/Turabian StyleWang, Rui, Xiaoou Lin, Changwei Yin, Zhongtao Liu, Yang Zhang, Wenping Liu, and Fuxin Du. 2025. "Robust Continuous Sliding-Mode-Based Assistive Torque Control for Series Elastic Actuator-Driven Hip Exoskeleton" Actuators 14, no. 5: 239. https://doi.org/10.3390/act14050239
APA StyleWang, R., Lin, X., Yin, C., Liu, Z., Zhang, Y., Liu, W., & Du, F. (2025). Robust Continuous Sliding-Mode-Based Assistive Torque Control for Series Elastic Actuator-Driven Hip Exoskeleton. Actuators, 14(5), 239. https://doi.org/10.3390/act14050239






