Composite Adaptive Control of Robot Manipulators with Friction as Additive Disturbance
Abstract
1. Introduction
Contributions
- A decomposition of the robot manipulator model into an adequate linear parametrization for the conservative part and another for the non-conservative part is presented.
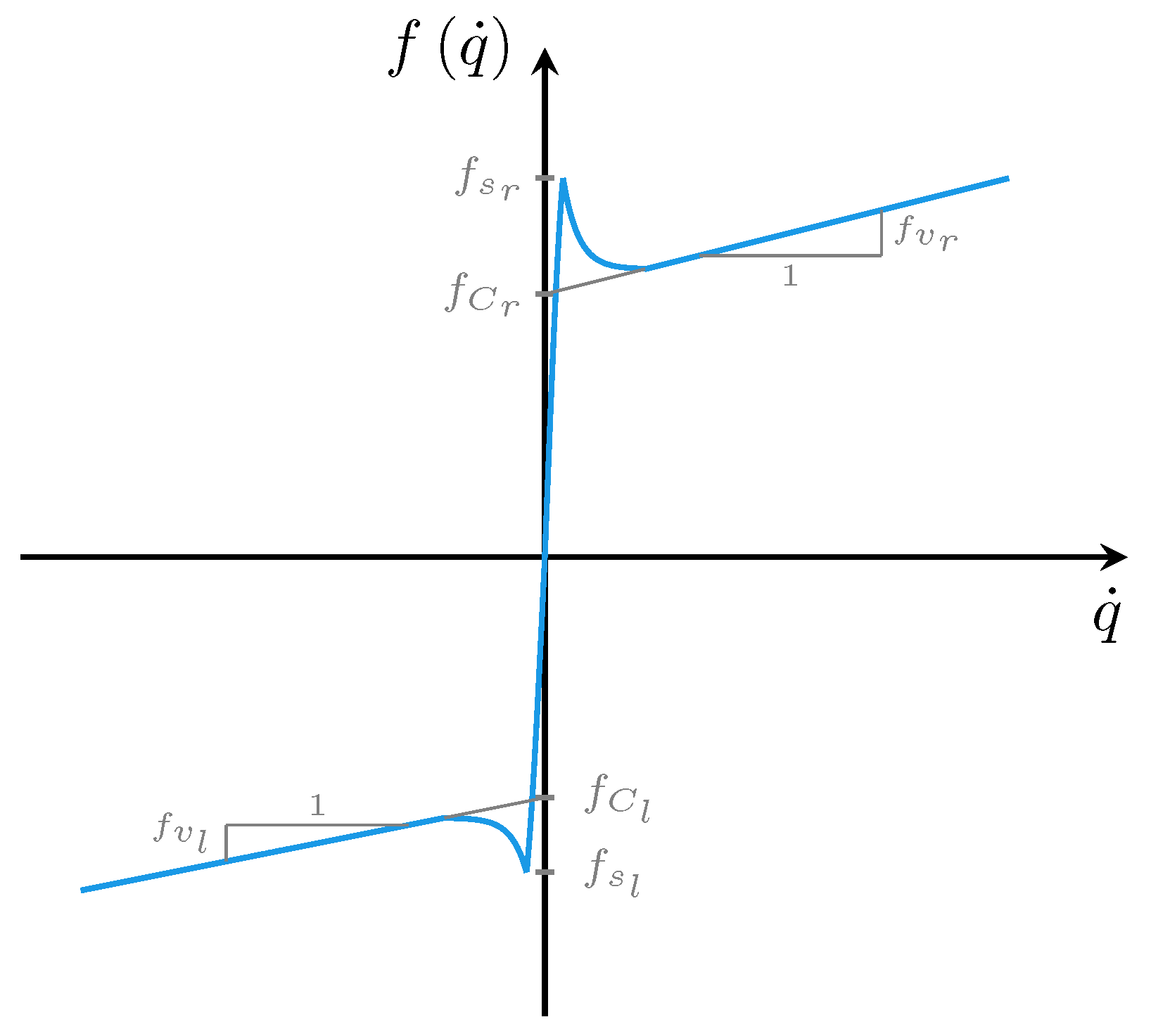
- The friction phenomenon is characterized as two independent additive disturbances that can be linearly parametrized in terms of the physical coefficients of friction with a quiet simple regression matrix.
- A separation into three simpler regression matrices is performed, which allows us to deal with them one by one and to find the upper and lower bounds that satisfy the persistent excitation condition for each of them.
- A relaxation in the persistent excitation condition is made for the overall regression matrix that arises when the well-known swapping technique is applied. Both concepts are presented in detail in Section 3.3.
- Lyapunov analysis is developed to support the fact that the robust control methodology in the designing stage of the controller is compensating for the disturbances while guaranteeing that the tracking position and velocity errors converge asymptotically to zero.
- An effective practical compensation for friction, not involving a cumbersome dynamic model of friction and staying as simple as possible in stability analysis within a passivity framework, is presented, performing the tracking of the desired trajectories in joint space successfully.
2. Problem Formulation
2.1. Robot Manipulator Model
2.2. Properties of the Dynamic Model
2.3. Control Objective and Identification Objective
2.4. Motivation of the Proposed Scheme
- It makes the control objective straightforward to conclude since the variable conveys enough information of and in order to show that its boundedness and convergence to zero imply those of and .
- It removes the computational complexity from the computed torque as the inverse inertia matrix does not have to be determined.
- Since it is a robust control method, and since the two major components of friction are considered as disturbances, it rejects the small changes in the disturbances, i.e., the transition between static and dynamic regimes.
3. Preliminaries
3.1. Lyapunov Stability
- Its partial derivatives are continuous.
- Its total time derivative along the trajectories of (8) satisfies .
3.2. Case of Study
3.3. Identification Algorithm
4. Controller Design
4.1. Control Law and Composite Update Law by Lyapunov Stability Analysis
4.2. Composite Adaptation
5. Additive Disturbances and Lyapunov Stability
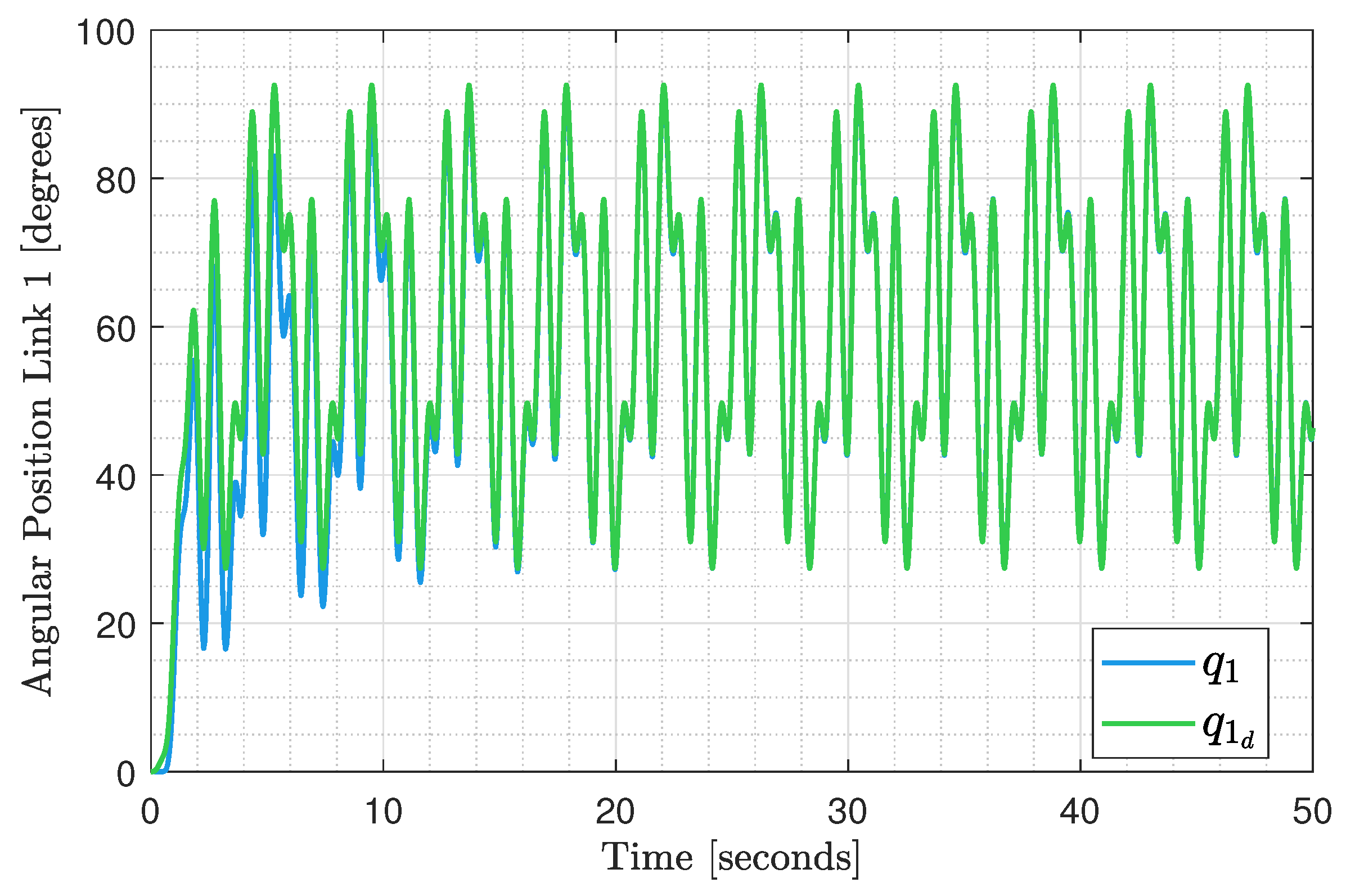
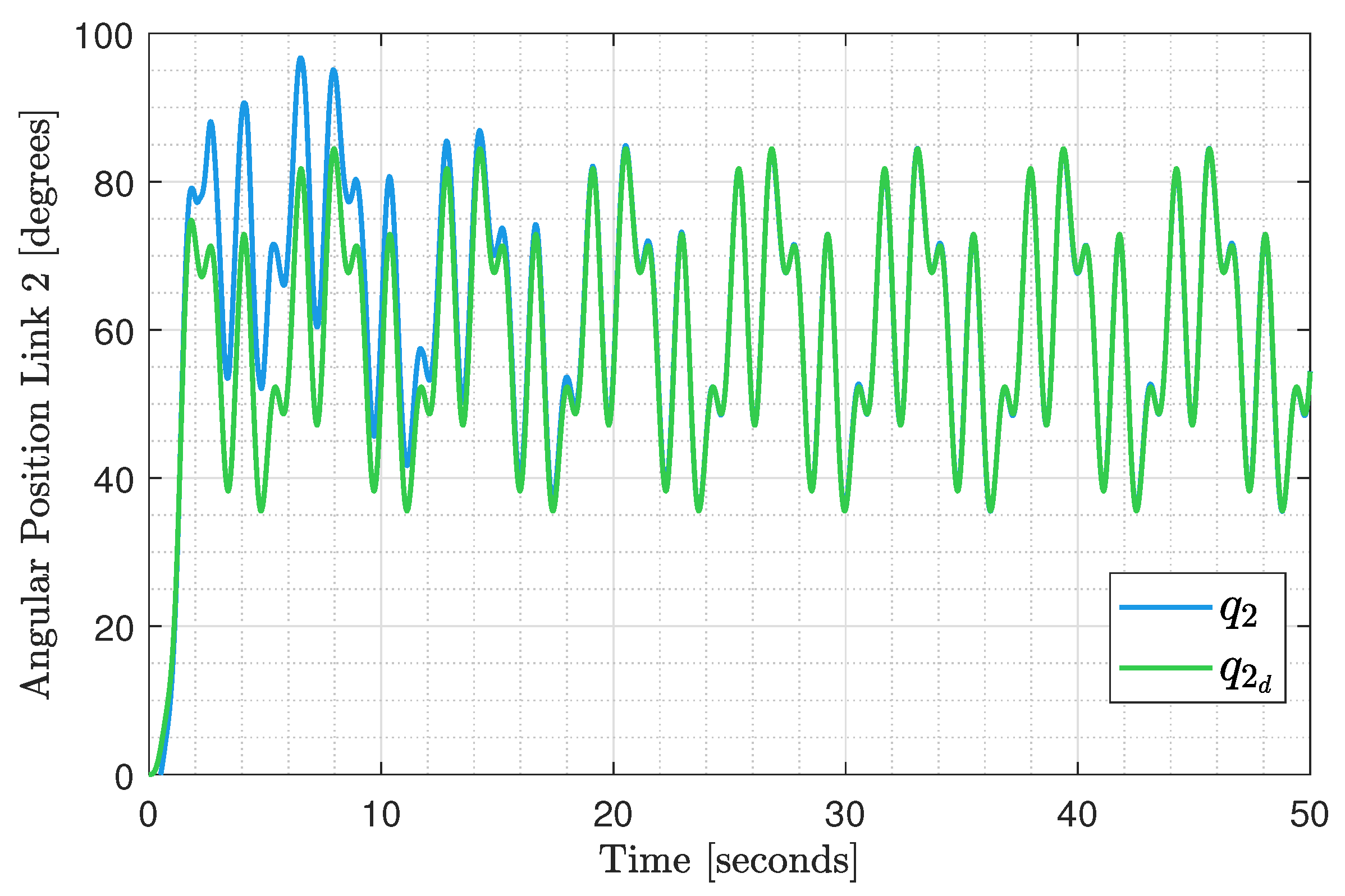
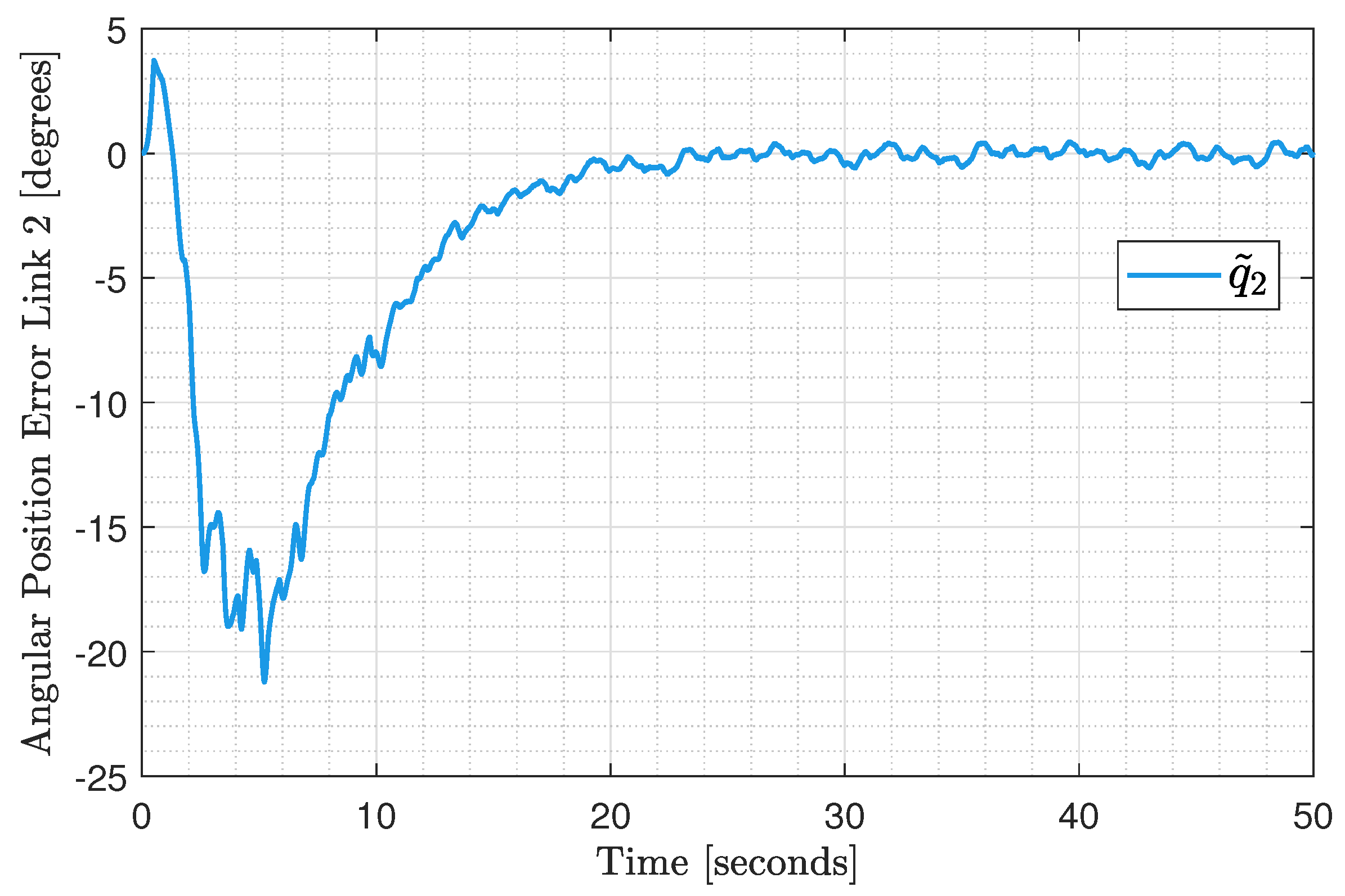
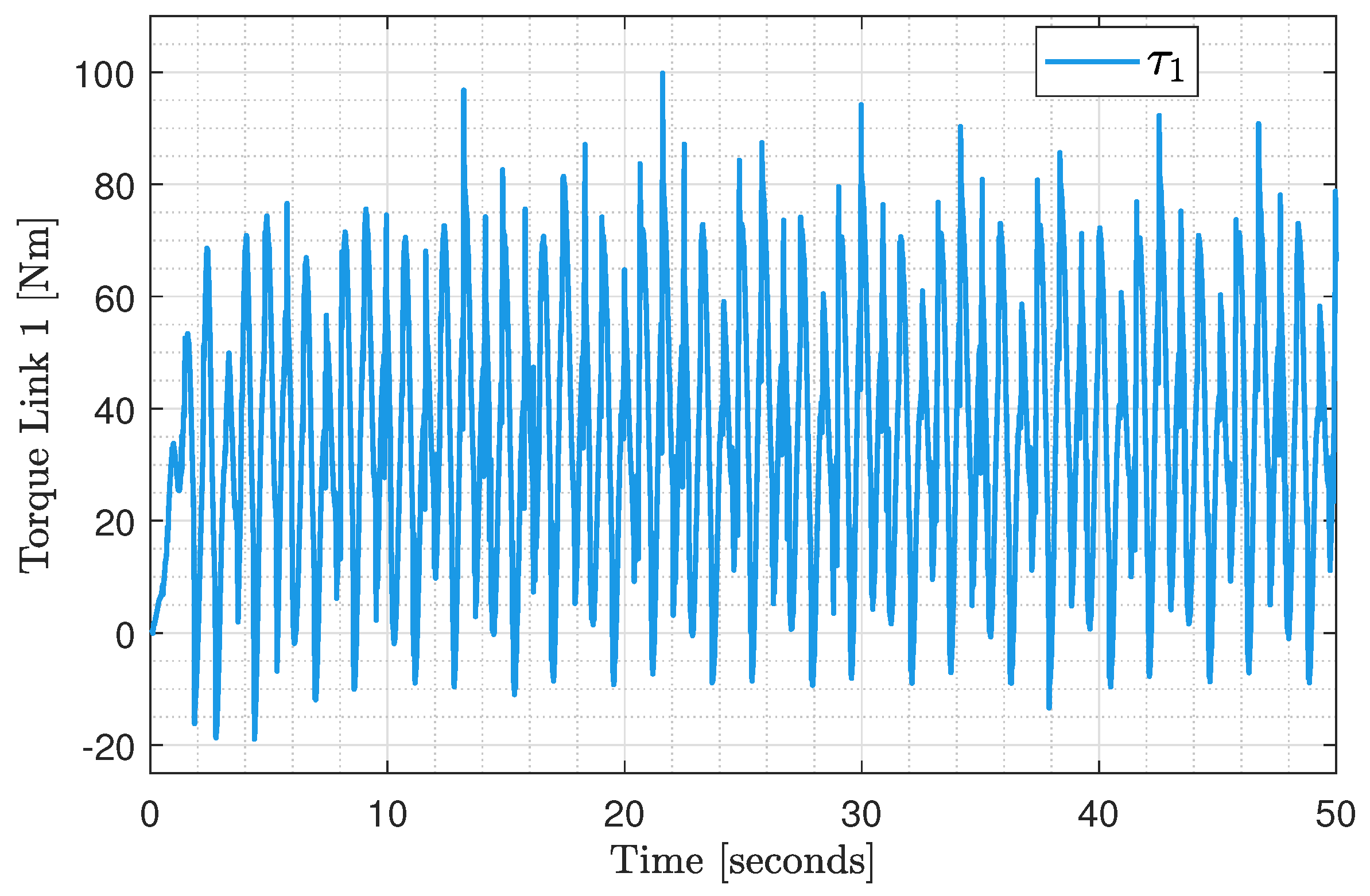
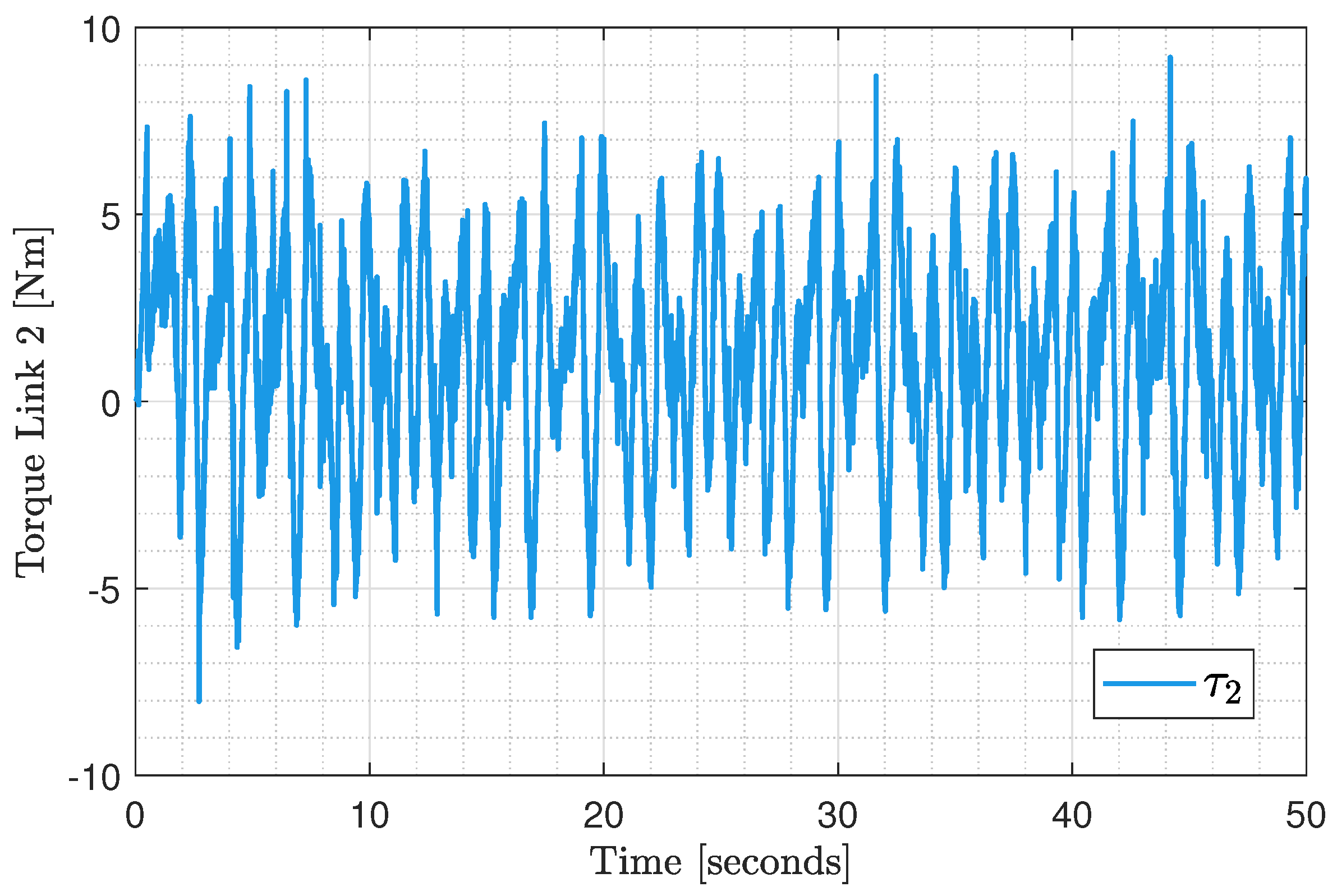
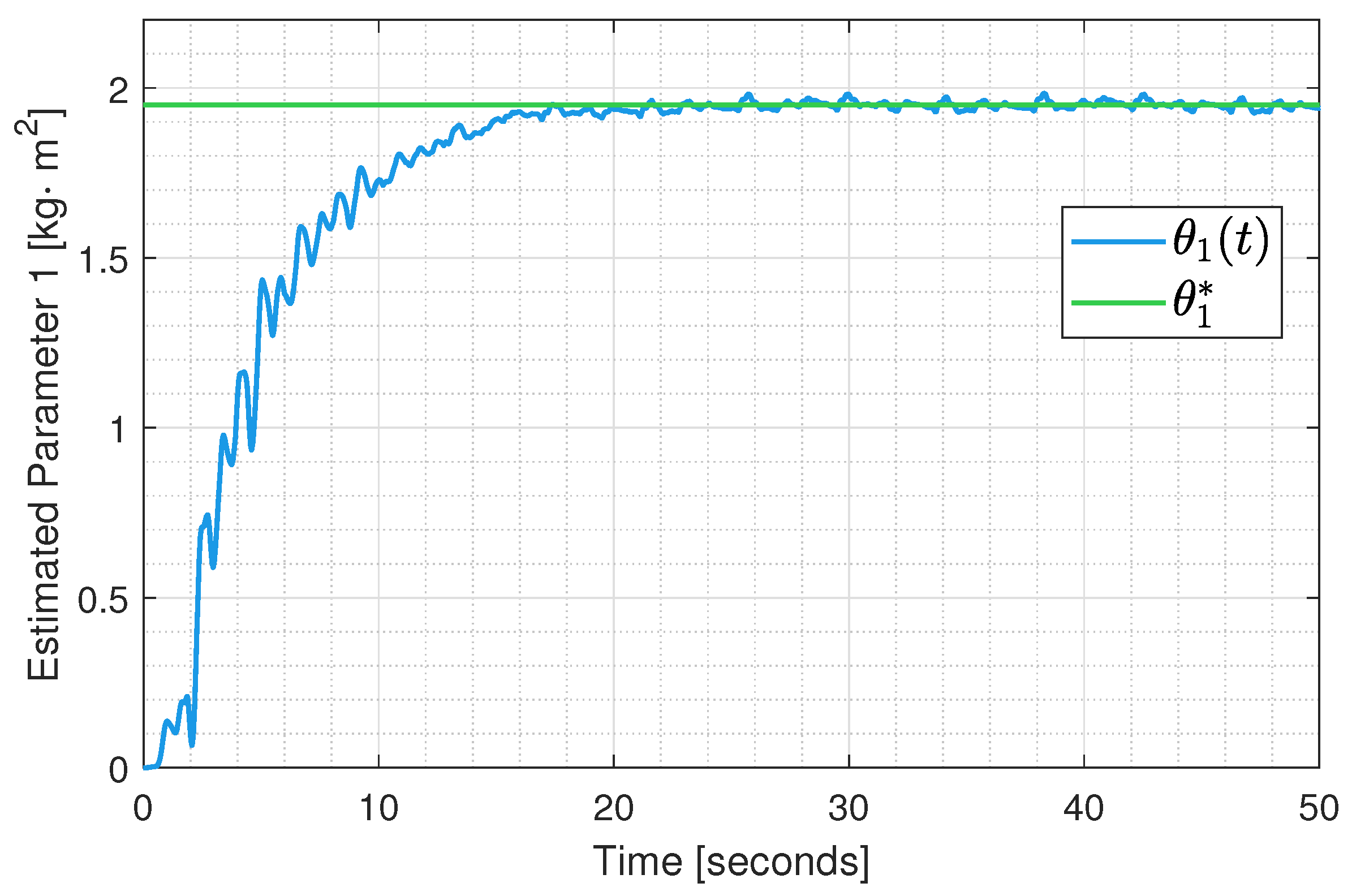
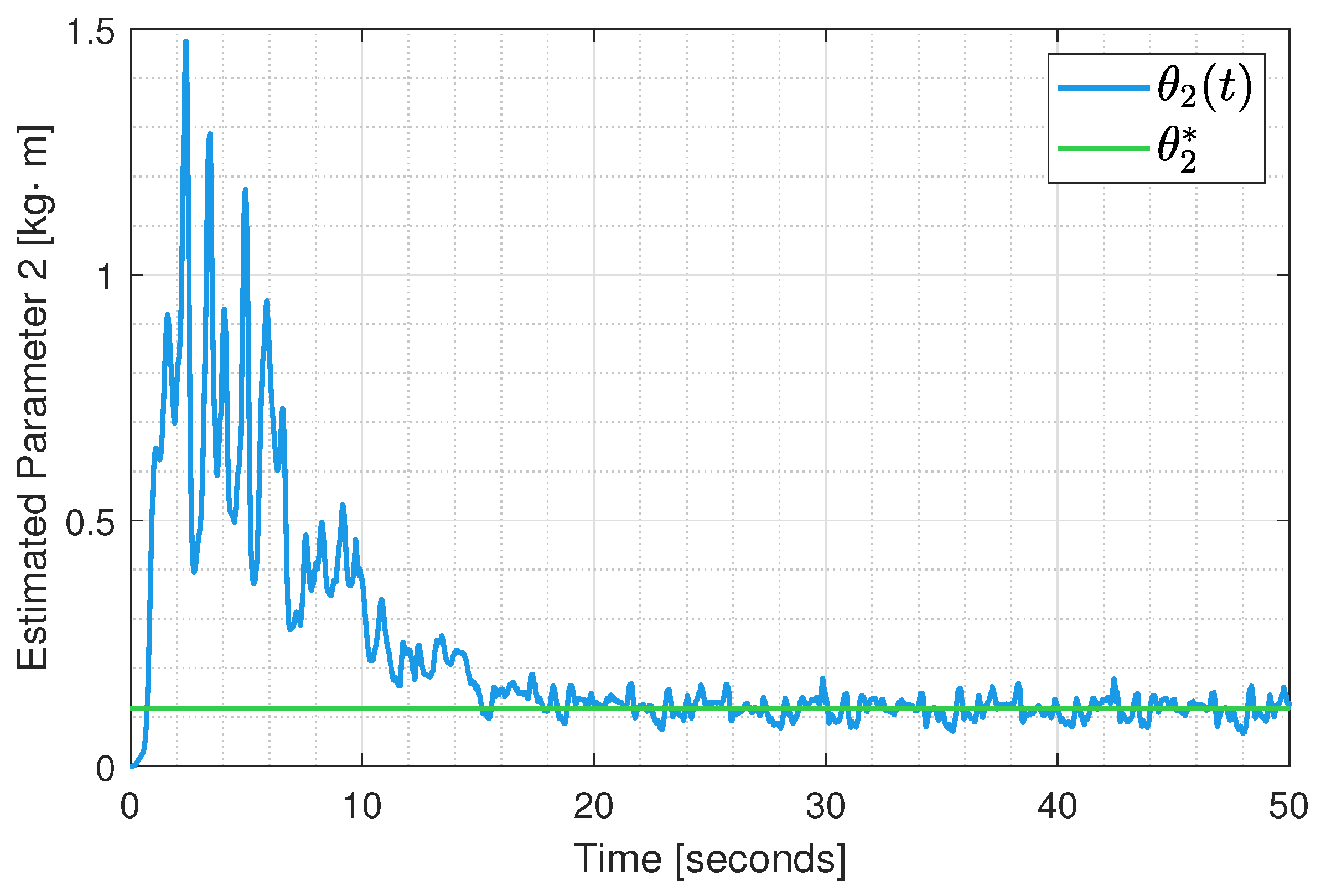
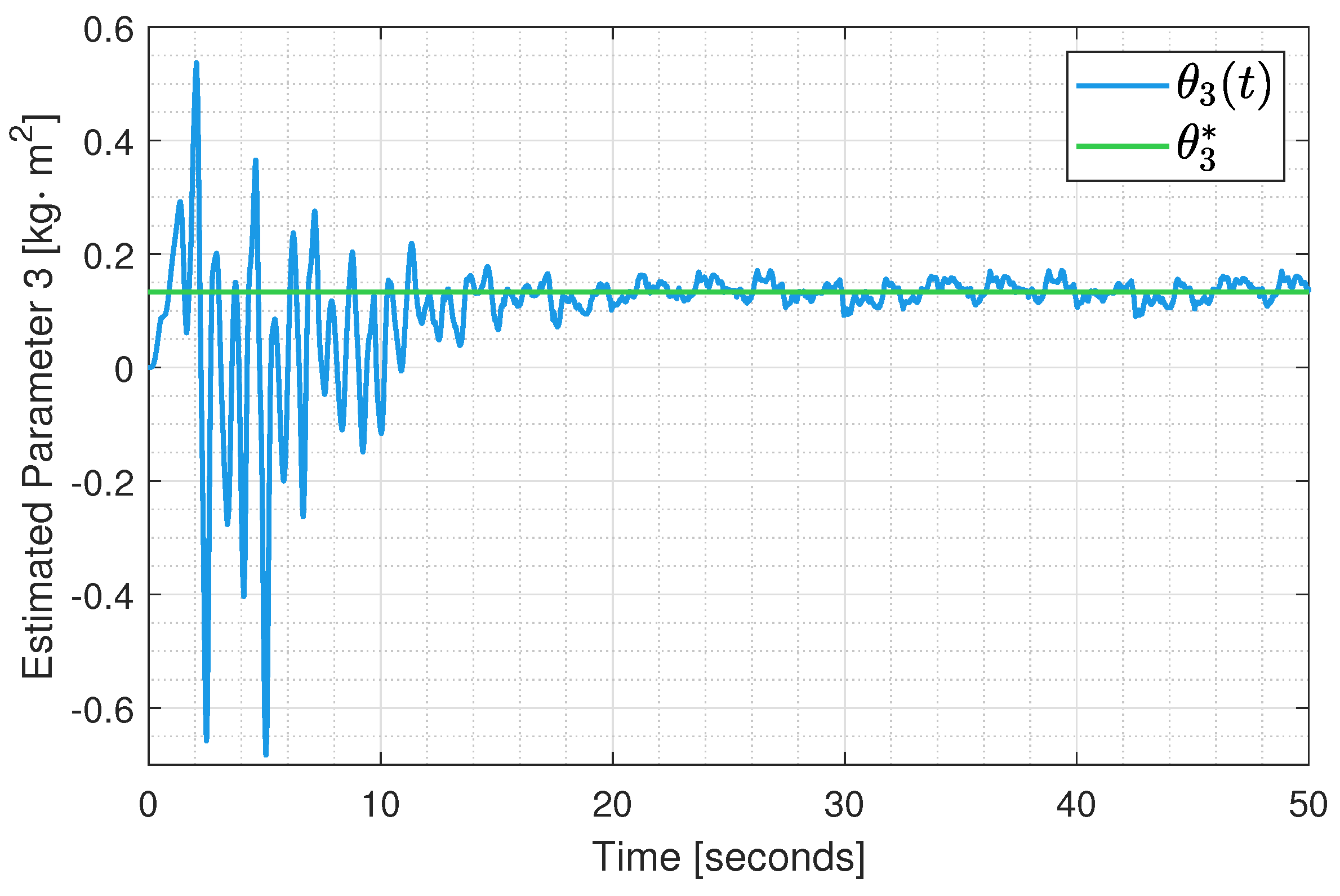
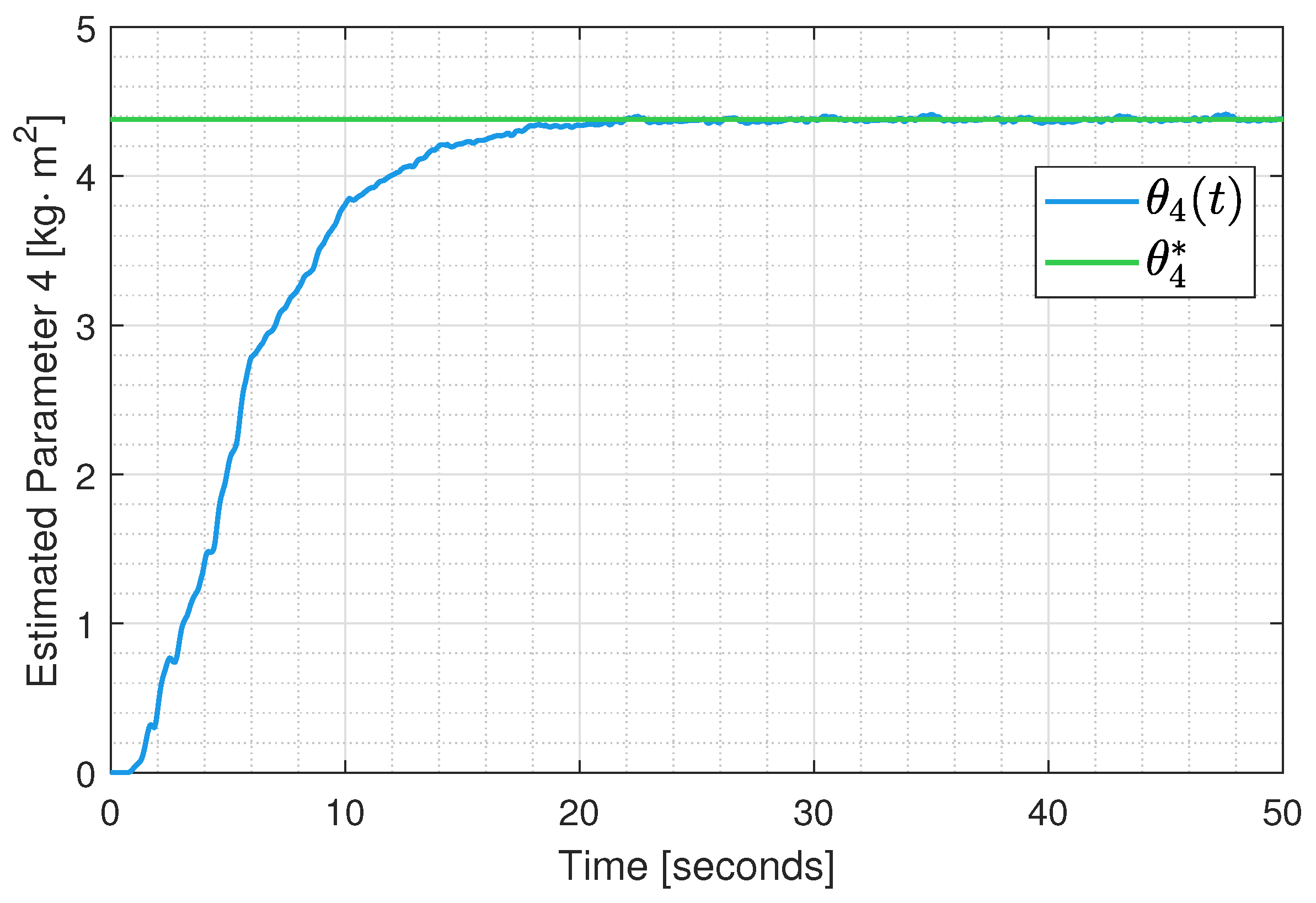
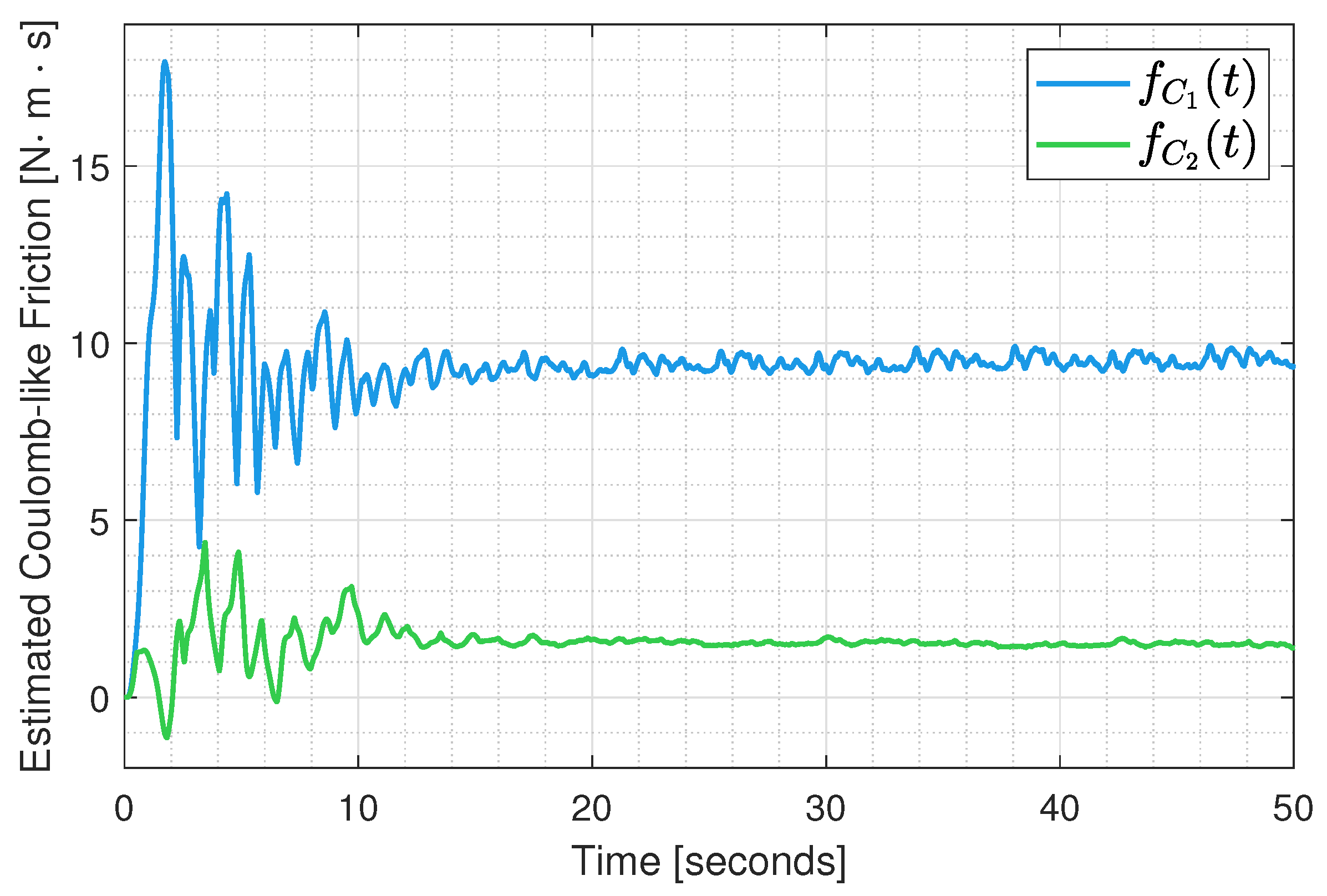
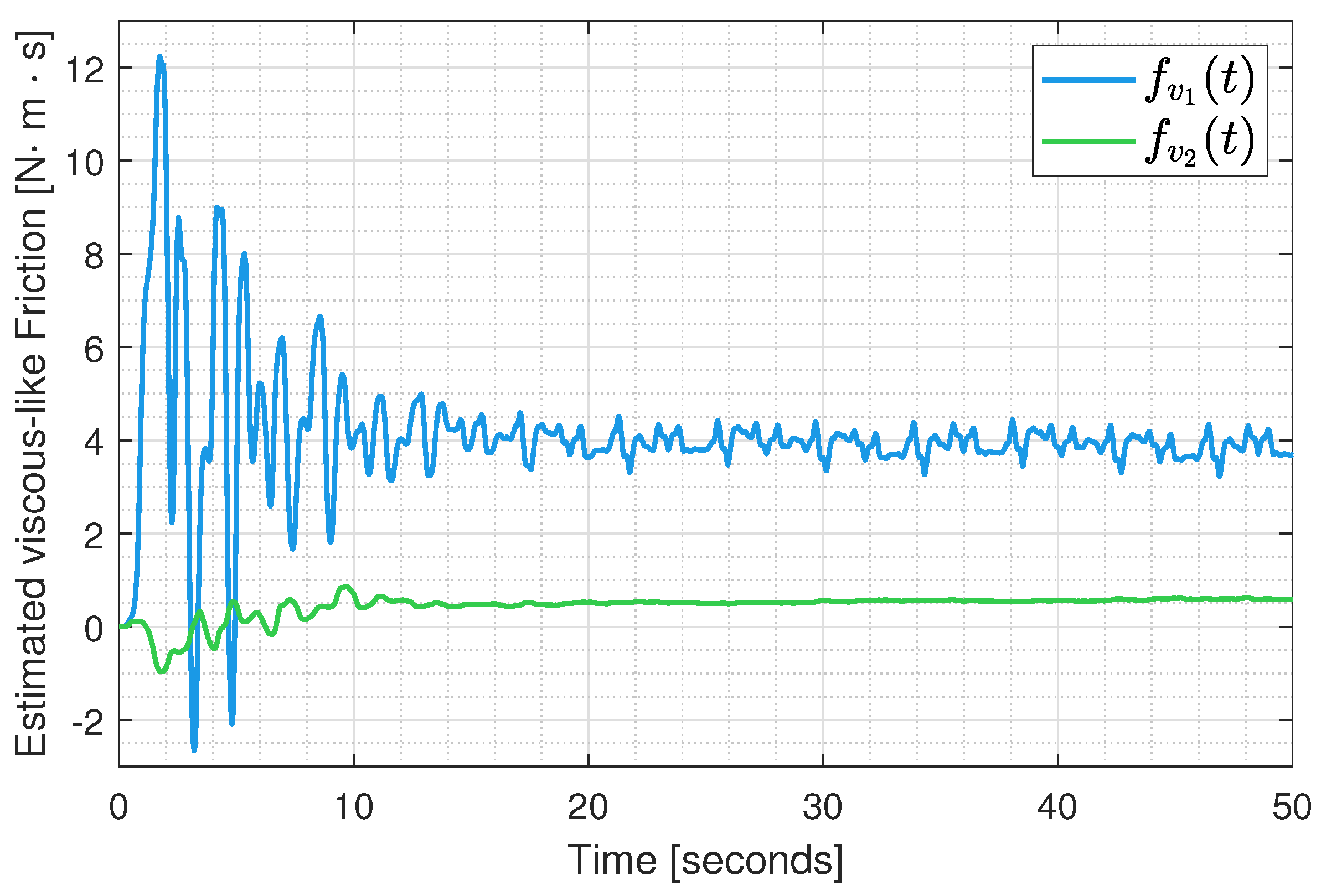
6. Results
Experimental Test Implementation
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Slotine, J.J.E.; Li, W. Composite adaptive control of robot manipulators. Automatica 1989, 25, 509–519. [Google Scholar] [CrossRef]
- Nielsen, H.A.; Madsen, H. Modelling the heat consumption in district heating systems using a grey-box approach. Energy Build. 2006, 38, 63–71. [Google Scholar] [CrossRef]
- Slotine, J.J.E.; Li, W. On the Adaptive Control of Robot Manipulators. Int. J. Robot. Res. 1987, 6, 49–59. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R. Varying-Coefficient Models. J. R. Stat. Soc. Ser. B (Methodol.) 1993, 55, 757–779. [Google Scholar] [CrossRef]
- Stokes, G. On the Variation of Gravity at the Surface of the Earth. In Mathematical and Physical Papers; Cambridge University Press: Cambridge, UK, 2009; pp. 131–171. [Google Scholar]
- Marques, F.; Flores, P.; Pimenta Claro, J.C.; Lankarani, H.M. A survey and comparison of several friction force models for dynamic analysis of multibody mechanical systems. Nonlinear Dyn. 2016, 86, 1407–1443. [Google Scholar] [CrossRef]
- Popova, E.; Popov, V.L. The research works of Coulomb and Amontons and generalized laws of friction. Friction 2015, 3, 183–190. [Google Scholar] [CrossRef]
- Armstrong-Hélouvry, B. Control of Machines with Friction, 1st ed.; Kluwer Academic Publishers: London, UK, 1991; pp. 24–35. [Google Scholar]
- Dahl, P.R. Solid Friction Damping of Mechanical Vibrations. AIAA J. 1976, 14, 1675–1682. [Google Scholar] [CrossRef]
- Olsson, H.; Åström, K.J.; Canudas de Wit, C.; Gäfvert, M.; Lischinsky, P. Friction Models and Friction Compensation. Eur. J. Control 1998, 4, 176–195. [Google Scholar] [CrossRef]
- Armstrong-Hélouvry, B.; Dupont, P.; Canudas de Wit, C. A Survey of Models, Analysis Tools and Compensation Methods for the Control of Machines with Friction. Automatica 1994, 30, 1083–1138. [Google Scholar] [CrossRef]
- Åström, K.J.; Canudas de Wit, C. Revisiting the LuGre Friction Model. IEEE Control Syst. Mag. 2008, 28, 101–114. [Google Scholar]
- Marques, F.; Woliński, Ł.; Wojtyra, M.; Flores, P.; Lankarani, H.M. An Investigation of a Novel LuGre-based Friction Force Model. Mech. Mach. Theory 2021, 166, 104493. [Google Scholar] [CrossRef]
- Niranjan, P.; Karinka, S.; Sairam, K.V.S.S.S.S.; Upadhya, A.; Shetty, S. Friction modeling in servo machines: A review. Int. J. Dynam. Control 2018, 6, 893–906. [Google Scholar] [CrossRef]
- Grami, S.; Okonkwo, P.C. Friction Compensation in Robot Manipulator Using Artificial Neural Network. In Advances in Automation, Signal Processing, Instrumentation, and Control; Komanapalli, V.L.N., Sivakumaran, N., Hampannavar, S., Eds.; Springer: Singapore, 2021; pp. 641–650. [Google Scholar]
- Sun, Y.; Liang, X.; Wan, Y. Tracking Control of Robot Manipulator with Friction Compensation Using Time-Delay Control and an Adaptive Fuzzy Logic System. Actuators 2023, 12, 184. [Google Scholar] [CrossRef]
- Ali, K.; Mehmood, A.; Iqbal, J. Fault-tolerant scheme for robotic manipulator—Nonlinear robust back-stepping control with friction compensation. PLoS ONE 2021, 16, e0256491. [Google Scholar] [CrossRef] [PubMed]
- Han, J.; Cheng, H.; Shan, X.; Liu, H.; Xiao, J.; Huang, T. A novel multi-pulse friction compensation strategy for hybrid robots. Mech. Mach. Theory 2024, 201, 105726. [Google Scholar] [CrossRef]
- Lewis, F.L.; Dawson, D.M.; Abdallah, C.T. Robot Manipulator Control: Theory and Practice, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2003; pp. 125–136. [Google Scholar]
- Spong, M.W.; Hutchinson, S.; Vidyasagar, M. Robot Dynamics and Control, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006; pp. 216–219. [Google Scholar]
- Rill, G.; Schaeffer, T.; Schuderer, M. LuGre or not LuGre. Multibody Syst. Dyn. 2024, 60, 191–218. [Google Scholar] [CrossRef]
- Kelly, R.; Santibáñez, V.; Loría, A. Control of Robot Manipulators in Joint Space, 1st ed.; Springer: London, UK, 2005; pp. 19–57, 95–101. [Google Scholar]
- Barahanov, N.; Ortega, R. Necessary and Sufficient Conditions for Passivity of the LuGre Friction Model. IEEE Trans. Autom. Control 2000, 45, 830–832. [Google Scholar] [CrossRef]
- Canudas-de-Wit, C.; Kelly, R. Passivity Analysis of a Motion Control for Robot Manipulators with Dynamic Friction. Asian J. Control 2007, 9, 30–36. [Google Scholar] [CrossRef]
- Istepanian, R.S.H.; Whidborne, J.F. Finite-Precision Computing for Digital Control Systems: Current Status and Future Paradigms. In Digital Controller Implementation and Fragility: A Modern Perspective; Istepanian, R.S.H., Whidborne, J.F., Eds.; Springer: London, UK, 2001; pp. 1–12. [Google Scholar]
- Soto, I.; Campa, R. Two-Loop Control of Redundant Manipulators: Analysis and Experiments on a 3-DOF Planar Arm. Int. J. Adv. Robot. Syst. 2013, 10, 85. [Google Scholar] [CrossRef]
- Sastry, S.S.; Boyd, M. Adaptive Control: Stability, Convergence and Robustness, 1st ed.; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1989; p. 141. [Google Scholar]
- Boyd, S.; Sastry, S.S. Necessary and Sufficient Conditions for Parameter Convergence in Adaptive Control. Automatica 1986, 22, 629–639. [Google Scholar] [CrossRef]
- Gilbert, E.G.; Ha, I.J. An approach to nonlinear feedback control with applications to robotics. In Proceedings of the 22nd IEEE Conference on Decision and Control, San Antonio, TX, USA, 14–16 December 1983; pp. 879–884. [Google Scholar]
- Slotine, J.J.; Sastry, S.S. Tracking Control of Non-linear Systems Using Sliding Surfaces with Application to Robot Manipulators. In Proceedings of the 1983 American Control Conference, San Francisco, CA, USA, 22–24 June 1983; pp. 132–135. [Google Scholar]
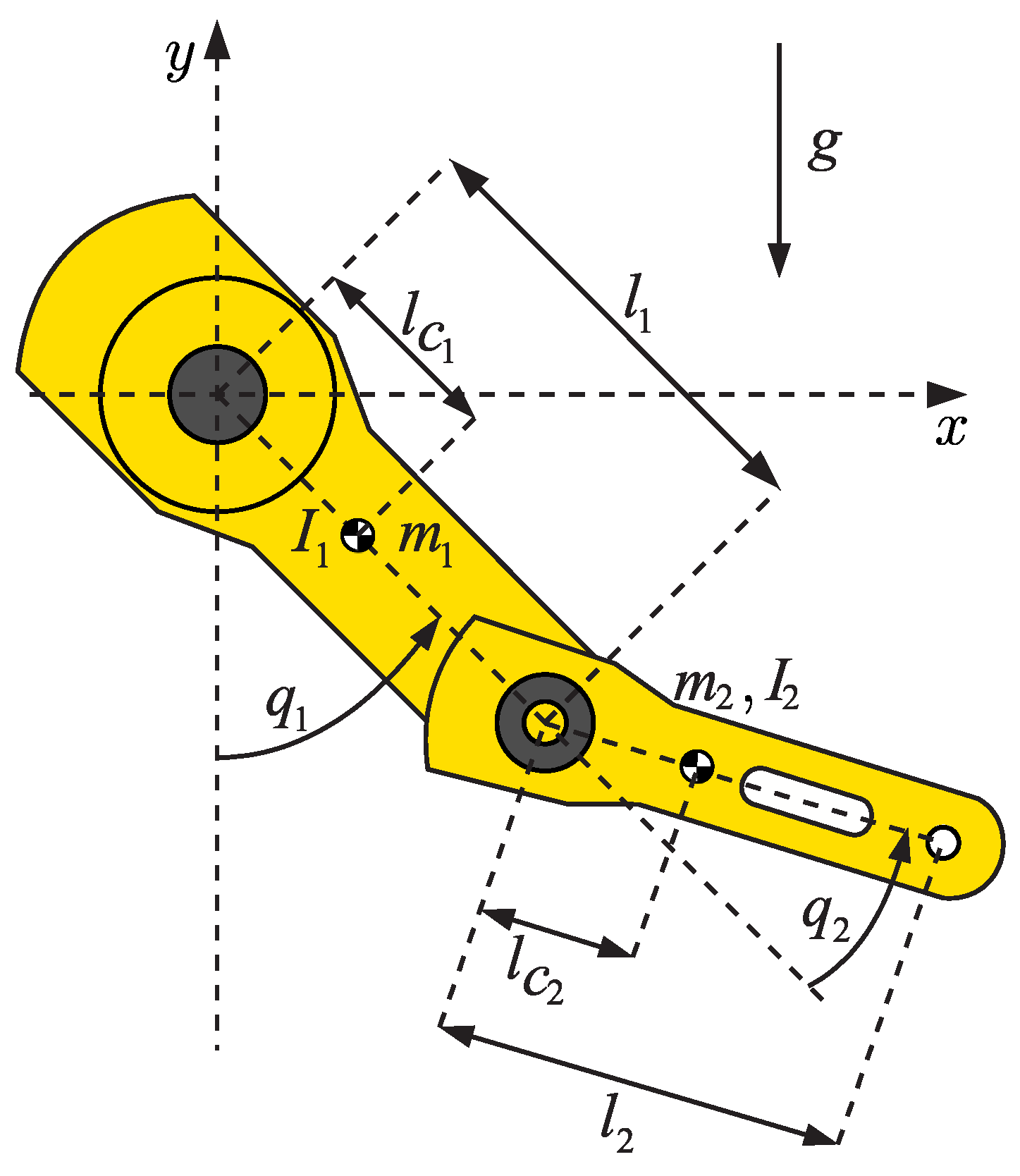


| Description | Notation | Units |
|---|---|---|
| Length of link 1 | m | |
| Length of link 2 | m | |
| Distance to the center of mass of link 1 | m | |
| Distance to the center of mass of link 2 | m | |
| Mass of link 1 | kg | |
| Mass of link 2 | kg | |
| Inertia related to center of mass of link 1 | ||
| Inertia related to center of mass of link 2 | ||
| Acceleration due to gravity | g |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gamez-Herrera, D.; Sifuentes-Mijares, J.; Santibañez, V.; Gandarilla, I. Composite Adaptive Control of Robot Manipulators with Friction as Additive Disturbance. Actuators 2025, 14, 237. https://doi.org/10.3390/act14050237
Gamez-Herrera D, Sifuentes-Mijares J, Santibañez V, Gandarilla I. Composite Adaptive Control of Robot Manipulators with Friction as Additive Disturbance. Actuators. 2025; 14(5):237. https://doi.org/10.3390/act14050237
Chicago/Turabian StyleGamez-Herrera, Daniel, Juan Sifuentes-Mijares, Victor Santibañez, and Isaac Gandarilla. 2025. "Composite Adaptive Control of Robot Manipulators with Friction as Additive Disturbance" Actuators 14, no. 5: 237. https://doi.org/10.3390/act14050237
APA StyleGamez-Herrera, D., Sifuentes-Mijares, J., Santibañez, V., & Gandarilla, I. (2025). Composite Adaptive Control of Robot Manipulators with Friction as Additive Disturbance. Actuators, 14(5), 237. https://doi.org/10.3390/act14050237






