Abstract
This work presents the design and experimental validation of a position-controlled rotating mechanism featuring multi-stage variable stiffness. Before designing the overall mechanism, three different compliant mechanisms, based on flexible beams, are parametrically optimized using a SolidWorks–Ansys co-simulation technique. The flexible beams are composed of multiple straight segments, Bezier curves, and multiple arc segments. The corresponding torque–deflection curves of the compliant mechanisms are collected and fitted into analytical expressions, from which the stiffness equation varying with the angular position is derived for stiffness regulation. A combination of three-stage compliant mechanisms connected in serial is realized to prototype the physical mechanism, which can have three different stiffness ranges of the output shaft. The maximum stiffness is about nine times higher than the lowest one, leading to a broader bandwidth of varying stiffness, which can make the mechanism more adaptive to the external payloads for safety consideration. Experimental measurements are carried out, and the comparison shows a good agreement between the experimental and simulation results, which experimentally validated the design concept. The compact and simple structure, as well as the multi-stage variable stiffness ranges, implies high adaptability of the designed mechanism.
1. Introduction
Compliant mechanisms with varying stiffness have found their applications in many environments for energy saving, equipment protection when overloaded, safe human–machine interaction, etc., such as industrial sectors [1,2,3], healthcare welfare [4], and medical devices [5,6,7]. In addition, considering the characteristics of varying stiffness, another possible application is that they can be used in the design of airplanes, morphing wings to be adaptive to the external load in different configurations. High-stiffness configurations can realize rapid response and high fidelity of the variable stiffness mechanisms, while low-stiffness configurations can help to reduce the impact and shock in collisions for safe contact and stable force/torque outputs.
Variable stiffness mechanisms can be categorized into antagonistic and serial configurations. An antagonistic variable stiffness mechanism utilizes an antagonistic configuration inspired by the biological musculoskeletal system [8], in which two motors actuate the output rod antagonistically via a nonlinear elastic transmission placed between the motors and the output rod, and the position and torque of the joint are controlled by both motors simultaneously. When a nonlinear transmission with quadratic torque rotation characteristics in the mechanism, the output stiffness is independent of the position of the output rod, which can significantly ease the control issue. For example, Palli et al. [9,10,11] realize the same stiffness regulation by replacing the nonlinear transmission device with a customized flexible element with quadratic torque-angle characteristics; the joint can rotate from −15° to 15°, and the range of stiffness adjustment after antagonistic coupling is [726, 1795] Nmm/rad. However, the deformation of its flexible element has exceeded the elastic yield limit, which leads to a short service life of the flexible element. Xiong et al. [12,13] derive the quadratic torque-angle characteristics by using a variable radius mechanism consisting of torsion springs, variable radius pulleys, and connecting rods. This joint uses only a single motor to drive the joint, which has a large range of stiffness adjustment, but its maximum deformation angle is only 14°, and the structure with variable radii makes the overall structure too complex. In addition, the antagonistic variable stiffness mechanisms include the variable stiffness actuator designed by Gaozhang et al. [14] that makes use of two pneumatic chambers for antagonistic control, while pneumatic control requires high sealing of the pneumatic chamber and is more difficult to control. In addition, the design of ADM-VSA by Ning et al. has a stiffness adjustment range of 1.5 to 5 Nmm/rad [15], and the flexible mechanism combined with the antagonistically normal force electromagnetic mechanism designed by Zhang et al. [16]. The main disadvantage of the antagonistic mechanism lies in that two motors need to be synchronized to change the equilibrium position or stiffness. Complex control and high energy consumption will decrease the performance of this type of variable mechanisms.
In contrast, the variable stiffness mechanism in serial configurations regulate the stiffness mainly by two ways, namely, changing the spring preload and changing their transmission ratio between the input force and the spring deflection through the rate of change in the lever mechanism. In the former approach, the first drive unit is connected to the output linkage through a spring that controls the position of the linkage while the second drive unit adjusts the preload tension of the spring. Since this spring is nonlinear, its stiffness can be changed by changing the pre-tension. Some examples of this type of actuator include the mechanically adjustable and controllable supple balanced position actuators MACCEPA [17], MACCEPA 2.0 [18], RVSA [19], variable stiffness actuators controlling the number of springs [20], logarithmic helical serial elastomeric actuators [21], etc. In these examples, linear springs are used; however, due to the stiffness adjustment used, the mechanism provides a nonlinear force deflection profile, and thus these springs can be considered nonlinear. In the latter approach, the lever mechanism has three main points: the pivot point, the point around which the lever can be rotated; the spring attachment point, the point at which the spring is located; and the force point, the point at which the force is applied to the lever. By changing the position of one of these major points, the stiffness of the lever can be changed. Examples of variable stiffness joints of this type are found as AwAS-I [22], AwAS-II [23], variable stiffness actuators based on steel plate springs [24], high-energy-efficiency variable stiffness actuators [25]. In addition, more recent uses of this approach include the iris-VSA [26], which forms the stiffness by changing the position of the intermediate force contact point of the torsion spring, and the theoretical range of stiffness adjustment, and joint angle is 0 to ∞. The SVSA-III designed by Yi et al. [27] is based on the linear stiffness profile of a symmetric variable rod arm mechanism, where the stiffness is adjusted by changing the position of the pivot located on an Archimedean Spiral Repositioning Mechanism (ASRM), and its rotational stiffness can be adjusted from 0.3 Nm/degree to infinity. Yang et al. [28] proposed a trapezoidal leaf spring brake (TLSA) with variable stiffness, which varies the stiffness by adjusting the force contact point between the trapezoidal leaf springs. And its simulation results show that the proposed TLSA is characterized by wide stiffness range, fast stiffness response capability, and large maximum load torque value. Shao et al. [29] proposed a variable stiffness articulation based on a cam-circular-beam mechanism, where the stiffness adjustment of the actuator is realized by simply rotationally adjusting the pivot position and by means of a circular beam. In addition, the ratio between the joint beam deformation and joint deflection is determined by the cam mechanism, so the stiffness profile and stiffness range can be customized.
Apart from the foregoing mechanically designed variable stiffness mechanisms, new materials and techniques have been applied to the design of variable stiffness joints in recent years, such as shape memory alloys (SMAs) [30,31], ionic polymers (EPAs) [32], origami structures [33], interlaminar interference techniques [34,35,36], and particle obstruction techniques [37], etc. Among the various methods, the laminar jamming technique mainly increases or reduces the bending stiffness by increasing or decreasing the interlayer friction, which has attracted plenty of research in recent years due to its simple structure and high stiffness adjustment bandwidth. In a recent study, Chen et al. [38] designed a variable stiffness actuator with a high stiffness bandwidth and a fast response speed of up to 5 mm by utilizing a hybrid interlaminar interference technique with electroadhesion and vacuum actuation. In addition, there is a trend to use vacuum pressure in combination with positive pressure pneumatic actuators [39], where the laminar jamming structure controls the stiffness and the positive pressure actuator is used to control the shape of the fingers, thus enabling objects to be gripped. On the other hand, the application of new technologies and materials still encounters a number of problems in nonlinear stiffness regulation, and the fabrication cost is high. Table 1 lists a brief summary of the advantages and disadvantages of different design approaches for variable stiffness mechanisms. In this light, the serial variable stiffness mechanisms to change the spring preload is simpler and easier to implement in terms of structure and principle, and it does not strictly require the nonlinear transmission mechanism to have a quadratic torque-deflection characteristic. The key to design such mechanism lies in the design of the flexible transmission unit with nonlinear torque rotation characteristics, and one of the typical ways is to realize it through the mechanical structure with elastic elements, but there are some drawbacks to this method; that is, it often leads to the increase in the number of parts and the increase in the complexity of the structure. Therefore, in this work, it is to use a one-piece fabricated flexible element for the design, which has the advantage of being able to significantly reduce the number of parts and greatly simplify the electromechanical system, thus improving the feasibility and practicality of the whole design scheme.

Table 1.
Comparison of the (dis)advantages of various stiffness regulation approaches.
The variable stiffness mechanism designed in this work adopts the serial configuration approach to regulate the stiffness by changing the spring preload, and multiple compliant mechanisms are connected in a series for wider and multi-stage stiffness ranges. The working principle of the variable stiffness mechanism and the compliant mechanism are shown in Figure 1. This structure avoids the antagonistic two-motor coupling control and increases the range of rotation angles and stiffness adjustment range by connecting the torsion springs in series. During the optimization of the compliant mechanism, it is ensured that the nonlinear characteristics of the torsional springs are provided entirely by geometric nonlinearities. The stiffness characteristic curve of the joint is generated with the help of finite element simulation and polynomial fitting methods.
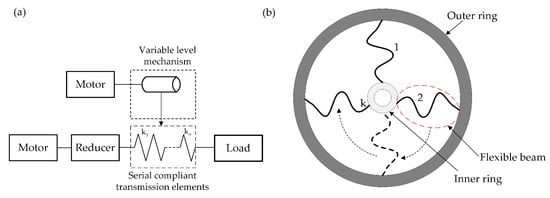
Figure 1.
(a) Schematic diagram of variable stiffness actuator based on serial multi-stage torsional compliant mechanisms. (b) Basic structure of torsional compliant mechanisms.
The remaining content of the paper is structured as follows. In Section 2, the working principle of the mechanism is described, and a detailed design optimization of compliant mechanism is interpreted. Section 3 presents the structure design of the variable stiffness mechanism with a CAD model developed as well as the torque deflection characteristics. In Section 4, a physical prototype of the mechanism is depicted, and experimental validation is carried out by measuring the angular displacement–torque curve to verify the mechanism design. The conclusions are drawn in Section 6.
2. Design Optimization of Compliant Mechanism with Different Shaped Flexures
As pointed out in the previous Introduction section, the primary task to design the actuation unit is to design the compliant mechanism; therefore, this section presents the corresponding design procedure. Here, the shape and size of the flexible beam is formed by means of the parametric design optimization, aiming at maximizing the load carrying capacity of the torsional spring subject to the elastic yield limit, which features nonlinear torque-angle characteristics.
2.1. Formulation of Optimization Problem
To illustrate the optimum design process, a flexible beam in terms of geometric Bezier curve beam is taken as an example, as depicted in Figure 2. The shape of the Bezier curve flexible beam is determined by five control points, of which the positions are to be optimized to realize nonlinear torque-deflection characteristics. In the design of compliant mechanism, the inner and outer rings are both considered as rigid compared to the flexible beam, on which the first p1 and last p5 control points are located. In this light, the design parameters include the orientation angles (φp1, φp2, φp3, φp4, φp5) of the control points relative to the mechanism center O, the radii (rp2, rp3, rp4) of the control points, and the cross-section of the beam by height h and thickness b.
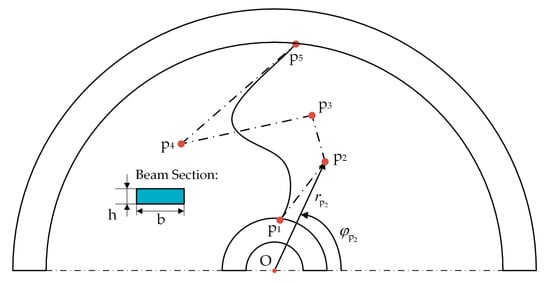
Figure 2.
Parameterized flexible beam of the compliant mechanism depicted by the Bezier curve.
The design objective is to achieve a prescribed torque-deflection profile between the external payload and elastic deformation, and it has been proved that a quadratic expression is a good candidate to describe the torque-deflection relationship, as it yields a linear stiffness equation which can ease the position control for stiffness regulation. Accordingly, the torque-angle characteristic of the Bezier curve beam is quadratically expressed as follows:
where τ and θ represent the external torque applied to the inner or outer ring and the corresponding angular deflection between the two rings when the mechanism is in the equilibrium position. Moreover, k1 and k2 are the stiffness coefficients with unit Nmm/rad2 and Nmm/rad, respectively, which can be determined after design optimization. Sequentially, the position determined stiffness equation can be derived by differentiating the previous equation, namely,
from which it is seen that the stiffness is in a linear relationship varying with the rotation angle. This means that the minimum and maximum stiffness (i.e., kmin and kmax) of the compliant mechanism can be reached when it has the minimum and maximum angular displacements. In order to maximize the varying stiffness range of the compliant mechanism, the maximum/minimum stiffness should correspond to the set of variables (θmax, τmax) and (θmin, τmin) that meet Equation (1); consequently, the first objective function is written as follows:
In addition, in order to maximize its carrying capacity, the second objective function is written as follows:
To ensure the safety of the designed compliant mechanism, a constraint about the stress is defined as below:
where represents the maximum stress in the torsional deformation of the compliant mechanism and stands for the yield strength of the material for the mechanism design.
2.2. Optimum Design of the Compliant Mechanism
To optimize the flexible beam as shown in Figure 3, a Solidworks 2020–ANSYS 2021R2 co-simulation approach is adopted in this work. Moreover, in order to reduce the computational time of optimum design, the model of compliant mechanism for design optimization is simplified by considering with the only one flexible beam. In the first step, a parameterized model is built with Solidworks, where the foregoing design parameters are set as variables. The model is then imported into ANSYS to optimize the previously defined variables, through which the design optimization problem can be solved by the parameter transferring between the two software. Since the compliant mechanism is to output relative rotational motion between the inner and outer rings under external torque, the flexible beam is treated as the cantilever beam. The simplified model to be optimized is depicted in Figure 3.
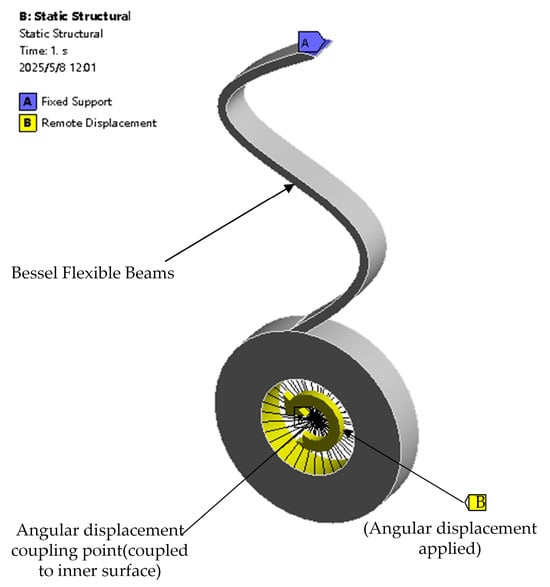
Figure 3.
Schematic diagram of the flexible beam represented by the Bezier curve for the design.
After building the model, simulation setting is made. Three-dimensional printing technology is an effective way for the fabrication of components, which will be adopted after structural optimization of the compliant mechanism. In this light, the material is selected as ABS, of which the elasticity modulus, Poisson’s ratio, and tensile yield strength are set to E = 1.8 GPa, υ = 0.4, σs = 29.7 MPa, respectively. Moreover, the maximum and minimum angular displacements are set to θmax = −θmin = 8°, according to the initial simulation for prediction. The next procedure is to design the flexible beam by iterative optimization of the design variables, wherein the Kriging response surface model is adopted and the multi-objective genetic algorithm (MOGA) is used to solve the formulated optimization problem. The flowchart of the design process is shown in Figure 4, of which the iterative optimization will terminate when the final optimal solution meets the expected result.
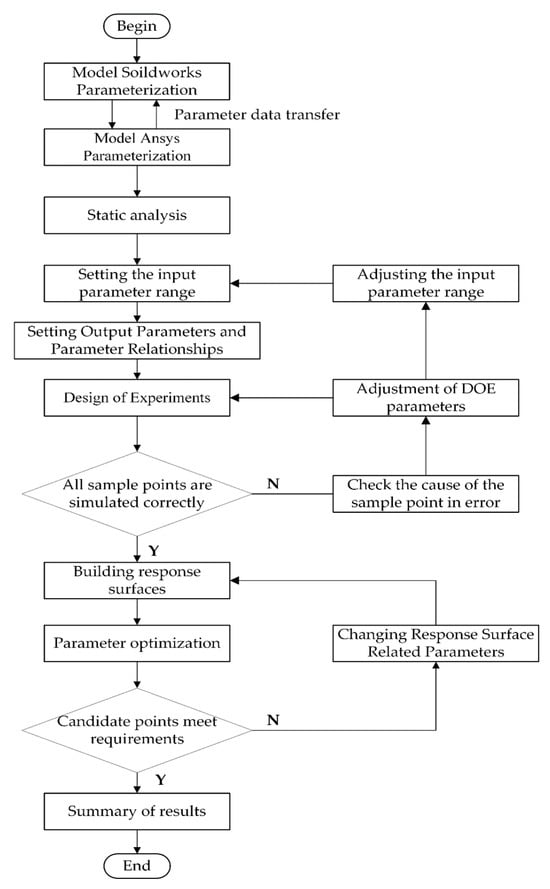
Figure 4.
Flowchart of parameter optimization by Soildworks-ANSYS co-simulation.
In the optimization design, the initial design variables are randomly selected, as listed in Table 2, as well as the lower/upper bounds and optimal results. After 32,000 iterations, the final design of the compliant mechanism with four flexible beams is shown in Figure 5. It can be seen that the optimized compliant mechanism ensures a nonlinear torque–deflection curve, reaching up to its maximum load carrying capacity. Moreover, the differential torque–deflection curve leads to a linear equation of the stiffness varying with the angular displacement, which is expressed as .

Table 2.
Initial, lower/upper bounds, and optimal values of design variables.
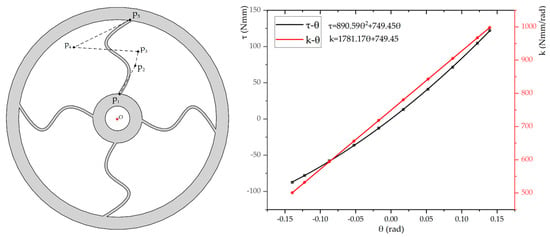
Figure 5.
Final design of the optimized compliant mechanism with four flexible beams (left) and the torque–deflection curve (right).
Figure 6 depicts the comparison of the torque–deflection curves before and after design optimization, from which it is seen that the optimized mechanism can ensure larger angular displacements when the maximum stress does not exceed the yield strength of the material. All the results show that the optimized complaint mechanism can meet the expected design requirements.
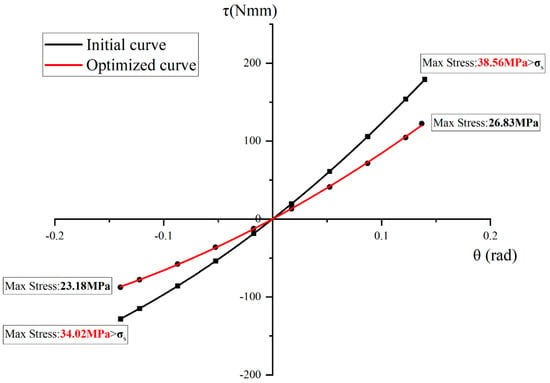
Figure 6.
Comparison of torque–deflection curves between the initial and optimized design.
By means of the previous optimum design technique and identical simulation settings, two more compliant mechanisms with different flexible beams are designed as shown in Figure 7. The flexible beams of the first compliant mechanism adopt multiple nonparallel straight segments, while the second one adopts two arc segments in each flexible beam, and their torque–deflection curves are displayed for comparison. The range of the variable stiffness of different compliant mechanisms and maximum torques are given in Table 3. It can be seen that the compliant mechanism with flexible beams composed of multiple straight segments has a larger torque capacity and range of variable stiffness, i.e., the maximum allowable torque being τmax = 137.62 Nmm when the deflection reaches up to the maximum angle θmax = 8°. The comparison also shows a larger bandwidth of variable stiffness of the flexible beams composed of multiple straight segments. It is noteworthy that the flexible beam by two arc segments forms a cubic torque–deflection curve, which leads to a quadratic equation of the stiffness, differing from the compliant mechanism with straight segments that forms a quadratic torque–deflection curve and linear stiffness-angle function.
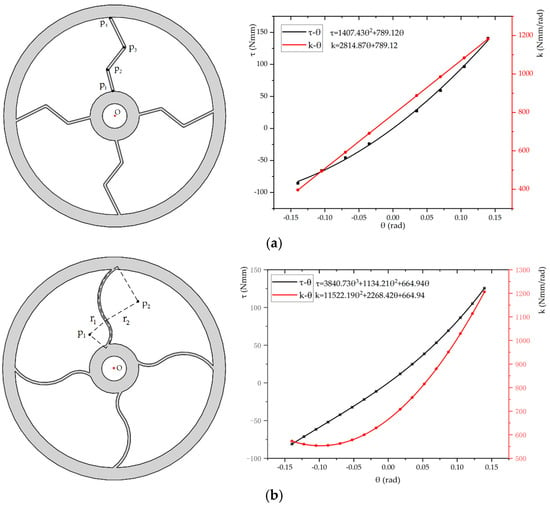
Figure 7.
Complaint mechanism design with flexible beams of multiple straight and arc segments. (a) Flexible beam of multiple straight segments (left) and torque–deflection curves (right). (b) Flexible beam of multiple arc segments (left) and torque–deflection curve (right).

Table 3.
Comparison of stiffness and torque ranges of the compliant mechanisms with different flexible beams.
3. Structural Design of the Compliant Actuation Mechanism
3.1. Working Principle
In this section, the structure of the compliant actuation module is designed by making use of the optimized compliant in the previous section. The stiffness regulation is realized by connecting three compliant mechanisms in serial, in order to make the actuation mechanism have different ranges of the variable stiffness. Figure 8 depicts the working principle of the actuation mechanism to be designed, of which the structure is a serial adjustable stiffness joint. One motor, called as major motor, works as the torque input, to generate the moment to the output shaft via the three compliant mechanisms in a series. The other motor drives the slider to change the position of the clamping jaws to select the compliant mechanisms to provide different stiffness. When the clamping jaw is close to the major motor, the overall stiffness of the actuation mechanism depends on the only the first complaint mechanism I (the second sub-figure in Figure 7), and in this case, the stiffness range is in the first level I, thus, the instantaneous stiffness of the output shaft is calculated as follows:
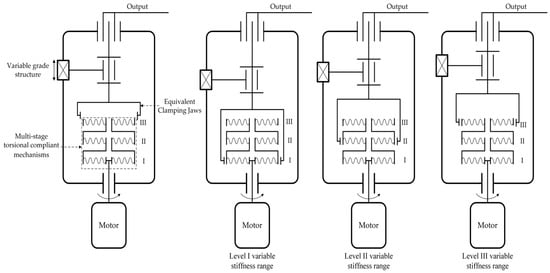
Figure 8.
Schematic diagram of the actuation mechanism with multi-stage compliant mechanisms.
In the case of the third sub-figure, when the clamping jaw is locked to the compliant mechanism II, the overall mechanism is in the lever II of variable stiffness range; sequentially, the output stiffness is written as follows:
In the case of the last sub-figure, the stiffness range of the overall mechanism is at the level III, and the output stiffness is expressed as follows:
where .
In accordance with the previous derivation of the output stiffness, different stiffness ranges of the output shaft of the actuation mechanism can be realized. With more complaint mechanisms connected in a series, the actuation mechanism can generate a larger deformed rotation angle under the same torque exerted to the output shaft, which can help to protect the overall mechanism if overload applied to the mechanism occurs.
3.2. Finite Element Evaluation of Multi-Stage Compliant Mechanisms
To find the combination of the multi-stage complaint mechanisms as shown in Figure 8, this section aims to analyze the static performance of the mechanism with different compliant mechanisms connected in a series by means of finite element modeling (FEM). Taking the combination of compliant mechanism with flexible beams of multiple straight segments and the Bezier curve as example, as shown in Figure 9a, the end labeled “B” of the combined mechanism is set as the “fixed” constraint, while the cylindrical surface “A” is selected as the free end. The “Static Mechanics” module of ANSYS is selected to analyze the relationship between torque and angular deflection, stress, etc., in which the simulation evaluation is carried out under “large deformation” condition. The meshed model and measured stress are given in Figure 9b, and the angular deflection is calculated by the equation uy/r, where uy is the linear deformation of a selected reference point on the free end along y-axis and r is the radius of the reference point to the center, as depicted in Figure 9c.
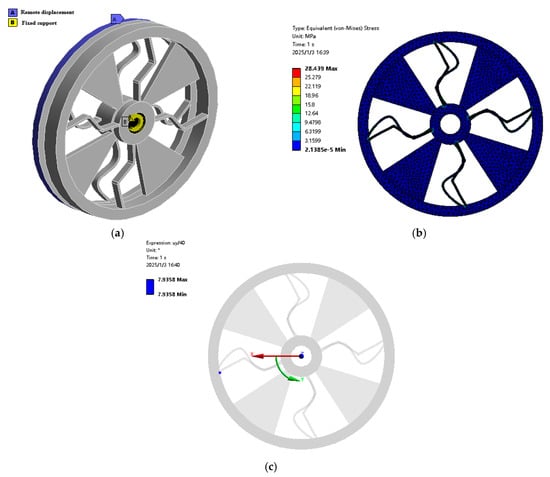
Figure 9.
FEM simulation analysis of the multi-stage complaint mechanism. (a) FE constraints of the combined compliant mechanism. (b) Max equivalent stress in the configuration of the maximum angular deformation. (c) User-defined rotation angle of the mechanism.
In order to deduce the torque–deflection curve, the rotation angle of the free compliant mechanism is discretized in the range [−16°, 16°], according to the previous optimized results. Collecting the simulation results, the varying torque–deflection curves with different combined compliant mechanisms are summarized in Figure 10, where the equations of torque and stiffness varying with angle can be fitted. It can be seen that when the compliant actuation mechanism includes the compliant mechanism unit with flexible beams of multiple arc segments, the torque–deflection curves are fitted into cubic equation, resulting in quadratic stiffness equation. In this view, the combinations of compliant mechanisms with flexible beams of multiple straight segments and the Bezier curve are preferable, as depicted in Figure 10b and 10e.
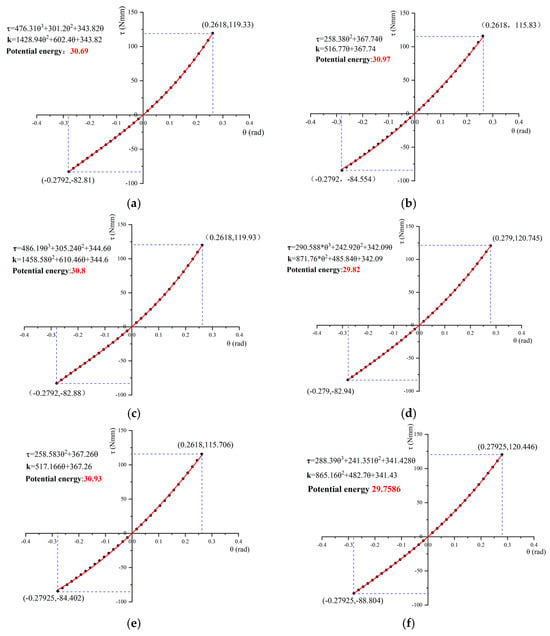
Figure 10.
Comparison of torque–deflection curves of combined compliant mechanisms: (a) multiple straight and arc segments; (b) multiple straight segments and the Bezier curve; (c) multiple arc and straight segments; (d) multiple arc segments and the Bezier curve; (e) the Bezier curve and multiple straight segments; (f) the Bezier curve and multiple arc segments. (Scattered dots: simulation results; solid lines: fitted curves).
The stiffness ranges of different combined compliant mechanisms are found as listed in Table 4, in comparison with the analytical solutions calculated by Equation (7) with the discrete torque-angle stiffness. The relative errors between the analytical and FEM results are calculated to find the maximum errors. Except the combined compliant mechanisms shown in Figure 10a,c, the maximum errors are very small, which implies that the previously derived stiffness equation is applicable for position-controlled stiffness regulation. It should be noted that the 20% difference between the FEM and analytical calculation occurs in the combination of compliant mechanisms with flexible beams of multiple straight and two arc segments. This discrepancy stems from the fact that the compliant mechanism with multiple straight segments will produce stress concentration at the connecting nodes, and the compliant mechanism with two arc segments featuring cubic torque-deflection characteristics is much more sensitive to the stress concentration. This makes the analytical Equation (7) is inapplicable in certain stiffness ranges of the two compliant mechanisms, as listed in Table 3. In particular, the upper bound of stiffness range of the compliant mechanism with two arc segments exceed that of the compliant mechanism with multiple straight segments, which leads to increased computation errors of the analytical equation with the increased torsional angles. In light of this, the combination of compliant mechanisms with flexible beams of multiple straight and two arc segments will not be considered in the design of the multi-stage compliant mechanism.

Table 4.
Comparison of static performances of the different combined compliant mechanisms.
In accordance with Figure 10 and Table 4, it can be observed that the six different combinations of compliant mechanisms do not show significant differences in terms of the energy storage capacity and maximum torque capacity. Taking the computation errors and variable stiffness ranges into consideration, a continuously varying stiffness of the overall mechanism is expected by ensuring an overlap of the first compliant mechanism with the serially connected ones. In this consideration, when the compliant mechanisms with flexible beams of multiple straight segments and the Bezier curve are, respectively, connected to the input and output shafts, the combined mechanism can have a relatively better stiffness range, which can be seen as a better design candidate. Thus, the stiffness range can be calculated in the range [223.43, 1182.07] Nmm/rad.
In order to make the actuation mechanism have more ranges of varying stiffness, the final design of the overall mechanism adopts three compliant mechanisms connected in a series, namely two compliant mechanisms with flexible beams of multiple straight segments to connect the input and output shaft and one Bezier curve-compliant mechanism in the middle. In this design, the torsional stiffness of the output shaft of the actuation mechanism can be written as follows:
with
In accordance with Figure 6 and Figure 7 and Equation (9), the ranges of angular deflections of the output shaft for the varying stiffness of levels 1–3 are found as [−8°, 8°], [−16°, 15°], and [−24°, 23°], respectively. The three-stage compliant mechanism connected in serial and the corresponding torque–deflection curves are shown in Figure 11.
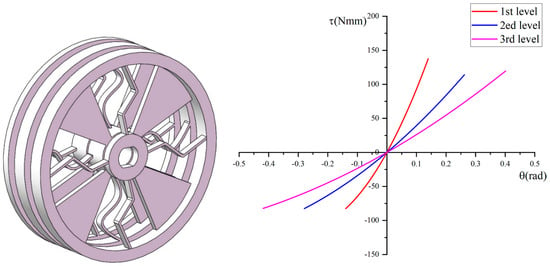
Figure 11.
The serially connected three-stage complaint mechanism (left) and the corresponding torque–deflection curves (right).
3.3. Strcuture of Variable Stiffness Mechanism
In accordance with Figure 7 and the stiffness analysis of the previous combination of multiple compliant mechanisms, the skeleton diagram of the variable stiffness mechanism is formed in Figure 12. The working principle is depicted as follows. The fork is driven linearly to change the position of the compression sleeve, which can make the clamping jaws produce elastic displacements have frictional contacts with the serial connected compliant mechanism. Since the clamping jaws without deformation are in the shape of a cone, the compression sleeve in different positions can make the compressed jaws connect to one, or two, or three of the compliant mechanisms in a series. When the input shaft rotates, it simultaneously drives the connected compliant mechanism, clamping jaws, compression sleeve, and output shaft (connected to fork by revolute joint) in order to generate the rotation of the output rod.
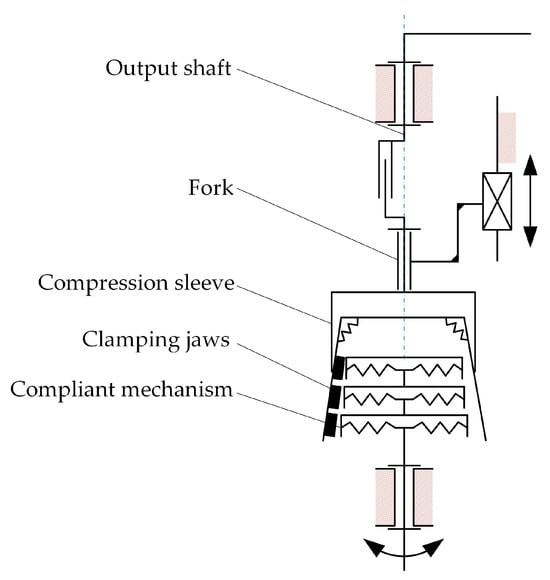
Figure 12.
The kinematic skeleton diagram of the position-controlled variable stiffness mechanism.
Accordingly, the detailed CAD model of the overall actuation mechanism is shown in Figure 13. The joint consists of three major modules: the input, the output, and the adjustable nonlinear flexible transmission module. The input part includes the actuation unit to provide the torque to the output shaft, and a second motor to select the combinations of the working compliant mechanism for the nonlinear stiffness adjustment. The output part is composed of the variable structure for stiffness tuning and the output shaft, where the variable stiffness is realized by driving the conical clamping jaws by the linear module. The combined compliant mechanism for varying nonlinear stiffness is depicted in Figure 11. It can be seen that the overall structure of the CAD model is compact and simple.
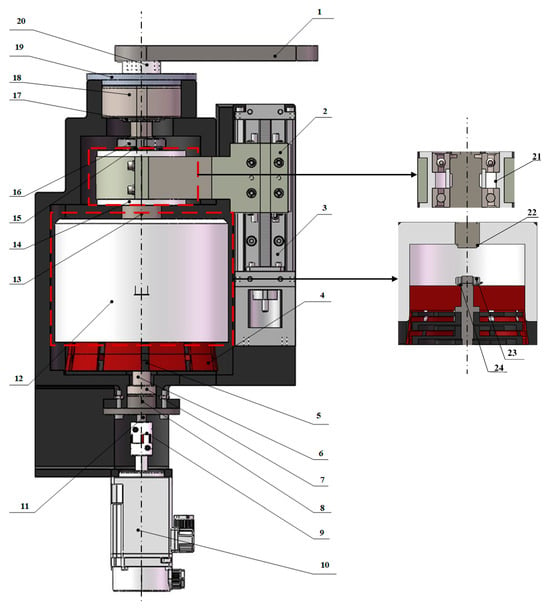
Figure 13.
CAD model of the compliant actuation mechanism with multi-level variable stiffness: 1. Output rod; 2. fork; 3. linear module; 4. special clamping jaws; 5. nonlinear series plane torsional spring; 6. input shaft sleeve; 7. rolling bearing; 8. output end cover; 9. coupling; 10. motor; 11. input shaft; 12. compression sleeve; 13. output shaft; 14. fork sleeve; 15. stop washer; 16. round nut; 17. elastic retaining ring for shaft; 18. double row angular contact ball bearing; 19. output end cover; 20. output shaft sleeve; 21. bearing sleeve; 22. elastic retaining ring for shaft; 23. round nut; 24. stop washer.
4. Experimental Verification of the Mechanism
In order to experimentally validate the mechanism design, a prototype is built as shown in Figure 14. The output shaft and output sleeve which are made of 7075 aluminum alloy, and the remaining components are made by 3D printing technology in order to realize the lightweight design. Moreover, material reduction treatment is performed on the compression sleeve and the shell, which is convenient for observing the position of the compression sleeve. The key components in the physical prototype are shown in Table 5.

Figure 14.
Physical prototype of the position-controlled variable stiffness mechanism.

Table 5.
Additional description of key components and functions in the physical prototype.
The experimental setup for static measurements is shown in Figure 15, of which the experimental steps consist of the external torque generation, angle reading, and stiffness adjustment. A standard static load is applied to the end of output rod, which is calculated by τ = mgLcosθ, and the corresponding torsion angle is read by an angular dial fixedly attached to the housing end cap. The resolution of the dial indicator is equal to 0.5°. The experimental results are shown in Figure 16, with the comparison to the simulation results. From the comparison, it can be seen that the errors between the experimental and simulation results are very small, i.e., the maximum and root-mean-squared deviations between them equal to 3.32% and 1.3121%, respectively, which implied that these two sets of results agree well with each other.

Figure 15.
Experimental setup of static measurement for the mechanism.
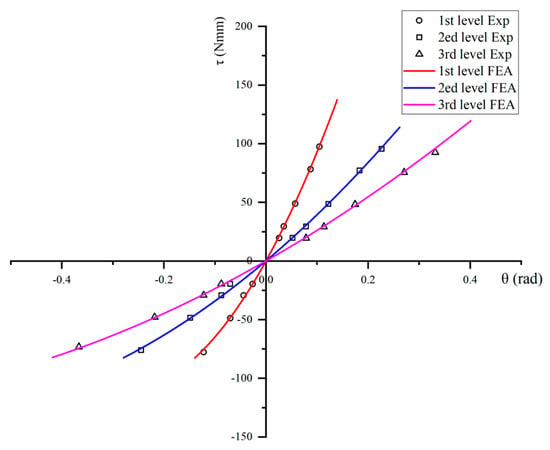
Figure 16.
Comparison of torque–deflection relationship between the FEM and experimental results.
5. Results Discussion
Based on the previous design analysis, it can be found that the variable stiffness mechanism designed in this work can move with a maximum rotation angle [−24°, 23°], together with a stiffness adjustment range [114.73, 1182.07] Nmm/rad, of which the maximum stiffness is about nine times greater than the minimum. This design allows a broader bandwidth of the stiffness regulation rather than the conventional single compliant mechanism. Different from the antagonistic joints, the multi-stage variable stiffness mechanism can realize the decoupled control of stiffness regulation and output motion. Moreover, the multi-stage compliant mechanism can produce different stiffness ranges of the output rod, which can make the designed mechanism more adaptive to different working environments. The multiple complaint mechanisms connected in a series still has quadratic torque-deflection characteristics of the designed mechanism, leading to a linear expression stiffness equation varying with the rotation angle, which results in a simple position-determined stiffness control approach.
In contrast to the serial variable stiffness mechanism in the introductory section, although the limitations of the material of the compliant element do not allow the stiffness adjustment range to reach infinity, the use of a multi-stage compliant element in a series structure makes it capable of adjusting three different stiffness adjustment ranges. In addition, the structure of this mechanism is simpler than most of the series-connected joints mentioned previously, and it does not require too many compliant elements and other components to cooperate to achieve the effect of nonlinear transmission. From the application point of view, this mechanism can be used in scenarios that do not require a large joint angle, such as rehabilitation robotic arms and other medical devices. In addition, the material of the compliant structure and the number of compliant beams can be changed according to the load during the application. In summary, the structure and working principle of the variable stiffness mechanism designed in this work are simple, offering a wide range of stiffness adjustment and demonstrating high potential for practical applications.
6. Conclusions
In this work, a compliant actuation mechanism with multi-stage variable stiffness was designed. Before developing the overall mechanism, three types of compliant beam structures—composed of multiple straight segments, Bezier curves, and multiple arc segments—were parametrically optimized using SolidWorks–ANSYS co-simulation techniques. The corresponding torque–deflection curves of the compliant mechanisms are collected and fitted into analytical expressions, from which the stiffness equation varying with the angular position is derived for stiffness regulation. Based on the comparison of the varying stiffness curves, compliant mechanisms with linear stiffness equations are selected, aiming to ease the control issue.
Based on the selected complaint mechanisms, a combination of three-stage compliant mechanisms connected in serial is realized to prototype the physical mechanism. This varying stiffness mechanism can have three ranges of varying stiffness of the output shaft, and the maximum stiffness is about nine times higher than the lowest one, i.e., leading to a broader bandwidth of varying stiffness, which can make the mechanism more adaptive to the external payloads for safety consideration. Experimental measurements are carried out, and the comparison shows a good agreement between the experimental and simulation results, which experimentally validated the design concept. The compact and simple structure as well as the multi-stage variable stiffness ranges imply high adaptability of the designed mechanism.
Author Contributions
Conceptualization, methodology, software, validation, formal analysis, writing—original draft preparation, K.W.; Conceptualization, methodology, data curation, writing—review and editing, supervision, G.W. All authors have read and agreed to the published version of the manuscript.
Funding
The support from the National Key R&D Program of China (2024YFF0505103), the National Natural Science Foundation of China (52375232), and the Liaoning (China) Revitalization Talents Program (XLYC2203031) are gratefully appreciated.
Data Availability Statement
Data available upon the request from the authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Villani, V.; Pini, F.; Leali, F.; Secchi, C. Survey on Human-Robot Collaboration in Industrial Settings: Safety, Intuitive Interfaces and Applications. Mechatronics 2018, 55, 248–266. [Google Scholar] [CrossRef]
- Heyer, C. Human-Robot Interaction and Future Industrial Robotics Applications. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 4749–4754. [Google Scholar]
- Brogårdh, T. Present and Future Robot Control Development—An Industrial Perspective. Annu. Rev. Control 2007, 31, 69–79. [Google Scholar] [CrossRef]
- Kim, Y.; Kim, D.-W.; Kang, B.-Y. Table-Balancing Cooperative Robot Based on Deep Reinforcement Learning. Sensors 2023, 23, 5235. [Google Scholar] [CrossRef] [PubMed]
- Alvi, M.H.; Fu, J.; Newell, B.A.; Gan, D. A Variable Stiffness Soft Actuator for Hand Rehabilitation. In Proceedings of the 2024 6th International Conference on Reconfigurable Mechanisms and Robots (Remar), Chicago, IL, USA, 23–26 June 2024; pp. 587–594. [Google Scholar]
- Du, W.; Yi, G.; Omisore, O.M.; Duan, W.; Oluwadra Akinyemi, T.; Chen, X.; Liu, J.; Lee, B.-G.; Wang, L. Analyzing Surgeon-Robot Cooperative Performance in Robot-Assisted Intravascular Catheterization. IEEE Trans. Hum.-Mach. Syst. 2024, 54, 698–710. [Google Scholar] [CrossRef]
- Li, X.; Hao, Y.; Zhang, J.; Wang, C.; Li, D.; Zhang, J. Design, Modeling and Experiments of a Variable Stiffness Soft Robotic Glove for Stroke Patients with Clenched Fist Deformity. IEEE Robot. Autom. Lett. 2023, 8, 4044–4051. [Google Scholar] [CrossRef]
- Li, Z.; Chu, X.; Hu, X.; Zhang, Z.; Li, N.; Li, J. Variable Stiffness Methods for Robots: A Review. Smart Mater. Struct. 2024, 33, 63002. [Google Scholar] [CrossRef]
- Bilancia, P.; Berselli, G.; Scarcia, U.; Palli, G. Design of a Beam-Based Variable Stiffness Actuator via Shape Optimization in a CAD/CAE Environment. In Proceedings of the ASME 2018 Conference on Smart Materials, Adaptive Structures and Intelligent Systems, San Antonio, TX, USA, 10 September 2018; American Society of Mechanical Engineers: New York, NY, USA, 2018; p. V001T03A013. [Google Scholar]
- Bilancia, P.; Berselli, G.; Palli, G. Virtual and Physical Prototyping of a Beam-Based Variable Stiffness Actuator for Safe Human-Machine Interaction. Robot. Comput.-Integr. Manuf. 2020, 65, 101886. [Google Scholar] [CrossRef]
- Palli, G.; Melchiorri, C.; Berselli, G.; Vassura, G. Design and Modeling of Variable Stiffness Joints Based on Compliant Flexures. In Proceedings of the ASME 2010 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Montreal, QC, Canada, 15 August 2010; ASMEDC: Washington, DC, USA, 2010; pp. 1069–1078. [Google Scholar]
- Sun, X.; Xiong, X.; Chen, W.; Chen, W.; Yang, G. Design and Control of a Novel Variable Stiffness Actuator Based on Antagonistic Variable Radius Principle. ISA Trans. 2024, 147, 567–576. [Google Scholar] [CrossRef]
- Xiong, X.; Sun, X.; Chen, W.; Zhi, Y.; Fang, X. Design of a Variable Stiffness Actuator Based on Variable Radius Mechanisms. In Proceedings of the 2022 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Sapporo, Japan, 11 July 2022; pp. 1567–1572. [Google Scholar]
- Gaozhang, W.; Li, Y.; Shi, J.; Wang, Y.; Stilli, A.; Wurdemann, H. A Novel Stiffness-Controllable Joint Using Antagonistic Actuation Principles. Mech. Mach. Theory 2024, 196, 105614. [Google Scholar] [CrossRef]
- Ning, Y.; Xu, W.; Huang, H.; Li, B.; Liu, F. Design Methodology of a Novel Variable Stiffness Actuator Based on Antagonistic-Driven Mechanism. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2019, 233, 6967–6984. [Google Scholar] [CrossRef]
- Zhang, W.; Yan, P. A Variable Stiffness Compliant Actuator Based on Antagonistic Normal-Stressed Electromagnetic Mechanism. Sens. Actuators A 2024, 366, 114983. [Google Scholar] [CrossRef]
- Van Ham, R.; Vanderborght, B.; Van Damme, M.; Verrelst, B.; Lefeber, D. MACCEPA, the Mechanically Adjustable Compliance and Controllable Equilibrium Position Actuator: Design and Implementation in a Biped Robot. Rob. Auton. Syst. 2007, 55, 761–768. [Google Scholar] [CrossRef]
- Vanderborght, B.; Tsagarakis, N.G.; Van Ham, R.; Thorson, I.; Caldwell, D.G. MACCEPA 2.0: Compliant Actuator Used for Energy Efficient Hopping Robot Chobino1D. Auton. Rob. 2011, 31, 55–65. [Google Scholar] [CrossRef]
- Xu, Y.; Guo, K.; Sun, J.; Li, J. Design, Modeling and Control of a Reconfigurable Variable Stiffness Actuator. Mech. Syst. Signal Proc. 2021, 160, 107883. [Google Scholar] [CrossRef]
- Cui, C.; Guo, K.; Sun, J. Variable Stiffness Actuator Structure for Robot. In Intelligent Robotics and Applications, ICIRA 2021, PT I; Liu, X.J., Nie, Z., Yu, J., Xie, F., Song, R., Eds.; Springer International Publishing Ag: Cham, Switzerland, 2021; Volume 13013, pp. 275–283. [Google Scholar]
- Abbood, W.T.; Nacy, S.M.; Youssef, G.; Abdullah, O.I. Dynamic Performance of a Series Elastic Actuator with Variable Stiffness Logarithmic Spiral Spring. Intell. Serv. Rob. 2022, 15, 275–287. [Google Scholar] [CrossRef]
- Jafari, A.; Tsagarakis, N.G.; Caldwell, D.G. A Novel Intrinsically Energy Efficient Actuator with Adjustable Stiffness (AwAS). IEEE/ASME Trans. Mechatron. 2013, 18, 355–365. [Google Scholar] [CrossRef]
- Jafari, A.; Tsagarakis, N.G.; Caldwell, D.G. AwAS-II: A New Actuator with Adjustable Stiffness Based on the Novel Principle of Adaptable Pivot Point and Variable Lever Ratio. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9 May 2011; pp. 4638–4643. [Google Scholar]
- Lu, Y.; Yang, Y.; Xue, Y.; Jiang, J.; Zhang, Q.; Yue, H. A Variable Stiffness Actuator Based on Leaf Springs: Design, Model and Analysis. Actuators 2022, 11, 282. [Google Scholar] [CrossRef]
- Visser, L.C.; Carloni, R.; Stramigioli, S. Energy-Efficient Variable Stiffness Actuators. IEEE Trans. Robot. 2011, 27, 865–875. [Google Scholar] [CrossRef]
- Ramadan, M.A.; Awad, M.I.; Boushaki, M.N.; Niu, Z.; Khalaf, K.; Hussain, I. irisVSA: Infinite-Rotation Infinite-Stiffness Variable Stiffness Actuator towards Physical Human–Robot-Interaction. Mechatronics 2023, 96, 103095. [Google Scholar] [CrossRef]
- Yi, S.; Liu, S.; Liao, J.; Guo, Z. Design and Modeling of a Compact Serial Variable Stiffness Actuator (SVSA-III) with Linear Stiffness Profile. In Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13 May 2024; pp. 7077–7082. [Google Scholar]
- Yang, T.; Zhang, H.; Zhang, S.; Wu, X.; Qiu, Y.; Zhang, J. Design and Modeling of a Trapezoidal Leaf Spring-Based Actuators with Valid Arm Length and Bending Deformation for Stiffness Adjustment. In Proceedings of the 2024 3rd Conference on Fully Actuated System Theory and Applications (FASTA), Shenzhen, China, 10 May 2024; pp. 121–126. [Google Scholar]
- Shao, Y.; Shi, D.; Feng, Y.; Zhang, W.; Ding, X. Design and Control of a Compact Variable Stiffness Actuator Based on a Cam-Circular Beam Mechanism. IEEE/ASME Trans. Mechatron. 2024, 29, 4131–4143. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, P.; Zhu, H.; Xia, K.; Ren, T.; Shen, Y.; Li, Y. A Variable Stiffness Soft Robotic Manipulator Based on Antagonistic Design of Supercoiled Polymer Artificial Muscles and Shape Memory Alloys. Sens. Actuators A 2024, 366, 114999. [Google Scholar] [CrossRef]
- Zhu, S.; Liu, M.; Min, X.; Dong, S. Research on Variable Stiffness Robotic Joint Actuator Based on Shape Memory Alloy. J. Mech. Sci. Technol. 2025, 39, 939–948. [Google Scholar] [CrossRef]
- Carloni, R.; Lapp, V.I.; Cremonese, A.; Belcari, J.; Zucchelli, A. A Variable Stiffness Joint with Electrospun P(VDF-TrFE-CTFE) Variable Stiffness Springs. IEEE Robot. Autom. Lett. 2018, 3, 973–978. [Google Scholar] [CrossRef]
- Giraud, F.H.; Mete, M.; Paik, J. Flexure Variable Stiffness Actuators. Adv. Intell. Syst. 2022, 4, 2100282. [Google Scholar] [CrossRef]
- Caro, F.; Carmichael, M.G. A Review of Mechanisms to Vary the Stiffness of Laminar Jamming Structures and Their Applications in Robotics. Actuators 2024, 13, 64. [Google Scholar] [CrossRef]
- Xu, F.; Ma, K.; He, X.; Wei, M.; Hu, C. Design, Analysis, and Testing of a Variable-Stiffness Soft Grabbing Robot Coupling Particle Jamming and Layer Jamming. Smart Mater. Struct. 2024, 33, 55036. [Google Scholar] [CrossRef]
- Arleo, L.; Lorenzon, L.; Cianchetti, M. Variable Stiffness Linear Actuator Based on Differential Drive Fiber Jamming. IEEE Trans. Robot. 2023, 39, 4429–4442. [Google Scholar] [CrossRef]
- Peng, H.; Wang, X.; Geng, D.; Xu, W. A Pneumatic Particle-Blocking Variable-Stiffness Actuator. Sensors 2023, 23, 9817. [Google Scholar] [CrossRef]
- Chen, C.; Ren, H.; Wang, H. Augment Laminar Jamming Variable Stiffness Through Electroadhesion and Vacuum Actuation. IEEE Trans. Robot. 2025, 41, 819–836. [Google Scholar] [CrossRef]
- Mikol, C.; Su, H.-J. An Actively Controlled Variable Stiffness Structure via Layer Jamming and Pneumatic Actuation. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 7555–7561. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).