Research on Active Lubrication Based on Piezoelectric Micropump
Abstract
1. Introduction
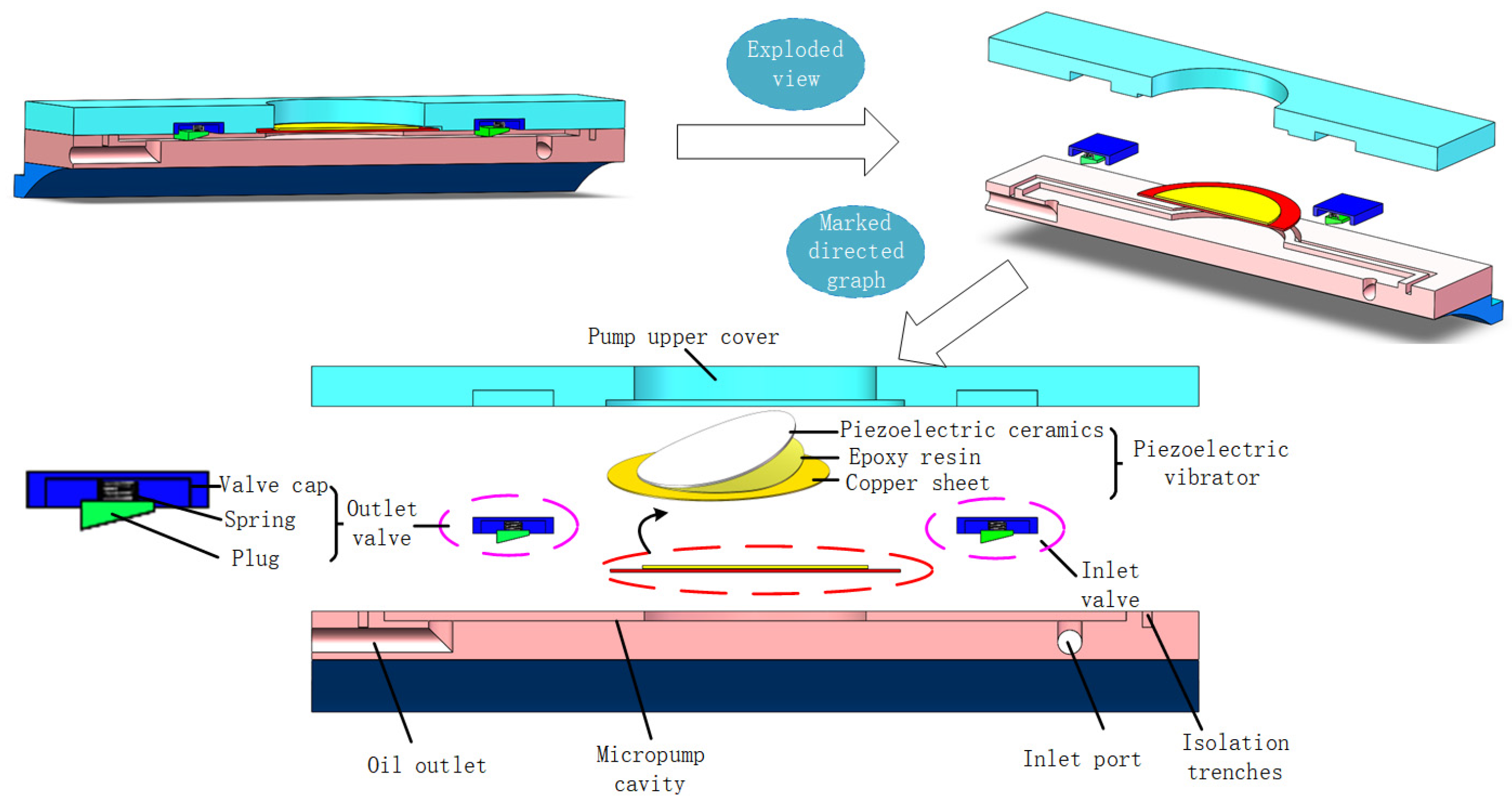
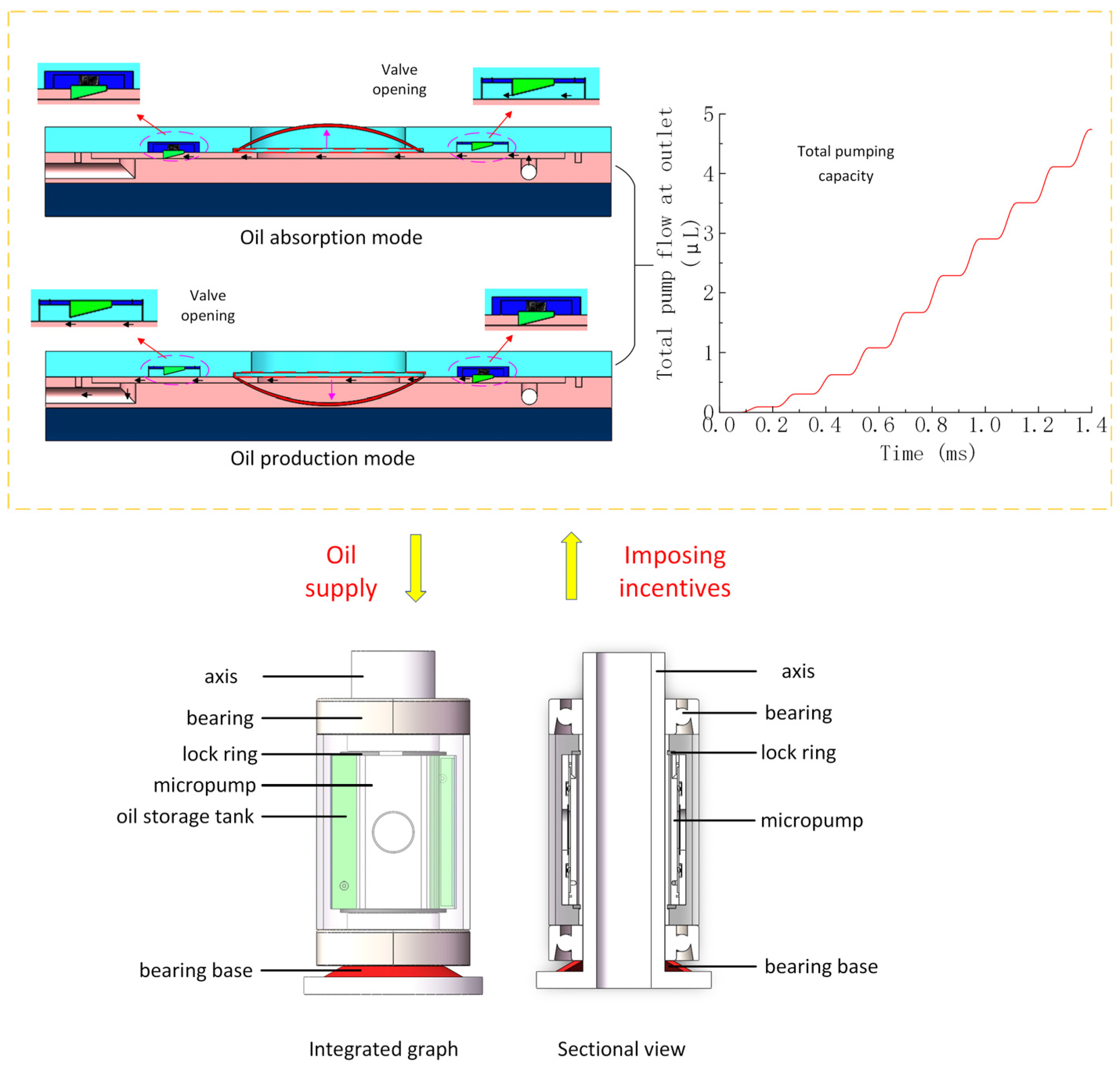
2. Structure and Mechanism
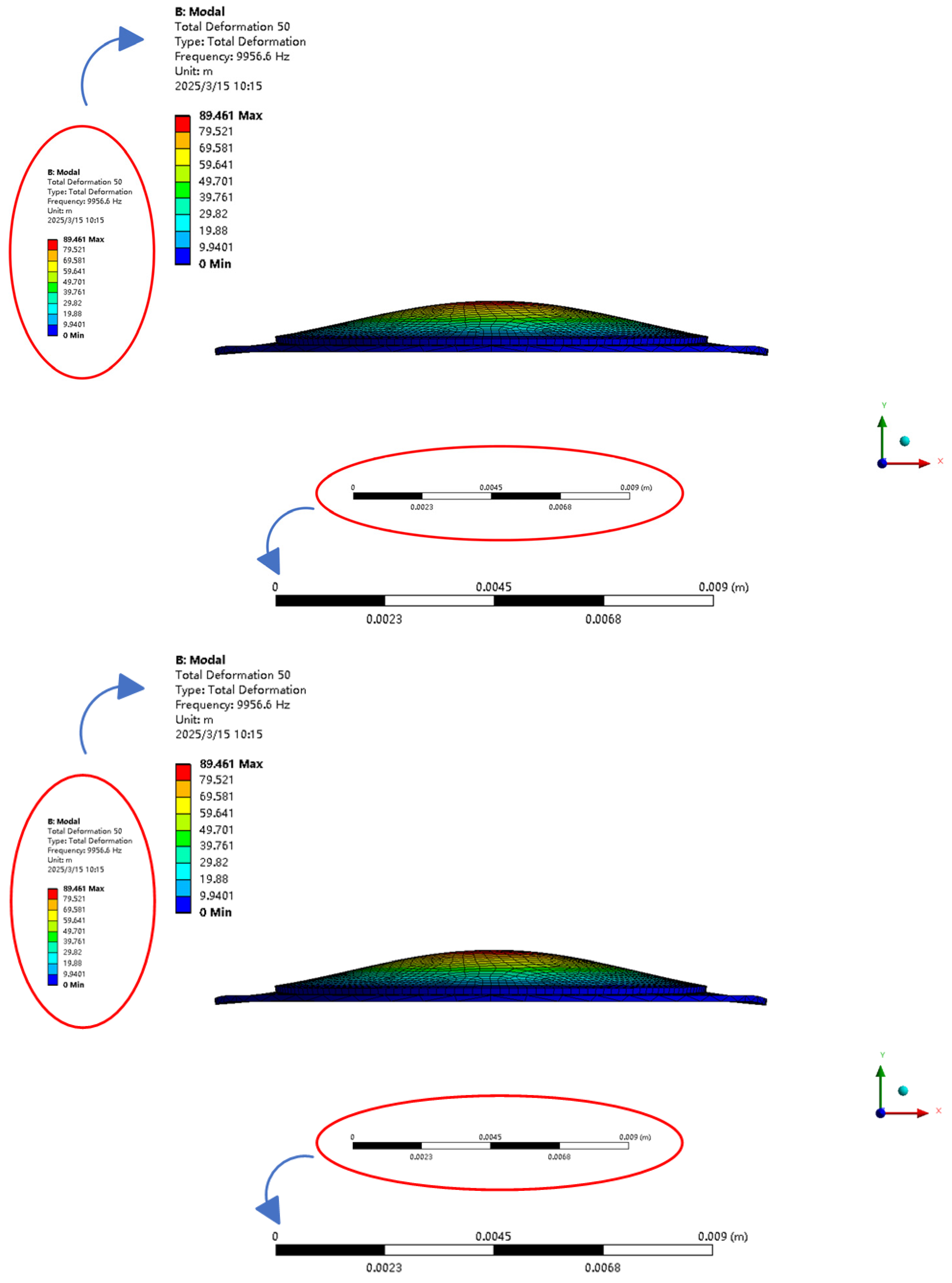
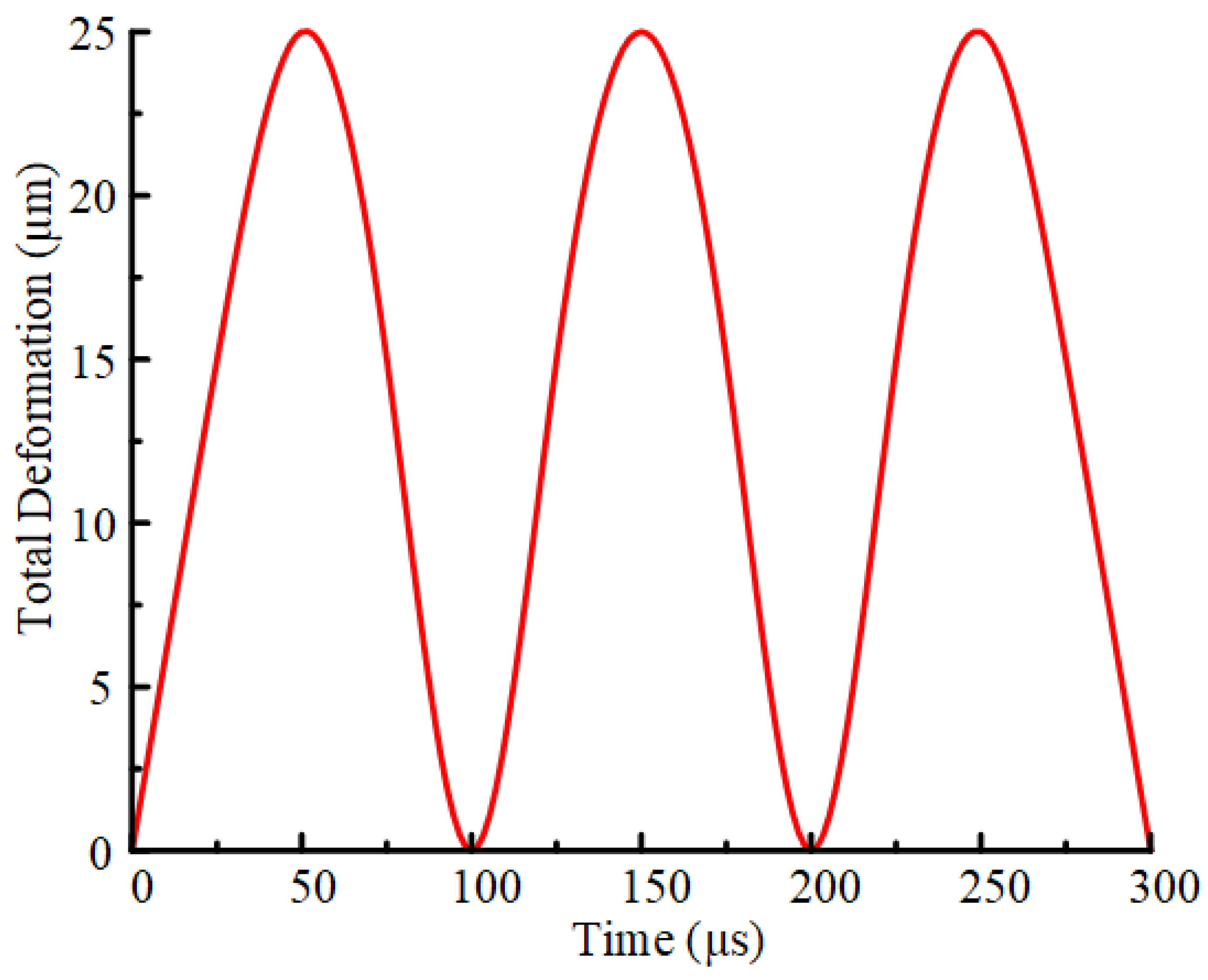
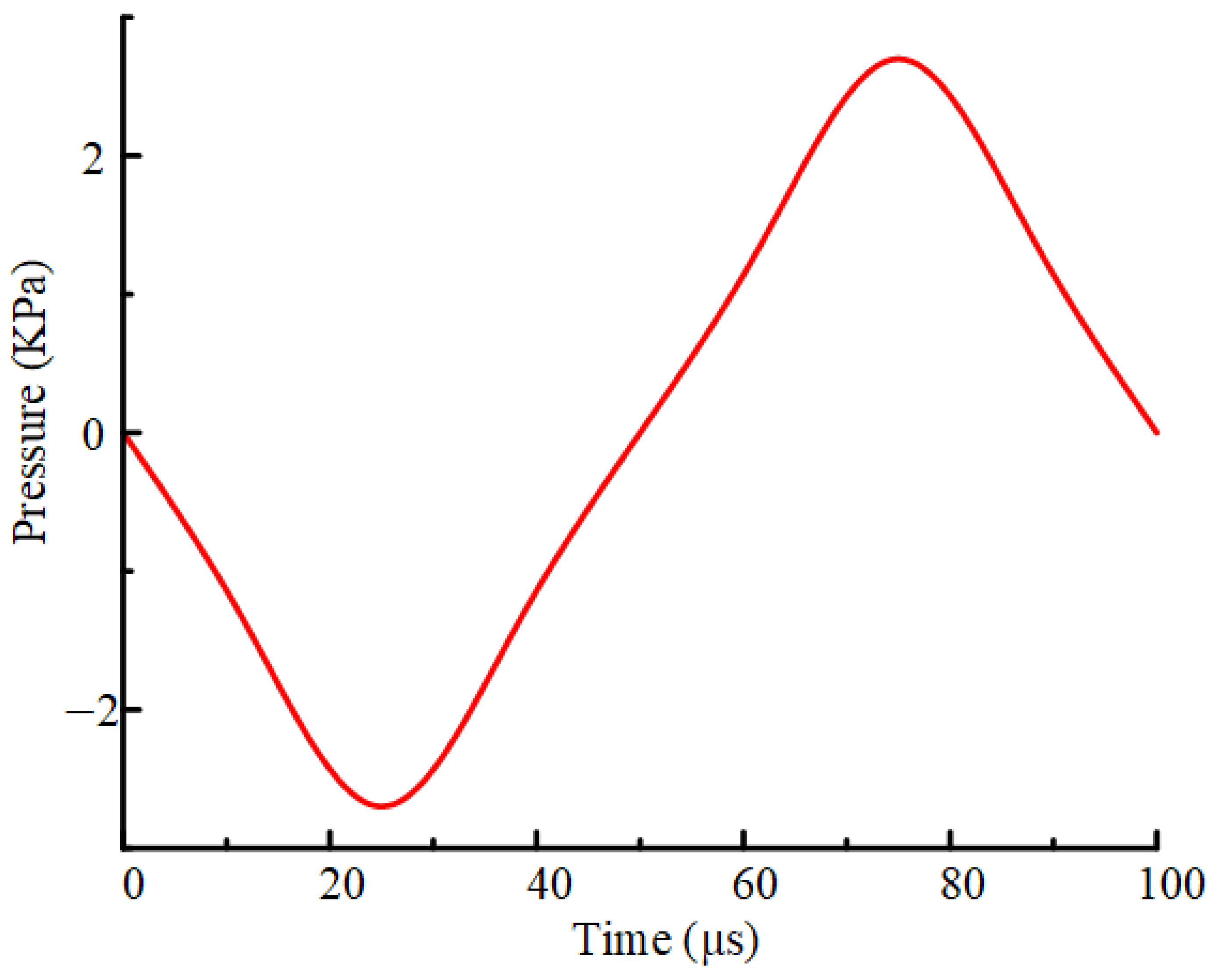
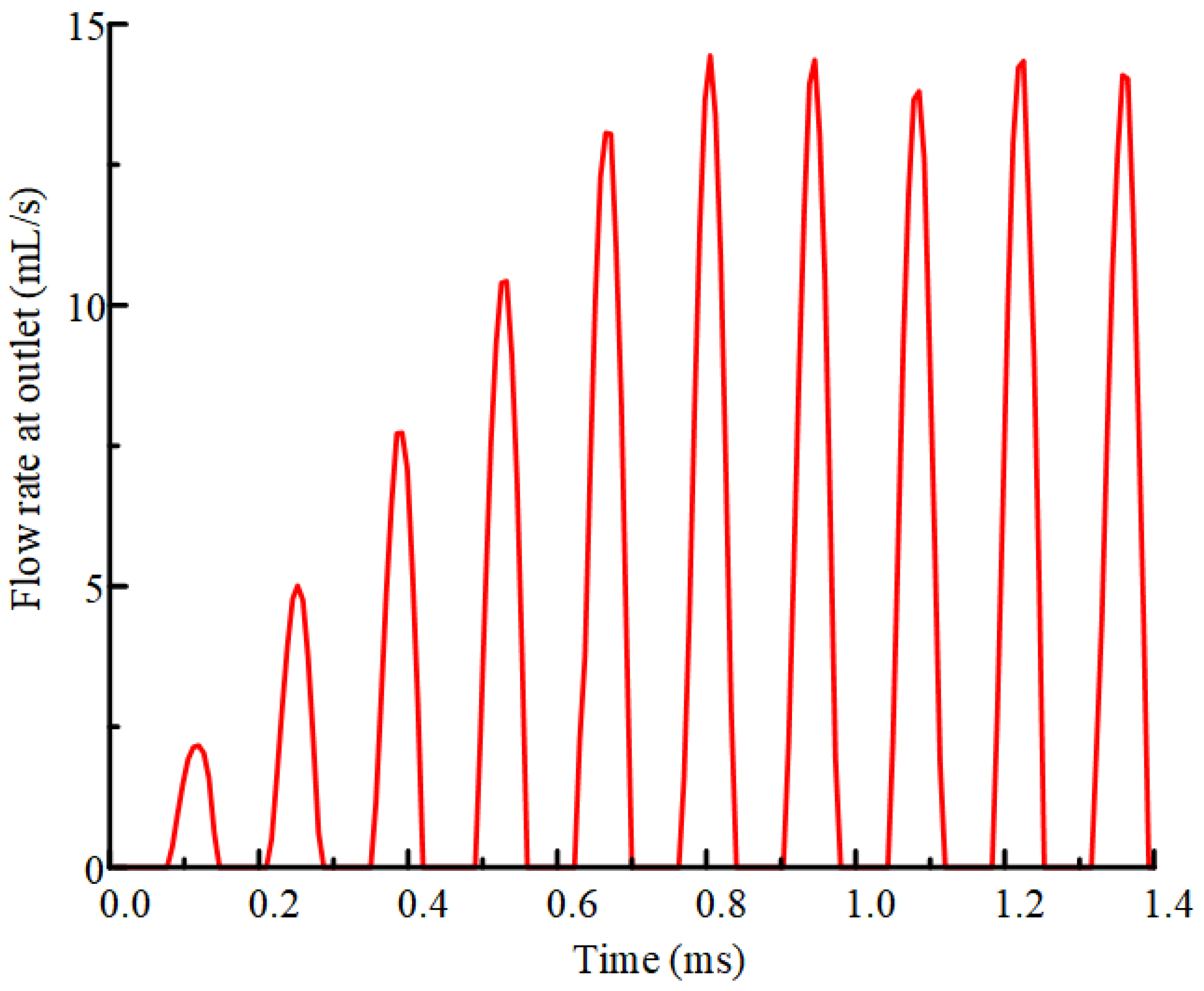
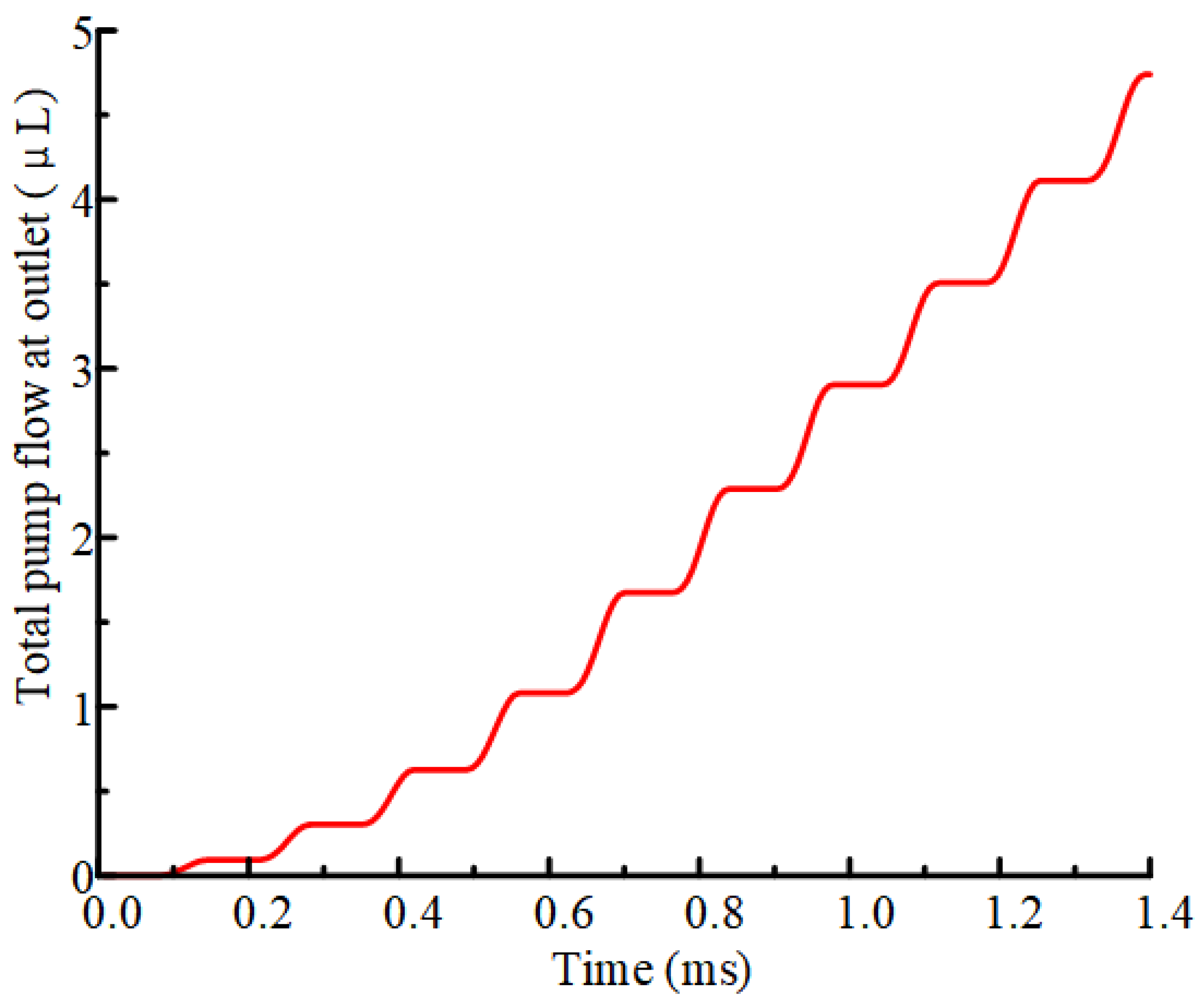
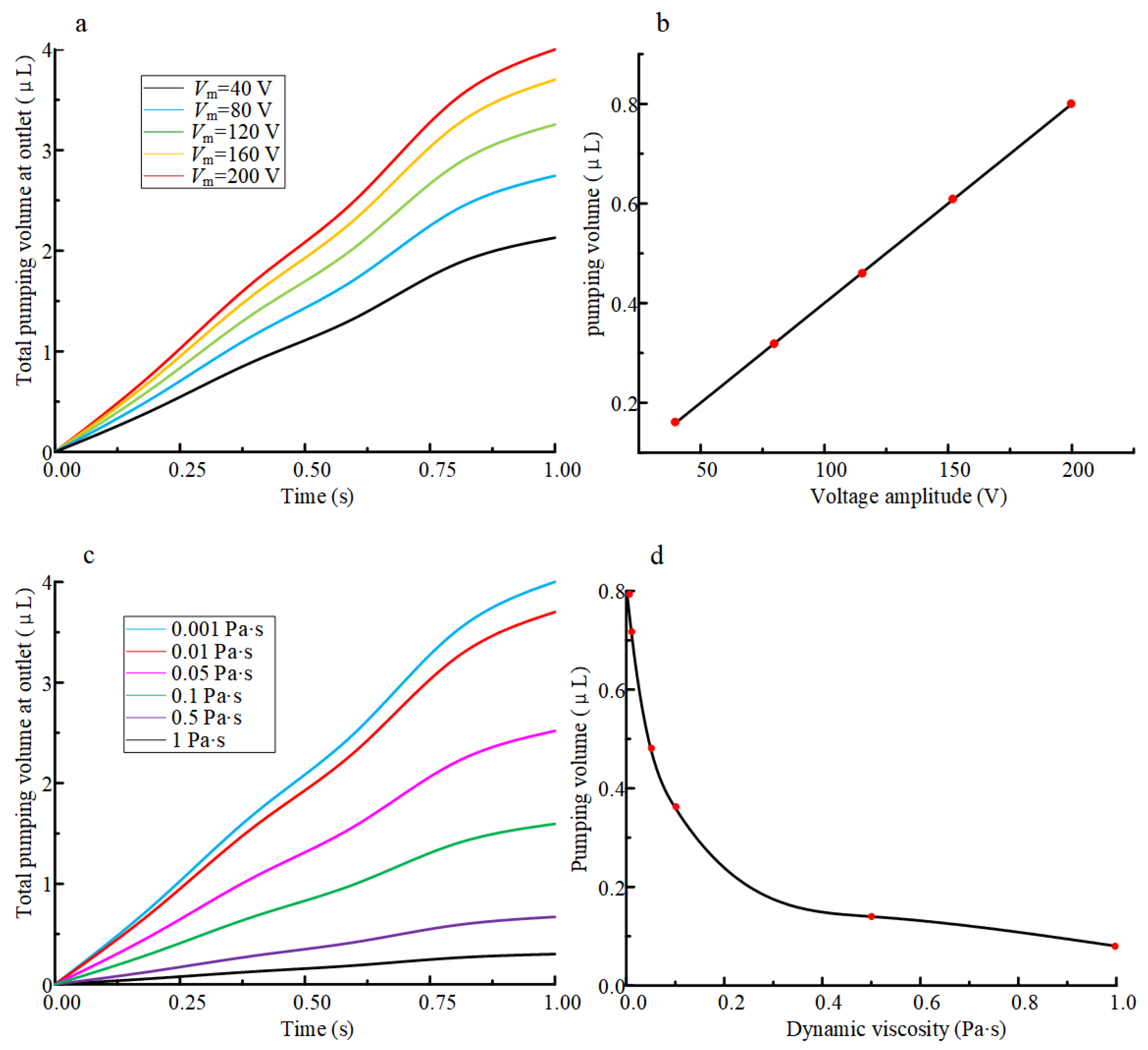
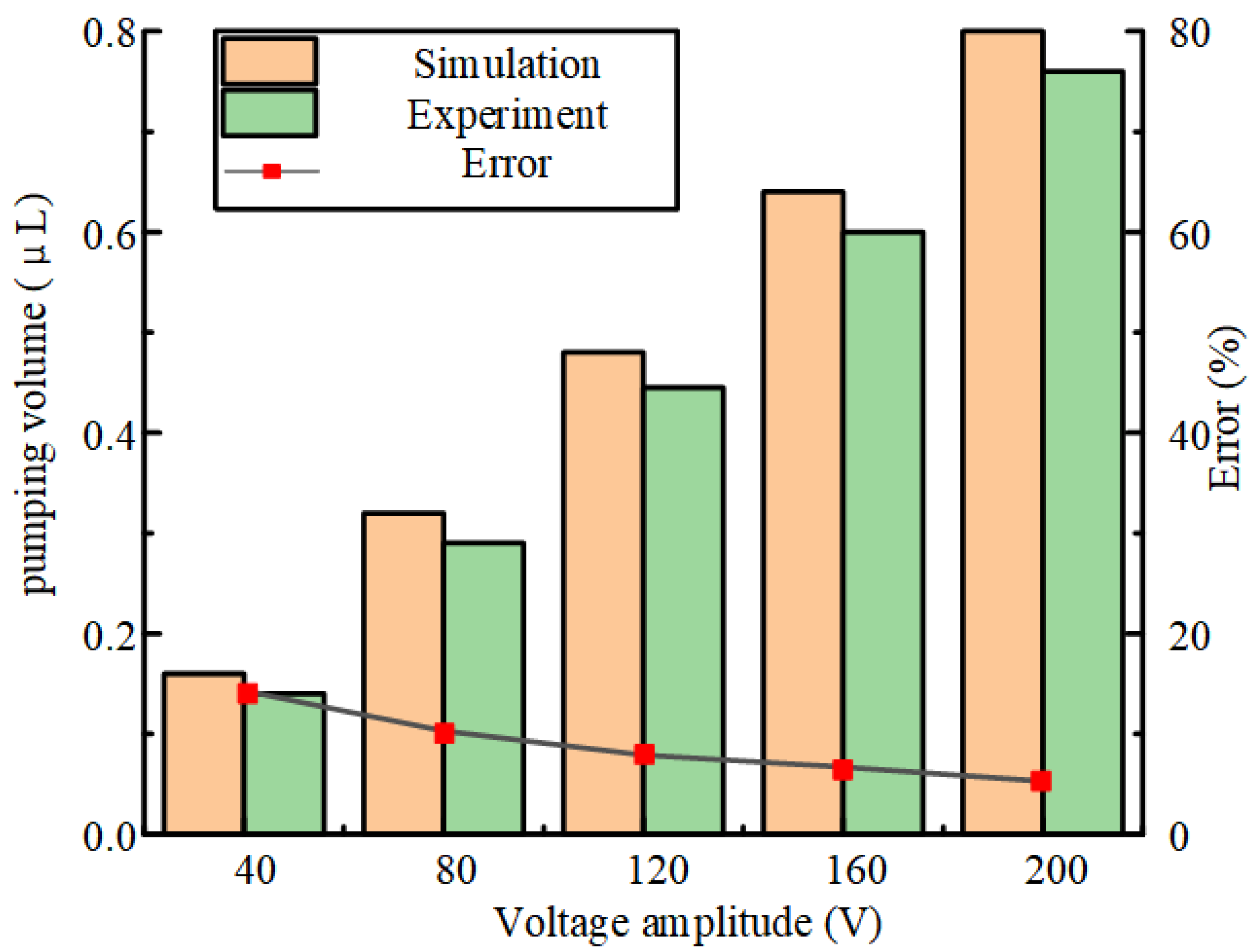
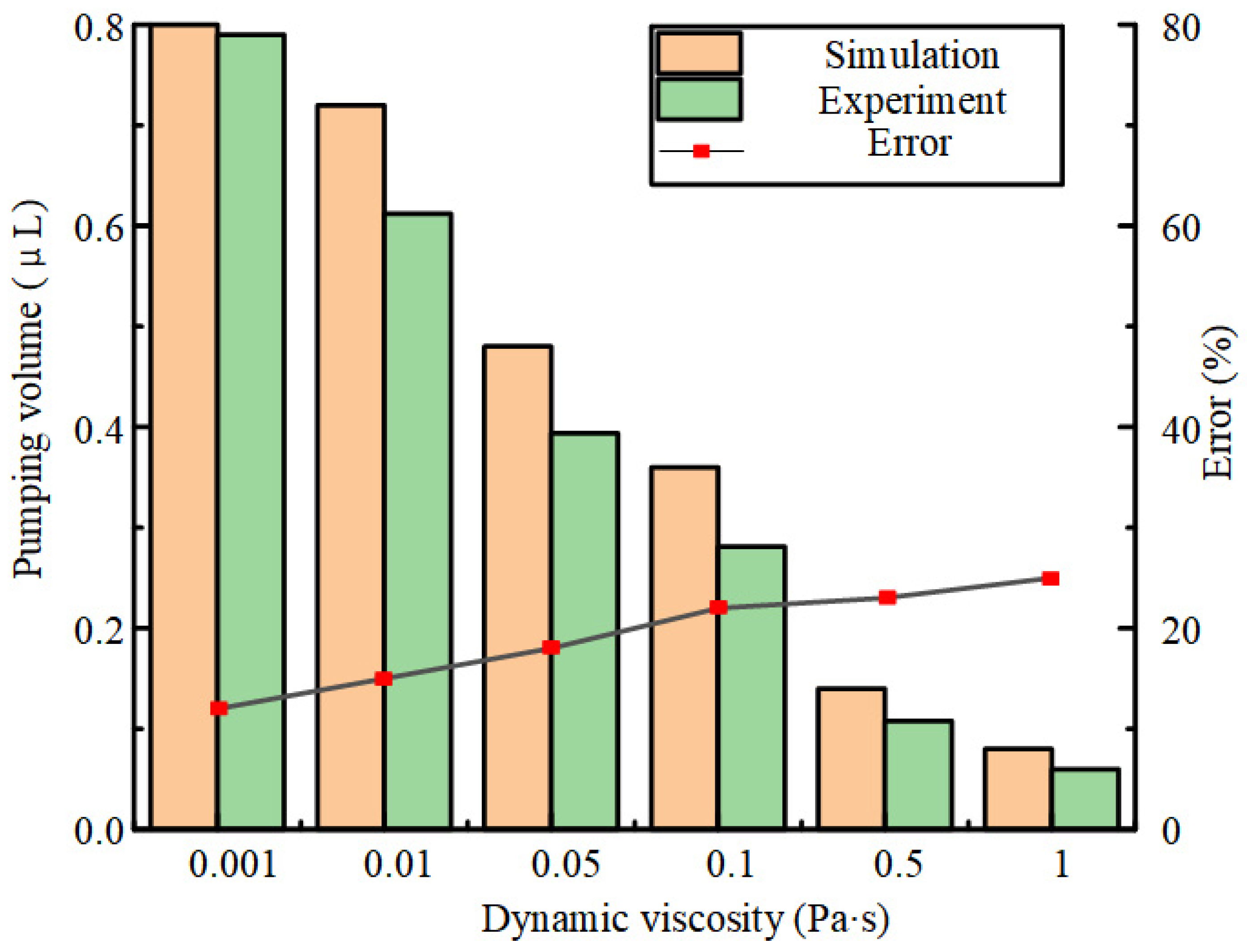
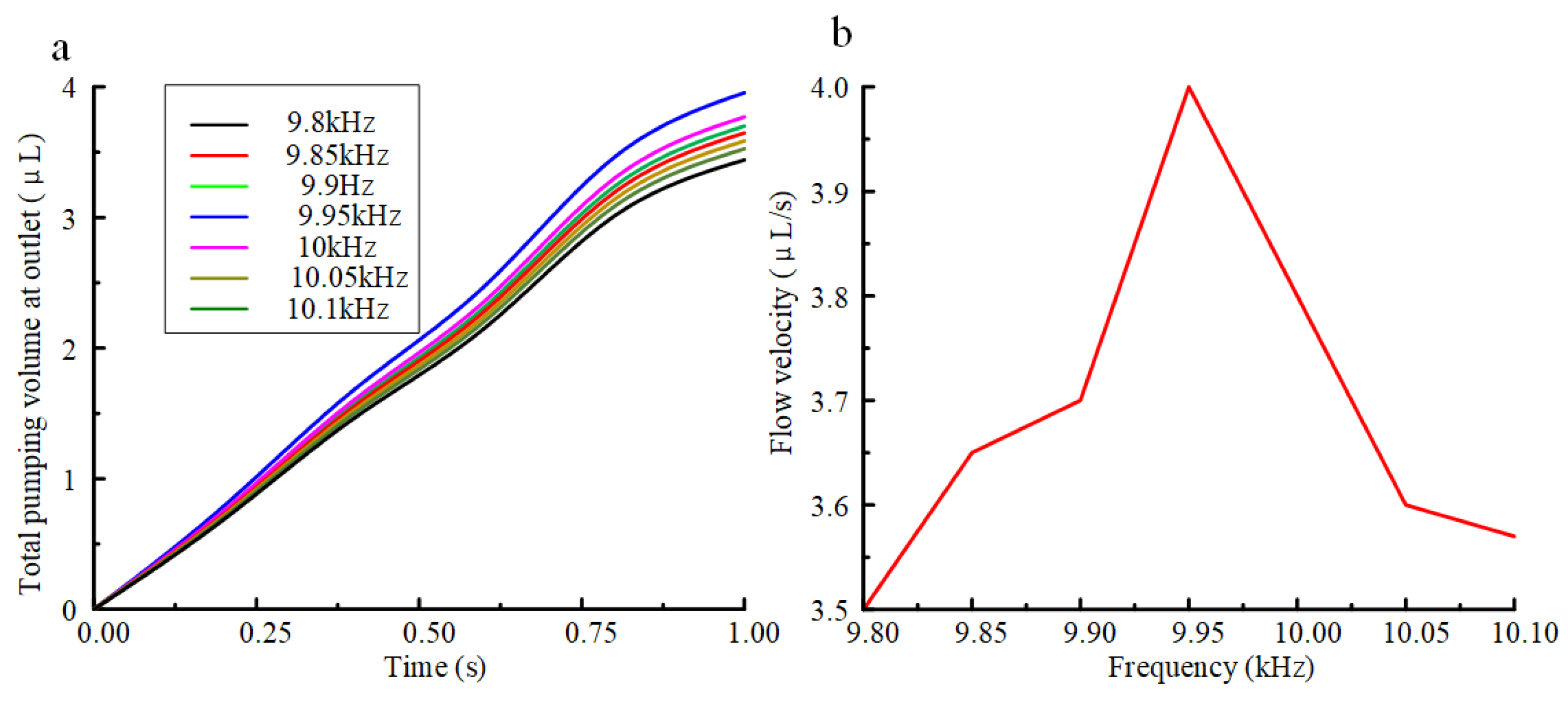
3. Performance Controlling
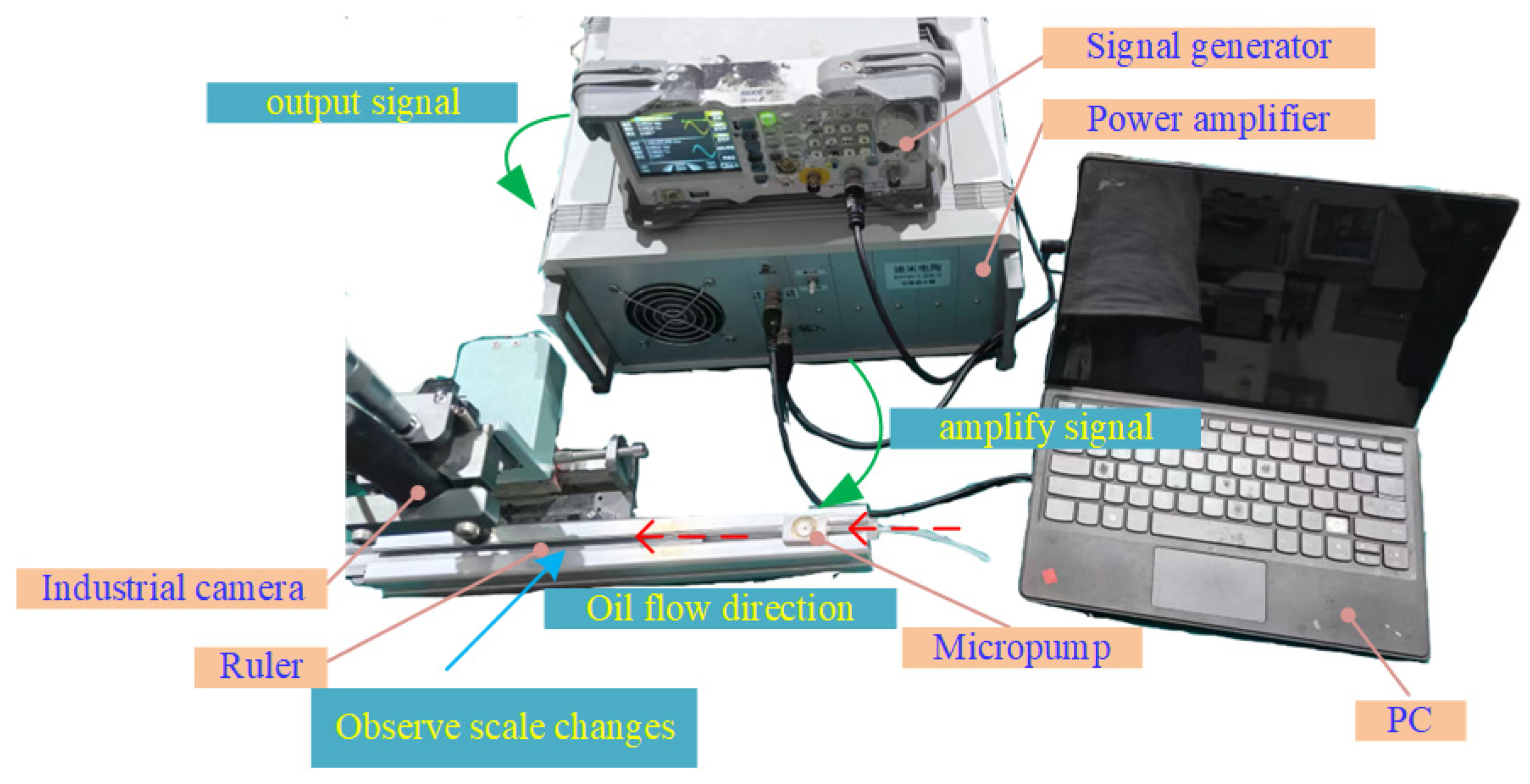
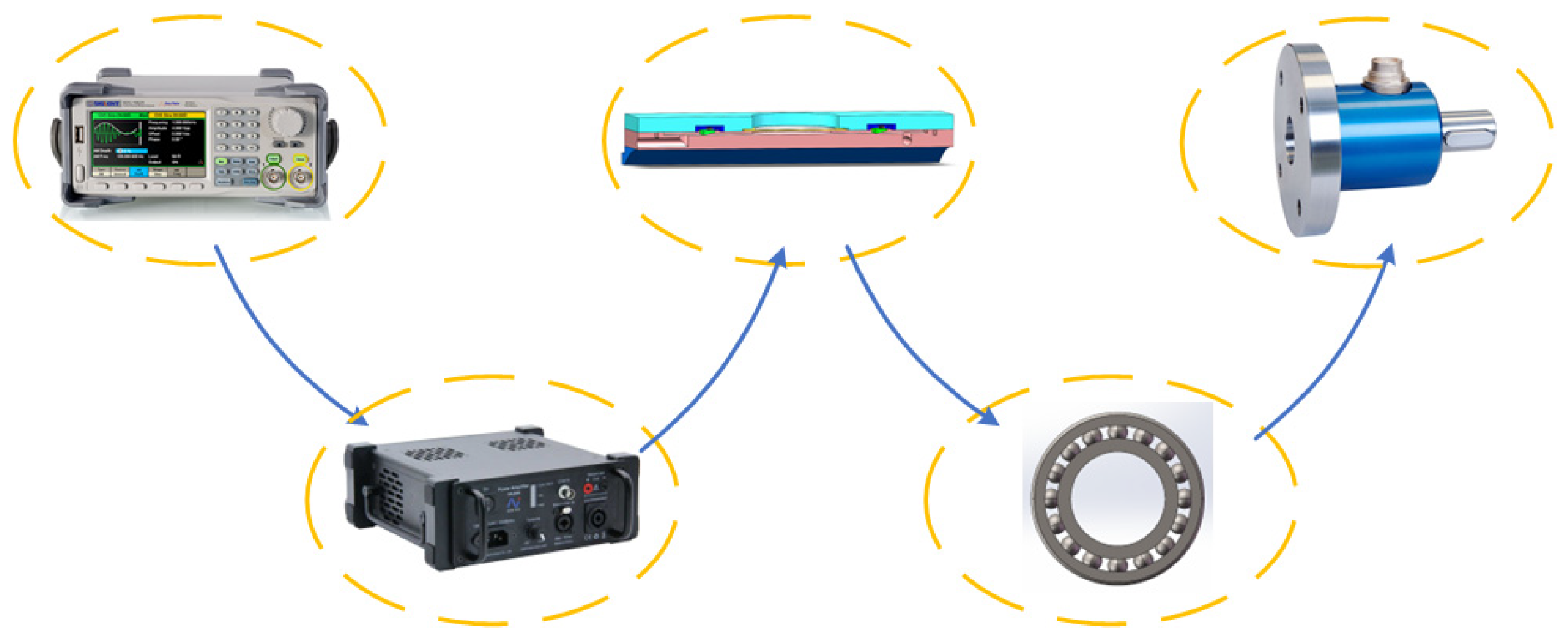
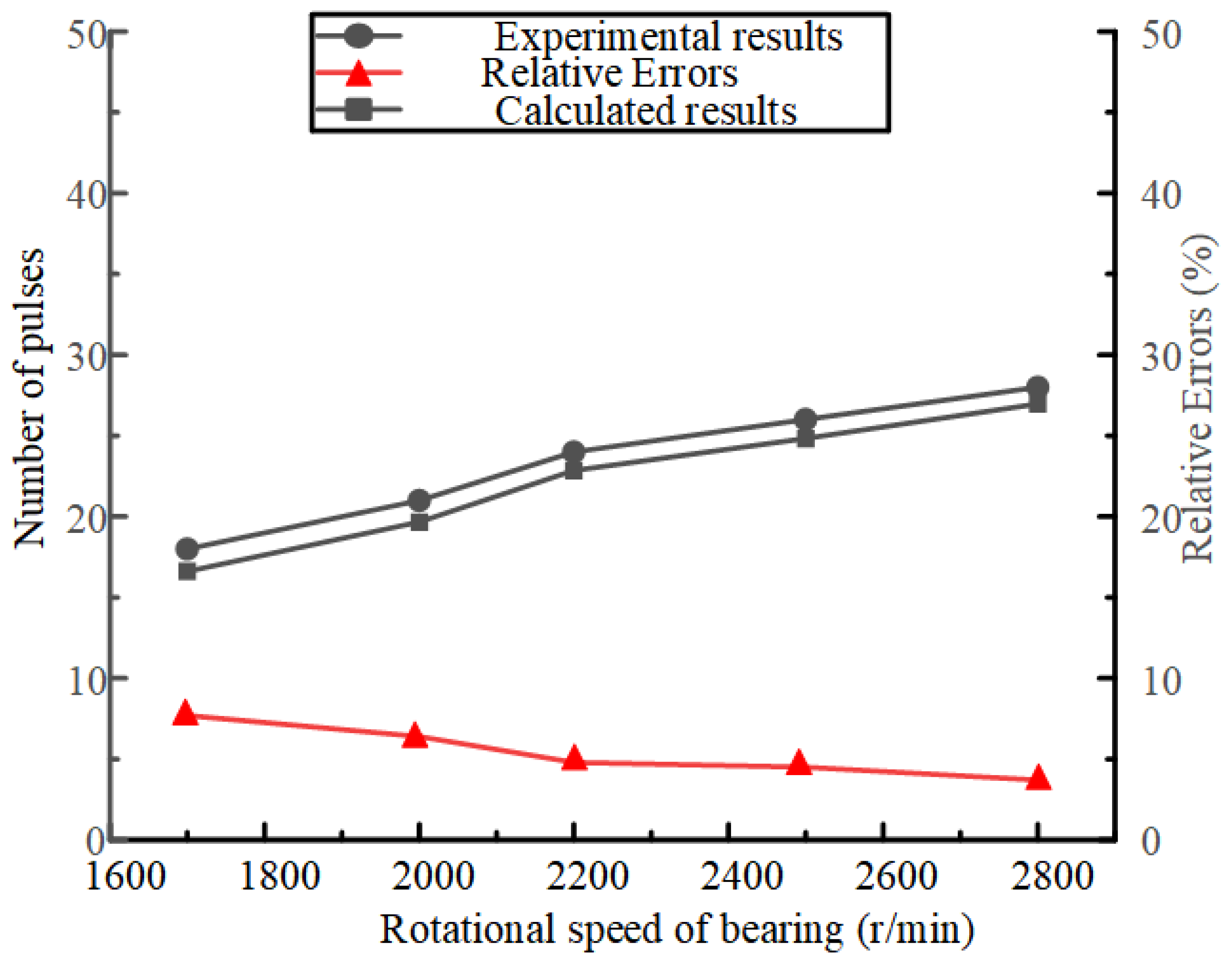
4. Experiments
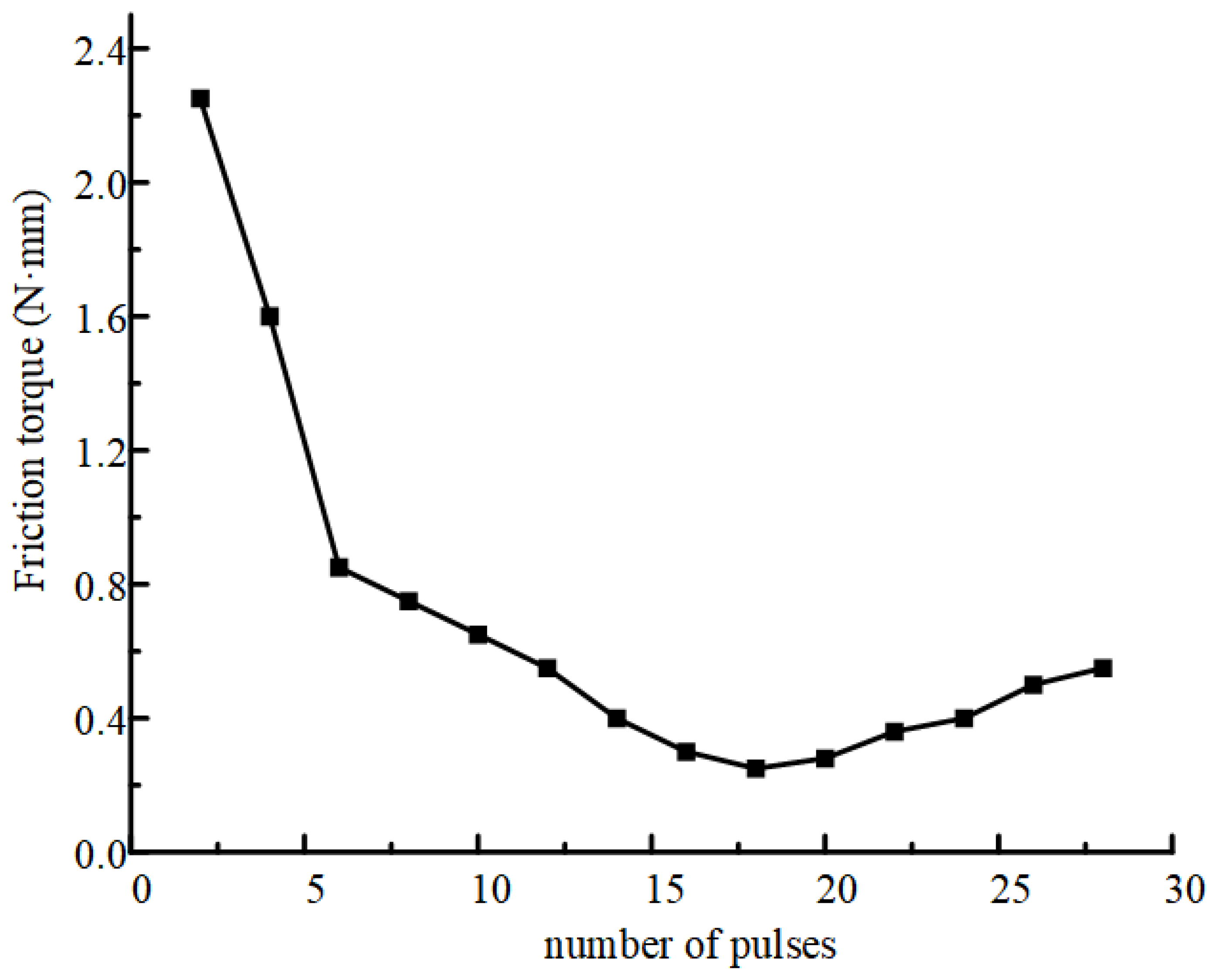
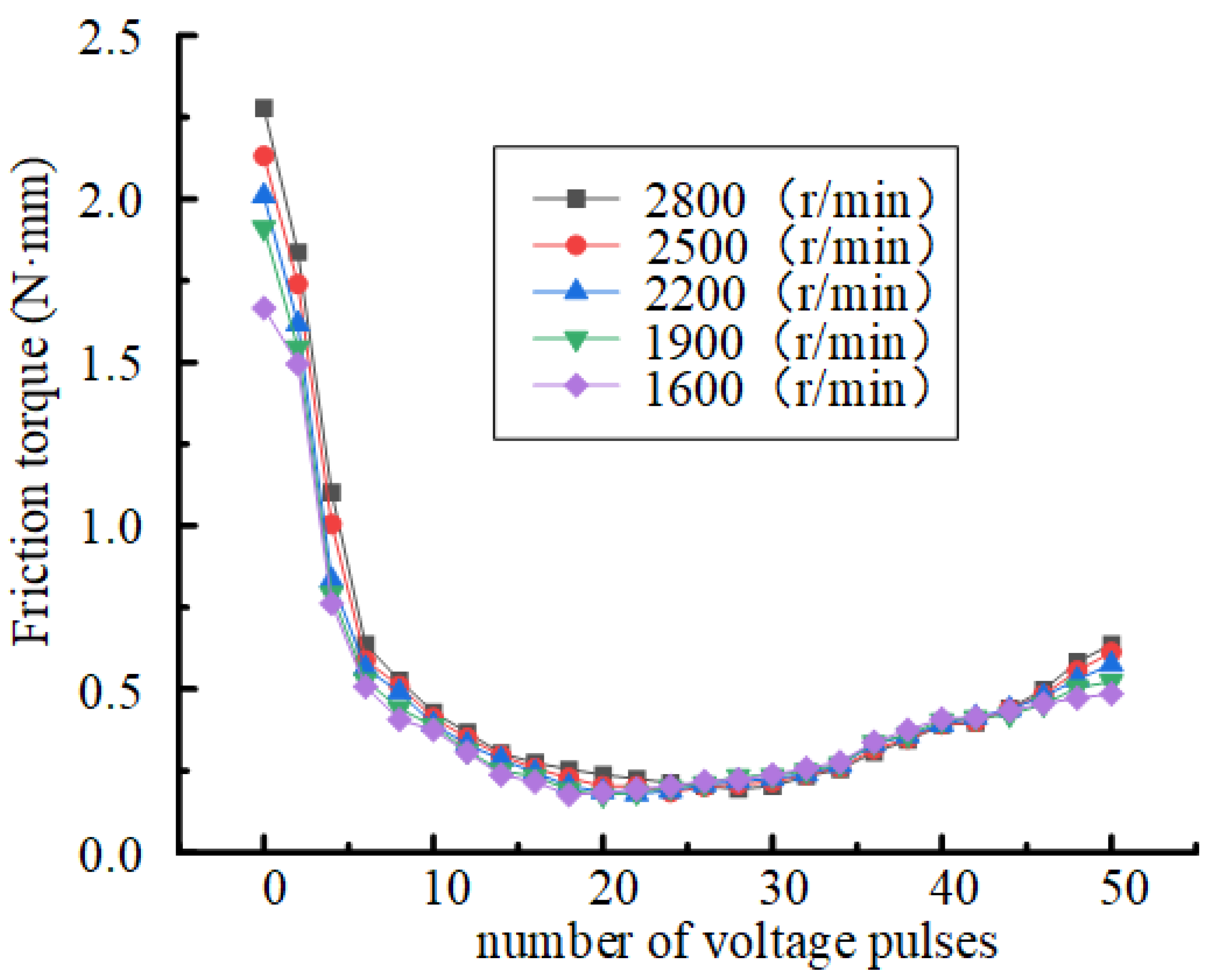
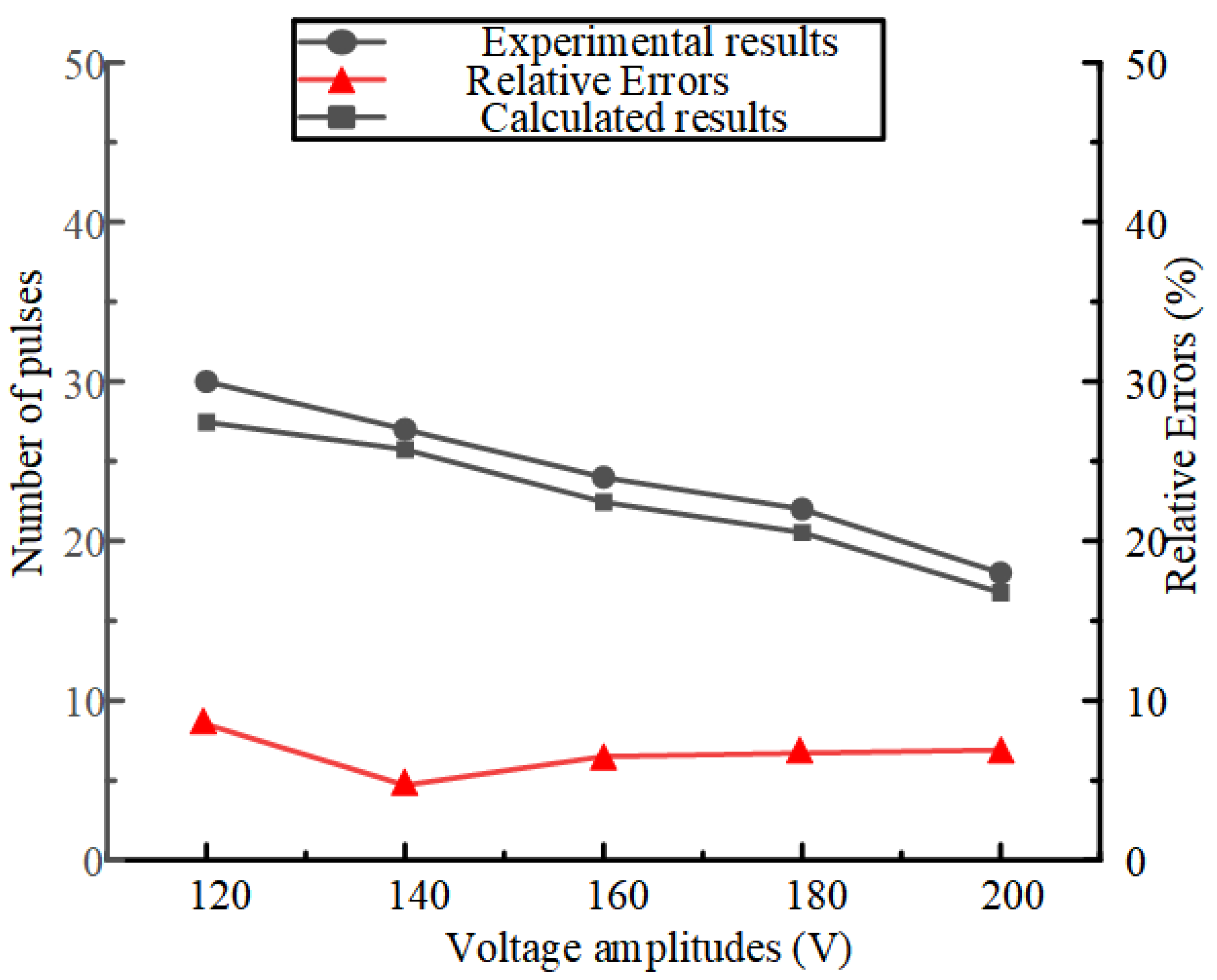
5. Lubrication Performance
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Krishnan, S.; Hsu, H.-Y.; Lee, S.-H.; Gopinath, K. A Bearing Cartridge Assembly for Long-term Performance of Momentum/Reaction Wheels used in Spacecraft. Tribol. Ind. 2014, 36, 22–32. [Google Scholar]
- Loewenthal, S.H.; Parker, R.J.; Zaretsky, E.V.; Scibbe, H.W. Operating Characteristics of a 0.87 kW-hr Flywheel Energy Storage Module. 1985. Available online: https://ntrs.nasa.gov/citations/19860040126 (accessed on 1 April 2025).
- Chen, W.B.; Wang, W.Z.; Liang, H.; Zhu, P.Z. Molecular Dynamics Simulations of Lubricant Outflow in Porous Polyimide Retainers of Bearings. Langmuir 2021, 37, 9162–9169. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zhao, H.; Huang, W.; Wang, X. Investigation of Porous Polyimide Lubricant Retainers to Improve the Performance of Rolling Bearings under Conditions of Starved Lubrication. Wear 2017, 380, 52–58. [Google Scholar] [CrossRef]
- Lugt, P.M. A Review on Grease Lubrication in Rolling Bearings. Tribol. Lubr. Technol. Rev. 2010, 66, 44. [Google Scholar] [CrossRef]
- Marchetti, M.; Jones, W.R.; Pepper, S.V.; Jansen, M.J.; Predmore, R.E. In-situ, on-demand lubrication system for space mechanisms. Tribol. Trans. 2003, 46, 452–459. [Google Scholar] [CrossRef][Green Version]
- Krishnan, S. Long-Term Lubrication Systems for Momentum Wheels Used in Spacecrafts. Tribol. Int. 2003, 43, 259–267. [Google Scholar]
- Estupinan, E.; Santos, I. Controllable Lubrication for Main Engine Bearings Using Mechanical and Piezoelectric Actuators. IEEE-ASME Trans. Mechatron. 2012, 17, 279–287. [Google Scholar] [CrossRef]
- Sathyan, K.; Hsu, H.Y.; Lee, S.H.; Gopinath, K. Long-term lubrication of momentum wheels used in spacecrafts-An overview. Tribol. Int. 2010, 43, 259–267. [Google Scholar] [CrossRef]
- Morosi, S.; Santos, I.F. Active lubrication applied to radial gas journal bearings. Part 1: Modeling. Tribol. Int. 2011, 44, 1949–1958. [Google Scholar] [CrossRef]
- Santos, I.F.; Watanabe, F.Y. Lateral dynamics and stability analysis of a gas compressor supported by hybrid and active lubricated multirecess journal bearing. J. Braz. Soc. Mech. Sci. Eng. 2006, 28, 485–495. [Google Scholar] [CrossRef]
- Li, K.; Yang, R.; Liu, J.; Chen, W.; Zhang, L.; Liu, Y. A Trace Redundant Lubrication Piezoelectric Micro-jet for Bearing System. IEEE/ASME Trans. Mechatron. 2018, 2018, 2862824. [Google Scholar] [CrossRef]
- Wegert, Z.J.; Roberts, A.P.; Challis, V.J. Multi-objective structural optimisation of piezoelectric materials. Int. J. Solids Struct. 2022, 248, 111666. [Google Scholar] [CrossRef]
- Zhang, L.; Zheng, H.; Liu, B.; Liang, Q.; Li, K.; Liu, J.; Chen, W. A piezoelectric energy harvester for multi-type environments. Energy 2024, 305, 132218. [Google Scholar] [CrossRef]
- Li, K.; Zhou, X.; Liu, Y.; Sun, J.; Tian, X.; Zheng, H.; Zhang, L.; Deng, J.; Liu, J.; Zhao, J.; et al. A 5 cm-Scale Piezoelectric Jetting Agile Underwater Robot. Adv. Intell. Syst. 2023, 5, 2200262. [Google Scholar] [CrossRef]
- Zhou, X.; Li, K.; Liu, Y.; Sun, J.; Li, H.; Chen, W. Development of an Anti-Hydropressure Miniature Underwater Robot with Multi-Locomotion Mode Using Piezoelectric Pulsed-Jet Actuator. IEEE Trans. Ind. Electron. 2022, 70, 5044–5054. [Google Scholar] [CrossRef]
- Shan, T.-Y.; Wu, X.-S.; Hu, Y.-W.; Lin, X.-D.; Sun, D.-F. Injection of Viscous Micro-Droplet via Nozzle-Driven Piezoelectric Micro-Jet and Its Performance Control Method. Micromachines 2023, 14, 1267. [Google Scholar] [CrossRef]
- Duque, M.; Leon-Salguero, E.; Sacristán, J.; Esteve, J.; Murillo, G. Optimization of a Piezoelectric Energy Harvester and Design of a Charge Pump Converter for CMOS-MEMS Monolithic Integration. Sensors 1895, 19, 1895. [Google Scholar] [CrossRef]
- Le, S.; Hegab, H. Investigation of a multistage micro gas compressor cascaded in series for increase pressure rise. Sens. Actuator A-Phys. 2017, 256, 66–76. [Google Scholar] [CrossRef]
- Gidde, R.R.; Pawar, P.M.; Dhamgaye, V.P. Fully coupled modeling and design of a piezoelectric actuation based valveless micropump for drug delivery application. Microsyst. Technol. 2020, 26, 633–645. [Google Scholar] [CrossRef]
- Yan, Q.F.; Yin, Y.K.; Sun, W.T.; Fu, J. Advances in Valveless Piezoelectric Pumps. Appl. Sci. 2021, 11, 7061. [Google Scholar] [CrossRef]
- Le, T.N.; Nguyen, V.A.; Bach, G.L.; Tran, L.D.; Cao, H. Design and Fabrication of a PDMS-Based Manual Micro-Valve System for Microfluidic Applications. Adv. Polym. Technol. 2020, 2020, 2460212. [Google Scholar] [CrossRef]
- Zhang, L.; Zheng, H.Y.; Zhou, X.X.; Liu, B.; Chen, S.; Li, K. A Universal Piezoelectric Micropump with Capabilities of Self-Cleaning, Stable Filtration and Precise Pumping. IEEE Trans. Ind. Electron. 2024, 71, 678–687. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, C.; Yue, Z.; Zhan, C.N.; Geng, W.D.; Liu, G.H. Travelling-wave piezoelectric micropump with low resistance microchannel. Electron. Lett. 2011, 47, 1065-U23. [Google Scholar] [CrossRef]
- Izzo, I.; Accoto, D.; Menciassi, A.; Schmitt, L.; Dario, P. Modeling and experimental validation of a piezoelectric micropump with novel no-moving-part valves. Sens. Actuator A-Phys. 2007, 133, 128–140. [Google Scholar] [CrossRef]
- Wu, X.Q.; He, L.P.; Hou, Y.; Tian, X.C.; Zhao, X.L. Advances in passive check valve piezoelectric pumps. Sens. Actuator A-Phys. Rev. 2021, 323, 112647. [Google Scholar] [CrossRef]
- Liu, C.; Zhu, Y.C.; Wu, C.W. Optimization of a synthetic jet based piezoelectric air pump and its application in electronic cooling. Microsyst. Technol. 2020, 26, 1905–1914. [Google Scholar] [CrossRef]
- Sun, Y.M.; Wang, J.Y. Digitally-controlled driving power supply for dual-active-valve piezoelectric pump. Microsyst. Technol. 2019, 25, 1257–1265. [Google Scholar] [CrossRef]
- He, L.P.; Wu, X.Q.; Zhang, Z.; Wang, Z.; Zhang, B.C.; Cheng, G.M. Experiment analysis of high output pressure piezoelectric pump with straight arm wheeled check valve. J. Intell. Mater. Syst. Struct. 2021, 32, 1987–1996. [Google Scholar] [CrossRef]
- Rao, K.S.; Hamza, M.; Kumar, P.A.; Sravani, K.G. Design and optimization of MEMS based piezoelectric actuator for drug delivery systems. Microsyst. Technol. 2020, 26, 1671–1679. [Google Scholar] [CrossRef]
- Ucar, H. Investigation of Piezoelectric Energy Harvesting From Structural Vibration Induced by Rotating Machinery. Int. J. Acoust. Vib. 2022, 27, 257–264. [Google Scholar] [CrossRef]
- Richter, M.; Anheuer, D.; Wille, A.; Congar, Y.; Wackerle, M. Multistage Micropump System towards Vacuum Pressure. Actuators 2023, 12, 227. [Google Scholar] [CrossRef]
- Truong, T.Q.; Nguyen, N.T. A polymeric piezoelectric micropump based on lamination technology. J. Micromech. Microeng. 2004, 14, 632–638. [Google Scholar] [CrossRef]
- Aksoy, B.; Besse, N.; Boom, R.J.; Hoogenberg, B.J.; Blom, M.; Shea, H. Latchable microfluidic valve arrays based on shape memory polymer actuators. Lab Chip 2019, 19, 608–617. [Google Scholar] [CrossRef] [PubMed]
- Hamrock, B.; Dowson, D. Isothermal Elastohydrodynamic Lubrication of Point Contacts: Part III-Fully Flooded Result. J. Lubr. Technol. 1976, 99, e3453074. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Zhao, Y.; Lin, L.; Wang, Y.; Shang, X.; Li, K. Research on Active Lubrication Based on Piezoelectric Micropump. Actuators 2025, 14, 227. https://doi.org/10.3390/act14050227
Zhang Z, Zhao Y, Lin L, Wang Y, Shang X, Li K. Research on Active Lubrication Based on Piezoelectric Micropump. Actuators. 2025; 14(5):227. https://doi.org/10.3390/act14050227
Chicago/Turabian StyleZhang, Zhiyuan, Yan Zhao, Long Lin, Yamen Wang, Xiuxin Shang, and Kai Li. 2025. "Research on Active Lubrication Based on Piezoelectric Micropump" Actuators 14, no. 5: 227. https://doi.org/10.3390/act14050227
APA StyleZhang, Z., Zhao, Y., Lin, L., Wang, Y., Shang, X., & Li, K. (2025). Research on Active Lubrication Based on Piezoelectric Micropump. Actuators, 14(5), 227. https://doi.org/10.3390/act14050227






