Time-Varying Control Strategy for Asymmetric Thrust Flight of Multi-Engines Aircraft
Abstract
1. Introduction
- (1)
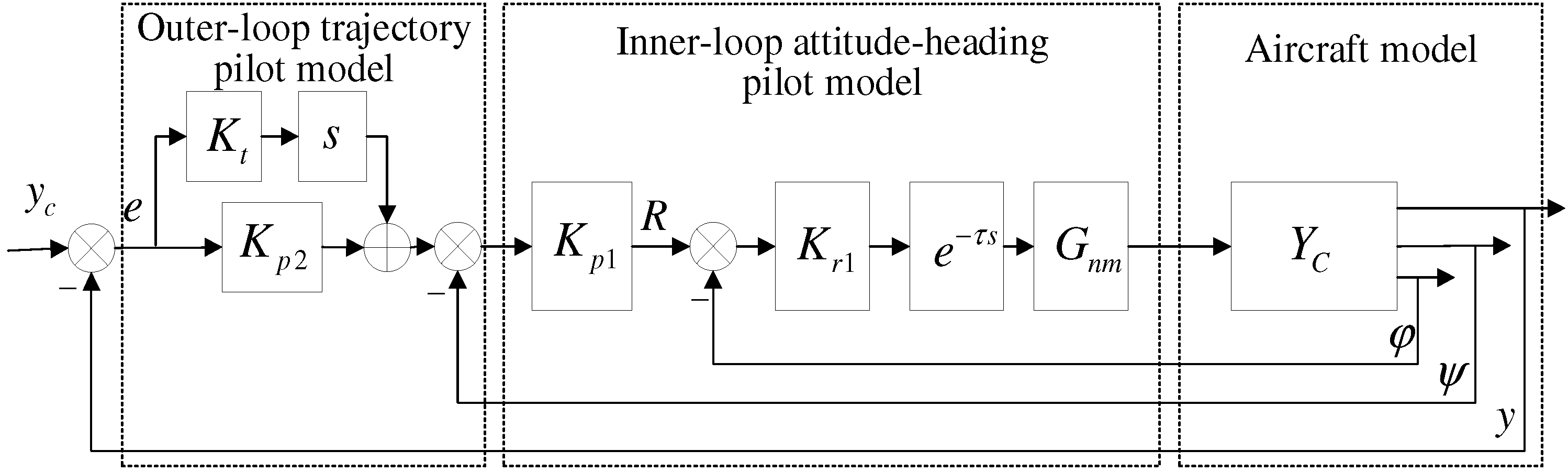
- A multi-loop pilot control behavior model structure is developed to describe the pilot’s control behavior characteristics under lateral-directional imbalance caused by asymmetric thrust.
- (2)
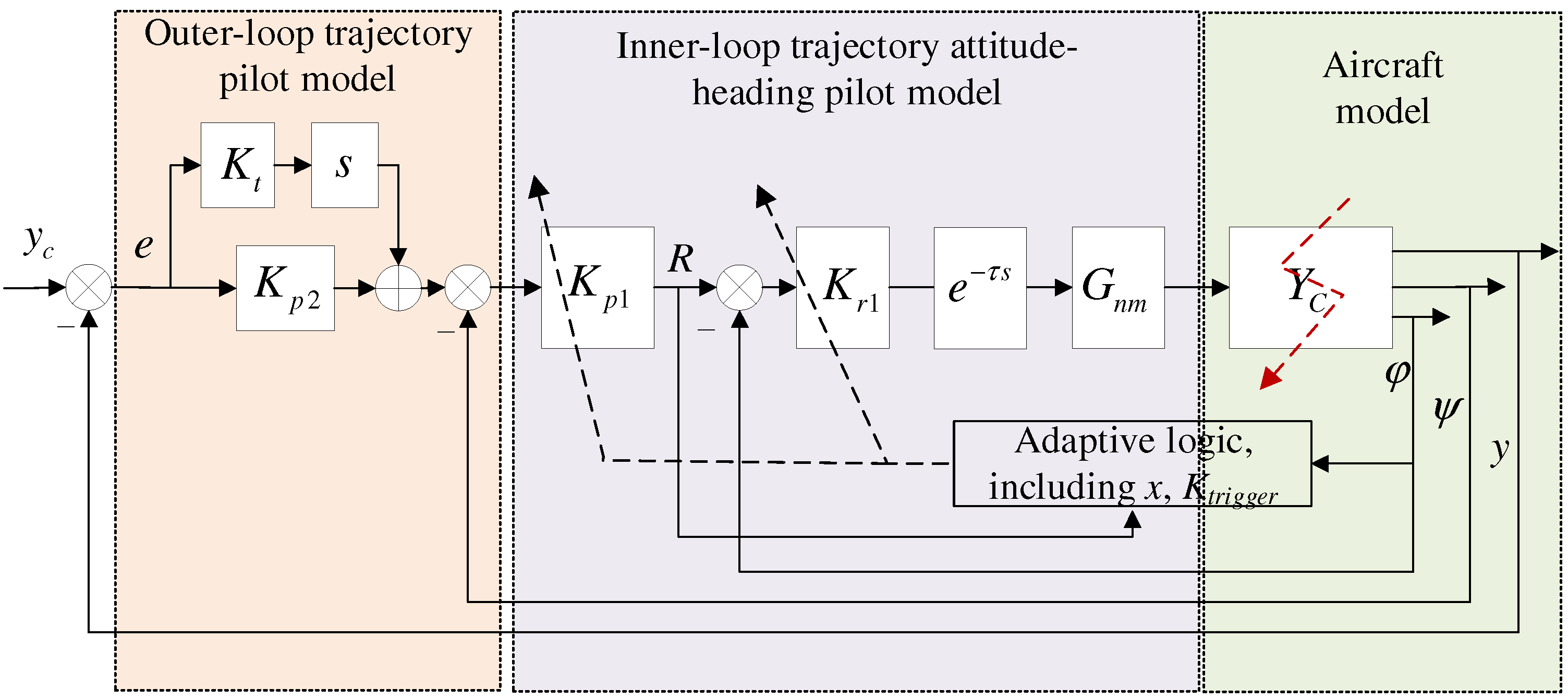
- In response to the pilot’s control characteristics under asymmetric thrust, including inner-loop attitude-heading control and outer-loop trajectory control, a time-varying model for pilot control of aileron manipulation is established to analyze control behavior during an asymmetric thrust flight.
- (3)
- The proposed time-varying control strategy is evaluated by combining pilot-aircraft system simulations and pilot-in-the-loop flight experiments, in terms of both time-domain results and time-varying flying quality evaluations.
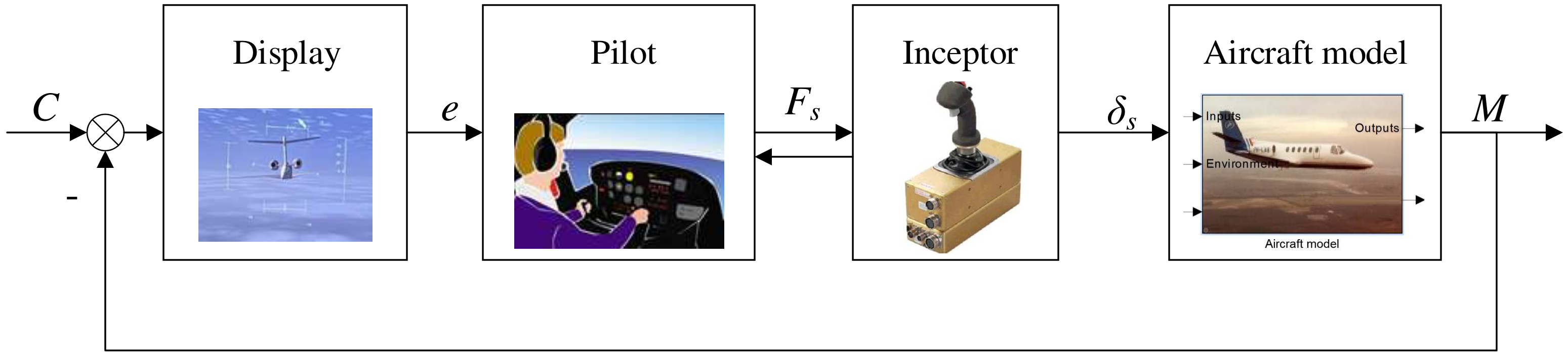
2. Analysis and Modeling of Pilot Control Behavior Under Asymmetric Thrust
2.1. Aileron Control Model for the Pilot Under Asymmetric Thrust Conditions
2.2. Pilot Rudder Control Model Under Asymmetric Thrust
3. Results and Discussions
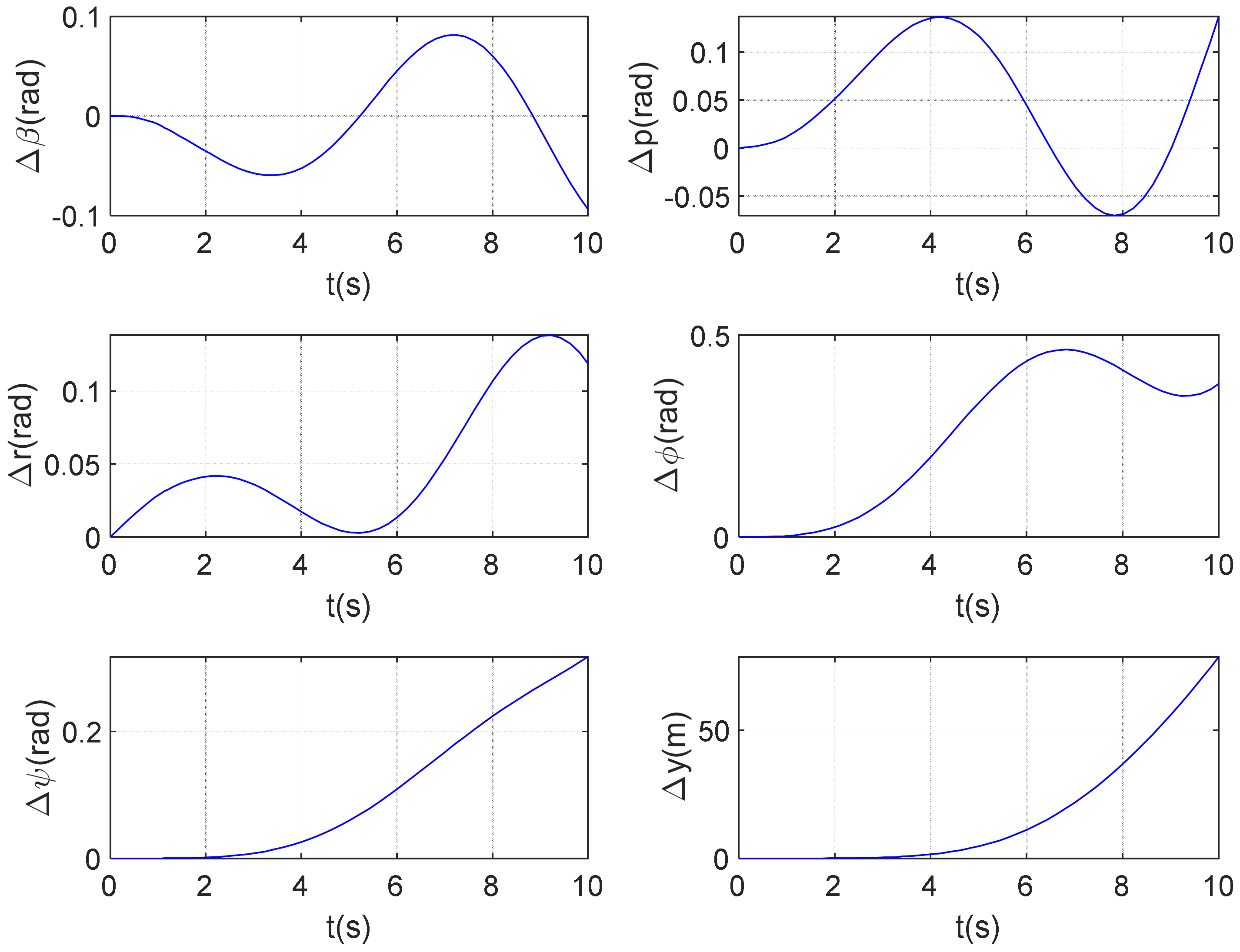
3.1. Analysis of Flight Motion Characteristics
3.1.1. Analysis of Yaw Motion Characteristics
3.1.2. Analysis of Lateral Motion Characteristics
3.1.3. Analysis of Aircraft Characteristics Under Asymmetric Thrust
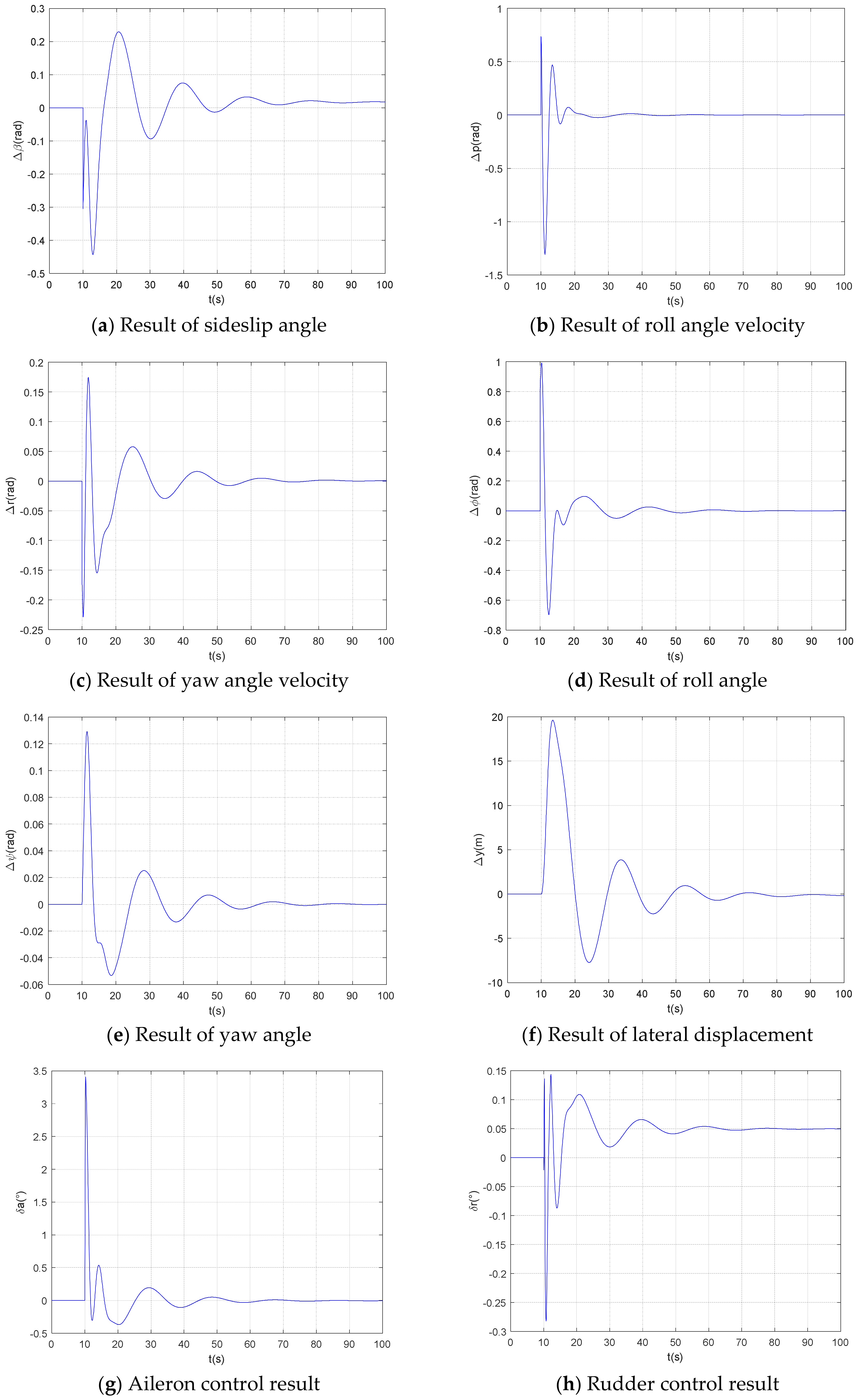
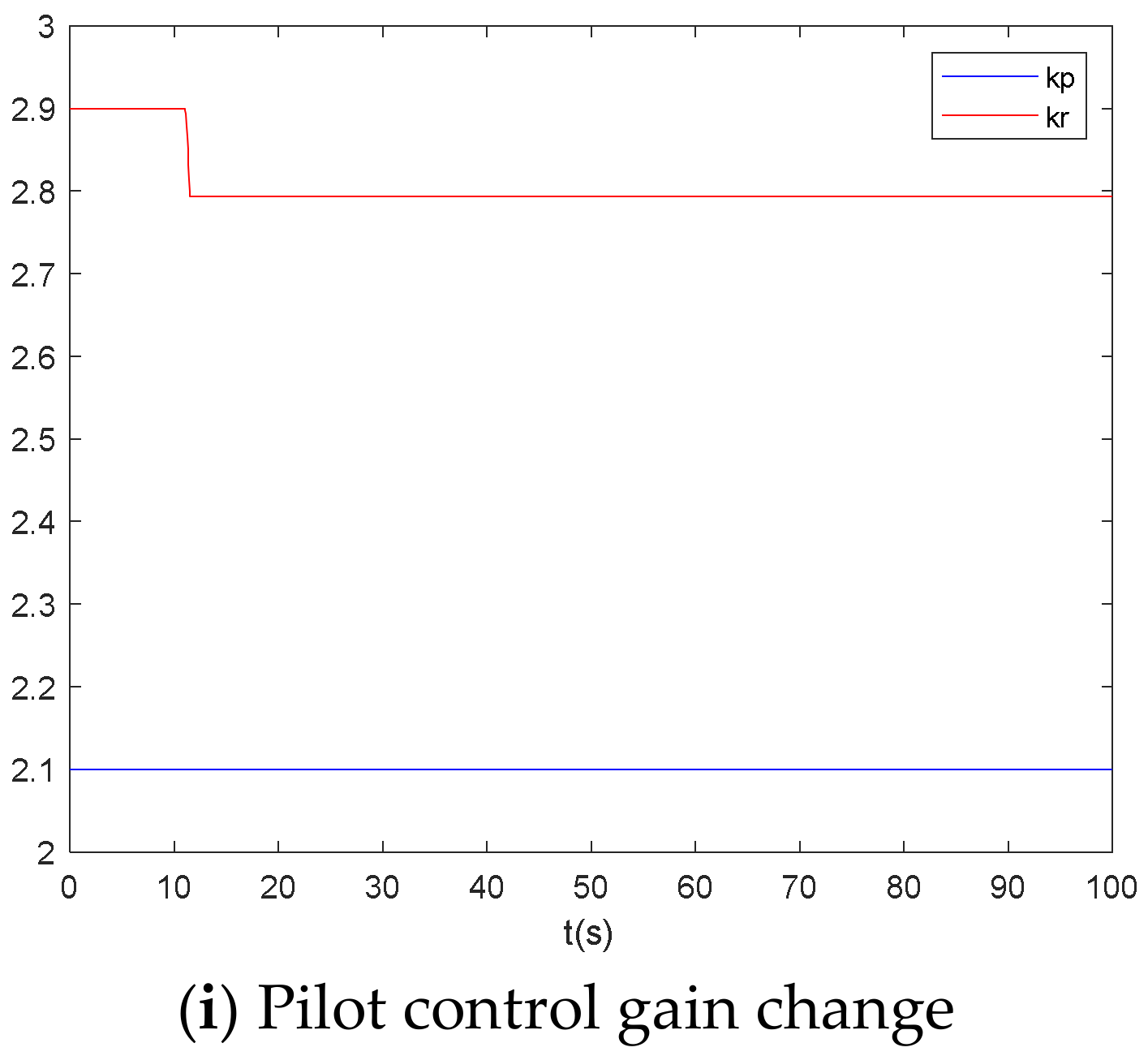
3.2. Pilot-Aircraft System Simulation and Analysis
4. Experimental Validation
4.1. Human-in-the-Loop Simulation Experiment Design
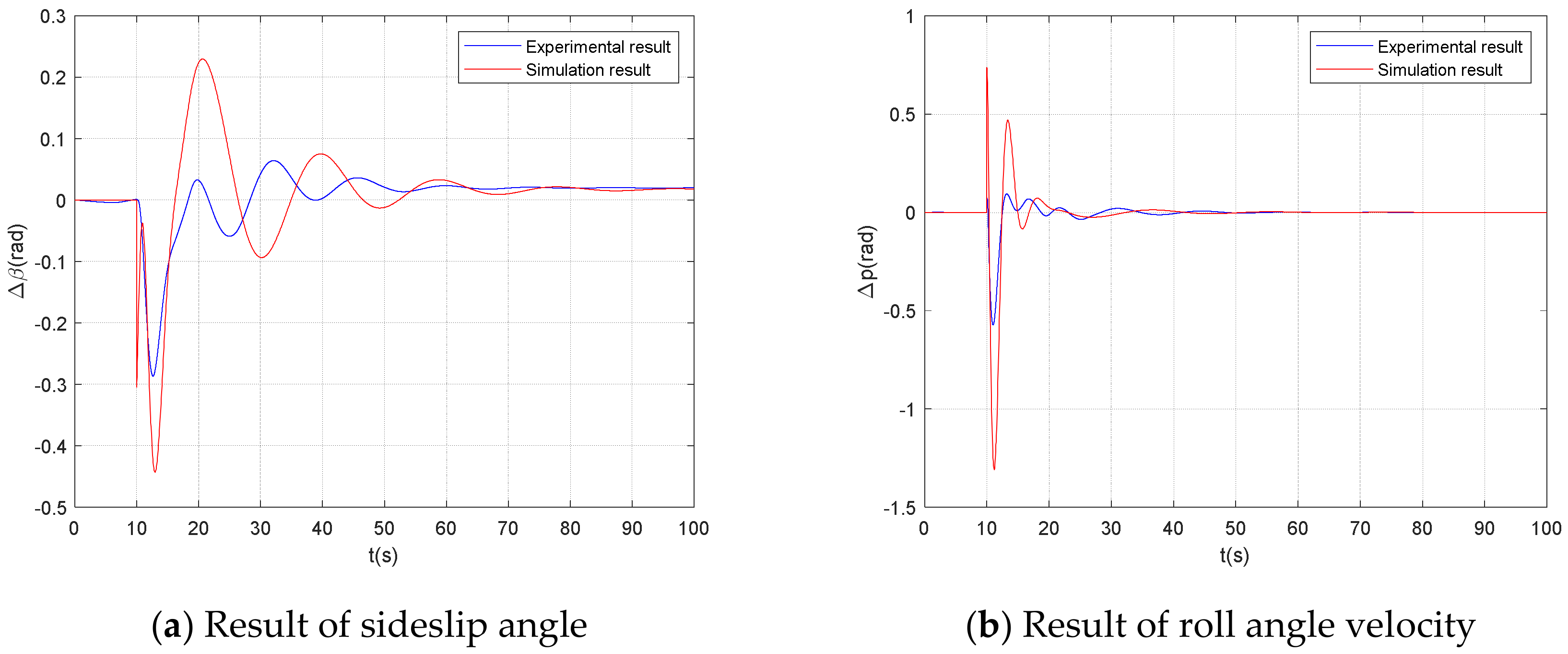
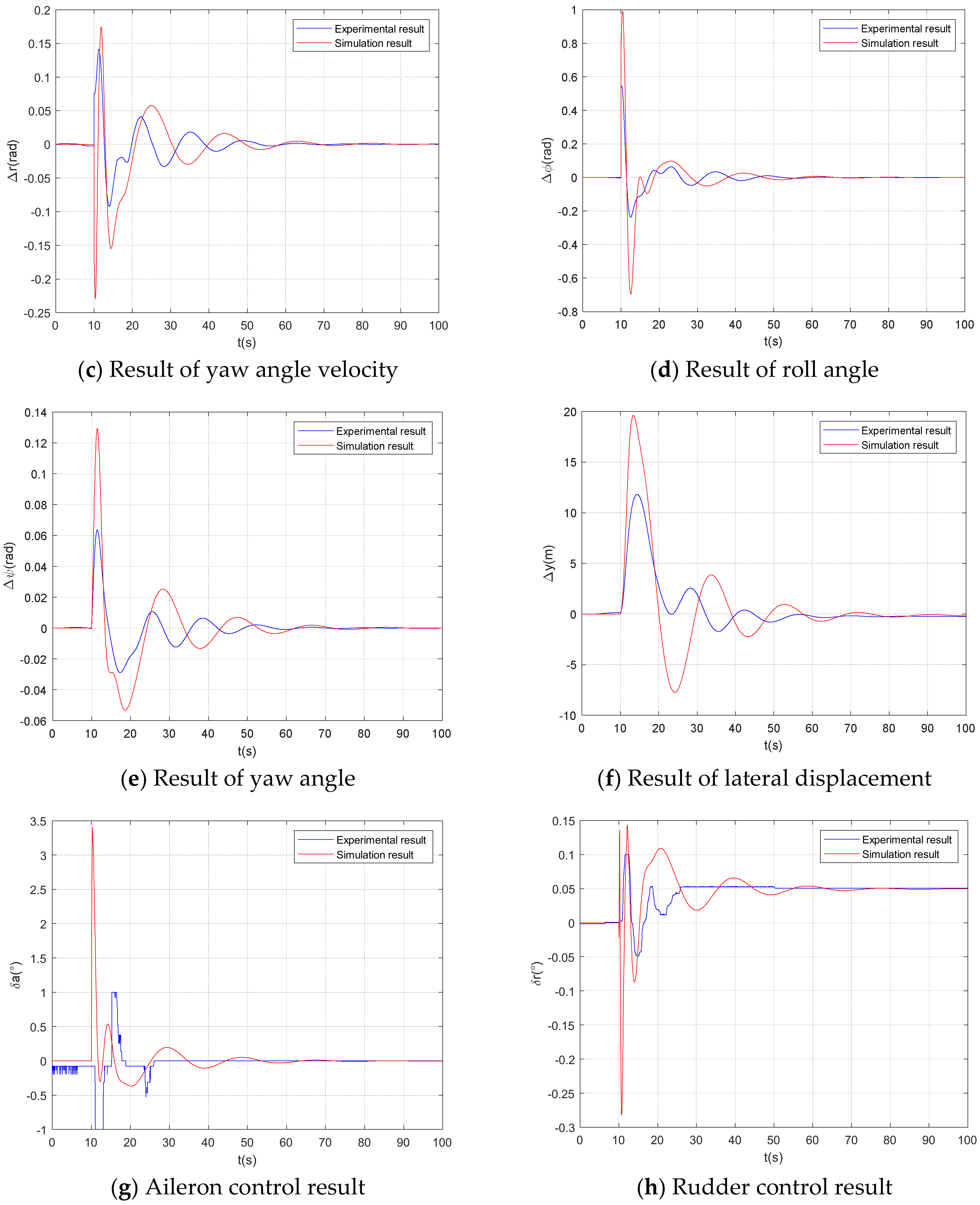
4.2. Experimental Results and Analysis
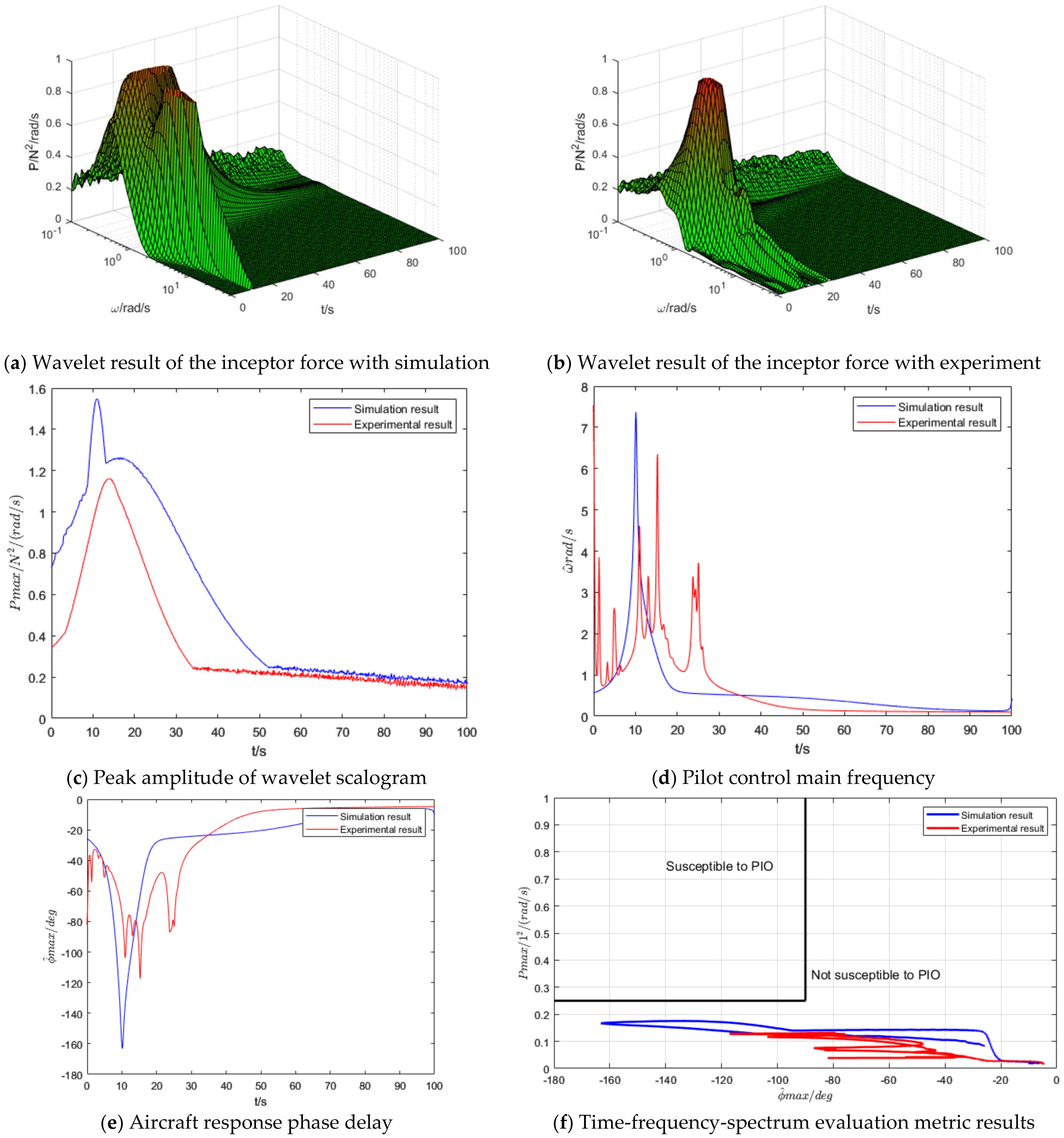
4.3. Aircraft-Pilot Couplings Evaluation Results
5. Conclusions
- (1)
- A multi-loop control behavior model for the pilot is developed, which includes the inner-loop attitude-heading control and outer-loop trajectory control under aileron manipulation, as well as command sideslip control under rudder manipulation. This model fully describes the pilot’s control behavior under asymmetric thrust, accounting for the resulting lateral-directional imbalance and strong coupling.
- (2)
- Considering the pilot’s time-varying and adaptive response to failure, the model integrates the pilot’s control demands under asymmetric thrust and extends the Hess time-varying pilot model in both structure and form. Based on this, a time-varying lateral-directional control strategy model for the pilot is established. Pilot-aircraft system simulation results show that this model maintains flight stability after a failure occurs.
- (3)
- Comparing the pilot-in-the-loop simulation results with the experimental data, the time-domain analysis indicates that the experimental and simulation results for the aircraft’s flight state are in good agreement. The time-varying aircraft-pilot coupling evaluation shows that both the experimental and simulation results fall within a range where pilot-induced oscillations are unlikely to occur, and their trends are consistent. This verifies the effectiveness of the proposed strategy model.
- (4)
- The human pilot model developed herein needs further investigation. (a) Some machine learning components will be built into the control scheme to make the control more realistic. (b) More experiments and models will be extended to address more issues, e.g., dual-engine failure, challenging weather conditions, etc.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, J.; Wang, Y.; Wang, Z.; Wang, X.; Zhao, Y. Transient gas path fault diagnosis of aero-engine based on domain adaptive offline reinforcement learning. Aerosp. Sci. Technol. 2024, 155, 109701. [Google Scholar] [CrossRef]
- Parnell, K.J.; Wynne, R.A.; Griffin, T.G.C.; Plant, K.L.; Stanton, N.A. Generating design requirements for flight deck applications: Applying the perceptual cycle model to engine failures on take-off. Int. J. Hum. Comput. Interact. 2021, 37, 611–629. [Google Scholar] [CrossRef]
- Neves, G.F.; de Souza, R.F.; Titton, C.C.; Messias, G.E.; Cruz, L.R. Wing aerodynamic loading asymmetry in engine failure condition for multi-propeller driven airplanes. In Proceedings of the AIAA SCITECH 2023 Forum, Online, 23–27 January 2023; p. 0219. [Google Scholar]
- Huang, Y.; Sun, G.; Tao, J.; Hu, Y.; Yuan, L. A modified fusion model-based/data-driven model for sensor fault diagnosis and performance degradation estimation of aero-engine. Meas. Sci. Technol. 2022, 33, 085105. [Google Scholar] [CrossRef]
- Wang, T.; Noori, M.; Altabey, W.A.; Wu, Z.; Ghiasi, R.; Kuok, S.C.; Silik, A.; Farhan, N.S.; Sarhosis, V.; Farsangi, E.N. From model-driven to data-driven: A review of hysteresis modeling in structural and mechanical systems. Mech. Syst. Signal Process. 2023, 204, 110785. [Google Scholar] [CrossRef]
- Chen, X.; Tong, Z.; Liu, Y.; Wang, Y.; Qing, X. A hybrid multi-model-based condition monitoring and sensor fault detection method for aero gas turbine. IEEE Sens. J. 2024, 24, 32729–32739. [Google Scholar] [CrossRef]
- Huang, Y.; Tao, J.; Zhao, J.; Sun, G.; Yin, K.; Zhai, J. Graph structure embedded with physical constraints-based information fusion network for interpretable fault diagnosis of aero-engine. Energy 2023, 283, 129120. [Google Scholar] [CrossRef]
- Parnell, K.J.; Banks, V.A.; Plant, K.L.; Griffin, T.G.; Beecroft, P.; Stanton, N.A. Predicting design-induced error on the flight deck: An aircraft engine oil leak scenario. Hum. Factors 2021, 63, 938–955. [Google Scholar] [CrossRef] [PubMed]
- Kordt, M.; Ackermann, J. Robust synergetic design of structural dynamic engine out controllers in parameter space. J. Guid. Control Dyn. 2001, 24, 305–314. [Google Scholar] [CrossRef]
- Zhou, X.; Huang, J.; Lu, F.; Zhou, W.; Liu, P. A novel compound fault-tolerant method based on online sequential extreme learning machine with cycle reservoir for turbofan engine direct thrust control. Aerosp. Sci. Technol. 2023, 132, 108059. [Google Scholar] [CrossRef]
- Liu, Y.; Tao, G.; Joshi, S.M. Modeling and model reference adaptive control of aircraft with asymmetric damage. J. Guid. Control Dyn. 2010, 33, 1500–1517. [Google Scholar] [CrossRef]
- Lian, G.; Chen, J.; Fan, Z.; Sun, C. Research on the Influence Factors of Ground Minimum Control Speed of Civil Aircraft Based on Dynamic Simulation. In Proceedings of the 2024 3rd International Symposium on Aerospace Engineering and Systems (ISAES), Nanjing, China, 22–24 March 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 312–317. [Google Scholar]
- Etherington, T.J.; Kramer, L.J.; Kennedy, K.D.; Bailey, R.E.; Last, M.C. Quantifying pilot contribution to flight safety during dual generator failure. In Proceedings of the 2017 IEEE/AIAA 36th Digital Avionics Systems Conference (DASC), St. Petersburg, FL, USA, 17–21 September 2017; IEEE: Piscataway, NJ, USA, 2017. [Google Scholar]
- Hariowibowo, H.; Arifianto, O.; Pasaribu, H.M.; Muhammad, H. Fighter Aircraft Closed Loop Handling Quality Simulation on Lateral-Directional Modes. J. Aeronaut. Astronaut. Aviat. 2021, 53, 129–135. [Google Scholar]
- Hess, R.A. Modeling Pilot Control Behavior with Sudden Changes in Vehicle Dynamics. J. Aircr. 2009, 46, 1584–1592. [Google Scholar] [CrossRef]
- Hess, R.A. Modeling Human Pilot Adaptation to Flight Control Anomalies and Changing Task Demands. J. Guid. Control Dyn. 2016, 39, 655–666. [Google Scholar] [CrossRef]
- Xu, S.; Wu, Y. Modeling multi-loop intelligent pilot control behavior for aircraft-pilot couplings analysis. Aerosp. Sci. Technol. 2021, 112, 106651. [Google Scholar] [CrossRef]
- Hess, R.A. Modeling the pilot detection of time-varying aircraft dynamics. J. Aircr. 2012, 49, 2100–2104. [Google Scholar] [CrossRef]
- Lu, L.; Jump, M. Multiloop pilot model for boundary-triggered pilot-induced oscillation investigations. J. Guid. Control Dyn. 2014, 37, 1863–1879. [Google Scholar] [CrossRef]
- Xu, S.T.; Tan, W.Q.; Wang, W.J.; Sun, L. Pilot time-varying control behavior modeling in refractory period with aircraft failures. Sci. China Technol. Sci. 2023, 66, 2000–2012. [Google Scholar] [CrossRef]
- Wang, L.; Zhu, Q.; Zhang, Z.; Dong, R. Modeling pilot behaviors based on discrete-time series during carrier-based aircraft landing. J. Aircr. 2016, 53, 1922–1931. [Google Scholar] [CrossRef]
- Xu, S.T.; Tan, W.Q.; Qu, X.J. Prediction of nonlinear pilot-induced oscillation using an intelligent human pilot model. Chin. J. Aeronaut. 2019, 32, 2592–2611. [Google Scholar] [CrossRef]
- Hess, R.A. Unified theory for aircraft handling qualities and adverse aircraft-pilot coupling. J. Guid. Control Dyn. 1997, 20, 1141–1148. [Google Scholar] [CrossRef]
- Ji, M. Research on Control Law Reconfiguration for Civil Aircraft with Asymmetric Thrust. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2011; pp. 31–34. [Google Scholar]


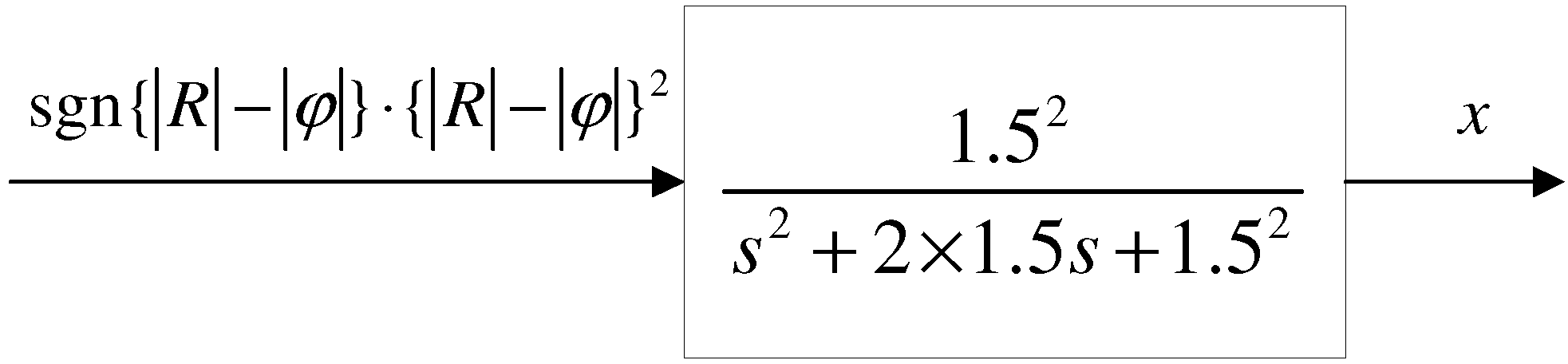


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, S.; Zhang, Z. Time-Varying Control Strategy for Asymmetric Thrust Flight of Multi-Engines Aircraft. Actuators 2025, 14, 222. https://doi.org/10.3390/act14050222
Xu S, Zhang Z. Time-Varying Control Strategy for Asymmetric Thrust Flight of Multi-Engines Aircraft. Actuators. 2025; 14(5):222. https://doi.org/10.3390/act14050222
Chicago/Turabian StyleXu, Shuting, and Zhe Zhang. 2025. "Time-Varying Control Strategy for Asymmetric Thrust Flight of Multi-Engines Aircraft" Actuators 14, no. 5: 222. https://doi.org/10.3390/act14050222
APA StyleXu, S., & Zhang, Z. (2025). Time-Varying Control Strategy for Asymmetric Thrust Flight of Multi-Engines Aircraft. Actuators, 14(5), 222. https://doi.org/10.3390/act14050222





