Fault Diagnosis of Rolling Element Bearing Based on BiTCN-Attention and OCSSA Mechanism
Abstract
1. Introduction
2. Bearing Data Decomposition Based on OCSSA-VMD
2.1. Osprey–Cauchy–Sparrow Search Algorithm
2.2. Variational Mode Decomposition
2.3. Optimize VMD Parameters Using OCCSA
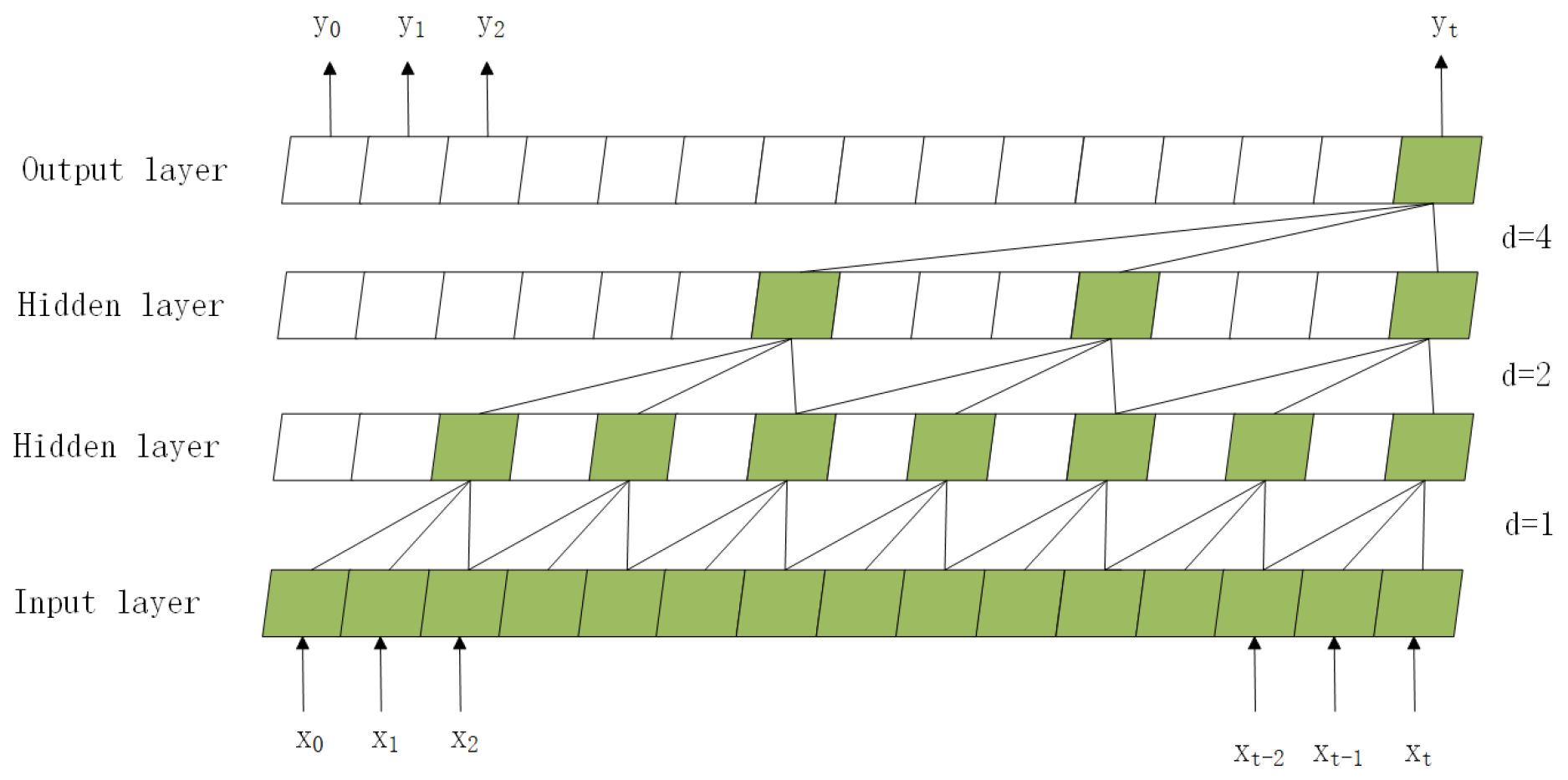
3. BiTCN-Attention Prediction Model
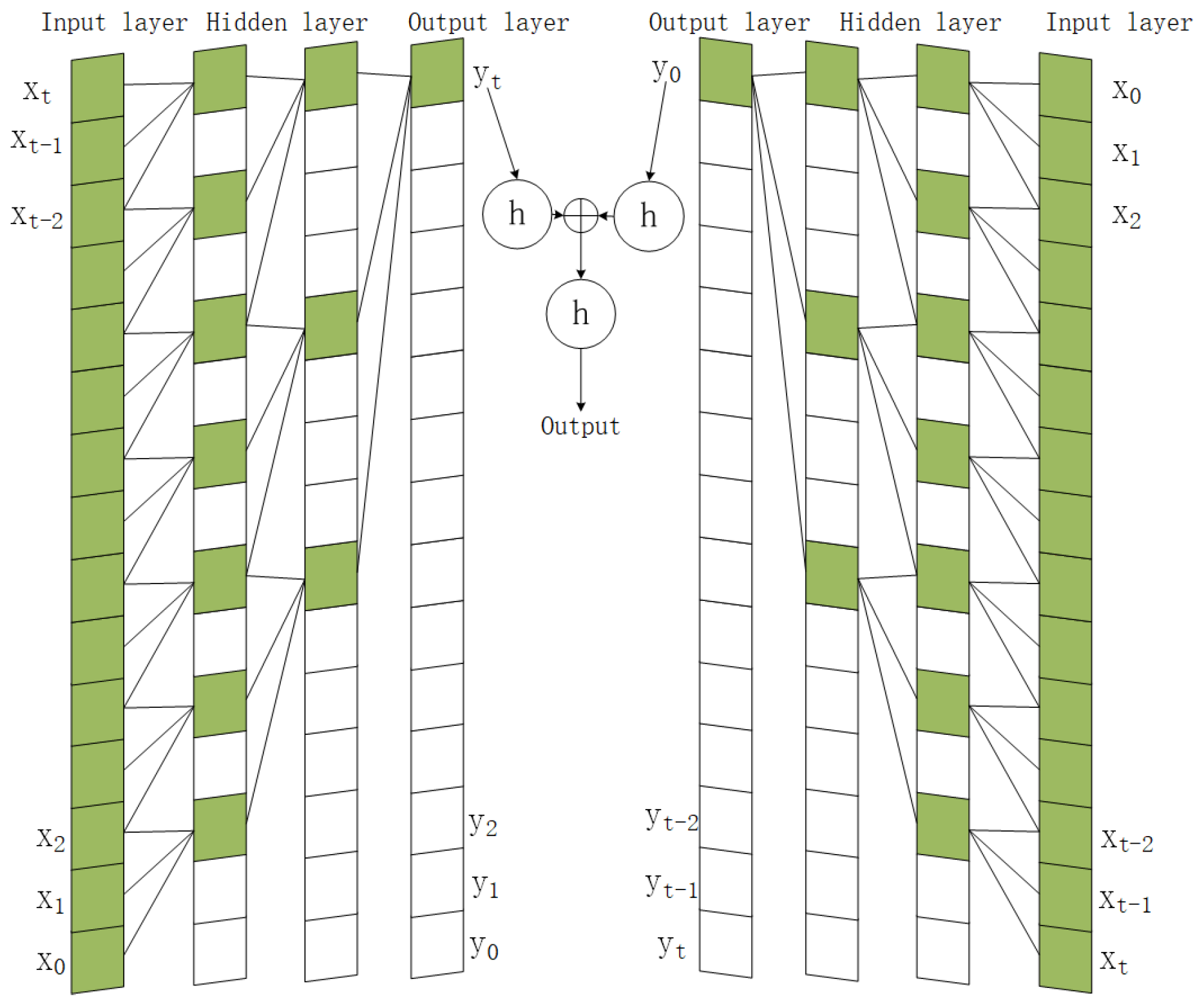
3.1. Temporal Convolutional Network
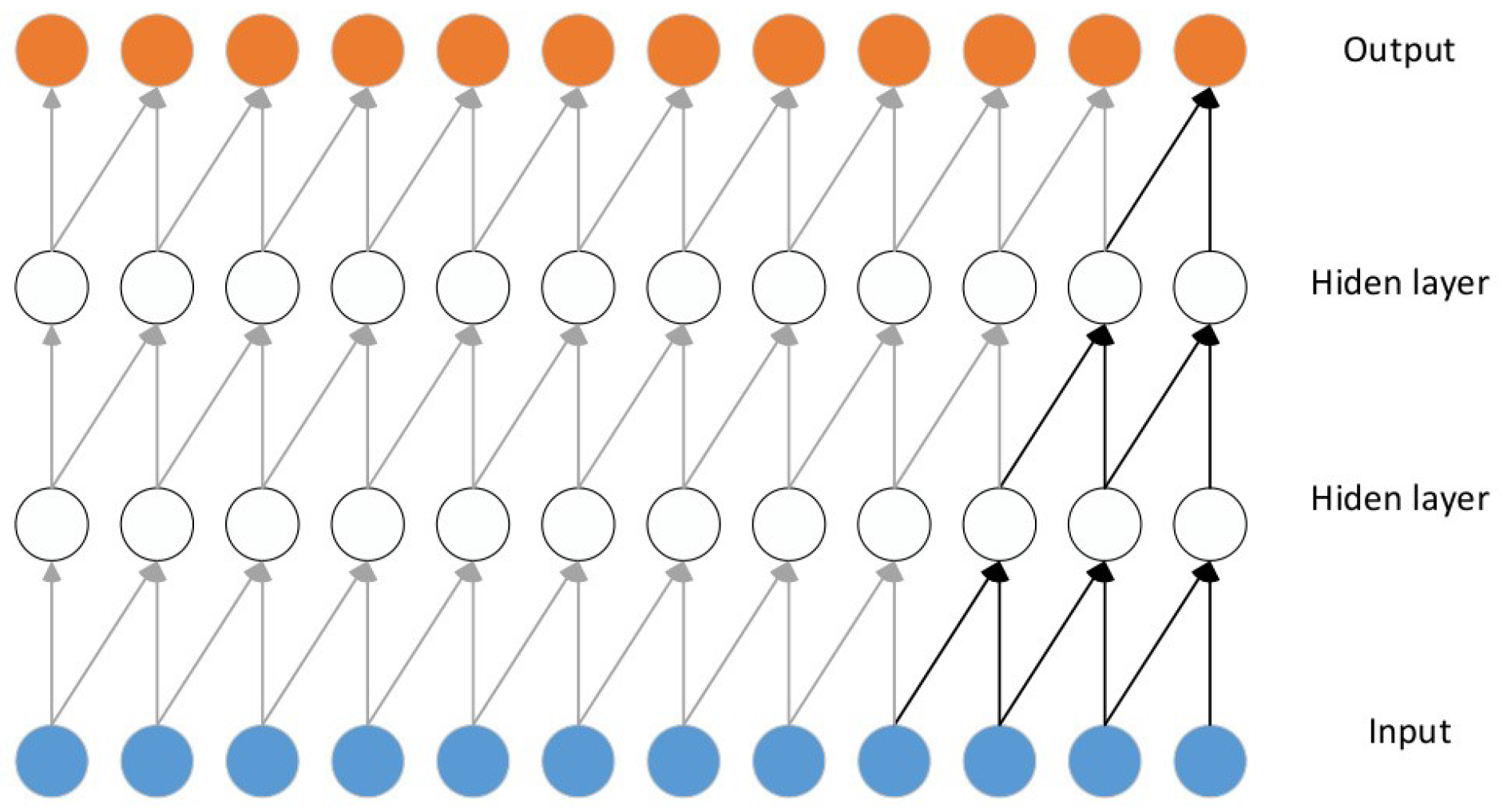
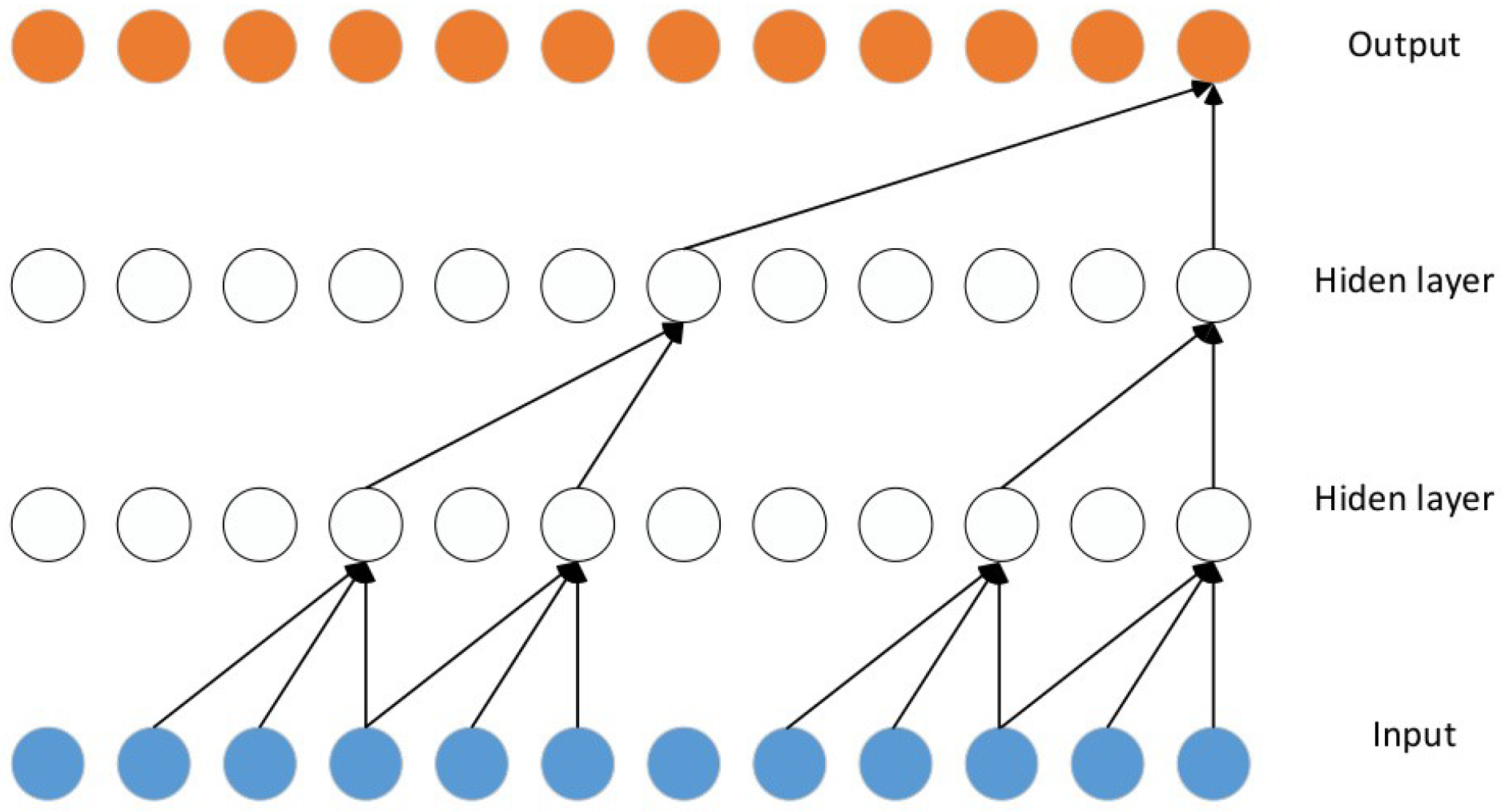
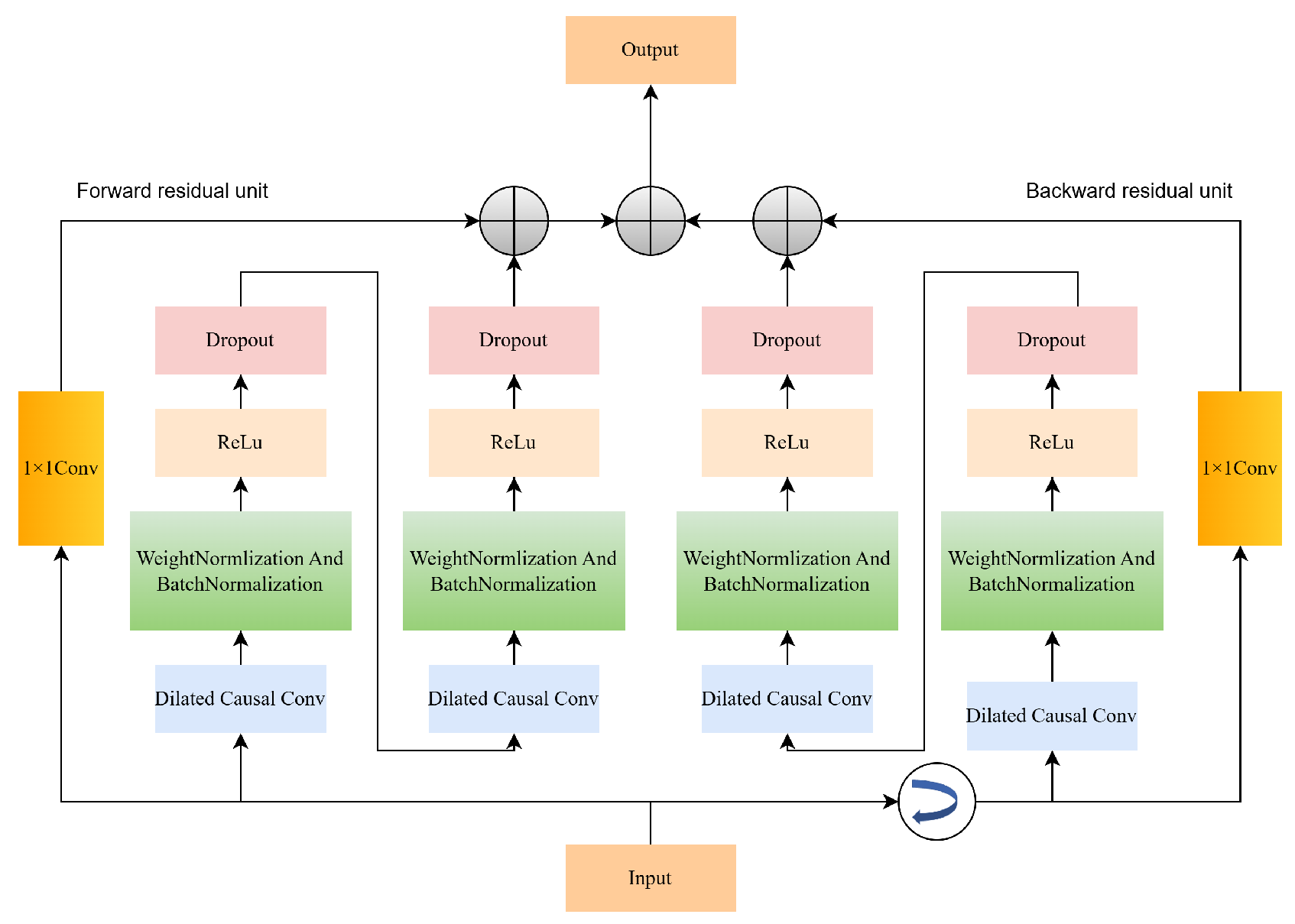
3.1.1. Dilated Causal Convolution
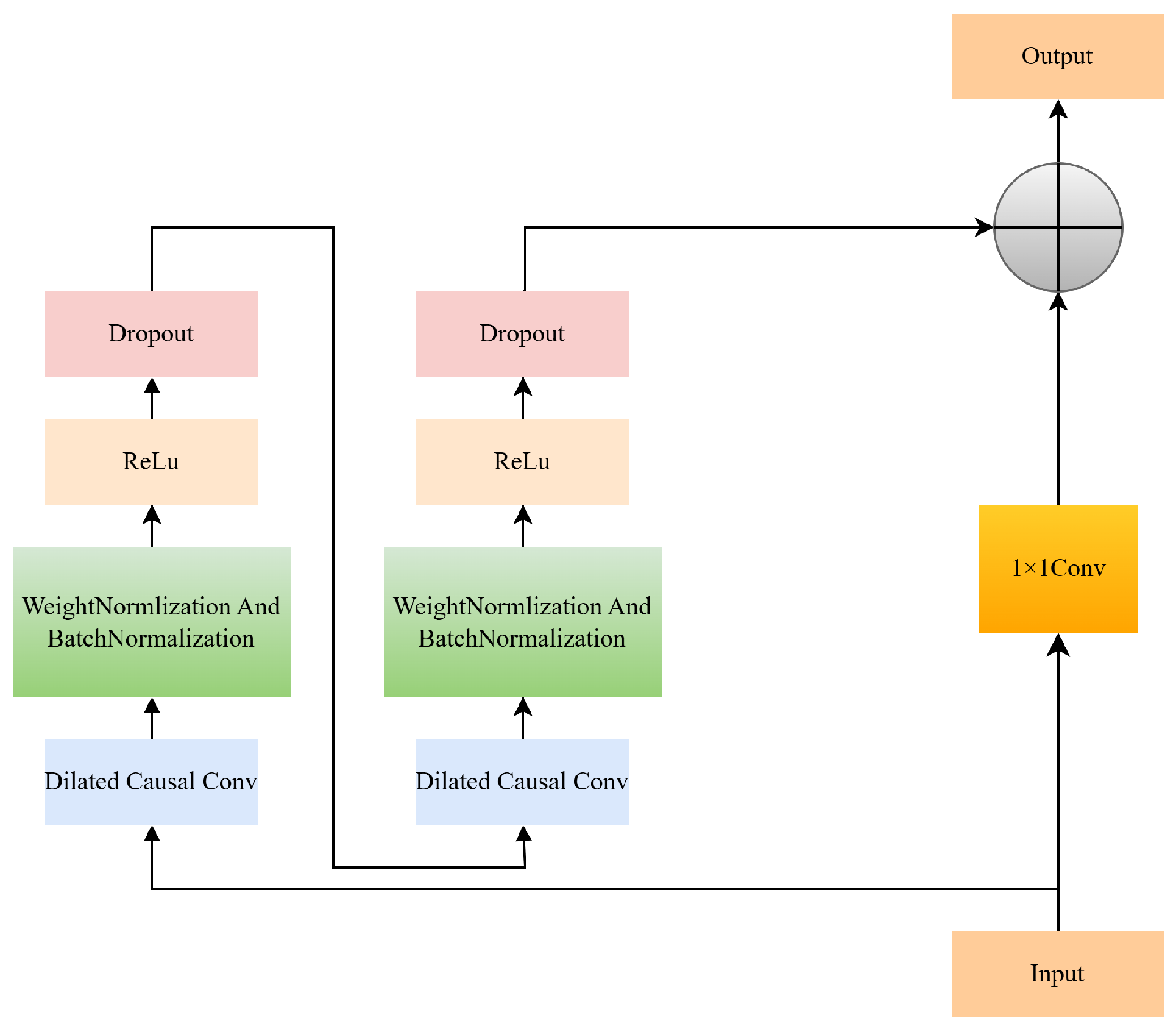
3.1.2. Residual Module
3.2. Self-Attention Layer
3.3. BiTCN-Attention
4. Research Results and Analysis
4.1. Data Source Selection
4.2. Signal Processing and Feature Extraction
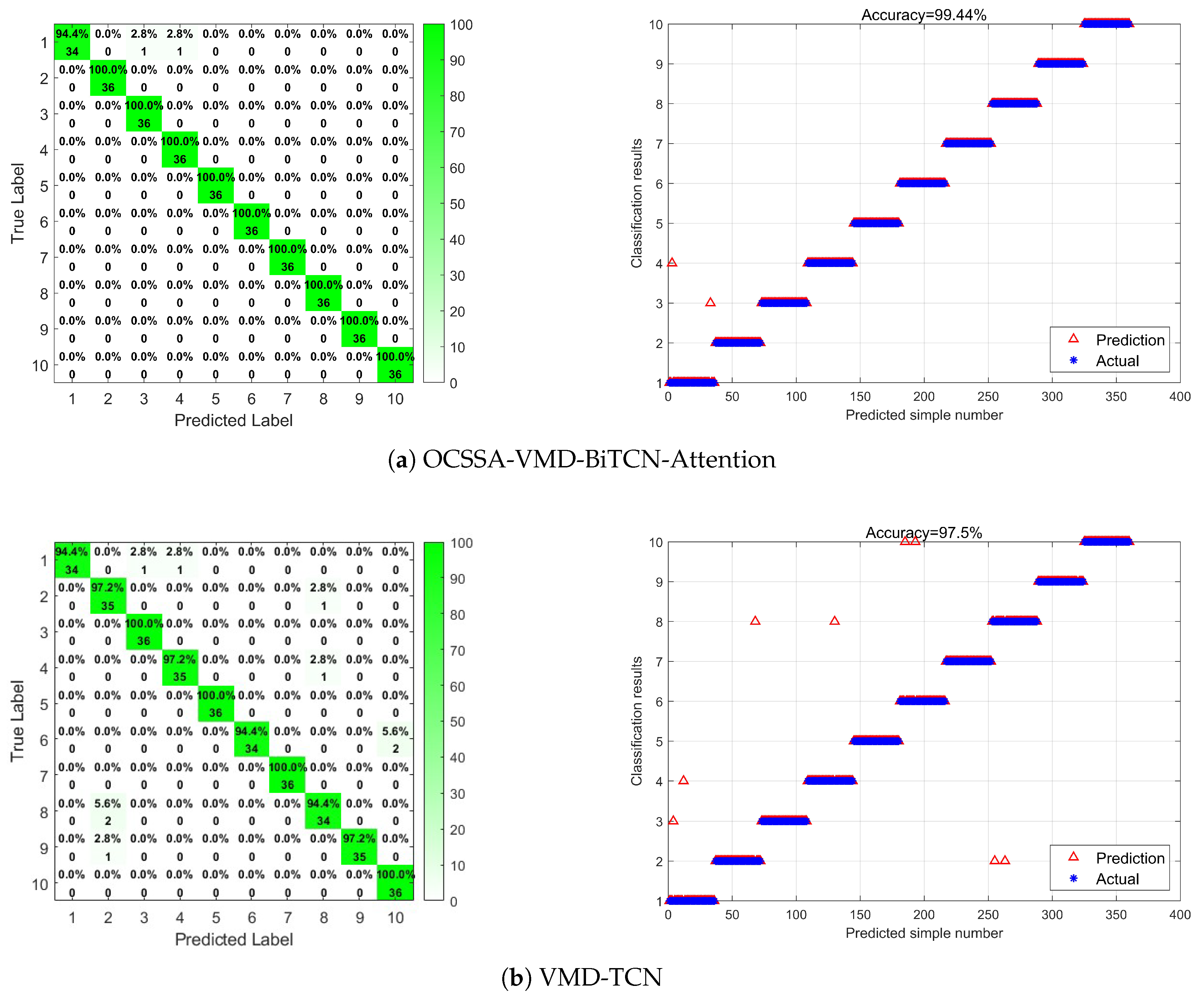
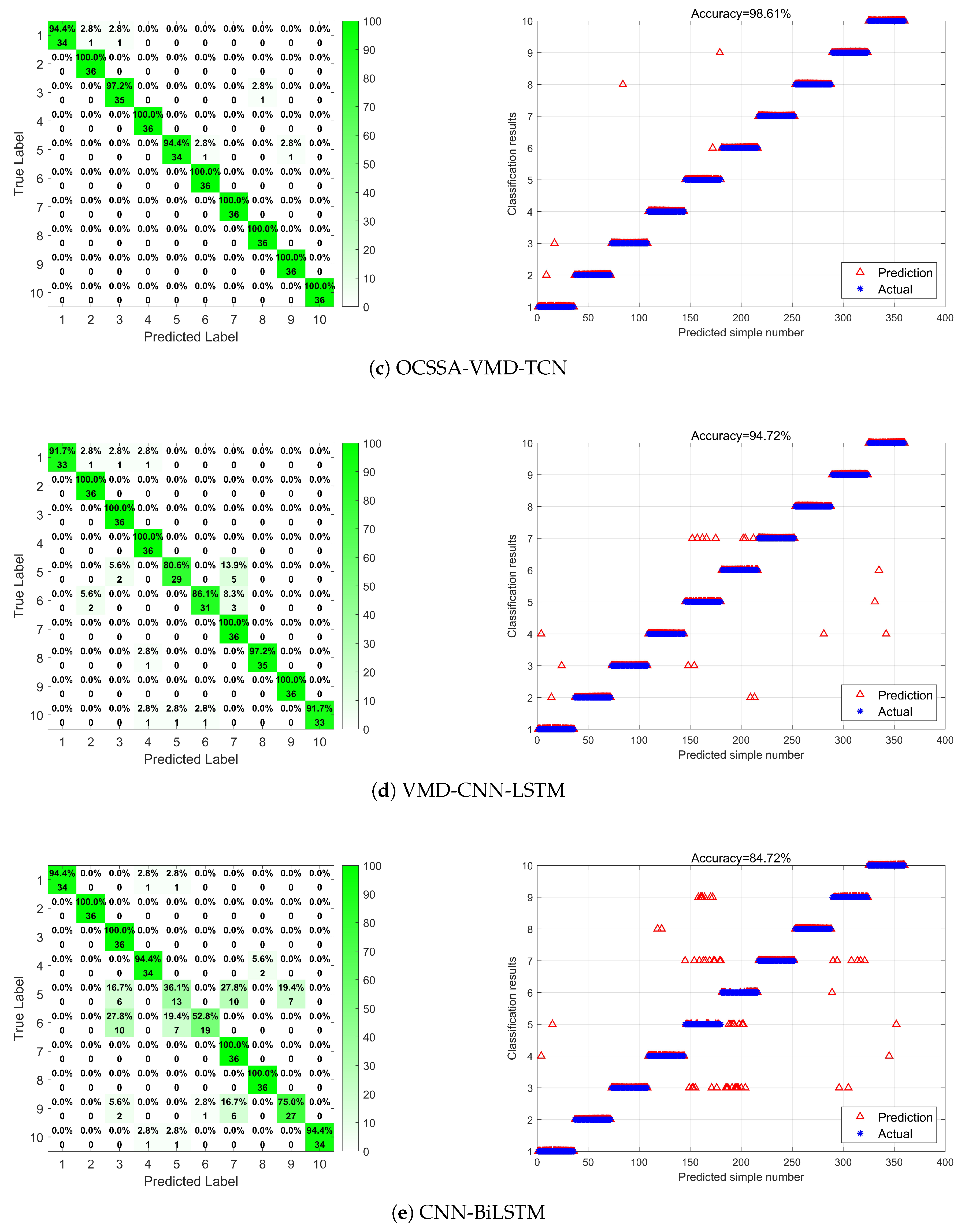
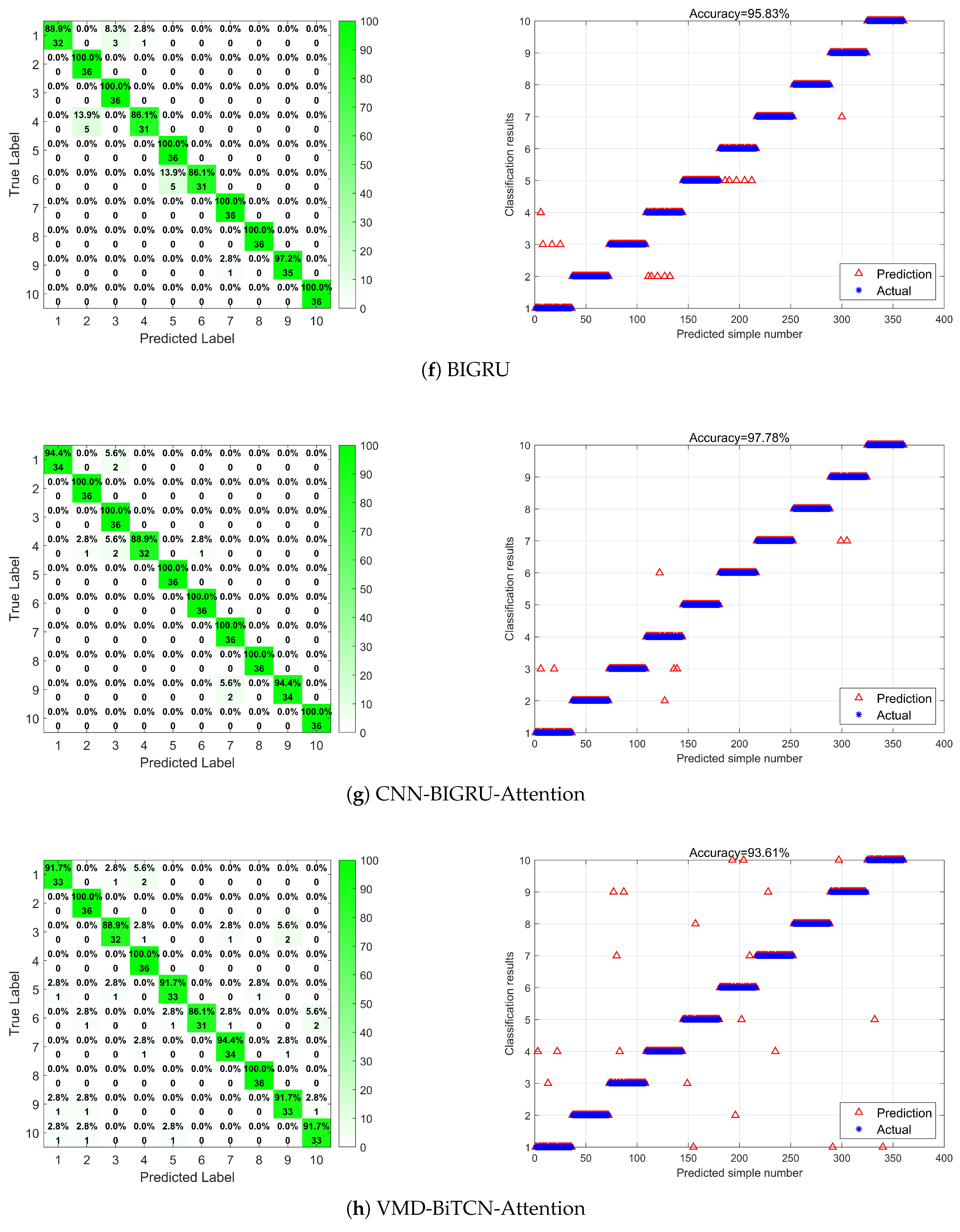
4.3. Comparison with Other Methods
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ran, G.; Chen, H.; Li, C.; Ma, G.; Jiang, B. A Hybrid Design of Fault Detection for Nonlinear Systems Based on Dynamic Optimization. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 5244–5254. [Google Scholar] [CrossRef] [PubMed]
- Gundewar, S.K.; Kane, P.V. Condition monitoring and fault diagnosis of induction motor. J. Vib. Eng. Technol. 2021, 9, 643–674. [Google Scholar] [CrossRef]
- Liu, R.; Yang, B.; Zio, E.; Chen, X. Artificial intelligence for fault diagnosis of rotating machinery: A review. Mech. Syst. Signal Process. 2018, 108, 33–47. [Google Scholar] [CrossRef]
- Chen, H.; Luo, H.; Verma, N.; Jiang, B. Guest Editorial: Special Issue on Artificial Intelligence Methods for Maintenance and Safety of Automation Systems. IEEE Trans. Artif. Intell. 2023, 4, 589–591. [Google Scholar] [CrossRef]
- Cerrada, M.; Sanchez, R.-V.; Li, C.; Pacheco, F.; Cabrera, D.; de Oliveira, J.V.; Vasquez, R.E. A review on data-driven fault severity assessment in rolling bearings. Mech. Syst. Signal Process. 2018, 99, 169–196. [Google Scholar] [CrossRef]
- Pandiyan, M.; Babu, T.N. Systematic Review on Fault Diagnosis on Rolling-Element Bearing. J. Vib. Eng. Technol. 2024, 12, 8249–8283. [Google Scholar] [CrossRef]
- Ran, G.; Liu, J.; Li, C.; Lam, H.-K.; Li, D.; Chen, H. Fuzzy-Model-Based Asynchronous Fault Detection for Markov Jump Systems With Partially Unknown Transition Probabilities: An Adaptive Event-Triggered Approach. IEEE Trans. Fuzzy Syst. 2022, 30, 4679–4689. [Google Scholar] [CrossRef]
- Atoui, I.; Meradi, H.; Boulkroune, R.; Saidi, R.; Grid, A. Fault detection and diagnosis in rotating machinery by vibration monitoring using FFT and Wavelet techniques. Syst. Signal Process. Their Appl. 2013, 5, 401–406. [Google Scholar]
- Rai, A.; Upadhyay, S.H. A review on signal processing techniques utilized in the fault diagnosis of rolling element bearings. Tribol. Int. 2016, 96, 289–306. [Google Scholar] [CrossRef]
- Li, D.Y.; Dong, J.; Peng, K.X. Motor fault classification using hybrid short-time Fourier transform and wavelet transform with vibration signal and convolutional neural networkA Novel Adaptive STFT-SFA Based Fault Detection Method for Nonstationary Processes. IEEE Sens. J. 2023, 23, 10748–10757. [Google Scholar] [CrossRef]
- Wu, F.; Qu, L. Diagnosis of subharmonic faults of large rotating machinery based on EMD. Mech. Syst. Signal Process. 2009, 23, 467–475. [Google Scholar] [CrossRef]
- Shifat, T.A.; Hur, J.W. EEMD assisted supervised learning for the fault diagnosis of BLDC motor using vibration signal. J. Mech. Sci. Technol. 2020, 34, 3981–3990. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Chen, H.; Zhong, K.; Ran, G.; Cheng, C. Deep Learning-Based Machinery Fault Diagnostics. Machines 2022, 10, 690. [Google Scholar] [CrossRef]
- Shen, Q.; Zhang, Z. Fault Diagnosis Method for Bearing Based on Attention Mechanism and Multi-Scale Convolutional Neural Network. IEEE Access 2024, 12, 12940–12952. [Google Scholar] [CrossRef]
- Wen, L.; Li, X.Y.; Gao, L.; Zhang, Y.Y. A New Convolutional Neural Network-Based Data-Driven Fault Diagnosis Method. IEEE Trans. Ind. Electron. 2018, 65, 5990–5998. [Google Scholar] [CrossRef]
- Ding, F.; Li, X.; Qu, J.X. ault diagnosis of rolling bearing based on improved CEEMDAN and distance evaluation technique. J. Vibroeng. 2017, 19, 260–275. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, B.; Gao, D. Bearing fault diagnosis base on multi-scale CNN and LSTM model. J. Intell. Manuf. 2021, 32, 971–987. [Google Scholar] [CrossRef]
- Pan, H.H.; He, X.X.; Tang, S.; Meng, F.M. An Improved Bearing Fault Diagnosis Method using One-Dimensional CNN and LSTM. Stroj. Vestn. J. Mech. Eng. 2018, 64, 443–452. [Google Scholar]
- Khorram, A.; Khalooei, M.; Rezghi, M. End-to-end CNN+LSTM deep learning approach for bearing fault diagnosis. Appl. Intell. 2021, 51, 736–751. [Google Scholar] [CrossRef]
- Jiao, J.; Zhao, M.; Lin, J.; Liang, K. A comprehensive review on convolutional neural network in machine fault diagnosis. Neurocomputing 2020, 417, 36–63. [Google Scholar] [CrossRef]
- Song, Y.; Gao, S.; Li, Y.; Jia, L.; Li, Q.; Pang, F. Distributed Attention-Based Temporal Convolutional Network for Remaining Useful Life Prediction. IEEE Internet Things J. 2021, 8, 9594–9602. [Google Scholar] [CrossRef]
- Shang, Z.W.; Liu, H.; Zhang, B.R.; Feng, Z.H.; Li, W.X. Multi-view feature fusion fault diagnosis method based on an improved temporal convolutional network. Insight 2023, 65, 559–569. [Google Scholar] [CrossRef]
- Xing, J.Q.; Xu, J.X. An Improved Convolutional Neural Network for Recognition of Incipient Faults. IEEE Sens. J. 2022, 22, 16314–16322. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, A.; Jiao, J.; Xie, J.; Chen, H. Short-Term PV Power Forecasting Based on CEEMDAN and Ensemble DeepTCN. IEEE Trans. Instrum. Meas. 2023, 72, 2526012. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Wen, X.D.; Liu, X.D.; Yu, C.H.; Gao, H.N.; Wang, J.; Liang, Y.J.; Yu, J.L.; Bai, Y. IOOA: A multi-strategy fusion improved Osprey Optimization Algorithm forglobal optimization. Electron. Res. Arch. 2024, 32, 2033–2074. [Google Scholar] [CrossRef]
- Li, C.; Liu, Y.; Zhou, A.; Kang, L.; Wang, H. A Fast Particle Swarm Optimization Algorithm with Cauchy Mutation and Natural Selection Strategy. Adv. Comput. Intell. 2007, 1, 334–343. [Google Scholar]
- Case Western Reserve University Bearing Data Center. Bearing Data Set. Available online: https://engineering.case.edu/bearingdatacenter (accessed on 21 November 2024).

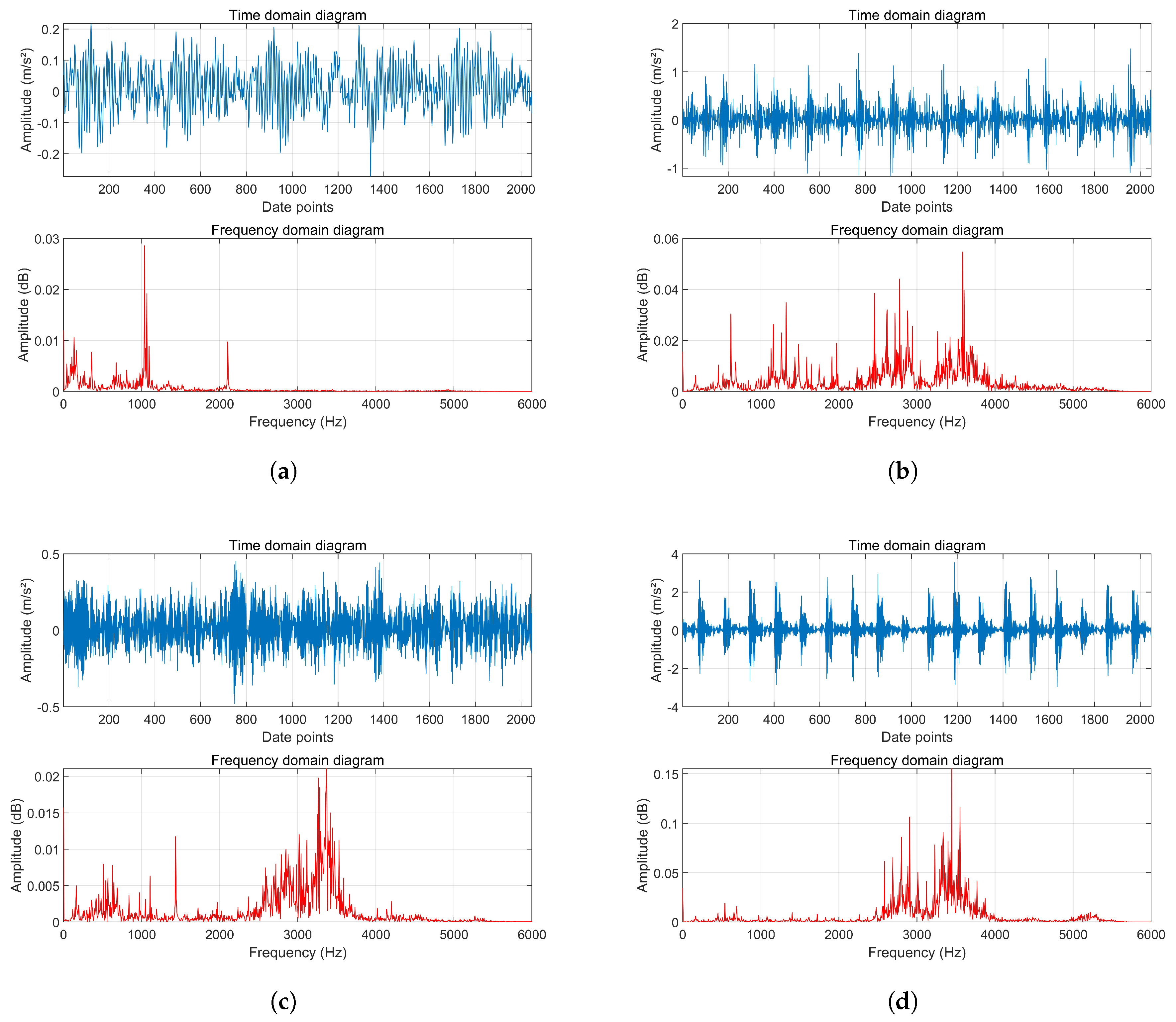
| Fault Type | Fault Diameter (mm) | Training Sample | Test Sample | Sample Data Size | Fault Label |
|---|---|---|---|---|---|
| Normal | - | 840 | 360 | 2048 | 1 |
| Inner ring fault | 0.1778 | 840 | 360 | 2048 | 2 |
| Rolling ball fault | 0.3556 | 840 | 360 | 2048 | 3 |
| Outer ring fault | 0.5334 | 840 | 360 | 2048 | 4 |
| Inner ring fault | 0.1778 | 840 | 360 | 2048 | 5 |
| Rolling ball fault | 0.3556 | 840 | 360 | 2048 | 6 |
| Outer ring fault | 0.5334 | 840 | 360 | 2048 | 7 |
| Inner ring fault | 0.1778 | 840 | 360 | 2048 | 8 |
| Rolling ball fault | 0.3556 | 840 | 360 | 2048 | 9 |
| Outer ring fault | 0.5334 | 840 | 360 | 2048 | 10 |
| Fault Type | Fault Diameter (mm) | Optimum Solutions | Optimum Solutions K | Optimum Parameters |
|---|---|---|---|---|
| Normal | - | 905 | 10 | 10 |
| Inner ring fault | 0.1778 | 2000 | 10 | 1 |
| Rolling ball fault | 0.3556 | 354 | 7 | 1 |
| Outer ring fault | 0.5334 | 100 | 9 | 1 |
| Inner ring fault | 0.1778 | 100 | 10 | 1 |
| Rolling ball fault | 0.3556 | 2144 | 10 | 4 |
| Outer ring fault | 0.5334 | 2500 | 10 | 1 |
| Inner ring fault | 0.1778 | 2491 | 10 | 1 |
| Rolling ball fault | 0.3556 | 1768 | 5 | 1 |
| Outer ring fault | 0.5334 | 2039 | 10 | 1 |
| Methods | Type1 | Type2 | Type3 | Type4 | Type5 | Type6 | Type7 | Type8 | Type9 | Type10 | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|
| OCSSA-VMD-BiTCN-Attention | 94.4% | 100% | 100% | 100% | 100% | 100% | 100% | 100% | 100% | 100% | 99.44% |
| OCSSA-VMD-TCN | 94.4% | 97.2% | 100% | 97.2% | 100% | 94.4% | 100% | 94.4% | 97.2% | 100% | 97.5% |
| VMD-TCN | 94.4% | 100% | 97.2% | 100% | 94.4% | 100% | 100% | 100% | 100% | 100% | 98.61% |
| VMD-CNN-LSTM | 91.7% | 100% | 100% | 100% | 80.6% | 86.1% | 100% | 97.2% | 100% | 91.7% | 94.72% |
| CNN-BiLSTM | 94.4% | 100% | 100% | 94.4% | 36.1% | 52.8% | 100% | 100% | 75% | 94.4% | 84.72% |
| BIGRU | 88.9% | 100% | 100% | 86.1% | 100% | 86.1% | 100% | 100% | 97.2% | 100% | 95.83% |
| CNN-BIGRU-Attention | 94.4% | 100% | 100% | 88.9% | 100% | 100% | 100% | 100% | 94.4% | 100% | 97.78% |
| VMD-BiTCN-Attention | 91.7% | 100% | 88.9% | 100% | 91.7% | 86.1% | 94.4% | 100% | 91.7% | 91.7% | 93.61% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Han, C.; Ran, G.; Ma, T.; Pan, J. Fault Diagnosis of Rolling Element Bearing Based on BiTCN-Attention and OCSSA Mechanism. Actuators 2025, 14, 218. https://doi.org/10.3390/act14050218
Yang Y, Han C, Ran G, Ma T, Pan J. Fault Diagnosis of Rolling Element Bearing Based on BiTCN-Attention and OCSSA Mechanism. Actuators. 2025; 14(5):218. https://doi.org/10.3390/act14050218
Chicago/Turabian StyleYang, Yuchen, Chunsong Han, Guangtao Ran, Tengyu Ma, and Juntao Pan. 2025. "Fault Diagnosis of Rolling Element Bearing Based on BiTCN-Attention and OCSSA Mechanism" Actuators 14, no. 5: 218. https://doi.org/10.3390/act14050218
APA StyleYang, Y., Han, C., Ran, G., Ma, T., & Pan, J. (2025). Fault Diagnosis of Rolling Element Bearing Based on BiTCN-Attention and OCSSA Mechanism. Actuators, 14(5), 218. https://doi.org/10.3390/act14050218






