Stability of Stochastic Coupled Networks with Time-Varying Coupling Under Intermittent Event-Triggered Control

Abstract

This paper studies the exponential stability in the mean square of the stochastic complex networks with time-varying coupling under an intermittent dynamic event-triggered control. A dynamic term and an exponential function are introduced into the event-triggered mechanism to reduce the number of control updates. Simultaneously, the minimum inter-execution time for every sample path solution of the stochastic complex networks, independent mathematical expectation, is obtained. Unlike previous research, the event-triggered mechanism under the stochastic version is more reasonable due to the absence of mathematical expectations in the event-triggered function. Furthermore, using the average control rate for intermittent strategy and the Lyapunov method, sufficient conditions for exponential stability in the mean square under intermittent dynamic event-triggered control are derived. Finally, an example with numerical simulations is provided to validate the feasibility of the theoretical results.

1. Introduction

Complex networks have attracted a tremendous amount of attention due to their diverse applications in a variety of fields such as brain science, engineering, sociology and linguistics [1,2,3,4]. In practical systems, the connections between nodes in complex networks are more likely to exhibit time-varying characteristics instead of remaining static over time. For instance, in the field of brain science, brain networks can be described as complex networks with time-varying coupling, as the nodal activity and connectivity patterns of brain nodes change over time [5,6]. Similarly, in a power grid, when a local power system experiences severe faults, it is disconnected from the network, leading to time-varying links [7]. Hence, time-varying coupling should be considered when simulating practical systems. In fact, several scholars have contributed to the investigations of the dynamical behaviors of complex networks with time-varying coupling [8,9].

In conjunction with the advancement of network control, many scholars used different controls to investigate the dynamical behaviors of complex networks [10,11,12,13]. Control cost is an important factor to consider when designing a control strategy due to the limited communication and computational resources as well as energy. Compared with the continuous control strategies, intermittent control is more efficient and economical since it has control subintervals (work time) and rest subintervals (rest time). Apart from that, intermittent control can choose the control width. Therefore, it has good flexibility. Hence, rapidly growing research results about intermittent control have been reported in [14,15,16,17]. The above-mentioned papers considered the intermittent control based on continuous-time states during work time. When considering cost and efficiency, discrete-time states (time-triggered) are more practical and economical than continuous-time states. In view of this, intermittent control based on time-triggered control during the work time was proposed in [9] to discuss the synchronization of the stochastic complex networks. However, time-triggered control may result in redundant transmission. In addition, the current results mainly consider intermittent strategies based on the minimum time activation rate of intermittent control [18]. Therefore, further improvement of intermittent control is needed. To avoid redundant transmission caused by time-triggered control, event-triggered control has become interesting, and some relevant results have been published in [19,20,21,22,23,24,25,26,27,28].

However, most of the references above mainly considered event-triggered control for deterministic systems. In actuality, the stochastic interference factor is unavoidable. For example, signals transmitted through communication networks are inevitably subject to stochastic interference from the external environment, which may cause the loss of information contained in these signals [29]. Meanwhile, stochastic interference may result in the poor performance and instability of the complex networks with time-varying coupling. Therefore, it is necessary to consider stochastic interference factors when studying the stabilization of complex networks by event-triggered control. The existing results related to the stabilization problem for the stochastic systems can be seen in [30,31,32,33]. For example, in [30], event-triggered control was investigated for uncertain stochastic systems. In [31], Ma et al. investigated event-triggered control for Markovian jump systems. However, the proposed event-triggered controls were based on mathematical expectation in [30] and [31]. In [32,33], Gao et al. and Wang et al. obtained the minimum inter-execution time by taking the mathematical expectations of the state. From a practical standpoint, this approach may not be implemented because the state measured by the controller is a sample path rather than statistics. Moreover, the minimum inter-execution time of every sample path solution of stochastic systems is required for the event-triggered control. To avoid the aforementioned two limitations, in [34], Luo and Deng designed event-triggered control based on dynamic event-generator control for nonlinear stochastic systems. The obtained results can ensure the existence of the minimum inter-execution time in a more reasonable way by utilizing a time-regularization design framework.

Most existing work considers either intermittent control or event-triggered control in the stochastic case. Considering the advantages of both event-triggered control and intermittent control, it is necessary to introduce the event-triggered control mechanism into intermittent control. As a matter of fact, in [35], Hu et al. considered the consensus of multi-agent systems under deterministic case by designing intermittent event-triggered control. However, the method of obtaining the minimum inter-execution time proposed in [35] might not be utilized for stochastic complex networks since the solution to stochastic complex networks is a stochastic process. Compared with the static event-triggered control considered in [35], the dynamic term should be added to the event-triggered mechanism to reduce the number of control updates, thereby making further efforts to improve energy utilization efficiency.

Motivated by the aforementioned discussions, we extend intermittent static event-triggered control into intermittent dynamic event-triggered control for complex networks with time-varying coupling under stochastic cases and investigate the exponential stability in the mean square of the stochastic complex networks with time-varying coupling under this novel control in this paper. Furthermore, the event-triggered control in the paper actually requires that every sample path solution of the system has a minimum inter-execution time. Meanwhile, the event-triggered condition designed in this paper is dependent on the topology structure of the stochastic complex networks. In addition, this article adopts the average control rate of intermittent strategy instead of the minimum time activation rate. What is more, based on the Lyapunov method and graph theory, some sufficient conditions with regard to the exponential stability in the mean square of the stochastic complex networks with time-varying coupling are established. Compared with relevant papers, the main contributions are as follows: (1) Unlike [17], an intermittent dynamic event-triggered control is developed where a dynamic term is added to the event-triggered condition to reduce the number of control updates. Moreover, an exponential function is added to the controller to better approximate the state of the stochastic complex networks with time-varying coupling, which can lower the error part and therefore reduce the number of control updates. Moreover, the average control rate of the intermittent strategy is proposed, which weakens the limitations of the intermittent strategy. (2) Compared with [19,22,23,25,26,28,30,31], the minimum inter-execution time of intermittent dynamic event-triggered control independent of mathematical expectation is guaranteed under the stochastic case, which is more reasonable. Meanwhile, the minimum inter-execution time has close relationship with the parameters of the stochastic complex networks with time-varying coupling. Moreover, the minimum inter-execution time can be estimated by the unique solution to Equation (3)). Unlike the results of existing intermittent strategies [15,17,18], this paper adopts the average control rate of intermittent strategies. We found that the larger the control rate of the intermittent strategy, the easier it is to satisfy the conditions of the theorem. Therefore, the results obtained in this article have less conservatism because the average control rate is greater than the minimum activation time rate.

The rest of this paper will be arranged as follows: We will begin with some notations and model formulation in Section 2. Then, the  exponential stability analysis for stochastic complex networks will be shown in Section 3. Next, in Section 4, we give an application and numerical simulations. Finally, the conclusions are given in Section 5.

2. Notations and Model Formulation

2.1. Notations

Let $\mathcal{Z}=\{0,1,2,\cdots \},$ ${\mathcal{R}}^{+}=[0,+\infty )$, and $\mathcal{N}=\{1,2,\cdots ,n\}$. For $x\in \mathcal{R}$, $\left|\right|x\left|\right|$ denotes the Euclidean norm of x. Moreover, let $(\Omega ,\mathcal{F},{\left\{{\mathcal{F}}_t\right\}}_{t\ge 0},\mathcal{P})$ be a complete probability space with the filtration ${\left\{{\mathcal{F}}_t\right\}}_{t\ge 0}$ satisfying the usual conditions if it is right continuous and ${\mathcal{F}}_0$ contains all $\mathcal{P}$-null sets, and $\mathbb{E}(·)$ is the mathematical expectation with regard to the given probability measure $\mathcal{P}$. In addition, $B\left(t\right)$ represents one-dimensional normal Brownian motion defined on the above probability space.

A digraph $\mathcal{G}=(\mathcal{N},\mathcal{E}(t\left)\right)$ is made up of a set $\mathcal{N}$ of nodes and a set $\mathcal{E}\left(t\right)$ of edges $(i,j)$. For a weighed digraph $\mathcal{G}$, each edge $(j,i)$ is assigned a nonzero weight $r_{ij}\left(t\right)$. And we define the weight matrix as $r\left(t\right)={\left(r_{ij}\left(t\right)\right)}_{n\times n}$. Meanwhile, the connecting edge $(j,i)$ exists in $\mathcal{G}$ if and only if $r_{ij}\left(t\right)>0$. If for any pair of distinct nodes of digraph $\mathcal{G}$, there is a directed path from one to the other, then the digraph is strongly connected. Furthermore, the Laplacian matrix of digraph $(\mathcal{G},r(t\left)\right)$ is defined as $L\left(t\right)={\left(p_{ij}\left(t\right)\right)}_{n\times n}$, where $p_{ij}\left(t\right)=-r_{ij}\left(t\right)$ for $i\ne j$, and  $p_{ii}\left(t\right)={\sum }_{j\ne i}{r}_{ij}\left(t\right)$.

2.2. Model Formulation

In this paper, we focus on a stochastic complex networks with time-varying coupling as follows:

$$\begin{array}{cc}\hfill \mathrm{d}{y}_i\left(t\right)=& \left(f_i(y_i\left(t\right),t)+\sum _{j=1}^n{d}_{ij}\left(t\right)h_{ij}(y_i\left(t\right),y_j\left(t\right))\right)\mathrm{d}t+k_i(y_i\left(t\right),t)\mathrm{d}B\left(t\right),i\in \mathcal{N},\hfill \end{array}$$

(1)

where $y_i\left(t\right)={(y_{i1}\left(t\right),y_{i2}\left(t\right),\cdots ,y_{im}\left(t\right))}^{\mathrm{T}}\in {\mathcal{R}}^m,$ $h_{ij}:{\mathcal{R}}^m\times {\mathcal{R}}^m\to {\mathcal{R}}^m$ is a coupling function, $f_i:{\mathcal{R}}^m\times {\mathcal{R}}^{+}\to {\mathcal{R}}^m$ represents the internal dynamic behaviors of the ith node, and $k_i:{\mathcal{R}}^m\times {\mathcal{R}}^{+}\to {\mathcal{R}}^m$ denotes the stochastic interference intensity. Suppose that $d_{ij}\left(t\right)$ is bounded, that is, $d_{ij}\left(t\right)\le d_{ij},$ where $d_{ij}>0$.

To make system (1) stable, the following intermittent dynamic event-triggered control strategy is proposed:

$$u_i\left(t\right)=\left\{\begin{array}{c}-b_i{y}_i\left(t_{l,k}\right)exp\{-a_i(t-t_{l,k})\},t\in I_{l,k}\cap I_l,\hfill \\ 0,t\in S_l,\hfill \end{array}\right.$$

(2)

where $I_{l,k}=[t_{l,k},t_{l,k+1})$, $I_l=[t_l,s_l)$, $S_l=[s_l,t_{l+1})$, $a_i,b_i$ are positive constants, $l,k\in \mathcal{Z}$, $[t_l,s_l)$ denotes the work time, and $[s_l,t_{l+1})$ represents the rest time. The event-triggered time sequences $\left\{t_{l,k}\right\}$ are determined by the following equation:

$$\begin{array}{cc}\hfill t_{l,k+1}=& inf\left\{t>t_{l,k}+\tau |\eta \left(\sum _{i=1}^n{c}_i\left(t\right)\left|\right|e_i{\left(t\right)\left|\right|}^2-\delta \sum _{i=1}^n{c}_i\left(t\right)\left|\right|y_i\left(t\right){\left|\right|}^2\right)>\theta \left(t\right)\right\},\hfill \end{array}$$

(3)

where parameters $\eta >0,$ $\delta >0,$ $\tau >0,$ $e_i\left(t\right)=exp\{-a_i(t-t_{l,k})\}{y}_i\left(t_{l,k}\right)-y_i\left(t\right),$ and $c_i\left(t\right)$ is a cofactor of the ith diagonal element of the Laplacian matrix of the strongly connected digraph $(\mathcal{G},r(t\left)\right),$ where $r\left(t\right)={\left(r_{ij}\left(t\right)\right)}_{n\times n},$ $r_{ij}\left(t\right)=max\{d_{ij}\left(t\right)b_{ij},d_{ij}^2\left(t\right)b_{ij}^2\}$. Suppose $t_{l,0}=t_l$ and the dynamic term $\theta \left(t\right)$ is given as follows:

$$\begin{array}{c}\hfill \dot{\theta }\left(t\right)=\left\{\begin{array}{c}-{\xi }_1\theta \left(t\right),t\in I_{l,k,\tau }\cap I_l,\hfill \\ {\displaystyle -{\xi }_1\theta \left(t\right)-\sum _{i=1}^n{c}_i\left(t\right)\left|\right|e_i{\left(t\right)\left|\right|}^2+\delta \sum _{i=1}^n{c}_i\left(t\right)\left|\right|y_i\left(t\right){\left|\right|}^2,t\in I_{l,k,\tau }^c\cap I_l,}\hfill \\ 0,t\in S_l,\hfill \end{array}\right.\end{array}$$

(4)

where $I_{l,k,\tau }=[t_{l,k},t_{l,k}+\tau )$, $I_{l,k,\tau }^c=[t_{l,k}+\tau ,t_{l,k+1})$, parameter ${\xi }_1>0$, and $\theta \left(0\right)>0$.

Now, system (1) with intermittent dynamic event-triggered control (2) is rewritten by

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill \mathrm{d}{y}_i\left(t\right)=& {\displaystyle \left(f_i(y_i\left(t\right),t)+\sum _{j=1}^n{d}_{ij}\left(t\right)h_{ij}(y_i\left(t\right),y_j\left(t\right))-b_i{y}_i\left(t_{l,k}\right)exp\{-a_i(t-t_{l,k})\}\right)\mathrm{d}t}\hfill \\ \hfill & +k_i(y_i\left(t\right),t)\mathrm{d}B\left(t\right),t\in I_{l,k}\cap I_l,\hfill \\ \hfill \mathrm{d}{y}_i\left(t\right)=& {\displaystyle \left(f_i(y_i\left(t\right),t)+\sum _{j=1}^n{d}_{ij}\left(t\right)h_{ij}(y_i\left(t\right),y_j\left(t\right))\right)\mathrm{d}t+k_i(y_i\left(t\right),t)\mathrm{d}B\left(t\right),t\in S_l.}\hfill \end{array}\right.\end{array}$$

(5)

Next, we present three assumptions and a definition.

Assumption 1. 

There exist ${\alpha }_{i1}>0$, ${\alpha }_{i2}>0$, and $b_{ij}>0$ such that

$$\left|\right|f_i(y_i,t)\left|\right|\le {\alpha }_{i1}\left|\right|y_i\left|\right|,\left|\right|k_i(y_i,t)\left|\right|\le {\alpha }_{i2}\left|\right|y_i\left|\right|,$$

and

$$\left|\right|h_{ij}(y_i,y_j)\left|\right|\le b_{ij}\left(\right||y_i\left|\right|+\left|\right|y_j\left|\right|),$$

for any $y_i,y_j\in {\mathcal{R}}^m.$

In this article, the functions $f_i,k_i,$ and $h_{ij}$ in the system (1) satisfy the inequalities in Assumption 1. In fact, Assumption 1 and the local Lipschitz condition are important for ensuring a unique solution to system (1) based on [36].

Assumption 2. 

Assuming a digraph $(\mathcal{G},r(t\left)\right)$ is strongly connected, the cofactor $c_i\left(t\right)$ of the ith diagonal element of the Laplacian matrix of the strongly connected digraph $(\mathcal{G},r(t\left)\right)$ satisfies

$${\underline{c}}_i\le c_i\left(t\right)\le {\overline{c}}_i,c_i^{\prime }\left(t\right)\le c_i,$$

where ${\overline{c}}_i$, ${\underline{c}}_i$, $c_i$ are positive constants and $c_i^{\prime }\left(t\right)$ represents the derivative of cofactor $c_i\left(t\right)$.

For the intermittent strategy, we make the following assumption:

Assumption 3 

(see [37]). For the intermittent strategy, there are $\vartheta \in (0,1)$ and $T_0\ge 0$ such that

$$\begin{array}{c}\hfill T_{con}(t_1,t_2)\ge \vartheta (t_1-t_2)-T_0,\forall t_1>t_2\ge 0,\end{array}$$

in which $T_{con}(t_1,t_2)$ stands for the total control interval length on $[t_2,t_1),\vartheta$ represents the average control rate, and $T_0$ is called the elasticity number.

In Assumption 3, $\vartheta$ is an average control rate, which can be calculated by $\vartheta ={\sum }_{l=0}^{\infty }\left(s_l-t_l\right)/{\sum }_{l=0}^{\infty }\left(t_{l+1}-t_l\right)$.

Definition 1. 

System (1) reaches the exponential stability in the mean square under intermittent dynamic event-triggered control (2) if there are constants $M_0>0$ and $\gamma >0$ such that

$$\begin{array}{c}\hfill {\mathbb{E}\left|\right|y\left(t\right)\left|\right|}^2\le M_{0}exp\{-\gamma t\},t\ge 0,\end{array}$$

where $y\left(t\right)={(y_1^{\mathrm{T}}\left(t\right),y_2^{\mathrm{T}}\left(t\right),\cdots ,y_n^{\mathrm{T}}\left(t\right))}^{\mathrm{T}}\in {\mathcal{R}}^{nm}$ is the state solution of system (5).

We can see from Definition 1 that the system (5) can achieve not only exponential convergence but also asymptotic convergence. If system (5) is exponentially convergent, it can achieve asymptotic convergence. But, if the system is asymptotically convergent, it is difficult to achieve exponential convergence.

3. Exponential Stability Analysis for Stochastic Complex Networks

This section gives the exponential stability in the mean square of the stochastic complex networks with time-varying coupling. Before proposing the exponential stability result, an important lemma is presented.

For the convenience of the following lemma description, we make the following notations. Let $\widetilde{c_1}={\displaystyle \frac{\overline{c}}{\underline{c}}}$ and $\widetilde{c_2}={\displaystyle \frac{\underline{c}}{\overline{c}}}$ with $\overline{c}={max}_{i\in \mathcal{N}}\left\{\overline{c_i}\right\},\underline{c}={min}_{i\in \mathcal{N}}\left\{\underline{c_i}\right\}.$ In addition, set $Z_1\left(\tau \right)=\widetilde{c_1}{\beta }_{1}exp\left\{\widetilde{c_1}{\beta }_2\tau \right\},$ where ${\beta }_1={max}_{i\in \mathcal{N}}\left\{{\beta }_{i1}\right\}$ with ${\beta }_{i1}=\tau \left[6\tau {(b_i-a_i)}^2+2(6\tau {\alpha }_{i1}^2+2{\alpha }_{i2}^2)+48\tau M{\displaystyle \frac{\overline{c}}{\underline{c}}}{\sum }_{j=1}^n{r}_{ij}\right],$ and ${\beta }_2={max}_{i\in \mathcal{N}}\left\{{\beta }_{i2}\right\}$ with ${\beta }_{i2}=2(6\tau {\alpha }_{i1}^2+2{\alpha }_{i2}^2)+48{\tau }^{2}M{\displaystyle \frac{\overline{c}}{\underline{c}}}{\sum }_{j=1}^n{r}_{ij}.$ And let $Z_2\left(\tau \right)={\displaystyle \frac{b}{\kappa }}(exp\{-\kappa \tau \}-1)\widetilde{c_2}+\widetilde{c_2}exp\{-\kappa \tau \}$ with $\kappa ={max}_{i\in \mathcal{M}}\left\{2{\alpha }_{i1}+{\alpha }_{i2}^2+b_i+4{\sum }_{j=1}^n{r}_{ij}+{\displaystyle \frac{c_i^{\prime }}{\underline{c_i}}}\right\}$ and $b={min}_{i\in \mathcal{N}}\left\{b_i\right\}$.

Lemma 1. 

Let Assumptions 1 and 2 hold. For each $t\in [t_{l,k},t_{l,k}+\tau )$, the following estimations are obtained:

$$\begin{array}{c}\hfill \mathbb{E}\left(\sum _{i=1}^n{c}_i\left(t\right)\left|\right|x_i\left(t\right){\left|\right|}^2\right)\ge Z_2\left(\tau \right)\mathbb{E}\left(\sum _{i=1}^n{c}_i\left(t\right)\left|\right|y_i\left(t_{l,k}\right){\left|\right|}^2\right),\\ \hfill \mathbb{E}\left(\sum _{i=1}^n{c}_i\left(t\right)\left|\right|e_i\left(t\right){\left|\right|}^2\right)\le Z_1\left(\tau \right)\mathbb{E}\left(\sum _{i=1}^n{c}_i\left(t\right)\left|\right|y_i\left(t_{l,k}\right){\left|\right|}^2\right),\end{array}$$

where $c_i\left(t\right)$ is cofactor of the ith diagonal element of the Laplacian matrix of the strongly connected digraph $(\mathcal{G},r(t\left)\right)$, and  the event-triggered time sequences $\left\{t_{l,k}\right\}$ are given in (3).

Proof. 

According to system (5), when $t\in I_{l,k,\tau },$ we can find

$$\begin{array}{cc}\hfill \mathrm{d}{e}_i\left(t\right)=& (-f_i(y_i\left(t\right),t)-\sum _{j=1}^n{d}_{ij}\left(t\right)h_{ij}(y_i\left(t\right),y_j\left(t\right))-a_{i}exp\{-a_i(t-t_{l,k})\}{y}_i\left(t_{l,k}\right)\hfill \\ \hfill & +b_{i}exp\{-a_i(t-t_{l,k})\}{y}_i\left(t_{l,k}\right))\mathrm{d}t-k_i(y_i\left(t\right),t)\mathrm{d}B\left(t\right).\hfill \end{array}$$

Therefore, based on Assumption 2, we can prove that  

$$\begin{array}{cc}\hfill & \mathbb{E}\left(\right|\left|e_i\left(t\right)\right|{|}^2\left|{\mathcal{F}}_{t_{l,k}}\right)\hfill \\ \hfill \le & \mathbb{E}\left(2\tau {\int }_{t_{l,k}}^t\right(3{(b_i-a_i)}^{2}exp\{-2a_i(s-t_{l,k})\}\left|\right|y_i\left(t_{l,k}\right){\left|\right|}^2\hfill \\ \hfill & +3\left|\right|f_i(y_i\left(s\right),s){\left|\right|}^2+3M\sum _{j=1}^n{d}_{ij}^2\left(s\right)\left|\right|h_{ij}(y_i\left(s\right),y_j\left(s\right)){\left|\right|}^2)\mathrm{d}s+2{\int }_{t_{l,k}}^t\left|\right|k_i(y_i\left(s\right),s){\left|\right|}^2\mathrm{d}s|{\mathcal{F}}_{t_{l,k}})\hfill \\ \hfill \le & \mathbb{E}\left({\int }_{t_{l,k}}^t\right(6\tau {(b_i-a_i)}^2\left|\right|y_i\left(t_{l,k}\right){\left|\right|}^2+6\tau {\alpha }_{i1}^2\left|\right|y_i\left(s\right){\left|\right|}^2\hfill \\ \hfill & +6\tau M\sum _{j=1}^n{d}_{ij}^2\left(s\right)b_{ij}^2\left(\right||y_i\left(s\right)\left|\right|+\left|\right|y_j{\left(s\right)\left|\right|)}^2+2{\alpha }_{i2}^2\left|\right|y_i\left(s\right){\left|\right|}^2\left)\mathrm{d}s\right|{\mathcal{F}}_{t_{l,k}})\hfill \\ \hfill \le & {\int }_{t_{l,k}}^t\left(\right(6\tau {(b_i-a_i)}^2\left|\right|y_i\left(t_{l,k}\right){\left|\right|}^2+(6\tau {\alpha }_{i1}^2+2{\alpha }_{i2}^2)\mathbb{E}\left|\right|y_i\left(s\right){\left|\right|}^2\hfill \\ \hfill & +12\tau M\sum _{j=1}^n{d}_{ij}^2\left(s\right)b_{ij}^2\left(\mathbb{E}\right||y_i{\left(s\right)\left|\right|}^2+\mathbb{E}\left|\right|y_j{\left(s\right)\left|\right|}^2\left)\right)|{\mathcal{F}}_{t_{l,k}})\mathrm{d}s.\hfill \end{array}$$

(6)

Making use of the elementary inequality, we can easily find that $\left|\right|y_i{\left(s\right)\left|\right|}^2\le 2\left|\right|e_i{\left(s\right)\left|\right|}^2+2\left|\right|y_i\left(t_{l,k}\right){\left|\right|}^2,$ which further implies that

$$\begin{array}{cc}\hfill & \mathbb{E}\left(\right|\left|e_i\left(t\right)\right|{|}^2\left|{\mathcal{F}}_{t_{l,k}}\right)\hfill \\ \hfill \le & {\int }_{t_{l,k}}^t(6\tau {(b_i-a_i)}^2+2(6\tau {\alpha }_{i1}^2+2{\alpha }_{i2}^2)\left|\right|y_i\left(t_{l,k}\right){\left|\right|}^2\hfill \\ \hfill & +2(6\tau {\alpha }_{i1}^2+2{\alpha }_{i2}^2)\mathbb{E}\left|\right|e_i\left(s\right){\left|\right|}^2+12\tau M\sum _{j=1}^n{d}_{ij}^2\left(s\right)b_{ij}^2\left(\mathbb{E}\right||y_i\left(s\right){\left|\right|}^2+\mathbb{E}\left|\right|y_j\left(s\right){\left|\right|}^2\left)\right|{\mathcal{F}}_{t_{l,k}})\mathrm{d}s\hfill \\ \hfill \le & \tau \left(6\tau {(b_i-a_i)}^2+2(6\tau {\alpha }_{i1}^2+2{\alpha }_{i2}^2)\right)\left|\right|y_i\left(t_{l,k}\right){\left|\right|}^2\hfill \\ \hfill & +{\int }_{t_{l,k}}^{t}2(6\tau {\alpha }_{i1}^2+2{\alpha }_{i2}^2)\mathbb{E}\left(\right||e_i\left(s\right){\left|\right|}^2|{\mathcal{F}}_{t_{l,k}})\mathrm{d}s\hfill \\ \hfill & +{\int }_{t_{l,k}}^t\left(12\tau M\mathbb{E}\sum _{j=1}^n{d}_{ij}^2\left(s\right)b_{ij}^2\left(\right||y_i{\left(s\right)\left|\right|}^2+\left|\right|y_j{\left(s\right)\left|\right|}^2\left)\right|{\mathcal{F}}_{t_{l,k}}\right)\mathrm{d}s.\hfill \end{array}$$

(7)

Based on (7), we can find that

$$\begin{array}{cc}\hfill & \sum _{i=1}^n{c}_i\left(t\right)\mathbb{E}\left(\right||e_i{\left(t\right)\left|\right|}^2\left|{\mathcal{F}}_{t_{l,k}}\right)\hfill \\ \hfill \le & \sum _{i=1}^n{c}_i\left(t\right)\tau (6\tau {(b_i-a_i)}^2+2(6\tau {\alpha }_{i1}^2+2{\alpha }_{i2}^2))\left|\right|y_i\left(t_{l,k}\right){\left|\right|}^2\hfill \\ \hfill & +{\int }_{t_{l,k}}^{t}2\sum _{i=1}^n{c}_i(6\tau {\alpha }_{i1}^2+2{\alpha }_{i2}^2)\mathbb{E}\left(\right||e_i\left(s\right){\left|\right|}^2\left|{\mathcal{F}}_{t_{l,k}}\right)\mathrm{d}s\hfill \\ \hfill & +{\int }_{t_{l,k}}^{t}12\tau M{\displaystyle \frac{\overline{c}}{\underline{c}}}\mathbb{E}\left(\sum _{i=1}^n\sum _{j=1}^n{c}_i\left(s\right)r_{ij}\left(s\right)\left(\right||y_j{\left(s\right)\left|\right|}^2-\left|\right|y_i{\left(s\right)\left|\right|}^2\left)\right|{\mathcal{F}}_{t_{l,k}}\right)\mathrm{d}s\hfill \\ \hfill & +{\int }_{t_{l,k}}^{t}24\tau M{\displaystyle \frac{\overline{c}}{\underline{c}}}\mathbb{E}\left(\sum _{i=1}^n\sum _{j=1}^n{c}_i\left(s\right)r_{ij}\left(s\right)\left|\right|y_i\left(s\right){\left|\right|}^2|{\mathcal{F}}_{t_{l,k}}\right)\mathrm{d}s\hfill \\ \hfill \le & \sum _{i=1}^n{c}_i\tau \left[6\tau {(b_i-a_i)}^2+2(6\tau {\alpha }_{i1}^2+2{\alpha }_{i2}^2)+48\tau M{\displaystyle \frac{\overline{c}}{\underline{c}}}\sum _{j=1}^n{r}_{ij}\right]\left|\right|y_i\left(t_{l,k}\right){\left|\right|}^2\hfill \\ \hfill & +{\int }_{t_{l,k}}^t\sum _{i=1}^n{c}_i[2(6\tau {\alpha }_{i1}^2+2{\alpha }_{i2}^2)+48{\tau }^{2}M{\displaystyle \frac{\overline{c}}{\underline{c}}}\sum _{j=1}^n{r}_{ij}]\mathbb{E}\left(\right||e_i\left(s\right){\left|\right|}^2\left|{\mathcal{F}}_{t_{l,k}}\right)\mathrm{d}s\hfill \\ \hfill & +{\int }_{t_{l,k}}^{t}12\tau M{\displaystyle \frac{\overline{c}}{\underline{c}}}\mathbb{E}\left(\sum _{i=1}^n\sum _{j=1}^n{c}_i\left(s\right)r_{ij}\left(s\right)\left(\right||y_j{\left(s\right)\left|\right|}^2-\left|\right|y_i{\left(s\right)\left|\right|}^2\left)\right|{\mathcal{F}}_{t_{l,k}}\right)\mathrm{d}s.\hfill \end{array}$$

(8)

According to Proposition 2.2 in [38], it is not difficult to find that

$$\sum _{i=1}^n\sum _{j=1}^n{c}_i\left(t\right)r_{ij}\left(t\right)\left(\right||y_j{\left(t\right)\left|\right|}^2-\left|\right|y_i{\left(t\right)\left|\right|}^2)=0.$$

(9)

Based on (9), we can find that

$$\begin{array}{cc}\hfill \sum _{i=1}^n{c}_i\left(t\right)\mathbb{E}\left(\right||e_i{\left(t\right)\left|\right|}^2\left|{\mathcal{F}}_{t_{l,k}}\right)\le & \sum _{i=1}^n{c}_i\tau \left[6\tau {(b_i-a_i)}^2+2(6\tau {\alpha }_{i1}^2+2{\alpha }_{i2}^2)+48\tau M{\displaystyle \frac{\overline{c}}{\underline{c}}}\sum _{j=1}^n{r}_{ij}\right]\left|\right|y_i\left(t_{l,k}\right){\left|\right|}^2\hfill \\ \hfill & +{\int }_{t_{l,k}}^t\sum _{i=1}^n{c}_i{\beta }_{i2}\mathbb{E}\left(\right||e_i{\left(t\right)\left|\right|}^2\left|{\mathcal{F}}_{t_{l,k}}\right)\mathrm{d}s\hfill \\ \hfill \le & \sum _{i=1}^n{c}_i{\beta }_{i1}\left|\right|y_i\left(t_{l,k}\right){\left|\right|}^2+{\int }_{t_{l,k}}^t{\beta }_2{\displaystyle \frac{\overline{c}}{\underline{c}}}\mathbb{E}\left(\sum _{i=1}^n{c}_i\left(s\right)\left|\right|e_i\left(t\right){\left|\right|}^2|{\mathcal{F}}_{t_{l,k}}\right)\mathrm{d}s.\hfill \end{array}$$

(10)

According to the Gronwall’s inequality, we have

$$\begin{array}{cc}\hfill \mathbb{E}\left(\sum _{i=1}^n{c}_i\left(t\right)\left|\right|e_i\left(t\right){\left|\right|}^2|{\mathcal{F}}_{t_{l,k}}\right)\le & {\tilde{c}}_1{\beta }_1\sum _{i=1}^n{c}_i\left(t\right)\left|\right|y_i\left(t_{l,k}\right){\left|\right|}^{2}exp\left\{{\tilde{c}}_1{\beta }_2\tau \right\}\hfill \\ \hfill =& Z_1\left(\tau \right)\sum _{i=1}^n{c}_i\left(t\right)\left|\right|y_i\left(t_{l,k}\right){\left|\right|}^2.\hfill \end{array}$$

(11)

Taking the mathematical expectation of both sides of inequality (11), we have

$$\mathbb{E}\left(\sum _{i=1}^n{c}_i\left|\right|e_i\left(t\right){\left|\right|}^2\right)\le Z_1\left(\tau \right)\mathbb{E}\left(\sum _{i=1}^n{c}_i\left(t\right)\left|\right|y_i\left(t_{l,k}\right){\left|\right|}^2\right).$$

On the other hand, if $V_i\left(t\right)=-\left|\right|y_i\left(t\right){\left|\right|}^2,$ we have

$$\mathbb{E}\left(V_i\left(t\right)\right|{\mathcal{F}}_{t_{l,k}})=V_i\left(t_{l,k}\right)+{\int }_{t_{l,k}}^t\mathbb{E}\left(\mathcal{L}{V}_i\left(s\right)\right|{\mathcal{F}}_{t_{l,k}})\mathrm{d}s,$$

where

$$\begin{array}{cc}\hfill \mathcal{L}{V}_i\left(t\right)=& -2y_i^{\mathrm{T}}\left(t\right)(f_i(y_i\left(t\right),t)+\sum _{j=1}^n{d}_{ij}\left(t\right)h_{ij}(y_i\left(t\right),y_j\left(t\right))\hfill \\ \hfill & -b_i{y}_i\left(t_{l,k}\right)exp\{-a_i(t-t_{l,k})\})+\left|\right|k_i(y_i\left(t\right),t){\left|\right|}^2\hfill \\ \hfill \le & 2{\alpha }_{i1}\left|\right|y_i{\left(t\right)\left|\right|}^2+b_i\left|\right|y_i{\left(t\right)\left|\right|}^2+b_i\left|\right|y_i\left(t_{l,k}\right){\left|\right|}^2\hfill \\ \hfill & +3\sum _{j=1}^n{d}_{ij}\left(t\right)b_{ij}\left|\right|y_i{\left(t\right)\left|\right|}^2+\sum _{j=1}^n{d}_{ij}\left(t\right)b_{ij}\left|\right|y_j\left(t\right){\left|\right|}^2.\hfill \end{array}$$

Therefore, we find that

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}\left(\mathbb{E}{V}_i\left(t\right)\right|{\mathcal{F}}_{t_{l,k}})}{\mathrm{d}t}}\le & \mathbb{E}\left(\right((2{\alpha }_{i1}+{\alpha }_{i2}^2+b_i)\left|\right|y_i\left(t\right){\left|\right|}^2+b_i\left|\right|y_i\left(t_{l,k}\right){\left|\right|}^2\hfill \\ \hfill & +3\sum _{j=1}^n{d}_{ij}\left(t\right)b_{ij}\left|\right|y_i{\left(t\right)\left|\right|}^2+\sum _{j=1}^n{d}_{ij}\left(t\right)b_{ij}\left|\right|y_j\left(t\right){\left|\right|}^2\left)\right|{\mathcal{F}}_{t_{l,k}}).\hfill \end{array}$$

Thus, we can derive that

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\displaystyle \mathrm{d}\mathbb{E}\left(\sum _{i=1}^n{c}_i\left(t\right)V_i\left(t\right)|{\mathcal{F}}_{t_{l,k}}\right)}}{\mathrm{d}t}}\le & \mathbb{E}\left(\sum _{i=1}^n{c}_i^{\prime }{V}_i\left(t\right)|{\mathcal{F}}_{t_{l,k}}\right)+\mathbb{E}(\sum _{i=1}^n{c}_i\left(t\right)(2{\alpha }_{i1}+{\alpha }_{i2}^2+b_i\hfill \\ \hfill & +4\sum _{j=1}^n{r}_{ij}\left)\right||y_i{\left(t\right)\left|\right|}^2\left|{\mathcal{F}}_{t_{l,k}}\right)+\sum _{i=1}^n{c}_i\left(t\right)b_i\left|\right|y_i\left(t_{l,k}\right){\left|\right|}^2\hfill \\ \hfill & +\mathbb{E}\left(\sum _{i=1}^n\sum _{j=1}^n{c}_i\left(t\right)r_{ij}\left(t\right)\left(\right||y_j{\left(t\right)\left|\right|}^2-\left|\right|y_i{\left(t\right)\left|\right|}^2\left)\right|{\mathcal{F}}_{t_{l,k}}\right).\hfill \end{array}$$

(12)

Based on (9), inequality (12) can be rewritten as

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\displaystyle \mathrm{d}\mathbb{E}\left(\sum _{i=1}^n{c}_i\left(t\right)V_i\left(t\right)|{\mathcal{F}}_{t_{l,k}}\right)}}{\mathrm{d}t}}\le & \sum _{i=1}^n{c}_i\left(t\right)b_i\left|\right|y_i\left(t_{l,k}\right){\left|\right|}^2+\mathbb{E}\left(\sum _{i=1}^n{c}_i\left(t\right)\right(2{\alpha }_{i1}+{\alpha }_{i2}^2+b_i\hfill \\ \hfill & +4\sum _{j=1}^n{r}_{ij}+{\displaystyle \frac{c_i^{\prime }}{\underline{c_i}}}\left)\right||y_i\left(t\right){\left|\right|}^2\left|{\mathcal{F}}_{t_{l,k}}\right)\hfill \\ \hfill \le & \sum _{i=1}^n{c}_i{b}_i\left|\right|y_i\left(t_{l,k}\right){\left|\right|}^2-\mathbb{E}\left(\kappa \sum _{i=1}^n{c}_i\left(t\right)V_i\left(t\right)|{\mathcal{F}}_{t_{l,k}}\right).\hfill \end{array}$$

According to the comparison principle, we can find that

$$\begin{array}{cc}\hfill \mathbb{E}\left(\sum _{i=1}^n{c}_i\left(t\right)V_i\left(t\right)|{\mathcal{F}}_{t_{l,k}}\right)\le & -{\displaystyle \frac{1}{\kappa }}\sum _{i=1}^n{c}_i{b}_i\left|\right|y_i\left(t_{l,k}\right){\left|\right|}^2(exp\{-\kappa (t-t_{l,k})\}-1)\hfill \\ \hfill & -\sum _{i=1}^n{c}_i\left(t_{l,k}\right)\left|\right|y_i\left(t_{l,k}\right){\left|\right|}^{2}exp\{-\kappa (t-t_{l,k})\}.\hfill \end{array}$$

Therefore, we can find that

$$\begin{array}{c}\hfill \mathbb{E}\left(\sum _{i=1}^n{c}_i\left(t\right)\left|\right|y_i\left(t\right){\left|\right|}^2|{\mathcal{F}}_{t_{l,k}}\right)\ge \left({\displaystyle \frac{1}{\kappa }}b(exp\{-\kappa \tau \}-1)c_2+c_{2}exp\{-\kappa \tau \}\right)\sum _{i=1}^n{c}_i\left(t\right)\left|\right|y_i\left(t_{l,k}\right){\left|\right|}^2.\end{array}$$

(13)

Taking the mathematical expectation of both sides of (13), we obtain the estimates of two inequalities. The proof is completed.    □

Based on Lemma 1, the exponential stability in the mean square of system (1) with the intermittent dynamic event-triggered control strategy (2) is shown.

Let ${\Lambda }_2=min\{{\epsilon }_1,{\Lambda }_1\},$ where ${\Lambda }_1=min\{\gamma ,{\xi }_1\}$ and ${\epsilon }_1=min\left\{{\overline{\epsilon }}_1,{\xi }_1-{\displaystyle \frac{\breve{b}}{\eta }}\right\}$ with ${\overline{\epsilon }}_1={min}_{i\in \mathcal{N}}\left\{b_i-\delta \breve{b}-\delta -{\displaystyle \frac{c_i^{\prime }}{\underline{c_i}}}-2{\alpha }_{i1}-4{\sum }_{j=1}^n{r}_{ij}-{\alpha }_{i2}^2\right\}$ and $\breve{b}={max}_{i\in \mathcal{N}}\left\{b_i\right\}$. And let ${\Lambda }_3={max}_{i\in \mathcal{N}}\left\{{\Lambda }_{3i}\right\},$ where ${\Lambda }_{3i}={\displaystyle \frac{c_i^{\prime }}{{\underline{c}}_i}}+2{\alpha }_{i1}+{\alpha }_{i2}^2+4{\sum }_{j=1}^n{r}_{ij}$ with $r_{ij}=max\{d_{ij}{b}_{ij},d_{ij}^2{b}_{ij}^2\}.$ ${\epsilon }_2={min}_{i\in \mathcal{N}}\left\{b_i-\left({\displaystyle \frac{c_i^{\prime }}{{\underline{c}}_i}}+2{\alpha }_{i1}+{\alpha }_{i2}^2+4{\sum }_{j=1}^n{r}_{ij}\right)\right\}.$

Theorem 1. 

Let Assumptions 1–3 hold. System (1) reaches exponential stability in the mean square under the intermittent dynamic event-triggered control strategy (2) if the following conditions are satisfied:

$$-{\Lambda }_2\vartheta +{\Lambda }_3(1-\vartheta )<0,0<\tau <{\tau }^{*},$$

where ${\tau }^{*}$ is the unique solution to the following equation:

$$-({\epsilon }_2-\gamma )Z_1\left(\tau \right)+\breve{b}{Z}_2\left(\tau \right)=0,$$

where $\gamma >0$, $Z_1\left(\tau \right)$ and $Z_2\left(\tau \right)$ are given in Lemma 1.

Proof. 

When $t\in I_{l,k,\tau },$ we can find that $\dot{\theta }\left(t\right)=-{\xi }_1\theta \left(t\right),$ which yields

$$\theta \left(t\right)=\theta \left(t_{l,k}\right)exp\{-{\xi }_1(t-t_{l,k})\}.$$

On the one hand, when $t\in I_{l,k,\tau }^c,$ we have

$$\begin{array}{cc}\hfill \dot{\theta }\left(t\right)=& -{\xi }_1\theta \left(t\right)-\sum _{i=1}^n{c}_i\left(t\right)\left|\right|e_i{\left(t\right)\left|\right|}^2+\delta \sum _{i=1}^n{c}_i\left(t\right)\left|\right|y_i\left(t\right){\left|\right|}^2.\hfill \end{array}$$

Combined with (3), we can find that

$$\begin{array}{cc}\hfill \dot{\theta }\left(t\right)\ge & -{\xi }_1\theta \left(t\right)-{\displaystyle \frac{1}{\eta }}\theta \left(t\right)=-\left({\xi }_1+{\displaystyle \frac{1}{\eta }}\right)\theta \left(t\right).\hfill \end{array}$$

Therefore, we have

$$\begin{array}{cc}\hfill \theta \left(t\right)\ge & \theta \left(t_{l,k}\right)exp\{-{\xi }_1\tau \}exp\left\{-\left({\xi }_1+{\displaystyle \frac{1}{\eta }}\right)(t-(t_{l,k}+\tau ))\right\}\hfill \\ \hfill \ge & \theta \left(t_{l,k}\right)exp\{-\left({\xi }_1+{\displaystyle \frac{1}{\eta }}\right)(t-t_{l,k})\}.\hfill \end{array}$$

(14)

Moreover, when $t\in S_l,$ we have $\dot{\theta }\left(t\right)=0$, which implies that

$$\theta \left(t\right)=\theta \left(s_l\right).$$

(15)

By combining (14) with (15), we can find that $\theta \left(t\right)>0.$

Now, a Lyapunov function is constructed as $V\left(t\right)={\sum }_{i=1}^n{c}_i\left(t\right)\left|\right|y_i\left(t\right){\left|\right|}^2+\theta \left(t\right).$ Hence, we can find

$$\begin{array}{cc}\hfill \mathcal{L}V\left(t\right)=& \sum _{i=1}^n{c}_i^{\prime }\left(t\right)\left|\right|y_i\left(t\right){\left|\right|}^2+\sum _{i=1}^n{c}_i\left(t\right)\left[2y_i^{\mathrm{T}}\left(t\right)\right(f_i(y_i\left(t\right),t)\hfill \\ \hfill & +\sum _{j=1}^n{d}_{ij}\left(t\right)h_{ij}(y_i\left(t\right),y_j\left(t\right))+u_i\left(t\right)+\left|\right|k_i(y_i\left(t\right),t){\left|\right|}^2\left)\right]+\dot{\theta }\left(t\right)\hfill \\ \hfill \le & \sum _{i=1}^n{c}_i^{\prime }\left(t\right)\left|\right|y_i{\left(t\right)\left|\right|}^2+\sum _{i=1}^n{c}_i\left(t\right)\left[2{\alpha }_{i1}+{\alpha }_{i2}^2+4\sum _{j=1}^n{r}_{ij}\left(t\right)\right]\left|\right|y_i\left(t\right){\left|\right|}^2\hfill \\ \hfill & +\sum _{i=1}^n\sum _{j=1}^n{c}_i\left(t\right)r_{ij}\left(t\right)\left(\right||y_j{\left(t\right)\left|\right|}^2-\left|\right|y_i{\left(t\right)\left|\right|}^2)+2\sum _{i=1}^n{c}_i\left(t\right)y_i^{\mathrm{T}}\left(t\right)u_i\left(t\right)+\dot{\theta }\left(t\right).\hfill \end{array}$$

(16)

According to (9), inequality (16) is rewritten by

$$\begin{array}{cc}\hfill \mathcal{L}V\left(t\right)\le & \sum _{i=1}^n{c}_i^{\prime }\left|\right|y_i{\left(t\right)\left|\right|}^2+\sum _{i=1}^n{c}_i\left(t\right)\left[2{\alpha }_{i1}+{\alpha }_{i2}^2+4\sum _{j=1}^n{r}_{ij}\left(t\right)\right]\left|\right|y_i\left(t\right){\left|\right|}^2\hfill \\ \hfill & +2\sum _{i=1}^n{c}_i\left(t\right)y_i^{\mathrm{T}}\left(t\right)u_i\left(t\right)+\dot{\theta }\left(t\right).\hfill \end{array}$$

(17)

When $t\in I_{l,k}\cap I_l,$ we have  

$$\begin{array}{cc}\hfill 2\sum _{i=1}^n{c}_i\left(t\right)y_i^{\mathrm{T}}\left(t\right)u_i\left(t\right)=& -2\sum _{i=1}^n{b}_i{c}_i\left(t\right)y_i^{\mathrm{T}}\left(t\right)y_i\left(t\right)\hfill \\ \hfill & +2\sum _{i=1}^n{b}_i{c}_i\left(t\right)y_i^{\mathrm{T}}\left(t\right)\left[y_i\left(t\right)-y_i\left(t_{l,k}\right)exp\{-a_i(t-t_{l,k})\}\right]\hfill \\ \hfill \le & -\sum _{i=1}^n{b}_i{c}_i\left(t\right)\left|\right|y_i{\left(t\right)\left|\right|}^2+\sum _{i=1}^n{b}_i{c}_i\left(t\right)\left|\right|e_i\left(t\right){\left|\right|}^2.\hfill \end{array}$$

(18)

According to (3), for $t\in I_{l,k,\tau }^c\cap I_k,$ it can be proven that

$$\begin{array}{c}\hfill \sum _{i=1}^n{c}_i\left(t\right)\left|\right|e_i{\left(t\right)\left|\right|}^2\le \delta \sum _{i=1}^n{c}_i\left(t\right)\left|\right|y_i\left(t\right){\left|\right|}^2+{\displaystyle \frac{1}{\eta }}\theta \left(t\right).\end{array}$$

(19)

By substituting (19) into (18), it yields

$$\begin{array}{c}\hfill 2\sum _{i=1}^n{c}_i\left(t\right)y_i^{\mathrm{T}}\left(t\right)u_i\left(t\right)\le \sum _{i=1}^n{c}_i\left(t\right)(-b_i+\delta \breve{b})\left|\right|y_i\left(t\right){\left|\right|}^2+{\displaystyle \frac{\breve{b}}{\eta }}\theta \left(t\right).\end{array}$$

(20)

By inserting (20) into (17), we have

$$\begin{array}{cc}\hfill \mathcal{L}V\left(t\right)\le & \sum _{i=1}^n{c}_i\left(t\right)\left[{\displaystyle \frac{c_i^{\prime }}{\underline{c_i}}}+2{\alpha }_{i1}+{\alpha }_{i2}^2+4\sum _{j=1}^n{r}_{ij}\left(t\right)-b_i+\delta \breve{b}\right]\left|\right|y_i\left(t\right){\left|\right|}^2+{\displaystyle \frac{\breve{b}}{\eta }}\theta \left(t\right)+\dot{\theta }\left(t\right).\hfill \end{array}$$

(21)

When $t\in [t_{l,k}+\tau ,t_{l,k+1})$, we can prove that

$$\begin{array}{cc}\hfill \mathcal{L}V\left(t\right)\le & \sum _{i=1}^n{c}_i\left(t\right)\left[{\displaystyle \frac{c_i^{\prime }}{\underline{c_i}}}+2{\alpha }_{i1}+{\alpha }_{i2}^2+4\sum _{j=1}^n{r}_{ij}-b_i+\delta \breve{b}+\delta \right]\left|\right|y_i\left(t\right){\left|\right|}^2-\left({\xi }_1-{\displaystyle \frac{\breve{b}}{\eta }}\right)\theta \left(t\right)\hfill \\ \hfill \le & -{\epsilon }_{1}V\left(t\right).\hfill \end{array}$$

(22)

For $t\in I_{l,k,\tau },$ by combining (16) with (18), it shows

$$\begin{array}{cc}\hfill \mathcal{L}V\left(t\right)\le & \sum _{i=1}^n{c}_i\left(t\right)\left[{\displaystyle \frac{c_i^{\prime }}{\underline{c_i}}}+2{\alpha }_{i1}+{\alpha }_{i2}^2+4\sum _{i=1}^n{r}_{ij}-b_i\right]\left|\right|y_i{\left(t\right)\left|\right|}^2+\sum _{i=1}^n{c}_i\left(t\right)b_i\left|\right|e_i\left(t\right){\left|\right|}^2-{\xi }_1\theta \left(t\right).\hfill \end{array}$$

(23)

Based on Lemma 1 and taking the mathematical expectation of both sides of (23), we have

$$\begin{array}{cc}\hfill \mathbb{E}\mathcal{L}V\left(t\right)\le & -\gamma \mathbb{E}\sum _{i=1}^n{c}_i\left(t\right)\left|\right|y_i{\left(t\right)\left|\right|}^2-({\epsilon }_2-\gamma )Z_2\left(\tau \right)\mathbb{E}\sum _{i=1}^n{c}_i\left(t\right)\left|\right|y_i\left(t_{l,k}\right){\left|\right|}^2\hfill \\ \hfill & +\breve{b}{Z}_1\left(\tau \right)\mathbb{E}\sum _{i=1}^n{c}_i\left(t\right)\left|\right|y_i\left(t_{l,k}\right){\left|\right|}^2-{\xi }_1\mathbb{E}\theta \left(t\right)\hfill \\ \hfill \le & -\gamma \mathbb{E}\sum _{i=1}^n{c}_i\left(t\right)\left|\right|y_i\left(t\right){\left|\right|}^2-{\xi }_1\mathbb{E}\theta \left(t\right)\hfill \\ \hfill \le & -{\Lambda }_1\mathbb{E}V\left(t\right).\hfill \end{array}$$

(24)

By combining (22) with (24), we can find that when $t\in I_{l,k},$

$$\begin{array}{c}\hfill \mathbb{E}\mathcal{L}V\left(t\right)\le -min\{{\epsilon }_1,{\Lambda }_1\}\mathbb{E}V\left(t\right)=-{\Lambda }_2\mathbb{E}V\left(t\right).\end{array}$$

When $t\in S_l,$ we have

$$\begin{array}{cc}\hfill \mathcal{L}V\left(t\right)=& \sum _{i=1}^n{c}_i^{\prime }\left(t\right)\left|\right|y_i\left(t\right){\left|\right|}^2+\sum _{i=1}^n{c}_i\left(t\right)[2y_i^{\mathrm{T}}\left(t\right)\left(f_i(y_i\left(t\right),t)\right)\hfill \\ \hfill & +\sum _{j=1}^n{d}_{ij}\left(t\right)h_{ij}(y_i\left(t\right),y_j\left(t\right))+\left|\right|k_i(y_i\left(t\right),t){\left|\right|}^2]\hfill \\ \hfill \le & \sum _{i=1}^n{c}_i^{\prime }\left(t\right)\left|\right|y_i{\left(t\right)\left|\right|}^2+\sum _{i=1}^n{c}_i\left(t\right)\left[2{\alpha }_{i1}+{\alpha }_{i2}^2+4\sum _{j=1}^n{r}_{ij}\right]\left|\right|y_i\left(t\right){\left|\right|}^2\hfill \\ \hfill & +\sum _{i=1}^n\sum _{j=1}^n{c}_i\left(t\right)r_{ij}\left(t\right)\left(\right||y_j{\left(t\right)\left|\right|}^2-\left|\right|y_i{\left(t\right)\left|\right|}^2).\hfill \end{array}$$

Based on (9), we have

$$\begin{array}{cc}\hfill \mathcal{L}V\left(t\right)\le & \sum _{i=1}^n{c}_i\left(t\right)\left[{\displaystyle \frac{c_i^{\prime }}{\underline{c_i}}}+2{\alpha }_{i1}+{\alpha }_{i2}^2+4\sum _{j=1}^n{r}_{ij}\right]\left|\right|y_i{\left(t\right)\left|\right|}^2\le {\Lambda }_3\sum _{i=1}^n{c}_i\left(t\right)\left|\right|y_i\left(t\right){\left|\right|}^2={\Lambda }_{3}V\left(t\right).\hfill \end{array}$$

(25)

Therefore, by combining (24) with (25), it yields

$$\begin{array}{c}\hfill \mathbb{E}\mathcal{L}V\left(t\right)\le \left\{\begin{array}{c}-{\Lambda }_2\mathbb{E}V\left(t\right),t\in I_l,\hfill \\ {\Lambda }_3\mathbb{E}V\left(t\right),t\in S_l.\hfill \end{array}\right.\end{array}$$

In fact, we can find $\mathbb{E}\mathcal{L}V\left(t\right)\le \Lambda \left(t\right)\mathbb{E}V\left(t\right)$ with $\Lambda \left(t\right)=-{\Lambda }_2$ for $t\in I_l$ and $\Lambda \left(t\right)={\Lambda }_3$ for $t\in S_l$. Thus, based on Assumption 3, we have

$$\begin{array}{cc}\hfill \mathbb{E}V\left(t\right)\le & \mathbb{E}V\left(0\right)exp\left\{{\int }_0^t\Lambda \left(s\right)\mathrm{d}s\right\}\hfill \\ \hfill =& \mathbb{E}V\left(0\right)exp\left\{-{\Lambda }_2{T}_{con}(t,0)+{\Lambda }_3{T}_{con}^c(t,0)\right\}\hfill \\ \hfill \le & \mathbb{E}V\left(0\right)exp\left\{(-{\Lambda }_2\vartheta +{\Lambda }_3(1-\vartheta ))t+({\Lambda }_2+{\Lambda }_3)T_0\right\}.\hfill \end{array}$$

Therefore, according to ${\displaystyle V\left(t\right)\ge \underset{i\in \mathcal{N}}{min}\left\{{\underline{c}}_i\right\}\left|\right|x\left(t\right){\left|\right|}^2,}$ we have

$$\begin{array}{cc}\hfill {\mathbb{E}\left|\right|x\left(t\right)\left|\right|}^2\le & {\displaystyle \frac{\mathbb{E}V\left(0\right)}{{\displaystyle \underset{i\in \mathcal{N}}{min}\left\{{\underline{c}}_i\right\}}}}exp\left\{({\Lambda }_2+{\Lambda }_3)T_0\right\}exp\left\{(-{\Lambda }_2\vartheta +{\Lambda }_3(1-\vartheta ))t\right\}.\hfill \end{array}$$

Hence, according to Definition 1, we find that system (1) achieves exponential stability in the mean square. We complete the proof.    □

Remark 1. 

Theorem 1 discusses the exponential stability in the mean square of stochastic complex networks with time-varying coupling. In fact, our results still hold when time-varying coupling $d_{ij}\left(t\right)$ degrades into constant coupling $l_{ij}$. Therefore, the results obtained in this paper are an extension of the existing literature.

Remark 2. 

Recently, we proposed intermittent control based on time-triggered control to investigate the synchronization of the stochastic complex networks and stochastic neural networks, as shown in [9,39]. References [9,39] presented the intermittent control based on the time-triggered control in work time (sampled every regular time interval τ). Compared with the intermittent control based on the time-triggered control, the unnecessary number of control updates and the waste of network resources can be reduced by applying intermittent dynamic event-triggered control. Therefore, we improve the control strategy in [9,39].

For the design of intermittent dynamic event-triggered control (2), an algorithm is presented in Algorithm  1.

Algorithm 1 Design of intermittent dynamic event-triggered control strategy.

1: Initialize the parameters $f_i,k_i,h_{ij},d_{ij}\left(t\right)$ in system (1). Based on Assumptions 1 and 2, we can obtain ${\alpha }_{i1},{\alpha }_{i2},b_{ij},{\overline{c}}_i,{\underline{c}}_i,c_i.$

2: Choose $a_i,b_i,\eta ,\delta ,{\xi }_1$ in intermittent dynamic event-triggered control strategy (2) with (3) and (4).

3: Choose $t_l$ and $s_l$. Calculate $\vartheta$ by Assumption 3.

4: Solve Equation $-({\epsilon }_2-\gamma )Z_1\left(\tau \right)+\breve{b}{Z}_2\left(\tau \right)=0$ in Theorem 1 to acquire ${\tau }^{*}$. Choose $\tau$ such that $0<\tau <{\tau }^{*}$.

5: Check whether condition $-{\Lambda }_2\vartheta +{\Lambda }_3(1-\vartheta )<0$ in Theorem 1 holds. If it does, output the values of $a_i,b_i,\eta ,\delta ,{\xi }_1$. Otherwise, return to Step 2.

Remark 3. 

In this paper, we present intermittent dynamic event-triggered control to study the exponential stability in the mean square of the stochastic complex networks with time-varying coupling. In [40,41], Ding and Zhu et al. investigated the dynamical behaviors of deterministic systems by designing event-triggered control. They excluded Zeno phenomena by ensuring the minimum lower bound for two triggered times based on the boundedness of $e_i\left(t\right)/x_i\left(t\right)$. But, for stochastic systems, $e_i\left(t\right)$ and $x_i\left(t\right)$ are stochastic processes. Therefore, this approach may not be applied to stochastic systems. In this paper, by utilizing a time-regularization design framework, the minimum inter-execution time can be obtained, that is, $t_{l,k+1}-t_{l,k}>\tau$. This overcomes the difficulty of excluding the Zeno phenomenon caused by stochastic interference.

Remark 4. 

We mainly propose intermittent dynamic event-triggered control (2) in this paper. In (3), when $\theta \left(t\right)=0$, the intermittent dynamic event-triggered control (2) strategy turns into the intermittent static event-triggered control strategy, that is, the dynamic event-triggered mechanism (3) degenerates into the static one as follows:

$$\begin{array}{cc}\hfill t_{l,k+1}=& inf\left\{t>t_{l,k}+\tau |\sum _{i=1}^n{c}_i\left(t\right)\left|\right|e_i{\left(t\right)\left|\right|}^2-\delta \sum _{i=1}^n{c}_i\left(t\right)\left|\right|y_i\left(t\right){\left|\right|}^2>0\right\}.\hfill \end{array}$$

(26)

Moreover, it is not difficult to know that the number of control updates of intermittent dynamic event-triggered control is less than that of intermittent static event-triggered control strategy. This fact is mainly analyzed as follows: Let $t_{l,k+1}^d$ and$t_{l,k+1}^s$be the triggering moments of the dynamic and static event-triggered mechanism (3) and (26), respectively. If $t_{l,k+1}^s>t_{l,k+1}^d$, when $t\in [t_{l,k+1}^d,t_{l,k+1}^s),$ based on static event-triggered mechanism (26), we can find ${\sum }_{i=1}^n{c}_i\left(t\right)\parallel e_i{\left(t\right)\parallel }^2-{\sum }_{i=1}^n\delta c_i\left(t\right){\parallel y_i\left(t\right)\parallel }^2\le 0$. Based on dynamic event-triggered mechanism (3), we can find that

$$\begin{array}{cc}\hfill 0\ge & \theta \left(t_{l,k+1}^d\right)-\eta \left(\sum _{i=1}^n{c}_i\left(t\right)\parallel e_i\left(t_{l,k+1}^d\right){\parallel }^2-\sum _{i=1}^n\delta c_i\left(t\right){\parallel y_i\left(t_{l,k+1}^d\right)\parallel }^2\right)\ge \theta \left(t_{l,k+1}^d\right),\hfill \end{array}$$

which is in contradiction to $\theta \left(t\right)>0$. Therefore, $t_{l,k+1}^s\le t_{l,k+1}^d$.

Remark 5. 

In Theorem 1, ${\tau }^{*}$ is the unique solution to Equation $-({\epsilon }_2-\gamma )Z_1\left(\tau \right)+b{Z}_2\left(\tau \right)=0$. For the uniqueness of solution, we can simply analyze as follows: Set function $g\left(\tau \right)=-({\epsilon }_2-\gamma )Z_1\left(\tau \right)+b{Z}_2\left(\tau \right)$. We can find that $g\left(0\right)=-({\epsilon }_2-\gamma )<0$ and $g(+\infty )=+\infty$. Therefore, based on the continuity and monotonicity of function g, there is a unique solution ${\tau }^{*}>0$, such that $g\left({\tau }^{*}\right)=0$.

Remark 6. 

In Assumption 3, the average control rate for intermittent strategy is shown. In the existing literature, most scholars use the lower bound of the control rate (the minimum activation time rate) for intermittent strategies. The average control rate is not less than the lower bound of the control rate. From the condition $-{\Lambda }_2\vartheta +{\Lambda }_3(1-\vartheta )<0$ in Theorem 1, we can see that the larger ϑ is, the easier it is to satisfy the condition of Theorem 1 when other parameters remain unchanged.

4. Applications and Numerical Simulations

Oscillator systems have been studied by many scholars [42,43]. Now, we consider the following oscillator system:

$$\ddot{x}\left(t\right)+\alpha \dot{x}\left(t\right)+g\left(x\left(t\right)\right)=0,$$

(27)

in which g is the nonlinear restoring force, and $\alpha \ge 0$ represents damping coefficient.

Considering stochastic interference, we assume that the damping coefficient $\alpha$ is disturbed and can be expressed as $\alpha +\gamma \dot{B}\left(t\right),$ in which $\gamma$ is interference intensity. Therefore, system (27) can be rewritten as

$$\ddot{x}\left(t\right)+\alpha \dot{x}\left(t\right)+g\left(x\left(t\right)\right)=-\gamma \dot{x}\left(t\right)\dot{B}\left(t\right).$$

(28)

Now, considering coupling factor into system (28), we can find an oscillator network with time-varying coupling as follows:

$$\begin{array}{cc}\hfill & {\ddot{x}}_i\left(t\right)+{\alpha }_i{\dot{x}}_i\left(t\right)+g_i\left(x_i\left(t\right)\right)+\sum _{j=1}^n{d}_{ij}\left(t\right)({\dot{x}}_i\left(t\right)-{\dot{x}}_j\left(t\right))=-{\gamma }_i{\dot{x}}_i\left(t\right)\dot{B}\left(t\right),i\in \mathcal{N},\hfill \end{array}$$

(29)

where a connecting edge from node j to node i exists at time t, then $d_{ij}\left(t\right)>0$; otherwise, $d_{ij}\left(t\right)=0$.

Now, system (29) can be transformed into

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\mathrm{d}{x}_i\left(t\right)=y_i\left(t\right)\mathrm{d}t,\hfill \\ \mathrm{d}{y}_i\left(t\right)=-({\alpha }_i{y}_i\left(t\right)+g_i\left(x_i\left(t\right)\right)\hfill \\ {\displaystyle +\sum _{j=1}^n{d}_{ij}\left(t\right)(y_i\left(t\right)-y_j\left(t\right)))\mathrm{d}t-{\gamma }_i{y}_i\left(t\right)\mathrm{d}B(t),i\in \mathcal{N}.}\hfill \end{array}\right.\end{array}$$

(30)

Set $Y_i\left(t\right)={(x_i\left(t\right),y_i\left(t\right))}^{\mathrm{T}}$ and then system (30) can be expressed in the following compact form:

$$\begin{array}{cc}\hfill \mathrm{d}{Y}_i\left(t\right)=& \left(\left(f_i(Y_i\left(t\right),t)\right)+\sum _{j=1}^n{d}_{ij}\left(t\right)h_{ij}(Y_i\left(t\right),Y_j\left(t\right))\right)\mathrm{d}t+k_i(Y_i\left(t\right),t)\mathrm{d}B\left(t\right),i\in \mathcal{N},\hfill \end{array}$$

(31)

where $f_i(Y_i\left(t\right),t)={(y_i\left(t\right),-{\alpha }_i{y}_i\left(t\right)-g_i\left(x_i\left(t\right)\right))}^{\mathrm{T}},$ $h_{ij}(Y_i\left(t\right),Y_j\left(t\right))={(0,y_j\left(t\right)-y_i\left(t\right))}^{\mathrm{T}},$ $k_i(Y_i\left(t\right),t)={(0,-{\gamma }_i{y}_i\left(t\right))}^{\mathrm{T}}.$

To make system (31) stable, we design an intermittent dynamic event-triggered control strategy as follows:

$$\begin{array}{c}\hfill u_i\left(t\right)=\left\{\begin{array}{c}-b_i{Y}_i\left(t_{l,k}\right)exp\{-a_i(t-t_{l,k})\},t\in I_{l,k}\cap I_l,\hfill \\ 0,t\in S_l,\hfill \end{array}\right.\end{array}$$

(32)

where the relevant parameters are similarly defined in Section 2.2. Now, we can obtain an oscillator network with time-varying coupling and control (32) below:

$$\begin{array}{cc}\hfill \mathrm{d}{Y}_i\left(t\right)=& \left(f_i(Y_i\left(t\right),t)+\sum _{j=1}^n{d}_{ij}\left(t\right)h_{ij}(Y_i\left(t\right),Y_j\left(t\right))+u_i\left(t\right)\right)\mathrm{d}t+k_i(Y_i\left(t\right),t)\mathrm{d}B\left(t\right),i\in \mathcal{N}.\hfill \end{array}$$

(33)

Next, we state a result with regard to the exponential stability in the mean square of system (33) as follows.:

Theorem 2. 

System (33) reaches the exponential stability in the mean square if Assumptions 2 and 3 and the following conditions are satisfied:

$$\begin{array}{cc}\hfill \left|\right|g_i\left(x_i\right)-g_i\left(y_i\right)\left|\right|& \le {\lambda }_i\left|\right|x_i-y_i\left|\right|,-{\Lambda }_2\vartheta +{\Lambda }_3(1-\vartheta )<0,\hfill \end{array}$$

where ${\lambda }_i$ is a positive constant, γ is an existing positive constant, ${\displaystyle {\Lambda }_2=min\{{\epsilon }_1,{\Lambda }_1\},{\Lambda }_3=\underset{i\in \mathcal{N}}{max}\left\{{\Lambda }_{3i}\right\},{\Lambda }_1=min\{\gamma ,{\xi }_1\},{\epsilon }_1=min\left\{{\overline{\epsilon }}_1,{\xi }_1-\frac{b}{\eta }\right\},{\overline{\epsilon }}_1=\underset{i\in \mathcal{N}}{min}\left\{b_i-\delta b-\delta -\frac{c_i^{\prime }}{\underline{c_i}}-2{\alpha }_{i1}-4\sum _{j=1}^n{r}_{ij}-{\gamma }_i^2\right\},{\Lambda }_{3i}=\frac{c_i^{\prime }}{{\underline{c}}_i}+2{\alpha }_{i1}+{\gamma }_i^2+4\sum _{j=1}^n{r}_{ij},{\theta }_1=\underset{k}{inf}\{t_k-s_k\},{\theta }_2=\underset{k}{sup}\{t_{k+1}-t_k\},{\epsilon }_2=\underset{i\in \mathcal{N}}{min}\left\{b_i-\left(\frac{c_i^{\prime }}{{\underline{c}}_i}+2{\alpha }_{i1}+{\gamma }_i^2+4\sum _{j=1}^n{r}_{ij}\right)\right\},{\alpha }_{i1}^2=\underset{i\in \mathcal{N}}{max}\{1+2{\alpha }_{i2}^2,2{\lambda }_i^2\},}$ $r_{ij}=max\{d_{ij}{b}_{ij},d_{ij}^2{b}_{ij}^2\},$ and $0<\tau <{\tau }^{*}$, in which ${\tau }^{*}$ is the unique solution to Equation $-({\epsilon }_2-\gamma )Z_1\left(\tau \right)+b{Z}_2\left(\tau \right)=0$, where $Z_1\left(\tau \right)$ and $Z_2\left(\tau \right)$ are defined in Lemma 1.

Proof. 

According to function $f_i$, we can find

$$\begin{array}{cc}\hfill \left|\right|f_i(X_i,t)-f_i(Y_i,t){\left|\right|}^2\le & \left|\right|y_i-{\tilde{y}}_i{\left|\right|}^2+\left|\right|-{\alpha }_i(y_i-{\tilde{y}}_i)-g_i\left(x_i\right)+g_i\left(\widetilde{x_i}\right){\left|\right|}^2\hfill \\ \hfill \le & (1+2{\alpha }_i^2)\left|\right|y_i-{\tilde{y}}_i{\left|\right|}^2+2{\lambda }_i^2\left|\right|x_i-\widetilde{x_i}{\left|\right|}^2\hfill \\ \hfill \le & {\alpha }_{i1}^2\left|\right|X_i-Y_i{\left|\right|}^2,\hfill \end{array}$$

which implies

$$\left|\right|f_i(X_i,t)-f_i(Y_i,t)\left|\right|\le {\alpha }_{i1}\left|\right|X_i-Y_i\left|\right|.$$

Thus, Assumption 1 and all conditions in Theorem 1 are satisfied. According to Theorem 1, it yields a system (33) that achieves the exponential stability in the mean square. The proof is completed. □

Now, set $n=26$. We consider an oscillator network with 26 nodes, and the network topology is given in Figure 1.

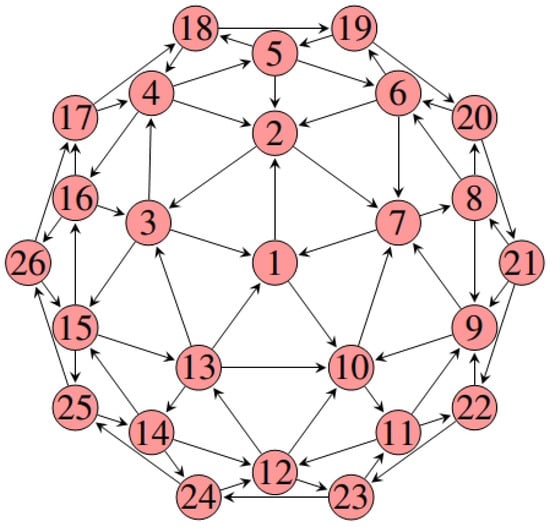
Figure 1. A digraph $(\mathcal{G},{\left(d_{ij}\left(t\right)\right)}_{26\times 26})$ with 26 nodes. Here, the red circles represent network nodes, and the arrows indicate the connection between the edges of the digraph.

Obviously, we can see from Figure 1 that digraph $(\mathcal{G},{\left(d_{ij}\left(t\right)\right)}_{n\times n})$ is strongly connected, and the nonzero components of weight matrix ${\left(d_{ij}\left(t\right)\right)}_{n\times n}$ are shown in Table 1.

Table 1. Nonzero components of weight matrix ${\left(d_{ij}\left(t\right)\right)}_{26\times 26}$.

Matrix Elements	Value
$d_{18,17}\left(t\right),d_{17,26}\left(t\right),d_{26,25}\left(t\right),d_{25,24}\left(t\right),d_{24,23}\left(t\right)$	$0.095+0.0095exp\{-2t\}$
$d_{23,22}\left(t\right),d_{22,21}\left(t\right),d_{21,20}\left(t\right),d_{20,19}\left(t\right),d_{19,18}\left(t\right)$	$0.025+0.0085exp\{-2t\}$
$d_{18,5}\left(t\right),d_{5,19}\left(t\right),d_{19,6}\left(t\right),d_{6,20}\left(t\right),d_{8,21}\left(t\right)$	$0.015+0.0015exp\{-3t\}$
$d_{20,8}\left(t\right),d_{9,22}\left(t\right),d_{9,21}\left(t\right),d_{11,23}\left(t\right),d_{22,11}\left(t\right)$	$0.015+0.0025exp\{-3t\}$
$d_{12,24}\left(t\right),d_{23,12}\left(t\right),d_{14,25}\left(t\right),d_{24,14}\left(t\right),d_{15,26}\left(t\right)$	$0.014+0.0015exp\{-3t\}$
$d_{25,15}\left(t\right),d_{17,16}\left(t\right),d_{26,16}\left(t\right),d_{4,17}\left(t\right),d_{4,18}\left(t\right)$	$0.013+0.0025exp\{-3t\}$
$d_{5,4}\left(t\right),d_{6,5}\left(t\right),d_{6,8}\left(t\right),d_{9,8}\left(t\right),d_{9,11}\left(t\right)$	$0.085+0.0075exp\{-2t\}$
$d_{12,11}\left(t\right),d_{12,14}\left(t\right),d_{15,14}\left(t\right),d_{16,15}\left(t\right),d_{16,4}\left(t\right)$	$0.085+0.0085exp\{-2t\}$
$d_{3,16}\left(t\right),d_{2,5}\left(t\right),d_{8,7}\left(t\right),d_{11,10}\left(t\right),d_{14,13}\left(t\right)$	$0.013+0.0035exp\{-3t\}$
$d_{2,4}\left(t\right),d_{2,6}\left(t\right),d_{7,6}\left(t\right),d_{7,9}\left(t\right),d_{10,9}\left(t\right)$	$0.085+0.0075exp\{-2t\}$
$d_{10,12}\left(t\right),d_{13,12}\left(t\right),d_{13,15}\left(t\right),d_{15,3}\left(t\right),d_{4,3}\left(t\right)$	$0.092+0.0065exp\{-2t\}$
$d_{7,2}\left(t\right),d_{7,10}\left(t\right),d_{10,13}\left(t\right),d_{3,13}\left(t\right),d_{3,2}\left(t\right)$	$0.092+0.0075exp\{-2t\}$
$d_{2,1}\left(t\right),d_{1,7}\left(t\right),d_{10,1}\left(t\right),d_{1,13}\left(t\right),d_{1,3}\left(t\right)$	$0.094+0.0085exp\{-2t\}$

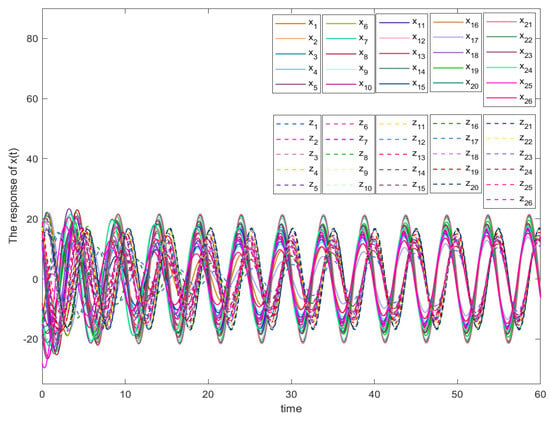
Set ${\alpha }_i=0.005,$ $g_i\left(x_i\right)=-x_i,$ and ${\gamma }_i=0.01.$ Figure 2 shows the state trajectories of the system (31) without a control strategy. From Figure 2, we can see that the state trajectories of system (31) are fluctuating. To make system (31) stable, we select parameters as follows: Letting $b_i=18,$ $a_i=2,$ and $\delta =0.01,$ we can find that ${\overline{\epsilon }}_1=10.7175.$ Then, choosing ${\xi }_1=15,$ $\gamma =3,$ and $\eta =2,$ we can find that ${\Lambda }_1=3,$ ${\epsilon }_1=6.$ By calculating, we find that ${\lambda }_i=0.01,$ ${\Lambda }_2=3,$ ${\Lambda }_3=7.0925,$ and ${\epsilon }_2=10.9075.$ Setting ${\theta }_1=2.9,$ ${\theta }_2=4$, it yields that $-{\Lambda }_2{\theta }_1+{\Lambda }_3({\theta }_2-{\theta }_1)=-0.8983$ and the unique solution ${\tau }^{*}=0.0014$ of Equation $-({\epsilon }_2-\gamma )Z_1\left(\tau \right)+b{Z}_2\left(\tau \right)=0.$ Hence, all the conditions in Theorem 2 are satisfied.

Figure 2. The state trajectories of system (31) without an intermittent dynamic event−triggered control strategy (32).

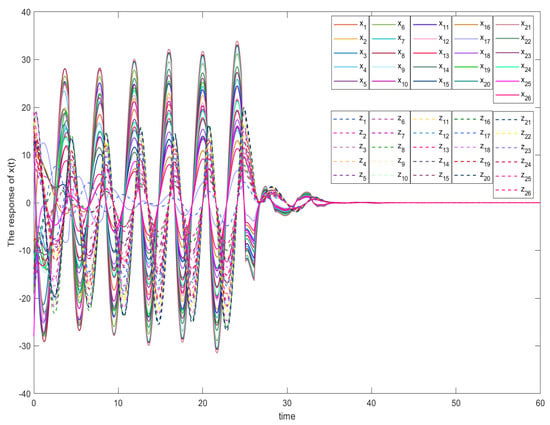
Now, the trajectories of system (31) under control (32) are given in Figure 3. From Figure 3, we can see that system (33) is stable, which verifies the effectiveness of our theoretical results.

Figure 3. The state trajectories of system (33) with an intermittent dynamic event−triggered control strategy (32).

Comparison 1. To compare intermittent dynamic event-triggered control with and without an exponential function, Figure 4 gives out the number of control updates under intermittent dynamic event-triggered control with an exponential function, and Figure 5 shows the number of control updates under intermittent dynamic event-triggered control without an exponential function. From Figure 4 and Figure 5, it can be found that the number of control updates is much smaller than the number of sampled signals shown in Figure 5. Consequently, by adding an exponential function into the intermittent dynamic event-triggered control, the number of control updates can be significantly reduced.

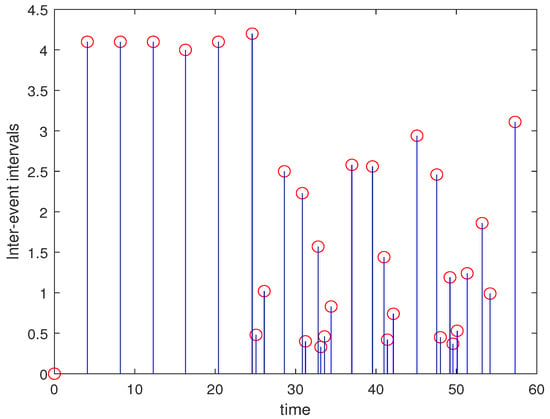
Figure 4. The triggering times under an intermittent dynamic event-triggered control strategy (32) with $\eta =2$ and $a_i=2$. The blue line with a red circle represents the time interval between adjacent triggering moments.

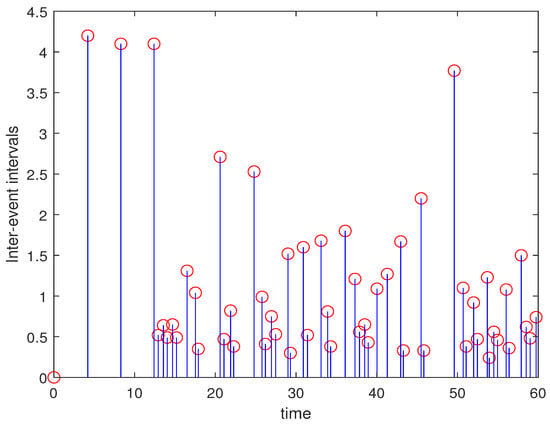
Figure 5. The triggering times under an intermittent dynamic event-triggered control strategy (32) with $\eta =2$ and $a_i=0$. The blue line with a red circle represents the time interval between adjacent triggering moments.

Comparison 2. In order to compare intermittent static event-triggered control strategy and intermittent dynamic event-triggered control, Figure 4 and Figure 6 are given. Figure 4 and Figure 6 denote simulations with $\eta =2$ in intermittent dynamic event-triggered control and intermittent static event-triggered control strategies, respectively. We can find that the number of control updates under an intermittent dynamic event-triggered control strategy is significantly reduced compared to the number of control updates under an intermittent static event-triggered control strategy. Therefore, the number of control updates for intermittent dynamic event-triggered control can be reduced.

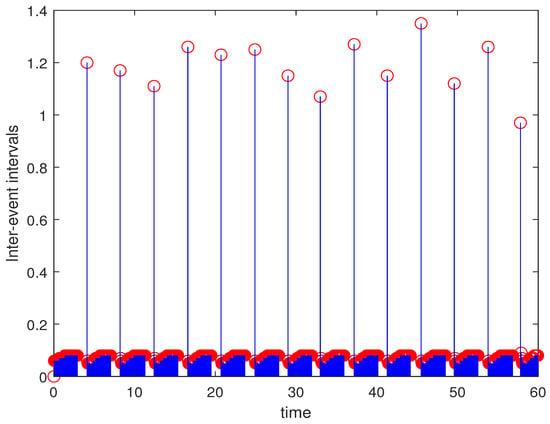
Figure 6. The triggering times under an intermittent static event-triggered control strategy with $\eta =2$. The blue line with a red circle represents the time interval between adjacent triggering moments.

5. Conclusions

This paper proposed an intermittent dynamic event-triggered control to discuss the exponential stability in the mean square of stochastic complex networks with time-varying coupling. For the intermittent dynamic event-triggered control, a dynamic term and an exponential function were introduced into the event-triggered mechanism to reduce the number of control updates. Furthermore, the minimum inter-execution time of intermittent dynamic event-triggered control, independent mathematical expectation, was guaranteed. Moreover, the event-triggered condition designed in this paper was dependent on the topology structure of the stochastic complex networks. In addition, the intermittent strategy considered in this article was based on the average control rate rather than the lower bound of the control rate. We found that this restriction had less conservatism. Based on the Lyapunov method and stochastic technique, some stability criteria were derived. Finally, an oscillator system was used, and some numerical simulations were given. In future work, considering the importance of delay factors, we will study delayed stochastic complex networks with time-varying coupling based on novel intermittent dynamic event-triggered control.