Non-Singular Fast Sliding Mode Control of Robot Manipulators Based on Integrated Dynamic Compensation
Abstract
1. Introduction
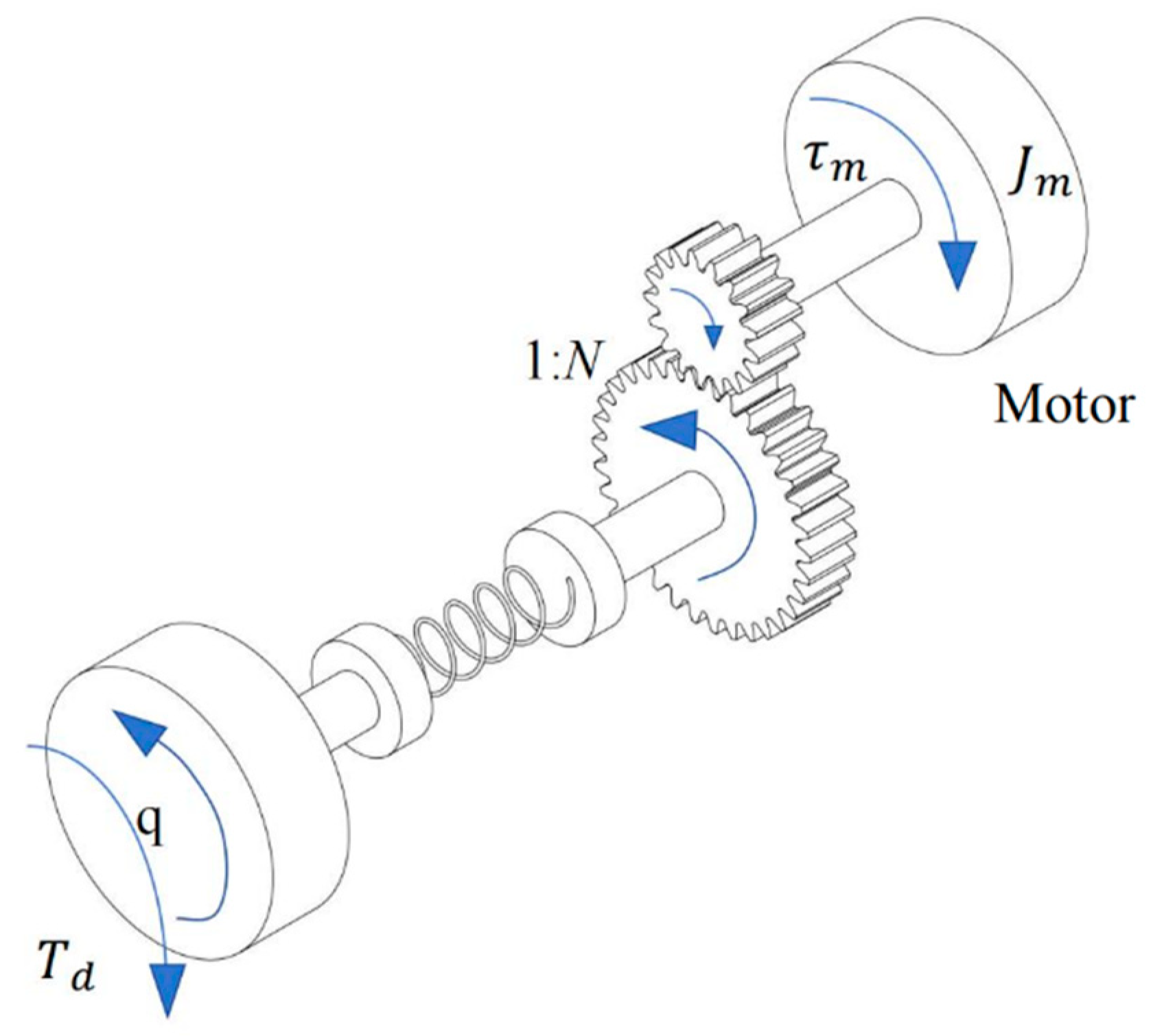
2. Robot Dynamics
2.1. Dynamics of n-DOF Robot Manipulators
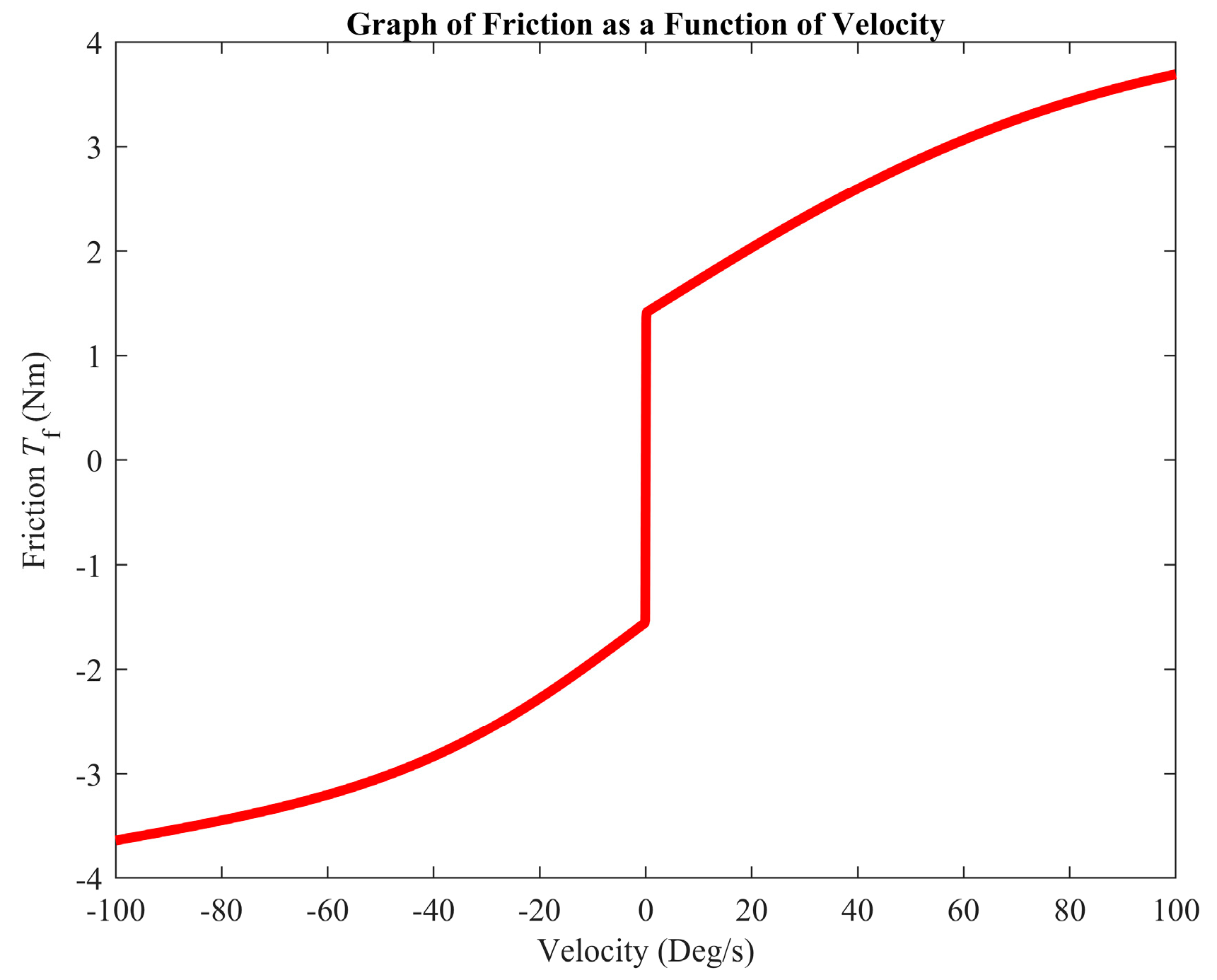
2.2. Integrated Friction and Joint Torque Dynamic Compensation
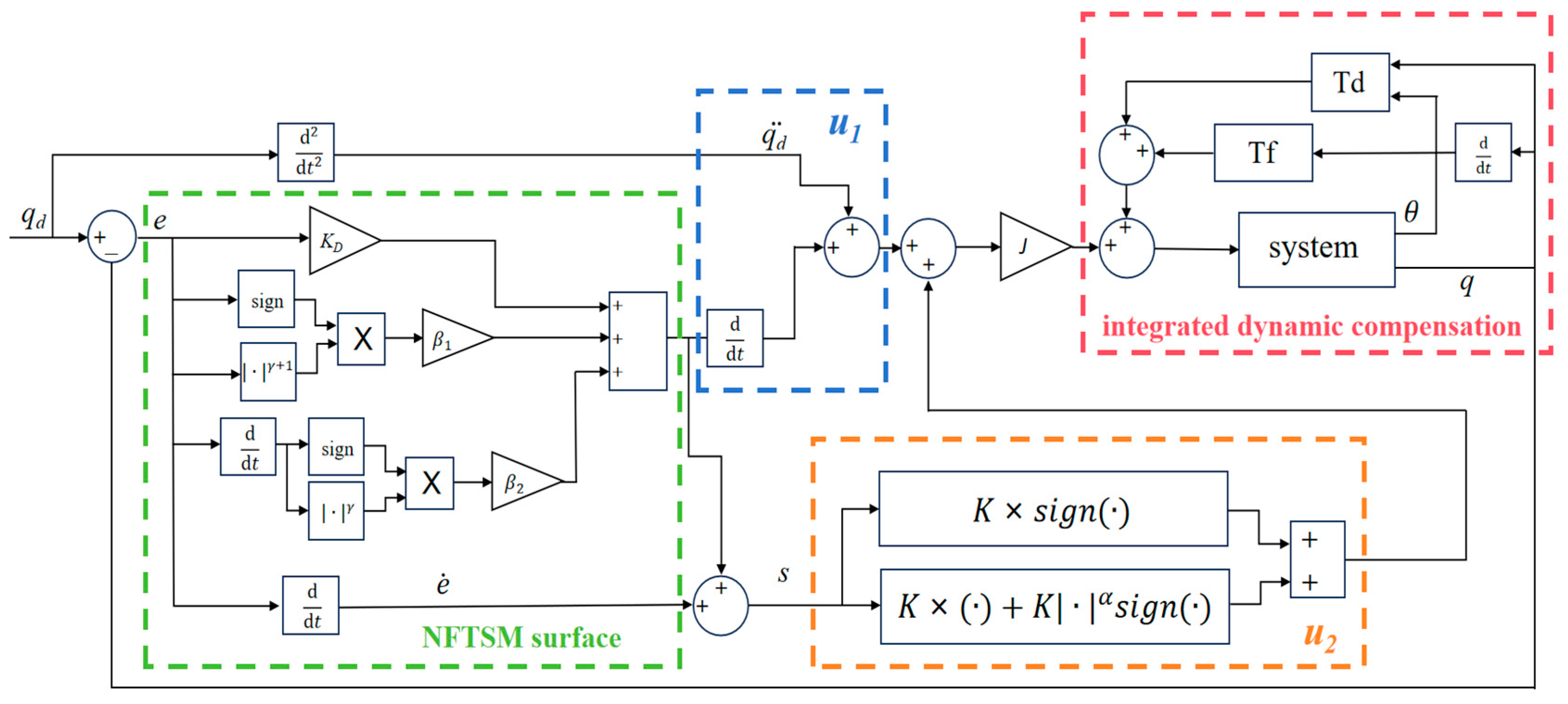
3. Controller Design and Stability Analysis
3.1. Control Design
3.2. Stability Analysis
4. Experiments
4.1. Experimental Setup
- Experiment 1: Trajectory tracking experiments using the four control schemes mentioned above under zero load conditions.
- Experiment 2: Trajectory tracking experiments using the four control schemes under a 5 (N) constant load.
- Experiment 3: Trajectory tracking experiments using the four control schemes under a sinusoidal load.
- Experiment 4: Trajectory tracking experiments using the four control schemes under a step load.
4.2. Experimental Results
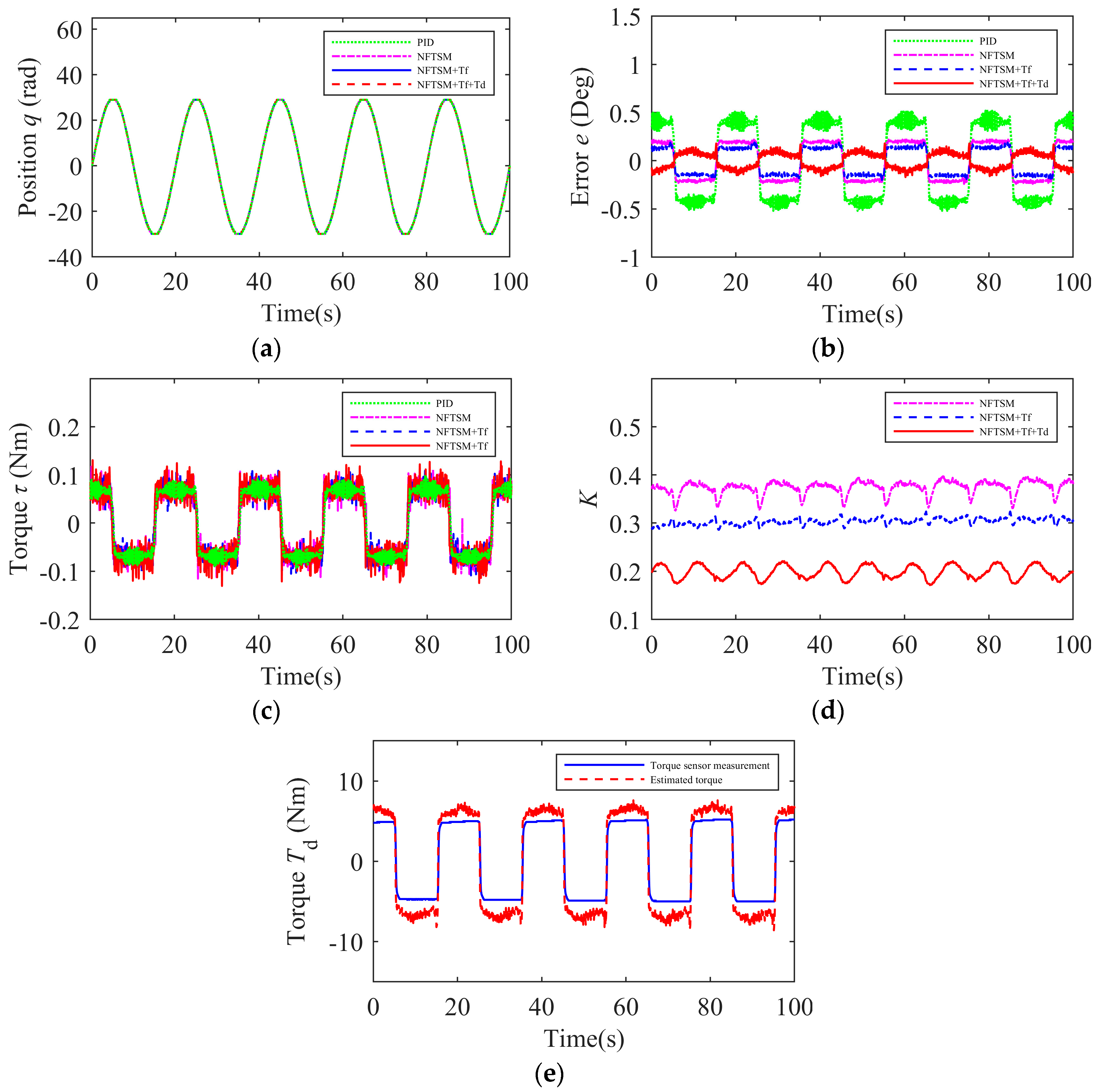
- Experiment 1: For all the control schemes, no load was applied. The actual position and tracking errors are shown in Figure 5a,b. Compared with the PID control scheme, the NFTSM scheme can significantly reduce the tracking error. The introduction of friction compensation further reduces the tracking error compared to using the NFTSM scheme alone. Under no-load conditions, friction exerts noticeable interference on the robot manipulators’ trajectory tracking. Adding friction compensation can reduce the tracking error. The motor input torque is shown in Figure 5c. When the system is not disturbed by external loads, the error mainly originates from internal factors of the system. The external torque estimation compensation has a negligible impact on the system dynamics. To simplify the control strategy, unnecessary compensation components are reduced under no-load conditions to lower the complexity and computational burden. As shown in Figure 5d, the dynamic changes in the adaptive factor indicate that when the system tracking error is large, the adaptive factor increases to enhance the control effect, thereby further reducing the error and improving the tracking accuracy. Conversely, when the system stabilizes or the control input is too large, the adaptive factor decreases to control the magnitude of the input, avoiding over-control or energy waste. As shown in Table 3, the experimental results of each algorithm in terms of the RMSE and MAXE for trajectory tracking under no-load conditions are presented. Comparisons reveal that the control algorithm proposed in this paper has smaller values for both the RMSE and MAXE compared to the other three control schemes. Therefore, the proposed algorithm can more accurately match the target trajectory, achieving a higher level of trajectory tracking performance.
- 2.
- Experiment 2: A constant load (5 Nm) was applied to all the control schemes. The actual position and tracking errors are shown in Figure 6a,b. The experimental results demonstrate that, under a constant load, the NFTSM scheme can significantly reduce the tracking error compared with PID control. Under a constant load, the impact of friction interference on the system is relatively small, and the addition of friction compensation has little effect on improving the control accuracy. However, when the NFTSM scheme is combined with both friction compensation and joint torque compensation, the root mean square error and maximum error values are further reduced, achieving even smaller tracking errors. As shown in Figure 6c, the motor input torque increases after adding friction compensation and joint torque compensation. As shown in Figure 6d, the adaptive factor K decreases after adding friction compensation and joint torque compensation. As shown in Figure 6e, the estimated torque is close to the load torque, which justifies the joint torque compensation in the scheme. The RMSE and MAXE values for trajectory tracking under the condition of a constant load for each control algorithm are shown in Table 4. Therefore, the proposed control algorithm can still maintain a higher level of trajectory tracking accuracy under constant load conditions.
- 3.
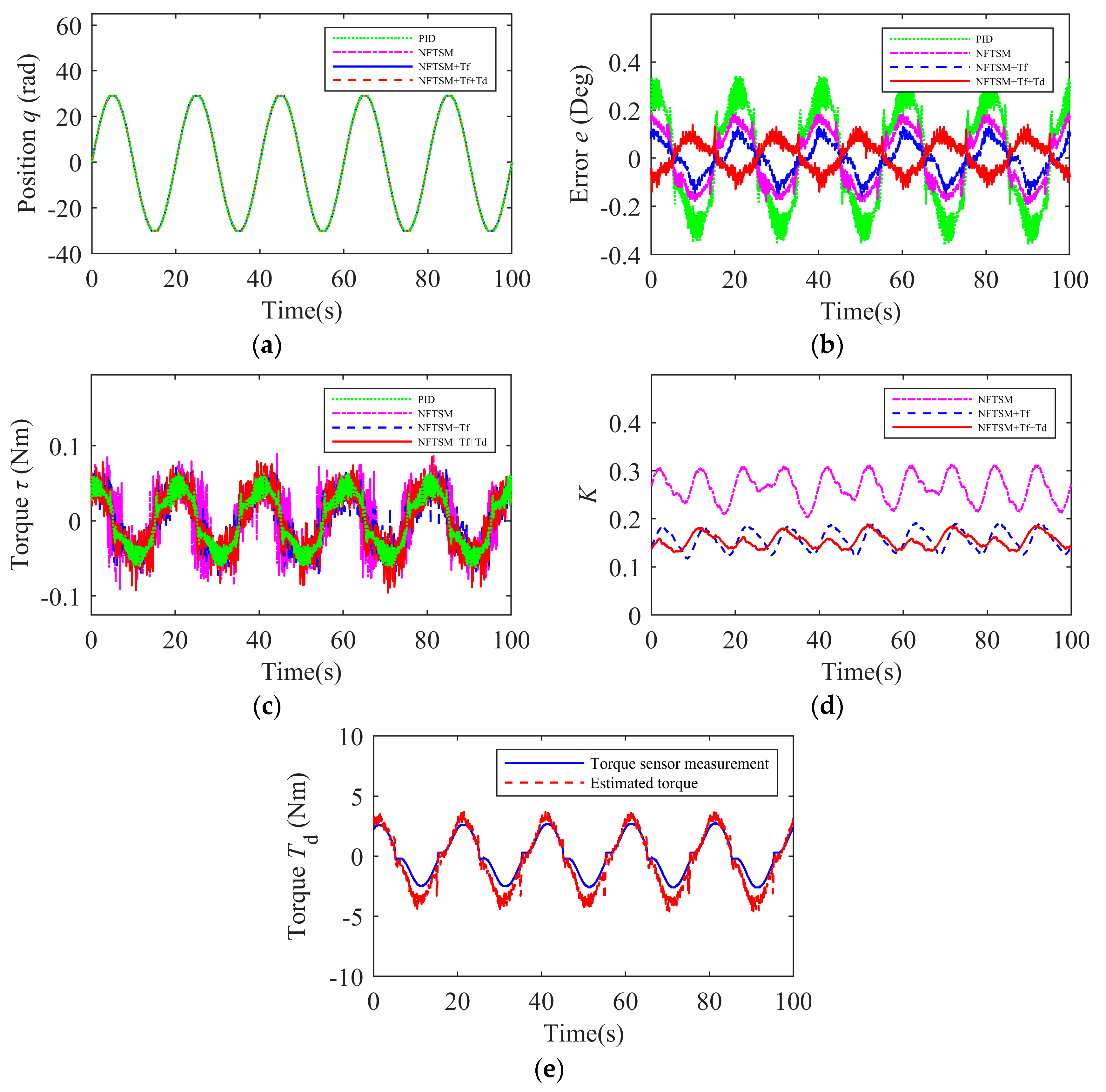
- Experiment 3: A sinusoidal load was applied to all the control schemes. The actual position and tracking errors are shown in Figure 7a,b. Figure 7c displays the motor input torque, Figure 7d shows the variation of the adaptive gain, and Figure 7e presents the estimation results of the load torque. The root mean square error and maximum error values for trajectory tracking under sinusoidal load conditions for each control algorithm are shown in Table 5. The experimental results indicate that, compared with the other three control schemes, the proposed control algorithm has smaller RMSE and MAXE values in terms of the tracking error. Therefore, it can be concluded that the proposed control algorithm can still maintain a higher level of trajectory tracking accuracy and rapid adaptability under sinusoidal load conditions.
- 4.
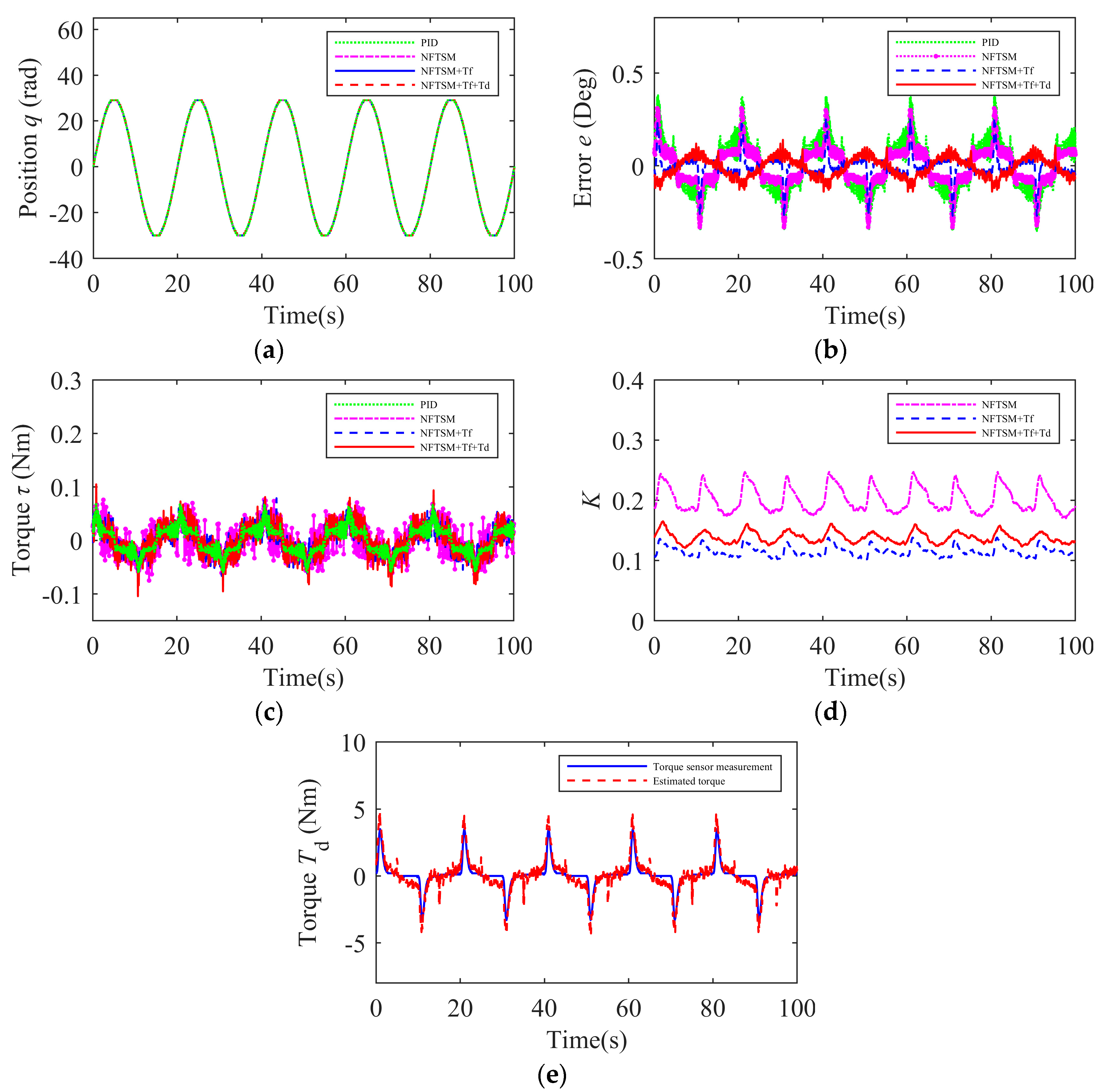
- Experiment 4: A step load was applied to all the control schemes. The actual position and tracking errors are shown in Figure 8a,b. Figure 8c displays the motor input torque, Figure 8d shows the variation of the adaptive gain, and Figure 8e presents the estimation results of the load torque. The root mean square error and maximum error values for trajectory tracking under step load conditions for each control algorithm are shown in Table 6. The experimental results indicate that, compared with the other three control schemes, the proposed control algorithm has smaller RMSE and MAXE values in terms of the tracking error. Therefore, it can be concluded that the proposed control algorithm can still maintain a higher level of trajectory tracking accuracy and rapid adaptability under step load conditions.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PID | Proportional–Integral–Derivative |
| SMC | Sliding Mode Control |
| NFTSM | Non-Singular Fast Terminal Sliding Mode Control |
| n-DOF | n-Degree of Freedom |
| RMSE | Root Mean Square Error |
| MAXE | Maximum Error |
References
- Li, Y.; Ang, K.H.; Chong, G.C. PID Control System Analysis and Design. IEEE Control Syst. Mag. 2006, 26, 32–41. [Google Scholar] [CrossRef]
- Zhao, Y.; Qi, J.; Li, W. Adaptive PID Feedback Tracking Control for 6-DOF Collaborative Robot. In Proceedings of the 2022 34th Chinese Control and Decision Conference (CCDC), Hefei, China, 15–17 August 2022; pp. 5525–5532. [Google Scholar] [CrossRef]
- Zhang, L.; Su, Y.; Wang, Z.; Wang, H. Fixed-Time Terminal Sliding Mode Control for Uncertain Robot Manipulators. ISA Trans. 2024, 144, 364–373. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Qiao, J.; Guo, L. Adaptive Sliding Mode Disturbance Observer-Based Composite Control with Prescribed Performance of Space Manipulators for Target Capturing. IEEE Trans. Ind. Electron. 2019, 66, 1973–1983. [Google Scholar] [CrossRef]
- Spong, M.W.; Ortega, R.; Kelly, R. Comments on “Adaptive Manipulator Control: A Case Study” by J. Slotine and W. Li. IEEE Trans. Autom. Control 1990, 35, 761–762. [Google Scholar] [CrossRef]
- Wang, H.; Xu, K.; Zhang, H. Adaptive Finite-Time Tracking Control of Nonlinear Systems With Dynamics Uncertainties. IEEE Trans. Autom. Control 2023, 68, 5737–5744. [Google Scholar] [CrossRef]
- Bouakrif, F.; Zasadzinski, M. Trajectory Tracking Control for Perturbed Robot Manipulators Using Iterative Learning Method. Int. J. Adv. Manuf. Technol. 2016, 87, 2013–2022. [Google Scholar] [CrossRef]
- Kou, Z.; Sun, J. Test-Based Model-Free Adaptive Iterative Learning Control with Strong Robustness. Int. J. Syst. Sci. 2023, 54, 1213–1228. [Google Scholar] [CrossRef]
- Chaoui, H.; Gueaieb, W. Type-2 Fuzzy Logic Control of a Flexible-Joint Manipulator. J. Intell. Robot. Syst. 2008, 51, 159–186. [Google Scholar] [CrossRef]
- Van, M.; Sun, Y.; Mcllvanna, S.; Nguyen, M.-N.; Khyam, M.O.; Ceglarek, D. Adaptive Fuzzy Fault Tolerant Control for Robot Manipulators With Fixed-Time Convergence. IEEE Trans. Fuzzy Syst. 2023, 31, 3210–3219. [Google Scholar] [CrossRef]
- Peng, R.; Guo, R.; Zheng, B.; Miao, Z.; Zhou, J. Neural Network-Based Robust Consensus Tracking for Uncertain Networked Euler-Lagrange Systems with Time-Varying Delays and Output Constraints. Appl. Math. Comput. 2024, 468, 128522. [Google Scholar] [CrossRef]
- Zhu, C.; Jiang, Y.; Yang, C. Fixed-Time Neural Control of Robot Manipulator With Global Stability and Guaranteed Transient Performance. IEEE Trans. Ind. Electron. 2023, 70, 803–812. [Google Scholar] [CrossRef]
- Shi, D.; Zhang, J.; Sun, Z.; Xia, Y. Adaptive Sliding Mode Disturbance Observer-Based Composite Trajectory Tracking Control for Robot Manipulator with Prescribed Performance. Nonlinear Dyn. 2022, 109, 2693–2704. [Google Scholar] [CrossRef]
- Yu, S.; Yu, X.; Shirinzadeh, B.; Man, Z. Continuous Finite-Time Control for Robotic Manipulators with Terminal Sliding Mode. Automatica 2005, 41, 1957–1964. [Google Scholar] [CrossRef]
- Feng, Y.; Yu, X.; Man, Z. Non-Singular Terminal Sliding Mode Control of Rigid Manipulators. Automatica 2002, 38, 2159–2167. [Google Scholar] [CrossRef]
- Yin, S.; Shi, Z.; Liu, Y.; Xue, G.; You, H. Adaptive Non-Singular Terminal Sliding Mode Trajectory Tracking Control of Robotic Manipulators Based on Disturbance Observer Under Unknown Time-Varying Disturbance. Processes 2025, 13, 266. [Google Scholar] [CrossRef]
- Zhang, Y.; Fang, L.; Song, T.; Zhang, M. Adaptive Non-singular Fast Terminal Sliding Mode Based on Prescribed Performance for Robot Manipulators. Asian J. Control 2023, 25, 3253–3268. [Google Scholar] [CrossRef]
- Jiang, J.; Zhang, H.; Jin, D.; Wang, A.; Liu, L. Disturbance Observer Based Non-Singular Fast Terminal Sliding Mode Control of Permanent Magnet Synchronous Motors. J. Power Electron. 2024, 24, 249–257. [Google Scholar] [CrossRef]
- Zhuang, X.; Guo, Y.; Tian, Y.; Wang, H. A Sampled Delayed Output Extended State Observer-Based Adaptive Feedback Control of Robot Manipulator with Unknown Dynamics. Nonlinear Dyn. 2023, 111, 22283–22301. [Google Scholar] [CrossRef]
- Saleki, A.; Fateh, M.M. Model-Free Control of Electrically Driven Robot Manipulators Using an Extended State Observer. Comput. Electr. Eng. 2020, 87, 106768. [Google Scholar] [CrossRef]
- Zhang, Z.; Hu, X.; Huang, P. Disturbance Observer-Based Tracking Controller for n-Link Flexible-Joint Robots Subject to Time-Varying State Constraints. Electronics 2024, 13, 1773. [Google Scholar] [CrossRef]
- Zhang, D.; Hu, J.; Cheng, J.; Wu, Z.-G.; Yan, H. A Novel Disturbance Observer Based Fixed-Time Sliding Mode Control for Robotic Manipulators with Global Fast Convergence. IEEECAA J. Autom. Sin. 2024, 11, 661–672. [Google Scholar] [CrossRef]
- Lee, J.; Chang, P.H.; Jin, M. Adaptive Integral Sliding Mode Control with Time-Delay Estimation for Robot Manipulators. IEEE Trans. Ind. Electron. 2017, 64, 6796–6804. [Google Scholar] [CrossRef]
- Taefi, M.; Khosravi, M.A. A Model Free Adaptive-robust Design for Control of Robot Manipulators: Time Delay Estimation Approach. Int. J. Robust Nonlinear Control 2024, 34, 8227–8247. [Google Scholar] [CrossRef]
- Wang, G.; Wang, Z.; Huang, B.; Gan, Y.; Min, F. Active Compliance Control Based on EKF Torque Fusion for Robot Manipulators. IEEE Robot. Autom. Lett. 2023, 8, 2668–2675. [Google Scholar] [CrossRef]
- Bona, B.; Indri, M. Friction Compensation in Robotics: An Overview. In Proceedings of the 44th IEEE Conference on Decision and Control, Seville, Spain, 15 December 2005; pp. 4360–4367. [Google Scholar] [CrossRef]
- Liang, X.; Yao, Z.; Deng, W.; Yao, J. Adaptive Control of N-Link Hydraulic Manipulators with Gravity and Friction Identification. Nonlinear Dyn. 2023, 111, 19093–19109. [Google Scholar] [CrossRef]
- Thenozhi, S.; Sanchez, A.C.; Rodriguez-Resendiz, J. A Contraction Theory-Based Tracking Control Design with Friction Identification and Compensation. IEEE Trans. Ind. Electron. 2022, 69, 6111–6120. [Google Scholar] [CrossRef]
- Ghorbel, F.H.; Gandhi, P.S.; Alpeter, F. On the Kinematic Error in Harmonic Drive Gears. J. Mech. Des. 1998, 123, 90–97. [Google Scholar] [CrossRef]
- Song, Y.; Huang, H.; Liu, F.; Xi, F.; Zhou, D.; Li, B. Torque Estimation for Robotic Joint with Harmonic Reducer Based on Deformation Calibration. IEEE Sens. J. 2020, 20, 991–1002. [Google Scholar] [CrossRef]


| −1.477 | −0.02592 | −7.865 | −2.967 | −4.188 | 0.01478 |
| −1.218 | 18.28 | 0.02605 | 2.692 | 18.62 | 0.01876 |
| Control Schemes | RMSE (Deg) | MAXE (Deg) |
|---|---|---|
| PID | 0.11380 | 0.20000 |
| NFTSM | 0.07194 | 0.11000 |
| NFTSM+Tf | 0.02923 | 0.07000 |
| Control Schemes | RMSE (Deg) | MAXE (Deg) |
|---|---|---|
| PID | 0.40422 | 0.53000 |
| NFTSM | 0.19836 | 0.24000 |
| NFTSM+Tf | 0.14700 | 0.20000 |
| NFTSM+Tf+Td | 0.08138 | 0.18000 |
| Control Schemes | RMSE (Deg) | MAXE (Deg) |
|---|---|---|
| PID | 0.21029 | 0.36000 |
| NFTSM | 0.11978 | 0.19000 |
| NFTSM+Tf | 0.06694 | 0.16000 |
| NFTSM+Tf+Td | 0.05867 | 0.14000 |
| Control Schemes | RMSE (Deg) | MAXE (Deg) |
|---|---|---|
| PID | 0.14108 | 0.38000 |
| NFTSM | 0.10290 | 0.33000 |
| NFTSM+Tf | 0.05796 | 0.27000 |
| NFTSM+Tf+Td | 0.05213 | 0.14000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Liang, X.; Hu, S.; Xin, Q. Non-Singular Fast Sliding Mode Control of Robot Manipulators Based on Integrated Dynamic Compensation. Actuators 2025, 14, 215. https://doi.org/10.3390/act14050215
Wang X, Liang X, Hu S, Xin Q. Non-Singular Fast Sliding Mode Control of Robot Manipulators Based on Integrated Dynamic Compensation. Actuators. 2025; 14(5):215. https://doi.org/10.3390/act14050215
Chicago/Turabian StyleWang, Xinyi, Xichang Liang, Shunjing Hu, and Qianqian Xin. 2025. "Non-Singular Fast Sliding Mode Control of Robot Manipulators Based on Integrated Dynamic Compensation" Actuators 14, no. 5: 215. https://doi.org/10.3390/act14050215
APA StyleWang, X., Liang, X., Hu, S., & Xin, Q. (2025). Non-Singular Fast Sliding Mode Control of Robot Manipulators Based on Integrated Dynamic Compensation. Actuators, 14(5), 215. https://doi.org/10.3390/act14050215




