Development of a Force Feedback Controller with a Speed Feedforward Compensator for a Cable-Driven Actuator
Abstract
1. Introduction
2. Methods
2.1. Mechanical Description
2.2. Force Control Strategy Development
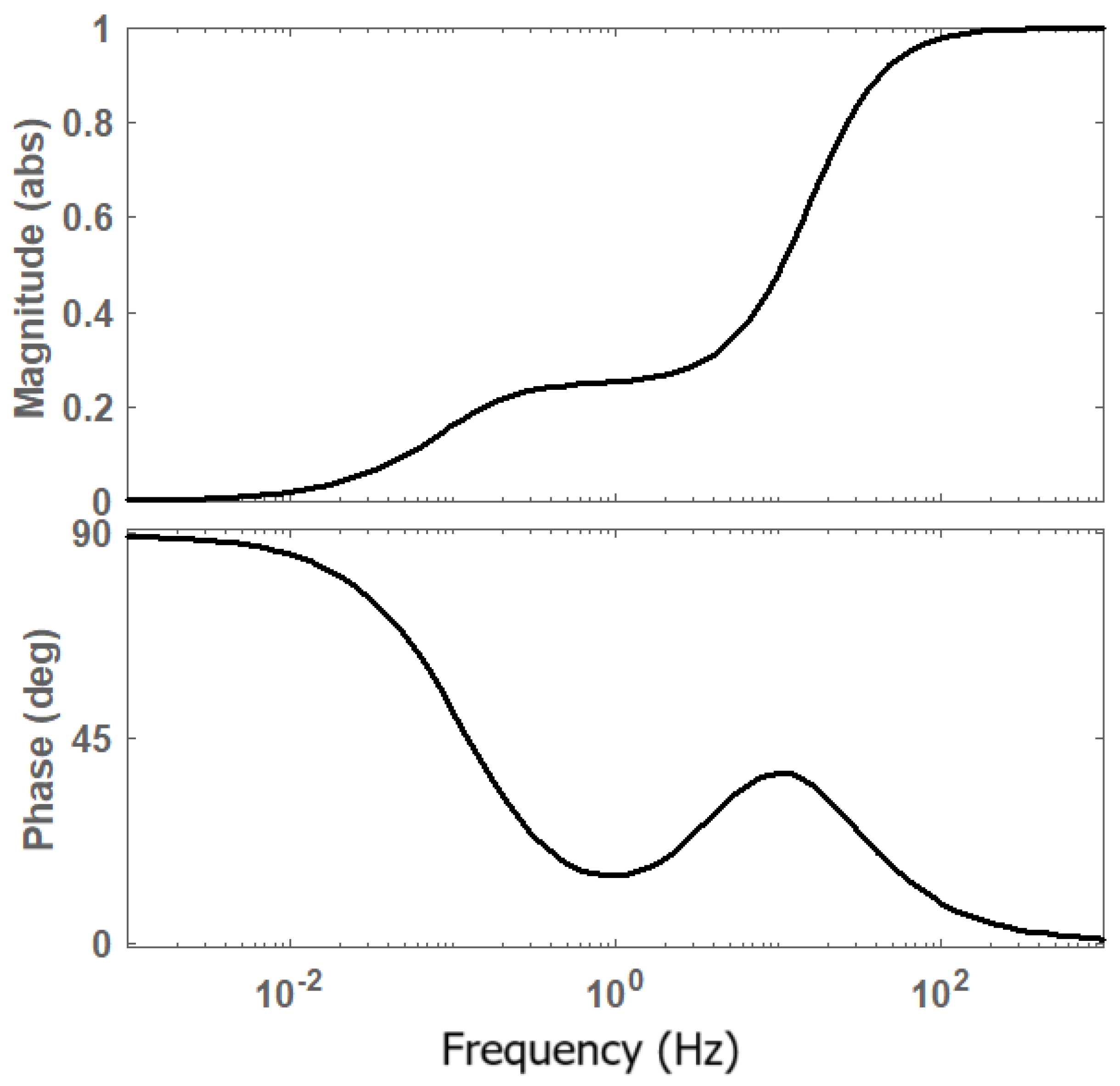
2.2.1. System Identification
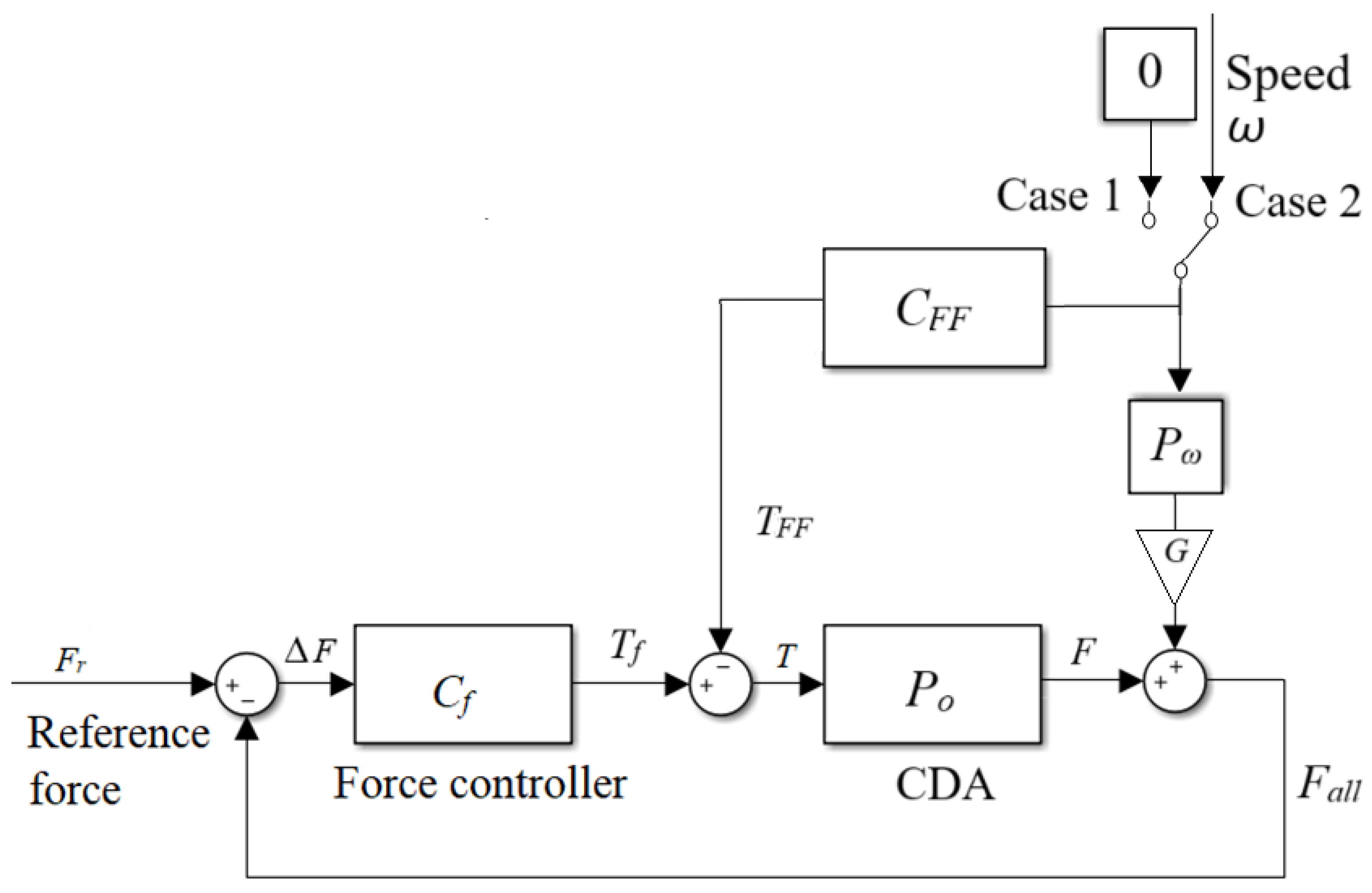
2.2.2. Derivation of Force Control Strategy
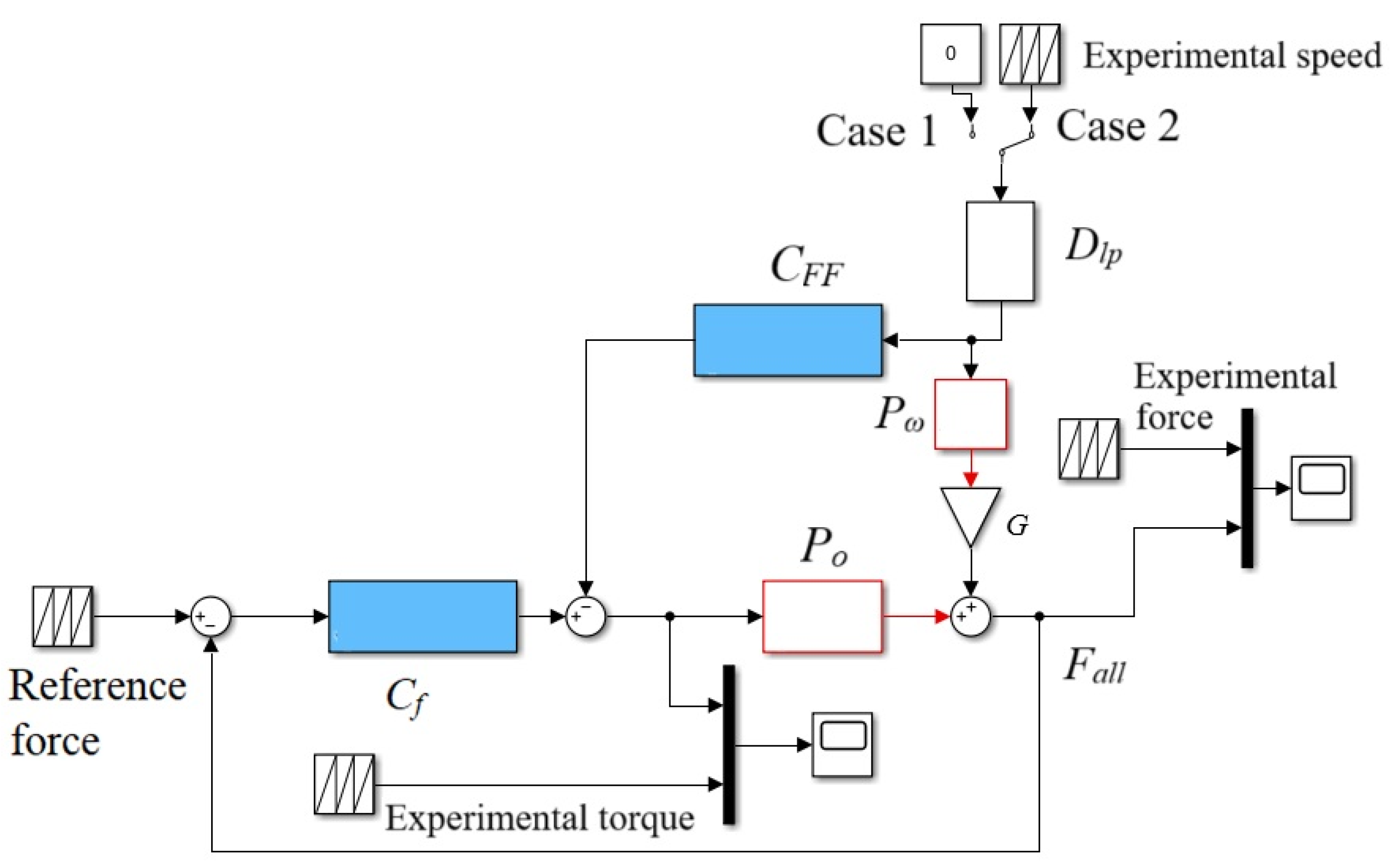
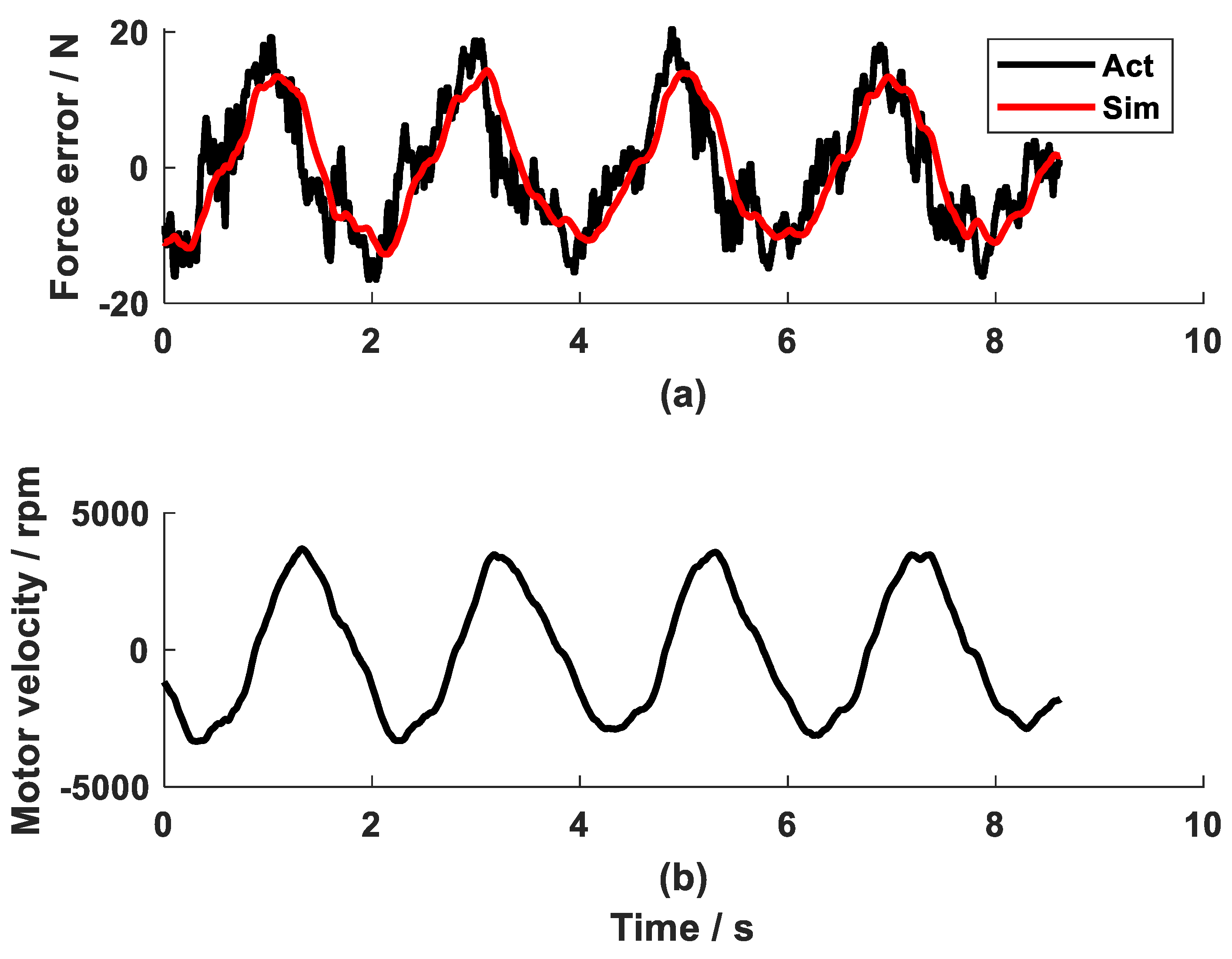
2.3. Simulation of Force Control Strategy
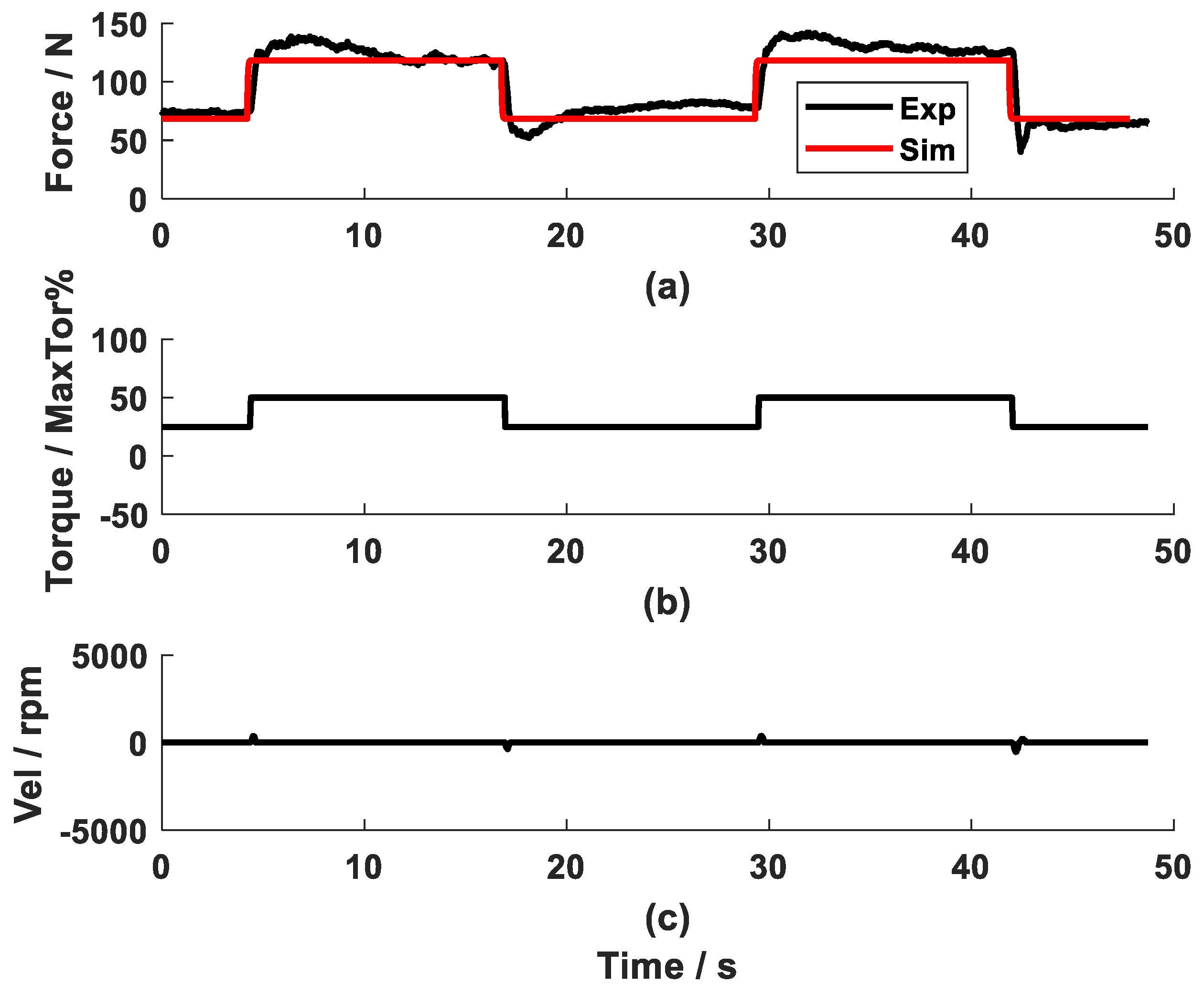
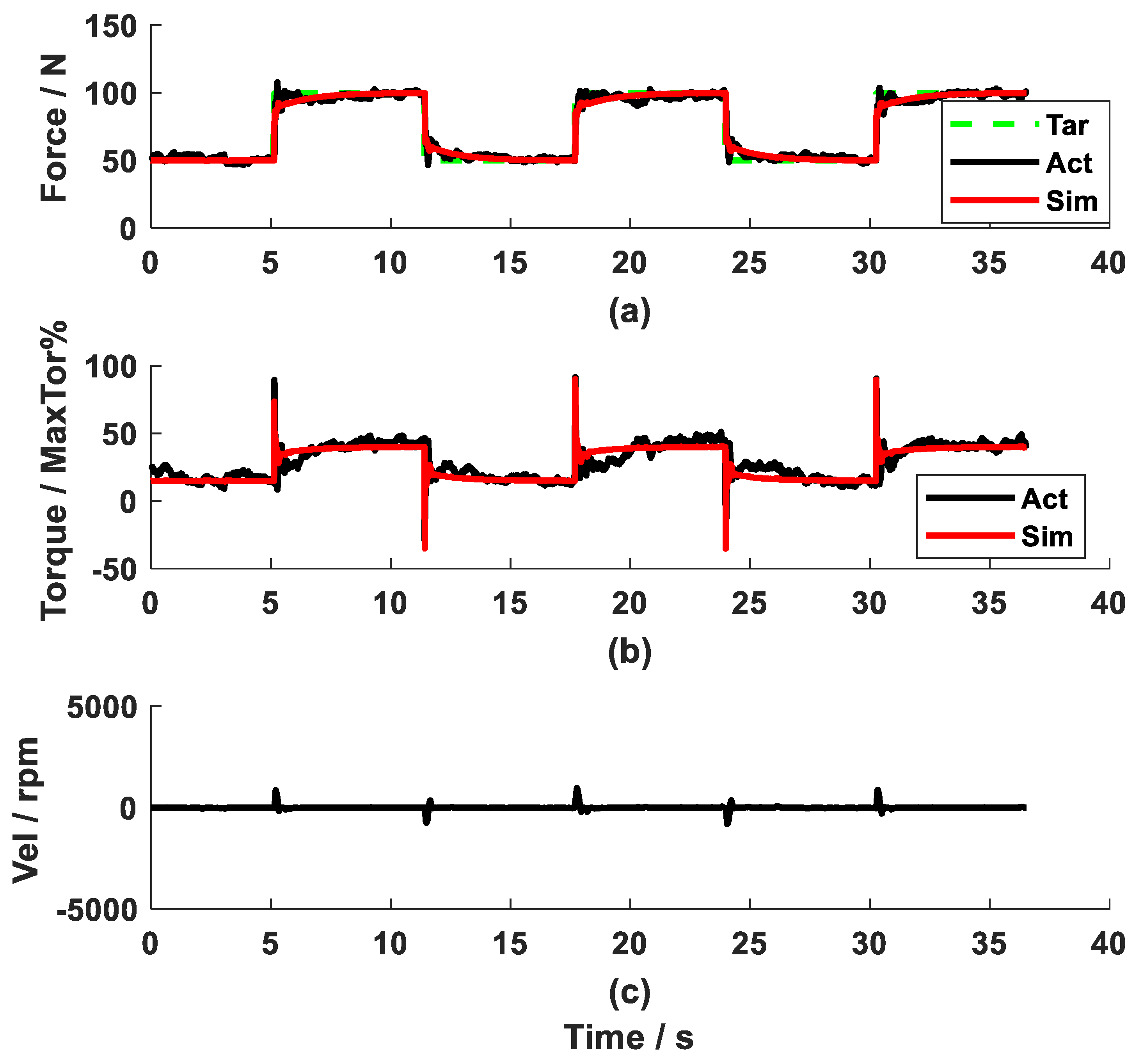
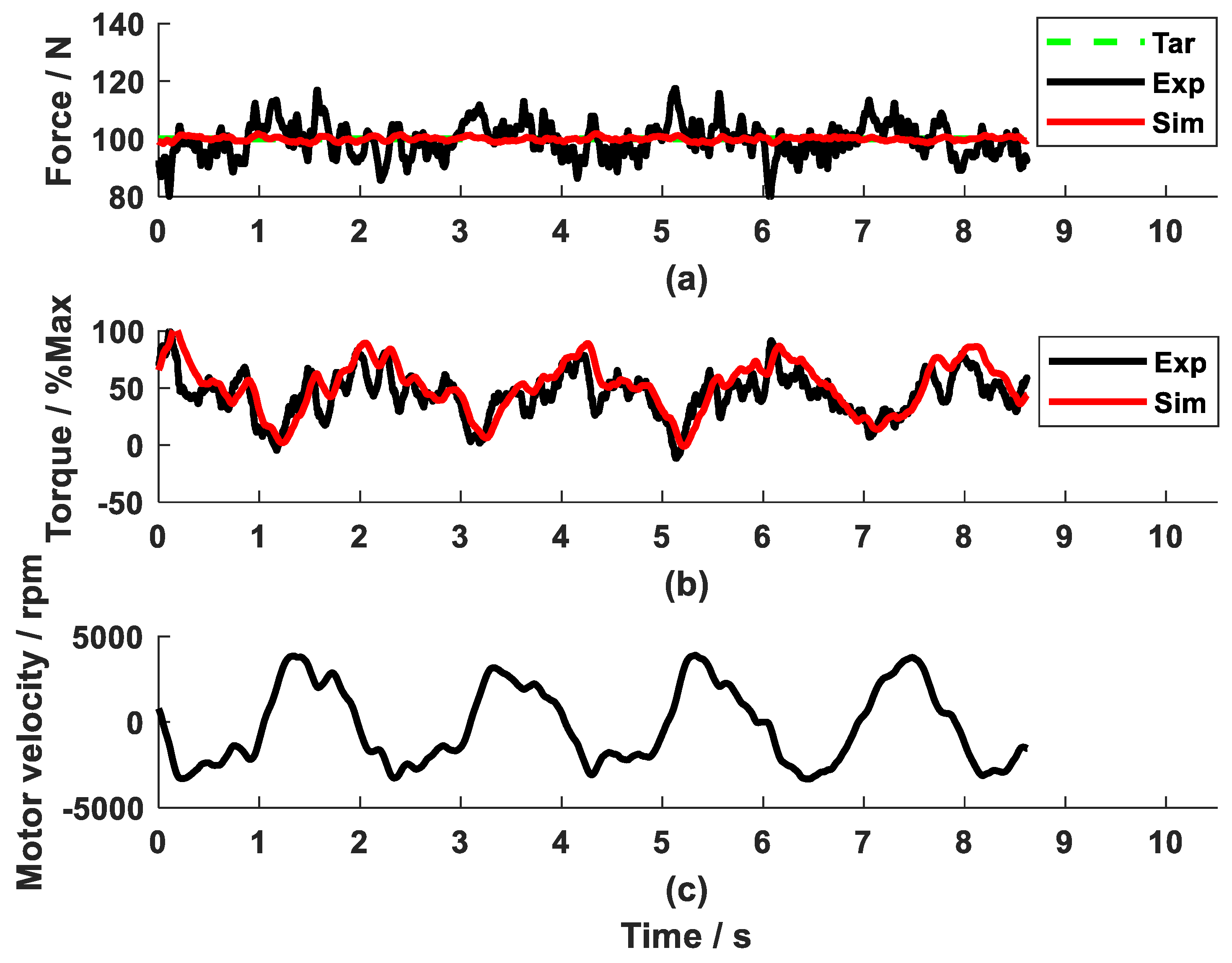
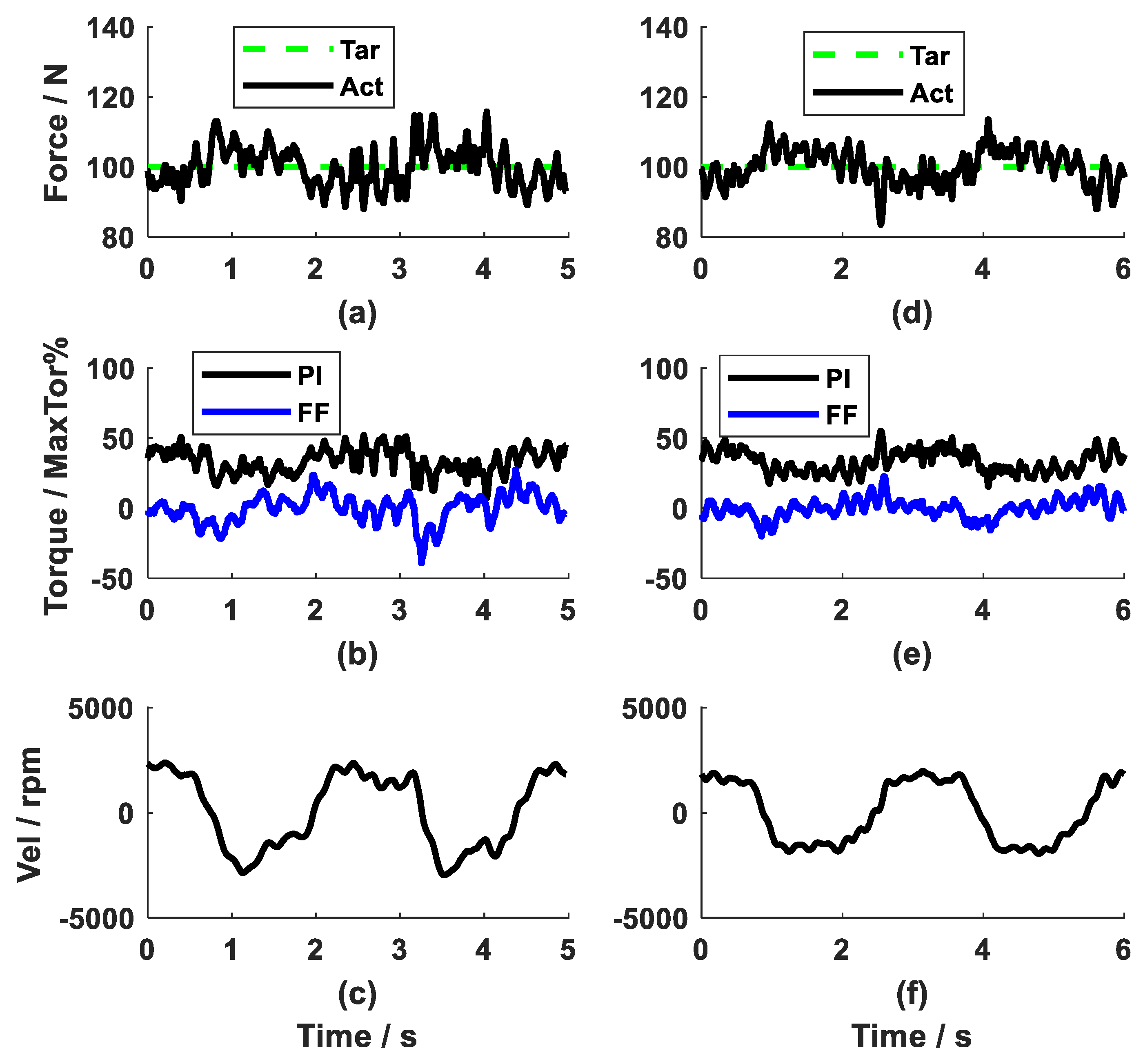
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mazzoleni, S.; Focacci, A.; Franceschini, M.; Waldner, A.; Spagnuolo, C.; Battini, E.; Bonaiuti, D. Robot-assisted end-effector-based gait training in chronic stroke patients: A multicentric uncontrolled observational retrospective clinical study. NeuroRehabilitation 2017, 40, 483–492. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Zhang, L.; Wang, B.; Xue, F.; Zou, Y.; Song, D. Running experimental research of a cable-driven astronaut on-orbit physical exercise equipment. Machines 2022, 10, 377. [Google Scholar] [CrossRef]
- Zou, Y.; Ma, H.; Han, Z.; Song, Y.; Liu, K. Force control of wire driving lower limb rehabilitation robot. Technol. Health Care 2018, 26, S399–S408. [Google Scholar] [CrossRef] [PubMed]
- Meunier, G.; Boulet, B.; Nahon, M. Control of an Overactuated Cable-Driven Parallel Mechanism for a Radio Telescope Application. IEEE Trans. Control. Syst. Technol. 2009, 17, 1043–1054. [Google Scholar] [CrossRef]
- Farcy, D.; Llibre, M.; Carton, P.; Lambert, C. SACSO: Wire-driven parallel set-up for dynamic tests in wind tunnel-review of principles and advantages for identification of aerodynamic models for flight mechanics. In Proceedings of the 8th ONERA-DLR Aerospace Symposium, Göttingen, Germany, 17–19 October 2007. [Google Scholar]
- Qian, S.; Zi, B.; Ding, H. Dynamics and trajectory tracking control of cooperative multiple mobile cranes. Nonlinear Dyn. 2016, 83, 89–108. [Google Scholar] [CrossRef]
- Troncoso, D.A.; Robles-Linares, J.A.; Russo, M.; Elbanna, M.A.; Wild, S.; Dong, X.; Mohammad, A.; Kell, J.; Norton, A.D.; Axinte, D. A continuum robot for remote applications: From industrial to medical surgery with slender continuum robots. IEEE Robot. Autom. Mag. 2023, 30, 94–105. [Google Scholar] [CrossRef]
- Gosselin, C. Cable-driven parallel mechanisms: State of the art and perspectives. Mech. Eng. Rev. 2014, 1, DSM0004. [Google Scholar] [CrossRef]
- Mao, Y.; Jin, X.; Gera, G.; Scholz, J.; Agrawal, S.K. Human movement training with a cable driven ARm EXoskeleton (CAREX). IEEE Trans. Neural Syst. Rehabil. Eng. 2015, 23, 84–92. [Google Scholar] [CrossRef]
- Zou, Y.; Wu, X.; Zhang, B.; Zhang, Q.; Zhang, A.; Qin, T. Stiffness analysis of parallel cable-driven upper limb rehabilitation robot. Micromachines 2022, 13, 253. [Google Scholar] [CrossRef]
- Rauter, G.; Zitzewitz, J.v.; Duschau-Wicke, A.; Vallery, H.; Riener, R. A tendon-based parallel robot applied to motor learning in sports. In Proceedings of the IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics, Tokyo, Japan, 26–29 September 2010. [Google Scholar]
- Marchal-Crespo, L.; Rauter, G.; Wyss, D.; Zitzewitz, J.v.; Riener, R. Synthesis and control of an assistive robotic tennis trainer. In Proceedings of the 4th IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics (BioRob), Rome, Italy, 24–27 June 2012. [Google Scholar]
- Von Zitzewitz, J.; Morger, A.; Rauter, G.; Marchal-Crespo, L.; Crivelli, F.; Wyss, D.; Bruckmann, T.; Riener, R. A reconfigurable, tendon-based haptic interface for research into human-environment interactions. Robotica 2013, 31, 441–453. [Google Scholar] [CrossRef]
- Vashista, V.; Jin, X.; Agrawal, S.K. Active Tethered Pelvic Assist Device (A-TPAD) to study force adaptation in human walking. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014. [Google Scholar]
- Khan, M.I.; Santamaria, V.; Kang, J.; Bradley, B.M.; Dutkowsky, J.P.; Gordon, A.M.; Agrawal, S.K. Enhancing seated stability using Trunk Support Trainer (TruST). IEEE Robot. Autom. Lett. 2017, 2, 1609–1616. [Google Scholar] [CrossRef]
- Zhang, L.; Li, L.; Zou, Y.; Wang, K.; Jiang, X.; Ju, H. Force control strategy and bench press experimental research of a cable driven astronaut rehabilitative training robot. IEEE Access 2017, 5, 9981–9989. [Google Scholar] [CrossRef]
- Ji, J.C.; Wang, Y.; Zhang, G.; Lin, Y.; Wang, G. Design and simulation analysis of a robot-assisted gait trainer with the PBWS system. J. Healthc. Eng. 2021, 2021, 2750936. [Google Scholar] [CrossRef]
- Hidayah, R.; Bishop, L.; Jin, X.; Chamarthy, S.; Stein, J.; Agrawal, S.K. Gait adaptation using a cable-driven active leg exoskeleton (C-ALEX) with post-stroke participants. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 28, 1984–1993. [Google Scholar] [CrossRef]
- Wu, M. A flexible cable-driven robotic system: Design and its clinical application for improving walking function in adults with stroke, SCI and children with CP. In Neurorehabilitation Technology; Reinkensmeyer, D.J., Marchal-Crespo, L., Dietz, V., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 717–743. [Google Scholar] [CrossRef]
- Idà, E.; Mattioni, V. Cable-driven parallel robot actuators: State of the art and novel servo-winch concept. Actuators 2022, 11, 290. [Google Scholar] [CrossRef]
- Gagliardini, L.; Gouttefarde, M.; Caro, S. Determination of a dynamic feasible workspace for cable-driven parallel robots. In Advances in Robot Kinematics 2016; Lenarčič, J., Merlet, J.-P., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 361–370. [Google Scholar] [CrossRef]
- Jamshidifar, H.; Khosravani, S.; Fidan, B.; Khajepour, A. Vibration decoupled modeling and robust control of redundant cable-driven parallel robots. IEEE/ASME Trans. Mechatron. 2018, 23, 690–701. [Google Scholar] [CrossRef]
- Zhang, Z.; Shao, Z.; You, Z.; Tang, X.; Zi, B.; Yang, G.; Gosselin, C.; Caro, S. State-of-the-art on theories and applications of cable-driven parallel robots. Front. Mech. Eng. 2022, 17, 37. [Google Scholar] [CrossRef]
- Qian, S.; Zi, B.; Shang, W.-W.; Xu, Q.-S. A review on cable-driven parallel robots. Chin. J. Mech. Eng. 2018, 31, 66. [Google Scholar] [CrossRef]
- Tempel, P.; Schnelle, F.; Pott, A.; Eberhard, P. Design and programming for cable-driven parallel robots in the German pavilion at the EXPO 2015. Machines 2015, 3, 223–241. [Google Scholar] [CrossRef]
- Lou, Y.n.; Lin, H.; Quan, P.; Wei, D.; Di, S. Robust adaptive control of fully constrained cable-driven serial manipulator with multi-segment cables using cable tension sensor measurements. Sensors 2021, 21, 1623. [Google Scholar] [CrossRef]
- Najafi, F.; Bakhshizadeh, M. Development a fuzzy PID controller for a parallel cable robot with flexible cables. In Proceedings of the 2016 4th International Conference on Robotics and Mechatronics (ICROM), Tehran, Iran, 26–28 October 2016. [Google Scholar]
- Nguyen, D.Q.; Gouttefarde, M. On the Improvement of Cable Collision Detection Algorithms. In Cable-Driven Parallel Robots; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
- Tho, T.P.; Thinh, N.T. An overview of cable-driven parallel robots: Workspace, tension distribution, and cable sagging. Math. Probl. Eng. 2022, 2022, 1–15. [Google Scholar] [CrossRef]
- Perreault, S.; Gosselin, C.M. Cable-driven parallel mechanisms: Application to a locomotion interface. J. Mech. Des. 2008, 130, 102301. [Google Scholar] [CrossRef]
- Hutter, M.; Leemann, P.; Hottiger, G.; Figi, R.; Tagmann, S.; Rey, G.; Small, G. Force control for active chassis balancing. IEEE/ASME Trans. Mechatron. 2017, 22, 613–622. [Google Scholar] [CrossRef]
- Xu, K.; Wang, S.; Shi, L.; Li, J.; Yue, B. Horizon-stability control for wheel-legged robot driving over unknow, rough terrain. Mech. Mach. Theory 2025, 205, 105887. [Google Scholar] [CrossRef]
- Georgarakis, A.-M.; Song, J.; Wolf, P.; Riener, R.; Xiloyannis, M. Control for gravity compensation in tendon-driven upper limb exosuits. In Proceedings of the 8th IEEE RAS/EMBS International Conference for Biomedical Robotics and Biomechatronics (BioRob), New York, NY, USA, 29 November–1 December 2020. [Google Scholar]
- Kraus, W.; Schmidt, V.; Rajendra, P.; Pott, A. Load identification and compensation for a cable-driven parallel robot. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation (ICRA), Karlsruhe, Germany, 6–10 May 2013; pp. 2485–2490. [Google Scholar]
- Kraus, W.; Miermeister, P.; Pott, A. Investigation of the influence of elastic cables on the force distribution of a parallel cable-driven robot. In Cable-Driven Parallel Robots; Bruckmann, T., Pott, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 103–115. [Google Scholar] [CrossRef]
- Vallery, H.; Ekkelenkamp, R.; Kooij, H.v.d.; Buss, M. Passive and accurate torque control of series elastic actuators. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems (IROS), San Diego, CA, USA, 29 October–2 November 2007. [Google Scholar]
- Kraus, W.; Schmidt, V.; Rajendra, P.; Pott, A. System identification and cable force control for a cable-driven parallel robot with industrial servo drives. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014. [Google Scholar]
- Santos, J.C.; Chemori, A.; Gouttefarde, M. Redundancy resolution integrated model predictive control of CDPRs: Concept, implementation and experiments. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020. [Google Scholar]
- Lee, G.; Ding, Y.; Bujanda, I.G.; Karavas, N.; Zhou, Y.M.; Walsh, C.J. Improved assistive profile tracking of soft exosuits for walking and jogging with off-board actuation. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017. [Google Scholar]
- Cavalcanti Santos, J.; Gouttefarde, M. A simple and efficient non-model based cable tension control. In Proceedings of the CableCon 2021—5th International Conference on Cable-Driven Parallel Robots, Virtual, France, 7–9 July 2021. [Google Scholar]
- Abdelaziz, S.; Barbé, L.; Renaud, P.; de Mathelin, M.; Bayle, B. Control of cable-driven manipulators in the presence of friction. Mech. Mach. Theory 2017, 107, 139–147. [Google Scholar] [CrossRef]
- Wu, M.; Hornby, T.G.; Landry, J.M.; Roth, H.; Schmit, B.D. A cable-driven locomotor training system for restoration of gait in human SCI. Gait Posture 2011, 33, 256–260. [Google Scholar] [CrossRef]
- Fang, J.; Haldimann, M.; Marchal-Crespo, L.; Hunt, K.J. Development of an active cable-driven, force-controlled robotic system for walking rehabilitation. Front. Neurorobot. 2021, 15, 651177. [Google Scholar] [CrossRef] [PubMed]
- Fang, J.; Hunt, K.J. Development of a cable-driven device for neuromuscular rehabilitation. In Converging Clinical and Engineering Research on Neurorehabilitation V, Proceedings of the International Conference on Neurorehabilitation (ICNR), La Granja, Spain, 5–8 November 2024; Springer Nature: Cham, Switzerland, 2024. [Google Scholar]
- Fang, S.; Franitza, D.; Torlo, M.; Bekes, F.; Hiller, M. Motion control of a tendon-based parallel manipulator using optimal tension distribution. Mechatron. IEEE/ASME Trans. 2004, 9, 561–568. [Google Scholar] [CrossRef]
- Khosravi, M.A.; Taghirad, H.D. Robust PID control of fully-constrained cable driven parallel robots. Mechatronics 2014, 24, 87–97. [Google Scholar] [CrossRef]
- Babaghasabha, R.; Khosravi, M.A.; Taghirad, H.D. Adaptive robust control of fully-constrained cable driven parallel robots. Mechatronics 2015, 25, 27–36. [Google Scholar] [CrossRef]
- Fang, J.; Haldimann, M. Technical development and preliminary physiological response investigation of a tendon-based robotic system for gait rehabilitation. Brain Netw. Modul. 2024, 3, 79–90. [Google Scholar] [CrossRef]
- Fang, J.; Haldimann, M.; Amiryavari, B.; Aksöz, E.A.; Riener, R. Development of a mobile gait trainer using pose estimation. In Converging Clinical and Engineering Research on Neurorehabilitation V, Proceedings of the International Conference on Neurorehabilitation (ICNR), La Granja, Spain, 5–8 November 2024; Springer Nature: Cham, Switzerland, 2024. [Google Scholar]
- Chrif, F.; Nef, T.; Lungarella, M.; Dravid, R.; Hunt, K.J. Control design for a lower-limb paediatric therapy device using linear motor technology. Biomed. Signal Process. Control 2017, 38, 119–127. [Google Scholar] [CrossRef]
- Bannwart, M.; Bolliger, M.; Lutz, P.; Gantner, M.; Rauter, G. Systematic analysis of transparency in the gait rehabilitation device the FLOAT. In Proceedings of the 14th International Conference on Control, Automation, Robotics and Vision (ICARCV), Phuket, Thailand, 13–15 November 2016. [Google Scholar]
- Vallery, H.; Lutz, P.; von Zitzewitz, J.; Rauter, G.; Fritschi, M.; Everarts, C.; Ronsse, R.; Curt, A.; Bolliger, M. Multidirectional transparent support for overground gait training. In Proceedings of the IEEE International Conference on Rehabilitation Robotics (ICORR), Seattle, WA, USA, 24–26 June 2013. [Google Scholar]
- Jamshidifar, H.; Fidan, B.; Gungor, G.; Khajepour, A. Adaptive vibration control of a flexible cable driven parallel robot. IFAC-PapersOnLine 2015, 48, 1302–1307. [Google Scholar] [CrossRef]
- Meziane, R.; Cardou, P.; Otis, M.J.D. Cable interference control in physical interaction for cable-driven parallel mechanisms. Mech. Mach. Theory 2019, 132, 30–47. [Google Scholar] [CrossRef]
- Wang, H.; Hunt, K.J. Self-paced heart rate control for treadmill exercise. Front. Control Eng. 2023, 4, 1158164. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, J.; Haldimann, M.; Amiryavari, B.; Riener, R. Development of a Force Feedback Controller with a Speed Feedforward Compensator for a Cable-Driven Actuator. Actuators 2025, 14, 214. https://doi.org/10.3390/act14050214
Fang J, Haldimann M, Amiryavari B, Riener R. Development of a Force Feedback Controller with a Speed Feedforward Compensator for a Cable-Driven Actuator. Actuators. 2025; 14(5):214. https://doi.org/10.3390/act14050214
Chicago/Turabian StyleFang, Juan, Michael Haldimann, Bardia Amiryavari, and Robert Riener. 2025. "Development of a Force Feedback Controller with a Speed Feedforward Compensator for a Cable-Driven Actuator" Actuators 14, no. 5: 214. https://doi.org/10.3390/act14050214
APA StyleFang, J., Haldimann, M., Amiryavari, B., & Riener, R. (2025). Development of a Force Feedback Controller with a Speed Feedforward Compensator for a Cable-Driven Actuator. Actuators, 14(5), 214. https://doi.org/10.3390/act14050214





