Disturbance Rejection Approach for Nonlinear Systems Using Kalman-Filter-Based Equivalent-Input-Disturbance Estimator

Abstract

In this paper, a novel disturbance rejection approach is developed for a class of nonlinear systems, which incorporates the Kalman filter into the equivalent-input-disturbance (EID) structure. First, the EID-based control system and the configuration of the Kalman Filter are illustrated. Then, an optimal estimation theorem is obtained by analyzing the dynamic of the Kalman filter, and a special Kalman gain is derived. Next, the dynamics of the closed-loop system are deduced, and stability is guaranteed based on the Lyapunov function. Finally, simulations with comparison are carried out to demonstrate the excellent performance of both disturbance rejection and noise attenuation.

1. Introduction

Disturbances are ubiquitous in industrial systems, arising from factors such as sensor noise [1], load variations, and external disturbances [2]. These disturbances will degrade the control performance and even lead to system instability. Consequently, disturbance rejection continues to be a fundamental challenge in control engineering, particularly for nonlinear systems [3,4,5]. On the other hand, due to the inevitable noise, it is crucial to consider the noise effect in the controller design process. This limitation highlights the necessity for novel control methods that integrate disturbance estimation, state observation, and noise attenuation into a comprehensive framework.

To effectively reject disturbances, there are some active disturbance rejection (ADR) methods, such as the Extended State Observer (ESO), the Disturbance Observer (DOB), and the Equivalent-Input-Disturbance (EID) method. The ESO method treats the lumped disturbance (including system uncertainties, external disturbances, and nonlinearities) as an extended state [6], but the states require availability in controller design. The DOB method uses the inverse of a nominal plant to estimate and reduce the effect of disturbances [7], which may not be realizable in practice. The EID method, as an active disturbance rejection method, has been widely used in physical systems due to its simple structure [8,9,10,11]. It applies an artificial disturbance to the control input, which produces an equivalent effect to the real disturbance on the system output [12]. Recently, a convenient version of the EID method (CEID) has been developed, which uses a linear gain in the CEID-based estimator to tune the disturbance rejection performance [13]. However, a large estimator gain may lead to increased sensitivity to noise, which burdens the actuators and even unstabilizes the whole control system.

As a cornerstone of optimal state estimation, the Kalman filter provides a robust framework for state estimation under noise in dynamic systems [14,15,16]. For systems with partially known nonlinear mapping, conventional Kalman filters usually handle nonlinearities through linearization [17] or sigma-point transformations [18,19]. However, these approaches use the complex error covariance update policy to calculate the Kalman gain online, resulting in high computational costs and poor real-time performance. Recently, a steady-state Kalman filter was developed to address disturbance and noise with an ESO, which shows advantages in noise attenuation and other control performance [20]. In particular, its steady-state Kalman gain shows excellent advantages in computational efficiency instead of a time-varying one, making it ideal for real-time applications.

Enlightened by the above discussion, this paper proposed a novel Kalman-Filter-based Equivalent-Input-Disturbance-based Estimator (KF-EIDE) for a class of nonlinear systems with disturbances and measurement noise. The primary objective of this study is to bridge the gap between disturbance rejection and noise attenuation in nonlinear control systems by integrating CEID and steady-state Kalman filter, while explicitly incorporating prior knowledge of system nonlinearities.

Unlike existing methods, key contributions are made:

• Novelty in methodology: a novel KF-EIDE scheme is organically proposed, which combines the disturbance rejection capability of CEID with the noise attenuation capability of the Kalman filter to improve the system tracking performance.
• Improvement of structure: nonlinear dynamics and the Kalman filter are organically integrated with the CEID control scheme, enabling accurate state estimation.
• Theoretical rigor: under the lumped disturbance, nonlinearity, and measurement noise, the stability of the closed-loop control system is guaranteed.

The rest of this paper is organized as follows: Section 2 demonstrates the problem and presents the nonlinear system model with disturbance dynamics. Section 3 details the design of the KF-EIDE and gives the related theorem, including nonlinearity incorporation mechanisms. Section 4 analyzes and proves the stability of the whole closed-loop control system. Section 5 validates the method through comparative simulations on a classic nonlinear system, while Section 6 gives the conclusion with future research directions.

In this paper, some mathematical symbols are first denoted as follows: ${\mathbb{R}}^{q\times p}$ presents the set of real matrices with q rows and p columns; $W\left(s\right)$ stands for the Laplace transform of a continuous-time signal $w\left(t\right)$; I denotes the identity matrix of appropriate dimensions; $\mathrm{diag}\{·\}$ refers to the diagonal matrix; $\left|a\right|$ and $∥A∥$ are the absolute value of a scalar a and the 2-norm of a matrix A, respectively; $∥\alpha \left(t\right)∥$ is the 2-norm of a vector $\alpha \left(t\right)$; and the time t will be excluded if the context provides clarity.

2. Methods and Materials

2.1. Problem Formulation

Consider a class of single-input single-output (SISO) nonlinear systems with measurement noise:

$$\left\{\begin{array}{c}\dot{x}\left(t\right)=Ax\left(t\right)+f\left(x\left(t\right)\right)+Bu\left(t\right)+B_{d}d\left(t\right)\hfill \\ y_o\left(t\right)=Cx\left(t\right)\hfill \\ y\left(t\right)=Cx\left(t\right)+v\left(t\right)\hfill \end{array}\right.$$

(1)

where $x\left(t\right)\in {\mathbb{R}}^n$ is the system state; $u\left(t\right)\in \mathbb{R}$, $y_o\left(t\right)\in \mathbb{R}$, and $y\left(t\right)\in \mathbb{R}$ are the control input, control output, and measurement output, respectively; $f(·):{\mathbb{R}}^n\to {\mathbb{R}}^n$ is a known nonlinear mapping; $v\left(t\right)$ is the measurement noise that is usually caused by sensors; $d\left(t\right)\in {\mathbb{R}}^d$ is a lumped disturbance term incorporating both system parameter perturbation and environmental disturbances; $B_d\in {\mathbb{R}}^{n\times n_d}$ is the unknown disturbance input matrix subject to $d\left(t\right)$; and A, B, and C are is the system parameter matrices with appropriate dimensions.

For the system in (1), some assumptions are made as follows.

Assumption  1.

The controllability of the pair $(A,B)$ and the observability of the pair $(A,C)$ hold.

Assumption  2.

The unknown lumped disturbance $d\left(t\right)$ of the system has an upper bound, i.e.,

$$∥d\left(t\right)∥\le d_m$$

(2)

where $d_m$ is an unknown positive constant.

Assumption  3.

The nonlinear mapping $f(·)$ is obtained by some techniques and satisfies

$$∥f\left(x_1\right)-f\left(x_2\right)∥\le f_m∥x_1-x_2∥f\left(0\right)=f_0$$

(3)

where $x_1,x_2\in {\mathbb{R}}^n$; $f_m$ is a known positive constant number; and $f_0$ is a known constant.

Remark  1.

Assumption 1 usually holds in controller design, and the boundedness constraints in Assumption 2 are universally valid in engineering practice.

Remark  2.

The prior knowledge of $f(·)$ can usually be known through system identification or other techniques. On the other hand, the lumped disturbance comprises identification errors, model simplification errors, system uncertainties, and external disturbances.

The control objective is to design a control law that tracks the reference trajectory $r\left(t\right)$ in the presence of lumped disturbance and measurement noise.

The control scheme of the KF-EIDE disturbance rejection approach consists of five parts (as shown in Figure 1): the internal model controller, state feedback controller, state observer, EID-based estimator, and Kalman filter.

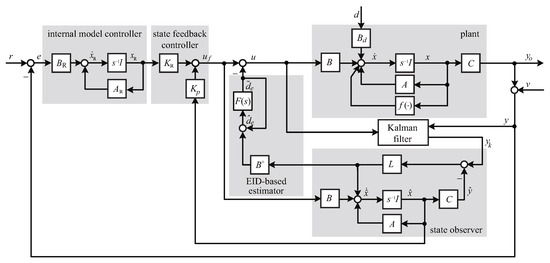
Figure 1. The control scheme of the KF-EIDE approach.

2.2. Conventional EID-Based Control System

According to the EID concept [12], an EID always exists in the input channel of the plant (1). Specifically, there exists an EID $d_e\left(t\right)$ that has an equivalent effect on the system output as the nonlinear function $f\left(x\right)$ and the lumped disturbance $d\left(t\right)$ do, i.e., [21]

$$\left\{\begin{array}{c}\dot{x}\left(t\right)=Ax\left(t\right)+B[u\left(t\right)+d_e\left(t\right)]\hfill \\ y\left(t\right)=Cx\left(t\right)+v\left(t\right).\hfill \end{array}\right.$$

(4)

Given the reference input $r\left(t\right)$, an internal model controller is designed to ensure asymptotic tracking. The controller is designed as follows:

$${\dot{x}}_{\mathrm{R}}\left(t\right)=A_{\mathrm{R}}{x}_{\mathrm{R}}\left(t\right)+B_{\mathrm{R}}[r\left(t\right)-y\left(t\right)]$$

(5)

where $x_{\mathrm{R}}\left(t\right)$ denotes the state; $A_{\mathrm{R}}$ and $B_{\mathrm{R}}$ are parameters to be designed.

A standard state observer is designed to estimate the state of (4), which is described as follows:

$$\left\{\begin{array}{c}\dot{\widehat{x}}\left(t\right)=A\widehat{x}\left(t\right)+B{u}_f\left(t\right)+L[y\left(t\right)-C\widehat{x}\left(t\right)]\hfill \\ \widehat{y}\left(t\right)=C\widehat{x}\left(t\right)\hfill \end{array}\right.$$

(6)

where $\widehat{x}\left(t\right)$ is the state of the observer; L is the observer gain to be determined; and $u_f\left(t\right)$ is the state feedback control law and is usually designed as follows:

$$u_f\left(t\right)=K_{\mathrm{R}}{x}_{\mathrm{R}}\left(t\right)+K_p\widehat{x}\left(t\right)$$

(7)

where $K_{\mathrm{R}}$ and $K_p$ are controller gains to be chosen.

Define the observed errors as follows:

$$\Delta x\left(t\right)=x\left(t\right)-\widehat{x}\left(t\right),\Delta y\left(t\right)=y\left(t\right)-\widehat{y}\left(t\right).$$

(8)

Then, the conventional EID estimation ${\widehat{d}}_e\left(t\right)$ is computed by [22]

$${\widehat{d}}_e\left(t\right)=B^{\star }L\Delta y\left(t\right)+u_f\left(t\right)-u\left(t\right)$$

(9)

where $B^{\star }$ is the pseudo-inverse matrix of B.

To have more freedom of disturbance rejection, a linear estimator gain $K_e$ is chosen instead of a fixed one $B^{\star }L$, i.e., [13]

$${\widehat{d}}_e\left(t\right)=K_e\Delta y\left(t\right)+u_f\left(t\right)-u\left(t\right).$$

(10)

There is non-causality in (10); in other words, the computation of ${\widehat{d}}_e\left(t\right)$ needs the control input $u\left(t\right)$. Therefore, the filter $F\left(s\right)$ is designed to cope with this problem and satisfies

$$\left|F\left(s\right)\right|\approx I\forall \omega \in [0,{\omega }_r]$$

(11)

where ${\omega }_r$ presents the highest frequency of the estimation. Furthermore, $F\left(s\right)$ can be given by a state space representation:

$$\left\{\begin{array}{c}{\dot{x}}_F\left(t\right)=A_F{x}_F\left(t\right)+B_F{\widehat{d}}_e\left(t\right)\hfill \\ {\tilde{d}}_e\left(t\right)=C_F{x}_F\left(t\right)\hfill \end{array}\right.$$

(12)

where $x_F\left(t\right)$ denotes the state of $F\left(s\right)$; $(A_F,B_F,C_F)$ are system parameters; and ${\tilde{d}}_e\left(t\right)$ is the filtered estimation of ${\widehat{d}}_e\left(t\right)$.

Then, the final control law is concluded to be

$$u\left(t\right)=u_f\left(t\right)-{\tilde{d}}_e\left(t\right)=K_{\mathrm{R}}{x}_{\mathrm{R}}\left(t\right)+K_p\widehat{x}\left(t\right)-{\tilde{d}}_e\left(t\right).$$

(13)

2.3. Configuration of the Kalman Filter

Considering the impact of measurement noise, a Kalman filter combined with known nonlinearity $f\left(x\right)$ is designed as follows:

$$\left\{\begin{array}{c}\dot{z}\left(t\right)=Az\left(t\right)+B{u}_f\left(t\right)+f\left(z\right)+K\left(t\right)[y\left(t\right)-y_k\left(t\right)]\hfill \\ y_k\left(t\right)=Cz\left(t\right)\hfill \end{array}\right.$$

(14)

where $z\left(t\right)$ is the state of the Kalman filter, $K\left(t\right)$ is the Kalman gain, and $y_k\left(t\right)$ is the estimation output.

Moreover, the filtered output $y_k\left(t\right)$ is applied in the conventional EID-based control scheme, and then the state observer is written as follows:

$$\left\{\begin{array}{c}\dot{\widehat{x}}\left(t\right)=A\widehat{x}\left(t\right)+B{u}_f\left(t\right)+L(y_k\left(t\right)-C\widehat{x}\left(t\right))\hfill \\ \widehat{y}\left(t\right)=C\widehat{x}\left(t\right).\hfill \end{array}\right.$$

(15)

Remark  3.

Since some nonlinearities are known, unlike [20], the dynamic equations of the Kalman filter (14) include prior knowledge of nonlinearity. Instead of treating nonlinearity as a disturbance, this approach can reduce the burden on the state observer; that is, it allows for the design of a smaller observer gain, thereby avoiding the excessive amplification of measurement noise on control inputs.

3. Analysis of Kalman Filter

In this section, $K\left(t\right)$ is to be designed through system analysis. Define the observed error of the Kalman filter and the estimated error of the EID-based estimator as follows:

$$x_{\delta }\left(t\right)=z\left(t\right)-x\left(t\right),\Delta d_e\left(t\right)={\tilde{d}}_e\left(t\right)-d_e\left(t\right).$$

(16)

Since measurement noise is a stochastic process, to facilitate the analysis of system dynamics and stability, the following assumptions are considered first:

Assumption  4.

The noise $v\left(t\right)$ is characterized as zero-mean Gaussian white noise [23], and the nonlinear term $f\left(z\right)$ of the Kalman filter and the EID estimation error $\Delta d_e\left(t\right)$ are independent of $v\left(t\right)$. Their covariance satisfies

$$\begin{array}{cc}\hfill E\left\{v\left(t\right)v^T\left(\tau \right)\right\}& =R\delta \left(t-\tau \right)\hfill \\ \hfill E\left\{\Delta d_e\left(t\right)\Delta d_e^T\left(\tau \right)\right\}& =Q_d\delta \left(t-\tau \right)\hfill \\ \hfill E\left\{f\left(z\right)f^T\left(z\right)\right\}& =F\delta \left(t-\tau \right)\hfill \end{array}$$

(17)

where R, $Q_d$, and F are the covariance matrices of $v\left(t\right)$, $f\left(z\right)$ of (14), and $\Delta d_e\left(t\right)$, respectively; δ is the Dirac function. Moreover, the measurement noise has an upper bound and satisfies

$$∥v\left(t\right)∥\le v_b$$

(18)

where $v_b$ is a positive constant.

Theorem  1.

Under Assumption 4, if the Kalman gain $K\left(t\right)$ is designed as

$$\begin{array}{cc}\hfill K\left(t\right)& =P_K\left(t\right)C^T{R}^{-1}\hfill \\ \hfill {\dot{P}}_K\left(t\right)& =\left[A-K\left(t\right)C\right]P_K\left(t\right)+P_K\left(t\right){\left[A-K\left(t\right)C\right]}^T+K\left(t\right)R{K}^T\left(t\right)+B{Q}_d{B}^T-F\hfill \end{array}$$

(19)

where $P_K\left(t\right)$ is the covariance matrix

$$P_K\left(t\right)=E\left\{x_{\delta }\left(t\right)x_{\delta }^T\left(t\right)\right\},$$

(20)

then the state estimation of the Kalman filter is optimal.

Proof. 

According to (4) and (14), the estimation dynamics of the Kalman filter are derived as follows:

$${\dot{x}}_{\delta }\left(t\right)=A_{\delta }\left(t\right)x_{\delta }\left(t\right)+\pi \left(t\right)$$

(21)

where

$$A_{\delta }\left(t\right)=A-K\left(t\right)C,\pi \left(t\right)=K\left(t\right)v\left(t\right)+B\Delta d_e\left(t\right)-f\left(z\right).$$

(22)

Then, the solution of (21) can be written as

$$x_{\delta }\left(t\right)=\mathrm{\Phi }(t,t_0)x_{\delta }\left(t_0\right)+{\int }_{t_0}^t\mathrm{\Phi }(t,\tau )\pi \left(t\right)d\tau$$

(23)

where $\mathrm{\Phi }(t,t_0)$ is the state transition matrix.

Invoking Assumption 4, we have

$$E\left\{\pi \left(t\right){\pi }^T\left(\tau \right)\right\}=[K\left(t\right)R{K}^T\left(t\right)+B{Q}_d{B}^T-F]\delta \left(t-\tau \right).$$

(24)

Supposing $x_{\delta }\left(t_0\right)$ and $\pi \left(t\right)$ are independent of each other and taking (23) into (20), we have

$$\begin{array}{c}\hfill P_K\left(t\right)=\mathrm{\Phi }(t,t_0)P_K\left(t_0\right){\mathrm{\Phi }}^T(t,t_0)+{\int }_{t_0}^t\mathrm{\Phi }(t,\tau )\left[K\left(\tau \right)R{K}^T\left(\tau \right)+B{Q}_d{B}^T-F\right]{\mathrm{\Phi }}^T(t,\tau )d\tau .\end{array}$$

(25)

The derivative of $P_K\left(t\right)$ with respect to t can be derived as follows:

$$\begin{array}{cc}\hfill {\dot{P}}_K\left(t\right)=& {\displaystyle \frac{\partial \mathrm{\Phi }(t,t_0)}{\partial t}}{P}_K\left(t_0\right){\mathrm{\Phi }}^T(t,t_0)+\mathrm{\Phi }(t,t_0)P_K\left(t_0\right){\displaystyle \frac{\partial {\mathrm{\Phi }}^T(t,t_0)}{\partial t}}\hfill \\ \hfill & +{\int }_{t_0}^t{\displaystyle \frac{\partial \mathrm{\Phi }(t,\tau )}{\partial t}}\left[K\left(\tau \right)R{K}^T\left(\tau \right)+B{Q}_d{B}^T-F\right]{\mathrm{\Phi }}^T(t,\tau )d\tau \hfill \\ \hfill & +{\int }_{t_0}^t\mathrm{\Phi }(t,\tau )\left[K\left(\tau \right)R{K}^T\left(\tau \right)+B{Q}_d{B}^T-F\right]{\displaystyle \frac{\partial {\mathrm{\Phi }}^T(t,\tau )}{\partial t}}d\tau \hfill \\ \hfill & +\mathrm{\Phi }(t,t)\left[K\left(\tau \right)R{K}^T\left(\tau \right)+B{Q}_d{B}^T-F\right]{\mathrm{\Phi }}^T(t,t).\hfill \end{array}$$

(26)

Since $\mathrm{\Phi }(t,t)=I$ and

$$\dot{\mathrm{\Phi }}(t,t_0)=A_{\delta }\left(t\right)\mathrm{\Phi }(t,t_0),$$

(27)

then (26) can be simplified as

$${\dot{P}}_K\left(t\right)=A_{\delta }\left(t\right)P_K\left(t\right)+P_K\left(t\right){A_{\delta }}^T\left(t\right)+K\left(t\right)R{K}^T\left(t\right)+B{Q}_d{B}^T-F.$$

(28)

To obtain the Kalman gain $K\left(t\right)$, define the trace of ${\dot{P}}_K\left(t\right)$ as the cost function:

$$J\left[K\left(t\right)\right]=\mathrm{tr}\left[{\dot{P}}_K\left(t\right)\right].$$

(29)

where $\mathrm{tr}(·)$ is the matrix trace operator.

Then, taking the derivative of $J\left[K\right(t\left)\right]$ with respect to $K\left(t\right)$, we have

$${\displaystyle \frac{\partial J}{\partial K\left(t\right)}}=2K\left(t\right)R-2P\left(t\right)C^T.$$

(30)

Let $\partial J/\partial K\left(t\right)=0$; finally $K\left(t\right)$ is derived as

$$K\left(t\right)=P_K\left(t\right)C^T{R}^{-1}.$$

(31)

This completes the proof. □

To avoid online computation of the Kalman gain and keep the system steady-state analysis within the time-invariant domain, this paper will adopt the steady-state Kalman gain $K_s$ instead of the dynamic one $K\left(t\right)$. In a time-invariant system, the Kalman filter estimation error covariance $P_K\left(t\right)$ also quickly converges to a steady-state value [24]. For the convenience of computation, the steady-state $P_K\left(t\right)$ is denoted as $P_{\infty }$; then, Equation (31) can be expressed as follows:

$$K_s=P_{\infty }{C}^T{R}^{-1}.$$

(32)

Remark  4.

By injecting the measurement noise $v\left(t\right)$, the state $x_{\delta }\left(t\right)$ of (21) contains a stochastic process. Hence, we use the expectation $P_K\left(t\right)$ of (20) to evaluate the average effect of $x_{\delta }^T\left(t\right)x_{\delta }\left(t\right)$. From (29), $tr\left\{{\dot{P}}_K\left(t\right)\right\}$, the rate of increase in $P_K\left(t\right)$ is expected to be minimized. On the other hand, the second derivative of (29) is a positive definite matrix $R\left(t\right)$, resulting in a minimization of $tr\left\{{\dot{P}}_K\left(t\right)\right\}$. Therefore, the optimal form of $K\left(t\right)$ can be deduced as (31).

4. Stability Analysis of the Closed-Loop Control System

In the subsequent analysis, the steady-state Kalman gain $K_s$ is to be used. Moreover, since (4) is only used to design the controller, the stability analysis will be based on (1).

Combining (1) and (14), another version of Kalman filter estimation error dynamics is given as

$${\dot{x}}_{\delta }=A_{\delta }{x}_{\delta }+B{C}_F{x}_F+K_{s}v+f\left(z\right)-f\left(x\right)-B_{d}d$$

(33)

where

$$A_{\delta }=A-K_{s}C.$$

(34)

According to (1) and (15), the dynamic of state observer error is derived as

$$\Delta \dot{x}=A_L\Delta x+B{C}_F{x}_F+LC{x}_{\delta }-B_{d}d-f\left(x\right)$$

(35)

where

$$A_L=A-LC.$$

(36)

Invoking (10) and (13), (12) can be rewritten as follows:

$${\dot{x}}_F=A_e{x}_F+B_F{K}_{e}C{x}_{\delta }-B_F{K}_{e}C\Delta x$$

(37)

where

$$A_e=A_F+B_F{C}_F.$$

(38)

Substituting (7) into (15), the dynamic of the state observer error can be written as

$$\dot{\widehat{x}}=A_K\widehat{x}+B{K}_{\mathrm{R}}{x}_{\mathrm{R}}+LC{x}_{\delta }-LC\Delta x$$

(39)

where

$$A_K=A+B{K}_p.$$

(40)

Likewise, the dynamic of internal model (5) can be expand as

$${\dot{x}}_{\mathrm{R}}=A_{\mathrm{R}}{x}_{\mathrm{R}}+B_{\mathrm{R}}C\Delta x-B_{\mathrm{R}}C\widehat{x}+B_{\mathrm{R}}r-B_{\mathrm{R}}v.$$

(41)

Define the generalized vector of the closed-loop control system as follows:

$$\overline{x}={\left[\begin{array}{ccccc}{x}_{\delta }^T& \Delta x^T& x_F^T& {\widehat{x}}^T& {x_{\mathrm{R}}}^T\end{array}\right]}^T.$$

(42)

According to (33), (35), (37), (39), and (41), the dynamic of the closed-loop control system is represented as

$$\left\{\begin{array}{c}\dot{\overline{x}}=\overline{A}\overline{x}+{\overline{B}}_{d}d+{\overline{B}}_{v}v+{\overline{B}}_{\mathrm{R}}r+\overline{f}-{\overline{f}}_0\hfill \\ y=\overline{C}\overline{x}\hfill \end{array}\right.$$

(43)

where

$$\overline{A}=\left[\begin{array}{ccccc}{A}_{\delta }& 0& B{C}_F& 0& 0\\ LC& A_L& B{C}_F& 0& 0\\ B_F{K}_{e}C& -B_F{K}_{e}C& A_e& 0& 0\\ LC& -LC& 0& A_K& B{K}_{\mathrm{R}}\\ 0& B_{\mathrm{R}}C& 0& -B_{\mathrm{R}}C& A_{\mathrm{R}}\end{array}\right]$$

(44)

$${\overline{B}}_d=\left[\begin{array}{c}-B_d\\ -B_d\\ 0\\ 0\\ 0\end{array}\right],{\overline{B}}_v=\left[\begin{array}{c}{K}_v\\ 0\\ 0\\ 0\\ -B_{\mathrm{R}}\end{array}\right],{\overline{B}}_{\mathrm{R}}=\left[\begin{array}{c}0\\ 0\\ 0\\ 0\\ B_{\mathrm{R}}\end{array}\right],\overline{f}=\left[\begin{array}{c}f\left(z\right)-f\left(x\right)\\ -f\left(x\right)+f\left(0\right)\\ 0\\ 0\\ 0\end{array}\right],{\overline{f}}_0=\left[\begin{array}{c}0\\ f\left(0\right)\\ 0\\ 0\\ 0\end{array}\right]$$

(45)

$$\overline{C}=\left[\begin{array}{ccccc}C\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \end{array}\right].$$

(46)

Let

$$\mathrm{\Theta }={\overline{B}}_{d}d+{\overline{B}}_{v}v+{\overline{B}}_{\mathrm{R}}r-{\overline{f}}_0.$$

(47)

In practice, the reference trajectory $r\left(t\right)$ is bounded. Invoking Assumptions 2 and 4, the lumped disturbance $d\left(t\right)$ and the measurement noise $v\left(t\right)$ are bounded. Therefore, it is clear that $\mathrm{\Theta }\left(t\right)$ is bounded, i.e.,

$$∥\mathrm{\Theta }∥\le {\mathrm{\Theta }}_m$$

(48)

where ${\mathrm{\Theta }}_m$ is a positive constant. Then, (43) is represented as

$$\left\{\begin{array}{c}\dot{\overline{x}}=\overline{A}\overline{x}+\overline{f}+\mathrm{\Theta }\hfill \\ y=\overline{C}\overline{x}.\hfill \end{array}\right.$$

(49)

Theorem  2.

Under the lumped disturbance, nonlinearity, and measurement noise described by Assumption 2–4, the closed-loop control system (42) is stable if there exists matrix $P=P^T>0$ and positive constants ${\epsilon }_1,{\epsilon }_2$ such that the following equation holds:

$$P\overline{A}+{\overline{A}}^{T}P+{\epsilon }_{1}P{P}^T+{\epsilon }_{2}P{P}^T+{\displaystyle \frac{f_m^2}{{\epsilon }_1}}<0.$$

(50)

with $\overline{A}$ of (44) and $f_m$ of Assumption 4.

Proof. 

Choose a Lyapunov candidate function as

$$V={\overline{x}}^{T}P\overline{x}$$

(51)

where $P=P^T$ is a positive definite matrix.

Under Assumption 3, the following inequality holds:

$$∥\overline{f}∥=\sqrt{{∥f\left(z\right)-f\left(x\right)∥}^2+{∥f\left(x\right)-f\left(0\right)∥}^2}\le f_m\sqrt{{∥x_{\delta }∥}^2+{∥\widehat{x}+\Delta x∥}^2}\le f_m∥\overline{x}∥$$

(52)

According to (49), differentiate V in terms of t:

$$\begin{array}{cc}\hfill \dot{V}& ={\overline{x}}^T(P\overline{A}+{\overline{A}}^{T}P)\overline{x}+2{\overline{x}}^{T}P\overline{f}+2{\overline{x}}^{T}P\mathrm{\Theta }\hfill \end{array}.$$

(53)

By Yong’s inequality, we have

$$\left\{\begin{array}{c}2{\overline{x}}^{T}P\overline{f}\le {\epsilon }_1{\overline{x}}^{T}P{P}^T\overline{x}+{\displaystyle \frac{1}{{\epsilon }_1}}{\overline{f}}^T\overline{f}\hfill \\ 2{\overline{x}}^{T}P\mathrm{\Theta }\left(t\right)\le {\epsilon }_2{\overline{x}}^{T}P{P}^T\overline{x}+{\displaystyle \frac{1}{{\epsilon }_2}}{\mathrm{\Theta }}^T\mathrm{\Theta }\hfill \end{array}\right.$$

(54)

where ${\epsilon }_1,{\epsilon }_2>0$ are constant numbers.

Invoking (52) and (54), (53) can be scaled as

$$\begin{array}{}\mathrm{(55)}& \hfill \dot{V}& \le {\overline{x}}^T(P\overline{A}+{\overline{A}}^{T}P+{\epsilon }_{1}P{P}^T+{\epsilon }_{2}P{P}^T)\overline{x}+{\displaystyle \frac{1}{{\epsilon }_1}}{∥\overline{f}∥}^2+{\displaystyle \frac{1}{{\epsilon }_2}}{∥\mathrm{\Theta }∥}^2\hfill \mathrm{(56)}& & \le -[{\lambda }_{min}\left(Q\right)-{\displaystyle \frac{f_m^2}{{\epsilon }_1}}]{∥\overline{x}∥}^2+{\displaystyle \frac{{\mathrm{\Theta }}_m^2}{{\epsilon }_2}}.\hfill \end{array}$$

Since ${\mathrm{\Theta }}_m^2/{\epsilon }_2$ is a bounded constant, and the term ${\lambda }_{min}\left(Q\right)-f_m^2/{\epsilon }_1$ is positive, system (49) is input-to-state stable [25]. The proof is completed. □

5. Simulation and Comparison Results

The system parameters of the plant described by

$$A=\left[\begin{array}{ccc}-8.807& -4.225& -0.4877\\ 8& 0& 0\\ 0& 0.25& 0\end{array}\right],B=\left[\begin{array}{c}8\\ 0\\ 0\end{array}\right],B_d=\left[\begin{array}{c}-12.94\\ 5.88\\ -6.072\end{array}\right],C={\left[\begin{array}{c}7.328\\ 31.71\\ 3.969\end{array}\right]}^T$$

(57)

are the same as [26] for the coupled rotational motor system.

To validate the effectiveness of the developed method, the nonlinearity $f\left(x\right)$ is chosen as [27]

$$f\left(x\right)={\left[\begin{array}{ccc}0& sin\left(x_1\right)sin\left(x_2\right)& 0\end{array}\right]}^T.$$

(58)

The lumped disturbance is given by

$$d\left(t\right)=\left\{\begin{array}{c}5,0\mathrm{s}<t<8\mathrm{s}\hfill \\ 0,\mathrm{others}.\hfill \end{array}\right.$$

(59)

The measurement noise $v\left(t\right)$ is added by the Band-Limited White Noise module in MATLAB R2024a and is shown as Figure 2.

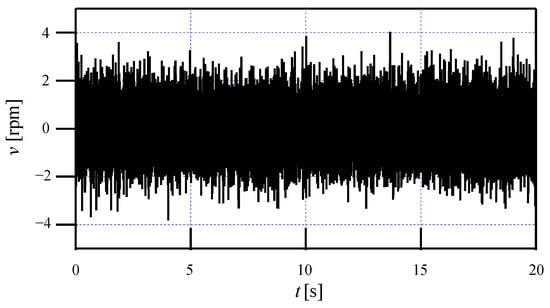
Figure 2. The measurement noise $v\left(t\right)$ in the simulation.

Set the reference as

$$r\left(t\right)=1000\left[\mathrm{r}/\min \right].$$

(60)

Then, for the asymptotic tracking of the reference $r\left(t\right)$, set $A_{\mathrm{R}}=-0.0001$ and $B_{\mathrm{R}}=1$.

Commonly, $F\left(s\right)$ is designed as a first-order low-pass filter and is selected here as

$$A_F=-2.9,B_F=2.5,C_F=1.$$

(61)

The linear quadratic regulation (LQR) method [28] is utilized to design observer gains for its simplicity, and it is utilized here to choose control parameters $(K_p,K_{\mathrm{R}})$, L, and $K_s$.

Let a part of $\overline{A}$ in (44) be

$$A^{\star }=\left[\begin{array}{cc}{A}_K& B{K}_{\mathrm{R}}\\ -B_{\mathrm{R}}C& A_{\mathrm{R}}\end{array}\right].$$

(62)

Rewrite $A^{\star }$ as

$$A^{\star }=\left[\begin{array}{cc}A& 0\\ -B_{\mathrm{R}}C& A_{\mathrm{R}}\end{array}\right]+\left[\begin{array}{c}B\\ 0\end{array}\right]\left[\begin{array}{cc}{K}_p& K_{\mathrm{R}}\end{array}\right].$$

(63)

Treat $[K_p,K_{\mathrm{R}}]$ of (63) as a state-feedback control gain [26]; then, we use the LQR method to select corresponding tunable matrices as follows:

$$\left\{\begin{array}{c}{Q}_1={10}^{-7}\times \mathrm{diag}\{1,1,1,100\}\hfill \\ R_1=1\hfill \end{array}\right.$$

(64)

where $\mathrm{diag}$ presents the diagonal matrix. Then, $K_p=[-0.0215,-0.0227,-0.0034]$ and $K_{\mathrm{R}}=0.0032$.

Likewise, the corresponding tunable matrices are selected as

$$\left\{\begin{array}{c}{Q}_2=100\times \mathrm{diag}\{1,1,1\}\hfill \\ R_2=1\hfill \end{array}\right.$$

(65)

for state observer gain L, and finally $L={[4.8350,8.7458,4.2950]}^T$.

The corresponding tunable matrices are chosen as

$$\left\{\begin{array}{c}{Q}_3=\mathrm{diag}\{1,1,1\}\hfill \\ R_3=1,\hfill \end{array}\right.$$

(66)

and then the steady-state Kalman filter gain is $K_s=[0.3107, 0.9355, 0.4339]$.

The estimator gain $K_e$ is designed to balance the performance of the speed of disturbance estimation and sensitivity to measurement noise in the estimator, which is finally set to be 1.

For the reference of (60), the simulation input and output results are illustrated in Figure 3 and Figure 4 under the disturbance of (59), which shows the robustness and rapid response to disturbances.

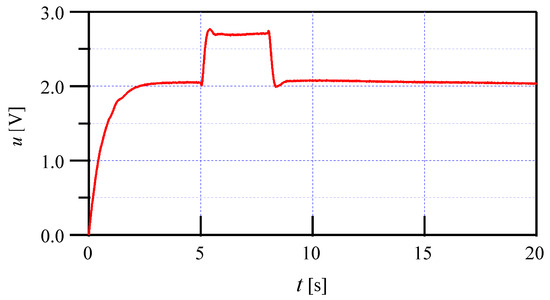
Figure 3. The control input $u\left(t\right)$ of the simulation under the KF-EIDE approach.

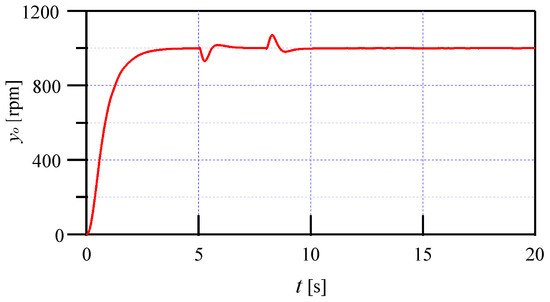
Figure 4. The control output $y_o\left(t\right)$ of the simulation under the KF-EIDE approach.

The disturbance estimation is shown in Figure 5, which demonstrates the lumped compensation of the simulation. When there is no disturbance, the estimator only compensates the nonlinearity $f\left(x\right)$; when the disturbance $d\left(t\right)$ is imposed, the estimator estimates the EID of both $f\left(x\right)$ and $d\left(t\right)$.

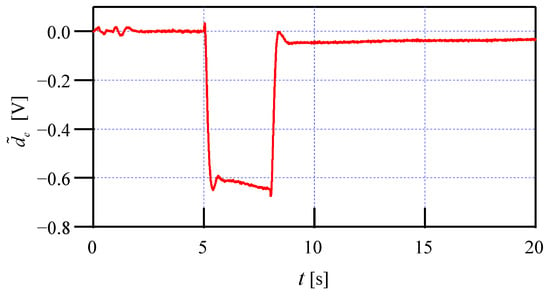
Figure 5. The disturbance estimation ${\tilde{d}}_e\left(t\right)$ of the simulation with the KF-EIDE approach.

To show the advancement of our method, a CEID approach is compared with the developed method. For fairness, except for the Kalman filter part, all parameters of the CEID approach are the same as those of the developed one.

The tracking errors of both methods, as shown in Figure 6 and Figure 7, are nearly identical. However, the control input in the CEID method is more sensitive to measurement noise, which could increase the burden on the actuators. In contrast, by incorporating the known nonlinearity into the Kalman filter, our control scheme shows improved performance, demonstrating the effectiveness of the KF-EIDE approach.

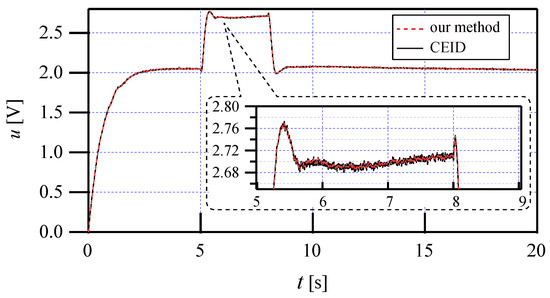
Figure 6. The control inputs $u\left(t\right)$ of the simulation using the CEID and our method.

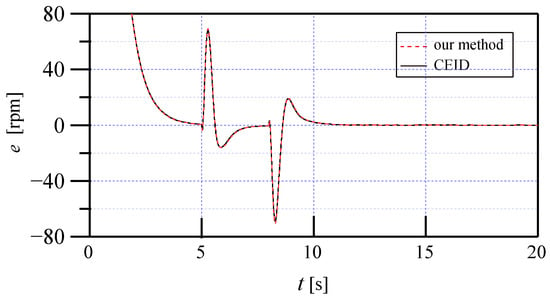
Figure 7. The tracking errors of $e\left(t\right)=r\left(t\right)-y_o\left(t\right)$ of the simulation using the CEID and our method.

6. Conclusions

This study proposed a steady-state Kalman filter integrated with the EID method to address disturbance rejection and state estimation in nonlinear systems. Unlike conventional approaches, the proposed control framework unifies disturbance rejection and noise attenuation by using prior knowledge of system nonlinearities and the steady-state Kalman filter gain. This design avoids complex time-varying gain while retaining robustness against disturbances and measurement noise. Furthermore, the Kalman gain is rigorously derived to obtain an optimal one with the close-loop stability guaranteed. From simulation and comparisons, our method shows an excellent disturbance rejection and noise attenuation performance compared with the CEID method, validating the effectiveness of the KF-EIDE control scheme. Future research will focus on extending the framework to handle coupled multivariable disturbances and experimental validation under real-world noise conditions.