Disturbance Rejection Approach for Nonlinear Systems Using Kalman-Filter-Based Equivalent-Input-Disturbance Estimator
Abstract
1. Introduction
- Novelty in methodology: a novel KF-EIDE scheme is organically proposed, which combines the disturbance rejection capability of CEID with the noise attenuation capability of the Kalman filter to improve the system tracking performance.
- Improvement of structure: nonlinear dynamics and the Kalman filter are organically integrated with the CEID control scheme, enabling accurate state estimation.
- Theoretical rigor: under the lumped disturbance, nonlinearity, and measurement noise, the stability of the closed-loop control system is guaranteed.
2. Methods and Materials
2.1. Problem Formulation
2.2. Conventional EID-Based Control System
2.3. Configuration of the Kalman Filter
3. Analysis of Kalman Filter
4. Stability Analysis of the Closed-Loop Control System
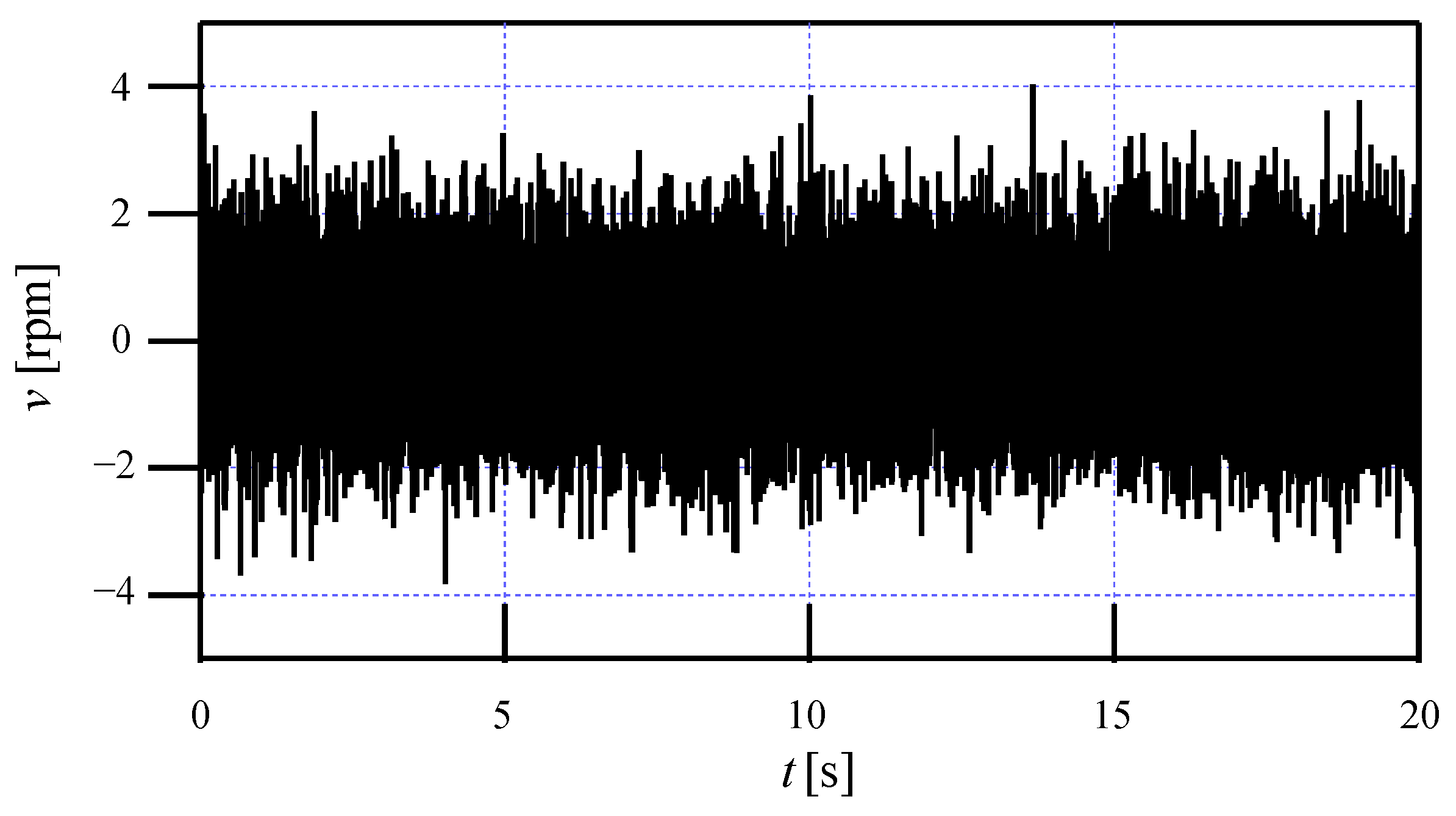
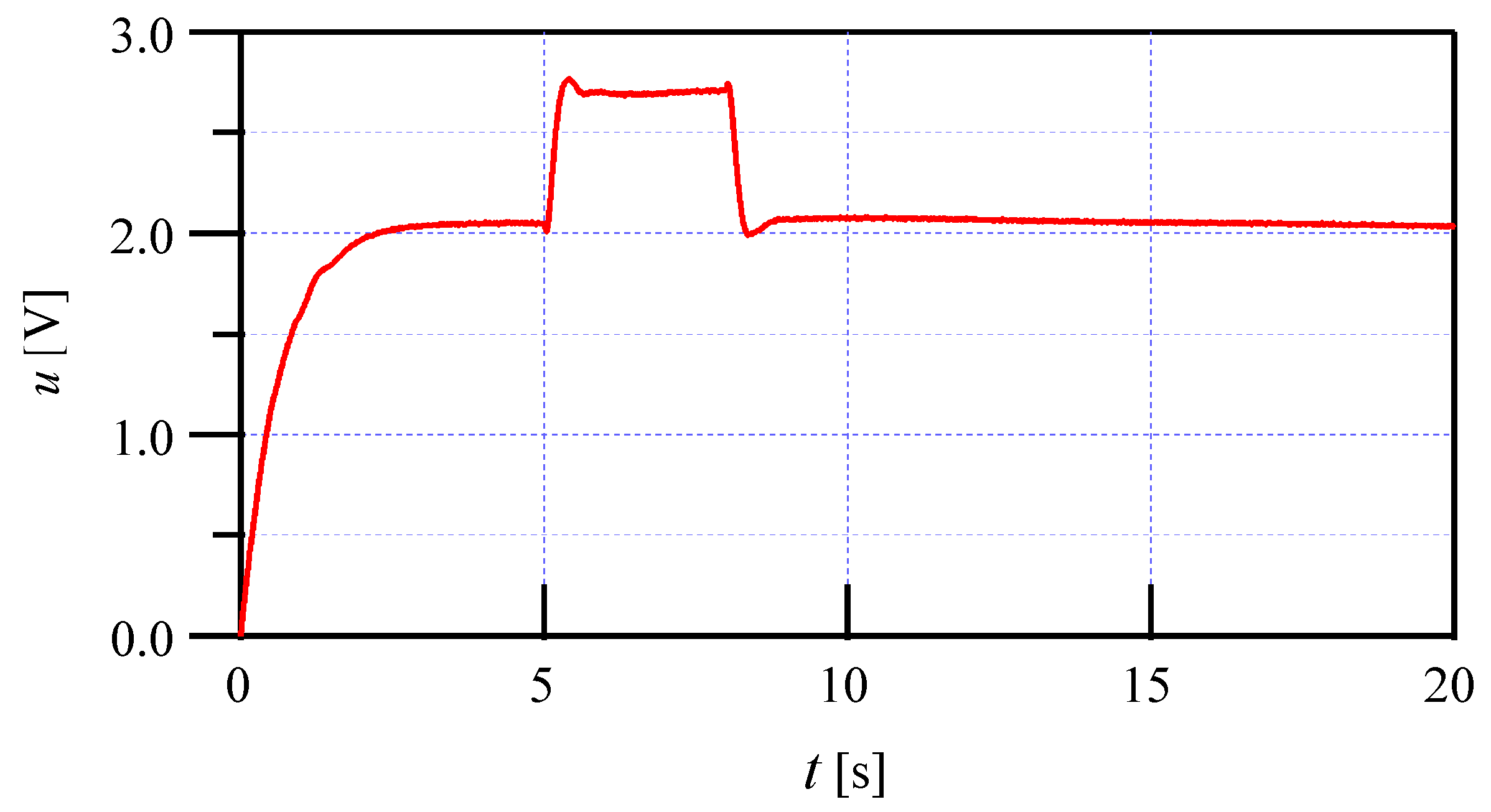
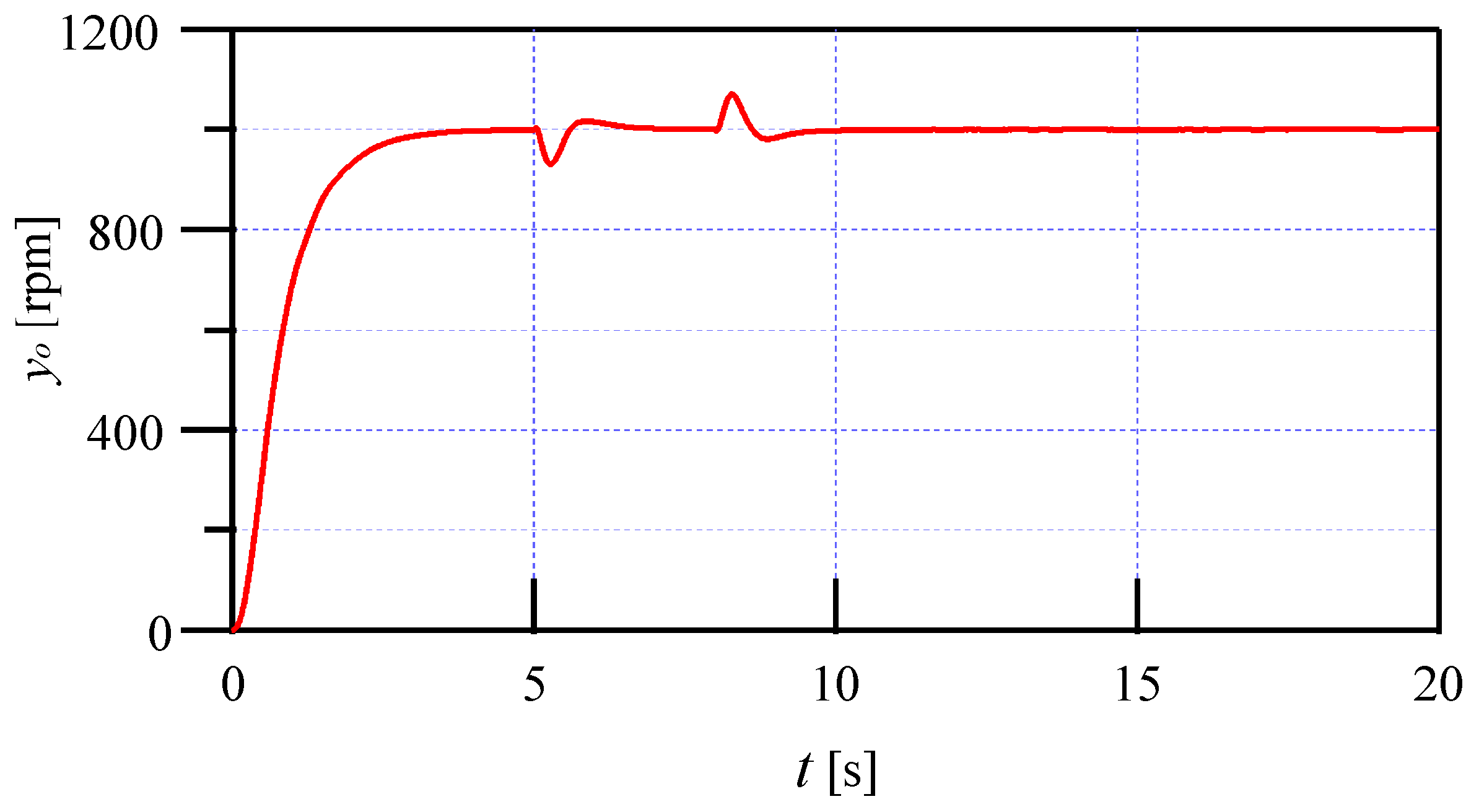
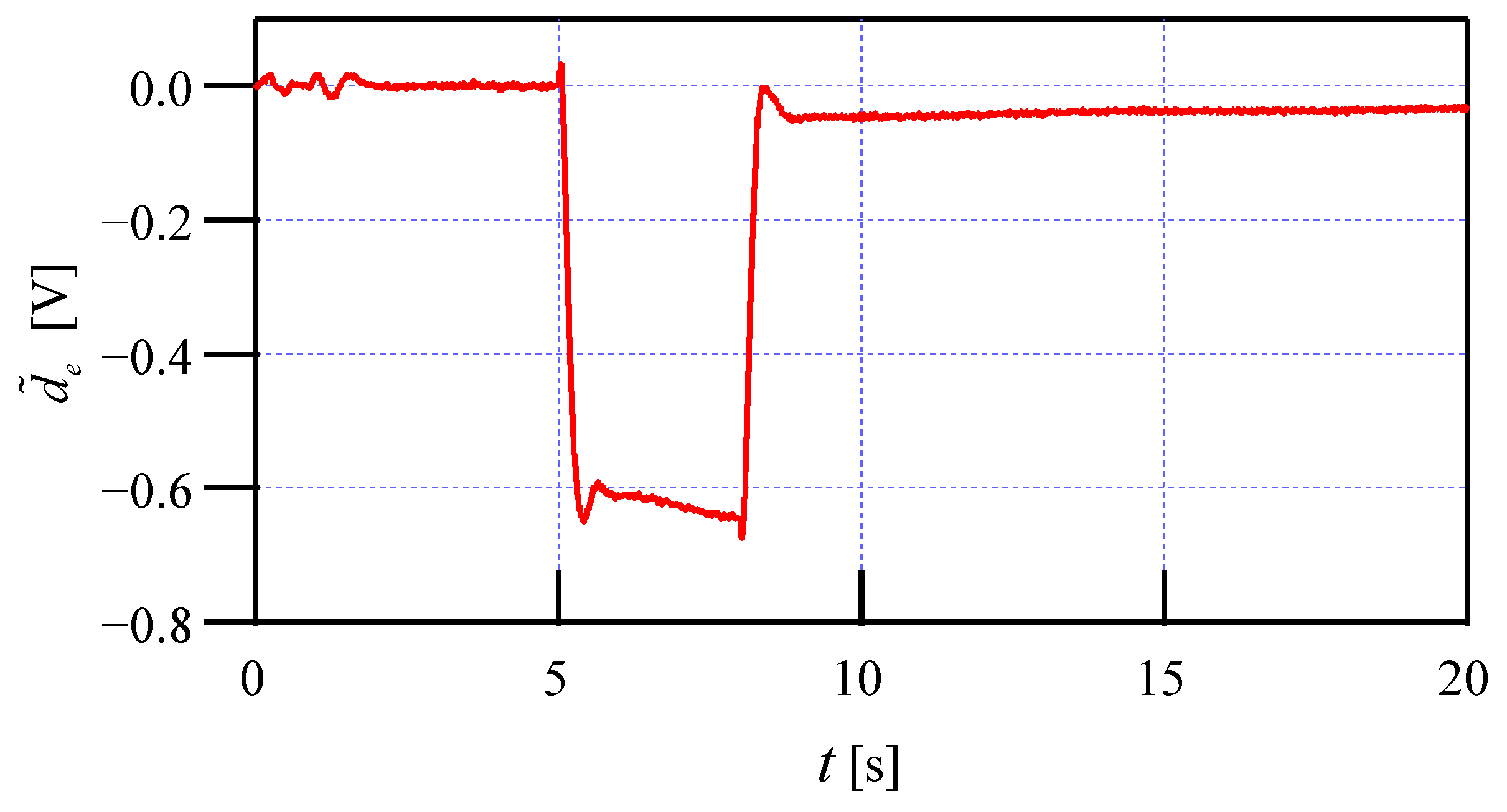
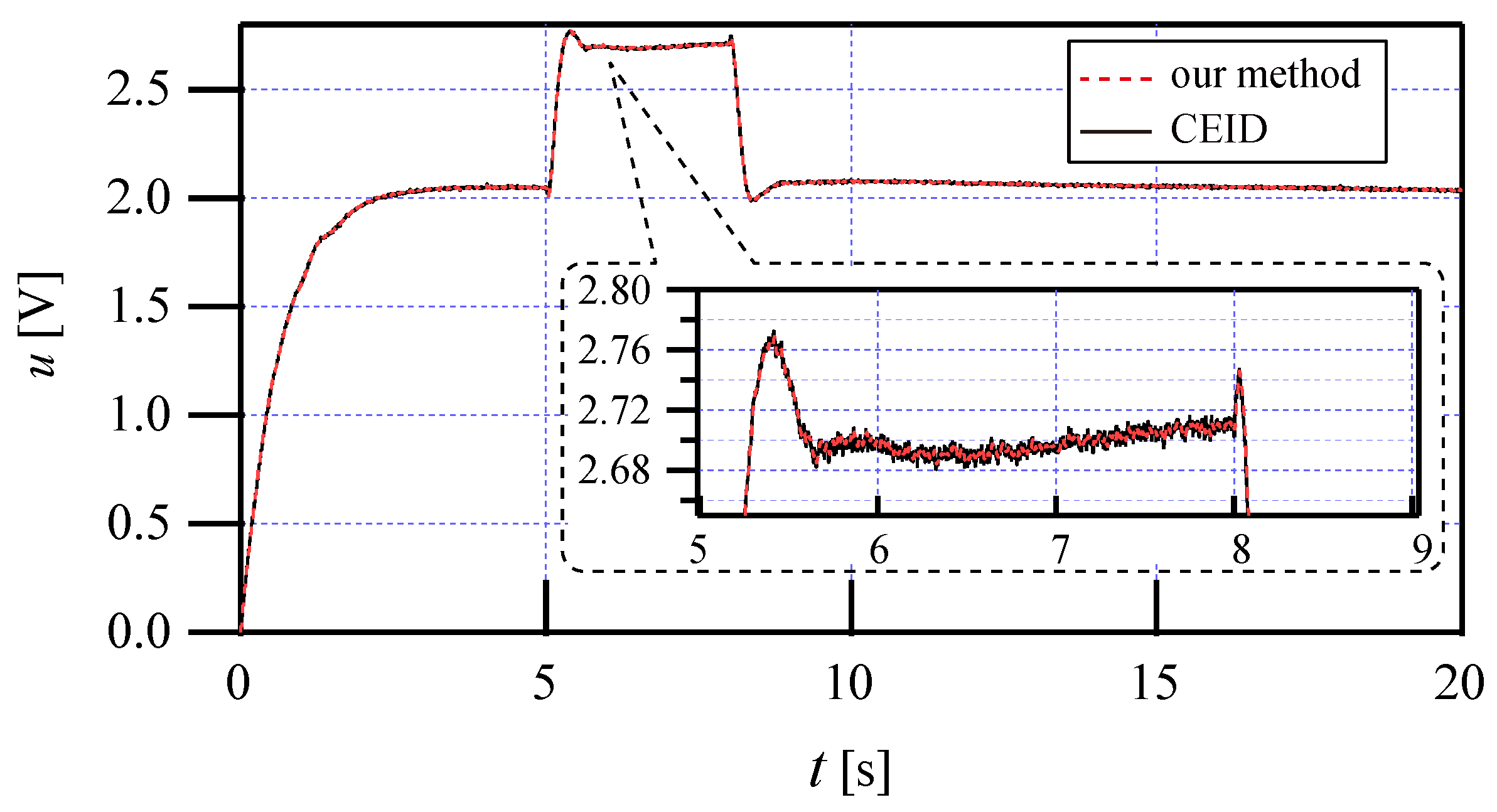
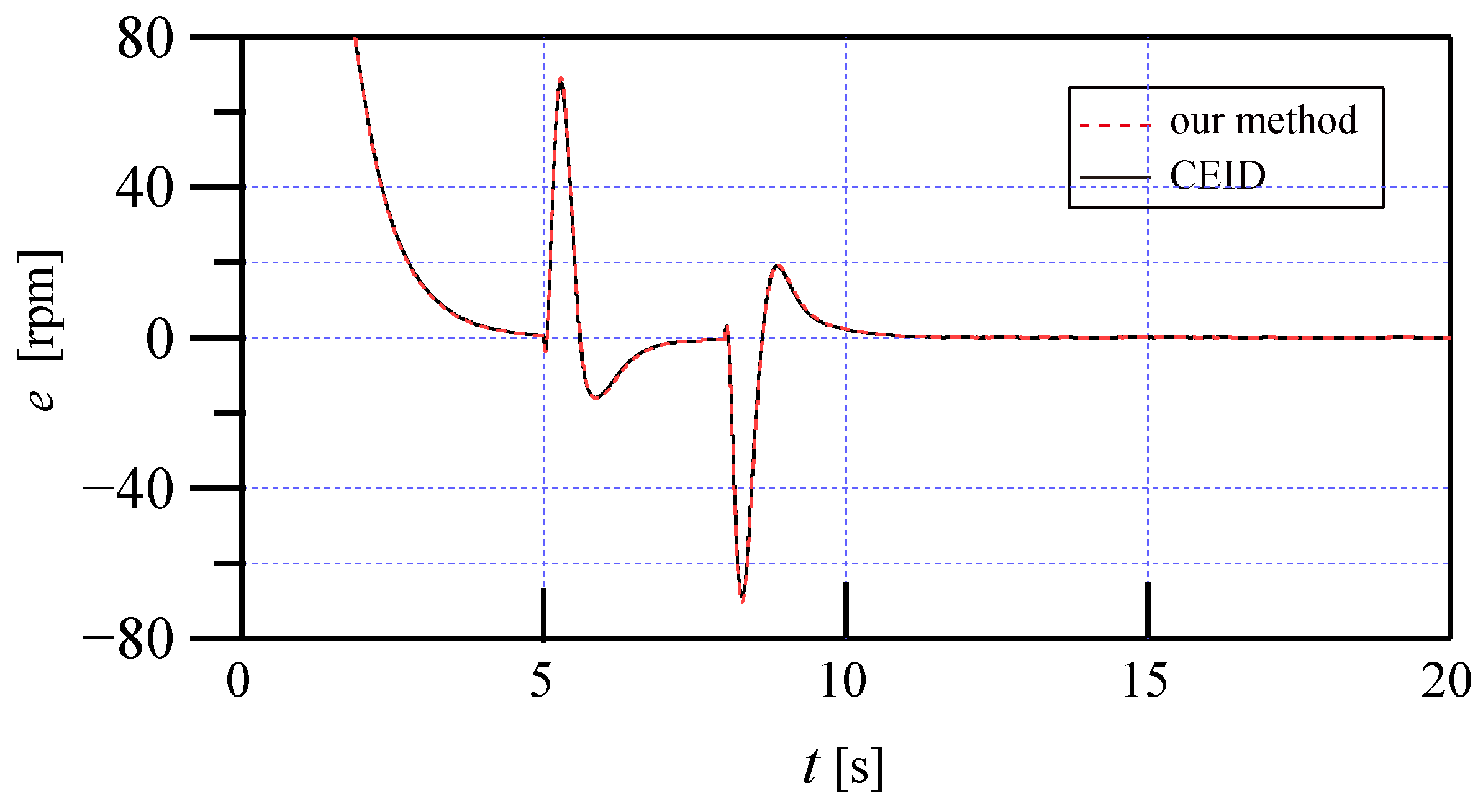
5. Simulation and Comparison Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gurauskis, D.; Przystupa, K.; Kilikevičius, A.; Skowron, M.; Matijošius, J.; Caban, J.; Kilikevičienė, K. Development and Experimental Research of Different Mechanical Designs of an Optical Linear Encoder’s Reading Head. Sensors 2022, 22, 2977. [Google Scholar] [CrossRef] [PubMed]
- Cheng, M.; Zhou, J.; Qian, W.; Wang, B.; Zhao, C.; Han, P. Advanced Electrical Motors and Control Strategies for High-quality Servo Systems—A Comprehensive Review. Chin. J. Electr. Eng. 2024, 10, 63–85. [Google Scholar] [CrossRef]
- Hu, K.; Ma, Z.; Zou, S.; Li, J.; Ding, H. Impedance Sliding-Mode Control Based on Stiffness Scheduling for Rehabilitation Robot Systems. Cyborg Bionic Syst. 2024, 5, 0099. [Google Scholar] [CrossRef] [PubMed]
- Tu, Y.H.; Wang, R.F.; Su, W.H. Active Disturbance Rejection Control—New Trends in Agricultural Cybernetics in the Future: A Comprehensive Review. Machines 2025, 13, 111. [Google Scholar] [CrossRef]
- Gu, X.; Ren, H. A Survey of Transoral Robotic Mechanisms: Distal Dexterity, Variable Stiffness, and Triangulation. Cyborg Bionic Syst. 2023, 4, 0007. [Google Scholar] [CrossRef]
- Sun, X.; Lin, X.; Guo, D.; Lei, G.; Yao, M. Improved Deadbeat Predictive Current Control With Extended State Observer for Dual Three-Phase PMSMs. IEEE Trans. Power Electron. 2024, 39, 6769–6782. [Google Scholar] [CrossRef]
- Chen, W.H.; Yang, J.; Guo, L.; Li, S. Disturbance-Observer-Based Control and Related Methods—An Overview. IEEE Trans. Ind. Electron. 2016, 63, 1083–1095. [Google Scholar] [CrossRef]
- Zhou, L.; Jia, F.; She, J.; Li, M.; Xiao, W. Parallel-Equivalent-Input-Disturbance-Approach-Based Spatial Repetitive Control for Rotating Systems. IEEE Trans. Ind. Electron. 2025; early access. [Google Scholar] [CrossRef]
- Zhu, Y.; Bao, Z.; Teng, H.; Yang, Y.; Cui, Y. Disturbance Separation-Based Enhanced Antidisturbance Attitude Control for Flexible Spacecrafts with Composite Disturbances. IEEE Trans. Ind. Electron. 2024, 71, 13146–13156. [Google Scholar] [CrossRef]
- Yin, X.; She, J.; Liu, Z.T.; Xiong, Y. Disturbance Suppression and System Design Based on Parallel-Equivalent-Input-Disturbance Approach. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 3654–3665. [Google Scholar] [CrossRef]
- Yin, X.; Shi, Y.; She, J.; Wang, H. Equivalent Input Disturbance-Based Control: Analysis, Development, and Applications. IEEE Trans. Cybern. 2024, 54, 2654–2667. [Google Scholar] [CrossRef]
- She, J.H.; Fang, M.; Ohyama, Y.; Hashimoto, H.; Wu, M. Improving Disturbance-Rejection Performance Based on an Equivalent-Input-Disturbance Approach. IEEE Trans. Ind. Electron. 2008, 55, 380–389. [Google Scholar] [CrossRef]
- Yu, P.; Liu, K.; Li, X.; Yokoyama, M. Robust control of pantograph-catenary system: Comparison of 1-DOF-based and 2-DOF-based control systems. IET Control Theory Appl. 2021, 15, 2258–2270. [Google Scholar] [CrossRef]
- Khodarahmi, M.; Maihami, V. A Review on Kalman Filter Models. Arch. Comput. Methods Eng. 2022, 30, 727–747. [Google Scholar] [CrossRef]
- Bian, Y.; Yang, Z.; Sun, X.; Wang, X. Speed Sensorless Control of a Bearingless Induction Motor Based on Modified Robust Kalman Filter. J. Electr. Eng. Technol. 2023, 19, 1179–1190. [Google Scholar] [CrossRef]
- Yu, K.; Li, S.; Zhu, W.; Wang, Z. Sensorless Control Scheme for PMSM Drive via Generalized Proportional Integral Observers and Kalman Filter. IEEE Trans. Power Electron. 2025, 40, 4020–4033. [Google Scholar] [CrossRef]
- Knox, J.; Blyth, M.; Hales, A. Advancing state estimation for lithium-ion batteries with hysteresis through systematic extended Kalman filter tuning. Sci. Rep. 2024, 14, 12472. [Google Scholar] [CrossRef]
- Park, G. Optimal vehicle position estimation using adaptive unscented Kalman filter based on sensor fusion. Mechatronics 2024, 99, 103144. [Google Scholar] [CrossRef]
- Lei, T.; Hou, M.; Li, L.; Cao, H. A State Estimation of Dynamic Parameters of Electric Drive Articulated Vehicles Based on the Forgetting Factor of Unscented Kalman Filter with Singular Value Decomposition. Actuators 2025, 14, 31. [Google Scholar] [CrossRef]
- Sun, H.; Madonski, R.; Li, S.; Zhang, Y.; Xue, W. Composite Control Design for Systems With Uncertainties and Noise Using Combined Extended State Observer and Kalman Filter. IEEE Trans. Ind. Electron. 2022, 69, 4119–4128. [Google Scholar] [CrossRef]
- Yin, X.; She, J.; Wu, M.; Sato, D.; Ohnishi, K. Disturbance rejection using SMC-based-equivalent-input-disturbance approach. Appl. Math. Comput. 2022, 418, 126839. [Google Scholar] [CrossRef]
- Zhou, Y.; She, J.; Wang, F.; Iwasaki, M. A Model-Predictive-Enabled Equivalent-Input-Disturbance Approach for Disturbance Rejection. In Proceedings of the 2023 IEEE 6th International Conference on Industrial Cyber-Physical Systems (ICPS), Wuhan, China, 8–11 May 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Žvirblis, T.; Pikšrys, A.; Bzinkowski, D.; Rucki, M.; Kilikevičius, A.; Kurasova, O. Data Augmentation for Classification of Multi-Domain Tension Signals. Informatica 2024, 35, 883–908. [Google Scholar] [CrossRef]
- Crassidis, J.L.; Junkins, J.L. Optimal Estimation of Dynamic Systems; Chapman and Hall/CRC: New York, NY, USA, 2004. [Google Scholar] [CrossRef]
- Sontag, E.D. Input to State Stability: Basic Concepts and Results. In Nonlinear and Optimal Control Theory; Springer: Berlin/Heidelberg, Germany, 2008; pp. 163–220. [Google Scholar] [CrossRef]
- Yu, P.; Wu, Q.; Liu, K.Z.; She, J.; Li, X. Tunable Nonlinear-Function-Based Estimators for Mismatched Disturbances and Performance Analysis. IEEE Trans. Ind. Electron. 2024, 71, 11453–11464. [Google Scholar] [CrossRef]
- Yin, X.; Shi, Y.; She, J.; Xie, M.; Wang, Z. Nonlinearity and Disturbance Compensation Based on Improved Equivalent-Input-Disturbance Approach. IEEE/ASME Trans. Mechatron. 2024, 29, 703–714. [Google Scholar] [CrossRef]
- Yu, P.; Liu, K.Z.; Liu, X.; Li, X.; Wu, M.; She, J. Robust Consensus Tracking Control of Uncertain Multi-Agent Systems With Local Disturbance Rejection. IEEE/CAA J. Autom. Sin. 2023, 10, 427–438. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, G.; Zhao, X.; Zhao, B.; Han, L.; Yu, P. Disturbance Rejection Approach for Nonlinear Systems Using Kalman-Filter-Based Equivalent-Input-Disturbance Estimator. Actuators 2025, 14, 189. https://doi.org/10.3390/act14040189
Huang G, Zhao X, Zhao B, Han L, Yu P. Disturbance Rejection Approach for Nonlinear Systems Using Kalman-Filter-Based Equivalent-Input-Disturbance Estimator. Actuators. 2025; 14(4):189. https://doi.org/10.3390/act14040189
Chicago/Turabian StyleHuang, Gao, Xuefei Zhao, Bohao Zhao, Lianqiang Han, and Pan Yu. 2025. "Disturbance Rejection Approach for Nonlinear Systems Using Kalman-Filter-Based Equivalent-Input-Disturbance Estimator" Actuators 14, no. 4: 189. https://doi.org/10.3390/act14040189
APA StyleHuang, G., Zhao, X., Zhao, B., Han, L., & Yu, P. (2025). Disturbance Rejection Approach for Nonlinear Systems Using Kalman-Filter-Based Equivalent-Input-Disturbance Estimator. Actuators, 14(4), 189. https://doi.org/10.3390/act14040189






