Abstract
A polymer-dispersed liquid crystal (PDLC) film is a device that can transition from opaque to transparent when electrically charged. These films can be used as actuators to control light levels in response to changing natural light. However, the current state of the art for controlling PDLC films is limited to on/off functionality, and few works in the current body of literature have explored continuous control. This study develops a novel nonlinear model for PDLCs in the context of the feedback control of light. This study also demonstrates the model’s utility by comparing experimental data of a PDLC in feedback with a proportional–integral (PI) controller for disturbance rejection and tracking of a desired light setpoint. This development is motivated by the need for a smart greenhouse that can provide programmable optimized light levels for plant growth. Specifically, a light sensor is composed of a circuit with photodiodes and calibrated for the photosynthetically active radiation range. The light sensor is placed under the film, separate from an exogenous light source, allowing for feedback control to be applied. A proportional–integral type control law is selected for stiffness and the ability to eliminate steady-state error, and it is implemented using a microcontroller. An equivalent analog control effort is applied to the PDLC via a PWM voltage signal and an H-bridge type driver. Details necessary for the driving of the PDLC are presented. Open-loop identification of the nonlinear quasi-static and dynamic step-response transients of the PDLC at different control levels are presented and modeled. Finally, closed-loop experimental and simulated results are presented for both light disturbance rejection and setpoint tracking. This shows that the proposed control framework allows for continuous control of light.
1. Introduction
There is a need to control the amount of external light entering a greenhouse in order to optimize seed germination and plant growth [1]. The ideal amount of photosynthetically active radiation (PAR) is generally different for different plant types and growth stages. For example, Li and Tan [2] studied the advantages of diffused light for horticultural production. Of course, exploiting natural sunlight is more energy efficient than using artificial light, but it is subject to disturbances such as sun movement, cloud movement, fluctuations in human-made light pollution, etc. [3], hence the need for active control [3]. One actuator technology for light control, which has shown potential but has not been fully explored, is polymer-dispersed liquid crystal (PDLC) films [4].
PDLC films can change transparency with voltage control [5]. They are made of three different layers: two outer layers of transparent electrodes and a polymer matrix with liquid crystal (LC) molecules in the middle [6]. By varying the voltage applied to the electrodes, two different states can be achieved: translucent and transparent [5]. When no voltage is applied, the refractive indices of the matrix do not match the indices of the LC microdroplets [7]. As a result, they are freely oriented and not aligned with the direction of the light [8]. The light is scattered, and PDLC appears translucent [6]. If sufficient voltage is applied, the electric field produces a high enough torque to overcome the elastic torque of the LC molecules. This aligns them with the electric field and the direction of the light [8]. Light travels through PDLC with high transmission [6,9]. The basic operation of PDLCs is illustrated in Figure 1, with (a) showing the off state and (b) showing the on state. PDLCs require an AC voltage signal [10,11]; therefore, a driver capable of changing polarity is needed. The voltage amplitude is related to the transparency [12], such that the driver must also provide variable voltage amplitude to achieve continuous control [13].
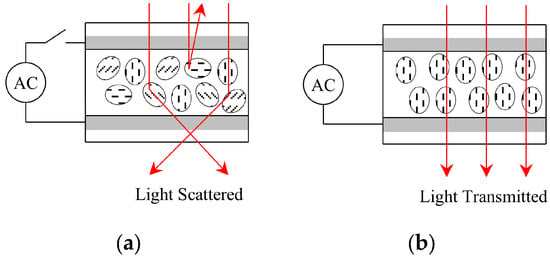
Figure 1.
PDLC basic operation: (a) switched off; (b) switched on.
PDLC films have a wide range of applications, including use as smart windows in buildings [14,15], the car industry [13,14], and as an alternative to blinds in smart homes and commercial buildings to control the illuminance and temperature of the room [16,17]. Additionally, they are studied to address various design requests for car windshields [14]. They are used to achieve energy and cost savings [16,18].
The control of PDLCs has mostly been studied for on/off controls, usually with user input [6,14]. Some have discrete steps in light transmission that are either controlled by a light sensor or through a manual input [19,20]. Others have an adaptive control that varies the voltage step size according to illuminance [16]. In [21,22], discrete light levels were achieved in feedback. Few works discuss the continuous controls required for an optimized light level for plant growth [15], as a constant light level is desired.
This study develops a feedback control scheme for controlling PAR inside a PDLC greenhouse. The scheme uses a PAR sensor positioned underneath the PDLC to measure PAR inside the greenhouse. A custom PAR sensor is constructed and calibrated in greenhouse conditions. A proportional–integral (PI) control law is implemented by a microcontroller and voltage driver to maintain a PAR setpoint. The developed scheme is demonstrated on a mini greenhouse test rig inside a laboratory. The setpoint is changed in software, and a disturbance is applied, with light bulbs illustrating the control scheme’s performance in setpoint tracking and disturbance rejection. A model is presented for the driver–PDLC combination, which predicts transmittance (ratio of light transmitted through the PDLC to that above the PDLC) as a function of driving voltage amplitude. The model comprises a linear dynamic part and a nonlinear static part.
The remainder of this work is as follows. Section 2 details the control scheme, and the experimental test rig. Then, Section 3 presents open-loop system identification and modeling of the driver-PDLC dynamics and static transmittance. Section 3 presents closed-loop disturbance rejection and setpoint tracking results, including simulation and experiment. Finally, Section 4 offers concluding remarks.
2. Materials and Methods
2.1. Control Scheme
The presented control scheme uses a proportional–integral (PI)-type control law to regulate a PDLC device, as shown in Figure 2. The microcontroller implements the PI control law. The error signal E is calculated by taking the difference between the setpoint signal r and feedback from the PAR sensor. The error signal is used by the PI controller to generate a PWM signal to drive the H-Bridge Driver, which powers the PDLC. By adjusting the Voltage signal to the Driver and, therefore, the PAM signal to the PDLC, its transmittance T is adjusted. The transmittance multiplied with the disturbance d, which represents the change in sunlight, forms the light measured by the PAR sensor. Additionally, the measured PAR is shown as the output, which is used for plant growth.
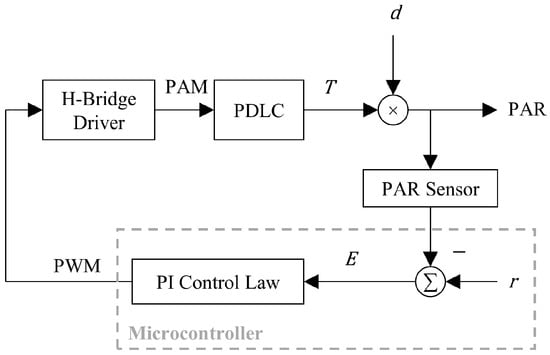
Figure 2.
Block diagram of feedback control of natural light using a PDLC actuator.
The sensor value is continuously compared to the setpoint and used to adjust the PI control value. Thereby, the closed-loop feedback system minimizes the error. Additionally, this continuous control enables the optimization of PDLC performance for maximum plant growth.
Initially, PID was selected. However, in manual tuning, it was noticed the derivative gain was not needed for the slow-moving sun. Also, the derivative gain tended to amplify noise; therefore, Pi control was selected. The control law is given in Equation (1).
Table 1 shows the parameters selected to achieve the desired PDLC performance, where and are proportion and integral gains, respectively. These gains are determined by manual tuning.

Table 1.
Controller gains.
2.2. Novel Control-Oriented Model
The control scheme, as shown in Figure 2, is necessary for the practical implementation of PDLCs. There is currently a lack of modeling of the PDLC as an actuator in this feedback context. That is, the static transmittance of the PDLC is often quantified, and the switching dynamics of the PDLC alone, due to the applied AC voltage, are documented. However, there has been insufficient quantification of the dynamics of the PDLC in conjunction with the driving circuit.
The authors propose the following control-oriented model for controlling natural light utilizing a PDLC actuator in feedback. The model is shown in Figure 3, where G(s) and T(v) represent the PDLC dynamic and static behavior, respectively.
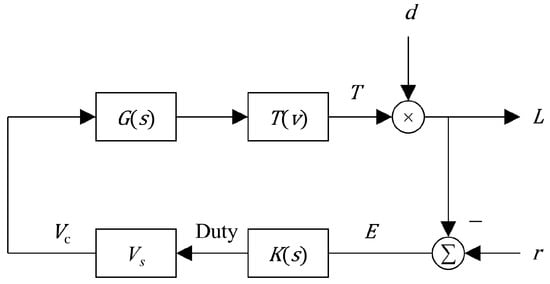
Figure 3.
Model block diagram.
This model is practical for predicting the actual closed-loop behavior of the actuator in the control loop. Some practical issues include the analog control signal from the microcontroller, which is a duty cycle affecting a PWM signal to the H-bridge driver, converting it into a PAM signal for the PDLC. The gain Vs is the supply voltage to the driver, scaling the duty cycle control signal to the voltage seen by the PDLC.
2.3. Test Rig
The conceptual sketch for the experiment is presented in Figure 4, along with a sketch illustrating a practical application example. The practical application is only an example of one possible application. The experiment demonstrating feedback control functionality is performed in the lab with an artificial light source and a parallel data logger.
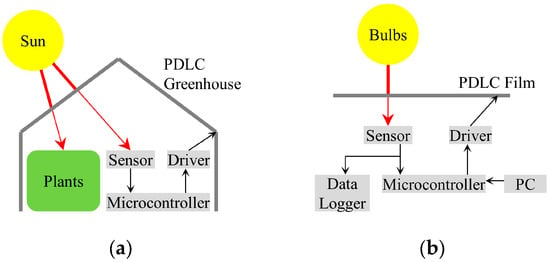
Figure 4.
Conceptual sketches for application of PDLC feedback control and validating experiment: (a) example application concept; (b) control experiment sketch.
The experimental test rig is shown in Figure 5. It includes a PDLC film in an aluminum frame with matte cardboard walls to prevent reflections inside the mini greenhouse. The PAR sensor is inside the mini greenhouse, and its voltage signal is sent to a microcontroller outside the mini greenhouse. The microcontroller is attached to a laptop PC for programming and has a voltage driver shield on top of it. Also shown is a power supply. These components comprise the feedback control scheme.

Figure 5.
Photograph of the overall test rig with PDLC under four light bulbs connected to a driver and a microcontroller.
Figure 5 also shows an array of four light bulb fixtures, approximately 330 mm above the PDLC, to effect light disturbance. The light bulbs used are Great Value brand LED General Purpose, model GVVLA1427ND4, and are 1500 lm at 2700 K (“Soft White”). Furthermore, a Siglent SDS 1104X-E oscilloscope is wired to the PAR sensor in parallel with the control loop and is used for data logging.
2.3.1. Light Sensor
The light sensor is made from a circuit of four photodiodes, distributed 50 mm apart from each other, to measure the average light level underneath the PLDC. The photodiodes comprise an OSRAM model SFH 203 P and have a range of 400 to 1100 nm. This includes the photosynthetically active radiation range (PAR) of 400 to 700 nm. Additionally, the diodes are equipped with a large viewing angle of 150° to gather a median of light.
In sequence with the diodes, two resistors R are used to establish the correct operating point and achieve a proportional response to light intensity. In parallel to the resistors, capacitor C is connected, as shown in Figure 6, to filter out noise and smooth the signal. The resistors have a nominal value of 10 kΩ, and the nominal value of the capacitor is 0.1 μF.
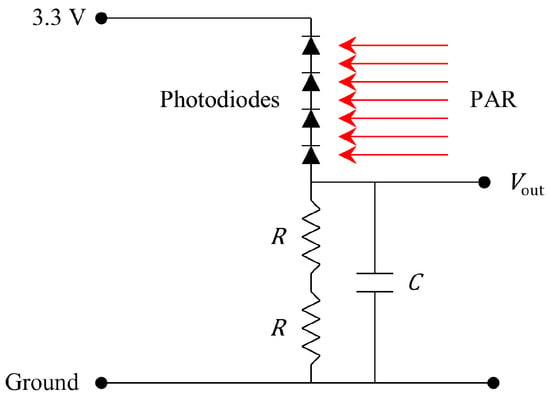
Figure 6.
PAR sensor circuit diagram.
The circuit is supplied with 3.3 V. To measure the light sensed by the photodiodes, the voltage across the resistors is measured. The measured voltage is compared to a PAR light sensor (AccuPAR PAR/LAI Ceptometer Model LP-80) at different light levels ranging from 0 to 300 PAR in natural sunlight. PAR is expressed in the typical unit of μmol·s/m2/s to express the rate of change in photons of hinting an area. As shown in Figure 7, a linear transfer function for the light sensor is obtained for this light range.
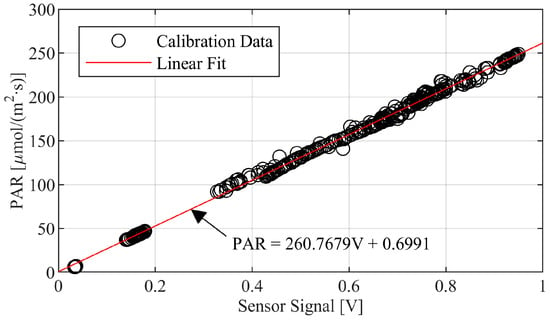
Figure 7.
PAR sensor calibration data and curve fit.
2.3.2. PDLC
The PDLC sample used is manufactured by FILMBASE. It is white and 190 × 270 mm. Two sheets are used. They are layered but wired in parallel. Also, the two sheets are wired in series with a resistor to produce a PWM driving voltage and an equivalent analog voltage. The equivalent PDLC circuit assumed is shown in Figure 8. R1 and C1 are the resistance and capacitance of the two PDLCs; R2 is the added resistance.
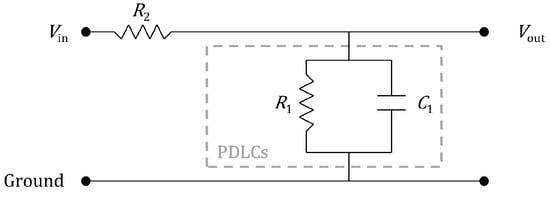
Figure 8.
PDLC circuit diagram.
The equivalent circuit has an electrical transfer function, as shown in (2). The resistance and capacitance of the two PDLC sheets together are measured via a Vici LCR meter model DM4070.
The resulting values are presented in Table 2.

Table 2.
PDLC circuit parameters.
To check that the assumed circuit and corresponding transfer function are a suitable approximation, an experiment is conducted using a Siglent SDG 2082 X waveform generator. The circuit is excited at Vin, and the voltage across the PDLCs Vout is measured using an oscilloscope. The results are shown in Figure 9. The left plot shows experimental input and output, and the right plot shows simulated output using the model in Equation (2).
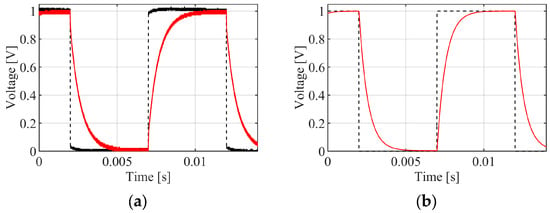
Figure 9.
PDLC circuit step response with the input given in a black dashed line and the output given in solid red: (a) experimental; (b) simulated.
A 0 to 1 V square wave is input at 100 Hz, and an approximate 1st-order transient is observed on the output. Agreement is found between the experimental and simulated results.
Interestingly, at approximately 0.007 s, the experimental result instantly jumps to 0.1 V when the step input is applied. This behavior occurs both upward and downward. This instantaneous jump is not predicted by the assumed circuit model but is deemed negligible for the purposes of the current study.
Next, to demonstrate that the PDLC circuit is sufficient to achieve an approximate analog voltage, a test is conducted in which the signal generator is switched at the same 1 kHz frequency as the shown microcontroller’s PWM, and the voltage across the PDLC film is measured. The results are shown in Figure 10, where the PWM signal is shown as a black dashed line, and the measured voltage is shown as a solid red line.
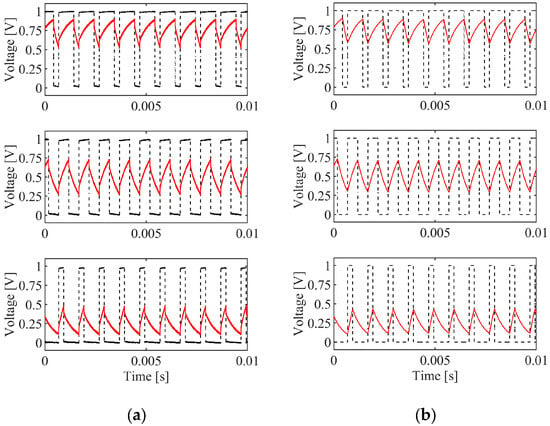
Figure 10.
PWM test for throughput of PDLC circuit at 75% (top), 50% (middle), and 25% (bottom) duty cycles: (a) experimental; (b) simulated.
The figure shows experimental input and output results on the left and simulated results using Equation (2) on the right. The test is performed at three different pulse widths: 25%, 50%, and 75%. The resulting mean voltages are 0.25 V, 0.5 V, and 0.75 V, indicating that an equivalent analog voltage can be assumed for this PDLC circuit with a PWM frequency of 1 kHz. Although additional tuning can be performed to reduce voltage ripple, the authors leave that to future work. Recall that the carrier wave is a 100 Hz alternating polarity PAM square wave.
2.3.3. Control Hardware
The microcontroller used is an Arduino Due, which runs an ARM Cortex-M3 Processor. It has a PWM frequency of 1 kHz. The control law is also evaluated at 1 kHz. However, the PWM is used to achieve a 100 Hz PAM square wave. The voltage driver is a Velleman KA03 power shield, which runs an ST L298P dual full-bridge driver IC. The power supply is Konrad KA3010D, and the supply voltage Vs is set to 30 V.
3. Results
3.1. Open-Loop Identification
The PDLC behavior is identified in situ with the driver and microcontroller used for feedback control. Two open-loop tests are conducted. One is a quasistatic test in which a PWM duty cycle is dictated by the microcontroller, and transients are allowed to die out to measure the transmittance of the PDLC. The other is a dynamic test in which the microcontroller changes the PWM duty cycle, and the resulting PAR transient under the PDLC is recorded.
3.1.1. Quasistatic Transmittance
To identify the correlation between PWM Equivalent Voltage and the transmittance of the PDLC, 11 different levels are measured, as shown in Figure 11. The levels are conducted by increasing the voltage from 0 V to 30 V in 10%-duty cycle increments. Recall that the PAR measured under the PDLC L is assumed to be the product of the transmittance T and the PAR measured with no PDLC present d, as shown in Figure 2.
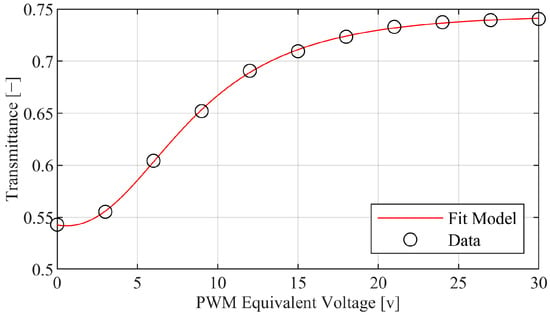
Figure 11.
Quasistatic PDLC transmittance for varying PWM levels.
A second-order biquadratic function is assumed for the obtained quasistatic data, as shown in Equation (3).
Recall that this model is used in the overall dynamic PDLC model shown in Figure 3, which will be used in the simulations in Section 3.2. Using the MATLAB Optimization Toolbox, the parameters shown in Table 3 are derived to achieve the desired performance of the system and align closely with the experimental results.

Table 3.
Fit PDLC static gain parameters.
The units of the coefficient are consistent with Equation (3), where is the equivalent voltage. The coefficient of determination is 0.99.
3.1.2. Dynamic Step Response
To characterize the dynamic behavior of the PDLC, a step response analysis is conducted from a 20% to 30% PWM duty cycle for a step up, and from a 30% to 20% duty cycle for a step down. The time needed to reach the new steady state is inspected, as are any oscillations or overshoots that occur during this process. PAR under the PDLC is recorded and normalized, as shown in Figure 12. The data are normalized so the fit transfer function captures the time dynamics, whereas the overall gain is accounted for by Equation (3). This distinction is what makes the proposed model useful for simulating PDLC in feedback control systems. Both directions are explored to make sure the correct time constant is captured.
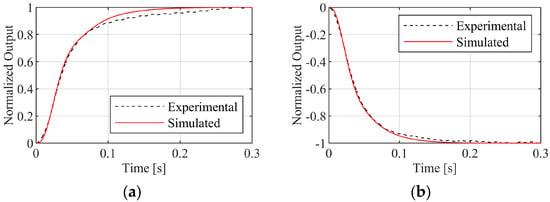
Figure 12.
Open-loop driver–PDLC step response from PWM equivalent voltage input to measured PAR output: (a) step up; (b) step down.
A third-order transfer function is assumed for both upward and downward transients, as shown in Equation (4).
The data are fit via the MATLAB R2022a System Identification Toolbox, resulting in the parameters shown in Table 4.

Table 4.
Fit PDLC transfer function parameters.
Simulations with the fit transfer function are also shown in Figure 12 and agree well with the presented data. The simulation is performed using MATLAB lsim. By utilizing both static and dynamic transfer functions, the PDLC characteristic is precisely modeled.
3.2. Closed-Loop Tests
Finally, closed-loop tests are performed with the manually tuned PI controller. These include disturbance rejection and set point tracking tests. Also, simulations are conducted in MATLAB Simulink via the ode45 variable step solver. The tests and simulations validate the proposed model shown in Figure 3.
3.2.1. Disturbance Rejection
For the upward disturbance test, three light bulbs were initially switched on, and the system was allowed to reach a steady state. At one second, a fourth light bulb was turned on. This corresponds to the input signal d increasing from 30.0 to 37.3 μmol/(m2∙s). The setpoint is maintained at 21.5 μmol/(m2∙s). The results are shown in Figure 13.
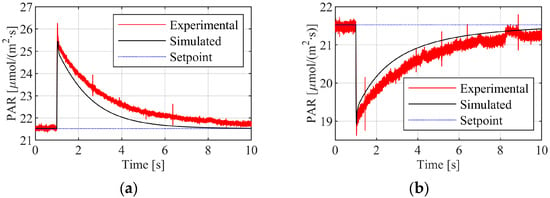
Figure 13.
Closed-loop disturbance rejection test from light disturbance input to measured PAR output: (a) up; (b) down.
At one second, there is an abrupt jump in PAR. Its direction depends on the direction of the disturbance. The amplitude of the jump is limited by the fast dynamics of the proportional gain. Then, over about nine seconds, the integral gain compensates to eliminate steady-state error. These results demonstrate the ability of the feedback control scheme to reject disturbances. Also, the simulation shows agreement with the data using all nominal values and PDLC fit models as previously described. Slight discrepancies may occur due to losses in the driver board, resulting in a lower effective supply voltage.
3.2.2. Setpoint Tracking
Next, a setpoint tracking test is performed. All four light bulbs are turned on. Then, the PAR setpoint is switched between 23.65 μmol/(m2∙s) and 25.80 μmol/(m2∙s) for one second. The resulting time history for PAR under the PDLC is shown in Figure 14.
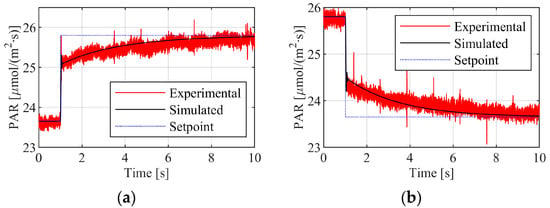
Figure 14.
Closed-loop setpoint tracking test from setpoint PAR input to measured PAR output: (a) up; (b) down.
The results show an immediate jump in PAR due to the proportional gain, which accounts for approximately one-third of the transient. Then, a slow ramping up of the integrator eliminates the remainder of the error over approximately nine seconds. These results show the ability of the feedback control scheme to track a PAR setpoint change. Also, simulation results are shown in Figure 14, which is in agreement with the data, confirming that the system model is a suitable approximation.
4. Discussion, Conclusions, and Future Work
This study develops a novel method for modeling PDLC films as actuators in the context of feedback control. The developed technique can be used to design systems to control the amount of PAR in a greenhouse using a PDLC film. In particular, a model for the driver–PDLC combination is presented, including a linear and dynamic part and a nonlinear and static part. The method was demonstrated in a laboratory setting by performing disturbance rejection and setpoint tracking experiments on a fully detailed test rig with a PI control law. The novel model is used for numerical simulations of the closed loop, demonstrating agreement with the experiments. This model can be used in the future for the optimization of hardware and controller settings through trial and error of the simulation. Eventually, it could also be used for model-based control.
The significance of the developed technique is that it offers the agricultural industry a more energy-efficient way to achieve optimum germination and growth PAR levels at all growth stages (compared to artificial lighting). This can enable higher profits for operators and lower costs for consumers. Also, its control ability is more consistent than passive methods due to the ability to reject disturbances. This can lead to improvement in overall product quality. The developed actuator can also serve as a valuable tool for botanists studying germination and growth.
Future work will involve using the developed test rig as a mini greenhouse placed inside a full-scale greenhouse to demonstrate the efficacy of the control actuation in situ, perhaps for an etiolation study. Then, a full-scale prototype greenhouse can be built, with all sides of the exterior glass coated with PDLC film. This strategy is inherently scalable as the PDLC functions on the induced electric field, allowing the device to draw minimal current. Therefore, a larger-area PDLC can be effectively controlled using the same sensor, microcontroller, and driver combination.
Author Contributions
A.H.P. and C.V. contributed equally to this paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
The authors would like to sincerely thank Ian Renne for many conversations and for sharing his deep insights in the area of botany. The authors would also like to thank J.T. Chesnes for helpful discussions on driver circuits.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| PAM | Pulse Amplitude Modulation |
| PAR | Photosynthetically Active Radiation |
| PDLC | Polymer-dispersed liquid crystal |
| PI | Proportional–integral |
| PWM | Pulse Width Modulation |
References
- Narvaez, F.Y.; Reina, G.; Torres-Torriti, M.; Kantor, G.; Cheein, F.A. A Survey of Ranging and Imaging Technologies for Precisio Agriculture Phenotyping. IEEE ASME Trans. Mech. 2017, 22, 2428–2439. [Google Scholar] [CrossRef]
- Li, T.; Yang, Q. Advantages of Diffuse Light for Horticultural Production and Perspectives for Further Research. Front. Plant Sci. 2015, 6, 704. [Google Scholar]
- Afzali, S.; Mosharafian, S.; van Iersel, M.W.; Velni, J.M. Development and Implementation of an IoT-Enabled Optimal and Predictive Lighting Control Strategy in Greenhouses. Plants 2021, 10, 2652. [Google Scholar] [CrossRef] [PubMed]
- Timmermans, G.H. Advanced Optical Materials for Light Control: On the Road towards Smart Greenhouses. Ph.D. Thesis, Technical University of Eindhoven, Eindhoven, The Netherlands, 6 April 2021. [Google Scholar]
- Hu, C.; Ma, D.; Hassan, M.; Hu, W. NLC: Natural Light Communication using Switchable Glass. In Proceedings of the IEEE INFOCOM 2020—IEEE Conference on Computer Communications Workshop, Toronto, ON, Canada, 6–9 July 2020. [Google Scholar]
- Uranus, H.P. Characterization and Driving of Polymer-dispersed Liquid-crystal Sheet for Smarthome Applications. In Proceedings of the 13th International Symposium on Modern Optics and Its Applications, Tangerang, Indonesia, 2–4 August 2021. [Google Scholar]
- Zhang, R.; Zhang, Z.; Han, J.; Yang, L.; Ii, J.; Song, Z.; Wang, T.; Zhu, J. Advanced Liquid Crystal-based Switchable Optical Devices for Light Protection Applications: Principles and Strategies. Light Sci. Appl. 2023, 12, 11. [Google Scholar] [PubMed]
- Abdulmohsin, H.; Aritra, G.; Senthilarasu, S.; Tapas, K.M. Evaluation of Thermal Performance for a Smart Switchable Adaptive Polymer Dispersed Liquid Crystal (PDLC) Glazing. Sol. Energy 2020, 195, 185–193. [Google Scholar]
- Marinov, Y.G.; Hadjichristov, G.B.; Petrov, A.G. Single-layered Microscale Linear-gradient PDLC Material for Electro-optics. Cryst. Res. Technol. 2009, 44, 870–878. [Google Scholar]
- Körner, W.; Scheller, H.; Beck, A.; Fricke, J. PDLC Films for Control of Light Transmission. J. Phys. D App. Phys. 1994, 27, 2145–2151. [Google Scholar]
- Ghosh, A.; Hafnaoui, R.; Mesloub, A.; Elkhayat, K.; Albaqawy, G.; Alnaim, M.M.; Mayhoub, M.S. Active Smart Switchable Glazing for Smart City: A Review. J. Build. Eng. 2024, 84, 108644. [Google Scholar]
- Jain, A.K.; Deshmukh, R.R. An Overview of Polymer-dispersed Liquid Crystal Composite Films and Their Applications. In Liquid Crystals and Display Technology; Ghamsar, M.S., Carlescu, I., Eds.; IntechOpen: London, UK, 2020; pp. 11–78. [Google Scholar]
- Prabakaran, B. Attaining Thermal Comfort by Utilizing Polymer Dispersed Liquid Crystal Embedded Wind Shield and Roof of a Passenger Car; SAE Technical Paper No. 2021-28-0151; SAE International Warrendale: Pittsburgh, PA, USA, 2021. [Google Scholar]
- Islam, M.S.; Chan, K.; Azmi, A.S.; Pang, W.; Wong, S. Internet of Things-enabled Smart Controller for Polymer Dispersed Liquid Crystal Films. Int. J. Electron. Comput. Eng. 2023, 13, 4708–4720. [Google Scholar]
- Jabbar, J.J.; Zaki, S.M. Smart-glass Glazing using Arduino and Android Application. Int. J. Interact. Mob. Technol. 2021, 15, 54–65. [Google Scholar] [CrossRef]
- Wang, N.; Wang, A.; Zhang, C.; Shan, H.S.; Jia, H.Z.; Zheng, J.H.; Liu, Y.R.; Zuo, L. Self-adaptive PDLC Control Strategy with Smart Light Intensity Adjustment using Photovoltaic-thermoelectric Hybrid Energy Supply Technology. IEEE Trans. Ind. Electron. 2022, 70, 10146–10155. [Google Scholar] [CrossRef]
- Stelzmann, M.; Zahner, F.; Navarro de Sosa, I.; Nemati, A.; Kahnt, A.; Maaß, B.; Drossel, W.-G. Development of a Self-Regulating Solar Shading Actuator Based on the Thermal Shape Memory Effect. Actuators 2024, 13, 85. [Google Scholar] [CrossRef]
- Gadgil, C.; Ghosh, A.; Bhattacharjee, A.; Praveen, P.L. Electrically Powered Active Smart Windows. Next Sustain. 2024, 3, 100027. [Google Scholar] [CrossRef]
- Lami, M.; Al-naemi, F.; Issa, W. Automated Quantification System for Vision through Polymer-dispersed Liquid Crystal Double-glazed Windows: Circuit Implementation. IET Circuits Devices Syst. 2022, 17, 38–52. [Google Scholar] [CrossRef]
- Chu, Y.; Miao, Z.; Wang, D. Stepwise Driving and Multi-transparency of Polymer Dispersed Liquid Crystals. Liq. Cryst. 2022, 50, 222–230. [Google Scholar]
- Sanchez-Pena, J.M.; Vazquez, C.; Perez, I.; Rodriguez, I.; Oton, M. Electro-optic System for Online Light Transmission Control of Polymer-dispersed Liquid Crystal Windows. Opt. Eng. 2002, 41, 1608–1611. [Google Scholar]
- Alghamdi, H.; Almawgani, A.H.M. Smart and Efficient Energy Saving System using PDLC Glass. In Proceedings of the 2019 Smart City Symposium, Prague, Czech Republic, 23–24 May 2019. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).