Adaptive Nonlinear Friction Compensation for Pneumatically Driven Follower in Force-Projecting Bilateral Control
Abstract
1. Introduction
1.1. Research Background
1.2. Related Works
1.3. Research Design
1.3.1. Objective
- (A1)
- Since the leader is operated by a human operator, it has a high design flexibility and can be driven by an electric motor or equipped with a force sensor.
- (A2)
- Depending on the application, the follower is mechanically or electromagnetically exposed to harsh working environments or requires high flexibility and ease of operation. It is difficult to mount a force sensor on the follower due to its small size and working environment. Thus, a pneumatic manipulator with high back-drivability is suitable for the follower device.
1.3.2. Contributions and Novelty
1.3.3. Organization of This Paper
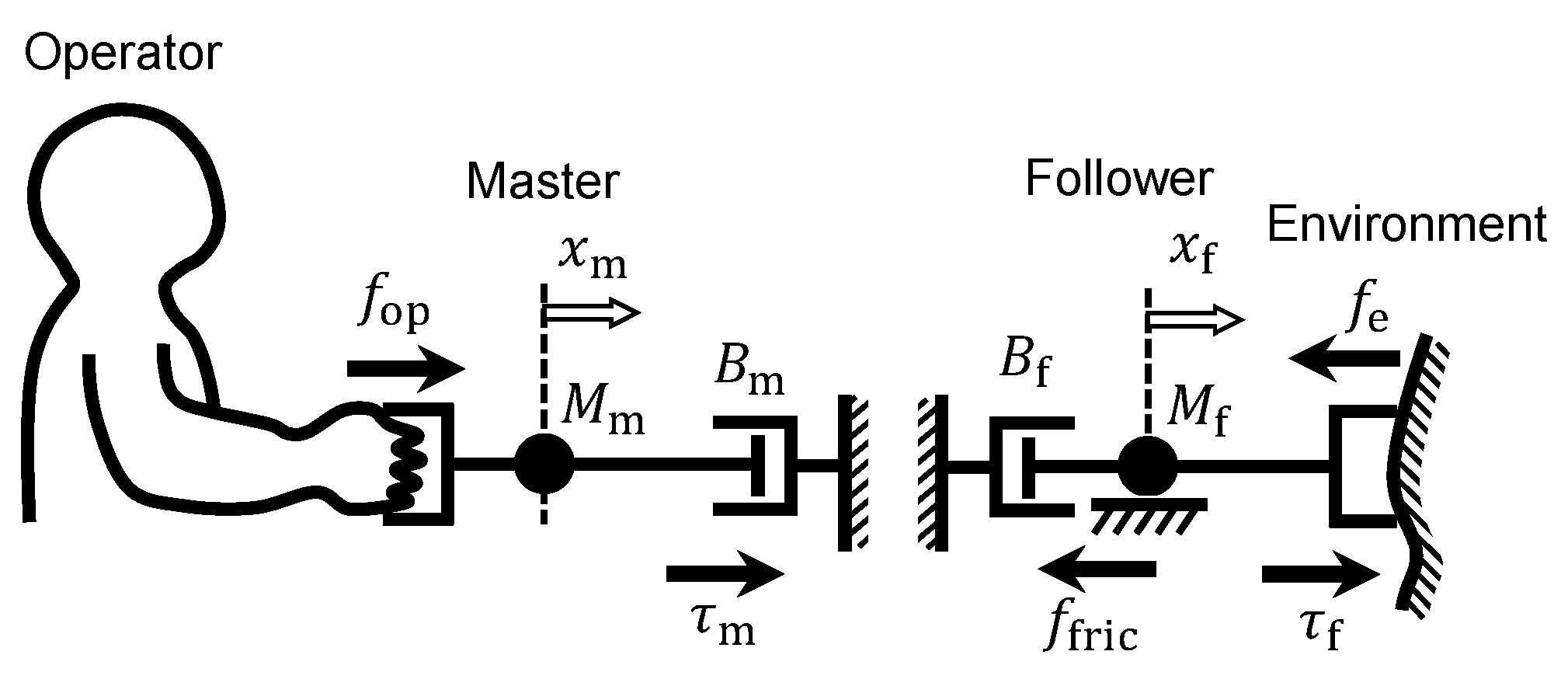
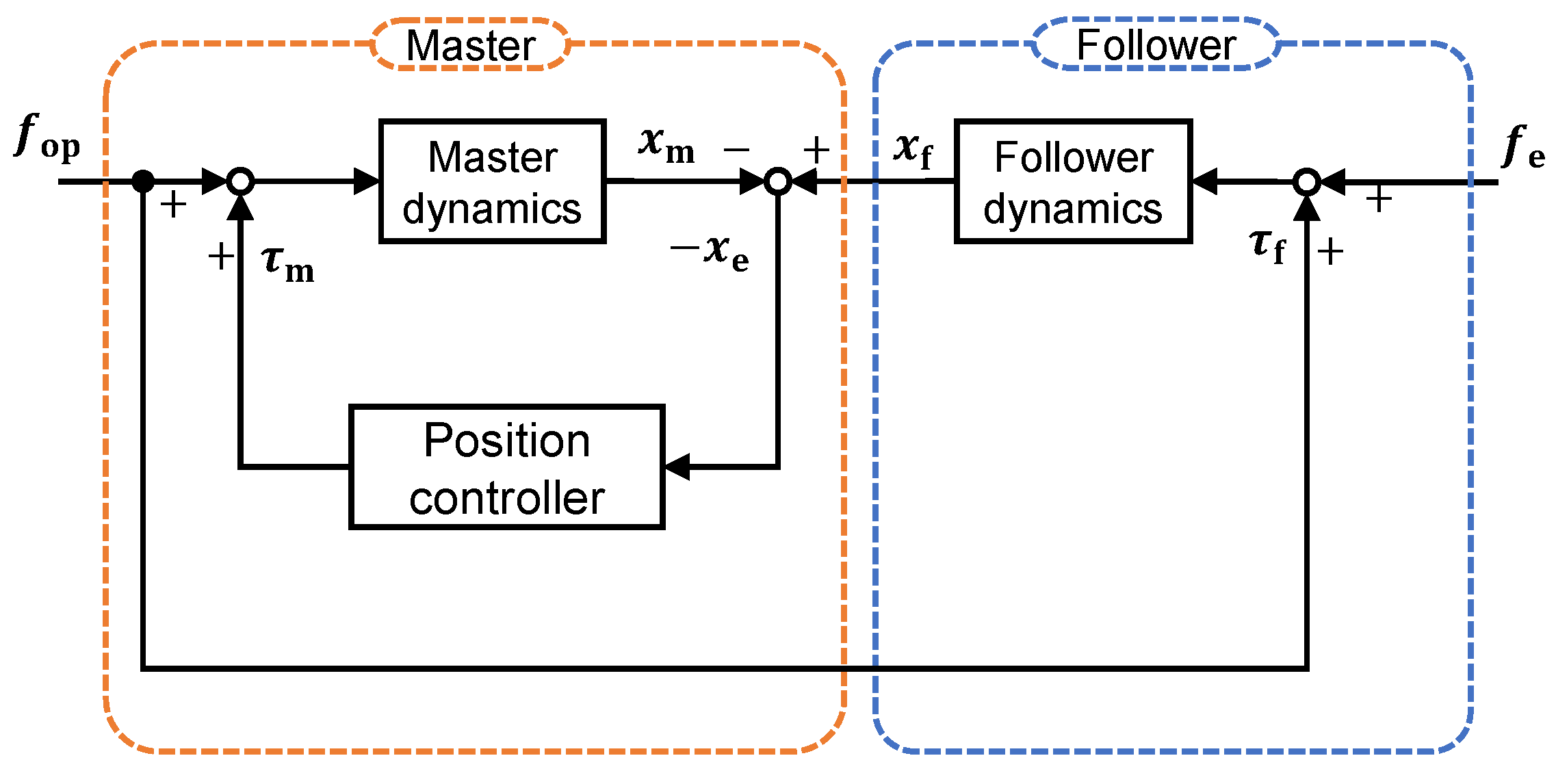
2. System Modeling
3. Proposal of Adaptive Nonlinear Friction Compensation Method
3.1. Concept
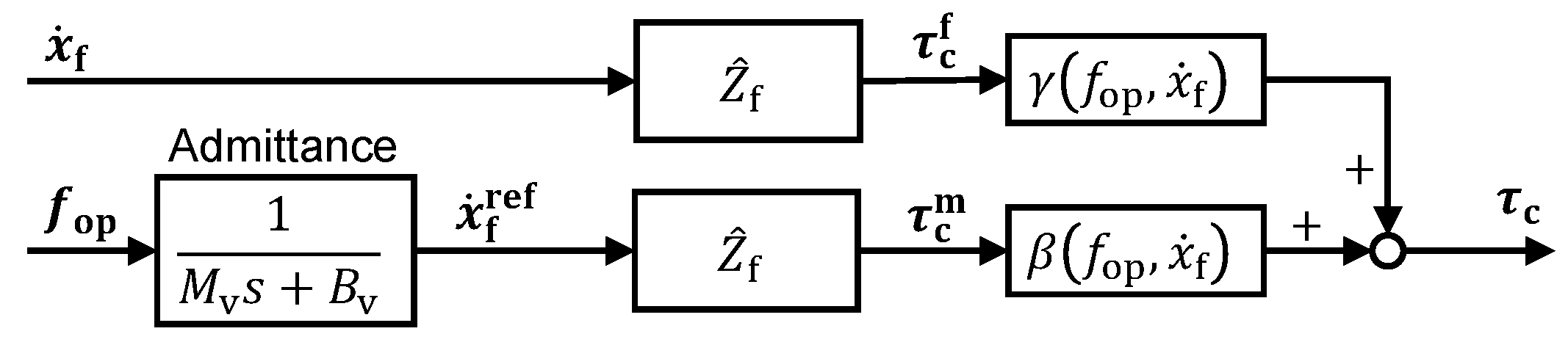
3.2. Scheme of Adaptive Nonlinear Friction Compensation
3.3. Setting the Mixing Ratio Parameters
- (a)
- Stationary state. ,
- (b)
- Moving in response to the operational force ,
- (c)
- Being pushed in the direction opposite to the operational force due to the environmental reaction force .
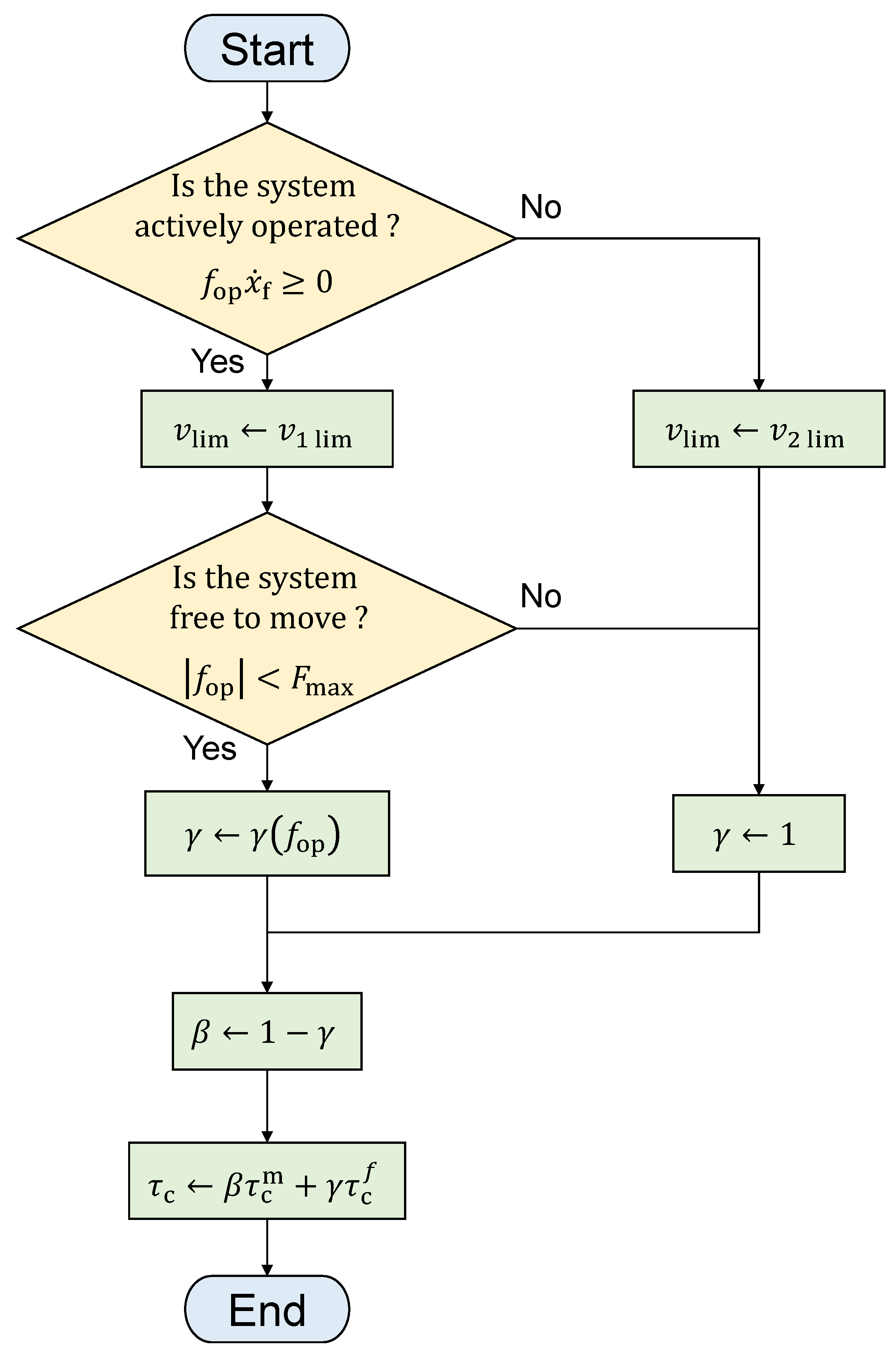
3.4. Algorithm Implementation
4. Experimental System Implementation
4.1. Hardware Configuration
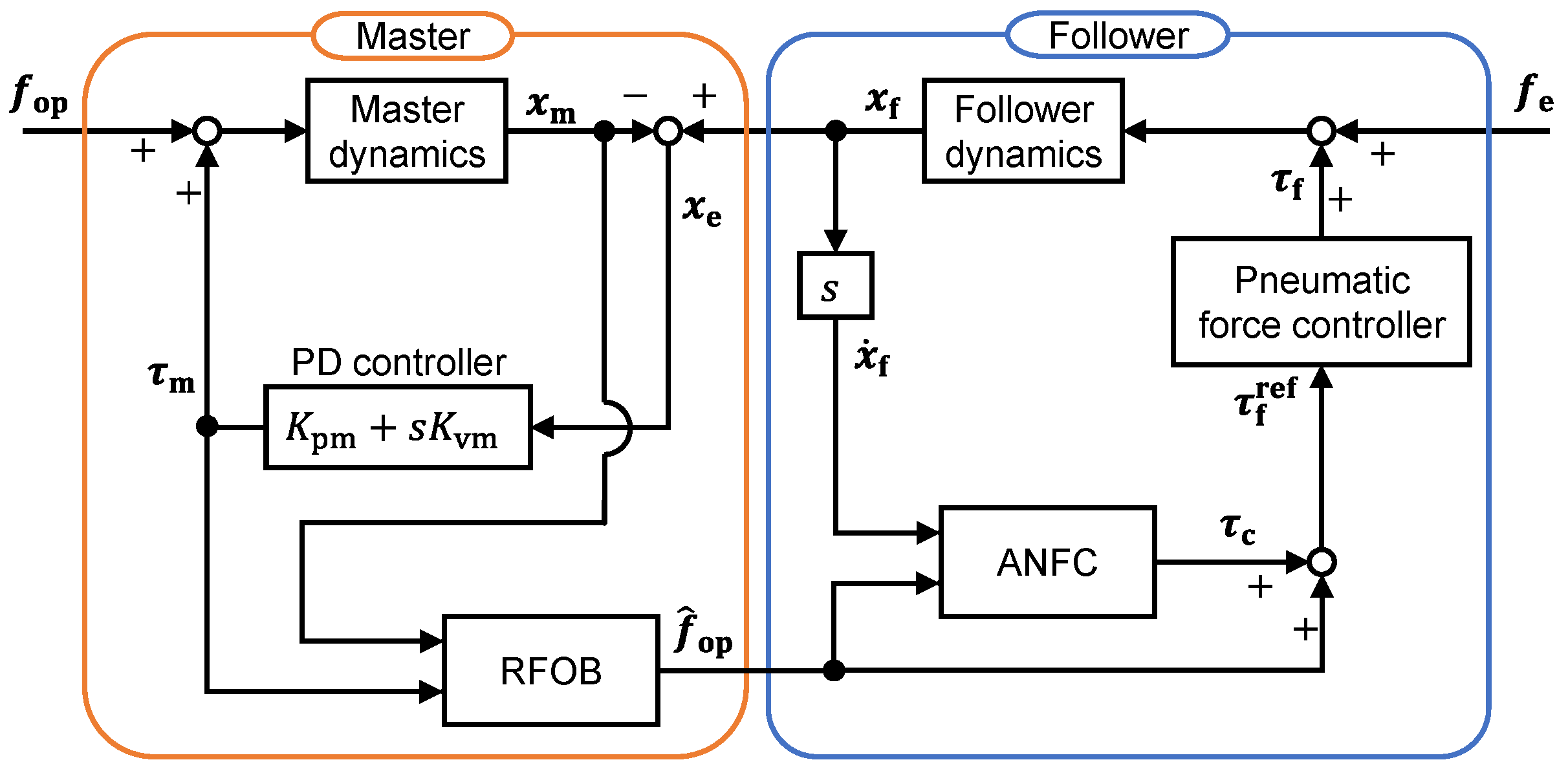
4.2. Design of the Bilateral Control System
5. Bilateral Control Experiment
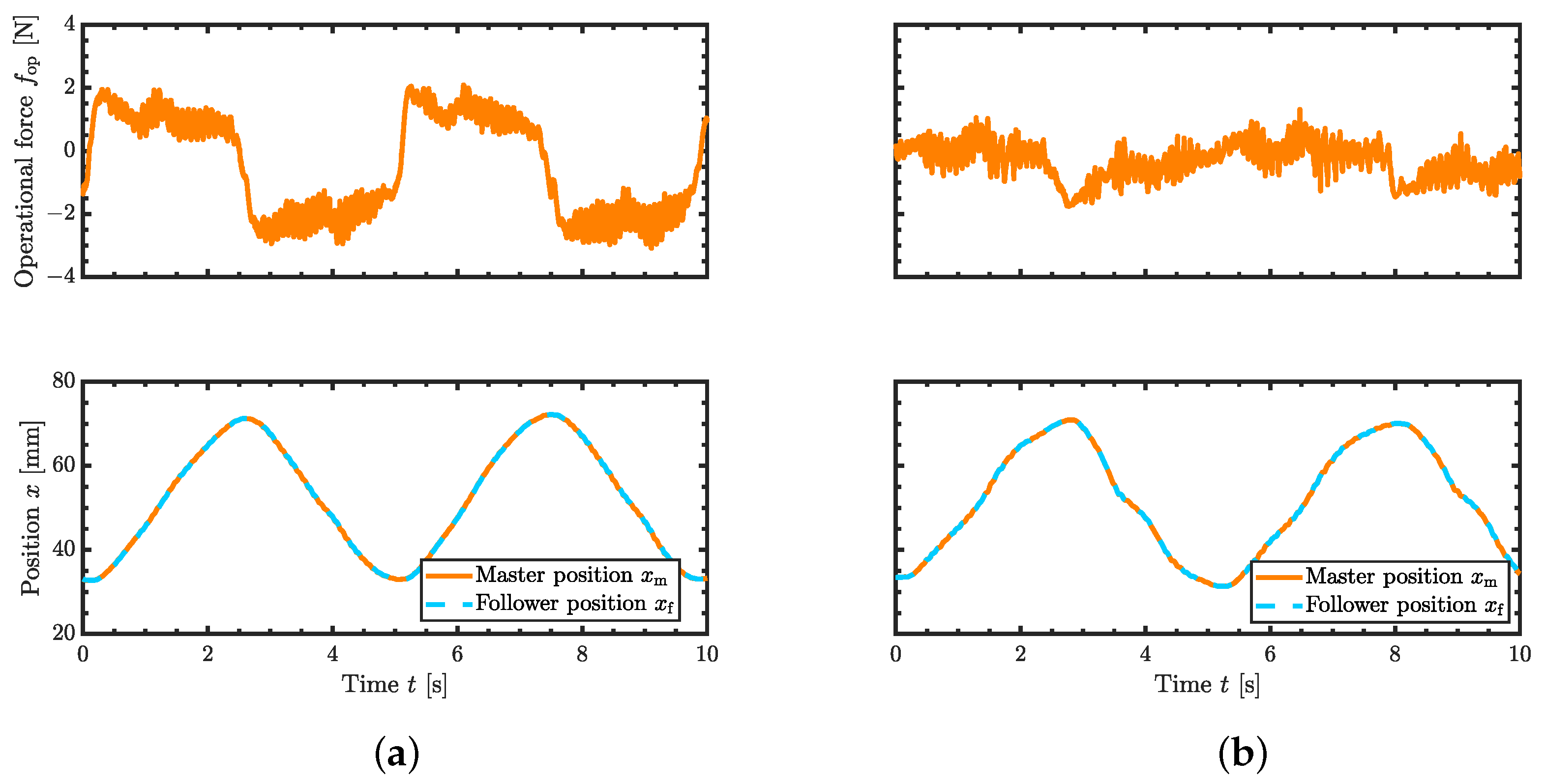
5.1. Operational Performance in No-Load Condition
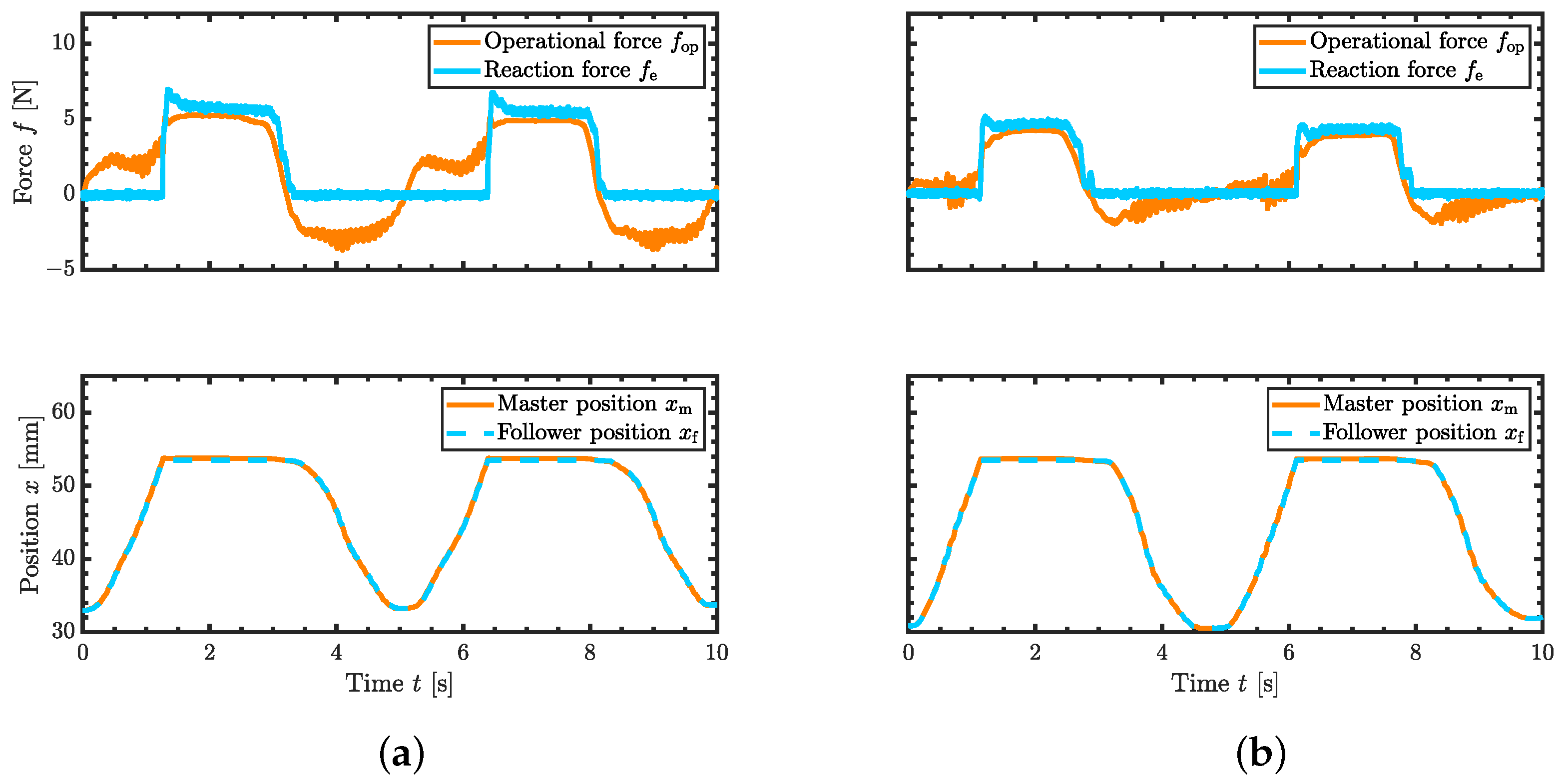
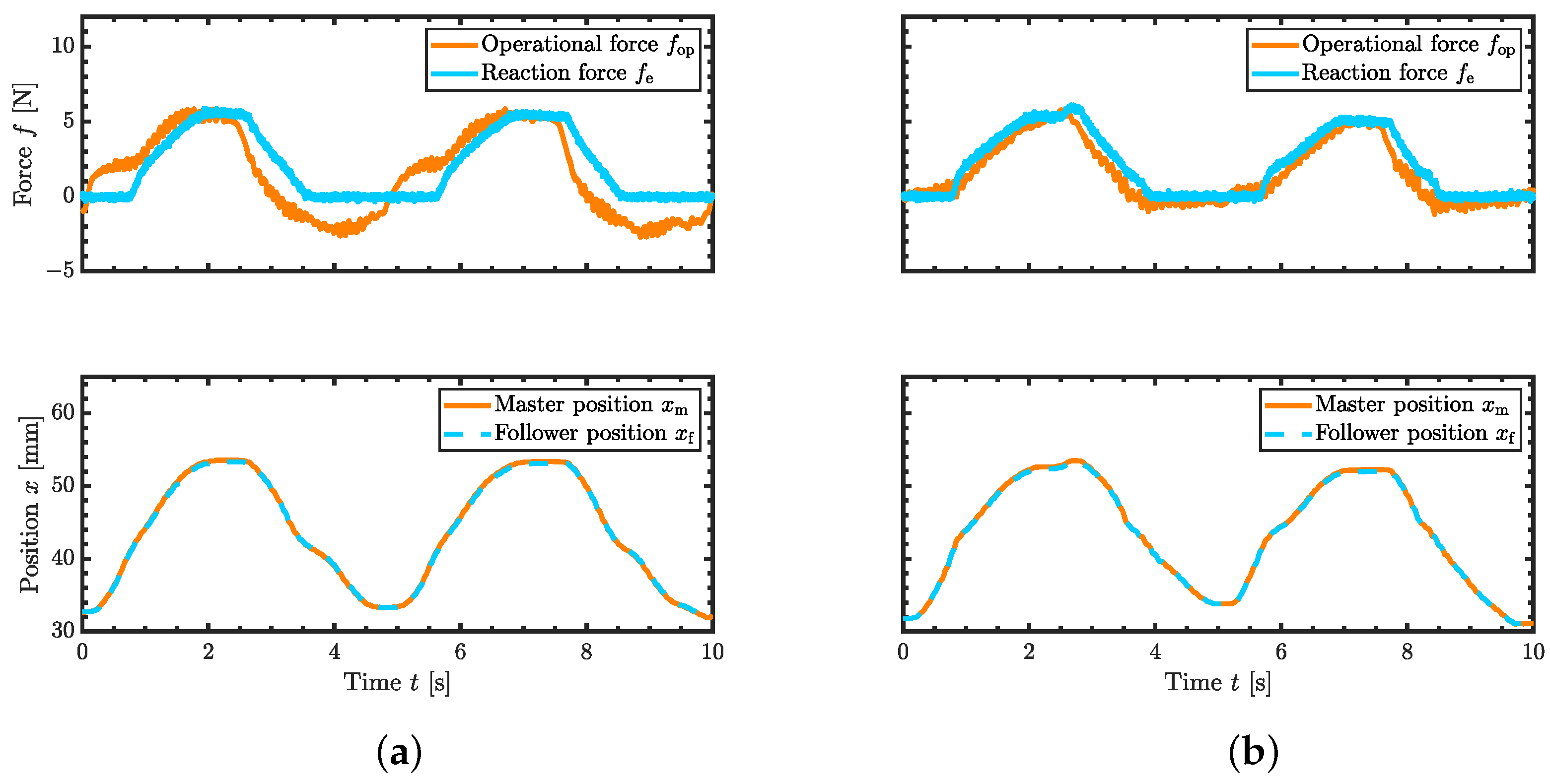
5.2. Control Response in Contact with Environment
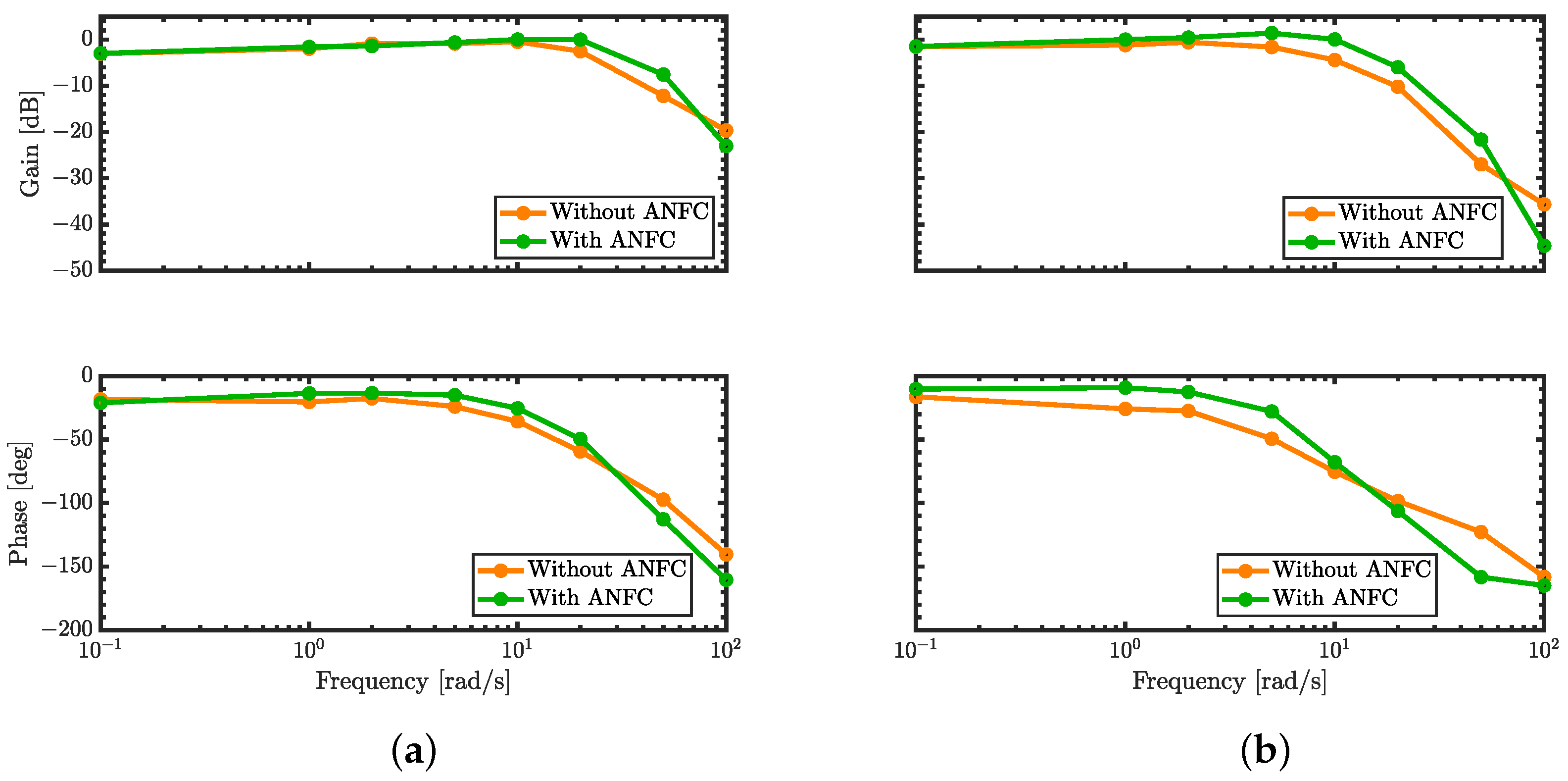
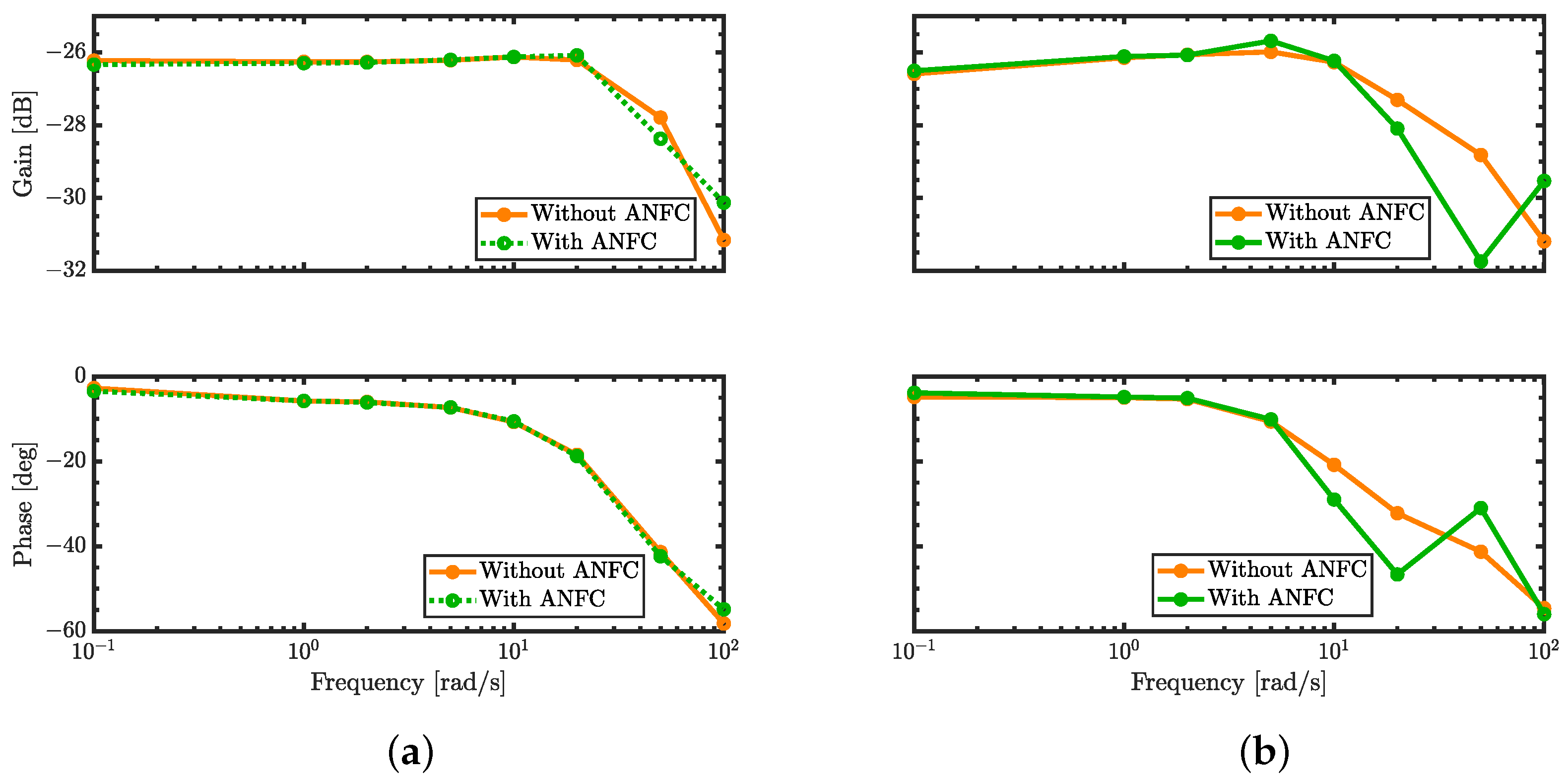
5.3. Frequency Response
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tadano, K.; Kawashima, K. Development of a Master Slave Manipulator with Force Display Using Pneumatic Servo System for Laparoscopic Surgery. Int. J. Assist. Robot. Syst. 2007, 8, 6–13. [Google Scholar]
- Tadano, K.; Kawashima, K. Development of a Master Slave System with Force Sensing Using Pneumatic Servo System for Laparoscopic Surgery. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Rome, Italy, 10–14 April 2007; pp. 947–952. [Google Scholar]
- Kanno, T.; Haraguchi, D.; Yamamoto, M.; Tadano, K.; Kawashima, K. A Forceps Manipulator with Flexible 4-DOF Mechanism for Laparoscopic Surgery. IEEE/ASME Trans. Mechatron. 2015, 20, 1170–1178. [Google Scholar] [CrossRef]
- Haraguchi, D.; Kanno, T.; Tadano, K.; Kawashima, K. A Pneumatically Driven Surgical Manipulator With a Flexible Distal Joint Capable of Force Sensing. IEEE/ASME Trans. Mechatron. 2015, 20, 2950–2961. [Google Scholar] [CrossRef]
- Kawashima, K.; Sasaki, T.; Miyata, T.; Nakamura, N.; Sekiguchi, M.; Kagawa, T. Development of Robot Using Pneumatic Artificial Rubber Muscles to Operate Construction Machinery. J. Robot. Mechatron. 2004, 16, 8–16. [Google Scholar] [CrossRef]
- Sasaki, T.; Kawashima, K. Remote control of backhoe at construction site with a pneumatic robot system. Autom. Constr. 2008, 17, 907–914. [Google Scholar] [CrossRef]
- Anderson, R.J.; Spong, M.W. Bilateral control of teleoperators with time delay. In Proceedings of the 1988 IEEE International Conference on Systems, Man, and Cybernetics, Beijing, China, 8–12 August 1988; Volume 1, pp. 131–138. [Google Scholar]
- Imaida, T.; Yokokohji, Y.; Doi, T.; Oda, M.; Yoshikawa, T. Ground–Space Bilateral Teleoperation of ETS-VII Robot Arm by Direct Bilateral Coupling Under 7-s Time Delay Condition. IEEE Trans. Robot. Autom. 2004, 20, 499–511. [Google Scholar] [CrossRef]
- Kim, W.S.; Hannaford, B.; Fejczy, A.K. Force-reflection and shared compliant control in operating telemanipulators with time delay. IEEE Trans. Robot. Autom. 1992, 8, 176–185. [Google Scholar] [CrossRef]
- Polushin, I.G.; Liu, P.X.; Lung, C.H. A Force-Reflection Algorithm for Improved Transparency in Bilateral Teleoperation With Communication Delay. IEEE/ASME Trans. Mechatron. 2007, 12, 361–374. [Google Scholar] [CrossRef]
- Lee, D.; Spong, M.W. Passive Bilateral Teleoperation With Constant Time Delay. IEEE Trans. Robot. 2006, 22, 269–281. [Google Scholar] [CrossRef]
- Kostyukova, O.; Vista, F.P.; Chong, K.T. Design of feedforward and feedback position control for passive bilateral teleoperation with delays. ISA Trans. 2019, 85, 200–213. [Google Scholar] [CrossRef]
- Yokokohji, Y.; Hosotani, N.; Yoshikawa, T. Analysis of maneuverability and stability of micro-teleoperation systems. In Proceedings of the 1994 IEEE International Conference on Robotics and Automation, San Diego, CA, USA, 8–13 May 1994; Volume 1, pp. 237–243. [Google Scholar]
- Yokokohji, Y.; Yoshikawa, T. Bilateral control of master-slave manipulators for ideal kinesthetic coupling-formulation and experiment. IEEE Trans. Robot. Autom. 1994, 10, 605–620. [Google Scholar] [CrossRef]
- Komada, S.; Ohnishi, K. Control of robotic manipulators by joint acceleration controller. In Proceedings of the 15th Annual Conference of IEEE Industrial Electronics Society, Philadelphia, PA, USA, 6–10 November 1989; Volume 3, pp. 623–628. [Google Scholar]
- Iida, W.; Ohnishi, K. Reproducibility and operationality in bilateral teleoperation. In Proceedings of the 8th IEEE International Workshop on Advanced Motion Control, 2004, AMC ’04, Kawasaki, Japan, 28 March 2004; pp. 217–222. [Google Scholar]
- Katsura, S.; Matsumoto, Y.; Ohnishi, K. Modeling of Force Sensing and Validation of Disturbance Observer for Force Control. IEEE Trans. Ind. Electron. 2007, 54, 530–538. [Google Scholar] [CrossRef]
- Murakami, T.; Yu, F.; Ohnishi, K. Torque sensorless control in multidegree-of-freedom manipulator. IEEE Trans. Ind. Electron. 1993, 40, 259–265. [Google Scholar] [CrossRef]
- Chen, Z.; Huang, F.; Yang, C.; Yao, B. Adaptive Fuzzy Backstepping Control for Stable Nonlinear Bilateral Teleoperation Manipulators With Enhanced Transparency Performance. IEEE Trans. Ind. Electron. 2020, 67, 746–756. [Google Scholar] [CrossRef]
- Chen, Z.; Huang, F.; Sun, W.; Gu, J.; Yao, B. RBF-Neural-Network-Based Adaptive Robust Control for Nonlinear Bilateral Teleoperation Manipulators With Uncertainty and Time Delay. IEEE/ASME Trans. Mechatron. 2020, 25, 906–918. [Google Scholar] [CrossRef]
- Batty, T.; Ehrampoosh, A.; Shirinzadeh, B.; Zhong, Y.; Smith, J. A Transparent Teleoperated Robotic Surgical System with Predictive Haptic Feedback and Force Modelling. Sensors 2022, 22, 9770. [Google Scholar] [CrossRef]
- Kikuuwe, R.; Kanaoka, K.; Kumon, T.; Yamamoto, M. Phase-Lead Stabilization of Force-Projecting Master-Slave Systems With a New Sliding Mode Filter. IEEE Trans. Control. Syst. Technol. 2015, 23, 2182–2194. [Google Scholar] [CrossRef]
- Monden, R.; Kanno, T.; Haraguchi, D. Analytical Evaluation of Force-Projecting Bilateral Control for Pneumatic Manipulators. IFAC-PapersOnLine 2023, 56, 9998–10003. [Google Scholar] [CrossRef]
- Haraguchi, D.; Monden, R. Fundamental Study on Force-Projecting Bilateral Control for Pneumatically Driven Follower Device. Actuators 2024, 13, 56. [Google Scholar] [CrossRef]
- Haraguchi, D.; Monden, R. Teleoperation of Pneumatic Manipulators using Force-Projecting Bilateral Control. Dyn. Des. Conf. 2023, A33. [Google Scholar] [CrossRef]
- Monden, Y.; Haraguchi, D. Sensorless Haptic Force Presentation using Force-Projecting Bilateral Control with Pneumatic Manipulator. In Proceedings of the 2024 IEEE 18th International Conference on Advanced Motion Control (AMC), Kyoto, Japan, 28 February–1 March 2024; pp. 1–6. [Google Scholar]
- Chen, W.H.; Ballance, D.J.; Gawthrop, P.J.; O’Reilly, J. A nonlinear disturbance observer for robotic manipulators. IEEE Trans. Ind. Electron. 2000, 47, 932–938. [Google Scholar] [CrossRef]
- Chen, W.H. Disturbance observer based control for nonlinear systems. IEEE/ASME Trans. Mechatron. 2004, 9, 706–710. [Google Scholar] [CrossRef]
- Iwasaki, M.; Shibata, T.; Matsui, N. Disturbance-observer-based nonlinear friction compensation in table drive system. IEEE/ASME Trans. Mechatron. 1999, 4, 3–8. [Google Scholar] [CrossRef]
- Wan, M.; Dai, J.; Zhang, W.H.; Xiao, Q.B.; Qin, X.B. Adaptive feed-forward friction compensation through developing an asymmetrical dynamic friction model. Mech. Mach. Theory 2022, 170, 104691. [Google Scholar] [CrossRef]
- Zhang, W.; Li, M.; Gao, Y.; Chen, Y.Q. Periodic adaptive learning control of PMSM servo system with LuGre model-based friction compensation. Mech. Mach. Theory 2022, 167, 104561. [Google Scholar] [CrossRef]
- Zhang, W.; Cao, B.; Nan, N.; Li, M.; Chen, Y.Q. An adaptive PID-type sliding mode learning compensation of torque ripple in PMSM position servo systems towards energy efficiency. ISA Trans. 2021, 110, 258–270. [Google Scholar] [CrossRef]
- Dai, K.; Zhu, Z.; Shen, G.; Tang, Y.; Li, X.; Wang, W.; Wang, Q. Adaptive force tracking control of electrohydraulic systems with low load using the modified LuGre friction model. Control. Eng. Pract. 2022, 125, 105213. [Google Scholar] [CrossRef]
- Zhang, B.; Wu, J.; Wang, L.; Yu, Z. Accurate dynamic modeling and control parameters design of an industrial hybrid spray-painting robot. Robot.Comput. Integr. Manuf. 2020, 63, 101923. [Google Scholar] [CrossRef]
- Chen, Y.; Ding, J.; Chen, Y.; Yan, D. Nonlinear Robust Adaptive Control of Universal Manipulators Based on Desired Trajectory. Appl. Sci. 2024, 14, 2219. [Google Scholar] [CrossRef]
- Li, A.; Qin, D. Adaptive model predictive control of dual clutch transmission shift based on dynamic friction coefficient estimation. Mech. Mach. Theory 2022, 173, 104804. [Google Scholar] [CrossRef]
- Schindele, D.; Aschemann, H. Adaptive friction compensation based on the LuGre model for a pneumatic rodless cylinder. In Proceedings of the 2009 35th Annual Conference of IEEE Industrial Electronics, Porto, Portugal, 3–5 November 2009; pp. 1432–1437. [Google Scholar]
- Liu, S.; Wang, L.; Wang, X.V. Sensorless force estimation for industrial robots using disturbance observer and neural learning of friction approximation. Robot. Comput. Integr. Manuf. 2021, 71, 102168. [Google Scholar] [CrossRef]
- Xiao, J.; Dou, S.; Zhao, W.; Liu, H. Sensorless Human-Robot Collaborative Assembly Considering Load and Friction Compensation. IEEE Robot. Autom. Lett. 2021, 6, 5945–5952. [Google Scholar] [CrossRef]
- Phuong, T.T.; Ohishi, K.; Yokokura, Y.; Miyasaki, T. Deep Learning Based Force-Sensor-Like Reaction Force Observer for Realization of Intelligent Force Sensing. In Proceedings of the 2024 IEEE 18th International Conference on Advanced Motion Control (AMC), Kyoto, Japan, 28 February–1 March 2024; pp. 1–6. [Google Scholar]
- Lawrence, D.A. Stability and transparency in bilateral teleoperation. IEEE Trans. Robot. Autom. 1993, 9, 624–637. [Google Scholar] [CrossRef]
- Fathollahi, A.; Andresen, B. Adaptive Fixed-Time Control Strategy of Generator Excitation and Thyristor-Controlled Series Capacitor in Multi-Machine Energy Systems. IEEE Access 2024, 12, 100316–100327. [Google Scholar] [CrossRef]
- Gheisarnejad, M.; Fathollahi, A.; Sharifzadeh, M.; Laurendeau, E.; Al-Haddad, K. Data-Driven Switching Control Technique Based on Deep Reinforcement Learning for Packed E-Cell as Smart EV Charger. IEEE Trans. Transp. Electrif. 2025, 11, 3194–3203. [Google Scholar] [CrossRef]


| Description | Symbol | Unit |
|---|---|---|
| First-order derivative | ||
| Second-order derivative | ||
| Estimated value | ||
| Reference value | ||
| Time | t | [s] |
| Leader position | [mm] | |
| Follower position | [mm] | |
| Position error between leader and follower | [mm] | |
| Leader driving force | [N] | |
| Follower driving force | [N] | |
| Operational force at leader | [N] | |
| Environmental reaction force at follower | [N] | |
| Nonlinear friction force of follower | [N] | |
| Mass of leader | [kg] | |
| Mass of follower | [kg] | |
| Viscous coefficient of leader | [Ns/mm] | |
| Viscous coefficient of follower | [Ns/mm] | |
| Coulomb friction force | [N] |
| Description | Symbol | Value | Unit |
|---|---|---|---|
| Smoothing range | 5.0 | [mm/s] | |
| Smoothing range | 0.20 | [mm/s] | |
| Estimated viscous coefficient of follower | 0.030 | [Ns/mm] | |
| Estimated maximum static friction force of follower | 1.0 | [N] | |
| Virtual mass | 0.10 | [kg] | |
| Virtual viscosity | 0.050 | [Ns/mm] | |
| Dynamics compensation force | Variable | [N] | |
| Compensation force derived from reference velocity | Variable | [N] | |
| Compensation force derived from current velocity | Variable | [N] | |
| Mixing ratio of | Variable | [–] | |
| Mixing ratio of | Variable | [–] |
| Leader | Linear motor | Maker | GMC Hillstone Co., Ltd., Yamagata, Japan |
| Model | s160Q | ||
| Stroke | 100 mm | ||
| Rated thrust | 20 N | ||
| Mass of moving part | 0.676 kg | ||
| Linear encoder | Maker | Technohands Co., Ltd., Kanagawa, Japan | |
| Model | TAi-200 | ||
| Position resolution | 1.0 m | ||
| Follower | Air cylinder | Maker | SMC Corp., Tokyo, Japan |
| Model | CJ2XE16-100Z | ||
| Bore | 16 mm | ||
| Stroke | 100 mm | ||
| Actuation type | Double acting | ||
| Mass of moving part | 0.125 kg | ||
| Linear encoder | Maker | Technohands Co., Ltd., Kanagawa, Japan | |
| Model | TAi-200 | ||
| Position resolution | 1.0 m |
| Description | Symbol | Value | Unit |
|---|---|---|---|
| Leader position gain | 20.0 | [N/mm] | |
| Leader velocity gain | [Ns/mm] | ||
| Mass of the leader | 0.676 | [kg] |
| Without ANFC | With ANFC | ||
|---|---|---|---|
| Force | RMSE [N] | 1.81 | 0.83 |
| NRMSE | 0.25 | 0.16 | |
| Standard deviation [N] | 1.73 | 0.71 | |
| Max error [N] | 3.92 | 2.41 | |
| Position | RMSE [mm] | 0.17 | 0.13 |
| NRMSE | 0.022 | 0.025 | |
| Standard deviation [mm] | 0.16 | 0.12 | |
| Max error [mm] | 0.37 | 0.26 |
| Without ANFC | With ANFC | ||
|---|---|---|---|
| Force | RMSE [N] | 1.62 | 0.73 |
| NRMSE | 0.21 | 0.13 | |
| Standard deviation [N] | 1.53 | 0.55 | |
| Max error [N] | 2.84 | 1.28 | |
| Position | RMSE [mm] | 0.18 | 0.13 |
| NRMSE | 0.023 | 0.022 | |
| Standard deviation [mm] | 0.16 | 0.10 | |
| Max error [mm] | 0.38 | 0.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haraguchi, D.; Monden, Y. Adaptive Nonlinear Friction Compensation for Pneumatically Driven Follower in Force-Projecting Bilateral Control. Actuators 2025, 14, 151. https://doi.org/10.3390/act14030151
Haraguchi D, Monden Y. Adaptive Nonlinear Friction Compensation for Pneumatically Driven Follower in Force-Projecting Bilateral Control. Actuators. 2025; 14(3):151. https://doi.org/10.3390/act14030151
Chicago/Turabian StyleHaraguchi, Daisuke, and Yuki Monden. 2025. "Adaptive Nonlinear Friction Compensation for Pneumatically Driven Follower in Force-Projecting Bilateral Control" Actuators 14, no. 3: 151. https://doi.org/10.3390/act14030151
APA StyleHaraguchi, D., & Monden, Y. (2025). Adaptive Nonlinear Friction Compensation for Pneumatically Driven Follower in Force-Projecting Bilateral Control. Actuators, 14(3), 151. https://doi.org/10.3390/act14030151






