Comparative Study on Active Suspension Controllers with Parameter Adaptive and Static Output Feedback Control
Abstract
1. Introduction
- SOFC is designed by the LQ cost function and state-space model and by SBOM with the quarter-car model with nonlinear elements in order to reduce the heave acceleration of the SPM. These two types of SOFC are compared through simulation
- PAC is designed by RLS and EKF in order to make the suspension force be zero.
- By comparing the simulation results, it is shown that PAC is equivalent to or better than SOFCs. More specifically, the structures of SOFCs and PAC are identical to each other, and the performances of those controllers are equivalent to each other.
2. Design of Active Suspension Controllers
2.1. Vehicle Model
2.2. Design of Static Output Feedback Controller
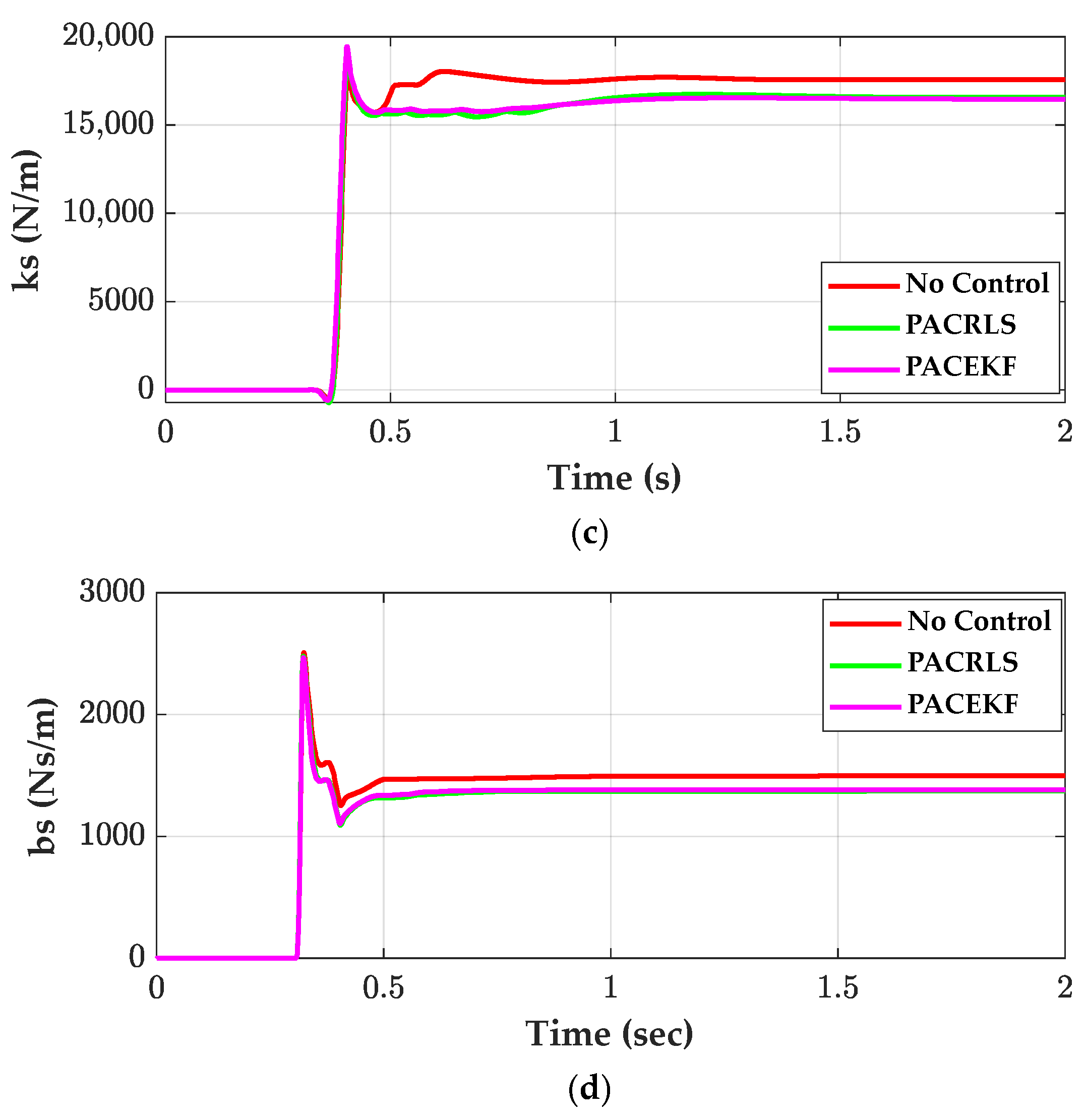
2.3. Design of Parameter Adaptive Controller
3. Simulation and Discussion
3.1. Simulation Environment
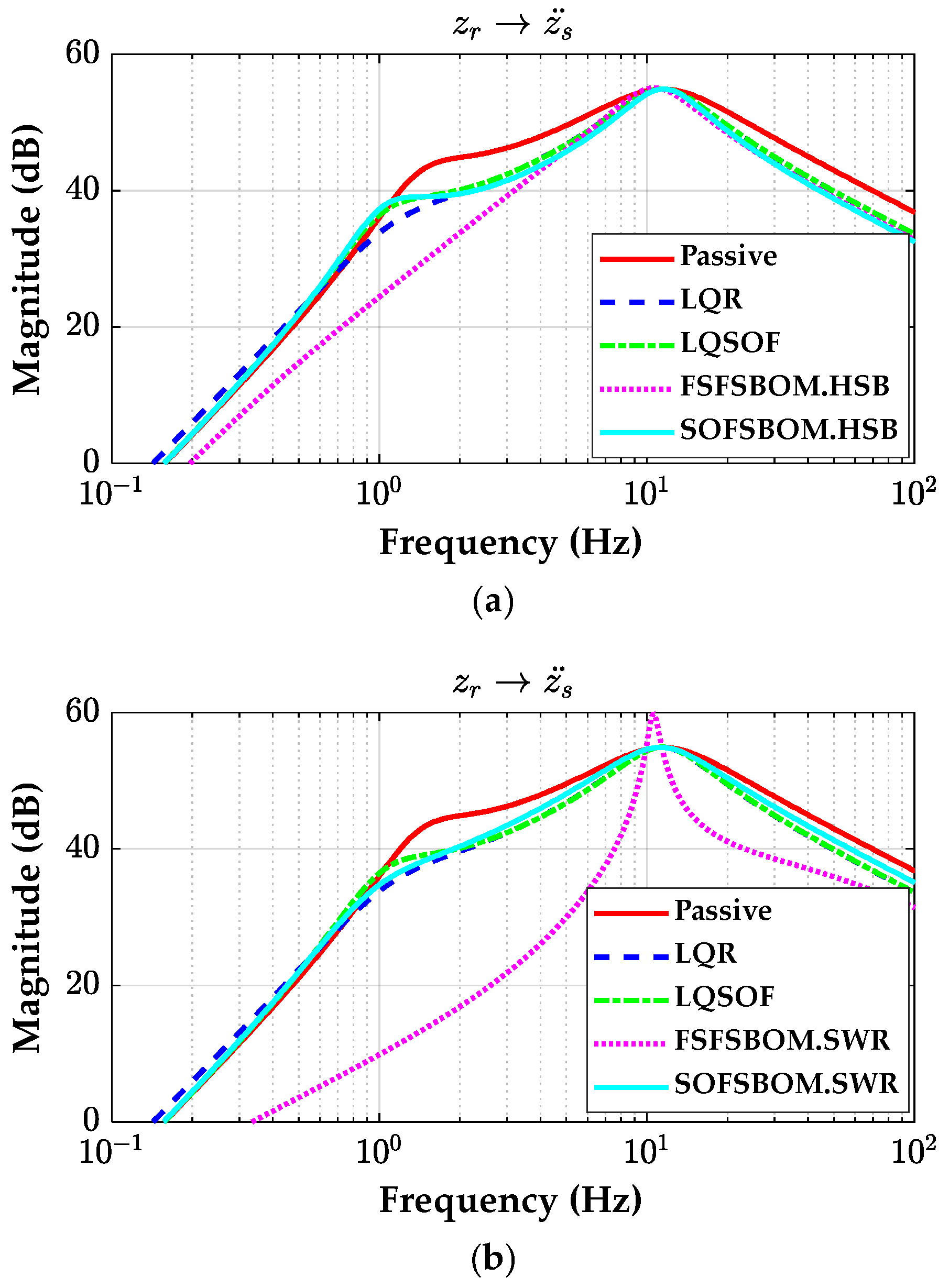
3.2. Frequency Response Analysis with the Designed Controllers
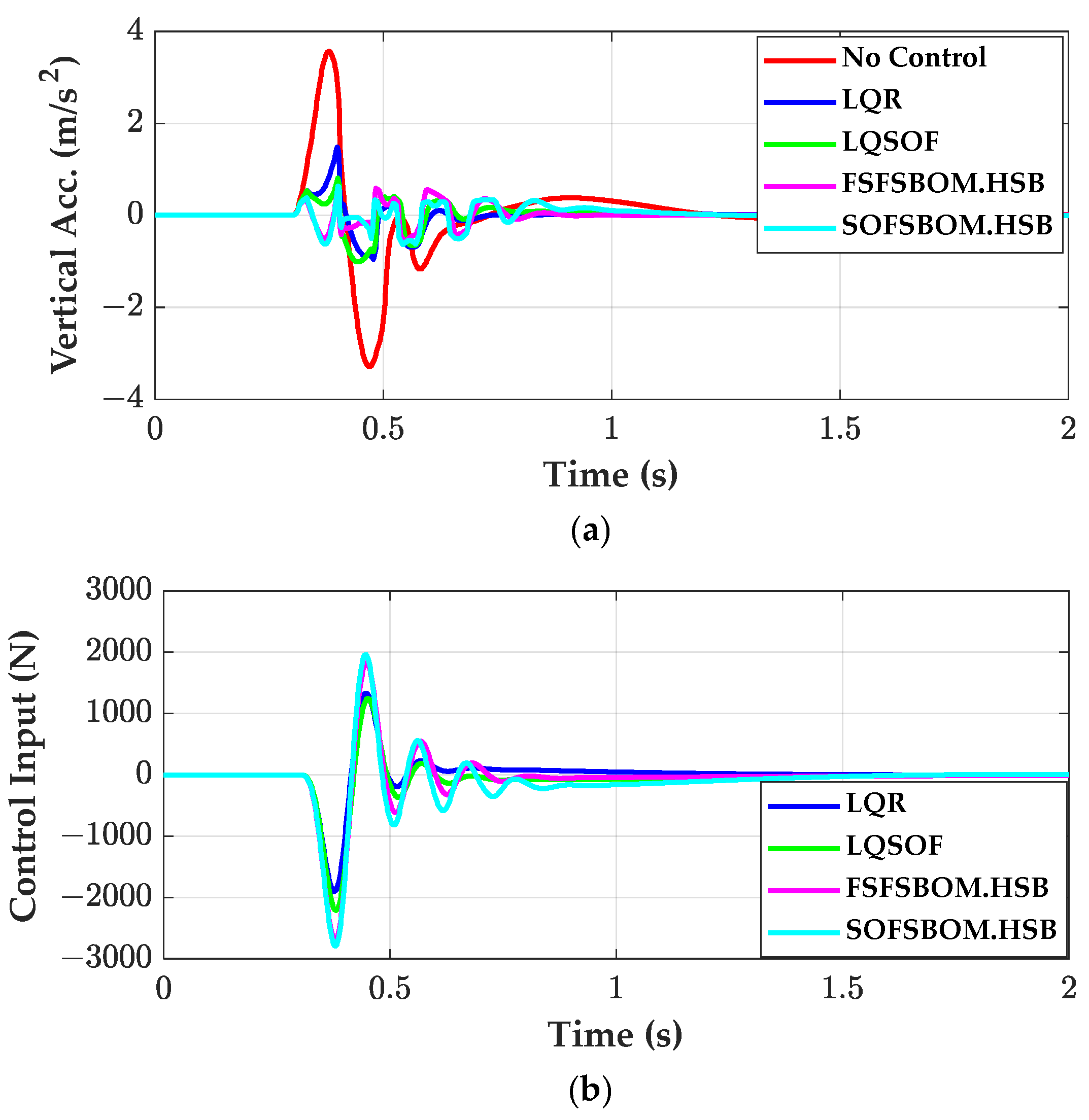
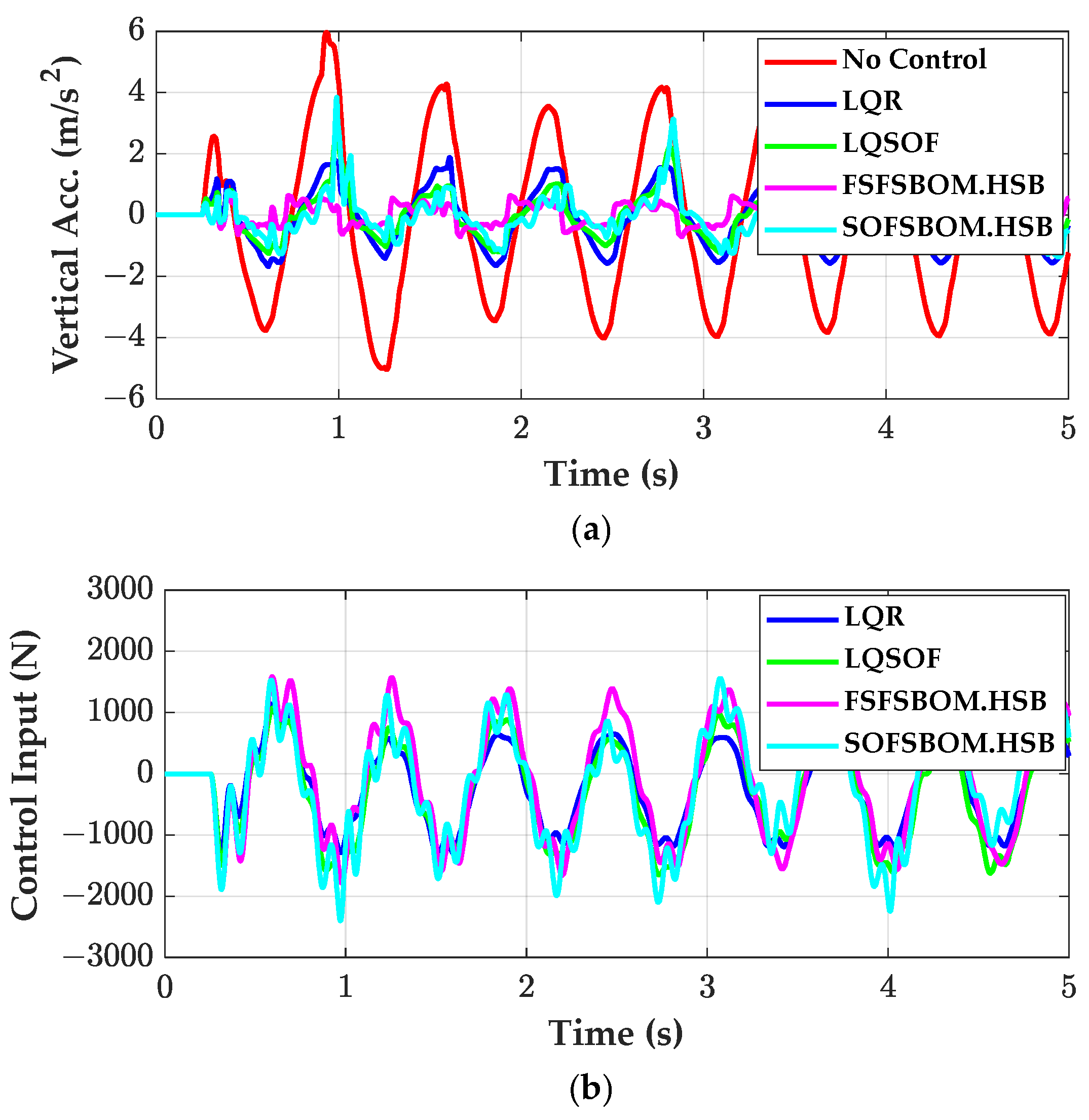
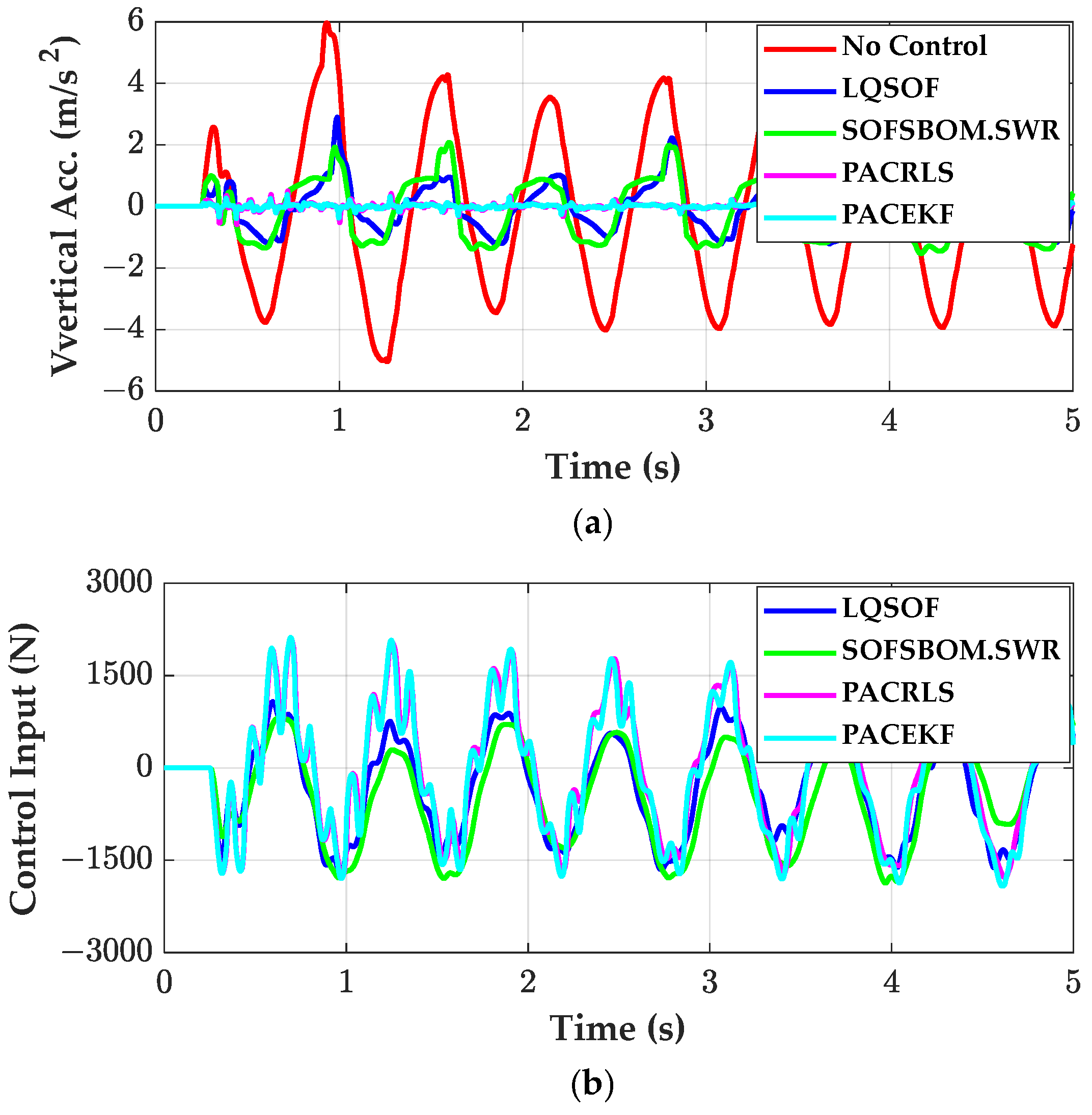
3.3. Simulation on Half-Sine Bump and Sine-Waved Road
4. Conclusions
- The SOF controllers designed with SBOM and PAC have identical control structure and show equivalent performance to each other in terms of ride comfort.
- FSFSBOM designed on the half-sine bump outperforms the other SOF controllers.
- PACRLS and PACEKF show equivalent performance to the SOF controllers on the half-sine bump in terms of ride comfort. On the other hand, PAC outperforms the other SOF controllers under periodic disturbances such as the sine-waved road.
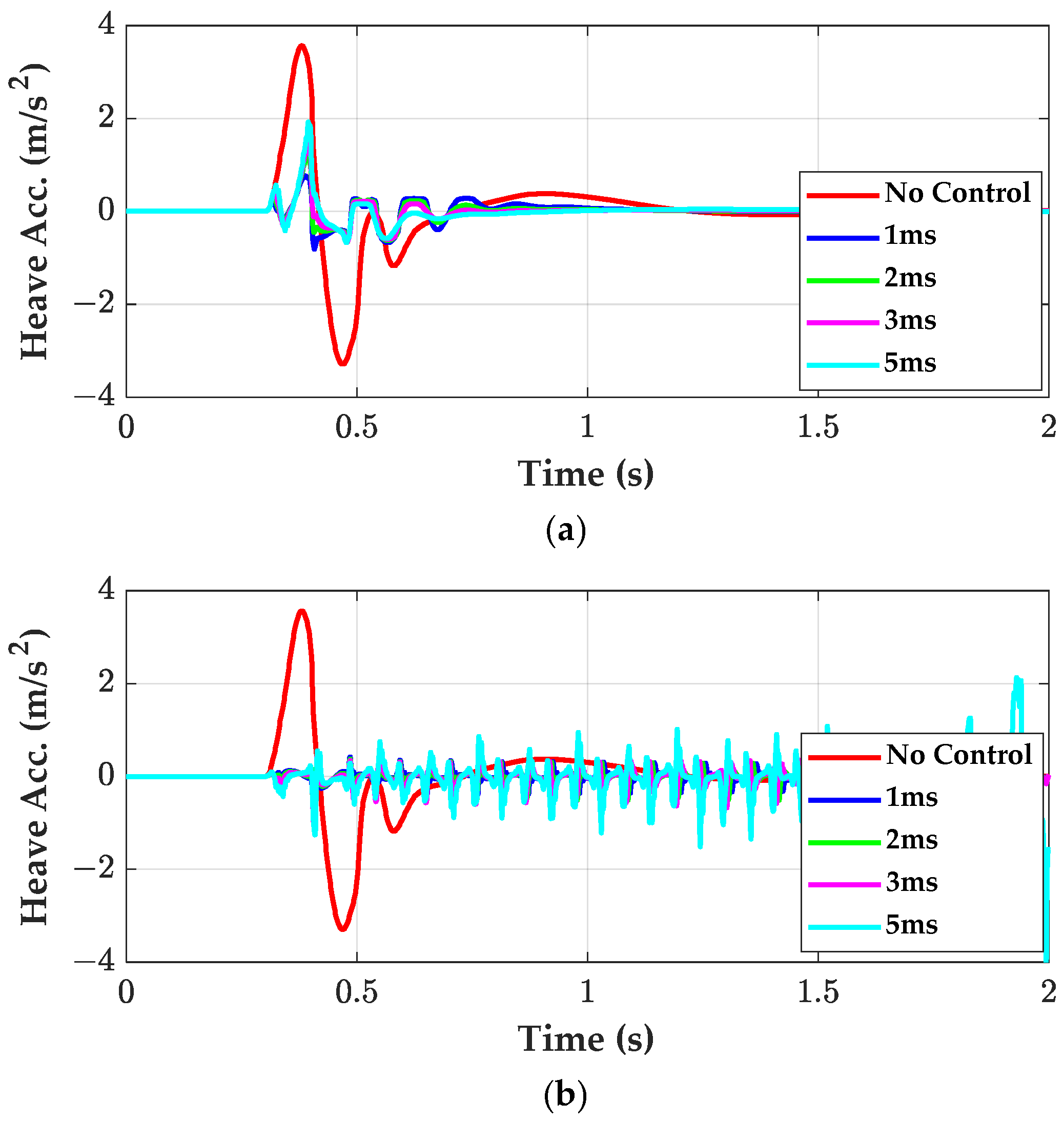
- The sampling period and the actuator bandwidth of PACs play a critical role in controlling the active suspension. For desired performance, the sampling period of PAC should be less than 5 ms and actuator bandwidth should be larger than 50 Hz.
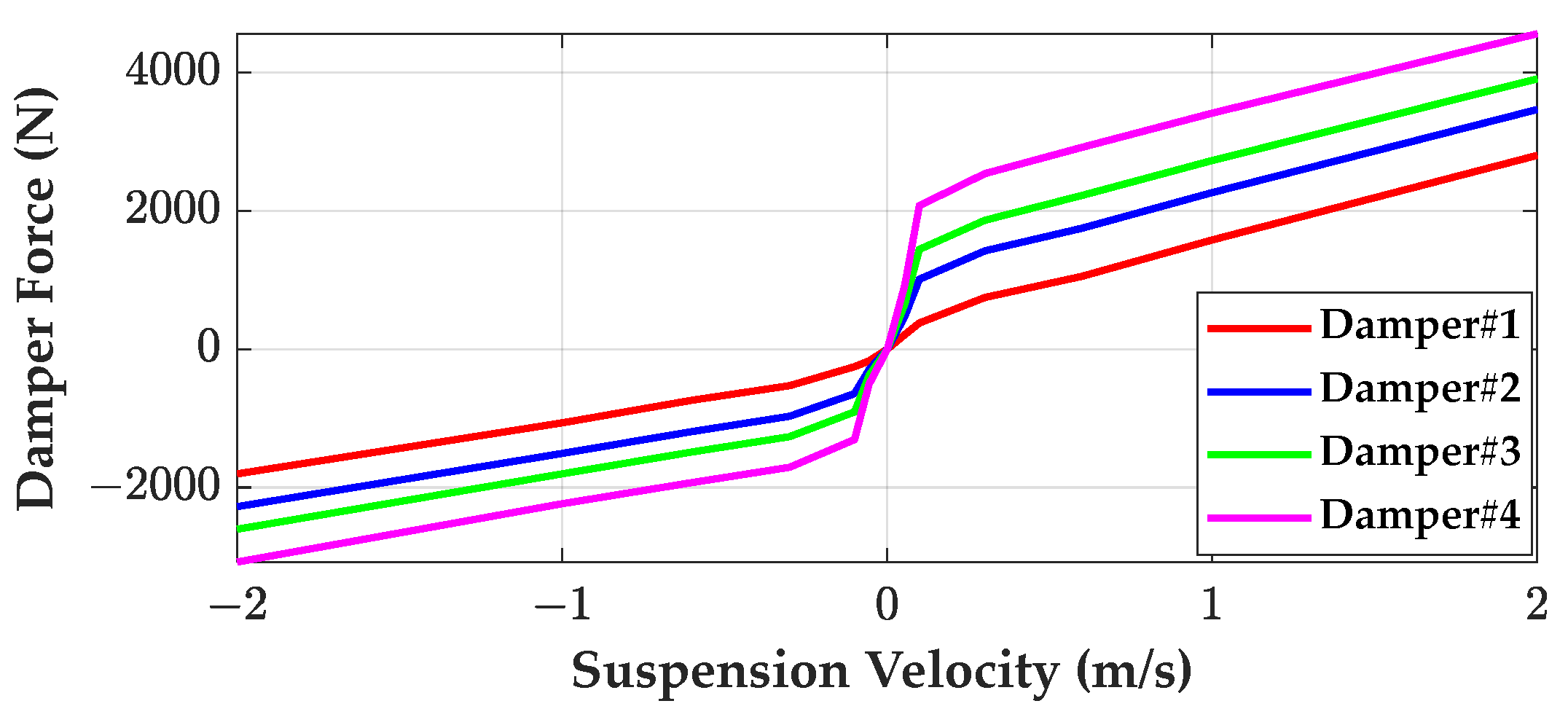
- If the damper has high damping coefficients, the control performance of PAC, i.e., PACRLS and PACEKF, is deteriorated.
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| EKF | Extended Kalman filter |
| FSF | Full-state feedback |
| HSB | Half-sine bump |
| LQR | Linear quadratic regulator |
| LQ SOF | Linear quadratic static output feedback |
| SBOM | Simulation-based optimization method |
| SOF | Static output feedback |
| SOFC | Static output feedback controller |
| SPM | Sprung mass |
| PAC | Parameter adaptive controller |
| PACEKF | Parameter adaptive controller with recursive least square |
| PACRLS | Parameter adaptive controller with extended Kalman filter |
| RLS | Recursive least square |
| SWR | Sine-waved road |
| USPM | Unsprung mass |
| Nomenclature | |
| bs | damping coefficient of a damper within a suspension (N·s/m) |
| f | suspension force acting on sprung and unsprung masses |
| J | LQ cost function used for LQR, LQSOF, and LQSSOF |
| JS | cost function of the simulation-based optimization |
| ks | stiffness of a spring within a suspension (N/m) |
| kt | stiffness of a tire (N/m) |
| ms | sprung mass (kg) |
| mu | unsprung mass under a suspension (kg) |
| u | forces generated by an actuator within a suspension (N) |
| zr | road elevation acting on a tire (m) |
| zs | vertical displacement of a sprung mass (m) |
| zu | vertical displacement of a wheel center (m) |
| ξi | maximum allowable value (MAV) of a weight in LQ cost function |
| λ | forgetting factor in the recursive least square |
| ρι | weight in LQ cost function |
References
- Sharp, R.S.; Crolla, D.A. Road vehicle suspension system design—A review. Veh. Syst. Dyn. 1987, 16, 167–192. [Google Scholar] [CrossRef]
- Hrovat, D. Survey of advanced suspension developments and related optimal control applications. Automatica 1997, 33, 1781–1817. [Google Scholar] [CrossRef]
- Tseng, H.E.; Hrovat, D. State of the art survey: Active and semi-active suspension control. Veh. Syst. Dyn. 2015, 53, 1034–1062. [Google Scholar] [CrossRef]
- ISO 2631-1:1997; Mechanical Vibration and Shock—Evaluation of Human Exposure to Whole-Body Vibration—Part 1: General Requirements. International Organization for Standardization: Geneva, Switzerland, 1997.
- Wilson, D.A.; Sharp, R.S.; Hassan, S.A. The application of linear optimal control theory to the design of active automobile suspensions. Veh. Syst. Dyn. 1987, 15, 105–118. [Google Scholar] [CrossRef]
- Cao, D.; Song, X.; Ahmadian, M. Editors’ perspectives: Road vehicle suspension design, dynamics, and control. Veh. Syst. Dyn. 2011, 49, 3–28. [Google Scholar] [CrossRef]
- Theunissen, J.; Tota, A.; Gruber, P.; Dhaens, M.; Sorniotti, A. Preview-based techniques for vehicle suspension control: A state-of-the-art review. Annu. Rev. Control 2021, 51, 206–235. [Google Scholar] [CrossRef]
- Sun, W.; Pan, H.; Zhang, Y.; Gao, H. Multi-objective control for uncertain nonlinear active suspension systems. Mechatronics 2014, 24, 318–327. [Google Scholar] [CrossRef]
- Hac, A. Optimal linear preview control of active vehicle suspension. Veh. Syst. Dyn. 1992, 21, 167–195. [Google Scholar] [CrossRef]
- Guo, L.; Zhang, L. Robust H∞ control of active vehicle suspension under non-stationary running. J. Sound Vib. 2012, 331, 5824–5837. [Google Scholar] [CrossRef]
- Sun, W.; Gao, H.; Kaynak, O. Adaptive backstepping control for active suspension systems with hard constraints. IEEE/ASME Trans. Mechatron. 2013, 18, 1072–1079. [Google Scholar] [CrossRef]
- Chen, S.-A.; Wang, J.-C.; Yao, M.; Kim, Y.-B. Improved optimal sliding mode control for a non-linear vehicle active suspension system. J. Sound Vib. 2017, 395, 1–25. [Google Scholar] [CrossRef]
- Pan, H.; Sun, W.; Jing, X.; Gao, H.; Yao, J. Adaptive tracking control for active suspension systems with non-ideal actuators. J. Sound Vib. 2017, 399, 2–20. [Google Scholar] [CrossRef]
- Yatak, M.O.; Sahin, F. Ride comfort-road holding trade-off improvement of full vehicle active suspension system by interval type-2 fuzzy control. Eng. Sci. Technol. Int. J. 2021, 24, 259–270. [Google Scholar] [CrossRef]
- Park, M.; Yim, S. Design of static output feedback and structured controllers for active suspension with quarter-car model. Energies 2021, 14, 8231. [Google Scholar] [CrossRef]
- Jeong, Y.; Sohn, Y.; Chang, S.; Yim, S. Design of static output feedback controllers for an active suspension system. IEEE Access 2022, 10, 26948–26964. [Google Scholar] [CrossRef]
- Kim, J.; Yim, S. Design of a suspension controller with an adaptive feedforward algorithm for ride comfort enhancement and motion sickness mitigation. Actuators 2024, 13, 315. [Google Scholar] [CrossRef]
- Attia, T.; Vamvoudakis, K.G.; Kochersberger, K.; Bird, J.; Furukawa, T. Simultaneous dynamic system estimation and optimal control of vehicle active suspension. Veh. Syst. Dyn. 2019, 57, 1467–1493. [Google Scholar] [CrossRef]
- Jeong, Y.; Sohn, Y.; Chang, S.; Yim, S. Design of virtual reference feedforward controller for an active suspension system. IEEE Access 2022, 10, 65671–65684. [Google Scholar] [CrossRef]
- Kim, J.; Yim, S. Design of static output feedback suspension controllers for ride comfort improvement and motion sickness reduction. Processes 2024, 12, 968. [Google Scholar] [CrossRef]
- Bryson, A.E., Jr.; Ho, Y. Applied Optimal Control; Hemisphere: New York, NY, USA, 1975. [Google Scholar]
- Hansen, N.; Muller, S.D.; Koumoutsakos, P. Reducing the time complexity of the derandomized evolution strategy with covariance matrix adaptation (CMA-ES). Evol. Comput. 2003, 11, 1–18. [Google Scholar] [CrossRef]
- Wenzel, T.A.; Burnham, K.J.; Blundell, M.V.; Williams, R.A. Dual extended Kalman filter for vehicle state and parameter estimation. Veh. Syst. Dyn. 2006, 44, 153–171. [Google Scholar] [CrossRef]
- Jiang, K.; Victorino, A.C.; Charara, A. Adaptive estimation of vehicle dynamics through RLS and Kalman filter approaches. In Proceedings of the 2015 IEEE 18th International Conference on Intelligent Transportation Systems, Canary Islands, Spain, 15–18 September 2015; pp. 1741–1746. [Google Scholar] [CrossRef]
- Hu, D.; Zong, C.; Na, X. Combined estimation of vehicle states and road friction coefficients using dual extended Kalman filter. Chin. J. Mech. Eng. 2013, 26, 313–324. [Google Scholar] [CrossRef]
- Park, M.; Yim, S. Design of robust observers for active roll control. IEEE Access 2019, 7, 173034–173043. [Google Scholar] [CrossRef]
- Haykin, S. Adaptive Filter Theory, 2nd ed.; Prentice-Hall: Hoboken, NJ, USA, 1991; pp. 760–761. [Google Scholar]
- Mechanical Simulation Corporation. CarSim Data Manual, Version 8; Mechanical Simulation Corporation: Ann Arbor, MI, USA, 2009.

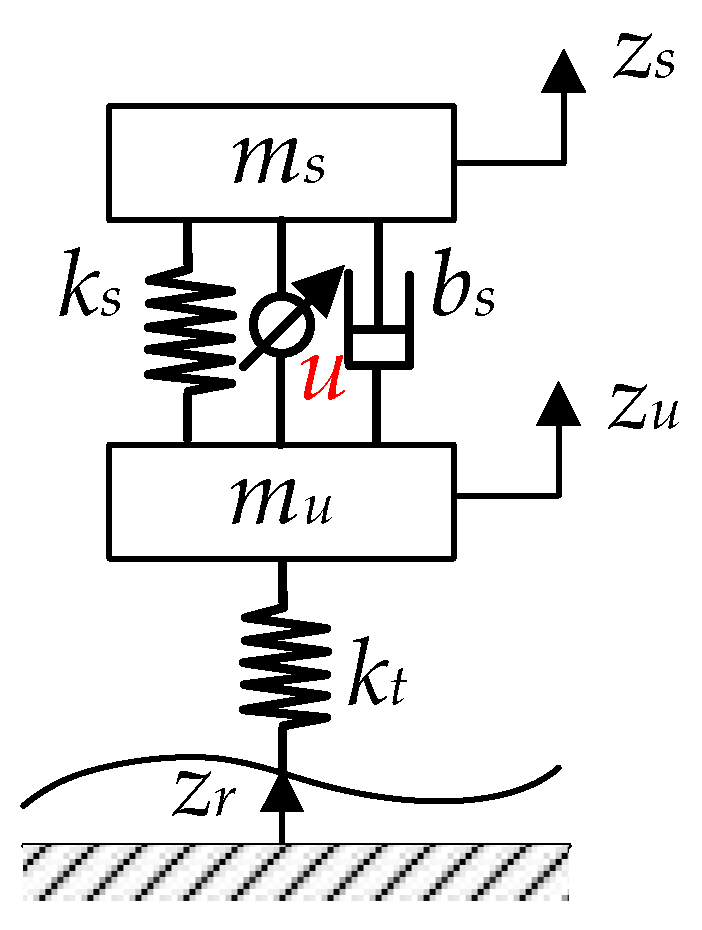
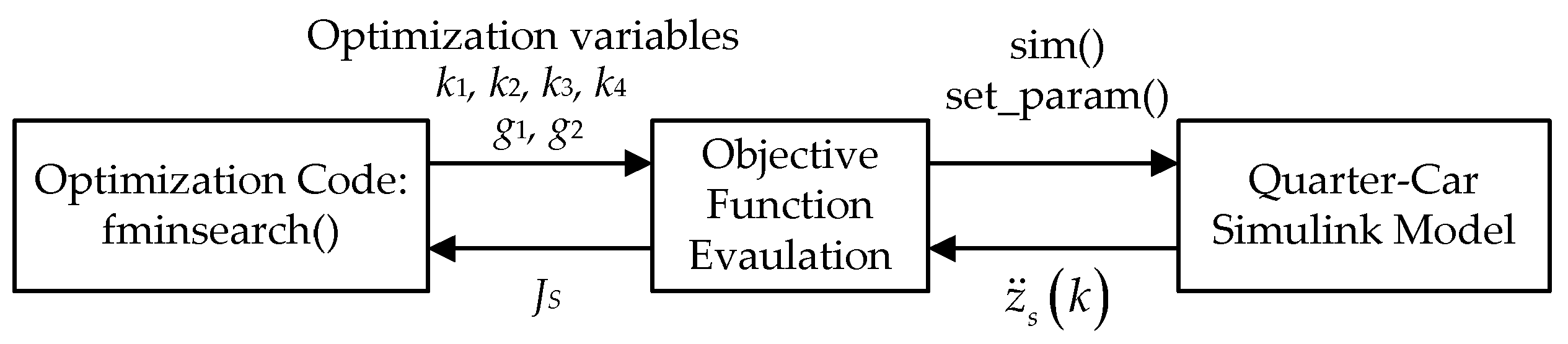
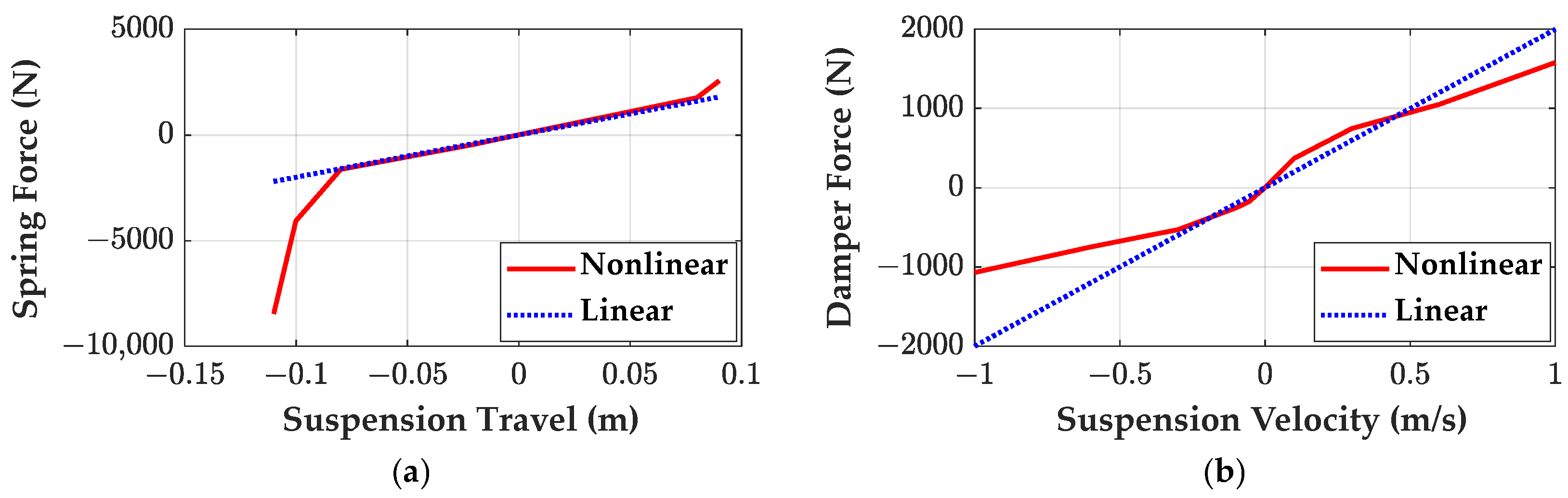







| Parameter | Value | Parameter | Value |
|---|---|---|---|
| ms | 413 kg | mu | 45 kg |
| ks | 34,000 N/m | bs | 3500 N·s/m |
| kt | 230,000 N/m |
| MAV | Value | MAV | Value |
|---|---|---|---|
| ξ1 | 1 m/s2 | ξ2 | 0.1 m |
| ξ3 | 0.01 m | ξ4 | 3000 N |
| Controller | Road Profile | Gain Matrix |
|---|---|---|
| LQR | ||
| LQSOF | ||
| FSFSBOM | HSB | |
| SOFSBOM | HSB | |
| FSFSBOM | SWR | |
| SOFSBOM | SWR | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yim, S. Comparative Study on Active Suspension Controllers with Parameter Adaptive and Static Output Feedback Control. Actuators 2025, 14, 150. https://doi.org/10.3390/act14030150
Yim S. Comparative Study on Active Suspension Controllers with Parameter Adaptive and Static Output Feedback Control. Actuators. 2025; 14(3):150. https://doi.org/10.3390/act14030150
Chicago/Turabian StyleYim, Seongjin. 2025. "Comparative Study on Active Suspension Controllers with Parameter Adaptive and Static Output Feedback Control" Actuators 14, no. 3: 150. https://doi.org/10.3390/act14030150
APA StyleYim, S. (2025). Comparative Study on Active Suspension Controllers with Parameter Adaptive and Static Output Feedback Control. Actuators, 14(3), 150. https://doi.org/10.3390/act14030150






