1. Introduction
Unmanned Aerial Vehicles (UAVs) have gained considerable attention within the scientific and aerospace engineering communities due to their various applications across both military and civilian sectors. Among these, Vertical Take-Off and Landing (VTOL) aircraft, such as quad-rotors, tilt-wings, and helicopters, are expected to play a critical role in the future of urban air mobility, reconnaissance missions, surveillance, disaster response, and other vital operations [
1,
2,
3].
One effective approach to improving the performance of VTOL UAVs is the incorporation of shrouds around the rotors. Shrouds have been shown to significantly enhance thrust, resulting in more efficient propulsion [
4,
5]. Additionally, shrouds play a key role in reducing acoustic emissions, making UAVs quieter and more suitable for urban environments and stealth operations.
Another major benefit is the reduction in rotor tip losses, which is achieved by limiting the high-energy airflow that escapes at the rotor tips, further improving aerodynamic efficiency and overall performance [
6,
7]. Despite these promising theoretical results, the practical application of shrouded rotors in aircraft has been limited, largely due to an incomplete understanding of the complex interactions between various geometrical features and their combined effects on aerodynamic performance [
8,
9].
In the aerodynamics area, one of the first to use a potential flow method to extend prior work on shrouded rotors in hover conditions to describe ducted fan aerodynamics in forward flight and the angle of attack was Kriebel [
10]. He researched stability derivatives for longitudinal flight and developed formulae to compute the forces and pitching moments experienced by shrouded rotors.
The understanding of the aerodynamic behavior of shrouded rotors has become more apparent as computing power has increased over time. An incompressible Navier–Stokes Computational Fluid Dynamics (CFD) solver for axisymmetric ducted fans was created in 2003 by Chang and Rajagopalan [
11] who modeled the fan as a “momentum source”. The approach, however, only considered pure axial flight (vertical climb). To further analyze the aerodynamics of ducted fans, Quackenbush et al. [
12] created a novel surface method combining fuselages and ducts with a free-wake potential flow method for propellers which showed good agreement with experimental data (e.g., X-22A ducted rotor-powered aircraft [
13] and isolated annular wings without propellers [
14]).
Research on the design and aerodynamic characteristics of shrouded rotors has increasingly focused on analyzing configuration characteristics. For instance, Zhongyun et al. [
15] developed a propeller design method capable of determining circulation distribution. Angelo et al. [
16] optimized the radial distributions of chord length and twist angle based on the blade’s working conditions and airfoil distribution. Additionally, Guo introduced a blade design method for ducted fans by refining blade element momentum theory using insights from CFD results [
17].
The growing adoption of computational research methods has led to a rise in the use of theoretical and low-order panel methods combined with rotor module techniques [
18,
19], as well as CFD simulations [
20,
21]. These methods have become increasingly common in recent studies. For example, Yu employed both the panel method and CFD to optimize shrouded rotor blades [
22]. Despite these advancements, the demand for highly accurate analytical models remains significant.
One-dimensional momentum theory can be used to estimate a shrouded rotor’s thrust. However, it is important to note that this theory alone cannot account for rotor geometric features such as rotor blade shape and the number of blades. The inlet cap model extends momentum theory for open rotors to shrouded ones. Adopting a one-dimensional analytical approach, it proposes an imaginary inlet surface model [
23,
24].
The inlet cap model provides insight into one-dimensional momentum theory by accounting for the thrust from the shroud’s inlet. However, because it is based on momentum theory, it still cannot account for the rotor blade shape or the number of blades. BET and BEMT can cover such a gap; however, the shroud effect on rotors can be accomplished by modifying the inflow ratio.
Blade element theory (BET) can be utilized to investigate the aerodynamic forces acting on each blade element comprising the rotor. The contribution of each segment is calculated to obtain the rotor’s overall performance. BET is considered for analyzing blade geometry and its impact on rotor performance. Such theory, however, is limited in accurately predicting induced velocities through the rotor. This limitation is particularly significant when dealing with shrouded rotors, which introduce increased induced velocity in the rotor plane and other complexities compared to open rotors. To overcome this challenge, combined BEMT is strategically employed. The purpose of using BEMT is to combine the strengths of both momentum and blade element theories. BEMT is used to enable accurate predictions of the induced flow velocities in each one of the shrouded rotor’s elements [
25,
26,
27].
In this research, a mathematical formulation for the aerodynamics of shrouded rotors is developed using a BEMT model, along with the integration of a previously developed sphere-cap model for shrouded rotors which depends on the shape of the shroud that was introduced by Dyer [
25]. This approach, which combines the strengths of both models, provides a more accurate and detailed description of the aerodynamics of shrouded rotors. The aerodynamic interactions between shrouded rotor blades and the surrounding flow can be more accurately captured. This development will significantly enhance the ability to optimize rotor designs and improve performance predictions, especially in applications such as VTOL aircraft.
2. Analytical Model
Achieving a perfect match between theoretical and real-world rotor blade performance is challenging due to the complexity of shrouded rotor aerodynamics. Therefore, simplifying assumptions are made in the present analytical work to streamline the calculations. The rotor blades are assumed to be rigid and the weight of the blades is ignored. Additionally, dynamic stall, which occurs under high angles of attack, and compressibility effects, which become significant at higher rotor speeds, are not accounted for in the present calculations. The flow is assumed to be steady and incompressible, with an ambient pressure, .
A set of mathematical formulations is developed to better understand the performance of shrouded rotors concerning various design parameters. The geometrical characteristics of the shroud’s inlet play an important role in calculating the shroud’s contribution to overall thrust using the sphere-cap model. Then, by combining that model with classical BEMT, a more accurate analysis of rotor performance is achieved.
2.1. Inlet Cap Area Definition
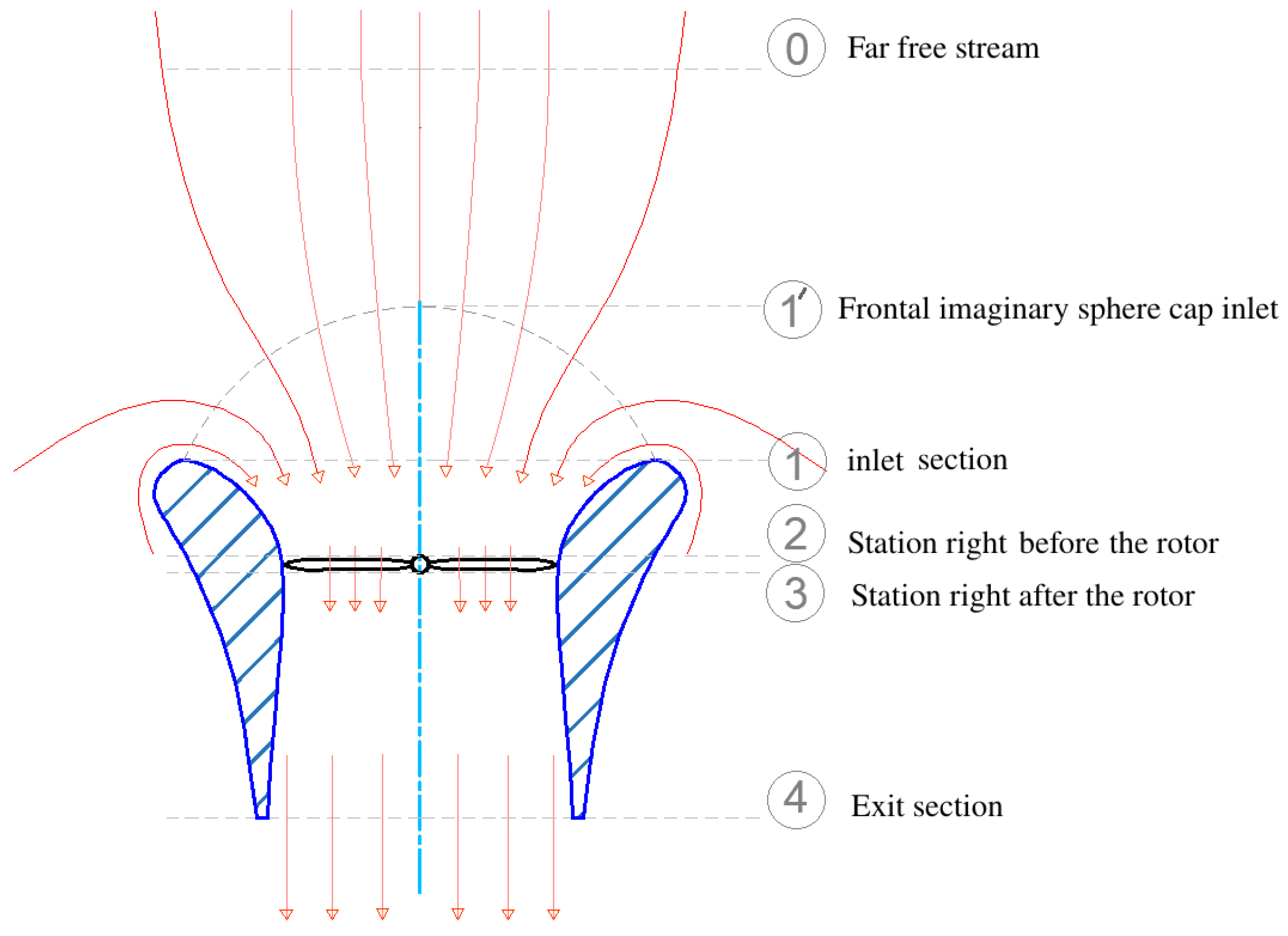
Figure 1 shows the numbered stations that are used to derive the total thrust and rotor thrust relations with the inlet cap representation. The stations along the longitudinal direction are as follows:
Section (0): the far free stream.
Section (1′): the frontal imaginary sphere-cap inlet.
Section (1): the shrouded rotor inlet.
Section (2): the station just before the rotor.
Section (3): the station right after the rotor.
Section (4): the exit section.
The definition of the inlet surface, shown in
Figure 1, required for setting up the model is not straightforward since the flow is highly distorted (i.e., strongly two-dimensional) at the shroud inlet [
23]. A sphere cap is an imaginary surface generated when a spherical shell is intersected by a plane, and the part of the shell above it (the “base plane”). The base plane can lay either above or below the sphere center. A sphere cap represents a potential surface to which the streamlines of the flow are assumed to be normal. The surface area of a sphere cap, as illustrated in
Figure 2, is given by the following equation:
where
is the radius of the sphere,
h is the height of the sphere cap, and
is the radius of the base circle. Applied to a shroud inlet,
and
h are given by
where
is the inlet angular coordinate that varies from
at the throat to
at the outer edge of the inlet lip,
is the duct throat radius, and
is the radius of the inlet lip.
2.2. BEMT
BEMT represents a synthesis of key concepts from both momentum theory and blade element theory, providing a more comprehensive understanding of the forces acting on rotor aerodynamics. This theory offers insights into how inflow is distributed along the radius of the rotor, allowing for a more precise calculation of local lift, drag, and induced velocity in each blade section [
28,
29,
30].
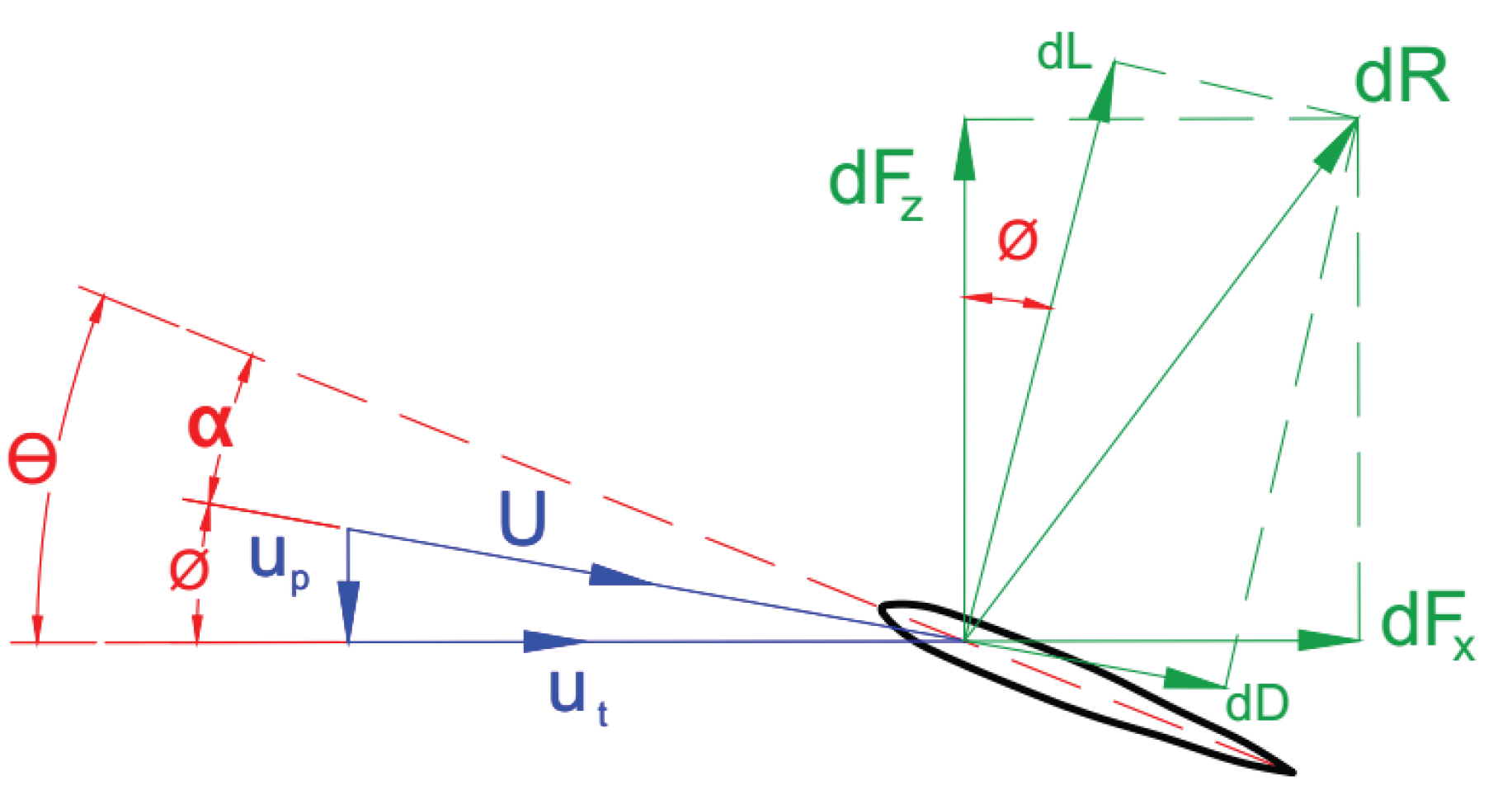
Considering the local velocities at a blade element (shown in
Figure 3), the tangential velocity,
, arises from the blade’s rotational motion (Equation (
1)). The perpendicular velocity,
, is formed by the induced velocity at the blade element. The tangential and the perpendicular velocity components for each of the rotor’s elements are presented as a function of the non-dimensional radial positions (
r) in Equation (
1) and Equation (
2), respectively.
The relative elementary angle of attack can be written as
where
is the local twist angle. Based on the value of the calculated local values of the angle of attack, Reynolds number, and cross-sectional airfoil type, the corresponding local lift coefficient, drag coefficient, and lift curve slope are obtained. So, the elementary lift,
, and drag,
, per unit spanning the corresponding blade element can be described as per Equation (
4) and Equation (
5), respectively.
where
is the air density,
c is the local chord,
U is the resultant total velocity,
, and
and
are the lift and drag coefficients, respectively, both obtained for each section of the rotor blade according to the sectional airfoil characteristics.
By resolving the lift and drag forces into parallel and normal components relative to the rotor disk, as shown in
Figure 3, Equations (
6) and (
7) are obtained.
Therefore, the elementary thrust, torque, and power of the disk can be defined as per Equation (
8), Equation (
9), and Equation (
10), respectively.
By integrating Equation (
8), Equation (
9), and Equation (
10) radially, the instantaneous thrust, torque, and power of the disk are obtained as shown by Equation (
11), Equation (
12), and Equation (
13), respectively.
Finally, the rotor’s average thrust, torque, and power can be obtained by integrating
,
, and
over the azimuth cycle for all blades,
, comprising the rotor, as represented by Equation (
14), Equation (
15), and Equation (
16), respectively.
Accounting for tip gap and root losses in shrouded rotors is essential for accurate performance prediction. Furthermore, the aerodynamic effect of the shroud on the rotor is characterized by the inflow ratio.
2.3. Tip Gap and Root Losses
Accurately predicting the performance of shrouded rotors requires accounting for both tip gap losses and root losses. The concept of tip loss, commonly applied to open rotors, is adapted to model the reduction in lift near the blade root [
28]. A more complex approach is needed to account for leakage losses due to the tip clearance gap. This is addressed using the tip correction factor introduced by Goodman [
31]. The overall loss correction factor for a shrouded rotor, denoted as
, is given by
where
and
represent the root loss factor (Equation (
18)) and the tip gap loss factor (Equation (
20)), respectively.
where
where
K is the complete elliptic integral of the first kind and
is the inverse of the Jacobi elliptic function. In the current modeling framework, both the elliptic integral of the first kind and the inverse of the Jacobi elliptic function are calculated using MATLAB R2021b functions. The modulus is defined as
, where
f and
g are defined in Equation (
21) and Equation (
22), respectively.
where
is the tip gap clearance (the difference between the shroud’s inner walls and the rotor tip).
2.4. Shrouded Rotor Inflow Ratio
We define
as the expansion ratio of the shroud’s diffuser (
), where
is the rotor disc area. Then, applying the conservation of momentum equation between just before and just after the rotor (i.e., from station 2 to station 3), the rotor thrust can be calculated as per Equation (
23).
By substituting
,
and
in Equation (
23), the rotor thrust can be found according to Equation (
24), where
is the induced velocity in the rotor plane.
As part of the proposed analysis of shrouded rotors, BEMT [
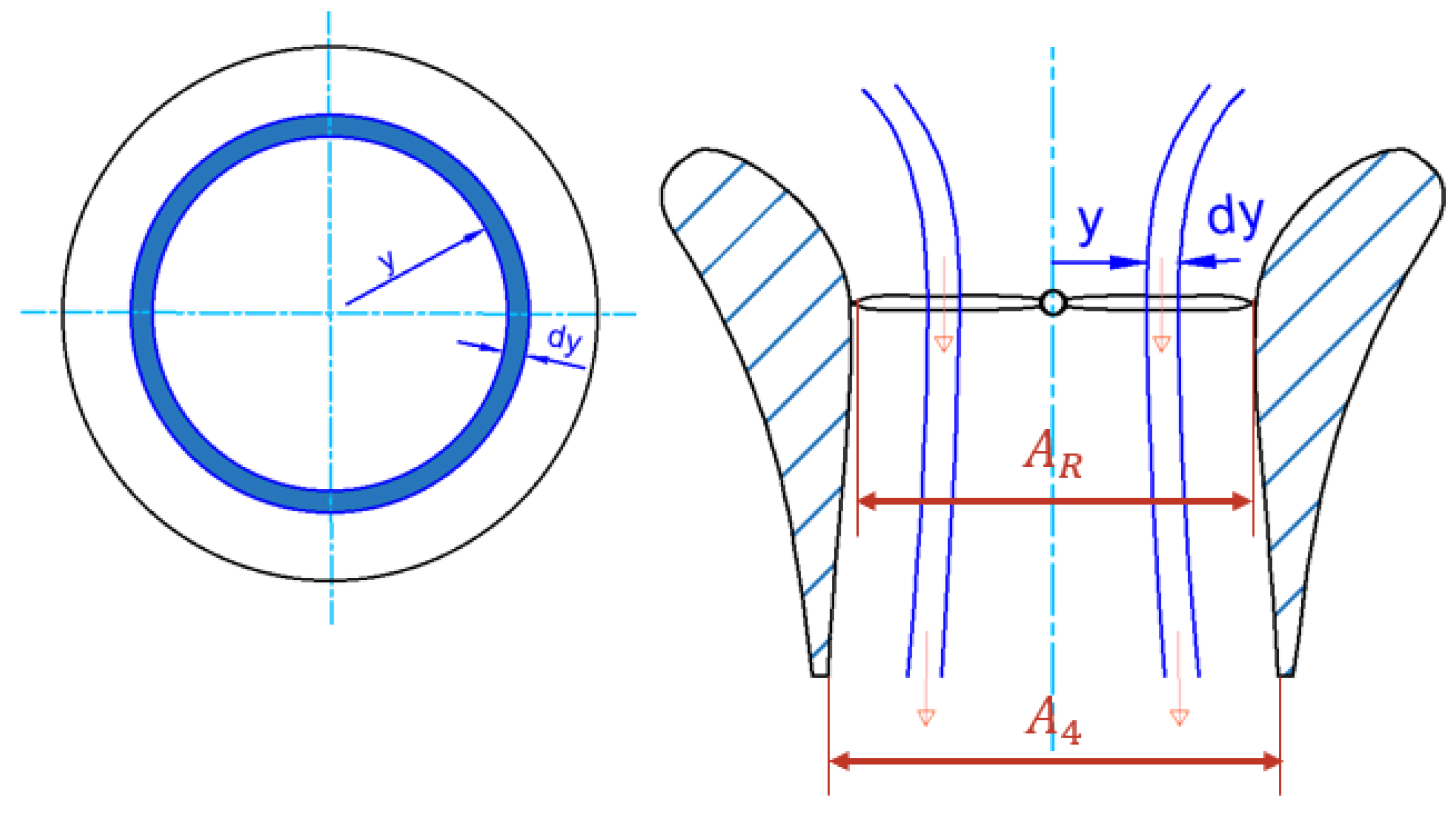
26] is used to predict the induced velocity experienced in shrouded rotors. From
Figure 4, the area of the specific blade element of interest can be found as
, where
y is the radial position. Thus, the elementary rotor thrust can be found as per Equation (
25).
Then, the elementary rotor thrust coefficient can be found as per Equation (
26).
where
is the inflow ratio (
),
r is the nondimensional radius (
), and
is the rotational velocity in
. By including the overall loss correction factor,
, the thrust coefficient becomes
A derivation of a linear equation for the induced velocity is needed for iterating a stable solution when modeling BEMT, similarly to the open rotor case [
28,
30]. As one blade element theory finding, the elementary rotor thrust coefficient can be obtained as follows [
28]:
where
is the local pitch angle, (
) is the rotor solidity ratio,
is local lift curve slope, and
is the local inflow angle (
).
By equating Equations (
27) and (
28), a quadratic function of the inflow ratio for the shrouded rotor can be obtained (Equation (
29)). Then, the solution of that equation provides the local inflow ratio for the shrouded rotor case (Equation (
31)).
Rearranging Equation (
29), we obtain
By solving the quadratic equation for
, we obtain
Since
typically represents a physical quantity that should be positive, the negative root is neglected. Finally, Equation (
30) can be simplified to
BEMT enables us to obtain accurate predictions of the induced flow velocities around and within shrouded rotors which relates to the induced power that is required to produce thrust at each one of the rotor’s elements [
32,
33]. To calculate the induced velocity at each element, Equation (
31) is used through an iteration process. Moreover, in the case of local angles of attack exceeding the critical angle of attack, the model needs to account for the post-stall effects.
2.5. Post-Stall Behavior
Viterna and Corrigan [
34,
35] modified classical BEMT to improve its correlation with measured data when aerodynamic stall occurs at high angles of attack. The model proposes the following expressions for the lift and drag coefficients (Equation (
32) and Equation (
33), respectively) being affected by post-stall behavior.
where
where
is the maximum drag coefficient,
is the aspect ratio of the blade element (
),
is the local airfoil thickness-to-chord ratio,
is the stall angle of attack, and
and
are the lift and drag coefficients at the stall angle of attack, respectively.
2.6. Total Thrust According to Inlet Cap Model
The total thrust can be calculated as per Equation (
34) according to the inlet cap model [
24].
where
is the inlet ratio (
) and
is the inlet cap ratio (
). Consequently, the shroud thrust can then be found as per Equation (
35) while the rotor thrust is calculated from BEMT, as illustrated in
Figure 5.
4. Case Study
The shroud used in this study was originally designed for the Navig8 UAV, shown in
Figure 8a, a maneuverable VTOL aircraft that incorporates shrouded rotors to improve the aerodynamic efficiency and overall performance of the rotor system. The shroud, as illustrated in
Figure 8b, is engineered to ensure that the rotor functions within optimal conditions for both thrust generation and maneuverability. It has a lip radius (
) of 0.01 m, the corresponding inlet angular coordinate
, and the diffuser expansion ratio
.
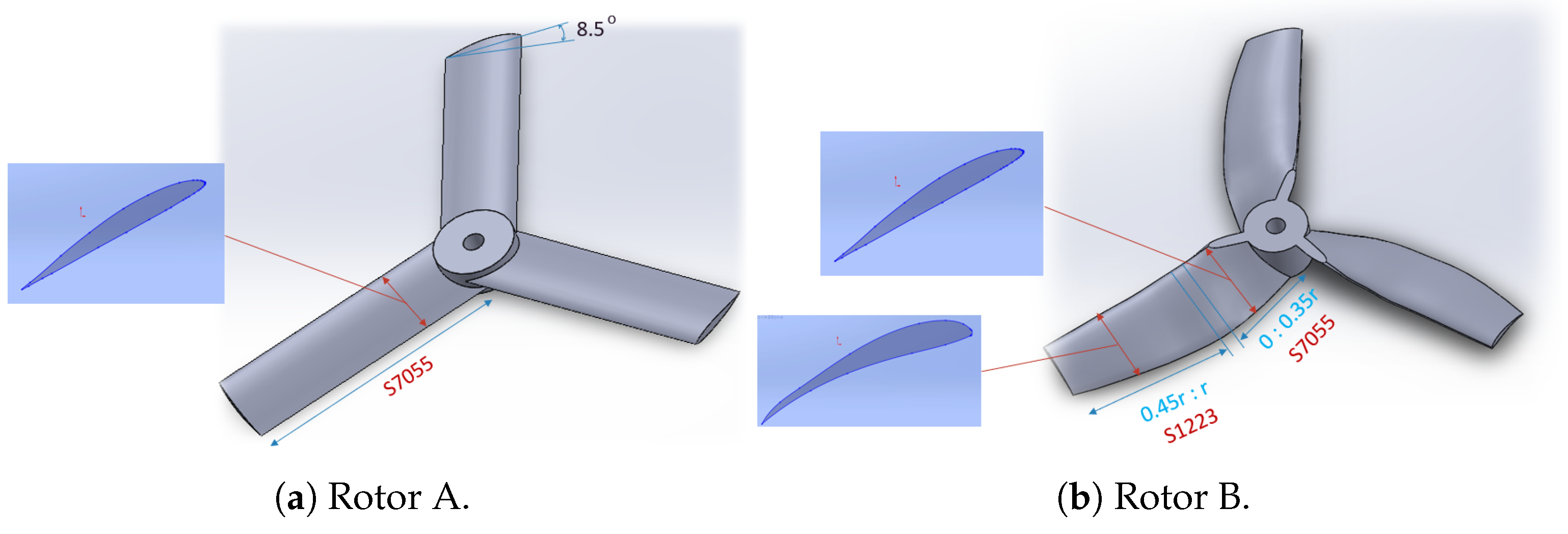
Two different rotors were chosen for the analytical modeling validation, which were Rotor A and Rotor B, with a radius 0.1143 m. Rotor A, shown in
Figure 9a, was designed to have a basic shape of one cross-sectional airfoil (S7055), constant chord (0.033 m), and no twist (8.5°) along its radius. Rotor B, shown in
Figure 9b, was designed by optimizing the chord and twist distributions, employing a third-degree variation for both the chord (
) and twist (
). The Navig8 UAV served as a reference framework to establish the feasible regions for the function coefficients. BEMT was applied to optimize the rotor, aiming to surpass the thrust-to-power ratio of the original Navig8 rotor [
36]. The equations governing the variations in the chord
and twist
are presented in Equation (
36) and Equation (
37), respectively.
It is important to note that the performance data for the S7055 and S1223 airfoils used in the analytical model were sourced from available experimental results to enhance the model’s accuracy [
37].
5. Computational Model
To simulate the flow structure and predict the aerodynamic effects of the designed test rig, ANSYS (2021 R1) FLUENT CFD software was used. The simulations were performed in a steady-state, 3D framework, with rotor rotation modeled using the Multiple Reference Frame (MRF) approach. The flow field was divided into two sub-domains: a stationary domain covering the entire computational area and a rotating domain surrounding the rotor, as shown in
Figure 10. The computational domain was cylindrical, measuring 2.5 m in length (about
) and 2 m in diameter (about
), with the shrouded rotor positioned 1 m downstream of the stationary domain’s entry point. The inlet boundary was defined as a velocity inlet with zero velocity, while the outlet boundary was set as a pressure outlet. The walls within the stationary domain were treated as symmetry boundaries, and all surfaces of the shrouded rotor were assigned no-slip wall conditions.
Figure 11 shows the two computational meshes, with and without the test rig with the same meshing properties. An unstructured mesh with tetrahedral cell meshing was generated for the entire flow domain using the ANSYS mesh tool due to the complex shrouded rotor configuration geometry. A CFD grid dependency study was carried out to verify that the simulation results were unaffected by mesh size. The grid was progressively refined until thrust and torque values stabilized, indicating minimal sensitivity to further refinement.
The Realizable
turbulence model, combined with enhanced wall functions, was employed in the simulations. This choice is particularly well-suited for applications involving rotating flows, which are typically characterized by high Reynolds numbers and complex vortex structures. The Realizable
model is known for its ability to accurately handle such flow conditions with delay in flow separation occurrences [
38,
39]. It offers a good balance between computational efficiency and the accuracy needed to capture essential flow dynamics, making it an appropriate and effective choice for these types of simulations [
40].
The simulation conditions are summarized in
Table 1. The air was assumed to have a constant density of
for Rotor A and
for Rotor B, in line with the experimental conditions. Equations (
38) and (
39) present the mathematical expressions for the turbulent kinetic energy (
k) and turbulent dissipation rate (
), respectively.
In contrast to the standard model, the Realizable variant treats
as a variable when computing the turbulent viscosity (
). The value of
is calculated using the following relation:
The modification in the
Realizable model allows for the accurate simulation of turbulent rotating flows, capturing the recirculation and boundary layer separation effectively. This makes it particularly suitable for rotor flow simulations [
41,
42].
7. Conclusions
The study employed a combination of BEMT and the sphere-cap model, alongside applying the inflow ratio for shrouded rotors. BEMT formed the foundation for calculating rotor performance, while the sphere-cap model accounted for the aerodynamic influence of the shroud. This provided a comprehensive analysis of shrouded rotors, capturing both the rotor dynamics and the shroud’s contribution to performance.
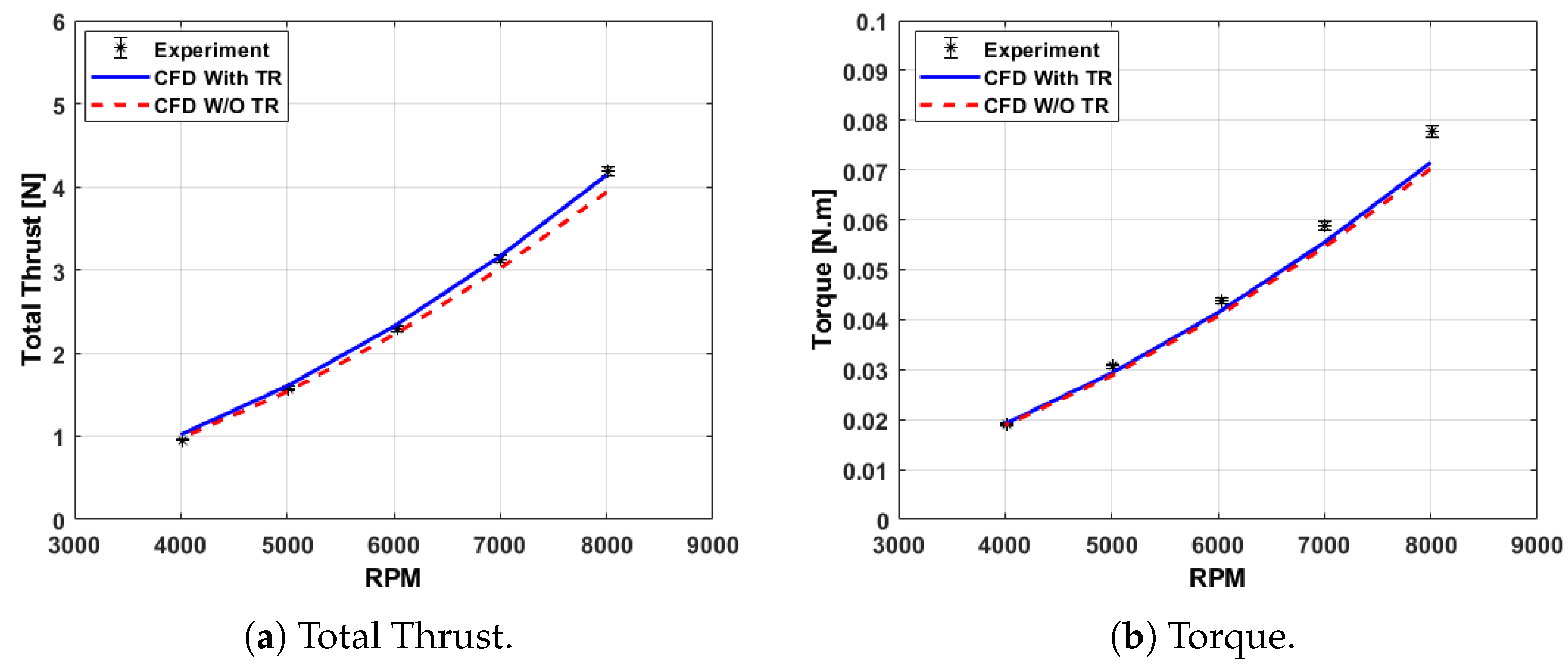
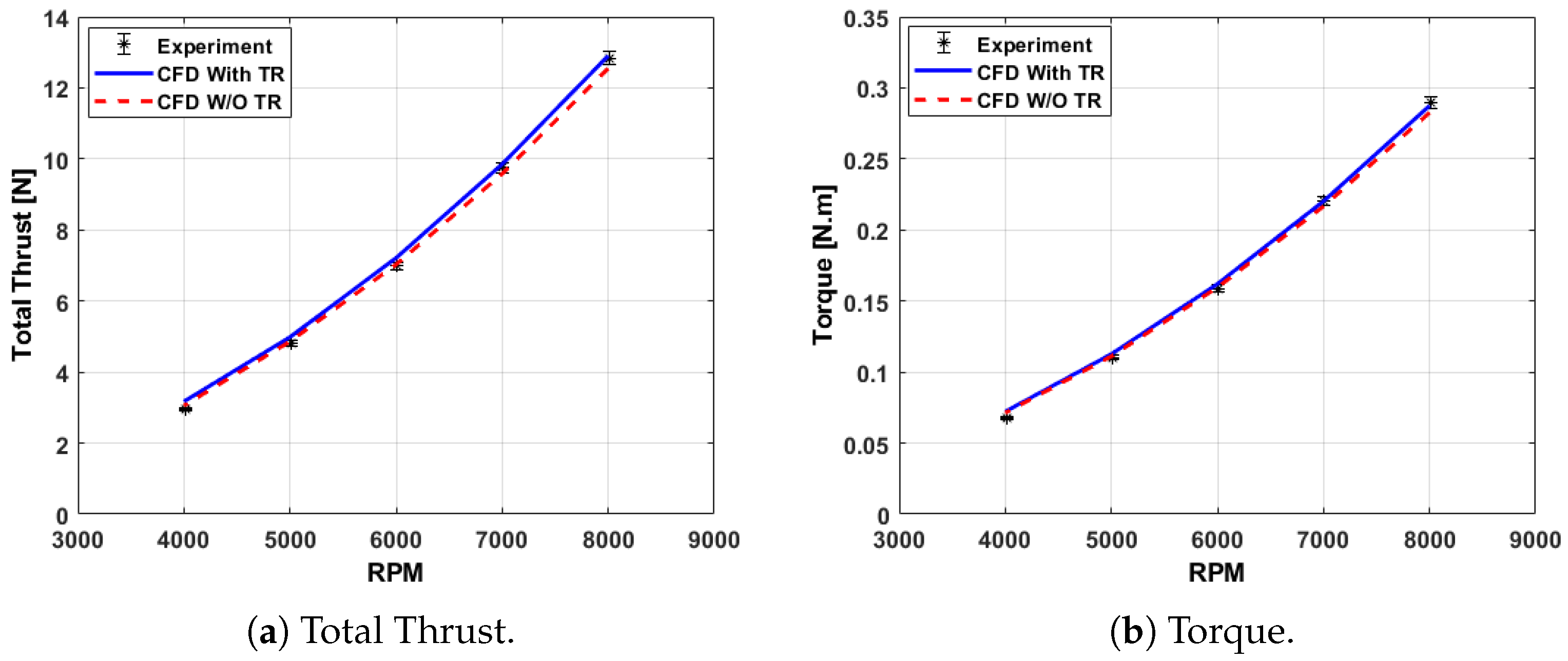
The effects of the test rig on shrouded rotor performance were investigated by conducting computational simulations with and without the test rig and comparing these results with experimental data. The agreement between the CFD without the test rig and the analytical model further suggested that the test rig’s influence could be reasonably disregarded, allowing for a more straightforward comparison between the analytical model and experimental results.
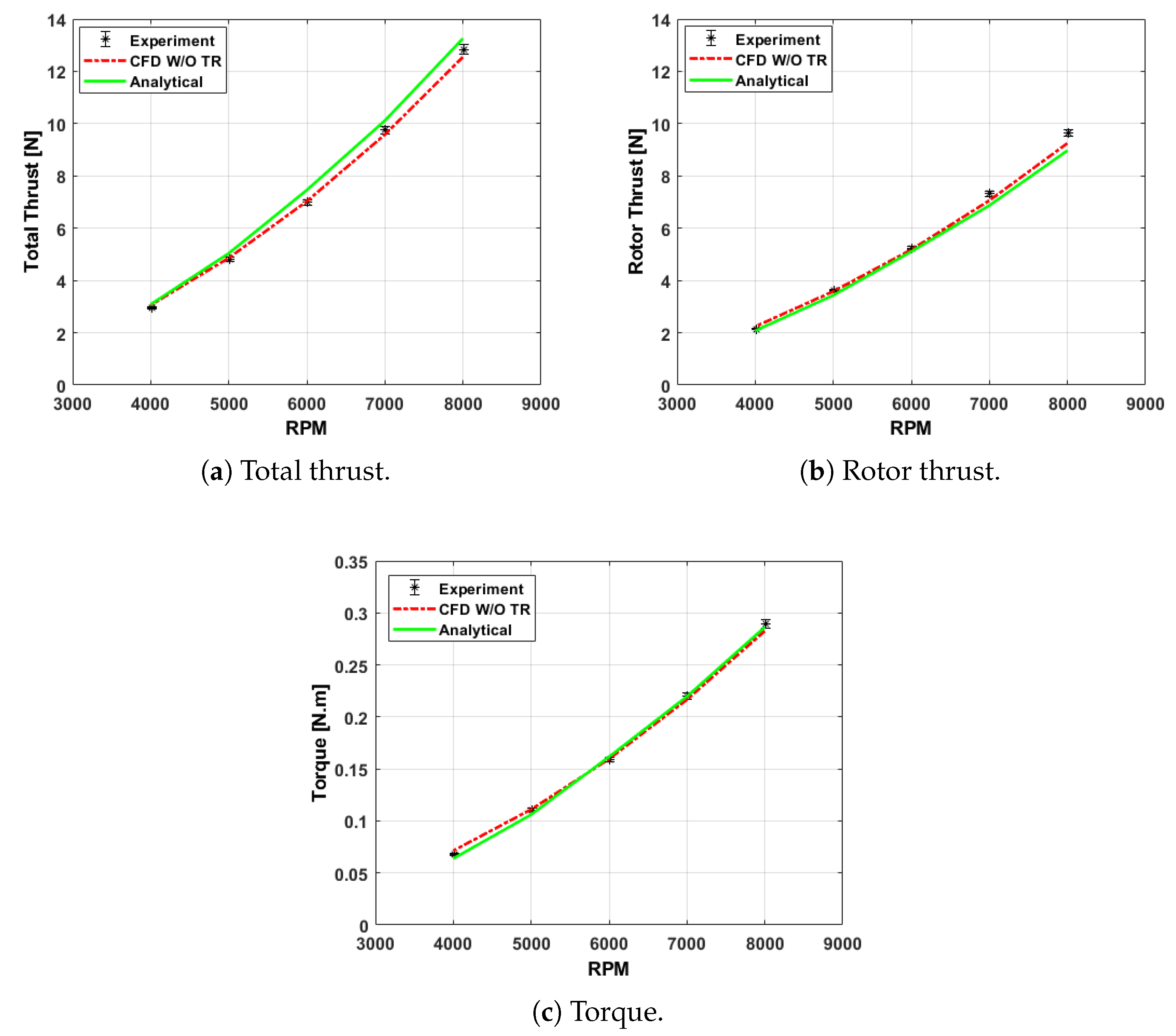
A comparison between the analytical model, experimental results, and computational simulations without the test rig was performed. The close match between the analytical model, experimental data, and CFD without the test rig across all three performance parameters (total thrust, rotor thrust, and torque) reinforces the accuracy of the analytical model in predicting rotor performance. Overall, these results suggest that the analytical model is a reliable tool for predicting the performance of the shrouded rotor, and the CFD simulations without the test rig provide additional validation by confirming that the test rig has minimal impact on the performance metrics.
The presented formula for the inflow ratio demonstrated its value and validity through the strong agreement between the predicted rotor thrust and both the experimental and CFD results. The close alignment across a wide range of RPMs indicated that the formula accurately captured the inflow characteristics of the shrouded rotor.
In summary, this study validated the analytical model for predicting the performance of the shrouded rotor with high accuracy. To assess the practical applicability and scalability of the analytical model, it was essential to consider the effects of scaling on the shrouded rotor performance. Variations in Reynolds numbers influenced aerodynamic forces, which was accounted for while calculating the lift and drag coefficients. While the analytical model predicts key performance metrics with reasonable accuracy, discrepancies may arise due to unmodeled scale-dependent effects, such as increased tip leakage at larger sizes or changes in boundary layer behavior within a shroud. Future research should evaluate the model’s accuracy across different rotor sizes, ensuring its reliability for both laboratory experiments and full-scale applications.