A Robust Cooperative Control Protocol Based on Global Sliding Mode Manifold for Heterogeneous Nonlinear Multi-Agent Systems Under the Switching Topology

Abstract

This study addresses the completely distributed consensus control problem for the heterogeneous nonlinear multi-agent system (MAS) with disturbances under switching topology. First, a global sliding mode manifold (GSMM) is designed for the overall MAS dynamic, which maintains stability without oscillations during topology switching after achieving the sliding mode. Subsequently, a consensus sliding mode control protocol (SMCP) is proposed, adopting the common sliding mode control (SMC) format and ensuring the finite-time reachability of the GSMM under topology switching. Finally, the proposed GSMM and SMCP are applied to the formation control of multiple-wheeled mobile robots (WMRs), and simulation results confirm their feasibility and effectiveness. The proposed SMCP design demonstrates key advantages, including a simple control structure, complete robustness to matched disturbance, and reduced-order dynamics under the sliding mode.

1. Introduction

Completely distributed cooperative control of multi-agent systems (MASs) has emerged as a significant research domain in recent years [1,2,3]. Cooperative control design has been successfully applied to various fields, including UAV formation control [4], multi-robot system (MRS) trajectory tracking [5] and satellite cluster attitude alignment [6]. Within multi-agent systems, cooperative control enables the execution of more complex and challenging control tasks, making significant contributions to humanity. Among these efforts, the consensus problem [7,8,9] is a fundamental objective in the cooperative control of MASs.

For the consensus problem, MASs can be categorized into two types: systems with leaders [10] and systems without leaders [11,12,13]. Research on consensus problems for MASs with linear structures has already been extensively developed. For instance, Rezaee and Abdollahi proposed a consensus control protocol that relies solely on relative positions in high-order MASs under undirected networks [14]. Chen et al. investigated the completely distributed consensus control problem for general linear MASs via a dynamic event-triggered scheme [15]. Some scholars have focused on finite-time stability and fixed-time stability in the context of the consensus problem for MASs [16,17,18,19,20]. For example, Wang et al. introduced a new distributed finite-time optimization algorithm for agents under directed graphs [21], while He et al. explored the fast finite-time tracking consensus problem for first-order nonlinear MASs [22]. In practical applications, methods based on the leader-following consensus framework are widely adopted.

In recent decades, sliding mode control (SMC) has undergone significant development, including methods such as the nonsingular terminal sliding mode [23] and the global sliding mode [24]. SMC methods have been applied to many industrial applications, including typical MASs, due to their simplicity and robustness. Cai et al. implemented sliding mode control for singular switched MASs by presenting a general integral-type sliding mode control rule based on mode-dependent average dwell time [25]. Ma et al. addressed the finite-time consensus problem for heterogeneous MASs with second-order linear and nonlinear agents, where communication between agents was described by directed graphs [26]. Nie et al. examined the finite-time consensus tracking problem of MASs with unknown follower states under SMC control in the presence of actuator attacks [27]. Jin et al. investigated predefined-time consensus for a class of second-order nonlinear MASs using a sliding mode technique [28]. Song et al. proposed an optimized leader-follower consensus control for multiple robot manipulator systems by combining sliding mode control with reinforcement learning [29].

Despite the significant progress in the research on various MASs, many of these studies have limitations. Some fail to provide a completely distributed control protocol. For instance, in tracking consensus control problems, the control protocol often relies on the leader’s control input information. Others neglect the nonlinear dynamic model of the followers. Numerous studies on switching topology cases focus on single or double-integrator systems or linear dynamic MASs without addressing the heterogeneous nature of MASs. Specifically, few studies tackle the tracking consensus control problem for both heterogeneous and high-order nonlinear dynamic MASs under switching topology. Moreover, only a limited number of results offer a completely distributed sliding mode control protocol that eliminates the need for the leader’s control input in such MASs.

This paper investigates the completely distributed consensus control problem for heterogeneous nonlinear MASs with disturbances under switching topology. To develop a sliding mode control protocol with a simple structure similar to common SMC, a global sliding mode manifold (GSMM) is designed for the overall MAS dynamic. The GSMM remains stable without oscillation during topology switching once the sliding mode is achieved. A corresponding consensus SMCP is proposed, guaranteeing finite-time reachability regardless of topology changes. The proposed SMCP design offers complete robustness to matched disturbances, similar to conventional SMC, and results in a reduced-order dynamic under the sliding mode. Finally, the proposed SMCP design is applied to the formation control of multiple-wheeled mobile robots (WMRs), validating its feasibility and effectiveness.

The contributions of the paper are summarized as follows.

(a).

A GSMM for MASs is proposed, which remains unaffected by topology switching. The consensus performance under the sliding mode is determined by the design of the sliding mode manifold parameters. Moreover, order reduction is realized.

(b).

A completely distributed control protocol based on the GSMM is proposed. It features a sliding mode control format, a simple structure, and strong robustness. The control protocol and its parameters depend solely on information from neighboring agents.

(c).

The proposed cooperative control protocol is applied to WMRs.

The remainder of the paper is organized as follows. Section 2 describes the problem. Section 3 introduces the design of the GSMM surface and analyzes its ideal sliding mode dynamics. Section 4 presents the control protocol design based on the GSMM and examines the finite-time reachability of the GSMM. Section 5 provides the application of the presented tracking consensus SMCP. Section 6 verifies the control protocol design through simulation results for WMRs. Finally, Section 7 concludes the paper.

2. Preliminary and Problem Formulation

2.1. Graph Theory

The communication topology among the M agents is characterized by an undirected switching graph. In particular, it is assumed that the topology switches within a given graph set $\widehat{\mathcal{G}}$, where $\widehat{\mathcal{G}}=\left\{{\mathcal{G}}^1,{\mathcal{G}}^2,\dots ,{\mathcal{G}}^{\kappa }\right\}$, $\kappa \in \mathbb{N},\kappa ⩾1$.

For analytical convenience consider an infinite sequence of non-overlapping time intervals $\left[t_k,t_{k+1}\right),k\in \mathbb{N}$, with $t_1=0,{\tau }_1⩾t_{k+1}-t_k⩾{\tau }_0$ where ${\tau }_1>{\tau }_0>0$. During each interval, the communication topology is fixed. In this context, the positive constant ${\tau }_0$ is referred to as the dwell time. The time sequence $t_1,t_2,\dots ,$ is defined as the switching sequence along which the communication topology changes. Based on this description, let ${\mathcal{G}}^{\sigma }$ be the communication topology of the considered MAS at time t, where $t⩾0$. The piecewise constant function $\sigma \left(t\right):\left[0,+\propto \right)\to \left\{1,2,\dots ,\kappa \right\}$ serves as the switching signal. Notably, ${\mathcal{G}}^{\sigma }\in \widehat{\mathcal{G}}$, for all $t⩾0$.

Directed graphs are used to model the information interaction among agents. Let ${\mathcal{G}}^{\sigma }=\left(\mathcal{V},\mathcal{E}\right)$ be a directed graph, where $\mathcal{V}=\left\{1,2,\dots ,M\right\}$ is a finite, nonempty set of nodes, and $\mathcal{E}\subseteq \mathcal{V}\times \mathcal{V}$ is the edge set. An edge of ${\mathcal{G}}^{\sigma }$ is denoted by $(i,j)$, which starts from i and ends at node j, indicating that node i can directly receive information from node j. The set of all neighbors of node i is denoted as ${\mathcal{N}}_i:=\left\{j|\left(i,j\right)\in \mathcal{E}\right\}$. A graph ${\mathcal{G}}^{\sigma }$ is called an undirected graph if and only if $(i,j)\in \mathcal{E}$ implies $(j,i)\in \mathcal{E}$, otherwise, it is considered a directed graph. An undirected path in an undirected graph is defined analogously. The weighted adjacency matrix $A^{\sigma }=\left[a_{ij}^{\sigma }\right]\in {\mathbb{R}}^{M\times M}$ of the graph ${\mathcal{G}}^{\sigma }$ is defined such that $a_{ij}^{\sigma }>0$ if $(i,j)\in \mathcal{E}$, and $a_{ij}^{\sigma }=0$, otherwise. For an undirected graph, we assume that $a_{ij}^{\sigma }=a_{ji}^{\sigma }$. The Laplacian matrix $L^{\sigma }=\left[l_{ij}^{\sigma }\right]\in {\mathbb{R}}^{M\times M}$ of ${\mathcal{G}}^{\sigma }$ is defined as $l_{ii}^{\sigma }={\sum }_{j=1}^M{a}_{ij}^{\sigma }$ and $l_{ij}^{\sigma }=-a_{ij}^{\sigma },\forall i\ne j$. Obviously, the Laplacian matrix and the weighted adjacency matrix are both symmetric for an undirected graph.

Consider a group consisting of M followers, labeled as agents 1 to M, and $N(N=1)$ leaders, labeled as agent $M+1$. The communication topology among the $M+1$ agents, denoted as ${\mathcal{G}}^{\sigma }$, is assumed to remain fixed during the interval $\left[t_k,t_{k+1}\right)$ when the switching signal $\sigma \left(t\right)=i,i\in \left\{1,2,\dots ,\kappa \right\}$. Let $A^{\sigma }=\left[a_{ij}^{\sigma }\right]\in {\mathbb{R}}^{\left(M+1\right)\times \left(M+1\right)}$ be the weighted adjacency matrix, and $L^{\sigma }=\left[l_{ij}^{\sigma }\right]\in {\mathbb{R}}^{\left(M+1\right)\times \left(M+1\right)}$ be the Laplacian matrix of the $M+1$ agents. Then, the following holds.

$$L^{\sigma }=\left(\begin{array}{cc}{L}_1^{\sigma }& L_2^{\sigma }\\ 0_{1\times M}& 0\end{array}\right)$$

(1)

where $L_1^{\sigma }\in {\mathbb{R}}^{M\times M},L_2^{\sigma }\in {\mathbb{R}}^{M\times 1}$.

2.2. The Consensus Control Problem

Consider multiple followers of general nonlinear systems

$${\dot{x}}_i=f_i+g_i{u}_i+d_i,i=1,2,\dots ,M,$$

(2)

where $x_i\in {\mathbb{R}}^n$ represents the agent state, $u_i\in {\mathbb{R}}^m$ is the control input, $d_i\in {\mathbb{R}}^n$ denotes the unknown disturbance, $f_i=f_i\left(x_i\right)\in {\mathbb{R}}^n$ is the nonlinear vector field, and $g_i\in {\mathbb{R}}^{n\times m}$ is the control matrix.

The leader is described as:

$${\dot{x}}_i\left(t\right)=f^0\left(x_i,t\right),i=M+1,$$

(3)

where $f^0:{\mathbb{R}}^n\times \mathbb{R}\to {\mathbb{R}}^n$ is a nonlinear vector function.

To facilitate the analysis, the following assumptions are made.

Assumption 1.

The nonlinear vector field $f_i\left(x_i\right)$ is piecewise Lipschitz continuous, satisfying $∥f_i\left(x_j\right)-f_i\left(x_i\right)∥⩽{\lambda }_i∥x_j-x_i∥$ where ${\lambda }_i>0$ is a positive scalar. Furthermore, $f_i\left(0\right)=0$.

Assumption 2.

The nonlinear vector function $f^0$ is Lipschitz continuous and satisfies $∥f^0\left(x_{M+1},t_1\right)-f^0\left(x_{M+1},t_2\right)∥⩽{\overline{\lambda }}_0∥x_{M+1}∥+{\lambda }_0$ where ${\overline{\lambda }}_0$ and ${\lambda }_0$ are positive scalars.

Assumption 3.

The control matrix $g_i$ is full-rank, i.e., $\mathrm{rank}\left(g_i\right)=min(m,n)$ ensuring the controllability of the agent.

Assumption 4.

The unknown disturbance $d_i=d_i\left(t\right)$ is bounded, satisfying $∥d_i∥\le {\overline{d}}_i$, where ${\overline{d}}_i$ is positive scalar.

Assumption 5.

The unknown disturbance $d_i$ does not affect the equilibrium of the nonlinear dynamic in (2).

Assumption 6.

For each $i\in \left\{1,2,\dots ,\kappa \right\}$, the directed graph ${\mathcal{G}}^i$ contains a directed spanning tree with node $M+1$ as the root.

3. The Global Sliding Mode Surface Design for the Multi-Agent System

The sliding mode surface for the MAS is designed as follows,

$$\begin{array}{cc}\hfill S& =\left(L_1^{\sigma }\otimes C\right)e\hfill \\ \hfill & =\left(L_1^{\sigma }\otimes I_m\right)\left[{\left(C{e}_1\right)}^T,{\left(C{e}_2\right)}^T,\cdots ,{\left(C{e}_M\right)}^T\right],\hfill \end{array}$$

(4)

where $e={\left[e_1^T,e_2^T,\dots ,e_M^T\right]}^T$, and $e_i=x_i-x_{M+1}$ is the consensus error of the i-th follower. The matrix $C\in {\mathbb{R}}^{m\times n}$ is the sliding mode parameter that satisfies $\mathrm{rank}\left(C\right)=m$ and ensures that matrix $C{g}_i$ is nonsingular and positive definite. The consensus error dynamics of the i-th follower are written as:

$$\begin{array}{cc}\hfill {\dot{e}}_i& ={\dot{x}}_i-{\dot{x}}_{M+1}\hfill \\ \hfill & =f_i+g_i{u}_i+d_i-f^0\left(x_{M+1},t\right).\hfill \end{array}$$

(5)

The following stacked vectors are defined for future use,

$$\begin{array}{cc}\hfill x_F=& {\left[x_1^T,x_2^T,\dots ,x_M^T\right]}^T,\hfill \\ \hfill F=& {\left[f_1^T\left(x_1\right),f_2^T\left(x_2\right),\dots ,f_M^T\left(x_M\right)\right]}^T,\hfill \\ \hfill d=& {\left[d_1^T,d_2^T,\dots ,d_M^T\right]}^T.\hfill \end{array}$$

(6)

By Assumption 6 and the properties of the Laplacian matrix, the following equality holds

$$\begin{array}{c}\hfill L_1^{\sigma }{1}_M+L_2^{\sigma }=L{1}_{M+1}^{\sigma }=0\end{array}$$

(7)

which implies $L_1^{\sigma }{1}_M=-L_2^{\sigma }$. According to (5), (6) and (7), the sliding mode surface in (4) can be written as:

$$\begin{array}{cc}\hfill S=& \left(L_1^{\sigma }\otimes C\right)(x_F-1_M\otimes x_{M+1})\hfill \\ \hfill =& \left(L_1^{\sigma }\otimes C\right)x_F+\left(L_2^{\sigma }\otimes C{x}_{M+1}\right)\hfill \\ \hfill =& \left(L_1^{\sigma }\otimes I_m\right){\left[{\left(C{x}_1\right)}^T,\cdots ,{\left(C{x}_M\right)}^T\right]}^T+L_2^{\sigma }\otimes C{x}_{M+1}\hfill \\ \hfill =& \left[\begin{array}{c}C{\sum }_{j=1}^{M+1}{a}_{1j}^{\sigma }\left(x_i-x_j\right)\\ C{\sum }_{j=1}^{M+1}{a}_{2j}^{\sigma }\left(x_i-x_j\right)\\ \dots \\ C{\sum }_{j=1}^{M+1}{a}_{Mj}^{\sigma }\left(x_i-x_j\right)\end{array}\right]\hfill \end{array}$$

$$\begin{array}{c}\hfill ={\left[S_1^T,S_2^T,\cdots ,S_M^T\right]}^T,\end{array}$$

(8)

where

$$\begin{array}{c}\hfill S_i=C\sum _{j=1}^{M+1}{a}_{ij}^{\sigma }\left(x_i-x_j\right),\forall i=1,2,\cdots ,M.\end{array}$$

(9)

The time derivative of the sliding mode is expressed as:

$$\begin{array}{cc}\hfill \dot{S}=& \left(L_1^{\sigma }\otimes C\right)\left({\dot{x}}_F-1_M\otimes {\dot{x}}_{M+1}\right)\hfill \\ \hfill =& \left(L_1^{\sigma }\otimes C\right)\left[F+d+\mathrm{diag}\left\{g_1,g_2,\dots ,g_M\right\}u\right]-\left(L_1^{\sigma }\otimes C\right)\left(1_M\otimes f^0\left(x_{M+1},t\right)\right),\hfill \end{array}$$

(10)

where $u={[u_1^T,u_2^T,\cdots ,u_M^T]}^T$.

Remark 1.

The sliding mode in (4) remains piecewise continuous during each topology switching dwell time interval ${\tau }_0$. Specifically, within the time interval $\left[t_k,t_{k+1}\right),k\in \mathbb{N}$, the sliding mode is continuous. However, when the topology switches, the coefficient in the sliding mode (4) undergoes a jump.

Remark 2.

When the sliding mode $S=0$ is reached and maintained, topology switching does not affect its stability and continuity. This is due to the property of the Laplacian matrix, where $L_1^{\sigma }>0$, implying $\left(L_1^{\sigma }\otimes I_M\right)>0$. Consequently, when the sliding mode is reached $S=0$, $C{e}_i=0$ according to (4), and $S_i=0$ according to (8). Therefore, the sliding mode equation $S=0$ remains unaffected, as $C{e}_i=0$, although the positive definite coefficient $L_1^{\sigma }$ transitions to another positive definite matrix during topology switching.

If the sliding mode $S=0$ is reached and maintained, $\dot{S}=0$, from (10), the equivalent control can be resolved as:

$$\begin{array}{cc}\hfill u_{eq}=& -{\left[\left(L_1^{\sigma }\otimes C\right)\mathrm{diag}\left\{g_1,g_2,\dots ,g_M\right\}\right]}^{-1}\left(L_1^{\sigma }\otimes C\right)\left[F+d-1_M\otimes f^0\left(x_{M+1},t\right)\right].\hfill \end{array}$$

(11)

In (11), the term is deduced as follows:

$$\begin{array}{cc}\hfill & {\left[\left(L_1^{\sigma }\otimes C\right)\mathrm{diag}\left\{g_1,g_2,\dots ,g_M\right\}\right]}^{-1}\left(L_1^{\sigma }\otimes C\right)\hfill \\ \hfill & ={\left[\left(L_1^{\sigma }\otimes I_m\right)\mathrm{diag}\left\{C{g}_1,C{g}_2,\dots ,C{g}_M\right\}\right]}^{-1}\left(L_1^{\sigma }\otimes C\right)\hfill \\ \hfill & =\mathrm{diag}\left\{{\left(C{g}_1\right)}^{-1},{\left(C{g}_2\right)}^{-1},\dots ,{\left(C{g}_M\right)}^{-1}\right\}{\left(L_1^{\sigma }\otimes I_m\right)}^{-1}\left(L_1^{\sigma }\otimes C\right)\hfill \\ \hfill & =\mathrm{diag}\left\{{\left(C{g}_1\right)}^{-1},{\left(C{g}_2\right)}^{-1},\dots ,{\left(C{g}_M\right)}^{-1}\right\}(I_m\otimes C)\hfill \\ \hfill & =\mathrm{diag}\left\{{\left(C{g}_1\right)}^{-1}C,{\left(C{g}_2\right)}^{-1}C,\dots ,{\left(C{g}_M\right)}^{-1}C\right\}.\hfill \end{array}$$

(12)

Substituting (12) into (11), the equivalent control can be obtained as:

$$\begin{array}{c}\hfill u_{i,eq}=-{\left(C{g}_i\right)}^{-1}C\left[f_i+d_i-f^0\left(x_{M+1},t\right)\right].\end{array}$$

(13)

Then, the i-th agent’s following error $e_i$ is partitioned as:

$$\begin{array}{cc}\hfill e_i& ={\left[{\left(e_i^1\right)}^T,{\left(e_i^2\right)}^T\right]}^T,\hfill \\ \hfill e_i^1& ={\left[e_{i,1},\cdots ,e_{n-m}\right]}^T,e_i^2={\left[e_{i,n-m+1},\cdots ,e_n\right]}^T,\hfill \end{array}$$

and the following equality holds,

$$C{e}_i=\left[C_1,C_2\right]e_i=C_1{e}_i^1+C_2{e}_i^2,$$

where $C=[C_1,C_2]$, $C_1\in R^{m\times \left(n-m\right)},$ and $C_2\in R^{m\times m}$. When the sliding mode is reached, $S_i=0$ and $C{e}_i=0$. It follows that $e_i^2=-C_2^{-1}{C}_1{e}_i^1$. (For simplicity, $C_2$ may be selected as $C_2=I_m$).

Consequently, the sliding mode equation of the i-th agent, based on the equivalent control (13), is given by:

$$\begin{array}{c}\left\{\begin{array}{c}{e}_i^2=-C_2^{-1}{C}_1{e}_i^1,\hfill \\ {\dot{e}}_i=[I_n-g_i{\left(C{g}_i\right)}^{-1}C](f_i+d_i-f^0\left(x_{M+1},t\right)).\hfill \end{array}\right.\hfill \end{array}$$

(14)

Define $g_i^{+}$ as the left P-inverse of the control matrix $g_i$, namely:

$$\begin{array}{c}\hfill g_i^{+}={\left(g_i^T{g}_i\right)}^{-1}{g}_i^T,\end{array}$$

and let $g_i^{\perp }\in R^{n\times \left(n-m\right)}$ denote the orthocomplement of the control matrix $g_i$ with $rank\left(g_i^{\perp }\right)=n-m$. Then, the following equality holds,

$$\begin{array}{c}\hfill g_i{g}_i^{+}+g_i^{\perp }{g}_i^{\perp +}=I_n,\end{array}$$

where $g_i^{\perp +}$ is the left P-inverse matrix of $g_i^{\perp }$, satisfying $g_i^{\perp +}{g}_i^{\perp }=I_{\left(n-m\right)}$.

One possible choice for the sliding mode surface parameter C is:

$$\begin{array}{c}\hfill C{g}_i=G(i.e.,C=G{g}_i^{+}),\forall i=1,2,\cdots ,M,\end{array}$$

(15)

where $G\in R^{m\times m}$ is an arbitrary full-rank matrix. Substituting the parameter (15) into (14), the sliding mode dynamic can be written as:

$$\begin{array}{c}\left\{\begin{array}{c}{e}_i^2=-C_2^{-1}{C}_1{e}_i^1,\hfill \\ {\dot{e}}_i=g_i^{\perp }{g}_i^{\perp +}\left[f_i+d_i-f^0\left(x_{M+1},t\right)\right].\hfill \end{array}\right.\hfill \end{array}$$

(16)

Corollary 1.

For the MASs (2), (3), when the sliding mode (4), (8), (9) is reached and maintained, (i.e., $S=0$), the stability (or convergence) of the consensus error of the i-th follower to the leader depends on the reduced-order error dynamics (14) or (16).

4. The Sliding Mode Control Protocol Design

4.1. The Control Protocol Design

The consensus control protocol is designed as follows:

$$\begin{array}{c}\hfill u_i=-\alpha {\eta }_i{S}_i-\beta k_i\mathrm{sgn}\left(S_i\right)-g_i^{+}{f}_i,\end{array}$$

(17)

where $\alpha ,\beta \in R$, $\alpha ,\beta >0$ are arbitrary positive scalars, $\mathrm{sgn}\left(S_i\right)={[\mathrm{sgn}\left(S_{i,1}\right),\cdots ,\mathrm{sgn}\left(S_{i,m}\right)]}^T$, and ${\eta }_i,k_i\in R^{m\times m},{\eta }_i,k_i>0$ are parameter matrices to be determined.

Substituting the control protocol (17) into the consensus error dynamics (5), the following is obtained:

$$\begin{array}{cc}\hfill {\dot{e}}_i=& f_i-f^0\left(x_{M+1},t\right)+d_i+g_i{u}_i\hfill \\ \hfill =& g_i^{\perp }{g}_i^{\perp +}{f}_i-f^0+d_i-\alpha g_i{\eta }_i{S}_i-\beta g_i{k}_i\mathrm{sgn}\left(S_i\right),\hfill \end{array}$$

(18)

and the overall consensus error dynamics are expressed as follows:

$$\begin{array}{cc}\hfill \dot{e}=& {\dot{x}}_F-1_M\otimes f^0\left(x_{M+1},t\right)\hfill \\ \hfill =& \overline{F}-1_M\otimes f^0+d-\alpha \mathrm{diag}\left\{g_1{\eta }_1,\dots ,g_M{\eta }_M\right\}S-\beta \mathrm{diag}\left\{g_1{k}_1,\dots ,g_M{k}_M\right\}\mathrm{sgn}\left(S\right),\hfill \end{array}$$

(19)

where

$$\begin{array}{cc}\hfill & \overline{F}={\left[{\left(g_1^{\perp }{g}_1^{\perp +}{f}_1\right)}^T,\cdots ,{\left(g_M^{\perp }{g}_M^{\perp +}{f}_M\right)}^T\right]}^T,\hfill \\ \hfill & \mathrm{sgn}\left(S\right)={\left[{\mathrm{sgn}}^T\left(S_1\right),\cdots ,{\mathrm{sgn}}^T\left(S_M\right)\right]}^T.\hfill \end{array}$$

4.2. Reachability of the Sliding Mode

The following results are obtained.

Theorem 1.

For the MAS (2), (3), the sliding mode (4), (8), (9) is achieved in finite time and maintained under the control protocol (17) if the parameter matrices satisfy

$$\begin{array}{cc}\hfill & L_1^{\sigma }\otimes I_m>{\beta }^{-1}{I}_{mM},\hfill \\ \hfill & k_i\ge [{\mu }_0+({\mu }_i+{\mu }_i^{\prime }+{\overline{\mu }}_i)\parallel C\parallel ]I_m,\hfill \end{array}$$

(20)

where ${\mu }_0>0$ is an arbitrary positive scalar,

$$\begin{array}{cc}\hfill {\mu }_i=& |a_{i(M+1)}^{\sigma }|({\overline{\lambda }}_0∥x_{M+1}∥+{\lambda }_0),\hfill \\ \hfill {\mu }_i^{\prime }=& \sum _{j=1}^M|l_{ij}^{\sigma }|{\overline{d}}_j,\hfill \\ \hfill {\overline{\mu }}_i=& \sum _{j=1}^M{\lambda }_j\parallel l_{ij}^{\sigma }{g}_j^{\perp }{g}_j^{\perp +}\parallel ·\parallel x_j\parallel .\hfill \end{array}$$

(21)

Proof. 

Consider the common Lyapunov function for the sliding mode surface dynamics (10) as $V=0.5S^{T}S$. Its time derivative along the overall consensus error dynamics (19) is:

$$\begin{array}{cc}\hfill \dot{V}=& S^T\left(L_1^{\sigma }\otimes C\right)\dot{e}\hfill \\ \hfill =& S^T\left(L_1^{\sigma }\otimes C\right)\left\{\overline{F}-1_M\otimes f^0+d\right\}-\alpha S^T\left(L_1^{\sigma }\otimes C\right)\mathrm{diag}\left\{g_1{\eta }_1,\dots ,g_M{\eta }_M\right\}S\hfill \\ \hfill & -\beta S^T\left(L_1^{\sigma }\otimes C\right)\mathrm{diag}\left\{g_1{k}_1,\dots ,g_1{k}_M\right\}\mathrm{sgn}\left(S\right)\hfill \\ \hfill =& S^T\left[(L_1^{\sigma }\otimes C)\overline{F}-\left(L_1^{\sigma }{1}_M\right)\otimes \left(C{f}^0\right)\right]+S^T\left(L_1^{\sigma }\otimes C\right)d\hfill \\ \hfill & -\beta S^T\left(L_1^{\sigma }\otimes I_m\right)\mathrm{diag}\left\{C{g}_1{k}_1,\dots ,C{g}_M{k}_M\right\}\mathrm{sgn}\left(S\right)\hfill \\ \hfill & -\alpha S^T\left(L_1^{\sigma }\otimes I_m\right)\mathrm{diag}\left\{C{g}_1{\eta }_1,\dots ,C{g}_M{\eta }_M\right\}S.\hfill \end{array}$$

(22)

On the right-hand side of (22), the first, second, and third terms satisfy the following inequalities based on the properties of the Laplacian matrix $L_1^{\sigma }$ and Assumption 1,

$$\begin{array}{cc}\hfill S^T(L_1^{\sigma }\otimes C)\overline{F}& ⩽\sum _{i=1}^M\sum _{j=1}^M∥l_{ij}^{\sigma }C{g}_j^{\perp }{g}_j^{\perp +}{f}_j∥∥S_i∥⩽\parallel C\parallel \sum _{i=1}^M{\overline{\mu }}_i\parallel S_i\parallel ,\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill S^T(L_1^{\sigma }\otimes C)d& ⩽\sum _{i=1}^M\sum _{j=1}^M∥l_{ij}^{\sigma }C{d}_j∥∥S_i∥⩽\parallel C\parallel \sum _{i=1}^M{\mu }_i^{\prime }∥S_i∥,\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill S^T\left[\left(L_1^{\sigma }{1}_M\right)\otimes \left(C{f}^0\right)\right]& ⩽\sum _{i=1}^M\left(∥a_{i(M+1)}^{\sigma }C{f}^0∥\right)∥S_i∥⩽\parallel C\parallel \sum _{i=1}^M{\mu }_i∥S_i∥.\hfill \end{array}$$

(25)

Combining (23), (24) and (25), the following inequality is obtained:

$$\begin{array}{cc}\hfill \dot{V}⩽& \parallel C\parallel \sum _{i=1}^M({\mu }_i+{\mu }_i^{\prime }+{\overline{\mu }}_i)∥S_i∥-\alpha S^T\left(L_1^{\sigma }\otimes I_m\right)\mathrm{diag}\left\{C{g}_1{\eta }_1,\dots ,C{g}_M{\eta }_M\right\}S\hfill \\ \hfill & -\beta S^T\left(L_1^{\sigma }\otimes I_m\right)\mathrm{diag}\left\{C{g}_1{k}_1,\dots ,C{g}_M{k}_M\right\}\mathrm{sgn}\left(S\right).\hfill \end{array}$$

(26)

By the properties of the Laplacian matrix $L_1^{\sigma }>0$, if the parameter matrix satisfies $C{g}_i>0$, the matrix inequalities

$$\begin{array}{c}\hfill \left(L_1^{\sigma }\otimes I_m\right)\mathrm{diag}\left\{C{g}_1{\eta }_1,\dots ,C{g}_M{\eta }_M\right\}>0,\\ \hfill \left(L_1^{\sigma }\otimes I_m\right)\mathrm{diag}\left\{C{g}_1{k}_1,\dots ,C{g}_M{k}_M\right\}>0\end{array}$$

easily hold. Therefore, under conditions (20) and (21), the following inequality is derived from (26),

$$\begin{array}{cc}\hfill \dot{V}⩽& \parallel C\parallel S^T\mathrm{diag}\left\{({\mu }_1+{\mu }_1^{\prime }+{\overline{\mu }}_1)I_m,\dots ,({\mu }_M+{\mu }_M^{\prime }+{\overline{\mu }}_M)I_m\right\}\mathrm{sgn}\left(S\right)\hfill \\ \hfill & -S^T\mathrm{diag}\left\{C{g}_1{k}_1,\dots ,C{g}_M{k}_M\right\}\mathrm{sgn}\left(S\right)\hfill \\ \hfill ⩽& -S^T\mathrm{diag}\left\{{\mu }_0{I}_m,\dots ,{\mu }_0{I}_m\right\}\mathrm{sgn}\left(S\right)\hfill \\ \hfill ⩽& -{\mu }_0\sum _{i=1}^M\parallel S_i{\parallel }_1.\hfill \end{array}$$

(27)

According to the Lyapunov stability theory, it is evident that the sliding mode $S=0$ is achieved in finite time. □

Lemma 1.

For the MAS (2), (3), the sliding mode (4), (8), (9), (15) is achieved in finite time and maintained under the control protocol (17) if the parameter matrices satisfy

$$\begin{array}{cc}\hfill & L_1^{\sigma }\otimes I_m>{\beta }^{-1}{I}_{mM},\hfill \\ \hfill & k_i\ge [{\mu }_0+({\mu }_1+{\mu }_i^{\prime })\parallel C\parallel ]I_m,\forall i=1,2,\cdots ,M,\hfill \end{array}$$

(28)

where ${\mu }_0>0$ is an arbitrary positive scalar.

Proof. 

If the sliding mode surface parameter $C=G{g}_i^{+}$, then the item $C{g}_i^{\perp }{g}_i^{\perp +}=0$ in (22). The proof directly follows the steps outlined in Theorem 1. □

Remark 3.

The control protocol (17) represents a completely distributed control in the SMC format for the MASs (2), (3) because its sliding mode (4), (8), (9) and its parameter conditions (20), (21), (28) rely solely on the information of the neighboring agents.

Remark 4.

The sliding surface dynamics (10) represent a switched system dynamic, in which the switching signal is the topology switching $\sigma \left(t\right)$. According to the stability analysis of switched systems, the switched dynamics (10) are finite-time stable if the time derivative of the common Lyapunov function (CLF) $V=0.5S^{T}S$ satisfies (27).

When the sliding mode is reached ($S_i=0$) and maintained, the consensus control protocol (17) simplifies to $u_i=-g_i^{+}{f}_i$. However, it cannot deal with the cooperative control requirements under the sliding mode unless the reduced-order system (14) or (16) is already stabilized. Therefore, an alternative consensus control protocol design, which utilizes the neighbors’ information more effectively, is proposed in the next section.

5. Application to Multiple WMRs

Consider the MAS where each agent is a wheeled mobile robot (WMR) modeled as in(2), (3), with

$$\begin{array}{cc}\hfill & f_i\left(x_i\right)=\left[\begin{array}{c}{x}_{i,3}cos{x}_{i,4}\\ x_{i,3}sin{x}_{i,4}\\ 0\\ 0\end{array}\right],g_i=\left[\begin{array}{cc}0& 0\\ 0& 0\\ 1& 0\\ 0& 1\end{array}\right],d_i=\left[\begin{array}{c}{d}_{i,1}\\ d_{i,2}\\ d_{i,3}\\ d_{i,4}\end{array}\right],\hfill \\ \hfill & u_i=\left[\begin{array}{c}{u}_{a,i}\\ u_{w,i}\end{array}\right],f^0(x_{M+1},t)=\left[\begin{array}{c}{v}_{d}cos{\phi }_d\\ v_{d}sin{\phi }_d\\ u_{F,d}\\ {\omega }_d\end{array}\right],\hfill \end{array}$$

(29)

where $x_{M+1}={[p_x,p_y,v_d,{\phi }_d]}^T$ represents the leader’s state, $p_x,p_y$ denote the position information in the horizontal and vertical directions, respectively; $v_d$ indicates the linear velocity and ${\phi }_d$ denotes the direction angle; The inputs $u_{F,d},$ and ${\omega }_d$ are the known control signals of the leader, while $u_{a,i},$ and $u_{w,i}$ are the control inputs of the followers.

5.1. Coordinate Transformation

Under the assumption that the agent speed $x_{i,3}\ne 0$ (the leader $v_d\ne 0$), the following control transformation is given:

$$\left\{\begin{array}{c}{u}_{a,i}=v_{1,i}cos{x}_{i,4}+v_{2,i}sin{x}_{i,4},\hfill \\ u_{w,i}={\displaystyle \frac{1}{x_{i,3}}}\left(v_{2,i}cos{x}_{i,4}-v_{1,i}sin{x}_{i,4}\right),\hfill \end{array}\right.$$

(30)

where $v_i={\left[v_{1,i},v_{2,i}\right]}^T$ represents the auxiliary control inputs to be designed.

Define the state transformation vector for the followers as:

$$\left\{\begin{array}{c}{z}_{i,1}=x_{i,1},\hfill \\ z_{i,2}=x_{i,2},\hfill \\ z_{i,3}=x_{i,3}cos{x}_{i,4},\hfill \\ z_{i,4}=x_{i,3}sin{x}_{i,4}.\hfill \end{array}\right.$$

(31)

The state vector $z_i={[z_{i,1},z_{i,2},z_{i,3},z_{i,4}]}^T$ is the transformed state vector of the $i$-th follower. Based on the transformations (30) and (31), the dynamics of the followers are expressed as:

$$\left\{\begin{array}{c}{\dot{z}}_{i,1}=z_{i,3}+d_{i,1},\hfill \\ {\dot{z}}_{i,2}=z_{i,4}+d_{i,2},\hfill \\ {\dot{z}}_{i,3}=v_{1,i}+cos{x}_{i,4}{d}_{i,3}-z_{i,4}{d}_{i,4},\hfill \\ {\dot{z}}_{i,4}=v_{2,i}+sin{x}_{i,4}{d}_{i,3}+z_{i,3}{d}_{i,4}.\hfill \end{array}\right.$$

(32)

Similarly, the leader dynamics are transformed using the state transformation $z_0={[z_{0,1},z_{0,2},z_{0,3},z_{0,4}]}^T={[p_x,p_y,v_{d}cos{\phi }_d,v_{d}sin{\phi }_d]}^T$, resulting in

$$\left\{\begin{array}{c}{\dot{z}}_{0,1}=z_{0,3},\hfill \\ {\dot{z}}_{0,2}=z_{0,4},\hfill \\ {\dot{z}}_{0,3}=v_1^0,\hfill \\ {\dot{z}}_{0,4}=v_2^0,\hfill \end{array}\right.$$

(33)

where

$$\left\{\begin{array}{c}{v}_1^0=u_{F,d}cos{\phi }_d-v_d{\omega }_{d}sin{\phi }_d,\hfill \\ v_2^0=u_{F,d}sin{\phi }_d+v_d{\omega }_{d}cos{\phi }_d.\hfill \end{array}\right.$$

Define the consensus error vector $e_i={[e_{i,1},e_{i,2},e_{i,3},e_{i,4}]}^T$, where $e_{i,j}=z_{i,j}-z_{0,j},\forall j=1,2,3,4$. Using(32) and (33), the consensus error dynamics are expressed as:

$$\left\{\begin{array}{c}{\dot{e}}_{i,1}=e_{i,3}+d_{i,1},\hfill \\ {\dot{e}}_{i,2}=e_{i,4}+d_{i,2},\hfill \\ {\dot{e}}_{i,3}=v_{1,i}-v_1^0+d_{i,3}^{\prime },\hfill \\ {\dot{e}}_{i,4}=v_{2,i}-v_2^0+d_{i,4}^{\prime },\hfill \end{array}\right.$$

(34)

where $d_{i,3}^{\prime }=cos{x}_{i,4}{d}_{i,3}-z_{i,4}{d}_{i,4}$, $d_{i,4}^{\prime }=sin{x}_{i,4}{d}_{i,3}+z_{i,3}{d}_{i,4}$.

Design the sliding mode surface as in (4), (8), (9) with

$$C=[C_1,C_2]=\left[\begin{array}{cccc}{c}_1& 0& 1& 0\\ 0& c_2& 0& 1\end{array}\right],$$

(35)

where $c_1,c_2>0$ are positive scalars.

As the sliding mode is reached and maintained,

$$S_i=C_1{e}_i^1+e_i^2=0,$$

which implies $e_i^2=-C_1{e}_i^1$, where $e_i^1={\left[e_{i,1},e_{i,2}\right]}^T$, $e_i^2={\left[e_{i,3},e_{i,4}\right]}^T$.

5.2. The Control Protocol Design

It is obvious that $g_i^{+}{f}_i=0$ for the WMRs. Therefore, the consensus control protocol $v_i$ is given by (17), with parameter matrices satisfying the conditions (20) and (21) as stated in Theorem 1. The sliding mode is achieved in finite time and remains at $S=0$.

5.3. The Stability of the Sliding Mode

By substituting (35) and the matrices $g_i$ of the WMR dynamics, the consensus error dynamics (14) become

$$\begin{array}{c}\left\{\begin{array}{c}{e}_i^2=-C_1{e}_i^1\hfill \\ {\dot{e}}_i^1=-C_1{e}_i^1+d_i^1\hfill \end{array}\right.\hfill \end{array}$$

(36)

where $d_i^1={[d_{i,1},d_{i,2}]}^T$.

For the WMRs, it is evident that the consensus error dynamics of the i-th follower under the sliding mode are order-reduced and linear. If the matrix $C_1$ is Hurwitz, the consensus error of the i-th follower is boundedly stable.

Theorem 2.

For the WMRs (2), (3), (29) under the sliding mode (4), (8), (9), (35), if there exist a positive definite symmetric matrix P, a positive scalar δ and the designed matrix $C_1$ satisfying the following linear matrix inequality

$$\begin{array}{cc}\hfill & \left[\begin{array}{cc}-C_1^{T}P-P{C}_1+I& P\\ P& -{\delta }^{2}I\end{array}\right]<0,\hfill \end{array}$$

(37)

then the consensus error is robustly asymptotically stable when $d_i=0$, and satisfies the $L_2$ gain δ when $d_i\ne 0$, assuming the same initial state condition or zero initial state conditions between the leader and followers.

Proof. 

Consider the Lyapunov function $V={\left(e_i^1\right)}^{T}P{e}_i^1$, and calculate its time derivative along with the dynamics (36),

$$\begin{array}{cc}\hfill \dot{V}=& -{\left(e_i^1\right)}^T[C_1^{T}P+P{C}_1]e_i^1+2{\left(e_i^1\right)}^{T}P\left(d_i^1\right).\hfill \end{array}$$

(38)

Based on the above equation, it can be easily obtained that

$$\begin{array}{cc}\hfill & \dot{V}+{\left(e_i^1\right)}^T{e}_i^1-{\delta }^2{\left(d_i^1\right)}^T{d}_i^1={\zeta }^T\left[\begin{array}{cc}-C_1^{T}P-P{C}_1+I& P\\ P& -{\delta }^{2}I\end{array}\right]\zeta ,\hfill \end{array}$$

where $\zeta ={[{\left(e_i^1\right)}^T,{\left(d_i^1\right)}^T]}^T$. If the condition (37) is satisfied, the following inequality can be obtained.

$$\begin{array}{cc}\hfill & \dot{V}+{\left(e_i^1\right)}^T{e}_i^1-{\delta }^2{\left(d_i^1\right)}^T{d}_i^1<0.\hfill \end{array}$$

Integrating over time,

$$\begin{array}{cc}\hfill & {\int }_0^t{\left(e_i^1\right)}^T{e}_i^{1}dt-{\delta }^2{\int }_0^t{\left(d_i^1\right)}^T{d}_i^{1}dt<V\left(0\right)-V\left(t\right).\hfill \end{array}$$

(39)

It follows that

$$\sup {\displaystyle \frac{\parallel e_i^1{\parallel }_2}{\parallel d_i^1{\parallel }_2}}<\delta ,$$

if the consensus error $e_i\left(0\right)=0$ under the same initial state condition or zero initial state conditions between the leader and the followers. Otherwise, if $d_i\equiv 0$, $\dot{V}<0$, and the consensus error becomes asymptotically stable. □

Remark 5.

For the multiple WMRs (2), (3), (29), when the sliding mode (4), (8), (9), (35) is achieved and maintained, the convergence of the consensus error is independent of topology switching, as determined by the reduced-order error dynamics (36).

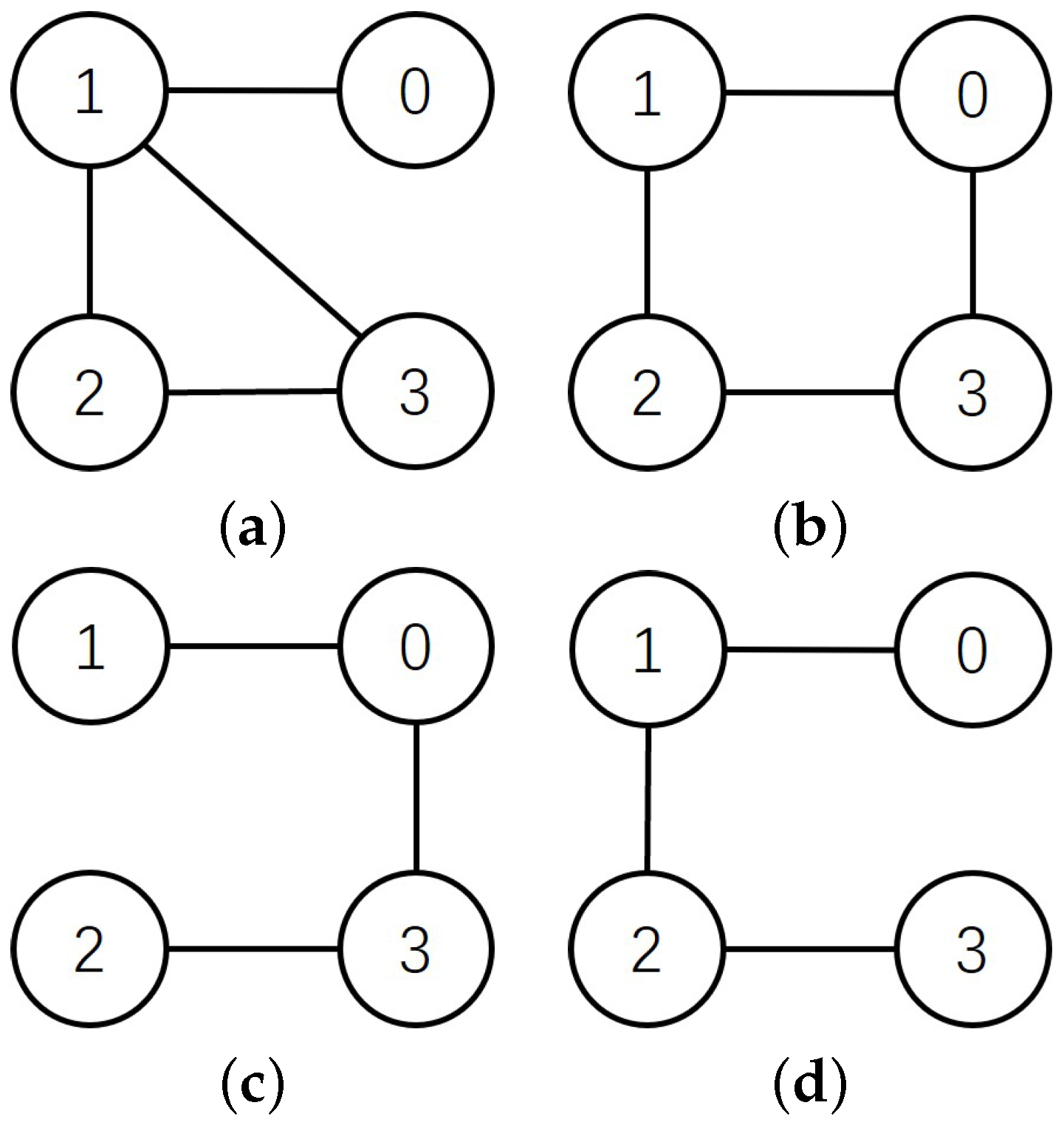
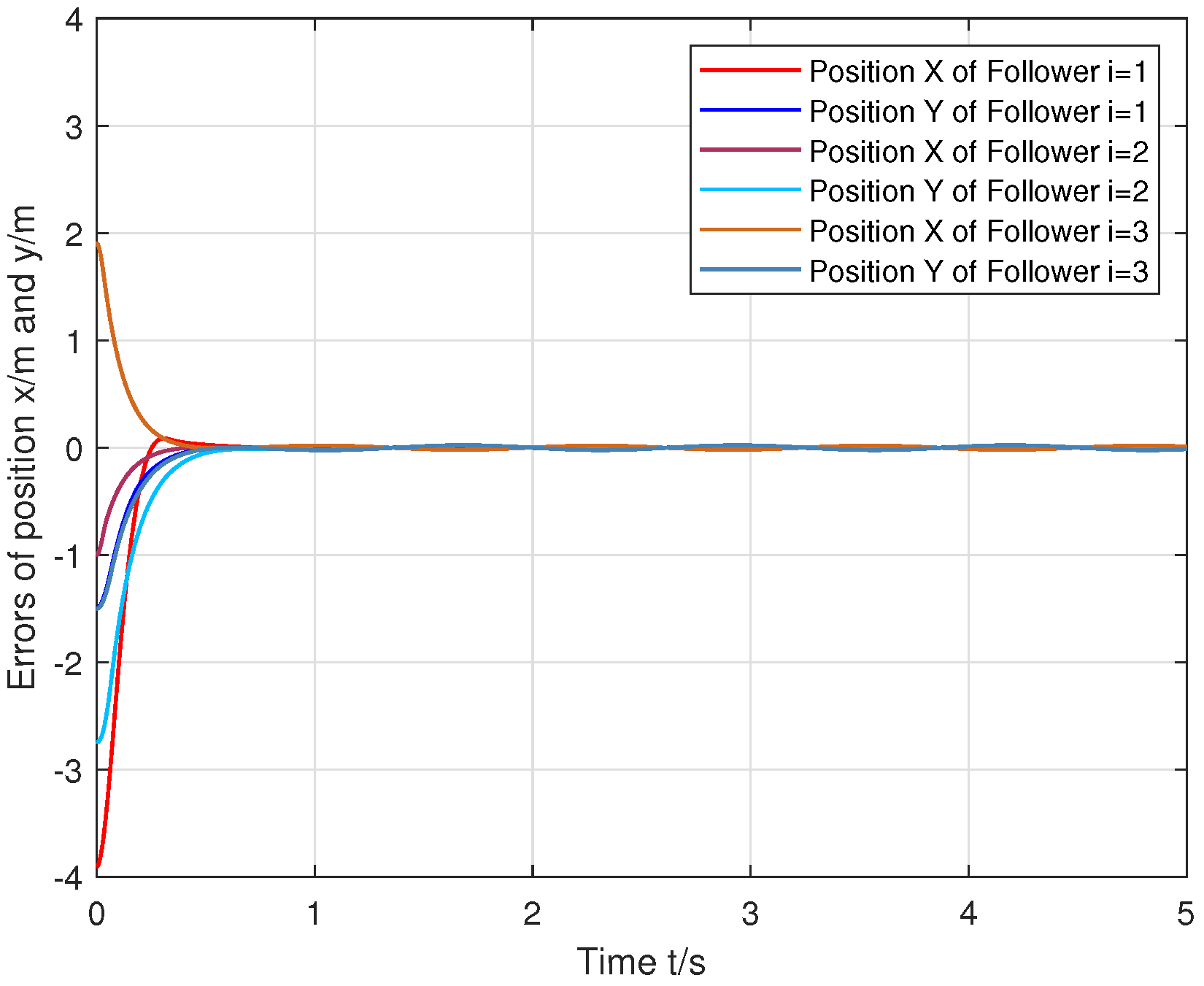
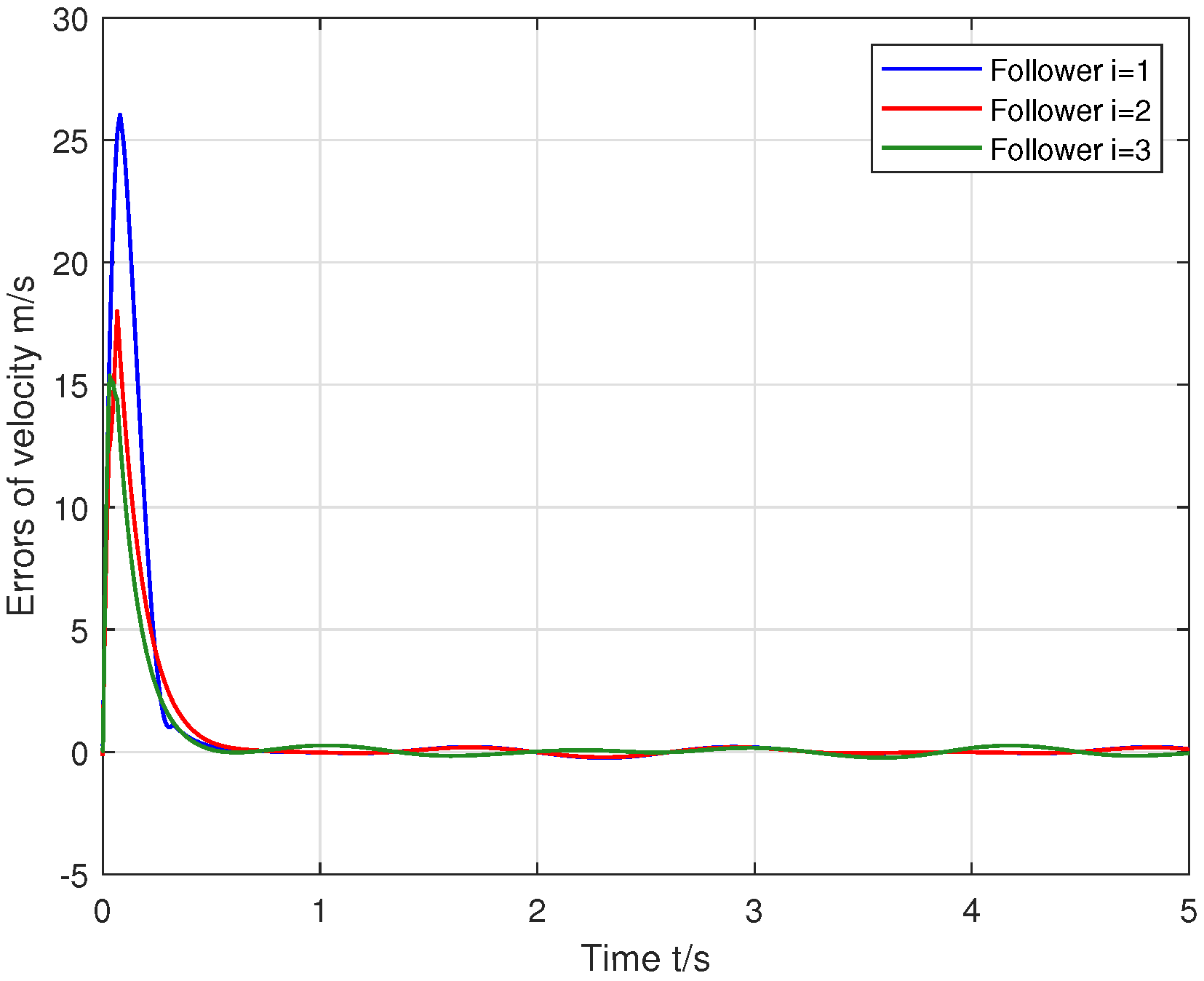
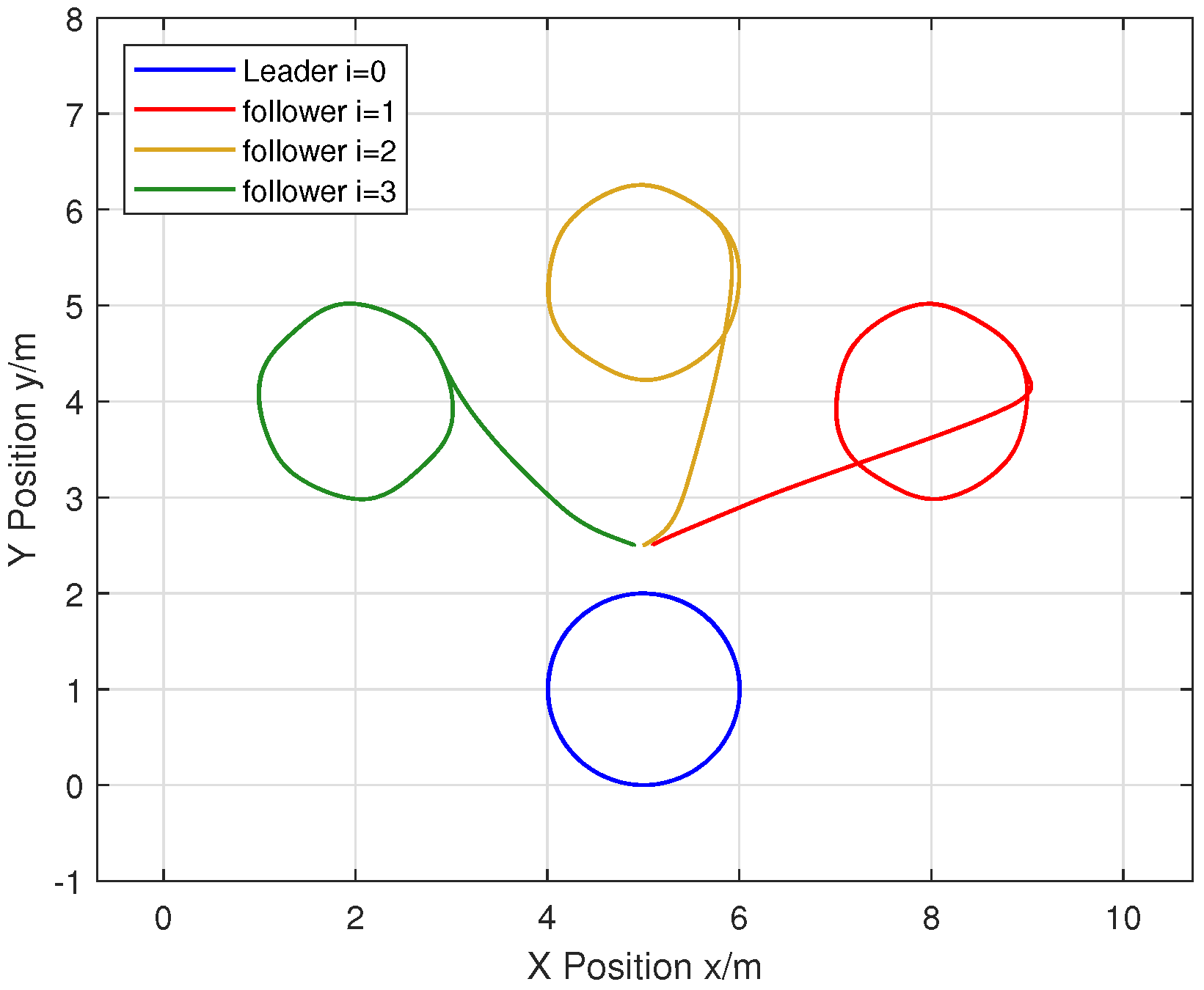
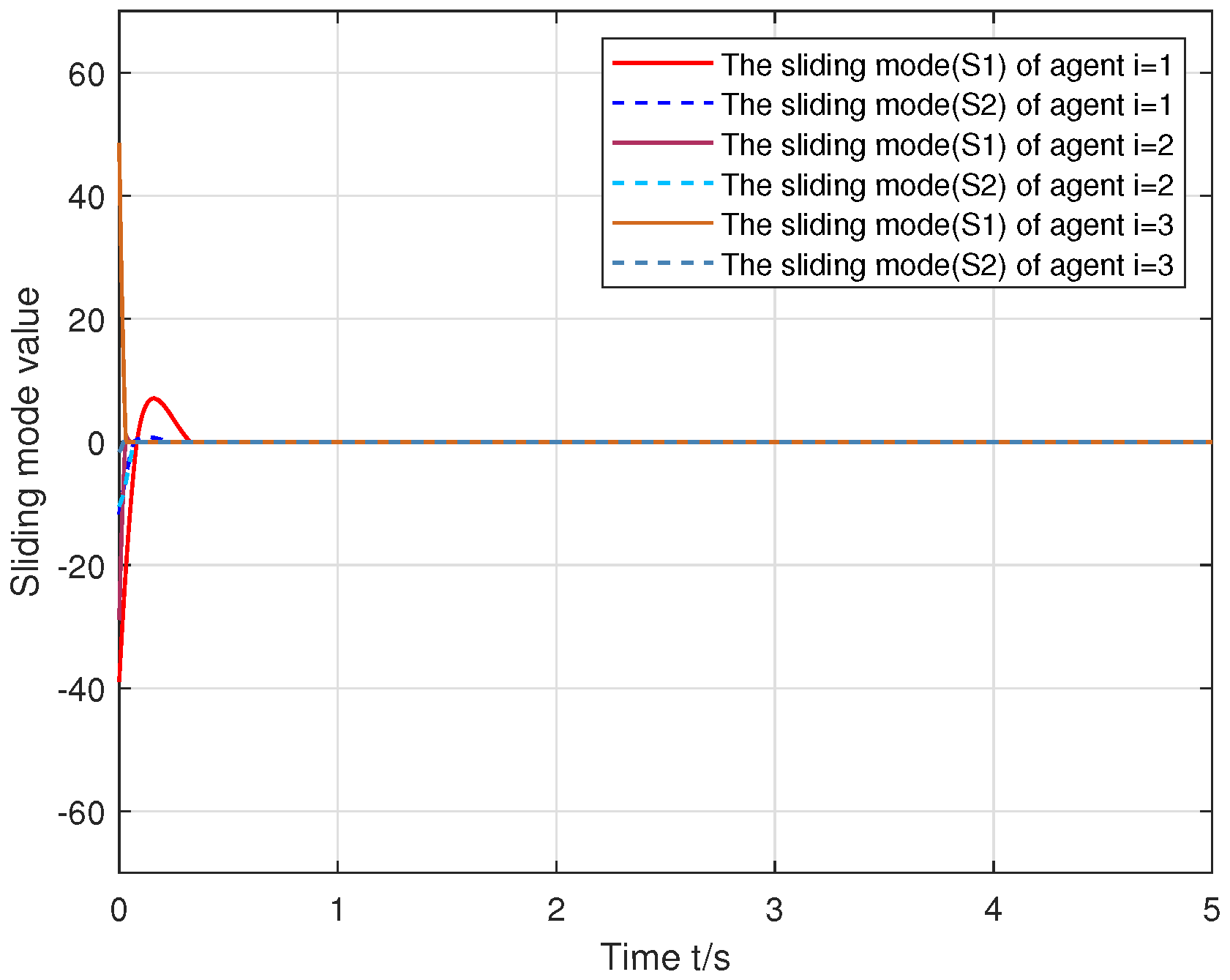
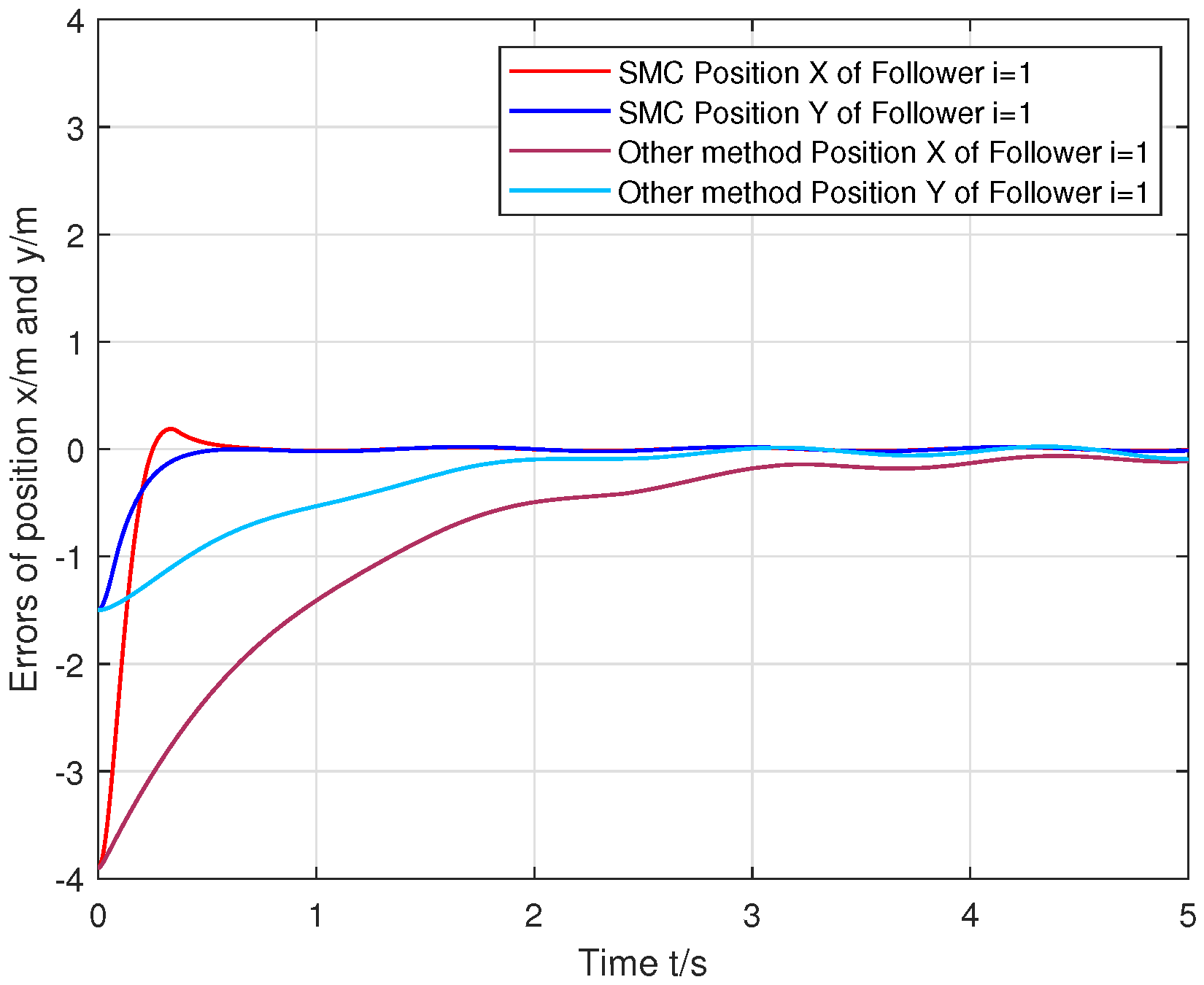
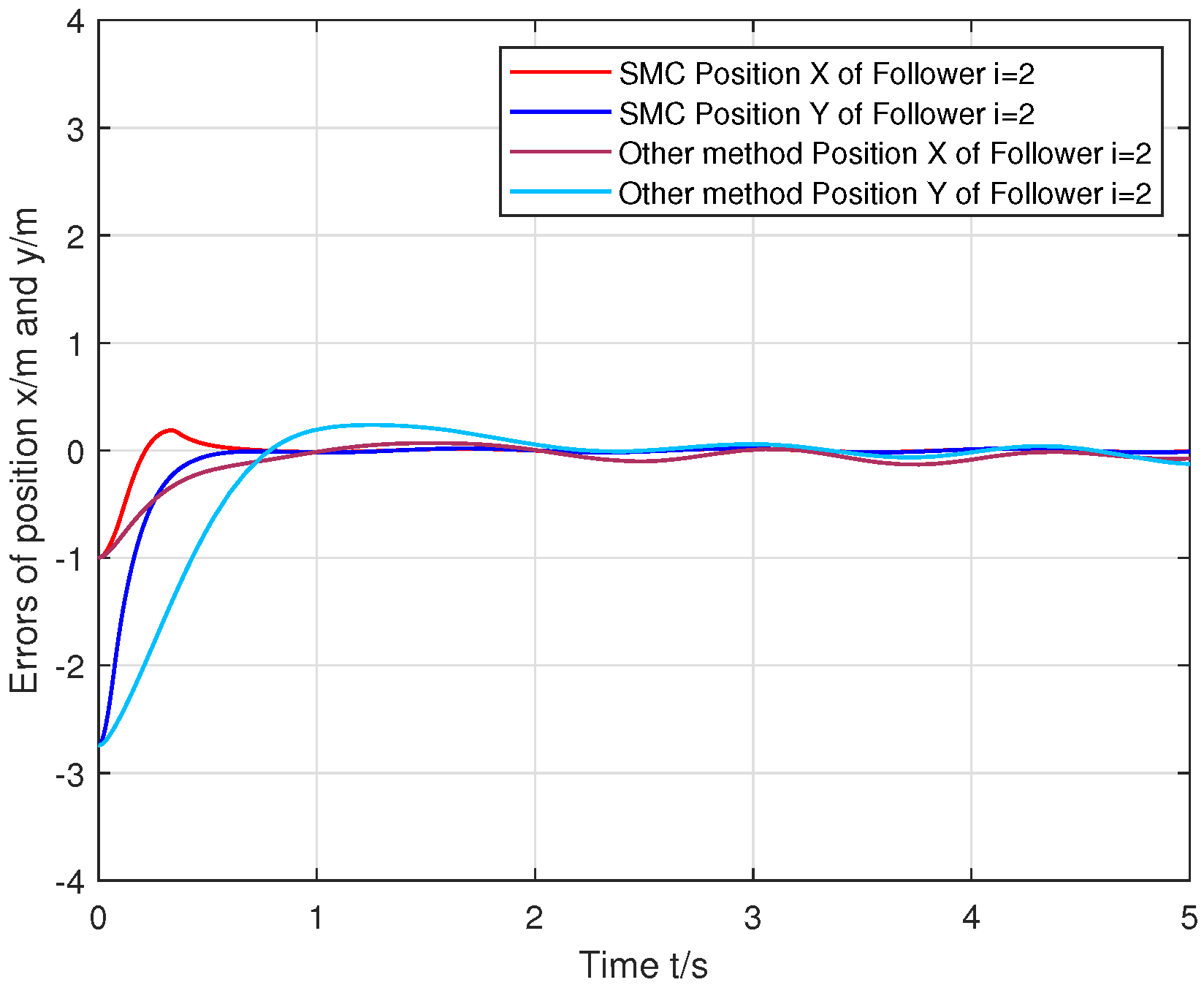
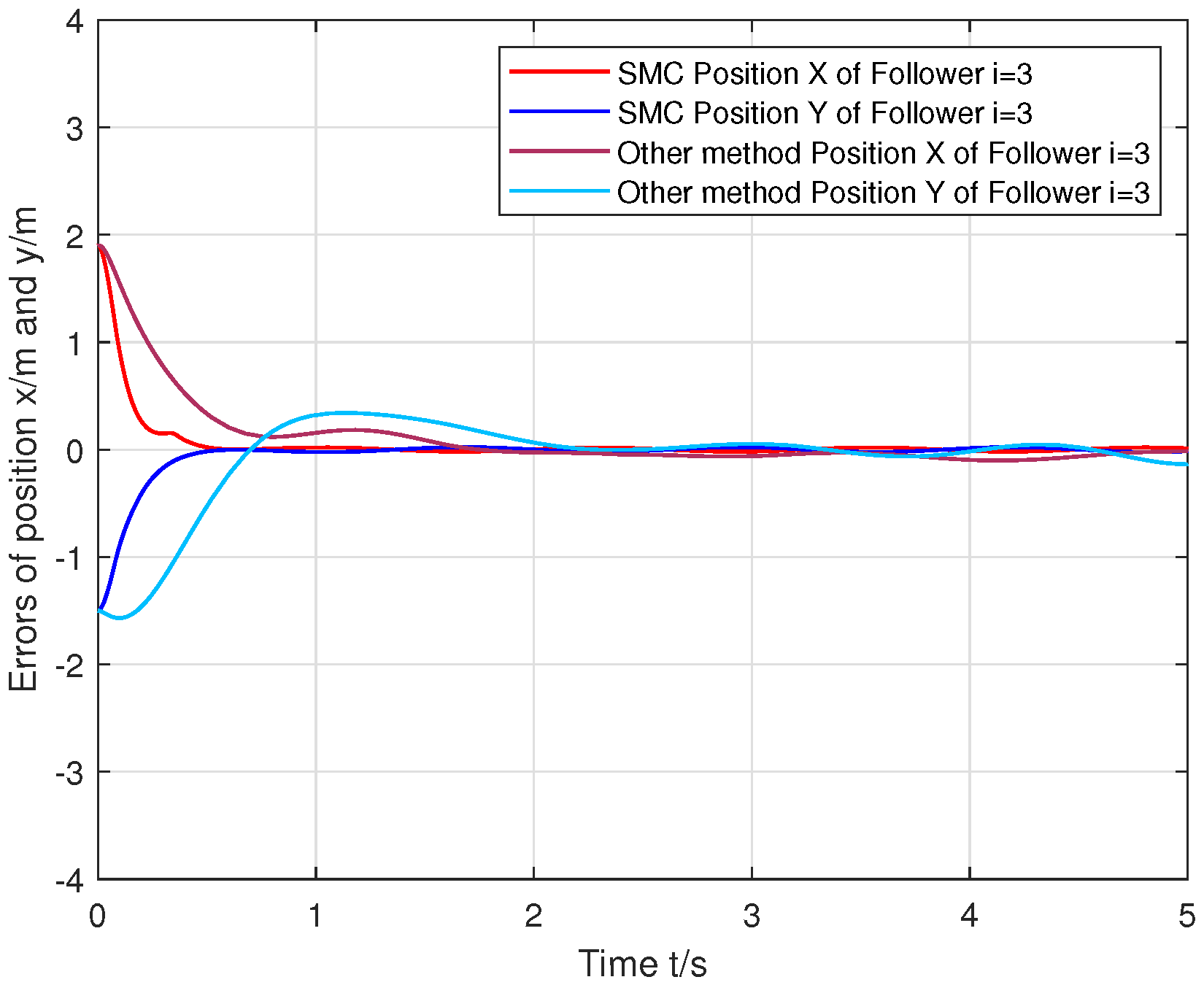
6. Simulation Tests

In this section, MATLAB2022a software was used to verify the proposed control protocol, and the Simulink module in MATLAB was employed to build and test the WMRs system. The computer specifications are as follows: CPU: Intel Core i7-12700K; Mainboard: Intel B660; RAM: DDR5, 5600MHz, 16GB; Graphics Card: NVIDIA GeForce RTX; Hard Disk: SSD 500GB.

A multiple WMRs system (29) was considered, consisting of one leader labeled as $i=0$ and three followers labeled as $i=1,2,3$. The sliding mode was designed based on (4), (8), (9) and (35). The interconnection topology was time-varying with a switching period of 0.8s among four graphs ${\mathcal{G}}^{\sigma }$, as shown in Figure 1, and the corresponding switching signal $\sigma \left(t\right)$ is depicted in Figure 2. The Laplacian matrices for the four graphs ${\mathcal{G}}^{\kappa }$($\kappa =1,2,3,4$) are:

$$\begin{array}{c}\hfill L_1^1=\left(\begin{array}{ccc}3& -1& -1\\ -1& 2& -1\\ -1& -1& 2\end{array}\right),L_2^1=\left(\begin{array}{c}-1\\ 0\\ 0\end{array}\right),\\ \\ \hfill L_1^2=\left(\begin{array}{ccc}2& -1& 0\\ -1& 2& -1\\ 0& -1& 2\end{array}\right),L_2^2=\left(\begin{array}{c}-1\\ 0\\ -1\end{array}\right),\\ \\ \hfill L_1^3=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& -1\\ 0& -1& 2\end{array}\right),L_2^3=\left(\begin{array}{c}-1\\ 0\\ -1\end{array}\right),\end{array}$$

 

$$\begin{array}{c}\hfill L_1^4=\left(\begin{array}{ccc}2& -1& 0\\ -1& 2& -1\\ 0& -1& 1\end{array}\right),L_2^4=\left(\begin{array}{c}-1\\ 0\\ 0\end{array}\right).\end{array}$$

The parameter values of the control protocol were designed as $\alpha$ = 2, $\beta$ = 0.5, $\gamma$ = 1, ${\eta }_1={\eta }_2={\eta }_3=\mathrm{diag}\left\{8,8\right\}$, and

$$C=\left[\begin{array}{cccc}10& 0& 1& 0\\ 0& 8& 0& 1\end{array}\right],$$

The parameter $k_i$ was designed to satisfy the conditions in (20) and (21).

The initial state of the leader was set to ${[6,1,1,0.5\pi ]}^T$. The initial state of the three followers ($i=1,2,3$) were set to ${[5.1,2.5,1.25,0.5\pi ]}^T$, ${[5,2.5,0.85,0.15\pi ]}^T$, and ${[4.9,2.5,1.15,0.3\pi ]}^T$, respectively. To validate the robust effectiveness, the simulation test considered the WMRs under both matched and unmatched disturbances. The disturbances for the three followers were assumed as follows:

$$\begin{array}{cc}\hfill & d_1={\left[\begin{array}{cccc}0.2sin5t& 0.2sin5t& 0.6sint& 0.8sin5t\end{array}\right]}^T,\hfill \\ \hfill & d_2={\left[\begin{array}{cccc}0.18sin5t& 0.18sin5t& 0.5sin2t& 0.7sin6t\end{array}\right]}^T,\hfill \\ \hfill & d_3={\left[\begin{array}{cccc}0.22sin5t& 0.22sin5t& 0.7sin1.5t& 0.9sin4t\end{array}\right]}^T.\hfill \end{array}$$

The $L_2$ gain was selected as $\delta =0.02$, and the parameters satisfied condition (37). The position tracking error in the X-Y directions, the linear velocity consensus error, and the yaw angle tracking error of the three followers are shown in Figure 3, Figure 4 and Figure 5.

Figure 3 shows that the X-Y position errors of the three followers converged to the origin at about 0.6 s. In the steady state, the position exhibited small oscillations due to the presence of mismatched disturbance. However, the oscillation amplitudes were suppressed within $\pm 0.02$. Compared with the unmatched disturbance amplitudes of 0.2, the control protocol displayed a robust suppression effect on the mismatched disturbances, validating Theorem 2.

From Figure 4, the line velocity tracking errors of the three followers converged to the origin at about 0.7 s despite the presence of external disturbances. Similarly, Figure 5 shows that the yaw angle tracking errors of the three followers also converged to the origin at about 0.7 s under external disturbances. The oscillation amplitudes of the line velocity and yaw angle tracking errors were greater than those of the position errors, which can be attributed to the relationship in the first line of (36) and the parameter $C_1$.

Based on the proposed control protocol, the formation control of the MAS can be achieved by adding a constant relative position vector to the consensus error $e_i$ for each follower. This is expressed as:

$$\begin{array}{cc}\hfill e_i=& z_i-z_0-p_i\hfill \end{array}$$

where $p_i\in {\mathbb{R}}^n$ is the constant relative position vector. For each follower, $e_i$ converges to 0 under the control protocol, leading to

$$z_i-z_0=p_i.$$

Each follower’s relative position vector is defined as $p_i={[p_{i,x},p_{i,y},0,0]}^T$. Consequently, the velocity of each follower aligns with the leader’s velocity, while position maintains a constant relative position value $(p_{i,x},p_{i,y})$. Setting $p_1={[3,3,0,0]}^T,p_2={[0,4.24,0,0]}^T,$ and $p_3={[-3,3,0,0]}^T$, the formation result is shown in Figure 6.

Figure 6 illustrates the motion path of the three followers and the leader. Despite the presence of external disturbances, the three followers successfully tracked the leader’s motion under the control protocol (17). Moreover, the motion trajectory tracking demonstrated strong robustness.

Figure 7 presents the sliding mode values of the three followers, validating that the sliding mode convergency and stability were unaffected by both matched and mismatched disturbances.

To explore the merits of the proposed SMC control protocol, a comparison was conducted, and the results are shown in Figure 8, Figure 9 and Figure 10. A prescribed-time formation tracking scheme for second-order MASs [30] was adopted for comparison. In [30], the follower model in the MAS is described as:

$$\begin{array}{c}\hfill {\dot{p}}_i\left(t\right)=v_i\left(t\right),\\ \hfill {\dot{v}}_i\left(t\right)=u_i\left(t\right),\end{array}$$

and the control protocol is defined as:

$$\begin{array}{c}\hfill u_i=-\left(c+b{\displaystyle \frac{\dot{\mu }}{\mu }}\right)\sum _{j\in N_i}{a}_{ij}^{\ast }\left[K_p\left(p_i-p_j\right)+K_v\left(v_i-v_j\right)\right],\end{array}$$

where $a_{ij}^{\ast }$ is the weights between agents, $K_p$ and $K_v$ are positive constant gains, $c>0$ and $b>0$ are selected parameters, and $\mu$ is a designed scaling function.

From the position tracking errors of the followers $i=1,2,3$ in Figure 8, Figure 9 and Figure 10, it can be seen that the response speed of the proposed SMC control protocol is faster than the compared method. Furthermore, the robustness performance of the proposed SMC control protocol in the steady state is significantly more efficient than the other method.

Several potential challenges exist in future experimental work. First, the effectiveness of the control may be influenced by robot hardware due to factors such as communication delays between actual vehicles, power limitations, or constraints on computational resources. Second, the path trajectory achieved in the current simulation is limited to a small range, and its cooperative control effectiveness in larger areas remains uncertain. Additionally, the designed expected trajectory does not account for the potential forced collisions between vehicles.

The simulation tests validated the proposed cooperative control scheme. However, the scheme has certain limitations. For example, the stability of the sliding mode relies on the dynamics of specific model components, denoted as $f_i$. While the $f_i$ is inapplicable, it may result in unstable sliding mode dynamics. Additionally, the control protocol outlined in this paper requires sufficient information from neighbor agents. In cases where unconnected communication typologies exist, parts of the neighbor state information may be unavailable. A possible solution would involve the use of agent state observers.

7. Conclusions

A completely distributed consensus sliding mode control protocol (SMCP) is proposed for heterogeneous nonlinear multi-agent systems (MAS) with disturbances under switching topology. The global sliding mode manifold (GSMM) is designed for the overall MAS dynamics, which results in reduced-order dynamics for each follower agent. The stability of these dynamics depends on the reduced-order nonlinear components. A corresponding consensus SMCP is proposed for the cooperative control of the MAS. The control protocol features a simple control structure and guarantees the finite-time reachability of the GSMM. Due to the common sliding mode control structure, the protocol achieves complete robustness against matched disturbances. Additionally, the control protocol realizes completely distributed cooperative control as the control signal only requires information from neighbor agents. The proposed SMCP design was applied to multiple-wheeled mobile robots (WMRs) formation and simulation test results confirmed its feasibility and effectiveness.