Abstract
This study addresses the completely distributed consensus control problem for the heterogeneous nonlinear multi-agent system (MAS) with disturbances under switching topology. First, a global sliding mode manifold (GSMM) is designed for the overall MAS dynamic, which maintains stability without oscillations during topology switching after achieving the sliding mode. Subsequently, a consensus sliding mode control protocol (SMCP) is proposed, adopting the common sliding mode control (SMC) format and ensuring the finite-time reachability of the GSMM under topology switching. Finally, the proposed GSMM and SMCP are applied to the formation control of multiple-wheeled mobile robots (WMRs), and simulation results confirm their feasibility and effectiveness. The proposed SMCP design demonstrates key advantages, including a simple control structure, complete robustness to matched disturbance, and reduced-order dynamics under the sliding mode.
1. Introduction
Completely distributed cooperative control of multi-agent systems (MASs) has emerged as a significant research domain in recent years [1,2,3]. Cooperative control design has been successfully applied to various fields, including UAV formation control [4], multi-robot system (MRS) trajectory tracking [5] and satellite cluster attitude alignment [6]. Within multi-agent systems, cooperative control enables the execution of more complex and challenging control tasks, making significant contributions to humanity. Among these efforts, the consensus problem [7,8,9] is a fundamental objective in the cooperative control of MASs.
For the consensus problem, MASs can be categorized into two types: systems with leaders [10] and systems without leaders [11,12,13]. Research on consensus problems for MASs with linear structures has already been extensively developed. For instance, Rezaee and Abdollahi proposed a consensus control protocol that relies solely on relative positions in high-order MASs under undirected networks [14]. Chen et al. investigated the completely distributed consensus control problem for general linear MASs via a dynamic event-triggered scheme [15]. Some scholars have focused on finite-time stability and fixed-time stability in the context of the consensus problem for MASs [16,17,18,19,20]. For example, Wang et al. introduced a new distributed finite-time optimization algorithm for agents under directed graphs [21], while He et al. explored the fast finite-time tracking consensus problem for first-order nonlinear MASs [22]. In practical applications, methods based on the leader-following consensus framework are widely adopted.
In recent decades, sliding mode control (SMC) has undergone significant development, including methods such as the nonsingular terminal sliding mode [23] and the global sliding mode [24]. SMC methods have been applied to many industrial applications, including typical MASs, due to their simplicity and robustness. Cai et al. implemented sliding mode control for singular switched MASs by presenting a general integral-type sliding mode control rule based on mode-dependent average dwell time [25]. Ma et al. addressed the finite-time consensus problem for heterogeneous MASs with second-order linear and nonlinear agents, where communication between agents was described by directed graphs [26]. Nie et al. examined the finite-time consensus tracking problem of MASs with unknown follower states under SMC control in the presence of actuator attacks [27]. Jin et al. investigated predefined-time consensus for a class of second-order nonlinear MASs using a sliding mode technique [28]. Song et al. proposed an optimized leader-follower consensus control for multiple robot manipulator systems by combining sliding mode control with reinforcement learning [29].
Despite the significant progress in the research on various MASs, many of these studies have limitations. Some fail to provide a completely distributed control protocol. For instance, in tracking consensus control problems, the control protocol often relies on the leader’s control input information. Others neglect the nonlinear dynamic model of the followers. Numerous studies on switching topology cases focus on single or double-integrator systems or linear dynamic MASs without addressing the heterogeneous nature of MASs. Specifically, few studies tackle the tracking consensus control problem for both heterogeneous and high-order nonlinear dynamic MASs under switching topology. Moreover, only a limited number of results offer a completely distributed sliding mode control protocol that eliminates the need for the leader’s control input in such MASs.
This paper investigates the completely distributed consensus control problem for heterogeneous nonlinear MASs with disturbances under switching topology. To develop a sliding mode control protocol with a simple structure similar to common SMC, a global sliding mode manifold (GSMM) is designed for the overall MAS dynamic. The GSMM remains stable without oscillation during topology switching once the sliding mode is achieved. A corresponding consensus SMCP is proposed, guaranteeing finite-time reachability regardless of topology changes. The proposed SMCP design offers complete robustness to matched disturbances, similar to conventional SMC, and results in a reduced-order dynamic under the sliding mode. Finally, the proposed SMCP design is applied to the formation control of multiple-wheeled mobile robots (WMRs), validating its feasibility and effectiveness.
The contributions of the paper are summarized as follows.
- (a).
- A GSMM for MASs is proposed, which remains unaffected by topology switching. The consensus performance under the sliding mode is determined by the design of the sliding mode manifold parameters. Moreover, order reduction is realized.
- (b).
- A completely distributed control protocol based on the GSMM is proposed. It features a sliding mode control format, a simple structure, and strong robustness. The control protocol and its parameters depend solely on information from neighboring agents.
- (c).
- The proposed cooperative control protocol is applied to WMRs.
The remainder of the paper is organized as follows. Section 2 describes the problem. Section 3 introduces the design of the GSMM surface and analyzes its ideal sliding mode dynamics. Section 4 presents the control protocol design based on the GSMM and examines the finite-time reachability of the GSMM. Section 5 provides the application of the presented tracking consensus SMCP. Section 6 verifies the control protocol design through simulation results for WMRs. Finally, Section 7 concludes the paper.
2. Preliminary and Problem Formulation
2.1. Graph Theory
The communication topology among the M agents is characterized by an undirected switching graph. In particular, it is assumed that the topology switches within a given graph set , where , .
For analytical convenience consider an infinite sequence of non-overlapping time intervals , with where . During each interval, the communication topology is fixed. In this context, the positive constant is referred to as the dwell time. The time sequence is defined as the switching sequence along which the communication topology changes. Based on this description, let be the communication topology of the considered MAS at time t, where . The piecewise constant function serves as the switching signal. Notably, , for all .
Directed graphs are used to model the information interaction among agents. Let be a directed graph, where is a finite, nonempty set of nodes, and is the edge set. An edge of is denoted by , which starts from i and ends at node j, indicating that node i can directly receive information from node j. The set of all neighbors of node i is denoted as . A graph is called an undirected graph if and only if implies , otherwise, it is considered a directed graph. An undirected path in an undirected graph is defined analogously. The weighted adjacency matrix of the graph is defined such that if , and , otherwise. For an undirected graph, we assume that . The Laplacian matrix of is defined as and . Obviously, the Laplacian matrix and the weighted adjacency matrix are both symmetric for an undirected graph.
Consider a group consisting of M followers, labeled as agents 1 to M, and leaders, labeled as agent . The communication topology among the agents, denoted as , is assumed to remain fixed during the interval when the switching signal . Let be the weighted adjacency matrix, and be the Laplacian matrix of the agents. Then, the following holds.
where .
2.2. The Consensus Control Problem
Consider multiple followers of general nonlinear systems
where represents the agent state, is the control input, denotes the unknown disturbance, is the nonlinear vector field, and is the control matrix.
The leader is described as:
where is a nonlinear vector function.
To facilitate the analysis, the following assumptions are made.
Assumption 1.
The nonlinear vector field is piecewise Lipschitz continuous, satisfying where is a positive scalar. Furthermore, .
Assumption 2.
The nonlinear vector function is Lipschitz continuous and satisfies where and are positive scalars.
Assumption 3.
The control matrix is full-rank, i.e., ensuring the controllability of the agent.
Assumption 4.
The unknown disturbance is bounded, satisfying , where is positive scalar.
Assumption 5.
The unknown disturbance does not affect the equilibrium of the nonlinear dynamic in (2).
Assumption 6.
For each , the directed graph contains a directed spanning tree with node as the root.
3. The Global Sliding Mode Surface Design for the Multi-Agent System
The sliding mode surface for the MAS is designed as follows,
where , and is the consensus error of the i-th follower. The matrix is the sliding mode parameter that satisfies and ensures that matrix is nonsingular and positive definite. The consensus error dynamics of the i-th follower are written as:
The following stacked vectors are defined for future use,
By Assumption 6 and the properties of the Laplacian matrix, the following equality holds
which implies . According to (5), (6) and (7), the sliding mode surface in (4) can be written as:
where
The time derivative of the sliding mode is expressed as:
where .
Remark 1.
Remark 2.
When the sliding mode is reached and maintained, topology switching does not affect its stability and continuity. This is due to the property of the Laplacian matrix, where , implying . Consequently, when the sliding mode is reached , according to (4), and according to (8). Therefore, the sliding mode equation remains unaffected, as , although the positive definite coefficient transitions to another positive definite matrix during topology switching.
If the sliding mode is reached and maintained, , from (10), the equivalent control can be resolved as:
In (11), the term is deduced as follows:
Substituting (12) into (11), the equivalent control can be obtained as:
Then, the i-th agent’s following error is partitioned as:
and the following equality holds,
where , and . When the sliding mode is reached, and . It follows that . (For simplicity, may be selected as ).
Consequently, the sliding mode equation of the i-th agent, based on the equivalent control (13), is given by:
Define as the left P-inverse of the control matrix , namely:
and let denote the orthocomplement of the control matrix with . Then, the following equality holds,
where is the left P-inverse matrix of , satisfying .
4. The Sliding Mode Control Protocol Design
4.1. The Control Protocol Design
The consensus control protocol is designed as follows:
where , are arbitrary positive scalars, , and are parameter matrices to be determined.
4.2. Reachability of the Sliding Mode
The following results are obtained.
Theorem 1.
Proof.
Consider the common Lyapunov function for the sliding mode surface dynamics (10) as . Its time derivative along the overall consensus error dynamics (19) is:
On the right-hand side of (22), the first, second, and third terms satisfy the following inequalities based on the properties of the Laplacian matrix and Assumption 1,
Combining (23), (24) and (25), the following inequality is obtained:
By the properties of the Laplacian matrix , if the parameter matrix satisfies , the matrix inequalities
easily hold. Therefore, under conditions (20) and (21), the following inequality is derived from (26),
According to the Lyapunov stability theory, it is evident that the sliding mode is achieved in finite time. □
Lemma 1.
Proof.
If the sliding mode surface parameter , then the item in (22). The proof directly follows the steps outlined in Theorem 1. □
Remark 3.
Remark 4.
The sliding surface dynamics (10) represent a switched system dynamic, in which the switching signal is the topology switching . According to the stability analysis of switched systems, the switched dynamics (10) are finite-time stable if the time derivative of the common Lyapunov function (CLF) satisfies (27).
When the sliding mode is reached () and maintained, the consensus control protocol (17) simplifies to . However, it cannot deal with the cooperative control requirements under the sliding mode unless the reduced-order system (14) or (16) is already stabilized. Therefore, an alternative consensus control protocol design, which utilizes the neighbors’ information more effectively, is proposed in the next section.
5. Application to Multiple WMRs
Consider the MAS where each agent is a wheeled mobile robot (WMR) modeled as in(2), (3), with
where represents the leader’s state, denote the position information in the horizontal and vertical directions, respectively; indicates the linear velocity and denotes the direction angle; The inputs and are the known control signals of the leader, while and are the control inputs of the followers.
5.1. Coordinate Transformation
Under the assumption that the agent speed (the leader ), the following control transformation is given:
where represents the auxiliary control inputs to be designed.
Define the state transformation vector for the followers as:
The state vector is the transformed state vector of the -th follower. Based on the transformations (30) and (31), the dynamics of the followers are expressed as:
Similarly, the leader dynamics are transformed using the state transformation , resulting in
where
Define the consensus error vector , where . Using(32) and (33), the consensus error dynamics are expressed as:
where , .
As the sliding mode is reached and maintained,
which implies , where , .
5.2. The Control Protocol Design
5.3. The Stability of the Sliding Mode
By substituting (35) and the matrices of the WMR dynamics, the consensus error dynamics (14) become
where .
For the WMRs, it is evident that the consensus error dynamics of the i-th follower under the sliding mode are order-reduced and linear. If the matrix is Hurwitz, the consensus error of the i-th follower is boundedly stable.
Theorem 2.
For the WMRs (2), (3), (29) under the sliding mode (4), (8), (9), (35), if there exist a positive definite symmetric matrix P, a positive scalar δ and the designed matrix satisfying the following linear matrix inequality
then the consensus error is robustly asymptotically stable when , and satisfies the gain δ when , assuming the same initial state condition or zero initial state conditions between the leader and followers.
Proof.
Consider the Lyapunov function , and calculate its time derivative along with the dynamics (36),
Based on the above equation, it can be easily obtained that
where . If the condition (37) is satisfied, the following inequality can be obtained.
Integrating over time,
It follows that
if the consensus error under the same initial state condition or zero initial state conditions between the leader and the followers. Otherwise, if , , and the consensus error becomes asymptotically stable. □
6. Simulation Tests
In this section, MATLAB2022a software was used to verify the proposed control protocol, and the Simulink module in MATLAB was employed to build and test the WMRs system. The computer specifications are as follows: CPU: Intel Core i7-12700K; Mainboard: Intel B660; RAM: DDR5, 5600MHz, 16GB; Graphics Card: NVIDIA GeForce RTX; Hard Disk: SSD 500GB.
A multiple WMRs system (29) was considered, consisting of one leader labeled as and three followers labeled as . The sliding mode was designed based on (4), (8), (9) and (35). The interconnection topology was time-varying with a switching period of 0.8s among four graphs , as shown in Figure 1, and the corresponding switching signal is depicted in Figure 2. The Laplacian matrices for the four graphs () are:
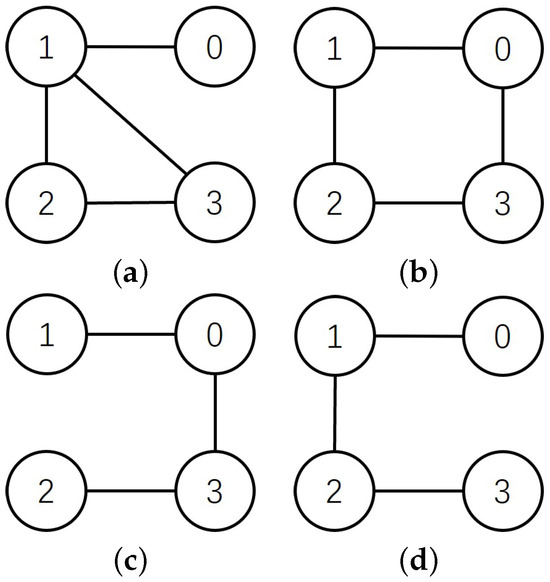
Figure 1.
Communication topologies (a), (b), (c) and (d) in numerical simulations.
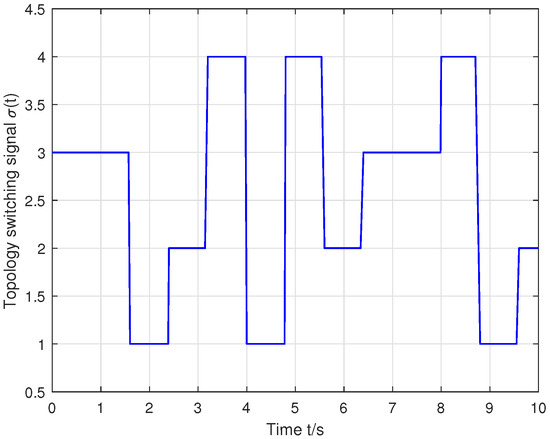
Figure 2.
The topology switching signal.
The parameter values of the control protocol were designed as = 2, = 0.5, = 1, , and
The parameter was designed to satisfy the conditions in (20) and (21).
The initial state of the leader was set to . The initial state of the three followers () were set to , , and , respectively. To validate the robust effectiveness, the simulation test considered the WMRs under both matched and unmatched disturbances. The disturbances for the three followers were assumed as follows:
The gain was selected as , and the parameters satisfied condition (37). The position tracking error in the X-Y directions, the linear velocity consensus error, and the yaw angle tracking error of the three followers are shown in Figure 3, Figure 4 and Figure 5.
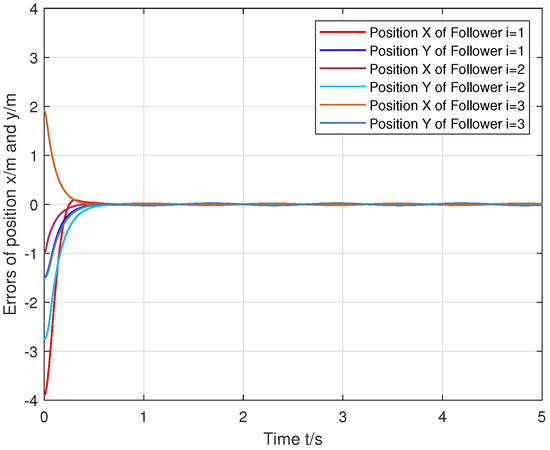
Figure 3.
Position errors of the followers (i = 1, 2, 3) in the X and Y directions.
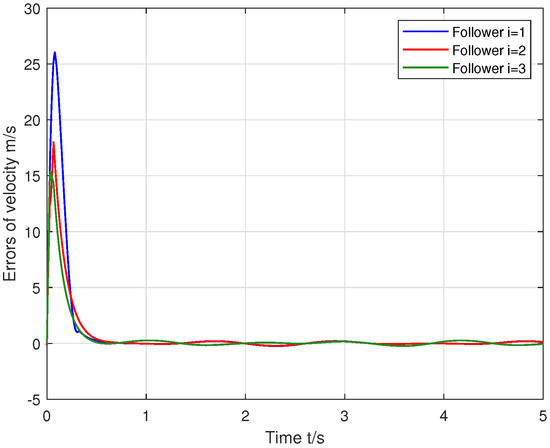
Figure 4.
Velocity errors of the followers (i = 1, 2, 3).
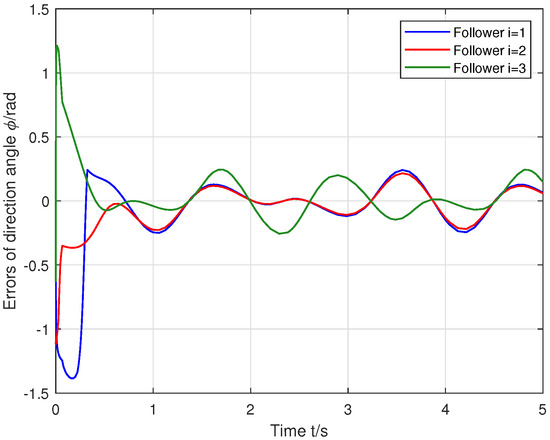
Figure 5.
Yaw angle errors of the followers (i = 1, 2, 3).
Figure 3 shows that the X-Y position errors of the three followers converged to the origin at about 0.6 s. In the steady state, the position exhibited small oscillations due to the presence of mismatched disturbance. However, the oscillation amplitudes were suppressed within . Compared with the unmatched disturbance amplitudes of 0.2, the control protocol displayed a robust suppression effect on the mismatched disturbances, validating Theorem 2.
From Figure 4, the line velocity tracking errors of the three followers converged to the origin at about 0.7 s despite the presence of external disturbances. Similarly, Figure 5 shows that the yaw angle tracking errors of the three followers also converged to the origin at about 0.7 s under external disturbances. The oscillation amplitudes of the line velocity and yaw angle tracking errors were greater than those of the position errors, which can be attributed to the relationship in the first line of (36) and the parameter .
Based on the proposed control protocol, the formation control of the MAS can be achieved by adding a constant relative position vector to the consensus error for each follower. This is expressed as:
where is the constant relative position vector. For each follower, converges to 0 under the control protocol, leading to
Each follower’s relative position vector is defined as . Consequently, the velocity of each follower aligns with the leader’s velocity, while position maintains a constant relative position value . Setting and , the formation result is shown in Figure 6.
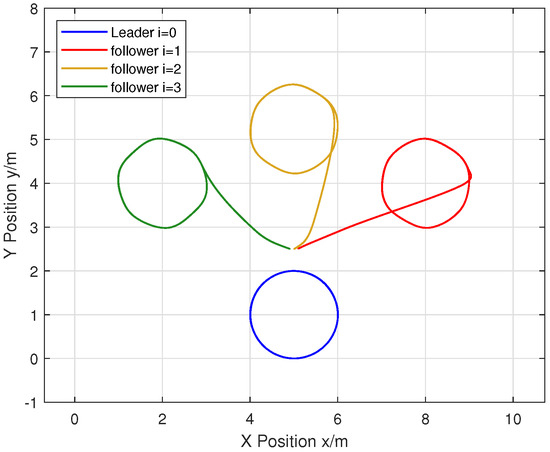
Figure 6.
States trajectories of the four agents.
Figure 6 illustrates the motion path of the three followers and the leader. Despite the presence of external disturbances, the three followers successfully tracked the leader’s motion under the control protocol (17). Moreover, the motion trajectory tracking demonstrated strong robustness.
Figure 7 presents the sliding mode values of the three followers, validating that the sliding mode convergency and stability were unaffected by both matched and mismatched disturbances.
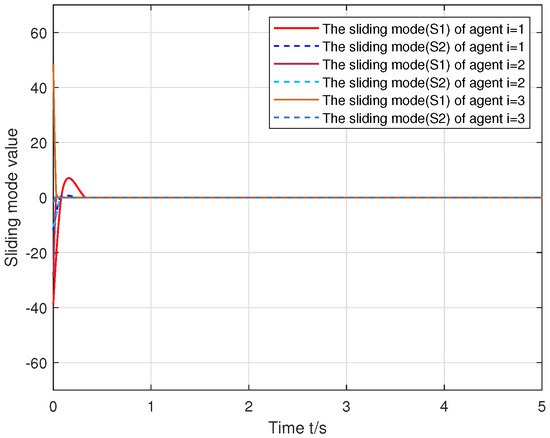
Figure 7.
Sliding mode values of the agents i = 1, 2, 3.
To explore the merits of the proposed SMC control protocol, a comparison was conducted, and the results are shown in Figure 8, Figure 9 and Figure 10. A prescribed-time formation tracking scheme for second-order MASs [30] was adopted for comparison. In [30], the follower model in the MAS is described as:
and the control protocol is defined as:
where is the weights between agents, and are positive constant gains, and are selected parameters, and is a designed scaling function.
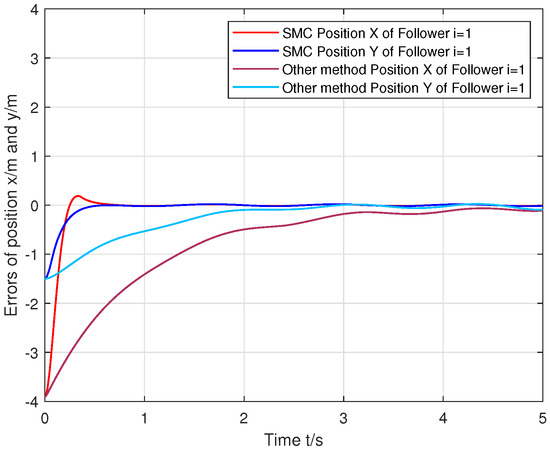
Figure 8.
Comparison between the proposed SMC protocol and the other method for agent i = 1.
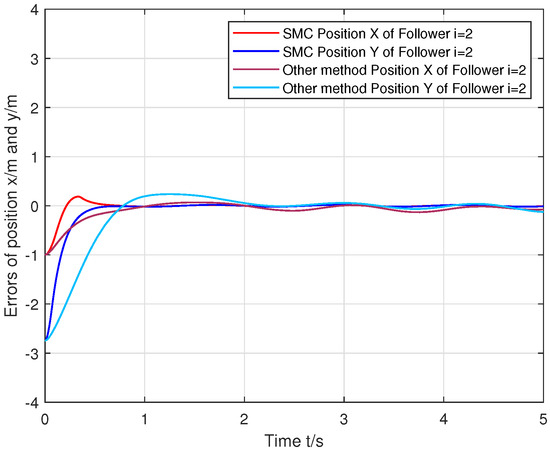
Figure 9.
Comparison between the proposed SMC protocol and the other method for agent i = 2.
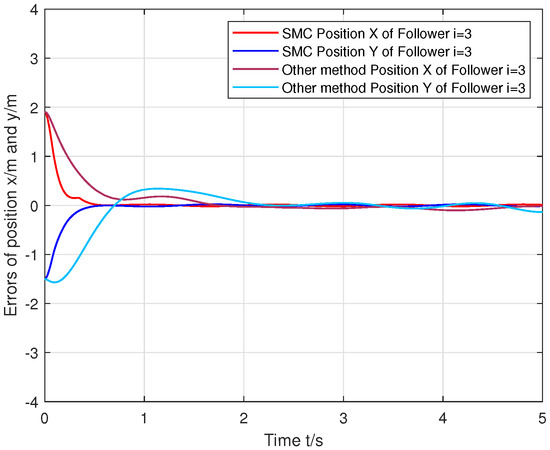
Figure 10.
Comparison between the proposed SMC protocol and the other method for agent i = 3.
From the position tracking errors of the followers in Figure 8, Figure 9 and Figure 10, it can be seen that the response speed of the proposed SMC control protocol is faster than the compared method. Furthermore, the robustness performance of the proposed SMC control protocol in the steady state is significantly more efficient than the other method.
Several potential challenges exist in future experimental work. First, the effectiveness of the control may be influenced by robot hardware due to factors such as communication delays between actual vehicles, power limitations, or constraints on computational resources. Second, the path trajectory achieved in the current simulation is limited to a small range, and its cooperative control effectiveness in larger areas remains uncertain. Additionally, the designed expected trajectory does not account for the potential forced collisions between vehicles.
The simulation tests validated the proposed cooperative control scheme. However, the scheme has certain limitations. For example, the stability of the sliding mode relies on the dynamics of specific model components, denoted as . While the is inapplicable, it may result in unstable sliding mode dynamics. Additionally, the control protocol outlined in this paper requires sufficient information from neighbor agents. In cases where unconnected communication typologies exist, parts of the neighbor state information may be unavailable. A possible solution would involve the use of agent state observers.
7. Conclusions
A completely distributed consensus sliding mode control protocol (SMCP) is proposed for heterogeneous nonlinear multi-agent systems (MAS) with disturbances under switching topology. The global sliding mode manifold (GSMM) is designed for the overall MAS dynamics, which results in reduced-order dynamics for each follower agent. The stability of these dynamics depends on the reduced-order nonlinear components. A corresponding consensus SMCP is proposed for the cooperative control of the MAS. The control protocol features a simple control structure and guarantees the finite-time reachability of the GSMM. Due to the common sliding mode control structure, the protocol achieves complete robustness against matched disturbances. Additionally, the control protocol realizes completely distributed cooperative control as the control signal only requires information from neighbor agents. The proposed SMCP design was applied to multiple-wheeled mobile robots (WMRs) formation and simulation test results confirmed its feasibility and effectiveness.
Author Contributions
Conceptualization, X.Z. and Y.L.; methodology, X.Z. and Y.L.; validation, X.Z., Y.L. and S.X.; analysis, X.Z. and X.L.; writing—original draft preparation, X.Z., Y.L. and R.G.; writing—review and editing, S.X.; project administration, S.X. and R.G. All authors have read and agreed to the submitted version of the manuscript.
Funding
This work was supported financially by the Open Project Fund of the Key Laboratory of AI and Information Processing (2022GXZDSY005), the National Natural Science Foundation of China (62371032), and the Cultivation Project Funds for Beijing University of Civil Engineering and Architecture (X23049).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors would like to thank the Editors and the Reviewers for their works. Additionally, the authors thank Yu Wang, Zerui Wei, and other graduated students in the team for their tidying up the materials.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liu, Y.; Liu, J.; He, Z.; Li, Z.; Zhang, Q.; Ding, Z. A survey of multi-agent systems on distributed formation control. Unmanned Syst. 2024, 12, 913–926. [Google Scholar] [CrossRef]
- Shah, M.I.A.; Wahid, A.; Barrett, E.; Mason, K. Multi-agent systems in Peer-to-Peer energy trading: A comprehensive survey. Eng. Appl. Artif. Intell. 2024, 132, 107847. [Google Scholar] [CrossRef]
- Jiang, Y.; Liu, L.; Feng, G. Fully distributed adaptive control for output consensus of uncertain discrete-time linear multi-agent systems. Automatica 2024, 162, 111531. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Q.; Shen, Y.; Dai, N.; He, B. Multi-AUV cooperative control and autonomous obstacle avoidance study. Ocean Eng. 2024, 304, 117634. [Google Scholar] [CrossRef]
- Nasir, M.; Maiti, A. Adaptive Sliding Mode Resilient Control of Multi-Robot Systems with a Leader–Follower Model under Byzantine Attacks in the Context of the Industrial Internet of Things. Machines 2024, 12, 205. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, M.; Sun, Y.; Chen, Z.; Duan, G.; Cao, X. Automated Design of Fault Diagnosis CNN Network for Satellite Attitude Control Systems. IEEE Trans. Cybern. 2024, 54, 4028–4038. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Zhou, B.; Duan, G.R. Leader-following consensus of multi-agent systems with time delays by fully distributed protocols. Syst. Control Lett. 2023, 178, 105582. [Google Scholar] [CrossRef]
- Zhou, Y.; Wen, G.; Wan, Y.; Fu, J. Consensus tracking control for a class of general linear hybrid multi-agent systems: A model-free approach. Automatica 2023, 156, 111198. [Google Scholar] [CrossRef]
- Wang, J.; Deng, X.; Guo, J.; Zeng, Z. Resilient consensus control for multi-agent systems: A comparative survey. Sensors 2023, 23, 2904. [Google Scholar] [CrossRef] [PubMed]
- Zhou, D.; Chen, W.H.; Lu, X. Leader-Following Consensus of Linear Multiagent Systems with Aperiodically Sampled Outputs: A Distributed Impulsive-Observer-Based Approach. IEEE Trans. Cybern. 2024, 55, 161–171. [Google Scholar] [CrossRef] [PubMed]
- Long, J.; Wang, W.; Wen, C.; Huang, J.; Guo, Y. Output-Feedback-Based Adaptive Leaderless Consensus for Heterogenous Nonlinear Multiagent Systems With Switching Topologies. IEEE Trans. Cybern. 2024, 54, 7905–7918. [Google Scholar] [CrossRef]
- Liu, Y.; Xie, X.; Chadli, M.; Sun, J. Leaderless Consensus Control of Fractional-Order Nonlinear Multi-Agent Systems with Measurement Sensitivity and Actuator Attacks. IEEE Trans. Control Netw. Syst. 2024, 1–10. [Google Scholar] [CrossRef]
- Zhang, W.; Huang, Q.; Alhudhaif, A. Event-triggered fixed-time bipartite consensus for nonlinear disturbed multi-agent systems with leader-follower and leaderless controller. Inf. Sci. 2024, 662, 120243. [Google Scholar] [CrossRef]
- Rezaee, H.; Abdollahi, F. Average consensus over high-order multiagent systems. IEEE Trans. Autom. Control 2015, 60, 3047–3052. [Google Scholar] [CrossRef]
- Chen, T.; Wang, F.; Feng, M.; Xia, C.; Chen, Z. Fully distributed consensus of linear multi-agent systems via dynamic event-triggered control. Neurocomputing 2024, 569, 127129. [Google Scholar] [CrossRef]
- Liu, Y.J.; Shang, X.; Tang, L.; Zhang, S. Finite-Time Consensus Adaptive Neural Network Control for Nonlinear Multiagent Systems Under PDE Models. IEEE Trans. Neural Netw. Learn. Syst. 2024, 1–11. [Google Scholar] [CrossRef]
- Luo, Y.; Huang, W.; Cao, J.; Cao, Z. Finite-time consensus of second-order multi-agent connectivity preserving based on adaptive sliding mode control. Commun. Nonlinear Sci. Numer. Simul. 2024, 137, 108142. [Google Scholar] [CrossRef]
- Zhuang, J.; Peng, S.; Peng, H. Finite-time and fixed-time consensus of nonlinear multi-agent systems: A unified two-phase control. Int. J. Robust Nonlinear Control 2024, 34, 9438–9455. [Google Scholar] [CrossRef]
- Wang, C.; Zhan, H.; Guo, Q.; Li, T. Distributed Neural Fixed-Time Consensus Control of Uncertain Multiple Euler-Lagrange Systems with Event-Triggered Mechanism. IEEE/ASME Trans. Mechatron. 2024, 1–12. [Google Scholar] [CrossRef]
- Li, H.; Niu, G.; Chen, Y. Fixed-time consensus of leader-following multi-agent systems subject to failed follower: Reconstructed topology approach. Appl. Math. Comput. 2024, 482, 128955. [Google Scholar] [CrossRef]
- Wang, Q.; Wu, W. A distributed finite-time optimization algorithm for directed networks of continuous-time agents. Int. J. Robust Nonlinear Control 2024, 34, 4032–4050. [Google Scholar] [CrossRef]
- He, S.; Wang, H.; Yu, W. Distributed Fast Finite-Time Tracking Consensus of Multi-Agent Systems With a Dynamic Leader. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 2176–2180. [Google Scholar] [CrossRef]
- Razmjooei, H.; Shafiei, M.H. Partial finite-time stabilization of perturbed nonlinear systems based on the novel concept of nonsingular terminal sliding mode method. J. Comput. Nonlinear Dyn. 2020, 15, 021005. [Google Scholar] [CrossRef]
- Chu, Y.; Fei, J.; Hou, S. Adaptive neural backstepping PID global sliding mode fuzzy control of MEMS gyroscope. IEEE Access 2019, 7, 37918–37926. [Google Scholar] [CrossRef]
- Cai, J.; Yi, C.; Wu, Y.; Liu, D.; Zhong, D. Leader-following consensus of nonlinear singular switched multi-agent systems via sliding mode control. Asian J. Control 2024, 26, 1997–2010. [Google Scholar] [CrossRef]
- Ma, Y.; Zhan, X.; Yang, Q.; Yan, H. Finite-time Consensus of Heterogeneous Multi-agent Systems by Integral Sliding Mode Control. Int. J. Control Autom. Syst. 2024, 22, 1819–1826. [Google Scholar] [CrossRef]
- Nie, R.; Du, W.; Li, Z.; He, S. Sliding mode-based finite-time consensus tracking control for multi-agent systems under actuator attacks. Inf. Sci. 2023, 640, 118971. [Google Scholar] [CrossRef]
- Jin, D.; Xiang, Z. Predefined-Time Consensus for Second-Order Nonlinear Multiagent Systems via Sliding Mode Technique. IEEE Trans. Fuzzy Syst. 2024, 32, 4534–4541. [Google Scholar] [CrossRef]
- Song, Y.; Li, Z.; Li, B.; Wen, G. Optimized leader-follower consensus control using combination of reinforcement learning and sliding mode mechanism for multiple robot manipulator system. Int. J. Robust Nonlinear Control 2024, 34, 5212–5228. [Google Scholar] [CrossRef]
- Li, X.; Zhu, Y.; Zhao, X.; Lu, J. Bearing-Based Prescribed Time Formation Tracking for Second-Order Multi-Agent Systems. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 3259–3263. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).