Prescribed-Time, Event-Triggered, Adaptive, Fault-Tolerant Formation Control of Heterogeneous Air–Ground Multi-Agent Systems Under Deception Attacks and Actuator Faults
Abstract
1. Introduction
- An innovative coordinate transformation combined with a constraint remapping mechanism is designed to accommodate corrupted states and filtered command signals. The method handles corrupted measurements and filtered commands. It maps tracking errors into a smooth, time-varying constrained domain, and overcoming the core difficulty of unavailable states caused by deception attacks.
- For unknown actuator efficiency loss and bias faults, we develop a rational adaptive law inside a command-filtered backstepping framework. The law estimates the efficiency loss and bias online, enabling the system to achieve reliable compensation and maintain closed-loop boundedness even under unknown control gains.
- An adaptive prescribed-time controller is developed based on a time-varying constraint. Tracking errors are driven into a user-specified accuracy region within a preset time, regardless of initial conditions. In addition, an event-triggered update rule is incorporated to reduce communication and to exclude Zeno behavior.
2. Problem Description and Preliminaries
2.1. Problem Description
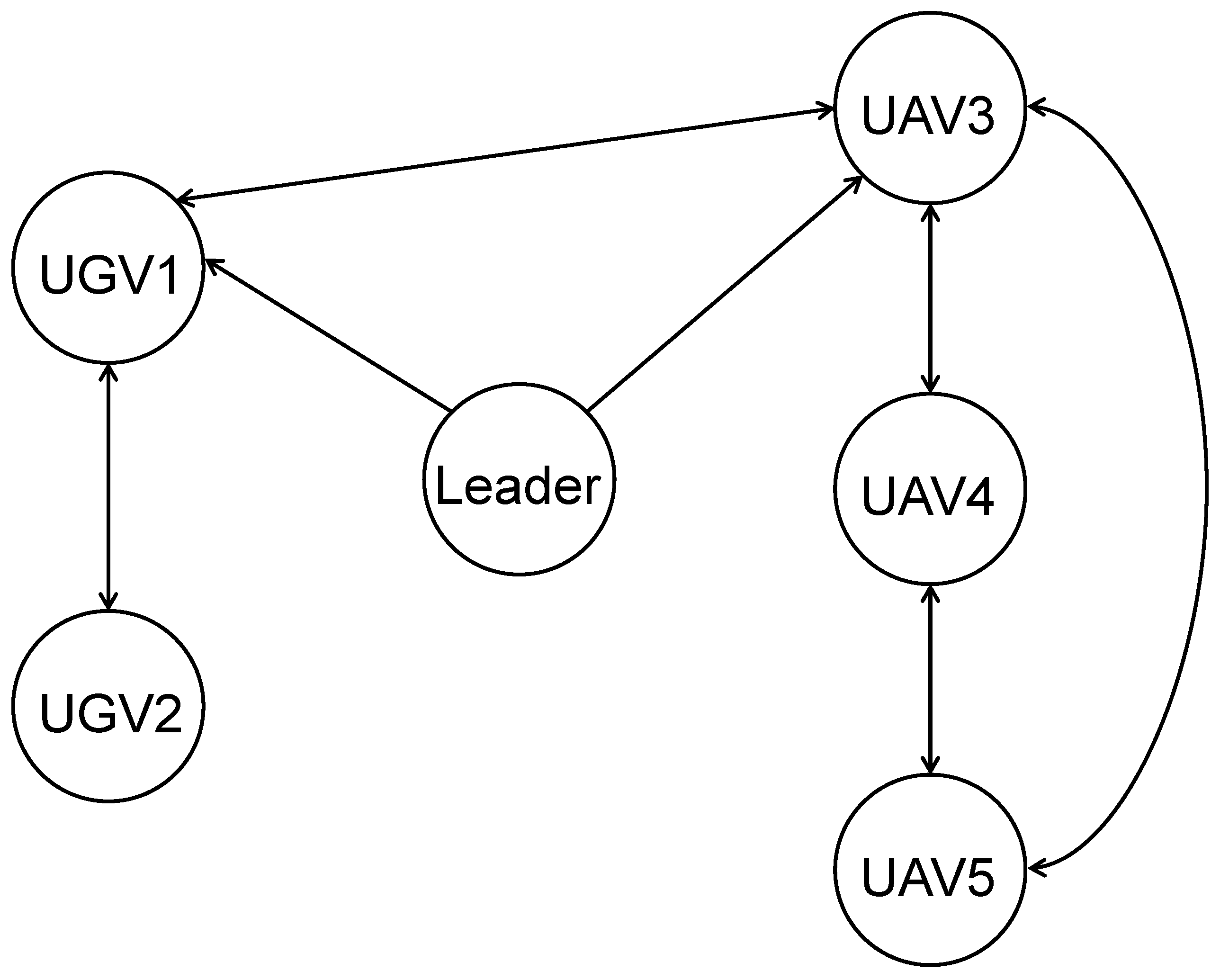
2.2. Graph Theory
2.3. Lemmas and Assumptions
3. Main Results
3.1. Adaptive Tracking Controller Design
3.2. Analysis of Stability
3.3. Zeno Behavior Analysis
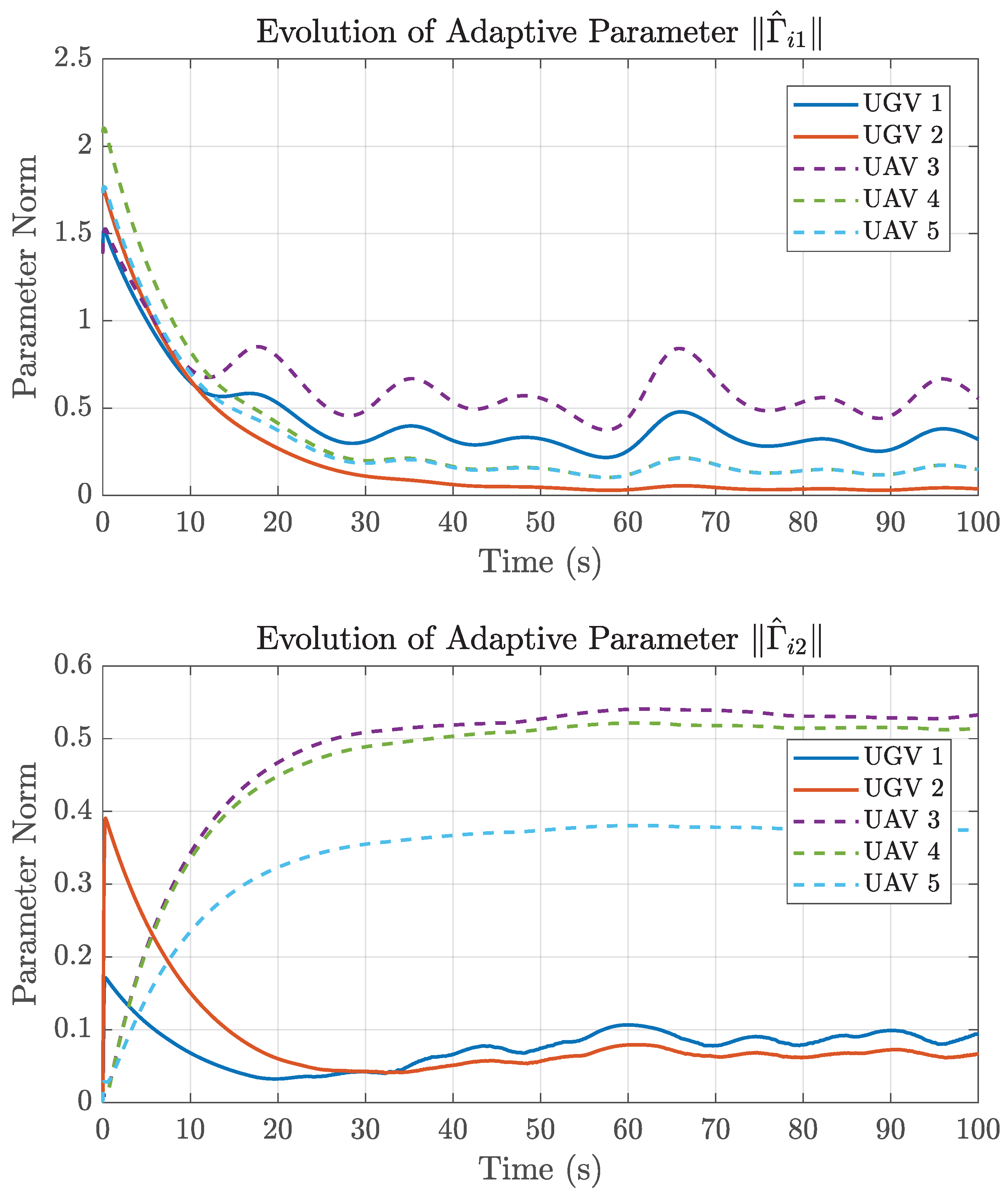
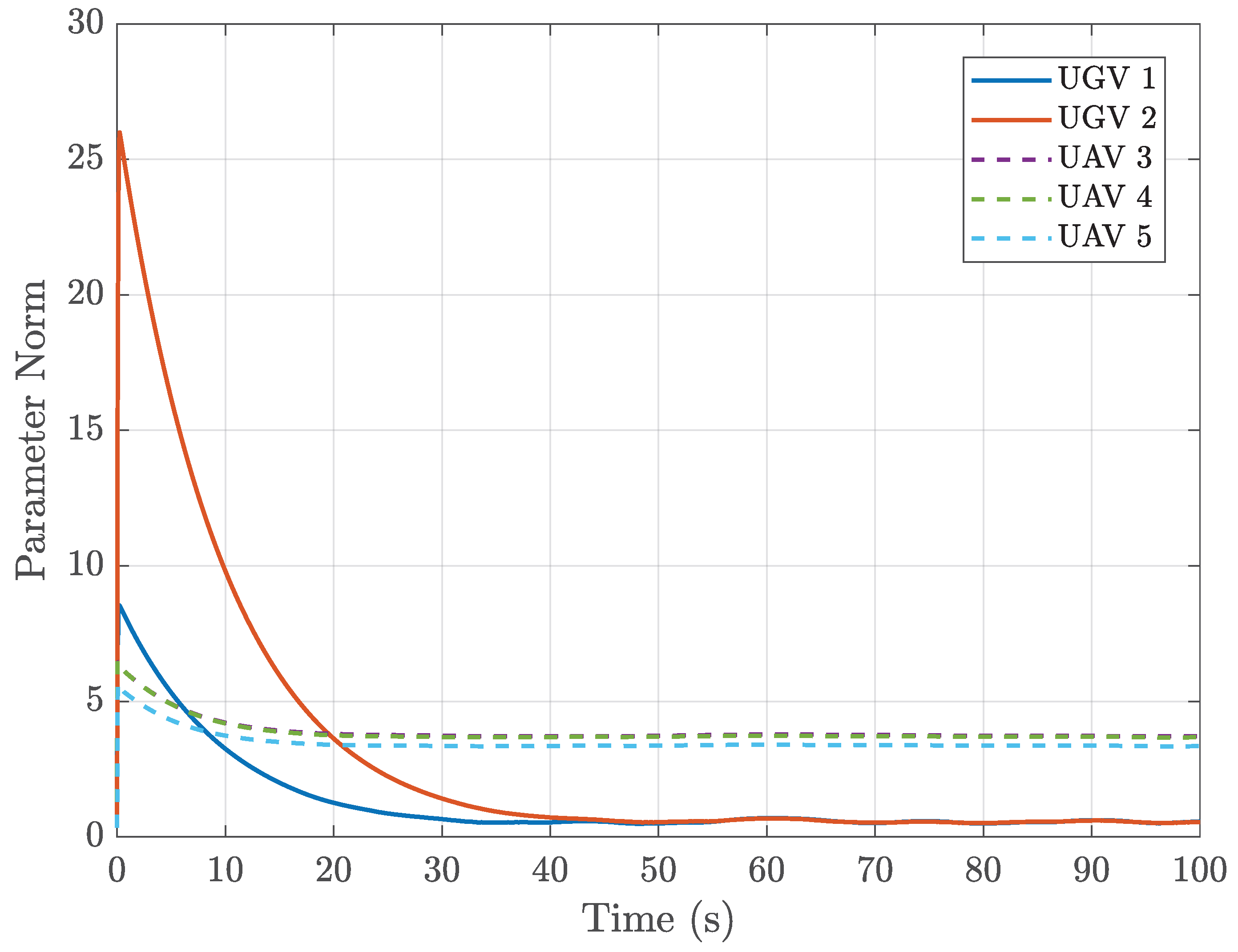
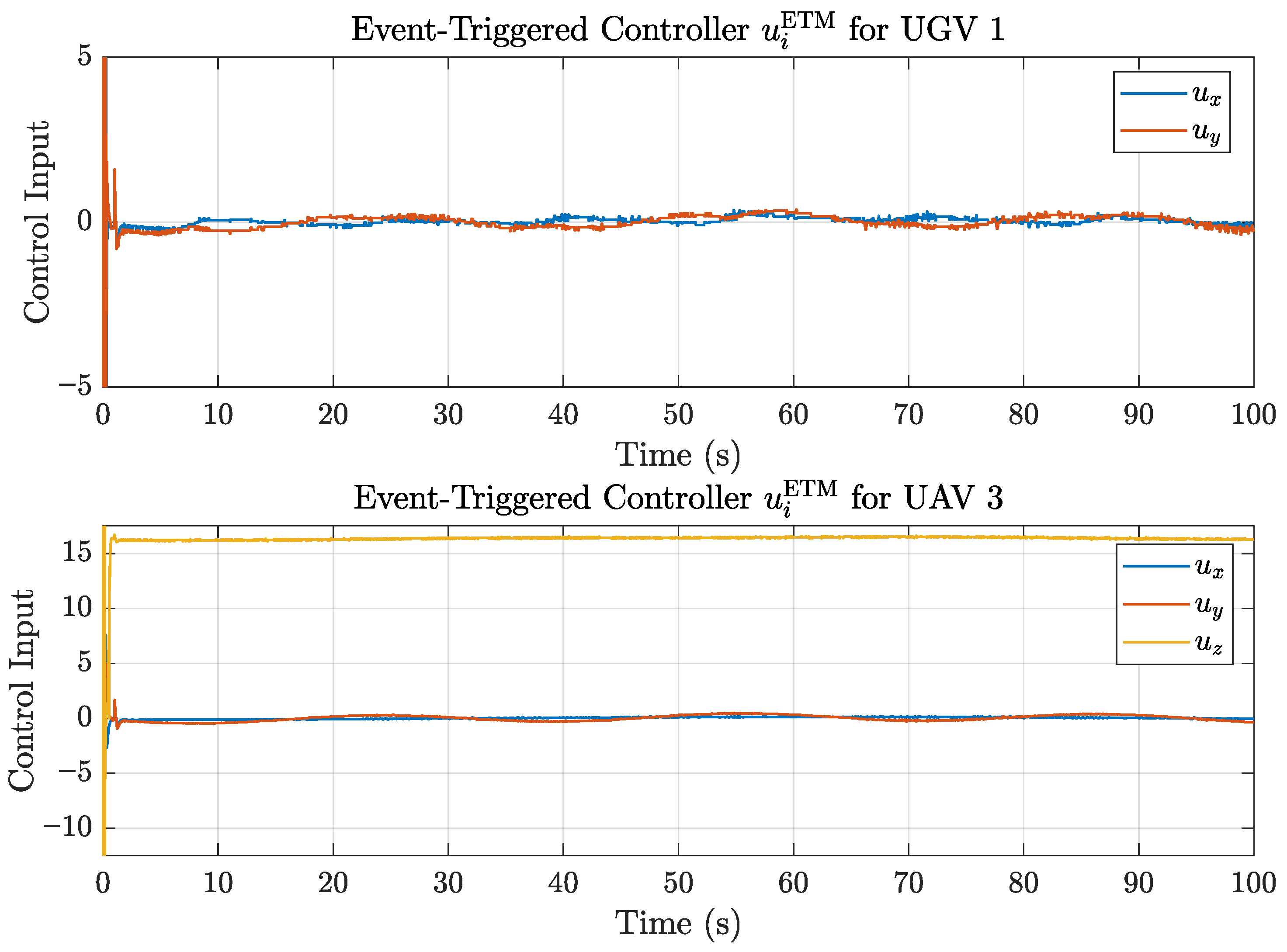
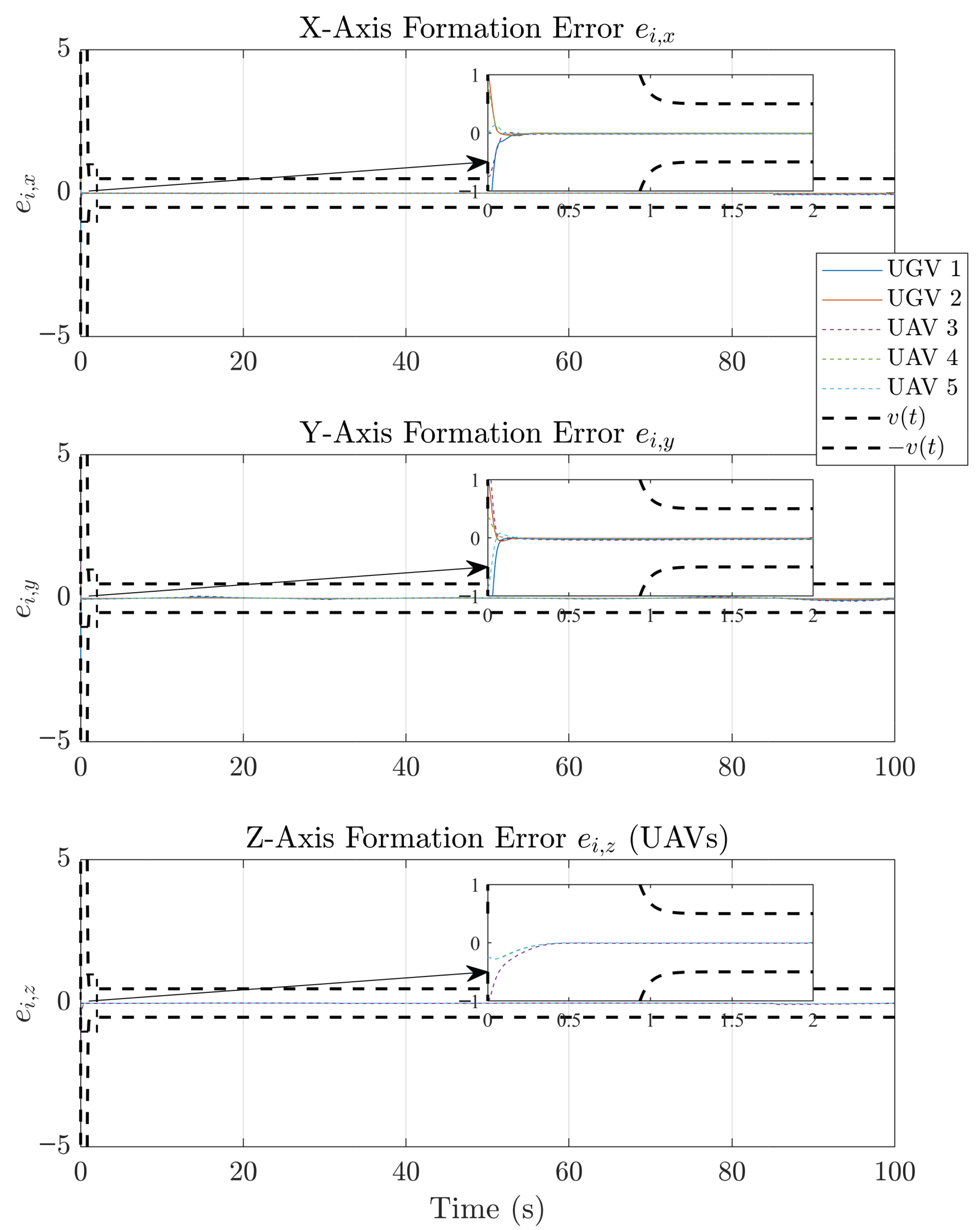
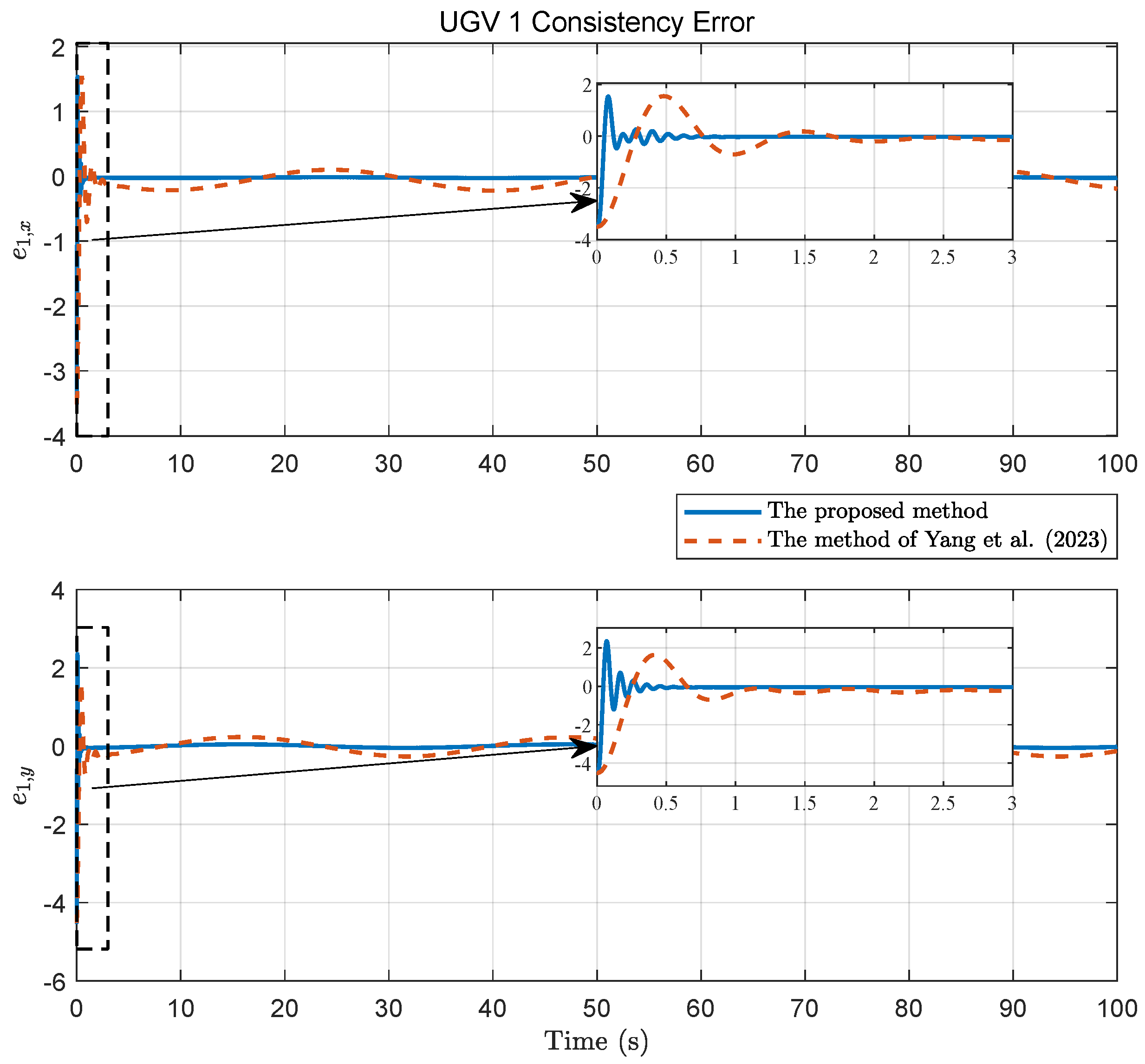
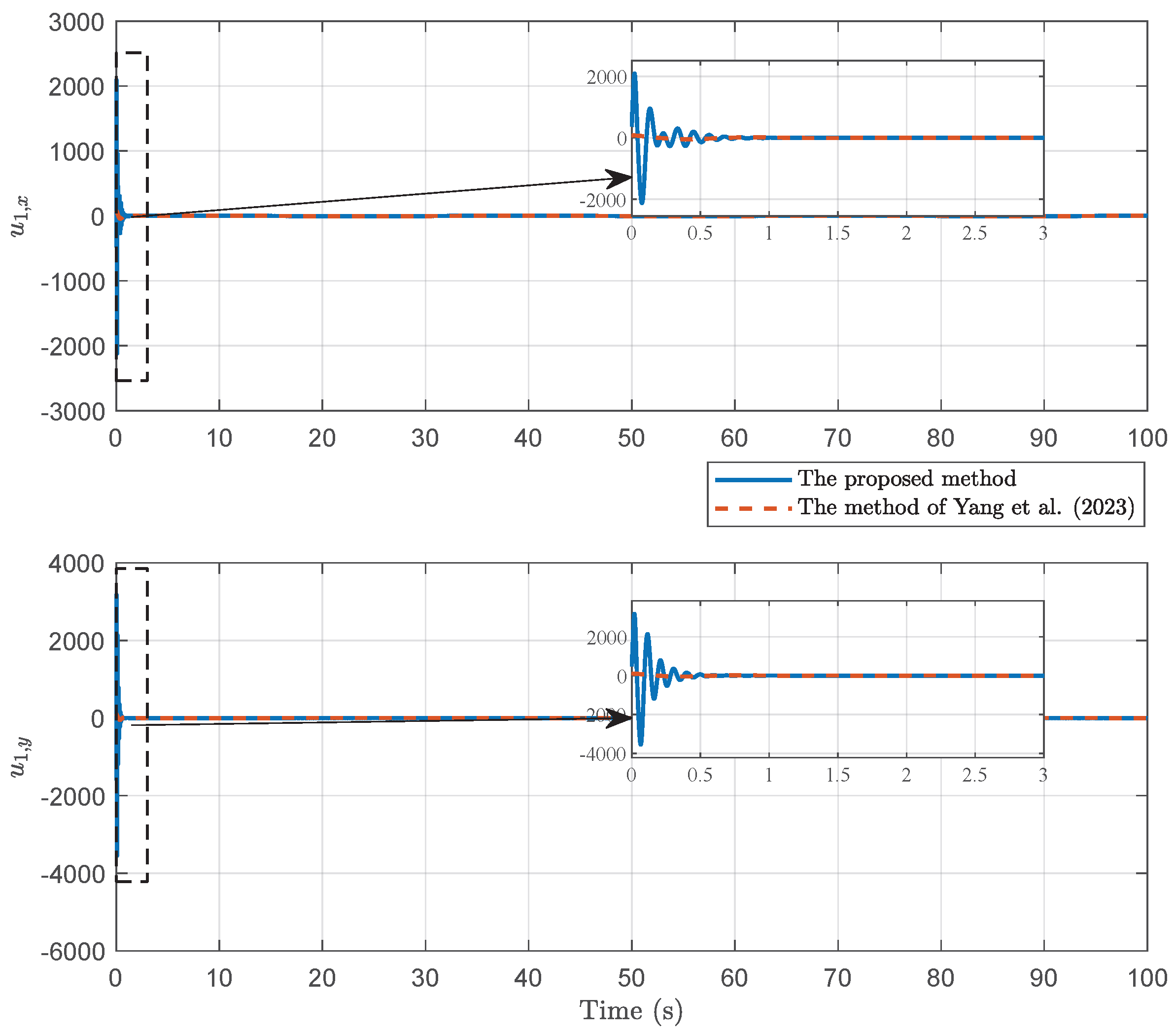
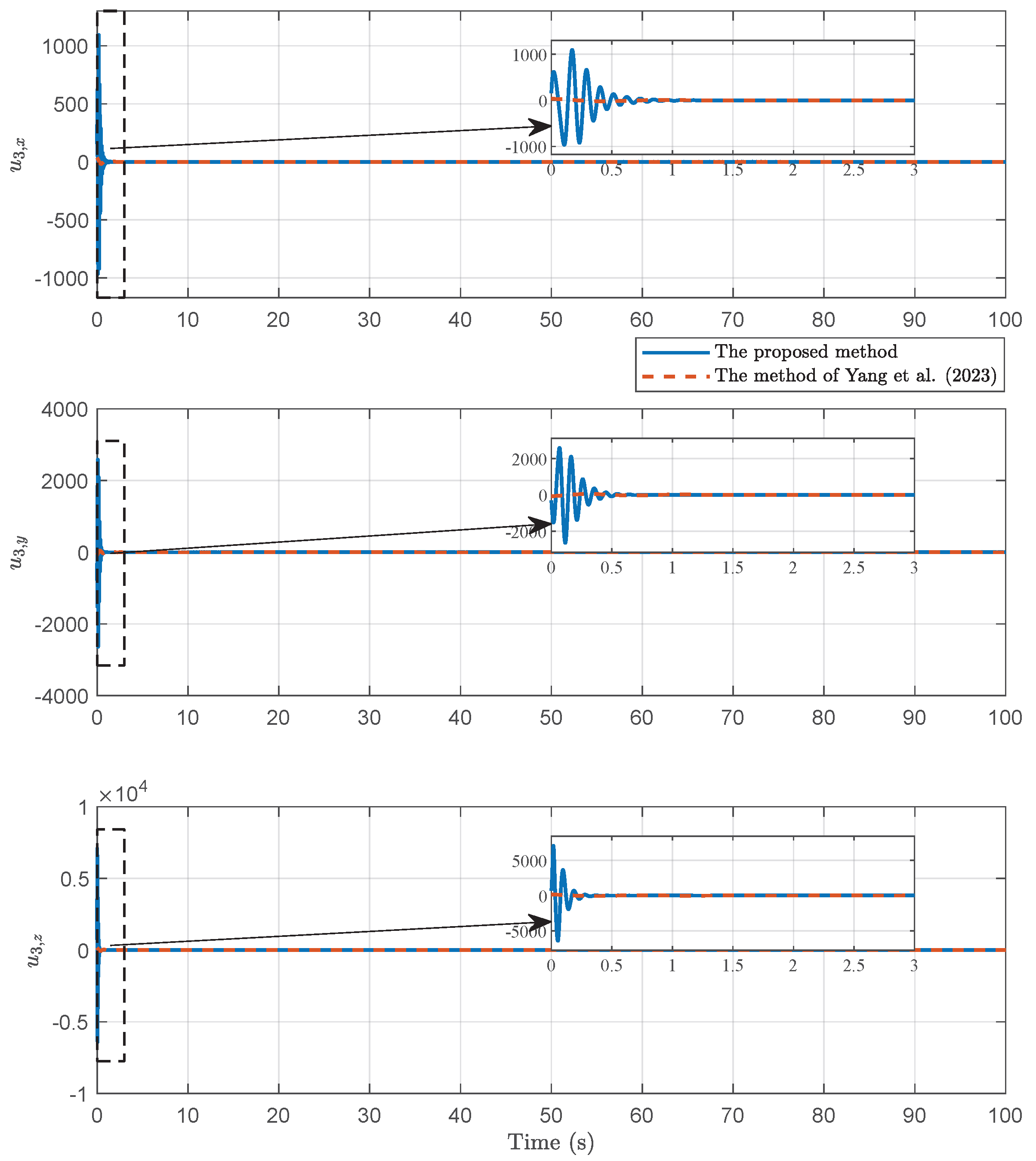
4. Simulation
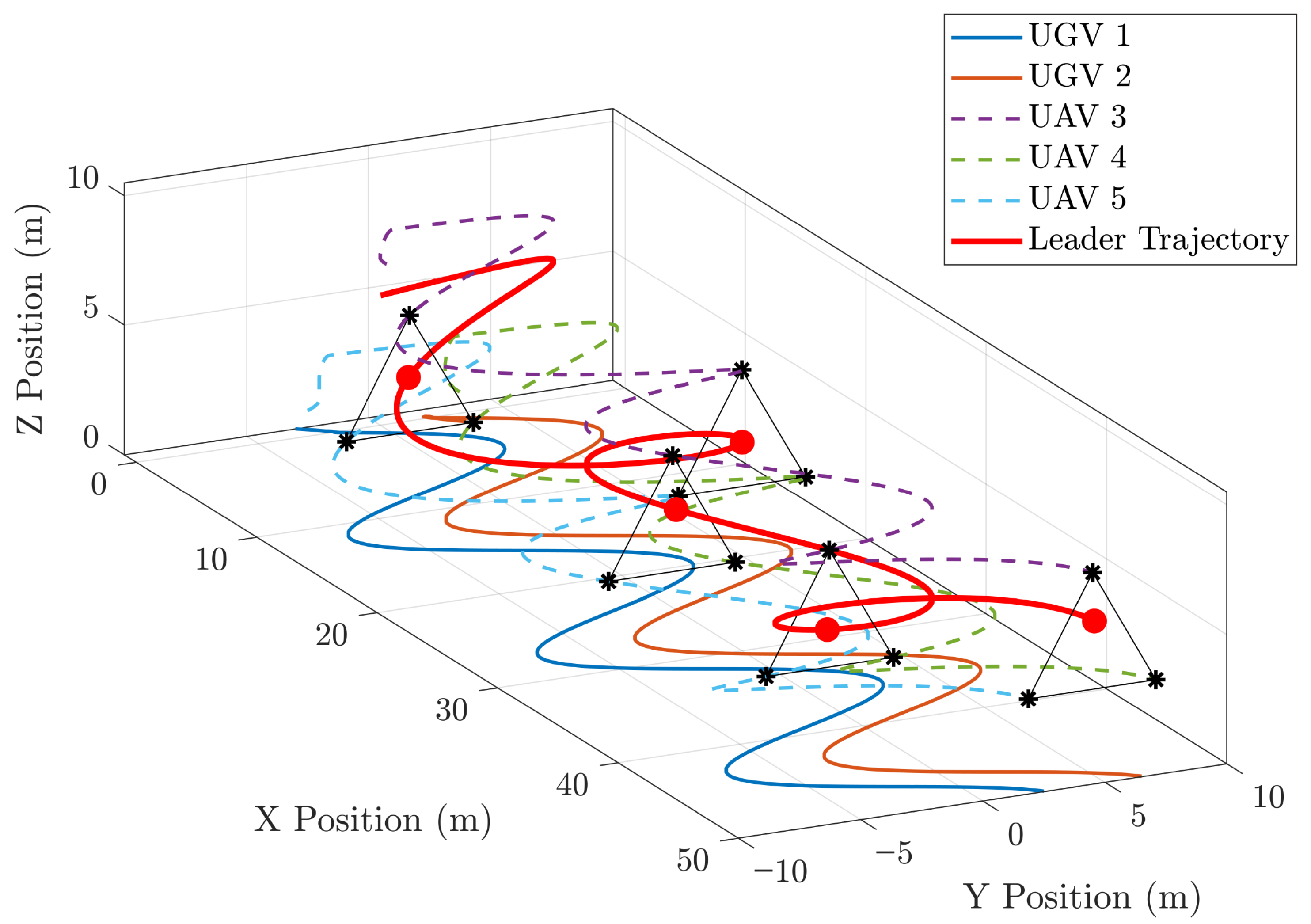
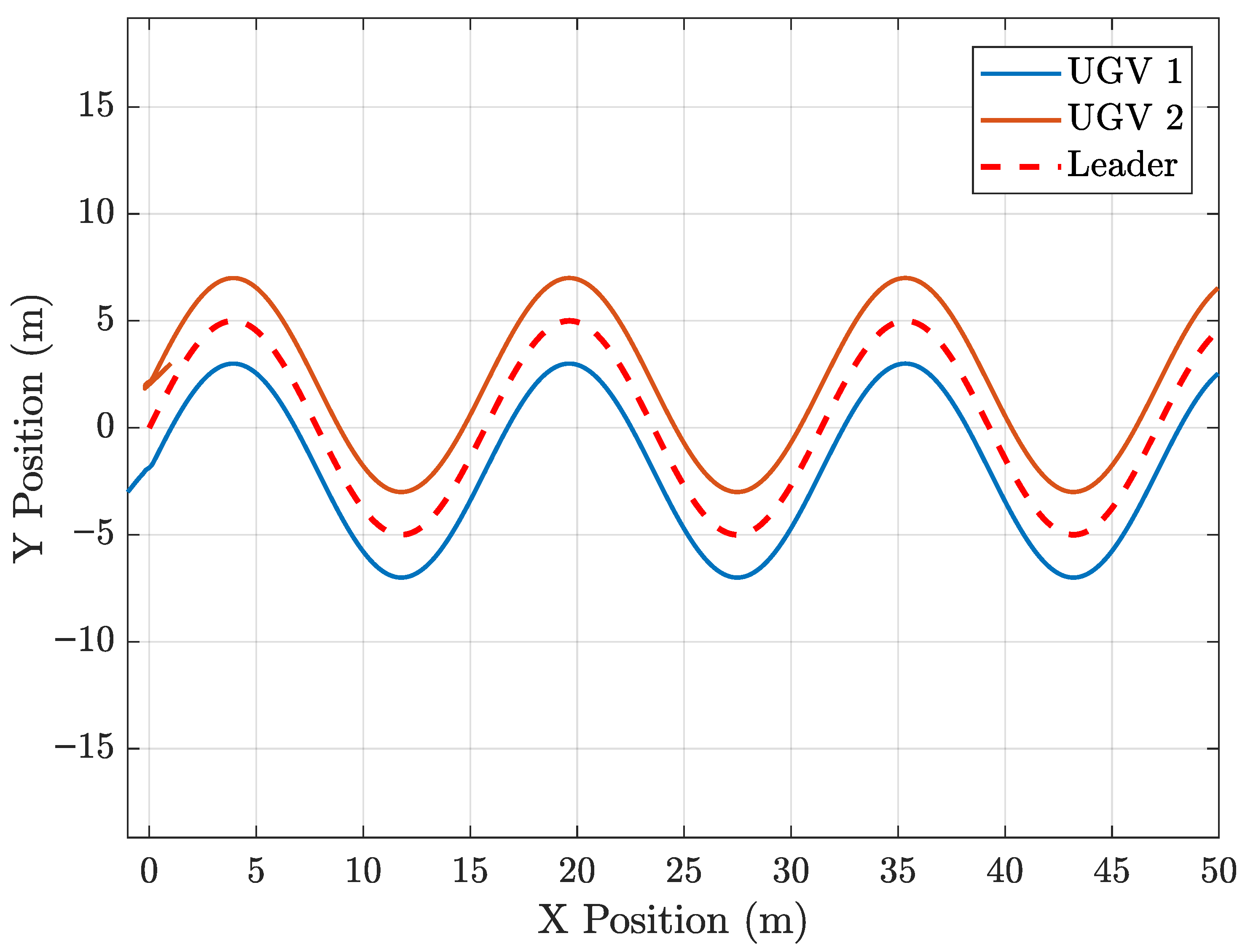
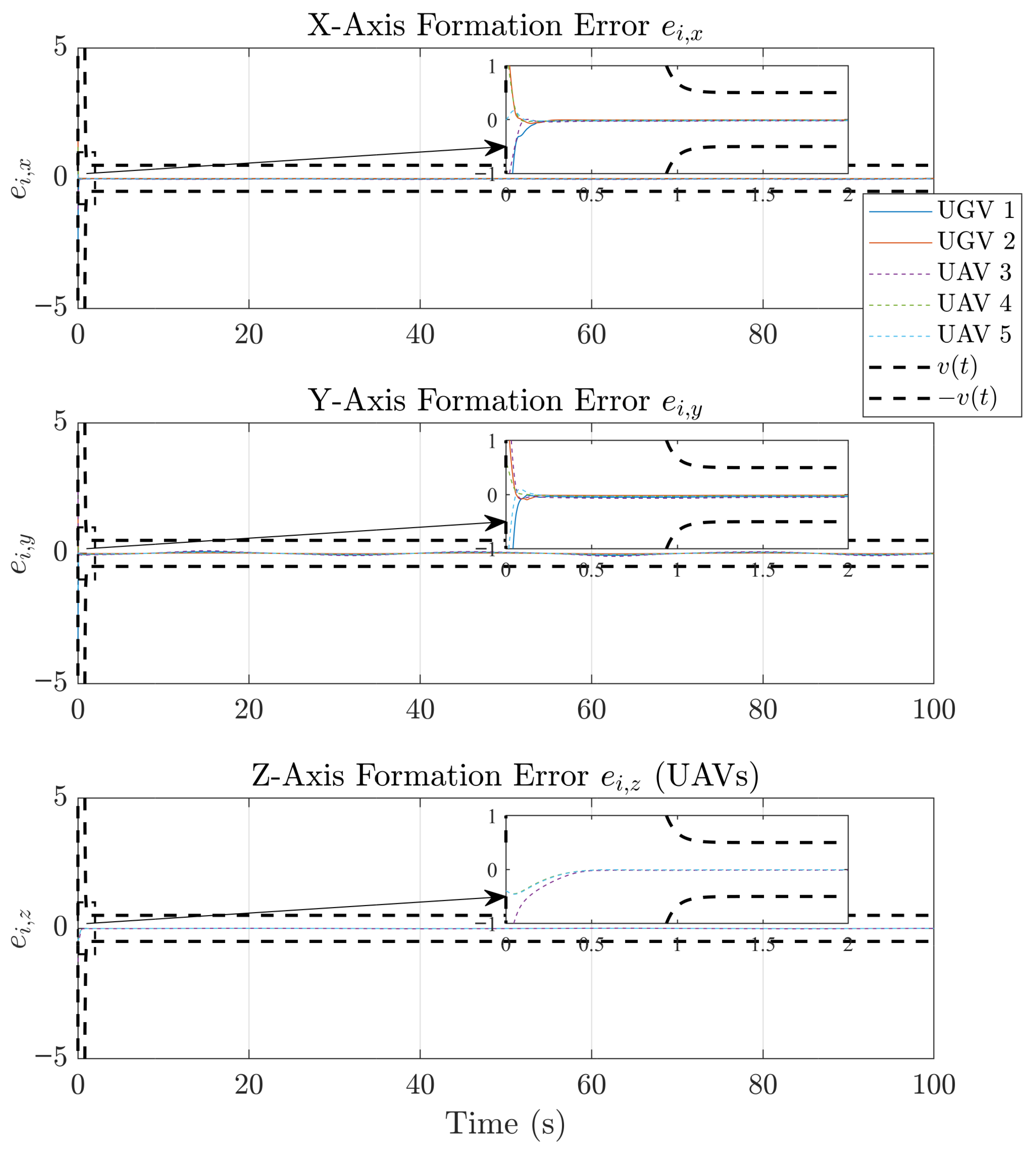
4.1. Example 1
4.2. Example 2
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yan, B.; Shi, P.; Lim, C.C. Robust formation control for nonlinear heterogeneous multiagent systems based on adaptive event-triggered strategy. IEEE Trans. Autom. Sci. Eng. 2022, 19, 2788–2800. [Google Scholar] [CrossRef]
- Xu, J.; Wang, Y.; Zhang, W. Containment control for high-order heterogeneous continuous-time multi-agent systems with input nonconvex constraints. Mathematics 2025, 13, 509. [Google Scholar] [CrossRef]
- Chang, X.; Yang, Y.; Zhang, Z.; Jiao, J.; Cheng, H.; Fu, W. Consensus-based formation control for heterogeneous multi-agent systems in complex environments. Drones 2025, 9, 175. [Google Scholar] [CrossRef]
- Talebi, S.P.; Werner, S. Distributed Kalman filtering and control through embedded average consensus information fusion. IEEE Trans. Autom. Control 2019, 64, 4396–4403. [Google Scholar] [CrossRef]
- Zhang, L.L.; Gao, F.; Deng, F.; Xi, L.L.; Chen, J. Distributed estimation of a layered architecture for collaborative air-ground target geolocation in outdoor environments. IEEE Trans. Ind. Electron. 2023, 70, 2822–2832. [Google Scholar] [CrossRef]
- Zheng, X.; Li, H.; Ahn, C.K.; Yao, D. NN-based fixed-time attitude tracking control for multiple unmanned aerial vehicles with nonlinear faults. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 1738–1748. [Google Scholar] [CrossRef]
- Loria, A.; Nuno, E.; Panteley, E. Observerless output-feedback consensus-based formation control of second-order nonholonomic systems. IEEE Trans. Autom. Control 2022, 67, 6934–6939. [Google Scholar] [CrossRef]
- Zhang, Q.; Yan, K.-X.; Xiao, B.; Han, T. Distributed observer-based adaptive formation-containment tracking for multi-agent systems on directed graphs. Mathematics 2025, 13, 558. [Google Scholar] [CrossRef]
- Feng, L.; Huang, B.; Sun, J.; Sun, Q.; Xie, X. Adaptive event-triggered time-varying output group formation containment control of heterogeneous multiagent systems. IEEE/CAA J. Autom. Sin. 2024, 11, 1398–1409. [Google Scholar] [CrossRef]
- Shi, J.L.; Hu, B.; Chen, L.; Zhang, D.X.; He, D.X.; Huang, J.; Guan, Z.H. Formation tracking of heterogeneous UGV-UAV systems with switching directed topologies. In Proceedings of the 2019 IEEE 4th International Conference on Advanced Robotics and Mechatronics (ICARM), Osaka, Japan, 3–5 July 2019; pp. 970–975. [Google Scholar] [CrossRef]
- Hua, H.A.; Fang, Y.C.; Zhang, X.T.; Lu, B.A. A novel robust observer-based nonlinear trajectory tracking control strategy for quadrotors. IEEE Trans. Control Syst. Technol. 2021, 29, 1952–1963. [Google Scholar] [CrossRef]
- Bhat, S.; Bernstein, D. Finite-time stability of continuous autonomous systems. SIAM J. Control Optim. 2000, 38, 751–766. [Google Scholar] [CrossRef]
- Yang, T.; Kang, H.; Ma, H.; Wang, X. Adaptive fuzzy finite-time fault-tolerant consensus tracking control for high-order multiagent systems with directed graphs. IEEE Trans. Cybern. 2023, 53, 607–616. [Google Scholar] [CrossRef]
- Defoort, M.; Polyakov, A.; Demesure, G.; Djemai, M.; Veluvolu, K. Leader-follower fixed-time consensus for multi-agent systems with unknown nonlinear inherent dynamics. IET Control Theory Appl. 2015, 9, 2165–2170. [Google Scholar] [CrossRef]
- Zuo, Z.; Tian, B.; Defoort, M.; Ding, Z. Fixed-time consensus tracking for multiagent systems with high-order integrator dynamics. IEEE Trans. Autom. Control 2017, 63, 563–570. [Google Scholar] [CrossRef]
- Luo, Y.; Tang, F.; Wei, Q. Event-based human-in-the-loop formation-containment control for heterogeneous UAV-USV systems with dual predefined-time prescribed performance. IEEE Trans. Veh. Technol. 2025; early access. [Google Scholar] [CrossRef]
- Jin, W.; Zhang, H.; Yang, Y.; Guo, X.; Chen, S. Distributed practical predefined-time output optimal allocation of resources for heterogeneous multi-agent systems. IEEE Trans. Autom. Sci. Eng. 2025, 22, 19646–19654. [Google Scholar] [CrossRef]
- Zhang, L.; Che, W.-W.; Deng, C.; Wu, Z.-G. Prescribed performance fuzzy resilient control for nonlinear systems under DoS attacks. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 3104–3116. [Google Scholar] [CrossRef]
- Ma, Y.S.; Che, W.W.; Deng, C.; Wu, Z.G. Distributed model-free adaptive control for learning nonlinear MASs under DoS attacks. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 1146–1155. [Google Scholar] [CrossRef]
- An, L.; Yang, G.-H. Decentralized adaptive fuzzy secure control for nonlinear uncertain interconnected systems against intermittent DoS attacks. IEEE Trans. Cybern. 2019, 49, 827–838. [Google Scholar] [CrossRef] [PubMed]
- Yue, D.; Deng, C.; Han, Q.-L. Distributed resilient optimization control for uncertain nonlinear MASs under DoS attacks. Automatica 2025, 173, 111997. [Google Scholar] [CrossRef]
- Porter, M.; Hespanhol, P.; Aswani, A.; Johnson-Roberson, M.; Vasudevan, R. Detecting generalized replay attacks via time-varying dynamic watermarking. IEEE Trans. Autom. Control 2021, 66, 3502–3517. [Google Scholar] [CrossRef]
- Franzè, G.; Tedesco, F.; Famularo, D. Resilience against replay attacks: A distributed model predictive control scheme for networked multi-agent systems. IEEE/CAA J. Autom. Sin. 2021, 8, 628–640. [Google Scholar] [CrossRef]
- Wang, H.; Wang, Y.; Zhuang, G.; Xia, J. Dynamic event-based prescribed-time practical consensus for nonlinear multi-agent systems under DoS and deception attacks. Nonlinear Dyn. 2025, 113, 16629–16642. [Google Scholar] [CrossRef]
- Liu, C.; Wang, W.; Yu, Z.; Patton, R.J. Distributed finite-time adaptive fault-tolerant consensus control of second-order multiagent systems under deception attacks. Int. J. Adapt. Control Signal Process. 2024, 38, 1309–1326. [Google Scholar] [CrossRef]
- Zhou, M.; Li, H.; Xue, T.; Wang, J.; Raïssi, T. Event-triggered state interval estimation and fault-tolerant control for multiagent systems under deception attacks. IEEE Trans. Autom. Control 2025, 70, 689–696. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, Z. Composite continuous high-order nonsingular terminal sliding mode control for flying wing UAVs with disturbances and actuator faults. Mathematics 2025, 13, 2375. [Google Scholar] [CrossRef]
- Wang, H.; Bai, W.; Zhao, X.; Liu, P.X. Finite-time-prescribed performance-based adaptive fuzzy control for strict-feedback nonlinear systems with dynamic uncertainty and actuator faults. IEEE Trans. Cybern. 2022, 52, 6959–6971. [Google Scholar] [CrossRef]
- Ding, L.; Han, Q.-L.; Ge, X.; Zhang, X.-M. An overview of recent advances in event-triggered consensus of multiagent systems. IEEE Trans. Cybern. 2018, 48, 1110–1123. [Google Scholar] [CrossRef]
- Wu, Z.-G.; Xu, Y.; Lu, R.; Wu, Y.; Huang, T. Event-triggered control for consensus of multiagent systems with fixed/switching topologies. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 1736–1746. [Google Scholar] [CrossRef]
- Zhu, B.; Zhang, L.; Niu, B.; Zhao, N. Adaptive reinforcement learning for fault-tolerant optimal consensus control of nonlinear canonical multiagent systems with actuator loss of effectiveness. IEEE Syst. J. 2024, 18, 1681–1692. [Google Scholar] [CrossRef]
- Lin, W.; Zhao, W.; Liu, H. Robust optimal formation control of heterogeneous multi-agent system via reinforcement learning. IEEE Access 2020, 8, 218424–218432. [Google Scholar] [CrossRef]
- Zhang, H.; Lewis, F.L.; Qu, Z. Lyapunov, adaptive, and optimal design techniques for cooperative systems on directed communication graphs. IEEE Trans. Ind. Electron. 2012, 59, 3026–3041. [Google Scholar] [CrossRef]
- Wang, H.; Chen, B.; Liu, K.; Liu, X.; Lin, C. Adaptive neural tracking control for a class of nonstrict-feedback stochastic nonlinear systems with unknown backlash-like hysteresis. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 947–958. [Google Scholar] [CrossRef]
- Sun, G.; Wang, D.; Peng, Z. Adaptive control based on single neural network approximation for non-linear pure-feedback systems. IET Control Theory Appl. 2012, 6, 2387–2396. [Google Scholar] [CrossRef]
- Lin, W.; Qian, C. Adaptive control of nonlinearly parameterized systems: The smooth feedback case. IEEE Trans. Autom. Control 2002, 47, 1249–1266. [Google Scholar] [CrossRef]
- Li, Y.-X. Command filter adaptive asymptotic tracking of uncertain nonlinear systems with time-varying parameters and disturbances. IEEE Trans. Autom. Control 2022, 67, 2973–2980. [Google Scholar] [CrossRef]
- Farrell, J.A.; Polycarpou, M.; Sharma, M.; Dong, W. Command filtered backstepping. IEEE Trans. Autom. Control 2009, 54, 1391–1395. [Google Scholar] [CrossRef]
- Gao, Z.; Zhang, Y.; Guo, G. Finite-time fault-tolerant prescribed performance control of connected vehicles with actuator saturation. IEEE Trans. Veh. Technol. 2023, 72, 1438–1448. [Google Scholar] [CrossRef]
- Guo, G.; Zhang, Q.; Zhou, Z.-D. Fixed-time cooperative control of vehicles with connectivity preservation. IEEE Trans. Veh. Technol. 2025, 74, 15109–15119. [Google Scholar] [CrossRef]




| Work | Hetero. | Attack Model | Prescribed-Time | Event-Triggered |
|---|---|---|---|---|
| This work | Yes (UGV + UAV) | Deception (state) | Yes | Yes |
| Ref. [24] | No | Deception (state) | Yes | Yes |
| Ref. [25] | No | Deception (actuator) | No (finite-time) | No |
| Ref. [26] | No | Deception (communication network) | No | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, J.; Xie, J.; Huang, J.; Liu, S. Prescribed-Time, Event-Triggered, Adaptive, Fault-Tolerant Formation Control of Heterogeneous Air–Ground Multi-Agent Systems Under Deception Attacks and Actuator Faults. Actuators 2025, 14, 575. https://doi.org/10.3390/act14120575
Huang J, Xie J, Huang J, Liu S. Prescribed-Time, Event-Triggered, Adaptive, Fault-Tolerant Formation Control of Heterogeneous Air–Ground Multi-Agent Systems Under Deception Attacks and Actuator Faults. Actuators. 2025; 14(12):575. https://doi.org/10.3390/act14120575
Chicago/Turabian StyleHuang, Jingli, Junjiang Xie, Jie Huang, and Shangkun Liu. 2025. "Prescribed-Time, Event-Triggered, Adaptive, Fault-Tolerant Formation Control of Heterogeneous Air–Ground Multi-Agent Systems Under Deception Attacks and Actuator Faults" Actuators 14, no. 12: 575. https://doi.org/10.3390/act14120575
APA StyleHuang, J., Xie, J., Huang, J., & Liu, S. (2025). Prescribed-Time, Event-Triggered, Adaptive, Fault-Tolerant Formation Control of Heterogeneous Air–Ground Multi-Agent Systems Under Deception Attacks and Actuator Faults. Actuators, 14(12), 575. https://doi.org/10.3390/act14120575






