Hysteresis Modeling of a Magnetic Shape Memory Alloy Actuator Using a NARMAX Model and a Long Short-Term Memory Neural Network
Abstract
1. Introduction
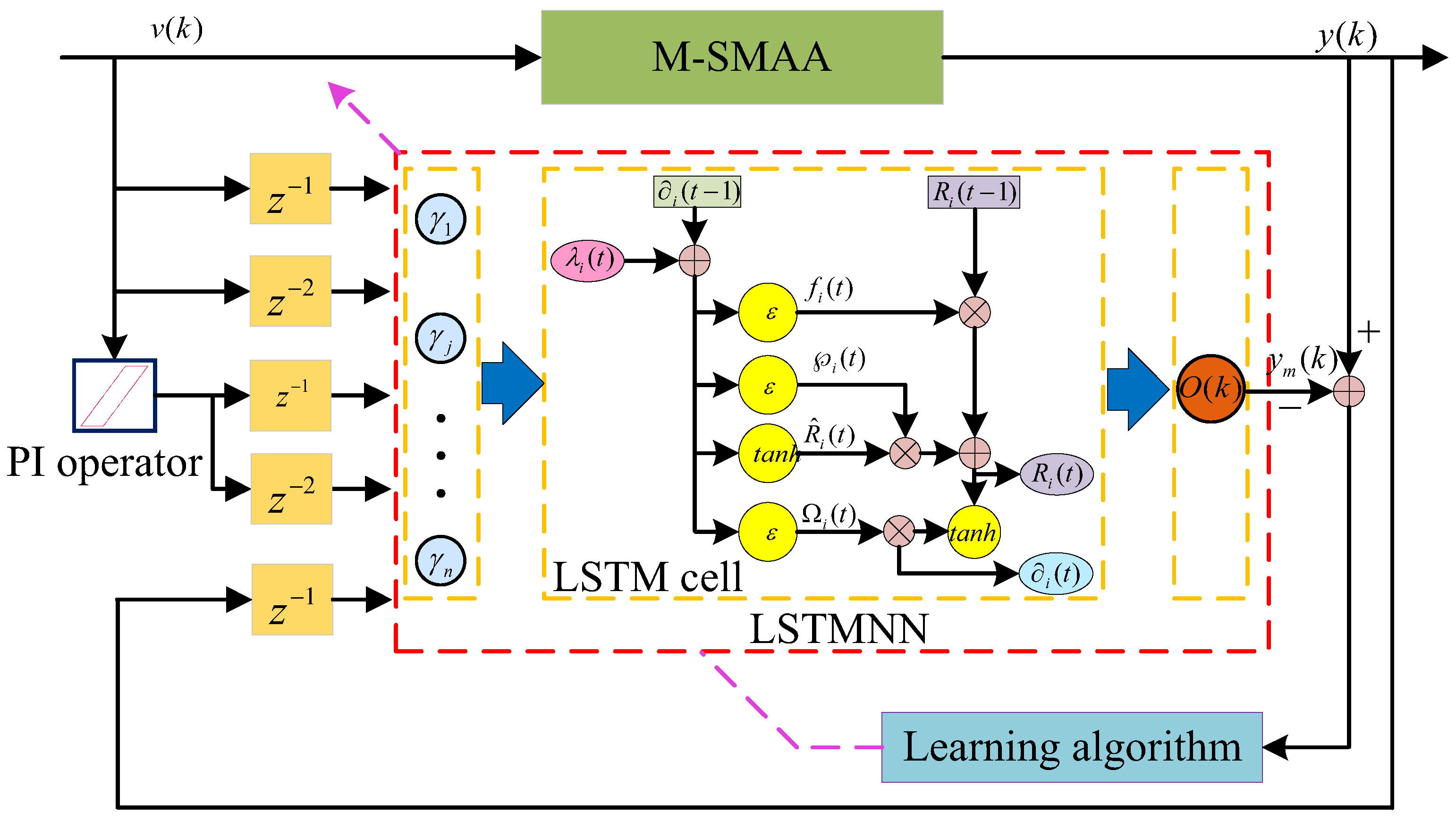
2. Modeling Method
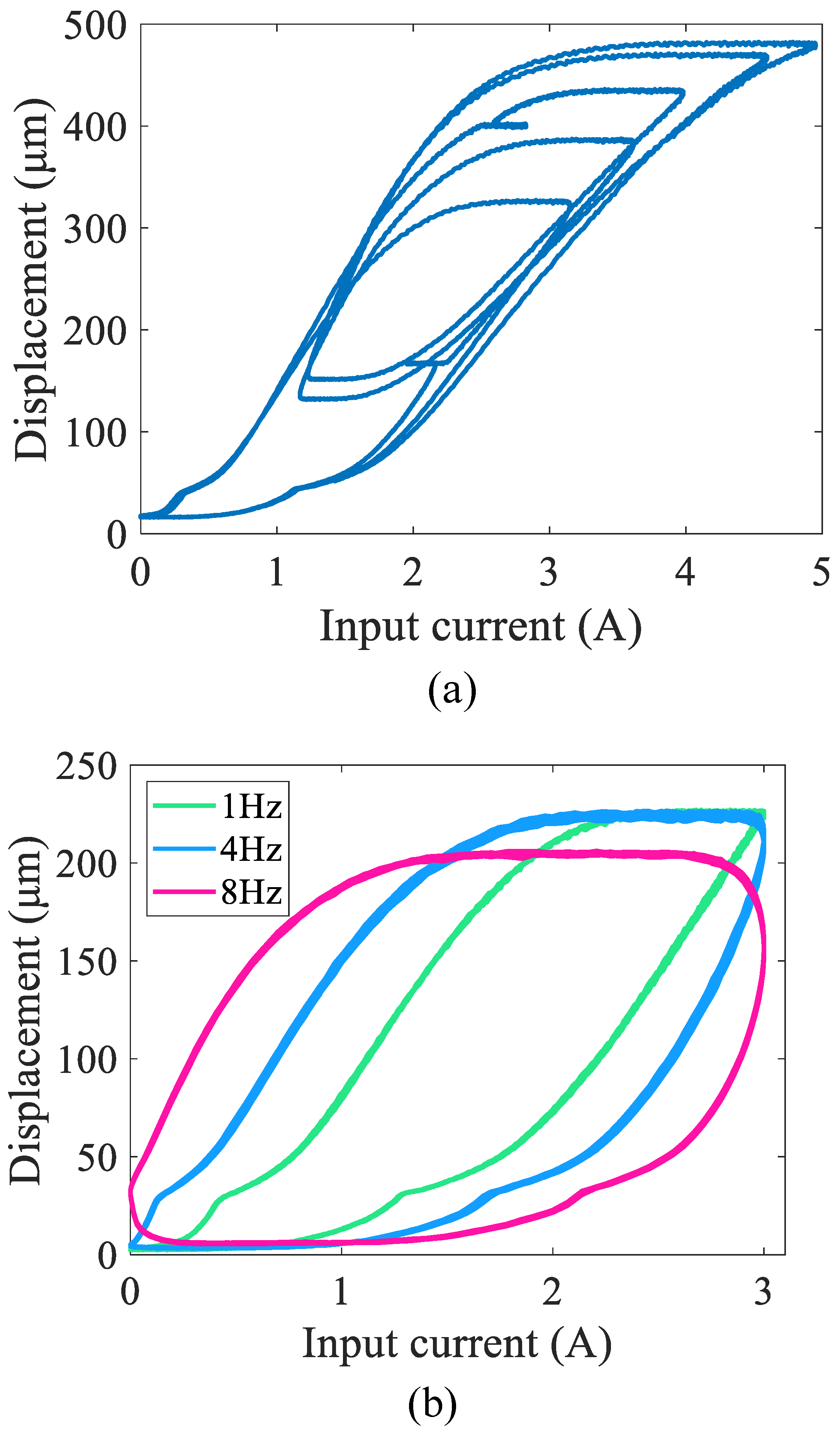
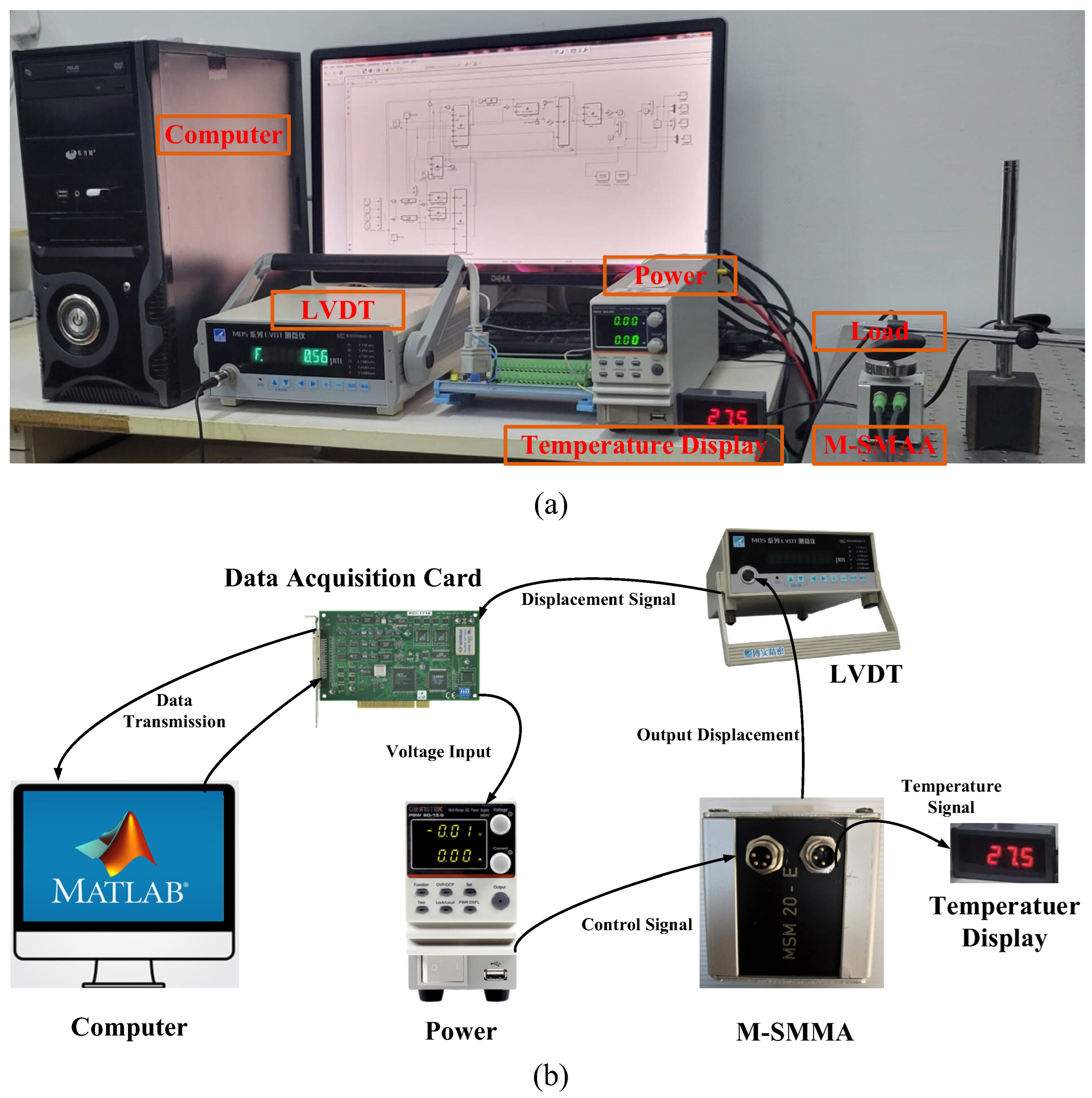
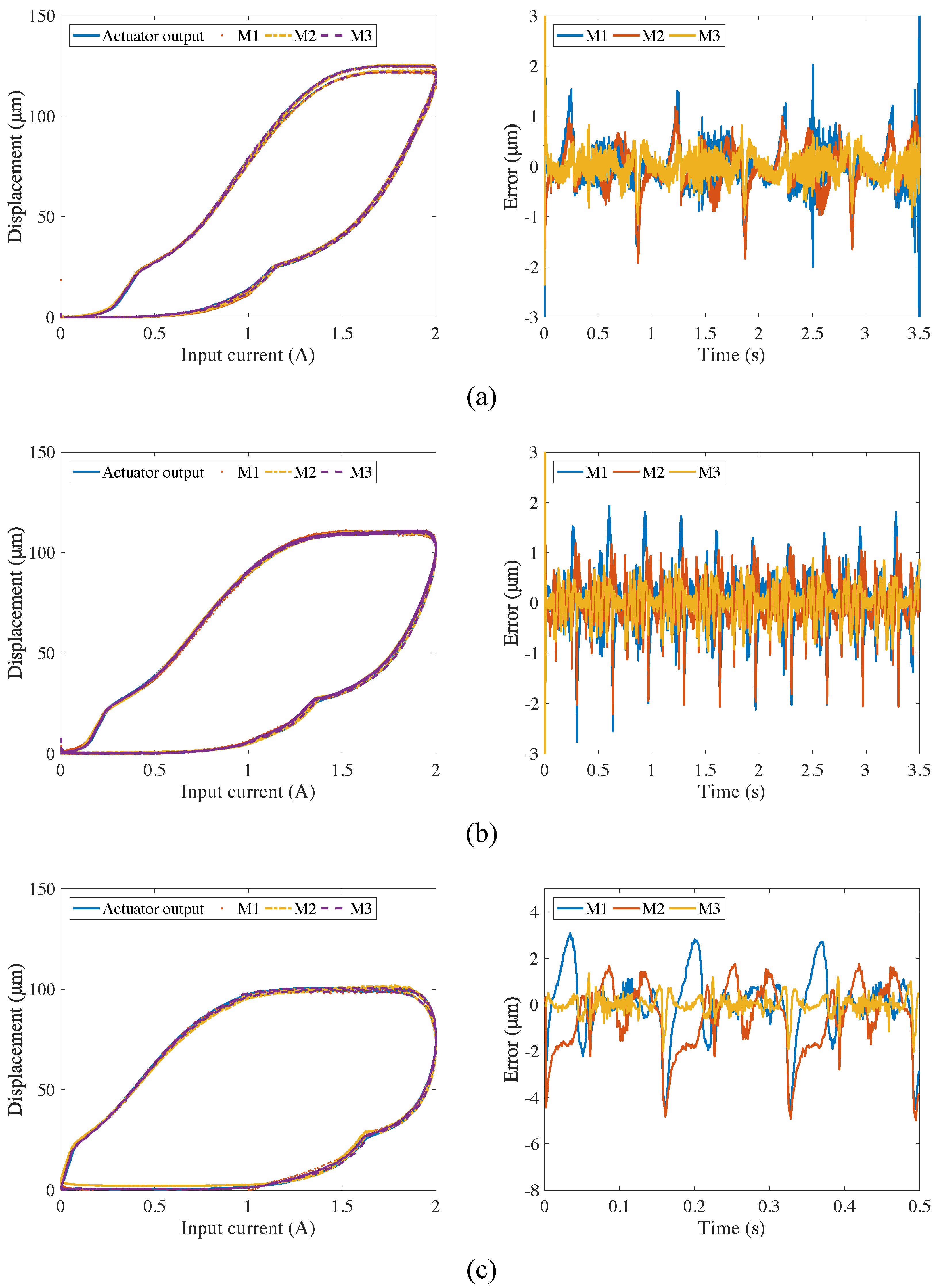
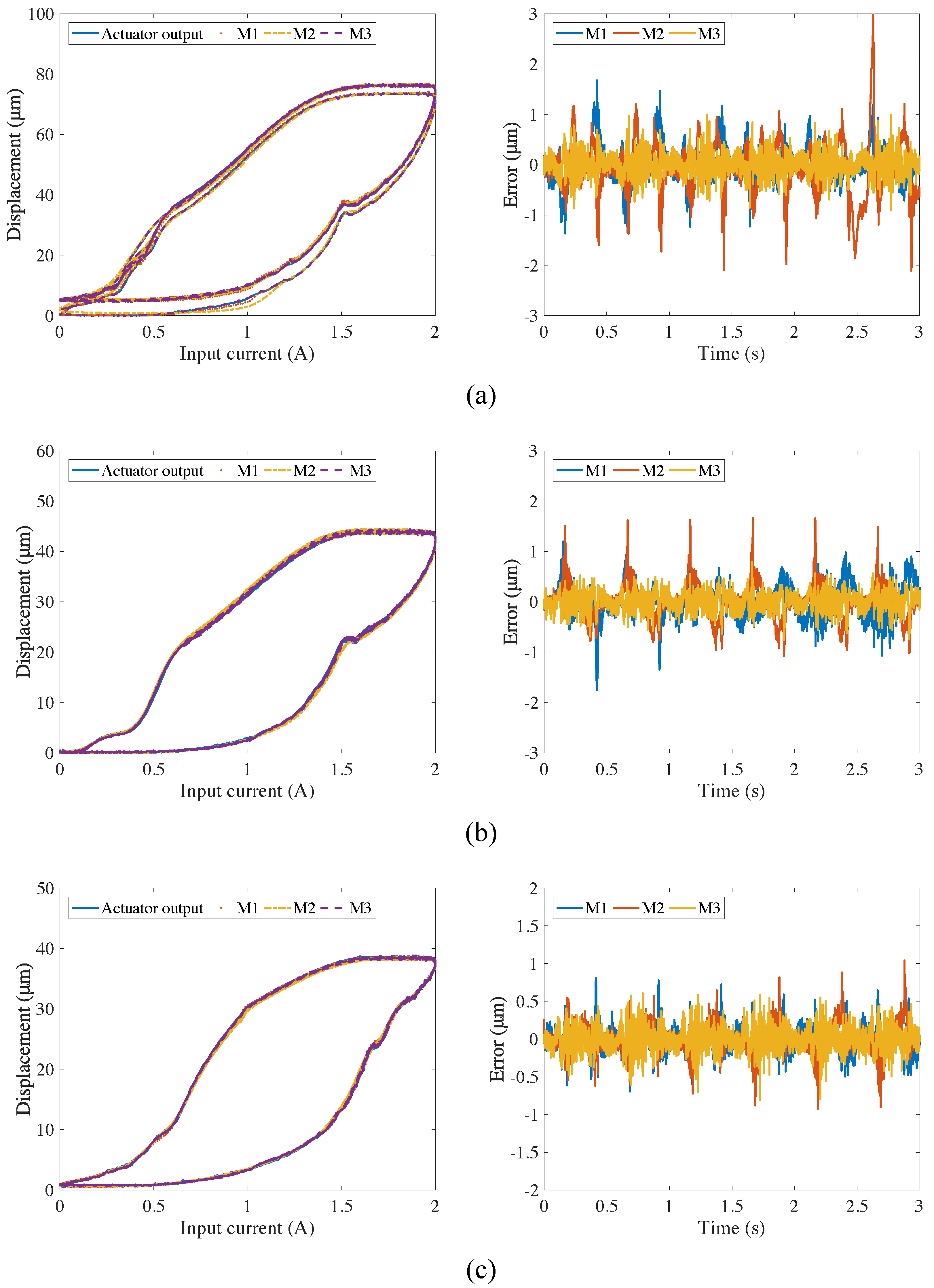
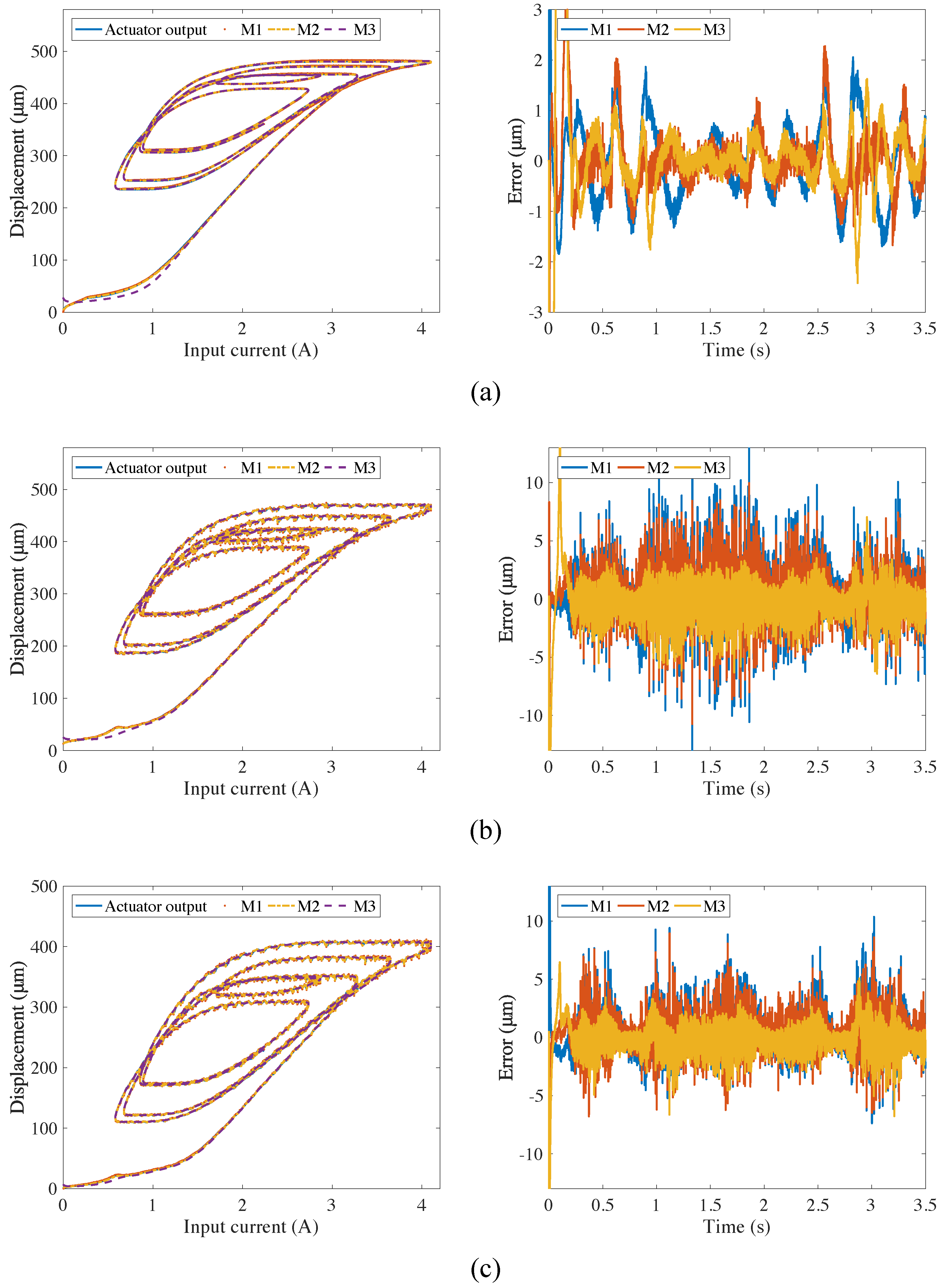
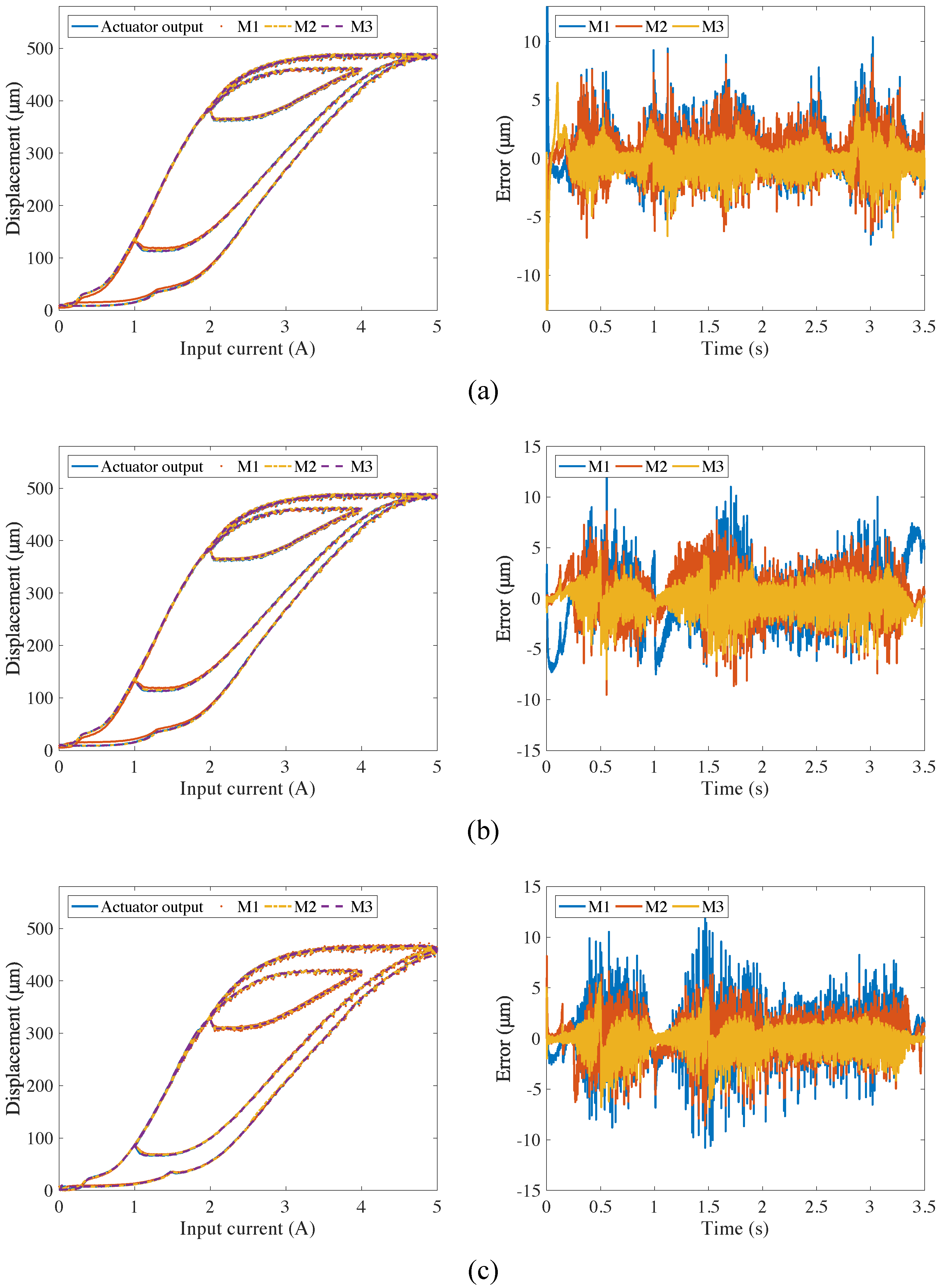
3. Experimental Results and Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yotov, I.; Todorov, G.; Gieva, E.; Todorov, T. Dynamics of a Self-Excited Vibrating Thermal Energy Harvester with Shape Memory Alloys and PVDF Cantilevers. Actuators 2024, 14, 8. [Google Scholar] [CrossRef]
- Kim, M.S.; Heo, J.K.; Rodrigue, H.; Lee, H.T.; Pané, S.; Han, M.W.; Ahn, S.H. Shape memory alloy (SMA) actuators: The role of material, form, and scaling effects. Adv. Mater. 2023, 33, 2208517. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Li, Y.; Cao, Y.; Zhang, F.; Cui, M.; Xu, R. High-precision position tracking control with a hysteresis observer based on the Bouc–Wen model for smart material-actuated systems. Actuators 2024, 13, 105. [Google Scholar] [CrossRef]
- Yu, Y.; Nie, L.; Zhang, X.; Su, C.Y.; Zhou, M. Finite-Iteration Learning Tracking Control of Magnetic Shape Memory Alloy Actuator Based on Neural Network. IEEE Trans. Circuits Syst. II 2025. early access. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, C.; Cao, W.; Huang, X.; Zhang, X.; Zhou, M. Neural network-based iterative learning control for magnetic shape memory alloy actuator with iteration-dependent uncertainties. Mech. Syst. Signal Proc. 2023, 187, 109950. [Google Scholar] [CrossRef]
- Hassani, V.; Tjahjowidodo, T.; Do, T.N. A survey on hysteresis modeling, identification and control. Mech. Syst. Signal Proc. 2014, 49, 209–233. [Google Scholar] [CrossRef]
- Wang, T.; Noori, M.; Altabey, W.A.; Wu, Z.; Ghiasi, R.; Kuok, S.C.; Silik, A.; Farhan, N.S.; Sarhosis, V.; Farsangi, E.N. From model-driven to data-driven: A review of hysteresis modeling in structural and mechanical systems. Mech. Syst. Signal Proc. 2023, 204, 110785. [Google Scholar] [CrossRef]
- Roussel, R.; Edelen, A.; Ratner, D.; Dubey, K.; Gonzalez-Aguilera, J.P.; Kim, Y.K.; Kuklev, N. Differentiable preisach modeling for characterization and optimization of particle accelerator systems with hysteresis. Phys. Rev. Lett. 2022, 128, 204801. [Google Scholar] [CrossRef]
- Manfredo, D.; Dörlich, V.; Linn, J.; Arnold, M. Data based constitutive modelling of rate independent inelastic effects in composite cables using Preisach hysteresis operators. Multibody Syst. Dyn. 2023, 62, 581–596. [Google Scholar] [CrossRef]
- Ruili, D.; Yonghong, T.; Yingjie, X.; Xiaoli, L. A dynamic hysteresis model of piezoelectric ceramic actuators. Chin. J. Electron. 2023, 32, 1278–1285. [Google Scholar] [CrossRef]
- Chai, G.; Tan, Y.; Tan, Q.; Dong, R.; Ke, C.; Gu, Y.; Wang, T. Modeling of Dynamic Systems With Hysteresis Using Predictive Gradient-Based Method. IEEE Trans. Autom. Sci. Eng. 2024, 22, 8976–8987. [Google Scholar] [CrossRef]
- Savoie, M.; Shan, J. Temperature-dependent asymmetric Prandtl-Ishlinskii hysteresis model for piezoelectric actuators. Smart Mater. Struct. 2022, 31, 055022. [Google Scholar] [CrossRef]
- Zhu, R.; Liu, L.; Wu, Y.; Chen, H.; Lou, W.; Yang, P.; Kong, M. Modeling and parameter identification of rate-dependent hysteresis behavior based on modified-generalized Prandtl–Ishlinskii model. Smart Mater. Struct. 2024, 33, 075003. [Google Scholar] [CrossRef]
- Fragassa, C.; Berardi, L.; Balsamini, G. Magnetorheological Fluid Devices: An Advanced Solution for Active Control of the Wood Manufacturing Process. FME Trans. 2016, 44, 333–339. [Google Scholar] [CrossRef]
- Xu, M.; Su, L.R.; Chen, S.T. Improved PI hysteresis model with one-sided dead-zone operator for soft joint actuator. Sens. Actuators A Phys. 2023, 349, 114072. [Google Scholar] [CrossRef]
- Xu, R.; Tian, D.; Zhou, M. A rate-dependent KP modeling and direct compensation control technique for hysteresis in piezo-nanopositioning stages. J. Intell. Mater. Syst. Struct. 2022, 33, 629–640. [Google Scholar] [CrossRef]
- Li, Z.; Shan, J.; Gabbert, U. Inverse compensation of hysteresis using Krasnoselskii-Pokrovskii model. IEEE-ASME Trans. Mechatron. 2018, 23, 966–971. [Google Scholar] [CrossRef]
- Li, Z.; Li, Z.; Xu, H.; Zhang, X.; Su, C.Y. Development of a butterfly fractional-order backlash-like hysteresis model for dielectric elastomer actuators. IEEE Trans. Ind. Electron. 2022, 70, 1794–1801. [Google Scholar] [CrossRef]
- Yang, L.; Zhong, R.; Li, D.; Li, Z. A fractional-order Duhem model of rate-dependent hysteresis for piezoelectric actuators. Meas. Control 2022, 55, 974–982. [Google Scholar] [CrossRef]
- Dai, Y.; Li, D.; Wang, D. Review on the nonlinear modeling of hysteresis in piezoelectric ceramic actuators. Actuators 2023, 12, 442. [Google Scholar] [CrossRef]
- Nguyen, X.B.; Komatsuzaki, T.; Truong, H.T. Adaptive parameter identification of Bouc-wen hysteresis model for a vibration system using magnetorheological elastomer. Int. J. Mech. Sci. 2022, 213, 106848. [Google Scholar] [CrossRef]
- Lin, M.; Cheng, C.; Zhang, G.; Zhao, B.; Peng, Z.; Meng, G. Identification of Bouc-Wen hysteretic systems based on a joint optimization approach. Mech. Syst. Signal Proc. 2022, 180, 109404. [Google Scholar] [CrossRef]
- Yin, R.; Xue, B.; Brousseau, E.; Geng, Y.; Yan, Y. Characterizing the electric field-and rate-dependent hysteresis of piezoelectric ceramics shear motion with the Bouc-Wen model. Sens. Actuators A Phys. 2024, 367, 115044. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, C.; Wang, E.; Zhou, M. Neural network adaptive control of magnetic shape memory alloy actuator with time delay based on composite NARMAX model. IEEE Trans. Circuits Syst. I-Regul. Pap. 2023, 70, 3336–3346. [Google Scholar] [CrossRef]
- Zhou, M.; Sun, Y.; Zhang, X.; Gao, W.; Su, C.Y. Enhanced neural-network-based iterative learning control considering iterative uncertainties for piezoelectric actuated micro-positioning platform. Eng. Appl. Artif. Intell. 2025, 161, 112134. [Google Scholar] [CrossRef]
- Sherstinsky, A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Phys. D 2020, 404, 132306. [Google Scholar] [CrossRef]
- Wu, D.; Zhang, Y.; Ourak, M.; Niu, K.; Dankelman, J.; Vander Poorten, E. Hysteresis modeling of robotic catheters based on long short-term memory network for improved environment reconstruction. IEEE Robot. Autom. Lett. 2021, 6, 2106–2113. [Google Scholar] [CrossRef]
- Zhou, M.; Su, L.; Zhang, C.; Liu, L.; Yu, Y.; Zhang, X.; Su, C.Y. Neural Network Based Iterative Learning Control for Dynamic Hysteresis and Uncertainties in Magnetic Shape Memory Alloy Actuator. IEEE Trans. Circuits Syst. I-Regul. Pap. 2024, 71, 2885–2896. [Google Scholar] [CrossRef]
- Wang, M.; Liu, Z.; Yu, Y.; Yang, X.; Gao, W. Rate-Dependent Hysteresis Model Based on LS-SVM for Magnetic Shape Memory Alloy Actuator. Actuator 2024, 14, 4. [Google Scholar] [CrossRef]
| Input Signal | M1 | M2 | M3 |
|---|---|---|---|
| 1 Hz, 0 g | 0.5783/1.03/0.39/1.39 | 0.4334/0.97/0.35/4.97 | 0.2434/0.67/0.21/2.56 |
| 3 Hz, 0 g | 0.5982/1.43/0.42/1.02 | 0.4625/1.22/0.37/3.34 | 0.3334/0.83/0.27/1.95 |
| 6 Hz, 0 g | 1.9974/1.99/1.40/0.33 | 1.6357/1.79/1.31/2.58 | 0.4438/1.21/0.36/0.85 |
| 2 Hz, 100 g | 0.2758/3.87/0.23/1.03 | 0.2047/3.06/0.16/5.32 | 0.1602/1.37/0.13/2.57 |
| 2 Hz, 200 g | 0.4893/3.94/0.39/1.47 | 0.3609/3.62/0.29/4.77 | 0.1880/1.72/0.15/2.50 |
| 2 Hz, 300 g | 0.6803/4.74/0.57/1.29 | 0.5584/4.20/0.45/5.01 | 0.2242/1.79/0.18/2.63 |
| CHS, 0 g | 0.6439/0.57/0.51/0.97 | 0.5222/0.49/0.42/4.58 | 0.4904/0.35/0.39/1.99 |
| CHS, 100 g | 1.7074/1.61/1.43/1.12 | 1.6734/1.52/1.34/4.21 | 1.2342/1.10/0.99/2.21 |
| CHS, 200 g | 2.3904/2.26/1.80/0.99 | 2.1751/2.16/1.74/4.02 | 1.5525/1.94/1.24/2.17 |
| TWS, 0 g | 2.0087/1.49/1.51/1.22 | 1.8241/1.37/1.46/5.35 | 1.4327/1.09/1.15/2.86 |
| TWS, 100 g | 2.4744/1.63/1.69/1.07 | 1.9943/1.53/1.60/5.01 | 1.6233/1.14/1.30/2.95 |
| TWS, 200 g | 2.8943/1.83/1.72/1.23 | 2.0180/1.77/1.61/5.27 | 1.7259/1.55/1.38/2.88 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, H.; Zhou, M. Hysteresis Modeling of a Magnetic Shape Memory Alloy Actuator Using a NARMAX Model and a Long Short-Term Memory Neural Network. Actuators 2025, 14, 573. https://doi.org/10.3390/act14120573
Wu H, Zhou M. Hysteresis Modeling of a Magnetic Shape Memory Alloy Actuator Using a NARMAX Model and a Long Short-Term Memory Neural Network. Actuators. 2025; 14(12):573. https://doi.org/10.3390/act14120573
Chicago/Turabian StyleWu, Haoran, and Miaolei Zhou. 2025. "Hysteresis Modeling of a Magnetic Shape Memory Alloy Actuator Using a NARMAX Model and a Long Short-Term Memory Neural Network" Actuators 14, no. 12: 573. https://doi.org/10.3390/act14120573
APA StyleWu, H., & Zhou, M. (2025). Hysteresis Modeling of a Magnetic Shape Memory Alloy Actuator Using a NARMAX Model and a Long Short-Term Memory Neural Network. Actuators, 14(12), 573. https://doi.org/10.3390/act14120573







