Rate-Dependent Hysteresis Model Based on LS-SVM for Magnetic Shape Memory Alloy Actuator
Abstract
1. Introduction
2. LS-SVM Hysteresis Model
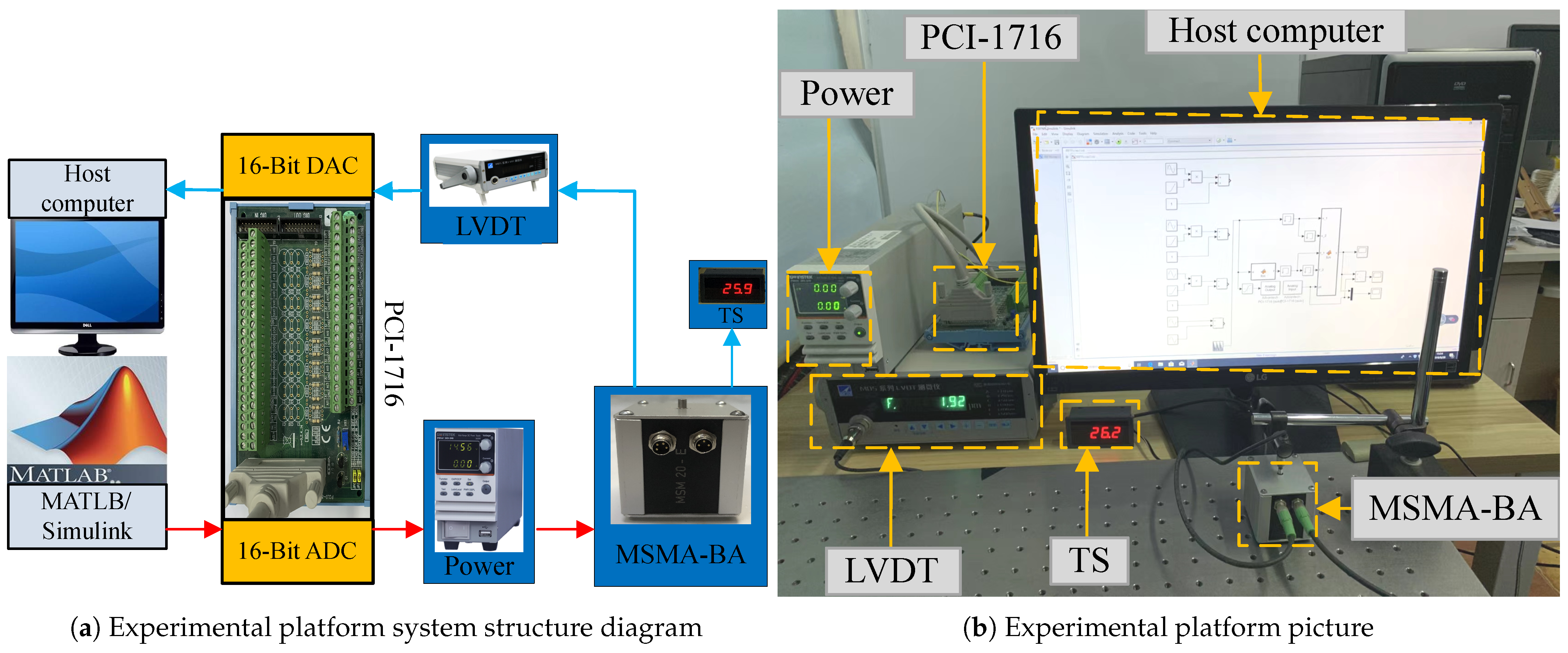
3. Experimental Verification
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, J.; Li, Y.; Cao, Y.; Zhang, F.; Cui, M.; Xu, R. High-precision position tracking control with a hysteresis observer based on the Bouc–Wen model for smart material-actuated systems. Actuators 2024, 13, 105. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, C.; Zhang, X.; Su, C.Y.; Zhou, M. Iterative Learning Control Based on Neural Network and Its Application to Ni-Mn-Ga Alloy Actuator With Local Lipschitz Nonlinearity. IEEE Trans. Industr. Inform. 2024, 20, 8138–8148. [Google Scholar] [CrossRef]
- Zhou, M.; Su, L.; Zhang, C.; Liu, L.; Yu, Y.; Zhang, X.; Su, C.Y. Neural Network Based Iterative Learning Control for Dynamic Hysteresis and Uncertainties in Magnetic Shape Memory Alloy Actuator. IEEE Trans. Circuits Syst. I Regul. Pap. 2024, 71, 2885–2896. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, C.; Cao, W.; Huang, X.; Zhang, X.; Zhou, M. Neural network based iterative learning control for magnetic shape memory alloy actuator with iteration-dependent uncertainties. Mech. Syst. Signal. Process. 2023, 187, 109950. [Google Scholar] [CrossRef]
- Zhang, C.; Yu, Y.; Zhou, M. Finite-time adaptive quantized motion control for hysteretic systems with application to piezoelectric-driven micropositioning stage. IEEE/ASME Trans. Mech. 2023, 28, 2541–2552. [Google Scholar] [CrossRef]
- Li, X.; Zhi, W.; Shi, E.; Fan, X.; Zhao, M.; Zhang, B. Adaptive Nonsingular Fast Terminal Sliding Mode Control for Shape Memory Alloy Actuated System. Actuators 2024, 13, 367. [Google Scholar] [CrossRef]
- Li, Z.; Shan, J.; Gabbert, U. Inverse Compensation of Hysteresis Using Krasnoselskii-Pokrovskii Model. IEEE/ASME Trans. Mech. 2018, 23, 966–971. [Google Scholar] [CrossRef]
- Xu, R.; Tian, D.; Wang, Z. Adaptive tracking control for the piezoelectric actuated stage using the Krasnosel’skii-Pokrovskii operator. Micromachines 2020, 11, 537. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Su, L.R.; Chen, S.T. Improved PI hysteresis model with one-sided dead-zone operator for soft joint actuator. Sens. Actuators A Phys. 2023, 349, 114072. [Google Scholar] [CrossRef]
- Jiang, H.; Ji, H.; Qiu, J.; Chen, Y. A modified prandtl-ishlinskii model for modeling asymmetric hysteresis of piezoelectric actuators. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2010, 57, 1200–1210. [Google Scholar] [CrossRef] [PubMed]
- Janaideh, M.A.; Su, C.Y.; Rakheja, S. Development of the rate-dependent Prandtl–Ishlinskii model for smart actuators. Smart Mater. Struct. 2008, 17, 035026. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, C.; Han, Z.; Zhou, M. Hysteresis modeling of magnetic shape memory alloy actuator based on volterra series. IEEE Trans. Magn. 2021, 57, 1–4. [Google Scholar] [CrossRef]
- Nie, L.; Zhou, M.; Zhang, X.; Su, C.Y. Observer-Based Finite-Time Adaptive Motion Control for Nonlinear Asymmetric Hysteresis Systems in Pure-Feedback Form. IEEE Trans. Ind. Electron. 2024, 71, 12900–12910. [Google Scholar] [CrossRef]
- Kang, S.; Wu, H.; Li, Y.; Yang, X.; Yao, J. A Fractional-Order Normalized Bouc–Wen Model for Piezoelectric Hysteresis Nonlinearity. IEEE/ASME Trans. Mech. 2022, 27, 126–136. [Google Scholar] [CrossRef]
- Cai, J.; Dong, W.; Nagamune, R. A survey of Bouc-Wen hysteretic models applied to piezo-actuated mechanical systems: Modeling, identification, and control. J. Intell. Mater. Syst. Struct. 2023, 34, 1843–1863. [Google Scholar] [CrossRef]
- Vasquez-Beltran, M.A.; Jayawardhana, B.; Peletier, R.F. Modeling and analysis of Duhem hysteresis operators with butterfly loops. IIEEE Trans. Automat. Contr. 2023, 68, 5977–5990. [Google Scholar] [CrossRef]
- Zhang, C.; Yu, Y.; Xu, J.; Zhou, M. Hysteresis modeling and analysis of magnetic shape memory alloy-driven actuator. IEEE Trans. Nanotechnol. 2022, 21, 390–398. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, C.; Wang, Y.; Zhou, M. Neural-network-based iterative learning control for hysteresis in a magnetic shape memory alloy actuator. IEEE/ASME Trans. Mech. 2021, 27, 928–939. [Google Scholar] [CrossRef]
- Nie, L.; Zhou, M.; Zhang, X.; Su, C.Y. Compound Estimation-Based Output-Feedback Hysteresis Compensation and Sensor Fault-Tolerant Control Strategy: Application to Piezoelectric Micropositioning Stage. IEEE/ASME Trans. Mech. 2024. early access. [Google Scholar] [CrossRef]
- Chen, G.; Chen, G.; Lou, Y. Diagonal Recurrent Neural Network-Based Hysteresis Modeling. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 7502–7512. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Yao, X.; Cui, J.; Yan, Y.; Dai, J.; Zhao, W. A novel piezoelectric hysteresis modeling method combining LSTM and NARX neural networks. Mod. Phys. Lett. B 2020, 34, 2050306. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, C.; Zhou, M. NARMAX model-based hysteresis modeling of magnetic shape memory alloy actuators. IEEE Trans. Nanotechnol. 2019, 19, 1–4. [Google Scholar] [CrossRef]
- Sudheer, C.; Maheswaran, R.; Panigrahi, B.K.; Mathur, S. A hybrid SVM-PSO model for forecasting monthly streamflow. Neural Comput. Appl. 2014, 24, 1381–1389. [Google Scholar] [CrossRef]
- Han, H.; Gu, B.; Kang, J.; Li, Z. Study on a hybrid SVM model for chiller FDD applications. Appl. Therm. Engi. 2011, 31, 582–592. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, C.; Wang, E.; Zhou, M. Neural network adaptive control of magnetic shape memory alloy actuator with time delay based on composite NARMAX model. IEEE Trans. Circuits Syst. I Regul. Pap. 2023, 70, 3336–3346. [Google Scholar] [CrossRef]
- Baziyad, A.G.; Nouh, A.S.; Ahmad, I.; Alkuhayli, A. Application of Least-Squares Support-Vector Machine Based on Hysteresis Operators and Particle Swarm Optimization for Modeling and Control of Hysteresis in Piezoelectric Actuators. Actuators 2022, 11, 217. [Google Scholar] [CrossRef]
- Baziyad, A.G.; Ahmad, I.; Salamah, Y.B.; Alkuhayli, A. Robust Tracking Control of Piezo-Actuated Nanopositioning Stage Using Improved Inverse LSSVM Hysteresis Model and RST Controller. Actuators 2022, 11, 324. [Google Scholar] [CrossRef]
- Suykens, J.A.; Vandewalle, J. Least squares support vector machine classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Xu, R.; Zhou, M. Elman Neural Network-Based Identification of Krasnosel’skii–Pokrovskii Model for Magnetic Shape Memory Alloys Actuator. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar]
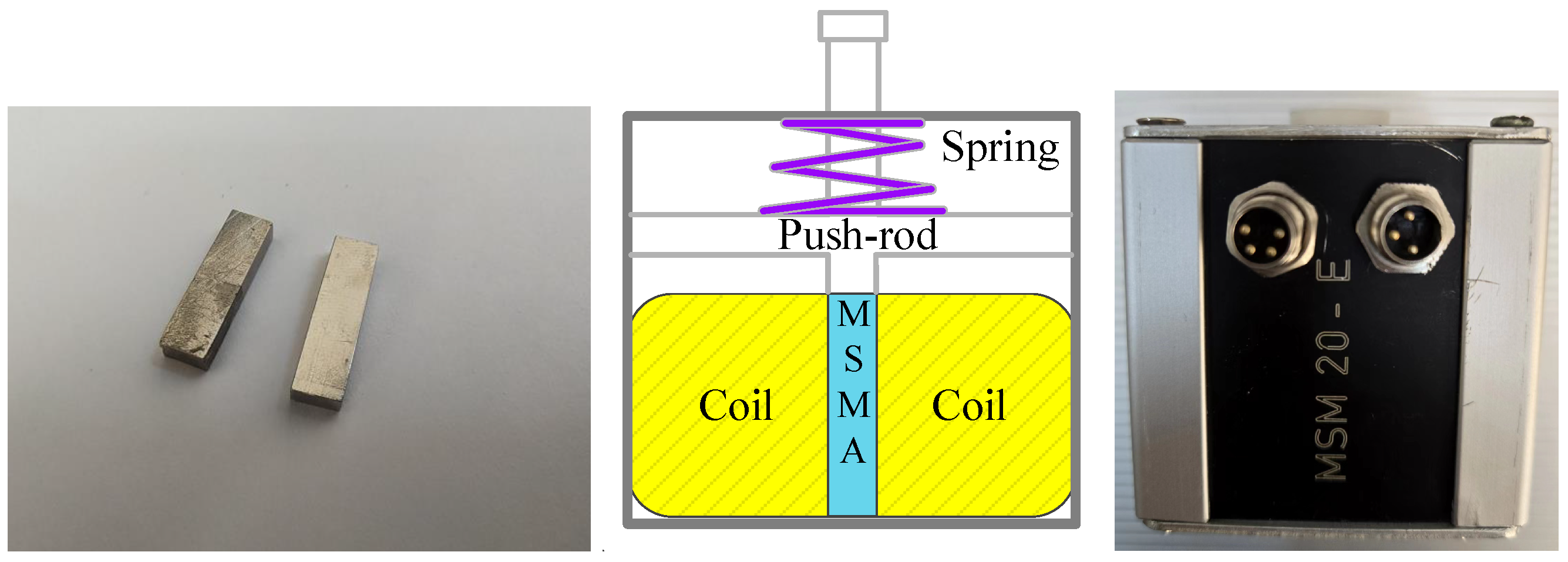



| Basic Properties | Values |
|---|---|
| Dimensions | 50 × 50 × 50 |
| Operating temperature range | 0–45 °C |
| Maximum output displacement | 450 m |
| Maximum input current | 8 |
| Resistance | 3 |
| Frequency | Model | RMSE | MAE | MER | Im. (RMSE / MAE) |
|---|---|---|---|---|---|
| (m) | (m) | (%) | (%) | ||
| 1 Hz | KP model | 1.0898 | 6.13 | 1.75 | 32.4/69.5 |
| LS-SVM model | 0.7368 | 1.87 | 0.53 | ||
| 10 Hz | KP model | 6.0826 | 11.36 | 3.79 | 35.7/57.5 |
| LS-SVM model | 3.9087 | 4.83 | 1.61 | ||
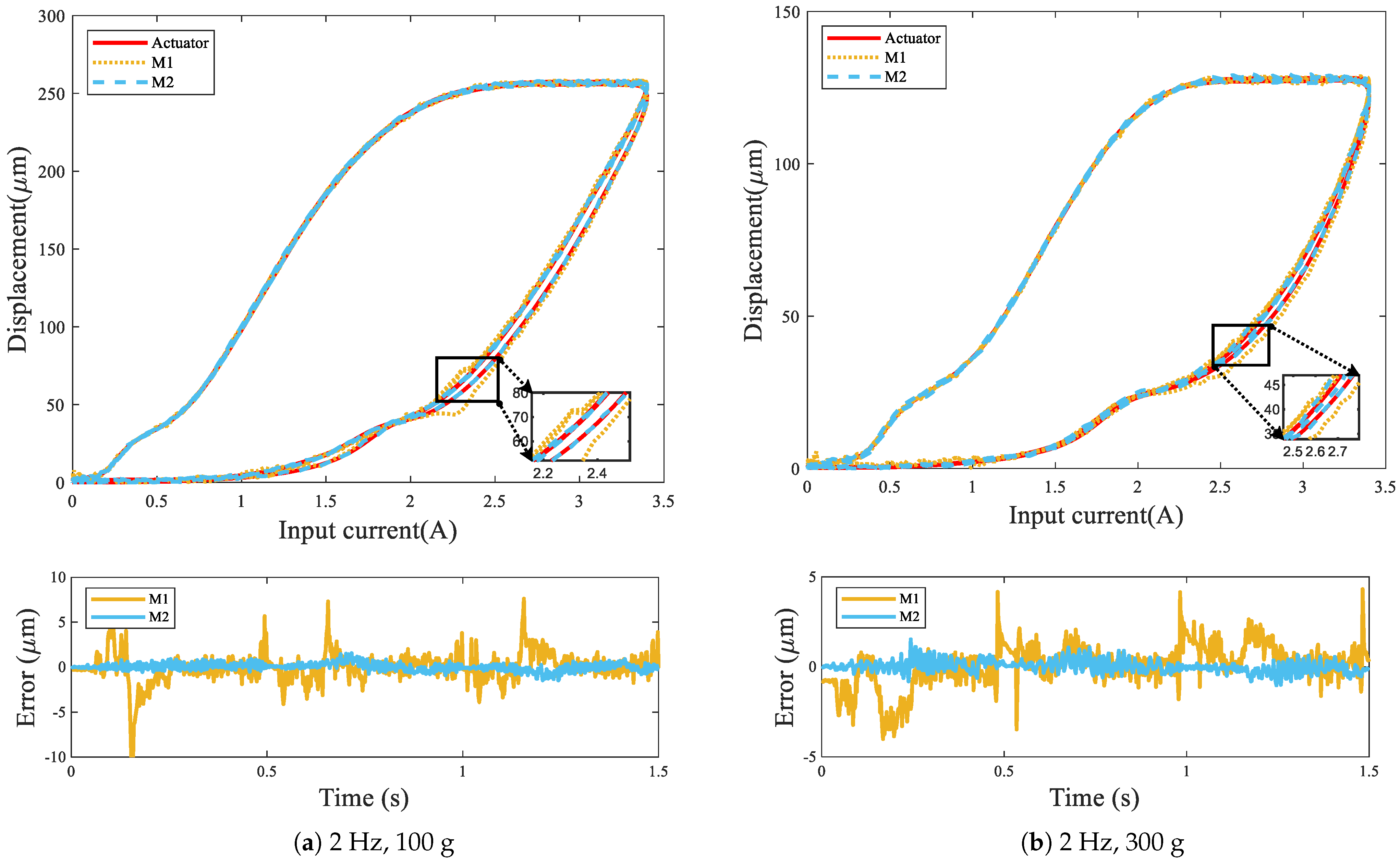
| 2 Hz, 100 g | KP model | 1.5162 | 7.13 | 2.85 | 26.1/71.1 |
| LS-SVM model | 1.1208 | 2.06 | 0.82 | ||
| 2 Hz, 300 g | KP model | 1.6017 | 4.87 | 3.83 | 10.8/56.7 |
| LS-SVM model | 1.4295 | 2.11 | 1.66 | ||
| Mixed Signal | KP model | 2.2899 | 9.10 | 2.17 | 25.7/55.3 |
| LS-SVM model | 1.7025 | 4.07 | 0.95 | ||
| Triangular Signal | KP model | 1.6959 | 21.62 | 5.54 | 22.1/28.7 |
| LS-SVM model | 1.3204 | 15.41 | 3.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Liu, Z.; Yu, Y.; Yang, X.; Gao, W. Rate-Dependent Hysteresis Model Based on LS-SVM for Magnetic Shape Memory Alloy Actuator. Actuators 2025, 14, 4. https://doi.org/10.3390/act14010004
Wang M, Liu Z, Yu Y, Yang X, Gao W. Rate-Dependent Hysteresis Model Based on LS-SVM for Magnetic Shape Memory Alloy Actuator. Actuators. 2025; 14(1):4. https://doi.org/10.3390/act14010004
Chicago/Turabian StyleWang, Mengyao, Zhenze Liu, Yewei Yu, Xiaoning Yang, and Wei Gao. 2025. "Rate-Dependent Hysteresis Model Based on LS-SVM for Magnetic Shape Memory Alloy Actuator" Actuators 14, no. 1: 4. https://doi.org/10.3390/act14010004
APA StyleWang, M., Liu, Z., Yu, Y., Yang, X., & Gao, W. (2025). Rate-Dependent Hysteresis Model Based on LS-SVM for Magnetic Shape Memory Alloy Actuator. Actuators, 14(1), 4. https://doi.org/10.3390/act14010004







