Abstract
Recently, the neural network control has been widely used in the field of wastewater treatment process (WWTP). However, most neural network (NN) control methods are time-driven, with a large number of transmissions and a large amount of neural network computation. To reduce the number of controller executions and save computational cost, the event-triggered neural network multivariate method is proposed to control WWTP. Firstly, different from the traditional NN-based control, the event-triggered mechanism based on sliding windows is designed to reduce the computation. Then, the multi-input and multi-output recurrent wavelet neural network (RWNN) controller is proposed for simultaneous control of dissolved oxygen and nitrate nitrogen. Furthermore, the stability of the RWNN controller is analyzed through the Lyapunov stability theorem. Experimental results demonstrate that the event-triggered RWNN delivers a significant 25% reduction in the number of executions without compromising control accuracy.
1. Introduction
Recently, frequent water shortages worldwide have affected economic development and society. To alleviate water shortages, the wastewater treatment process (WWTP) has attracted a lot of attention as an important way to reduce the need for natural water and weaken the pollution of the water environment [1,2]. Meanwhile, discharge standards for WWTPs have become stricter as water quality deteriorates, leading to an increase in the operating cost of WWTP [3]. On the other hand, the WWTP is a dynamic and nonlinear process due to its multiple biochemical reactions [4,5]. Therefore, it is a challenge to reduce the operating costs of WWTP while maintaining the desired control performance.
In WWTP, the activated sludge method (ASM) has become a widely used method for nitrogen removal and phosphorus removal with the development of technology [6,7]. During the process of ASM, the dissolved oxygen (DO) in the fifth tank and the nitrate nitrogen (NO3−) in the second tank are two important control variables. The nitrification reaction and denitrification reaction, as the core of ASM, are affected by DO and NO3− concentrations [8,9]. Therefore, the precise control of DO and NO3− is important to improve the efficiency of nitrogen and phosphorus removal in WWTP. Effective removal of DO and NO3− can prevent water eutrophication and substandard water quality. Furthermore, since high concentrations of DO and NO3− can inhibit microbial activity, their efficient elimination is essential for maintaining the metabolic function of microorganisms in activated sludge and ensuring the stable operation of the treatment system.
Traditional control methods such as feedforward control, proportional integral (PI) control and proportional integral derivative (PID) control have been widely applied to the control of WWTP [10,11]. These methods are simple in structure, but the control accuracy is low due to the fact that the WWTP is a complex nonlinear system [12]. To address this issue, with the development of technology, some intelligent control methods have attracted attention [13,14,15]. For example, the data-driven adaptive control based on the deep belief network was proposed to improve the stabilization of process control in WWTP [16]. To solve the problem of disturbances in the laboratory-activated sludge bioreactor process, the boundary-based predictive controller was designed to control the DO concentration within the desired range [17]. Wei et al. combined the state observer and adaptive sliding mode control to compensate for disturbances, effectively enhancing the robustness of the control system [18]. These intelligent methods can effectively improve the control accuracy of WWTP. However, the WWTP is a typical multivariate process, and these univariate control methods can only control the DO concentration, which cannot ensure the efficient operation of WWTP.
To deal with the problem of univariate control [19,20,21], multivariate control methods have been proposed, such as the reinforcement learning control [22], the sliding mode control [23] and the neural network control [24]. Among these methods, neural network control can realize precise control due to its powerful self-learning capability. For example, the self-organizing fuzzy neural network was proposed to control the DO concentration and NO3− concentration simultaneously. The results demonstrate the proposed controller can achieve high-precision multivariable control [25]. To deal with the local optimization problem of the traditional gradient descent algorithm of the neural network, Bai et al. designed the multi-gradient recurrent reinforcement learning algorithm to train the radial basis function neural network to control uncertain nonlinear systems. Experimental results show that the proposed algorithm effectively improves the learning accuracy of the network [26]. The recurrent fuzzy neural network with two hidden layers was combined with the sliding mode control to improve the control accuracy of the nonlinear system [27]. However, most neural network controls are time-driven, with large amounts of transmitted data and high computational load.
Unlike time-driven controls, event-triggered controls operate only when a specific event occurs, reducing the computational load. Recently, event-triggered controls have been studied in many fields. For example, the switching-like event-triggered scheme was proposed to counter denial-of-service attacks, thereby improving the communication efficiency of network control systems [28]. Liu et al. constructed the event-triggered controller to ensure the stability of repeated scalar nonlinear systems [29]. Moreover, the event-triggered distributed hybrid control scheme was designed to realize the safe and economic operation of the integrated energy system [30]. Experimental results have demonstrated that these event-triggered mechanisms can be successfully applied. However, the event-triggered algorithm in the framework of neural network control has not been well addressed.
Based on the above analysis, to reduce the computational cost of WWTP control, the event-triggered recurrent wavelet neural network (ERWNN) multivariate controller is designed in this paper. Unlike the previous neural network controls, the control process is event-driven to reduce the computational load of the neural network. The main contributions of this paper can be summarized as follows:
(1) Based on the control errors within a sliding window, the event-triggered mechanism is designed. Unlike traditional control methods that execute periodically at fixed time intervals, the mechanism only initiates control actions when the error meets specific conditions. This methodology effectively reduces the computational burden while improving overall control performance.
(2) The recurrent wavelet neural network is employed as the controller for WWTP. Otherwise, the control performance of the ERWNN is evaluated using the Benchmark Simulation Model No. 1 (BSM1) platform.
2. Activated Sludge Process
The activated sludge process (ASP), as an aerobic biological treatment method, is the most widely used method for WWTP. A typical ASP is composed of the biochemical reaction tank, the secondary settling tank, the sludge return system and the residual sludge discharge system, as shown in Figure 1. Among them, the biochemical reactor is the core of the ASP. The red part and blue part are the anoxic and aerobic zones, respectively, where denitrification and nitrification reactions are carried out.
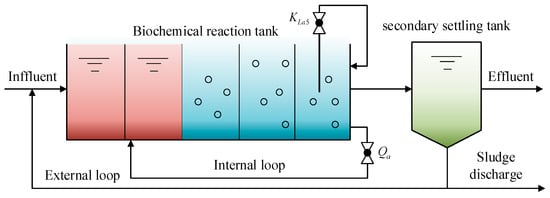
Figure 1.
The process of ASP.
In the biochemical reaction tank, the DO concentration and NO3− concentration have a great influence on the nitrification and denitrification reactions. Moreover, when the DO concentration is too high or too low, it will have an inhibitory effect on the denitrification reaction, thus affecting the NO3− concentration. Coupling exists between the control loops of DO and NO3−. Therefore, it is very important to design a high-performance multivariable controller for DO and NO3− concentration to improve the efficiency of WWTP.
According to the reaction mechanism of ASP, the kinetic equations of DO and NO3− concentration are as follows
where and are the flow rate of kth tank and internal flow of the second tank, and are the volume of the kth tank and component concentration, is the oxygen transfer coefficient of the kth tank, and and are the DO concentration and DO saturation concentration of the kth tank. Based on Equation (1) and the mechanism of biochemical reaction, the main factors affecting the DO and NO3− are and . Thus, the and are chosen as the operating variables for NO3− of the second tank and DO of the fifth tank.
3. Event-Triggered Neural Network Control
In this section, to reduce the control cost while ensuring control accuracy, the event-triggered recurrent wavelet neural network (ERWNN) is proposed to control DO and NO3− concentrations in WWTP, as shown in Figure 2.
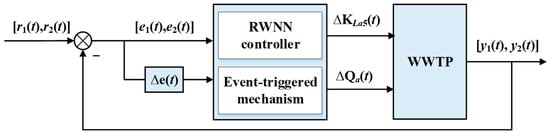
Figure 2.
The structure of multi-variable control.
The structure of the RWNN controller is displayed in Figure 3, which contains four layers: input layer, mother wavelet layer, wavelet layer and output layer. It is assumed that the number of wavelet nodes is q, then the input to the controller at time t is
where , , and are the set-points of DO and NO3− concentration, and are the actual values of DO and NO3− concentration and and are the changes in error, respectively.
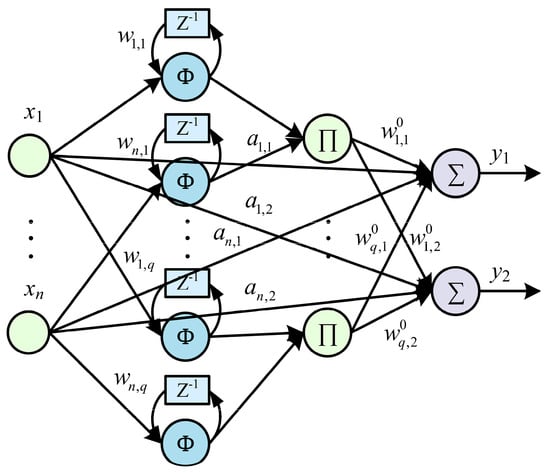
Figure 3.
The structure of the RWNN controller.
Then the output of the controller can be calculated as
where is the weight between input and output, is the ith input, is the output weight and is the output of jth wavelet neuron which is shown as follows
where is the output of the mother wavelet layer, and are the translation and dilation coefficients, respectively and is the feedback weight.
Remark 1.
In practice, the WWTP is a dynamic and nonlinear process. The RWNN combines the dynamic performance of the recurrent neural network and the capability of wavelet analysis, which effectively improves the learning ability of neural networks. Therefore, the RWNN is selected as the controller in this paper. Furthermore, there is a coupling between the control loops of DO and NO3−. Thus, a single controller is used to weaken the influence of the coupling problem on the control results.
3.1. Parameter Learning Mechanism
In this subsection, the parameter learning algorithm combined with adaptive learning rates is designed to obtain the desired control accuracy. The cost function of RWNN controller is defined as
where and are the control error of DO and NO3− concentration, respectively, and is the proportionality factor.
Then, according to the gradient descent mechanism, the parameters can be updated as follows
where that can be defined as
where , which is described for clarity.
The RWNN transforms the input error into control signals and via Equations (3)–(6), directing the WWTP to update the DO and NO3− concentrations. Concurrently, parameters are updated in real-time by the online learning algorithm specified in Equations (7)–(9). This forms a closed-loop where the learning algorithm refines parameters using the feedback error, thereby forcing the output of RWNN to converge toward the desired values and consequently regulating the actual DO and NO3− concentrations to match their targets.
3.2. Event-Triggered Mechanism
The traditional neural network controls are time-driven, i.e., the controller executes at every time, resulting in a large computational load on the controller. To reduce the computational cost of WWTP, the event-triggered mechanism based on the control error is designed for the RWNN controller in this subsection. The procedure of the event-triggered mechanism is described as follows:
Step 1: Define a sliding window of window size m and the confidence level as .
Step 2: Calculate the confidence intervals of DO and NO3− errors as and .
Step 3: Define the events which are shown as follows
where are the artificially set thresholds.
Step 4: Design an event-triggered learning strategy. When events E1 or E2 occur, the system is poorly controlled, which means that the controller is required to make adjustments to the DO and NO3− concentrations. Thus, we have the following rule
where and are the outputs of RWNN controller at time t.
Remark 2.
Based on the event-triggered mechanism, the controller executes only when event E1 or E2 occurs.
3.3. Control Process of WWTP
Based on the above introduction, the details of the ERWNN-based multivariate control of WWTP are described in Table 1 and Figure 4.

Table 1.
The control process of WWTP.
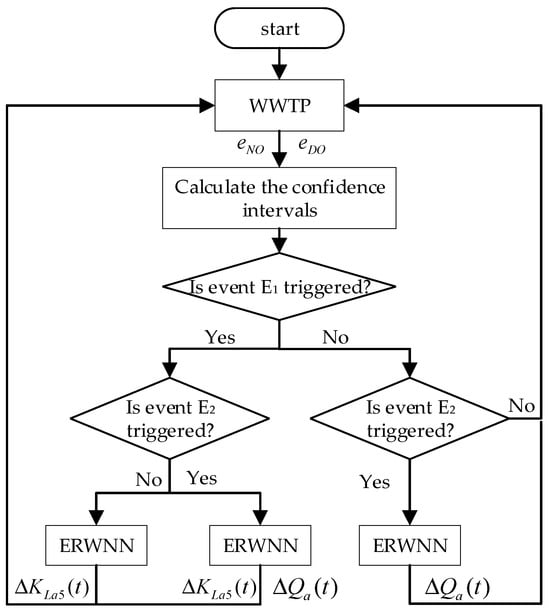
Figure 4.
The control flow of ERWNN.
3.4. Stability Analysis
In practice, the stability of the controller is very important for successful application. Thus, the stability of the ERWNN controller is analyzed based on the Lyapunov stability theorem in this subsection.
Theorem 1.
Assuming that the wavelet node of ERWNN is q, if the adaptive learning rates satisfy Equation (9), the stability of the ERWNN controller can be guaranteed.
Proof.
Define the Lyapunov function as
where and are the control errors of the DO and NO3− concentrations, respectively.
Then the change in Lyapunov function is as follows
According to [25], the change in control error can be calculated as
Based on the update rule of Equation (8), we have
Then Equation (14) can be further described as
It can be seen that when , . Then when the learning rates satisfy Equation (9), we have , i.e., Theorem 1 is proved. □
4. Simulation Results and Discussion
Based on the BSM1 platform, the performance of the ERWNN controller is analyzed in this section. The set-points of DO and NO3− concentrations are chosen as fixed and variable values to measure the control performance more comprehensively. The parameters of ERWNN are determined by the trail-and-error method in the experiment. The control accuracy of different methods is measured by the maximal derivation from set point (Devmax), integral of squared error (ISE) and integral of absolute error (IAE), as shown in the following formulas.
where N is the total number of samples, d(t) and y(t) are the desired output and actual output. The smaller IAE, ISE and Devmax represent better control performance.
4.1. Constant Set-Points of DO and NO3− Concentration
In this subsection, the control performance of the ERWNN controller is fist measured at the constant set-points, i.e., and .
Under the dry condition, the control errors of DO and NO3− concentrations are shown in Figure 5. Obviously, the control results of ERWNN are better than RWNN. Most of the control errors of ERWNN are contributed in the range of [−0.008, 0.008] and [−0.01, 0.01], while most of the control errors of RWNN are in the range of [−0.02, 0.02] and [−0.04, 0.02]. As shown in Figure 6 and Figure 7, the ERWNN can also obtain good control effects in rainy and rainstorm weather. The control performance of ERWNN on the DO concentration is better than that of RWNN. Moreover, the control results of ERWNN and RWNN are comparable in NO3−, which is due to the coupling between DO and NO3−.
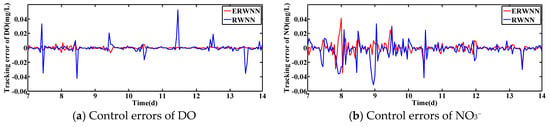
Figure 5.
Control errors under dry weather with constant set-points.
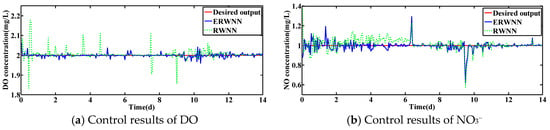
Figure 6.
Control results under rainy weather with constant set-points.
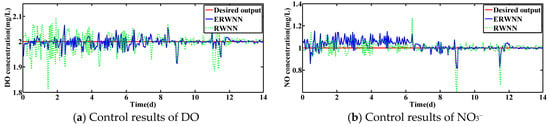
Figure 7.
Control results under rainstorm weather with constant set-points.
To further measure the control performance of ERWNN under the dry condition, the control results are compared with the RWNN, NNOMC, RARFNNC and DRFNNC. Moreover, under two other operating conditions, the control performances are compared with the RFNN and RBFNN. The comparison results are summarized in Table 2, which include the IAE, ISE and Devmax of the DO and NO3− concentrations. Otherwise, the Events column in Table 2 refers to the number of executions of the controller. It can be seen that the control error of ERWNN is smaller than other methods under any of the operating conditions. In practical applications, the event-triggered mechanism offers a significant reduction in controller executions, improving overall control efficiency without compromising performance.

Table 2.
Comparison of different control methods for fixed set-point.
4.2. Changed Set-Points of DO and NO3− Concentrations
In this subsection, to further analyze the dynamic characteristics of the ERWNN controller, the set-points of DO and NO3− are set to step values as follows,
where .
Under the dry condition, the control results of ERWNN and RWNN are shown in Figure 8. It can be seen that the proposed ERWNN can obtain good control results when the set-point is dynamically changed. Moreover, the simulation results of the DO concentration and NO3− concentration under the other two conditions are displayed in Figure 9 and Figure 10. Obviously, the actual value of DO and NO3− concentrations can track the set-points well.
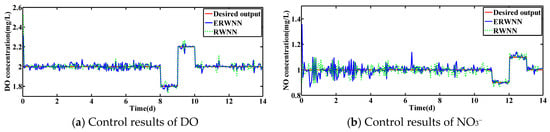
Figure 8.
Control results under dry weather with changed set-points.
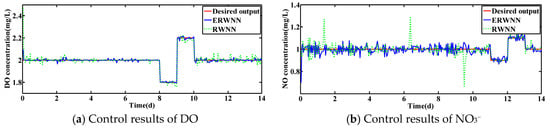
Figure 9.
Control results under rainy weather with changed set-points.
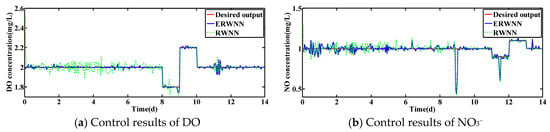
Figure 10.
Control results under rainstorm weather with changed set-points.
The corresponding control errors under the rainy and rainstorm conditions are displayed in Figure 11 and Figure 12, respectively. As shown in Figure 11, the control errors of ERWNN are contributed in the range of [−0.02, 0.02] and [−0.09, 0.06], where the control errors of RWNN are in the range of [−0.07, 0.05] and [−0.1, 0.3]. Furthermore, under the rainstorm condition, most of the errors of ERWNN are contributed in [−0.02, 0.02] and [−0.05, 0.05], where most of the errors of RWNN are in [−0.05, 0.05] and [−0.1, 0.1]. It can be concluded that the control errors of ERWNN are smaller than that of RWNN, which indicates that the ERWNN can obtain better control performance than RWNN.
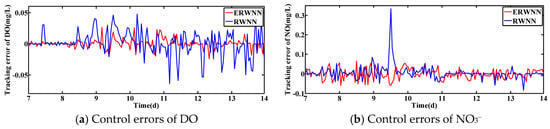
Figure 11.
Control errors under rainy weather with changed set-points.
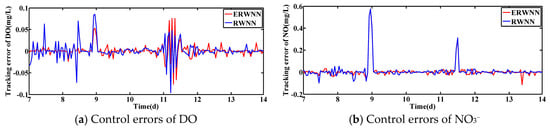
Figure 12.
Control errors under rainstorm weather with changed set-points.
To further measure the dynamic performance of ERWNN, the control indicators are compared with the RWNN, PID, RFNN, and RBFNN, respectively. The comparison results are shown in Table 3. It can be seen that the ERWNN can ensure the control accuracy while reducing the number of executions in the three operating conditions. Among them, the control error of ERWNN is minimized under both dry and rainy conditions. Moreover, the control performance of the DO concentration is better than other methods under the rainstorm condition, while the control error of the NO3− concentration is about the same as that of RWNN. It can be concluded that the ERWNN can also achieve better control performance than other control methods when the set-points change.

Table 3.
Comparison of different control methods for changed set-points.
Experimental results demonstrate that the ERWNN achieves superior control performance under both fixed and varied set-points. This effectiveness stems from three key design elements. First, the incorporation of wavelet functions enhances the nonlinear approximation capability of the model, which is crucial for handling the inherent nonlinearity of WWTPs. Second, the recurrent structure enables the network to dynamically adapt to process changes. Furthermore, the event-triggered mechanism reduces unnecessary controller updates, thereby improving control efficiency without compromising accuracy.
5. Conclusions
In this paper, the event-triggered recurrent wavelet neural network (ERWNN) control method is proposed to address the computational cost issue in controller execution. First, the event-triggered mechanism is designed to reduce the computational burden. Then, a RWNN controller is introduced to simultaneously regulate the concentrations of DO and NO3−. Based on this, the stability of the closed-loop system is analyzed using the Lyapunov stability theory. Finally, the control performance of ERWNN is evaluated through two sets of experiments on the BSM1 platform. Experimental results demonstrate that the proposed method significantly reduces the number of controller executions while maintaining high control accuracy, effectively balancing computational efficiency and control performance.
Author Contributions
Conceptualization, Y.S.; methodology, Y.S.; software, Y.S.; validation, J.G., Y.H. and D.W.; formal analysis, Y.S.; investigation, J.G.; resources, Y.H. and D.W.; data curation, Y.S.; writing—original draft preparation, Y.S.; writing—review and editing, J.G., Y.H. and D.W.; visualization, Y.H. and D.W.; supervision, D.W.; project administration, Y.S.; funding acquisition, Y.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Jiaxing Public Welfare Research Program Project under grant 2024AY10050.
Data Availability Statement
Dataset available on request from the authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Jacobs, D.; McDaniel, T.; Varsani, A.; Halden, R.; Lee, H. Wastewater monitoring raises privacy and ethical considerations. IEEE Trans. Technol. Soc. 2021, 2, 116–121. [Google Scholar] [CrossRef]
- Oikonomou, K.; Parvania, M.; Khatami, R. Optimal demand response scheduling for water distribution systems. IEEE Trans. Ind. Inform. 2018, 14, 5112–5122. [Google Scholar] [CrossRef]
- Yang, R.Y.; Wang, D.; Qiao, J.F. Policy gradient adaptive critic design with dynamic prioritized experience replay for wastewater treatment process control. IEEE Trans. Ind. Inform. 2022, 18, 3150–3158. [Google Scholar] [CrossRef]
- Xiang, H.; Lei, B.; Yuan, X.; Lv, Q.; Zhang, Q. Design and simulation of new type reactor in the wastewater treatment system based on discharge plasma. IEEE Trans. Plasama Sci. 2019, 47, 952–957. [Google Scholar] [CrossRef]
- Heo, S.; Nam, K.; Loy-Benitez, J.; Yoo, C. Data-driven hybrid model for forecasting wastewater influent loads based on multimodal and ensemble deep learning. IEEE Trans. Ind. Inform. 2021, 17, 6925–6934. [Google Scholar] [CrossRef]
- Nawaz, Z.; Arora, A.; Ali, W.; Saxena, N.; Khan, M.; Yun, C.; Lee, M. Intelligent human–machine interface: An agile operation and decision support for an ANAMMOX SBR system at a pilot-scale wastewater treatment plant. IEEE Trans. Ind. Inform. 2022, 18, 6224–6232. [Google Scholar] [CrossRef]
- Zhou, P.; Wang, X.; Chai, T. Multiobjective operation optimization of wastewater treatment process based on reinforcement self-learning and knowledge guidance. IEEE Trans. Cybern. 2023, 53, 6869–6909. [Google Scholar] [CrossRef]
- Wang, D.; Ha, M.M.; Qiao, J.F. Data-Driven iterative adaptive critic control toward an urban wastewater treatment plant. IEEE Trans. Ind. Electron. 2021, 68, 7362–7369. [Google Scholar] [CrossRef]
- Chang, P.; Zhang, S.; Wang, W. Soft sensor of the key effluent index in the municipal wastewater treatment process based on transformer. IEEE Trans. Ind. Inform. 2024, 20, 4021–4028. [Google Scholar] [CrossRef]
- Camcioglu, S.; Ozyurt, B.; Dogan, I.C.; Hapoglu, H. Application of response surface methodology as a new PID tuning method in an electrocoagulation process control case. Water Sci. Technol. 2017, 76, 3410–3427. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.Q.; Liu, S.H.; Li, J.H.; Han, W.J. Wastewater treatment PH value control based on fuzzy self-tuning PID cascade control. Tech. Autom. Appl. 2019, 2, 22–27. [Google Scholar] [CrossRef]
- Chen, Q.; Fan, J.; Chen, W.; Zhang, A.; Pan, G. A dimensionality-reducible operational optimal control for wastewater treatment process. IEEE Trans. Neur. Net. Learn. Syst. 2023, 34, 5418–5426. [Google Scholar] [CrossRef]
- Wang, D.; Liu, T.; Li, L.; Yang, W.; Jin, Y.; Zhao, H.; He, Y.; Zhang, R. Performance analysis of UAV-RIS assisted short-packet secure communications. IEEE Internet Things J. 2025. [Google Scholar] [CrossRef]
- Li, J.W.; Wang, D.; Zhao, H.; Jin, Y.; He, Y.; Zhou, F. Enhancing secrecy energy efficiency in UAC-RIS assisted mobile IoV networks through DRL. IEEE Trans. Wirel. Commun. 2025. [Google Scholar] [CrossRef]
- He, Y.X.; Huang, F.H.; Wang, D.; Chen, B.; Li, T.; Zhang, R. Performance Analysis and optimization design of AAV-Assisted vehicle platooning in NOMA-Enhanced internet of vehicles. IEEE Trans. Intell. Transp. Syst. 2025, 26, 8810–8819. [Google Scholar] [CrossRef]
- Wang, G.; Zhao, Y.; Liu, C.; Qiao, J.F. Data-Driven robust adaptive control with deep learning for wastewater treatment process. IEEE Trans. Ind. Inform. 2024, 20, 149–157. [Google Scholar] [CrossRef]
- Stebel, K.; Pospiech, J.; Nocon, W.; Czeczot, J.; Skupin, P. Boundary-based predictive controller and its application to control of dissolved oxygen concentration in activated sludge bioreactor. IEEE Trans. Ind. Electron. 2022, 69, 10541–10551. [Google Scholar] [CrossRef]
- Wei, W.; Chen, N.; Zhang, Z.; Liu, Z.; Zuo, M.; Liu, K.; Xia, Y. A scalable-bandwidth extended state observer-based adaptive sliding-mode control for the dissolved oxygen in a wastewater treatment process. IEEE Trans. Cybern. 2022, 52, 13448–13457. [Google Scholar] [CrossRef]
- He, Y.X.; Huang, F.H.; Wang, D.; Zhang, R. Outage probanbility analysis of MISO-NOMA downlink communications in UAV-Assisted Agri-IoT with SWIPT and TAS enhancement. IEEE Trans. Netw. Sci. Eng. 2025, 12, 2151–2164. [Google Scholar] [CrossRef]
- He, Y.X.; Huang, F.H.; Wang, D.; Chen, B.; Zhang, R. Emergency communications in post-disaster scenarios: IoT-enhanced airship and buffer support. IEEE Internet Things 2025, 12, 11457–11468. [Google Scholar] [CrossRef]
- He, Y.; Huang, F.; Wang, D.; Zhou, X.; Zhang, R. Uplink outage probability analysis of AAV and intelligent connected vehicle cooperative communication using full-duplex MIMO. IEEE Commun. Lett. 2025, 29, 2068–2072. [Google Scholar] [CrossRef]
- Yang, Q.; Cao, W.; Meng, W.; Si, J. Reinforcement-learning-based tracking control of waste water treatment process under realistic system conditions and control performance requirements. IEEE Trans. Syst. Man Cybern. 2022, 52, 5284–5294. [Google Scholar] [CrossRef]
- Du, P.; Zhong, W.; Peng, X.; Li, L.; Li, Z. Self-healing control for wastewater treatment process based on variable-gain state observer. IEEE Trans. Ind. Inform. 2023, 19, 10412–10424. [Google Scholar] [CrossRef]
- Han, H.G.; Liu, H.X.; Qiao, J.F. Knowledge-data-driven flexible switching control for wastewater treatment process. IEEE Trans. Contr. Syst. Technol. 2022, 30, 1116–1129. [Google Scholar] [CrossRef]
- Han, H.G.; Liu, H.X.; Li, J.; Qiao, J.F. Cooperative fuzzy-neural control for wastewater treatment process. IEEE Trans. Ind. Inform. 2021, 17, 5971–5981. [Google Scholar] [CrossRef]
- Bai, W.; Zhou, Q.; Li, T.; Li, H. Adaptive reinforcement learning neural network control for uncertain nonlinear system with input saturation. IEEE Trans. Cybern. 2020, 50, 3433–3443. [Google Scholar] [CrossRef]
- Fei, J.; Chen, Y.; Liu, L.; Fang, Y. Fuzzy multiple hidden layer recurrent neural control of nonlinear system using terminal sliding-mode controller. IEEE Trans. Cybern. 2022, 52, 9519–9534. [Google Scholar] [CrossRef] [PubMed]
- Peng, C.; Sun, H. Switching-like event-triggered control for networked control systems under malicious denial of service attacks. IEEE Trans. Automat. Contr. 2020, 65, 3943–3949. [Google Scholar] [CrossRef]
- Liu, X.X.; Su, X.J.; Shi, P.; Shen, C.; Peng, Y. Event-triggered sliding mode control of nonlinear dynamic systems. Automatica 2020, 112, 108738. [Google Scholar] [CrossRef]
- Zhang, N.; Sun, Q.; Yang, L.; Li, Y. Event-triggered distributed hybrid control scheme for the integrated energy system. IEEE Trans. Ind. Inform. 2022, 18, 835–846. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).