Data-Driven Forward Kinematics for Robotic Spatial Augmented Reality: A Deep Learning Framework Using LSTM and Attention

Abstract

Robotic Spatial Augmented Reality (RSAR) systems present a unique control challenge as their end-effector is a projection, whose final position depends on both the actuator’s pose and the external environment’s geometry. Accurately controlling this projection first requires predicting the 6-DOF pose of a projector-camera unit from joint angles; however, loose kinematic specifications in many RSAR setups make precise analytical models unavailable for this task. This study proposes a novel deep learning model combining Long Short-Term Memory (LSTM) and an Attention Mechanism (LSTM–Attention) to accurately estimate the forward kinematics of a 2-axis Pan-Tilt actuator. To ensure a fair evaluation of intrinsic model performance, a simulation framework using Unity and unified robot description format was developed to generate a noise-free benchmark dataset. The proposed model utilizes a multi-task learning architecture with a geodesic distance loss function to optimize 3-dimensional position and 4-dimensional quaternion rotation separately. Quantitative results show that the proposed LSTM–Attention model achieved the lowest errors (Position MAE: 18.00 mm; Rotation MAE: 3.723 deg), consistently outperforming baseline models like Random Forest by 9.5% and 17.6%, respectively. Qualitative analysis further confirmed its superior stability and outlier suppression. The proposed LSTM–Attention architecture proves to be a effective and accurate methodology for modeling the complex non-linear kinematics of RSAR systems.

1. Introduction

Spatial Augmented Reality (SAR) is a technology that enhances real-world tasks by projecting relevant information directly onto the surfaces of the work environment, instead of relying on external displays such as glasses or smartphones [1]. Traditional SAR systems utilize a method of installing a fixed projector near the ceiling to secure a wide projection area; however, this approach has limitations in its application to dynamic work environments or ad-hoc spaces [2]. To overcome these limitations, Robotic Spatial Augmented Reality (RSAR) systems, which integrate robotics technology with SAR, have been proposed [3]. RSAR dynamically changes the position and pose of the Projector-Camera Unit (PCU) via robotic actuators, thereby offering the potential for a much larger and more flexible workspace than fixed systems.

SAR technology is being actively applied across various industrial and academic fields, demonstrating its effectiveness. For example, in the manufacturing sector, it is widely utilized as a guidance system that projects assembly sequences or part information directly onto work objects, reducing operator errors and increasing efficiency [4]. Furthermore, pioneering research such as Shader Lamps, which precisely projects computer graphics images onto the surfaces of static physical objects to make them appear as if they are alive and moving, has significantly expanded the artistic and commercial possibilities of SAR technology [5]. Moreover, systems that combine small, user-worn projectors with retro-reflective materials to provide personalized augmented reality information have extended the application scope of SAR into the personal domain [6].

To overcome the limitation of a fixed projection area in SAR, recent attempts have been actively made to mobilize the system itself or to combine it with robotics technology [7]. In the initial stages, the concept of Movable SAR was proposed, where the projector-camera unit is mounted on a movable cart to relocate the workspace as needed. This has further evolved into RSAR, where the projector is directly attached to a multi-joint robotic arm or a mobile robot, enabling an active response to changes in the work environment and objects. In particular, research combining collaborative robots with RSAR to project real-time construction information to workers in unstructured and dynamic environments, such as construction sites, is a clear example of how effectively RSAR can be used in complex real-world industrial settings [8].

The flexibility of RSAR systems introduces fundamental challenges that are difficult to solve with traditional robotic control methods. For a typical robotic arm, a forward kinematics relationship, $p=f\left(q\right)$, exists where the 6-Degrees-of-Freedom (6-DOF) pose p of the end-effector is generally determined given the joint angles q [9]. However, in an RSAR system, the final end-effector perceived by the user is the image formed by the light projected from the projector onto the surface of the real environment. This final output depends not only on the actuator’s pose but also on the external environment, such as the position of the wall or the shape of objects where the light lands, making it impossible to establish an analytical model to predict it directly from joint angles alone.

To solve this problem, this study adopts an approach that simplifies the control pipeline. In an RSAR system, the camera and projector are fixed on each other as a single unit at the end of the robotic arm; therefore, the relative transformation relationship between them is constant. Consequently, if the 6-DOF pose of the camera relative to the world coordinate system can be accurately determined, the projector’s pose can be easily calculated analytically. Ultimately, the complex control problem of RSAR converges to the core task of “accurately predicting the camera’s 6-DOF pose, an intermediate parameter, from the actuator’s joint angle inputs.”

While the 2-DOF actuator might suggest simple kinematics, the core RSAR challenge lies in mapping these two joint inputs to a 6-DOF camera pose ($t_x,t_y,t_z$ and $q_w,q_x,q_y,q_z$). This $2\to 7$ mapping, particularly for the non-Euclidean $SO\left(3\right)$ rotation manifold, is inherently complex and highly non-linear. User-Created Robotics (UCR) or ad-hoc assembled RSAR systems often exacerbate this challenge, making it difficult to obtain precise kinematic specifications, such as computer-aided design models, or assembly processes may introduce minute errors, causing theoretical analytical models to fail to represent the actual system. Thus, the problem is not easily solvable by lightweight regression or simple analytical models, necessitating a more powerful data-driven approach. This loose kinematic specifications problem is a common challenge in other robotics fields as well, such as soft robotics, where analytical modeling is difficult, and data-driven approaches, which directly learn the system’s input–output relationship based on actual operational data, are being researched as an effective alternative [10].

Prior research has utilized B-spline surface fitting techniques for such data-driven control [3]. This method approximates and represents the relationship between joint angles and camera extrinsic parameters as a B-spline surface derived from sampled data. While this demonstrated the possibility of controlling kinematics without an analytical model, B-splines alone have limitations in accurately representing the relationship when the actuator’s movement becomes complex and exhibits high non-linearity. Therefore, a more sophisticated machine learning or deep learning-based approach is required to learn the complex and subtle intrinsic patterns within the data. This study focuses on providing this foundational, data-driven kinematic model, which is a prerequisite for the subsequent implementation of dynamic controllers, especially in systems where analytical models are unavailable.

The final objective of this study is to propose an optimal data-driven model that most accurately and stably predicts the 6-DOF pose of the camera from the joint angle information of a 2-axis Pan-Tilt actuator. To this end, this paper makes the following three key contributions. First, we propose a novel deep learning model based on LSTM–Attention, which combines Long Short-Term Memory (LSTM) [11], known for its strength in time-series data processing, with an Attention Mechanism [12] that focuses on important features for prediction. Second, we quantitatively and qualitatively compare the performance of the proposed model with classic machine learning models such as Polynomial Regression [13], Support Vector Regression (SVR) [14], and Random Forest [15], demonstrating the superior ability of the proposed model to model complex non-linear kinematic relationships. Third, we present a simulation-based verification framework. This approach is intentionally chosen to fundamentally eliminate measurement noise from physical sensors, allowing for a clear comparison of the models’ intrinsic performance and theoretical upper bounds [16]. We acknowledge this as a clear limitation, as the study does not account for critical real-world factors such as calibration errors, mechanical backlash, or complex environmental dynamics. Therefore, this work aims to establish a methodological foundation for evaluating the theoretical validity of data-driven models, which serves as a crucial preceding step before addressing real-world robustness.

2. Materials and Methods

2.1. Principle of Pose Estimation in RSAR

The geometric modeling of the RSAR system discussed in this study is based on the pinhole camera model. To express geometric transformations in 3D space as linear transformations, a 3D point $(X_w,Y_w,Z_w)$ in the world coordinate system is represented as a homogeneous coordinates vector $P_w={[X_w,Y_w,Z_w,1]}^T$ by adding an additional dimension (w = 1). This representation allows 3D rotation and translation transformations to be concisely combined into a single 4 × 4 matrix multiplication. The process of projecting this 3D point $P_w$ onto the 2D camera image plane at pixel coordinates $p_c={[u,v,1]}^T$ is determined by the camera’s intrinsic and extrinsic parameters, and can be expressed by the following homogeneous equalityrelation:

$$s\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=K_c\left[R\right|t]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]$$

(1)

Here, s is a non-zero scale factor proportional to the depth of the 3D point, $K_c$ is the camera intrinsic parameter matrix, and $\left[R\right|t]$ denotes the extrinsic parameter matrix. The above equation implies that the result of projecting the 3D point differs from the final pixel coordinates by a constant factor; the actual pixel coordinates $(u,v)$ are obtained by normalizing the resulting vector on the right-hand side by dividing by its last element.

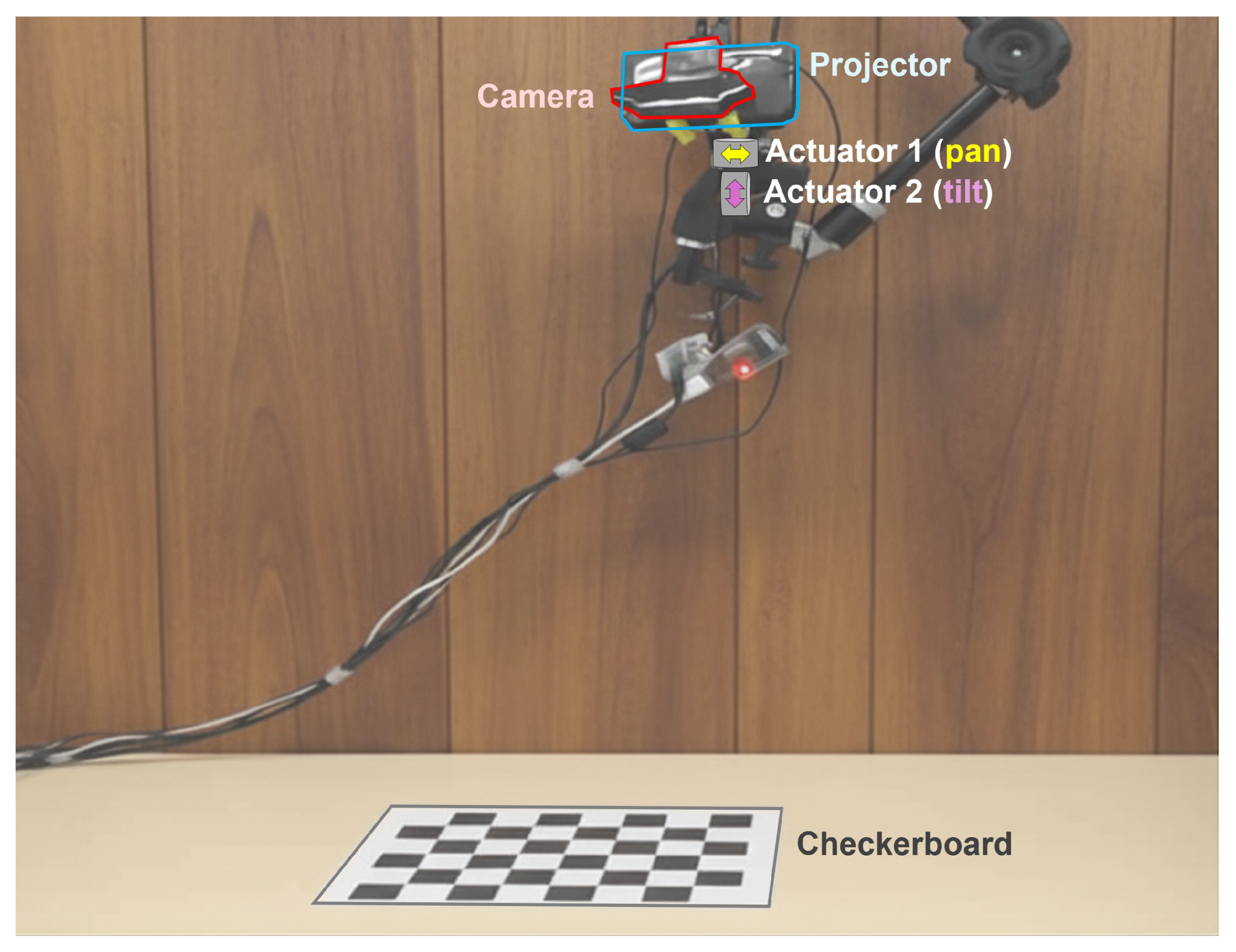
The RSAR system proposed in this study is based on a 2-axis Pan-Tilt actuator (Dynamixel XC430-T150BB-T), as shown in Figure 1, instead of a complex multi-DOF robotic arm. This is because the primary purpose of the RSAR envisioned in this research is not complex manipulation, such as grasping or handling objects, but rather effectively changing the projector’s pose towards a target plane, like a flat wall or screen. To achieve this objective, 2-DOF rotation is sufficient to cover a wide area and determine the pose of the PCU. Therefore, the Pan-Tilt mechanism is the most suitable and efficient actuator configuration for performing the core functions of RSAR while reducing system complexity. Consequently, the control problem in this study is defined as predicting the 3D spatial pose of the PCU from the two joint angle inputs of this Pan-Tilt actuator.

The camera intrinsic parameter matrix $K_c$ defines the unique optical characteristics of the camera lens; it is determined through a one-time calibration process after system assembly and remains a constant value thereafter. This matrix consists of the focal lengths ($f_x,f_y$) and the principal point ($c_x,c_y$).

$$K_c=\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]$$

(2)

In contrast, the extrinsic parameters represent the relative position and orientation of the camera with respect to the world coordinate system, and these values change in real time as the actuator moves. The extrinsic parameters are expressed as a combination of a 3 × 3 rotation matrix R and a 3 × 1 translation vector t and can be represented as a 4 × 4 matrix $X_{wc}$ for Homogeneous Transformation.

$$X_{wc}=\left[\begin{array}{cc}R& t\\ \mathbf{0}& 1\end{array}\right]=\left[\begin{array}{cccc}{r}_{11}& r_{12}& r_{13}& t_x\\ r_{21}& r_{22}& r_{23}& t_y\\ r_{31}& r_{32}& r_{33}& t_z\\ 0& 0& 0& 1\end{array}\right]$$

(3)

Here, the rotation matrix R represents the 3D orientation of the camera, and the translation vector t represents its 3D position. This combined 6-DOF pose is the target we must predict according to the actuator’s movement.

In the RSAR system’s PCU, the projector is modeled on the same principle as the camera. The core assumption of the system is that the relative transformation relationship between the camera and the projector $X_{cp}$ is fixed as a rigid-body transformation. Therefore, a clear relationship holds between the camera’s extrinsic parameters $X_{wc}$ and the projector’s extrinsic parameters $X_{wp}$:

$$X_{wp}=X_{cp}{X}_{wc}$$

(4)

The above equation reduces the complexity of the RSAR control problem. Since $K_c$ and $X_{cp}$ are both predetermined constant values, the only variable we need to determine as the actuator’s Pan-Tilt joint angles ($\theta ,\varphi$) change is the camera’s extrinsic parameter $X_{wc}$, which varies in real-time. Therefore, the core task of this study is to learn a non-linear function f from data that accurately estimates the camera’s extrinsic parameter matrix $X_{wc}$ from the joint angles ($\theta ,\varphi$).

$$X_{wc}=f(\theta ,\varphi )$$

(5)

Finding the most effective method to model this function f is the main objective of this paper.

2.2. Experimental Setup and Data Preprocessing

To train the proposed models and objectively evaluate their performance, a large-scale dataset consisting of numerous pan-tilt joint angles ($\theta ,\varphi$) and their precisely corresponding 6-DOF camera poses $X_{wc}$ is essential. However, fundamental limitations exist in the process of acquiring such ground-truth data using a physical RSAR system. The reference position of extrinsic parameters, such as the camera’s optical center, is nearly impossible to measure directly physically and must typically be estimated indirectly through camera calibration techniques using vision markers like checkerboards. This estimation process, however, inevitably generates data containing measurement noise due to various factors such as camera lens distortion, marker corner detection errors, and lighting variations [17].

This data contamination problem can act as a serious confounding variable in model performance evaluation. If a model is evaluated using noisy data as the ground-truth, the result measures not only the model’s pure predictive ability but also its robustness to noise, making a fair comparison difficult. Therefore, to overcome this limitation and to most clearly compare the pure learning and prediction capabilities (intrinsic performance) of various models, this study adopted an approach of constructing an ideal simulation environment. This ensures that the experimental results aim to primarily reflect the performance of the model itself, rather than external factors.

To construct a virtual RSAR system, the robot’s kinematic properties were first defined using the Unified Robot Description Format (URDF). URDF is a standard framework in robotics for describing physical specifications—such as link lengths, joint positions and rotation axes, and the relative attachment position of the PCU—in an extensible markup language format. This URDF-defined robot model was imported into the Unity game engine to configure the entire simulation environment. The Unity environment provides a precise physics engine, making it possible to issue specific joint angle commands to the virtual Pan-Tilt actuator and accurately extract the resulting 6-DOF camera pose values without error. Figure 2 shows the Unity simulation environment constructed in this manner.

Using this simulation environment, the dataset was generated by systematically moving the Pan and Tilt joints within their respective operating ranges and recording the camera’s 6-DOF pose corresponding to each joint angle combination. Although the simulation can generate virtually limitless data, this study intentionally limited the dataset size to over 3000 samples. This was to simulate the realistic constraint that, when collecting data in a real environment, considerable time is required to capture a checkerboard and calculate the pose for each sample. Therefore, a sample size of 3000 represents a scale sufficient for comparing the performance of various machine learning models while considering realistic data acquisition costs, which enhances the practical validity of this study’s results. The structure of the generated dataset is as specified in

Table 1. Structure of the 3000-sample dataset generated from the simulation environment.

Category	Variable Name	Description
Input	p_deg	Rotational state of the pan (horizontal) actuator joint, measured in degrees.
	t_deg	Rotational state of the tilt (vertical) actuator joint, measured in degrees.
Output	Camera Position (World Coordinates)
	camPosX	X-axis component.
	camPosY	Y-axis component.
	camPosZ	Z-axis component.
	Camera Orientation (Euler Angles)
	camEulerX_deg	Roll component, measured in degrees.
	camEulerY_deg	Pitch component, measured in degrees.
	camEulerZ_deg	Yaw component, measured in degrees.

.

To effectively use the raw data obtained from the simulation for model training, preprocessing steps tailored to the characteristics of the input and output data were applied respectively. First, the input data, the Pan-Tilt angles ($\theta ,\varphi$), have a cyclical characteristic. For example, 0 degrees and 360 degrees represent the same physical direction, but the numbers themselves show a large difference. To resolve this discontinuity problem, trigonometric encoding was applied, converting each angle value into its sine and cosine values.

$$\theta \to \left(\sin \right(\theta ),\cos (\theta \left)\right),\varphi \to \left(\sin \right(\varphi ),\cos (\varphi \left)\right)$$

(6)

Through this transformation, the model can geometrically recognize that 359 degrees and 1 degree are close to each other, enabling more continuous and consistent learning.

Second, Euler angles, which represent the orientation component of the 6-DOF pose output data, are vulnerable to the Gimbal Lock phenomenon, where two or more axes overlap at specific poses, resulting in a loss of degrees of freedom [18]. This is a major cause of instability in training regression models; therefore, this study used Quaternions ($q=[q_w,q_x,q_y,q_z]$), which represent rotation with four elements, instead of the three Euler angles. Quaternions are free from the Gimbal Lock problem and are more suitable for deep learning model training as they are advantageous for continuous rotational interpolation. Finally, all models were designed to predict a total of seven variables, combining the 3D position ($t_x,t_y,t_z$) and the 4D quaternion ($q_w,q_x,q_y,q_z$).

2.3. Proposed Model: LSTM–Attention for Pose Prediction

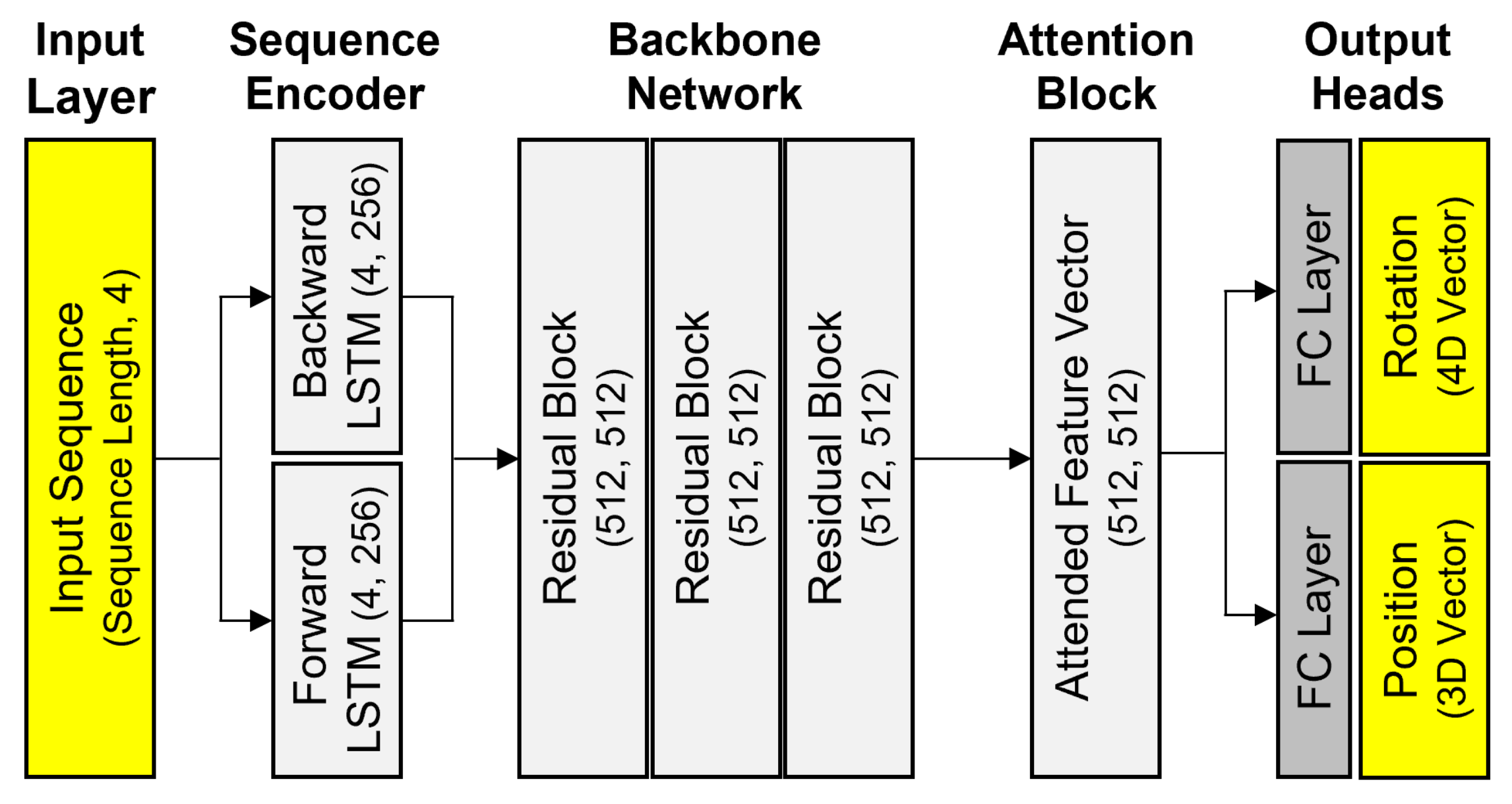
In this study, to model the complex and non-linear relationship between the Pan-Tilt actuator’s joint angles and the camera’s 6-DOF pose, we propose a novel deep learning architecture combining LSTM, which has strengths in sequential data processing, with an Attention Mechanism. The overall architecture of the proposed model is illustrated in Figure 3, and it consists of a bidirectional LSTM layer to extract sequential features from the input data, residual blocks to deepen the expressive power of the extracted features, an attention block to re-weight the importance of features, and multi-task learning heads that independently predict position and rotation. Each component is organically designed to maximize prediction accuracy and the model’s generalization performance.

2.3.1. Model Architecture Overview

The data processing flow of the proposed model is as follows. First, the 4-dimensional input vector, preprocessed through trigonometric encoding, is expanded into 2nd-degree polynomial features to represent non-linear interactions between input features. This expanded feature vector is then structured into a sequence for time-series processing and passed to the bidirectional LSTM layer. The bidirectional LSTM learns both the forward and backward contexts of the input sequence, generating a fixed-size feature vector that compresses temporal characteristics. This feature vector passes through a backbone network composed of several residual blocks, where it is transformed into more sophisticated features via a deep network addressing the vanishing gradient problem. Subsequently, a self-attention mechanism dynamically calculates and applies weights based on the inter-relationships between elements within this feature vector. Finally, the attention-applied feature vector is fed into two independent fully-connected layers, which predict the position and rotation respectively, to output the final predictions.

2.3.2. Sequential Feature Extraction with Bidirectional LSTM and Residual Blocks

Since the actuator’s movement has continuous characteristics over time, this study adopted LSTM, a type of Recurrent Neural Network (RNN), to learn this time-series dependency [11]. In particular, noting that the camera pose at the current time step can be influenced not only by previous angles but also by subsequent angle changes, a Bidirectional LSTM (Bi-LSTM) was used instead of a unidirectional one. Bi-LSTM processes the input sequence in both forward and backward directions and then generates the final features by concatenating the hidden states from each time step. For an input sequence $X=(x_1,x_2,...,x_L)$ with sequence length L and input feature dimension $F_{in}$, the Bi-LSTM calculates a forward hidden state $\overrightarrow{h_t}$ and a backward hidden state $\overleftarrow{h_t}$ at each time step t. In this model, with a structure stacking two LSTM layers, the final forward hidden state ($\overrightarrow{h_L}$) and final backward hidden state ($\overleftarrow{h_L}$) from the last layer are concatenated to generate a feature vector $h_{final}$ that compresses the information of the entire sequence.

$$h_{final}=[\overrightarrow{h_L};\overleftarrow{h_L}]$$

(7)

This generated $h_{final}$ vector then passes through a backbone network composed of residual blocks. The residual block is a key mechanism that helps ensure stable learning even as the network deepens by directly adding the input signal to the output via a skip connection structure [19]. Thanks to this structure, the model can effectively extract deeper and richer features from the time-series information.

2.3.3. Attention Mechanism for Feature Refinement

The feature vector refined by passing through the residual blocks is transferred to the attention block to be further sophisticated. The attention mechanism is a technique based on the idea that not all elements of a feature vector are equally important, dynamically assigning higher weights to elements that have a more decisive impact on the final prediction [12]. This model adopts a Multi-Head Self-Attention structure, where the query, key, and value are all derived from the same input feature vector [20]. This allows the model to learn the inter-relationships among features from different perspectives by dividing the feature vector into multiple heads and performing attention in parallel.

When the input feature vector is denoted as $f_{in}$, the attention score is calculated through the dot product of the query and key, and then converted into weights $\alpha$ after scaling and passing through a soft-max function. Finally, the attention-applied feature vector $f_{att}$ is obtained by a weighted sum of these weights and the value vectors. Finally, the attention-applied feature vector $f_{att}$ is obtained by a weighted sum of these weights and the value vectors, using the standard scaled dot-product attention formula [20]:

$$\mathrm{Attention}(Q,K,V)=\mathrm{softmax}\left({\displaystyle \frac{Q{K}^T}{\sqrt{d_k}}}\right)V$$

(8)

Here, $Q,K,V$ are all generated from $f_{in}$ through a linear transformation, and $d_k$ is the dimension of the key vector. Through this process, the model learns to identify which feature combinations are most important in the complex mapping relationship between the Pan-Tilt angles and the camera pose, suppressing noisy features unnecessary for prediction and focusing on core features to enhance prediction accuracy.

2.3.4. Multi-Task Learning for Pose Prediction

Finally, the feature vector $f_{att}$, refined through attention, is split into two independent branches to predict the 6-DOF pose. This is a Multi-Task Learning structure that simultaneously learns two sub-tasks with different physical and mathematical characteristics: position (3D vector) and rotation (4D quaternion) [21]. Instead of predicting all variables at once in a single large output layer, separate heads specialized for each task are used to induce the model to learn the unique characteristics of each task more effectively.

The position prediction head is a fully-connected layer that takes $f_{att}$ as input and outputs a 3D position vector $\widehat{t}=[{\widehat{t}}_x,{\widehat{t}}_y,{\widehat{t}}_z]$. This head is trained to minimize the Mean Squared Error (MSE) between the predicted position vector $\widehat{t}$ and the ground-truth position vector t. The MSE loss function is defined as follows:

$$L_{pos}={\displaystyle \frac{1}{N}}\sum _{i=1}^N\left|\right|{\widehat{t}}_i-t_i{\left|\right|}_2^2$$

(9)

Here, N is the batch size, and $\left|\right|·{\left|\right|}_2^2$ denotes the squared Euclidean distance.

The rotation prediction head outputs a 4D quaternion $\widehat{q}=[{\widehat{q}}_w,{\widehat{q}}_x,{\widehat{q}}_y,{\widehat{q}}_z]$. Since the predicted quaternion must be a unit vector, it is normalized to a magnitude of 1 via L2 normalization before calculating the loss. To measure the quaternion rotation error, this study used a Geodesic Loss, which directly calculates the actual angular difference between two unit quaternions [18]. The dot product of the normalized predicted quaternion ${\widehat{q}}_{norm}$ and the ground-truth quaternion q is computed, and the absolute value of this dot product is taken to account for the two ways a quaternion can represent the same rotation (q and $-q$). This value is then passed through an arc-cosine (arc-cos) function to calculate the shortest angle (in radians) between the two quaternions.

$$L_{rot}={\displaystyle \frac{1}{N}}\sum _{i=1}^N\mathrm{acos}\left(\right|{\widehat{q}}_{i,norm}·q_i\left|\right)$$

(10)

In this multi-task learning structure, the two loss functions are combined via a weighted sum using the hyper-parameter ${\lambda }_{rot}$ for the rotation loss to constitute the model’s final loss, $L_{total}$.

$$L_{total}=L_{pos}+{\lambda }_{rot}{L}_{rot}$$

(11)

This integrated loss function is used to update all parameters of the model through back-propagation, and it provides a regularization effect that encourages the shared backbone network to learn generalized features useful for both the position and rotation tasks, contributing to an improvement in overall prediction performance.

2.4. Baseline Models

To objectively validate the performance of the proposed LSTM–Attention model, three classic algorithms widely used in the machine learning field were selected as baseline models. These models were trained and evaluated using data that underwent the same preprocessing steps as the proposed model. Specifically, the 4-dimensional input vector $\left(\sin \right(\theta ),\cos (\theta ),\sin (\varphi ),\cos (\varphi \left)\right)$ with trigonometric encoding applied was used as the input for all baseline models.

Furthermore, the 7-dimensional output vector (three for position, four for quaternion) was normalized using Standard Scaler to enhance the stability and efficiency of the training process [22]. Standard Scaler is a standardization technique that transforms each output variable to have a mean of 0 and a variance of 1. This process prevents the error of a specific variable from having an excessive influence on the overall loss function when output variables have different scales, helping the model to learn all output variables in a balanced manner. The results predicted by the model were scaled back to the original data’s scale for final performance evaluation.

Since the baseline models used in this study were inherently designed for single-output prediction, the Multi Output Regressor wrapper from the Scikit-learn library was commonly used to apply them to the multi-output prediction problem [22]. Multi Output Regressor is a strategy for solving multi-target regression problems, which trains one independent single model for each output variable. For example, to predict 7 output variables, 7 independent SVR models are created, and each model is trained individually to predict only one output variable. This method has the advantage of simple implementation but cannot learn the potential correlations between output variables.

2.4.1. Polynomial Regression

Polynomial Regression is a statistical technique that models non-linear relationships by assuming the relationship between independent and dependent variables is an n-degree polynomial [13]. Whereas linear regression can only express linear relationships in data, polynomial regression can learn complex curve patterns inherent in the data by creating new features through exponentiation of input features and applying these to a linear regression model. This model has the advantages of simple implementation and low computational cost, so it is often utilized as a basic baseline for gauging the performance of complex models. However, if the degree is too high, overfitting to the training data can occur, and conversely, if it is too low, underfitting can occur, failing to sufficiently express the complexity of the data.

The mathematical model of Polynomial Regression begins by generating an expanded feature vector $\varphi \left(\mathbf{x}\right)$ for an input feature vector $\mathbf{x}={[x_1,...,x_k]}^T$. For example, when expanding 2 features $x_1,x_2$ into a 2nd-degree polynomial, it is expressed as $\varphi \left(\mathbf{x}\right)={[x_1,x_2,x_1{x}_2,x_1^2,x_2^2]}^T$. The predicted value $\widehat{y}$ is calculated as a linear combination of this generated expanded feature vector and a weight vector $\mathbf{w}$.

$$\widehat{y}={\mathbf{w}}^T\varphi \left(\mathbf{x}\right)+b=w_0+\sum _{j=1}^M{w}_j{\varphi }_j\left(\mathbf{x}\right)$$

(12)

Here, M is the total number of expanded features, and the model aims to find the weights $\mathbf{w}$ and bias b that minimize the loss function (typically MSE).

In this study, the four input features $\left(\sin \right(\theta ),\cos (\theta ),\sin (\varphi ),\cos (\varphi \left)\right)$ were expanded into a 3rd-degree polynomial using polynomial features from the Scikit-learn library. This creates a high-dimensional feature space that includes not only the original features but also interaction terms and polynomial terms between features. A standard Linear Regression model, using these expanded features as input, was trained to predict the seven output variables. The Multi Output Regressor wrapper performs the role of training an independent polynomial regression model for each of the seven output variables, thereby enabling the simultaneous prediction of multi-dimensional output.

2.4.2. Support Vector Regression

SVR is an algorithm that extends the principles of Support Vector Machines, which show excellent performance in classification problems, to regression problems [14]. The core idea of SVR is to define an $ϵ$-insensitive tube, which allows for a certain level of error between the predicted and actual values. The error of data points existing within this tube is disregarded in the loss calculation, and the model is trained to minimize only the errors of data points that fall outside the tube. Simultaneously, the model maximizes the margin, which in regression can be interpreted as an attempt to maintain the widest possible tube. This approach makes SVR less sensitive to small noise in the data and helps it achieve good generalization performance.

SVR controls model complexity by minimizing the L2-norm of the weight vector $\mathbf{w}$ and imposes penalties for errors exceeding the $ϵ$-tube through slack variables ${\xi }_i,{\xi }_i^{*}$. The objective function for this is formulated as follows:

$$\underset{\mathbf{w},b,\xi ,{\xi }^{*}}{\min }{\displaystyle \frac{1}{2}}{\left|\right|\mathbf{w}\left|\right|}^2+C\sum _{i=1}^N({\xi }_i+{\xi }_i^{*})$$

(13)

The above equation is minimized under the following constraints:

$$y_i-(\mathbf{w}·\varphi \left({\mathbf{x}}_{\mathbf{i}}\right)+b)\le ϵ+{\xi }_i$$

(14)

$$(\mathbf{w}·\varphi \left({\mathbf{x}}_{\mathbf{i}}\right)+b)-y_i\le ϵ+{\xi }_i^{*}$$

(15)

$${\xi }_i,{\xi }_i^{*}\ge 0$$

(16)

Here, $C>0$ is the regularization parameter, which adjusts the balance between model complexity and the allowable training error range. $\varphi (·)$ is the kernel function that maps the input data ${\mathbf{x}}_{\mathbf{i}}$ into a high-dimensional feature space.

This optimization problem is typically solved by converting it into a dual problem using Lagrangian duality, with the Lagrange multipliers ${\alpha }_i,{\alpha }_i^{*}\ge 0$ as variables. Using the solution to this dual problem, the weight vector $\mathbf{w}$ can be expressed as a linear combination of the input data: $\mathbf{w}={\sum }_{i=1}^N({\alpha }_i-{\alpha }_i^{*})\varphi \left({\mathbf{x}}_{\mathbf{i}}\right)$. The data points ${\mathbf{x}}_{\mathbf{i}}$ for which the $({\alpha }_i-{\alpha }_i^{*})$ values are non-zero are called the support vectors. SVR can model non-linear relationships without explicitly transforming the input data into a high-dimensional space by using the Kernel Trick. In this study, the Radial Basis Function (RBF) kernel, which is highly effective for modeling non-linear relationships, was used, and its definition is as follows:

$$K({\mathbf{x}}_{\mathbf{i}},{\mathbf{x}}_{\mathbf{j}})=\exp (-\gamma ||{\mathbf{x}}_{\mathbf{i}}-{\mathbf{x}}_{\mathbf{j}}{\left|\right|}^2)$$

(17)

By substituting the dual representation of $\mathbf{w}$ into the prediction function $f\left(\mathbf{x}\right)=\mathbf{w}·\varphi \left(\mathbf{x}\right)+b$ and applying the kernel trick, the final prediction function is obtained. Once training is complete, the prediction for a new input $\mathbf{x}$ is made through the following function, where only the support vectors (where ${\alpha }_i-{\alpha }_i^{*}\ne 0$) contribute to the prediction.

$$f\left(\mathbf{x}\right)=\sum _{i=1}^N({\alpha }_i-{\alpha }_i^{*})K({\mathbf{x}}_{\mathbf{i}},\mathbf{x})+b$$

(18)

The overall training and prediction process of SVR is shown in Algorithm 1.

In this study, SVR using the RBF kernel was adopted as a baseline model to learn the complex non-linear relationship between the Pan-Tilt angles and the camera pose. The main hyper-parameters of the model were set to the default values of the Scikit-learn library: the regularization parameter $C=1.0$ and $ϵ=0.1$, which determines the size of the $ϵ$-insensitive tube. Through Multi Output Regressor, SVR models for each of the 7 output variables were trained independently, thereby effectively performing multi-dimensional pose prediction.

Algorithm 1 Support Vector Regression (SVR) Process

1: Input: Training data $D={\left\{({\mathbf{x}}_{\mathbf{i}},y_i)\right\}}_{i=1}^N$, Hyperparameters $C,ϵ,\gamma$ 2: Training Phase: 3: Solve the optimization problem defined in Equation (13) to find the Lagrange multipliers ${\alpha }_i,{\alpha }_i^{*}$ and the bias b. 4: Identify the support vectors (data points where ${\alpha }_i-{\alpha }_i^{*}\ne 0$). 5: Output: The prediction model $f\left(\mathbf{x}\right)$. 6: Prediction Phase: 7: Input: A new data point $\mathbf{x}$. 8: Compute the predicted value using the support vectors and the learned parameters:         $f\left(\mathbf{x}\right)={\sum }_{i\in \mathrm{SV}}({\alpha }_i-{\alpha }_i^{*})K({\mathbf{x}}_{\mathbf{i}},\mathbf{x})+b$ 9: Return$f\left(\mathbf{x}\right)$.

2.4.3. Random Forest

Random Forest is a type of ensemble learning technique that generates multiple Decision Trees during the training process and derives the final prediction value by aggregating (averaging) the prediction results of each tree [15]. The two core features of Random Forest are Bagging (Bootstrap Aggregating) and feature randomness. Bagging is a technique that independently trains each tree using multiple bootstrap samples, which are generated by random sampling with replacement from the entire training dataset. Furthermore, when finding the optimal feature for a split at each node of a tree, instead of considering all features, it randomly selects a subset of features and finds the best split only from that subset.

These two randomness factors serve to reduce the correlation between individual trees. Consequently, this mitigates the high variance problem that a single decision tree can have and significantly reduces the model’s tendency to overfit the training data. By averaging the prediction results of numerous trees, Random Forest can build a predictive model that is robust to noise, stable, and highly accurate. The training and prediction process of Random Forest is shown in Algorithm 2.

Algorithm 2 Random Forest Algorithm

1: for b = 1 to B (number of trees) do 2:       Draw a bootstrap sample $D_b$ of size N from the training data D. 3:       Grow a regression tree $T_b$ on $D_b$ by recursively repeating the following steps for each node, until the stopping criterion (e.g., max_depth) is met:            - Select m features at random from the full set of p features.            - Pick the best feature and split-point among the m features.            - Split the node into two child nodes. 4: end for 5: Output: The ensemble of trees ${\left\{T_b\right\}}_1^B$. 6: Prediction: For a new input $\mathbf{x}$, the prediction is the average of all individual tree predictions: $\widehat{y}={\displaystyle \frac{1}{B}}{\sum }_{b=1}^B{T}_b\left(\mathbf{x}\right)$.

In this experiment, a total of 100 decision trees were generated. Furthermore, to prevent over-fitting of each tree and control model complexity, the maximum depth of each tree was limited to max_depth = 10. Similar to the other baseline models, Multi Output Regressor was used to configure and train an independent Random Forest model for each of the seven output variables. This has the effect of allowing each output variable to be predicted by the ensemble of trees best suited to it.

3. Results

In this section, the performance of the proposed LSTM–Attention model and the three baseline models is quantitatively and qualitatively compared and analyzed. All experiments were conducted using the simulation-based dataset described in Section 2.2, focusing on a fair evaluation of the models’ intrinsic performance. First, the metrics and experimental environment used for model performance evaluation are clearly defined, followed by a quantitative numerical analysis and an in-depth analysis of the error distribution.

3.1. Evaluation Metrics and Experimental Environment

3.1.1. Performance Metrics

The objective of this study, predicting the 6-DOF pose of the camera from the actuator’s joint angles, can be viewed as a multi-task regression problem that simultaneously estimates two heterogeneous physical quantities. One is Position in 3D space, and the other is Orientation in 3D space. Position belongs to a continuous vector space with units of meters, whereas orientation belongs to a non-Euclidean space represented by $SO\left(3\right)$, the Special Orthogonal group, which is the set of 3D rotation matrices. Therefore, to fairly and meaningfully evaluate the prediction errors of these two components, it is essential to use separate evaluation metrics suited to their respective characteristics. In this study, the position and rotation errors were measured separately and then combined to evaluate the overall performance of the models.

The accuracy of the position prediction was measured using the Euclidean distance between the predicted 3D camera coordinates $\widehat{\mathbf{t}}={[{\widehat{t}}_x,{\widehat{t}}_y,{\widehat{t}}_z]}^T$ and the actual ground-truth coordinates $\mathbf{t}={[t_x,t_y,t_z]}^T$. This represents the physical straight-line distance between the two points and is the most intuitive metric for expressing prediction error. The position error $d_{pos}$ is calculated as follows:

$$d_{pos}=\left|\right|\mathbf{t}-\widehat{\mathbf{t}}{\left|\right|}_2=\sqrt{{(t_x-{\widehat{t}}_x)}^2+{(t_y-{\widehat{t}}_y)}^2+{(t_z-{\widehat{t}}_z)}^2}$$

(19)

A smaller value of this metric signifies that the model predicted the camera’s position more accurately. In this paper, all position errors are converted to and reported in millimeters.

Rotation error is evaluated by measuring the angular difference between the predicted orientation and the actual orientation. Since this study used quaternions, which are free from the Gimbal Lock problem, as the model’s output, the rotation error was also measured by calculating the geodesic distance, i.e., the shortest angular distance, between the two quaternions. Given the ground-truth quaternion q and the predicted quaternion $\widehat{q}$, the angular error ${\theta }_{err}$ (in degrees) between the two rotations is calculated as follows [18]:

$${\theta }_{err}={\displaystyle \frac{180}{\pi }}·2·\arccos \left(\right|\langle q,\widehat{q}\rangle \left|\right)={\displaystyle \frac{180}{\pi }}·2·\arccos \left(\right|q_w{\widehat{q}}_w+q_x{\widehat{q}}_x+q_y{\widehat{q}}_y+q_z{\widehat{q}}_z\left|\right)$$

(20)

Here, $\langle ·,·\rangle$ denotes the dot product of the two quaternion vectors. The absolute value is taken on the dot product because q and $-q$ represent the same 3D rotation, and this selects the angle of the shorter path between the two representations as the error. A smaller value of this metric signifies that the model predicted the camera’s orientation more accurately.

To evaluate the overall performance and prediction stability of the models on the entire test dataset, the position and rotation errors calculated for each sample were consolidated using the following three statistical metrics.

• Mean Absolute Error (MAE): The arithmetic mean of the absolute values of the errors, which intuitively represents the average magnitude of the model’s prediction error. It is relatively less sensitive to the influence of outliers.

  $$\mathrm{MAE}={\displaystyle \frac{1}{N}}\sum _{i=1}^N|y_i-{\widehat{y}}_i|$$

  (21)
• Root Mean Square Error (RMSE): The square root of the average of the squared errors. Due to the squaring process, it assigns greater weight to large errors and thus reacts sensitively to the variance and outliers of the predictions. It is useful for evaluating the variability of the model’s performance.

  $$\mathrm{RMSE}=\sqrt{{\displaystyle \frac{{\sum }_{i=1}^N{(y_i-{\widehat{y}}_i)}^2}{N}}}$$

  (22)
• Standard Deviation (Std): A metric indicating how spread out the prediction errors are from the mean (MAE). A smaller standard deviation implies that the model’s prediction errors are consistent and stable, serving as an important measure for judging the model’s reliability.

Here, N is the total number of samples in the test dataset, $y_i$ represents the individual error values such as $d_{pos}$ or ${\theta }_{err}$, and ${\widehat{y}}_i$ represents the mean of the errors.

3.1.2. Experimental Environment and Data Splitting

To ensure the reproducibility and fairness of all experiments, training and evaluation were conducted in a controlled environment. The total 3000-sample dataset generated via simulation was randomly split into a Training dataset and a Test dataset at an 8:2 ratio for model training, validation, and final performance evaluation. That is, 2400 samples were used to train the model parameters, and the remaining 600 samples were used exclusively for final performance evaluation, having not been used at all during the training process. For the deep learning model, 20% of the training dataset (16% of the total) was further split as a Validation dataset to monitor overfitting during training and to select the optimal model. The baseline models were implemented based on the Scikit-learn library, and the proposed LSTM–Attention model was implemented using the PyTorch framework. The key specifications of the hardware and software environment used for model training and evaluation are shown in

Table 2. Specifications of the experimental hardware and software environment.

Component	Specification
Hardware
CPU	Intel Core i9-11900 2.50GHz Processor
GPU	NVIDIA GeForce RTX 3080 10 GB
Memory	32 GB DDR4 RAM
Software
Operating System	Windows 11
CUDA Version	12.1
Key Libraries	Python 3.10.18, PyTorch 2.5.1, Scikit-learn 1.7.2, NumPy 2.0.1, Pandas 2.3.3

.

The main hyper-parameters for training the proposed model are as follows. The sequence length was set to 10. These sequences were constructed using a sliding window approach with a stride of 1, where each sequence comprises 10 consecutive time steps from the dataset. This is a deliberate choice reflecting the data acquisition process, which was done via continuous kinematic control, resulting in smooth trajectories. While a non-sequential ($L=1$) model is feasible, using a short sequence allows the LSTM to leverage this temporal structure to learn the continuous kinematic manifold and its local dynamics, providing a richer feature representation than a simple point-to-point mapping. For the optimizer, AdamW [23], which improves upon the weight decay method of the existing Adam, was used, with an initial learning rate set to $1\times {10}^{-4}$ and weight decay set to $1\times {10}^{-4}$. The learning rate was dynamically adjusted during the training process using a CosineAnnealingWarmRestarts scheduler [24], which periodically and gradually decreases the learning rate and then restores it to the initial value (restarts).

The total training was conducted for 500 epochs, but it was set for early stopping if the validation loss did not improve for 50 epochs. The batch size was set to 256, and the rotation loss weight ${\lambda }_{rot}$ was set to 20.0. This value is a critical, empirically-tuned hyperparameter. It is necessary to balance the different scales and units of the $L_{pos}$ (MSE) and $L_{rot}$ (Geodesic Loss), ensuring the network does not bias optimization toward one task at the expense of the other. This value was found to provide the most stable and balanced optimization during validation.

3.2. Performance Comparison

The results of a quantitative comparison of the performance of the proposed LSTM–Attention model and the three baseline models on the 600-sample test dataset are summarized in

Table 3. Quantitative performance comparison on the test dataset (600 samples). The table includes baseline models, an ablation study of the proposed architecture, and the final proposed model. The best performance is highlighted in bold.

Model	Position Error (mm)			Rotation Error (deg)
	MAE	RMSE	Std	MAE	RMSE	Std
Baseline Models
Polynomial Regression	24.30	27.60	13.00	5.536	6.352	3.115
Support Vector Reg. (SVR)	24.40	27.80	13.30	5.554	6.409	3.198
Random Forest	19.90	22.50	10.60	4.519	5.186	2.543
Ablation Study
Attention-Only	19.83	22.65	10.55	4.159	5.130	2.490
LSTM-Only	20.78	23.36	10.76	4.851	5.490	2.710
Proposed (LSTM–Attention)	18.00	20.40	9.60	3.723	4.428	2.398

. This table details the position error (mm) and rotation error (deg) for each model, divided into three metrics: MAE, RMSE, and Std. The experimental results clearly demonstrate that the proposed LSTM–Attention model achieved the lowest error across all metrics for both position and rotation prediction, significantly outperforming the other baseline models.

The experimental results summarized in Table 3 provide two key insights: the justification for the proposed model’s architecture via an ablation study, and its superior performance against traditional baselines. First, the ablation study quantitatively validates the contribution of each core component. The LSTM-Only model, which removes the attention block, demonstrates a clear performance drop compared to the full model. This result confirms that the attention mechanism is not a superficial addition but a meaningful component providing a critical feature refinement step. Similarly, the poor performance of the Attention-Only model underscores the importance of the LSTM’s sequential feature extraction. The full proposed LSTM–Attention model outperforms both ablated versions, confirming the synergistic contribution of combining both mechanisms.

Second, when compared to the baseline models, the now-validated proposed architecture demonstrates clear superiority. In the MAE metric, the proposed model (Position: 18.00 mm; Rotation: 3.723 deg) shows a performance improvement of approximately 9.5% and 17.6%, respectively, compared to the strongest baseline, Random Forest (Position: 19.90 mm; Rotation: 4.519 deg). The improvement is even more significant over Polynomial Regression and SVR. In particular, the proposed model also maintained the lowest standard deviation for rotation prediction (2.398 degrees), demonstrating its capability for generally consistent pose prediction without the problem of errors increasing sharply in specific angular ranges. These quantitative results strongly support that the LSTM–Attention architecture effectively learned the complex temporal and non-linear relationship between the Pan-Tilt actuator’s joint angles and the camera’s pose, more so than the other models.

The average error metrics presented in Table 3 summarize the overall performance of the models, but they have limitations in assessing whether a model exhibits systematically large errors under specific conditions or how stable the prediction errors are. Therefore, to evaluate the reliability of the models in-depth, the position and rotation error distributions of each model for the entire 3000 dataset samples were visualized and qualitatively analyzed. Figure 4 shows the errors generated by each model for all data points in the form of a scatter plot, allowing for an intuitive comparison of the overall error distribution, as well as the frequency and magnitude of outliers.

Looking at the positional error distribution in Figure 4a, it can be clearly confirmed that the errors of the proposed LSTM–Attention model (red dots) are densely distributed mostly within a very low range below 20 mm. In contrast, the Polynomial Regression and SVR models not only show a generally high error distribution but also exhibit an unstable prediction pattern with frequent occurrences of extreme outliers exceeding 90 mm. The Random Forest model shows improved performance over Polynomial Regression or SVR, but considerable errors exceeding 60 mm still appear sporadically. Compared to this, the upper bound of the proposed model’s prediction error is effectively suppressed, visually demonstrating that the model performs consistent and reliable predictions across the entire workspace.

This trend is even more starkly revealed in the rotational error distribution in Figure 4b. While the baseline models frequently generate very large rotational errors exceeding 15 degrees, or even 20 degrees, the proposed model’s errors are mostly concentrated within a narrow region below 5 degrees. Considering that even a small rotational error in an RSAR system can be a serious problem capable of distorting the projected image’s position by tens of centimeters or more, the low rotational error and stable distribution of the proposed model are very significant strengths from a practical perspective. This qualitative analysis strongly supports that the superiority of the proposed model lies not only in its low average error but also in its significant advantage over other models in terms of prediction stability and reliability.

To analyze the cause and characteristics of the errors in more detail, the prediction errors for each component of the 6-DOF pose (camPosX, Y, Z and camEulerX, Y, Z) were visualized in 3D across the entire operating range of the Pan-Tilt joint angles. Figure 5 shows these individual error distributions, where the x-axis and y-axis represent the actuator’s Pan and Tilt angles, respectively, and the z-axis represents the prediction error of each model. This component-wise analysis clearly reveals the vulnerabilities that each model exhibits on specific axes or in specific operating regions. This component-wise analysis clearly reveals the vulnerabilities that each model exhibits on specific axes or in specific operating regions. Notably, the Z-axis rotation error (camEulerZ_deg) shown in Figure 5f presents a unique case, which stems from the fundamental difference between the proposed model’s holistic quaternion loss and the baselines’ independent axis regression, as will be detailed in the Section 4.

4. Discussion

The experimental results presented in Section 3 clearly demonstrate that the proposed LSTM–Attention model is the most effective approach for solving the forward kinematics problem of RSAR systems. In both the quantitative figures in Table 3 and the qualitative distribution in Figure 4, the proposed model demonstrated significant accuracy and stability over the baseline models. This performance gap demonstrates that simpler, traditional methods (e.g., lightweight regression) have clear limitations and are insufficient for this task. Our baseline models, Polynomial Regression and SVR, represent this exact category. This performance difference is analyzed to stem from the fundamental differences in the models’ architectures and learning strategies. Polynomial Regression and SVR showed clear limitations in capturing the data’s complex non-linearity, and while Random Forest showed respectable performance, it did not demonstrate as much consistency (low Std) or outlier suppression capability as the proposed model. This is interpreted as the proposed model’s bidirectional LSTM layer effectively learning the time-series dependency of the pose according to the continuous changes in Pan-Tilt angles, and the attention mechanism increasing prediction accuracy by selecting features important for the prediction.

The most core insight of this study is found in the 6-DOF component-wise error analysis of Figure 5, particularly in Figure 5f, which deals with the Z-axis rotation (camEulerZ_deg) error. In the case of position error (a–c), while all models commonly show a tendency for the error to increase at the boundaries of the operating range, the error of the proposed model (purple crosses) generally remains close to 0 and is stably distributed within a very narrow bandwidth. In contrast, Polynomial Regression (blue circles) and SVR (green triangles) frequently generate spike-shaped errors where predictions deviate significantly in specific regions, clearly showing the instability of the predictions. In the rotation error (d–f) analysis, the proposed model demonstrates superior performance with a significantly lower error distribution compared to the baseline models for X-axis (d) and Y-axis (e) rotations. However, a contrary result appears in Figure 5f, which shows the Z-axis rotation error. The baseline models, including Random Forest (red squares), show errors close to almost 0, whereas the proposed model’s (purple crosses) error is relatively more widely distributed and shows the largest error. This phenomenon originates from the fundamental difference in the learning methods of the baseline models and the proposed model.

As described in Section 2.4, the baseline models were individually trained to predict each of the seven outputs, including the Z-axis rotation independently. Due to the characteristics of the Pan-Tilt simulation system in this study, the Z-axis rotation (camEulerZ) value is close to almost 0 across the entire dataset; therefore, the baseline models are easily optimized to predict this Z-axis value close to 0. In contrast, the proposed model, as defined in Section 2.3.4, uses a multi-task learning method that minimizes the overall geodesic distance (Equation (20)) between quaternions by integrating the 3-axis rotation. Therefore, the proposed model is trained in a direction that minimizes the error of the entire 3D rotation, including the X-axis and Y-axis, even if some individual error occurs in the Z-axis. This result, as shown in Figure 5f, occurred due to the specificity of the current simulation data where the Z-axis error is close to 0, and this should be interpreted as a result signifying that the proposed model achieved the most accurate and robust comprehensive pose estimation performance in 3D space, as already demonstrated in Table 3.

This study focused on verifying the ideal performance of the model based on simulation data. We acknowledge that this simulation-only approach is a significant limitation, as it does not capture the complexities of a physical system. Future research must, therefore, prioritize verifying the model’s robustness and applicability using data collected from actual RSAR hardware. This validation must address critical factors omitted in this study, such as measurement noise from physical sensors, calibration errors, and mechanical backlash inherent in the actuators. It is anticipated that such real-world noise will degrade prediction accuracy. Overcoming this sim-to-real gap will likely require adaptation strategies; for example, transfer learning could be employed by fine-tuning the simulation-trained model with a smaller, calibrated real-world dataset, or a residual model could be trained to predict the discrepancy between simulation and reality. Furthermore, incorporating online adaptation techniques to respond to real-time environmental dynamics, such as varying surface geometries, remains a crucial challenge. Exploring the generalization possibility by applying this modeling method to more complex multi-DOF robotic arms, beyond the current Pan-Tilt 2-axis system, will also be a meaningful follow-up study.

5. Conclusions

This study addressed the unique control challenge of RSAR systems, whose end-effector is a projection form, and its final position depends on both the actuator’s pose and the external environment’s geometry. This characteristic, combined with the loose kinematic specifications problem that makes analytical modeling difficult, raises the necessity for a data-driven approach to solve the system’s forward kinematics problem. To this end, a deep learning architecture based on LSTM–Attention was designed to accurately predict the 6-DOF pose of the camera from the joint angles of a 2-axis Pan-Tilt actuators. The proposed model features a bidirectional LSTM for time-series feature extraction, an Attention Mechanism for feature refinement, and a multi-task learning structure that optimizes position and rotation separately. In particular, for 3D rotation prediction, a Geodesic Loss between quaternions was applied to stably learn the pose without the Gimbal Lock problem.

To verify the proposed model’s pure intrinsic performance, a simulation environment based on Unity and URDF, which excluded actual measurement noise, was constructed to generate a benchmark dataset. As a result of comparing the proposed model’s performance with the three baseline models—Polynomial Regression, SVR, and Random Forest—it was demonstrated that the proposed model achieved the most superior performance across all quantitative evaluation metrics (MAE, RMSE, Std). The position error MAE was 18.00 mm, and the rotation error MAE was recorded at 3.723 degrees, showing performance improvements of approximately 9.5% and 17.6%, respectively, compared to the second-place model, Random Forest.

As a result of the qualitative error distribution analysis, the proposed model, unlike the baseline models, effectively suppressed the occurrence of extreme outliers and showed very stable prediction reliability. In particular, the characteristics of the Z-axis rotation error identified in the 6-DOF individual axis analysis are a key result proving that the proposed model, unlike the baselines that learn each axis independently, achieved a more accurate and holistic comprehensive pose estimation performance in 3D space. This suggests that the proposed LSTM–Attention model is an effective methodology for accurately modeling the complex non-linear kinematic relationship of the RSAR system.