The Structural Design and Pressure Characteristics Analysis of a Magnetic Fluid Sealing Device with Dual Magnetic Sources
Abstract
1. Introduction
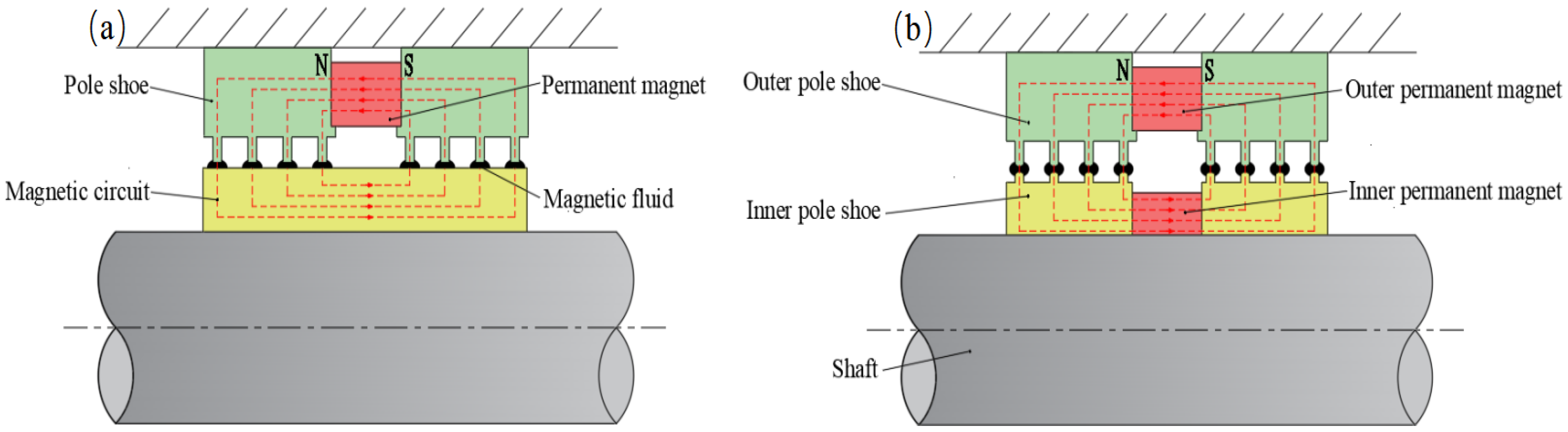
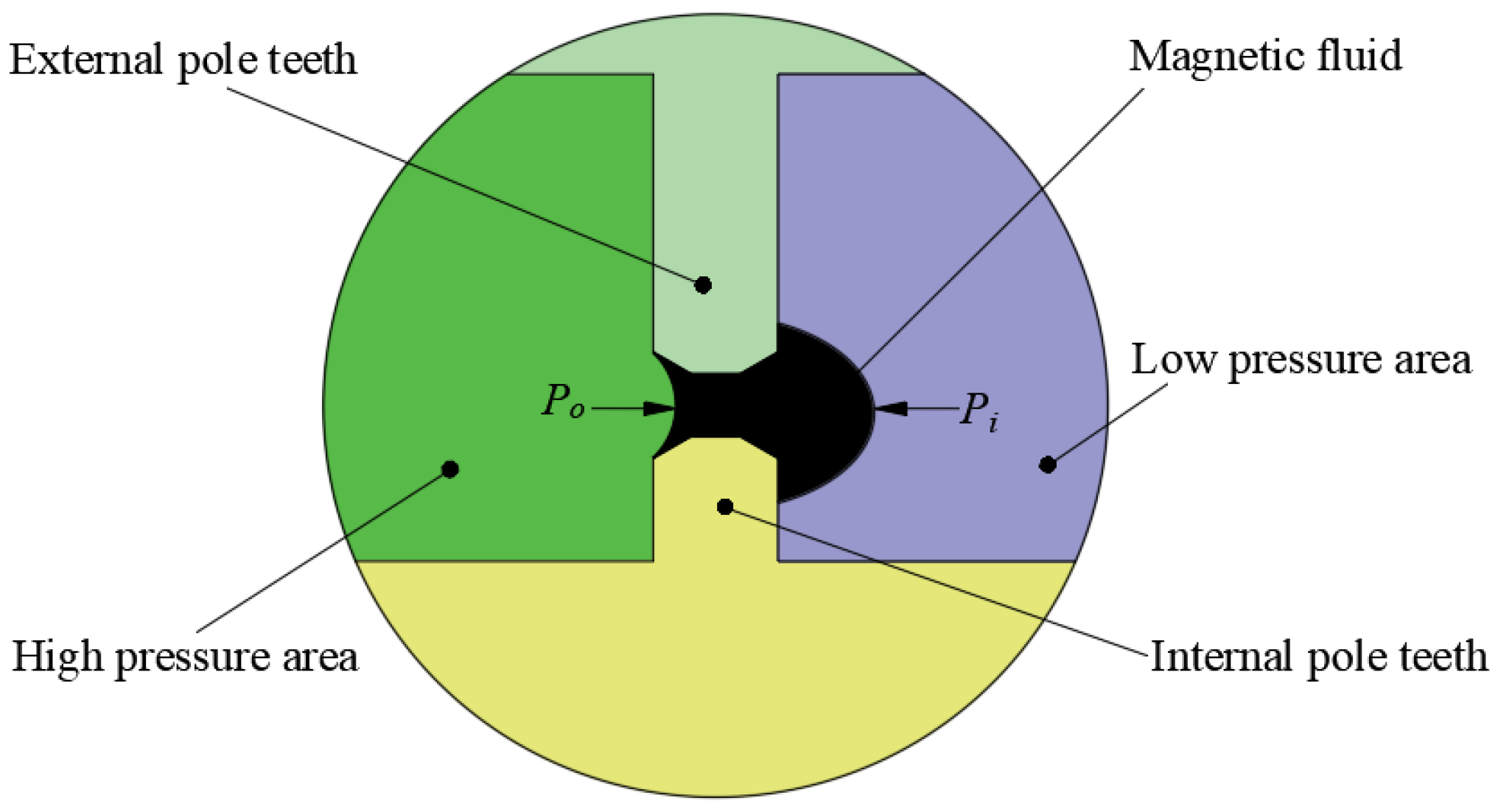
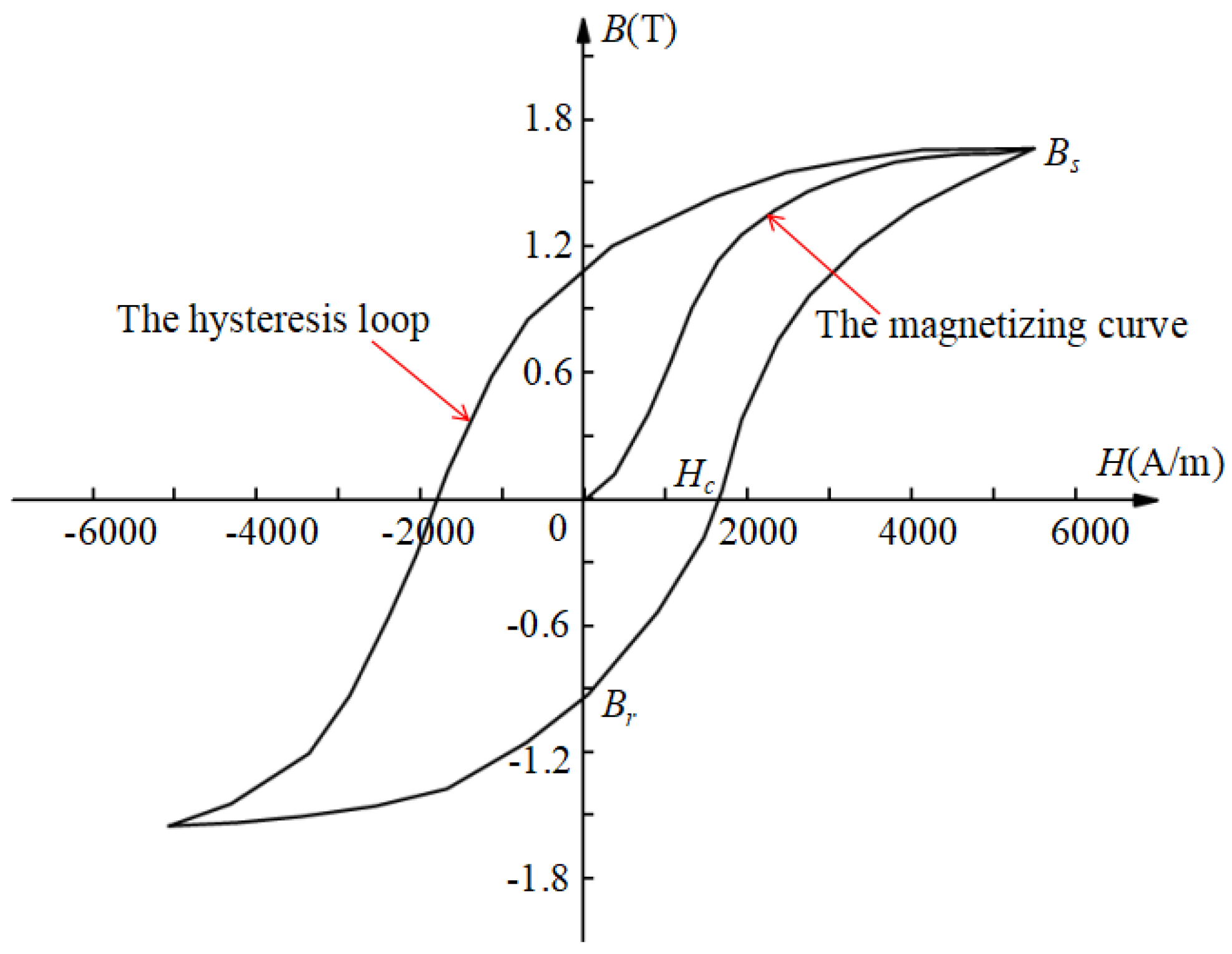
2. Theoretical Foundations
3. Simulation Analysis of Pressure Characteristics
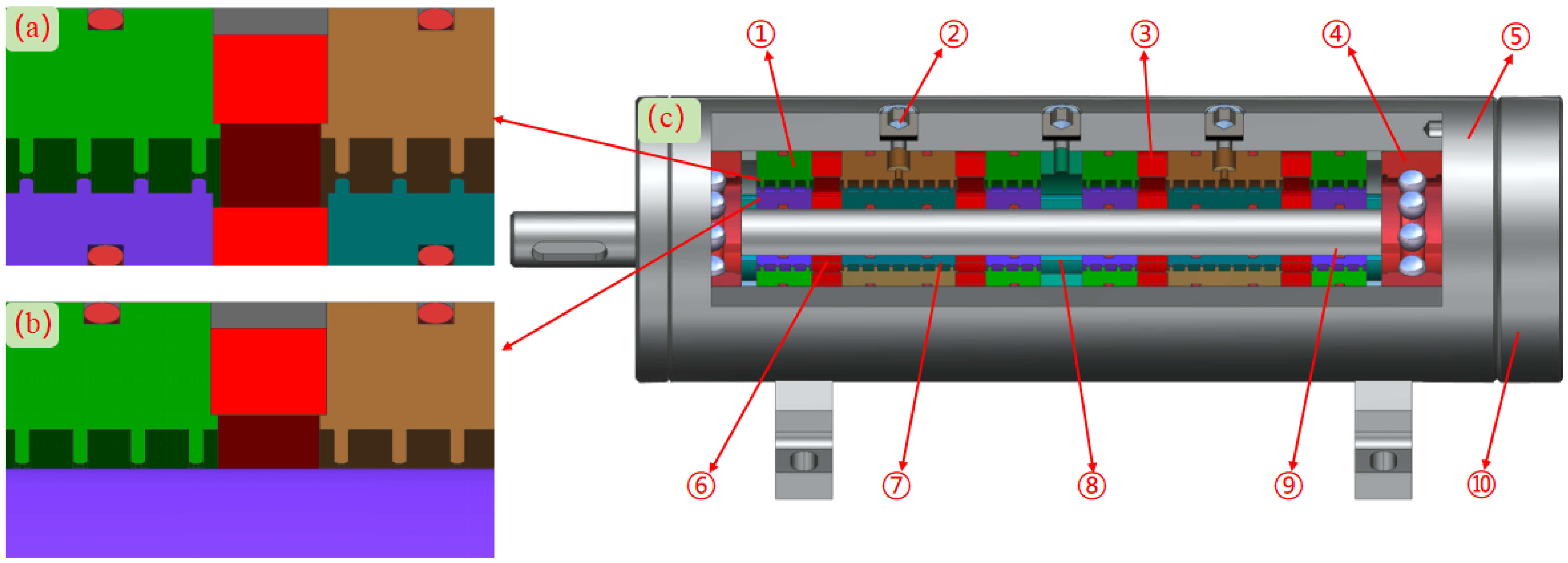
3.1. Introduction to Model
3.2. Material Selection and Boundary Condition Setting
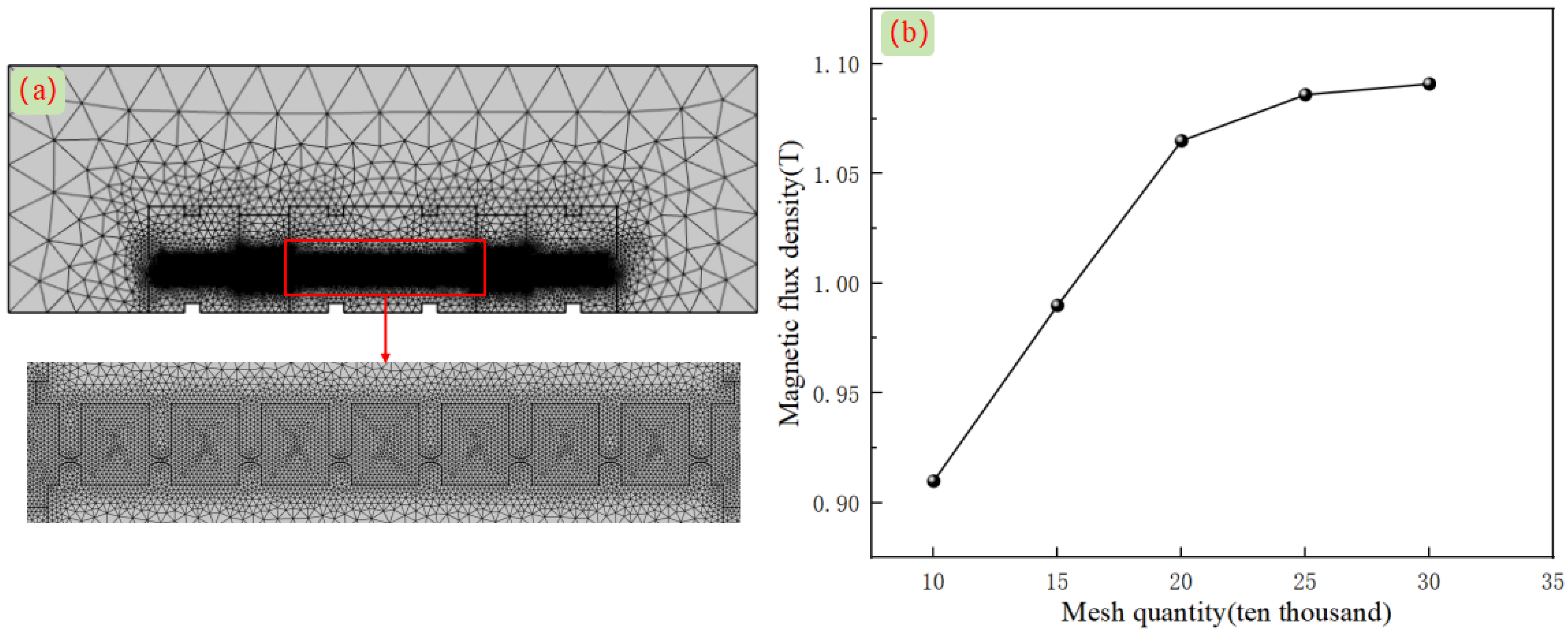
3.3. Mesh Spacing and Irrelevance Verification
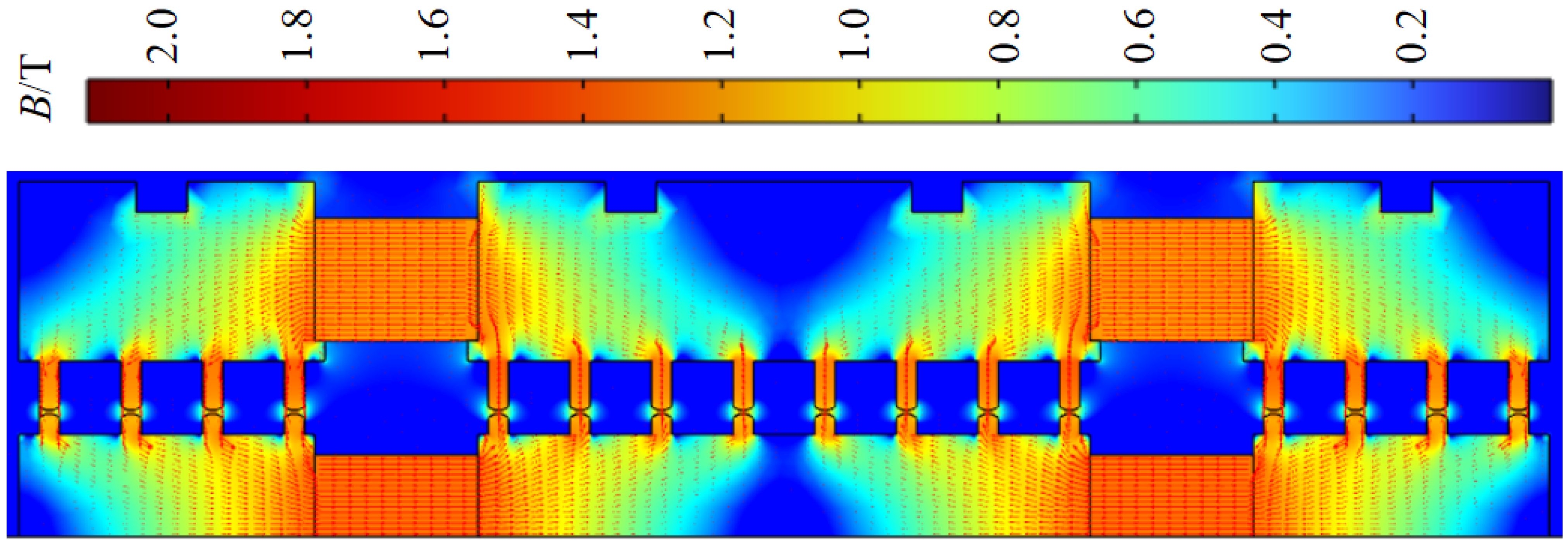
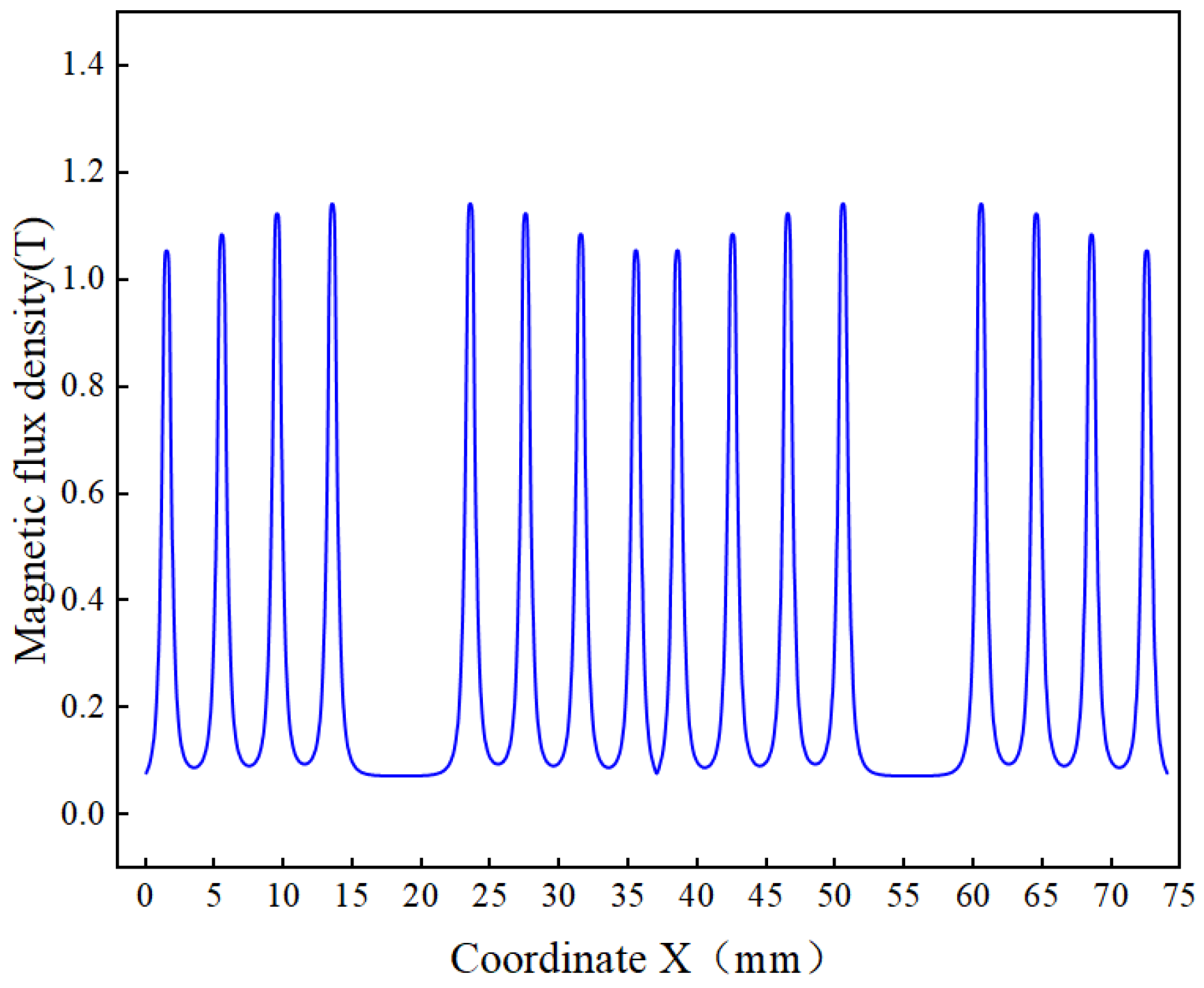
3.4. Numerical Simulation
3.5. The Effect of Each Parameter on the Sealing Pressure
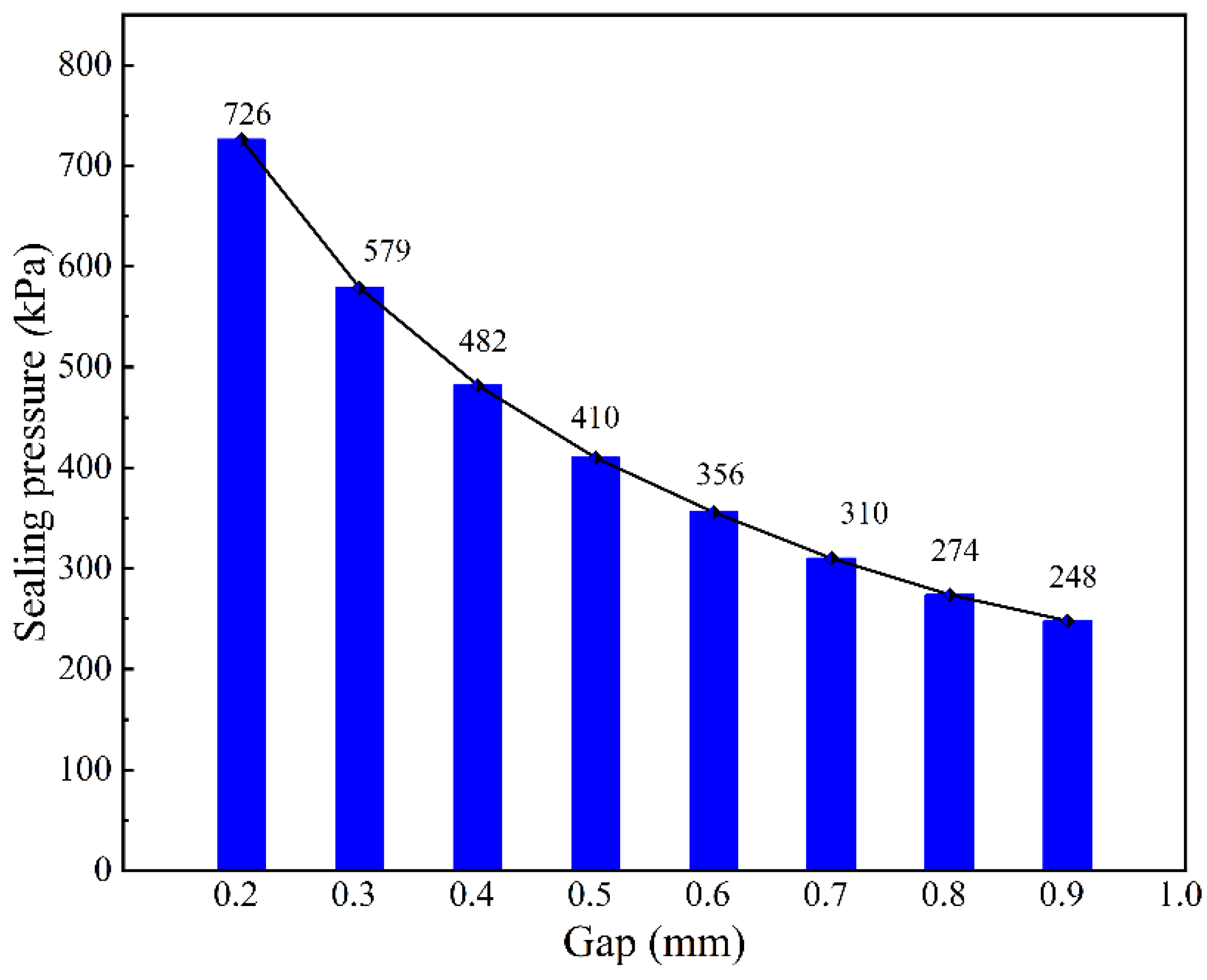
3.5.1. The Effect of Gap on Sealing Pressure
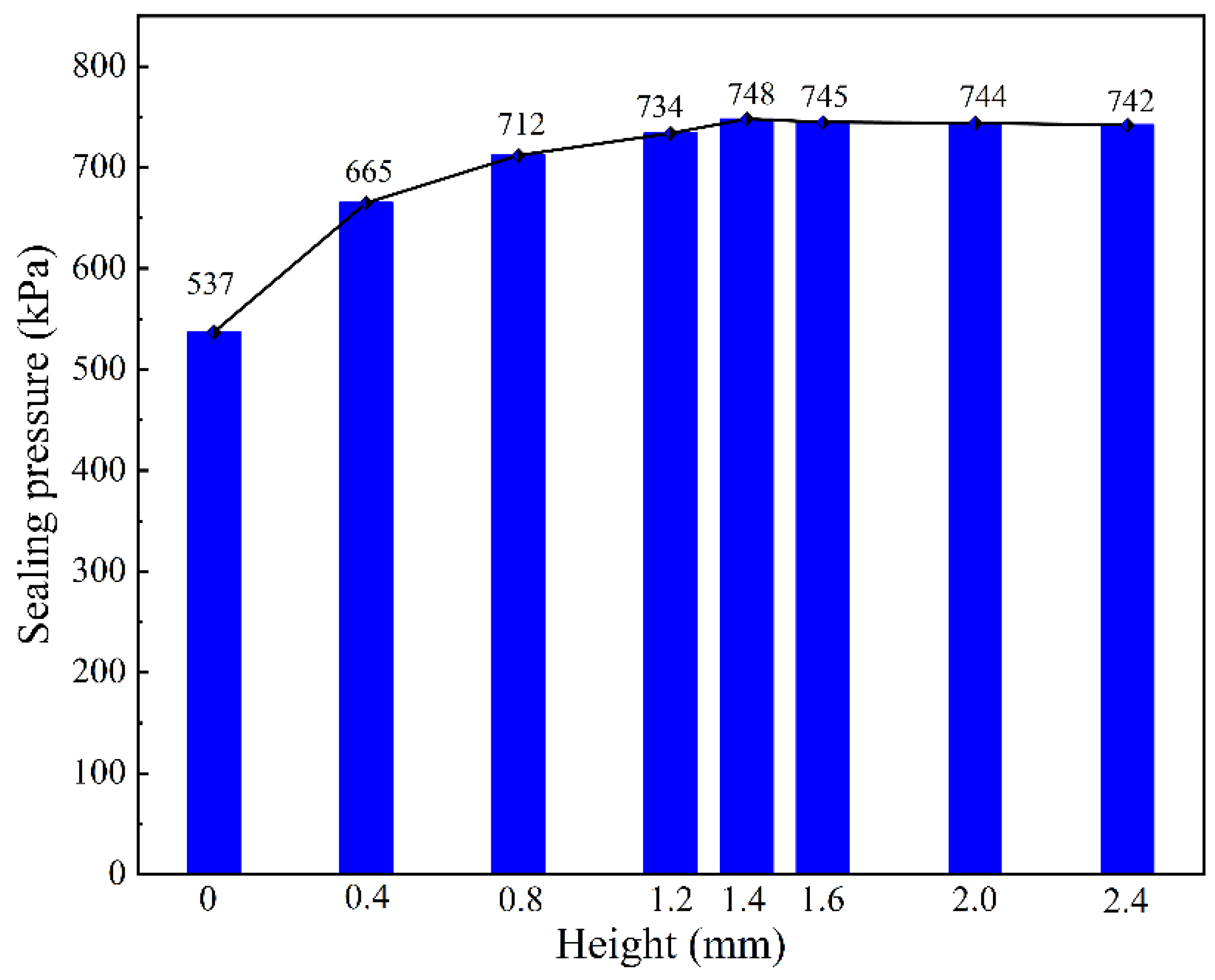
3.5.2. The Effect of Tooth Height on Sealing Pressure
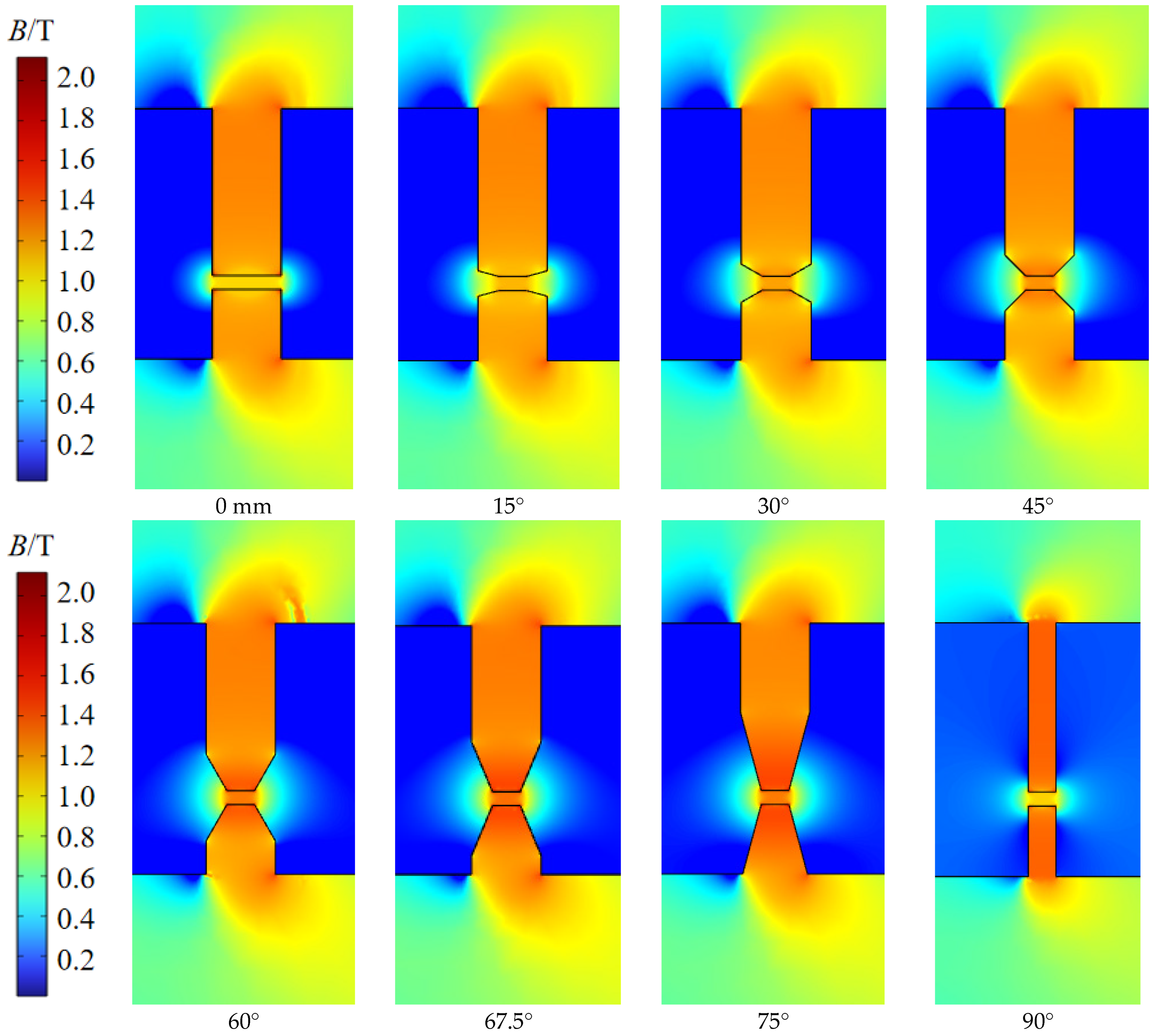
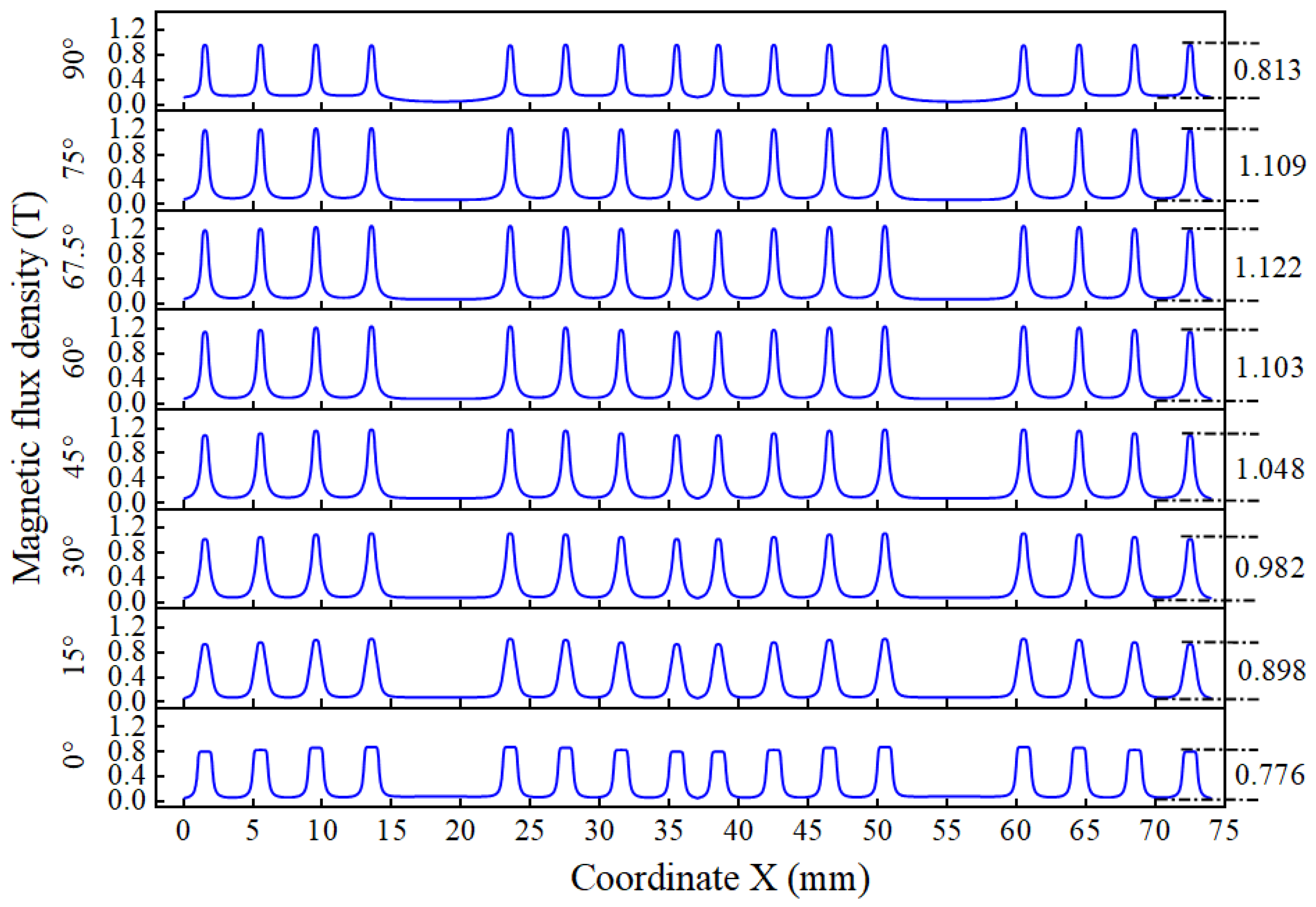
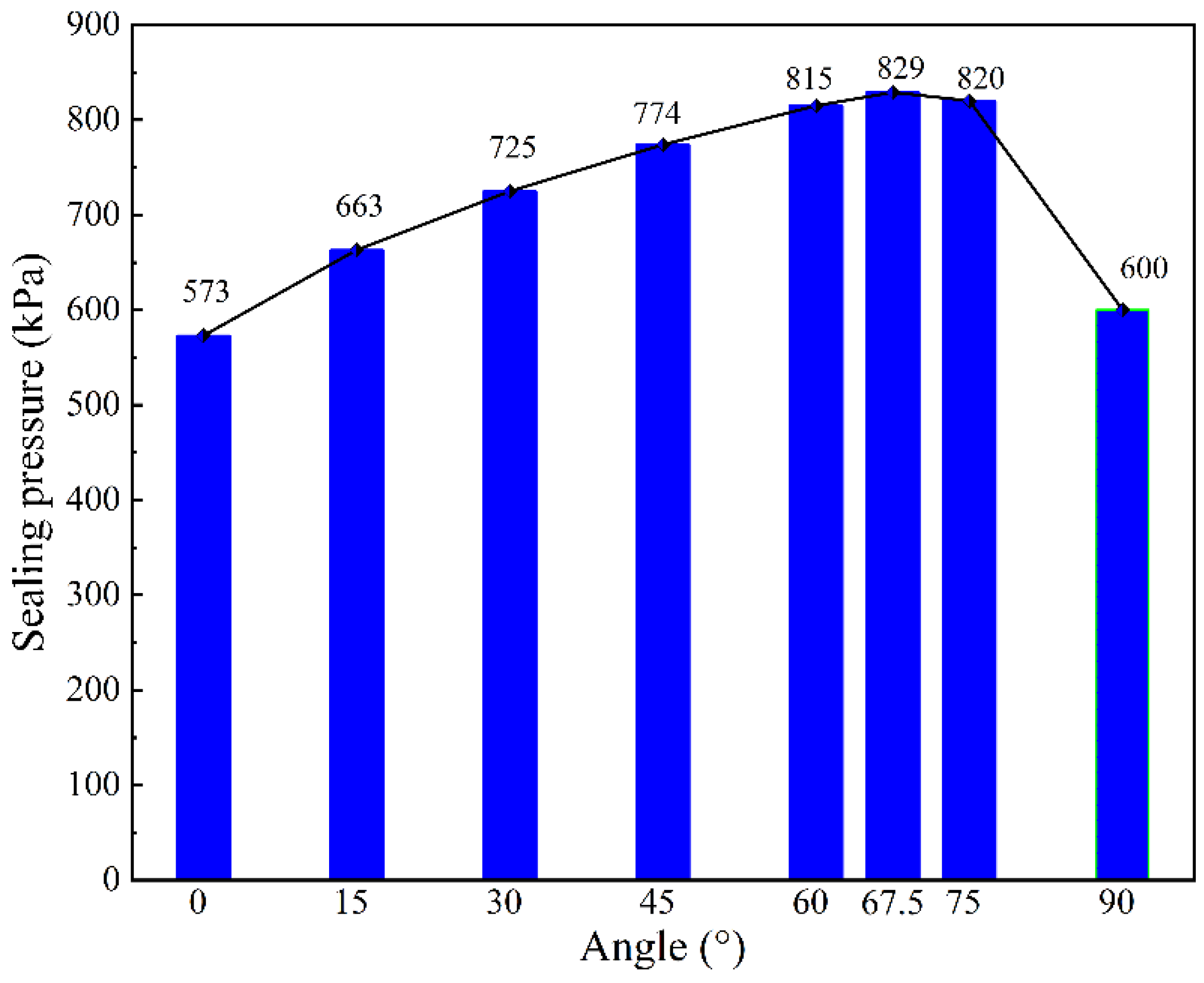
3.5.3. The Effect of Angle on Sealing Pressure
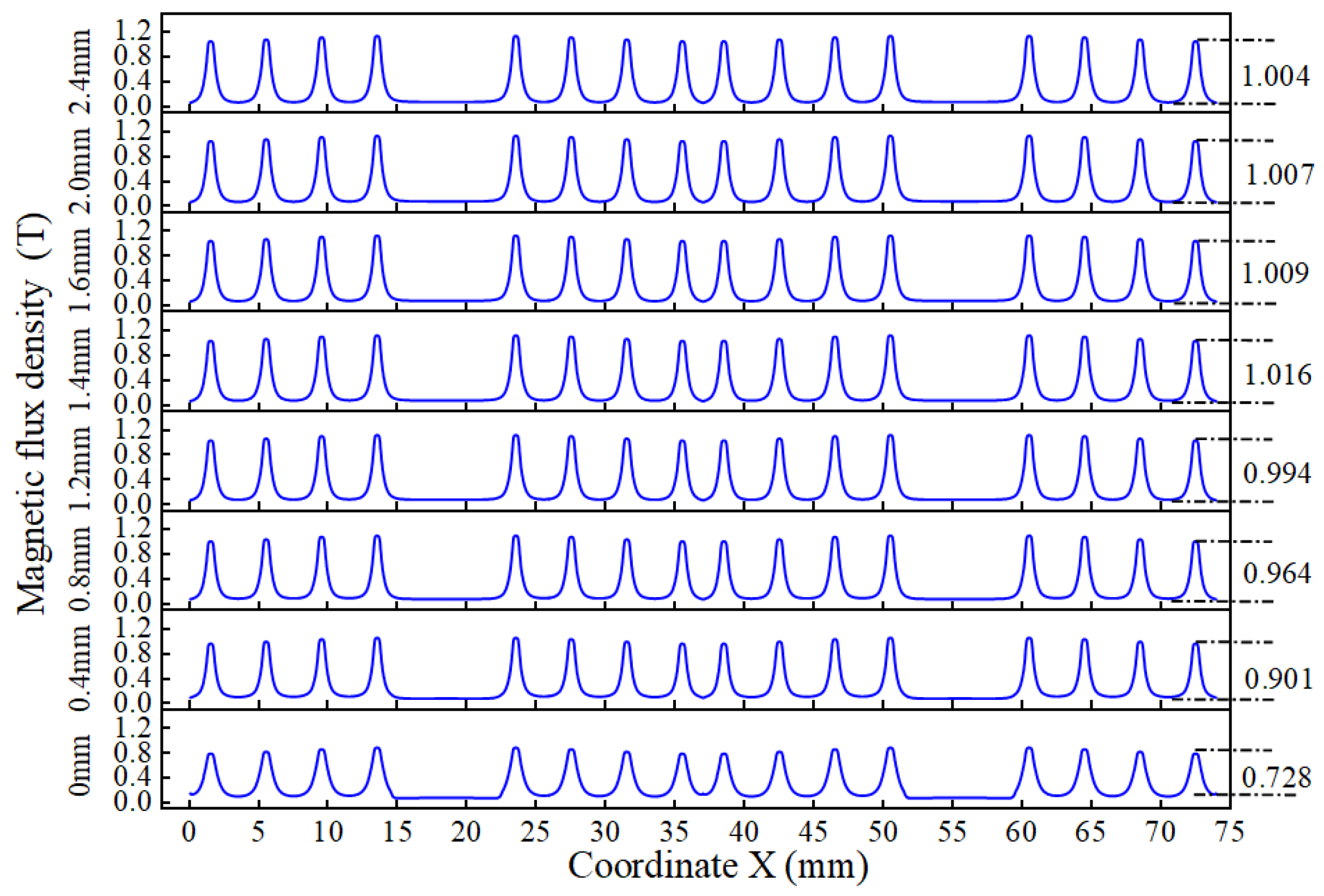
3.5.4. The Effect of Eccentricity Distance on Sealing Pressure
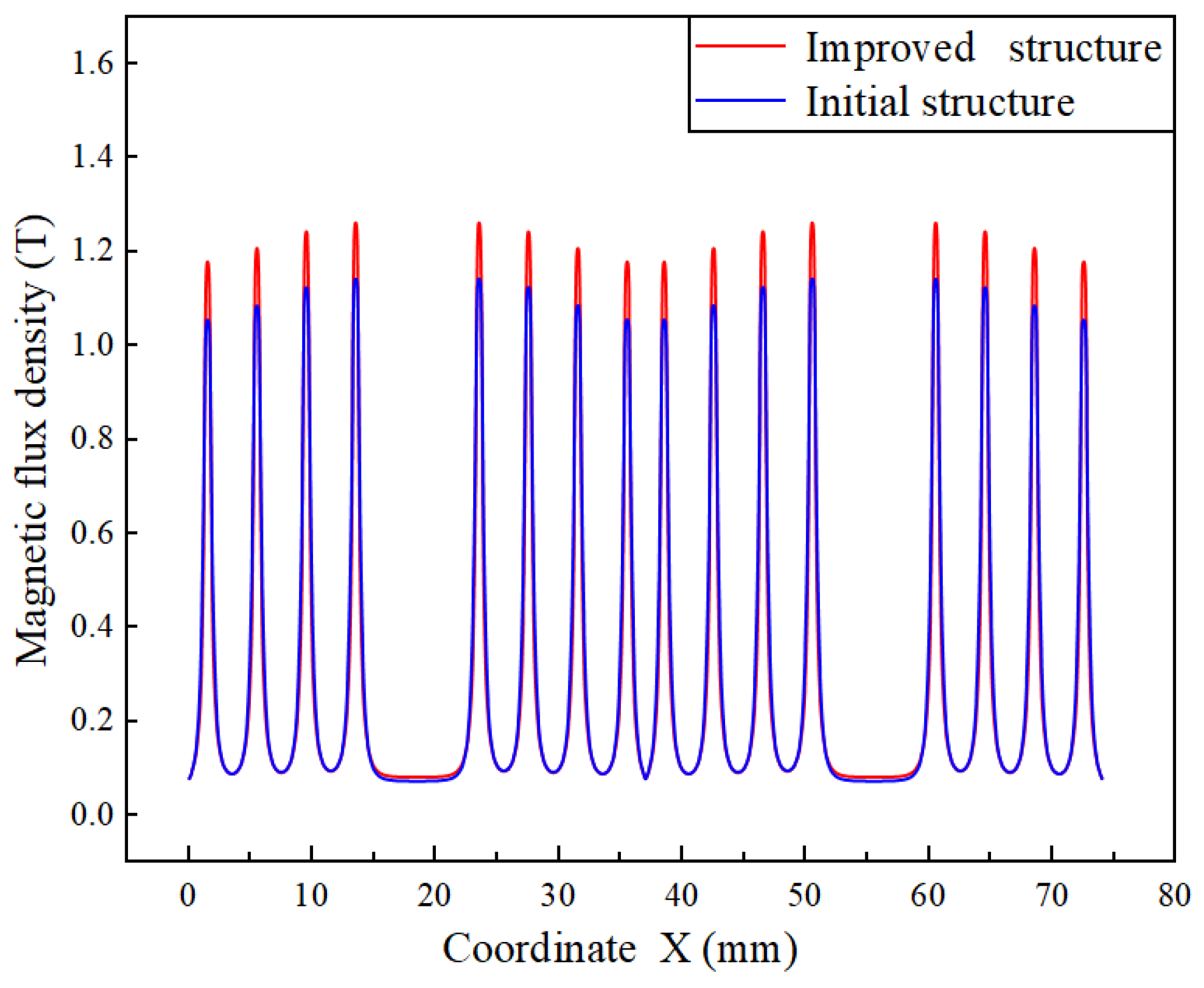
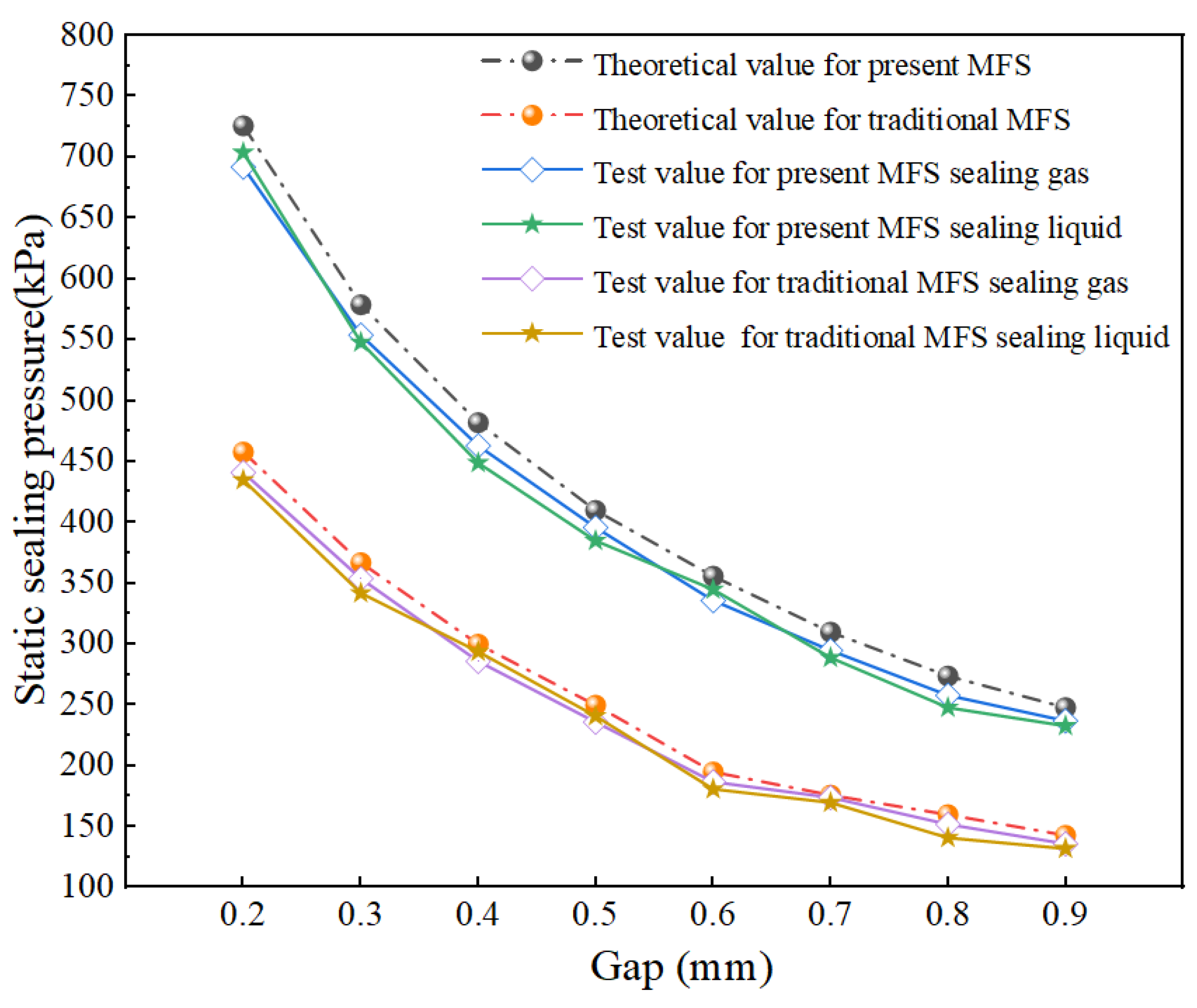
3.6. Comparison of Results Before and After Improved Structure
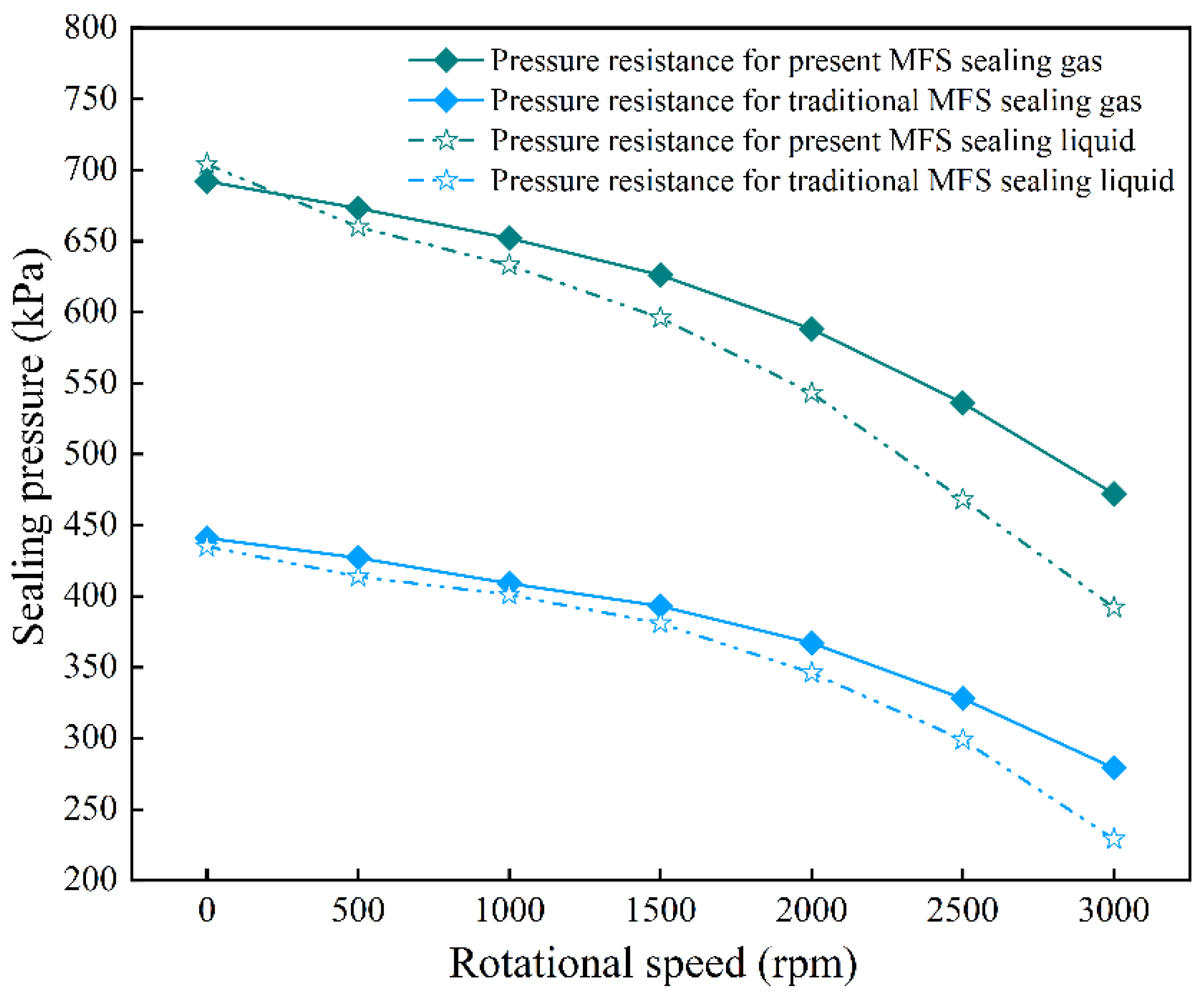
4. Test Validation
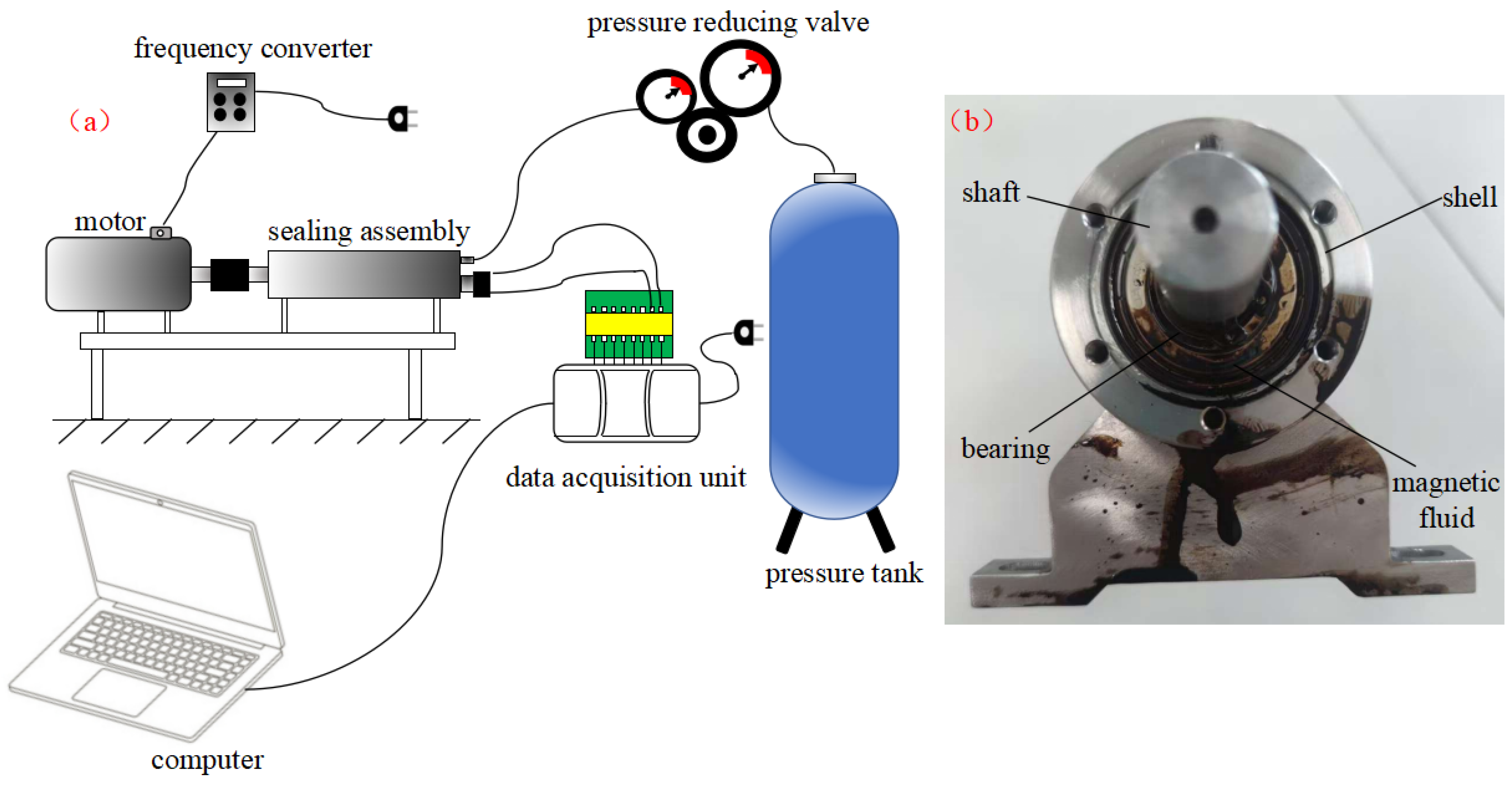
4.1. Test Equipment
4.2. Test Method
4.3. Analysis of Test Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Khan, N.; Katiyar, A.; Nandi, T.; Abhyankar, A.; Eswara Prasad, N. Tunable thermal conductivity and rheology of in-house synthesized Fe55Co25Ni20 complex fluids under the external magnetic field. J. Mol. Liq. 2019, 294, 111662. [Google Scholar] [CrossRef]
- Li, W.; Li, Z.; Han, W.; Wang, Y.; Zhao, J.; Zhou, J. Morphologic transformation of ferrofluid during micropump driving under field control. Ann. N. Y. Acad. Sci. 2025, 1543, 194–203. [Google Scholar] [CrossRef]
- Yamasaki, H.; Kishimoto, T.; Tazawa, T.; Yamaguchi, H. Dynamic behavior of gas bubble detached from single orifice in magnetic fluid. J. Magn. Magn. Mater. 2020, 501, 166446. [Google Scholar] [CrossRef]
- Li, W.; Li, Z.; Han, W.; Li, R.; Zhang, Y. Mechanism of bubble generation in ferrofluid micro-pumps and key parameters influencing performance. Powder Technol. 2025, 467, 121562. [Google Scholar] [CrossRef]
- Mitamura, Y.; Sekine, K.; Okamoto, E. Magnetic fluid seals working in liquid environments: Factors limiting their life and solution methods. J. Magn. Magn. Mater. 2020, 500, 166293. [Google Scholar] [CrossRef]
- Radionov, A.; Podoltsev, A.; Peczkis, G. The specific features of high-velocity magnetic fluid sealing complexes. Mech. Adv. Technol. 2018, 2, 57–63. [Google Scholar]
- Trbušić, M.; Goričan, V.; Beković, M.; Jesenik, M.; Trlep, M.; Hamler, A. An experimental study on magnetic field distribution above a magnetic liquid free surface. J. Magn. Magn. Mater. 2020, 509, 166903. [Google Scholar] [CrossRef]
- Guo, Y.; Li, D.; Zang, G.; Qi, Z.; Zhang, Z. Research on a large diameter magnetic fluid seal with thin-wall parts. Front. Mater. 2022, 9, 932662. [Google Scholar] [CrossRef]
- Li, X.; Fan, X.; Li, Z.; Zhu, M. Failure mechanism of magnetic fluid seal for sealing liquids. Tribol. Int. 2023, 187, 108700. [Google Scholar] [CrossRef]
- Szczęch, M. Magnetic fluid seal critical pressure calculation based on numerical simulations. Simulation 2020, 96, 403–413. [Google Scholar] [CrossRef]
- Urreta, H.; Aguirre, G.; Kuzhir, P.; Lopez de Lacalle, L. Seals based on magnetic fluids for high precision spindles of machine tools. Int. J. Precis. Eng. Manuf. 2018, 19, 495–503. [Google Scholar] [CrossRef]
- Yang, X.; Shi, M.; Guan, Y.; Li, D. Numerical and experimental study of convergent integral embedded magnetic fluid seal. J. Magn. Magn. Mater. 2023, 570, 170522. [Google Scholar] [CrossRef]
- Li, W.; Li, Z.; Han, W.; Tan, S.; Yan, S.; Wang, D.; Yang, S. Time-mean equation and multi-field coupling numerical method for low-Reynolds-number turbulent flow in ferrofluid. Phys. Fluids 2023, 35, 125145. [Google Scholar] [CrossRef]
- Zhou, W.; Su, H.; Liu, H.; Zhang, Y.; Qiu, N.; Gao, B. Leakage and rotordynamic performance of a semi-Y labyrinth seal structure for centrifugal pump based on multi-frequency whirl method. J. Eng. Gas Turbines Power 2025, 147, 101022. [Google Scholar] [CrossRef]
- Li, D.; Li, Y.; Li, Z.; Wang, Y. Theory analyses and applications of magnetic fluids in sealing. Friction 2021, 11, 1771–1793. [Google Scholar] [CrossRef]
- Rosensweig, R.E. Buoyancy and stable levitation of a magnetic body immersed in a magnetizable fluid. Nature 1966, 210, 613–614. [Google Scholar] [CrossRef]
- Chen, Y.; Li, D.; Zhang, Y.; Li, Z.; Zhou, H. The influence of the temperature rise on the sealing performance of the rotating magnetic fluid seal. IEEE Trans. Magn. 2020, 56, 4600510. [Google Scholar] [CrossRef]
- Parmar, S.; Ramani, V.; Upadhyay, R.V.; Parekh, K. Two stage magnetic fluid vacuum seal for variable radial clearance. Vacuum 2020, 172, 109087. [Google Scholar] [CrossRef]
- Li, W.; Li, Z.; Wang, Z.; Wu, F.; Xu, L.; Peng, S. Turbulence intensity characteristics of a magnetoliquid seal interface in a liquid environment. Coatings 2021, 11, 1333. [Google Scholar] [CrossRef]
- Zhang, T.; Li, D.; Li, Y. Design and Optimization of Combined Magnetic Fluid Seal and Labyrinth Seal. J. Mech. Eng. 2022, 58, 172–181. [Google Scholar]
- Wang, H.; He, X.; Gao, Z.; Xu, X. Performance of Combined Magnetic Fluid Seal and Spiral Seal for Sealing Water. Chin. J. Vac. Sci. Technol. 2022, 42, 809–814. [Google Scholar]
- Chen, J.; Guan, Y.; Xu, W.; Zhang, T. Structural design and parameter analysis of a modular magnetic fluid rotary seal for robot joints. Vacuum 2023, 212, 112037. [Google Scholar] [CrossRef]
- Jiang, Y.; Chen, Y.; Lv, L.; Lu, J.; Li, D..; Zhou, H. Multi-parameter optimization of ferrofluid seal pole teeth based on magnetic-flow coupling and taboo genetic algorithm. J. Magn. Magn. Mater. 2023, 587, 171364. [Google Scholar] [CrossRef]
- Yang, X.; Xia, Y.; Huang, G. Numerical analysis and orthogonal optimization design of magnetic fluid reciprocating seals. J. Magn. Magn. Mater. 2024, 592, 171782. [Google Scholar] [CrossRef]
- Liu, L.; Li, D.; Li, L.; Wei, Y.; Li, Q.; Qi, Z. Design and study of sealing performance for ultra-clean and highly reliable magnetic fluid seals. Tribol. Int. 2025, 213, 111091. [Google Scholar] [CrossRef]
- Li, D. Theory and Application of Magnetic Liquid Sealing; Science Press: Beijing, China, 2010. [Google Scholar]
- Rosensweig, R. Magnetic fluids. Annu. Rev. Fluid Mech. 1987, 19, 437–461. [Google Scholar] [CrossRef]
- Chi, C. Fundamentals of Physics and Applications of Ferrofluid; Beihang University Press: Beijing, China, 2011. [Google Scholar]
- Yang, X.; Liu, G.; Li, Y.; Gao, S. Structural optimization of reciprocating seal with magnetic fluid based on orthogonal test design. J. Magn. 2021, 26, 229–237. [Google Scholar] [CrossRef]
- Li, Z.; Yuan, Z.; Li, X.; Wang, M.; Zhu, G. Research on dynamic coupling characteristics of magnetic fluid and gas medium interface in sealing devices. Phys. Fluids 2023, 35, 062004. [Google Scholar] [CrossRef]
- Li, Z.; Zhu, G.; Li, X.; Li, W.; Wang, Z.; Yuan, Z. Experimental visualization of the lifetime and self-healing of magnetic fluid seals. Vacuum 2023, 216, 112399. [Google Scholar] [CrossRef]
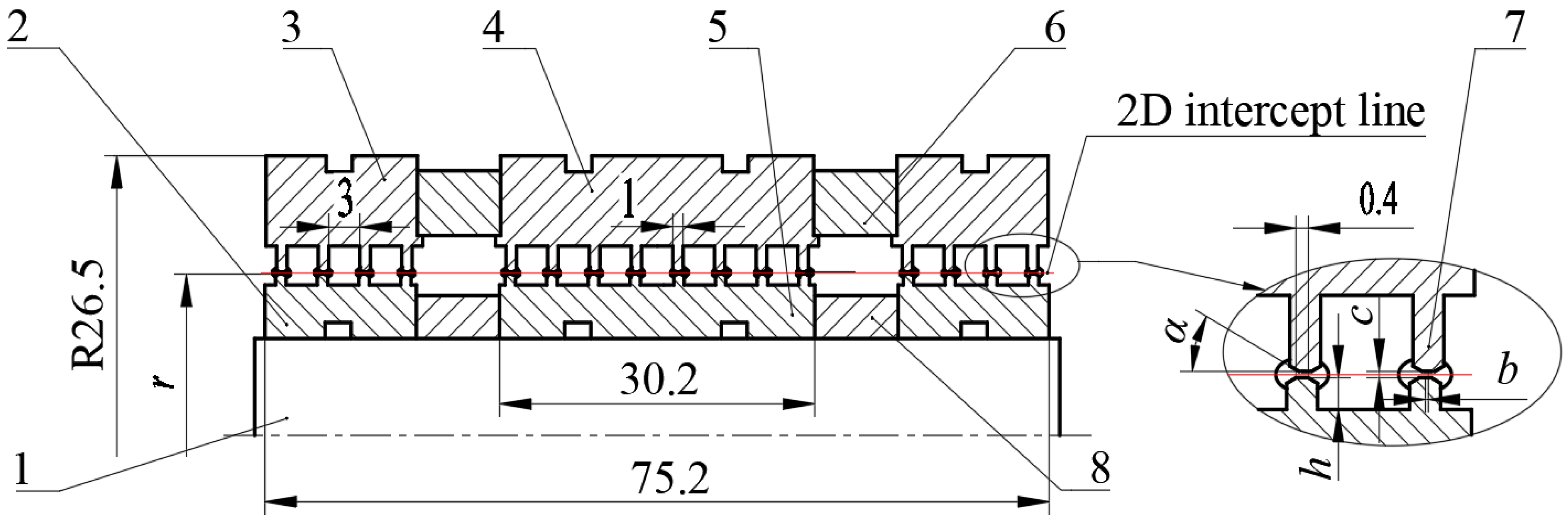
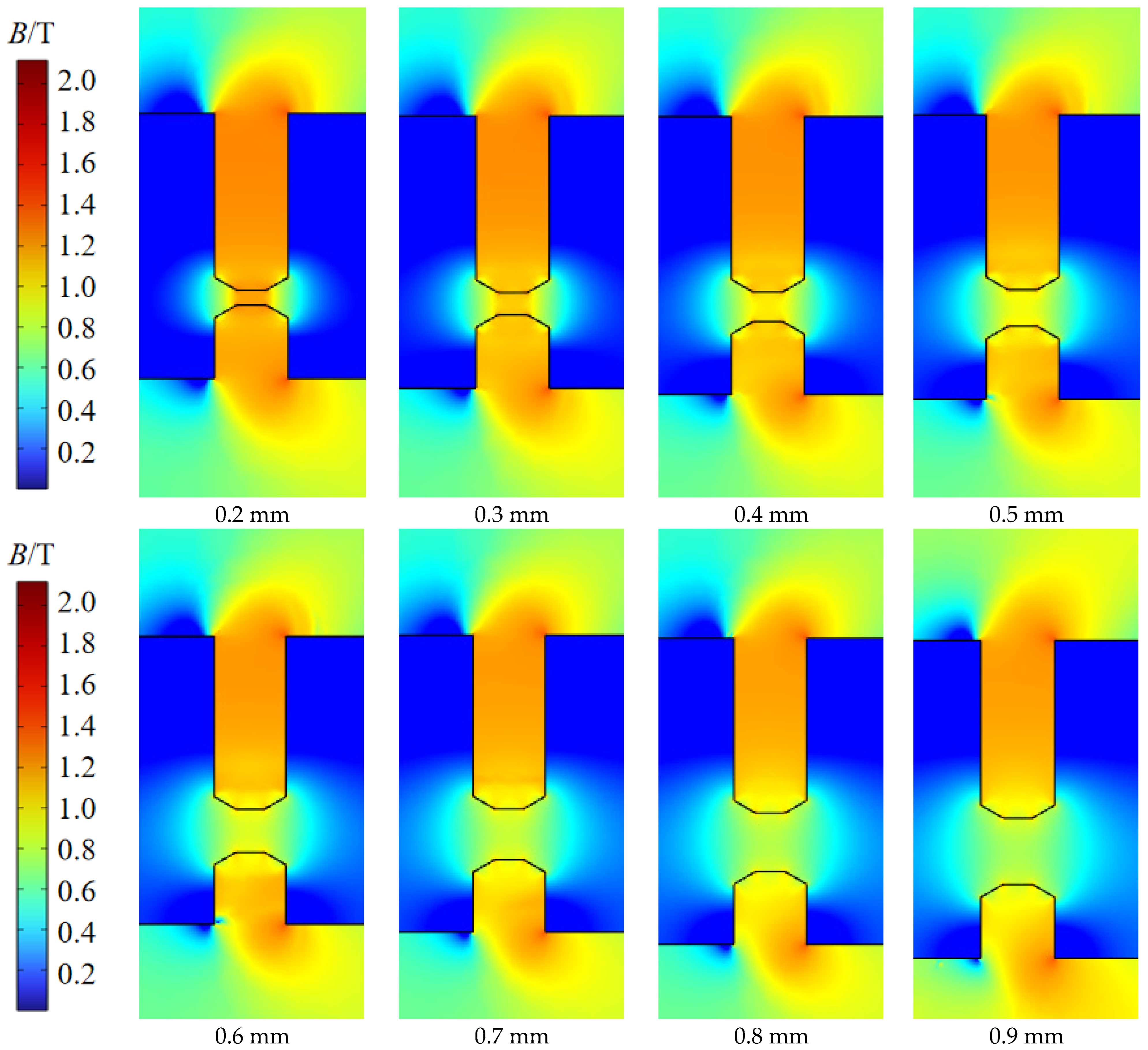

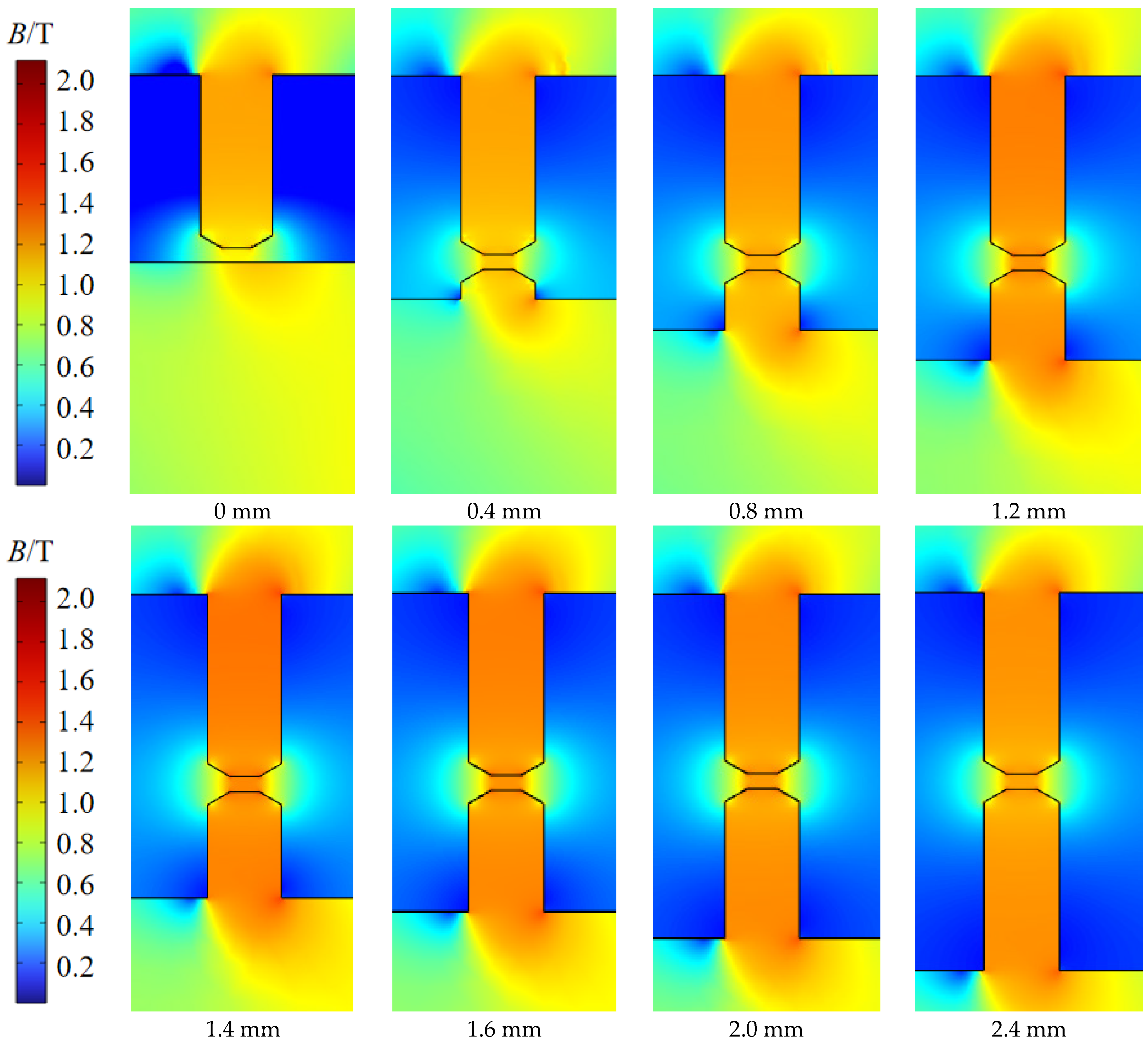
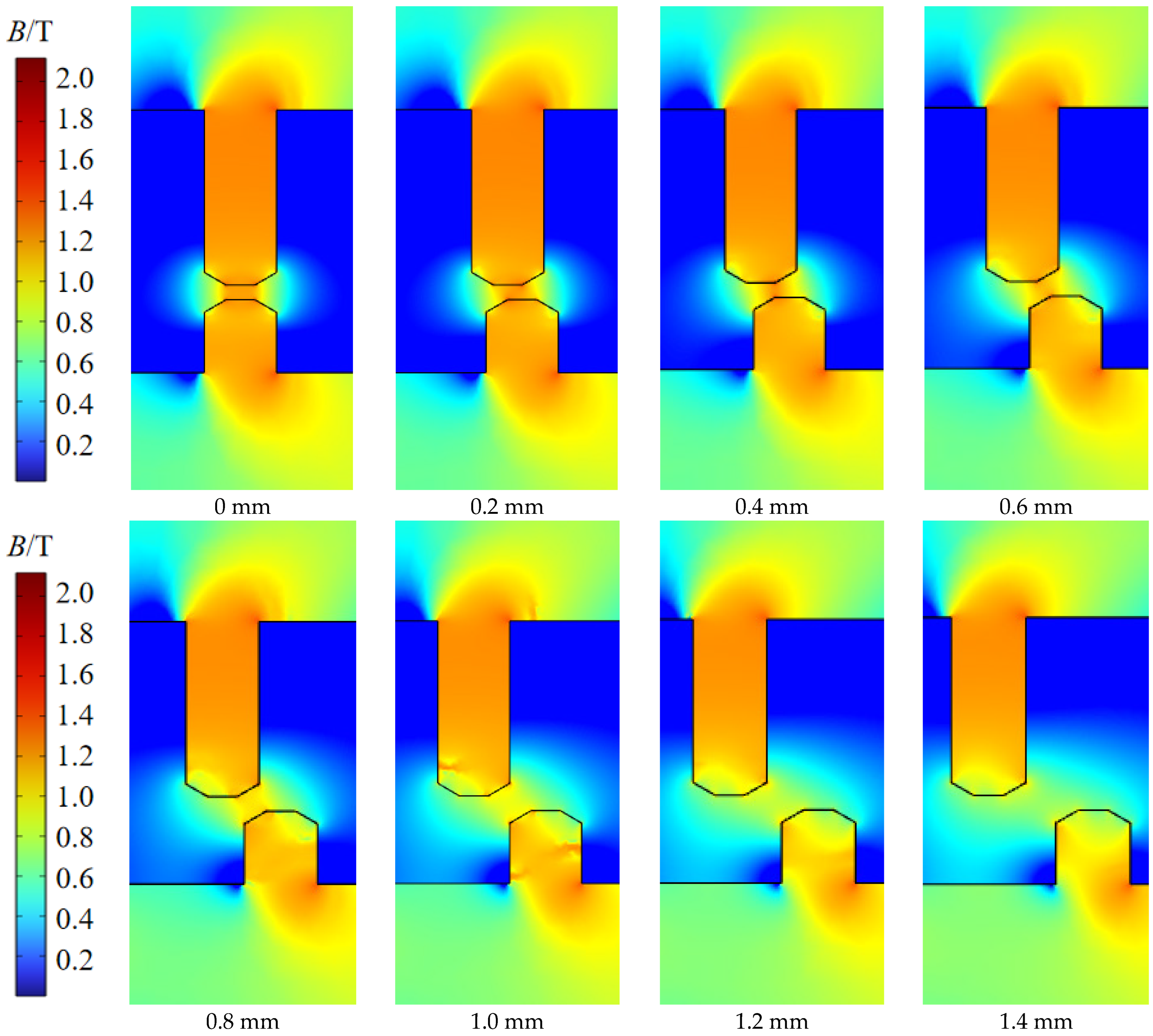

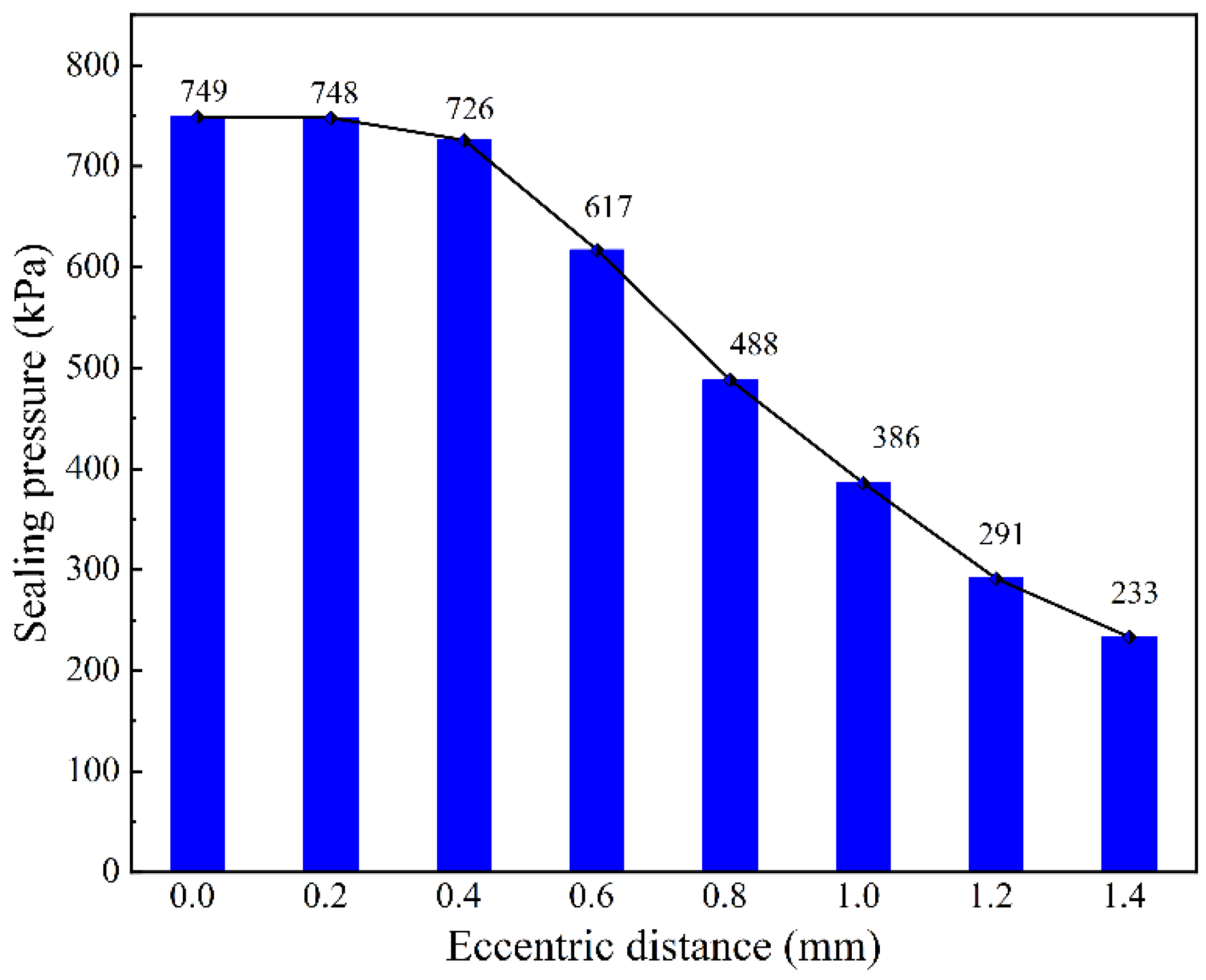

| Sealing Gap c | Inner Pole Tooth Height h | Angle α | Eccentricity Distance b | Radius of Shaft r |
|---|---|---|---|---|
| 0.2 mm | 1 mm | 30° | 0 mm | 15 mm |
| Number | Instrument | Manufacturer | Model | Range | Precision |
|---|---|---|---|---|---|
| 1 | Motor | JINYING | YVF2-71M | 300–3000 rpm | N/A |
| 2 | Pressure-reducing valve | Lightinglok | R21 | 0~2500 kPa | Level 1.6 |
| 3 | Pressure sensor | YBPCM | PCM300 | 0~1600 kPa | Level 0.25 |
| 4 | Data acquisition unit | NI | USB-6211 | / | / |
| 5 | Frequency converter | SHZK | ZK880 | 0~0.75 kW | Level 0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qing, J.; Li, Z.; Cheng, C.; Shen, C.; Cai, L. The Structural Design and Pressure Characteristics Analysis of a Magnetic Fluid Sealing Device with Dual Magnetic Sources. Actuators 2025, 14, 561. https://doi.org/10.3390/act14110561
Qing J, Li Z, Cheng C, Shen C, Cai L. The Structural Design and Pressure Characteristics Analysis of a Magnetic Fluid Sealing Device with Dual Magnetic Sources. Actuators. 2025; 14(11):561. https://doi.org/10.3390/act14110561
Chicago/Turabian StyleQing, Jie, Zhenggui Li, Chuanshi Cheng, Changrong Shen, and Lin Cai. 2025. "The Structural Design and Pressure Characteristics Analysis of a Magnetic Fluid Sealing Device with Dual Magnetic Sources" Actuators 14, no. 11: 561. https://doi.org/10.3390/act14110561
APA StyleQing, J., Li, Z., Cheng, C., Shen, C., & Cai, L. (2025). The Structural Design and Pressure Characteristics Analysis of a Magnetic Fluid Sealing Device with Dual Magnetic Sources. Actuators, 14(11), 561. https://doi.org/10.3390/act14110561





